Next Article in Journal
A New Model for Transfer Learning-Based Mapping of Burn Severity
Next Article in Special Issue
Land Cover Classification using Google Earth Engine and Random Forest Classifier—The Role of Image Composition
Previous Article in Journal
Improved Detection of Inundation below the Forest Canopy using Normalized LiDAR Intensity Data
Previous Article in Special Issue
Temporal Patterns in Illumination Conditions and Its Effect on Vegetation Indices Using Landsat on Google Earth Engine
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 12
Issue 4
10.3390/rs12040709
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

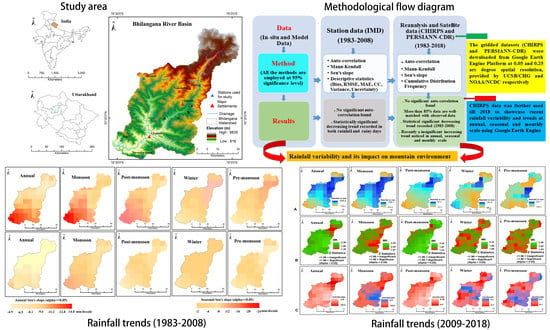
An Analysis of Long-Term Rainfall Trends and Variability in the Uttarakhand Himalaya Using Google Earth Engine

by
Abhishek Banerjee
1,
Ruishan Chen
1,*,
Michael E. Meadows
1,2,
R.B. Singh
3,
Suraj Mal
4 and
Dhritiraj Sengupta
1
1
Key Laboratory of Geographic Information Science, Ministry of Education, and School of Geographical Science, Institute of Eco-Chongming, East China Normal University, 500 Dongchuan Road, Shanghai 200241, China
2
Department of Environmental and Geographical Science, University of Cape Town, Cape Town 7701, South Africa
3
Department of Geography, Delhi School of Economics, University of Delhi, New Delhi 110007, India
4
Department of Geography, Shaheed Bhagat Singh College, University of Delhi, New Delhi 110017, India
*
Author to whom correspondence should be addressed.
Remote Sens. 2020, 12(4), 709; https://doi.org/10.3390/rs12040709
Submission received: 4 January 2020 / Revised: 13 February 2020 / Accepted: 19 February 2020 / Published: 21 February 2020
(This article belongs to the Special Issue Google Earth Engine and Cloud Computing Platforms: Methods and Applications in Big Geo Data Science)
Browse Figures
Versions Notes

Abstract

:
This paper analyses the spatio-temporal trends and variability in annual, seasonal, and monthly rainfall with corresponding rainy days in Bhilangana river basin, Uttarakhand Himalaya, based on stations and two gridded products. Station-based monthly rainfall and rainy days data were obtained from the India Meteorological Department (IMD) for the period from 1983 to 2008 and applied, along with two daily rainfall gridded products to establish temporal changes and spatial associations in the study area. Due to the lack of more recent ground station rainfall measurements for the basin, gridded data were then used to establish monthly rainfall spatio-temporal trends for the period 2009 to 2018. The study shows all surface observatories in the catchment experienced an annual decreasing trend in rainfall over the 1983 to 2008 period, averaging 15.75 mm per decade. Analysis of at the monthly and seasonal trend showed reduced rainfall for August and during monsoon season as a whole (10.13 and 11.38 mm per decade, respectively); maximum changes were observed in both monsoon and winter months. Gridded rainfall data were obtained from the Climate Hazard Infrared Group Precipitation Station (CHIRPS) and Precipitation Estimation from Remotely Sensed Information Using Artificial Neural Networks-Climate Data Record (PERSIANN-CDR). By combining the big data analytical potential of Google Earth Engine (GEE), we compare spatial patterns and temporal trends in observational and modelled precipitation and demonstrate that remote sensing products can reliably be used in inaccessible areas where observational data are scarce and/or temporally incomplete. CHIRPS reanalysis data indicate that there are in fact three significantly distinct annual rainfall periods in the basin, viz. phase 1: 1983 to 1997 (relatively high annual rainfall); phase 2: 1998 to 2008 (drought); phase 3: 2009 to 2018 (return to relatively high annual rainfall again). By comparison, PERSIANN-CDR data show reduced annual and winter precipitation, but no significant changes during the monsoon and pre-monsoon seasons from 1983 to 2008. The major conclusions of this study are that rainfall modelled using CHIRPS corresponds well with the observational record in confirming the decreased annual and seasonal rainfall, averaging 10.9 and 7.9 mm per decade respectively between 1983 and 2008, although there is a trend (albeit not statistically significant) to higher rainfall after the marked dry period between 1998 and 2008. Long-term variability in rainfall in the Bhilangana river basin has had critical impacts on the environment arising from water scarcity in this mountainous region.

Graphical Abstract

1. Introduction

Rainfall is a key component of the hydrological cycle and has a diverse range of impacts on human society, for example, agricultural activities [1], hydropower generation [2], vegetation phenology [3], and sustainability of biodiversity [4]. It is widely accepted that recent climate change has altered annual and seasonal patterns of rainfall along with its spatial distribution. The particular significance of rainfall variability has been highlighted for the high mountain regions of the Indian Himalayan Region (IHR) [5,6]. High mountain regions are in fact potentially ideal localities for evaluating climate change and associated impacts because of its large elevation range and vulnerable biota. As about one-fifth of the world’s mountain inhabitants is found in the wider Himalayan region [7], with an ongoing increasing population, the region is likely to play a crucial role in livelihoods of future generations [8]. However, recent studies suggest that over the past century, there have been several phases of rapid warming and that climate variability here exceeds the global average [9]. Therefore, understanding rainfall variability in the Himalayan region becomes extremely critical for integrated Himalayan spatial planning.
As the Himalayan region receives summer precipitation from the Indian Summer Monsoon (ISM) and winter precipitation from the Westerlies, much of the area that falls under the dominant influence of the south-westerly winds receives significant amounts of summer rainfall (~80%), but this gradually declines towards the north-western Himalayan region (i.e., the Monsoon shadow zone). Contrastingly, during the winter season, north, and northwest slopes of the Himalaya receive more rainfall from frontal disturbances and mid-latitude westerly cyclones, which originate in the North Atlantic, Mediterranean and Caspian Sea [10]. Accordingly, precipitation distribution and amount across the region depend on a range of climatic drivers, including the North Atlantic Oscillation (NAO) and El Niño Southern Oscillation (ENSO) and Jet Stream etc.
A growing literature suggests above normal increasing trend in temperature around the Western Himalayan region [11,12,13,14]. The decreasing thermal contrast between the Indian Ocean and Tibetan Plateau has led to the weakening of the ISM and hence the rainfall in the Himalayan region [13,14]. A range of regional precipitation attributes, such as rainfall amount, distribution, intensity, and frequency of rainy days, have been studied previously in the IHR and propose reduced rainfall intensity between 1951 and 2004 [15,16,17]. Such inconsistency in seasonal rainfall and rainy-day results in extreme rainfall events that, in turn, lead to flash floods and associated damages in low-lying areas [18]. Monitoring such inconsistencies of rainfall and reduction related forfeiture in mountainous regions are major challenges for the scientific community [19] and requires suitable data on its spatio-temporal variability [20,21]. Although paucity of station data in such regions is a significant obstacle, advances in cloud computing technology enable computation of satellite-derived information of rainfall characteristics using web-based remote sensing platforms such as Google Earth Engine (GEE). Indeed, access to gridded satellite data has become significantly more accessible in the recent past [22,23] and numerous satellite and reanalysis rainfall observations are available with higher spatial and temporal resolution such as TRMM, GPCC, APHRODITE, ERA-Interim, CFSR, GPM, IMERG, CHIRPS, PERSIANN. We used CHIRPS and PERSIANN-CDR datasets based on their higher spatio-temporal resolution, suitability over mountainous terrain such as the IHR and recent data availability over our study area.
Given the importance of evaluating amount, seasonality, variability, and long-term trends in precipitation characteristics of the Indian Himalaya, the aim of this study is to assess the spatio-temporal dynamics of rainfall and rainy days for the Bhilangana river basin during the period from 1983 to 2008. In so doing, we seek to explain the patterns of rainfall change and its potential impacts on the regional environment. The aim is achieved in relation to the following objectives.
  • To collect, tabulate and analyse rainfall data collected from i) available surface observatories managed by IMD ii) reanalysis rainfall data from CHIRPS and iii) satellite rainfall data PERSIANN-CDR
  • To map annual and seasonal time series of rainfall dynamics and juxtapose the performance of reanalysis and satellite-based data products compared to ground station data
  • To evaluate annual, seasonal, and monthly distributions and trends in rainfall and rainy days and compare the results from the three sources through the application of non-parametric tests
  • To briefly discuss the regional socio-economic implications of observed rainfall variability

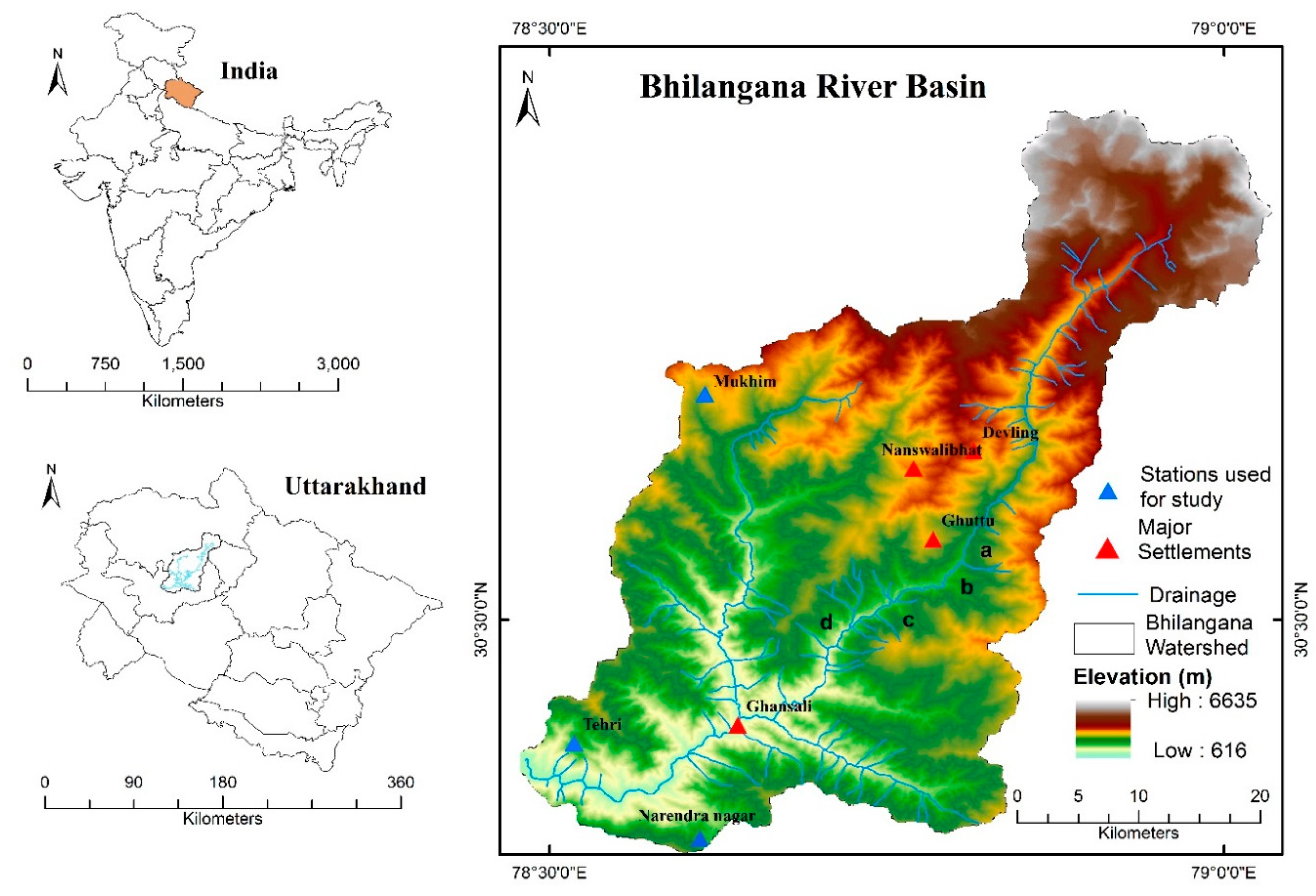
2. Environmental Characteristics of the Bhilangana River Basin

The Bhilangana river basin, a sub-basin of the upper Bhagirathi, is located in Uttarakhand State, western Himalaya, India. The basin, which occupies a total area of 1482 km2, lies between 30°32′71″N to 30°87′79″N latitude and 78°48′22″E to 79°03′53″E longitude (Figure 1) at elevations ranging between 616 to 6635 m amsl. The headwaters originate at the terminus of the Khatling glacier (3718 m asl) and flow ~ 80 km southwest to confluence with another river and feeds into the Tehri dam (India’s highest elevation river dam), after which it is known as the Bhagirathi river. The dam supports a 2400-megawatt hydropower system which provides electricity to adjacent states (Punjab, Haryana, Uttar Pradesh, Jammu and Kashmir) including the national capital (New Delhi). Indeed, the Bhilangana river is the lifeline for approximately 1.3 million people (around 13 percent of Uttarakhand’s population) and 295 villages [24] in terms of fresh water, irrigation, household activities and social wellbeing. Geologically, this area is primarily underlain by the Garhwal formation [25]. The major litho-tectonic units in the area are a) Central Crystalline and b) Garhwal groups [26]. Tectonically, this area is located in an earthquake zone “V”, (i.e., seismically more active) and is frequently impacted by mass movements including landslides and debris flow following monsoonal precipitation in summer months (June–September) [27,28]. The area is prone to extreme rainfall events, such as cloudbursts and torrential downpour, some of which together with other extreme events such as glacier lake outburst floods have resulted in loss of life, property, and infrastructure in the region during recent past [18,29].

3. Materials and Methods

3.1. Observed Data

Observed monthly rainfall and rainy days data for the period from 1983 to 2008 were obtained from the India Meteorological Department (IMD, Pune) (Table 1). Since both rainfall and rainy-day records of IMD have data gaps, we carefully selected suitable stations for this study based on a) more than 30 years of data, b) up to 80% of data availability, and c) the most recent records. In some cases, we interpolated the missing data by applying long-term monthly averages. Eventually, three surface observatories were selected for both rainfall and rainy-day parameters. As per the IMD, a rainy-day is defined as a day with a minimum of 2.5 mm rainfall. Reliable and reasonably continuous monthly data for these ground stations were only available for the period from 1983 to 2008.

3.2. Gridded Rainfall Data

Along with observed data, one reanalysis (CHIRPS) and one satellite-based (PERSIANN-CDR) gridded rainfall product was derived using GEE. Conspicuously, the CHIRPS gridded daily rainfall product is a combination of observed and satellite rainfall and has low systematic bias [30,31,32,33,34,35] with an extended period of record. CHIRPS data is accessed from the website of the Climate Hazard Group (https://www.chc.ucsb.edu) (USAID, NASA, and NOAA).PERSIANN-CDR data is satellite-derived daily rainfall estimate using artificial neural networks (ANN), with high spatio-temporal resolution and accuracy [36,37,38,39], and retrieved from the website of NCAR and UCAR (https://climatedataguide.ucar.edu). The ANN estimates precipitation from cold cloud pixels and adjacent features using gridded satellite brightness temperature details. In addition to this, two intensive field visits were conducted in 2016 to assess the environmental and socio-economic impacts of rainfall changes.
To estimate long-term trends, observed monthly rainfall and rainy-day data were collected from 1983 to 2008, as per the existing observation records of IMD. This was further compared with gridded data available between 1983 and 2008, based on high spatial resolution and a similar period of record. Thereafter, the more recent spatial and temporal trends were carried out using reanalysis data for the period 2009 to 2018.

3.3. Data Handling and Statistical Applications in GEE

Annual, seasonal and monthly gridded rainfall products were derived from the GEE platform [40] using the ee.ImageCollection algorithm and applying a filter command (ee.Filter.calendarRange) to cover the study period (1983–2018). After processing the images (.sum), the clip function was used to confine the boundaries to the Bhilangana study region (Supplementary code 1). Both high-resolution modelled datasets were downloaded and analysed in the GEE code editor. To ensure spatial similarity in both gridded datasets, bilinear interpolation resampling technique was used [41]. To match the similar spatial information with station data, nearest point-pixel rainfall values of both the gridded datasets were extracted in GEE platform for station localities (Supplementary code 2) [33,36]. Subsequently, pixel-based long-term spatio-temporal trend for both gridded data sets was performed in GEE using ee.Reducer.senSlope algorithm (Supplementary code 3). The Sen’s slope (magnitude of trend) was tested through Mann–Kendall (alpha ≤ 0.05 and Z statistics = 1.96, obtained from the standard normal table) expression.
Additionally, gridded daily rainfall records were then aggregated to monthly and seasonal totals viz., pre-monsoon (MAM), monsoon (JJAS), post-monsoon (ON), and winter (DJF), following the scheme of Basistha et al. [13] and Singh and Mal [42]. Thereafter, Lag-1 autocorrelation technique (alpha ≤ 0.05) was employed to check the presence of positive and negative autocorrelation in rainfall data, since this may affect the observed magnitude of trends in a dataset [13,43,44,45]. As observed rainfall records in a high mountainous region like IHR are poorly available and remain a challenge for the scientific community, several descriptive statistics were then applied to check data distribution and relative performance of the gridded datasets to ensure high- quality satellite rainfall data with respect to station observed data be used for further investigation. This statistical metrics includes determination of (a) mean-variance between observed and satellite/model rainfall values (Bias), (b) multiplicative bias (MBias) to measure the mean magnitude of bias, (c) relative bias (RBias) to reveal systematic standard error (d) mean absolute error (MAE) to obtain the average slope of error (e) root mean square error (RMSE) to assess the average magnitude of error, and (f) correlation coefficient (CC) to evaluate the degree of relationship between observed and satellite data, (g) coefficient of variation used as a estimation of variability when the average is proportional to standard deviation, (h) uncertainty to measure the amount of error in an average of large scale estimation, together with an (i) empirical cumulative distribution frequency (CDF) and (j) the Taylor diagram [22,33,34,46] (Appendix A). A normalised standard deviation method was applied to the Taylor diagram to exhibit relative performance of both gridded and station datasets [47]. Furthermore, Sen’s slope estimator was used to calculate the long-term magnitude of change in station observed data, the Mann–Kendall (MK) test was applied using MATLAB programming language to evaluate their statistical significance (Appendix B).

4. Results

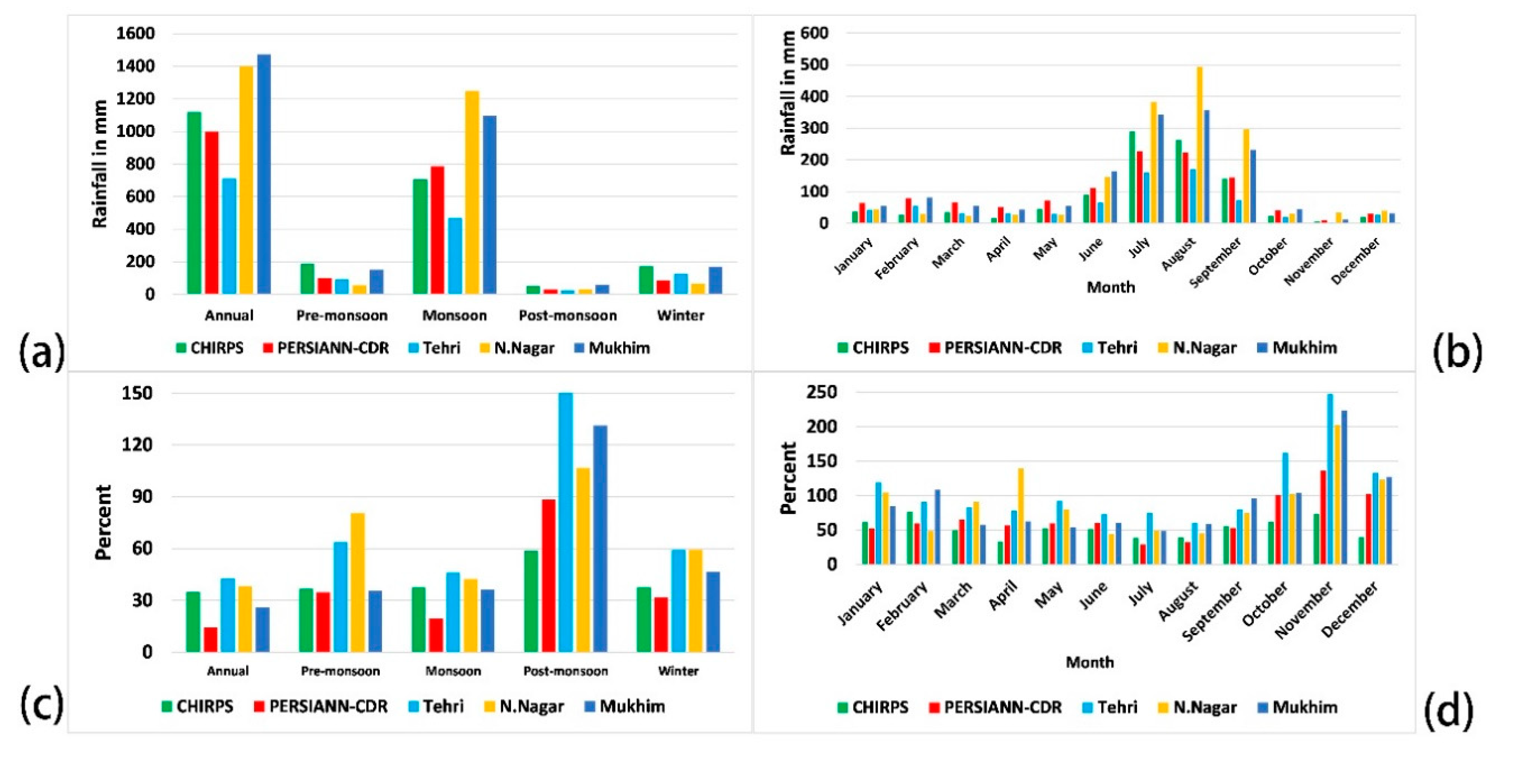
4.1. Spatio-Temporal Distribution of Rainfall and Rainy Days in the Bhilangana River Basin (1983–2008)

Mean annual rainfall (1983–2018) in the Bhilangana river basin is observed as 1196 mm across an average of 66 rainy days per year, although with marked spatial variability and seasonality. Rainfall is highest in the mountainous northeast (1473.6 mm), and somewhat less (710.8 mm) in the lower elevation areas in the southwest (Figure 2). Maximum rainfall is recorded during the monsoon season (78.6%), along with an average of 44 rainy days, followed by the winter (10.1%), pre-monsoon (8.4%), and post-monsoon (3.0%) along with around 8, 11, and 3 rainy days correspondingly. Within the Indian Summer Monsoon (ISM) monsoon season, August exhibits maximum rainfall (28.5%) followed by July (24.7%), September (16.8%) and June (10.5%) with 15, 13, 8, and 7 rainy days respectively. Station observed data on the other hand revealed mean annual rainfall of the basin is 1313.4. Monsoon is the highest rainfall season followed by pre-monsoon, winter, and post-monsoon (Table 2). Out of the two gridded datasets, CHIRPS reveals similar spatial information with station observed data in compare to PERSIANN-CDR. Mean annual rainfall revealed by the CHIRPS was 1119.7 mm, where PERSIANN-CDR underestimate rainfall counts by 998.1 mm. Seasonal and monthly distribution highlights similar spatial integrity with observed and CHIRPS dataset, where PERSIANN-CDR overestimate rainfall counts during pre-monsoon, post-monsoon and winter season (Figure 3a,b, Table 3). In both station and gridded datasets, there is greater annual and seasonal spatial variability at lower elevation stations such as Tehri and Narendra Nagar, than the higher elevation observatory (Mukhim) (Figure 3c,d). Both gridded datasets indicate similar spatial variability, although CHIRPS has better match with all the observed stations at seasonal and monthly scale (Figure 3c,d).

4.2. Detailed Outcomes of Descriptive Statistics

The autocorrelation assessment indicates that no significant homogeneity between both observed and gridded data sources (alpha ≤ 0.05). According to the results of descriptive statistics, the PERSIANN-CDR, for example, overestimates rainfall in the higher elevation region (Mukhim) with a positive MBias, but underestimates it in the low elevation part of catchment (higher spatial bias and lower CC (Table 3). Figure 4a–c illustrates linear regression and CC for both gridded and individual observational data, revealing strong spatial agreement with CHIRPS and somewhat less correspondence in the case of PERSIANN-CDR. Both the datasets were well matched with lower elevation station data, although CHIRPS has better agreement (r = 0.85) than the PERSIANN-CDR (r = 0.74) with an average lower uncertainty value (±6.2 mm). Higher elevation surface observatories have a similar spatial relationship with gridded datasets. Statistical indices indicated better performance of CHIRPS data in corresponding with direct observation, showing less bias at Tehri (4.59 mm) and Nagendra Nagar (6.26 mm), and a little higher, albeit not beyond the acceptance level, in Mukhim (bias acceptance level = 10 mm) (Figure 4d,e). The positive bias for each station indicates that CHIRPS sometimes underestimates rainfall amount. However, MBias and RBias values are low suggesting that the existing error is not systematic. PERSIANN-CDR, on the other hand, overestimates rainfall with both greater bias and lower spatial agreement (CC), therefore signifying systematic errors (Table 3), exception for Tehri. The maximum RMSE was detected by the PERSIANN-CDR in the high elevation region, i.e., Mukhim (111.30 mm), followed by Nagendra Nagar (96.2 mm) and Tehri (81.24 mm) whereas CHIRPS shows better performance with all the observed stations. Moreover, empirical CDF reveals spatial distribution for mean monthly rainfall (Figure 4f); notably, more than 80% of the data are evenly distributed among CHIRPS and station records, where PERSIANN-CDR show a relatively higher distribution in respect to observed data due to greater RMSE and systematic error.

4.3. Spatio-Temporal Trends: Observational Data

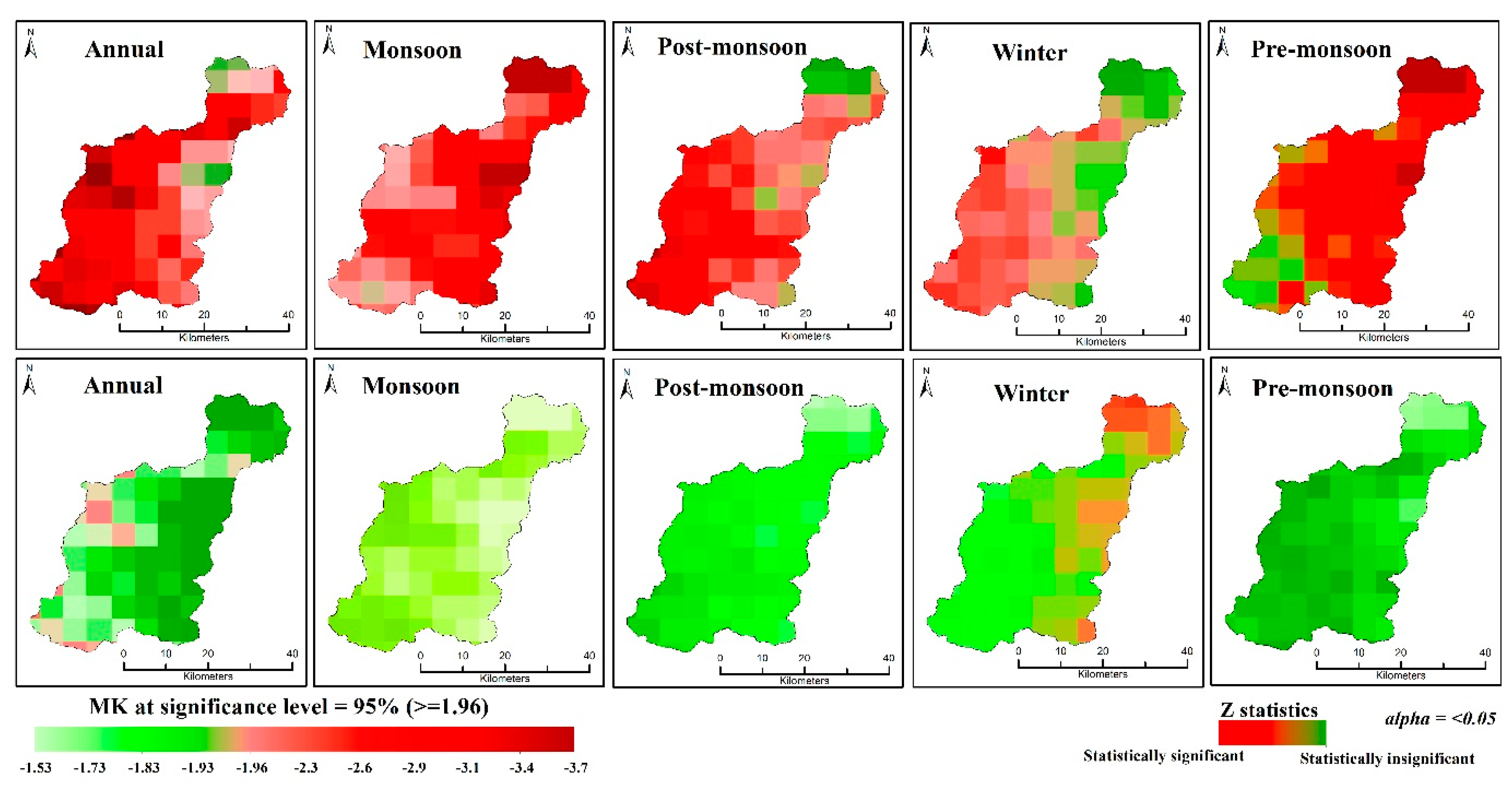
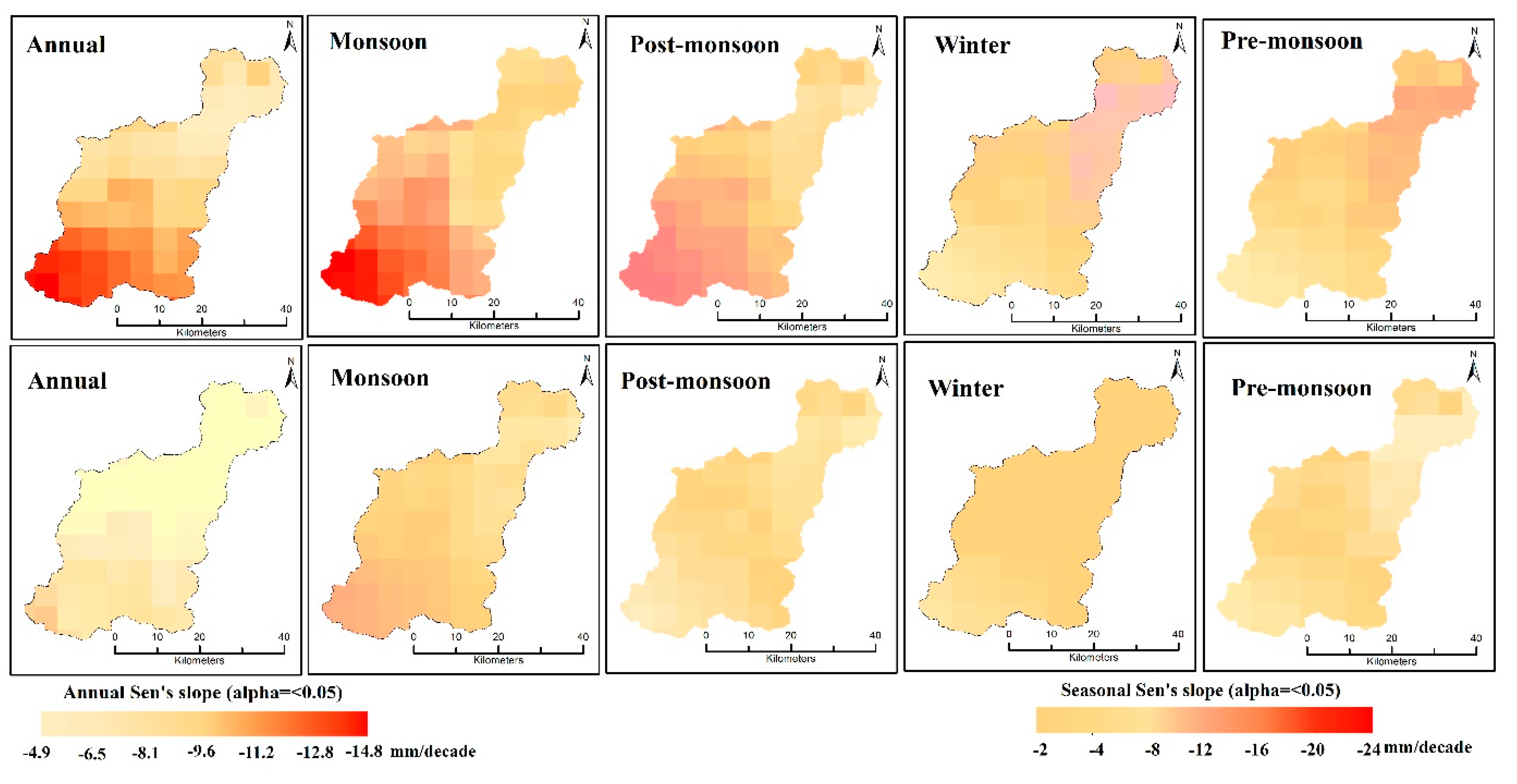
4.3.1. Annual and Seasonal Trends in Observatory Rainfall Data (1983–2008)

This study reveals annual and seasonal rainfall distribution and trend for the period from 1983 to 2008. Maximum annual rainfall occurred in highest elevation surface observatory (Mukhim) followed by Narendra Nagar and Tehri. Seasonally, Narendra Nagar received maximum rainfall than the Mukhim and Tehri (Table 4). The analysis also reveals that the three surface observatories experienced decreasing rainfall trends, some of which are statistically significant. Narendra Nagar showed the maximum decrease (−32.82 mm/decade) followed by Tehri (−12.26 mm/decade) and Mukhim (−2.04 mm/decade) between 1983 and 2008 (Table 4). Stations at a lower elevation (Tehri) witnessed rainfall changes of lower magnitude (statistically insignificant). All surface observatories experienced a decreasing trend in rainfall throughout the year, except Mukhim during the winter season. The most marked rainfall changes occurred during the monsoon season (−11.23 mm/decade) followed by winter (−1.1 mm/decade), pre-monsoon season (0.63 mm) and post-monsoon (0.53 mm) seasons. Narendra Nagar recorded the maximum decrease in monsoon season rainfall (−22.37 mm/decade) and also for the winter (−2.56 mm/decade) followed by post-monsoon (−0.82 mm/decade) and pre-monsoon (−0.676) rainfall. The station at Tehri also witnessed significant rainfall decline during monsoon (−7.45 mm/decade), although the reductions during winter (−0.71 mm/decade) and pre-monsoon (−0.31 mm/decade) were not statistically significant. This was also the case, for Mukhim in the monsoon (3.79 mm/decade) and winter (−0.009 mm/decade); the negative trend (0.91 mm/decade) in the post-monsoon season was, however, statistically significant at this locality.

4.3.2. Monthly Trends in Observatory Data (1983–2008)

Analysis of monthly distribution and trend of rainfall offers a more detailed picture of rainfall change in the region over the study period. Maximum rainfall was observed in July, August, and September in all the surface observatories. However, Narendra Nagar experienced maximum rainfall in the last 26 years followed by Mukhim and Tehri (Table 5). Furthermore, statistical trend analysis shows marked decreases in Narendra Nagar for July (−8.4 mm/decade), August (−12.4 mm/decade) and October (−0.5 mm/decade) (Table 5). Tehri also recorded significant decreases but mainly in July (0.8 mm/decade) and September (0.1 mm/decade). Monthly values for Mukhim show no statistically significant trends, although rainfall for June, July, October, and November did decrease over the study period.

4.3.3. Trends in Rainy Days (1983–2008)

Annually, all surface observatories witnessed a statistically significant reduction in the number of rainy days (Table 6). Narendra Nagar recorded the most marked frequency reduction during the monsoon season, followed by Mukhim and Tehri (Table 6). Mukhim and Tehri stations experienced fewer rainy days in post-monsoon and winter seasons respectively. The negative trend in rainy days during monsoon season indicates a declining rainfall pattern for June through September. Significant changes in annual and seasonal rainy days have direct influence on long-term rainfall patterns in the study area.

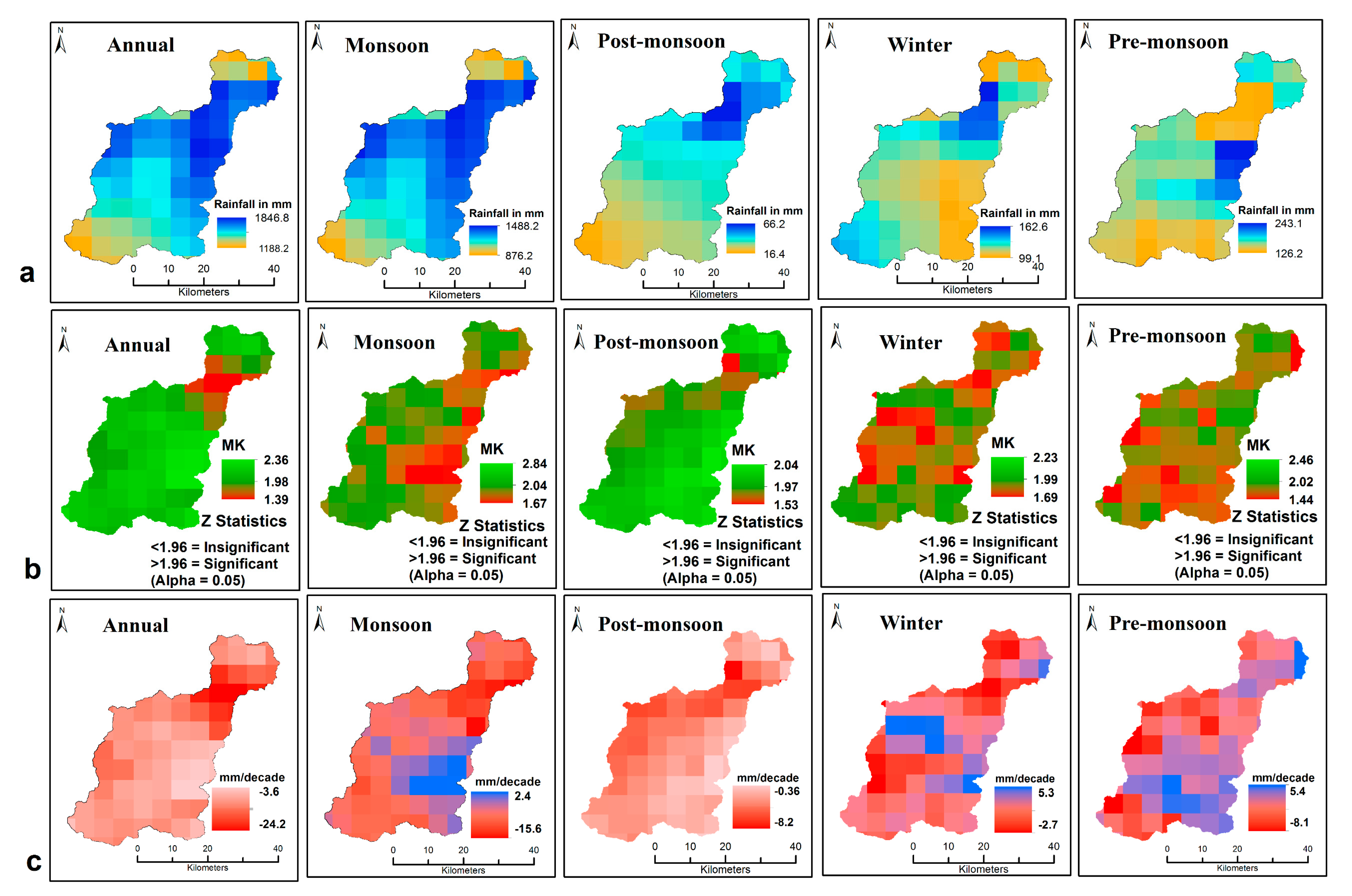
4.4. Spatio-Temporal Trends: CHIRPS and PERSIANN-CDR

4.4.1. Annual and Seasonal Trends (1983–2008)

Statistically significant declining annual rainfall trends were recorded in both gridded data products, averaging 10.9 mm/decade (Table 7). CHIRPS exhibited the most prominent changes (−14.8 mm/decade), followed by PERSIANN-CDR (−6.9 mm/decade). Modelled rainfall declined in all seasons across the study period, with CHIRPS revealing a greater magnitude of change during monsoon, pre-monsoon, winter, and post-monsoon (significant) seasons compared with PERSIANN-CDR (not significant). The magnitude of rainfall reduction revealed by PERSIANN-CDR is lower, due to higher spatial bias and greater mean absolute error. Due to the underestimation of rainfall counts (beyond the acceptance level), PERSIANN-CDR showed very fewer changes in seasonal and monthly values in comparison to observed station datasets, whereas CHIRPS has better agreement over the study period exhibited by the higher correlation coefficient (r2 = 0.74). Spatially, the statistically significant reduced rainfall trend is confined to the south-western parts of the study area (Figure 5). The decreased rainfall trend in the north-western windward parts of the area over the area is not statistically significant. Low elevation regions exhibit less rainfall variability throughout the decades, because both models (CHIRPS and PERSIANN-CDR) underestimate rainfall amounts (bias = 4.6 and 16.88 mm respectively).
Lower elevation parts of the basin record greater magnitude changes both annually and seasonally supported by lower systematic errors and bias with high spatial integrity. CHIRPS data also indicated more change in low-lying areas with higher spatial agreement between station observed data, whereas PERSIANN-CDR show no significant trend due to its underestimation of rainfall counts (Bias = 16.88). The eastern side of the basin showed maximum changes in both the datasets, which suggests lower monsoonal rainfall (Figure 6). The north and north-western areas exhibit lower winter rainfall changes from 1983 to 2008.

4.4.2. Monthly Trends: CHIRPS and PERSIANN-CDR (1983–2008)

Markedly reduced rainfall is exhibited by CHIRPS for the months May through November (Table 8). In contrast, the PERSIANN-CDR output showed a (statistically insignificant) slightly increasing trend for May, June, and October. Maximum changes are recorded in July and August (CHIRPS), whereas PERSIANN-CDR data reflect a lower magnitude of change over all due to higher spatial bias and systematic errors compared to observe rainfall.

5. Inter-Annual Rainfall Variability and Trends (1983 to 2018) from Station Observed and CHIRPS Data

Inter-annual rainfall variability was tested using station observed and gridded data sets for the period from 1983 to 2008. Due to the unavailability or unreliability of ground station records for the basin in the post-2008 period, annual, seasonal, and monthly rainfall trends and variability need to be assessed using modelled data. The study suggests an overall increasing tendency for the period from1983 to 2018 of approximately 8.76 mm/decade, although there is substantial inter-annual variability across the entire study period. CHIRPS is shown here to produces values that are more consistent with observed data, and we selected this to estimate long-term inter-annual rainfall variability and trends as illustrated in Figure 7a indicate three distinct phases are evident in the annual, seasonal and monthly records, such that 1983 to 1997 (phase I) exhibits mean annual precipitation fluctuating around 1270 mm with lower uncertainty (±18 mm); phase II (1998–2008) is associated with significantly lower annual totals (less than 620 mm), strongly suggested by station observed data (Figure 7d,e); phase III indicates sharply increased annual rainfall of around 1586mm with high uncertainty values. More recently, there is a suggestion of an increasing trend (4.11 mm/decade), although this is not statistically significant. This investigation further revealed that monthly and seasonal rainfall has increased in recent years (2009–2018) in comparison to previous decades, whereas phase II experienced severely less rainfall and the significant reduction rate was −4.24 mm/decade (Figure 7a).
This recent (phase III) increase is primarily due to higher rainfall during the pre-monsoon season in particular (Table 9; Figure 7b). However, there are significant decreasing changes in rainfall during monsoon, pre-monsoon, and winter season in the north-western part of the basin in particular. The eastern and south-eastern parts on the other hand experienced increasing rainfall during these same seasons (not statistically significant) (Figure 8). Analysis of monthly trends indicate statistically insignificant decreasing rainfall with lower uncertainty values in September (−8.2 mm/decade) followed by February (−2.1mm/decade) and October (−1.9 mm/decade) with higher uncertainty. However, January exhibits a significant increasing trend (0.79 mm/decade) with relatively greater uncertainty (±11.4 mm), while March to July recorded an increasing but not significant trend in rainfall with an average of ± 2.9 mm uncertainty (Table 9). This study also highlights that the highest increases are for June (7.5 mm/decade) and July (6.1 mm/decade) (Figure 7c, Table 9). This increasing tendency in monthly rainfall is most likely to be a result of extreme rainfall events in the study area.

6. Discussion

This study presents an analysis of annual, seasonal, and monthly trends and variability in rainfall and rainy days using three surface observatories and two high-resolution gridded datasets at different elevation ranges (from 6635 to 616 m amsl) over the last four decades. These three datasets were calibrated and compared using several non-parametric statistical techniques which reveals significance levels (alpha ≤ 0.05) for a wide range of data characteristics. The present study reveals that maximum annual rainfall is observed during the monsoon season (79%) followed by the winter, pre-monsoon, and post-monsoon, which is corroborated by the studies in the adjacent regions of Uttarakhand and Nepal Himalaya, during the presence of ISM (monsoon) and Westerly Disturbances (winter) [13,14,17].

6.1. Temporal Trends in Observed Rainfall (1983–2008)

Significance changes in annual, seasonal, and monthly rainfall are observed using station-based records. Spatial variability in rainfall trends and orographic effects on the distribution of rainfall are apparent in the study area. Narendra Nagar witnessed the significant reductions in annual and monsoonal rainfall (−32.82 and −22.37 mm/decade) followed by Tehri and Mukhim. The trends align well with the previous studies in the western Himalaya and in the abject Nepal Himalaya [13,42]. In such circumstances, topography, relief, and aspects are dominant factors influencing rainfall distribution, for instance, Tehri is located on the western side of the Gangotri range and receives more rainfall from frontal systems in the winter compared to Narendra Nagar [48,49].
Significant inter-seasonal variations are also apparent, whereby average monsoon rainfall changes (−11.23 mm-decade) are most considerable across the basin. Similar outcomes have been reported by others, for example Ramesh and Goswami [15] described the increased occurrence of “monsoon-breaks” across India between 1951 and 2008, which is attributed largely to less atmospheric water vapour reaching the subcontinent. Shekhar et al. [5] and Kumar and Jain [16] highlighted decline in frequency and intensity of westerly disturbances in winters along with shrinkage of monsoonal cloud cover in the Himalayan region from 1971 to 2000. A growing body of work concerning rainfall distribution and trends in the IHR describes declining thermal contrast between the Indian Ocean and Tibetan Plateau, resulting in less moisture reaching the Indian landmass, and contributes to decreased rainfall in higher elevation regions [16,17,50]. Besides, anthropogenic factors such as large scale land use transformation from forest to agricultural land and settlement in low elevation regions under the ‘Tehri Dam Rehabilitation Program’ [51,52] and the ‘Terai Colonization Scheme’ also play a dominant role in altering local rainfall patterns [53].
Significant reduction in the annual frequency of rainy days was identified from observational data in the Bhilangana river basin. Several other studies on rainfall in India and Himalayan region have reached similar conclusions [13,16,17,54,55]. This temporal pattern is perhaps due to a combination of factors, including substantial decrease in the frequency and intensity of westerly disturbances from 1977 to 2007 [16], population migration from high to low elevation regions with associated land use change and weakening of the land-ocean thermal contrast between the Tibetan plateau and Indian Ocean [50]. In general, large scale deforestation [56], global climate shift [57], dynamics of the El Niño Southern Oscillation [58] and North Atlantic Oscillation [10] are also the possible drivers of the rainfall trend.

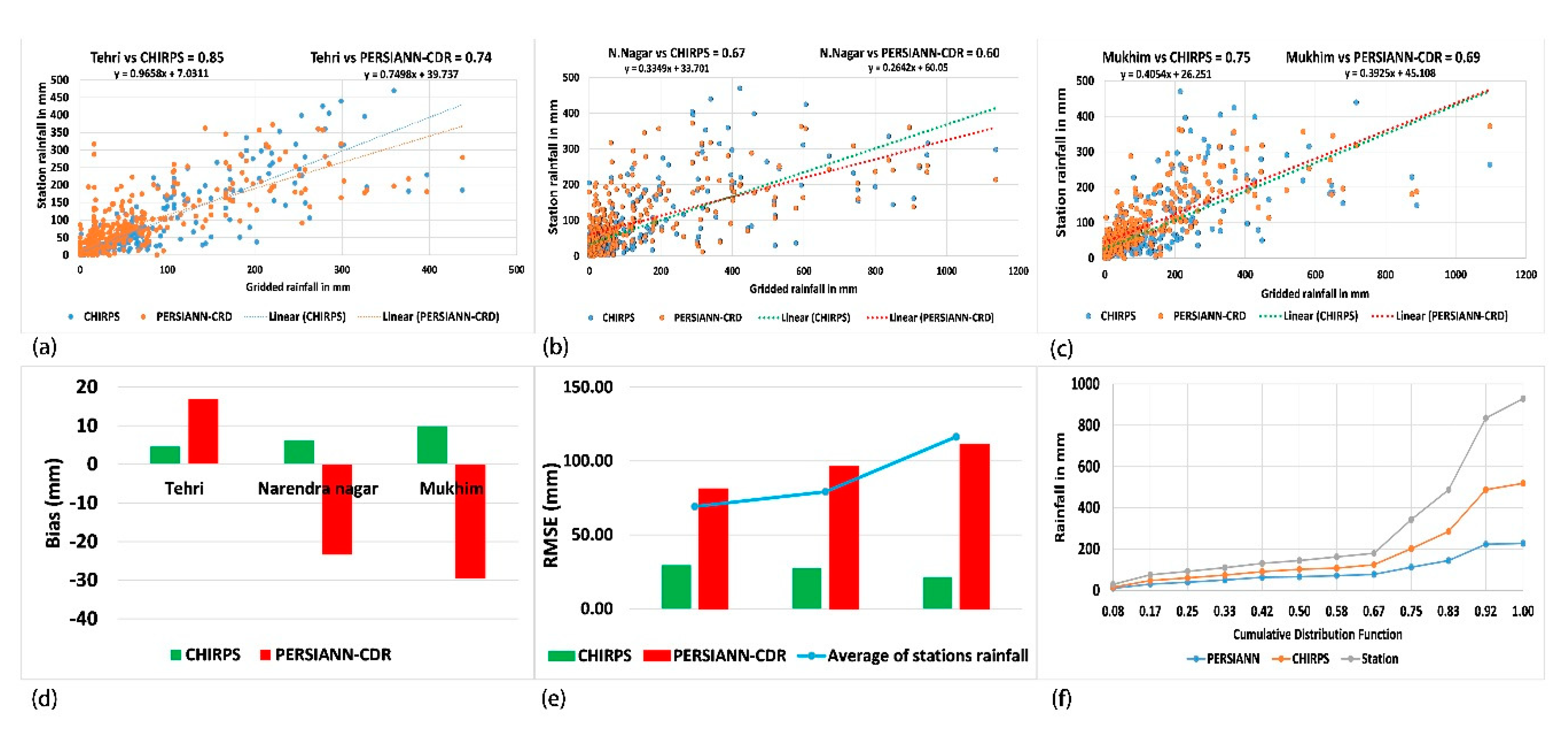
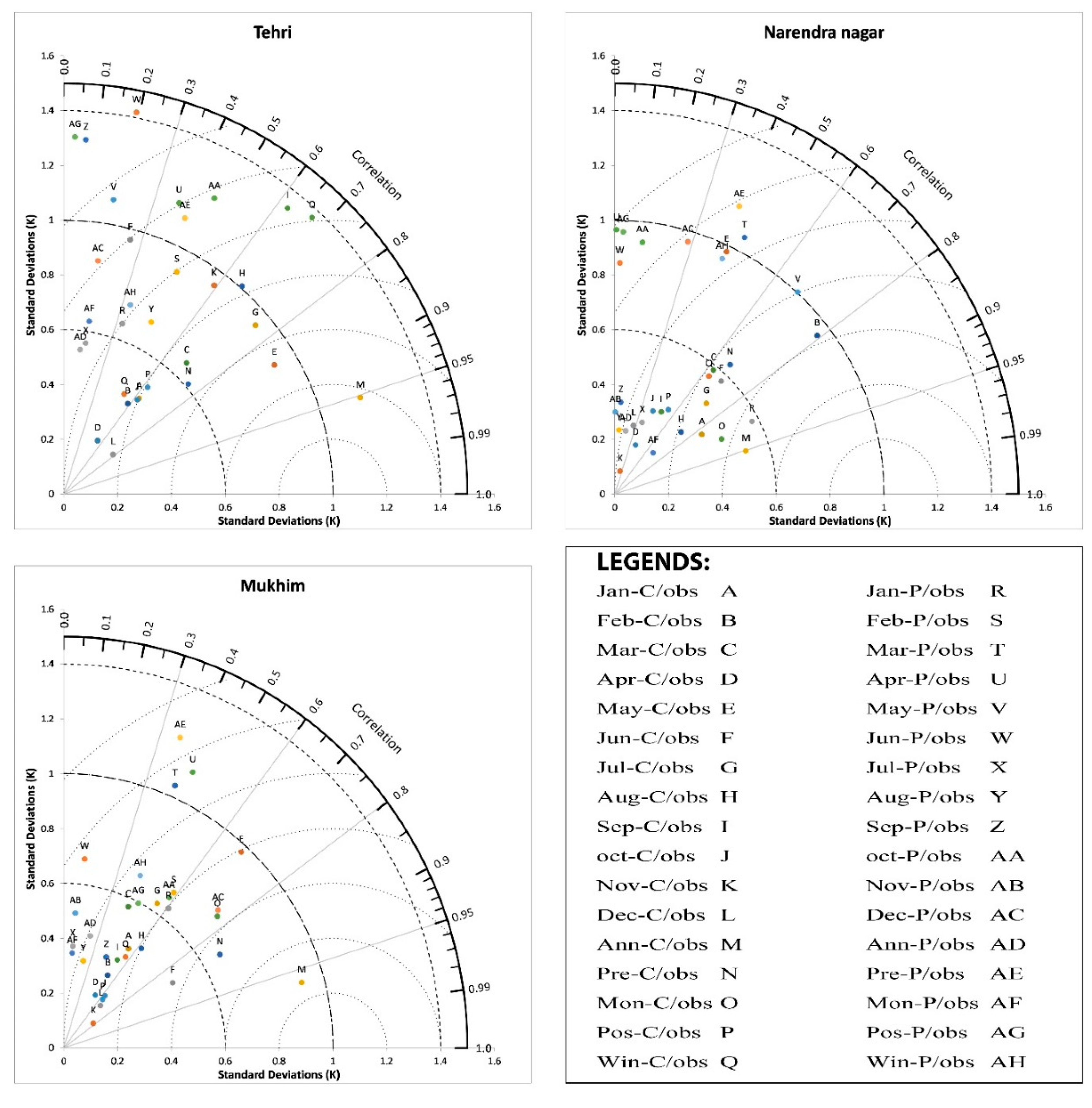
6.2. Appropriateness of Gridded Datasets in Compared to Observed Data (1983–2008)

There remains controversy, however, around long-term climate changes in the Himalaya. This is largely a consequence of the complexity of monsoon system itself, coupled with heterogeneity of surface topography [59]. Long-term observation stations are few and far between due to the inhospitable climate and inaccessibility, and remotely sensed and reanalysis products must be relied upon to estimate uncertainties that cannot be addressed with station rainfall data. Using the facility of GEE cloud computing, reanalysis (CHIRPS) and satellite-derived (PERSIANN-CDR) rainfall products may be compared and statistically analysed in terms of relative performance against the limited observational data.
Satellite products do have limitation in regard to estimate rainfall in mountainous regions due to the presence of cold cloud, ice, and snow [32,33,59,60]. Moreover, the role of local topography in orographic rainfall is widely described [61,62,63,64] and this certainly impacts on the resolution and accuracy of satellite-derived rainfall data. Prakash [34] and Beck et al. [35] demonstrated the suitability of CHIRPS rainfall data through several statistical methods and concluded that the product adequately estimates annual and seasonal long-term rainfall trends with respect to observed data. Which seems in general to underestimate changes relative to the observational data. Ullash et al. [33] noted the proficiency of CHIRPS data to estimate seasonal and monthly rainfall counts in different climate zones of Pakistan, with low bias.
However, Ashouri et al. [38] established the proficiency of PERSIANN-CDR in terms of long-term rainfall-runoff modelling with low bias. In recent years, there has been growing literature in the performance of PERSIANN-CDR daily rainfall product to acquire rainfall information in Asian mountainous regions and assess its efficiency in terms of long-term performance for rainfall and hydrological modelling [32,37,65,66,67,68,69].
Our study further highlights the performance of these two gridded data products whereby CHIRPS a greater degree of correspondence with observed rainfall compared to PERSIANN-CDR. The monthly, annual, and seasonal distribution from 1983 to 2008 depicts similar temporal trends and spatial patterns to the three surface observatories (Figure 9). Statistical analysis supports this interpretation of rainfall, in that CHIRPS shows lower systematic bias and spatial distributional errors (RMSE). Annual, seasonal, and monthly trends from 1983 to 2008 reflect the ground station data well, whereas the trends in PERSIANN-CDR data are variable.

6.3. Estimation of 1983 to 2008 Rainfall with Gridded Data

Observed rainfall variability based on the gridded data presented here exhibit similar temporal trends to station data, with slight differences in annual, seasonal, and monthly rainfall, with a mean annual reduction of around 11 mm/decade across the basin. CHIRPS with a greater degree of agreement with station data, shows reduction in annual and seasonal rainfall by comparison with PERSIANN-CDR., because this product appears to systematically underestimate rainfall counts in the region. The study shows that most of the low-lying regions in the Bhilangana river basin have experienced a significantly decreasing trend in both annual and monsoon season rainfall, whereas PERSIANN-CDR showed much less change. Similar results are noted by Ullah et al. [33] in the mountainous regions of Karakoram and found CHIRPS data has better performance than PERSIANN-CDR to estimate rainfall counts.

6.4. Estimation of 2009–2018 Rainfall with CHIRPS

The CHIRPS analysis of rainfall pattern from 2009 to 2018 indicates a tendency towards increasing annual rainfall, although this is not statistically significant, however, other studies have suggested increased rainfall over the western Himalaya after 2008 due to fluctuation in monsoonal rainfall, the formation of deep and wide convective cores in the Arabian seas and release at the foothills of western Himalaya, might be the cause of substantial rainfall at the south-eastern area due to orographic uplifting [70,71].
An increased frequency of extreme events in the recent past, including cloudbursts, lake avulsion floods and avalanches have been recorded for the Bhagirathi and Bhilangana basins, more especially in the monsoon season [18,29]. Although Dimri et al. [29] indicate that gridded data products may not capture such short term events in high mountain regions, CHIRPS data in this study do successfully record extreme rainfall events during the monsoon seasons of July and August 2012 and 2013.

6.5. Variability of Rainfall (1983–2018) from CHIRPS Data

Temporal variability in annual and seasonal rainfall was analysed using the CHIRPS dataset for the period from 1983 to 2018. Based on our analysis, we identified three distinctive rainfall phases (1983 to 1997, 1998 to 2008, and 2009 to 2018). This pattern is notably due to a particularly dry period, although this has not previously been shown for this or other parts of the Himalaya. However, Bhutiyani et al. [11] conducted a spatial-temporal analysis of teleconnections between two meteorological phenomena (NAO, ENSO) and monsoon rainfall and found that these systems brought less moisture to the upland areas between 1983 and 2005. They further suggested that reduced rainfall during 2004 and 2005 was due to rapidly increasing temperatures in the mountainous areas of the Himalaya. Archer and Fowler [48] highlighted the importance of local topography in influencing the amount and distribution of moisture during the onset of the ISM.

6.6. Regional Environmental Impacts of Rainfall Changes

Rainfall change is certain to have significant environmental and socio-economic consequences, especially in vulnerable high mountain regions. Aside from the historical changes highlighted in this paper, has been predicted that future surface temperatures will increase [72] and that surface runoff of Himalayan major river basins will increase due to melting glaciers and early melting of snow [73]. Higher temperatures impact rainfall mechanisms, which will, in turn, affect spatial and temporal patterns of rainfall in the study region. Such scenarios are potentially very important for people living in mountainous areas. Appollo, [74] stated that in the last few decades (1961–2011), the Himalayan population has increased by 2.5 times from 19.9 to 52.8 million with a growth rate of 3.3 percent, which was three times the global average. The temporal patterns of rainfall reported here suggests that the population has already faced considerable challenges in this regard and will be increasingly exposed. Almost 70 percent of the population of the basin is dependent on agriculture and small-scale industries for their livelihoods and is therefore entirely reliant on the river water supply of the Bhilangana river [24].

6.6.1. Effects of Decreasing Rainfall: 1983 to 2008

The long-term trend analysis of the Bhilangana river basin has revealed a decreasing rainfall pattern, averaging roughly 15 mm/decade using both stations observed and gridded datasets. Of the total area of the Bhilangana community development block (21350.67 hectares), more than 40 percent of the land is cultivable and, within this, more than one-quarter is irrigated [24]. This changing rainfall pattern presents a major challenge to the people of the study area, since less water availability impacts agriculture and other related activities directly. Several other studies have noted that rainfall in the Himalayan mountains has become more strongly seasonal, whereby the pre- and post-monsoon seasons exhibit prominent drying trends [13,42]. The negative trends in the pre-monsoon rainfall have significant implications for the economy and local livelihoods. Since the pre-monsoon season marks the beginning of the growing season, when the demands for water for irrigation is high. Decreasing rainfall has led to abandonment of agricultural lands (Figure 10a). Moreover, small-scale household industries, such as small hydropower stations have been discontinued due to lack of water in the streams and rivers (Figure 10b).

6.6.2. Effects of Increasing Rainfall: 2009 to 2018

Recent trends in inter-annual rainfall patterns suggest the long-term reduction in rainfall has been reversed and, while this is not statistically significant at the annual scale, an increase in the frequency and magnitude of extreme events has become an additional threat for local people as well as infrastructure. Dimri et al. [29] describes several recent major cloudburst and associated mass movement events that affected the area between 800 to 1800 m amsl and resulted in losses of livestock and destruction of houses during the monsoon months. Banerjee et al. [28] reported that almost 10 percent of the total basin area falls within the high landslide risk zone and increased rainfall further heightens the risk of such disasters. Dramatic evidence of the impact of such events changes can be seen in the damage to buildings and infrastructure (Figure 10d). During a flood event in 2012 flood, a medium-scale (24 mega-watts) hydropower station was partially destroyed (Figure 10c).

7. Conclusions

The prime aim of this study was to evaluate the spatio-temporal dynamics of rainfall and rainy days for the Bhilangana river basin during the period from 1983 to 2018 using both in situ and gridded rainfall data. Non-parametric statistical indices were applied coupled with advance web-based cloud computing platform (GEE). This basin was studied because of its diverse topography, large extent of population dynamics, heterogeneous land use and limited availability of ground data. The present study adequately uses big data applications using GEE platform, alongside MATLAB programming language to delineate the monotonic trend of gridded and observed data. The main conclusions of the study can be summarised as follows.
1) This study provided a comprehensive understanding of the long-term historical trend of observed rainfall and rainy days, together with satellite and reanalysis data sets. The statistical indices indicated CHIRPS data show relatively better performance and accuracy than PERSIANN-CDR, when compared to observational data. However, associating the two results, it can be seen that both station and gridded data products record statistically significant decreasing trends in rainfall from 1983 to 2018. CHIRPS showed similar tendency corresponding with station data, averaging 11 mm rainfall/decade over the period of record.
Notably, The PERSIANN-CDR showed less alteration in annual rainfall (6.9 mm/decade) due to high RMSE and systematic bias, resulted in miscounting rainfall totals. From the observational data exposed, Narendra Nagar has exclusively witnessed very substantial reduced annual rainfall (32.82 mm/decade). Seasonally there is a statistically significant decreasing trend in monsoon, winter, and post-monsoon rainfall of all the data products. Areas at lower elevation were subject to a greater degree of rainfall decrease while the magnitude of change was highest in the monsoon season.
2) The temporal pattern of rainfall change can bring about substantial impacts on the regional economy, including reduced water supply for crop cultivation, hydropower generation, tourism, and livelihoods in general. In addition, the increasing recent rainfall pattern from 2009 to 2018, has caused loss of life and damage of property and infrastructure.
3) Understanding spatial and temporal patterns, trends, and variability of rainfall in the Himalaya remain a challenge to assess due to a combination of complex topography and low spatial coverage of observation stations and inhospitable climatic conditions. Eventually, the systematic bias of gridded rainfall in mountainous regions specify that precise estimation by satellite-based rainfall products remains a big task for the scientific community. Sometimes low spatial resolution of satellites is also another cause to detect short term changes at micro level regions. Nevertheless, high-resolution reanalysis data products (CHIRPS) can be analysed through powerful cloud computing applications such as GEE and provide valuable information about the dynamics of rainfall in vulnerable high mountain regions.

Supplementary Materials

The following are available online, Code:1—to export annual and seasonal images https://code.earthengine.google.com/2bc1f4840c718a35b5e1357cad4a801f, Code:2—Pixel wise data for gridded rainfall product https://code.earthengine.google.com/a0e5dc887d4fccc054c444e06430c95f, Code:3—to calculate pixel wise trend and statistical significance (alpha ≤ 0.05) https://code.earthengine.google.com/f4753d0b3eaeb6f16df7aec96e3c1bab.

Author Contributions

Conceptualization, A.B. and M.E.M.; methodology, A.B.; software, A.B. and D.S.; validation, A.B., D.S., M.E.M., R.C., R.B., and S.M.; formal analysis, A.B.; investigation A.B., and D.S.; resources, A.B., and M.E.M.; data curation, A.B., and D.S.; writing—original draft preparation, A.B., and M.E.M.; writing—review and editing, A.B., M.E.M., R.C., R.B.S., S.M., and D.S.; visualization, A.B.; supervision, M.E.M., R.C., R.B.S., S.M.; project administration, A.B.; funding acquisition, R.C. All authors have read and agreed to the published version of the manuscript.

Funding

This study has been conducted with the support of the National Key R&D Program of China (2017YFC1503001), the National Natural Science Foundation of China [grant number 41771119], and funding from Institute of Eco-Chongming (IEC). A.B. and S.M. would like to acknowledge funding for the field visits, which were conducted within the HINEX project supported by the International Water Management Institute and the Water, Land and Ecosystems (WLE) program of the Consultative Group for International Agricultural Research (CGIAR).

Acknowledgments

We gratefully acknowledge the anonymous reviewers and editor of the paper in providing critical and constructive comments, which has helped us to significantly improve the manuscript. We are also grateful to the India Meteorological Department, NOAA, NCDC, UCSB and Climate Hazard Groups for providing long-term observatory data. We also appreciate the assistance of Ehsan Sharifi (Institute of Meteorology and Climatology, University of Natural Resources and Life Sciences, Vienna, Austria), Kishore Pangaluru (Department of Earth System Sciences, University of California, Irvine, CA 92697, USA) for their valuable suggestions regarding the methodology section of this paper.

Conflicts of Interest

There are no conflicts of interest among the researchers. All authors contributed equally to this work.

Abbreviations

APHRODITE: Asian Precipitation - Highly Resolved Observational Data Integration towards Evaluation of Water Resources; CFSR: Climate Forecast System Reanalysis; ERA-Interim: European Reanalysis; GPM: Global Precipitation Measurement; GPCC: Global Precipitation Climatology Centre; IMERG: Integrated Multi-satellite Retrievals for GPM; NASA: National Aeronautics and Space Administration; NOAA: National Oceanic and Atmospheric Administration; TRMM: Tropical Rainfall Measuring Mission; USAID: United States Agency for International Development.

Appendix A

Appendix A.1. Auto-Correlation

Occurrence of positive and negative autocorrelation may affect the analysis of trend in dataset [13,43]. The autocorrelation coefficient was tasted using the interval of Lag-1 (at 95% significance level) and computed as follows
{ − 1 − 1.645 ∗ ( N − 2 ) 0.5 } N − 1 = < R = < { 1 + 1.645 ∗ ( N − 2 ) 0.5 } N − 1

Appendix A.2. Bias

Bias denotes mean variance between in situ and satellite or model data. The positive bias indicates underestimation and negative bias specifics overestimation of rainfall.
B i a s = ∑ i = 1 N ( R S i − R O i ) N ( mm )
whereas, R S i and R O i depicts satellite and observed rainfall values respectively. N is showing number of observations.

Appendix A.3. Multiplicative Bias

Multiplicative Bias is the average magnitude of gridded precipitation over observed counts, where underestimation seems to count less than unity and overestimation is greater than unity [22]. This is actually estimate probability mass function to distinct kernels of a set of observations including variance and mean integrated standard error.
M B i a s = ∑ i = 1 N R S i ∑ i = 1 N R O i
where R S i and R O i depict satellite and observed rainfall values respectively. N is the number of observation days over a particular grid.

Appendix A.4. Relative Bias

Relative bias illustrates the systematic bias of satellite precipitation and acts as parallel to bias. This actually estimates the standard error between the observed and modelled datasets.
R B i a s = ∑ i = 1 N ( R S i − R O i ) ∑ i = 1 N P O i × 100
where R S i and R O i depict satellite and observed rainfall values respectively. N is the number of observations.

Appendix A.5. Mean Absolute Error

Mean absolute error is employed to demonstrate average magnitude of error in satellite and observed rainfall values.
M A E = ∑ i = 1 N | R S i − R O i | N ( mm )
where R S i and R O i depict satellite and observed rainfall values respectively. N is the number of observations days over a particular grid.

Appendix A.6. Root Mean Square Error

Root mean square error is similar to MAE. However, it gives higher priority to calculate the mean magnitude of error in satellite and in situ measurement [33].
R M S E = 1 N ∑ i = 1 N ( R S i − R O i )   2 ( mm )
where R S i and R O i depict satellite and observed rainfall values respectively. N is the number of observations.

Appendix A.7. Correlation Coefficient

The correlation coefficient is widely used to portrait spatial agreement between observed and gridded data sets. Perfect relationship specifies towards +1.
C C = ∑ i = 1 N ( R S i − R ¯ S ) ( R O i − R ¯ O ) ∑ i = 1 N ( R S i − R ¯ S )   2 ∑ i = 1 N ( R O i − R ¯ O )   2

Appendix A.8. Coefficient of Variation

The coefficient of variance is used to determine the degree of variability from one data series to another by simply the ratio of mean and standard deviation.
C V = Mean Standard   Deviation × 100
where R S i and R O i depict satellite and observed rainfall values respectively. N is the number of observations.

Appendix A.9. Uncertainty

The uncertainty is estimated using the amount of random fluctuations in an observation. This can be measured by difference of maximum and minimum value in a series of observations, divided by two. Such undercities arise mainly due to observation error from the instrument.
U n c e r t a i n t y = Max − Min 2

Appendix A.10. Normalised Standard Deviation

Normalised standard deviation (NSD) standardises the values of SDs. The ranges of NSD varies from zero to one [75].
N S D = Standard   Deviation   of   gridded   rainfall Standard   Deviation   of   observed   rainfall

Appendix B

Appendix B.1. Mann–Kendall

The MK test [76,77] computes S statistics as:
S = ∑ k = 1 n − 1 ∑ j = k − 1 n s g n ( x j − x k )
where S = normal distribution with the mean, n = number of observation ( ≥ 10) and xj is the jth observation and sgn () is the sign function, defined as sgn (θ) = 1 if θ > 0; sgn (θ) = 0 if θ = 0; and sgn (θ) = −1 if θ < 0 [78].
As per the autocorrelation result, all selected datasets are individually independent and normally distributed, then mean and variance of S statistics are given by Kendall, [77], Basistha et al. [13].
E(S) = 0
Var [ S ] = ( n ( n − 1 ) ( 2 n + 5 ) − ∑ t t ( t − 1 ) ( 2 t + 5 ) ) / 18
where n = number of groups of tried ranks, each with ti tied observations and t = limitation of the data in any given nexus. The actual MK statistic, designed by Z, can computed as:
Z = { s − 1 [ v a r ( s ) ] 1 2 } , If S > 0
Z = 0, if S = 0
Z = { s + 1 [ v a r ( s ) ] 1 2 } , If S < 0
Theoretically: if the statistic value lies within ±1.96 (alpha ≤ 0.05) then there is no statistically significant trend at the 95% significance level and vice-a-versa [79]. Two hypotheses are made, i.e., H0 (null hypothesis) and H1 (alternative hypothesis). H0 indicates no statistically significant trend, while H1 indicates a statistically significant trend [80].

Appendix B.2. Sen.’s Slope Estimation

Identification of magnitude in any particular dataset is known as Sen.’s slope [81]. This is a simple linear regression method, which can estimate the slope of the median of two different variables (dependent and independent). The slope of in the data series can be estimated on following equation:
d i j k = X i j − x i k j − k
where xij and xik are the data value, j and k are the time series.

References

  1. Bhatt, D.; Maskey, S.; Babel, M.S.; Uhlenbrook, S.; Prasad, K.C. Climate trends and impacts on crop production in the Koshi river basin of Nepal. Reg. Environ. Chang. 2014, 14, 1291–1301. [Google Scholar] [CrossRef] [Green Version]
  2. Gaddam, V.K.; Kulkarni, A.V.; Gupta, A.K. Assessment of snow-glacier melt and rainfall contribution to stream runoff in Baspa Basin, Indian Himalaya. Environ. Monit. Assess. 2018, 190, 154. [Google Scholar] [CrossRef] [PubMed]
  3. Chakraborty, A.; Saha, S.; Sachdeva, K.; Joshi, P.K. Vulnerability of forests in the Himalayan region to climate change impacts and anthropogenic disturbances: A systematic review. Reg. Environ. Chang. 2018, 18, 1783–1799. [Google Scholar] [CrossRef]
  4. Kishore, P.; Jyothi, S.; Basha, G.; Rao, S.V.B.; Rajeevan, M.; Velicogna, I.; Sutterley, T.C. Precipitation climatology over India: Validation with observations and reanalysis darasets and spatial trends. Clim. Dyn. 2016, 46, 541–556. [Google Scholar] [CrossRef] [Green Version]
  5. Shekhar, M.S.; Chand, H.; Kumar, S.; Srinivasan, K.; Ganju, A. Climate-change studies in the western Himalaya. Ann. Glaciol. 2010, 51, 315–322. [Google Scholar] [CrossRef] [Green Version]
  6. Mishra, B.; Babel, M.; Tripathi, N.K. Analysis of climate variability and snow cover in the Kaligandaki river basin, Himalaya, Nepal. Theor. Appl. Climatol. 2014, 116, 681–694. [Google Scholar] [CrossRef]
  7. Hoy, A.; Katel, O.; Thapa, P.; Dendup, N. Climate change and their impact on socio-economic sectors in the Bhutan Himalaya: An implementation strategy. Reg. Environ. Chang. 2016, 16, 1401–1415. [Google Scholar] [CrossRef]
  8. Meybeck, M.; Green, P.; Vorosmarty, C. A new topology for mountains and other relief classes. Mt. Res. Dev. 2001, 21, 34–45. [Google Scholar] [CrossRef] [Green Version]
  9. Hartmann, D.L.; Klein Tank, A.M.G.; Rusticucci, M.; Alexander, L.V.; Brönnimann, S.; Charabi, Y.; Dentener, F.J.; Dlugokencky, E.J.; Easterling, D.R.; Kaplan, A.; et al. Observations: Atmosphere and surface. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013; pp. 159–254. [Google Scholar] [CrossRef] [Green Version]
  10. Yadav, R.R. Tree ring evidence of a 20th century precipitation surge in the monsoon shadow zone of the western Himalaya, India. J. Geophys. Res. 2011, 116. [Google Scholar] [CrossRef]
  11. Bhutiyani, M.R.; Kale, S.V.; Pawar, J.N. Long-term trends in maximum, minimum and mean annual air temperatures across the Northwestern Himalaya during the twentieth century. Clim. Chang. 2007, 85, 159–177. [Google Scholar] [CrossRef]
  12. Dash, S.K.; Hunt, J.C.R. Variability of climate change in India. Curr. Sci. 2007, 93, 782–788. [Google Scholar]
  13. Basistha, A.; Arya, D.S.; Goel, N.K. Analysis of historical changes in rainfall in the Indian Himalayas. Int. J. Climatol. 2009, 29, 555–572. [Google Scholar] [CrossRef]
  14. Pal, I.; Al-Tabbaa, A. Long-term changes and variability of monthly extreme temperatures in India. Theor. Appl. Climatol. 2010, 100, 45–56. [Google Scholar] [CrossRef]
  15. Ramesh, K.V.; Goswami, P. Reduction in temporal and spatial extent of the Indian summer monsoon. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
  16. Kumar, V.; Jain, S.K. Trends in rainfall amount and number of rainy days in river basins of India (1951–2004). Hydrol. Res. 2011, 42, 290. [Google Scholar] [CrossRef]
  17. Das, P.K.; Chakraborty, A.; Seshasai, M.V.R. Spatial analysis of temporal trend of rainfall and rainy days during the Indian Summer Monsoon season using daily gridded (0.5° × 0.5°) rainfall data for the period of 1971–2005. Meteorol. Appl. 2014, 21, 481–493. [Google Scholar] [CrossRef]
  18. Allen, S.; Rastner, P.; Arora, M.; Huggel, C.; Stoffel, M. Lake outburst and debris flow disaster at Kedarnath, June 2013: Hydro meteorological triggering and topographic predisposition. Landslides 2015, 13, 1479–1491. [Google Scholar] [CrossRef]
  19. Wang, Z.; Zhong, R.; Lai, C.; Chen, J. Evaluation of the GPM IMERG satellite-based precipitation products and the hydrological utility. Atmos. Res. 2017, 196, 151–163. [Google Scholar] [CrossRef]
  20. Mei, Y.W.; Anagnostou, E.N.; Nikolopoulos, E.I.; Borga, M. Error analysis of satellite precipitation products in mountainous basins. J. Hydrometeorol. 2014, 15, 1778–1793. [Google Scholar] [CrossRef]
  21. Guo, H.; Chen, S.; Bao, A.; Behrangi, A.; Hong, Y.; Ndayisaba, F.; Hu, J.; Stepanian, P.M. Early assessment of integrated multi-satellite retrievals for global precipitation measurement over China. Atmos. Res. 2016, 176–177, 121–133. [Google Scholar] [CrossRef]
  22. Sharifi, E.; Steinacker, R.; Saghafian, B. Assessment of GPM-IMERG and other precipitation products against gauge data under different topographic and climatic conditions in Iran: Preliminary results. Remote Sens. 2016, 8, 135. [Google Scholar] [CrossRef] [Green Version]
  23. Sidhu, N.; Pebesma, E.; Camara, G. Using Google Earth Engine to detect land cover change: Singapore as a use case. Eur. J. Remote Sens. 2018, 51, 486–500. [Google Scholar] [CrossRef]
  24. District Census Handbook. Village and Town Directory, Tehri Garhwal. Directorate of Census Operations, Uttarakhand; 2011; Series-06, Part XII-A; Dehradun, Uttarakhand. Available online: http://www.censusindia.gov.in (accessed on 2 December 2019).
  25. Auden, J.B. Director’s General Report of 1935. Rec. Geol. Surv. India Calcutta 1936, 71, 73–75. [Google Scholar]
  26. Agarwal, N.C.; Kumar, G. Geology of the upper Bhagirathi and Yamuna Valleys, Uttarakashi District, Kumaun Himalaya. Himal. Geol. 1973, 3, 1–23. [Google Scholar]
  27. Dasgupta, S.; Mazumdar, K.; Pande, P.; Sanyal, S. Seismotectonic Atlas of Indian and Its Environs; Geological Survey of India: Kolkata, India, 2000.
  28. Banerjee, A.; Singh, R.B.; Mal, S. Assessment of landslide hazards in mountainous terrain: A case study of Bhilangana river basin, Uttarakhand Himalaya. Hill Geog. 2018, 34, 51–61. [Google Scholar]
  29. Dimri, A.P.; Chevuturi, A.; Niyogi, D.; Thayyen, R.J.; Ray, K.; Tripathi, S.N.; Pandey, A.K.; Mohanty, U.C. Cloudbursts in Indian Himalaya: A review. Earth Sci. Rev. 2017, 168, 1–23. [Google Scholar] [CrossRef]
  30. Lopez-Carr, D.; Pricope, N.G.; Aukema, J.E.; Jankowska, M.M.; Funk, C.; Husak, G.; Michaelsen, J. A spatial analysis of population dynamics and climate change in Africa: Potential vulnerability hot spots emerge where precipitation declines and demographic presuures coincide. Popul. Environ. 2014, 35, 323–339. [Google Scholar] [CrossRef]
  31. Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, J.; Hoell, A.; et al. The climate hazards infrared precipitation with stations—A new environmental record for monitoring extremes. Sci. Data 2015, 2, 1–21. [Google Scholar] [CrossRef] [Green Version]
  32. Hussain, Y.; Satge, F.; Hussain, M.B.; Carvajal, H.M.; Bonnet, M.P.; Soto, M.C.; Roig, H.L.; Akhter, G. Performance of CMORPH, TMPA and PERSIANN rainfall datasets over plain, mountains, and glacial regions of Pakistan. Theor. Appl. Climatol. 2017. [Google Scholar] [CrossRef]
  33. Ullah, W.; Wang, G.; Ali, G.; Hagan, D.F.T.; Bhatti, A.S.; Lou, D. Comparing multiple precipitation products against in situ observations over different climate regions of Pakistan. Remote Sens. 2018, 11, 628. [Google Scholar] [CrossRef] [Green Version]
  34. Prakash, S. Performance assessment of CHIRPS, MSWEP, SM2RAIN-CCI, and TMPA precipitation products across India. J. Hydrol. 2019, 57, 50–59. [Google Scholar] [CrossRef]
  35. Beck, H.E.; Vergopolan, N.; Pan, M.; Levizzani, V.; Albert, I.J.M.; Dijk, V.; Weedon, G.P.; Brocca, L.; Pappenberger, F.; Huffman, G.J.; et al. Global-scale evaluation of 22 precipitation datasets using gauge observations and hydrological modelling. Hydrol. Earth Syst. Sci. 2019, 21, 6201–6217. [Google Scholar] [CrossRef] [Green Version]
  36. Guo, H.; Chen, S.; Bao, A.; Hu, J.; Gebregiorgis, A.; Xue, X.; Zhang, X. Inter-comparison of high-resolution satellite precipitation products over Central Asia. Remote Sens. 2015, 7, 7181–7211. [Google Scholar] [CrossRef] [Green Version]
  37. Yang, X.; Yong, B.; Hong, Y.; Chen, S.; Zhang, X. Error analysis of multi-satellite precipitation estimates with an independent rain gauge observation network over a medium-sized humid basin. Hydrol. Sci. J. 2016, 61, 1813–1830. [Google Scholar] [CrossRef]
  38. Ashouri, H.; Nguyen, P.; Thorstensen, A.; Hsu, K.L.; Sorooshian, S.; Braithwaite, D. Assessing the efficacy of high-resolution satellite-based PERSIANN-CDR precipitation product in simulating streamflow. J. Hydrometeorol. 2016, 17, 2061–2076. [Google Scholar] [CrossRef]
  39. Mondal, A.; Lakshmi, V.; Hashemi, H. Intercomparison of trend analysis of multisatellite monthly precipitation products and gauge measurements for river basins of India. J. Hydrol. 2018, 565, 779–790. [Google Scholar] [CrossRef]
  40. Gorelick, N.; Hancher, M.; Dixon, M.; Llyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
  41. Vos, K.; Splinter, K.D.; Harley, M.D.; Joshua, A.S.; Turner, S.I. CoastSat: A Google Earth Engine-enabled Python toolkit to extract shorelines from publicly available satellite imagery. Environ. Model. Softw. 2019, 122, 104528. [Google Scholar] [CrossRef]
  42. Singh, R.B.; Mal, S. Trend and variability of monsoon and other rainfall seasons in Western Himalaya, India. Atmos. Sci. Lett. 2014, 15, 218–226. [Google Scholar] [CrossRef]
  43. Hamed, K.H.; Rao, A.R. A modified Mann-Kendall trend test for auto correlated data. J. Hydrol. 1998, 204, 182–196. [Google Scholar] [CrossRef]
  44. Kumar, M.; Denis, D.M.; Suryavanshi, S. Long-term climatic trend analysis of Giridih district, Jharkhand (India) using statistical approach. Model Earth Syst. Environ. 2016, 2, 116. [Google Scholar] [CrossRef] [Green Version]
  45. Zelenakova, M.; Vido, J.; Portela, M.M.; Purcz, P.; Blistan, H.H.; Hlustik, P. Precipitation trend over Slovakia in the period 1981–2013. Water 2017, 9, 922. [Google Scholar] [CrossRef] [Green Version]
  46. Anjum, M.N.; Ding, Y.; Shangguan, D.; Ahmad, I.; Ijaz, M.W.; Farid, H.U.; Yagoub, Y.E.; Zaman, M. Performance evalution of latest integrated multi-satellite retrievals for Global Precipitation Measurement (IMERG) over northern highlands of Pakistan. Atmos. Res. 2018, 205, 134–146. [Google Scholar] [CrossRef]
  47. Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
  48. Archer, D.R.; Fowler, H.J. Spatial and temporal variations in precipitation in the upper Indus Basin, global teleconnections and hydrological implications. Hydrol. Earth Syst. Sci. 2004, 8, 47–61. [Google Scholar] [CrossRef] [Green Version]
  49. Dimri, A.P.; Niyogi, D. Regional climate model application at subgrid scale on Indian winter monsoon over the western Himalaya. Int. J. Climatol. 2013, 33, 2185–2205. [Google Scholar] [CrossRef]
  50. Palazzi, E.; Hardeberg, J.V.; Provenzale, A. Precipitation in the Hindu-Kush Karakoram Himalaya: Bbservations and future scenarios. J. Geophys. Res. Atmos. 2013, 118, 85–100. [Google Scholar] [CrossRef]
  51. Paranjpye, V. (Ed.) Evaluating the Tehri Dam: An Extended Cost-Benefit Appraisal. In Indian National Trust for Art and Culture; Indian National Trust for Art and Cultural Heritage: New Delhi, India, 1988; ISBN 10: 819000610X. [Google Scholar]
  52. Sinha, B.K.; Pokhriyal, H.C. Rehabilitation in Tehri Dam: An evaluation. Soc. Chang. 2001, 31, 110–143. [Google Scholar] [CrossRef]
  53. Randhawa, M.S. (Ed.) A History of Agriculture in India. In Indian Council of Agricultural Research; Indian Council of Agricultural Research: New Delhi, India, 1986; Volume IV, Record Number 19846751450. [Google Scholar]
  54. Joshi, S.; Kumar, K.; Joshi, V.; Pande, B. Rainfall variability and indices of extreme rainfall-analysis and perception study for two stations over Central Himalaya, India. Nat. Hazards 2014, 72, 361–374. [Google Scholar] [CrossRef]
  55. Kumar, N.; Yadav, B.P.; Gahlot, S.; Singh, M. Winter frequency of western disturbances and precipitation indices over Himachal Pradesh, India: 1977–2007. Atmósfera 2015, 28, 63–70. [Google Scholar] [CrossRef]
  56. Gupta, R.P.; Haritashya, U.K.; Singh, P. Mapping dry/wet snow cover in the Indian Himalaya using IRS multispectral imagery. Remote Sens. Environ. 2005, 97, 458–469. [Google Scholar] [CrossRef]
  57. Baines, P.G. The late 1960s Global Climate Shift and its influence on the Southern Hemisphere. In Proceedings of the 8 ICSHMO, Foz do Iguaçu, Brazil, 24–28 April 2006; pp. 1477–1482. [Google Scholar]
  58. Lhara, C.; Kushnir, Y.; Cane, M.A.; Pene, V.D.L. Indian summer monsoon rainfall and its link with ENSO and Indian Ocean climate indices. Int. J. Climatol. 2007, 27, 179–187. [Google Scholar] [CrossRef]
  59. Li, H.; Haugen, J.E.; Xu, C.Y. Precipitation pattern in the Western Himalayas revealed by four datasets. Hydrol. Earth Syst. Sci. 2018, 22, 5097–5110. [Google Scholar] [CrossRef] [Green Version]
  60. Bollasina, M.A.; Ming, Y.; Ramaswamy, V. Anthropogenic Aerosols and the Weakening of the South Asian Summer Monsoon. Science 2011, 334, 502–505. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  61. Chiao, S.; Lin, Y.L.; Kaplan, M.L. Numerical study of orographic forcing of heavy precipitation during MAP IOP-2B. Mon. Weather Rev. 2004, 132, 2184–2203. [Google Scholar] [CrossRef]
  62. Barros, A.P.; Kim, G.; Williams, E.; Nesbitt, S.W. Probing orographic controls in the Himalayas during the monsoon using satellite imagery. Nat. Hazards Earth Syst. Sci. 2004, 4, 29–51. [Google Scholar] [CrossRef] [Green Version]
  63. Chen, J.; Li, C.; He, G. A diagnostic analysis of the impact of complex terrain in the Eastern Tibetan Plateau, China, on a severe storm, Arctic. Arct. Antarct. Alp. Res. 2007, 39, 699–707. [Google Scholar] [CrossRef] [Green Version]
  64. Medina, S.; Houze, R.A., Jr.; Kumar, A.; Niyogi, D. Summer monsoon convection in the Himalayan region: Terrain and land cover effects. Q. J. R. Meteorol. Soc. 2010, 136, 593–616. [Google Scholar] [CrossRef] [Green Version]
  65. Bhardwaj, A.; Ziegler, A.D.; Wasson, R.J.; Chow, W.T.L. Accuracy of rainfall estimates at high altitude in the Garhwal Himalaya (India): A comparison of secondary precipitation products and station rainfall measurements. Atmos. Res. 2017, 188, 30–38. [Google Scholar] [CrossRef]
  66. Bhuiyan, M.A.E.; Nikolopoulos, E.I.; Anagnostou, E.N.; Pere, Q.S.; Ortiz, A.B. A nonparametric statistical technique for combining global precipitation datasets: Development and hydrological evaluation over the Iberian Peninsula. Hydrol. Earth Syst. Sci. 2018, 22, 1371–1389. [Google Scholar] [CrossRef] [Green Version]
  67. Ba, K.M.; Balcazar, L.; Diaz, V.; Qrtiz, F.; Miguel, A.G.; Carlos, D.D. Hydrological evaluation of PERSIANN-CDR rainfall over Upper Senegal River and Bani River basins. Remote Sens. 2018, 10, 1884. [Google Scholar] [CrossRef] [Green Version]
  68. Liu, J.; Xu, Z.; Junrui, B.; Peng, D.; Ren, M. Assessment and correction of the PERSIANN-CDR product in the Yarlung Zangbo River basin, China. Remote Sens. 2018, 10, 2031. [Google Scholar] [CrossRef] [Green Version]
  69. Sun, S.; Zhou, S.; Shen, H.; Chai, R.; Chen, H.; Liu, Y.; Shi, W.; Wang, J.; Wang, G.; Zhou, Y. Dissecting performance of PERSIANN-CDR precipitation product over Huai River basin, China. Remote Sens. 2019, 11, 1805. [Google Scholar] [CrossRef] [Green Version]
  70. Romatschke, U. Regional, seasonal, and diurnal variations of extreme convection in the south Asian region. J. Clim. 2010, 23, 419–439. [Google Scholar] [CrossRef] [Green Version]
  71. Bharti, V.; Singh, C. Evaluation of error in TRMM 3B42V7 precipitation estimates over the Himalaya region. J. Geophy. Res. Atmos. 2015, 120, 458–473. [Google Scholar] [CrossRef]
  72. IPCC. 2013: Climate Change 2013: The Physical Science Basis. In Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013; p. 1535. [Google Scholar] [CrossRef] [Green Version]
  73. Lutz, A.F.; Immerzeel, W.W.; Shrestha, A.B.; Bierkens, M.F.P. Consistent increase in High Asia’s runoff due to increasing glacier melt and precipitation. Nat. Clim. Chang. 2014, 4, 587–592. [Google Scholar] [CrossRef] [Green Version]
  74. Apollo, M. The population of Himalayan regions—By the numbers: Past, present and future. In Contemporary Studies in Environment and Tourism; Efe, R., Ozturk, M., Eds.; Cambridge Scholar Publishing: Cambridge, UK, 2017; pp. 145–159. ISBN 978-1-4438-7283-6. [Google Scholar]
  75. Sharma, C.; Ojha, C.S.P.; Shukla, A.K.; Pham, Q.B.; Linh, N.T.T.; Fai, C.M.; Ho, H.L.; Dung, T.D. Modified approach to reduce GCM bias in downscaled Precipitation: A study in Ganga River basin. Water 2019, 11, 2097. [Google Scholar] [CrossRef] [Green Version]
  76. Maan, H.B. Non-parametric tests against trend. Econometrica 1945, 33, 245–259. [Google Scholar] [CrossRef]
  77. Kendall, M.G. Rank Correlation Method, 4th ed.; Charles Griffin: London, UK, 1975. [Google Scholar]
  78. Jhajharia, D.; Dinpashoh, Y.; Kahya, E.; Chowdhury, R.R.; Singh, P.V. Trends in temperature over Godavari River basin in Southern Peninsular India. Int. J. Climatol. 2014, 34, 1369–1384. [Google Scholar] [CrossRef]
  79. Jhajharia, D.; Singh, P.V. Trends in temperature, diurnal temperature range and sunshine duration in Northeast India. Int. J. Climatol. 2011, 31, 1353–1367. [Google Scholar] [CrossRef]
  80. Drapela, K.; Drapelova, I. Application of Mann-Kendall test and the Sen’s slope estimates for trend detection in deposition data from Bily Kriz (Beskydy Mts, the Czech Republic) 1997–2010. Beskydy 2011, 4, 133–146. [Google Scholar]
  81. Sen, P.K. Estimates of the regression coefficient based on Kendall’s tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
Remotesensing 12 00709 g001 550
Figure 1. Location of the Bhilangana river basin in Uttarakhand, India. The IMD meteorological observatories and major settlements in the study region are indicated by blue and red solid triangles respectively. The background image is ASTER GDEMV2, derived from USGS.
Figure 1. Location of the Bhilangana river basin in Uttarakhand, India. The IMD meteorological observatories and major settlements in the study region are indicated by blue and red solid triangles respectively. The background image is ASTER GDEMV2, derived from USGS.
Remotesensing 12 00709 g001
Remotesensing 12 00709 g002 550
Figure 2. Spatial distribution of mean annual and seasonal rainfall (mm). Top panel distribution is from reanalysis and bottom panel from satellite-based gridded datasets derived using GEE.
Figure 2. Spatial distribution of mean annual and seasonal rainfall (mm). Top panel distribution is from reanalysis and bottom panel from satellite-based gridded datasets derived using GEE.
Remotesensing 12 00709 g002
Remotesensing 12 00709 g003 550
Figure 3. Mean distribution and variance of station-based and gridded rainfall products. Annual, seasonal (a,c), monthly (b,d) rainfall and variance, respectively for the period from 1983 to 2008.
Figure 3. Mean distribution and variance of station-based and gridded rainfall products. Annual, seasonal (a,c), monthly (b,d) rainfall and variance, respectively for the period from 1983 to 2008.
Remotesensing 12 00709 g003
Remotesensing 12 00709 g004 550
Figure 4. (a–c) are showing the relationship between the gridded and observed datasets (r2), (d) Bias, (e) RMSE and (f) CDF for all datasets with the corresponding station for the period from 1983 to 2008.
Figure 4. (a–c) are showing the relationship between the gridded and observed datasets (r2), (d) Bias, (e) RMSE and (f) CDF for all datasets with the corresponding station for the period from 1983 to 2008.
Remotesensing 12 00709 g004
Remotesensing 12 00709 g005 550
Figure 5. Spatial distribution of trends in annual and seasonal rainfall along with their statistical significance (1983–2008) (Top panel showing CHIRPS reanalysis and bottom PERSIANN-CDR satellite-based data products respectively).
Figure 5. Spatial distribution of trends in annual and seasonal rainfall along with their statistical significance (1983–2008) (Top panel showing CHIRPS reanalysis and bottom PERSIANN-CDR satellite-based data products respectively).
Remotesensing 12 00709 g005
Remotesensing 12 00709 g006 550
Figure 6. Spatial distribution of magnitude of trend in annual and seasonal rainfall, (Top panel showing a spatial tendency of CHIRPS and bottom panel PERSIANN-CDR data respectively).
Figure 6. Spatial distribution of magnitude of trend in annual and seasonal rainfall, (Top panel showing a spatial tendency of CHIRPS and bottom panel PERSIANN-CDR data respectively).
Remotesensing 12 00709 g006
Remotesensing 12 00709 g007 550
Figure 7. Long-term temporal distribution of monthly rainfall and annual magnitude of trends in mm/decade (a) monthly values from 1983 to 2018, (b) mean annual and seasonal rainfall for three distinct rainfall phases with error bars from 1983 to 2018 (c) box and whisker plots show monthly rainfall values from 2009 to 2018 (d,e) mean annual, seasonal and monthly rainfall of station observed data for two different time periods (1983–1997; 1998–2008).
Figure 7. Long-term temporal distribution of monthly rainfall and annual magnitude of trends in mm/decade (a) monthly values from 1983 to 2018, (b) mean annual and seasonal rainfall for three distinct rainfall phases with error bars from 1983 to 2018 (c) box and whisker plots show monthly rainfall values from 2009 to 2018 (d,e) mean annual, seasonal and monthly rainfall of station observed data for two different time periods (1983–1997; 1998–2008).
Remotesensing 12 00709 g007
Remotesensing 12 00709 g008 550
Figure 8. (a) Spatial distribution, (b) statistical significance level and (c) trends in annual and seasonal rainfall from 2009 to 2018 respectively. Top panel showing annual and seasonal rainfall distribution from 2009 to 2018, Middle panel indicate the level of significance (at 95% confidence level based on MK test), Bottom panel showing annual and seasonal trends of rainfall for the same period, where blue and red color indicates increasing and decreasing trends, respectively.
Figure 8. (a) Spatial distribution, (b) statistical significance level and (c) trends in annual and seasonal rainfall from 2009 to 2018 respectively. Top panel showing annual and seasonal rainfall distribution from 2009 to 2018, Middle panel indicate the level of significance (at 95% confidence level based on MK test), Bottom panel showing annual and seasonal trends of rainfall for the same period, where blue and red color indicates increasing and decreasing trends, respectively.
Remotesensing 12 00709 g008
Remotesensing 12 00709 g009 550
Figure 9. Taylor diagram compares observed and gridded datasets (Notations, “Jan to Dec” are used for defining months, “Ann to Win” for annual and seasons, “obs” for the observation stations and “C” and “P” denote CHIRPS and PERSIANN-CDR respectively).
Figure 9. Taylor diagram compares observed and gridded datasets (Notations, “Jan to Dec” are used for defining months, “Ann to Win” for annual and seasons, “obs” for the observation stations and “C” and “P” denote CHIRPS and PERSIANN-CDR respectively).
Remotesensing 12 00709 g009
Remotesensing 12 00709 g010 550
Figure 10. (a–d) Regional consequences of alternations in annual, seasonal and monthly rainfall pattern from 1983 to 2018. (a,b) show some effects of decreased rainfall; (c,d) the state of property after a major rainfall event. Localities of photos a-d are shown in Figure 1. Photos: A.B.
Figure 10. (a–d) Regional consequences of alternations in annual, seasonal and monthly rainfall pattern from 1983 to 2018. (a,b) show some effects of decreased rainfall; (c,d) the state of property after a major rainfall event. Localities of photos a-d are shown in Figure 1. Photos: A.B.
Remotesensing 12 00709 g010
Table
Table 1. Data used to estimate long-term rainfall variability in the Bhilangana river basin.
Table 1. Data used to estimate long-term rainfall variability in the Bhilangana river basin.
Station Observed Data (Collected from IMD)
StationLocationPeriodElevation (m)Available Observations (%)
Lat.Long.
Mukhem30.3478.281983–2008198195.8
Tehri30.2278.261983–200867691.3
Narendra Nagar30.0978.171983–2008103781.3
Gridded Data (Downloaded through Google Earth Engine Platform)
Data productYearSourceGrid Spacing
CHIRPS1983–2018UCSB/CHG0.05 arc degree
PERSIANN-CDR1983–2008NOAA/NCDC0.25 arc degree
Table
Table 2. Mean annual, seasonal, and monthly distribution of station and gridded datasets in the Bhilangana river basin for the period from 1983 to 2008.
Table 2. Mean annual, seasonal, and monthly distribution of station and gridded datasets in the Bhilangana river basin for the period from 1983 to 2008.
DataJANFEBMARAPRMAYJUNJULAUGSEPTOCTNOVDEC
Station63.778.366.850.671.3112.3227.9223.8144.540.010.330.3
CHIRPS36.827.135.417.446.190.0290.6263.8141.023.65.420.8
PERSIANN-CDR55.754.940.431.736.1140.5347.1410.5201.542.413.428.1
DataAnnualPre-monsoonMonsoonPost-monsoonWinter
Station1313.4154.31014.848.396.0
CHIRPS1119.7188.7708.650.3172.3
PERSIANN-CDR998.098.9785.429.187.7
Table
Table 3. Statistical indices to check the spatial similarity between observed and gridded datasets (CHIRPS and PERSIANN-CDR) for the period from 1983 to 2008.
Table 3. Statistical indices to check the spatial similarity between observed and gridded datasets (CHIRPS and PERSIANN-CDR) for the period from 1983 to 2008.
Statistical Indices with UnitsCHIRPSPERSIANN-CDR
TehriN.NagarMukhimTehriN.NagarMukhim
RMSE (mm)29.6024.6621.5881.2496.20111.30
MAE (mm)30.2026.3166.5449.7683.0966.54
Bias (mm)4.596.269.8816.88−23.4−29.5
MBias (mm)0.930.991.620.772.111.61
RBias (%)0.060.080.410.290.350.39
CC0.850.670.690.740.600.75
Table
Table 4. Annual and seasonal rainfall distributions and trends (1983–2008) in the Bhilangana river basin for ground station records.
Table 4. Annual and seasonal rainfall distributions and trends (1983–2008) in the Bhilangana river basin for ground station records.
StationSen.’s Slope (mm/decade)
AnnualMonsoonPost-MonsoonWinterPre-Monsoon
MukhimDistribution1473.71095.856.7169.9151.2
Trend−2.04−3.79−0.88−0.01−0.68
Tehri Distribution710.8469.922.2125.692.9
Trend−12.26−7.460.00−0.71−0.31
Narendra NagarDistribution1400.41249.929.565.555.5
Trend−32.82−22.37−0.82−2.56−0.95
Bold numbers are statistically significant (alpha ≤ 0.05).
Table
Table 5. Monthly rainfall distributions and trends in the Bhilangana river basin (mm/decade, 1983–2008) based on station observed data.
Table 5. Monthly rainfall distributions and trends in the Bhilangana river basin (mm/decade, 1983–2008) based on station observed data.
Station JANFEBMARAPRMAYJUNJULAUGSEPTOCTNOVDEC
MukhimDistribution56.281.553.842.854.6163.4342.9357.9231.745.011.732.3
Trend−0.340.710.200.420.42−0.31−0.700.620.10−0.600.000.00
TehriDistribution42.556.032.032.029.066.0159.8170.473.720.51.727.1
Trend−0.13−0.00−0.00−0.00−0.110.10−0.80−0.10−0.11−0.100.000.00
Narendra NagarDistribution43.729.223.326.528.0145.7382.7493.7296.230.533.139.6
Trend−0.62−0.42−0.700.00−0.30−0.91−8.43−12.40−2.92−0.510.000.00
Bold numbers are statistically significant (alpha ≤ 0.05).
Table
Table 6. Annual and seasonal trends in frequency of rainy days in the Bhilangana river basin (days/decade, 1983–2008).
Table 6. Annual and seasonal trends in frequency of rainy days in the Bhilangana river basin (days/decade, 1983–2008).
StationAnnualMonsoonPost-MonsoonWinterPre-Monsoon
Mukhim −6−8−2−10.00
Tehri−7−30.000.000.00
Narendra Nagar−9−110.0000.00
Bold numbers are statistically significant (alpha ≤ 0.05). Zero values represent no statistically significant trend.
Table
Table 7. Annual and seasonal rainfall trends in the Bhilangana river basin (mm/decade, 1983–2008).
Table 7. Annual and seasonal rainfall trends in the Bhilangana river basin (mm/decade, 1983–2008).
DataAnnualMonsoonPost-MonsoonWinterPre-Monsoon
CHIRPS−14.82−24.14−9.60−12.60−3.12
PERSIANN-CRD−6.91−5.12−0.71−2.91−1.32
Bold numbers are statistically significant (alpha ≤ 0.05).
Table
Table 8. Monthly rainfall trend of gridded datasets (mm/decade, 1983–2008).
Table 8. Monthly rainfall trend of gridded datasets (mm/decade, 1983–2008).
DATAJANFEBMARAPRMAYJUNJULAUGSEPTOCTNOVDEC
CHIRPS−1.08−0.51−1.130.12−1.60−3.10−9.42−9.44−5.71−0.81−0.30−0.42
PERSIANN-CDR−1.11−0.12−0.50−0.601.211.42−2.31−3.50−0.601.12−0.11−1.41
Bold numbers are statistically significant (alpha ≤ 0.05).
Table
Table 9. Monthly distribution, trends, and uncertainty (mm/ decade, 1983 to 2018).
Table 9. Monthly distribution, trends, and uncertainty (mm/ decade, 1983 to 2018).
DistributionJANFEBMARAPRMAYJUNJULAUGSEPTOCTNOVDEC
1983–2008 (CHIRPS)36.8227.1135.4417.4446.1189.90290.60263.83141.1123.615.6020.84
1983–2008 (Station)47.455.636.433.837.2125.0295.1340.6200.632.015.533.0
2009–2018 (CHIRPS)40.655.558.9135.6267.52161.62460.92434.82207.9236.333.912.42
Relative Uncertainty11.415.93.93.63.26.50.30.13.015.918.216.3
Sen’s slope using CHIRPS (2009–2018)0.79−2.12.911.613.697.546.09−2.02−8.21−1.88−0.06−1.18
Bold numbers are statistically significant (alpha ≤ 0.05).

Share and Cite

MDPI and ACS Style

Banerjee, A.; Chen, R.; E. Meadows, M.; Singh, R.B.; Mal, S.; Sengupta, D. An Analysis of Long-Term Rainfall Trends and Variability in the Uttarakhand Himalaya Using Google Earth Engine. Remote Sens. 2020, 12, 709. https://doi.org/10.3390/rs12040709

AMA Style

Banerjee A, Chen R, E. Meadows M, Singh RB, Mal S, Sengupta D. An Analysis of Long-Term Rainfall Trends and Variability in the Uttarakhand Himalaya Using Google Earth Engine. Remote Sensing. 2020; 12(4):709. https://doi.org/10.3390/rs12040709

Chicago/Turabian Style

Banerjee, Abhishek, Ruishan Chen, Michael E. Meadows, R.B. Singh, Suraj Mal, and Dhritiraj Sengupta. 2020. "An Analysis of Long-Term Rainfall Trends and Variability in the Uttarakhand Himalaya Using Google Earth Engine" Remote Sensing 12, no. 4: 709. https://doi.org/10.3390/rs12040709

APA Style

Banerjee, A., Chen, R., E. Meadows, M., Singh, R. B., Mal, S., & Sengupta, D. (2020). An Analysis of Long-Term Rainfall Trends and Variability in the Uttarakhand Himalaya Using Google Earth Engine. Remote Sensing, 12(4), 709. https://doi.org/10.3390/rs12040709

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop