An Assessment of the GOCE High-Level Processing Facility (HPF) Released Global Geopotential Models with Regional Test Results in Turkey
Abstract
1. Introduction
2. Materials and Methods
2.1. Practical Need of Global Geopotential Model Validation Results
2.2. Overview the Tested Global Geopotential Models
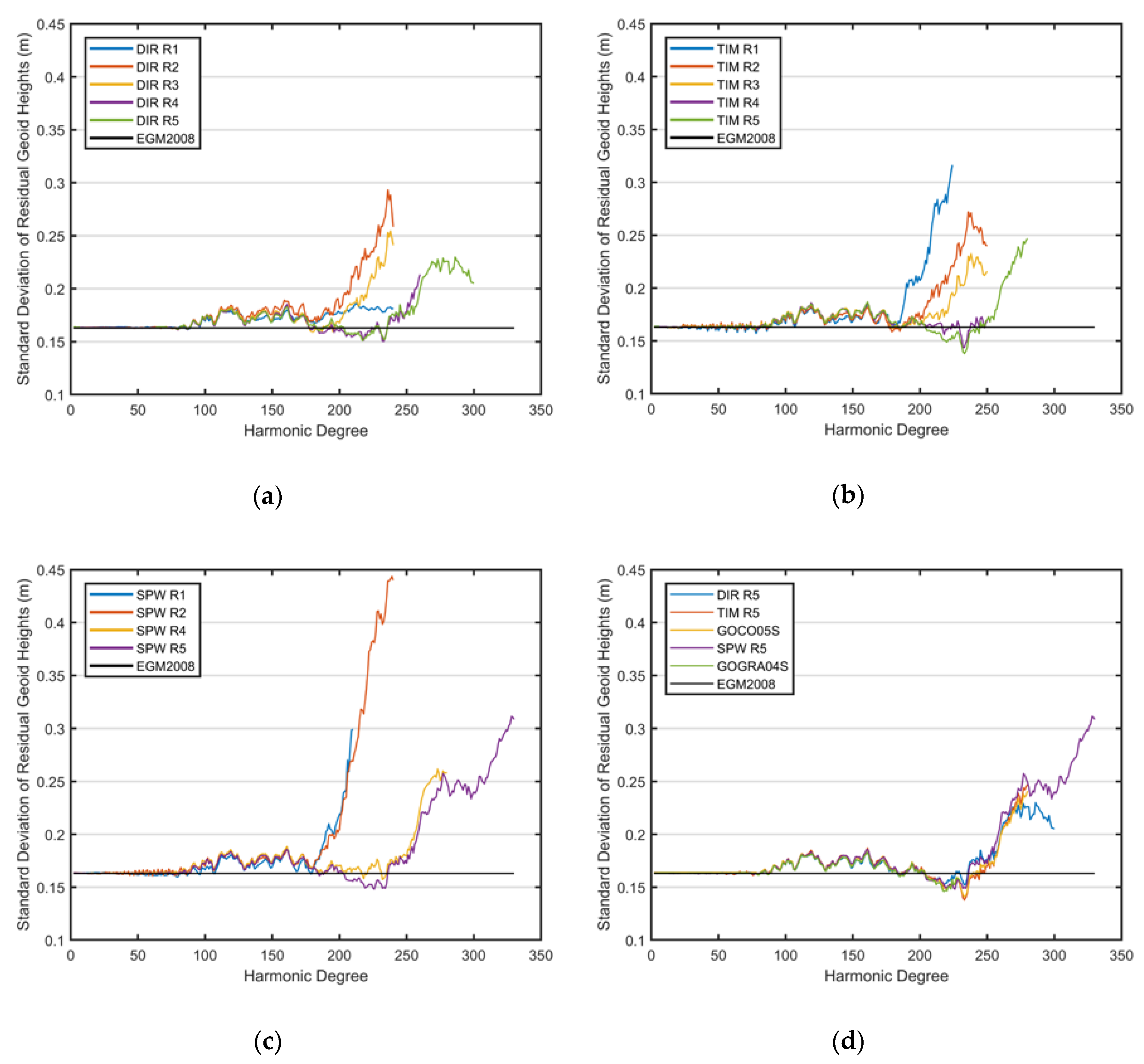
- DIR models contain GRACE observations in the lower to medium degrees of the expansions (in addition to GOCE gravity gradient data).
- As a priori gravity field information EIGEN5C (≤d/o 360) was introduced in DIR RL1, whereas the ITG-GRACE2010S (≤d/o 150) solution was the background model in RL2.
- In RL3, RL4 and RL5 models, GRACE was combined with GOCE and SLR data on the basis of the normal equations (including the SLR data (LAGEOS-1 and -2)) in order to improve the gravity field solution, since the very low-degree harmonics (in particular degrees 2 and 3) cannot be estimated with GRACE and GOCE data).
- In order to overcome the polar gap of GOCE’s observations caused by the orbit inclination of the satellite (inclined at 96.7° [18]), a spherical cap regularization (SCR) in accordance to [44] was applied using EIGEN-51C (≤d/o 240). In the later releases after RL1, the SCR was applied using GRACE and LAGEOS data. In the RL3, RL4, RL5 of DIR models, additionally, the predecessor release was used as a priori information (≤d/o 240, 260, 300, respectively, in the releases) and a Kaula regularization [44] was used beyond degrees 200 (for RL3, RL4) and 180 (for RL5).
- In the DIR RL1 solution, the gravity tensor elements, which are measured with GOCE on-board SGG, were accumulated with the relative weights of Txx 1.0, Tyy 0.5 and Tzz 1.0. They were equally weighted in combination for the releases after RL1. In RL4, RL5 and RL6 models, the off-diagonal tensor elements Txz were also included.
- In RL4 and RL5 models, the spectral bandwidth of the bandpass filter used to filter the SGG observations was extended by 1.7 MHz toward the lower frequency domain.
- Reference [16] notes that contrary to the TIM approach, the DIR approach employs the GOCE gravity gradient information as restricted in a certain spectral band, which is close to the gradiometer measurement bandwidth (5–100 MHz [45]). However, the filtering procedure in the TIM approach allows the use of information on the gradient observations over the entire spectrum.
- The TIM models were constrained using Kaula’s rule regularization applied to (near-) zonal coefficients, improving the signal-to-noise ratio (constraints for high degree coefficients).
- The off-diagonal tensor element Vxz was included in the models TIM RL3, RL4, RL5 and RL6. The stochastic models for the gravity gradient observations rely on optimum weighting based on variance component estimation.
- TIM RL6e includes additional terrestrial gravity field observations over GRACE’s polar gap areas (>83° S, N) [46].
- The SPW RL1 model includes the first GOCE quick-look model as the a priori information and the EGM2008 was used for error calibration of the estimated gravitational potential along the orbit that affects the low degrees of the solution. However, the later releases, RL2 and RL4, were not corrected using any a priori model, thus they are the GOCE-only models. EIGEN5C and EIGEN6C3stat models were respectively used in SPW RL2 and RL4 models’ computations for signal covariance modeling, in addition to FES2004 for ocean tide modeling.
- In all SPW models, the off-diagonal tensor elements Vxz were included.
2.3. Synthesis of the Gravity Field Parameters Using GGMs Spherical Harmonic Coefficients
2.4. Assessments of the Global Geopotential Models Using Spectral Enhancement Method (SEM)
2.5. Spectral Analysis of GGMs
2.6. GGMs’ Contribution in High-resolution Regional Geoid Modeling
3. Results and Discussion
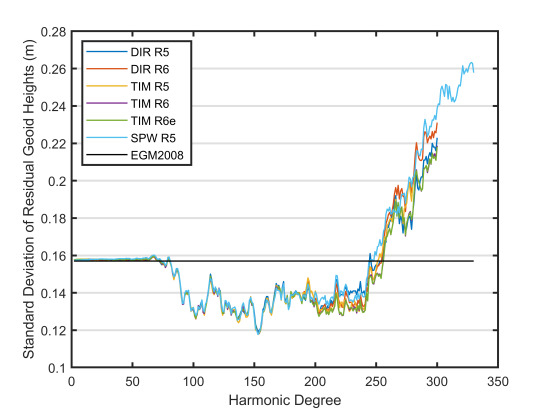
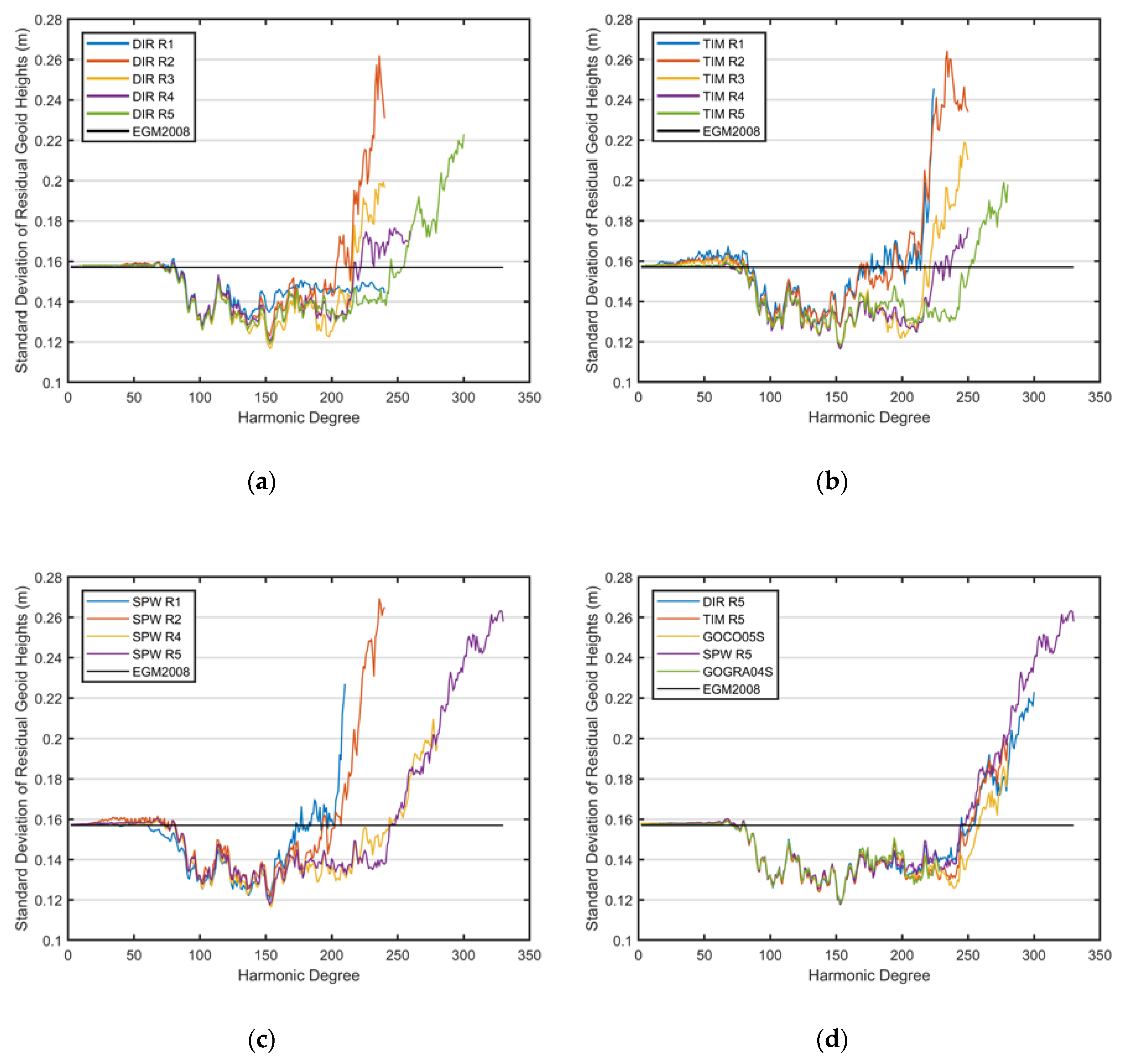
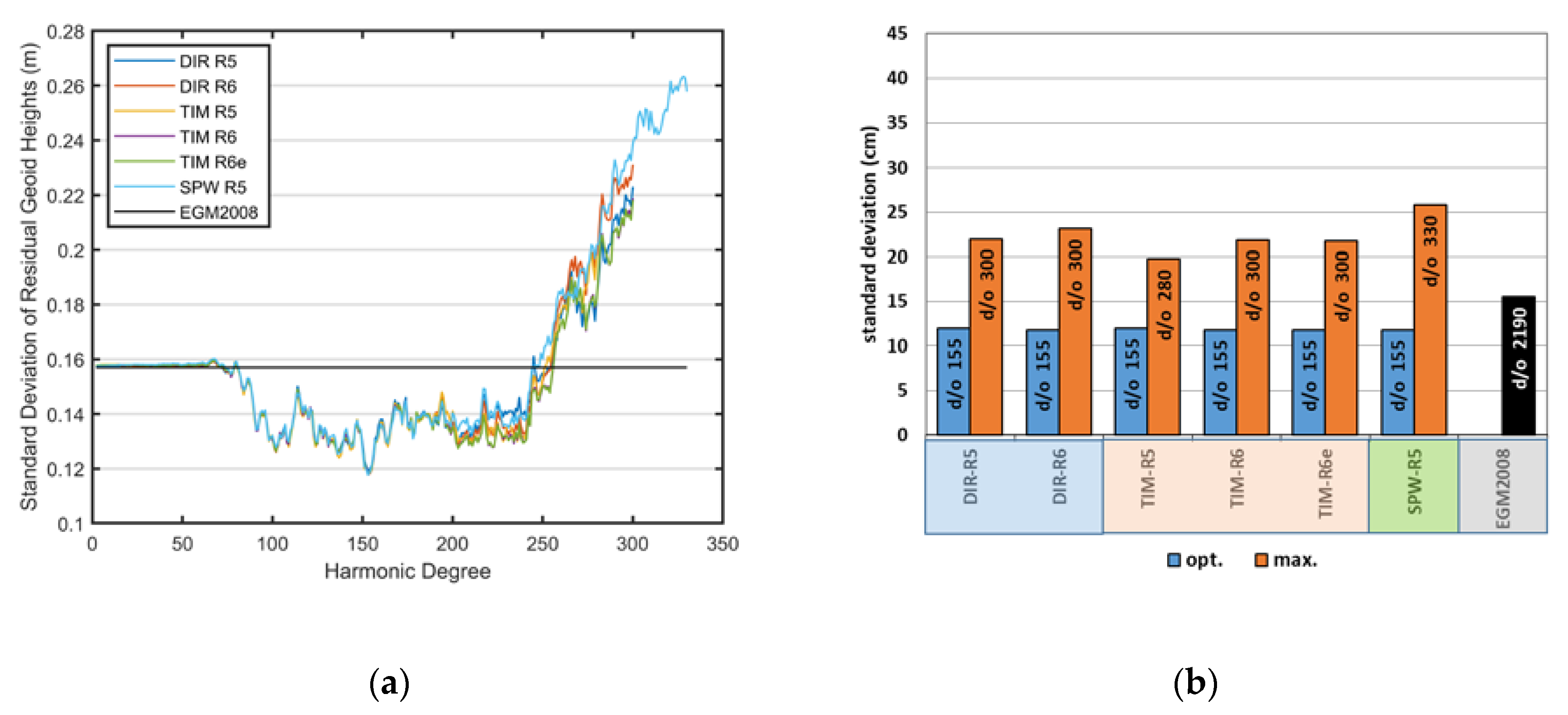
3.1. Internal Error Estimates of Tested GGMs
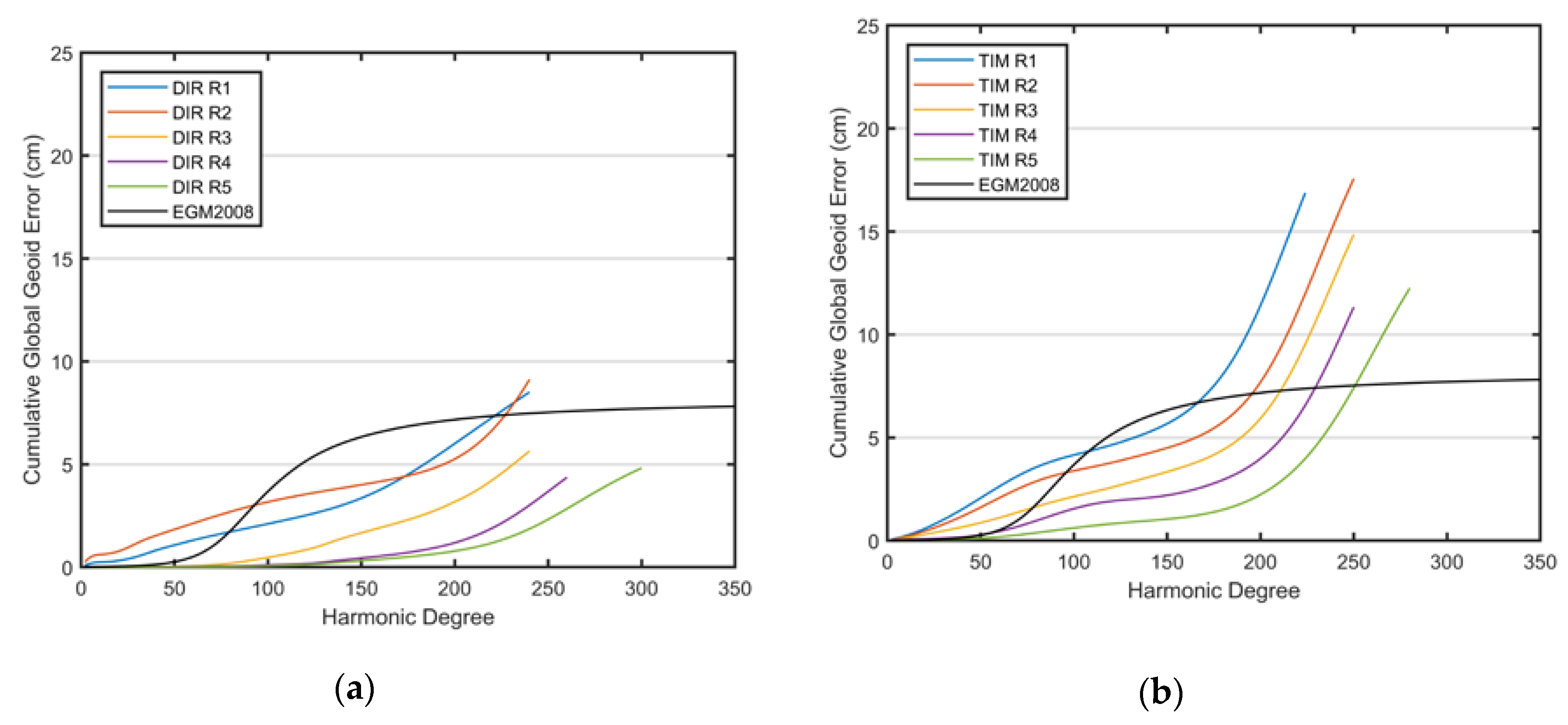
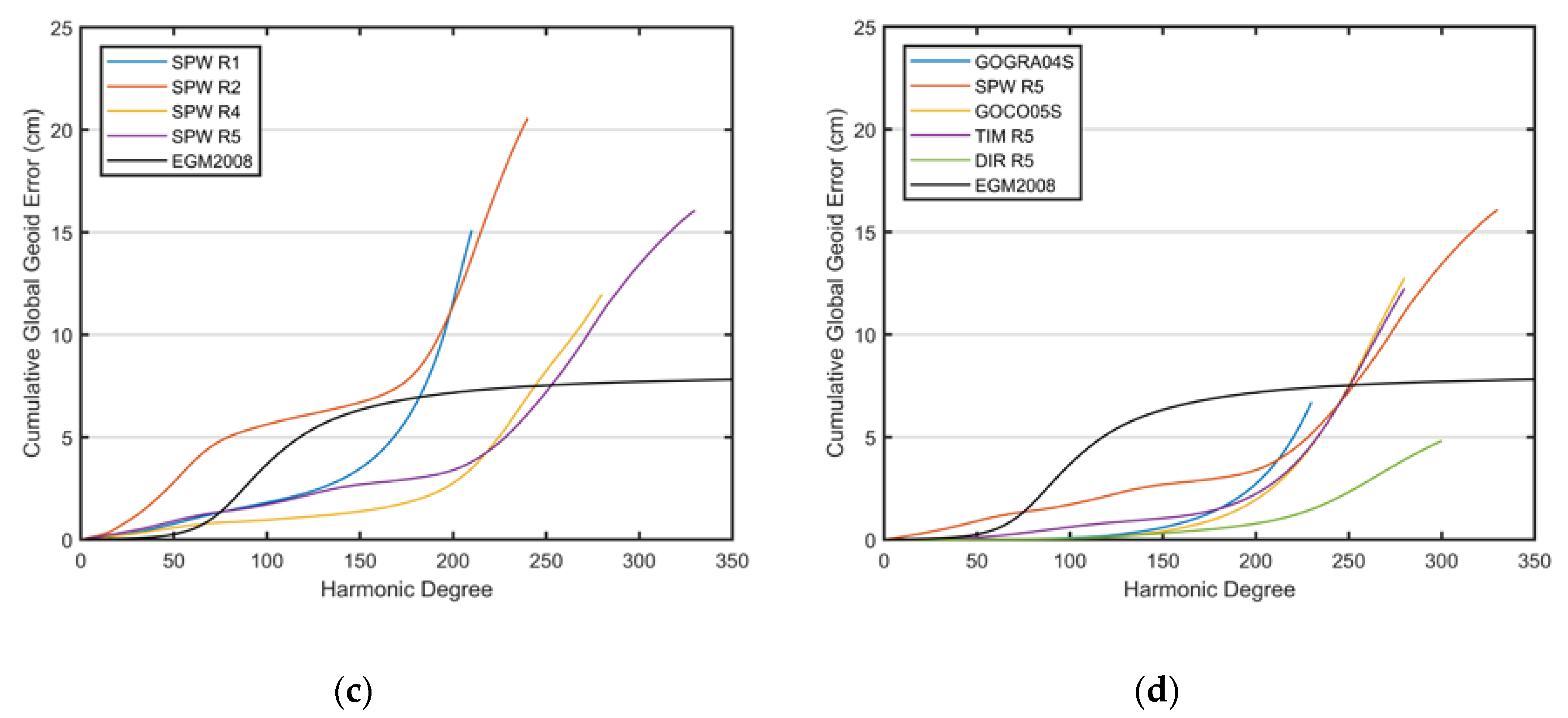
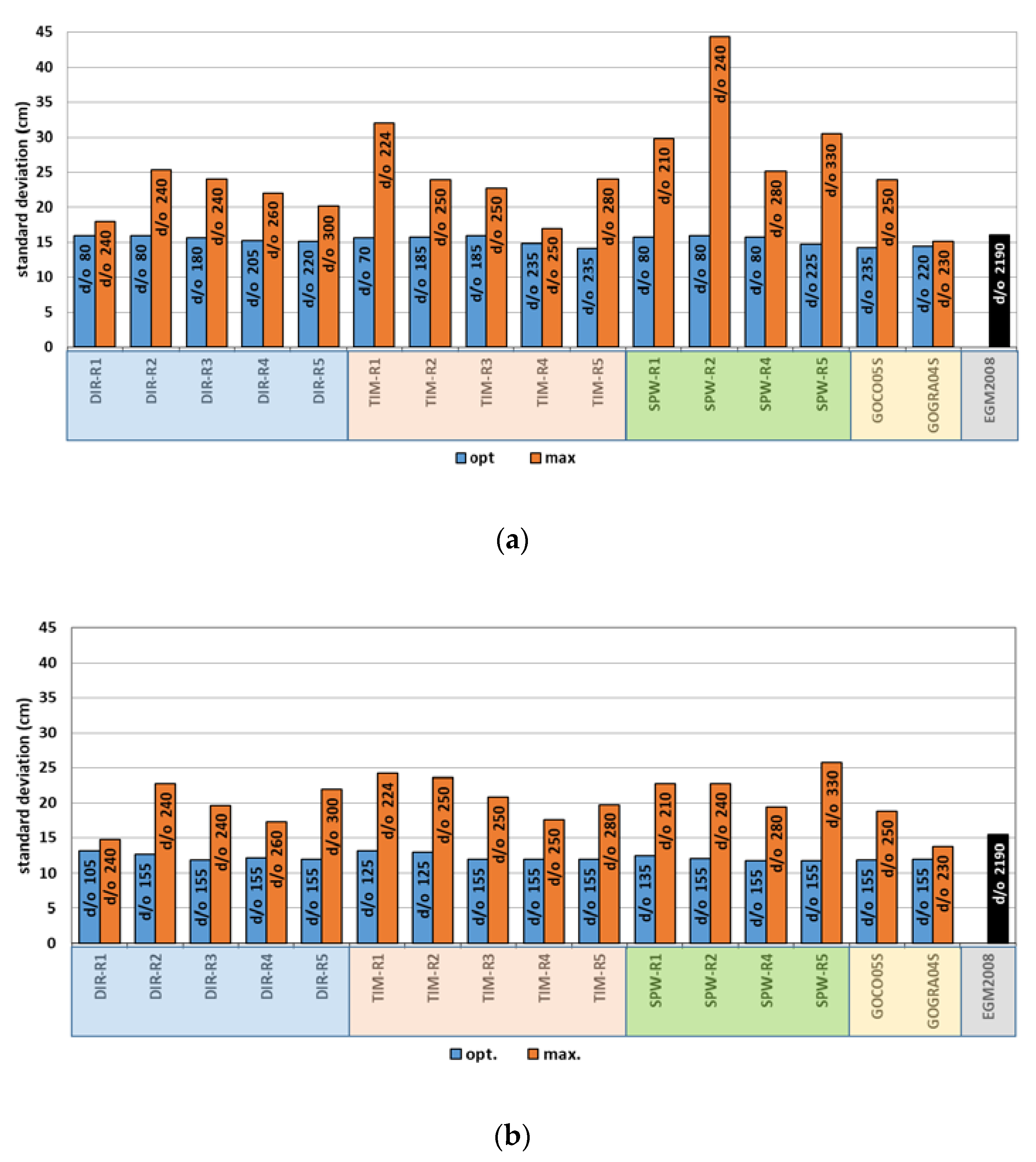
3.2. Overview of the Regional Accuracies of the GGMs
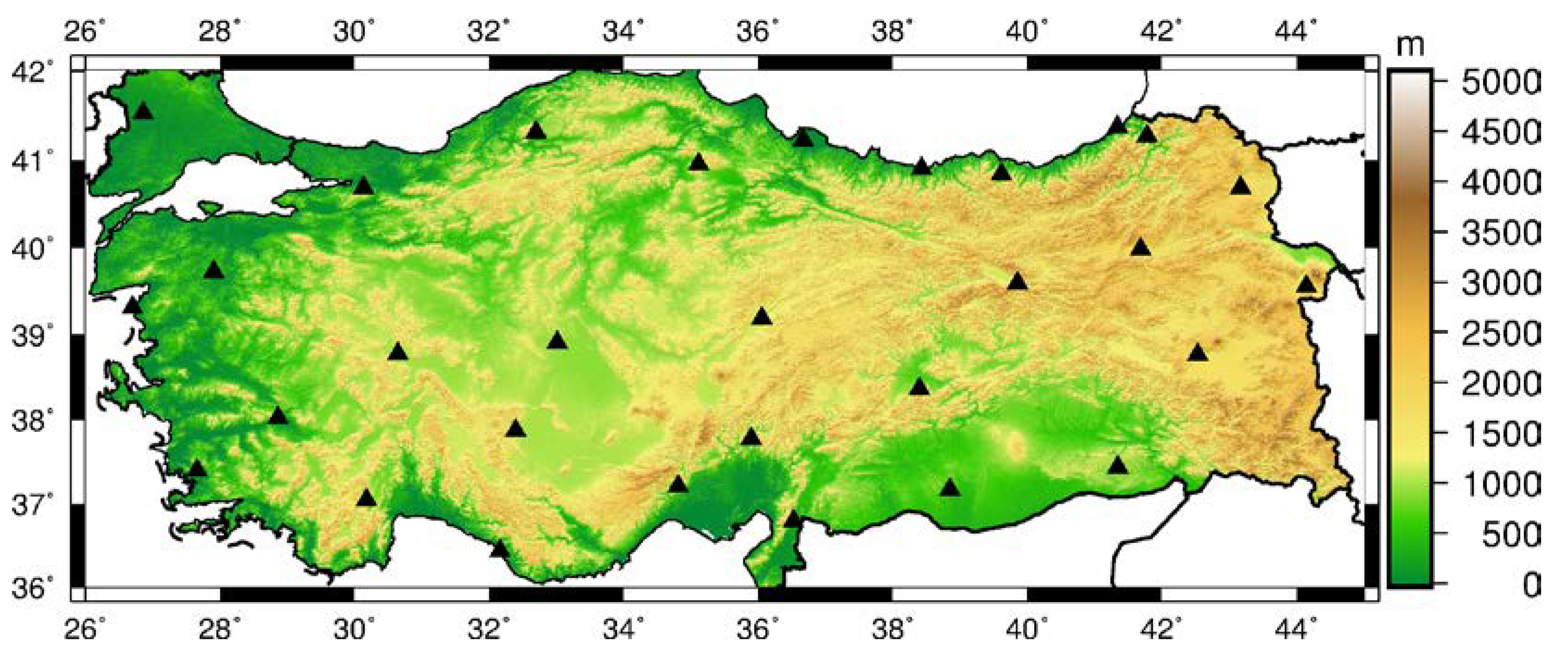
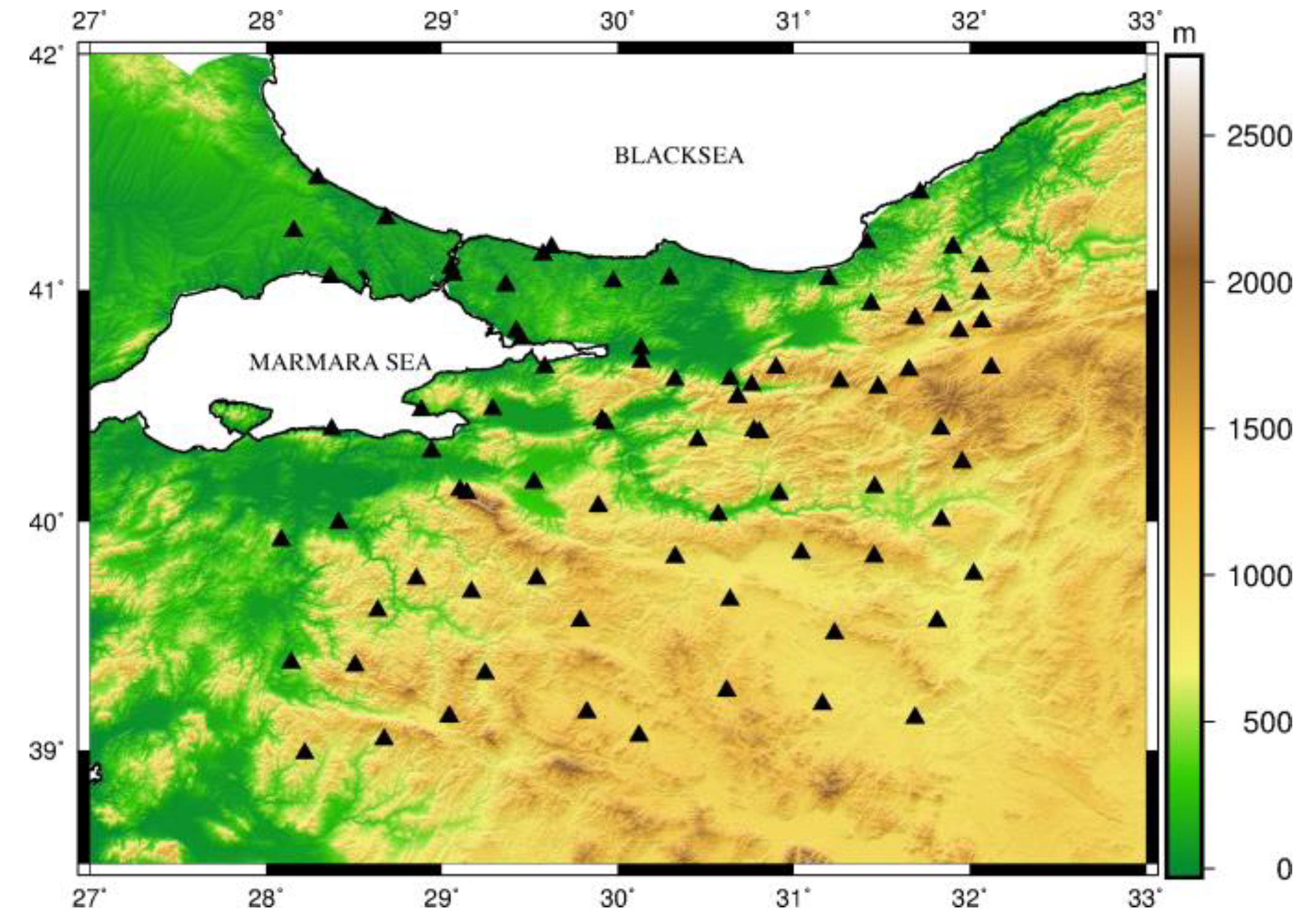
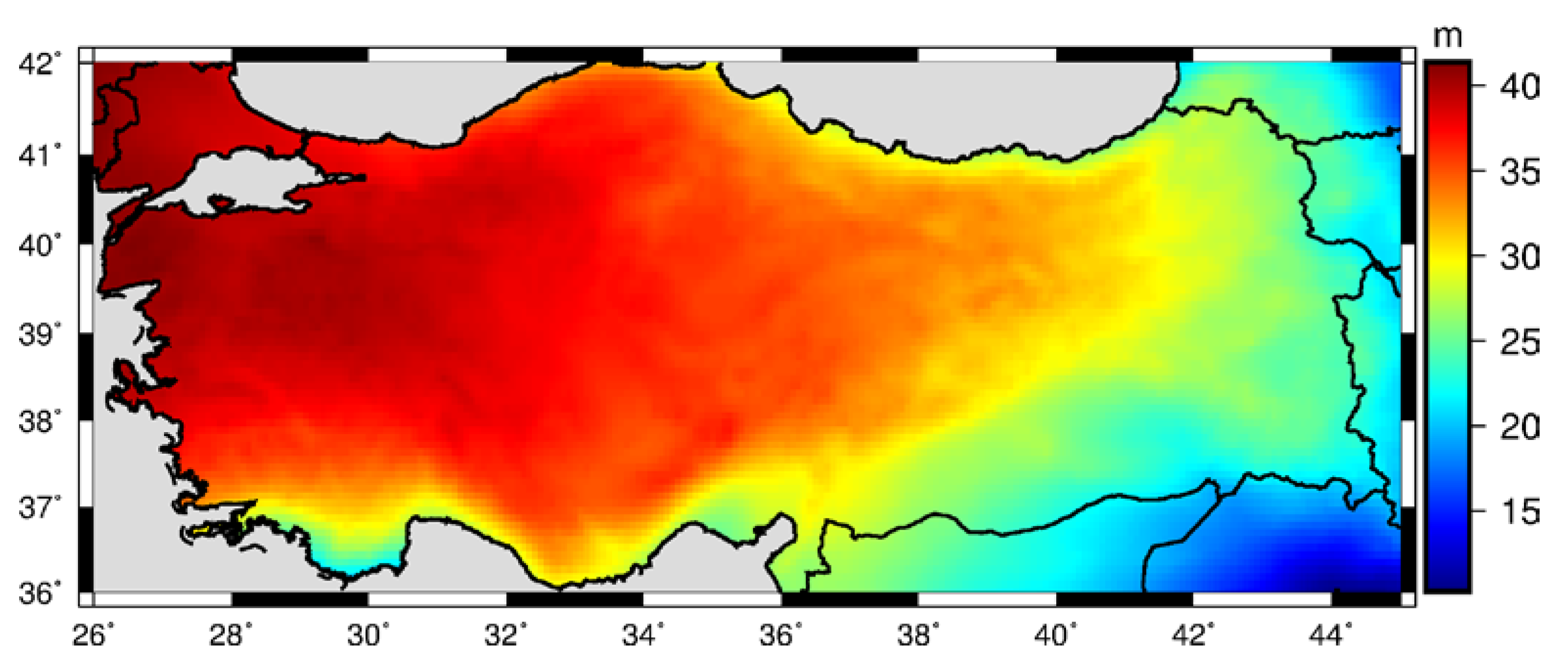
3.2.1. Assessment of GGMs’ Accuracies in Turkey
3.2.2. Testing the GGMs Contribution in Detailed Geoid Modeling
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tapley, B.D.; Schutz, B.E.; Eanes, R.J.; Ries, J.C.; Watkins, M.M. Lageos laser ranging contributions to geodynamics, geodesy, and orbital dynamics. Contrib. Space Geod. Geodyn. Earth Dyn. Geodyn. Ser. 1993, 24, 147–173. [Google Scholar]
- Huang, J.; Kotsakis, C. External Quality Evaluation Reports of EGM08. Newton’s Bulletin 2009, 4, 1–331. [Google Scholar]
- Jin, S.; Van Dam, T.; Wdowinski, S. Observing and understanding the Earth system variations from space geodesy. J. Geodyn. 2013, 72, 1–10. [Google Scholar] [CrossRef]
- Wolff, M. Direct measurements of the Earth’s gravitational potential using a satellite pair. J. Geophys. Res. Space Phys. 1969, 74, 5295–5300. [Google Scholar] [CrossRef]
- Rummel, R.; Balmino, G.; Johannessen, J.; Visser, P.; Woodworth, P. Dedicated gravity field missions—Principles and aims. J. Geodyn. 2002, 33, 3–20. [Google Scholar] [CrossRef]
- Drinkwater, M.R.; Floberghagen, R.; Haagmans, R.; Muzi, D.; Popescu, A. VII: CLOSING SESSION: GOCE: ESA’s First Earth Explorer Core Mission. Space Sci. Rev. 2003, 108, 419–432. [Google Scholar] [CrossRef]
- Tapley, B.D.; Bettadpur, S.; Watkins, M.; Reigber, C. The gravity recovery and climate experiment: Mission overview and early results. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Rummel, R.; Gruber, T.; Flury, J.; Schlicht, A. ESA’s gravity field and steady-state ocean circulation explorer GOCE. ZfV-Zeitschrift für Geodäsie. Geoinf. Landmanag. 2009, 134, 125–130. [Google Scholar]
- CHAMP Satellite Mission, GFZ German Research Centre for Geosciences. Available online: http://op.gfz-potsdam.de/champ/ (accessed on 21 September 2019).
- GRACE (Gravity Recovery and Climate Experiment) Satellite Mission, University of Texas at Austin Center 795 for Space Research. Available online: http://www.csr.utexas.edu/grace/ (accessed on 7 February 2020).
- Tapley, B.D.; Bettadpur, S.; Ries, J.C.; Thompson, P.F.; Watkins, M.M. GRACE Measurements of Mass Variability in the Earth System. Science 2004, 305, 503–505. [Google Scholar] [CrossRef]
- Flechtner, F.; Morton, P.; Watkins, M.; Webb, F. Status of the GRACE Follow-on Mission, in Gravity, Geoid and Height Systems; Springer: Berlin/Heidelberg, Germany, 2014; pp. 117–121. [Google Scholar]
- Rummel, R. Satellite Gradiometry; Springer: Berlin/Heidelberg, Germany, 1986. [Google Scholar]
- Rummel, R.; Colombo, O.L. Gravity field determination from satellite gradiometry. J. Geod. 1985, 59, 233–246. [Google Scholar] [CrossRef]
- Hirt, C.; Gruber, T.; Featherstone, W.E. Evaluation of the first GOCE static gravity field models using terrestrial gravity, vertical deflections and EGM2008 quasigeoid heights. J. Geod. 2011, 85, 723–740. [Google Scholar] [CrossRef]
- Rexer, M.; Hirt, C.; Pail, R.; Claessens, S. Evaluation of the third- and fourth-generation GOCE Earth gravity field models with Australian terrestrial gravity data in spherical harmonics. J. Geod. 2014, 88, 319–333. [Google Scholar] [CrossRef]
- ESA. The Four Candidate Earth Explorer Core Missions–Gravity Field and Steady-State Ocean Circulation; Battrick, B., Ed.; ESA: Noordwijk, The Netherlands, 1999. [Google Scholar]
- Pail, R.; Bruinsma, S.; Migliaccio, F.; Förste, C.; Goiginger, H.; Schuh, W.-D.; Höck, E.; Reguzzoni, M.; Brockmann, J.M.; Abrikosov, O.; et al. First GOCE gravity field models derived by three different approaches. J. Geod. 2011, 85, 819–843. [Google Scholar] [CrossRef]
- Gruber, T.; Visser, P.N.A.M.; Ackermann, C.; Hosse, M. Validation of GOCE gravity field models by means of orbit residuals and geoid comparisons. J. Geod. 2011, 85, 845–860. [Google Scholar] [CrossRef]
- Barthelmes, F. Definition of Functionals of the Geopotential and Their Calculation from Spherical Harmonic Models. Available online: http://icgem.gfz-potsdam.de/str-0902-revised.pdf (accessed on 7 February 2020).
- ICGEM—International Centre for Global Earth Models (ICGEM), GFZ Potsdam, Germany. Available online: http://icgem.gfz-potsdam.de/ (accessed on 7 February 2020).
- Pavlis, N.K.; Holmes, S.A.; Kenyon, S.C.; Factor, J.K. The development and evaluation of the Earth Gravitational Model 2008 (EGM2008). J. Geophys. Res. Space Phys. 2012, 117. [Google Scholar] [CrossRef]
- Gruber, T.; Gerlach, C.; Haagmans, R. Intercontinental height datum connection with GOCE and GPS-levelling data. J. Géod. Sci. 2012, 2, 270–280. [Google Scholar] [CrossRef]
- Gruber, T. Validation concepts for gravity field models from new satellite missions. In Proceedings of the 2nd International GOCE User Workshop: GOCE The Geoid and Oceanography, Bratislava, Slovakia, 8–10 March 2004. [Google Scholar]
- Ihde, J.; Wilmes, H.; Müller, J.; Denker, H.; Voigt, C.; Hosse, M. Validation of Satellite Gravity Field Models by Regional Terrestrial Data Sets. In Advanced Technologies in Earth Sciences; Springer Science and Business Media: Berlin/Heidelberg, Germany, 2010; pp. 277–296. [Google Scholar]
- Erol, S.; Isik, M.S.; Erol, B. Assessments on GOCE-based Gravity Field Model Comparisons with Terrestrial Data Using Wavelet Decomposition and Spectral Enhancement Approaches. In Proceedings of the EGU General Assembly 2016, Vienna, Austria, 17–22 April 2016. [Google Scholar]
- Sansò, F.; Sideris, M.G. Geoid Determination: Theory and Methods; Springer: San Francisco, CA, USA, 2013; ISBN 978-3-540-74699-7. [Google Scholar]
- Erol, B.; Sideris, M.G.; Çelik, R.N. Comparison of global geopotential models from the champ and grace missions for regional geoid modelling in Turkey. Stud. Geophys. Geod. 2009, 53, 419–441. [Google Scholar] [CrossRef]
- Isık, M.S.; Erol, B. Geoid determination using GOCE-based models in Turkey. In Proceedings of the EGU General Assembly 2016, Vienna, Austria, 17–22 April 2016. [Google Scholar]
- Sjöberg, L.E.; Bagherbandi, M. Gravity Inversion and Integration; Springer Science and Business Media: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Halicioglu, K.; Deniz, R.; Ozener, H. Digital astro-geodetic camera system for the measurement of the deflections of the vertical: Tests and results. Int. J. Digit. Earth 2016, 9, 914–923. [Google Scholar] [CrossRef]
- Kiamehr, R.; Eshagh, M.; Sjoberg, L.E. Interpretation of general geophysical patterns in Iran based on GRACE gradient component analysis. Acta Geophys. 2008, 56, 440–454. [Google Scholar] [CrossRef]
- Mintourakis, I. Adjusting altimetric sea surface height observations in coastal regions. Case study in the Greek Seas. J. Géod. Sci. 2014, 4. [Google Scholar] [CrossRef]
- Kotsakis, C.; Katsambalos, K. Quality Analysis of Global Geopotential Models at 1542 GPS/levelling Benchmarks Over the Hellenic Mainland. Surv. Rev. 2010, 42, 327–344. [Google Scholar] [CrossRef]
- Ihde, J.; Sánchez, L.; Barzaghi, R.; Drewes, H.; Foerste, C.; Gruber, T.; Liebsch, G.; Marti, U.; Pail, R.; Sideris, M. Definition and Proposed Realization of the International Height Reference System (IHRS). Surv. Geophys. 2017, 38, 549–570. [Google Scholar] [CrossRef]
- Gerlach, C.; Rummel, R. Global height system unification with GOCE: A simulation study on the indirect bias term in the GBVP approach. J. Geod. 2013, 87, 57–67. [Google Scholar] [CrossRef]
- Vergos, G.S.; Erol, B.; Natsiopoulos, D.A.; Grigoriadis, V.N.; Işık, M.S.; Tziavos, I.N. Preliminary results of GOCE-based height system unification between Greece and Turkey over marine and land areas. Acta Geod. Geophys. 2018, 53, 61–79. [Google Scholar] [CrossRef]
- Van Der Meijde, M.; Pail, R.; Bingham, R.; Floberghagen, R. GOCE data, models, and applications: A review. Int. J. Appl. Earth Obs. Geoinf. 2015, 35, 4–15. [Google Scholar] [CrossRef]
- Bruinsma, S.; Marty, J.; Balmino, G.; Biancale, R.; Förste, C.; Abrikosov, O.; Neumayer, H. GOCE gravity field recovery by means of the direct numerical method. In Proceedings of the ESA Living Planet Symposium 2010, Bergen, Norway, June 27–2 July 2010. [Google Scholar]
- Pail, R.; Goiginger, H.; Mayrhofer, R.; Höck, E.; Schuh, W.D.; Brockmann, J.M. GOCE gravity field model derived from orbit and gradiometry data applying the time-wise method. In Proceedings of the ESA Living Planet Symposium 2010, Bergen, Norway, 27 June–2 July 2010. [Google Scholar]
- Migliaccio, F.; Reguzzoni, M.; Sansò, F.; Tscherning, C.C.; Veicherts, M. GOCE data analysis: The space-wise approach and the first space-wise gravity field model. In Proceedings of the ESA Living Planet Symposium 2010, Bergen, Norway, 27 June–2 July 2010. [Google Scholar]
- Rummel, R.; Gruber, T.; Koop, R. High level processing facility for GOCE: Products and processing strategy. In Proceedings of the 2nd International GOCE User Workshop GOCE, The Geoid and Oceanography, ESA SP-569, Bratislava, Slovakia, 8–10 March 2004. [Google Scholar]
- Gruber, T.; Rummel, R.; Abrikosov, O.; van Hees, R. GOCE Level 2 Product Data Handbook; The European GOCE Gravity Consortium EGG-C: Paris, France, 2010. [Google Scholar]
- Metzler, B.; Pail, R. GOCE Data Processing: The Spherical Cap Regularization Approach. Stud. Geophys. Geod. 2005, 49, 441–462. [Google Scholar] [CrossRef]
- ESA. Gravity Field and Steady-State Ocean Circulation Explorer (GOCE) Mission. Available online: http://www.esa.int/Our_Activities/Observing_the_Earth/GOCE (accessed on 21 September 2019).
- Zingerle, P.; Brockmann, J.M.; Pail, R.; Gruber, T.; Willberg, M. The polar extended gravity field model TIM_R6e. In GFZ Data Services; GFZ: Potsdam, Germany, 2019. [Google Scholar]
- Pail, R.; Fecher, T.; Murböck, M.; Rexer, M.; Stetter, M.; Gruber, T.; Stummer, C. Impact of GOCE Level 1b data reprocessing on GOCE-only and combined gravity field models. Studia Geophys. Geod. 2013, 57, 155–173. [Google Scholar] [CrossRef]
- Reguzzoni, M. From the time-wise to space-wise GOCE observables. Adv. Geosci. 2003, 1, 137–142. [Google Scholar] [CrossRef][Green Version]
- Migliaccio, F.; Reguzzoni, M.; Sansò, F.; Tselfes, N. On the use of gridded data to estimate potential coefficients. In Proceedings of the 3rd International GOCE User Workshop, Frascati, Italy, 6–8 November 2006. [Google Scholar]
- Gruber, T.; Rummel, R. GOCE gravity field models-Overview and performance analysis. In Proceedings of the 3rd International Gravity Field Service (IGFS) General Assembly, Shanghai, China, 30 June–6 July 2014. [Google Scholar]
- Bruinsma, S.L.; Förste, C.; Abrikosov, O.; Lemoine, J.-M.; Marty, J.-C.; Mulet, S.; Rio, M.-H.; Bonvalot, S. ESA’s satellite-only gravity field model via the direct approach based on all GOCE data. Geophys. Res. Lett. 2014, 41, 7508–7514. [Google Scholar] [CrossRef]
- Förste, C.; Abrykosov, O.; Bruinsma, S.; Dahle, C.; König, R.; Lemoine, J.M. ESA’s Release 6 GOCE gravity field model by means of the direct approach based on improved filtering of the reprocessed gradients of the entire mission. In GFZ Data Services; GFZ: Potsdam, Germany, 2019. [Google Scholar]
- Brockmann, J.M.; Zehentner, N.; Höck, E.; Pail, R.; Loth, I.; Mayer-Gürr, T.; Schuh, W.-D. EGM_TIM_RL05: An independent geoid with centimeter accuracy purely based on the GOCE mission. Geophys. Res. Lett. 2014, 41, 8089–8099. [Google Scholar] [CrossRef]
- Brockmann, J.M.; Schubert, T.; Mayer-Gürr, T.; Schuh, W.D. The Earth’s gravity field as seen by the GOCE satellite—An improved sixth release derived with the time-wise approach. In GFZ Data Services; GFZ: Potsdam, Germany, 2019. [Google Scholar]
- Migliaccio, F.; Reguzzoni, M.; Gatti, A.; Sansò, F.; Herceg, M. A GOCE-only global gravity field model by the space-wise approach. In Proceedings of the 4th International GOCE User Workshop, Munich, Germany, 31 March–1 April 2011. [Google Scholar]
- Gatti, A.; Reguzzoni, M.; Migliaccio, F.; Sansò, F. Space-wise grids of gravity gradients from GOCE data at nominal satellite altitude. In Proceedings of the 5th International GOCE User Workshop, Paris, France, 25–28 November 2014. [Google Scholar]
- Gatti, A.; Reguzzoni, M.; Migliaccio, F.; Sansò, F. Computation and assessment of the fifth release of the GOCE-only space-wise solution. In Proceedings of the the 1st Joint Commission 2 and IGFS Meeting, Thessaloniki, Greece, 19–23 September 2016. [Google Scholar]
- Mayer-Guerr, T. The combined satellite gravity field model GOCO05s. In Proceedings of the EGU General Assembly Conference, Vienna, Austria, 12–17 April 2015. [Google Scholar]
- Yi, W.; Rummel, R.; Gruber, T. Gravity field contribution analysis of GOCE gravitational gradient components. Stud. Geophys. Geod. 2013, 57, 174–202. [Google Scholar] [CrossRef]
- Ince, E.S.; Barthelmes, F.; Reißland, S.; Elger, K.; Förste, C.; Flechtner, F.; Schuh, H. ICGEM—15 years of successful collection and distribution of global gravitational models, associated services, and future plans. Earth Syst. Sci. Data 2019, 11, 647–674. [Google Scholar] [CrossRef]
- Hofmann-Wellenhof, B.; Moritz, H. Physical Geodesy; Springer: New York, NY, USA, 2006. [Google Scholar]
- Ellmann, A.; Kaminskis, J.; Parseliunas, E.; Jürgenson, H.; Oja, T. Evaluation Results of the Earth Gravitational Model EGM08 over the Baltic Countries. Newton’s Bulletin 2009, 4, 110–121. [Google Scholar]
- Kirby, J.; Featherstone, W. A study of zero-and first-degree terms in geopotential models over Australia. Geomat. Res. Australas. 1997, 66, 93–108. [Google Scholar]
- Sánchez, L.; Čunderlík, R.; Dayoub, N.; Mikula, K.; Minarechová, Z.; Šíma, Z.; Vatrt, V.; Vojtíšková, M. A conventional value for the geoid reference potential $$ W_ {0} $$. J. Geod. 2016, 90, 815–835. [Google Scholar] [CrossRef]
- Smith, D.A. There is no such thing as “The” EGM96 geoid: Subtle points on the use of a global geopotential model. IGeS Bull. Int. Geoid Serv. 1998, 8, 17–27. [Google Scholar]
- Ekman, M. Impacts of geodynamic phenomena on systems for height and gravity. J. Geod. 1989, 63, 281–296. [Google Scholar] [CrossRef]
- Kiamehr, R. A strategy for determining the regional geoid by combining limited ground data with satellite-based global geopotential and topographical models: A case study of Iran. J. Geod. 2006, 79, 602–612. [Google Scholar] [CrossRef]
- Voigt, C.; Denker, H. Validation of GOCE Gravity Field Models in Germany. Newton’s Bulletin 2015, 5, 37–49. [Google Scholar]
- Tscherning, C.C.; Arabelos, D. Gravity anomaly and gradient recovery from GOCE gradient data using LSC and comparisons with known ground data. In Proceedings of the 4th International GOCE user workshop, Munich, Germany, 31 March–1 April 2011. [Google Scholar]
- Šprlák, M.; Gerlach, C.; Pettersen, B. Validation of GOCE global gravity field models using terrestrial gravity data in Norway. J. Géod. Sci. 2012, 2, 134–143. [Google Scholar] [CrossRef]
- Bouman, J.; Fuchs, M.J. GOCE gravity gradients versus global gravity field models. Geophys. J. Int. 2012, 189, 846–850. [Google Scholar] [CrossRef]
- Abdalla, A.; Fashir, H.; Ali, A.; Fairhead, D. Validation of recent GOCE/GRACE geopotential models over Khartoum state-Sudan. J. Géod. Sci. 2012, 2, 88–97. [Google Scholar] [CrossRef]
- Guimarães, G.; Matos, A.; Blitzkow, D. An evaluation of recent GOCE geopotential models in Brazil. J. Géod. Sci. 2012, 2, 144–155. [Google Scholar] [CrossRef]
- Szűcs, E. Validation of GOCE time-wise gravity field models using GPS-levelling, gravity, vertical deflections and gravity gradient measurements in Hungary. Period. Polytech. Civ. Eng. 2012, 56, 3–11. [Google Scholar] [CrossRef][Green Version]
- Huang, J.; Reguzzoni, M.; Gruber, T. Assessment of GOCE Geopotential Models. Newton’s Bulletin 2015, 5, 1–192. [Google Scholar]
- Ayhan, M.E.; Demir, C.; Lenk, O.; Kılıçoğlu, A.; Aktug, B.; Acikgoz, M.; Firat, O.; Sengun, Y.S.; Cingoz, A.; Gurdal, M.A.; et al. Türkiye Ulusal Temel GPS Ağı. Harit. Derg. 2002, 16, 1–80. [Google Scholar]
- Andersen, O.B.; Knudsen, P.; Berry, P.A. The DNSC08GRA global marine gravity field from double retracked satellite altimetry. J. Geod. 2010, 84, 191–199. [Google Scholar] [CrossRef]
- Şaroğlu, F.; Emre, Ö.; Kuşçu, İ. Turkish Active Faults Map; Directorate of Mineral Research and Exploration: Ankara, Turkey, 1992. [Google Scholar]
- Kılıçoğlu, A.; Direnç, A.; Simav, M.; Lenk, O.; Aktuğ, B.; Yıldız, H. Evaluation of the Earth Gravitational Model 2008 in Turkey. Newton’s Bulletin 2009, 4, 164–171. [Google Scholar]
- Aktuğ, B.; Kilicoglu, A.; Lenk, O.; Gürdal, M.A.; Aktuğ, B. Establishment of regional reference frames for quantifying active deformation areas in Anatolia. Stud. Geophys. Geod. 2009, 53, 169–183. [Google Scholar] [CrossRef]
- International Service for the Geoid (ISG) at DICA Politecnico di Milano. Available online: http://www.isgeoid.polimi.it/ (accessed on 7 February 2020).
- Erol, B.; Işık, M.S.; Erol, S. Assessment of Gridded Gravity Anomalies for Precise Geoid Modeling in Turkey. J. Surv. Eng. 2020. [Google Scholar] [CrossRef]
- Kearsley, A.H.W. Data requirements for determining precise relative geoid heights from gravimetry. J. Geophys. Res. Space Phys. 1986, 91, 9193–9201. [Google Scholar] [CrossRef]
- Farahani, H.H.; Klees, R.; Slobbe, C. Data requirements for a 5-mm quasi-geoid in the Netherlands. Stud. Geophys. Geod. 2017, 25, 17–702. [Google Scholar] [CrossRef]
| Model | (Max. d/o) | Data | Difference w.r.t. Previous Version | Literature |
|---|---|---|
| DIR_RL1 (240) | GOCE (2 m), CHAMP (6 y) | [18,39] |
| The model is more accurate than GRACE models for d/o 130-150 and up, less accurate for the lower degrees. | ||
| DIR_RL2 (240) | GOCE (8 m) | [18,39] |
| SST ≤ d/o 130 | ||
| DIR_RL3 (240) | GOCE (18m), GRACE (6.5y), SLR (6.5y) | [18,39] |
| Combined GRACE as normal equations. and LAGEOS as normal equations., SGG components: equal relative weights 1.0. | ||
| DIR_RL4 (260) | GOCE (33 m), GRACE (9 y), SLR (>10 y) | [51] |
| SGG: inclusion of Txz-component.8.3–125 MHz filter. GRACE: a blended combination of GRGS-RL02 ≤ d/o 54 and GFZ-RL05 from d/o 55 to 180. | ||
| DIR_RL5 (300) | GOCE (48 m), GRACE (>10 y), SLR (>10 y) | [51] |
| The GRACE contribution up to d/o 130. Very low-degree harmonics of (esp. d/o 2 and 3) cannot be estimated accurately with GRACE and GOCE data, therefore LAGEOS-1 and -2 normal equations are used in the combination | ||
| DIR_RL6 (300) | GOCE (48 m), GRACE (>10 y), SLR (>10 y) | [52] |
| Based on improved filtering of the reprocessed gradients of the full mission observations | ||
| TIM_RL1 (224) | GOCE (2 m) | [40] |
| The model is independent of any other gravity field information. In the low degrees, it is not competitive with GRACE models. Kaula reg. is to improve SNR. | ||
| TIM_RL2 (250) | GOCE (8 m) | [18] |
| No change in data processing strategy w.r.t. its predecessor. | ||
| TIM_RL3 (250) | GOCE (18 m) | [18] |
| In addition to Vxx, Vyy, Vzz, the inclusion of Vxz component in the SGG observations. | ||
| TIM_RL4 (250) | GOCE (32 m) | [18] |
| Applying the short-arc integral method to the kinematic orbits. | ||
| TIM_RL5 (280) | GOCE (48 m) | [53] |
| SST ≤ d/o 150, SGG ≤ d/o 280, Kaula ≥ 201 | ||
| TIM_RL6 (300) | GOCE (48 m) | [54] |
| SGG ≤ d/o 300, digital decorrelation filter to observation equations | ||
| TIM_RL6e (300) | GOCE (48 m) | [46] |
| Included terrestrial gravity field observations over GOCES’s polar gap areas | ||
| SPW_RL1 (210) | GOCE (2 m) | [18,41] |
| Applying an iterative procedure based on the Wiener orbital filter to reduce time correlated noise of the gradiometer. Including Txz in the gravity gradients. | ||
| SPW_RL2 (240) | GOCE (8 m) | [55] |
| No corrections to any a priori model. Using EIGEN5C for signal covariance modeling and FES2004 for ocean tide modeling. | ||
| SPW_RL4 (280) | GOCE (32 m) | [56] |
| Using EIGEN6C3stat for signal covariance modeling. | ||
| SPW_RL5 (330) | GOCE (48 m) | [57] |
| Using EIGEN6C4 and GOCO05S for signal covariance modeling. | ||
| GOCO05S (280) | GOCE (48 m), GRACE (~10 y), CHAMP (6y), SLR (>10y) | [58] |
| Combined satellite gravity field model, estimated with over 800,000,000 observations. | ||
| GOGRA04S (230) | GOCE (48 m), GRACE (>10y) | [59] |
| In the solution: the normal equations combine SST ≤ d/o 120, SGG ≤ d/o 230, GRACE ≤ d/o 180 | ||
| EGM2008 (2190) | GRACE, Gravity (terrestrial, airborne), Altimetry Data | [22] |
| Dataset | I | II |
|---|---|---|
| Size of area | 6° × 19° | 3° × 4° |
| Number of BMs | 30 | 81 |
| BM density | 1 BM/200 km | 1 BM/45 km |
| The distribution of BMs | Homogenous and quite sparse | Homogenous and sparse |
| 1 Coordinate datum | ITRF96 | ITRF96 |
| 2D coordinate accuracy | ±1.0 cm | ±1.0 cm |
| H-accuracy | ±2.0 cm | ±2.0 cm |
| 1 Vertical datum | TUDKA99 | TUDKA99 |
| H-accuracy | ±2.5 cm | ±2.0 cm |
| Topography | 0–5000 m | 0–2500 m |
| Reference | [76] | [76] |
| GGMs and Detailed Geoid Model | Ref. GGM (d/o) | Statistics | |||||
|---|---|---|---|---|---|---|---|
| Min | Max | Mean | Std. | ||||
| Optimum d/o of GGMs | DIR RL5 (155) | − | − | −192.8 | 61.8 | −72.8 | 61.0 |
| expTG-Opt-1 | DIR RL5 (155) | Before fit | −174.1 | −94.4 | −127.9 | 16.5 | |
| After fit | −37.2 | 31.6 | 0.0 | 9.8 | |||
| TIM RL5 (155) | − | − | −192.8 | 61.2 | −72.7 | 61.1 | |
| expTG-Opt-2 | TIM RL5 (155) | Before fit | −174.5 | −94.6 | −128.2 | 16.5 | |
| After fit | −37.2 | 31.5 | 0.0 | 9.8 | |||
| SPW RL5 (155) | − | − | −204.8 | 62.7 | −72.6 | 63.7 | |
| expTG-Opt-3 | SPW RL5 (155) | Before fit | −164.9 | −83.8 | −119.6 | 16.3 | |
| After fit | −34.3 | 29.7 | 0.0 | 11.4 | |||
| GOCO05S (155) | − | − | −192.8 | 61.1 | −72.9 | 60.8 | |
| expTG-Opt-4 | GOCO05S (155) | Before fit | −174.3 | −94.4 | −128.0 | 16.5 | |
| After fit | −37.2 | 31.6 | 0.0 | 9.8 | |||
| EGM2008 (155) | − | − | −89.9 | 171.0 | 23.1 | 63.1 | |
| expTG-Opt-5 | EGM2008 (155) | Before fit | −170.3 | −89.7 | −124.2 | 16.5 | |
| After fit | −37.2 | 31.6 | 0.0 | 9.8 | |||
| Maximum d/o of GGMs | DIR RL5 (300) | − | − | −42.2 | 67.4 | 8.7 | 26.4 |
| expTG-M-1 | DIR RL5 (300) | Before fit | −162.2 | −66.6 | −112.9 | 19.4 | |
| After fit | −35.0 | 30.2 | 0.0 | 9.7 | |||
| TIM RL5 (280) | − | − | −50.2 | 67.3 | 8.6 | 27.2 | |
| expTG-M-2 | TIM RL5 (280) | Before fit | −164.8 | −69.8 | −115.2 | 19.6 | |
| After fit | −34.3 | 30.0 | 0.0 | 9.6 | |||
| SPW RL5 (330) | − | − | −57.5 | 88.8 | 9.1 | 31.3 | |
| expTG-M-3 | SPW RL5 (330) | Before fit | −161.8 | −75.4 | −115.9 | 18.4 | |
| After fit | −31.1 | 27.7 | 0.0 | 10.7 | |||
| GOCO05S (280) | − | − | −48.2 | 62.7 | 8.0 | 26.2 | |
| expTG-M-4 | GOCO05S (280) | Before fit | −163.6 | −68.2 | −113.9 | 19.7 | |
| After fit | −34.4 | 30.9 | 0.0 | 9.6 | |||
| EGM2008 (280) | − | − | −44.7 | 69.3 | 8.3 | 26.4 | |
| expTG-M-5 | EGM2008 (280) | Before fit | −163.6 | −68.2 | −113.9 | 19.7 | |
| After fit | −34.6 | 30.8 | 0.0 | 9.6 | |||
| EGM2008 (300) | − | − | −43.1 | 66.6 | 8.7 | 25.7 | |
| expTG-M-6 | EGM2008 (300) | Before fit | −163.6 | −68.2 | −113.9 | 19.7 | |
| After fit | −33.0 | 33.6 | 0.0 | 11.7 | |||
| EGM2008 (330) | − | − | −38.6 | 59.8 | 8.3. | 23.8 | |
| expTG-M-7 | EGM2008 (330) | Before fit | −151.0 | −63.7 | −104.5 | 18.6 | |
| After fit | −31.1 | 29.0 | 0.0 | 10.8 | |||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Erol, B.; Işık, M.S.; Erol, S. An Assessment of the GOCE High-Level Processing Facility (HPF) Released Global Geopotential Models with Regional Test Results in Turkey. Remote Sens. 2020, 12, 586. https://doi.org/10.3390/rs12030586
Erol B, Işık MS, Erol S. An Assessment of the GOCE High-Level Processing Facility (HPF) Released Global Geopotential Models with Regional Test Results in Turkey. Remote Sensing. 2020; 12(3):586. https://doi.org/10.3390/rs12030586
Chicago/Turabian StyleErol, Bihter, Mustafa Serkan Işık, and Serdar Erol. 2020. "An Assessment of the GOCE High-Level Processing Facility (HPF) Released Global Geopotential Models with Regional Test Results in Turkey" Remote Sensing 12, no. 3: 586. https://doi.org/10.3390/rs12030586
APA StyleErol, B., Işık, M. S., & Erol, S. (2020). An Assessment of the GOCE High-Level Processing Facility (HPF) Released Global Geopotential Models with Regional Test Results in Turkey. Remote Sensing, 12(3), 586. https://doi.org/10.3390/rs12030586