Spectral Imagery Tensor Decomposition for Semantic Segmentation of Remote Sensing Data through Fully Convolutional Networks
Abstract
1. Introduction
1.1. Related Work
1.2. Contribution
- RS-CNNMSI or -HSI, or third order tensors are compressed in the spectral domain through TKD preprocessing, preserving the pixel spatial structure and obtaining a core tensor representative of the original. These core tensors, with less new tensor bands, which belong to subspaces of the original space, build the new input space for any supervised classifier at pixel level, which delivers the corresponding prediction matrix of pixels classified element-wise. This approach achieves high or competitive performance metrics but with less computational complexity, and consequently, lower computational time.
- This approach outperforms other methods in normalized difference indexes, PCA, particularly the same FCN with original data. Each core tensor is calculated using the HOOI algorithm, which achieves high orthogonality degree for the core tensor (all-orthogonality) and for its factor matrices (column-wise orthogonal); besides, it converges faster than others, such as TUCKALS3 [17].
- The efficiency of this approach can be measured by one or more performance metrics, e.g., pixel accuracy (PA), as a function of the number of new tensor bands, orthogonality degree of the factor matrices and the core tensor, reconstruction error of the original tensor, and execution time. These results are shown in Section 6: Experimental Results.
2. Tensor Algebra Basic Concepts
2.1. Matricization
2.2. Outer Product
2.3. Inner Product
2.4. N-Mode Product
2.5. Rank-One Tensor
2.6. Rank-R Tensor
2.7. N-Rank
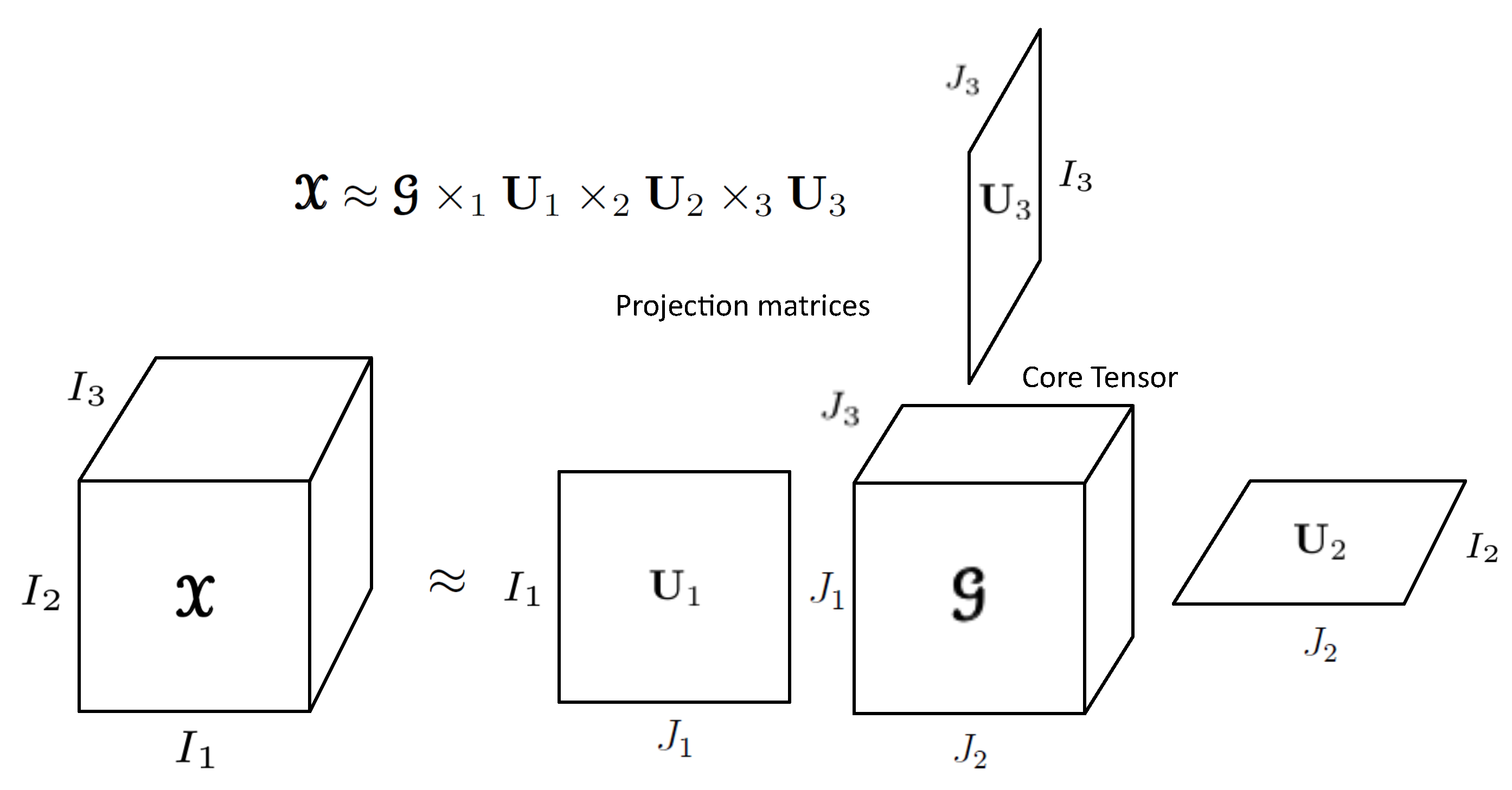
2.8. Tucker Decomposition (Tkd)
3. Problem Statement and Mathematical Definition
3.1. Problem Statement
3.2. Mathematical Definition
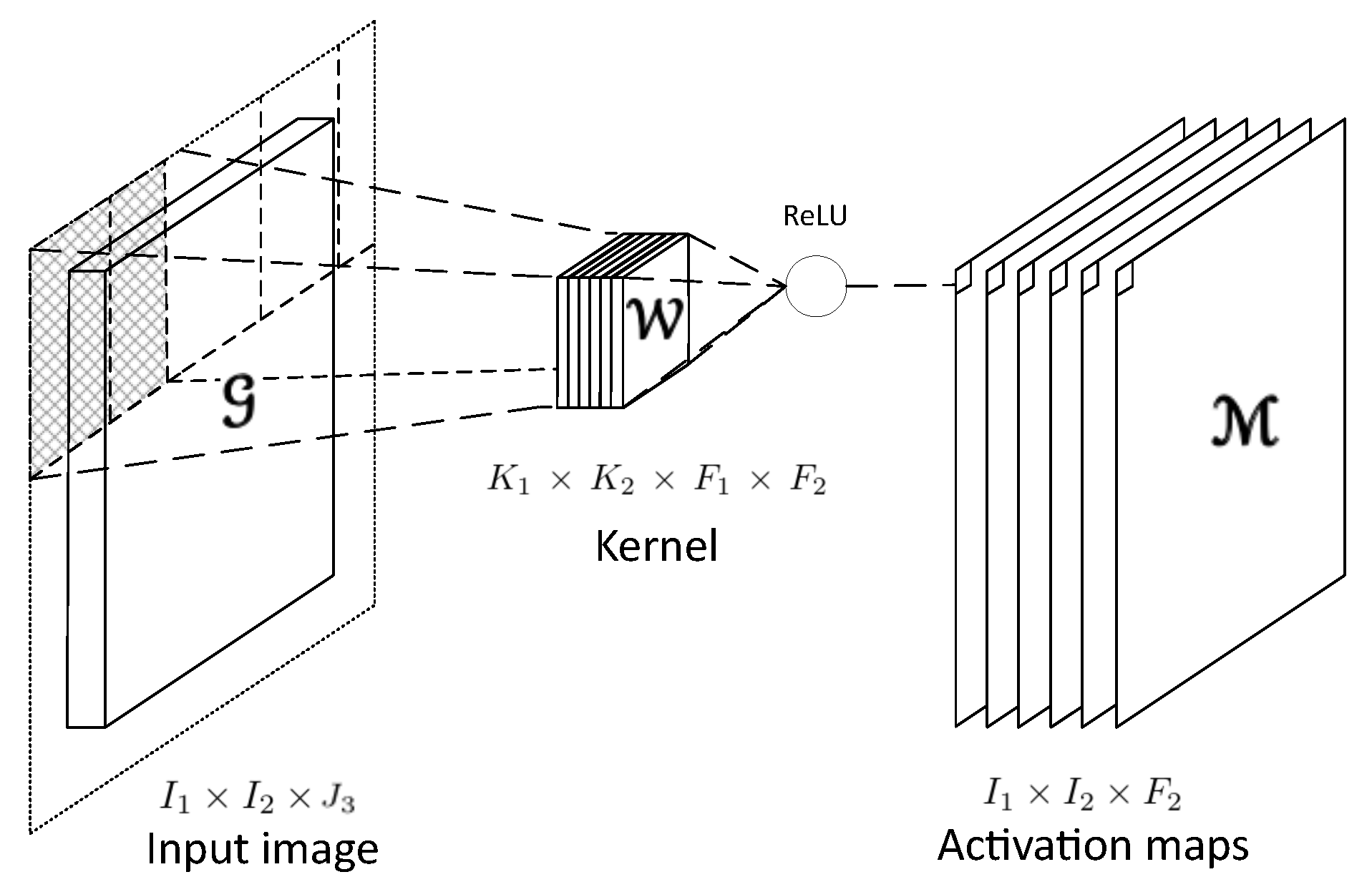
4. Convolutional Neural Networks (CNNs)
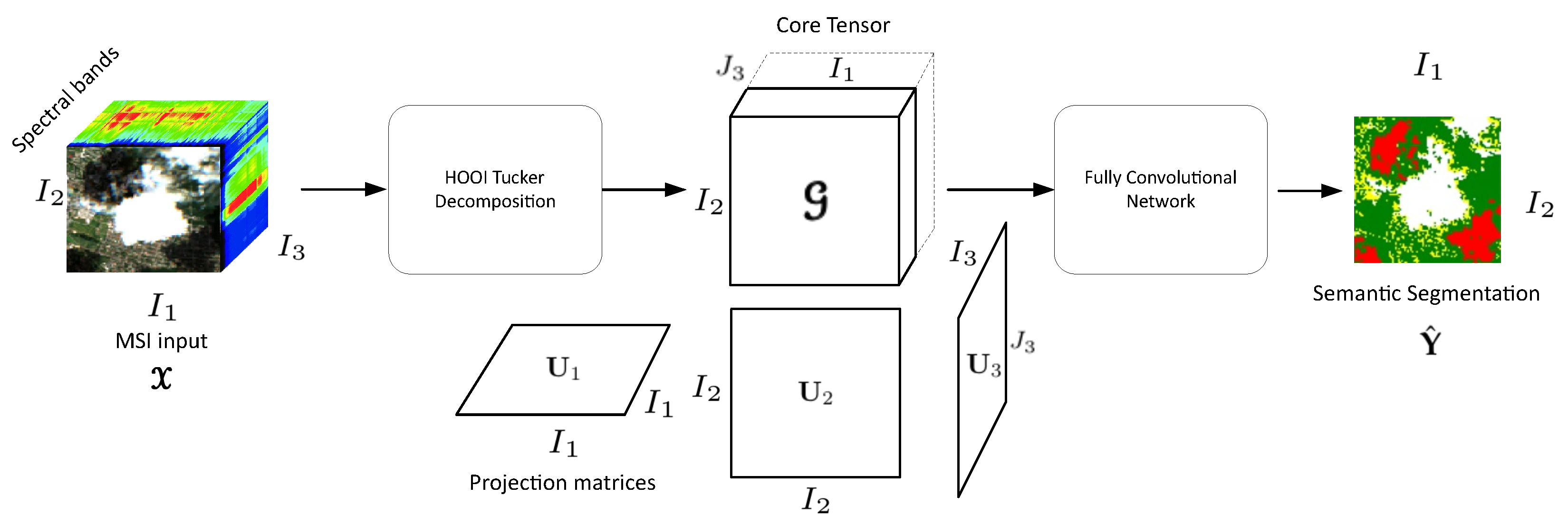
5. Hooi-Fcn Framework
5.1. Higher Order Orthogonal Iteration (HOOI) for Spectral Image Compression
| Algorithm 1: HOOI for MSI. ALS algorithm to compute the core tensor . |
 |
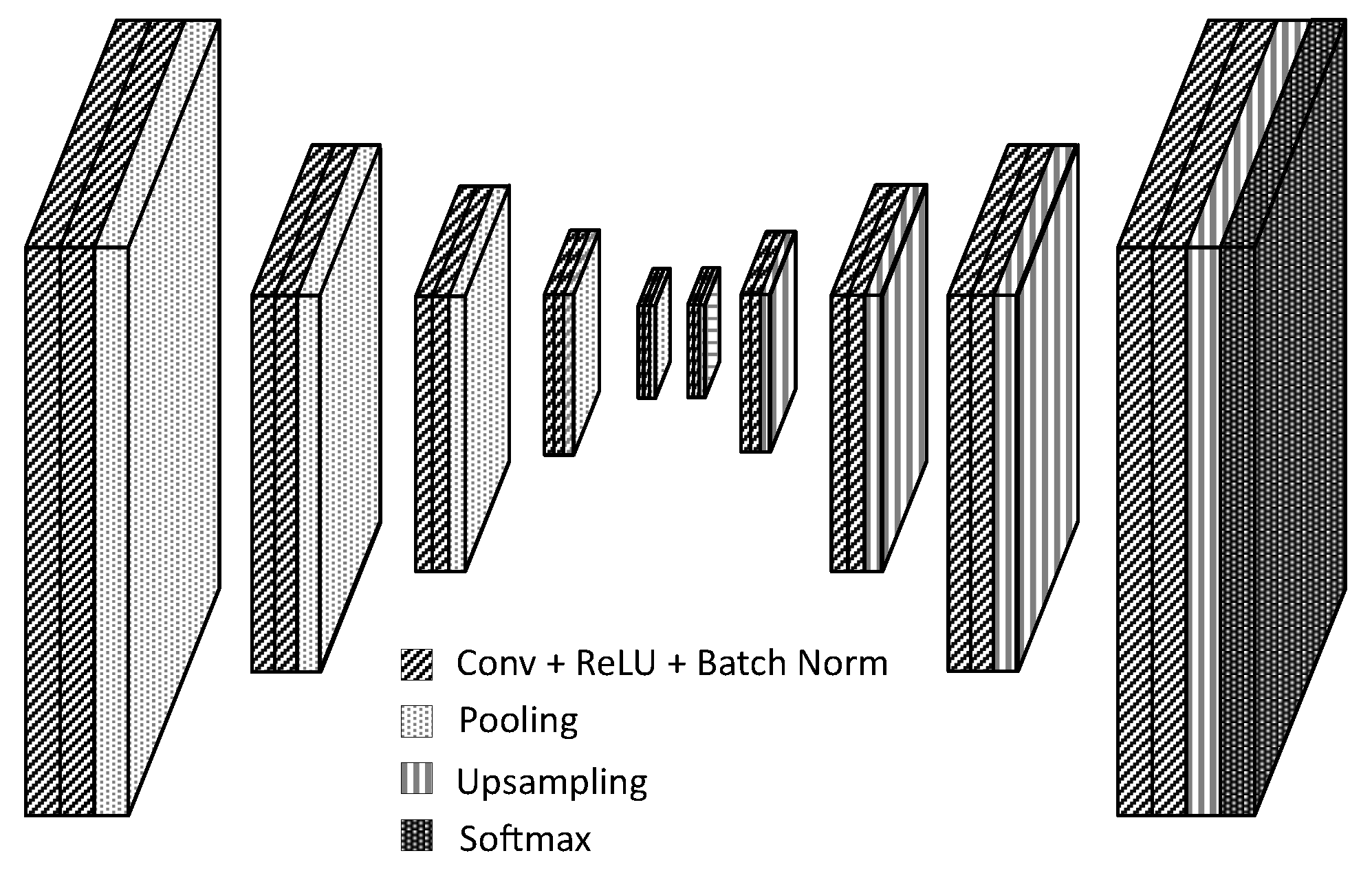
5.2. Fcn for Semantic Segmentation of Spectral Images
6. Experimental Results
6.1. Our Data
6.1.1. The Training Space
6.1.2. The Labels
6.1.3. The Testing Space
6.1.4. Downloading Data
- The training dataset is in the file S2_TrainingData.npy.
- Labels of the training dataset are in the file S2_TrainingLabels.npy.
- A true color representation of the training dataset can be found in S2_Trainingtruecolor.npy.
- The testing dataset and the corresponding labels are in the file S2_TestData.npy.
- Labels of the test dataset are in the file S2_TestLabels.npy.
- Last, a true color representation of the test data can be found in S2_Testtruecolor.npy.
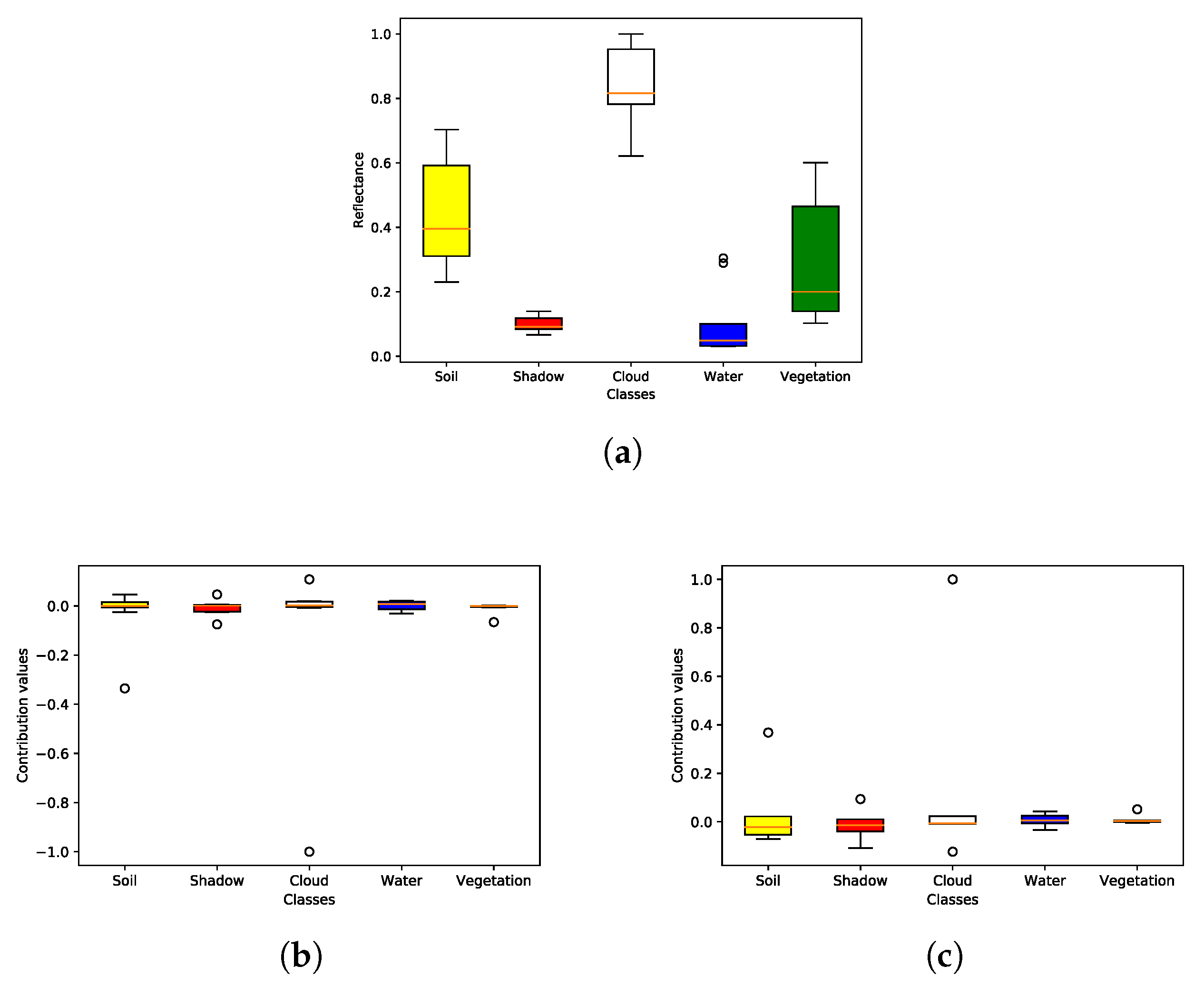
6.2. Classes
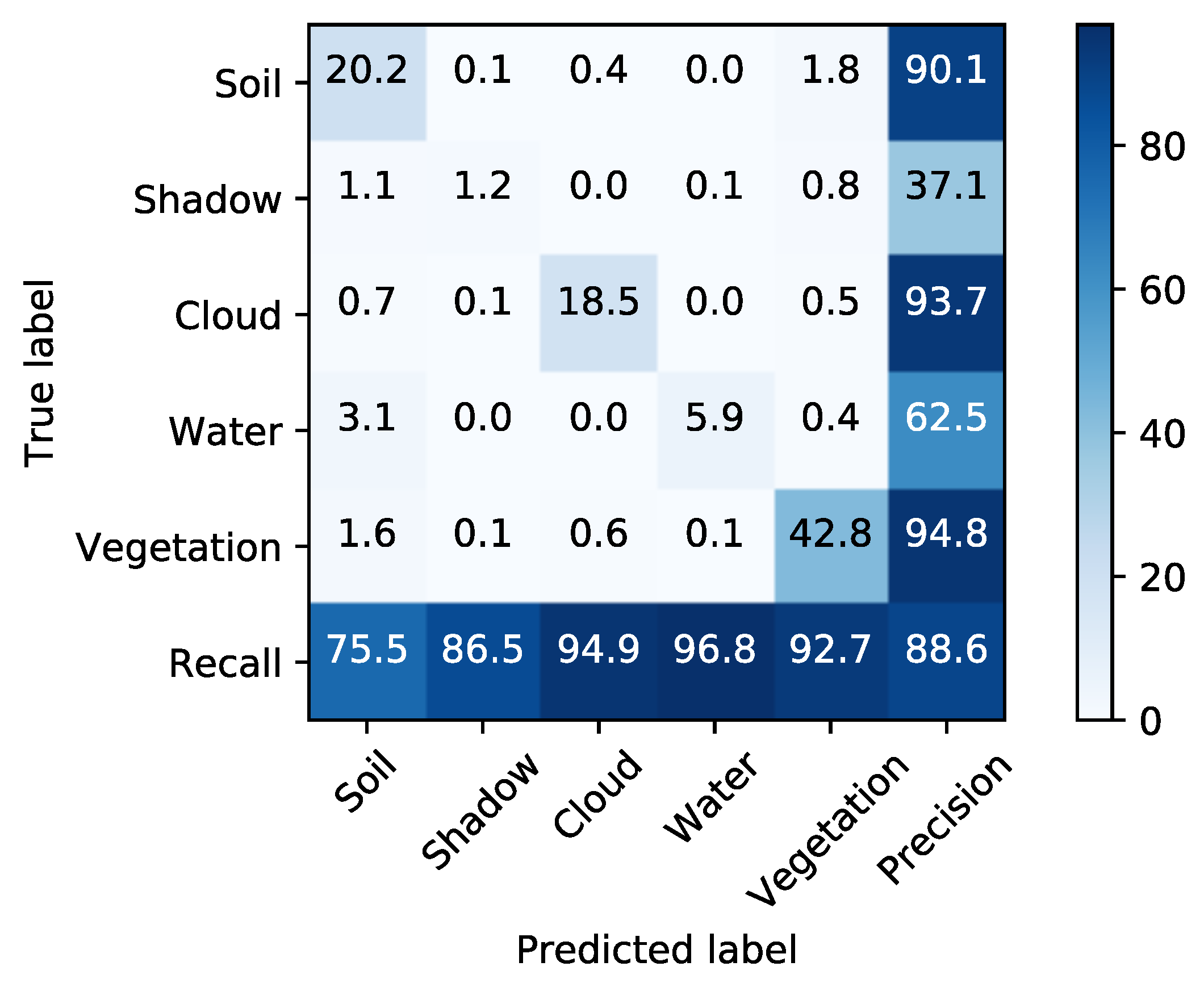
6.3. Metrics
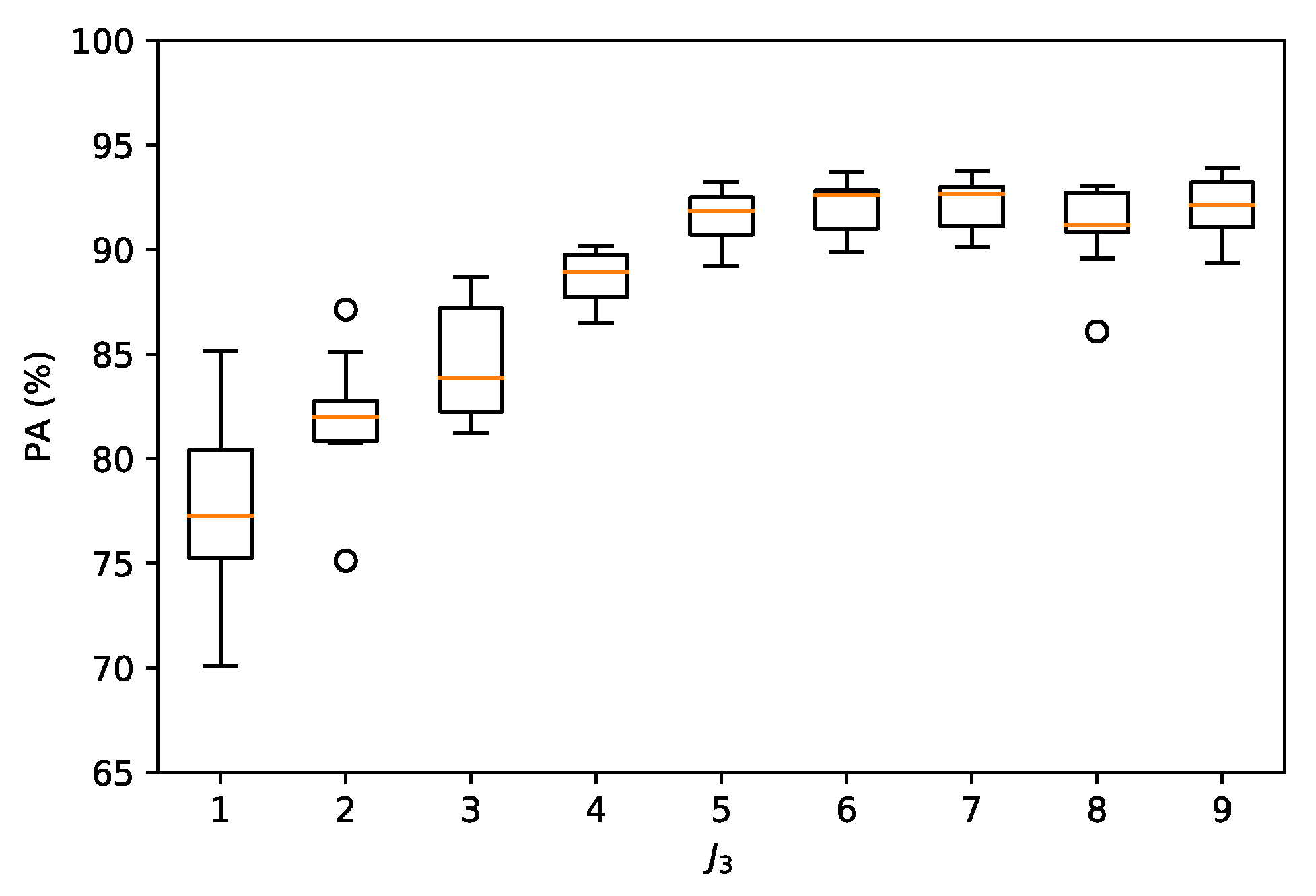
6.3.1. Pixel Accuracy (PA)
- Indexes NDI are important references for pixel-wise classification but they show one of the lowest PAs and the highest computational time.
- Classic PCA with five components shows the lowest PA, although the computational time is similar to HOOI-FCN with five tensor bands.
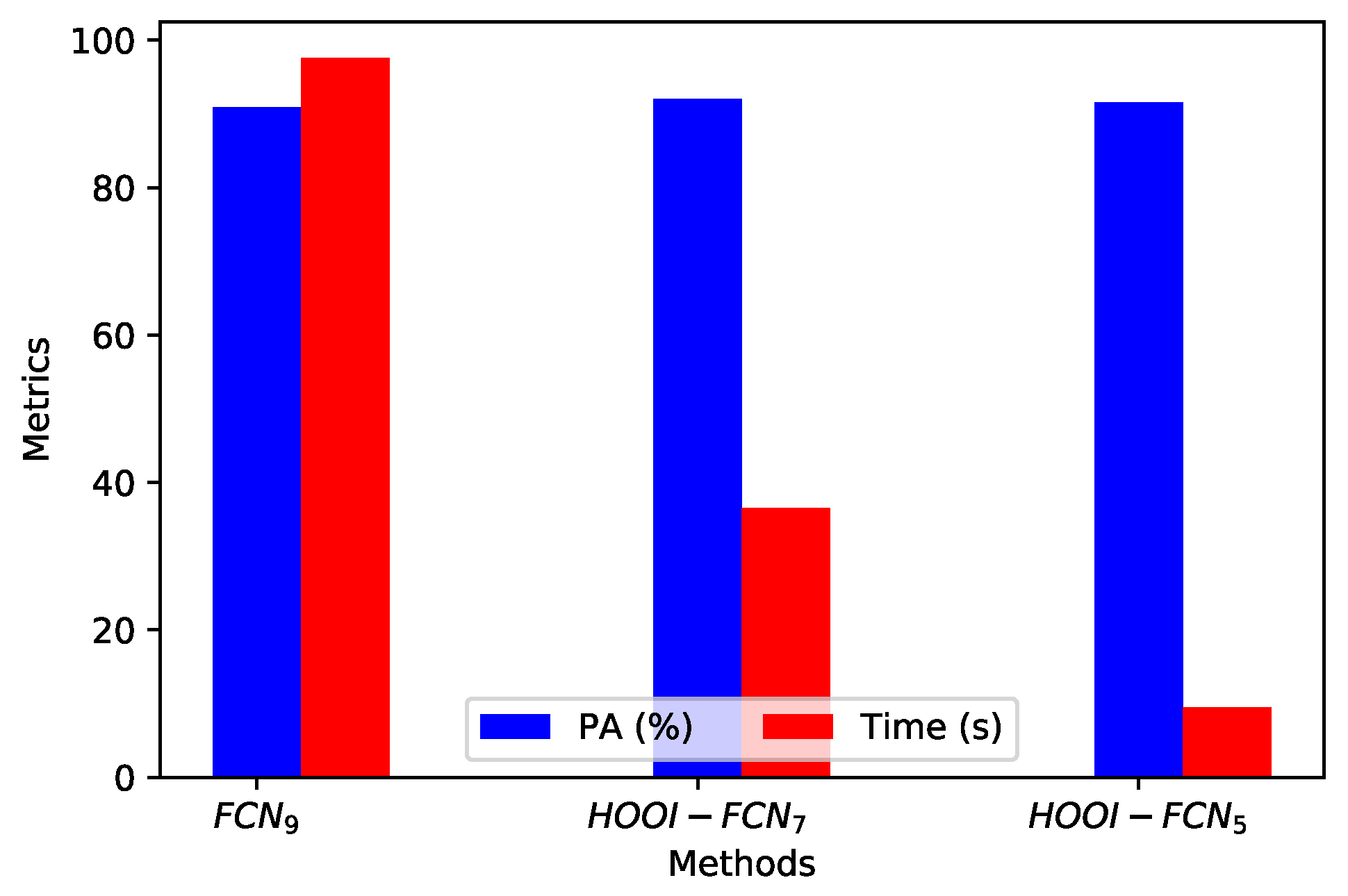
- Due to the poor results of NDI and classical PCA, FCN (with raw data and nine components) is a good reference in terms of performance and computational time, and HOOI-FCN with seven and five tensor bands achieves the highest PA and the lowest computational time.
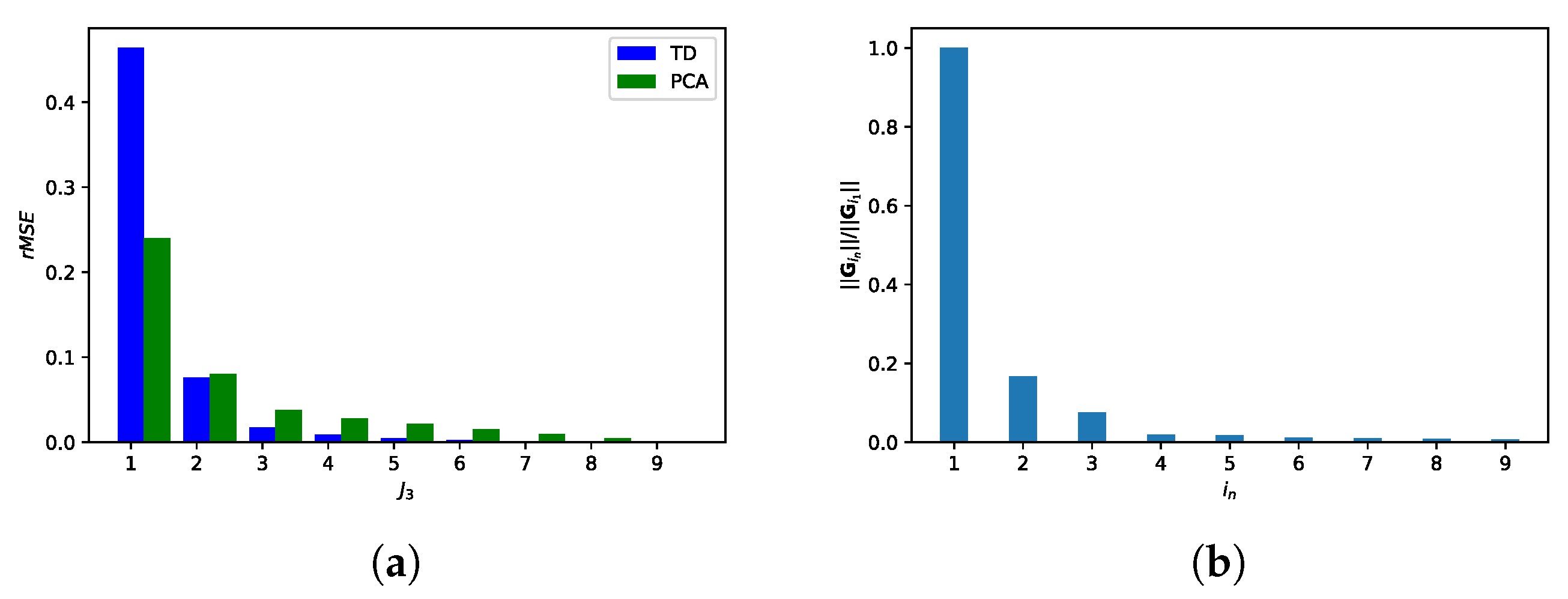
6.3.2. Relative Mean Square Error (rMSE)
6.3.3. Orthogonality Degree of Factor Matrices and Tensor Bands
6.4. Fcn Specifications
6.5. Hardware/Software Specifications
7. Discussion and Comparison with Other Methods
8. Conclusions
Open Issues
- Compression affects not only the input data, but also the CNN network to reduce overall complexity and/or create new ANN architectures for specific RS-CNNMSI or HSI image applications.
- Instead of the HOOI algorithm, use greedy HOOI and other algorithms that determine the core tensor for a broad comparison.
- For classification purposes, use other machine learning algorithms, such as a SVM or random forest.
- Increase the input data with more scenarios and their corresponding ground truth to a deeper study of the behaviors of several classifiers, including those based on ANN, and the scope of the TD methods.
- Denoise the original input data for an improvement of the new subspace of reduced dimensionality.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ANN | artificial neural network |
| CNN | convolutional neural network |
| CPD | canonical polyadic decomposition |
| ESA | european space agency |
| DL | deep learning |
| FCN | fully convolutional network |
| GPU | graphics processing unit |
| HSI | hyperspectral image |
| HOOI | higher order orthogonal iteration |
| HOSVD | higher order singular value decomposition |
| MSE | mean square error |
| ML | machine learning |
| MSI | multispectral image |
| NIR | near-infrared |
| NTD | nonnegative Tucker decomposition |
| NDVI | normalized difference vegetation index |
| NDWI | normalized difference water index |
| PA | pixel accuracy |
| PCA | principal components analysis |
| ReLU | rectified linear unit |
| rMSE | relative mean square error |
| RS | remote sensing |
| SVD | singular value decomposition |
| SWIR | short wave infrared |
| SVM | support vector machine |
| T-MLRD | tensor-based multiscale low rank decomposition |
| TD | tensor decomposition |
| TDA | tensor discriminant analysis |
| TKD | tucker decomposition |
References
- Tempfli, K.; Huurneman, G.; Bakker, W.; Janssen, L.; Feringa, W.; Gieske, A.; Grabmaier, K.; Hecker, C.; Horn, J.; Kerle, N.; et al. Principles of Remote Sensing: An Introductory Textbook, 4th ed.; ITC: Geneva, Switzerland, 2009. [Google Scholar]
- He, Z.; Hu, J.; Wang, Y. Low-rank tensor learning for classification of hyperspectral image with limited labeled sample. IEEE Signal Process. 2017, 145, 12–25. [Google Scholar] [CrossRef]
- Richards, A.; Xiuping, J.J. Band selection in sentinel-2 satellite for agriculture applications. In Remote Sensing Digital Image Analysis, 4th ed.; Springer-Verlag: Berlin, Germany, 2006. [Google Scholar]
- Zhang, T.; Su, J.; Liu, C.; Chen, W.; Liu, H.; Liu, G. Band selection in sentinel-2 satellite for agriculture applications. In Proceedings of the 23rd International Conference on Automation & Computing, University of Huddersfield, Huddersfield, UK, 7–8 September 2017. [Google Scholar]
- Xie, Y.; Zhao, X.; Li, L.; Wang, H. Calculating NDVI for Landsat7-ETM data after atmospheric correction using 6S model: A case study in Zhangye city, China. In Proceedings of the 18th International Conference on Geoinformatics, Beijing, China, 18–20 June 2010. [Google Scholar]
- Gao, B. NDWI—A normalized difference water index for remote sensing of vegetation liquid water from space. Remote Sens. Environ. 1996, 58, 1–6. [Google Scholar] [CrossRef]
- Ham, J.; Chen, Y.; Crawford, M.; Ghosh, J. Investigation of the random forest framework for classification of hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2005, 43, 492–501. [Google Scholar] [CrossRef]
- Hearst, M.A. Support Vector Machines. IEEE Intell. Syst. J. 1998, 13, 18–28. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, L. An SVM Ensemble Approach Combining Spectral, Structural, and Semantic Features for the Classification of High-Resolution Remotely Sensed Imagery. IEEE Trans. Geosci. Remote Sens. 2013, 51, 257–272. [Google Scholar] [CrossRef]
- Delalieux, S.; Somers, B.; Haest, B.; Spanhove, T.; Vanden Borre, J.; Mucher, S. Heathland conservation status mapping through integration of hyperspectral mixture analysis and decision tree classifiers. Remote Sens. Environ. 2012, 126, 222–231. [Google Scholar] [CrossRef]
- Kemker, R.; Salvaggio, C.; Kanan, C. Algorithms for semantic segmentation of multispectral remote sensing imagery using deep learning. ISPRS J. Photogramm. Remote Sens. 2018, 145, 60–77. [Google Scholar] [CrossRef]
- Pirotti, F.; Sunar, F.; Piragnolo, M. Benchmark of machine learning methods for classification of a sentinel-2 image. In Proceedings of the XXIII ISPRS Congress, Prague, Czech Republic, 12–19 July 2016. [Google Scholar]
- Mateo-García, G.; Gómez-Chova, L.; Camps-Valls, G. Convolutional neural networks for multispectral image cloud masking. In Proceedings of the IGARSS, Fort Worth, TX, USA, 23–28 July 2017. [Google Scholar]
- Guo, X.; Huang, X.; Zhang, L.; Zhang, L.; Plaza, A.; Benediktsson, J.A. Support Tensor Machines for Classification of Hyperspectral Remote Sensing Imagery. IEEE Trans. Geosci. Remote Sens. 2016, 54, 3248–3264. [Google Scholar] [CrossRef]
- Cichocki, A.; Mandic, D.; De Lathauwer, L.; Zhou, G.; Zhao, Q.; Caiafa, C.; Phan, H. Tensor Decompositions for Signal Processing Applications: From two-way to multiway component analysis. IEEE Signal Process. Mag. 2015, 32, 145–163. [Google Scholar] [CrossRef]
- Jolliffe, I.T. Principal Component Analysis, 2nd ed.; Springer Verlag: New York, NY, USA, 2002. [Google Scholar]
- Kolda, T.; Bader, B. Tensor Decompositions and Applications. SIAM Rev. 2009, 51, 455–500. [Google Scholar] [CrossRef]
- Lopez, J.; Santos, S.; Torres, D.; Atzberger, C. Convolutional Neural Networks for Semantic Segmentation of Multispectral Remote Sensing Images. In Proceedings of the LATINCOM, Guadalajara, Mexico, 14–16 November 2018. [Google Scholar]
- European Space Agency. Available online: https://sentinel.esa.int/web/sentinel/missions/sentinel-2 (accessed on 15 July 2019).
- Kemker, R.; Kanan, C. Deep Neural Networks for Semantic Segmentation of Multispectral Remote Sensing Imagery. arXiv 2017, arXiv:abs/1703.06452. [Google Scholar]
- Hamida, A.; Benoît, A.; Lambert, P.; Klein, L.; Amar, C.; Audebert, N.; Lefèvre, S. Deep learning for semantic segmentation of remote sensing images with rich spectral content. In Proceedings of the IGARSS, Fort Worth, TX, USA, 23–28 July 2017. [Google Scholar]
- Wang, Q.; Lin, J.; Yuan, Y. Salient Band Selection for Hyperspectral Image Classification via Manifold Ranking. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 1279–1289. [Google Scholar] [CrossRef]
- Li, S.; Qiu, J.; Yang, X.; Liu, H.; Wan, D.; Zhu, Y. A novel approach to hyperspectral band selection based on spectral shape similarity analysis and fast branch and bound search. Eng. Appl. Artif. Intell. 2014, 27, 241–250. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, L.; Tao, D.; Huang, X.; Du, B. Compression of hyperspectral remote sensing images by tensor approach. Neurocomputing 2015, 147, 358–363. [Google Scholar] [CrossRef]
- Astrid, M.; Lee, S.I. CP-decomposition with Tensor Power Method for Convolutional Neural Networks compression. In Proceedings of the BigComp, Jeju, Korea, 13–16 February 2017. [Google Scholar]
- Chien, J.; Bao, Y. Tensor-factorized neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 1998–2011. [Google Scholar] [CrossRef] [PubMed]
- An, J.; Lei, J.; Song, Y.; Zhang, X.; Guo, J. Tensor Based Multiscale Low Rank Decomposition for Hyperspectral Images Dimensionality Reductio. Remote Sens. 2019, 11, 1485. [Google Scholar] [CrossRef]
- Li, J.; Liu, Z. Multispectral Transforms Using Convolution Neural Networks for Remote Sensing Multispectral Image Compression. Remote Sens. 2019, 11, 759. [Google Scholar] [CrossRef]
- An, J.; Song, Y.; Guo, Y.; Ma, X.; Zhang, X. Tensor Discriminant Analysis via Compact Feature Representation for Hyperspectral Images Dimensionality Reduction. Remote Sens. 2019, 11, 1822. [Google Scholar] [CrossRef]
- Absil, P.-A.; Mahony, R.; Sepulchre, R. Optimization Algorithms on Matrix Manifolds, 1st ed.; Princeton University Press: Princeton, NJ, USA, 2007. [Google Scholar]
- De Lathauwer, L.; De Moor, B.; Vandewalle, J. On the best rank-1 and rank-(R 1, R 2, ···, R N) approximation of higher-order tensors. SIAM J. Matrix Anal. Appl. 2000, 21, 1324–1342. [Google Scholar] [CrossRef]
- De Lathauwer, L.; De Moor, B.; Vandewalle, J. A Multilinear Singular Value Decomposition. SIAM J. Matrix Anal. Appl. 2000, 21, 1253–1278. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning, 1st ed.; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Sheehan, B.N.; Saad, Y. Higher Order Orthogonal Iteration of Tensors (HOOI) and its Relation to PCA and GLRAM. In Proceedings of the 7th SIAM International Conference on Data Mining, Minneapolis, MN, USA, 26–28 April 2007. [Google Scholar]
- Badrinarayanan, V.; Kendall, A.; Cipolla, R. SegNet: A Deep Convolutional Encoder-Decoder Architecture for Image Segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 2481–2495. [Google Scholar] [CrossRef] [PubMed]
- Rodes, I.; Inglada, J.; Hagolle, O.; Dejoux, J.; Dedieu, G. Sampling strategies for unsupervised classification of multitemporal high resolution optical images over very large areas. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012. [Google Scholar]
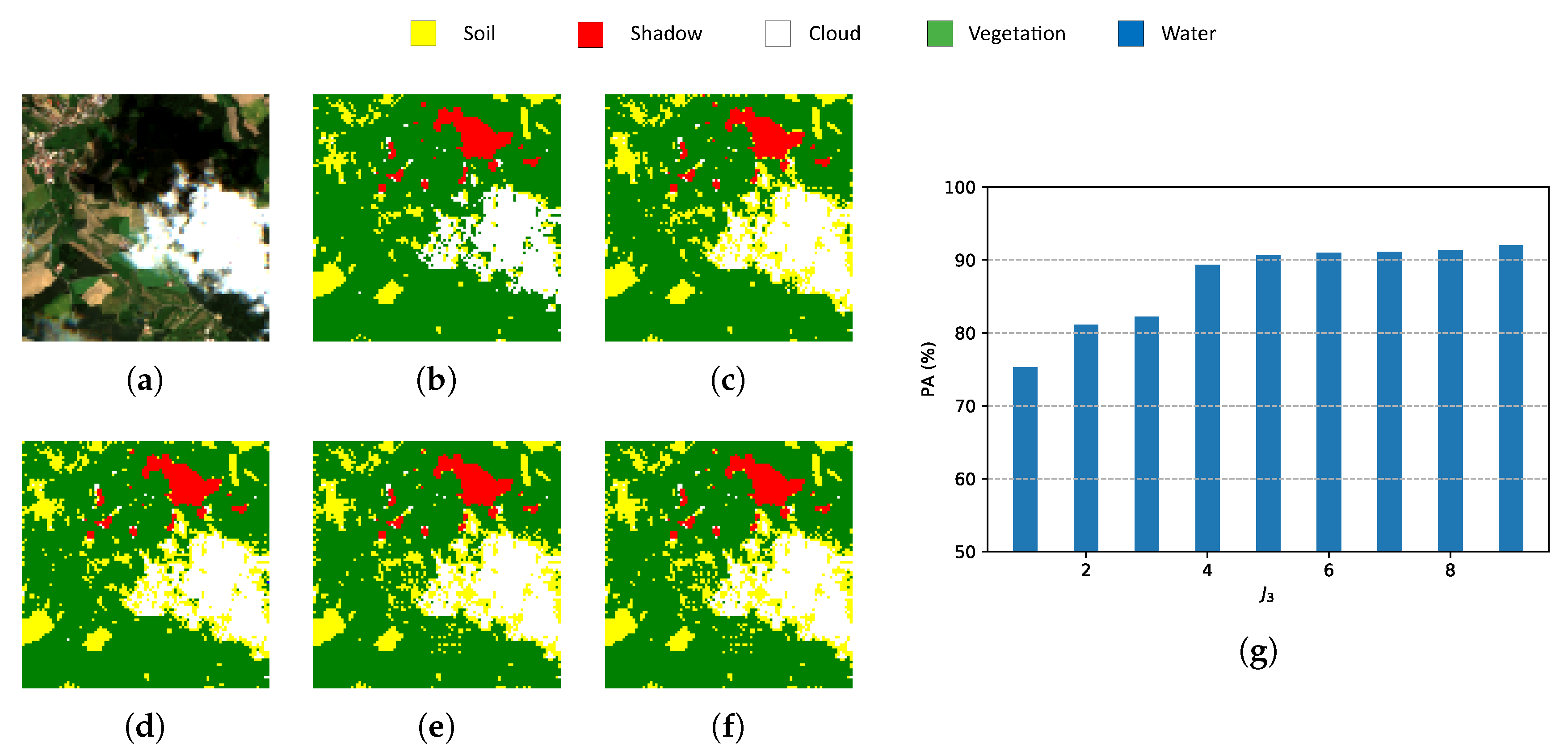
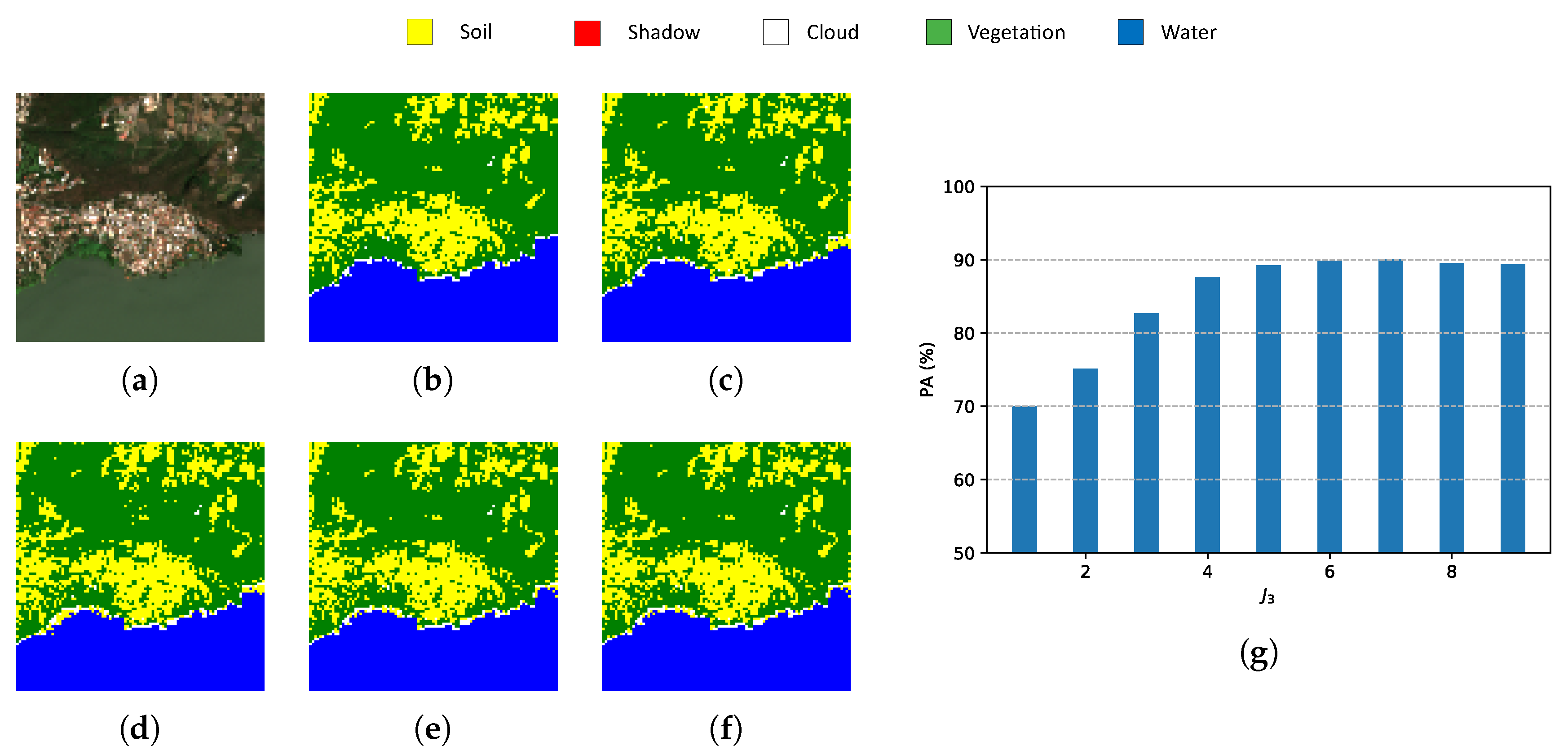
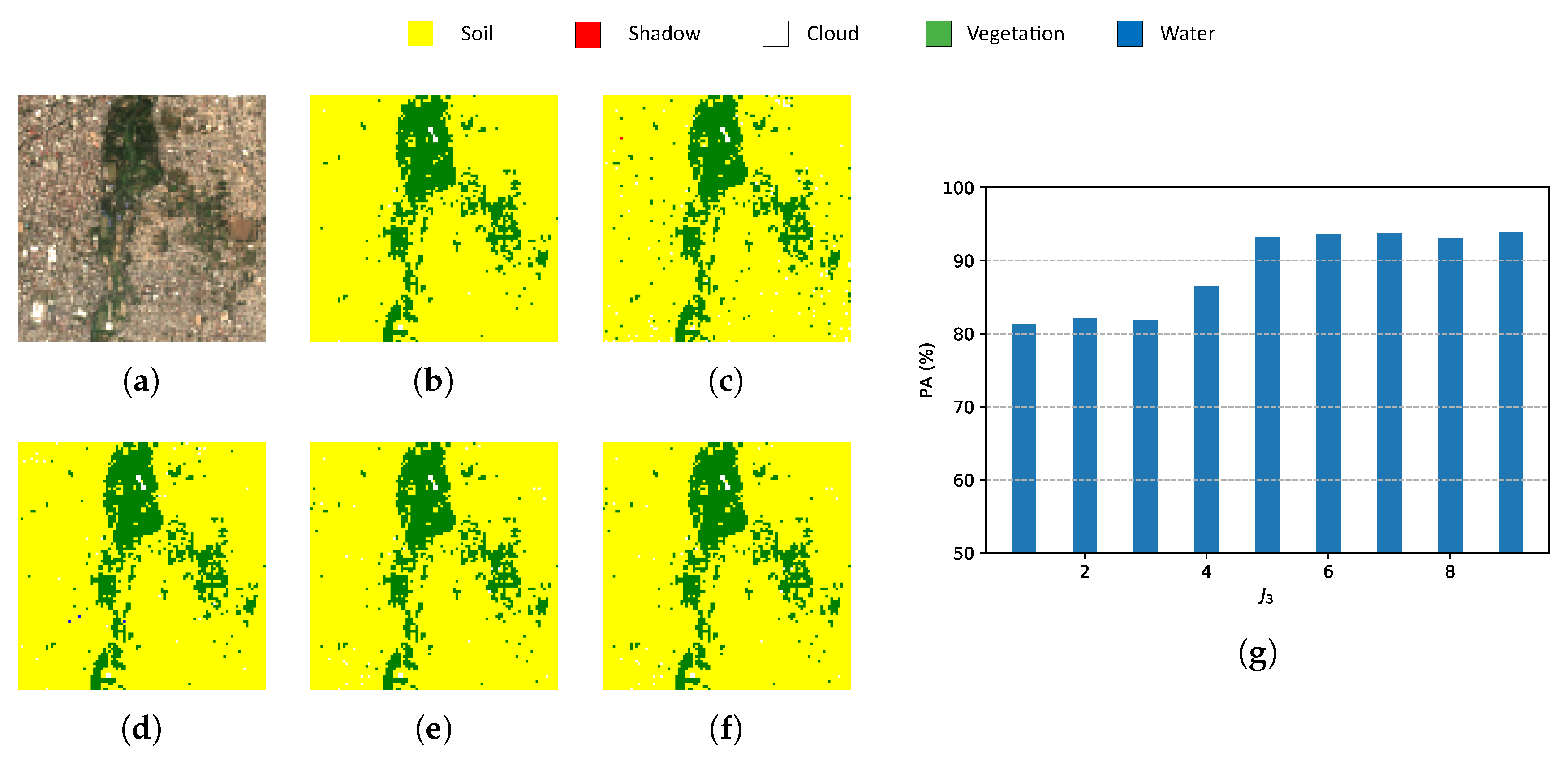
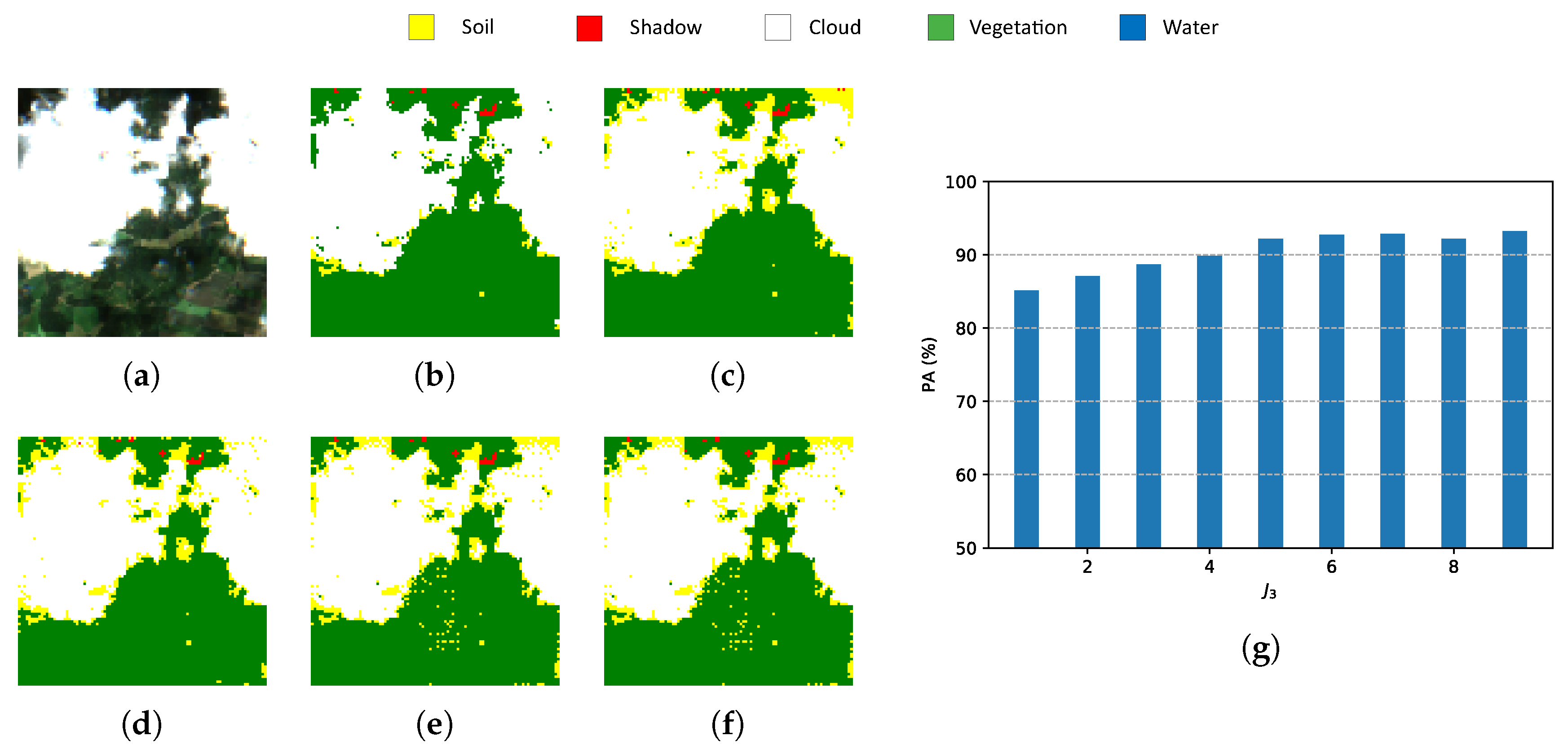
| Reference | Input | Decomposition | Reduction | Classifier |
|---|---|---|---|---|
| Li, S. et al. [23] (2014) | HSI | - | Band selection | SVM |
| Zhang, L. et al. [24] (2015) | HSI | TKD | Spatial-Spectral | - |
| Wan, Q. et al. [22] (2016) | HSI | - | Band selection | SVM/kNN/CART |
| Kemke, R. et al. [11] (2017) | MSI | - | - | CNN |
| Hamida, A. et al. [21] (2017) | MSI | - | - | CNN |
| Li, J. et al. [28] (2019) | MSI | NTD-CNN | Spatial-spectral | - |
| An, J. et al. [27] (2019) | HSI | T-MLRD | Spatial-spectral | SVM/1NN |
| An, J. et al. [29] (2019) | HSI | TDA | Spatial-spectral | SVM/1NN |
| Our framework (2019) | MSI | HOOI | Spectral | FCN |
| , A, a, a | Tensor, matrix, vector and scalar respectively |
|---|---|
| N-order tensor of size . | |
| An element of a tensor | |
| , , and | Column, row and tube fibers of a third order tensor |
| , , | Horizontal, lateral and frontal slices for a third order tensor |
| , | A matrix/vector element from a sequence of matrices/vectors |
| Mode-n matricization of a tensor. | |
| Outer product of N vectors, where | |
| Inner product of two tensors. | |
| n-mode product of tensor by a matrix along axis n. |
| Scenarios | NDI | FCN9 | PCA-FCN5 | HOOI-FCN7 | HOOI-FCN5 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| PA (%) | Time (s) | PA (%) | Time (s) | PA (%) | Time (s) | PA (%) | Time (s) | PA (%) | Time (s) | |
| 1 | 88.20 | 363.03 | 91.05 | 101.21 | 85.12 | 9.85 | 91.12 | 37.84 | 90.63 | 9.13 |
| 2 | 84.75 | 412.89 | 92.21 | 87.54 | 84.60 | 9.83 | 90.12 | 36.54 | 89.23 | 9.06 |
| 3 | 92.34 | 307.56 | 93.67 | 93.45 | 88.32 | 10.00 | 93.75 | 36.02 | 93.22 | 9.03 |
| 4 | 90.08 | 382.31 | 91.72 | 98.92 | 86.08 | 9.73 | 92.85 | 36.79 | 92.18 | 8.93 |
| 5 | 87.14 | 400.12 | 89.91 | 103.57 | 86.36 | 9.12 | 92.13 | 35.88 | 91.84 | 9.67 |
| 6 | 89.75 | 312.15 | 90.95 | 95.21 | 87.65 | 10.15 | 92.95 | 37.23 | 92.71 | 10.09 |
| 7 | 85.73 | 373.84 | 89.92 | 107.13 | 88.47 | 9.63 | 93.06 | 35.56 | 92.59 | 9.55 |
| 8 | 91.49 | 308.00 | 90.17 | 95.45 | 85.78 | 9.76 | 90.23 | 36.34 | 90.12 | 9.14 |
| 9 | 89.38 | 397.92 | 90.74 | 80.33 | 87.91 | 10.26 | 92.50 | 37.09 | 92.18 | 10.11 |
| 10 | 90.01 | 352.66 | 88.52 | 112.85 | 84.32 | 9.88 | 91.17 | 35.53 | 90.97 | 9.85 |
| Average | 88.87 | 361.04 | 90.88 | 97.56 | 86.46 | 9.82 | 91.97 | 36.48 | 91.56 | 9.45 |
| Tensor Band | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | - | ||||||||
| 2 | - | - | |||||||
| 3 | - | - | - | ||||||
| 4 | - | - | - | - | |||||
| 5 | - | - | - | - | - | ||||
| 6 | - | - | - | - | - | - | |||
| 7 | - | - | - | - | - | - | - | ||
| 8 | - | - | - | - | - | - | - | - |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
López, J.; Torres, D.; Santos, S.; Atzberger, C. Spectral Imagery Tensor Decomposition for Semantic Segmentation of Remote Sensing Data through Fully Convolutional Networks. Remote Sens. 2020, 12, 517. https://doi.org/10.3390/rs12030517
López J, Torres D, Santos S, Atzberger C. Spectral Imagery Tensor Decomposition for Semantic Segmentation of Remote Sensing Data through Fully Convolutional Networks. Remote Sensing. 2020; 12(3):517. https://doi.org/10.3390/rs12030517
Chicago/Turabian StyleLópez, Josué, Deni Torres, Stewart Santos, and Clement Atzberger. 2020. "Spectral Imagery Tensor Decomposition for Semantic Segmentation of Remote Sensing Data through Fully Convolutional Networks" Remote Sensing 12, no. 3: 517. https://doi.org/10.3390/rs12030517
APA StyleLópez, J., Torres, D., Santos, S., & Atzberger, C. (2020). Spectral Imagery Tensor Decomposition for Semantic Segmentation of Remote Sensing Data through Fully Convolutional Networks. Remote Sensing, 12(3), 517. https://doi.org/10.3390/rs12030517






