An Assessment of Using Remote Sensing-based Models to Estimate Ground Surface Soil Heat Flux on the Tibetan Plateau during the Freeze-thaw Process
Abstract
1. Introduction
2. Study Regions and Data
2.1. Study Regions
2.2. Data Sources
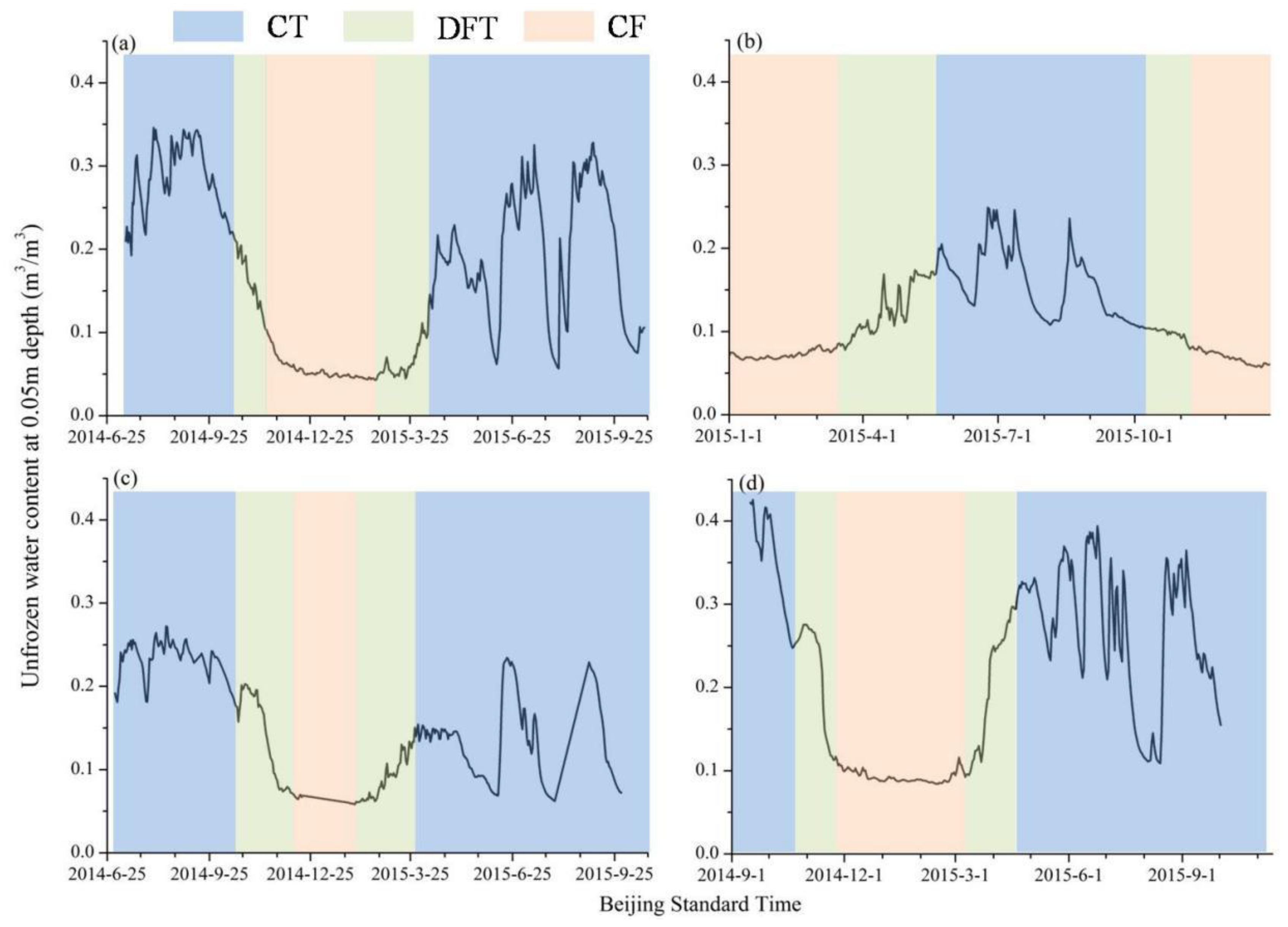
2.2.1. In-Situ Measurement Data
2.2.2. Remote Sensing Data (MODIS) and China Meteorological Forcing Dataset
3. Methods
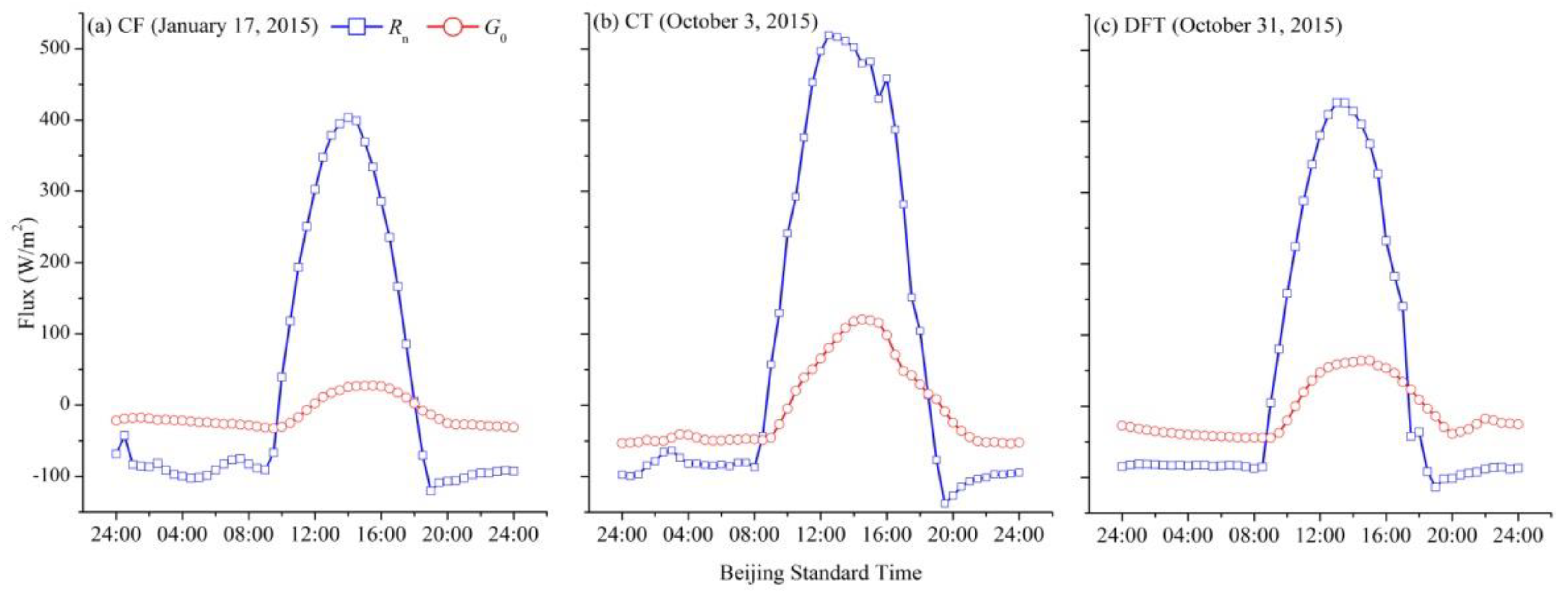
3.1. Estimate G0 at a Site
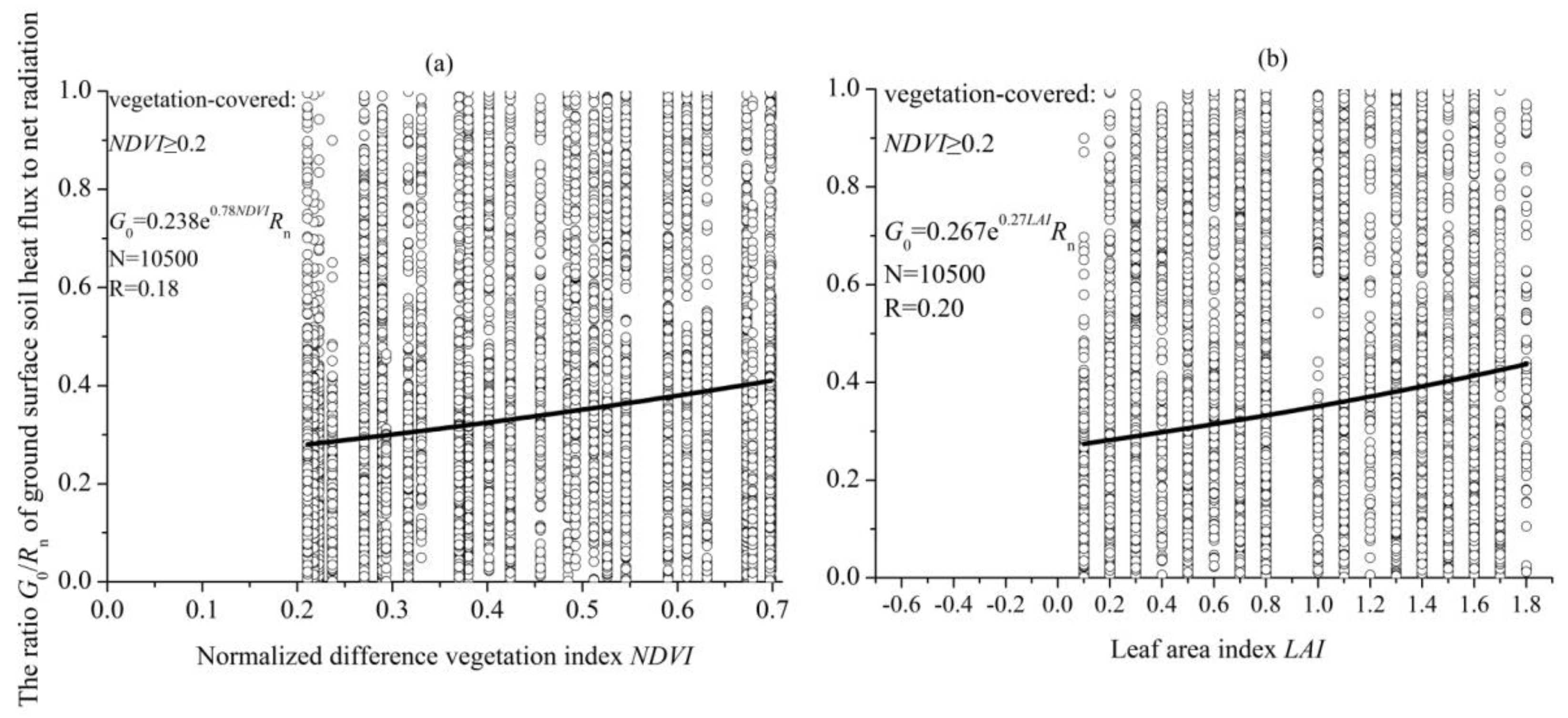
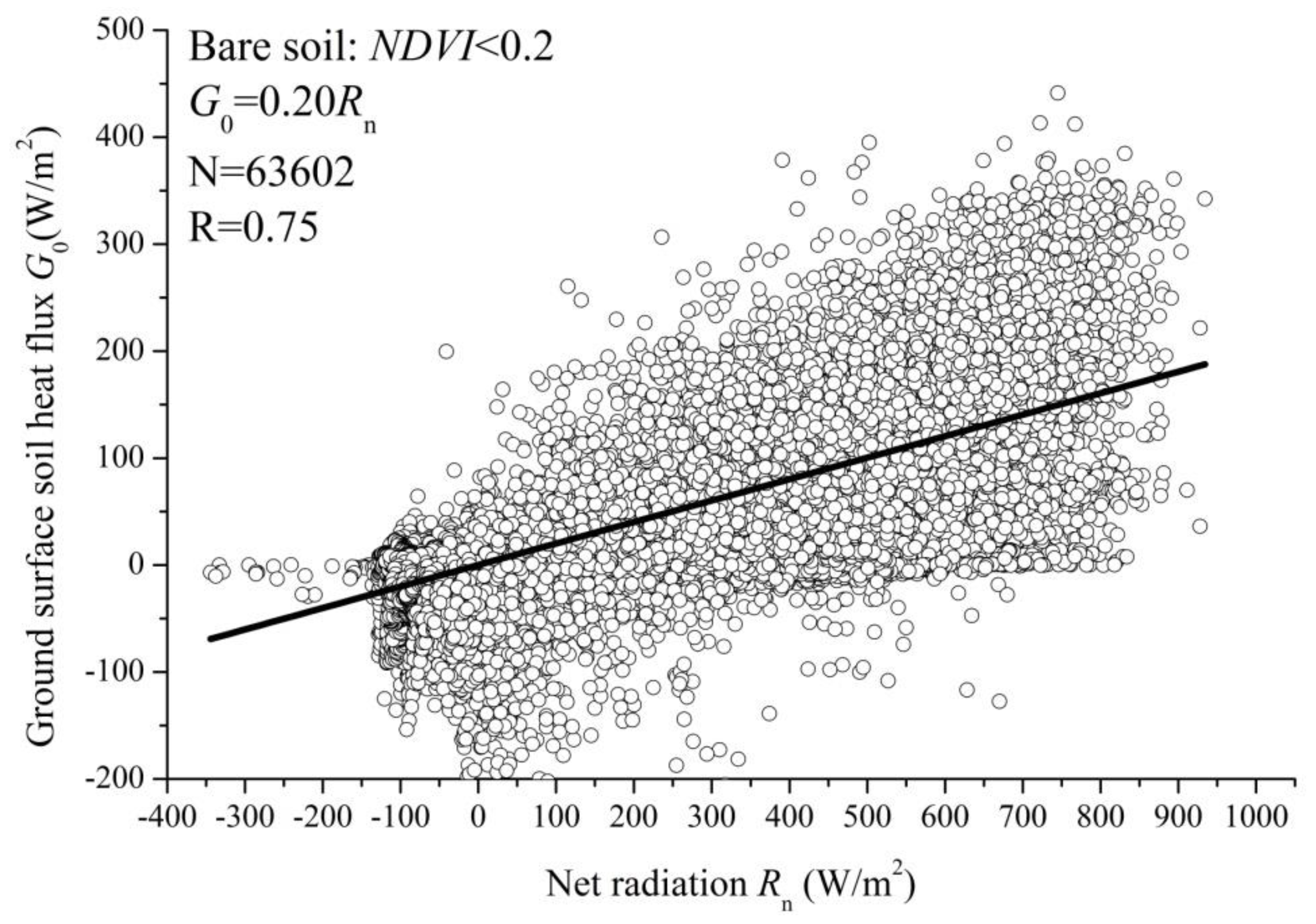
3.2. Introduction and Adjustments to G0 Parameterization Schemes
3.2.1. Introduction and Adjustments to G0 Parameterization Schemes
3.2.2. Indicators to Evaluate the Applicability of G0 Parameterization Schemes
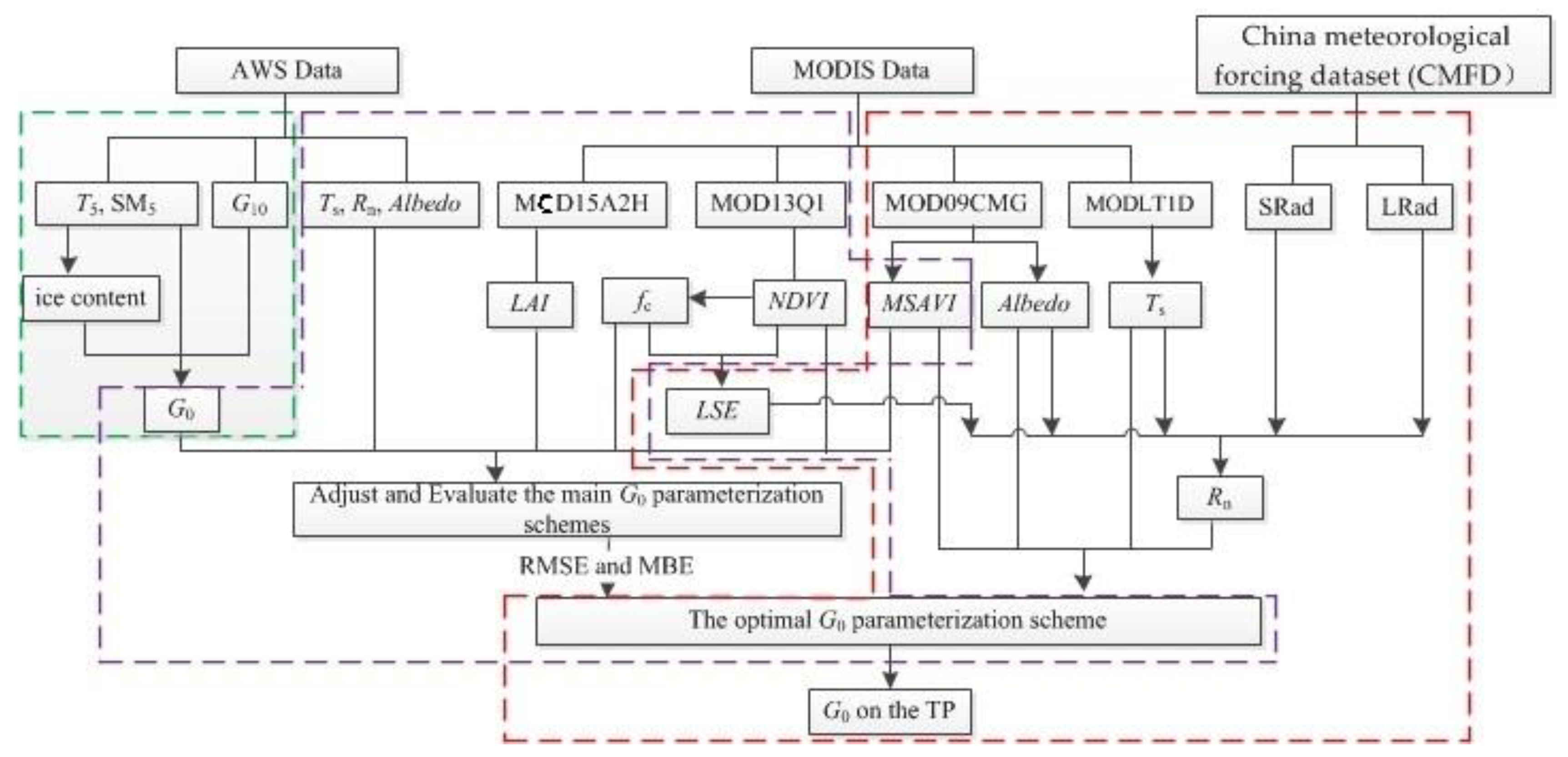
3.3. Estimating Regional G0 on the TP
4. Results
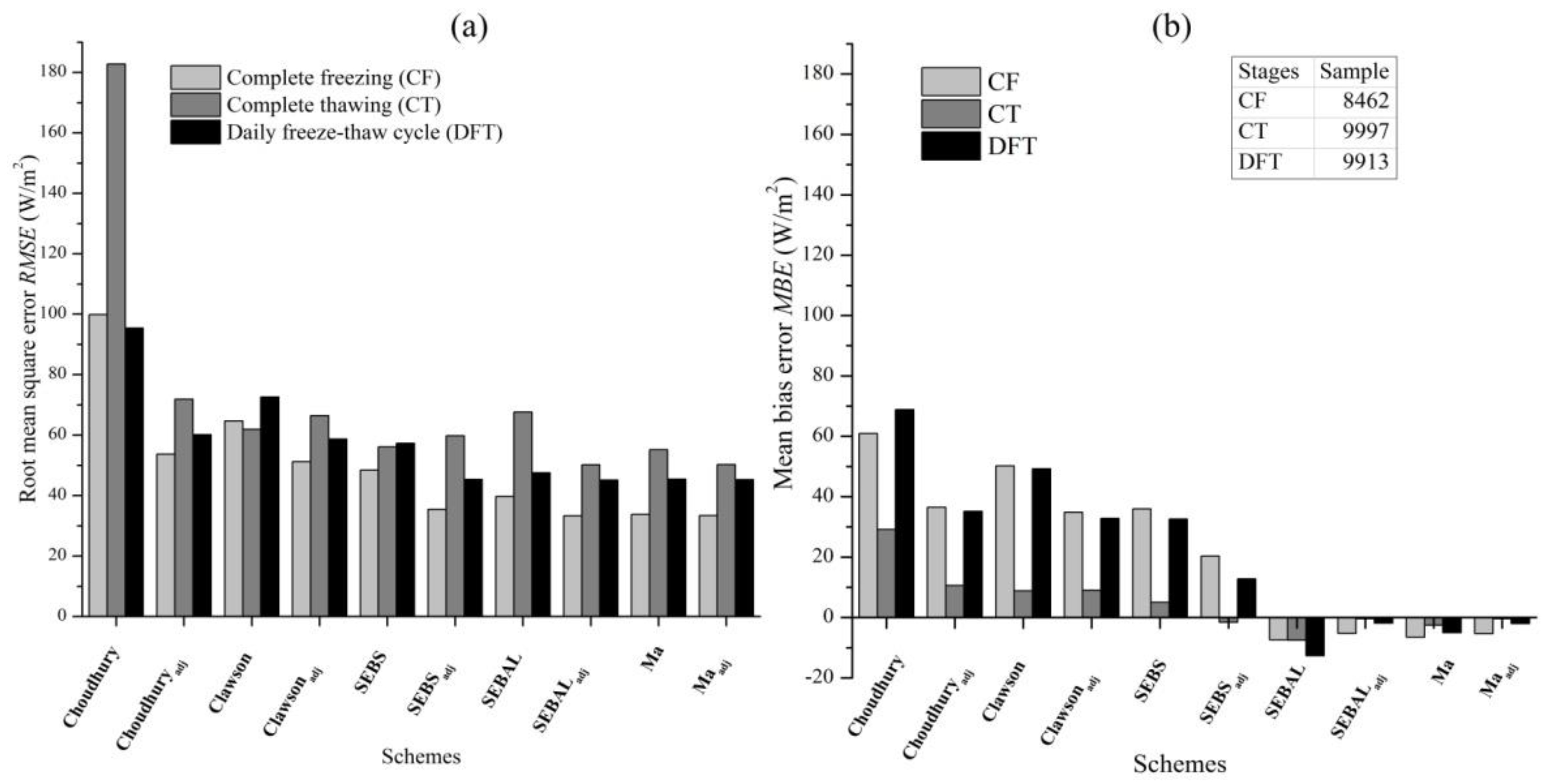
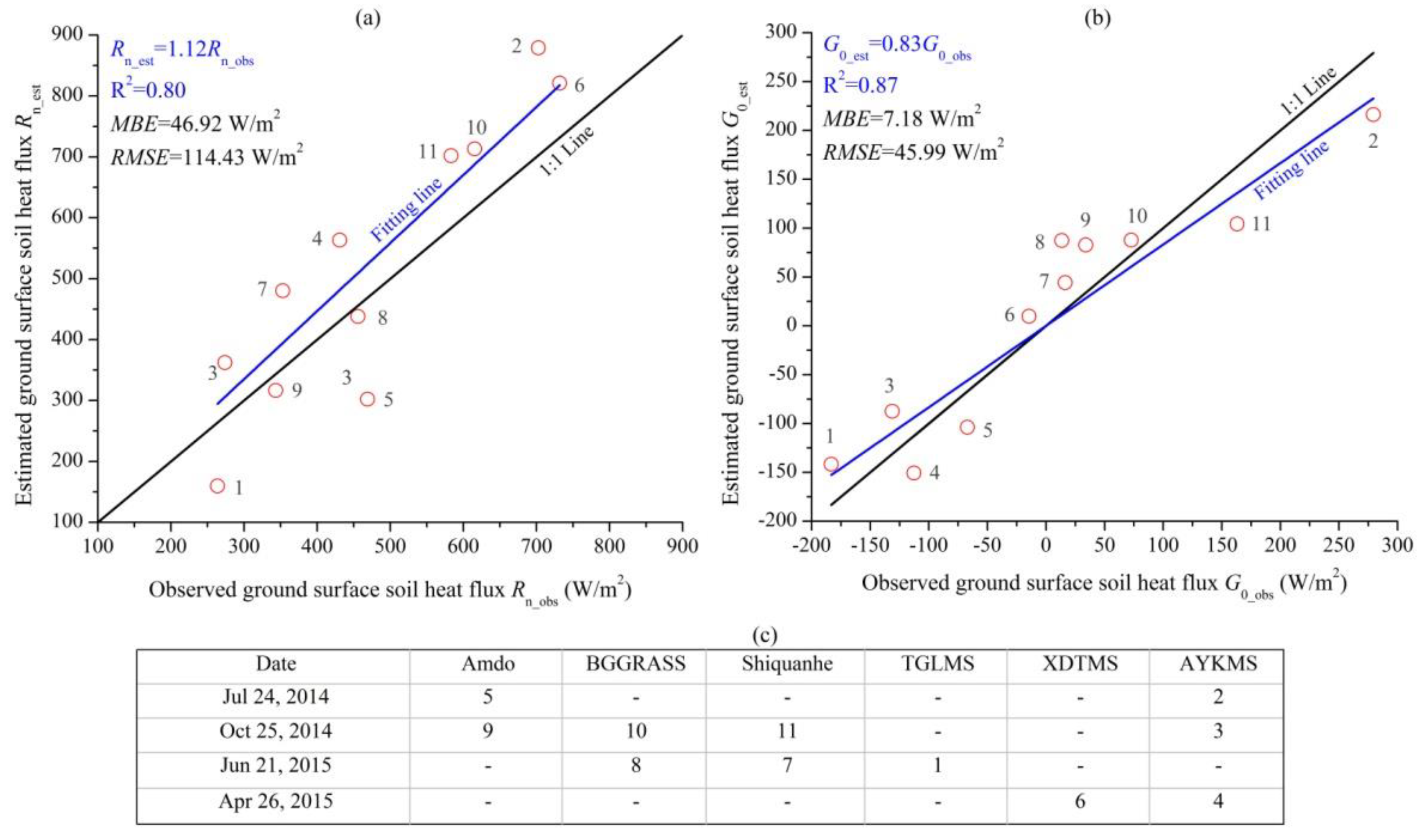
4.1. Errors of the Schemes during the Freeze-Thaw Process
4.2. Regional G0 on the TP
5. Discussion
5.1. The Sensitivity of Remote Sensing-Based Schemes to Land Surface Parameters
5.2. Analysis of the Causes of the Scheme Errors
6. Conclusions
- (1)
- The RMSE of each scheme was significantly different during the freeze-thaw cycle on the TP; meanwhile, the RMSE values of the three stages can be roughly presented as a whole: CF < DFT < CT. The MBE of the CT stage, whether overestimated or underestimated, was less than that of the other two stages, while the MBE values of the other two stages were close. Overall, RMSE values of the second group of schemes (SEBAL, Ma, SEBALadj, and Maadj) were smaller than that of the first group of schemes (Choudhury, Clawson, SEBS, Choudhuryadj, Clawsonadj, and SEBSadj). The MBE values tell us the G0 values simulated by the first group of schemes were obviously overestimated, and those of the second group of schemes are weakly underestimated.
- (2)
- In the absence of measured data, the Maadj scheme can be considered for estimating G0 on the TP; its RMSE and MBE were the least among all the schemes.
- (3)
- AVaccuracy of the second group of schemes was less and their simulated results were relatively more stable than those of the first group of schemes during the freeze-thaw process on the TP.
- (4)
- We discussed four possible reasons for the errors of the main schemes. Soil moisture, the phase difference between G0 and Rn, whether each main scheme can correctly capture the propagation direction of G0, and the accuracy of remote sensing data resulted in errors for the scheme analog results.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. (Adjustments to G0 Parameterization Schemes)
- (1)
- Maadj/SEBALadj
| Parameters | a | b | c | d | e | R2 | N |
|---|---|---|---|---|---|---|---|
| Value | 0.0084 | 0.0018 | 0.00116 | 0.96 | 4 | 0.45 | 38,368 |
- (2)
- Clawsonadj/Choudhuryadj
- (3)
- SEBSadj
References
- Ma, W.; Ma, Y.; Hu, Z.; Li, M.; Sun, F.; Gu, L.; Wang, J.; Qian, Z. The contrast between the radiation budget plus seasonal variation and remote sensing over the northern Tibetan Plateau. J. Arid Land Resour. Environ. 2005, 19, 109–115. [Google Scholar]
- Xiao, Y.; Zhao, L.; Li, R.; Yao, J. Seasonal variation characteristics of surface energy budget components in permafrost regions of northern Tibetan Plateau. J. Glaciol. Geocryol. 2011, 33, 1033–1039. [Google Scholar]
- Ye, D.; Gao, Y. Meteorology of Qinghai-Tibet Plateau; Science press: Beijing, China, 1979. [Google Scholar]
- Wu, G. Recent progress in the study of the Qinghai-Xizang Plateau climate dynamics in China. Quat. Sci. 2004, 24, 1–9. [Google Scholar]
- Shan, C.H.; Bo, S.Z. Simulation of Land-Atmosphere Exchange Processes at Amdo and Gaize Stations over Qinghai-Xizang Plateau. Plateau Meteorol. 2005, 24, 9–15. [Google Scholar]
- Ma, Y.M.; Yao, T.D.; Wang, J.M. Experimental Study of Energy and Water Cycle in Tibetan Plateau—The Progress Introduction on the Study of GAME/Tibet and CAMP/Tibet. Plateau Meteorol. 2006, 25, 344–351. [Google Scholar]
- Yang, K.; Wang, J. A temperature prediction-correction method for estimating surface soil heat flux from soil temperature and moisture data. Sci. China Ser. D 2008, 51, 721–729. [Google Scholar] [CrossRef]
- Li, S.X.; Nan, Z.; Lin, Z. Impact of Soil Freezing and Thawing Process on Thermal Exchange between Atmosphere and Ground Surface. J. Glaciol. Geocryol. 2002, 24, 506–511. [Google Scholar]
- Yang, M.X.; Yao, T.; Hirose, N.; Fujii, H. Diurnal freezing-thawing cycle of topsoil in Qinghai-Tibet Plateau. Chin. Sci. Bull. 2006, 51, 1974–1976. [Google Scholar]
- Guo, D.L.; Xue, Y.M.; Min, L.; Peng, Q. Analysis on Simulation of Characteristic of Land Surface Energy Flux in Seasonal Frozen Soil Region of Central Tibetan Plateau. Plateau Meteorol. 2009, 28, 978–987. [Google Scholar]
- William, P.J.; Smith, M.W. The Frozen Earth: Fundamentals of Geocryology; Cambridge University Press: Cambridge, UK, 1989. [Google Scholar]
- Xu, Z.W.; Liu, S.M.; Xu, T.R.; Ding, C. The observation and calculation method of soil heat flux and its impact on the energy balance closure. Adv. Earth Sci. 2013, 28, 875–889. [Google Scholar]
- Bastiaanssen, W.G.M. SEBAL-based sensible and latent heat fluxes in the irrigated Gediz Basin, Turkey. J Hydrol. 2000, 229, 87–100. [Google Scholar] [CrossRef]
- Wang, J.M.; Ma, Y.M.; Menenti, M.; Bastiaanssen, W.; Mitsuta, Y. The scaling-up of processes in the heterogeneous landscape of HEIFE with the aid of satellite remote sensing. J. Meteorol. Soc. Jpn. 1995, 73, 1235–1244. [Google Scholar] [CrossRef]
- Jackson, R.D.; Moran, M.S.; Gay, L.W.; Raymond, L.H. Evaluating Evaporation from Field Crops Using Airborne Radiometry and Ground-Based Meteorological Data. Irrig. Sci. 1987, 8, 81–90. [Google Scholar] [CrossRef]
- Moran, M.S.; Jackson, R.D.; Raymond, L.H.; Gay, L.W.; Slater, P.N. Mapping surface energy balance components by combining Landsat thermatic mapper and ground-based meteorological data. Remote Sens. Environ. 1989, 30, 77–87. [Google Scholar] [CrossRef]
- Choudhury, B.J.; Bjso, S.B.; Rejinato, R.J. Analysis of an empirical model for soil heat flux under a growing wheat crop for estimating evaporation by an infrared-temperature based energy balance equation. Agric. For. Meteorol. 1987, 39, 283–297. [Google Scholar] [CrossRef]
- Su, Z. The Surface Energy Balance System (SEBS) for estimation of turbulent heat fluxes. Hydrol. Earth Syst. Sci. 2002, 6, 85–100. [Google Scholar] [CrossRef]
- Ma, Y.M.; Ishikawa, H.; Tsukamoto, O.; Menenti, M.; Su, Z.B.; Yao, T.D.; Koike, T.; Yasunari, T. Regionalization of surface fluxes over heterogeneous landscape of the Tibetan Plateau by using satellite remote sensing data. J. Meteorol. Soc. Jpn. 2003, 81, 277–293. [Google Scholar] [CrossRef]
- Ma, Y.M.; Wang, J.M.; Huang, R.H.; Wei, G.; Menenti, M.; Su, Z.B.; Hu, Z.Y.; Gao, F.; Wen, J. Remote sensing parameterization of land surface heat fluxes over arid and semi-arid areas. Adv. Atmos. Sci. 2003, 20, 530–539. [Google Scholar]
- Ma, Y.M.; Ma, W.Q.; Li, M.S.; Sun, F.L.; Wang, J.M. Remote Sensing Parameterization of Land Surface Heat Fluxes over the Middle Reaches of the Heihe River. J. Desert Res. 2004, 24, 392–399. [Google Scholar]
- Ma, Y.M.; Xue, D.Y.; Ma, W.Q.; Li, M.S.; Wang, J.M.; Wen, J.; Sun, F.L. Satellite Remote Sensing Parameterization of Regional Land Surface Heat Fluxes over Heterogeneous Surface of Arid and Semi-Arid Areas. Plateau Meteorol. 2004, 23, 139–146. [Google Scholar]
- Cheng, Y.; Wu, T.; Wang, J.; Yao, J.; Li, R.; Zhao, L.; Xie, C.; Zhu, X.; Ni, J.; Hao, J. Estimating Surface Soil Heat Flux in Permafrost Regions Using Remote Sensing-Based Models on the Northern Qinghai-Tibetan Plateau under Clear-Sky Conditions. Remote Sens. 2019, 11, 416. [Google Scholar]
- Min, W. Analysis of adaptabilities of remote sensing models for heat flux over hilly land. Sci. Meteorol. Sin. 2009, 29, 386–389. [Google Scholar]
- Cheng, W.M.; Zhao, S.M.; Zhou, C.H.; Chen, X. Simulation of the Decadal Permafrost Distribution on the Qinghai-Tibet Plateau (China) over the Past 50 Years. Permafr. Periglac. Process. 2012, 23, 292–300. [Google Scholar]
- Zhu, Z.K.; Hu, Z.Y.; Ma, Y.M.; Li, M.S.; Sun, F.L. Net ecosystem carbon dioxide exchange in alpine meadow of Nagchu region over Qinghai-Xizang Plateau. Plateau Meteorol. 2015, 34, 1217–1223. [Google Scholar]
- Yang, L.W.; Gao, X.Q.; Hui, X.Y.; Gao, N.; Zhou, Y.; Hou, X.H. Study on turbulence characteristics in the atmospheric surface layer over Nyainrong grassland in central Qinghai-Tibetan Plateau. Plateau Meteorol. 2017, 36, 875–885. [Google Scholar]
- Duan, L.J.; Duan, A.M.; Hu, W.T.; Gong, Y.F. Low frequency oscillation of precipitation and daily variation characteristic of air–land process at Shiquanhe station and Linzhi station in Tibetan Plateau in the summer of 2014. Chin. J. Atmos. Sci. 2017, 41, 767–783. [Google Scholar]
- Yu, W.P.; Ma, M.G.; Wang, X.F.; Geng, L.Y.; Tan, J.L.; Shi, J.A. Evaluation of MODIS LST Products Using Longwave Radiation Ground Measurements in the Northern Arid Region of China. Remote Sens. 2014, 6, 11494–11517. [Google Scholar] [CrossRef]
- Duan, S.B.; Li, Z.L.; Leng, P. A framework for the retrieval of all-weather land surface temperature at a high spatial resolution from polar-orbiting thermal infrared and passive microwave data. Remote Sens. Environ. 2017, 195, 107–117. [Google Scholar] [CrossRef]
- Liu, S.M.; Xu, Z.W.; Wang, W.Z.; Jia, Z.Z.; Zhu, M.J.; Bai, J.; Wang, J.M. A comparison of eddy-covariance and large aperture scintillometer measurements with respect to the energy balance closure problem. Hydrol. Earth Syst. Sci. 2011, 15, 1291–1306. [Google Scholar] [CrossRef]
- Wang, B.B.; Ma, Y.M.; Ma, W.Q. Estimation of land surface temperature retrieved from EOS/MODIS in Naqu area over Tibetan Plateau. J. Remote Sens. 2012, 16, 1289–1309. [Google Scholar]
- Myneni, R.; Knyazikhin, Y.; Park, T. MCD15A2H MODIS/Terra+Aqua Leaf Area Index/FPAR 8-day L4 Global 500m SIN Grid V006. 2015. Available online: http://doi.org/10.5067/MODIS/MCD15A2H.006 (accessed on 1 February 2020).
- Qi, J.; Chehbouni, A.; Huete, A.R.; Kerr, Y.H.; Sorooshian, S. A Modified Soil Adjusted Vegetation Index. Remote Sens. Environ. 1994, 48, 119–126. [Google Scholar] [CrossRef]
- Carlson, T.N.; Ripley, D.A. On the relation between NDVI, fractional vegetation cover, and leaf area index. Remote Sens. Environ. 1997, 62, 241–252. [Google Scholar] [CrossRef]
- He, J. Development of Surface Meteorological Dataset of Chinawith High Temporal and Spatial Resolution. Master’s Thesis, Inst. of Tibetan Plateau Res., Chin. Acad. of Sci., Beijing, China, 2010. [Google Scholar]
- Yang, K.; He, J.; Tang, W.J.; Qin, J.; Cheng, C.C.K. On downward shortwave and longwave radiations over high altitude regions: Observation and modeling in the Tibetan Plateau. Agric. For. Meteorol. 2010, 150, 38–46. [Google Scholar] [CrossRef]
- Zhong, L.; Ma, Y.M.; Hu, Z.Y.; Fu, Y.F.; Hu, Y.Y.; Wang, X.; Cheng, M.L.; Ge, N. Estimation of hourly land surface heat fluxes over the Tibetan Plateau by the combined use of geostationary and polar-orbiting satellites. Atmos. Chem. Phys. 2019, 19, 5529–5541. [Google Scholar] [CrossRef]
- Yao, J.M.; Zhao, L.; Gu, L.L.; Qiao, Y.P.; Jiao, K.Q. The surface energy budget in the permafrost region of the Tibetan Plateau. Atmos. Res. 2011, 102, 394–407. [Google Scholar] [CrossRef]
- Tanaka, K.; Tamagawa, I.; Ishikawa, H.; Ma, Y.M.; Hu, Z.Y. Surface energy budget and closure of the eastern Tibetan Plateau during the GAME-Tibet IOP 1998. J. Hydrol. 2003, 283, 169–183. [Google Scholar] [CrossRef]
- Osterkamp, T.E. Freezing and Thawing of Soils and Permafrost Containing Unfrozen Water or Brine. Water Resour. Res. 1987, 23, 2279–2285. [Google Scholar] [CrossRef]
- Jackson, R.D.; Pinter, P.J.; Reginato, R.J. Net-Radiation Calculated from Remote Multispectral and Ground Station Meteorological Data. Agric. For. Meteorol. 1985, 35, 153–164. [Google Scholar] [CrossRef]
- Park, H.; Iijima, Y.; Yabuki, H.; Ohta, T.; Walsh, J.; Kodama, Y.; Ohata, T. The application of a coupled hydrological and biogeochemical model (CHANGE) for modeling of energy, water, and CO2 exchanges over a larch forest in eastern Siberia. J. Geophys. Res.-Atmos. 2011, 116. [Google Scholar] [CrossRef]
- Amaty, P.M.; Ma, Y.M.; Han, C.B.; Wang, B.B.; Devkota, L.P. Recent trends (2003–2013) of land surface heat fluxes on the southern side of the central Himalayas, Nepal. J. Geophys. Res. Atmos. 2015, 120, 11957–11970. [Google Scholar] [CrossRef]
- Liang, S.L. Narrowband to broadband conversions of land surface albedo I Algorithms. Remote Sens. Environ. 2001, 76, 213–238. [Google Scholar]
- Wan, Z.M.; Li, Z.L. A physics-based algorithm for retrieving land-surface emissivity and temperature from EOS/MODIS data. IEEE Trans. Geosci. Remote Sens. 1997, 35, 980–996. [Google Scholar]
- Liang, S.L.; Shuey, C.J.; Russ, A.L.; Fang, H.L.; Chen, M.Z.; Walthall, C.L.; Daughtry, C.S.T.; Hunt, R. Narrowband to broadband conversions of land surface albedo: II. Validation. Remote Sens. Environ. 2003, 84, 25–41. [Google Scholar] [CrossRef]
- Qin, Z.L.; Li, W.J.; Xu, B.; Chen, Z.X.; Liu, J. The estimation of land surface emissivity for Landsat TM6. Remote Sens. Land Resour. 2011, 16, 28–32. [Google Scholar]
- Ma, Y.M.; Tsukamoto, O.; Ishikawa, H.; Su, Z.B.; Menenti, M.; Wang, J.M.; Wen, J. Determination of regional land surface heat flux densities over heterogeneous landscape of HEIFE integrating satellite remote sensing with field observations. J. Meteorol. Soc. Jpn. 2002, 80, 485–501. [Google Scholar] [CrossRef]
- Idso, S.B.; Aase, J.K.; Jackson, R.D. Net radiation–soil heat flux relations as influenced by soil water content variations. Bound.-Layer Meteorol. 1975, 9, 113–122. [Google Scholar] [CrossRef]
- Fuchs, M.; Hadas, A. The heat flux density in a nonhomogeneous bare loessial soil. Bound.-Layer Meteorol. 1972, 3, 191–200. [Google Scholar] [CrossRef]
- Clothier, B.E.; Clawson, K.L.; Pinter, P.J.; Moran, M.S.; Reginato, R.J.; Jackson, R.D. Estimation of Soil Heat-Flux from Net-Radiation during the Growth of Alfalfa. Agric. For. Meteorol. 1986, 37, 319–329. [Google Scholar] [CrossRef]
- Ogee, J.; Lamaud, E.; Brunet, Y.; Berbigier, P.; Bonnefond, J.M. A long-term study of soil heat flux under a forest canopy. Agric. For. Meteorol. 2001, 106, 173–186. [Google Scholar] [CrossRef]
- Santanello, J.A.; Friedl, M.A. Diurnal covariation in soil heat flux and net radiation. J. Appl. Meteorol. 2003, 42, 851–862. [Google Scholar] [CrossRef]
- Colaizzi, P.D.; Kustas, W.P.; Anderson, M.C.; Agam, N.; Tolk, J.A.; Evett, S.R.; Howell, T.A.; Gowda, P.H.; O’Shaughnessy, S.A. Two-source energy balance model estimates of evapotranspiration using component and composite surface temperatures. Adv. Water Resour. 2012, 50, 134–151. [Google Scholar] [CrossRef]
- Zhao, L.; Sheng, Y.; Wu, T.H.; Li, R.; Xie, C.W.; Wu, J.C.; Li, J.; Yao, J.M.; Wu, X.D.; Hu, G.J.; et al. Permafrost and Its changes on Qinghai-Tibet Plateau; Science press: Beijing, China, 2019. [Google Scholar]

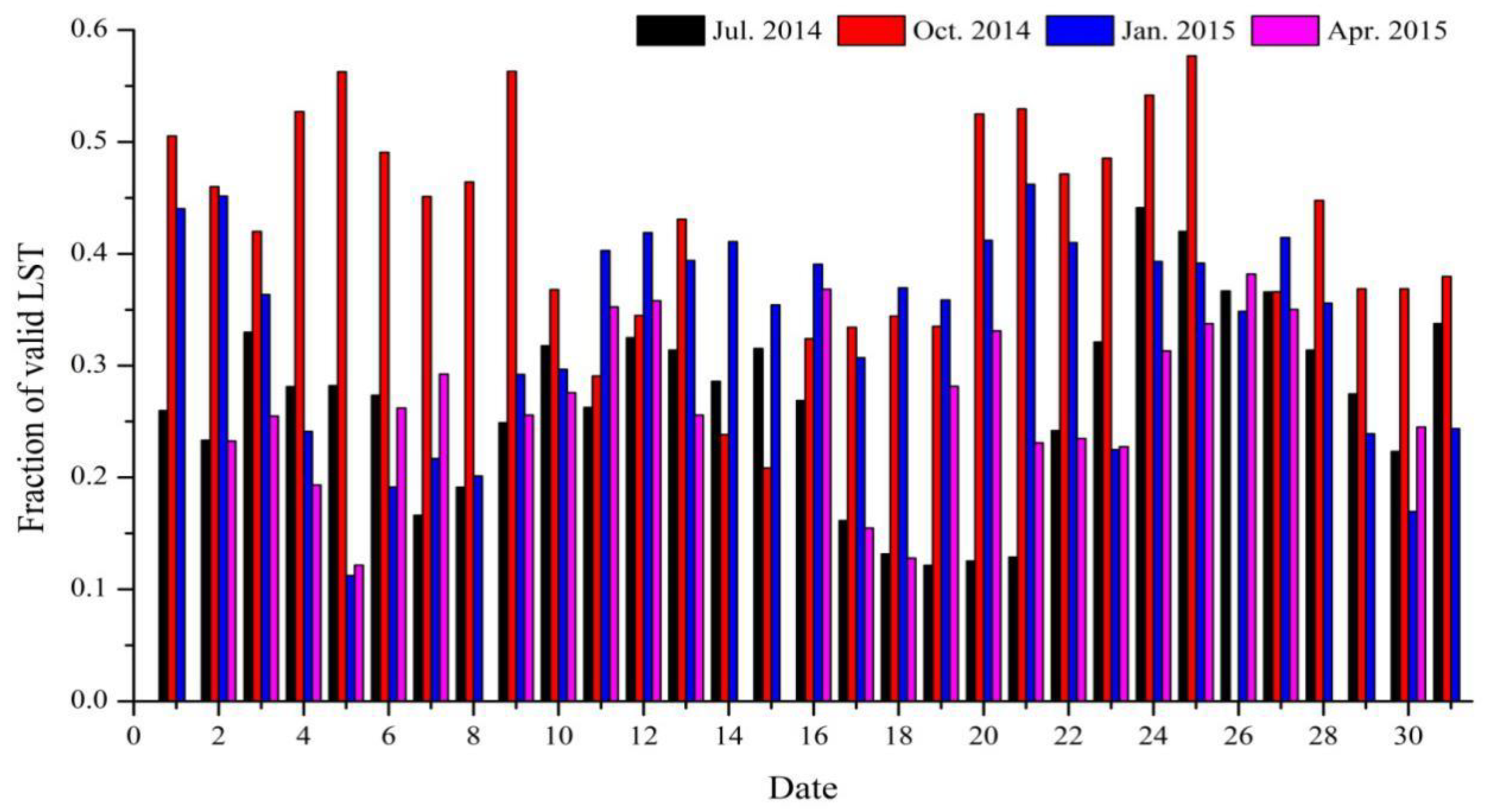
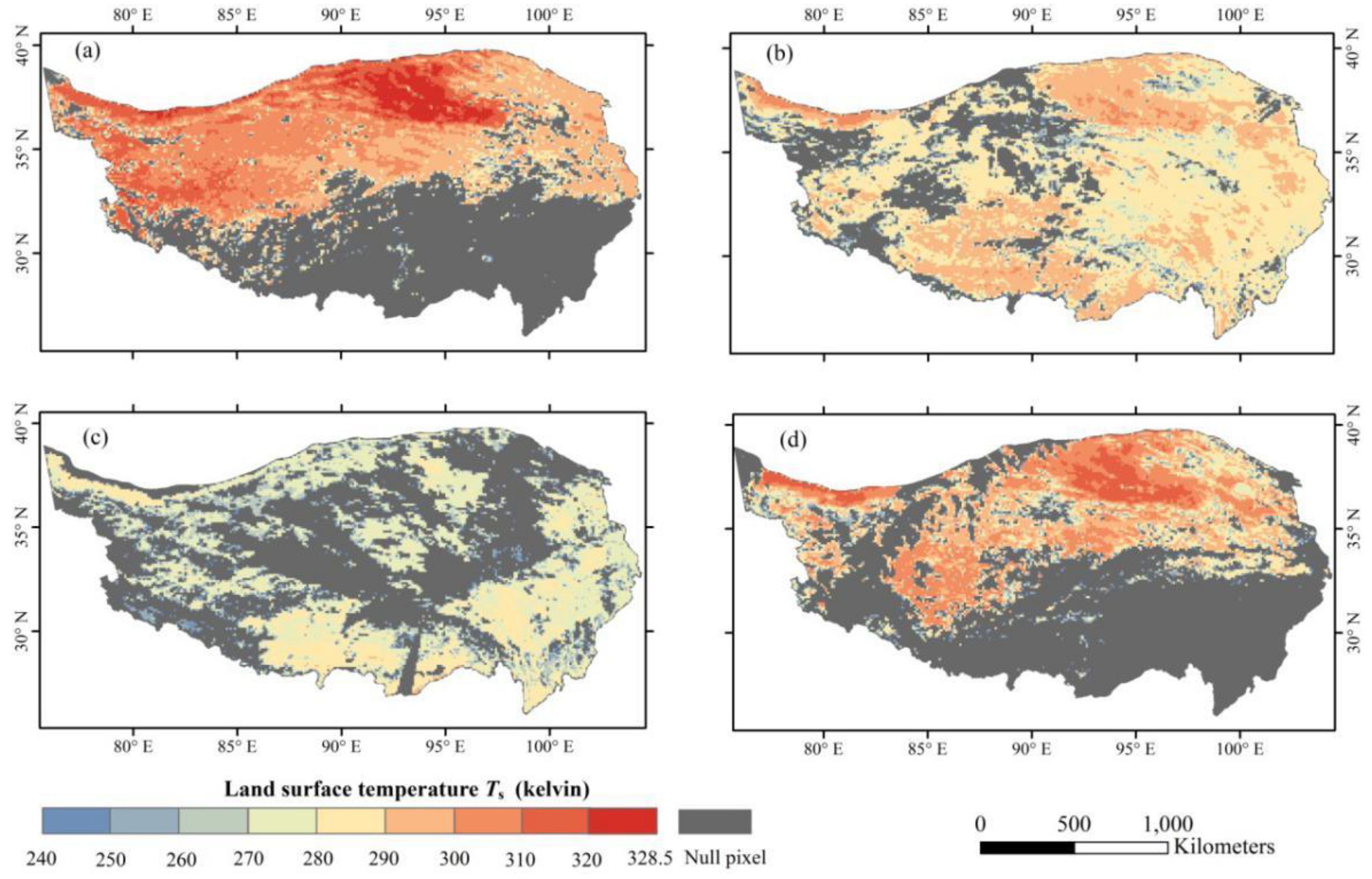
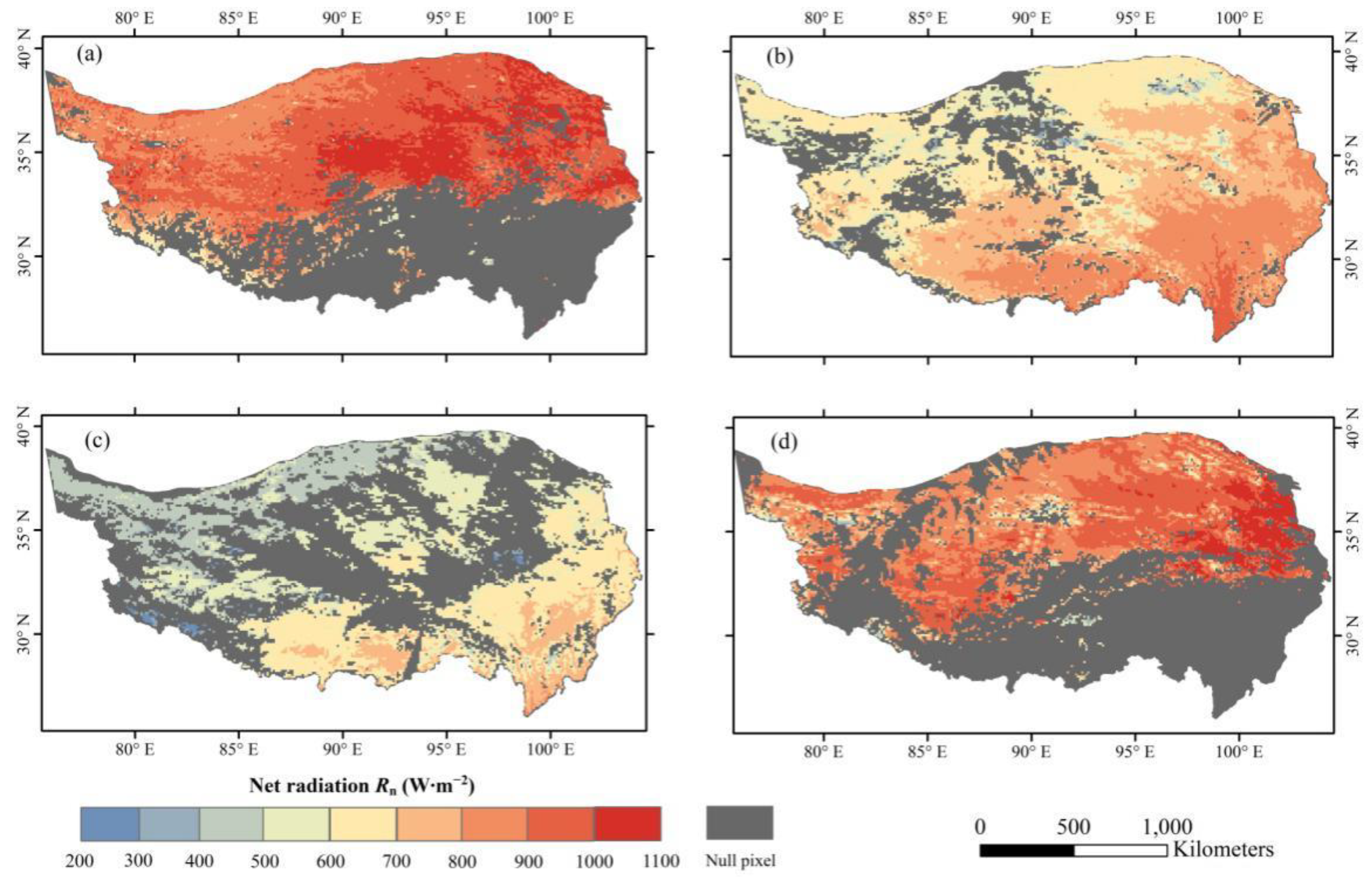

| AWS | Location (lon/lat/alt) | Ground Surface Condition | Observation Period (Beijing Time: dd.mm.yyyy) | Observation Items | Depth/Height |
|---|---|---|---|---|---|
| AYKMS | 88°48′E 37°32′N 4300 m | Desert steppe | 12.06.2014–24.02.2015 | DSR/USR | 2 m |
| DLR/ULR | 2 m | ||||
| G | 5, 10, 20 cm | ||||
| SM | 5, 10, 20, 40 cm | ||||
| ST | 5, 10, 20, 40 cm | ||||
| Ts | 1.5 m | ||||
| prec | 1.5 m | ||||
| TGLMS | 91°56′E 33°04′N 5100 m | Alpine meadow | 01.01–31.12.2015 | DSR/USR | 2 m |
| DLR/ULR | 2 m | ||||
| G | 5, 10, 20 cm | ||||
| SM | 35, 70, 105, 140, 175, 210, 245, 280, 300 cm | ||||
| ST | 2, 5, 10, 20, 50, 70, 90, 105, 140, 175, 210, 245, 280, 300 cm | ||||
| Ts | 1.5 m | ||||
| prec | 1.5 m | ||||
| XDTMS | 94°08′E 35°43′N 4538 m | Alpine steppe | 01.01.2015–31.12.2016 | DSR/USR | 2 m |
| DLR/ULR | 2 m | ||||
| G | 5, 10, 20 cm | ||||
| SM | 35, 70, 105, 140, 175, 210, 245, 280, 300 cm | ||||
| ST | 2, 5, 10, 20, 50, 70, 90, 105, 140, 175, 210, 245, 280, 300 cm | ||||
| Ts | 1.5 m | ||||
| prec | 1.5 m | ||||
| Binggou | 100°13.31′E 38°4.05′N 3449.4 m | Alpine meadow | 16.03–17.10.2008, 01.01–31.07.2009 | DSR/USR | 1.5 m |
| DLR/ULR | 1.5 m | ||||
| SM | 5, 10, 20, 40, 80, 120 cm | ||||
| ST | 5, 10, 20, 40, 80, 120 cm | ||||
| G | 5, 15 cm | ||||
| prec | 4.11 m | ||||
| Amdo | 91°37.2′E 32°14.4′N 4695 m | Alpine steppe | 01.07.2014–30.09.2015 | DSR/USR | 1.5 m |
| DLR/ULR | 1.5 m | ||||
| SM | 5, 10, 20, 40, 80, 160 cm | ||||
| ST | 5, 10, 20, 40, 80, 160 cm | ||||
| G | 5, 10 cm | ||||
| prec | 1.5 m | ||||
| BGGRASS | 90°1.68′E 31°25.07′N 4700 m | Alpine steppe | 15.07.2014–23.09.2015 | DSR/USR | 2 m |
| DLR/ULR | 2 m | ||||
| SM | 5, 10, 20, 40, 100 cm | ||||
| ST | 5, 10, 20, 40, 100 cm | ||||
| G | 5, 10 cm | ||||
| prec | 1.5 m | ||||
| Biru | 93°9.5′E 31°39.8′N 4408 m | Alpine steppe | 14.09.2014–02.10.2015 | DSR/USR | 2 m |
| DLR/ULR | 2 m | ||||
| SM | 5, 10, 20, 40, 100 cm | ||||
| ST | 5, 10, 20, 40, 100 cm | ||||
| G | 5, 10 cm | ||||
| prec | 1.5 m | ||||
| Jiali | 93°13.95′E 30°38.456′N 4509 m | Alpine meadow | 17.09.2014–28.06.2015, 06.09.2015–11.10.2015 | DSR/USR | 2 m |
| DLR/ULR | 2 m | ||||
| SM | 5, 10, 20, 40, 100 cm | ||||
| ST | 5, 10, 20, 40, 100 cm | ||||
| G | 5, 10 cm | ||||
| prec | 1.5 m | ||||
| Naqu | 91°54′E 31°22.2′N 4509 m | Alpine steppe | 01.07–10.09.2014, 16.09–07.12.2014, 28.01–01.08.2015, 01.09–30.09.2015 | DSR/USR | 1.5 m |
| DLR/ULR | 1.5 m | ||||
| SM | 5, 10, 20, 40, 80, 160 cm | ||||
| ST | 5, 10, 20, 40, 80, 160 cm | ||||
| G | 5, 10 cm | ||||
| prec | 1.5 m | ||||
| Nierong | 92°18.27′E 32°7.33′N 4607 m | Alpine meadow | 11.07.2014–21.10.2015 | DSR/USR | 1.5 m |
| DLR/ULR | 1.5 m | ||||
| SM | 5, 10, 20, 50, 100 cm | ||||
| ST | 5, 10, 20, 50, 100 cm | ||||
| G | 5, 10 cm | ||||
| prec | 1 m | ||||
| Linzhou | 91°16.25′E 29°53.93′N 3756 m | Alpine desert | 19.09.2015–09.03.2016 | DSR/USR | 1.5 m |
| DLR/ULR | 1.5 m | ||||
| SM | 5, 10, 20, 40, 80 cm | ||||
| ST | 5, 10, 20, 40, 80 cm | ||||
| G | 8 cm | ||||
| Ts | 1.5 m | ||||
| prec | 1.5 m | ||||
| Shiquanhe | 80°6′E 32°29.4′N 4278.6 m | Alpine desert | 16.09.2014–30.09.2015 | DSR/USR | 2 m |
| DLR/ULR | 2 m | ||||
| SM | 5, 10, 20, 40, 80 cm | ||||
| ST | 5, 10, 20, 40, 80 cm | ||||
| G | 5, 10, 20, 40, 80 cm | ||||
| Ts | 1.5 m | ||||
| prec | 1.5 m |
| Product Name | Description | Time Range (Beijing Time: dd.mm.yyyy) | Time Granularity | Spatial Resolution |
|---|---|---|---|---|
| MOD13Q1 | Normalized difference vegetation index (NDVI), enhanced vegetation index (EVI) | 01.01.2008–31.12.2009, 01.01.2014–31.12.2016 | 16 day | 250 m |
| MCD15A2H | Fraction of photosynthetically active radiation (FPAR), leaf area index (LAI) | 8 day | 500 m | |
| MODLT1D | Daytime/Nighttime Land Surface Temperature | 01.07–31.07.2014, 01.10–31.10.2014, 01.01–31.01.2015, 01.04–30.04.2015 | Daily | 1000 m |
| MOD09CMG | Surface reflectance band 1–7 | 24.07.2014, 25.10.2014, 21.01.2015, 26.04.2015 | Daily | 5600 m |
| CMFD-SRad | Downwelling shortwave radiation | 3 h | 10,000 m | |
| CMFD-LRad | Downwelling longwave radiation | 3 h | 10,000 m |
| Model Name | Mathematical Form | References |
|---|---|---|
| SEBAL | [13] | |
| SEBALadj | This study | |
| Ma | [19] | |
| Maadj | This study | |
| Choudhury | [17] | |
| Choudhuryadj | This study | |
| Clawson | [42] | |
| Clawsonadj | This study | |
| SEBS | [18] | |
| SEBSadj | This study |
| Choudhury | CT | DFT | CF |
|---|---|---|---|
| +α | 2.19 | 2.45 | 3.15 |
| −α | 2.19 | 2.45 | 3.15 |
| +α, +LAI | 1.25 | 1.08 | 1.16 |
| +α, −LAI | 4.89 | 5.06 | 6.04 |
| −α, +LAI | 5.25 | 5.44 | 6.51 |
| −α, −LAI | 1.25 | 1.07 | 1.11 |
| +LAI | 3.07 | 2.98 | 3.32 |
| −LAI | 2.92 | 2.84 | 3.16 |
| +Ts | 3.16 | 2.02 | 1.81 |
| +Ts, +α | 5.34 | 4.47 | 4.96 |
| +Ts, −α | 1.80 | 1.54 | 1.96 |
| +Ts, +α, +LAI | 3.27 | 2.37 | 2.35 |
| +Ts, +α, −LAI | 7.34 | 6.54 | 7.50 |
| +Ts, −α, +LAI | 4.33 | 4.45 | 5.30 |
| +Ts, −α, −LAI | 3.21 | 1.95 | 1.66 |
| +Ts, +LAI | 2.86 | 2.43 | 2.48 |
| +Ts, −LAI | 5.27 | 4.22 | 4.52 |
| −Ts | 3.12 | 2.00 | 1.79 |
| −Ts, +α | 1.79 | 1.54 | 1.96 |
| −Ts, −α | 5.31 | 4.45 | 4.94 |
| −Ts, +α, +LAI | 3.38 | 2.01 | 1.68 |
| −Ts, +α, −LAI | 4.05 | 4.17 | 4.96 |
| −Ts, −α, +LAI | 7.96 | 7.07 | 8.12 |
| −Ts, −α, −LAI | 2.84 | 2.05 | 2.02 |
| −Ts, +LAI | 5.66 | 4.51 | 4.82 |
| −Ts, −LAI | 2.68 | 2.32 | 2.39 |
| MAX | 7.96 | 7.07 | 8.12 |
| N | 11249 | 5171 | 5676 |
| Scheme | CT | DFT | CF |
|---|---|---|---|
| Choudhury | 7.96 | 7.07 | 8.12 |
| Choudhuryadj | 3.60 | 3.70 | 4.28 |
| Clawson | 7.54 | 14.21 | 17.95 |
| Clawsonadj | 4.87 | 13.20 | 6.23 |
| SEBS | 8.89 | 22.52 | 29.57 |
| SEBSadj | 2.52 | 3.53 | 4.28 |
| SEBAL | 0.56 | 0.63 | 1.05 |
| SEBALadj | 1.61 | 1.47 | 1.69 |
| Ma | 0.88 | 1.11 | 1.68 |
| Maadj | 1.45 | 1.46 | 1.72 |
| Scheme | CT | DFT | CF | |
|---|---|---|---|---|
| G0 is the opposite direction from Rn | 5102 | 2117 | 2270 | |
| Under the premise that G0 is opposite to Rn, the simulated G0 direction is consistent with the “measured” G0 | Choudhury | 0 | 0 | 0 |
| Choudhuryadj | ||||
| Clawson | ||||
| Clawsonadj | ||||
| SEBS | ||||
| SEBSadj | ||||
| SEBAL | 853 | 1127 | 2051 | |
| SEBALadj | ||||
| Ma | ||||
| Maadj | ||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, C.; Wu, T.; Yao, J.; Li, R.; Xie, C.; Hu, G.; Zhu, X.; Zhang, Y.; Ni, J.; Hao, J.; et al. An Assessment of Using Remote Sensing-based Models to Estimate Ground Surface Soil Heat Flux on the Tibetan Plateau during the Freeze-thaw Process. Remote Sens. 2020, 12, 501. https://doi.org/10.3390/rs12030501
Yang C, Wu T, Yao J, Li R, Xie C, Hu G, Zhu X, Zhang Y, Ni J, Hao J, et al. An Assessment of Using Remote Sensing-based Models to Estimate Ground Surface Soil Heat Flux on the Tibetan Plateau during the Freeze-thaw Process. Remote Sensing. 2020; 12(3):501. https://doi.org/10.3390/rs12030501
Chicago/Turabian StyleYang, Cheng, Tonghua Wu, Jimin Yao, Ren Li, Changwei Xie, Guojie Hu, Xiaofan Zhu, Yinghui Zhang, Jie Ni, Junming Hao, and et al. 2020. "An Assessment of Using Remote Sensing-based Models to Estimate Ground Surface Soil Heat Flux on the Tibetan Plateau during the Freeze-thaw Process" Remote Sensing 12, no. 3: 501. https://doi.org/10.3390/rs12030501
APA StyleYang, C., Wu, T., Yao, J., Li, R., Xie, C., Hu, G., Zhu, X., Zhang, Y., Ni, J., Hao, J., Li, X., Ma, W., & Wen, A. (2020). An Assessment of Using Remote Sensing-based Models to Estimate Ground Surface Soil Heat Flux on the Tibetan Plateau during the Freeze-thaw Process. Remote Sensing, 12(3), 501. https://doi.org/10.3390/rs12030501







