Attention-Based Residual Network with Scattering Transform Features for Hyperspectral Unmixing with Limited Training Samples
Abstract
1. Introduction
- A novel network model is proposed, which is a combination of the scattering transform and a deep neural network, such as the CNN and the ResNet. The scattering transform extracts deep-level features from hyperspectral images and the resulting high-order information is processed through neural networks.
- Hyperspectral unmixing using ResNet and attention-based ResNet are introduced. The attention mechanism is helpful in paying attention to important features in HSIs during learning.
- Under the condition of limited training data, the proposed approach with only a few parameters to be configured can achieve more accurate results than state-of-the-art methods.
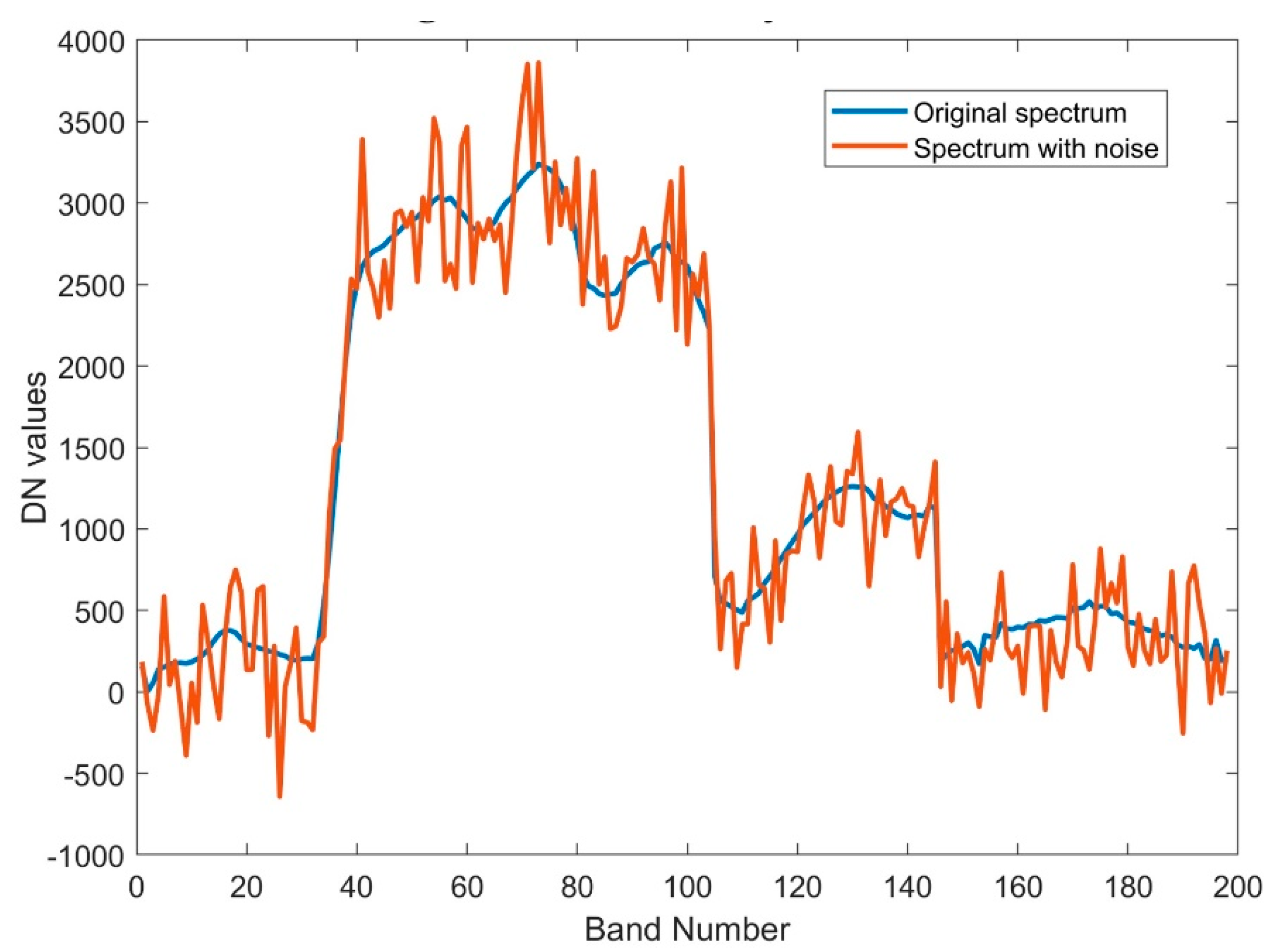
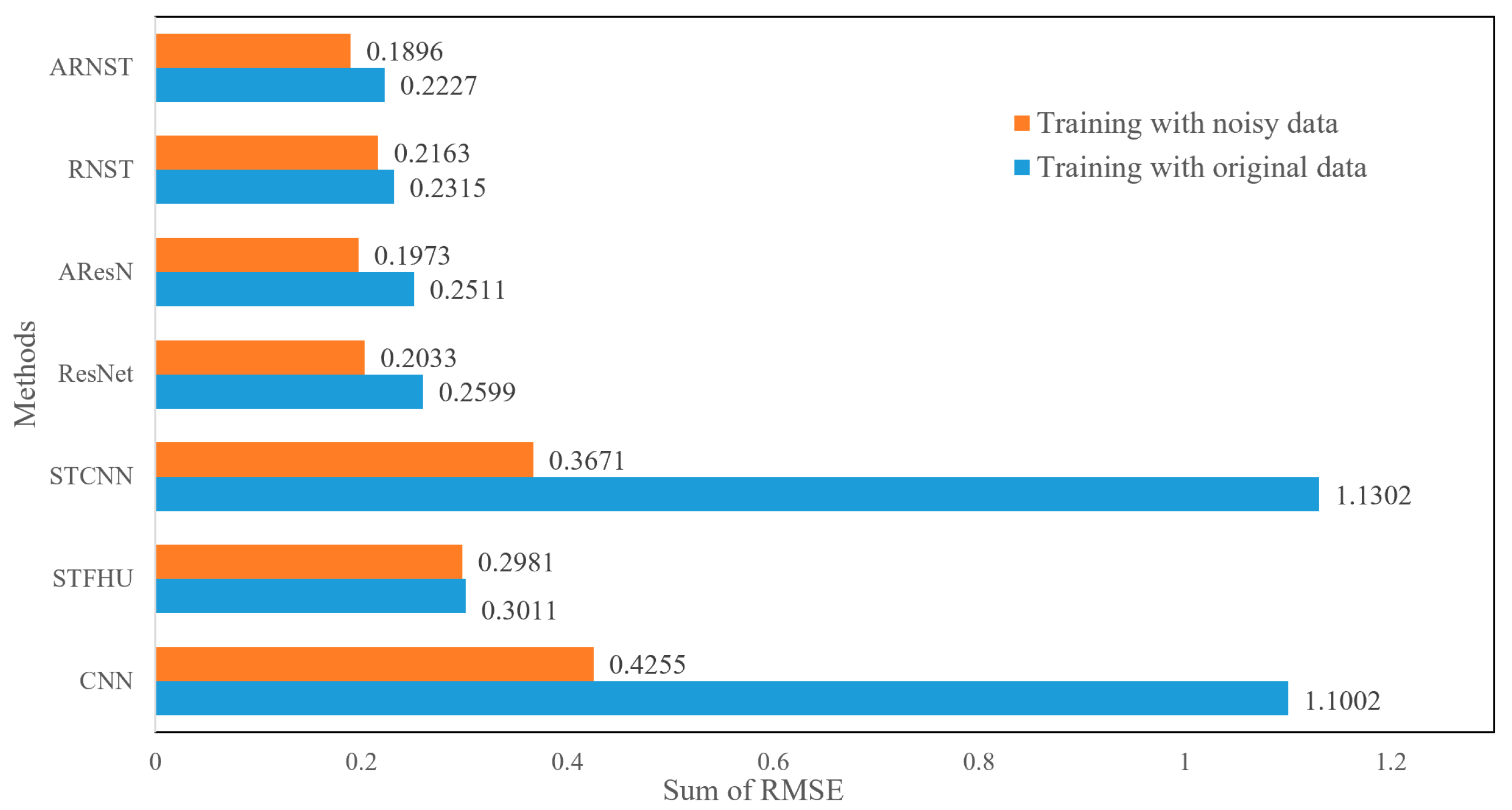
- When unmixing HSI images corrupted by additive noise, the proposed approach utilizes the scattering transform combined with deep learning to reduce the effect of noise, which is shown to be more robust in terms of suffering a smaller reduction in accuracy compared to the CNN applied directly to the HSI images, which requires retraining with noisy data to achieve satisfactory results.
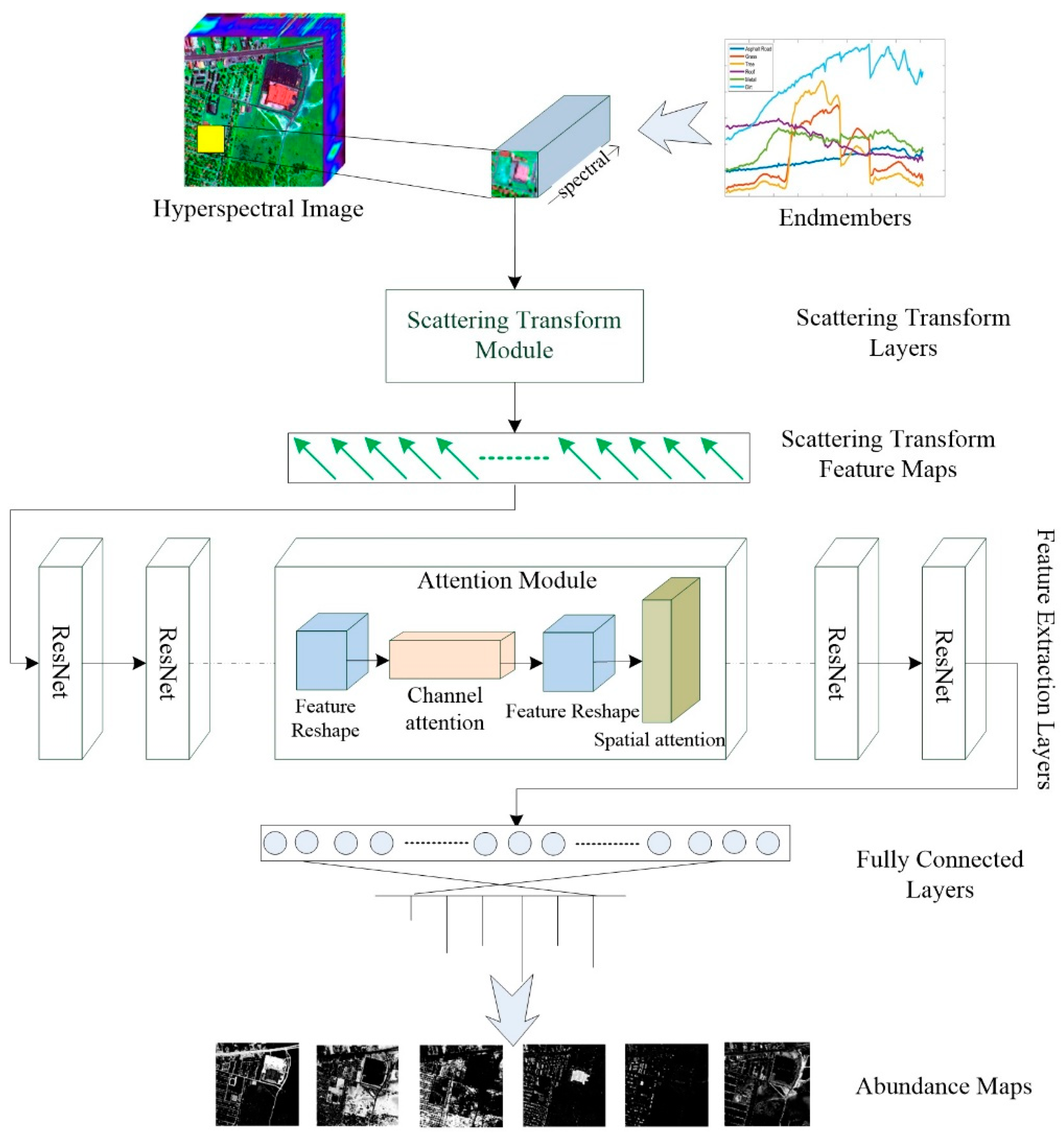
2. Methods
2.1. Scattering Transform Module
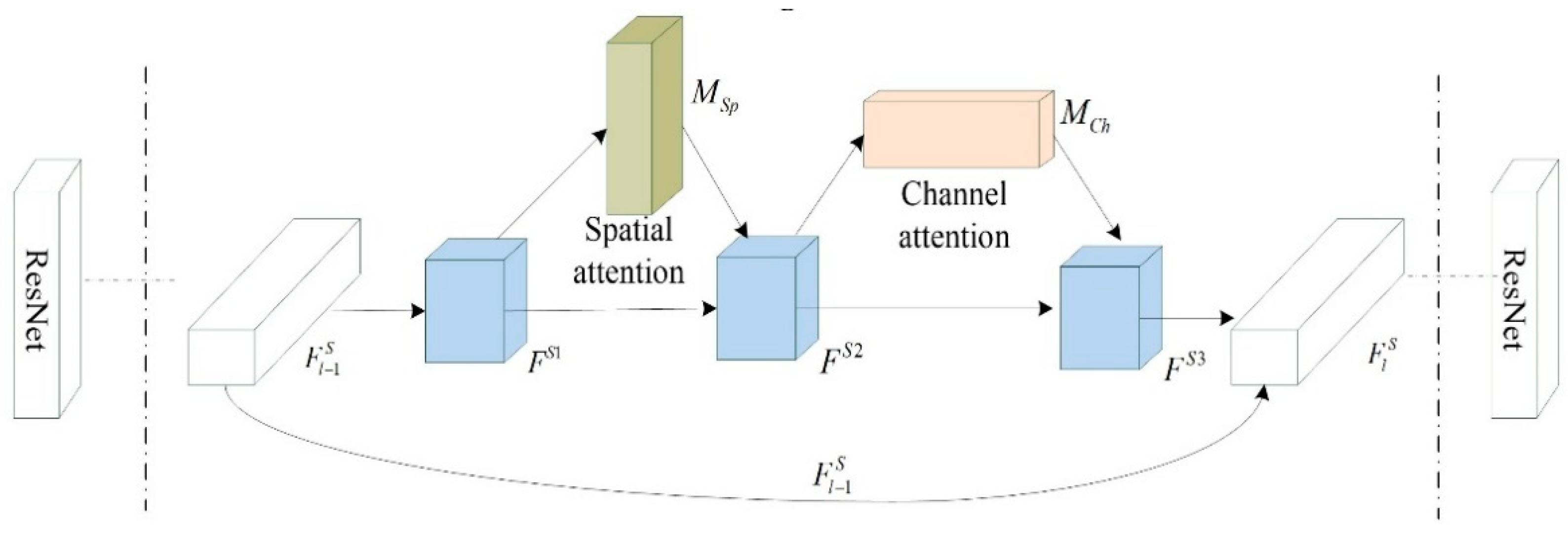
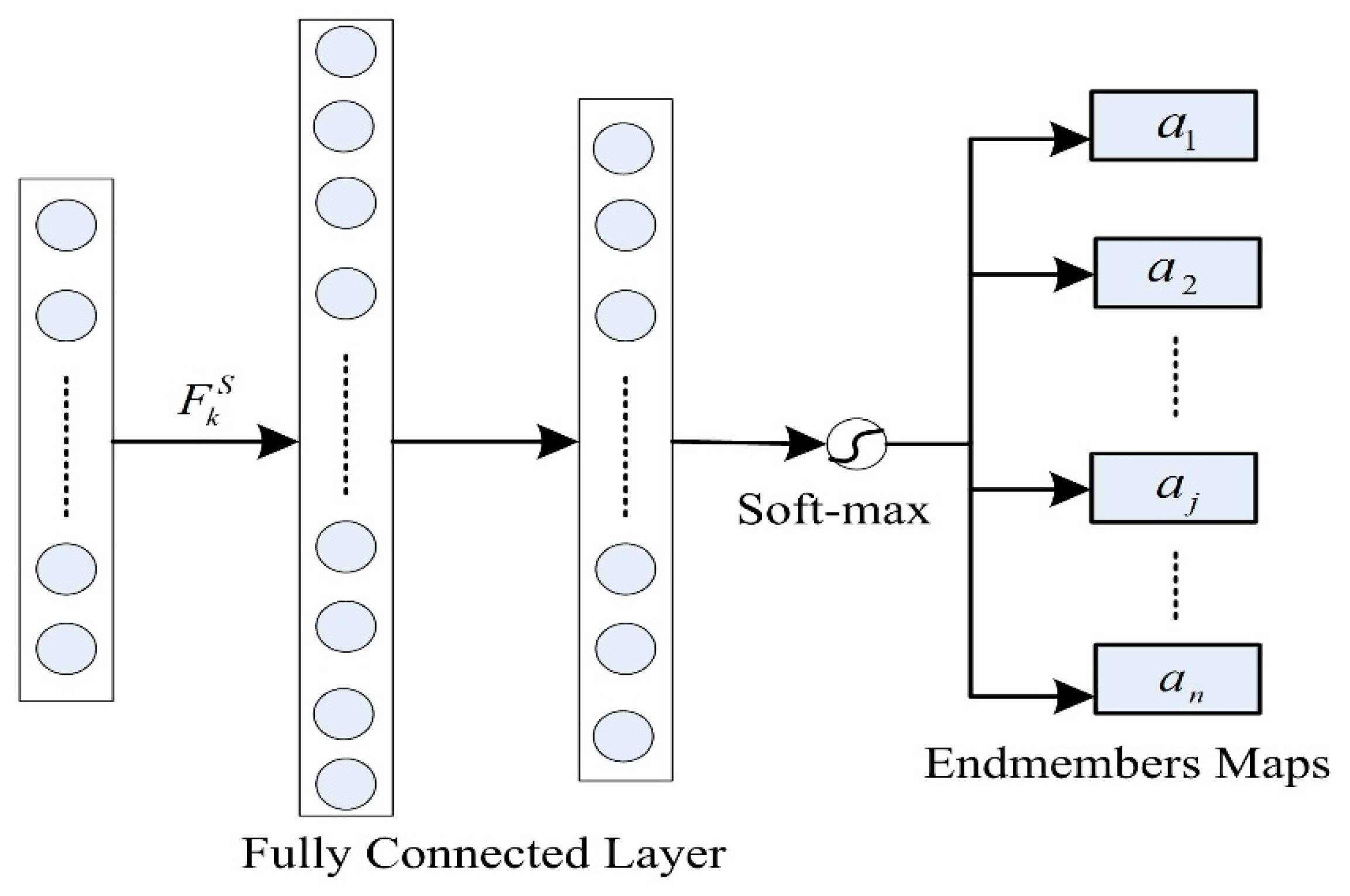
2.2. Deep Neural Network Feature Extraction Module
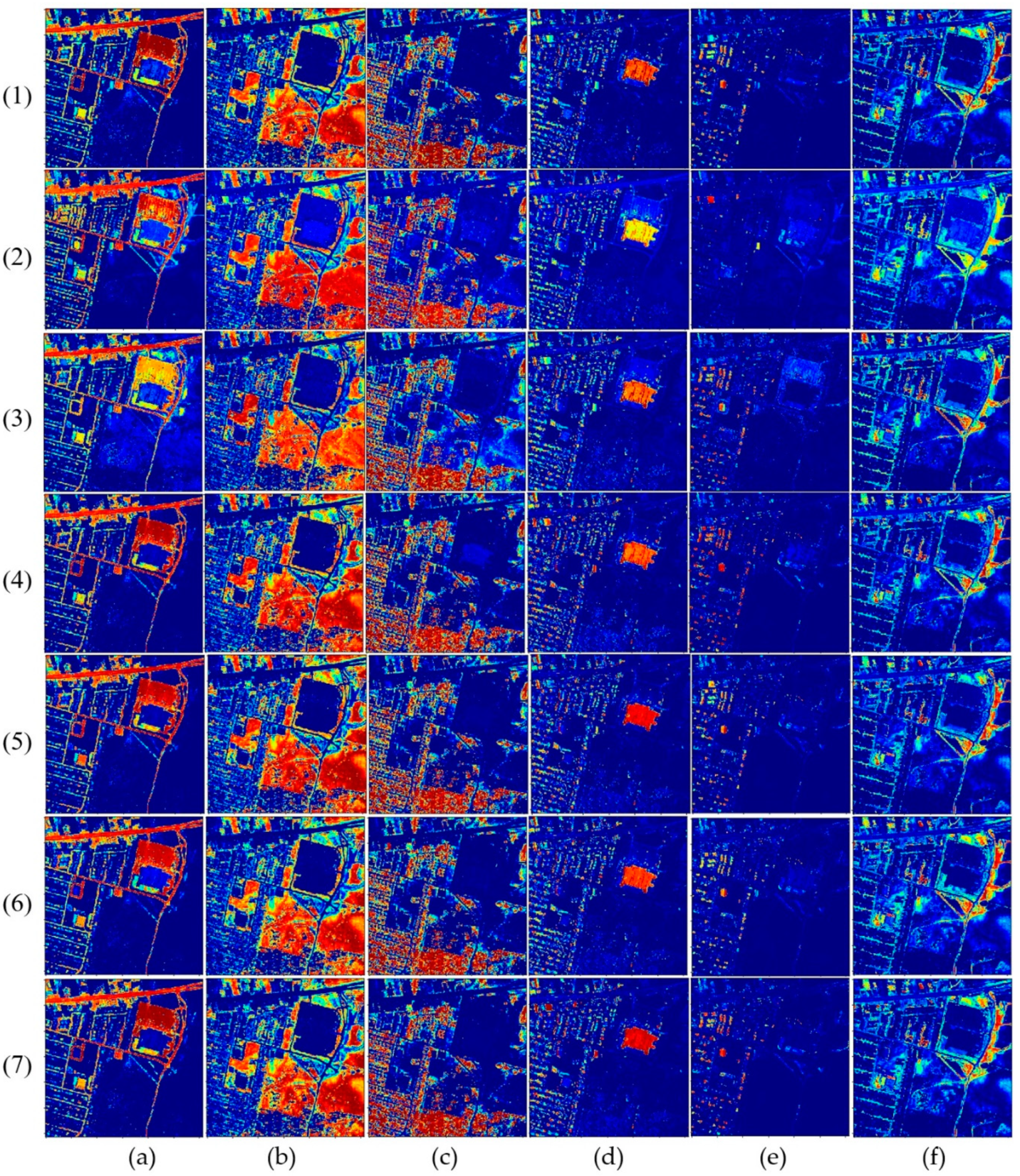
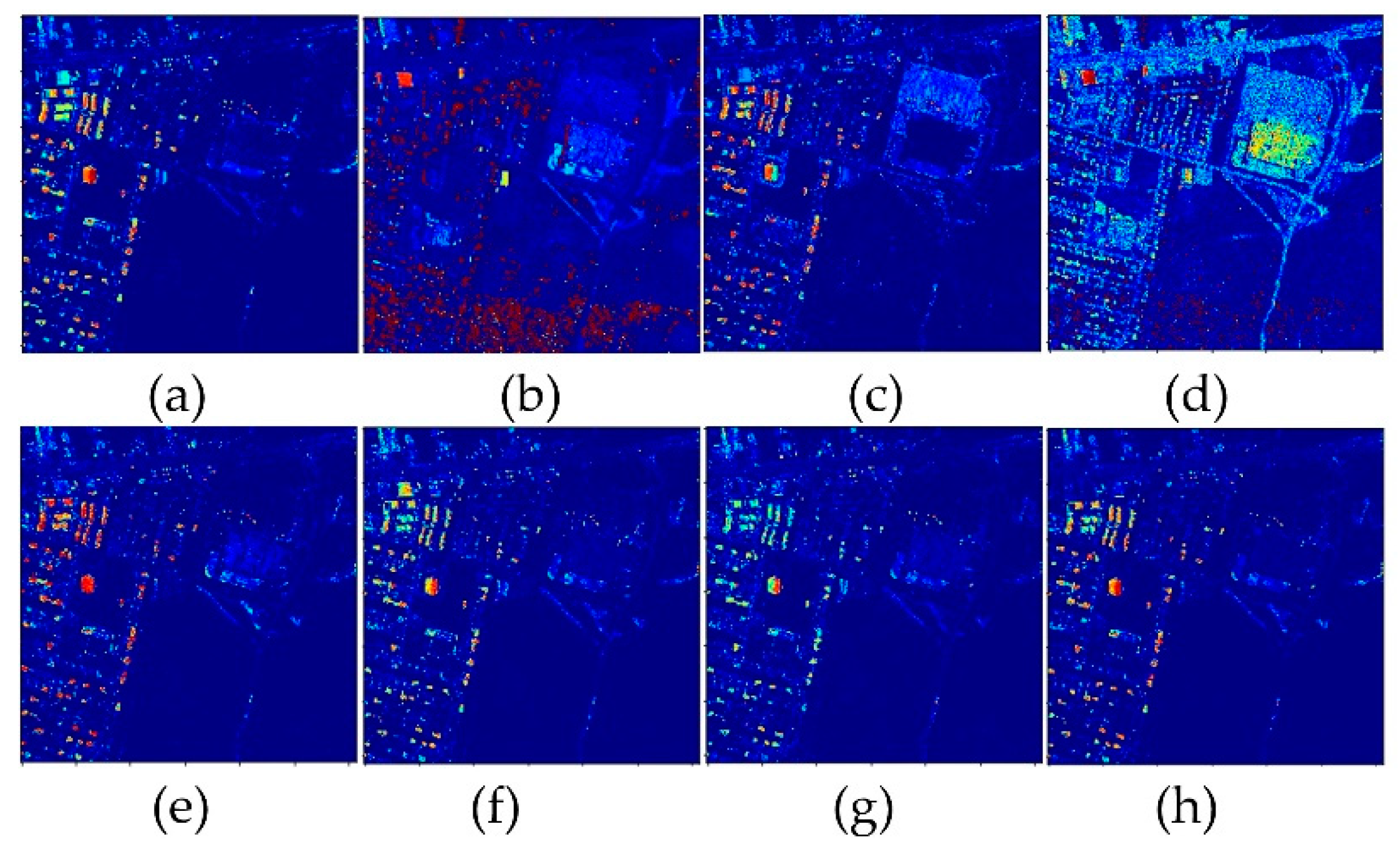
3. Experimental Results
3.1. Description of Hyperspectral Datasets
3.2. Experimental Setup
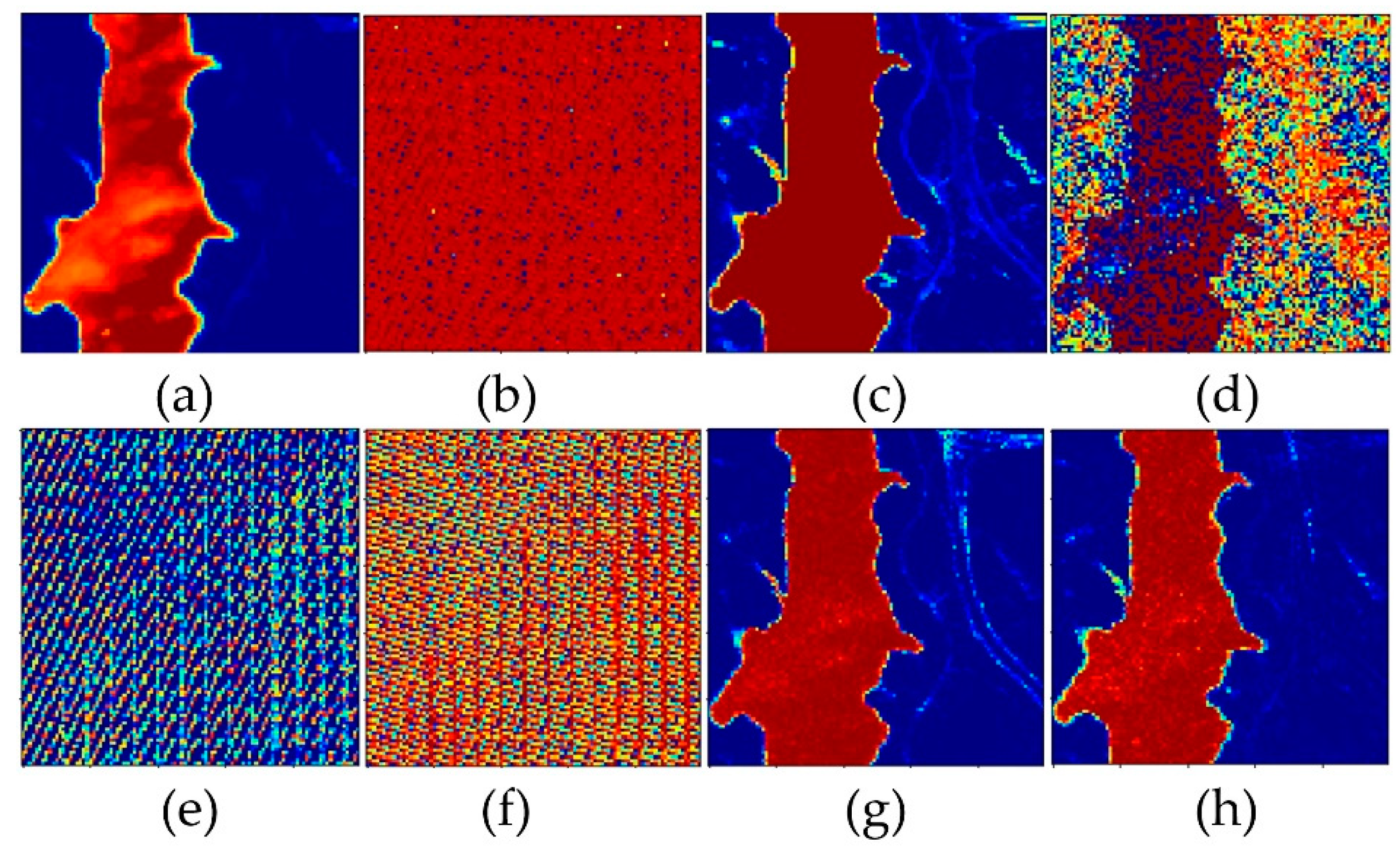
3.3. Results for the Urban Dataset
3.4. Results for the Jasper Ridge Dataset
3.5. Results for the Samson Dataset
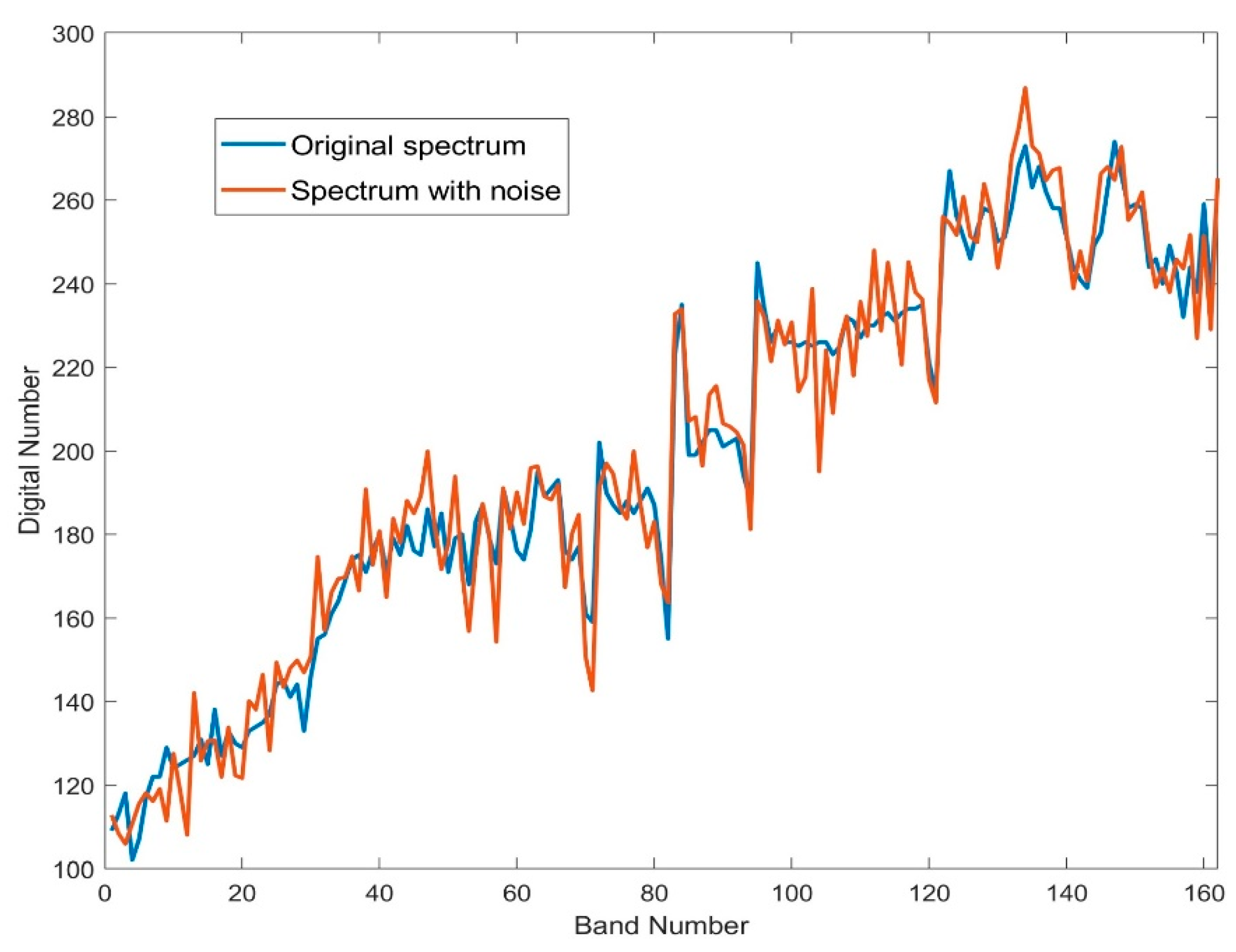
3.6. Results when Training on Noisy Data
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Landgrebe, D. Hyperspectral image data analysis. IEEE Signal. Process. Mag. 2002, 19, 17–28. [Google Scholar] [CrossRef]
- Bioucas-Dias, J.M.; Plaza, A.; Camps-Valls, G.; Scheunders, P.; Nasrabadi, N.; Chanussot, J. Hyperspectral remote sensing data analysis and future challenge. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–36. [Google Scholar] [CrossRef]
- Bioucas-Dias, J.M.; Plaza, A.; Dobigeon, N.; Parente, M.; Du, Q.; Gader, P.; Chanussot, J. Hyperspectral unmixing overview: Geometrical, statistical, and sparse regression-based approaches. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 354–379. [Google Scholar] [CrossRef]
- Zou, J.; Lan, J.; Shao, Y. A Hierarchical Sparsity Unmixing Method to Address Endmember Variability in Hyperspectral Image. Remote Sens. 2018, 10, 738. [Google Scholar] [CrossRef]
- Parra, L.C.; Spence, C.; Sajda, P.; Ziehe, A.; Müller, K.R. Unmixing Hyperspectral Data. In Advances in Neural Information Processing Systems; Available online: http://papers.nips.cc/paper/1714-unmixing-hyperspectral-data.pdf (accessed on 15 January 2020).
- Iordache, M.D.; Bioucas-Dias, J.M.; Plaza, A. Total variation spatial regularization for sparse hyperspectral unmixing. IEEE Trans. Geosci. Remote Sens. 2012, 50, 4484–4502. [Google Scholar] [CrossRef]
- Heylen, R.; Parente, M.; Gader, P. A review of nonlinear hyperspectral unmixing methods. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1844–1868. [Google Scholar] [CrossRef]
- Xu, X.; Shi, Z.; Pan, B. A supervised abundance estimation method for hyperspectral unmixing. Remote Sens. Letter. 2018, 9, 383–392. [Google Scholar] [CrossRef]
- Nguyen, N.H.; Chen, J.; Richard, C.; Honeine, P.; Theys, C. Supervised nonlinear unmixing of hyperspectral images using a pre-image methods. Eur. Astron. Soc. Publ. Ser. 2013, 59, 417–437. [Google Scholar] [CrossRef]
- Zhang, X.; Sun, Y.; Zhang, J.; Wu, P.; Jiao, L. Hyperspectral unmixing via deep convolutional neural networks. Ieee Geosci. Remote Sens. Lett. 2018, 15, 1755–1759. [Google Scholar] [CrossRef]
- Palsson, F.; Sigurdsson, J.; Sveinsson, J.R.; Ulfarsson, M.O. Neural network hyperspectral unmixing with spectral information divergence objective. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 755–758. [Google Scholar]
- Plaza, J.; Plaza, A.; Perez, R.; Martinez, P. On the use of small training sets for neural network-based characterization of mixed pixels in remotely sensed hyperspectral images. Pattern Recogn. 2009, 42, 3032–3045. [Google Scholar] [CrossRef]
- Shen, D.; Wu, G.; Suk H, I. Deep learning in medical image analysis. Ann. Rev. Biomed. Engineer. 2017, 19, 221–248. [Google Scholar] [CrossRef] [PubMed]
- Zhao, W.; Du, S. Spectral–spatial feature extraction for hyperspectral image classification: A dimension reduction and deep learning approach. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4544–4554. [Google Scholar] [CrossRef]
- Bayar, B.; Stamm M, C. A deep learning approach to universal image manipulation detection using a new convolutional layer. In Proceedings of the 4th ACM Workshop on Information Hiding and Multimedia Security, Vigo, Spain, 20–22 June 2016; pp. 5–10. [Google Scholar]
- Druzhkov P, N.; Kustikova V, D. A survey of deep learning methods and software tools for image classification and object detection. Pattern Recogn. Image Analys. 2016, 26, 9–15. [Google Scholar] [CrossRef]
- Pouyanfar, S.; Sadiq, S.; Yan, Y.; Tian, H.; Tao, Y.; Reyes, M.P.; yengar, S.S. A survey on deep learning: Algorithms, techniques, and applications. ACM Comput. Surve. 2019, 51, 92. [Google Scholar] [CrossRef]
- Guo, R.; Wang, W.; Qi, H. Hyperspectral image unmixing using autoencoder cascade. In Proceedings of the Seventh Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Tokyo, Japan, 2–5 June 2015; pp. 1–4. [Google Scholar]
- Su, Y.; Marinoni, A.; Li, J.; Plaza, J.; Gamba, P. Stacked nonnegative sparse autoencoders for robust hyperspectral unmixing. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1427–1431. [Google Scholar] [CrossRef]
- Hong, D.; Chanussot, J.; Yokoya, N.; Heiden, U.; Heldens, W.; Zhu, X.X. WU-Net: A Weakly-Supervised Unmixing Network for Remotely Sensed Hyperspectral Imagery. In Proceedings of the 2019 IEEE International Geoscience and Remote Sensing Symposium (IGARSS 2019), 28 July–2 August 2019; pp. 373–376. [Google Scholar]
- Arun, P.; Buddhiraju, K.; Porwal, A. CNN based sub-pixel mapping for hyperspectral images. Neurocomputing 2018, 311, 51–64. [Google Scholar] [CrossRef]
- Ozkan, S.; Akar, G.B. Improved Deep Spectral Convolution Network For Hyperspectral Unmixing With Multinomial Mixture Kernel and Endmember Uncertainty. arXiv 2018, arXiv:1808.01104. [Google Scholar]
- He, Z.; Liu, H.; Wang, Y.; Hu, J. Generative adversarial networks based semi-supervised learning for hyperspectral image classification. Remote Sens. 2017, 9, 1042. [Google Scholar] [CrossRef]
- Yang, J.; Zhao, Y.Q.; Chan, C.W. Learning and transferring deep joint spectral–spatial features for hyperspectral classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4729–4742. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Y.; Jiang, Y.; Wang, P.; Shen, Q.; Shen, C. Hyperspectral Classification Based on Lightweight 3-D-CNN With Transfer Learning. IEEE Trans. Geosci. Remote Sens. 2019, 57, 5813–5828. [Google Scholar] [CrossRef]
- Zhong, Z.; Li, J.; Luo, Z.; Chapman, M. Spectral–spatial residual network for hyperspectral image classification: A 3-d deep learning framework. IEEE Trans. Geosci. Remote Sens. 2018, 56, 847–858. [Google Scholar] [CrossRef]
- Ma, X.; Wang, H.; Geng, J. Spectral-spatial classification of hyperspectral image based on deep auto-encoder. Ieee J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4073–4085. [Google Scholar] [CrossRef]
- Makantasis, K.; Doulamis, A.D.; Doulamis, N.D.; Nikitakis, A. Tensor-based classification models for hyperspectral data analysis. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6884–6898. [Google Scholar] [CrossRef]
- Pan, B.; Shi, Z.; Xu, X. MugNet: Deep learning for hyperspectral image classification using limited samples. ISPRS J. Photogramm. Remote Sens. 2018, 145, 108–119. [Google Scholar]
- Fang, B.; Li, Y.; Zhang, H.; Chan, J.W. Hyperspectral Images Classification Based on Dense Convolutional Networks with Spectral-Wise Attention Mechanism. Remote Sens. 2019, 11, 159. [Google Scholar] [CrossRef]
- Bioucas-Dias, J.M.; Figueiredo, M.A. Alternating direction algorithms for constrained sparse regression: Application to hyperspectral unmixing. In Proceedings of the 2010 2nd Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing, Reykjavik, Iceland, 14–16 June 2010; pp. 1–4. [Google Scholar]
- Zeng, Y.; Ritz, C.; Zhao, J.; Lan, J. Scattering Transform Framework for Unmixing of Hyperspectral Data. Remote Sens. 2019, 11, 2868. [Google Scholar] [CrossRef]
- Mei, X.; Pan, E.; Ma, Y.; Dai, X.; Huang, J.; Fan, F.; Du, Q.; Zheng, H.; Ma, J. Spectral-Spatial Attention Networks for Hyperspectral Image Classification. Remote Sens. 2019, 11, 963. [Google Scholar] [CrossRef]
- Cai, Y.; Dong, Z.; Cai, Z.; Liu, X.; Wang, G. Discriminative Spectral-Spatial Attention-Aware Residual Network for Hyperspectral Image Classification. In Proceedings of the 2019 10th Workshop on Hyperspectral Imaging and Signal Processing: Evolution in Remote Sensing (WHISPERS), Amsterdam, The Netherlands, 24–26 September 2019; pp. 1–5. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 26 June–1 July 2016; pp. 770–778. [Google Scholar]
- Woo, S.; Park, J.; Lee, J.Y.; also, K.I. Cbam: Convolutional block attention module[C]. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 3–19. [Google Scholar]
- TensorFlow Software. Available online: https://www.tensorflow.org (accessed on 20 July 2019).
- Scikit-Learn Software. Available online: https://scikit-learn.org (accessed on 20 July 2019).
- Keras Software. Available online: https://keras.io (accessed on 20 July 2019).
- Hyperspectral Unmixing Datasets & Ground Truths. Available online: http://www.escience.cn/people/feiyunZHU/Dataset_GT.html (accessed on 10 August 2019).
- Zhu, F.; Wang, Y.; Xiang, S.; Fan, B.; Pan, C. Structured sparse method for hyperspectral unmixing. ISPRS J. Photogram. Remote Sens. 2014, 88, 101–118. [Google Scholar] [CrossRef]
- Shao, Y.; Lan, J. A Spectral Unmixing Method by Maximum Margin Criterion and Derivative Weights to Address Spectral Variability in Hyperspectral Imagery. Remote Sens. 2019, 11, 1045. [Google Scholar] [CrossRef]
- Andén, J.; Mallat, S. Deep scattering spectrum. IEEE Trans. Signal Process. 2014, 62, 4114–4128. [Google Scholar] [CrossRef]
- Complexity of Self-Attention. Available online: https://www.cnblogs.com/nxf-rabbit75/p/11945195.html (accessed on 15 January 2020).
- Computational Complexity of Neural Networks. Available online: https://kasperfred.com/series/computational-complexity/computational-complexity-of-neural-networks. (accessed on 15 January 2020).
| Training Ratio | Total Pixels | |||||
|---|---|---|---|---|---|---|
| 20% | 10% | 5% | 1% | 0.5% | ||
| Total training pixels | 14,736 | 7122 | 3438 | 491 | 245 | 94,249 |
| Total validation pixels | 3684 | 1781 | 860 | 123 | 62 | |
| Total testing pixels | 75,829 | 85,346 | 89,951 | 93,635 | 93,942 | |
| Endmembers | Number of training and validation pixels for each endmember | |||||
| Asphalt road | 9630 | 4015 | 1378 | 171 | 82 | 33,153 |
| Grass | 11,216 | 6135 | 3256 | 471 | 233 | 61,978 |
| Tree | 7251 | 4499 | 2328 | 318 | 159 | 48,244 |
| Roof | 8350 | 4354 | 1899 | 263 | 134 | 36,303 |
| Metal | 5677 | 2768 | 1068 | 141 | 66 | 18,446 |
| Dirt | 13,966 | 6515 | 3008 | 390 | 192 | 56,082 |
| Layers | K | Network Structure | Output Size | |
|---|---|---|---|---|
| Input | - | - | 1 × 1 × 162 | |
| Scattering Transform | m = 2, j = 3 | Scattering transform | 1 × 1 × 648 | |
| Feature Reshape | - | Reshape | 9 × 9 × 8 | |
| Residual Block 1 |  | 3 × 3 | Conv-BN-ReLU | 9 × 9 × 16 |
| - | Channel attention | 1 × 1 × 16, 81 | ||
| 7 × 7 | Spatial attention | 9 × 9 × 1, 16 | ||
| - | Add | 9 × 9 × 16 | ||
| Residual Block 2 |  | 3 × 3 | Conv-BN-ReLU | 5 × 5 × 32 |
| - | Channel attention | 1 × 1 × 32, 25 | ||
| 7 × 7 | Spatial attention | 5 × 5 × 1, 32 | ||
| - | Add | 5 × 5 × 32 | ||
| Residual Block 3 |  | 3 × 3 | Conv-BN-ReLU | 3 × 3 × 64 |
| - | Channel attention | 1 × 1 × 64, 9 | ||
| 7 × 7 | Spatial attention | 3 × 3 × 1, 64 | ||
| - | Add | 3 × 3 × 64 | ||
| AveragePooling2D | 8 × 8 | Pooling-Flatten | 576 | |
| FC layer | 1 × 1 | FC-softmax | 6 | |
| Training Ratio | CNN | STFHU | STCNN | ResNet | AResN | RNST | ARNST | |
|---|---|---|---|---|---|---|---|---|
| Original | 20% | 0.4324 | 0.2930 | 0.3577 | 0.1896 | 0.1716 | 0.1864 | 0.1715 |
| 10% | 0.4761 | 0.4125 | 0.4159 | 0.2356 | 0.2222 | 0.2324 | 0.2158 | |
| 5% | 0.5717 | 0.4738 | 0.4964 | 0.3217 | 0.2913 | 0.2997 | 0.2817 | |
| 1% | 0.8162 | 0.9208 | 0.7756 | 0.5456 | 0.4913 | 0.5395 | 0.4382 | |
| 0.5% | 1.0803 | 1.2889 | 1.0246 | 0.6095 | 0.5246 | 0.5836 | 0.5129 | |
| Noisy | 20% | 1.1002 | 0.3011 | 1.1302 | 0.2599 | 0.2511 | 0.2315 | 0.2227 |
| 10% | 1.1291 | 0.4192 | 1.1924 | 0.3148 | 0.2970 | 0.2717 | 0.2643 | |
| 5% | 1.3143 | 0.4812 | 1.2826 | 0.3835 | 0.3776 | 0.3522 | 0.3365 | |
| 1% | 1.1435 | 0.9308 | 1.3196 | 0.6138 | 0.5382 | 0.5667 | 0.4706 | |
| 0.5% | 1.7159 | 1.3014 | 1.1140 | 0.6504 | 0.5683 | 0.5986 | 0.5468 |
| Training Ratio | CNN | STFHU | STCNN | ResNet | AResN | RNST | ARNST | |
|---|---|---|---|---|---|---|---|---|
| Original | 30% | 0.1986 | 0.4856 | 0.1725 | 0.1330 | 0.1162 | 0.1238 | 0.1087 |
| 20% | 0.2246 | 0.4952 | 0.1837 | 0.1473 | 0.1240 | 0.1436 | 0.1106 | |
| 10% | 0.3237 | 0.5647 | 0.2009 | 0.1685 | 0.1487 | 0.1567 | 0.1320 | |
| 5% | 0.3360 | 0.6026 | 0.2295 | 0.2058 | 0.1795 | 0.2046 | 0.1432 | |
| Noisy | 30% | 1.9703 | 0.5509 | 1.9539 | 1.8460 | 1.6932 | 0.2967 | 0.2943 |
| 20% | 1.9239 | 0.5531 | 2.2657 | 1.8541 | 1.8152 | 0.3356 | 0.3055 | |
| 10% | 1.8982 | 0.5720 | 2.0489 | 1.9129 | 1.7395 | 0.3866 | 0.3657 | |
| 5% | 1.8149 | 0.6067 | 2.0297 | 1.7578 | 1.7047 | 0.4102 | 0.3766 |
| Training Ratio | CNN | STFHU | STCNN | ResNet | AResN | RNST | ARNST | |
|---|---|---|---|---|---|---|---|---|
| Original | 30% | 0.1383 | 0.3738 | 0.1221 | 0.0986 | 0.0800 | 0.0595 | 0.0439 |
| 20% | 0.1658 | 0.8253 | 0.1466 | 0.1168 | 0.0866 | 0.1047 | 0.0751 | |
| 10% | 0.8930 | 1.6998 | 0.7241 | 0.7416 | 0.9706 | 0.9819 | 0.5255 | |
| 5% | 0.9393 | 1.8950 | 1.2546 | 1.1362 | 0.9849 | 1.2985 | 0.8546 | |
| Noisy | 30% | 1.1581 | 0.7345 | 0.9467 | 0.9284 | 0.8741 | 0.1785 | 0.1320 |
| 20% | 1.7946 | 0.8983 | 1.8845 | 1.1437 | 1.2148 | 0.3514 | 0.3372 | |
| 10% | 1.6485 | 1.8237 | 1.7618 | 1.6752 | 1.7553 | 1.2196 | 1.0743 | |
| 5% | 2.0059 | 1.9029 | 1.9864 | 1.7114 | 1.8828 | 1.3821 | 1.3608 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, Y.; Ritz, C.; Zhao, J.; Lan, J. Attention-Based Residual Network with Scattering Transform Features for Hyperspectral Unmixing with Limited Training Samples. Remote Sens. 2020, 12, 400. https://doi.org/10.3390/rs12030400
Zeng Y, Ritz C, Zhao J, Lan J. Attention-Based Residual Network with Scattering Transform Features for Hyperspectral Unmixing with Limited Training Samples. Remote Sensing. 2020; 12(3):400. https://doi.org/10.3390/rs12030400
Chicago/Turabian StyleZeng, Yiliang, Christian Ritz, Jiahong Zhao, and Jinhui Lan. 2020. "Attention-Based Residual Network with Scattering Transform Features for Hyperspectral Unmixing with Limited Training Samples" Remote Sensing 12, no. 3: 400. https://doi.org/10.3390/rs12030400
APA StyleZeng, Y., Ritz, C., Zhao, J., & Lan, J. (2020). Attention-Based Residual Network with Scattering Transform Features for Hyperspectral Unmixing with Limited Training Samples. Remote Sensing, 12(3), 400. https://doi.org/10.3390/rs12030400






