A Comparative Assessment of Ensemble-Based Machine Learning and Maximum Likelihood Methods for Mapping Seagrass Using Sentinel-2 Imagery in Tauranga Harbor, New Zealand
Abstract
1. Introduction
2. Materials and Methods
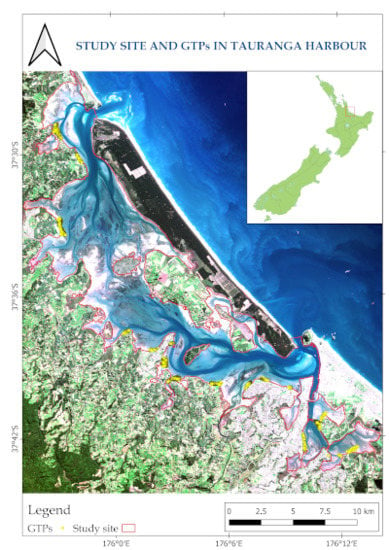
2.1. Study Site
2.2. Field Survey
2.3. Satellite Data Acquisition and Image Pre-Processing
2.3.1. Atmospheric Correction
2.3.2. Water Column Correction
2.4. Image Classification with Machine Learning Ensemble-Based and Maximum Likelihood Methods
2.4.1. Selection of Maximum Likelihood, Random Forest, Rotation Forest, and Canonical Correlation Forest Classifiers
2.4.2. Training and Testing Dataset
2.4.3. Use of Maximum Likelihood, Random Forest, Rotation Forest, and Canonical Correlation Forest Models
2.4.4. Evaluation Criteria
3. Results
3.1. Hyper-Parameter Tuning for Random Forest, Rotation Forest, and Optimizing the Number of Trees for Canonical Correlation Forest Models
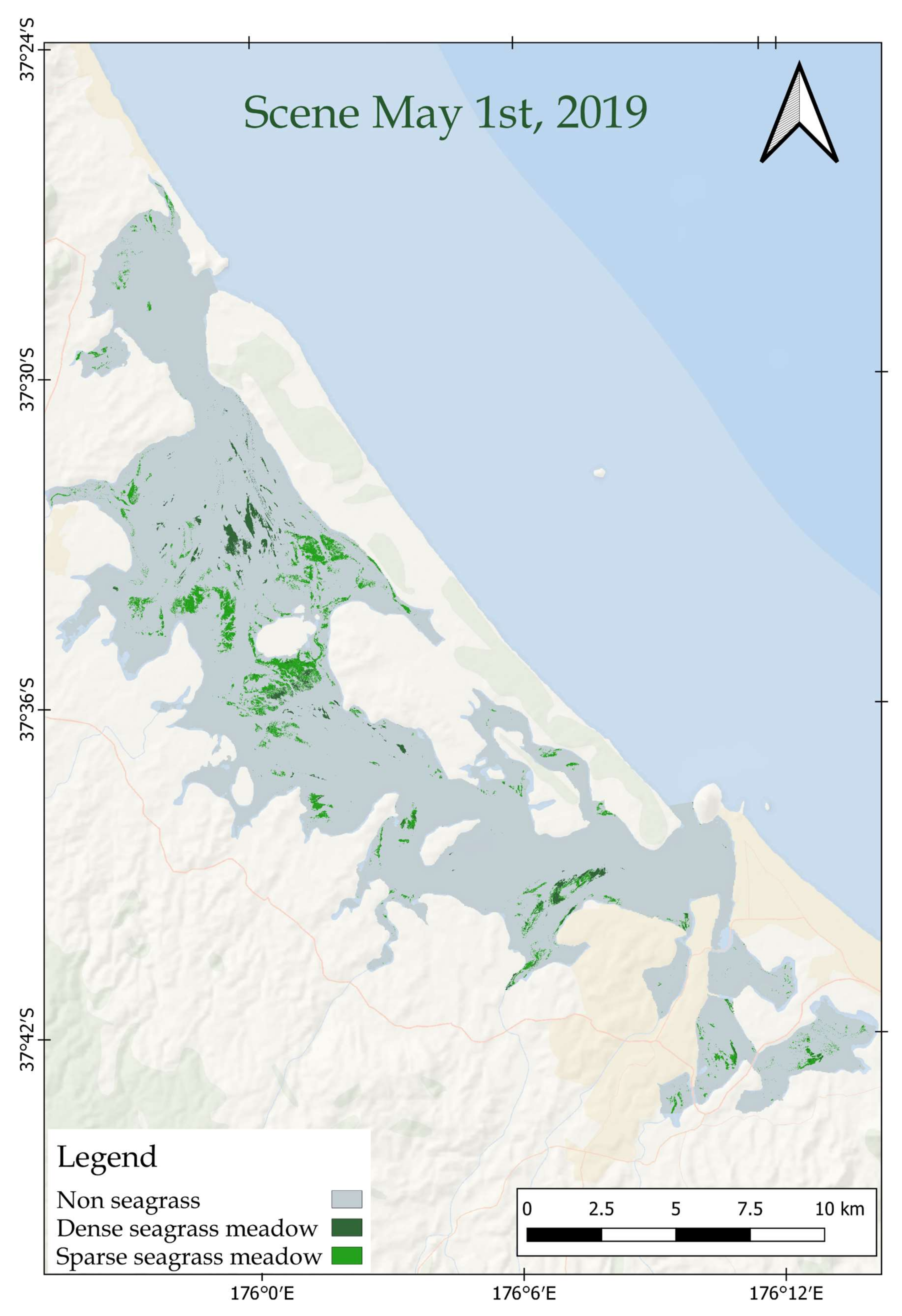
3.2. Comparing the Performance of Random Forest, Rotation Forest, Canonical Correlation Forest, and Maximum Likelihood Models for Seagrass Mapping
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gullström, M.; Lyimo, L.D.; Dahl, M.; Samuelsson, G.S.; Eggertsen, M.; Anderberg, E.; Rasmusson, L.M.; Linderholm, H.W.; Knudby, A.; Bandeira, S.; et al. Blue carbon storage in tropical seagrass meadows relates to carbonate stock dynamics, plant–sediment processes, and landscape context: Insights from the Western Indian ocean. Ecosystems 2018, 21, 551–566. [Google Scholar]
- Oreska, M.P.J.; McGlathery, K.J.; Porter, J.H. Seagrass blue carbon spatial patterns at the meadow-scale. PLoS ONE 2017, 12, e0176630. [Google Scholar] [CrossRef] [PubMed]
- Duarte, C.M.; Krause-Jensen, D. Export from seagrass meadows contributes to marine carbon sequestration. Front. Mar. Sci. 2017, 4. [Google Scholar] [CrossRef]
- Waycott, M.; Duarte, C.M.; Carruthers, T.J.B.; Orth, R.J.; Dennison, W.C.; Olyarnik, S.; Calladine, A.; Fourqurean, J.W.; Heck, K.L.; Hughes, A.R.; et al. Accelerating loss of seagrasses across the globe threatens coastal ecosystems. Proc. Natl. Acad. Sci. 2009, 106, 12377–12381. [Google Scholar] [CrossRef]
- Herold, M.; Skutsch, M. Monitoring, reporting and verification for national REDD + programmes: Two proposals. Environ. Res. Lett. 2011, 6, 014002. [Google Scholar] [CrossRef]
- Pham, T.D.; Xia, J.; Ha, N.T.; Bui, D.T.; Le, N.N.; Tekeuchi, W. A review of remote sensing approaches for monitoring blue carbon ecosystems: Mangroves, seagrassesand salt marshes during 2010–2018. Sensors 2019, 19, 1933. [Google Scholar] [CrossRef]
- ESA Sentinel—2 User Handbook; ESA: Paris, France, 2015; p. 64.
- Hossain, M.S.; Bujang, J.S.; Zakaria, M.H.; Hashim, M. The application of remote sensing to seagrass ecosystems: An overview and future research prospects. Int. J. Remote Sens. 2015, 36, 61–114. [Google Scholar] [CrossRef]
- Winters, G.; Edelist, D.; Shem-Tov, R.; Beer, S.; Rilov, G. A low cost field-survey method for mapping seagrasses and their potential threats: An example from the northern Gulf of Aqaba, Red Sea: Mapping seagrasses and their potential threats in the Gulf of Aqaba. Aquat. Conserv. Mar. Freshw. Ecosyst. 2017, 27, 324–339. [Google Scholar] [CrossRef]
- Gumusay, M.U.; Bakirman, T.; Tuney Kizilkaya, I.; Aykut, N.O. A review of seagrass detection, mapping and monitoring applications using acoustic systems. Eur. J. Remote Sens. 2019, 52, 1–29. [Google Scholar] [CrossRef]
- Wicaksono, P.; Lazuardi, W. Assessment of PlanetScope images for benthic habitat and seagrass species mapping in a complex optically shallow water environment. Int. J. Remote Sens. 2018, 39, 5739–5765. [Google Scholar] [CrossRef]
- Poursanidis, D.; Topouzelis, K.; Chrysoulakis, N. Mapping coastal marine habitats and delineating the deep limits of the Neptune’s seagrass meadows using very high resolution Earth observation data. Int. J. Remote Sens. 2018, 1–18. [Google Scholar] [CrossRef]
- Poursanidis, D.; Traganos, D.; Reinartz, P.; Chrysoulakis, N. On the use of Sentinel-2 for coastal habitat mapping and satellite-derived bathymetry estimation using downscaled coastal aerosol band. Int. J. Appl. Earth Obs. Geoinformation 2019, 80, 58–70. [Google Scholar] [CrossRef]
- Asmala, A. Analysis of Maximum Likelihood Classification on Multispectral Data. Appl. Math. Sci. 2012. [Google Scholar]
- Richards, J.A. Supervised Classification Techniques. In Remote Sensing Digital Image Analysis; Springer: Berlin/Heidelberg, Germany, 2013; ISBN 978-3-642-30062-2. [Google Scholar]
- Holloway, J.; Mengersen, K. Statistical machine learning methods and remote sensing for sustainable development goals: A review. Remote Sens. 2018, 10, 1365. [Google Scholar] [CrossRef]
- Liu, Y. Python Machine Learning by Example: Easy-to-follow Examples that Get You up and Running with Machine Learning; Packt Publishing: Birmingham, UK; Mumbai, India, 2017; ISBN 978-1-78355-311-2. [Google Scholar]
- Mohamed, H.; Nadaoka, K.; Nakamura, T. Assessment of machine learning algorithms for automatic benthic cover monitoring and mapping using towed underwater video camera and high-resolution satellite images. Remote Sens. 2018, 10, 773. [Google Scholar] [CrossRef]
- Bonin-Font, F.; Campos, M.M.; Codina, G.O. Towards visual detection, mapping and quantification of Posidonia Oceanica using a lightweight AUV. IFAC-Pap. 2016, 49, 500–505. [Google Scholar] [CrossRef]
- Traganos, D.; Reinartz, P. Mapping Mediterranean seagrasses with Sentinel-2 imagery. Mar. Pollut. Bull. 2017. [Google Scholar] [CrossRef] [PubMed]
- Pe’eri, S.; Morrison, J.R.; Short, F.; Mathieson, A.; Lippmann, T. Eelgrass and macroalgal mapping to develop nutrient criteria in New Hampshire’s estuaries using hyperspectral imagery. J. Coast. Res. 2016, 76, 209–218. [Google Scholar] [CrossRef]
- Colkesen, I.; Kavzoglu, T. Ensemble-based canonical correlation forest (CCF) for land use and land cover classification using sentinel-2 and Landsat OLI imagery. Remote Sens. Lett. 2017, 8, 1082–1091. [Google Scholar] [CrossRef]
- Sahin, E.K.; Colkesen, I.; Kavzoglu, T. A comparative assessment of canonical correlation forest, random forest, rotation forest and logistic regression methods for landslide susceptibility mapping. Geocarto Int. 2018, 33, 1–23. [Google Scholar] [CrossRef]
- Moughal, T.A. Hyperspectral image classification using Support Vector Machine. J. Phys. Conf. Ser. 2013, 439, 012042. [Google Scholar] [CrossRef]
- Adriano, B.; Xia, J.; Baier, G.; Yokoya, N.; Koshimura, S. Multi-source data fusion based on ensemble learning for rapid building damage mapping during the 2018 sulawesi earthquake and tsunami in Palu, Indonesia. Remote Sens. 2019, 11, 886. [Google Scholar] [CrossRef]
- Probst, P.; Wright, M.; Boulesteix, A.-L. Hyperparameters and tuning strategies for random forest. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2019, 9, e1301. [Google Scholar] [CrossRef]
- Xiu, Y.; Liu, W.; Yang, W. An improved rotation forest for multi-feature remote-sensing imagery classification. Remote Sens. 2017, 9, 1205. [Google Scholar] [CrossRef]
- Bagnall, A.; Bostrom, A.; Cawley, G.; Flynn, M.; Large, J.; Lines, J. Is rotation forest the best classifier for problems with continuous features? arXiv 2018, arXiv:1809.06705. [Google Scholar]
- Belgiu, M.; Drăguţ, L. Random forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Feng, W.; Sui, H.; Tu, J.; Huang, W.; Xu, C.; Sun, K. A Novel Change Detection Approach for Multi-Temporal High-Resolution Remote Sensing Images Based on Rotation Forest and Coarse-to-Fine Uncertainty Analyses. Remote Sens. 2018, 10, 1015. [Google Scholar] [CrossRef]
- Rainforth, T.; Wood, F. Canonical Correlation Forests. arXiv 2015, arXiv:150705444. [Google Scholar]
- Park, S.G. Changes in abundance of seagrass (Zostera spp.) in Tauranga Harbour from 1959–96; Environmental Report 99/30; Environment BOP: Whakatane, New Zealand, 1999; p. 19. [Google Scholar]
- Collier, C.J.; Villacorta-Rath, C.; van Dijk, K.; Takahashi, M.; Waycott, M. Seagrass proliferation precedes mortality during hypo-salinity events: A stress-induced morphometric response. PLoS ONE 2014, 9, e94014. [Google Scholar] [CrossRef]
- Collier, C.J.; Ow, Y.X.; Langlois, L.; Uthicke, S.; Johansson, C.L.; O’Brien, K.R.; Hrebien, V.; Adams, M.P. Optimum Temperatures for Net Primary Productivity of Three Tropical Seagrass Species. Front. Plant Sci. 2017, 8. [Google Scholar] [CrossRef]
- York, P.H.; Gruber, R.K.; Hill, R.; Ralph, P.J.; Booth, D.J.; Macreadie, P.I. Physiological and Morphological Responses of the Temperate Seagrass Zostera muelleri to Multiple Stressors: Investigating the Interactive Effects of Light and Temperature. PLoS ONE 2013, 8, e76377. [Google Scholar] [CrossRef] [PubMed]
- Collier, C.J.; Uthicke, S.; Waycott, M. Thermal tolerance of two seagrass species at contrasting light levels: Implications for future distribution in the Great Barrier Reef. Limnol. Oceanogr. 2011, 56, 2200–2210. [Google Scholar] [CrossRef]
- Turner, S.J. Growth and productivity of intertidal Zostera capricorni in New Zealand estuaries. N. Z. J. Mar. Freshw. Res. 2007, 41, 77–90. [Google Scholar] [CrossRef]
- Ramage, D.L.; Schiel, D.R. Reproduction in the seagrass Zostera novazelandica on intertidal platforms in southern New Zealand. Mar. Biol. 1998, 130, 479–489. [Google Scholar] [CrossRef]
- Schwarz, A.-M.; Turner, S. Management and Conservation of Seagrass in New Zealand: An Introduction; Wellington, New Zeland, 2006; p. 90. [Google Scholar]
- Reeve, G.; Stephens, S.; Wadhwa, A. Tauranga Harbour Inundation Modelling; NIWA: Tauranga, New Zealand, 2018; p. 107. [Google Scholar]
- Past Weather for Tauranga Airport. Available online: https://www.metservice.com/towns-cities/locations/tauranga/past-weather (accessed on 5 January 2020).
- Tauranga Sea Temperature. Available online: https://www.seatemperature.org/australia-pacific/new-zealand/tauranga.htm (accessed on 5 January 2020).
- Park, S. Extent of Seagrass in the Bay of Plenty in 2011; Environmental publication; Bay of Plenty Reginal Council: Whakatane, New Zealand, 2011. [Google Scholar]
- Glovis. Available online: https://glovis.usgs.gov (accessed on 12 October 2019).
- RBINS Acolite Atmospheric Correction Processor. Available online: https://odnature.naturalsciences.be/remsem/software-and-data/acolite (accessed on 1 October 2018).
- Vanhellemont, Q. Adaptation of the dark spectrum fitting atmospheric correction for aquatic applications of the Landsat and Sentinel-2 archives. Remote Sens. Environ. 2019, 225, 175–192. [Google Scholar] [CrossRef]
- Green, E.P.; Mumby, P.J.; Edwards, A.J.; Clark, C.D. A review of remote sensing for the assessment and management of tropical coastal resources. Coast. Manag. 1996, 24, 1–40. [Google Scholar] [CrossRef]
- Thang, H.N.; Yoshino, K.; Hoang Son, T.P. Seagrass mapping using ALOS AVNIR-2 data in Lap An Lagoon, Thua Thien Hue, Vietnam; Frouin, R.J., Ebuchi, N., Pan, D., Saino, T., Eds.; SPIE: Kyoto, Japan, 2012; p. 85250S. [Google Scholar]
- Garcia, R.; Hedley, J.; Tin, H.; Fearns, P. A method to analyze the potential of optical remote sensing for benthic habitat mapping. Remote Sens. 2015, 7, 13157–13189. [Google Scholar] [CrossRef]
- Remote Sensing Handbook for Tropical Coastal Management; Green, E.P., Edwards, A.J., Eds.; Coastal management sourcebooks; Unesco Pub: Paris, France, 2000; ISBN 978-92-3-103736-8. [Google Scholar]
- Chen, Q.; Yu, R.; Hao, Y.; Wu, L.; Zhang, W.; Zhang, Q.; Bu, X. A new method for mapping aquatic vegetation especially underwater vegetation in lake Ulansuhai using GF-1 satellite data. Remote Sens. 2018, 10, 1279. [Google Scholar] [CrossRef]
- Sagawa, T.; Boisnier, E.; Komatsu, T.; Mustapha, K.B.; Hattour, A.; Kosaka, N.; Miyazaki, S. Using bottom surface reflectance to map coastal marine areas: A new application method for Lyzenga’s model. Int. J. Remote Sens. 2010, 31, 3051–3064. [Google Scholar] [CrossRef]
- Lyzenga, D.R.; Malinas, N.P.; Tanis, F.J. Multispectral bathymetry using a simple physically based algorithm. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2251–2259. [Google Scholar] [CrossRef]
- Hogland, J.; Billor, N.; Anderson, N. Comparison of standard maximum likelihood classification and polytomous logistic regression used in remote sensing. Eur. J. Remote Sens. 2013, 46, 623–640. [Google Scholar] [CrossRef]
- Breiman, L. Random Forest. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Rodriguez, J.J.; Kuncheva, L.I.; Alonso, C.J. Rotation Forest: A New Classifier Ensemble Method. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 1619–1630. [Google Scholar] [CrossRef] [PubMed]
- Koedsin, W.; Intararuang, W.; Ritchie, R.; Huete, A. An Integrated Field and Remote Sensing Method for Mapping Seagrass Species, Cover, and Biomass in Southern Thailand. Remote Sens. 2016, 8, 292. [Google Scholar] [CrossRef]
- Kovacs, E.; Roelfsema, C.; Lyons, M.; Zhao, S.; Phinn, S. Seagrass habitat mapping: How do Landsat 8 OLI, Sentinel-2, ZY-3A, and Worldview-3 perform? Remote Sens. Lett. 2018, 9, 686–695. [Google Scholar] [CrossRef]
- Meyer, C.A.; Pu, R. Seagrass resource assessment using remote sensing methods in St. Joseph Sound and Clearwater Harbor, Florida, USA. Environ. Monit. Assess. 2012, 184, 1131–1143. [Google Scholar] [CrossRef]
- Tsujimoto, R.; Terauchi, G.; Sasaki, H.; Sakamoto, S.X.; Sawayama, S.; Sasa, S.; Yagi, H.; Komatsu, T. Damage to seagrass and seaweed beds in Matsushima Bay, Japan, caused by the huge tsunami of the Great East Japan Earthquake on 11 March 2011. Int. J. Remote Sens. 2016, 37, 5843–5863. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Joshua, L. Rotation Forest 2016. Available online: https://github.com/joshloyal/RotationForest (accessed on 13 February 2019).
- Albanese, D.; Visintainer, R.; Merler, S.; Riccadonna, S.; Jurman, G.; Furlanello, C. Mlpy: Machine Learning Python. arXiv 2012, arXiv:12026548. [Google Scholar]
- Davide, A. Non Linear Methods for Classification: Maximum Likelihood Classifier. Available online: http://mlpy.sourceforge.net/docs/3.5/nonlin_class.html#maximum-likelihood-classifier (accessed on 15 February 2019).
- Rainforth, T. Canonical Correlation Forests 2018. Available online: https://github.com/twgr/ccfs (accessed on 17 February 2019).
- Raschka, S. MLxtend: Providing machine learning and data science utilities and extensions to Python’s scientific computing stack. J. Open Source Softw. 2018, 3, 638. [Google Scholar] [CrossRef]
- Traganos, D.; Reinartz, P. Interannual Change Detection of Mediterranean Seagrasses Using RapidEye Image Time Series. Front. Plant Sci. 2018, 9. [Google Scholar] [CrossRef] [PubMed]
- Pham, T.D.; Xia, J.; Baier, G.; Le, N.N.; Yokoya, N. Mangrove Species Mapping Using Sentinel-1 and Sentinel-2 Data in North Vietnam. In Proceedings of the IGARSS 2019 - 2019 IEEE International Geoscience and Remote Sensing Symposium; IEEE: Yokohama, Japan, 2019; pp. 6102–6105. [Google Scholar]
- Lemenkova, P. Processing oceanographic data by python libraries Numpy, Scipy, and Pandas. Aquat. Res. 2019, 73–91. [Google Scholar] [CrossRef]
- Raschka, S.; Mirjalili, V. Python machine learning: Machine learning and deep learning with Python, scikit-learn, and TensorFlow, 2nd ed.; Packt Publishing: Birmingham, UK; Mumbai, India, 2017; ISBN 978-1-78712-593-3. [Google Scholar]
- Yan, J.; Ma, Y.; Wang, L.; Choo, K.-K.R.; Jie, W. A cloud-based remote sensing data production system. Future Gener. Comput. Syst. 2018, 86, 1154–1166. [Google Scholar] [CrossRef]
- Yao, X.; Li, G.; Xia, J.; Ben, J.; Cao, Q.; Zhao, L.; Ma, Y.; Zhang, L.; Zhu, D. Enabling the Big Earth Observation Data via Cloud Computing and DGGS: Opportunities and Challenges. Remote Sens. 2019, 12, 62. [Google Scholar] [CrossRef]


| Date of Acquisition | Time of Acquisition a | Spatial Resolution (m) | Cloud Coverage (%) | First Low Tide | Second Low Tide |
|---|---|---|---|---|---|
| 5/1/2019 | 10:16 AM | 10 | 0 | 10:33 AM | 22:52 PM |
| Parameters | Values |
|---|---|
| Ancillary data | |
| Gas transmittance | True |
| Ozone concentration (cm−1) | 0.3 |
| Water vapor concentration (g/cm2) | 1.5 |
| Pressure | Normal pressure |
| Masking | |
| Level 2 water masking (nm) | 1600 |
| Negative reflectance masking | True |
| Cirrus masking | True |
| Other parameters | |
| Sky correction | True |
| Dark spectrum fitting | Fixed |
| Sun glint correction | False |
| Output parameter | |
| Surface reflectance for water pixel () | |
| Sentinel Acquisition Date | Number of Pixels | |
|---|---|---|
| 60% for training | 40% for testing | |
| 5/1/2019 | 8586 | 5724 |
| RF | RoF | |
|---|---|---|
| Bootstrap | True | True |
| Max depth | 20 | 30 |
| Max feature | Auto | Auto |
| Min sample leaf | 1 | 3 |
| Min sample split | 9 | 7 |
| Number of tree | 100 | 100 |
| Number of subset | 3 |
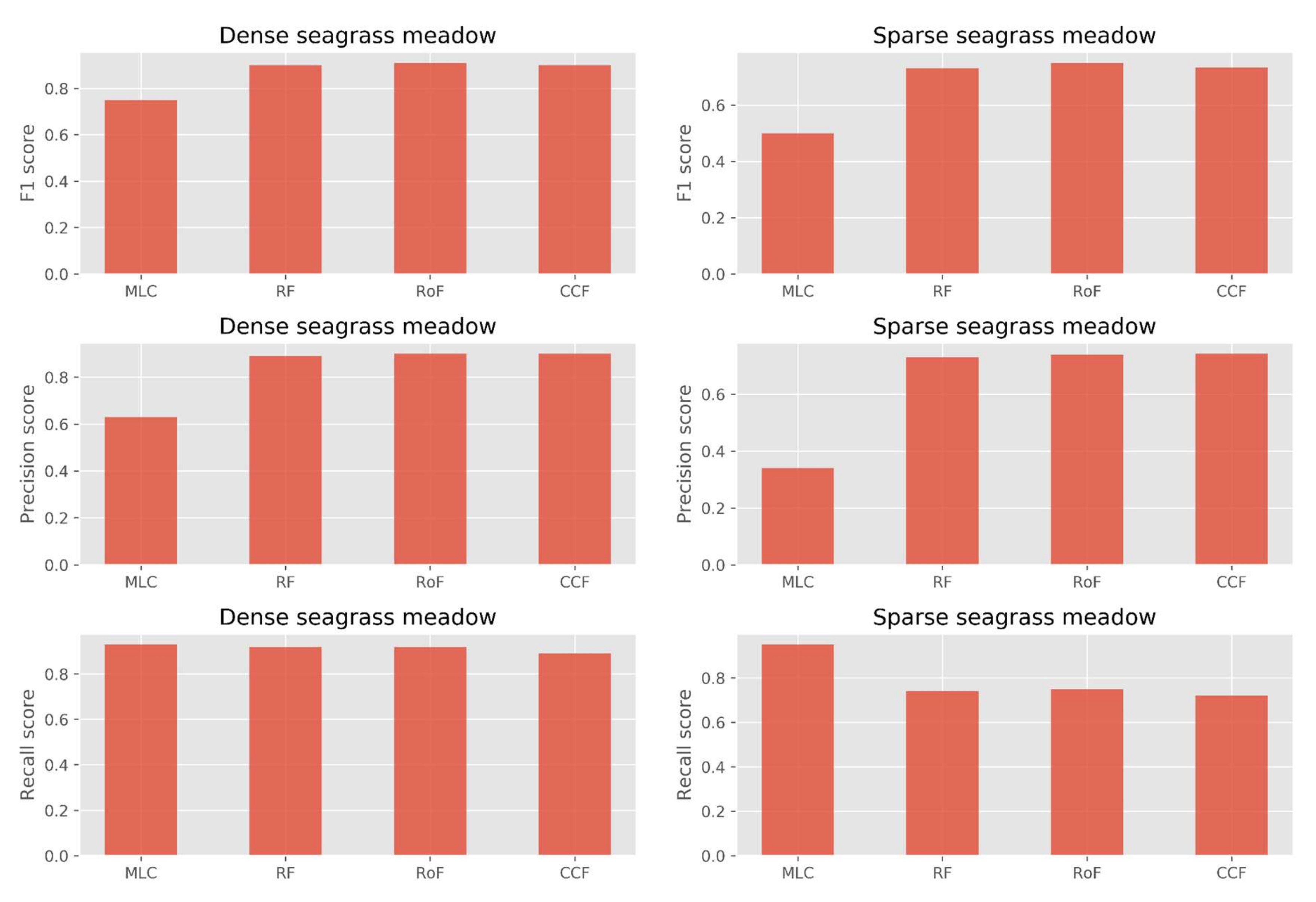
| Model | Accuracy | Precision DS a | Precision SS a | Recall DS | Recall SS | F1 DS | F1 SS | Training time (s) | Prediction time (s) |
|---|---|---|---|---|---|---|---|---|---|
| RoF | 0.88 | 0.90 | 0.74 | 0.92 | 0.75 | 0.91 | 0.75 | 3.54 | 0.37 |
| CCF | 0.87 | 0.90 | 0.74 | 0.89 | 0.72 | 0.90 | 0.73 | 27.06 | 4.57 |
| RF | 0.87 | 0.89 | 0.73 | 0.92 | 0.74 | 0.90 | 0.73 | 0.07 | 0.00 |
| MLC | 0.51 | 0.63 | 0.34 | 0.93 | 0.95 | 0.75 | 0.50 | 0.00 | 0.01 |
| χ2 | p Value | |
|---|---|---|
| Scene 05/01/2019 | ||
| RoF–RF | 9.03 | 0.00 |
| RoF–MLC | 1667.29 | 0.00 |
| RoF–CCF | 2069.37 | 0.00 |
| RF–MLC | 1599.46 | 0.00 |
| RF–CCF | 1995.93 | 0.00 |
| CCF–MLC | 42.51 | 0.00 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ha, N.T.; Manley-Harris, M.; Pham, T.D.; Hawes, I. A Comparative Assessment of Ensemble-Based Machine Learning and Maximum Likelihood Methods for Mapping Seagrass Using Sentinel-2 Imagery in Tauranga Harbor, New Zealand. Remote Sens. 2020, 12, 355. https://doi.org/10.3390/rs12030355
Ha NT, Manley-Harris M, Pham TD, Hawes I. A Comparative Assessment of Ensemble-Based Machine Learning and Maximum Likelihood Methods for Mapping Seagrass Using Sentinel-2 Imagery in Tauranga Harbor, New Zealand. Remote Sensing. 2020; 12(3):355. https://doi.org/10.3390/rs12030355
Chicago/Turabian StyleHa, Nam Thang, Merilyn Manley-Harris, Tien Dat Pham, and Ian Hawes. 2020. "A Comparative Assessment of Ensemble-Based Machine Learning and Maximum Likelihood Methods for Mapping Seagrass Using Sentinel-2 Imagery in Tauranga Harbor, New Zealand" Remote Sensing 12, no. 3: 355. https://doi.org/10.3390/rs12030355
APA StyleHa, N. T., Manley-Harris, M., Pham, T. D., & Hawes, I. (2020). A Comparative Assessment of Ensemble-Based Machine Learning and Maximum Likelihood Methods for Mapping Seagrass Using Sentinel-2 Imagery in Tauranga Harbor, New Zealand. Remote Sensing, 12(3), 355. https://doi.org/10.3390/rs12030355