Spatiotemporal Analysis of Hydrological Variations and Their Impacts on Vegetation in Semiarid Areas from Multiple Satellite Data
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data
2.2.1. Meteorological Data
2.2.2. Actual Evapotranspiration (ET)
2.2.3. Terrestrial Water Storage
2.2.4. Auxiliary Data from Global Land Data Assimilation System (GLDAS)
2.2.5. Normalized Difference Vegetation index (NDVI)
2.3. Methods
2.3.1. Determination of Terrestrial Water Storage Change (TWSC)
2.3.2. Estimation of Groundwater Change (GWC)
2.3.3. Analysis of NDVI
Maximum-Value Composite
Analysis of Spatial Trend
Analysis of Hurst Index
Analysis of Trend Test
3. Results
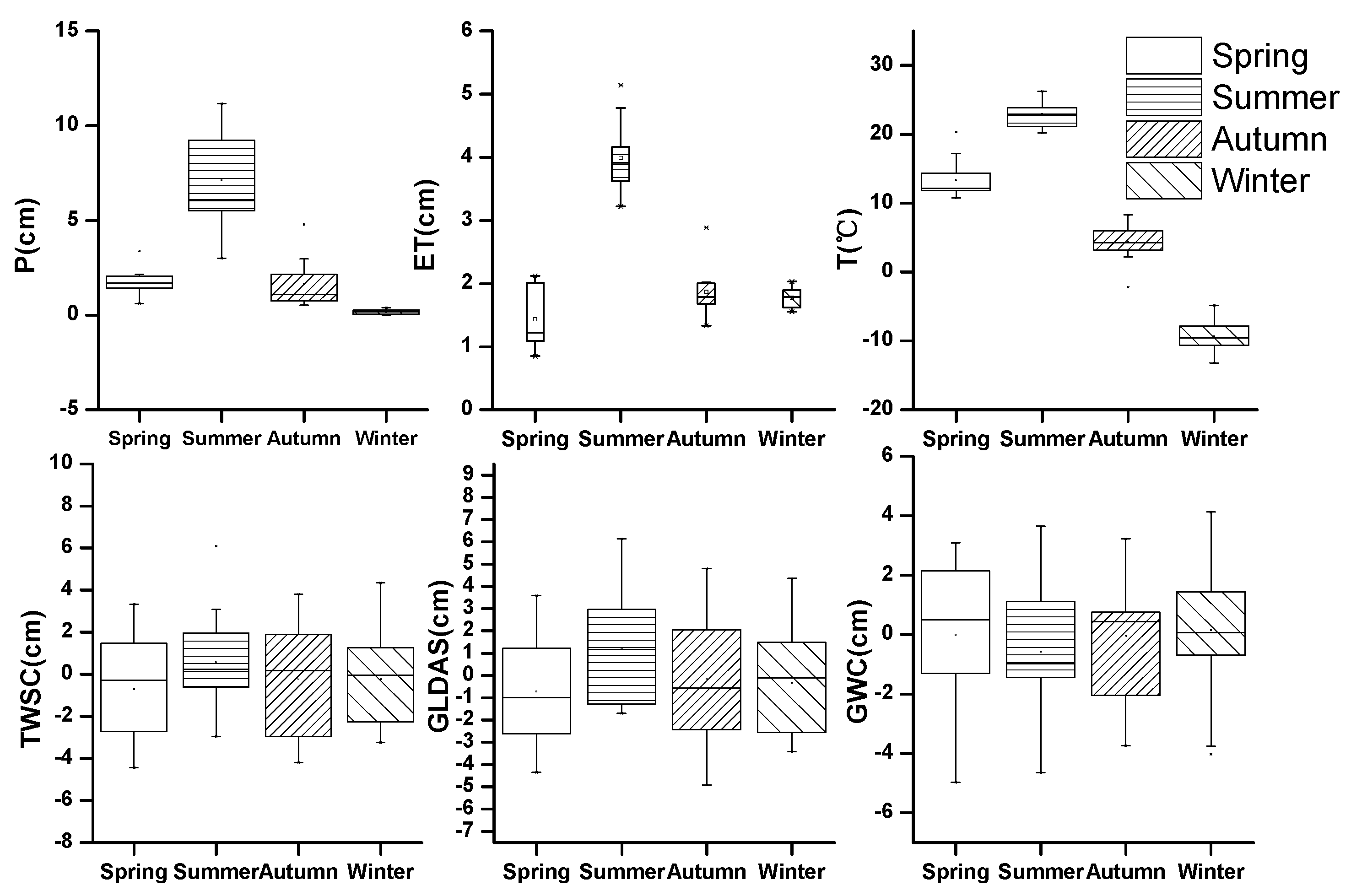
3.1. Changes of Hydrological Factors over Time
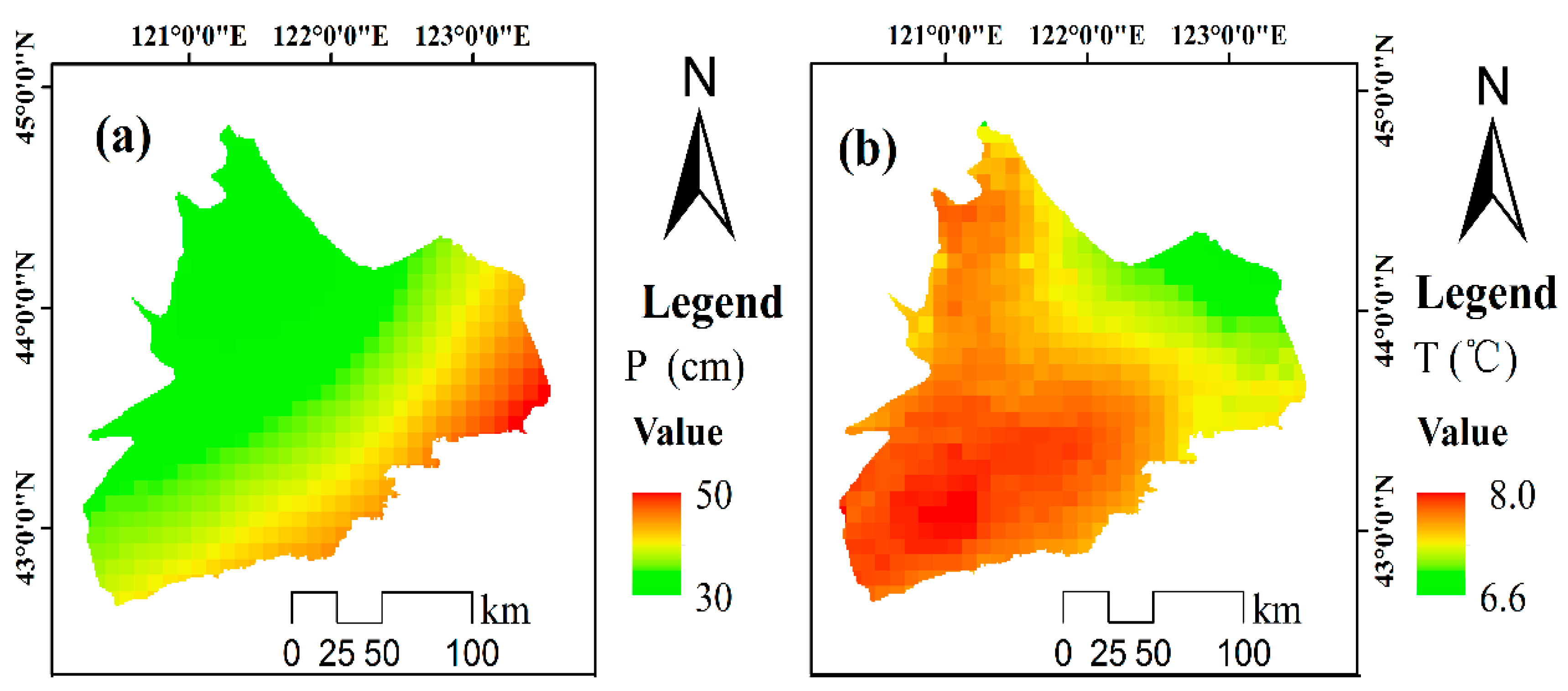
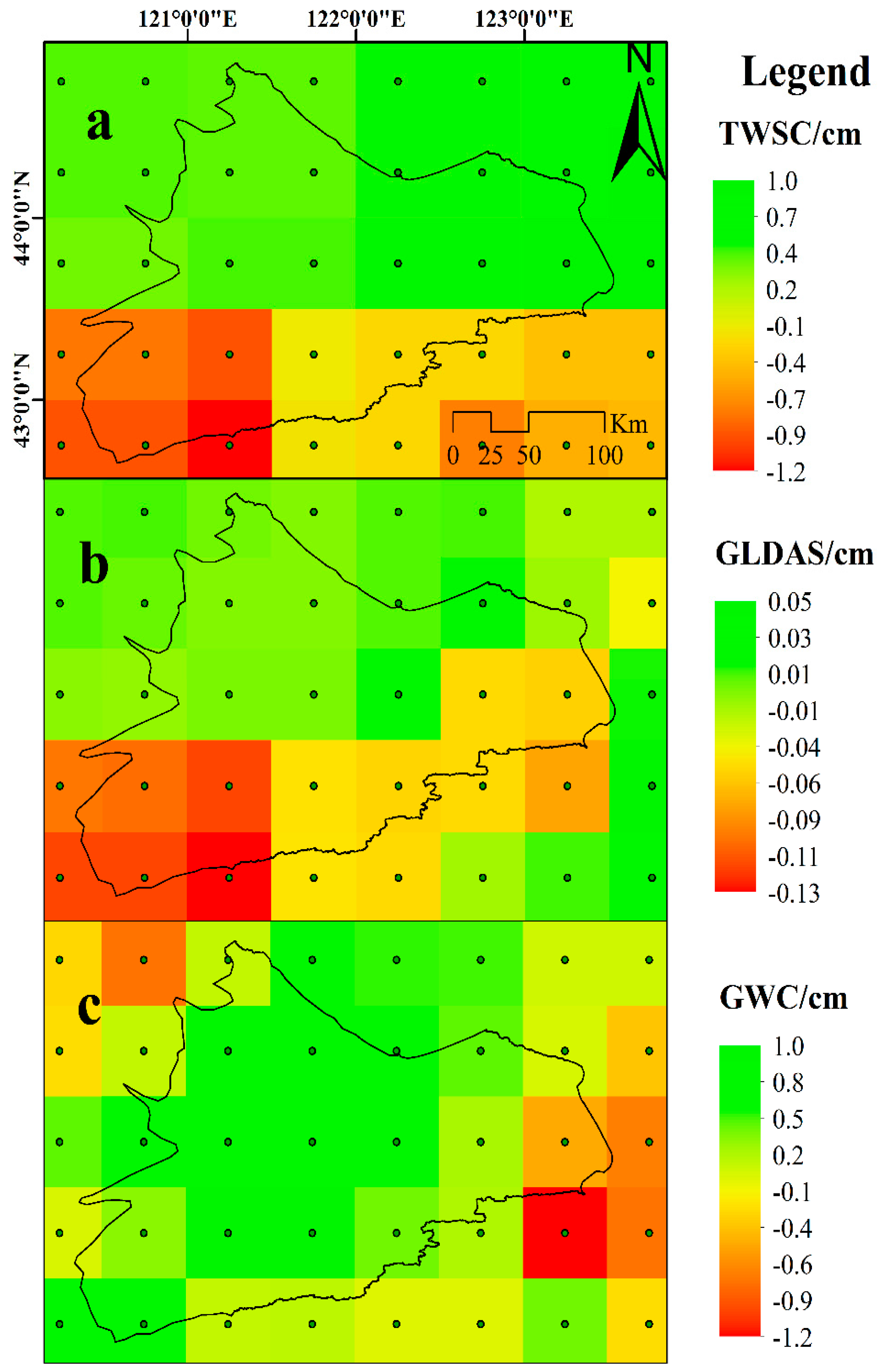
3.2. Spatial Distribution of Annual Hydrological Factors
3.2.1. Situ Observation of Hydrological Factors
3.2.2. Hydrological Factors from Satellite Data
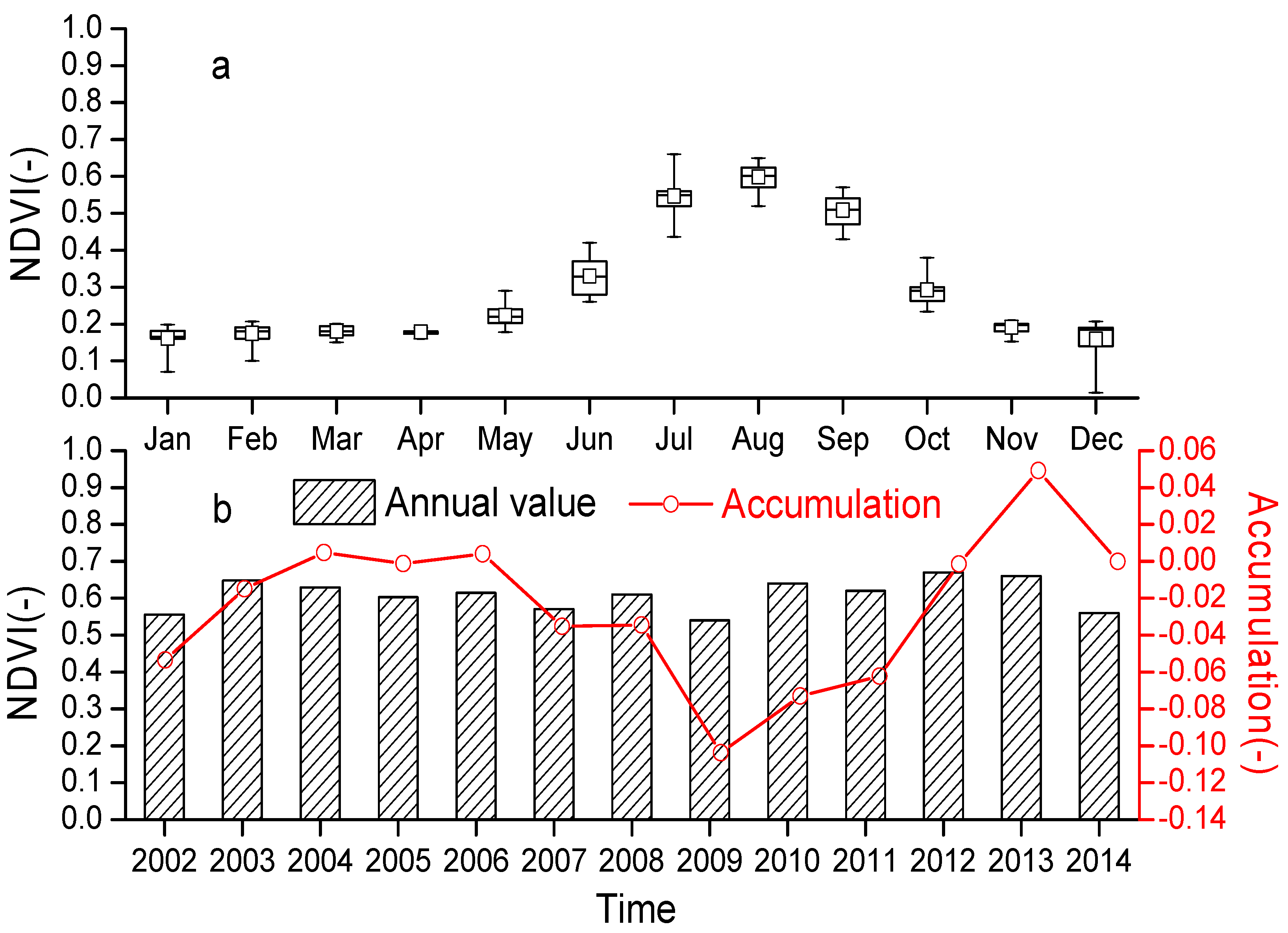
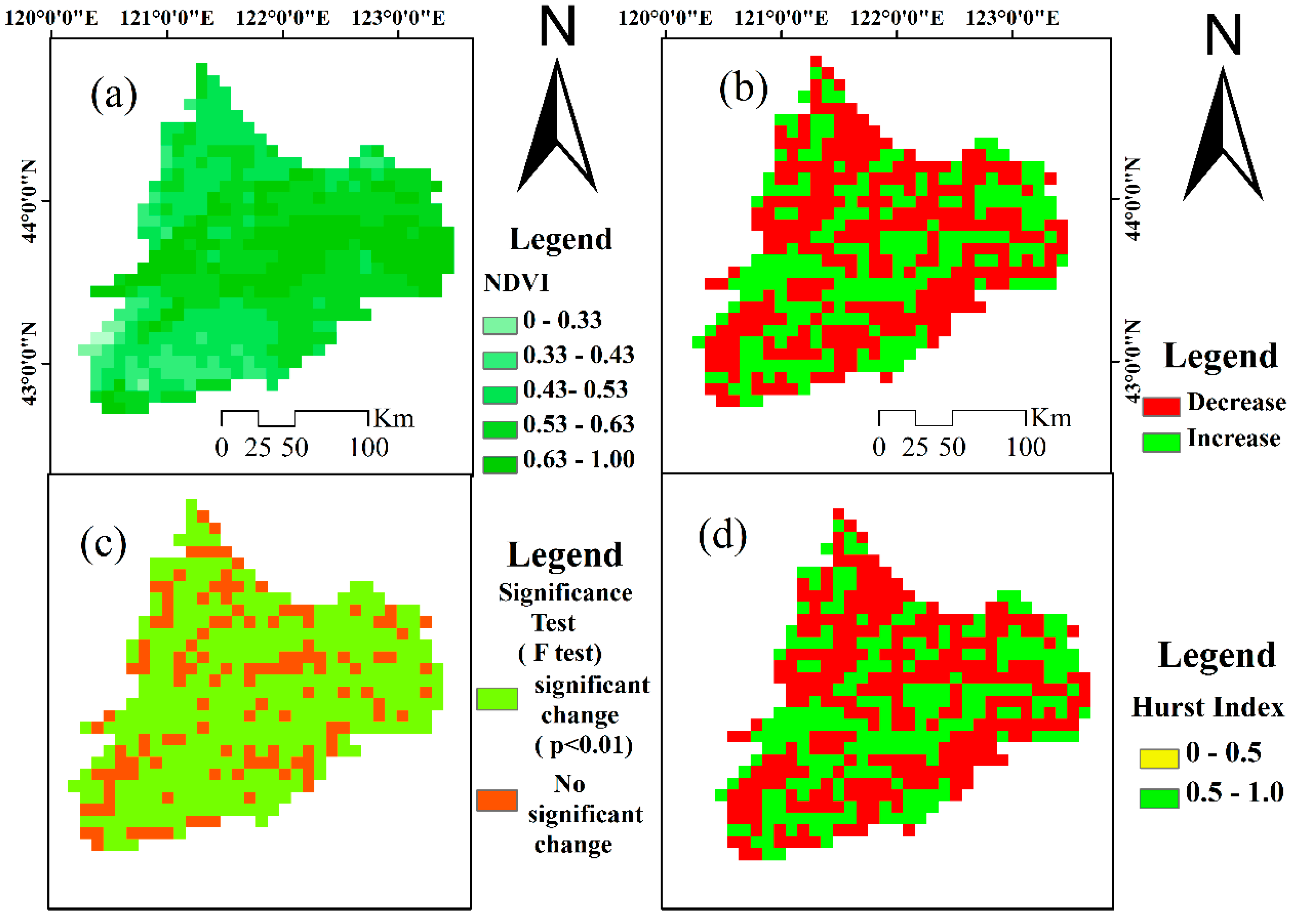
3.3. Spatiotemporal Variations of Normalized Difference Vegetation Index (NDVI)
3.3.1. Temporal Variation
3.3.2. Spatial Variations
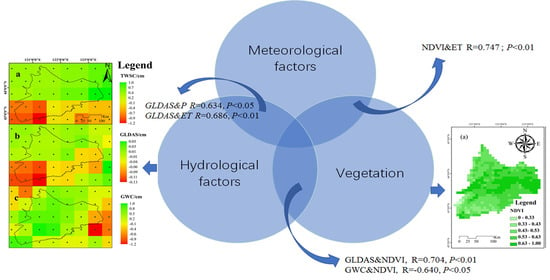
3.4. Relationships between Hydrological Factors
3.5. Relationships between Hydrological Factors and NDVI
4. Discussion
4.1. Dynamics of Hydroecological Elements in Semiarid Area
4.2. Impacts of Hydrological Factors on Vegetation
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Huang, J.; Zhang, W.; Zuo, J.; Fu, C.; Chou, J.; Feng, G.; Yuan, J.; Zhang, L.; Wang, S.; Zuo, H.; et al. Development of the semi-arid climate and environment research observatory over Loess Plateau. Adv. Atmos. Sci. 2008, 25, 906–921. [Google Scholar] [CrossRef]
- Nielsen, U.N.; Ball, B.A. Impacts of altered precipitation regimes on soil communities and biogeochemistry in arid and semi-arid ecosystems. Glob. Chang. Biol. 2015, 21, 1407–1421. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Liu, T.X.; Paredes, P.; Duan, L.M.; Wang, H.Y.; Wang, T.S.; Pereira, L.S. Ecohydrology of groundwater-dependent grasslands of the semi-arid Horqin sandy land of inner Mongolia focusing on evapotranspiration partition. Ecohydrology 2016, 9, 1052–1067. [Google Scholar] [CrossRef]
- Villalobos-Vega, R.; Salazar, A.; Miralles-Wilhelm, F.; Haridasan, M.; Franco, A.C.; Goldstein, G.; Wesche, K. Do groundwater dynamics drive spatial patterns of tree density and diversity in Neotropical savannas? J. Veg. Sci. 2014, 25, 1465–1473. [Google Scholar] [CrossRef]
- Dai, X.Q.; Shi, H.B.; Li, Y.S.; Ouyang, Z.; Huo, Z.L. Artificial neural network models for estimating regional reference evapotranspiration based on climate factors. Hydrol. Process. 2009, 23, 442–450. [Google Scholar] [CrossRef]
- He, D.; Liu, Y.; Pan, Z.; An, P.; Wang, L.; Dong, Z.; Zhang, J.; Pan, X.; Zhao, P. Climate change and its effect on reference crop evapotranspiration in central and western Inner Mongolia during 1961–2009. Front. Earth Sci. 2013, 7, 417–428. [Google Scholar] [CrossRef]
- Zhang, F.; Zhou, G.S.; Wang, Y.; Yang, F.L.; Nilsson, C. Evapotranspiration and crop coefficient for a temperate desert steppe ecosystem using eddy covariance in Inner Mongolia, China. Hydrol. Process. 2012, 26, 379–386. [Google Scholar] [CrossRef]
- Miao, L.; Jiang, C.; Xue, B.; Liu, Q.; He, B.; Nath, R.; Cui, X. Vegetation dynamics and factor analysis in arid and semi-arid Inner Mongolia. Environ. Earth Sci. 2014, 73, 2343–2352. [Google Scholar] [CrossRef]
- Li, S.G.; He, Z.Y.; Chang, X.L.; Harazono, Y.; Oikawa, T.; Zhao, H.L. Grassland desertification by grazing and the resulting micrometeorological changes in Inner Mongolia. Agric. For. Meteorol. 2000, 102, 125–137. [Google Scholar]
- Zunya, W.; Yihui, D.; Jinhai, H.; Jun, Y. An updating analysis of the climate change in china in recent 50 years. Acta Meteorol. Sin. 2004, 62, 228–236. [Google Scholar]
- Zhong, Y.L.; Zhong, M.; Feng, W.; Zhang, Z.Z.; Shen, Y.C.; Wu, D.C. Groundwater Depletion in the West Liaohe River Basin, China and Its Implications Revealed by GRACE and In Situ Measurements. Remote Sens. 2018, 10, 493. [Google Scholar] [CrossRef]
- Li, B.; Yu, W.; Wang, J. An Analysis of Vegetation Change Trends and Their Causes in Inner Mongolia, China from 1982 to 2006. Adv. Meteorol. 2011, 2011, 13–30. [Google Scholar] [CrossRef]
- Huang, J.; Sun, S.; Xue, Y.; Zhang, J. Changing characteristics of precipitation during 1960–2012 in Inner Mongolia, northern China. Meteorol. Atmos. Phys. 2014, 127, 257–271. [Google Scholar] [CrossRef]
- Yang, H.S.; Liu, J.; Liang, H.Y. Change characteristics of climate and water resources in west Liaohe River Plain. J. Appl. Ecol. 2009, 20, 84–90. (In Chinese) [Google Scholar]
- Gao, Z.; He, J.; Dong, K.; Bian, X.; Li, X. Sensitivity study of reference crop evapotranspiration during growing season in the West Liao River basin, China. Theor. Appl. Climatol. 2015, 124, 865–881. [Google Scholar] [CrossRef]
- Schaffrath, D.; Bernhofer, C. Variability and distribution of spatial evapotranspiration in semiarid Inner Mongolian grasslands from 2002 to 2011. Springerplus 2013, 2, 547. [Google Scholar] [CrossRef]
- Liu, X.P.; He, Y.H.; Zhao, X.Y.; Zhang, T.H.; Li, Y.L.; Yun, J.Y.; Wei, S.L.; Yue, X.F. The response of soil water and deep percolation under Caragana microphylla to rainfall in the Horqin Sand Land, northern China. Catena 2016, 139, 82–91. [Google Scholar] [CrossRef]
- Yao, S.X.; Zhao, C.C.; Zhang, T.H.; Liu, X.P. Response of the soil water content of mobile dunes to precipitation patterns in Inner Mongolia, northern China. J. Arid. Environ. 2013, 97, 92–98. [Google Scholar] [CrossRef]
- Zhu, L.; Gong, H.L.; Dai, Z.X.; Xu, T.B.; Su, X.S. An integrated assessment of the impact of precipitation and groundwater on vegetation growth in arid and semiarid areas. Environ. Earth Sci. 2015, 74, 5009–5021. [Google Scholar] [CrossRef]
- Feng, W.; Zhong, M.; Lemoine, J.M.; Biancale, R.; Hsu, H.T.; Xia, J. Evaluation of groundwater depletion in North China using the Gravity Recovery and Climate Experiment (GRACE) data and ground-based measurements. Water Resour. Res. 2013, 49, 2110–2118. [Google Scholar] [CrossRef]
- Wahr, J.; Molenaar, M.; Bryan, F. Time variability of the Earth’s gravity field: Hydrological and oceanic effects and their possible detection using GRACE. J. Geophys. Res. Solid Earth 1998, 103, 30205–30229. [Google Scholar] [CrossRef]
- Chen, Z.; Jiang, W.; Wu, J.; Chen, K.; Deng, Y.; Jia, K.; Mo, X. Detection of the spatial patterns of water storage variation over China in recent 70 years. Sci. Rep. 2017, 7, 6423. [Google Scholar] [CrossRef] [PubMed]
- Yang, P.; Xia, J.; Zhan, C.; Qiao, Y.; Wang, Y. Monitoring the spatio-temporal changes of terrestrial water storage using grace data in the Tarim river basin between 2002 and 2015. Sci. Total Environ. 2017, 595, 218–228. [Google Scholar] [CrossRef] [PubMed]
- Yeh, P.J.-F.; Swenson, S.C.; Famiglietti, J.S.; Rodell, M. Remote sensing of groundwater storage changes in illinois using the gravity recovery and climate experiment (grace). Water Resour. Res. 2006, 42, 4. [Google Scholar] [CrossRef]
- Singh, A.K.; Tripathi, J.N.; Kotlia, B.S.; Singh, K.K.; Kumar, A. Monitoring groundwater fluctuations over india during indian summer monsoon (ism) and northeast monsoon using grace satellite: Impact on agriculture—Sciencedirect. Quat. Int. 2019, 507, 342–351. [Google Scholar] [CrossRef]
- Han, Z.; Huang, S.; Huang, Q.; Leng, G.; Wang, H.; He, L.; Fang, W. Assessing grace-based terrestrial water storage anomalies dynamics at multi-timescales and their correlations with teleconnection factors in yunnan province, china. J. Hydrol. 2019, 574, 836–850. [Google Scholar] [CrossRef]
- Lv, M.; Ma, Z.; Li, M.; Zheng, Z. Quantitative Analysis of Terrestrial Water Storage Changes under the Grain for Green Program in the Yellow River Basin. J. Geophys. Res. Atmos. 2019, 124, 1336–1351. [Google Scholar] [CrossRef]
- Zhang, Q.; Singh, V.P.; Sun, P.; Chen, X.; Zhang, Z.X.; Li, J.F. Precipitation and streamflow changes in China: Changing patterns, causes and implications. J. Hydrol. 2011, 410, 204–216. [Google Scholar] [CrossRef]
- Long, W.H.; Chen, H.H.; Li, Z.; Pan, H.J. Evaluation of the groundwater intrinsic vulnerability in West Liaohe plain, Inner Mongolia, China. Geological Bulletin of China. Geol. Bull. China 2010, 29, 598–602. [Google Scholar]
- Zhu, Y.H.; Zhang, S.; Sun, B.; Yan, L.; Wang, Y. Relationship of dominant herbaceous plant species and groundwater depth in tongliao plain, northwestern china. Appl. Ecol. Environ. Res. 2019, 17, 15363–15374. [Google Scholar] [CrossRef]
- Jia, X.; Lee, H.F.; Zhang, W.C.; Wang, L.; Sun, Y.G.; Zhao, Z.J.; Yi, S.W.; Huang, W.B.; Lu, H.Y. Human-environment interactions within the West Liao River Basin in Northeastern China during the Holocene Optimum. Quat. Int. 2016, 426, 10–17. [Google Scholar] [CrossRef]
- Hutchinson, M.F. Interpolation of rainfall data with thin plate smoothing splines I. two-dimensional smoothing of data with shortrange correlation. Geogr. Inf. Decis. Anal. 1998, 2, 153–167. [Google Scholar]
- Mu, Q.; Heinsch, F.A.; Zhao, M.; Running, S.W. Development of a global evapotranspiration algorithm based on MODIS and global meteorology data. Remote Sens. Environ. 2007, 111, 519–536. [Google Scholar] [CrossRef]
- Mu, Q.; Zhao, M.; Heinsch, F.A.; Liu, M.; Tian, H.; Running, S.W. Evaluating water stress controls on primary production in biogeochemical and remote sensing based models. J. Geophys. Res. Biogeosci. 2015, 112, 863–866. [Google Scholar] [CrossRef]
- Ouyang, W.; Liu, B.; Wu, Y.Y. Satellite-based estimation of watershed groundwater storage dynamics in a freeze-thaw area under intensive agricultural development. J. Hydrol. 2016, 537, 96–105. [Google Scholar] [CrossRef]
- Feixiao, G.; Zhongmiao, S.; Feilong, R.; Yun, X. Comparison and Analysis of Different Mascon Model Results. J. Geod. Geodyn. 2019, 39, 1022–1026. [Google Scholar]
- Cheng, M.; Tapley, B.D. Variations in the Earth’s Oblateness during the Past 28 Years. J. Geophys. Res. Solid Earth 2004, 109. [Google Scholar] [CrossRef]
- Swenson, S.; Chambers, D.; Wahr, J. Estimating Geocenter Variations from a Combination of GRACE and Ocean Model Output. J. Geophys. Res. Solid Earth 2008, 113. [Google Scholar] [CrossRef]
- Geruo, A.; Wahr, J.; Zhong, S. Computations of the Viscoelastic Response of a 3-D Compressible Earth to Surface Loading: An Application to Glacial Isostatic Adjustment in Antarctica and Canada. Geophys. J. Int. 2013, 192, 557–572. [Google Scholar]
- Watkins, M.M.; Wiese, D.N.; Yuan, D.-N.; Boening, C.; Landerer, F.W. Improved Methods for Observing Earth’s Time Variable Mass Distribution with GRACE Using Spherical Cap Mascons. J. Geophys. Res. Solid Earth 2015, 120, 2648–2671. [Google Scholar]
- Rodell, M.; Chen, J.; Kato, H.; Famiglietti, J.S.; Nigro, J.; Wilson, C.R. Estimating groundwater storage changes in the Mississippi River basin (USA) using GRACE. Hydrogeol. J. 2006, 15, 159–166. [Google Scholar] [CrossRef]
- Save, H.; Bettadpur, S.; Tapley, B.D. High-resolution CSR GRACE RL05 mascons. J. Geophys. Res. Sol. Earth 2016, 121, 7547–7569. [Google Scholar] [CrossRef]
- Holger, S.; Patrick, W.; Hansheng, W. Determination of the Earth’s structure in Fennoscandia from GRACE and implications for the optimal post-processing of GRACE data. Geophys. J. Int. 2010, 182, 1295–1310. [Google Scholar]
- Rodell, M.; Velicogna, I.; Famiglietti, J.S. Satellite-based estimates of groundwater depletion in India. Nature 2009, 460, 999–1002. [Google Scholar] [CrossRef]
- Nanteza, J.; De Linage, C.R.; Thomas, B.F.; Famiglietti, J.S. Monitoring groundwater storage changes in complex basement aquifers: An evaluation of the grace satellites over eastafrica. Water Resour. Res. 2016, 52, 9542–9564. [Google Scholar]
- Long, D.; Yang, Y.; Wada, Y.; Hong, Y.; Liang, W.; Chen, Y.; Chen, L. Deriving scaling factors using a global hydrological model to restore. J. Remote Sens. Environ. 2015, 168, 177–193. [Google Scholar] [CrossRef]
- Holben, B.N. Characteristics of maximum-value composite images from temporal AVHRR data. Int. J. Remote Sens. 1986, 7, 1417–1434. [Google Scholar] [CrossRef]
- Jiang, L.; Bao, A.; Guo, H.; Ndayisaba, F. Vegetation dynamics and responses to climate change and human activities in central Asia. Sci. Total Environ. 2017, 599–600, 967–980. [Google Scholar] [CrossRef]
- Hou, W.; Hou, X. Spatial–temporal changes in vegetation coverage in the global coastal zone based on gimms ndvi3g data. Int. J. Remote Sens. 2019, 41, 1118–1138. [Google Scholar] [CrossRef]
- Tong, S.; Zhang, J.; Bao, Y.; Lai, Q.; Lian, X.; Li, N.; Bao, Y. Analyzing vegetation dynamic trend on the Mongolian Plateau based on the Hurst exponent and influencing factors from 1982–2013. J. Geogr. Sci. 2018, 28, 595–610. [Google Scholar] [CrossRef]
- Thompson, S.E.; Harman, C.J.; Troch, P.A.; Brooks, P.D.; Sivapalan, M. Spatial scale dependence of ecohydrologically mediated water balance partitioning: A synthesis framework for catchment ecohydrology. Water Resour. Res. 2011, 47, W00J03. [Google Scholar] [CrossRef]
- Abelen, S.; Seitz, F. Relating satellite gravimetry data to global soil moisture products via data harmonization and correlation analysis. Remote Sens. 2013, 136, 89–98. [Google Scholar] [CrossRef]
- Clark, M.P.; Hendrikx, J.; Slater, A.G.; Kavetski, D.; Anderson, B.; Cullen, N.J.; Kerr, T.; Örn Hreinsson, E.; Woods, R.A. Representing spatial variability of snow water equivalent in hydrologic and land-surface models: A review. Water Resour. Res. 2011, 47, W07539. [Google Scholar] [CrossRef]
- Lee, Y.G.; Ho, C.-H.; Kim, J.; Kim, J. Potential impacts of northeastern Eurasian snow cover on generation of dust storms in northwestern China during spring. Clim. Dyn. 2012, 41, 721–733. [Google Scholar] [CrossRef]
- Jackson, T.J. Remote sensing of soil moisture: Implications for groundwater recharge. Hydrogeol. J. 2002, 10, 40–51. [Google Scholar] [CrossRef]
- Zheng, Y.; Rimmington, G.M.; Xie, Z.; Zhang, L.; An, P.; Zhou, G.; Li, X.; Yu, Y.; Chen, L.; Shimizu, H. Responses to air temperature and soil moisture of growth of four dominant species on sand dunes of central Inner Mongolia. J. Plant Res. 2008, 121, 473–482. [Google Scholar] [CrossRef]
- Rabelo, J.L.; Wendland, E. Assessment of groundwater recharge and water fluxes of the guarani aquifer system, brazil. Hdrgeol. J. 2009, 17, 1733–1748. [Google Scholar] [CrossRef]
- Zhang, G.H.; Fei, Y.H.; Shen, J.M.; Yang, L.Z. Influence of unsaturated zone thickness on precipitation infiltration for recharge of groundwater. J. Hydraul. Eng. 2007, 38, 611–617. (In Chinese) [Google Scholar]
- Morris, C.; Badik, K.J.; Morris, L.R.; Weltz, M.A. Integrating precipitation, grazing, past effects and interactions in long-term vegetation change. J. Arid. Environ. 2016, 124, 111–117. [Google Scholar] [CrossRef]
- Zhou, J.; Fu, B.; Gao, G.; Lü, Y.; Liu, Y.; Lü, N.; Wang, S. Effects of precipitation and restoration vegetation on soil erosion in a semi-arid environment in the Loess Plateau, China. Catena 2016, 137, 1–11. [Google Scholar] [CrossRef]
- Irmak, S.; Burgert, M.J.; Yang, H.S.; Cassman, K.G.; Walters, D.T.; Rathje, W.R.; Payero, J.O.; Grassini, P.; Kuzila, M.S.; Brunkhorst, K.J.; et al. Large-Scale On-Farm Implementation of Soil Moisture-Based Irrigation Management Strategies for Increasing Maize Water Productivity. Trans. Asabe 2012, 55, 881–894. [Google Scholar] [CrossRef]
- Ibrahim, M.; Favreau, G.; Scanlon, B.R.; Seidel, J.L.; Le Coz, M.; Demarty, J.; Cappelaere, B. Long-term increase in diffuse groundwater recharge following expansion of rainfed cultivation in the Sahel, West Africa. Hydrogeol. J. 2014, 22, 1293–1305. [Google Scholar] [CrossRef]
- Li, P.; Ren, L. Evaluating the effects of limited irrigation on crop water productivity and reducing deep groundwater exploitation in the North China Plain using an agro-hydrological model: II. Scenario simulation and analysis. J. Hydrol. 2019, 574, 715–732. [Google Scholar]
- Liu, X.; He, Y.; Zhang, T.H.; Zhao, X.; Li, Y.; Zhang, L.; Wei, S.; Yun, J.; Yue, X. The response of infiltration depth, evaporation, and soil water replenishment to rainfall in mobile dunes in the horqin sandy land, northern china. Environ. Earth Sci. 2015, 73, 8699–8708. [Google Scholar] [CrossRef]
- Baldocchi, D.; Knox, S.; Dronova, I.; Verfaillie, J.; Oikawa, P.; Sturtevant, C.; Matthes, J.H.; Detto, M. The impact of expanding flooded land area on the annual evaporation of rice. Agric. For. Meteorol. 2016, 223, 181–193. [Google Scholar] [CrossRef]
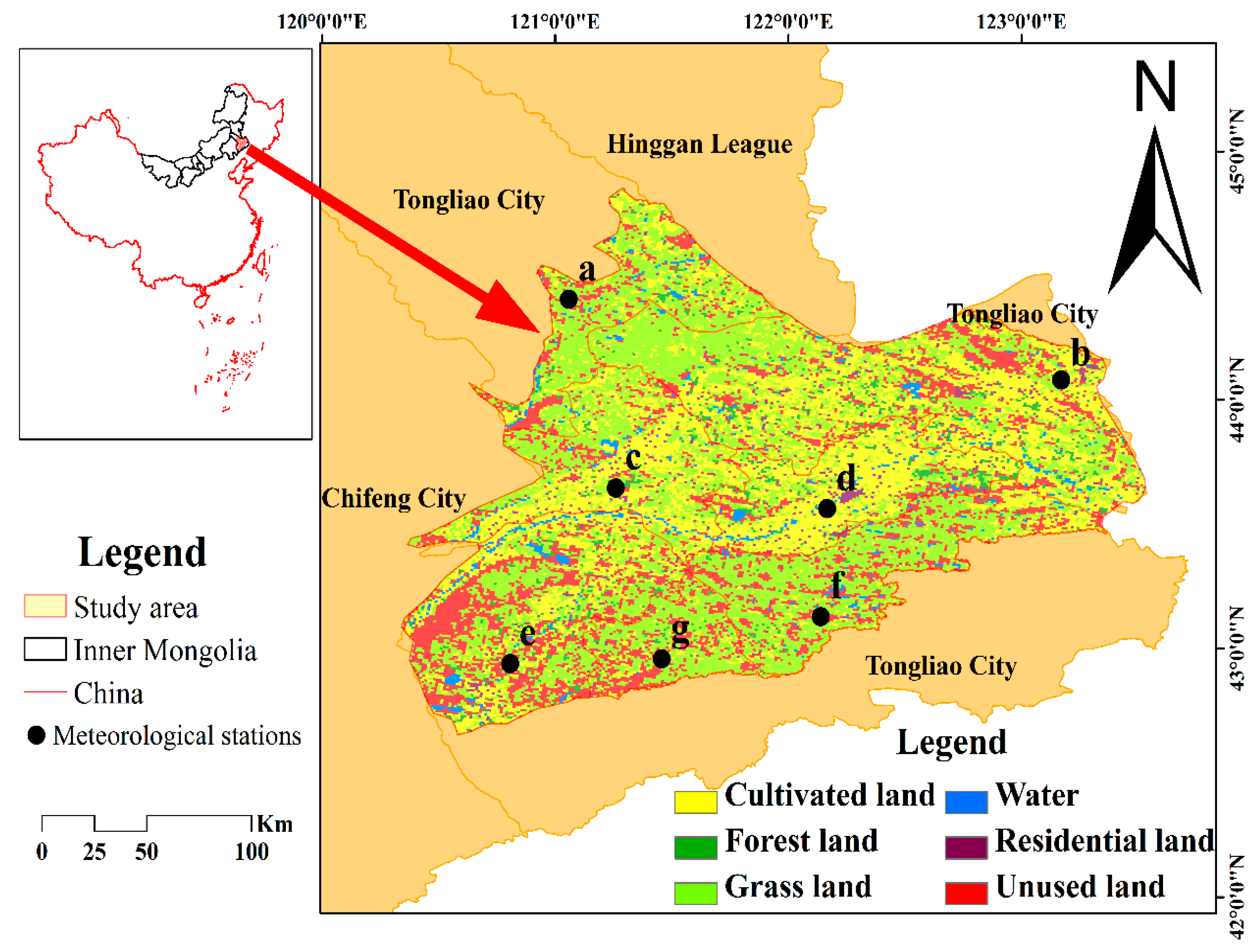

| Meteorological Stations (2002–2014) | Code | Location (Lat & Lon) | Data | ||||||
|---|---|---|---|---|---|---|---|---|---|
| P (cm) | T (°C) | ||||||||
| X | Y | Max | Min | Avg | Max | Min | Avg | ||
| Zhalute | a | 120.54 | 44.34 | 55.0 | 22.1 | 35.8 | 8.9 | 6.4 | 7.5 |
| Kezuozhongqi | b | 123.17 | 44.08 | 55.6 | 18.7 | 34.3 | 8.0 | 6.4 | 7.4 |
| Kailu | c | 121.17 | 43.36 | 49.6 | 21.3 | 31.9 | 8.5 | 6.0 | 7.3 |
| Tongliao | d | 122.16 | 43.36 | 45.2 | 22.7 | 31.0 | 8.6 | 6.4 | 7.5 |
| Naiman | e | 120.39 | 42.51 | 39.1 | 21.3 | 30.1 | 9.0 | 6.6 | 7.5 |
| Kezuohouqi | f | 122.21 | 42..58 | 51.5 | 21.7 | 41.8 | 8.6 | 6.4 | 7.3 |
| Kulun | g | 121.45 | 42.44 | 56.2 | 29.3 | 34.7 | 9.0 | 6.6 | 7.5 |
| P | ET | T | TWSC | GLDAS | GWC | |
|---|---|---|---|---|---|---|
| P | 1 | 0.685 ** | −0.470 | 0.472 | 0.634 * | 0.065 |
| ET | 1 | −0.245 | 0.387 | 0.686 ** | −0.096 | |
| T | 1 | 0.021 | −0.481 | 0.570 * | ||
| TWSC | 1 | 0.518 | 0.680 * | |||
| GLDAS | 1 | −0.193 | ||||
| GWC | 1 |
| P | ET | |||||||
|---|---|---|---|---|---|---|---|---|
| Lag0-M | Lag1-M | Lag2-M | Lag3-M | Lag0-M | Lag1-M | Lag2-M | Lag3-M | |
| TWSC | 0.230 ** | 0.312 ** | 0.275 ** | 0.195 * | 0.276 ** | 0.276 ** | 0.131 | 0.025 |
| GLDAS | 0.324 ** | 0.382 ** | 0.281 ** | 0.181 * | 0.378 ** | 0.331 ** | 0.142 | 0.045 |
| GWC | 0.007 | 0.03 | 0.067 | 0.049 | −0.012 | 0.005 | 0.011 | −0.017 |
| P | ET | T | TWSC | GLDAS | GWC | ||
|---|---|---|---|---|---|---|---|
| NDVI | Spring | −0.075 | 0.024 | −0.226 | 0.151 | 0.226 | −0.123 |
| Summer | 0.425 | 0.418 | −0.073 | −0.162 | 0.446 | −0.357 | |
| Autumn | −0.140 | 0.063 | 0.220 | 0.370 | 0.411 | 0.046 | |
| Winter | −0.585 * | 0.407 | −0.250 | −0.151 | −0.484 | 0.074 | |
| Growing season | 0.542 | 0.747 ** | −0.242 | 0.154 | 0.704 ** | −0.640 * |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Y.; Luo, P.; Zhang, S.; Sun, B. Spatiotemporal Analysis of Hydrological Variations and Their Impacts on Vegetation in Semiarid Areas from Multiple Satellite Data. Remote Sens. 2020, 12, 4177. https://doi.org/10.3390/rs12244177
Zhu Y, Luo P, Zhang S, Sun B. Spatiotemporal Analysis of Hydrological Variations and Their Impacts on Vegetation in Semiarid Areas from Multiple Satellite Data. Remote Sensing. 2020; 12(24):4177. https://doi.org/10.3390/rs12244177
Chicago/Turabian StyleZhu, Yonghua, Pingping Luo, Sheng Zhang, and Biao Sun. 2020. "Spatiotemporal Analysis of Hydrological Variations and Their Impacts on Vegetation in Semiarid Areas from Multiple Satellite Data" Remote Sensing 12, no. 24: 4177. https://doi.org/10.3390/rs12244177
APA StyleZhu, Y., Luo, P., Zhang, S., & Sun, B. (2020). Spatiotemporal Analysis of Hydrological Variations and Their Impacts on Vegetation in Semiarid Areas from Multiple Satellite Data. Remote Sensing, 12(24), 4177. https://doi.org/10.3390/rs12244177