Unsupervised Haze Removal for High-Resolution Optical Remote-Sensing Images Based on Improved Generative Adversarial Networks

Abstract

One major limitation of remote-sensing images is bad weather conditions, such as haze. Haze significantly reduces the accuracy of satellite image interpretation. To solve this problem, this paper proposes a novel unsupervised method to remove haze from high-resolution optical remote-sensing images. The proposed method, based on cycle generative adversarial networks, is called the edge-sharpening cycle-consistent adversarial network (ES-CCGAN). Most importantly, unlike existing methods, this approach does not require prior information; the training data are unsupervised, which mitigates the pressure of preparing the training data set. To enhance the ability to extract ground-object information, the generative network replaces a residual neural network (ResNet) with a dense convolutional network (DenseNet). The edge-sharpening loss function of the deep-learning model is designed to recover clear ground-object edges and obtain more detailed information from hazy images. In the high-frequency information extraction model, this study re-trained the Visual Geometry Group (VGG) network using remote-sensing images. Experimental results reveal that the proposed method can recover different kinds of scenes from hazy images successfully and obtain excellent color consistency. Moreover, the ability of the proposed method to obtain clear edges and rich texture feature information makes it superior to the existing methods.

1. Introduction

With the continuous development and growth of space technology, the applications of remote-sensing images are growing, and the quality requirements are increasing [1]. Remote-sensing images play an important role in the fields of object extraction [2], seismic detection [3], and automatic navigation [4]. However, in bad weather conditions, remote-sensing images may be obscured by haze, which decreases the visibility of ground objects and affects the accuracy of image interpretation [5]. Therefore, image dehazing is essential for remote-sensing image applications [6,7].

Recently, many researchers have focused on the problem of haze affecting the precision processing of remote-sensing images. In the field of remote-sensing image dehazing, the research can be divided into multiple-image dehazing and single-image dehazing, which use different numbers of images in the dehazing process. There is currently a focus on single-image dehazing methods for their advantages in not requiring other images. In particular, many pretreatment methods that remove the haze in remote-sensing images have been proposed. These methods are mostly based on traditional morphological methods, which use some special structuring elements to measure or extract the shape and characteristic information, such as dilation, erosion, opening, white top hat, and black top hat. However, these methods depend largely on prior information and cannot batch process a data set. These methods can be classified into non-model-based [8,9,10,11,12,13] and model-based methods [14,15,16,17,18,19]. Under the non-model-based methods, studies [8,9] describe the mathematics of a lightness scheme that generates lightness numbers, the biological analog of reflectance, independent of the flux from objects. Moreover, paper [10] proposed a scheme for adaptive image-contrast enhancement based on a generalization of histogram equalization. Analogously, paper [11] presented a new method for unsharp masking for contrast enhancement. Studies [12,13] unified previous methods, yielding an improved Retinex theory that addresses the problem of separating the illumination from the reflectance in a given image, thereby compensating for non-uniform lighting. They modeled global and local adaptations of the human visual system. Among the model-based methods, the study [14] introduced a method for reducing degradation in situations where the scene geometry is known. Papers [15,17] proposed enhancements to color image methods based on the underlying physics of the degradation process, and the parameters required for enhancement were estimated from the image itself. Paper [16] developed models and methods for recovering pertinent scene properties, such as three-dimensional structure, from images taken under poor weather conditions. Papers [18,19] derived approaches for blindly recovering the parameters needed for separating the sky from the measurements, thus recovering contrast, with neither user interaction nor the existence of the sky in the frame.

These methods used traditional morphological algorithms and a deep-learning model to recover ground objects. However, they did not remove the problems of paired image preparation, model training efficiency, and the recovery effect. To explore further the limitations of current remote-sensing image dehazing methods, we analyzed dehazing in both non-model-based methods and model-based methods.

Non-model-based methods, also known as image-enhancement methods, neither consider the reason for image degradation in the dehazing process nor the quality of optical imaging. For example, a multiple linear regression model was applied to learn the transmittance of hazy images in [20]. However, the transmittance obtained is relatively smooth, and its effect on images with sharp depth changes is very poor. An image-enhancing contrast method [21] was introduced to dehaze images in gray and color. Unfortunately, the image-enhancement algorithm is extremely complex as it must perform multi-scale transformations and inverse transformations, which makes it unsuitable for processing large data sets of hazy remote-sensing images.

Model-based methods use the theory of image degradation to dehaze images. A novel method based on soft matting, named the dark channel method, was recently proposed [22] to repair the transmittance in hazy images. However, this method includes several complicated calculations, which implies that large periods are required for dehazing. Meanwhile, the original algorithm [23] was also optimized for extracting dark channel values according to the dark a priori theory. However, it still needs atmospheric a priori information and includes relatively complicated calculations. A two-step method [24] was designed to process the white balance of atmospheric light and simplify atmospheric scattering to improve the dark channel method. This method is based on a data hypothesis and cannot automatically process hazy remote-sensing images. Generally, such methods always require a priori information, such as scene depth and atmospheric conditions, and hence are inappropriate for dehazing remote-sensing images.

Recently, researchers have begun using deep-learning methods to solve problems in remote-sensing images [25,26,27,28,29]. Specifically, papers [25,26,27] proposed deep-learning multi-model data fusion methods to extract landscape features or discover spatial and temporal dependencies; paper [29] proposed a convolutional neural network (CNN) to classify POLarimetric Synthetic Aperture Radar (PolSAR) images; specifically, the major deep-learning concepts pertinent to remote sensing were introduced, and more than 200 publications in the field, most of which were published during the last two years, were reviewed and analyzed [28]. It is limited by the amount of information from remote-sensing satellites, and in most instances, we cannot obtain much a priori information [30,31]. Therefore, the traditional method is not suitable for this problem. Deep learning is an outstanding method that can be automatically used for dehazing images. Deep-learning models using multiple graphics processing units can greatly reduce the computing time, and hence they exhibit high efficiency. Moreover, these methods can be trained using complex datasets without any a priori environmental information. Such advancements are beneficial to train models for dehazing remote-sensing images.

Currently, several applications are being developed based on the generative adversarial network (GAN) [32] in the field of image denoising, such as image inpainting [33,34,35], image deblurring [36], and super-resolution image reconstructing [37,38,39,40]. Furthermore, there are many remote-sensing applications processed by deep-learning methods, such as the crop classification method [41], cloud detection method [42], and change detection method [43]. Because of the complex ground environment, the traditional methods cannot learn complicated high-frequency features. Deep-learning algorithms can learn features from different data sets. The deep-learning methods described above obtained outstanding processing accuracy in remote-sensing images, so we can conclude that deep-learning methods have an advantage in extracting complex high-frequency information and can process large data sets. The use of these methods led to the realization that it is more efficient to process remote-sensing data using a batch model. GAN has excellent ability in producing images, as it contains a discrimination network in the model when training the generation network. Unlike CNN, GAN is optimized by a countermeasure scheme between discrimination and generation networks. This new training process avoids the loss of errors due to artificial design. The discrimination network can learn an appropriate loss to match the training data set, which makes GAN more robust. However, when using GAN for image denoising, insufficient constraints may lead to the network generating monotonous images. To tackle this problem, cycle generative adversarial networks (CycleGAN) [44] was proposed. The cycle structure generates two types of image, and those images can be swapped with each other by the cycle structure. By optimizing cycle-consistency loss in the generated and the original images, scene information can be recovered. The generation network of CycleGAN is an end-to-end structure into which the Visual Geometry Group (VGG) network (ResNet) block [45] was introduced to enhance features. The discrimination network is a traditional CNN classification structure used to predict the class of images.

In recent years, several dehazing methods based on GAN have been developed. Conditional GAN [46] and its corresponding improved model with circle consistency [47] were used to remove haze from remote-sensing images. However, such methods use the structure of GAN alone and do not consider the concrete features of remote-sensing images. Cyclic perceptual-consistency loss was designed to help in dehazing and improve the quality of textures in recovered images [48].

A VGG network [49] is a CNN model developed at Oxford University in 2014. This method is widely used in image classification and object detection. VGG has the advantage of a simple structure, as all its convolutional layers use the same parameters. Because VGG is very simple and deep, it is widely used to extract features from images. A super-resolution generative adversarial network (SRGAN) [50] uses VGG16 to calculate the perceptual loss. Generally speaking, the model is trained by the ImageNet data set and a yield-loss function to calculate the difference between images. In a previous study, the mean square error (MSE) was used to evaluate pixel error and optimize networks. However, MSE is sensitive to pixel errors, but the pixel error is not sensitive to perceptual changes. Thus, to enhance perceptual detail, the perceptual loss is widely used in image processing.

In this paper, we propose an unsupervised remote-sensing image dehazed method based on CycleGAN that the training data consists of hazed remote-sensing image and haze-free remote-sensing image, that image is composed of different remote-sensing scenes, the dehazed method is named edge-sharpening cycle-consistent adversarial network (ES-CCGAN). The main contributions of this work are summarized as follows:

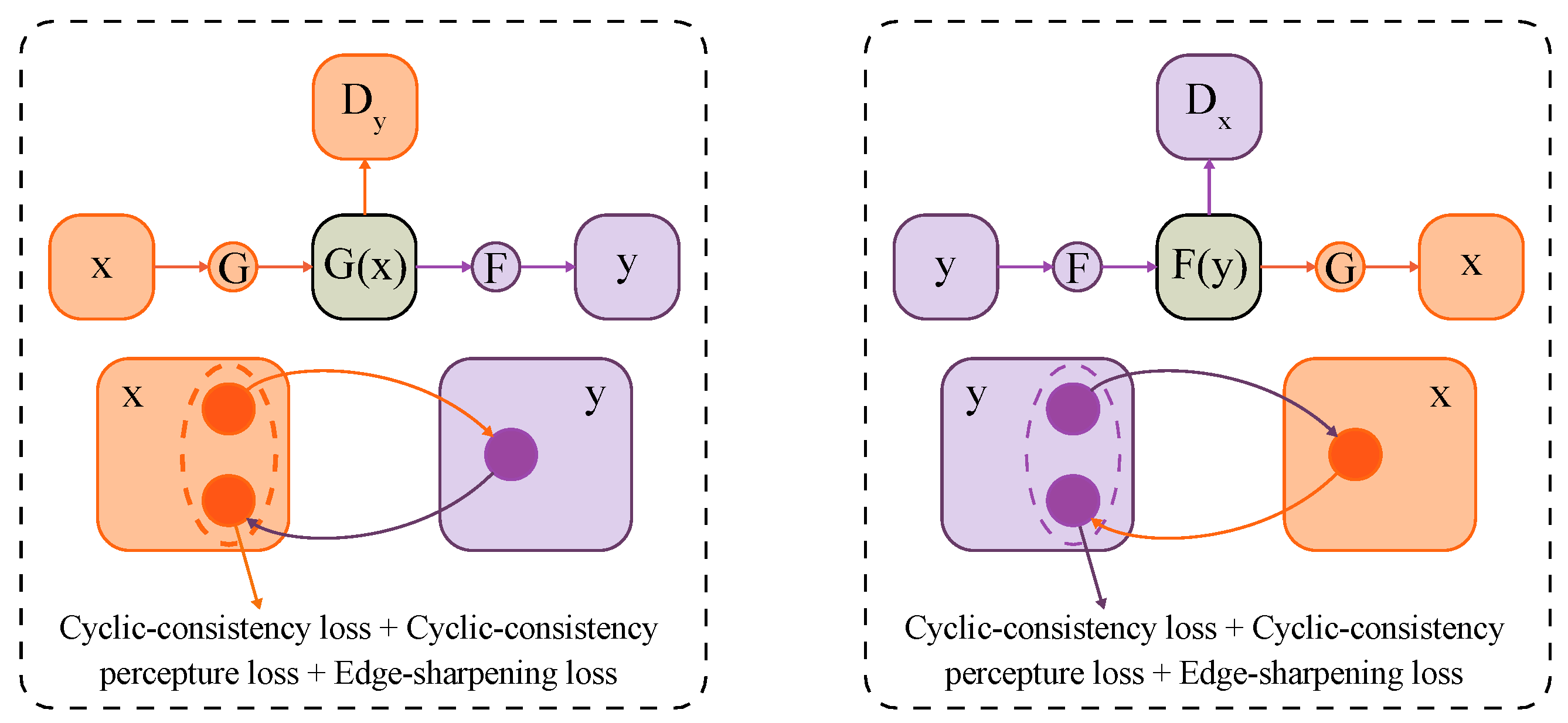
• The training and testing data sets are several unpaired haze and haze-free remote-sensing images. The cycle structure can achieve unsupervised training that can largely reduce the pressure in preparing data sets.
• In the generators G (dehazing model) and F (add-haze model), DenseNet blocks, which can recover the high-frequency information from remote-sensing images, are introduced to replace ResNet.
• In remote-sensing interpretation applications, sharpened edges and haze-free remote-sensing images can reflect contour texture information clearly, leading to more accurate results. In this study, we designed an edge-sharpening loss and introduced cyclic perceptual-consistency loss into the loss function.
• This model uses a transfer learning training model for the cyclic perceptual-consistency loss, and the homemade classified remote-sensing image is used to retrain the perceptual extracted model. This model can accurately learn the feature information of ground objects.

The rest of this study is organized as follows. Section 2 introduces the proposed method. Section 3 explains the experimental details, compares several haze-removal methods, and verifies the effectiveness of edge-sharpening loss. Section 4 discusses the obtained results, and the conclusions are presented in Section 5.

2. Remote-Sensing Image Dehazing Algorithm

In this study, we propose a remote-sensing image dehazing method named ES-CCGAN, which is based on CycleGAN. This method is unsupervised. The training dataset is composed of unpaired remote-sensing images, and the loss function is optimized as in CycleGAN. To produce dehazed remote-sensing images with abundant texture information, this method uses a DenseNet block for the generator, which replaces the ResNet block. Furthermore, to restore clear edges in the images, an edge-sharpening loss is designed for the loss function. Moreover, transfer learning is used in the training process, and a VGG16 network is re-trained by our remote-sensing image data set to preserve contour information. In this section, we will focus on the structure and loss function of ES-CCGAN. Irrespective of image resolution, this network will crop the training image to a fixed size to match the dimensions of the network. Using these settings, the dehazed model will not influence the size of the input images.

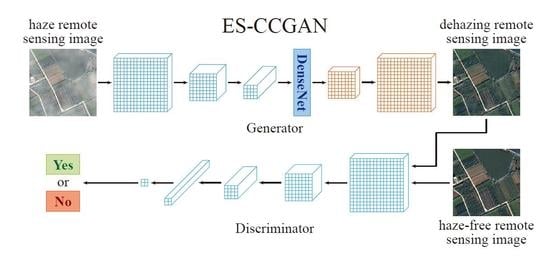
2.1. Edge-Sharpening Cycle-Consistent Adversarial Network (ES-CCGAN) Dehazing Architecture

GAN is one of the most promising deep-learning methods for image denoising. Compared with conventional deep-learning structures, GAN has an extra discriminator network, which can learn a loss function while it is suitable for the training data and avoid error in the traditional artificial loss function. Generally, GAN frameworks are made up of a generator (G) and discriminator (D). The generator is trained to generate images and fool the discriminator. Meanwhile, the discriminator is trained to discriminate whether an image is original or synthetic.

Unlike traditional GAN, ES-CCGAN includes two generation networks (G and F) and two discriminant networks (D_x and D_y). G and F transform remote-sensing images between hazy and haze-free in opposite directions, while discriminant networks D_x and D_y determine whether the input remote-sensing images are original or synthetic. Besides, to improve the ability of the model to dehaze remote-sensing images further, a DenseNet [51] block is introduced in both G and F. From Figure 1, we can see the processing procedure of ES-CCGAN. In this figure, the different line colors indicate the different generator processing; x is the hazy image; y is the haze-free image; G is the dehazed network; F is the haze-added network; G(x) is the image dehazed by generator G; F(y) is the haze-added image by generator F; G(F(y)) is the dehazed result processed by F then G; F(G(x)) is the hazy result processed by G then F.

2.1.1. Generation Network

The architecture of generation networks G and F is an end-to-end structure based on CNN. G is designed to learn hazy-to-haze-free mapping while F is designed to learn haze-free-to-hazy mapping. Because the objective of this work is to dehaze remote-sensing images, ultimately, we use model G to dehaze the hazy remote-sensing image.

Normally, the ES-CCGAN model is based on the structure of CycleGAN, which uses a ResNet block to extract features. However, the structure of ResNet is too simple and may lose significant feature information in the training process. Therefore, to improve textural information about the dehazed image, we use a DenseNet block to replace the ResNet block. The generator framework is shown in Figure 2.

The DenseNet block connection provides a unique perspective of the connections between convolution layers. Instead of connecting layers in a simple linear sequence (normal CNN), the DenseNet block connects each layer to all previous layers. Unlike the ResNet block that merges the values of information from previous layers, the DenseNet block uses deeper and more non-linear connections, which can effectively alleviate the problem of gradient disappearance and boost the performance. This allows all the channels in the front layer to merge, and feature information from remote-sensing images can be re-trained more effectively while maintaining the original object information.

2.1.2. Discriminant Network

In the GAN structure, a discriminant network is used to classify whether an input image is original or synthetic. To classify images produced by the two different generation networks, G and F, we adopted two discriminant networks, D_y and D_x, in our ES-CCGAN model. The structure of D_x and D_y is shown in Figure 3.

D_y discriminates between generated dehazed remote-sensing images and haze-free remote-sensing images, while D_x discriminates between generated hazy remote-sensing images and haze-free remote-sensing images. In this manner, the discriminator can guide generator G to generate the corresponding dehazed remote-sensing image and generator F to generate the corresponding hazy remote-sensing image.

In the training process, the discriminant network cannot identify destroyed remote-sensing images with blurred boundaries. This phenomenon will cause generator synthesized remote-sensing images with blurred edges. To solve this problem, we improved the ES-CCGAN method by adding blurred-edge haze-free images into the input to control the training process. Consequently, the discriminant network can discriminate blurred features and guide the generator to avoid this feature. In the case of discriminant network D_y, inputs include haze-free remote-sensing images with blurred edges (y^~) set to label 0 (False), haze-free remote-sensing images (y) set to label 1 (True), and generated dehazed remote-sensing images (G(x)) set to label 0 (False). Meanwhile, for discriminant network D_x, inputs include haze-free remote-sensing images with blurred edges (y^~) set to label 1 (True), hazy remote-sensing images (x) set to label 1 (True), and generated hazy remote-sensing images (F(y)) set to label 0 (False).

In summary, ES-CCGAN consists of two generator networks (G and F) and two discriminant networks (D_x and D_y). To guide the generator networks to produce images with clear edges, blurred-edge images were added in the input to train discriminators D_x and D_y.

2.2. ES-CCGAN Loss Function

In the training process, because of the optimization of the model parameters for ES-CCGAN, the loss function plays an essential role. To improve its performance, four losses are combined, namely adversarial loss, cycle-consistency loss, cyclic perceptual-consistency loss, and edge-sharpening loss. The optimization processes are shown in Figure 4.

In most GAN models, the adversarial loss is included in the training process and can enable the generator and discriminator to combat. Inspired by EnhanceNet [52], to improve the texture quality for the images, the perceptual loss is proposed for the loss function. Additionally, ES-CCGAN compares original remote-sensing images with generated dehazed remote-sensing images in both pixel and feature spaces. The cycle-consistency loss ensures a high peak signal to noise ratio (PSNR) score in the pixel space, and cyclic perceptual-consistency loss preserves texture information in the feature space. Moreover, to generate dehazed remote-sensing images with clear edges, the edge-sharpening loss in the ES-CCGAN model has been designed to enhance edge information during dehazing.

2.2.1. Adversarial Loss

The key to the success of GAN models is the idea of an adversarial loss that controls the generated images to be indistinguishable from real images. In this study, adversarial losses were used to train generation networks G and F and their corresponding discriminant networks D_y and D_x. Model training was carried out by minimaxing the loss function and iteratively adjusting the network parameters. In this way, the generator can match the distribution of the generated dehazed images with the target haze-free images.

Generation network G is a mapping from hazy images to dehazed images (yˆ = G(x)), where x represents the hazy image, and yˆ is the generated dehazed image. D_y is trained to distinguish the generated dehazed image yˆ from the haze-free image y. Generator F is simply an inverse mapping of G (the structures of G and F are similar). This study uses adversarial loss to train G and D_y, which can be expressed as follows,

$$\underset{G}{\min } \underset{D_y}{\max } L_{G\_adv}\left(G,D_y,X,Y\right)=E_y\left[\log \left(D_y\left(y\right)\right)\right]+E_x\left[\log \left(1-D_y\left(G\left(x\right)\right)\right)\right],$$

(1)

where L_{G_adv} represents the adversarial loss of G and D_y; D_y(y) represents the perspective of the haze-free image corresponding to the real haze-free image by the discriminator D_y, and D_y(G(x)) represents the probability of the generated dehazed image being the real haze-free image.

For network F, which maps haze-free images to hazy images, and its discriminator D_x, the loss function can be expressed as:

$$\underset{F}{\min } \underset{D_x}{\max } L_{F\_adv}\left(F,D_x,X,Y\right)=E_x\left[\log \left(D_x\left(x\right)\right)\right]+E_y\left[\log \left(1-D_x\left(F\left(y\right)\right)\right)\right],$$

(2)

where L_{F_adv} represents the adversarial loss of F and D_x, and D_x(x) and D_x(F(y)) represent the probability of the hazy image and the generated hazy image being the hazy remote-sensing image, respectively.

2.2.2. Cycle-Consistency Loss and Cyclic Perceptual-Consistency Loss

Theoretically, by optimizing the adversarial loss function, networks G and F can produce an output with a distribution identical to that of haze-free remote-sensing images and hazy remote-sensing images, respectively. However, the generation network G can fool discriminator D_y by mapping several hazy images to the same dehazed image. Thus, optimization using adversarial losses alone will result in generator G lacking the ability to dehaze an individual hazy image. To solve this problem, an additional loss function was designed to compare the generated images with the original images at the pixel level; this function is called the cycle-consistency loss function.

In SRGAN, the pixel-wise loss function cannot capture high-frequency details and thus results in an overly smooth texture. This problem leads to blurred texture information in recovered images and poor perceptual quality. To render remote-sensing images similar to human visual perception, in this study, we designed a perception-loss function, named cyclic perceptual-consistency loss, to evaluate the error in restored images. This loss can avoid the problem of generated remote-sensing images lacking texture information. Recently, significant research attention has been given to the idea of loss. A classification neural network named VGG has been designed to evaluate the perceptual loss. It is widely used in image classification and has achieved excellent results in this field. In the area of image denoising, VGG16 is used as a feature extracting tool for calculating perceptual loss.

In our investigation, to extract more feature information, transfer learning is included in the training process. The VGG16 network is re-trained by a remote-sensing data set with five categories of data to calculate cyclic perceptual-consistency loss. Cyclic-consistency and cyclic perceptual-consistency losses are calculated as shown in Equations (3) and (4), respectively.

$$L_{con}\left(G,F,X,Y\right)=E_x[\Vert F\left(G\left(x\right)\right)-x{\Vert }_1]+E_y\left[\Vert G\left(F\left(y\right)\right)-y{\Vert }_1\right],$$

(3)

$$L_{perceptual}\left(G,F,X,Y\right)=\Vert \phi \left(x\right)-\phi {\left(F\left(G\left(x\right)\right)\right)\Vert }_2^2+\Vert \phi \left(y\right)-\phi {\left(G\left(F\left(y\right)\right)\right)\Vert }_2^2,$$

(4)

where F(G(x)) represents the cyclic hazy image generated by networks G and F; G(F(y)) represents the cyclic dehazed image generated by networks F and G, and φ(x) and φ(y) represent feature maps extracted by the re-trained model VGG16.

2.2.3. Edge-Sharpening Loss

Clear boundary information plays an important role in potential remote-sensing image applications, such as in road extraction and semantic segmentation [53]. However, conventional dehazing algorithms cannot recover clear ground-object edges in hazy images. In this work, the solution to this problem is to enhance the constraints for generators G and F, which can determine the effect of the generated results. In particular, this dehazing method is an end-to-end algorithm, which can integrate the dehazing processing. Thus, we tried to use a method that can be added to the network and does not need post-processing. In this unsupervised cycle structure network, the designed edge-sharping loss function shows that it is possible to further remove the transition point for ground object edge, while retaining minutiae feature and enhanced the quality for ground object edge. To guide generator G to produce remote-sensing images with sharpened edge information, we designed an edge-sharpening loss for discriminators D_x and D_y. This function was designed for this cycle structure, which has different roles in the generator. Specifically, blurred-edge haze-free remote-sensing images are added to the input of D_y and D_x with False (0) and True (1) labels, respectively. The blurred-edge haze-free images can make D_y and D_x distinguish blurred-edge features. D_y can guide G-generated sharpened-edge images, and D_x can guide F-generated blurred-edge images, which are more like hazy images.

Using edge-sharpening loss, discriminator D_y can better identify haze-free remote-sensing images with blurred edges, which will help in training network G to generate dehazed remote-sensing images with clear edges. Meanwhile, for discriminant network D_x, the input is required as haze-free remote-sensing images with blurred edges, hazy remote-sensing images, and generated hazy remote-sensing images. Using edge-sharpening loss, the performance of D_x concerning blurred-edge haze-free images can be improved. For this, F can be guided to generate better hazy remote-sensing images. Edge-sharpening loss for D_x and D_y can be expressed as follows,

$$\underset{D_y}{\max } L_{D_{y\_sharp}}\left(D_y,y^{~}\right)=E_{y^{~}}\left[1-D_y\left(y^{~}\right)\right]$$

(5)

$$\underset{D_x}{\max } L_{D_{x\_sharp}}\left(D_x,y^{~}\right)=E_{y^{~}}\left[D_y\left(y^{~}\right)\right]$$

(6)

where y^~ represents haze-free remote-sensing images with blurred edges; they are treated as true labels during D_x training and as false labels during D_y training.

In practical conditions, we cannot obtain numerous haze-free remote-sensing images with blurred edges. To circumvent this problem, in this study, haze-free remote-sensing images were processed by an algorithm to generate a blurred-edge haze-free remote-sensing image data set. The details are as follows:

(1)

Ground-object edge pixels are detected from haze-free remote-sensing images by a standard Canny edge detector, which can accurately locate edge pixels.

(2)

Edge regions of the ground object are dilated based on the detected edge pixels.

(3)

Gaussian smoothing is applied to the dilated edge regions to obtain y~, which can reduce the edge weights and obtain a more natural effect.

2.2.4. Full Objective of ES-CCGAN

To train ES-CCGAN, we optimized the loss function L_loss, which can be calculated by adding all the losses mentioned earlier, as shown in Equation (7).

$$\begin{array}{l}{L}_{loss}=L_{adv}\left(G,F,D_x,D_y,X,Y\right)+L_{con}\left(G,F,X,Y\right)+L_{perceptual}\left(G,F,X,Y\right)\\ +L_{sharp}\left(D_x,D_y,y^{~}\right)\end{array}$$

(7)

Here, L_adv (G, F, D_x, D_y, X, Y) represents adversarial loss; L_con (G, F, D_x, D_y, X, Y) represents cycle-consistency loss; L_perceptual (G, F, D_x, D_y, X, Y) represents cyclic perceptual-consistency loss, and L_sharp (D_x, D_y, y^~) indicates an edge-sharpening loss.

3. Experiments

3.1. Experimental Data Set

Owing to difficulties in selecting hazy and clear remote-sensing images, there is no suitable public dataset of hazy remote-sensing images to train our method; hence, we created both the training and testing data sets. Clear remote-sensing images were processed by an additional haze algorithm where the Perlin noise [54], interpolated noise [55], smoothed noise [56], and cosine interpolate [57] are superimposed on the haze-free remote-sensing images. During the test, real hazy images were processed to confirm the effectiveness of the dehazing model. Moreover, to validate this method, a real-image data set was created. This data set was collected from the Qinling mountains in the south-central Shaanxi province of China and the Guanzhong Plain in the northern part of the Qinling mountains. These data cover the period from 2015 to 2018. To avoid the influence of chromatic aberration on the images, we used remote-sensing images captured in spring and summer, ensuring the same colors in the images. This terrain includes plains, mountains, water systems, cities, and other features. All data were collected using the Gaofen-2 satellite (GF-2), which has a 1-m spatial resolution, high radiometric accuracy, high positioning accuracy, and fast attitude maneuverability. The obtained data set was subjected to orthorectification and atmospheric correction. Later, 4-m multi-spectral images and 1-m panchromatic images were fused to obtain some red, green and blue (RGB) images. In this study, data were chosen from two image classes (hazy and clear images).

The training data set contained haze-free remote-sensing images, hazy remote-sensing images, and haze-free remote-sensing images with blurred edges, while the test data set included only hazy remote-sensing images, reflecting the purpose of this work. In particular, the test hazy remote-sensing images were separate from the training data. Moreover, hazy and haze-free remote-sensing images in the training data set do not need to be paired; in other words, ES-CCGAN is an unsupervised method. The training data set consisted of 52,376 haze-free images, 52,376 hazy images, and 52,376 haze-free images with blurred edges. All the images were 256 × 256 pixels in size. Besides, the perceptual network VGG16 was re-trained with a remote-sensing image data set with five different topography categories, urban, industrial, suburban, river, and forest. That image is selected by artificial that the images of similar scenes are classified into one group. Moreover, to ensure the convergence of perceptual models, each ground-object category included 700 images. In the perceptual model, the classified images are divided into 256 × 256 pixels. During the training of the dehazing method, the images are resized to 224 × 224 to calculate the perceptual loss in the feature map. In particular, the sequence of training images will be disordered and make the training process completely unsupervised. This method was implemented on TensorFlow, and the training data set was converted to the TFRecord for efficiency.

3.2. Network Parameters

The designed ES-CCGAN network is based on CycleGAN. The structures of the generator networks and discriminator networks in the model are shown in

Table 1. The framework of generators G and F.

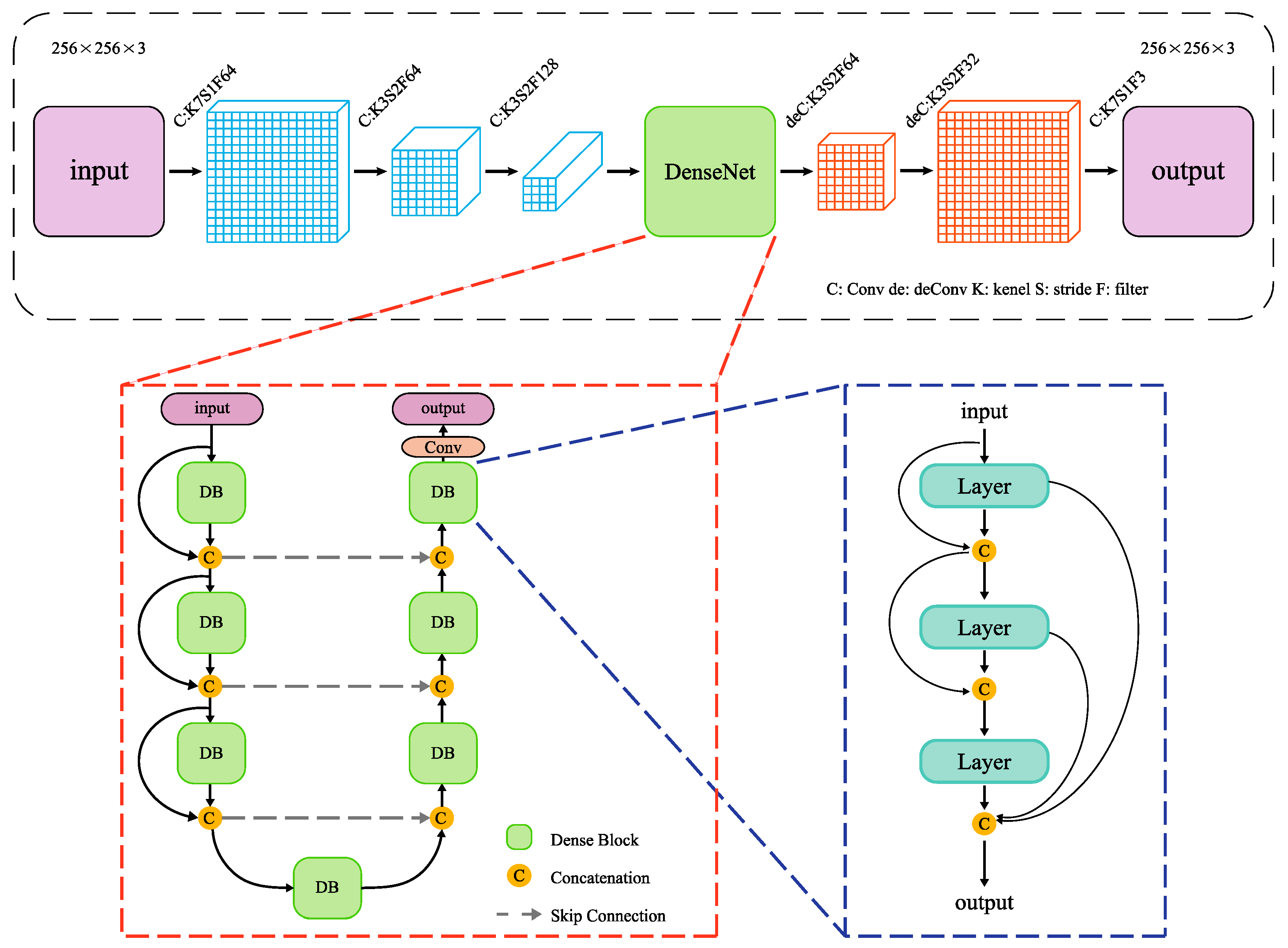
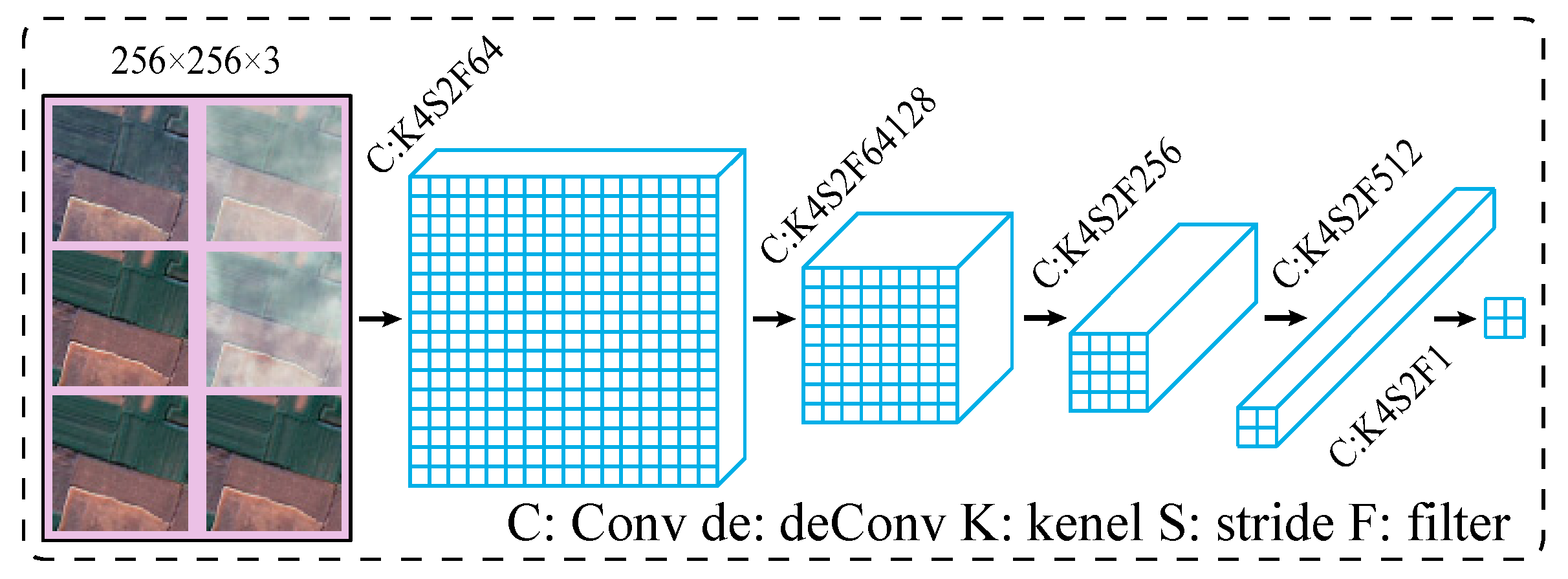
Operation	Kernel Size	Strides	Filters	Normalization	Activation Function
Conv1	7 × 7	1 × 1	32	Yes	tanh
Conv2	3 × 3	2 × 2	64	Yes	relu
Conv3	3 × 3	2 × 2	128	Yes	relu
DenseNet	--	--	--	--	--
deConv1	3 × 3	2 × 2	64	Yes	relu
deConv2	3 × 3	2 × 2	32	Yes	relu
deConv3	7 × 7	1 × 1	3	Yes	relu

and

Table 2. The framework of D_y and D_x.

Operation	Kernel Size	Strides	Normalization	Activation Function
Conv1	4 × 4	2 × 2	Yes	leaky-relu
Conv2	4 × 4	2 × 2	Yes	leaky-relu
Conv3	4 × 4	2 × 2	Yes	leaky-relu
Conv4	4 × 4	2 × 2	Yes	leaky-relu
Conv5	4 × 4	1 × 1	No	None

. Details of the DenseNet block are presented in

Table 3. DenseNet framework.

Structure
Input, Filters = 3
Dense block (2 layers), Filters = 288
Dense block (4 layers), Filters = 352
Dense block (5 layers), Filters = 432
Dense block (5 layers), Filters = 512
Dense block (3 layers), Filters = 432
Dense block (2 layers), Filters = 368
Dense block (1 layer), Filters = 64
1 × 1 Convolution, Filters = 256

. The output of each layer in the generator and discriminator is normalized in batches, which reduces the dependencies between layers. Moreover, in the dehazed structure, this study used batch normalization to improve training efficiency. We performed about 40 epochs on each dataset to ensure convergence. During training, Adam [58] was used to optimize the neural network, with the learning rate set to β₁ = 0.9 (first-moment estimation of exponential decay rate) and β₂ = 0.999 (second-moment estimation of exponential decay rate), which can control the attenuation rate of the exponential moving average. This dehazing method was trained with a learning rate of 1e-4. This dehazing method was trained with a learning rate of 1 × 10⁻⁴. For each mini-batch, we cropped 4 distinct random 256 × 256 hazy and haze-free training images in generators F and G. We alternated updates to the generator and discriminator networks, where the adversarial loss weight is 1; the cycle-consistency loss weight is 10, and the cycle perceptual-consistency loss weight is 5 × 10⁻⁵. We trained our model on a Linux OS with four NVIDIA Titan XP Graphics Processing Units (GPU) and 12 GB of RAM. In particular, this model is convergence in step 80,000 to 200,000, and the score of PSNR is more than 20 that is the excellent score in image processing, and the results are shown in Figure 5.

As shown in Figure 5, the PSNR scores of the proposed method are more than 20 and the best value has been achieved at 22.75. We can see from those results that the model’s results obtained were relatively average in the step 130,000 to 200,000. Moreover, we compared the dehazing results in visual effect, which has the most texture information during step 180,000. Thus, the model in step 180,000 is the final dehazing model.

3.3. Experimental Results

In this work, we compared five scenarios dehazed by ES-CCGAN, including urban and industrial areas, suburbs, rivers, and forests. In the obtained results, the hazy remote-sensing images preserved the original information even in complex environments.

Three rows of sub-pictures are shown in Figure 6. The pictures in the first row are hazy remote-sensing images, while those in the second row are the corresponding dehazed versions produced using the proposed method. By comparing the details of these two sets of images, it can be clearly understood that the proposed ES-CCGAN effectively dehazes remote-sensing images and restores contour texture information. In each patch, the proposed method recovered clear edges from blurred hazy remote-sensing images.

There are many researchers have developed a lot of methods for evaluating the quality of images or vector [6,59], To quantify better the advantages of this method, two evaluation indicators, called PSNR, structural similarity index measure (SSIM) and feature similarity (FSIM), are used. PSNR is defined by mean square error (MSE) and is commonly used as an indicator to assess the quality of processed images. SSIM is an indicator used to measure the similarity of two images in the presence of noise or distortion. FSIM is improved from SSIM so that this method is used to evaluate the feature texture similarity for the dehazing results.

$$PSNR=20\ast lo{g}_{10}\left(\frac{MA{X}_I}{\sqrt{MSE}}\right),$$

(8)

where MAX_I represents the maximum value of the image points. In this study, the sampling points are represented by 8 bits; therefore, MAX_I is 255. MSE represents the mean square deviation between the two pictures.

$$SSIM\left(x,y\right)=\frac{\left(2{\mu }_x{\mu }_y+C_1\right)\left(2{\sigma }_{xy}+C_2\right)}{\left({\mu }_x^2+{\mu }_y^2+C_1\right)+\left({\sigma }_x^2+{\sigma }_y^2+C_2\right)},$$

(9)

where µ_x and µ_y are the average values of all the pixels in the image; σ_x and σ_y represent image variance, and C₁ and C₂ are constants used to maintain stability.

$$FSIM=\frac{{{\displaystyle \sum }}_{x\in \Omega }{S}_L\left(x\right)\ast P{C}_m\left(x\right)}{{{\displaystyle \sum }}_{x\in \Omega }P{C}_m\left(x\right)},$$

(10)

where PC_m(x) is the phase congruency and is the maximum of PC₁(x) and PC₂(x); S_L(x) is the coupling of S_pc(x) and S_G(x), the S_pc(x) and S_G(x) is calculated by PC₁(x) and PC₂(x).

As shown in

Table 4. Structural similarity index measure (SSIM) and PSNR scores in five categories.

Category	Urban	Industrial	Suburban	River	Forest
SSIM(SD)	0.92 (0.02)	0.74 (0.06)	0.91 (0.01)	0.90 (0.01)	0.90 (0.01)
FSIM(SD)	0.94 (0.01)	0.84 (0.01)	0.93 (0.01)	0.93 (0.01)	0.93 (0.01)
PSNR(SD)	23.55 (2.40)	19.43 (0.97)	23.96 (0.78)	24.03 (1.41)	26.47 (0.94)

, the proposed method achieved outstanding SSIM, PSNR and FSIM scores while dehazing all five categories of remote-sensing images, especially in the urban category. In particular, to ensure the accuracy of the results, we used the average results (30 pieces of remote-sensing images) in each of the categories. Moreover, the standard deviations are shown in the table. We can confirm that ES-CCGAN can be widely used in various remote-sensing scenarios and will not be influenced by the type of image.

4. Discussion

4.1. Some Effects of the Proposed Method

In this investigation, we made several improvements to the baseline CycleGAN method. The proposed method uses a remote-sensing classification data set for transfer learning; furthermore, an edge-sharpening loss function, and a DenseNet block were used to improve the generator networks. To validate the proposed method, several remote-sensing images were selected as experimental samples. By comparing the results of each method with the ground truth in the same remote-sensing image, its performance can be analyzed. The experimental results are shown in Figure 7. A refers to the VGG16 model trained by the ImageNet data set; B is the VGG16 model trained by the remote-sensing classification data set; C refers to the edge-sharpening loss for training; D refers to the generator composed of ResNet blocks, and E refers to the generator composed by DenseNet blocks.

The components of the proposed method, ES-CCGAN, include the remote-sensing classification data set for transfer learning (B), edge-sharpening loss (C), and the DenseNet block to improve the generator network (E). In the last column, we can see that ES-CCGAN achieved significant results. By comparing the results of other groups, it can be inferred that the proposed method recovers a remote-sensing image with more texture and edge information.

For evaluating the optimization factor in this work, B, C, and E will be evaluated in this experiment. After adding the edge-sharpening loss component to the proposed model, we compared the results of ‘A+D’ and ‘A+C+D’ and found that edge-sharpening loss enhanced the ability of the model to recover clear edges. While comparing ‘A+C+D’ and ‘B+C+D,’ it can be noted that the color information of a remote-sensing image can be recovered well using transfer learning. After replacing the ResNet block with the DenseNet block in the generator, we compared ‘B+C+D’ and the ‘B+C+E’ and found that the DenseNet block yielded better texture information. Moreover, compared to those results with ground truth, ES-CCGAN’s results are more similar to it in ground object structure and ‘B+C+D’ method has a lot of artifacts. For those experiments, we can see that ES-CCGAN achieved outstanding performance in the results. The innovation of this work can greatly enhance the ability to restore feature information.

4.2. Comparison with Other Dehazing Methods

In this investigation, we used the same remote-sensing image data set to train different dehazing models and compared the results obtained with ES-CCGAN. The result can be seen in Figure 8. In the dark channel method, it is clear that the color of some parts of the ground is too dark after dehazing. Upon comparing the details of the ground truth image and the dehazed image generated by CycleDehaze, it can be seen that the color of the vegetation in the generated image is incorrect. This result indicates that CycleDehaze cannot be used to recover hazy remote-sensing images of areas covered by plants. In the case of the ES-CCGAN model, the results obtained showed clear edges and natural texture information.

To compare the results of different methods quantitatively, we calculated the average PSNR, FSIM and SSIM values of the analyzed remote-sensing images. In particular, the classic dehazed method (dark channel method), the deep learning dehazed methods (DehazeNet [60] and GFN [61]) and the baseline method (CycleDehaze) are training with the same data, the PSNR and SSIM results are shown in

Table 5. The SSIM and PSNR score on the four methods.

Method	Dark Channel	CycleDehaze	Intermediate Result	DehazeNet	GFN	Ours
SSIM(SD)	0.93 (0.02)	0.55 (0.08)	0.90 (0.01)	0.69 (0.19)	0.86 (0.054)	0.91 (0.02)
FSIM(SD)	0.95 (0.02)	0.77 (0.02)	0.93 (0.01)	0.84 (0.09)	0.92 (0.02)	0.93 (0.01)
PSNR(SD)	21.16 (2.19)	17.28 (2.69)	21.66 (3.05)	14.85 (3.39)	18.82 (1.96)	22.46 (3.81)

. Both DehazeNet and GFN is the supervised method, and the CycleDehaze method is unsupervised.

In Table 5, ‘Intermediate Result’ means the results using CycleDehaze [48] optimization by VGG16′s transfer training and edge-sharpening loss. ES-CCGAN achieves better PSNR values, which prove that it is better than the other state-of-the-art methods for restoring remote-sensing images. Because the confirm of the SRGAN that the too much pixel-wise loss optimization will produce texture overly-smooth and poorly the perceptual quality. Thus, the cyclic perceptual-consistency loss can solve this problem well. On the other hand, the perceptual information will lead to reducing the score of SSIM and FSIM, which is used to maintain the pixel similar. In particular, the Dark Channel method is higher than ES-CCGAN in that the Dark Channel method has no change for the ground object and just removes haze by the degenerate process of haze. Due to a large amount of restored information, the images generated by ES-CCGAN are close to real haze-free remote-sensing images in terms of texture. This work proposed a remote-sensing image dehazing method that can remove the redundant occluded information in hazy images. However, in practical application, the input could be haze-free remote-sensing images; the proposed method cannot ensure the input. To further verify the robustness of the dehazing method, we used it to test haze-free images and compared the results of those images.

From Figure 9, we can see that, although the input is not a hazy image, the result can retain the texture information, edge details, and spatial information in the haze-free image. However, the work removes the haze information, and the color of the hazy remote-sensing images is dull. Thus, generator G will brighten the color for dehazed images, which will make the image clearer. For this reason, the generated haze-free image, which is transformed from an already haze-free image, is brighter than the original haze-free image, but the texture information, edge details, and spatial information is largely retained.

5. Conclusions

In this study, we proposed a model, named edge-sharpening cycle-consistent adversarial network, based on the structure of CycleGAN, to dehaze remote-sensing images. This method can take hazy remote-sensing images as input and produce dehazed images as output. To mitigate the pressure of preparing training data, this model, whose training data set includes unpaired hazy and haze-free images, uses an unsupervised method. Unlike the traditional atmospheric scattering model dehazing algorithm, our model does not require many prior parameters and can dehaze remote-sensing images in complex environments. In the dehazing network, DenseNet block was used to replace the ResNet block, yielding dehazed images with good texture feature information. As the baseline method of CycleGAN leads to remote-sensing images with blurred ground objects, we designed an edge-sharpening loss function to enhance edge information. As the main objective of this study was to dehaze remote-sensing images, when calculating cyclic perceptual-consistency loss, the perceptual neural network was re-trained using an in-house generated remote-sensing image data set. Our experimental results showed that the ES-CCGAN model produces outstanding results and detailed texture information. To validate the effectiveness of this method, real hazy remote-sensing images were processed, and the results obtained conformed to the ground-truth situation. Furthermore, we compared this method with four other dehazing methods for different topographies and found that the results yielded by ES-CCGAN provide a valuable reference for remote-sensing image applications. However, this method still has some limitations. During training, the performance of deep-learning methods is always influenced by training data. Thus, we need many remote-sensing images to train this algorithm. To solve this problem, the network will be enhanced to feature fusion. In our next work, we will focus on clouds in remote-sensing images for haze removal. We will also concentrate on dehazing super-resolution remote-sensing images to recover richer and more detailed information. In particular, the time complexity is also an important study point, and we will try to find a more retrenched network to implement the dehazing effect.