Estimation of Land Surface Albedo from MODIS and VIIRS Data: A Multi-Sensor Strategy Based on the Direct Estimation Algorithm and Statistical-Based Temporal Filter
Abstract
1. Introduction
2. Data and Methods
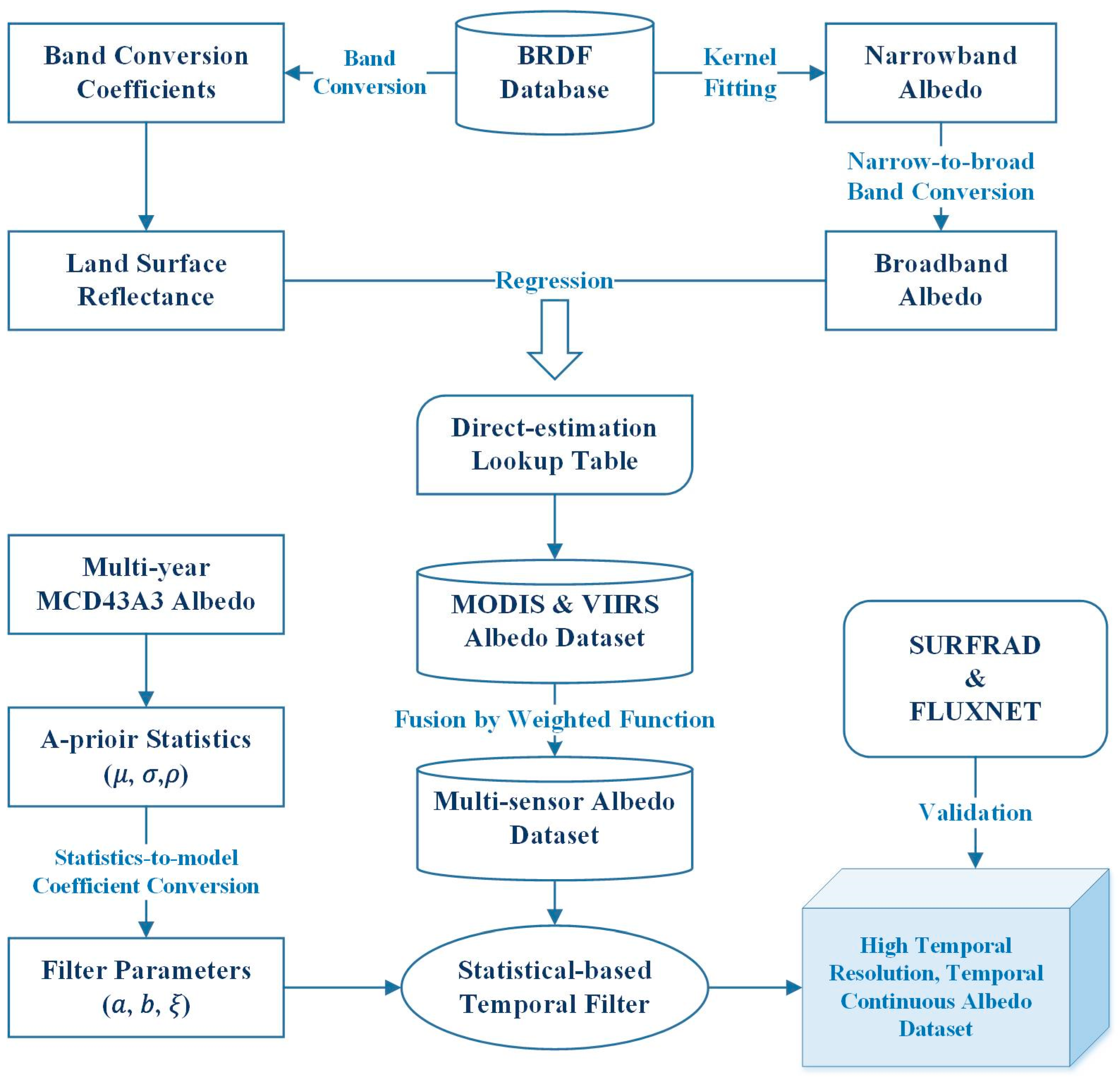
2.1. Overall Framework
2.2. Methods
2.2.1. Direct Estimation Algorithm
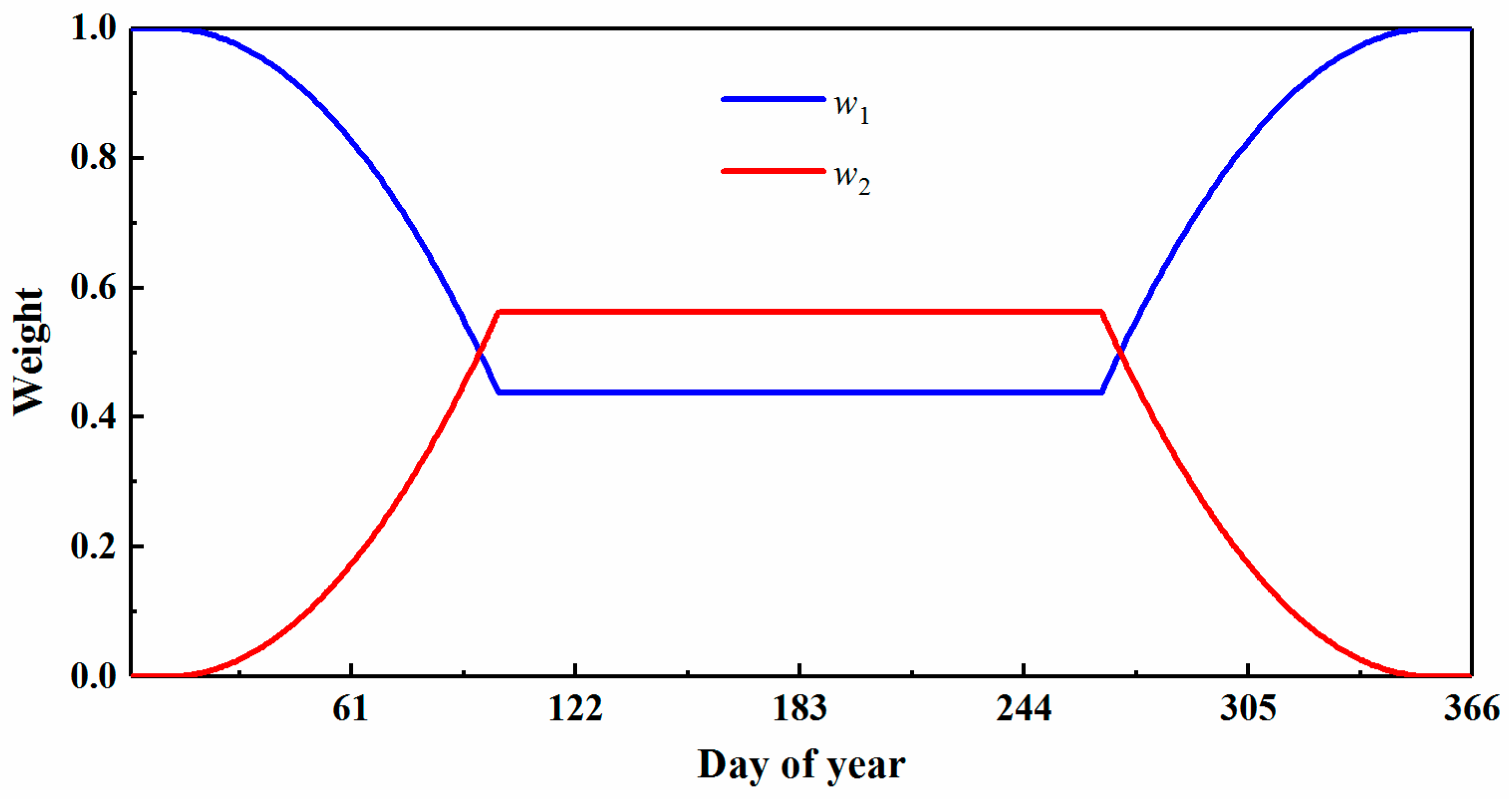
2.2.2. Band Conversion and Fusion of Multi-Sensor Data
2.2.3. Statistical-Based Temporal Filter
2.3. Satellite Data
2.4. Validation Data
2.4.1. MODIS Albedo Product
2.4.2. In Situ Measurements
3. Results and Discussion
3.1. Estimations of Land Surface Albedo
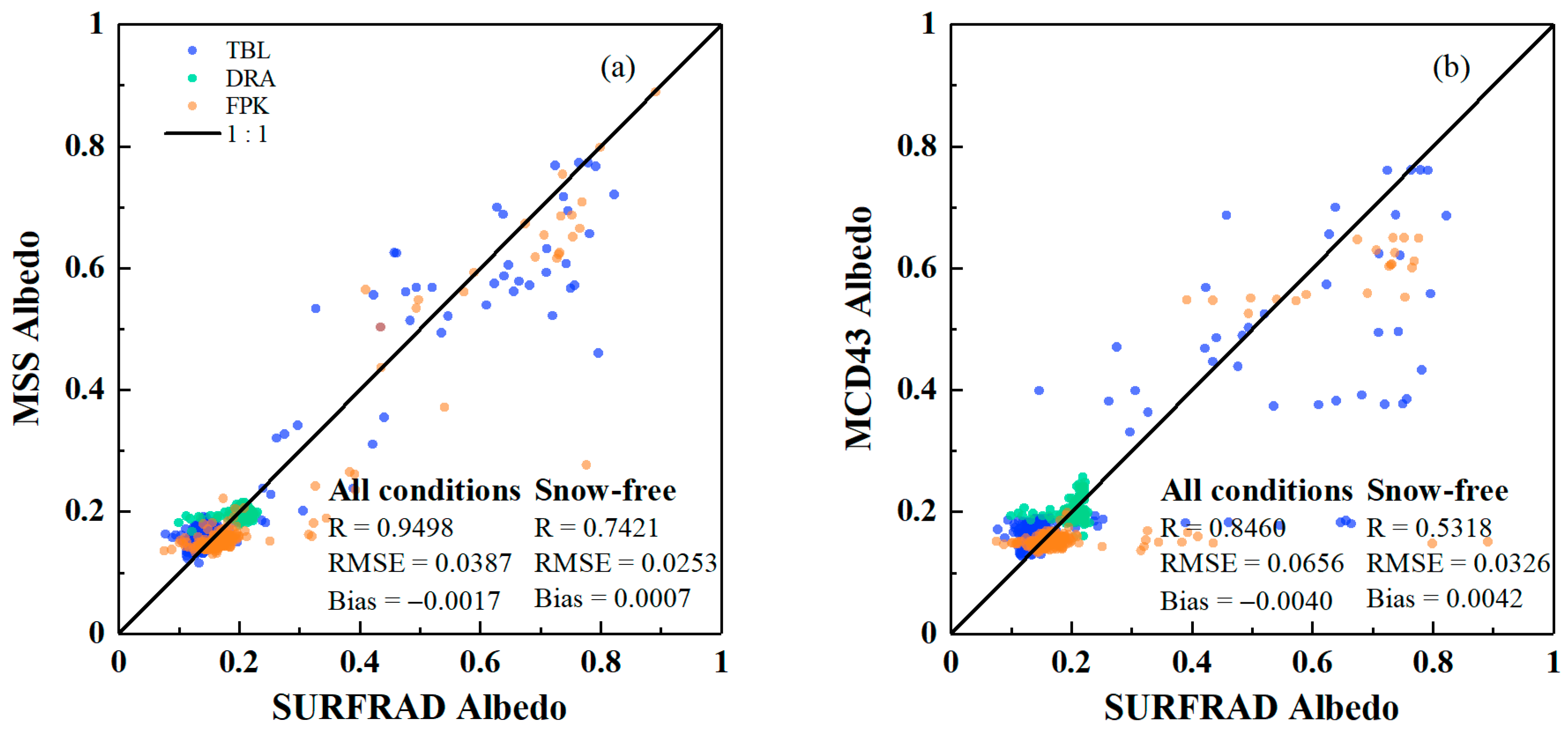
3.2. Validation with In Situ Measurements
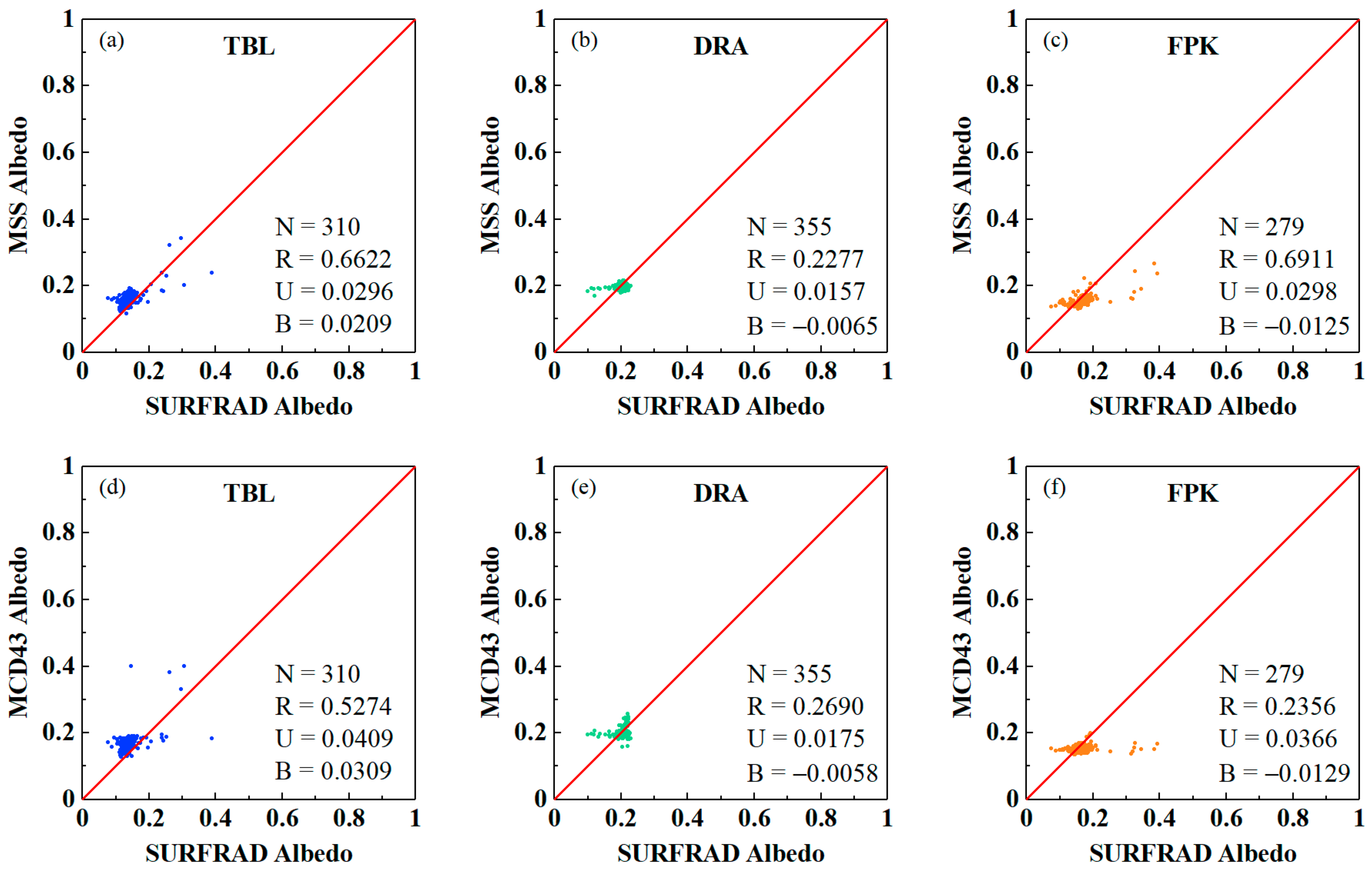
3.2.1. Validation with SURFRAD Sites
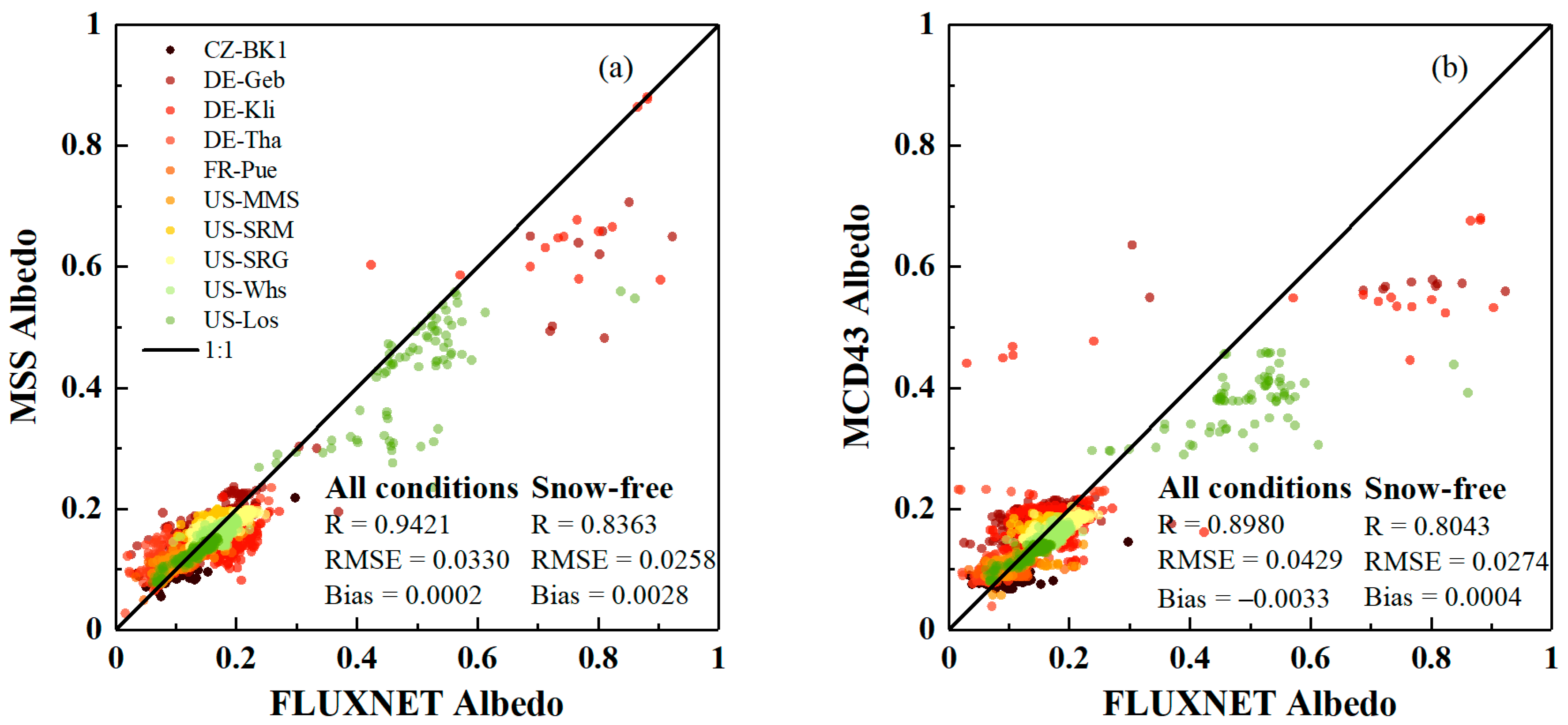
3.2.2. Validation with FLUXNET Sites
3.3. Assessment of the Temporal Continuity
3.4. Comparison of the Estimation Results Derived by DEA and MSS Approaches
3.5. Discussion
4. Conclusions
- (1)
- We obtained more accurate estimations of land surface albedo during snow-covered period using the proposed MSS method. The albedo estimated by the MSS method was consistent with the measurements of SURFRAD (R = 0.9498, RMSE = 0.0387, and bias = −0.0017) and FLUXNET (R = 0.9421, RMSE = 0.0330, and bias = 0.0002) sites.
- (2)
- The temporal continuity of the land surface albedo dataset was significantly improved by employing the multi-sensor data and STF. We found that the number of effective days per year increased with the number of valid satellite observations from multi-sensor data, and temporally continuous, gap-free land surface albedo datasets can be obtained using the proposed MSS method.
- (3)
- By incorporating the DEA and STF approaches, the MSS method could be used to generate long-term, spatiotemporal continuous land surface albedo datasets with high temporal resolution (e.g., daily). The results of this study demonstrated that this is a promising method for generating global climate datasets with high temporal resolution and spatiotemporal continuity.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Dickinson, R. Land processes in climate models. Remote Sens. Environ. 1995, 51, 27–38. [Google Scholar] [CrossRef]
- Dickinson, R.E. Land surface processes and climate—Surface albedos and energy balance. Adv. Geophys. 1983, 25, 305–353. [Google Scholar]
- Liang, S.; Wang, K.; Zhang, X.; Wild, M. Review on estimation of land surface radiation and energy budgets from ground measurement, remote sensing and model simulations. IEEE J. Spec. Top. Appl. Earth Obs. Remote Sens. 2010, 3, 225–240. [Google Scholar] [CrossRef]
- He, T.; Liang, S.; Song, D. Analysis of global land surface albedo climatology and spatial-temporal variation during 1981–2010 from multiple satellite products. J. Geophys. Res. Atmos. 2014, 119, 10281–10298. [Google Scholar] [CrossRef]
- Sagan, C.; Toon, O.B.; Pollack, J.B. Anthropogenic albedo changes and the earth’s climate. Science 1979, 206, 1363–1368. [Google Scholar] [CrossRef] [PubMed]
- Charney, J.G. Dynamics of deserts and drought in the Sahel. QJR Meteorol. Soc. 2006, 101, 193–202. [Google Scholar] [CrossRef]
- Myhre, G.; Govaerts, Y.; Haywood, J.M.; Berntsen, T.K.; Lattanzio, A. Radiative effect of surface albedo change from biomass burning. Geophys. Res. Lett. 2005, 32, L20812. [Google Scholar] [CrossRef]
- Zhai, J.; Liu, R.; Liu, J.; Zhao, G.; Huang, L. Radiative forcing over China due to albedo change caused by land cover change during 1990–2010. J. Geogr. Sci. 2014, 24, 789–801. [Google Scholar] [CrossRef]
- He, T.; Wang, D.; Qu, Y. Land Surface Albedo. In Comprehensive Remote Sensing; Liang, S., Ed.; Elsevier: Cambridge, MA, USA, 2017; pp. 140–162. [Google Scholar]
- Zhang, X.; Liang, S.; Wang, K.; Li, L.; Gui, S. Analysis of global land surface shortwave broadband albedo from multiple data sources. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2010, 3, 296–305. [Google Scholar] [CrossRef]
- Qu, Y.; Liang, S.; Liu, Q.; He, T.; Liu, S.; Li, X. Mapping surface broadband albedo from satellite observations: A review of literatures on algorithms and products. Remote Sens. 2015, 7, 990–1020. [Google Scholar] [CrossRef]
- Lucht, W.; Schaaf, C.; Strahler, A. An algorithm for the retrieval of albedo from space using semiempirical BRDF models. IEEE Trans. Geosci. Remote Sens. 2000, 38, 977–998. [Google Scholar] [CrossRef]
- Schaaf, C.; Gao, F.; Strahler, A.; Lucht, W.; Li, X.; Tsang, T.; Strugnell, N.; Zhang, X.; Jin, Y.; Muller, J. First operational BRDF, albedo nadir reflectance products from MODIS. Remote Sens. Environ. 2002, 83, 135–148. [Google Scholar] [CrossRef]
- Wang, Z.; Schaaf, C.B.; Strahler, A.H.; Chopping, M.J.; Román, M.O.; Shuai, Y.; Woodcock, C.E.; Hollinger, D.Y.; Fitzjarrald, D.R. Evaluation of MODIS albedo product (MCD43A) over grassland, agriculture and forest surface types during dormant and snow-covered periods. Remote Sens. Environ. 2014, 140, 60–77. [Google Scholar] [CrossRef]
- Wang, Z.; Schaaf, C.B.; Sun, Q.; Shuai, Y.; Román, M.O. Capturing rapid land surface dynamics with Collection V006 MODIS BRDF/NBAR/Albedo (MCD43) products. Remote Sens. Environ. 2018, 207, 50–64. [Google Scholar] [CrossRef]
- Wang, D.; Liang, S.; He, T.; Yu, Y. Direct estimation of land surface albedo from VIIRS data: Algorithm improvement and preliminary validation. J. Geophys. Res. Atmos. 2013, 118, 12577–12586. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Z.; Sun, Q.; Erb, A.M.; Li, Z.; Schaaf, C.B.; Zhang, X.; Román, M.O.; Scott, R.L.; Zhang, Q. Evaluation of the VIIRS BRDF, Albedo and NBAR products suite and an assessment of continuity with the long term MODIS record. Remote Sens. Environ. 2016, 201, 256–274. [Google Scholar] [CrossRef]
- Peng, J.; Yu, Y.; Yu, P.; Liang, S. The VIIRS Sea-Ice Albedo Product Generation and Preliminary Validation. Remote Sens. 2018, 10, 1826. [Google Scholar] [CrossRef]
- Liu, Q.; Wang, L.; Qu, Y.; Liu, N.; Tang, H.; Liang, S.; Liu, S. Preliminary evaluation of the long-term GLASS albedo product. Int. J. Digit. Earth 2013, 6 (Suppl. 1), 5–33. [Google Scholar] [CrossRef]
- Qu, Y.; Liang, S.; Liu, Q.; Li, X.; Feng, Y.; Liu, S. Estimating shortwave Arctic sea-ice albedo from MODIS data. Remote Sens. Environ. 2016, 186, 32–46. [Google Scholar] [CrossRef]
- Qu, Y.; Liu, Q.; Liang, S.; Wang, L.; Liu, N.; Liu, S. Direct-estimation algorithm for mapping daily land-surface broadband albedo from MODIS data. IEEE Trans. Geosci. Remote Sens. 2014, 52, 907–919. [Google Scholar] [CrossRef]
- Riihelä, A.; Manninen, T.; Laine, V.; Andersson, K.; Kaspar, F. CLARA-SAL: A global 28 yr timeseries of Earth’s black-sky surface albedo. Atmos. Chem. Phys. 2013, 13, 3743–3762. [Google Scholar] [CrossRef]
- Karlsson, K.G.; Anttila, K.; Trentmann, J.; Stengel, M.; Meirink, J.F.; Devasthale, A.; Hanschmann, T.; Kothe, S.; Jääskeläinen, E.; Sedlar, J.; et al. CLARA-A2: The second edition of the CM SAF cloud and radiation data record from 34 years of global AVHRR data. Atmos. Chem. Phys. 2017, 17, 5809–5828. [Google Scholar] [CrossRef]
- Muller, J.-P.; López, G.; Watson, G.; Shane, N.; Kennedy, T.; Yuen, P.; Lewis, P.; Fischer, J.; Guanter, L.; Domench, C.; et al. The ESA GlobAlbedo Project for mapping the Earth’s land surface albedo for 15 years from European sensors. In Proceedings of the European Geophysical Union Conference, Geophysical Research Abstracts, Vienna, Austria, 3–8 April 2011; p. 10969. [Google Scholar]
- Bréon, F.; Maignan, F.; Leroy, M.; Grant, I. Analysis of hot spot directional signatures measured from space. J. Geophys. Res. 2002, 107, 4282–4296. [Google Scholar]
- Maignan, F.; Bréon, F.; Lacaze, R. Bidirectional reflectance of Earth targets: Evaluation of analytical models using a large set of spaceborne measurements with emphasis on the Hot Spot. Remote Sens. Environ. 2004, 90, 210–220. [Google Scholar] [CrossRef]
- Diner, D.J.; Martonchik, J.V.; Borel, C.; Gerstl, S.A.W.; Gordon, H.R.; Knyazikhin, Y.; Myneni, R.; Pinty, B.; Verstraete, M. Multi-Angle Imaging Spectro-Radiometer Level 2 Surface Retrieval Algorithm Theoretical Basis; Jet Propulsion Laboratory: Pasadena, CA, USA, 2008. [Google Scholar]
- Martonchik, J.; Diner, D.; Pinty, B.; Verstraete, M.; Myneni, R.; Knyazikhin, Y.; Gordon, H. Determination of land and ocean reflective, radiative, and biophysical properties using multiangle imaging. IEEE Trans. Geosci. Remote Sens. 2002, 36, 1266–1281. [Google Scholar] [CrossRef]
- Martonchik, J.; Pinty, B.; Verstraete, M. Note on an improved model of surface BRDF-atmospheric coupled radiation. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1637–1639. [Google Scholar] [CrossRef]
- Muller, J.; Zuhlke, M.; Brockmann, C.; Preusker, R.; Fischer, J.; Regner, P. ALBEDOMAP: MERIS land surface albedo retrieval using data fusion with MODIS BRDF and its validation using contemporaneous EO and in situ data products. In Proceedings of the IEEE Geoscience and Remote Sensing Symposium (IGARSS), Bacelona, Spain, 23–28 July 2007; Volume 23–28, pp. 2404–2407. [Google Scholar]
- He, T.; Liang, S.; Wang, D.; Cao, Y.; Gao, F.; Yu, Y.; Feng, M. Evaluating land surface albedo estimation from Landsat MSS, TM, ETM+, and OLI data based on the unified direct estimation approach. Remote Sens. Environ. 2018, 204, 181–196. [Google Scholar] [CrossRef]
- Shuai, Y.; Masek, J.G.; Gao, F.; Schaaf, C.B. An algorithm for the retrieval of 30-m snow-free albedo from Landsat surface reflectance and MODIS BRDF. Remote Sens. Environ. 2011, 115, 2204–2216. [Google Scholar] [CrossRef]
- Shuai, Y.; Masek, J.G.; Gao, F.; Schaaf, C.B.; He, T. An approach for the long-term 30-m land surface snow-free albedo retrieval from historic Landsat surface reflectance and MODIS-based a priori anisotropy knowledge. Remote Sens. Environ. 2014, 152, 467–479. [Google Scholar] [CrossRef]
- Liu, Q.; Wen, J.; Qu, Y.; He, T.; Zhang, X. Broadband Albedo. In Advanced Remote Sensing: Terrestrial Information Extraction and Applications; Liang, S., Wang, J., Li, X., Eds.; Academic Press: San Diego, CA, USA, 2013. [Google Scholar]
- Liu, S.H.; Liu, Q.A.; Liu, Q.H.; Wen, J.G.; Li, X.W. The Angular and Spectral Kernel Model for BRDF and Albedo Retrieval. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2010, 3, 241–256. [Google Scholar] [CrossRef]
- Salomon, J.G.; Schaaf, C.B.; Strahler, A.H.; Gao, F.; Jin, Y. Validation of the MODIS bidirectional reflectance distribution function and albedo retrievals using combined observations from the aqua and terra platforms. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1555–1565. [Google Scholar] [CrossRef]
- Wen, J.; Dou, B.; You, D.; Tang, Y.; Xiao, Q.; Liu, Q.; Liu, Q. Forward a small-timescale BRDF/Albedo by multisensor combined brdf inversion model. IEEE Trans. Geosci. Remote Sens. 2017, 55, 683–697. [Google Scholar] [CrossRef]
- Liu, N.; Liu, Q.; Wang, L.; Liang, S.; Wen, J.; Qu, Y.; Liu, S. A statistics-based temporal filter algorithm to map spatiotemporally continuous shortwave albedo from MODIS data. Hydrol. Earth Syst. Sci. 2013, 17, 2121–2129. [Google Scholar] [CrossRef]
- Moody, E.G.; King, M.D.; Platnick, S.; Schaaf, C.B.; Gao, F. Spatially complete global spectral surface albedos: Value-added datasets derived from terra MODIS land products. IEEE Trans. Geosci. Remote Sens. 2005, 43, 144–158. [Google Scholar] [CrossRef]
- Bacour, C.; Breon, F. Variability of biome reflectance directional signatures as seen by POLDER. Remote Sens. Environ. 2005, 98, 80–95. [Google Scholar] [CrossRef]
- Samain, O.; Geiger, B.; Roujean, J. Spectral normalization and fusion of optical sensors for the retrieval of BRDF and albedo: Application to VEGETATION, MODIS, and MERIS data sets. IEEE Trans. Geosci. Remote Sens. 2006, 44, 3166–3179. [Google Scholar] [CrossRef]
- Xiao, Z.; Liang, S.; Wang, J.; Xiang, Y.; Zhao, X.; Song, J. Long-time-series global land surface satellite leaf area index product derived from MODIS and AVHRR surface reflectance. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5301–5318. [Google Scholar] [CrossRef]
- Wang, Z.; Schaaf, C.B.; Sun, Q.; Kim, J.; Erb, A.M.; Gao, F.; Román, M.O.; Yang, Y.; Petroy, S.; Taylor, J.R. Monitoring land surface albedo and vegetation dynamics using high spatial and temporal resolution synthetic time series from Landsat and the MODIS BRDF/NBAR/albedo product. Int. J. Appl. Earth Obs. Geoinf. 2017, 59, 104–117. [Google Scholar] [CrossRef]
- Augustine, J.A.; DeLuisi, J.J.; Long, C.N. SURFRAD-A national surface radiation budget network for atmospheric research. Bull. Am. Meteorol. Soc. 2000, 81, 2341–2357. [Google Scholar] [CrossRef]
- Baldocchi, D.; Falge, E.; Gu, L.; Olson, R.; Hollinger, D.; Running, S.; Anthoni, P.; Bernhofer, C.; Davis, K.; Evans, R. FLUXNET: A new tool to study the temporal and spatial variability of ecosystem-scale carbon dioxide, water vapor, and energy flux densities. Bull. Am. Meteorol. Soc. 2001, 82, 2415–2434. [Google Scholar] [CrossRef]
- Cescatti, A.; Marcolla, B.; Santhana Vannan, S.K.; Pan, J.Y.; Román, M.O.; Yang, X.; Ciais, P.; Cook, R.B.; Law, B.E.; Matteucci, G. Intercomparison of MODIS albedo retrievals and in situ measurements across the global FLUXNET network. Remote Sens. Environ. 2012, 121, 323–334. [Google Scholar] [CrossRef]
- Roman, M.O.; Schaaf, C.B.; Woodcock, C.E.; Strahler, A.H.; Yang, X.Y.; Braswell, R.H.; Curtis, P.S.; Davis, K.J.; Dragoni, D.; Goulden, M.L.; et al. The MODIS (Collection V005) BRDF/albedo product: Assessment of spatial representativeness over forested landscapes. Remote Sens. Environ. 2009, 113, 2476–2498. [Google Scholar] [CrossRef]
- Pinty, B.; Lattanzio, A.; Martonchik, J.V.; Verstraete, M.M.; Gobron, N.; Taberner, M.; Widlowski, J.-L.; Dickinson, R.E.; Govaerts, Y. Coupling Diffuse Sky Radiation and Surface Albedo. J. Atmos. Sci. 2005, 62, 2580–2591. [Google Scholar] [CrossRef]
- Stokes, G.M.; Schwartz, S.E. The Atmospheric Radiation Measurement (ARM) Program: Programmatic Background and Design of the Cloud and Radiation Test Bed. Bull. Am. Meteorol. Soc. 1994, 75, 1201–1221. [Google Scholar] [CrossRef]
- Wang, Z.; Schaaf, C.B.; Chopping, M.J.; Strahler, A.H.; Wang, J.; Román, M.O.; Rocha, A.V.; Woodcock, C.E.; Shuai, Y. Evaluation of Moderate-resolution Imaging Spectroradiometer (MODIS) snow albedo product (MCD43A) over tundra. Remote Sens. Environ. 2012, 117, 264–280. [Google Scholar] [CrossRef]
- Wu, X.; Wen, J.; Xiao, Q.; YOu, D. Upscaling of single-site-based measurements for validation of long-term coarse-pixel albedo products. IEEE Trans. Geosci. Remote Sens. 2020, 58, 3411–3425. [Google Scholar] [CrossRef]
- Nguyen, H.; Katzfuss, M.; Cressie, N.; Braveman, A. Spatio-Temporal Data Fusion for Very Large Remote Sensing Datasets. Technometrics 2014, 56, 174–185. [Google Scholar] [CrossRef]






| Bands | MODIS | ||||||
|---|---|---|---|---|---|---|---|
| 648 nm | 859 nm | 466 nm | 554 nm | 1244 nm | 1631 nm | 2119 nm | |
| c1-VIIRS (412 nm) | −0.00348 | 0.00131 | −0.11369 | −0.00040 | −0.00647 | −0.00044 | −0.02538 |
| c2-VIIRS (445 nm) | 0.05024 | −0.00516 | 0.57152 | 0.00992 | −0.00654 | 0.08790 | 0.00602 |
| c3-VIIRS (488 nm) | −0.07806 | 0.00564 | 0.60739 | −0.05882 | 0.01662 | −0.15338 | −0.03737 |
| c4-VIIRS (555 nm) | 0.20236 | −0.00732 | −0.08842 | 1.04364 | −0.00025 | 0.05368 | 0.09303 |
| c5-VIIRS (672 nm) | 0.84309 | 0.03519 | 0.02749 | 0.01159 | −0.01245 | −0.00336 | −0.11199 |
| c6-VIIRS (865 nm) | −0.02485 | 0.97967 | −0.01269 | −0.00732 | 0.00792 | 0.02334 | 0.01635 |
| c7-VIIRS (1240 nm) | 0.02032 | −0.00991 | 0.00673 | 0.00230 | 0.97682 | −0.05595 | −0.20074 |
| c8-VIIRS (1610 nm) | −0.00822 | −0.00038 | −0.00169 | −0.00071 | 0.00588 | 0.99118 | 0.53446 |
| c9-VIIRS (2250 nm) | 0.00087 | −0.00095 | 0.00183 | −0.00003 | 0.00920 | 0.05602 | 0.70410 |
| c0 (Offset) | −0.00044 | 0.00085 | −0.00124 | −0.00025 | 0.00203 | 0.00284 | 0.01492 |
| RMSE | 0.00974 | 0.00583 | 0.00620 | 0.00212 | 0.00654 | 0.03002 | 0.04987 |
| Code | Site Name | Land Cover | Latitude (Degree) | Longitude (Degree) | Elevation (m) |
|---|---|---|---|---|---|
| TBL | Table Mountain | Grasslands | 40.12498 | −105.23680 | 1689 |
| DRA | Desert Rock | Barren, sparse grass | 36.62373 | −116.01947 | 1007 |
| FPK | Fort Peck | Grasslands | 48.30783 | −105.10170 | 634 |
| Code | Site Name | Land Cover | Latitude (Degree) | Longitude (Degree) | Elevation (m) |
|---|---|---|---|---|---|
| CZ-BK1 | Bily Kriz Forest | Evergreen needleleaf forest | 49.50208 | 18.53688 | 875 |
| DE-Geb | Gebesee | Croplands | 51.09973 | 10.91463 | 161.5 |
| DE-Kli | Klingenberg | Croplands | 50.89306 | 13.52238 | 478 |
| DE-Tha | Tharandt | Evergreen needleleaf forest | 50.96256 | 13.56515 | 385 |
| FR-Pue | Puechabon | Evergreen broadleaf forest | 43.7413 | 3.5957 | 270 |
| US-Los | Lost Creek | Wetlands | 46.0827 | −89.9792 | 480 |
| US-MMS | Morgan Monroe State Forest | Deciduous broadleaf forest | 39.3232 | −86.4131 | 275 |
| US-SRM | Santa Rita Mesquite | Woody savannas | 31.8214 | −110.8661 | 1120 |
| US-SRG | Santa Rita Grassland | Grasslands | 31.78938 | −110.82768 | 1291 |
| US-Whs | Walnut Gulch Lucky Hills Shrub | Open shrublands | 31.7438 | −110.0522 | 1370 |
| Site | MOD | MOD + MYD | MODIS + VIIRS | MSS | MCD43A3 |
|---|---|---|---|---|---|
| TBL | 153 | 161 | 201 | 365 | 352 |
| DRA | 166 | 187 | 260 | 365 | 361 |
| FPK | 145 | 152 | 204 | 365 | 311 |
| CZ-BK1 | 59 | 66 | 256 | 365 | 199 |
| DE-Geb | 69 | 79 | 145 | 365 | 303 |
| DE-Kli | 74 | 82 | 127 | 365 | 342 |
| DE-Tha | 88 | 92 | 140 | 365 | 304 |
| FR-Pue | 146 | 157 | 217 | 365 | 350 |
| US-MMS | 96 | 106 | 177 | 365 | 308 |
| US-SRM | 241 | 249 | 291 | 365 | 365 |
| US-SRG | 232 | 243 | 280 | 365 | 365 |
| US-Whs | 233 | 246 | 275 | 365 | 365 |
| US-Los | 76 | 79 | 267 | 362 | 260 |
| Methods | R | RMSE |
|---|---|---|
| DEA (MODIS) | 0.8399 | 0.0390 |
| DEA (VIIRS) | 0.8623 | 0.0412 |
| DEA (MODIS + VIIRS) | 0.8627 | 0.0404 |
| MSS (without gap-filled data) | 0.9025 | 0.0351 |
| MSS (with gap-filled data) | 0.9402 | 0.0385 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, M.; Fan, X.; Li, X.; Liu, Q.; Qu, Y. Estimation of Land Surface Albedo from MODIS and VIIRS Data: A Multi-Sensor Strategy Based on the Direct Estimation Algorithm and Statistical-Based Temporal Filter. Remote Sens. 2020, 12, 4131. https://doi.org/10.3390/rs12244131
Wang M, Fan X, Li X, Liu Q, Qu Y. Estimation of Land Surface Albedo from MODIS and VIIRS Data: A Multi-Sensor Strategy Based on the Direct Estimation Algorithm and Statistical-Based Temporal Filter. Remote Sensing. 2020; 12(24):4131. https://doi.org/10.3390/rs12244131
Chicago/Turabian StyleWang, Mengsi, Xianlei Fan, Xijia Li, Qiang Liu, and Ying Qu. 2020. "Estimation of Land Surface Albedo from MODIS and VIIRS Data: A Multi-Sensor Strategy Based on the Direct Estimation Algorithm and Statistical-Based Temporal Filter" Remote Sensing 12, no. 24: 4131. https://doi.org/10.3390/rs12244131
APA StyleWang, M., Fan, X., Li, X., Liu, Q., & Qu, Y. (2020). Estimation of Land Surface Albedo from MODIS and VIIRS Data: A Multi-Sensor Strategy Based on the Direct Estimation Algorithm and Statistical-Based Temporal Filter. Remote Sensing, 12(24), 4131. https://doi.org/10.3390/rs12244131






