Characteristics of the Bright Band Based on Quasi-Vertical Profiles of Polarimetric Observations from an S-Band Weather Radar Network
Abstract
1. Introduction
2. Materials and Methods
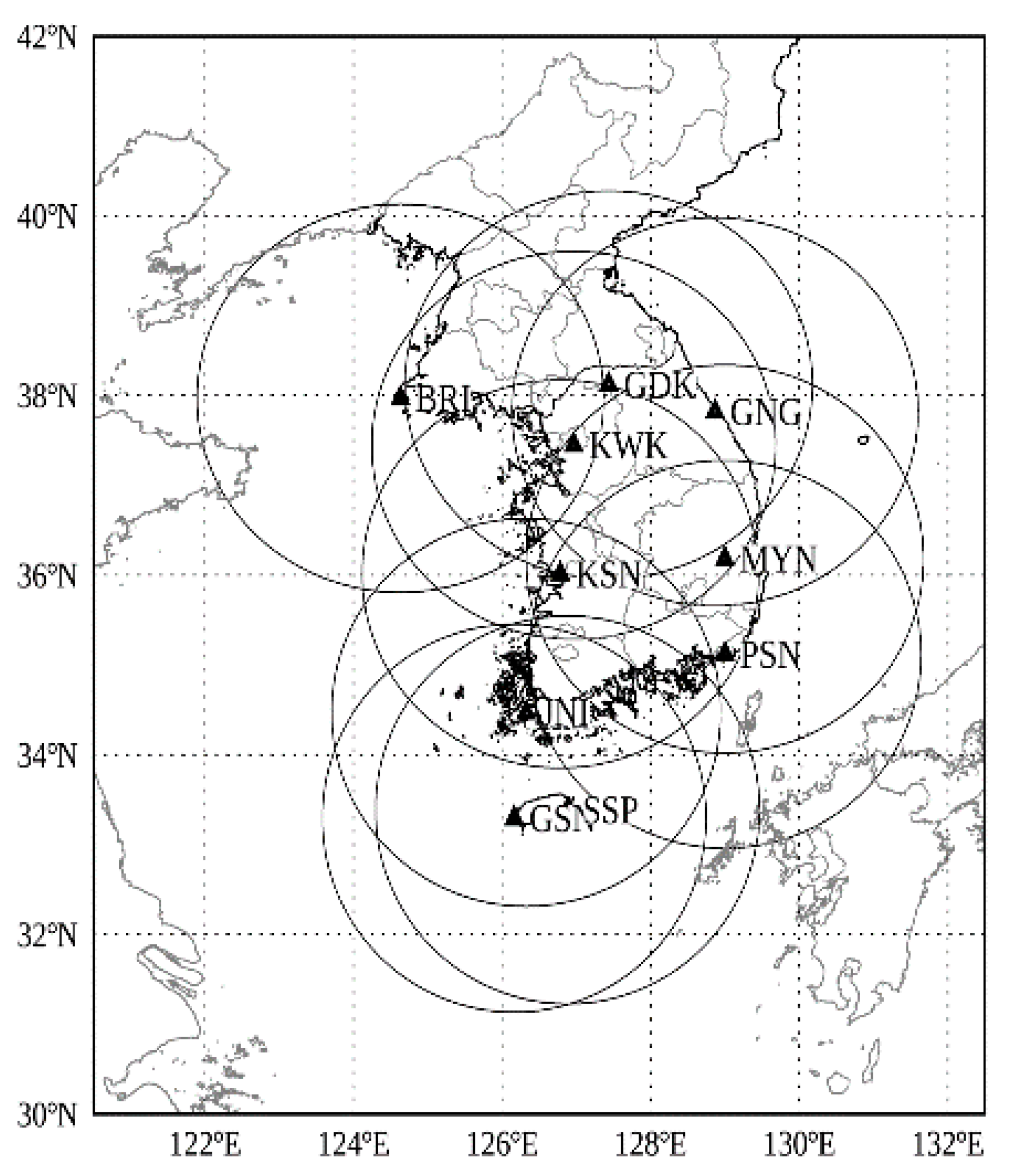
2.1. Materials and Data
2.2. Methodology
2.2.1. Construction of the QVPs
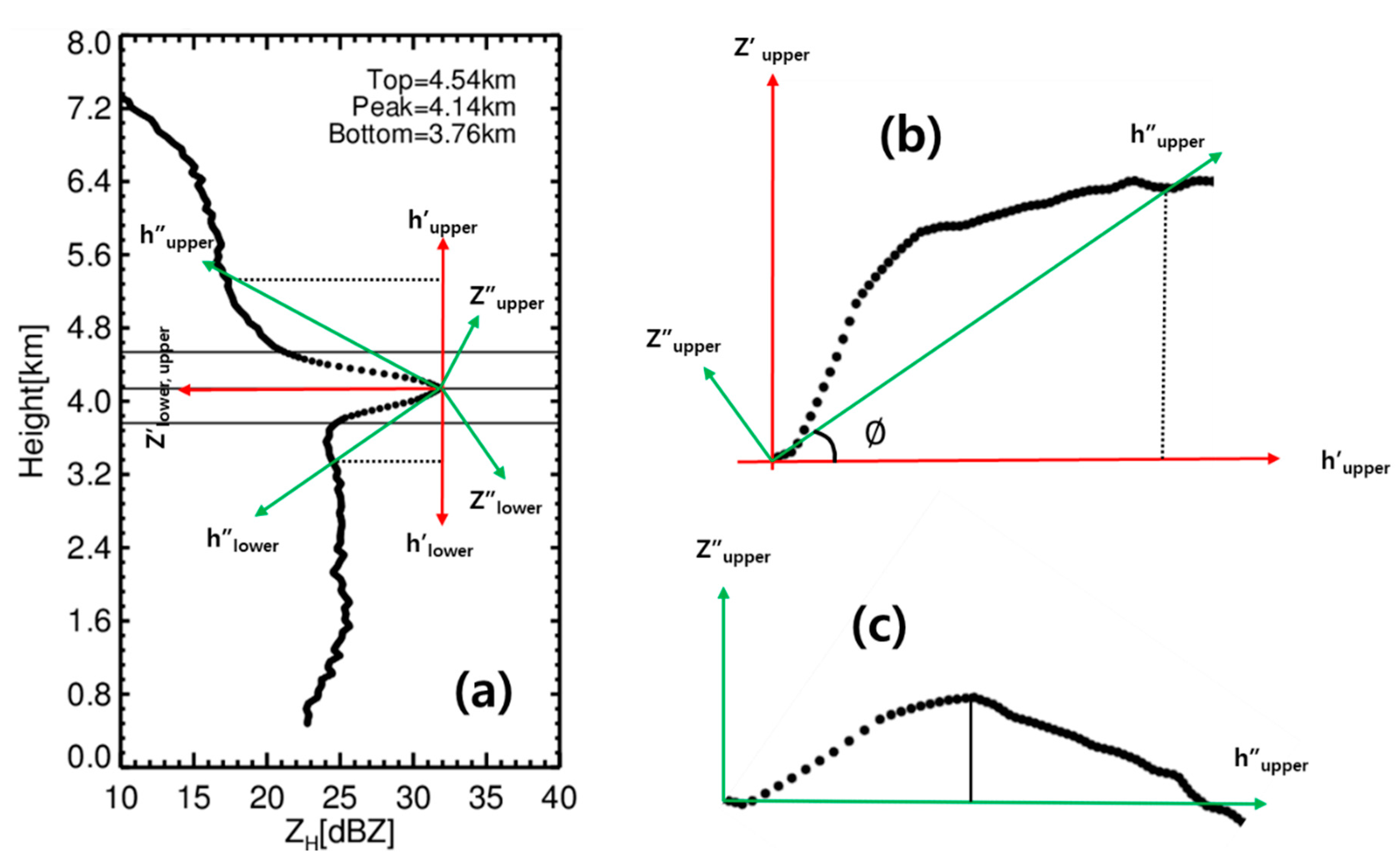
2.2.2. Detection of the Bright Band (BB)
2.2.3. Variables for Characterizing the BB
3. Results and Discussion
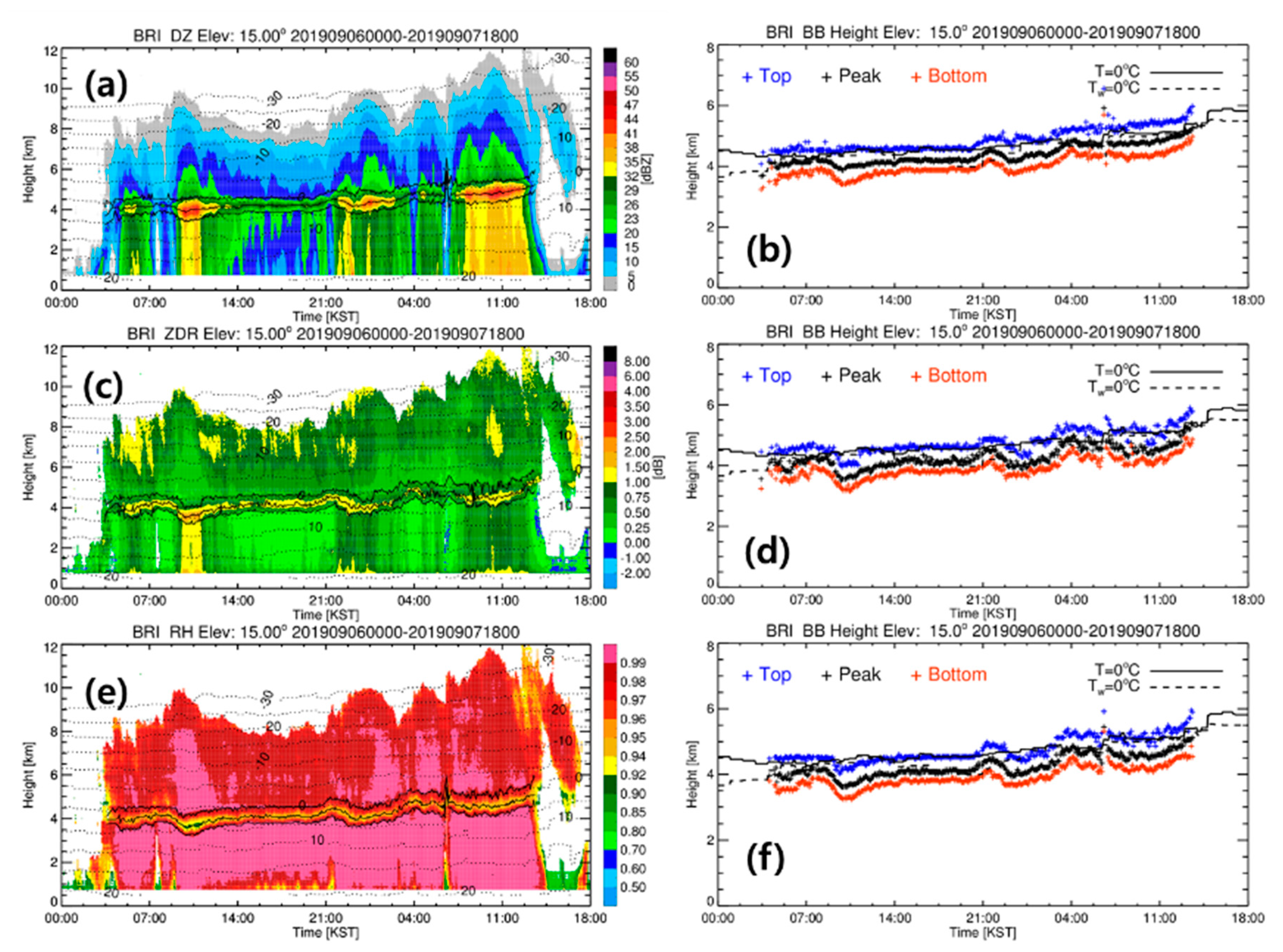
3.1. Characterization of the BB
3.1.1. Height of the BB
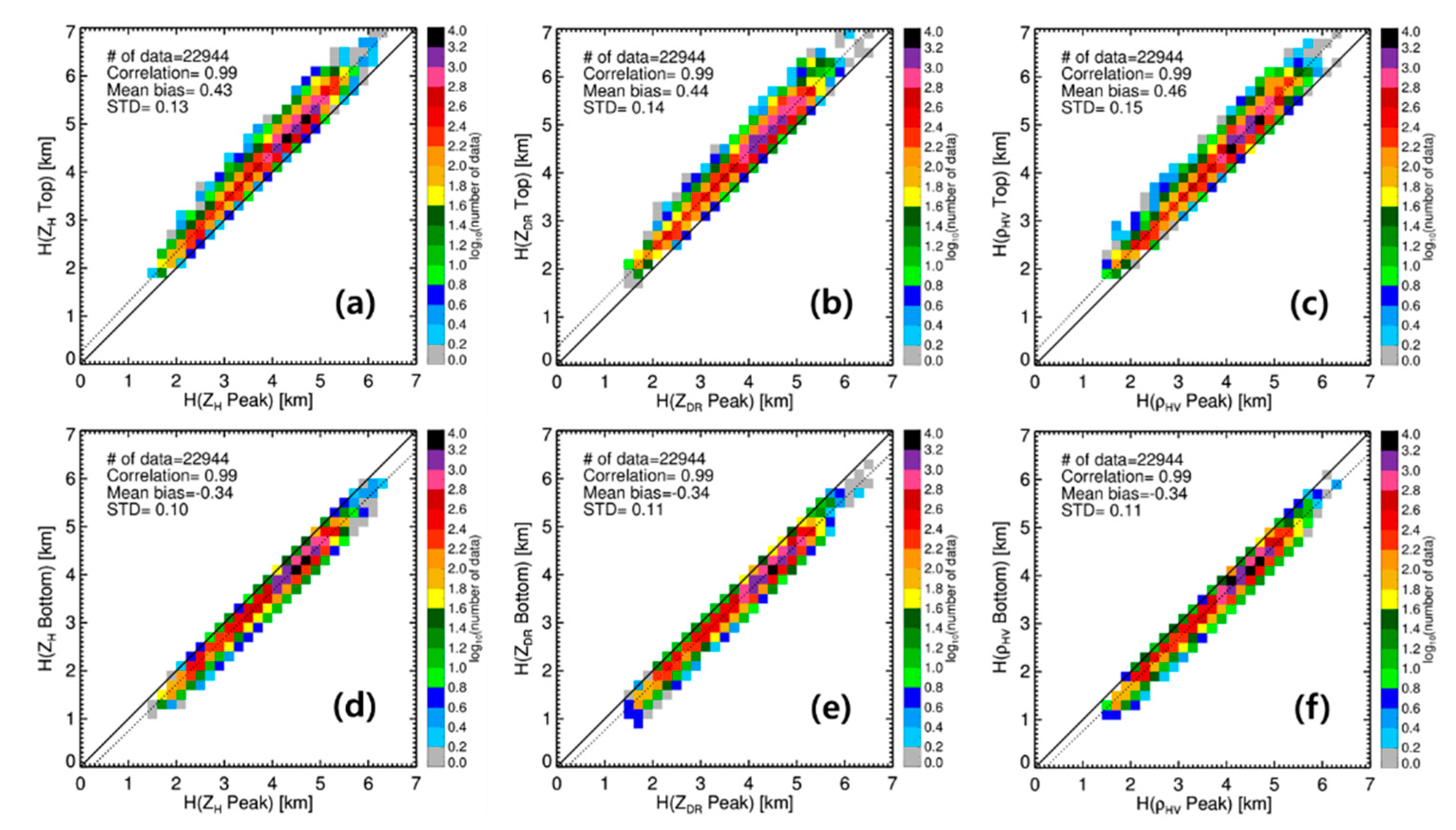
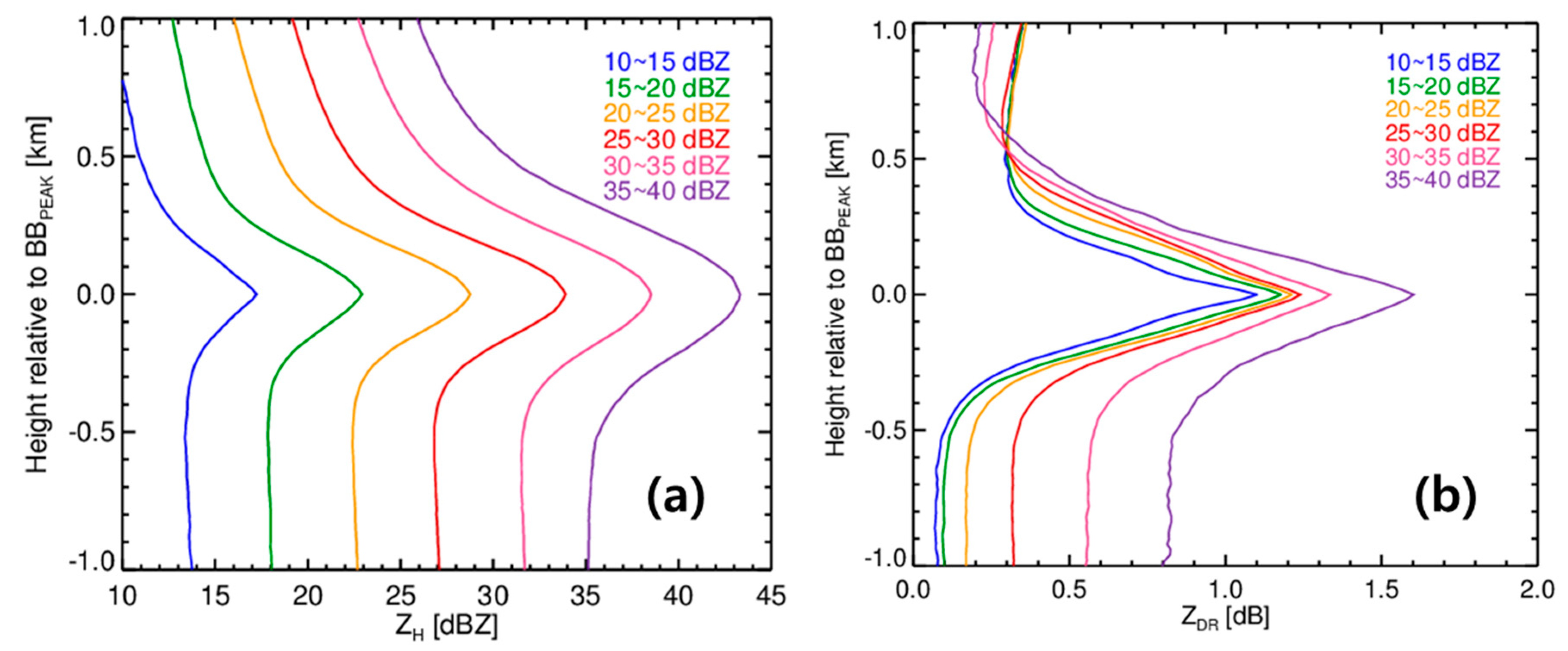
3.1.2. Geometric Structure of the BB
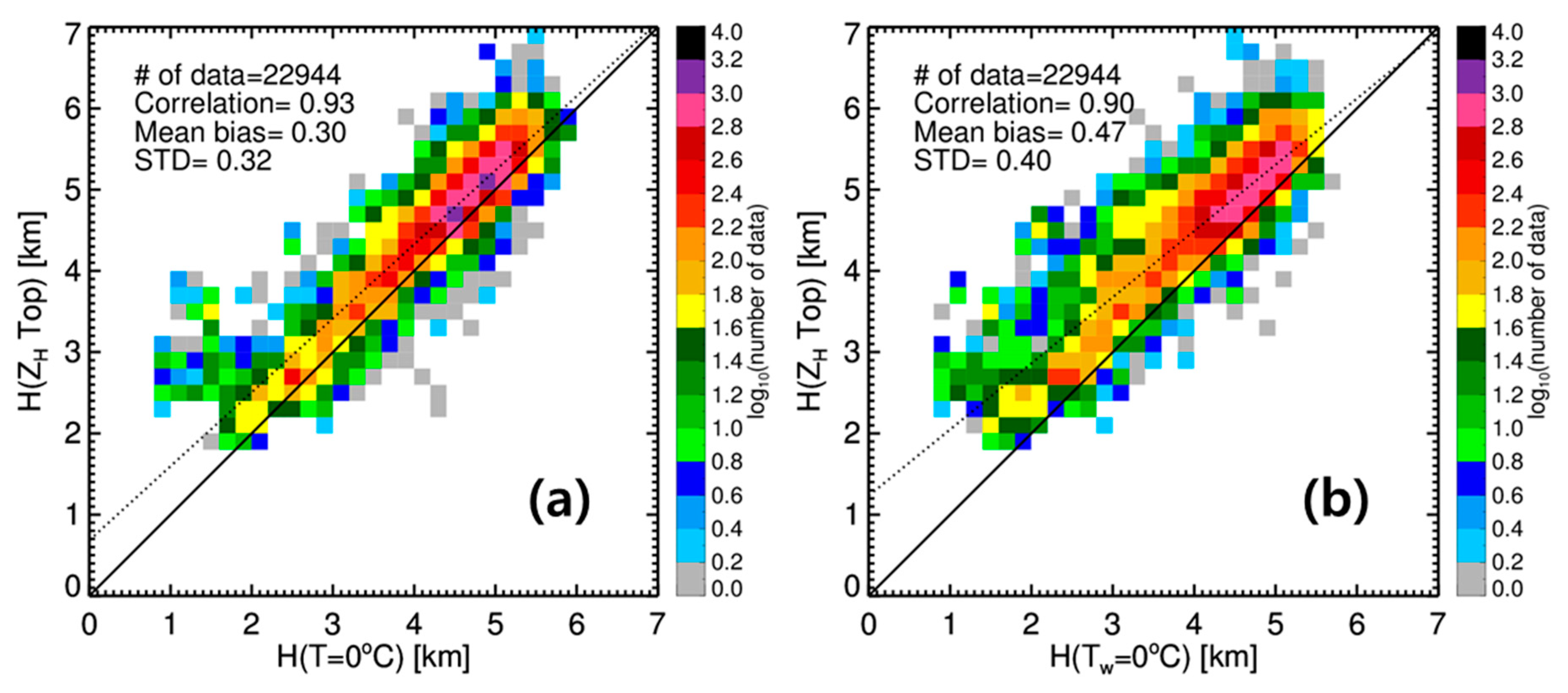
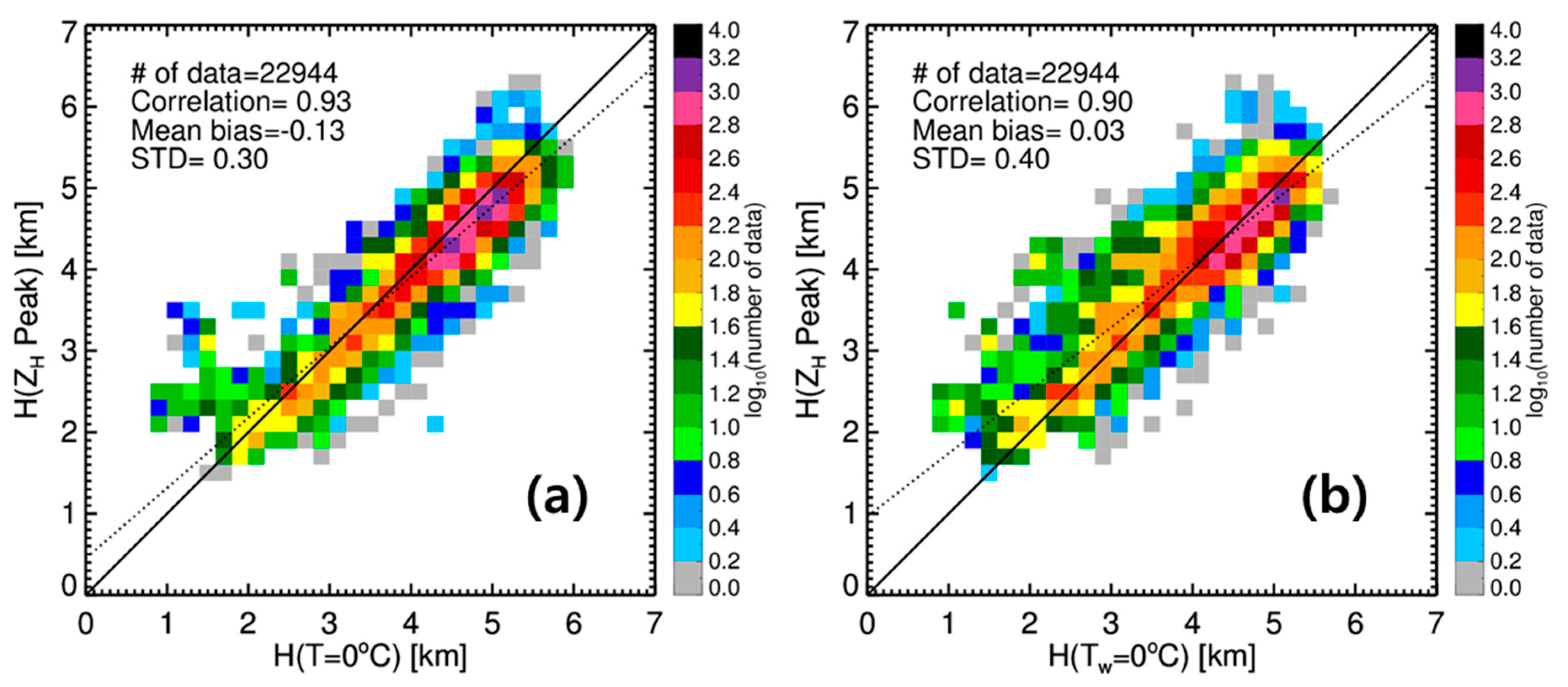
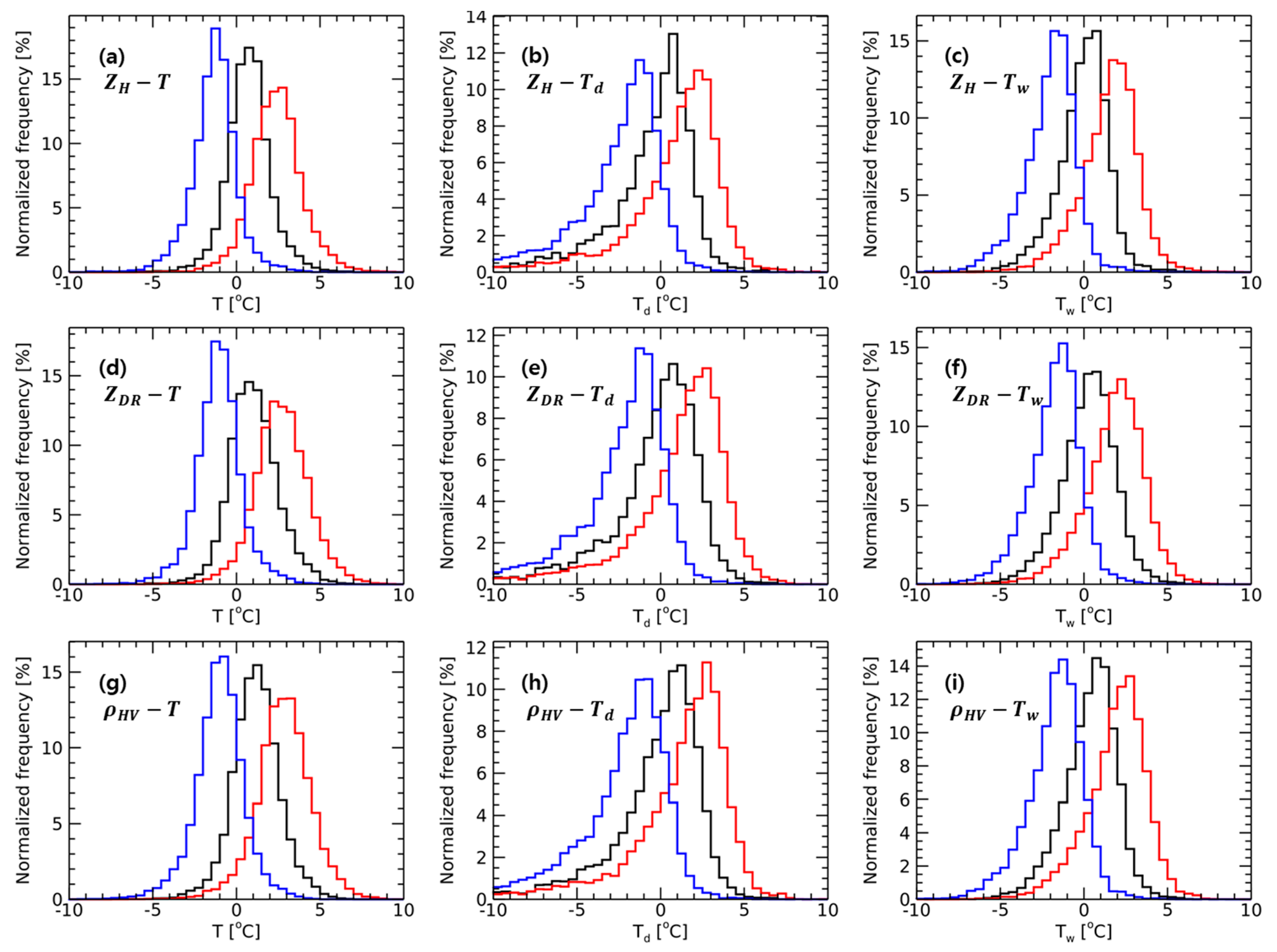
3.1.3. Thermodynamic Characteristic of the BB
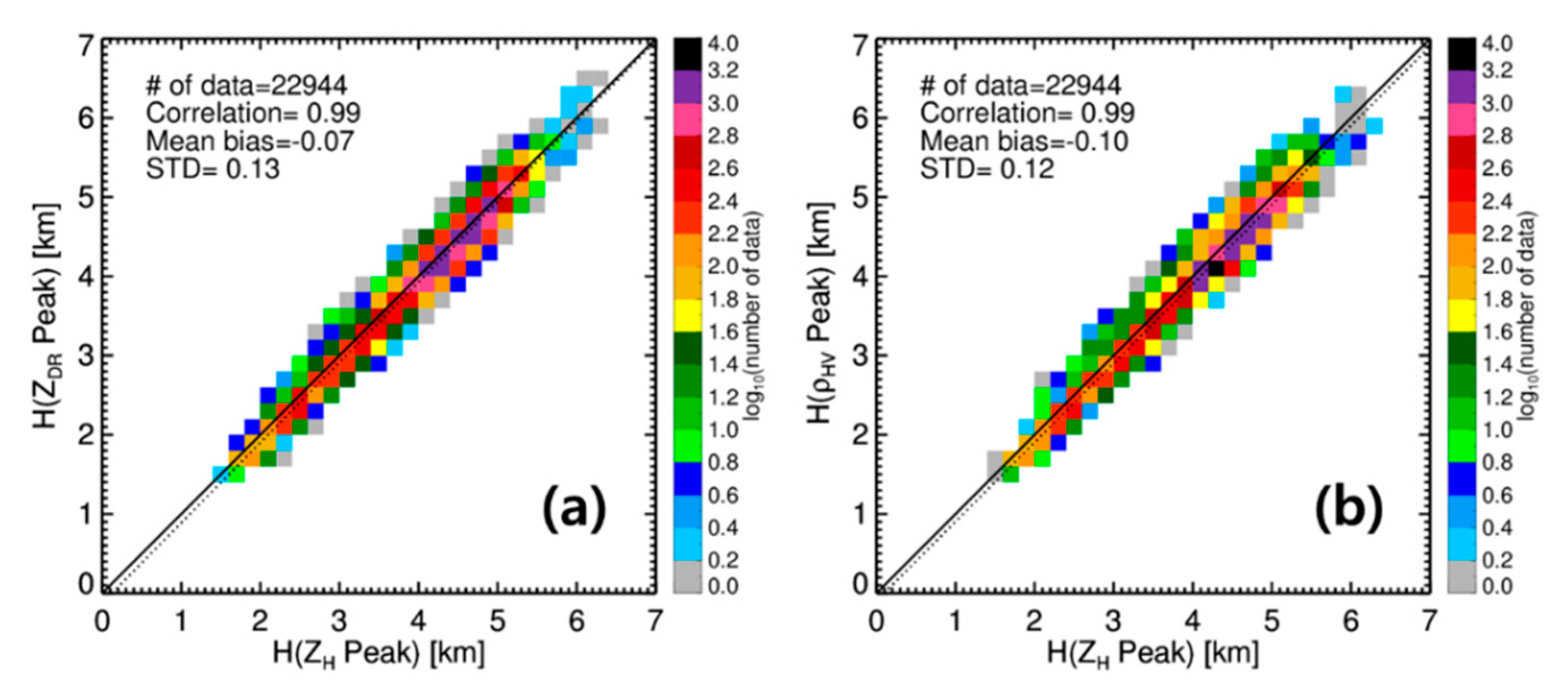
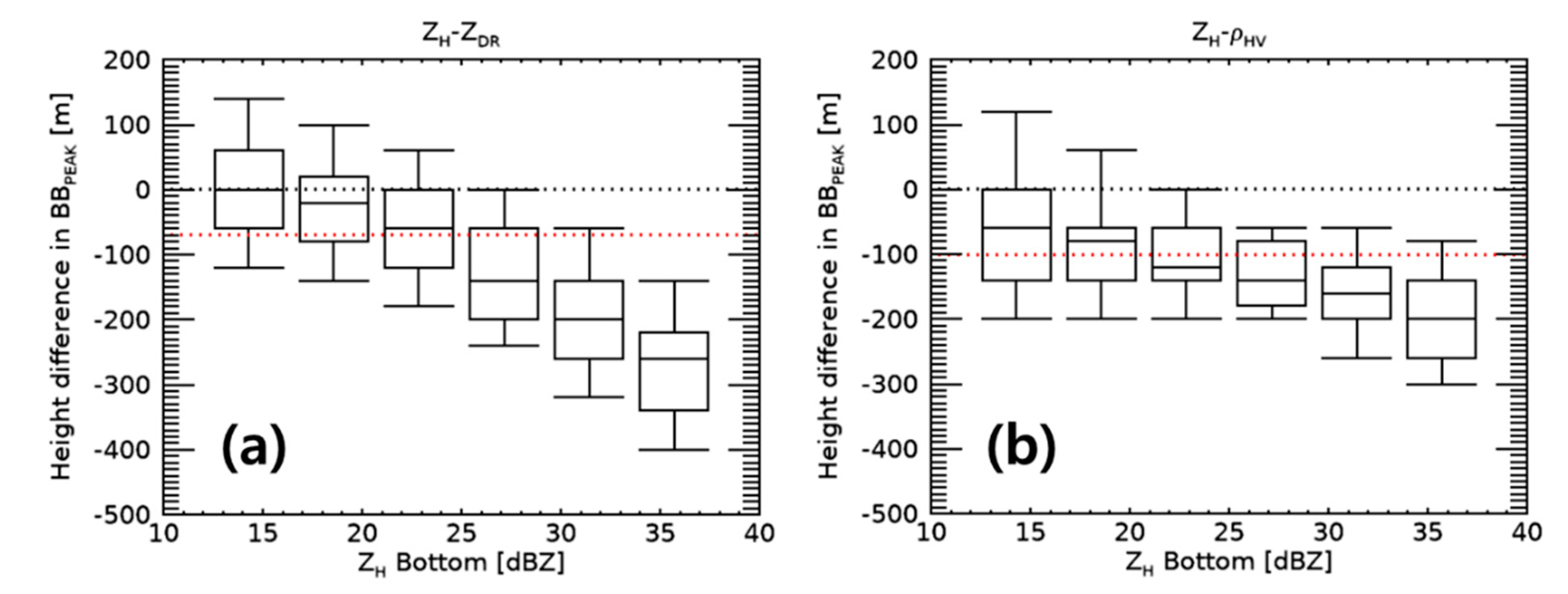
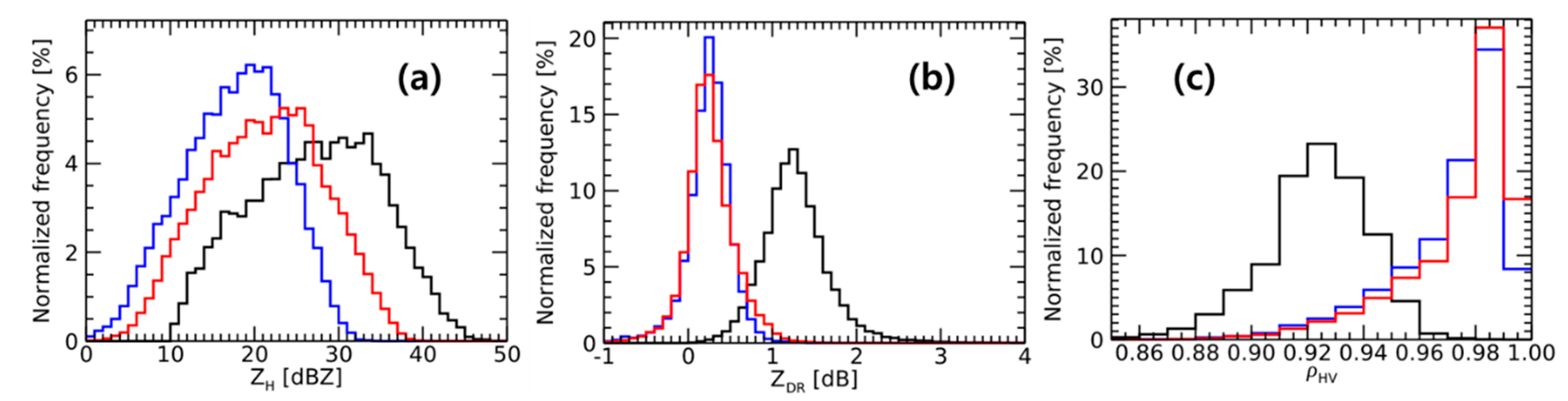
3.2. Polarimetric Observation of the BB
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Fabry, F.; Zawadzki, I. Long-term radar operations of the melting layer of precipitation and their interpretation. J. Atmos. Sci. 1995, 52, 838–851. [Google Scholar] [CrossRef]
- Szyrmer, W.; Zawadzki, I. Modeling of the melting layer. Part I: Dynamics and microphysics. J. Atmos. Sci. 1999, 56, 3573–3592. [Google Scholar]
- Bellon, A.; Lee, G.W.; Zawadzki, I. Error statistics of VPR corrections in stratiform precipitation. J. Appl. Meteor. 2005, 44, 998–1015. [Google Scholar] [CrossRef]
- Germann, U.; Joss, J. Mesobeta profiles to extrapolate radar precipitation measurements above the Alps to the ground level. J. Appl. Meteor. 2002, 41, 542–557. [Google Scholar] [CrossRef]
- Vignal, B.; Krajewski, W. Large-sample evaluation of two methods to correct range-dependent error for WSR-88D rainfall estimates. J. Hydrometeor. 2001, 2, 490–504. [Google Scholar] [CrossRef]
- Tilford, K.A.; Cluckie, I.D.; Griffith, R.J.; Lane, A. Vertical reflectivity characteristics and bright band correction. In Radar Hydrology for Real Time Flood Forecasting, Proceedings of an Advanced Study Course; Griffith, R.J., Cluckie, I.D., Austin, G.L., Han, D., Eds.; EUR-OP: Luxembourg, 2001; pp. 47–65. [Google Scholar]
- Gray, W.R.; Uddstrom, M.J.; Larsen, H.R. Radar surface rainfall estimates using a typical shape function approach to correct for the variations in the vertical profile of reflectivity. Int. J. Remote Sens. 2002, 23, 2489–2504. [Google Scholar] [CrossRef]
- Gourley, J.J.; Calvert, C.M. Automated detection of the bright band using WSR-88D data. Weather Forecast. 2003, 18, 585–598. [Google Scholar] [CrossRef]
- Rico-Ramirez, M.A.; Cluckie, I.D. Bright-band detection from radar vertical reflectivity profiles. Int. J. Remote Sens. 2007, 28, 4013–4025. [Google Scholar] [CrossRef]
- Zhang, J.; Langston, C.; Howard, K. Bright band identification based on vertical profiles of reflectivity from the WSR-88D. J. Atmos. Ocean. Technol. 2008, 25, 1859–1872. [Google Scholar] [CrossRef]
- Klaassen, W. Radar observations and simulations of the melting layer of precipitation. J. Atmos. Sci. 1988, 45, 3741–3753. [Google Scholar] [CrossRef]
- White, A.B.; Gottas, D.J.; Strem, E.T.; Ralph, F.M.; Neiman, P.J. An automated bright band height detection algorithm for use with Doppler radar spectral moments. J. Atmos. Ocean. Technol. 2002, 19, 687–697. [Google Scholar] [CrossRef]
- Ryzhkov, A.; Zrnić, D. Discrimination between rain and snow with a polarimetric radar. J. Appl. Meteor. 1998, 37, 1228–1440. [Google Scholar] [CrossRef]
- Brandes, E.; Ikeda, K. Freezing-level estimation with polarimetric radar. J. Appl. Meteorol. 2004, 43, 1541–1553. [Google Scholar] [CrossRef]
- Tabary, P.; Henaff, A.; Vulpiani, G.; Parent-du-Chatelet, J.; Gourley, J. Melting layer characterization and identification with a C-band dual-polarization radar: A long term analysis. In Proceedings of the Fourth European Conference on Radar in Meteorology and Hydrology (ERAD 2006), Barcelona, Spain, 18–22 September 2006; Servei Meteorològic de Catalunya: Barcelona, Spain, 2006; pp. 17–20. [Google Scholar]
- Giangrande, S.E.; Krause, J.M.; Ryzhkov, A.V. Automated designation of the melting layer with a polarimetric prototype of the WSR-88D radar. J. Appl. Meteor. Climatol. 2008, 47, 1354–1364. [Google Scholar] [CrossRef]
- Islam, T.; Rico-Ramirez, M.A.; Han, D.W.; Bray, M.; Srivastava, P.K. Fuzzy logic based melting layer recognition from 3 GHz dual polarization radar: Appraisal with NWP model and radio sounding observations. Theor. Appl. Climatol. 2013, 112, 317–338. [Google Scholar] [CrossRef]
- Boodoo, S.; Hudak, D.; Donaldson, N.; Leduc, M. Application of dual-polarization radar melting-layer detection algorithm. J. Appl. Meteorol. Climatol. 2010, 49, 1779–1793. [Google Scholar] [CrossRef]
- Illingworth, A.; Thompson, R. Radar bright band correction using the linear depolarisation ratio. In Proceedings of the Eighth International Symposium on Weather Radar and Hydrology, Exeter, UK, 18–21 April 2011; IAHS Publication: Wallingford, UK, 2011; Volume 351, pp. 64–68. [Google Scholar]
- Zawadzki, I.; Szyrmer, W.; Bell, C.; Fabry, F. Modeling of the melting layer. Part III: The density effect. J. Atmos. Sci. 2005, 62, 3705–3723. [Google Scholar] [CrossRef]
- Wolfensberger, D.; Scipion, D.; Berne, A. Detection and characterization of the melting layer based on polarimetric radar scans. Q. J. R. Meteorol. Soc. 2015, 142, 108–124. [Google Scholar] [CrossRef]
- Kumjian, M.R.; Ryzhkov, A.V.; Reeves, H.D.; Schuur, T.J. A dual polarization radar signature of hydrometeor refreezing in winter storms. J. Appl. Meteor. Climatol. 2013, 52, 2549–2566. [Google Scholar] [CrossRef]
- Kumjian, M.R.; Lombardo, K.A. Insights into the evolving microphysical and kinematic structure of northeastern U.S. winter storms from dual-polarization Dopper radar. Mon. Weather Rev. 2017, 145, 1033–1061. [Google Scholar] [CrossRef]
- Ryzhkov, A.V.; Zhang, P.; Reeves, H.D.; Kumjian, M.R.; Tschallener, T.; Trömel, S.; Simmer, C. Quasi-vertical profiles—A new way to look at polarimetric radar data. J. Atmos. Ocean. Technol. 2016, 33, 551–562. [Google Scholar] [CrossRef]
- Kim, H.L.; Jung, S.H.; Jang, K.I. Estimating rain microphysical characteristics using S-band dual-polarization radar in South Korea. J. Atmos. Ocean. Technol. 2020, 33, 551–562. [Google Scholar] [CrossRef]
- Trömel, S.; Ryzhkov, A.V.; Hickman, B.; Muhlbauer, K.; Simmer, C. Polarimetric radar variables in the layers of melting and dendritic growth at X band—Implications for a nowcasting strategy in stratiform rain. J. Appl. Meteorol. Climatol. 2019, 58, 2497–2522. [Google Scholar] [CrossRef]
- Griffin, E.M.; Schuur, T.J.; Ryzhkov, A.V. A polarization radar analysis of ice microphysical processes in melting layers of winter storms using S-band qusai-vertical profiles. J. Appl. Meteorol. Climatol. 2020, 59, 751–767. [Google Scholar] [CrossRef]
- Lee, J.-E.; Jung, S.-H.; Kim, J.-S.; Jang, K. Sensitivity analysis of polarimetric observations by two different pulse lengths of dual-polarization weather radar. Atmosphere 2019, 29, 192–211, (In Korean with English abstract). [Google Scholar]
- Kim, M.; Lee, K.; Lee, Y.H. Visibility Data Assimilation and Prediction Using an Observation Network in South Korea. Pure Appl. Geophys. 2019, 177, 1125–1141. [Google Scholar] [CrossRef]
- Lee, G.W.; Zawadzki, I. Radar calibration by gate, disdrometer, and polarimetry: Theoretical limit caused by the variability of drop size distribution and application to fast scanning operational radar data. J. Hydrol. 2006, 328, 83–97. [Google Scholar] [CrossRef]
- Kwon, S.; Lee, G.W.; Kim, G. Rainfall estimation from an operational S-band dual-polarization radar: Effect of radar calibration. J. Meteor. Soc. Jpn. 2015, 93, 65–79. [Google Scholar] [CrossRef]
- Ryzhkov, A.; Zrnić, D. Radar Polarimetry for Weather Observations; Springer: Cham, Switzerland, 2019; p. 486. [Google Scholar]
- Durden, S.L.; Kitiyakara, A.; Eastwood, I.; Tanner, A.B.; Haddad, Z.S.; Li, F.K.; Wilson, W.J. ARMAR observations of the melting layer during TOGA COARE. IEEE Trans. Geosci. Remote Sens. 1997, 35, 1453–1456. [Google Scholar] [CrossRef]
- Khanal, A.K.; Delrieu, G.; Cazenave, F.; Boudevillain, B. Radar Remote Sensing of Precipitation in High Mountains: Detection and Characterization of Melting layer in the Grenoble Valley, French Alps. Atmosphere 2019, 10, 784. [Google Scholar] [CrossRef]



| Radar | Elevation Angle (°) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| GDK | −0.40 | 0.01 | 0.31 | 0.80 | 1.41 | 2.50 | 4.20 | 7.11 | 15.01 |
| BRI | 0.10 | 0.42 | 0.81 | 1.41 | 2.20 | 3.41 | 5.10 | 7.61 | 15.01 |
| KWK | −0.19 | 0.00 | 0.30 | 0.81 | 1.50 | 2.60 | 4.40 | 7.30 | 15.01 |
| MYN | −0.80 | −0.39 | 0.01 | 0.41 | 0.91 | 1.91 | 3.60 | 7.00 | 15.01 |
| KSN | 0.00 | 0.30 | 0.70 | 1.30 | 2.10 | 3.21 | 5.00 | 7.61 | 15.01 |
| PSN | −0.09 | 0.20 | 0.60 | 1.10 | 1.81 | 3.00 | 4.71 | 7.40 | 15.01 |
| JNI | −0.09 | 0.20 | 0.60 | 1.10 | 1.81 | 3.00 | 4.71 | 7.42 | 15.02 |
| SSP | 0.20 | 0.50 | 1.01 | 1.60 | 2.41 | 3.50 | 5.20 | 7.60 | 15.00 |
| GSN | 0.20 | 0.50 | 1.01 | 1.60 | 2.41 | 3.50 | 5.20 | 7.60 | 15.01 |
| Feature Parameters | Definition |
|---|---|
| H(ZH Top) | Height of identified by QVP of ZH |
| H(ZH Peak) | Height of identified by QVP of ZH |
| H(ZH Bottom) | Height of identified by QVP of ZH |
| H(ZDR Top) | Height of identified by QVP of ZDR |
| H(ZDR Peak) | Height of identified by QVP of ZDR |
| H(ZDR Bottom) | Height of identified by QVP of ZDR |
| H(ρHV Top) | Height of identified by QVP of ρHV |
| H(ρHV Peak) | Height of identified by QVP of ρHV |
| H(ρHV Bottom) | Height of identified by QVP of ρHV |
| H( = 0 °C) | Height where is 0° |
| H( = 0 °C) | Height where is 0° |
| H( = 0 °C) | Height where is 0° |
| ZH Top | ZH value at H(ZH Top) |
| ZH Peak | ZH value at H(ZH Peak) (i.e., Maximum ZH in BB) |
| ZH Bottom | ZH value at H(ZH Bottom) |
| ZDR Top | ZDR value at H(ZDR Top) |
| ZDR Peak | ZDR value at H(ZDR Peak) (i.e., Maximum ZDR in BB) |
| ZDR Bottom | ZDR value at H(ZDR Bottom) |
| ρHV Top | ρHV value at H(ρHV Top) |
| ρHV Peak | ρHV value at H(ρHV Peak) (i.e., Minimum ρHV in BB) |
| ρHV Bottom | ρHV value at H(ρHV Bottom) |
| Radar | MAR | APR | MAY | JUN | JUL | AUG | SEP | OCT | NOV |
|---|---|---|---|---|---|---|---|---|---|
| GDK | 2.58 | 1.79 | - | 3.54 | 4.56 | 4.83 | 4.35 | 3.45 | 2.44 |
| BRI | 1.96 | 1.85 | 4.20 | 3.57 | 4.37 | 4.15 | 4.36 | 2.59 | 1.80 |
| KWK | 2.53 | 2.24 | - | 4.12 | 4.46 | 4.74 | 4.29 | 3.71 | 2.25 |
| MYN | 3.10 | 2.99 | 3.21 | 4.54 | 4.75 | 4.77 | 4.29 | 3.35 | 3.14 |
| KSN | 2.17 | 3.33 | 3.35 | 4.55 | 4.86 | 5.00 | 4.44 | 4.09 | 2.87 |
| PSN | 2.28 | 2.81 | 3.58 | 4.36 | 4.81 | 4.85 | 4.55 | 3.70 | - |
| JNI | 2.73 | 2.94 | 3.94 | 4.39 | 4.58 | 4.68 | 4.51 | 4.25 | 3.15 |
| SSP | 1.83 | 3.59 | 4.04 | 4.11 | 4.81 | 4.70 | 4.52 | 3.92 | 2.68 |
| GSN | 1.93 | 3.20 | 4.09 | 4.06 | 4.84 | 4.66 | 4.61 | 4.14 | 2.68 |
| Mean | 2.35 | 2.75 | 3.77 | 4.14 | 4.67 | 4.71 | 4.43 | 3.69 | 2.62 |
| at H(ZH Bottom/Peak/Top) | at H(ZH Bottom/Peak/Top) | at H(ZH Bottom/Peak/Top) | |||||||
| MEAN | 2.41 | 0.73 | −1.33 | 0.64 | −0.89 | −2.90 | 1.53 | −0.04 | −2.03 |
| STD | 1.55 | 1.32 | 1.39 | 3.34 | 3.24 | 3.36 | 1.71 | 1.52 | 1.58 |
| at H(ZDR Bottom/Peak/Top) | at H(ZDR Bottom/Peak/Top) | at H(ZDR Bottom/Peak/Top) | |||||||
| MEAN | 2.71 | 1.04 | −1.96 | 0.92 | −0.61 | −2.63 | 1.82 | 0.25 | −1.76 |
| STD | 1.63 | 1.47 | 1.42 | 3.39 | 3.31 | 3.38 | 1.79 | 1.65 | 1.60 |
| at H(ρHV Bottom/Peak/Top) | at H(ρHV Bottom/Peak/Top) | at H(ρHV Bottom/Peak/Top) | |||||||
| MEAN | 2.84 | 1.16 | −1.03 | 1.03 | −0.49 | −2.60 | 1.93 | 0.37 | −1.73 |
| STD | 1.65 | 1.44 | 1.51 | 3.39 | 3.28 | 3.40 | 1.79 | 1.60 | 1.69 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.-E.; Jung, S.-H.; Kwon, S. Characteristics of the Bright Band Based on Quasi-Vertical Profiles of Polarimetric Observations from an S-Band Weather Radar Network. Remote Sens. 2020, 12, 4061. https://doi.org/10.3390/rs12244061
Lee J-E, Jung S-H, Kwon S. Characteristics of the Bright Band Based on Quasi-Vertical Profiles of Polarimetric Observations from an S-Band Weather Radar Network. Remote Sensing. 2020; 12(24):4061. https://doi.org/10.3390/rs12244061
Chicago/Turabian StyleLee, Jeong-Eun, Sung-Hwa Jung, and Soohyun Kwon. 2020. "Characteristics of the Bright Band Based on Quasi-Vertical Profiles of Polarimetric Observations from an S-Band Weather Radar Network" Remote Sensing 12, no. 24: 4061. https://doi.org/10.3390/rs12244061
APA StyleLee, J.-E., Jung, S.-H., & Kwon, S. (2020). Characteristics of the Bright Band Based on Quasi-Vertical Profiles of Polarimetric Observations from an S-Band Weather Radar Network. Remote Sensing, 12(24), 4061. https://doi.org/10.3390/rs12244061




