1. Introduction
Night light remote sensing, as an active branch of remote sensing [
1], can obtain the information of visible light and near infrared electromagnetic wave emitted from the ground surface on cloudless nights [
2] It can reflect the urban night lighting and capture the night lighting of fishing boats [
3], natural gas combustion [
4], and forest fire light [
5]. It intuitively reflects the human activities and social development rules [
6] and is widely applied in the estimation of socioeconomic parameters such as GDP [
7], population density [
8], electric power consumption (EPC) [
9], greenhouse gas emissions [
10] and poverty index [
11]; urban expansion [
12] and urbanization research [
13]; major events assessment such as energy crisis [
14], earthquake [
15] and war [
16]; environmental effect analysis of urban expansion [
17]; light pollution [
18] and effect analysis [
19]. Consequently, it has become the main data source for monitoring human socioeconomic activities and natural phenomena.
The Defense Meteorological Satellite Program’s Operational Linescan System (DMSP/OLS) and Soumi National Polar-Orbiting Partnership Visible Infrared Imaging Radiometer Suite (NPP/VIIRS) are the most widely used to obtain the nighttime light data. In this research, it provides nighttime light (NTL) data from 1992 to 2013 and 2012 to 2018, which are named as DMSP/OLS and NPP/VIIRS, respectively.
The Operational Linescan System is one of the principal sensors on the DMSP satellite platform. The radiation value detected by OLS sensors at night is four orders of magnitude lower than that of other sensors [
20]. Due to the superior performance of OLS sensors, the NTL data is often used for exploring human activities. However, DMSP/OLS data also has a series of shortcomings [
21]. Light saturation in the city center, blooming effect, and lack of airborne calibration are the major obstacles to the application of DMSP/OLS data. The light saturation phenomenon is caused by the low 6-bit radiation resolution of OLS sensor. The pixel value of DMSP/OLS data ranges from 0 to 63. When the radiation brightness of a light source in the city center exceeds to the detection upper limit (10
−8 W/ (cm
2*sr*um)), the DN values of DMSP/OLS data are all forced to be 63 [
22]. Therefore, it is impossible to distinguish the spatial difference of actual lighting intensity in the urban central area where the lighting intensity exceeds the detection limit [
23]. Furthermore, the correlation between the detected NTL and economic activity is reduced, which increases errors in the established model [
24,
25], and limits the application of NTL data [
26]. At the same time, DMSP/OLS dataset is made up of NTL data collected by different satellite sensors in different years. In the absence of airborne calibration [
4], the night stable light data was affected by the difference of sensors, the difference of satellite cross time, and the influence of the sensor performance degradation [
27]. Therefore, the data cannot be directly compared [
28]. In addition, the illumination area is overestimated due to the reflection of urban light to urban edge and internal water body, and then increases the error of distribution estimation [
29].
In order to improve the accuracy of nighttime light data in representing social and economic activities, many studies have attempted to solve the problems in DMSP/OLS data. Aiming at the saturation problem of DMSP/OLS data, scholars have proposed a series of methods to correct the saturation. The correction method is mainly divided into only using the NTL data and using other satellite data to correct the NTL data. There are three calibration methods that only use the NTL data: (1) radiation calibration desaturation method. This method is used to adjust the sensor gain to make it lower than the typical work settings and obtain the nighttime light change in the city center [
30]. The limited nighttime light data obtained can be combined with the nighttime light data obtained under the high gain setting to generate the unsaturated nighttime light data [
23]. Although this method can effectively reduce the saturation effect of NTL data, it is labor intensive and cost intensive. Therefore, calibration data only can be obtained with a limited number of years (1996, 1999, 2000, 2002, 2004, 2006, and 2010). (2) Desaturation method based on frequency distribution of the DN value of light pixels [
31]. This method is based on the assumption that the variation trend of the DN value of night light in saturated regions which is consistent with that in unsaturated regions, the number of pixels in saturated regions can be predicted by establishing a linear correction model of the number of pixels in unsaturated regions and the DN value [
32]. Letu et al. used the cubic regression model to construct the DN value frequency of light pixels to correct the saturation problem of light images on the basis of the linear correction model [
33]. This method is a desaturation method on the regional scale which is not suitable for the pixel scale. (3) The desaturation method based on the invariant target area. This method realizes the saturation correction of the NTL image by determining the corresponding relationship between DN value in the invariant target area of the stable image and Radiance Calibrated Nighttime Lights (RCNTL). Letu et al. realized the correction of the light data of the saturated region in the year of 1999 by constructing a regression model of the nighttime light data of the unsaturated region of the target region in 1999 and the nighttime light data of the radiometric calibration image in 1996–1997 [
24]. Wu et al. used the NTL data of RCNTL in 2006 to achieve the correction of DMSP/OLS saturated images by defining Mauritius, Puerto Rico, and Okinawa as invariant target areas [
34]. This correction method can reduce the saturation of the pixel to a certain extent, but the saturated pixel is corrected to the same DN value through the regression model, which means that the corrected pixels lack spatial difference and cannot reflect the real nighttime light data. At the same time, saturation correction will lead to distortion of unsaturated pixels in suburban and rural areas of underdeveloped areas [
35]. There are also three calibration methods that use other satellite data to correct the NTL data: (1) correction of nighttime light data based on vegetation index. Vegetation adjusted normalized urban index (VANUI) [
36,
37] was proposed by combining normalized difference vegetation index (NDVI) with DMSP/OLS data based on the principle that urban characteristics (including nighttime light) should be inversely proportional to vegetation coverage [
38]. Enhanced vegetation index adjusted nighttime light index (EANTLI) [
39,
40] was proposed combined with the advantages of enhanced vegetation index (EVI) [
41] to make it impossible for VANUI to effectively highlight the difference of nighttime light intensity in saturated areas under the rapid urbanization process in China and other countries. EVI data is the vegetation index obtained by the calculation of infrared band, near-infrared band, and blue light band [
42] in remote sensing data. It is an important numerical expression method for monitoring the growth information of surface vegetation, which can effectively describe the growth and biomass information of green plants. However, at present, this method is mostly used to correct DMSP/OLS images of specific years, and rarely to correct long time series DMSP/OLS datasets. Moreover, rare studies have been conducted on the consistency correction of DMSP/OLS data based on EVI correction and NPP/VIIRS data. (2) NTL data was corrected based on surface temperature and vegetation index spatial distribution difference of vegetation was a natural factor and the influence of human factors on the evolution of urban internal structure. LST and EVI Regulated NTL City Index (LERNCI) based on EVI, land surface temperature (LST), and nighttime light data was proposed [
43]. LERNCI based on the double correction of LST and EVI can better improve the spatial difference caused by single index correction. (3) Other data to correct the NTL data: GDP data can effectively reflect the urban development vitality. Therefore, a linear model between the GDP grid data of corresponding time and the NTL data of unsaturated areas is constructed, and the NTL data of saturated areas can be calculated by the model to eliminate the saturation phenomenon [
44].
In view of the lack of airborne calibration, the invariant region method was used to realize intercalibration of DMSP/OLS data [
45]. Assuming that there are relatively unchangeable pixels in the multi time nighttime light image, and building calibration model of invariant pixels in different images, the calibration model is used to correct the corresponding night light image to get comparable night light images. Elvidge et al. [
4] assumed that the NTL data of Sicily in Italy remained basically unchanged from 1994 to 2008. Based on the baseline image in F121999, the regression model of other images from 1994 to 2008 was constructed to achieve intercalibration. Liu et al. [
46] used the second order regression model to realize intercalibration of Chinese DMSP/OLS data from 1992 to 2008 by taking Jixi city of Heilongjiang province as the invariant target area. The above two intercalibration methods solve the problem of incomparability of DMSP/OLS data, but do not effectively correct the saturation problem in the image. How to effectively solve the problem of data saturation in DMSP/OLS data while solving the problem of data incomparability in DMSP/OLS data is still a hot research topic.
With the attenuation and failure of DMSP/OLS, NPP/VIIRS data became the new generation of NTL data [
47]. As NPP/VIIRS data with higher spatial and radiating quality than DMSP/OLS data [
48], it addresses the shortcomings existing in DMSP/OLS data (saturation of city center light data and lack of airborne calibration), but the published NPP/VIIRS monthly composites is a preliminary product which has not been filtered to screen out lights from aurora, fires, boats, and other temporal lights. To solve this problem, Li et al. [
26] proposed to extract the corresponding pixel in NPP/VIIRS data as the stable pixel in NPP/VIIRS data by using the bright pixel in DMSP/OLS data of 2010. Wu et al. [
49] used the bright pixel of an annual composite of 2015 to extract the corresponding pixel in the NPP/VIIRS data from 2015 to 2017 as the stable pixel in the NPP/VIIRS data of respective years. Although the above methods can remove some unstable pixels in the NPP/VIIRS data, the first method to extract the NPP/VIIRS data from 2012 to 2018 will cause more information to be lost in later years due to the rapid urbanization process in China. The second method can better retain the information in NPP/VIIRS data, but some information will be lost from 2016 to 2018.
Moreover, combination of DMSP/OLS data and NPP/VIIRS data to study continuity over long time series has great advantages and prospects in the significant application of NTL data in socioeconomic activity studies. However, the inconsistency between NPP/VIIRS data and DMSP/OLS data is more serious than that between the different products of the DMSP/OLS data [
50]. Xu et al. [
51] achieved the evaluation of urban land expansion in China from 1992 to 2015 by comparing DMSP/OLS data from 1992 to 2013 and NPP/VIIRS data in 2015, but failed to achieve the fitting of the two data. Li et al. [
50] fitted NPP/VIIRS monthly composite product and DMSP/OLS monthly composite product by power function and gaussian low-pass filter, but the data set used was not accessible to the public. Researchers [
22,
52] constructed the regression model between stable image and RCNTL to realize the correction of DMSP/OLS data, and realized the fitting between the two data by establishing the regression relationship between the total nighttime light of DMSP/OLS data and NPP/VIIRS data on the county scale in 2012 and 2013. However, there are still defects in the process of correcting DMSP/OLS data and NPP/VIIRS data, which reduces the correlation between NTL data and socioeconomic indicators.
Scholars have done a lot of research on the processing of DMSP/OLS data and NPP/VIIRS data, but there are still some limitations in the existing research results: (1) in the saturation correction of DMSP/OLS data, the existing research did not distinguish the spatial differences of the saturated pixels and carried out the saturation correction of the unsaturated pixels, thus failed to effectively correct the saturation of the DMSP/OLS data. (2) When processing the NPP/VIIRS annual image data, the existing research usually mistakenly classified some stable pixels as unstable pixels and lost some effective information. (3) When fitting DMSP/OLS data and NPP/VIIRS data, some scholars used the same fitting function to fit the data of 31 provinces, without considering the data differences of each province, thus reducing the ability of night light data to represent economic data.
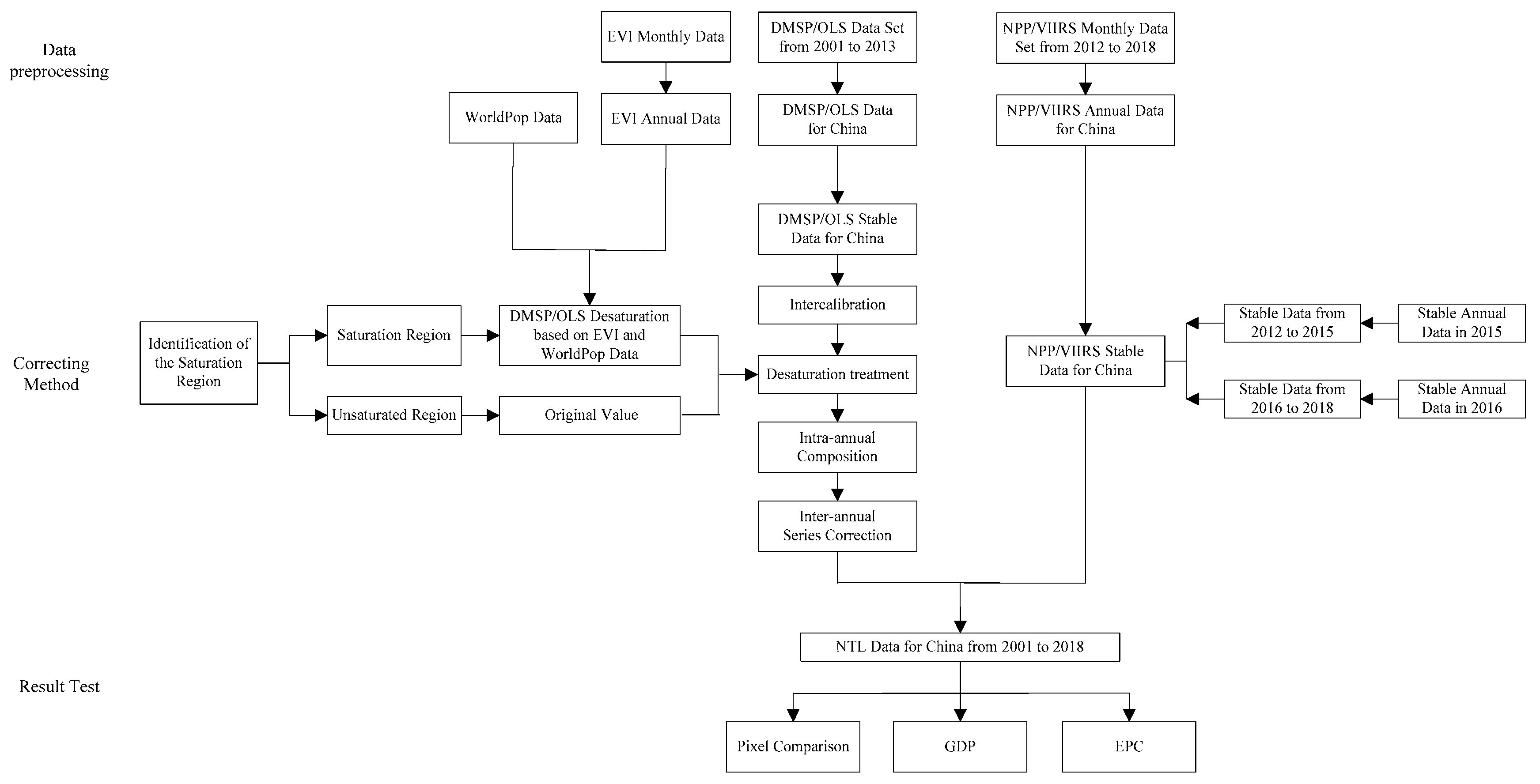
Aiming at the problems in the current research, this paper proposes a correction method of nighttime light data using EVI and WorldPop data based on the principle that urban characteristics (including nighttime light) should be inversely proportional to vegetation coverage [
38] and directly proportional to population distribution data [
53,
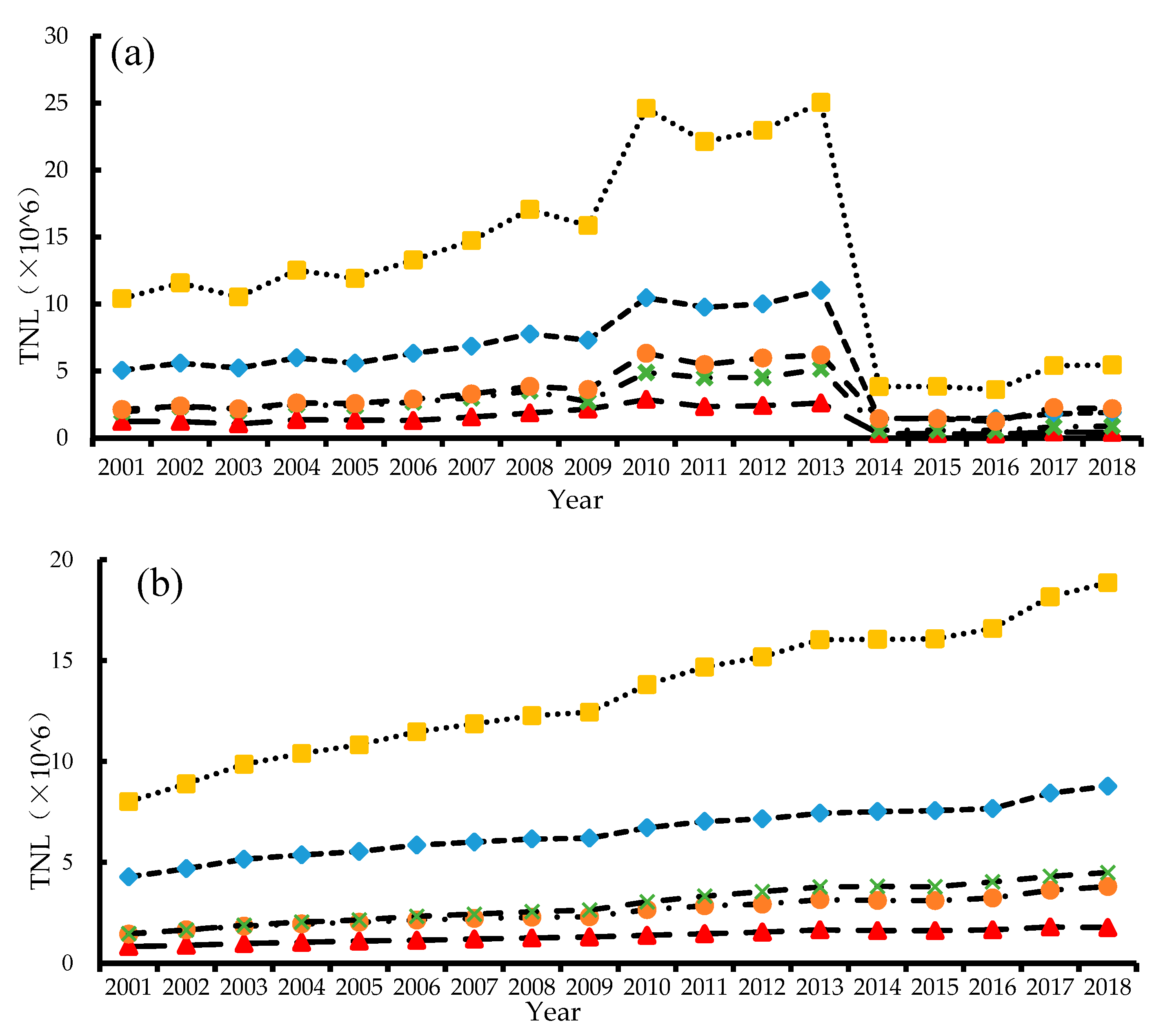
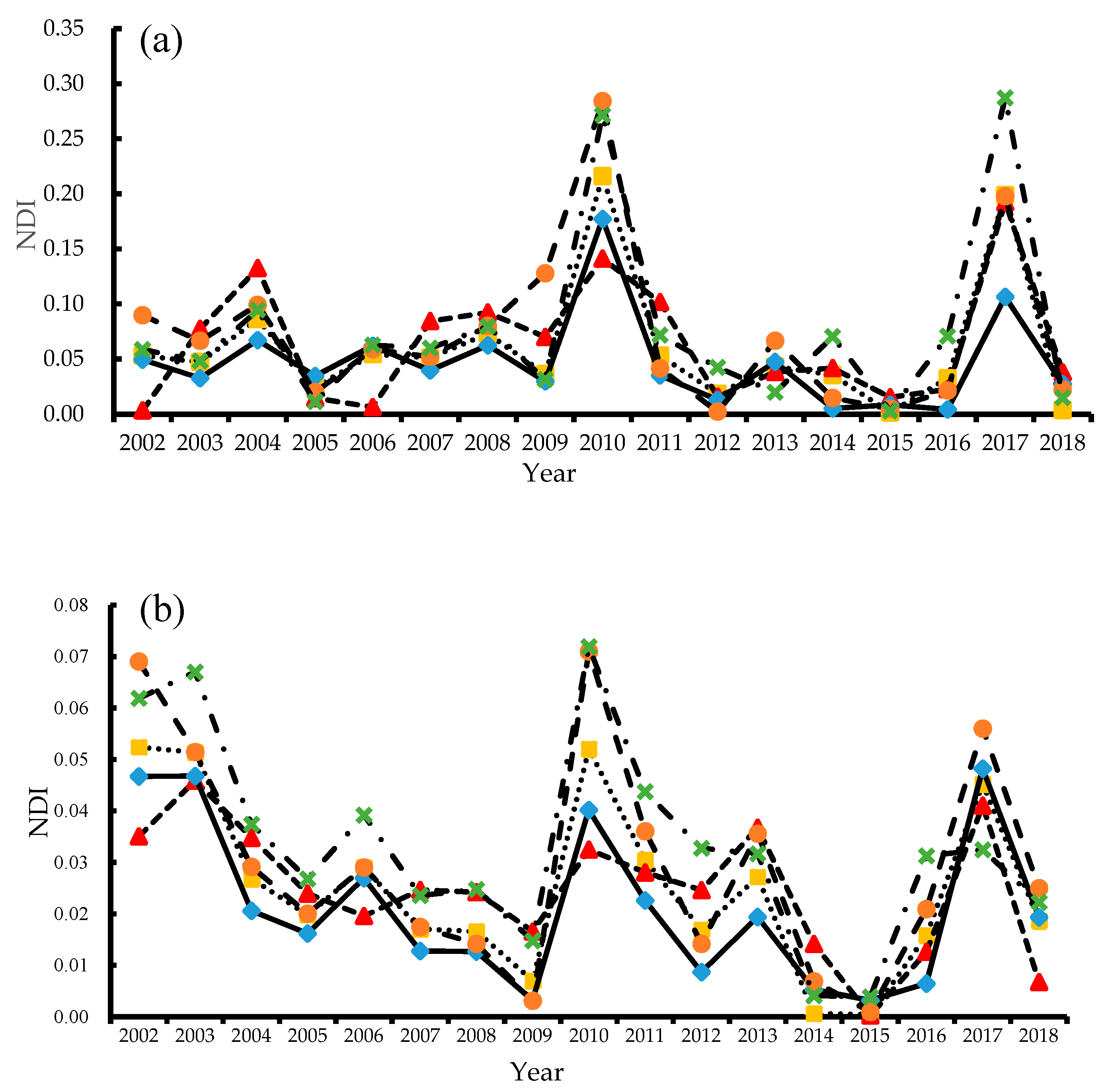
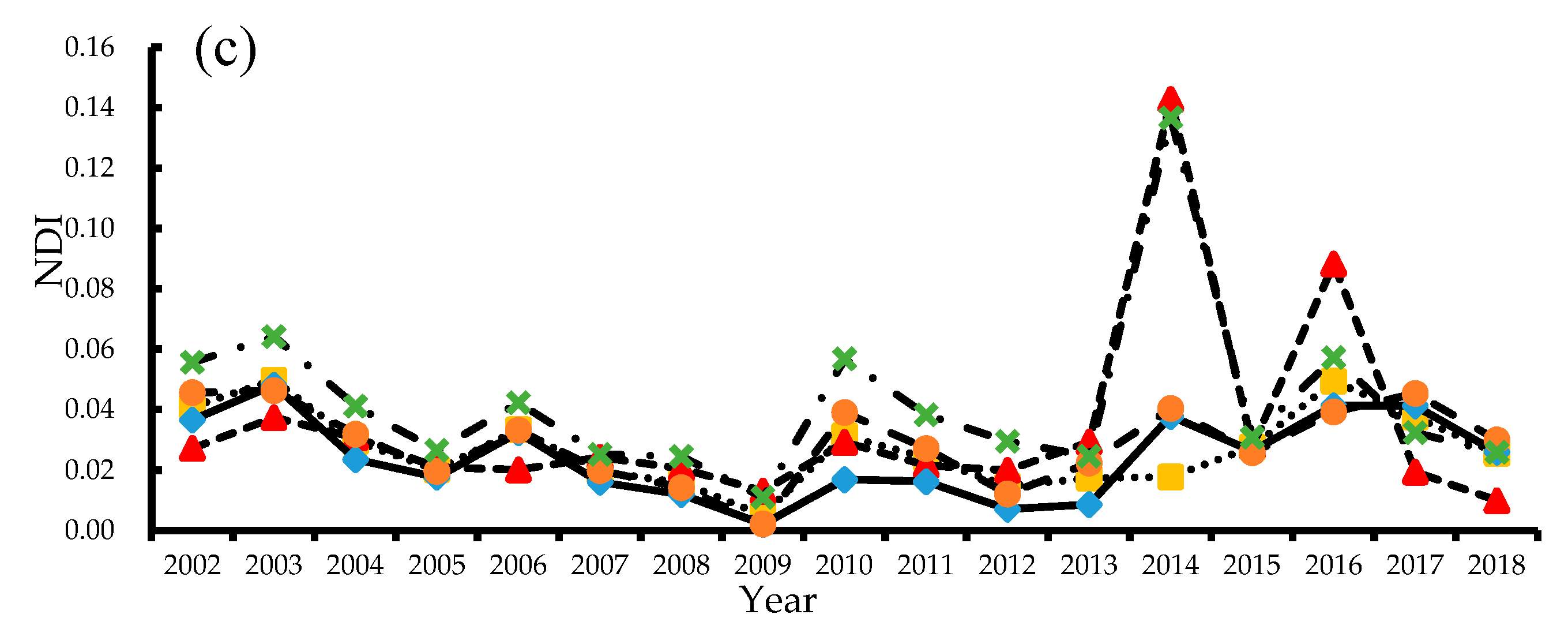
54], so as to obtain the nighttime light dataset from 2001 to 2018 to represent economic data reliably and accurately. On the basis of related research, the invariant region method is used to realize the intercalibration of the DMSP/OLS data from 2001 to 2013. The annual EVI and WorldPop data from 2001 to 2013 is used to realize the saturation correction of DMSP/OLS data. The corrected unsaturated DMSP/OLS data from 2001 to 2013 is obtained. The corrected DMSP/OLS data and NPP/VIIRS data are fitted by using a regression model to obtain the regional scale DMSP/OLS data from 2001 to 2018. The validity of the correction method is evaluated by constructing indexes such as total nighttime light (TNL), normalized difference index (NDI), and the sum of normalized difference index (SNDI). The correlation between NTL data and GDP or EPC and the relative error of the estimation model are calculated.
2. Study Area and Data
A total of 30 provinces were chosen as the study areas in mainland of China due to the lack of economic statistics from Hong Kong, Macau, Taiwan, and Tibet. For regional comparison, the study area was divided into four regions (Northeast, East, Central and West). These regions, in addition to their geographical location, are a broad reflection of overall differences in socioeconomic development.
Eight types of data were used in this study, including DMSP/OLS data, NPP/VIIRS data, EVI data, WorldPop data, gas combustion area mask, county level administrative boundary vector map, river and lake data, and socioeconomic statistics.
DMSP/OLS night lighting data set from 2001 to 2013 was collected from the website (
https://eogdata.mines.edu/dmsp/downloadV4composites.html) of Paynes Institute for Public Policy, Colorado School of Mines. There are three annual average data types in the dataset which are cloud-free coverage, average visible light, and stable light. Among the three types of data, the stable light data contains light from cities, towns, and other locations with continuous lighting, while fires, volcanoes, background noise, and other transient events are discarded [
27]. The 20 images were captured by four different DMSP satellites, F14 (2001–2003), F15 (2001–2007), F16 (2004–2009), and F18 (2010–2013). In this paper, the radiometric calibration product of F162010 (
https://eogdata.mines.edu/dmsp/download_radcal.html) was used to compare the influence of calibration method on the saturation effect of nighttime lighting data.
NPP/VIIRS data from 2012 to 2018 was also collected from the website of Paynes Institute for Public Policy, Colorado School of Mines (
https://eogdata.mines.edu/download_dnb_composites.html). The images used for this study were monthly VIIRS DNB composite from 2012 to 2018 and two annual composites of 2015 and 2016. However, the NPP/VIIRS monthly composite was not filtered to eliminate light detection associated with gas flares, fires, volcanoes or auroras, and the data set was not processed to eliminate background noise. Temporary lighting and background noise were eliminated in the annual composite image.
EVI data is the EVI monthly composite of the moderate resolution imaging spectroradiometer (MODIS). The data set was provided by Geospatial Data Cloud site, Computer Network Information Center, Chinese Academy of Sciences. (
http://www.gscloud.cn).
The WorldPop dataset was developed by the WorldPop Project (
https://www.worldpop.org). The dataset provides annual gridded population data from the 2000–2020 period, with a spatial resolution of 100 m. The input variables of WorldPop include the most recent official census population data and a wide range of spatial ancillary datasets. The spatial datasets include settlement locations and extents, nighttime satellite images, land cover, roads, building maps, health facility locations, vegetation, topography, and refugee camps. A random forest regression tree-based mapping approach was used to generate a predictive weighting layer to reallocate population counts into gridded pixels [
55]. The WorldPop dataset has two products, one is the number of people per hectare, the other is the number of people per grid, and the latter dataset was used in this paper.
Gas burning zones are generated due to insufficient infrastructure in the oil producing areas to make full use of natural gas. The data of the gas burning area used in this paper can be downloaded from the website of Paynes Institute for Public Policy, Colorado School of Mines (
https://eogdata.mines.edu/download_global_flare.html).
Vector maps of China’s county-level administrative boundaries and rivers and lakes data were obtained from 1:400 million database in the National Fundamental Geographic Information System. All nighttime lighting data were extracted according to China’s administrative boundary.
The socioeconomic statistics from 2002 to 2019 were provided by the China statistical yearbook which was published by China National Bureau of statistics (
http://www.stats.gov.cn/tjsj/ndsj/). These include two attributes for reference: gross domestic product (GDP) and electric power consumption (EPC). The unit of the GDP is billion RMB, and the unit of EPC is billion·kilowatt·h
−1.
Agriculture is an important part of social and economic activities, especially in a traditional agricultural country like China. However, most of the agricultural production is located in the darker area of the nighttime light image, so the nighttime light data cannot represent the agricultural part of economic activities [
56]. Therefore, it is necessary to remove the contribution of agricultural sector to economic activities when using nighttime data to predict GDP. The GDP data in the following paragraphs are all subtracting the data of the agricultural sector.
5. Discussion
DMSP/OLS data and NPP/VIIRS data are the most widely used to obtain the nighttime light data for monitoring human socioeconomic activities and natural phenomena [
6]. Light saturation in the city center, blooming effect, and lack of airborne calibration are the major obstacles to the application of DMSP/OLS data. In addition, when building a long time series of nighttime light datasets, the inconsistency between NPP/VIIRS data and DMSP/OLS data is more serious than that between the different products of the DMSP/OLS data [
50]. Although, scholars have done a lot of research on the processing of DMSP/OLS Data and NPP/VIIRS data, but there are still some limitations in the existing research results.
Aiming at the problems in the current research, this paper proposes the WorldPop and the enhanced vegetation index adjusted nighttime light (WEANTL) using EVI and WorldPop data based on the principle that urban characteristics (including nighttime light) should be inversely proportional to vegetation coverage [
38] and directly proportional to population distribution data [
53,
54], so as to obtain the nighttime light dataset from 2001 to 2018 to represent economic data reliably and accurately. The result shows that the extended nighttime light data set has good quality and reliable time consistency. Considering that the use of nighttime light data to reflect social and economic development is carried out by constructing the statistical relationship between TNL and socioeconomic parameters [
7,
9,
35,
74,
75], this paper also evaluates the accuracy of the correction method proposed in this paper in predicting socioeconomic parameters by constructing a regression model between TNL and socioeconomic parameters.
In the saturation correction of DMSP/OLS data, the existing research did not distinguish the spatial differences of the saturated pixels and carried out the saturation correction of the unsaturated pixels, thus failed to effectively correct the saturation of the DMSP/OLS data. When fitting DMSP/OLS data and NPP/VIIRS data, some scholars used the same fitting function to fit the data of 30 provinces, without considering the data differences of each province, thus reducing the ability of night light data to represent economic data. Compared with the previous models [
63,
77], it can effectively distinguish the spatial differences of the nighttime light data because EVI and WorldPop data was used to realize the saturation correction of DMSP/OLS data.
In this paper, when fitting DMSP/OLS data and NPP/VIIRS data, considering the differences of economic development of each province, linear regression models were developed for each province. It can be seen from the above paper, the TNL-GDP model and TNL-EPC model of 30 provinces obtained in this paper all passed the F-test at the level of 0.001, while the TNL-GDP model and TNL-EPC model of 28 provinces besides Tianjin and Shandong obtained under the reference correction method passed the F-test at the level of 0.001. Tianjin and Shandong failed to pass the F-test mainly because when fitting DMSP/OLS and NPP/VIIRS data, the model was fitted on all county-level scales in China in 2012 and 2013. NPP/VIIRS data from 2014 to 2018 were fitted to DMSP/OLS data according to the fitting model, which can ensure that the DMSP/OLS data in later years after fitting on a national scale is almost larger than that in previous years. However, there is no guarantee that DMSP/OLS data in later years after fitting of all the provincial units in the provincial scale is greater than the DMSP/OLS data in previous years. For example, the DMSP/OLS data of Beijing in 2014 or 2015 after fitting is less than that in 2013, leading to the R2 values of the TNL-GDP model and TNL-EPC model being below the average. The DMSP/OLS data of Tianjin and Shandong after fitting from 2014 to 2018 is all less than that in 2013. As a result, the established regression model could not pass the F test at the 0.001 level. Therefore, it is necessary to establish the fitting equation between the DMSP/OLS and NPP/VIIRS data in 2012 and 2013 for the specific research area when studying the research area on and below the provincial scale.
Compared with the existing research, the main contributions of this paper are as follows: (1) DMSP/OLS image is divided into saturation and unsaturated regions, WEANTL was put forward to correct the image data in the saturation region by using EVI and WorldPop data of the corresponding year, and pixel points in the unsaturated region kept the original value. Therefore, the saturation correction of DMSP/OLS image data from 2001 to 2013 is realized by using EVI and WorldPop data. (2) The unstable pixels in 2012–2015 and 2015–2018 NPP/VIIRS annual images are removed by the annual night light images of NPP/VIIRS in 2015 and 2016, respectively, which retain more effective information than previous studies. (3) The total nighttime lights on the county scale of 30 provinces is calculated. The regression model carried out the regression analysis on the total nighttime lights of DMSP/OLS data and NPP/VIIRS data in 2012 and 2013, respectively. Compared with previous studies, it can better fit and correct night light data and economic data on a provincial scale.
As a correction method for fitting DMSP/OLS data and NPP/VIIRS data to obtain a long time series of nighttime light data sets for continuous monitoring of society, this method has made some contributions, but there are still some limitations. Firstly, although the prediction accuracy of the proposed correction method in establishing long-term GDP and EPC dynamic models is better than that of the reference correction method, the saturation problem in the DMSP/OLS data and the noise data in NPP/VIIRS data are not removed completely. These problems reduce the accuracy of long time series nighttime light datasets and the prediction accuracy of establishing long-term GDP and EPC dynamic models. Secondly, considering that regression models (quadratic polynomial model and power function model) have been applied in this paper to model socioeconomic activities using nighttime light data, more complex models need to be developed to predict socioeconomic activities more accurately. Therefore, with the updating of NPP/VIIRS data and more sources of nighttime light data, such as luojia1-01 satellite, new methods for multisensor nighttime light data to model social and economic dynamic situations can be developed in future research.