Weakly Supervised Change Detection Based on Edge Mapping and SDAE Network in High-Resolution Remote Sensing Images
Abstract
1. Introduction
1.1. Background and Motivation
1.2. Proposed Method
1.3. Key Contributions
- Aiming at high-resolution remote sensing images, a novel weakly supervised change detection framework based on edge mapping and SDAE is proposed, which can extract both the obvious and subtle change information efficiently.
- A pre-classification algorithm based on the difference of the edge maps of the image pair is designed to obtain prior knowledge. Besides, a selection rule is defined and employed to select as high-quality label data as possible for the latter classification stage.
- SDAE-based deep neural networks are designed to establish a classification model with strong robustness and generalization capability, which reduces noises and extracts the features of difference of image pair. The classification model facilitates the identification of complex regions with subtle changes and improves the accuracy of the final change detection result.
- The experimental results of three datasets prove the high efficiency of our method, in which accuracy and Kappa coefficient increase to 91.18% and by 27.19% on average in the first two datasets compared with the IR-MAD, PCA-k-means, CaffeNet, USFA, and DSFA methods [15,25,26,27,28] (The code implementation of the proposed method has been published on the website https://github.com/ChenAnRn/EM-DL-Remote-sensing-images-change-detection).
2. Related Work
3. Problem Formulation
3.1. Problem Definition
3.2. Problem Decomposition
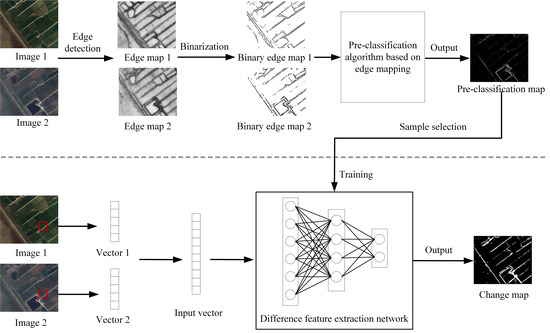
4. Methodology
4.1. Change Detection Framework
4.2. Pre-Classification Based on Edge Mapping
4.2.1. Image Edge Detection
4.2.2. Image Edge Binarization
4.2.3. Pre-Classification Algorithm Based on Edge Mapping
| Algorithm 1 Pre-classification based on Edge Mapping |
| Input:, , , and |
Output: and
|
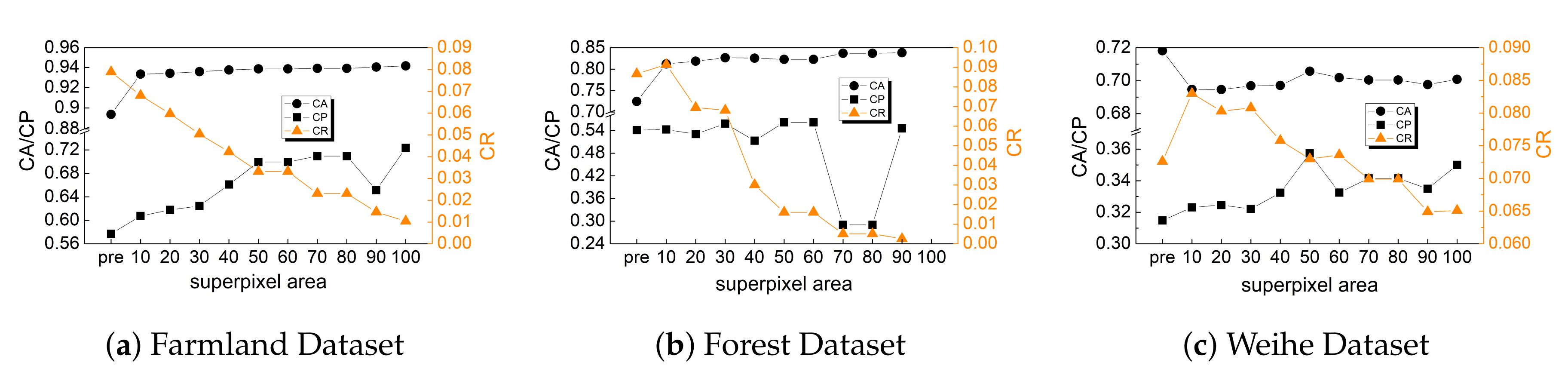
4.2.4. Sample Selection
4.3. Classification Based on Difference Extraction Network
5. Experimental Studies
5.1. Experimental Setup
5.2. Pre-Classification Evaluation
5.3. Classification Evaluation
5.3.1. Experimental Settings
5.3.2. Results of the Farmland Dataset
5.3.3. Results of the Forest Dataset
5.3.4. Results of the Weihe Dataset
5.3.5. Influence of Pre-Training on Change Detection
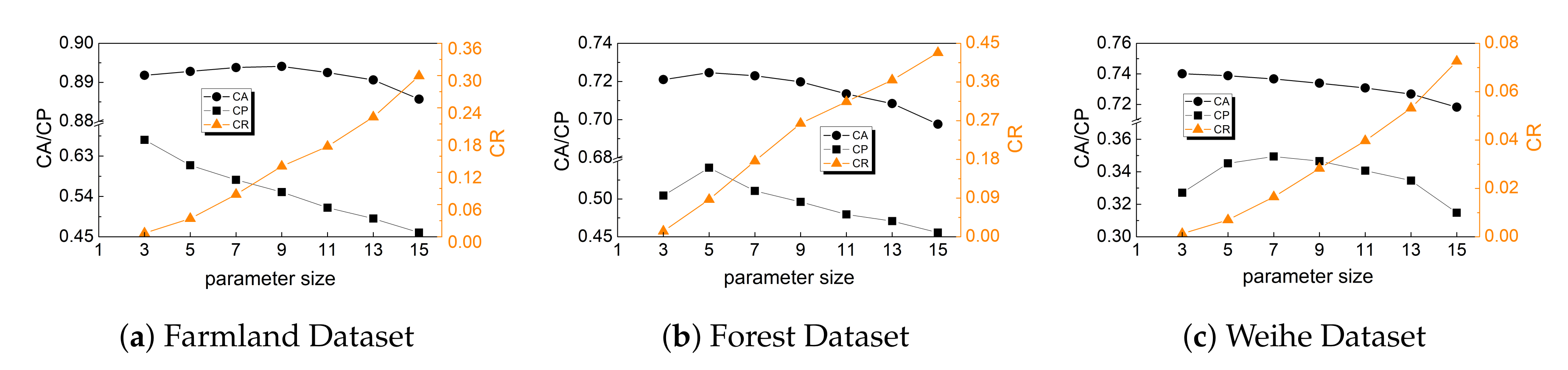
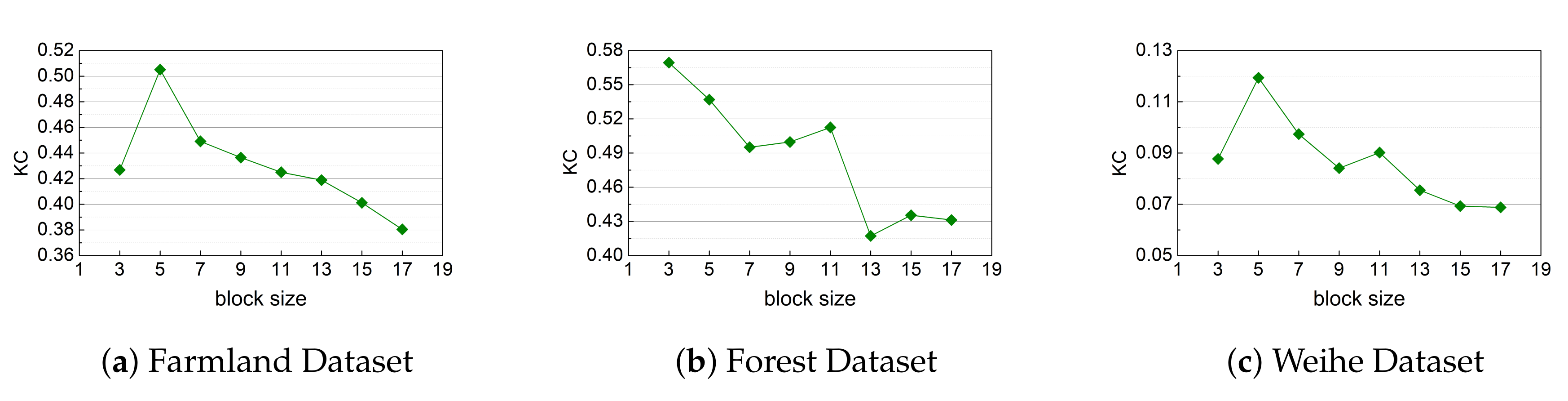
5.3.6. Size of The Pixel Block
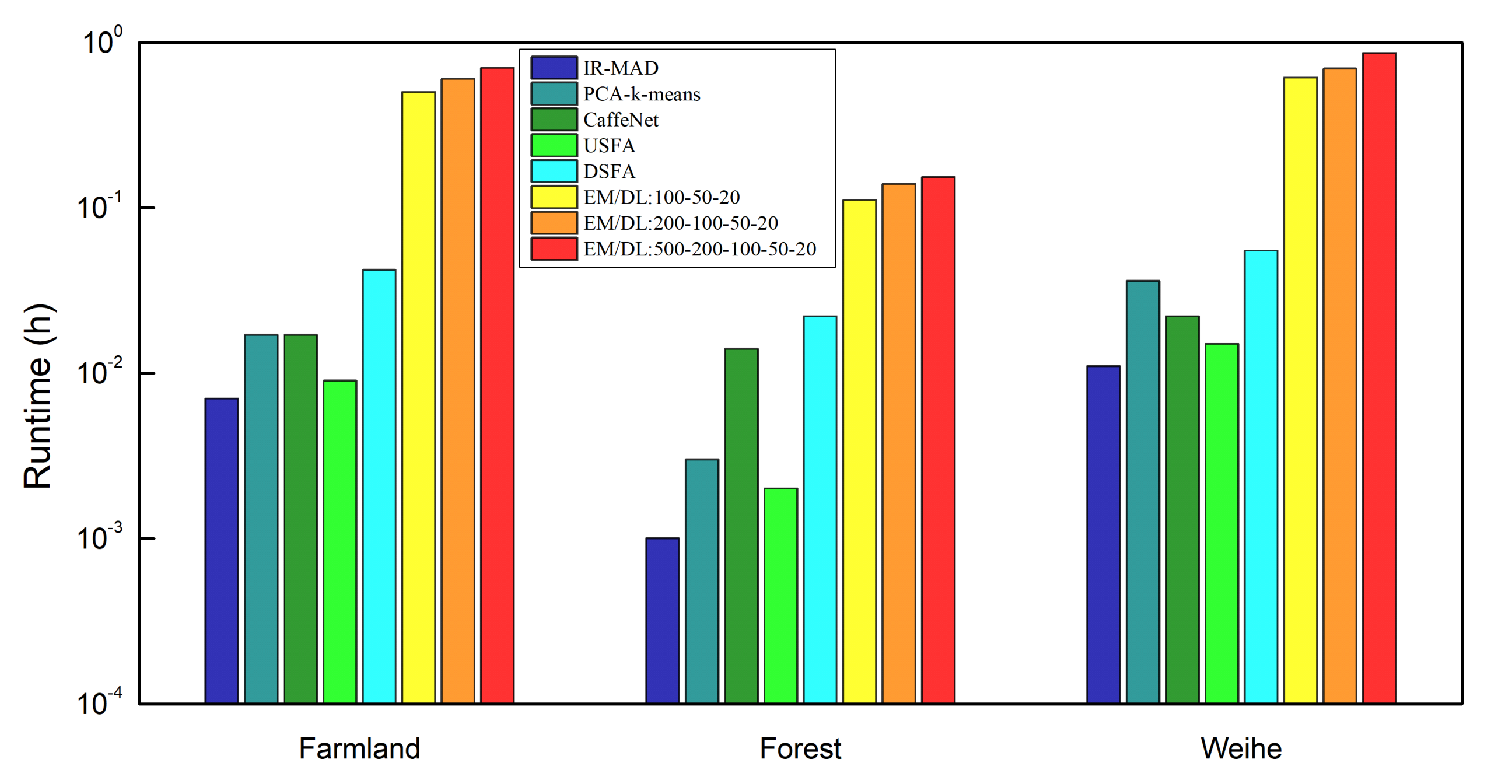
5.4. Runtime Analysis
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Amici, V.; Marcantonio, M.; La Porta, N.; Rocchini, D. A multi-temporal approach in MaxEnt modelling: A new frontier for land use/land cover change detection. Ecol. Inform. 2017, 40, 40–49. [Google Scholar] [CrossRef]
- Zadbagher, E.; Becek, K.; Berberoglu, S. Modeling land use/land cover change using remote sensing and geographic information systems: Case study of the Seyhan Basin, Turkey. Environ. Monit. Assess. 2018, 190, 494–508. [Google Scholar] [CrossRef] [PubMed]
- Gargees, R.S.; Scott, G.J. Deep Feature Clustering for Remote Sensing Imagery Land Cover Analysis. IEEE Geosci. Remote Sens. Lett. 2019. [Google Scholar] [CrossRef]
- Feizizadeh, B.; Blaschke, T.; Tiede, D.; Moghaddam, M.H.R. Evaluating fuzzy operators of an object-based image analysis for detecting landslides and their changes. Geomorphology 2017, 293, 240–254. [Google Scholar] [CrossRef]
- De Alwis Pitts, D.A.; So, E. Enhanced change detection index for disaster response, recovery assessment and monitoring of accessibility and open spaces (camp sites). Int. J. Appl. Earth Obs. Geoinf. 2017, 57, 49–60. [Google Scholar] [CrossRef]
- Hao, Y.; Sun, G.; Zhang, A.; Huang, H.; Rong, J.; Ma, P.; Rong, X. 3-D Gabor Convolutional Neural Network for Damage Mapping from Post-earthquake High Resolution Images. In International Conference on Brain Inspired Cognitive Systems; Springer: Berlin/Heidelberg, Germany, 2018; pp. 139–148. [Google Scholar]
- Gong, M.; Zhao, J.; Liu, J.; Miao, Q.; Jiao, L. Change detection in synthetic aperture radar images based on deep neural networks. IEEE Trans. Neural Networks Learn. Syst. 2015, 27, 125–138. [Google Scholar] [CrossRef]
- Zhuang, H.; Deng, K.; Fan, H.; Yu, M. Strategies combining spectral angle mapper and change vector analysis to unsupervised change detection in multispectral images. IEEE Geosci. Remote Sens. Lett. 2016, 13, 681–685. [Google Scholar] [CrossRef]
- Asokan, A.; Anitha, J. Change detection techniques for remote sensing applications: A survey. Earth Sci. Inform. 2019, 12, 143–160. [Google Scholar] [CrossRef]
- Feng, W.; Sui, H.; Tu, J.; Huang, W.; Xu, C.; Sun, K. A novel change detection approach for multi-temporal high-resolution remote sensing images based on rotation forest and coarse-to-fine uncertainty analyses. Remote Sens. 2018, 10, 1015. [Google Scholar] [CrossRef]
- Volpi, M.; Tuia, D.; Bovolo, F.; Kanevski, M.; Bruzzone, L. Supervised change detection in VHR images using contextual information and support vector machines. Int. J. Appl. Earth Obs. Geoinf. 2013, 20, 77–85. [Google Scholar] [CrossRef]
- Mai, D.S.; Ngo, L.T. Semi-supervised fuzzy C-means clustering for change detection from multispectral satellite image. In Proceedings of the 2015 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), Istanbul, Turkey, 2–5 August 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1–8. [Google Scholar]
- Malila, W.A. Change Vector Analysis: An Approach for Detecting Forest Changes with Landsat; Institute of Electrical and Electronics Engineers: West Lafayette, IN, USA, 1980. [Google Scholar]
- Nielsen, A.A.; Conradsen, K.; Simpson, J.J. Multivariate Alteration Detection (MAD) and MAF Postprocessing in Multispectral, Bitemporal Image Data: New Approaches to Change Detection Studies. Remote Sens. Environ. 1998, 64, 1–19. [Google Scholar] [CrossRef]
- Celik, T. Unsupervised change detection in satellite images using principal component analysis and k-means clustering. IEEE Geosci. Remote Sens. Lett. 2009, 6, 772–776. [Google Scholar] [CrossRef]
- Wang, Q.; Yuan, Z.; Du, Q.; Li, X. GETNET: A general end-to-end 2-D CNN framework for hyperspectral image change detection. IEEE Trans. Geosci. Remote Sens. 2018, 57, 3–13. [Google Scholar] [CrossRef]
- Song, A.; Choi, J.; Han, Y.; Kim, Y. Change Detection in Hyperspectral Images Using Recurrent 3D Fully Convolutional Networks. Remote Sens. 2018, 10, 1827. [Google Scholar] [CrossRef]
- Xiang, M.; Li, C.; Zhao, Y.; Hu, B. Review on the new technologies to improve the resolution of spatial optical remote sensor. In International Symposium on Advanced Optical Manufacturing and Testing Technologies: Large Mirrors and Telescopes; International Society for Optics and Photonics: San Diego, CA, USA, 2019; Volume 10837, p. 108370C. [Google Scholar]
- Yu, H.; Yang, W.; Hua, G.; Ru, H.; Huang, P. Change detection using high resolution remote sensing images based on active learning and Markov random fields. Remote Sens. 2017, 9, 1233. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, X.; Chen, G.; Dai, F.; Gong, Y.; Zhu, K. Change detection based on Faster R-CNN for high-resolution remote sensing images. Remote Sens. Lett. 2018, 9, 923–932. [Google Scholar] [CrossRef]
- Lim, K.; Jin, D.; Kim, C.S. Change Detection in High Resolution Satellite Images Using an Ensemble of Convolutional Neural Networks. In Proceedings of the 2018 Asia-Pacific Signal and Information Processing Association Annual Summit and Conference (APSIPA ASC), Honolulu, HI, USA, 12–15 November 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 509–515. [Google Scholar]
- Xv, J.; Zhang, B.; Guo, H.; Lu, J.; Lin, Y. Combining iterative slow feature analysis and deep feature learning for change detection in high-resolution remote sensing images. J. Appl. Remote Sens. 2019, 13, 024506. [Google Scholar]
- Tan, K.; Jin, X.; Plaza, A.; Wang, X.; Xiao, L.; Du, P. Automatic change detection in high-resolution remote sensing images by using a multiple classifier system and spectral–spatial features. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 3439–3451. [Google Scholar] [CrossRef]
- Cao, G.; Zhou, L.; Li, Y. A new change-detection method in high-resolution remote sensing images based on a conditional random field model. Int. J. Remote Sens. 2016, 37, 1173–1189. [Google Scholar] [CrossRef]
- El Amin, A.M.; Liu, Q.; Wang, Y. Convolutional neural network features based change detection in satellite images. In First International Workshop on Pattern Recognition; International Society for Optics and Photonics: Tokyo, Japan, 2016; Volume 10011, p. 100110W. [Google Scholar]
- Du, B.; Ru, L.; Wu, C.; Zhang, L. Unsupervised Deep Slow Feature Analysis for Change Detection in Multi-Temporal Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9976–9992. [Google Scholar] [CrossRef]
- Nielsen, A.A. The regularized iteratively reweighted MAD method for change detection in multi-and hyperspectral data. IEEE Trans. Image Process. 2007, 16, 463–478. [Google Scholar] [CrossRef] [PubMed]
- Wu, C.; Du, B.; Zhang, L. Slow Feature Analysis for Change Detection in Multispectral Imagery. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2858–2874. [Google Scholar] [CrossRef]
- Awrangjeb, M. Effective Generation and Update of a Building Map Database Through Automatic Building Change Detection from LiDAR Point Cloud Data. Remote Sens. 2015, 7, 14119–14150. [Google Scholar] [CrossRef]
- Guo, J.; Zhou, H.; Zhu, C. Cascaded classification of high resolution remote sensing images using multiple contexts. Inf. Sci. 2013, 221, 84–97. [Google Scholar] [CrossRef]
- Long, T.; Liang, Z.; Liu, Q. Advanced technology of high-resolution radar: Target detection, tracking, imaging, and recognition. Sci. China Inf. Sci. 2019, 62, 40301. [Google Scholar] [CrossRef]
- Lv, Z.; Liu, T.; Wan, Y.; Benediktsson, J.A.; Zhang, X. Post-processing approach for refining raw land cover change detection of very high-resolution remote sensing images. Remote Sens. 2018, 10, 472. [Google Scholar] [CrossRef]
- Guo, Q.; Zhang, J. Change Detection for High Resolution Remote Sensing Image Based on Co-saliency Strategy. In 2019 10th International Workshop on the Analysis of Multitemporal Remote Sensing Images (MultiTemp); IEEE: Piscataway, NJ, USA, 2019; pp. 1–4. [Google Scholar]
- Saha, S.; Bovolo, F.; Bruzzone, L. Unsupervised Deep Change Vector Analysis for Multiple-Change Detection in VHR Images. IEEE Trans. Geosci. Remote Sens. 2019, 57, 3677–3693. [Google Scholar] [CrossRef]
- Lv, Z.Y.; Liu, T.F.; Zhang, P.; Benediktsson, J.A.; Lei, T.; Zhang, X. Novel adaptive histogram trend similarity approach for land cover change detection by using bitemporal very-high-resolution remote sensing images. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9554–9574. [Google Scholar] [CrossRef]
- Peng, D.; Zhang, Y.; Guan, H. End-to-End Change Detection for High Resolution Satellite Images Using Improved UNet++. Remote Sens. 2019, 11, 1382. [Google Scholar] [CrossRef]
- Hou, B.; Wang, Y.; Liu, Q. A saliency guided semi-supervised building change detection method for high resolution remote sensing images. Sensors 2016, 16, 1377. [Google Scholar] [CrossRef]
- Zhang, P.; Gong, M.; Su, L.; Liu, J.; Li, Z. Change detection based on deep feature representation and mapping transformation for multi-spatial-resolution remote sensing images. ISPRS J. Photogramm. Remote Sens. 2016, 116, 24–41. [Google Scholar] [CrossRef]
- Gong, M.; Niu, X.; Zhang, P.; Li, Z. Generative Adversarial Networks for Change Detection in Multispectral Imagery. IEEE Geoence Remote Sens. Lett. 2017, 14, 2310–2314. [Google Scholar] [CrossRef]
- Lei, Y.; Liu, X.; Shi, J.; Lei, C.; Wang, J. Multiscale superpixel segmentation with deep features for change detection. IEEE Access 2019, 7, 36600–36616. [Google Scholar] [CrossRef]
- Li, X.; Yuan, Z.; Wang, Q. Unsupervised Deep Noise Modeling for Hyperspectral Image Change Detection. Remote Sens. 2019, 11, 258. [Google Scholar] [CrossRef]
- Liu, Y.; Cheng, M.M.; Hu, X.; Wang, K.; Bai, X. Richer convolutional features for edge detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 3000–3009. [Google Scholar]
- Xie, S.; Tu, Z. Holistically-nested edge detection. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 1395–1403. [Google Scholar]
- Xu, J.; Jia, Y.; Shi, Z.; Pang, K. An improved anisotropic diffusion filter with semi-adaptive threshold for edge preservation. Signal Process. 2016, 119, 80–91. [Google Scholar] [CrossRef]
- Achanta, R.; Shaji, A.; Smith, K.; Lucchi, A.; Fua, P.; Süsstrunk, S. SLIC superpixels compared to state-of-the-art superpixel methods. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 2274–2282. [Google Scholar] [CrossRef]
- Gong, M.; Zhan, T.; Zhang, P.; Miao, Q. Superpixel-based difference representation learning for change detection in multispectral remote sensing images. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2658–2673. [Google Scholar] [CrossRef]
- Bengio, Y.; Lamblin, P.; Popovici, D.; Larochelle, H. Greedy layer-wise training of deep networks. In Advances in Neural Information Processing Systems; MIT Press: Vancouver, BC, Canada, 2007; pp. 153–160. [Google Scholar]
- Vincent, P.; Larochelle, H.; Bengio, Y.; Manzagol, P.A. Extracting and composing robust features with denoising autoencoders. In Proceedings of the 25th International Conference on Machine Learning, Helsinki, Finland, 5–9 July 2008; ACM: New York, NY, USA, 2008; pp. 1096–1103. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Available online: http://www.rivermap.cn/index.html (accessed on 23 November 2020).
- Available online: https://www.harrisgeospatial.com/Software-Technology/ENVI/ENVICapabilities/OneButton (accessed on 23 November 2020).
- Available online: https://github.com/wkentaro/labelme (accessed on 23 November 2020).














| Datasets description | Dataset | Size | Spatial resolution | Region | ||||||
| Farmland Dataset | 0.3 m | 2009 | 2013 | Huaxi Village, Chongming District, Shanghai, China | ||||||
| Forest Dataset | 0.3 m | 2011 | 2015 | Wenzhou City, Zhejiang Province, China | ||||||
| Weihe Dataset | 0.3 m | 2014 | 2017 | Tongguan County, Weinan City, China | ||||||
| Evaluation criteria | Criteria | Description | ||||||||
| FA | The proportion of pixels in the change map that are misjudged as changed | |||||||||
| MA | The proportion of pixels in the change map that are actually change but are not detected | |||||||||
| OE | The overall error rate, which is the sum of FA and MA | |||||||||
| CA | The proportion of pixels in the change map that are classified correctly | |||||||||
| KC | The degree of similarity between the change map and the ground truth | |||||||||
| Comparison methods | IR-MAD [27] | The iteratively reweighted multivariate alteration detection method for change detection | ||||||||
| PCA-k-means [15] | Unsupervised change detection method using principal component analysis and k-means clustering | |||||||||
| CaffeNet [25] | A novel deep Convolutional Neural Networks features based change detection method | |||||||||
| USFA [28] | Slow feature analysis algorithm based change detection method | |||||||||
| DSFA [26] | Unsupervised change detection method based on deep network and slow feature analysis theory | |||||||||
| Dataset | Before Sample Selection | After Sample Selection | ||||
|---|---|---|---|---|---|---|
| Farmland | Forest | Weihe | Farmland | Forest | Weihe | |
| Acuuracy | 0.8938 | 0.7246 | 0.7182 | 0.9385 | 0.8229 | 0.7057 |
| Precision | 0.5770 | 0.5412 | 0.3148 | 0.6994 | 0.5615 | 0.3573 |
| Positive sample number | - | - | - | 7077 | 894 | 111636 |
| Negative sample number | - | - | - | 2,374,299 | 174,379 | 2,971,483 |
| Different Methods | FA | MA | OE | CA | KC |
|---|---|---|---|---|---|
| IR-MAD | 0.1194 | 0.0667 | 0.1861 | 0.8139 | 0.2068 |
| PCA-k-means | 0.0006 | 0.0959 | 0.0965 | 0.9035 | 0.1506 |
| CaffeNet | 0.0506 | 0.0565 | 0.1070 | 0.8930 | 0.3227 |
| USFA | 0.3975 | 0.0585 | 0.4560 | 0.5440 | 0.0062 |
| DSFA | 0.0909 | 0.0491 | 0.1400 | 0.8600 | 0.3813 |
| EM-SDAE:100-50-20/with dropout | 0.0410 | 0.0509 | 0.0919 | 0.9081 | 0.5054 |
| EM-SDAE:200-100-50-20/with dropout | 0.0345 | 0.0537 | 0.0882 | 0.9118 | 0.5059 |
| EM-SDAE:500-200-100-50-20/with dropout | 0.0342 | 0.0547 | 0.0889 | 0.9111 | 0.4991 |
| EM-SDAE:100-50-20/no dropout | 0.0531 | 0.0504 | 0.1035 | 0.8965 | 0.4708 |
| EM-SDAE:200-100-50-20/no dropout | 0.0360 | 0.0595 | 0.0955 | 0.9045 | 0.4546 |
| EM-SDAE:500-200-100-50-20/no dropout | 0.0376 | 0.0563 | 0.0939 | 0.9061 | 0.4750 |
| Different Methods | FA | MA | OE | CA | KC |
|---|---|---|---|---|---|
| IR-MAD | 0.2712 | 0.1498 | 0.4210 | 0.5790 | 0.0768 |
| PCA-k-means | 0.0181 | 0.1590 | 0.1771 | 0.8229 | 0.4792 |
| CaffeNet | 0.0670 | 0.2057 | 0.2728 | 0.7272 | 0.1823 |
| USFA | 0.3316 | 0.0759 | 0.4075 | 0.5925 | 0.2092 |
| DSFA | 0.1003 | 0.1325 | 0.2327 | 0.7673 | 0.4413 |
| EM-SDAE:100-50-20/with dropout | 0.0668 | 0.0790 | 0.1458 | 0.8542 | 0.6326 |
| EM-SDAE:200-100-50-20/with dropout | 0.0387 | 0.1050 | 0.1437 | 0.8563 | 0.6148 |
| EM-SDAE:500-200-100-50-20/with dropout | 0.0436 | 0.0869 | 0.1305 | 0.8695 | 0.6594 |
| EM-SDAE:100-50-20/no dropout | 0.1680 | 0.0651 | 0.2331 | 0.7669 | 0.4794 |
| EM-SDAE:200-100-50-20/no dropout | 0.1199 | 0.0617 | 0.1816 | 0.8184 | 0.5759 |
| EM-SDAE:500-200-100-50-20/no dropout | 0.1093 | 0.0615 | 0.1708 | 0.8292 | 0.5967 |
| Different Methods | FA | MA | OE | CA | KC |
|---|---|---|---|---|---|
| IR-MAD | 0.0002 | 0.2586 | 0.2585 | 0.7415 | 0.0083 |
| PCA-k-means | 0.0160 | 0.2084 | 0.2245 | 0.7758 | 0.2314 |
| CaffeNet | 0.0060 | 0.2391 | 0.2451 | 0.7549 | 0.0189 |
| USFA | 0.2693 | 0.0259 | 0.2952 | 0.7048 | 0.4112 |
| DSFA | 0.1238 | 0.1980 | 0.3218 | 0.6782 | 0.0770 |
| EM-SDAE:100-50-20/with dropout | 0.1726 | 0.1685 | 0.3410 | 0.6590 | 0.1173 |
| EM-SDAE:200-100-50-20/with dropout | 0.1621 | 0.1750 | 0.3370 | 0.6630 | 0.1088 |
| EM-SDAE:500-200-100-50-20/with dropout | 0.1777 | 0.1696 | 0.3473 | 0.6527 | 0.1056 |
| EM-SDAE:100-50-20/no dropout | 0.2343 | 0.1550 | 0.3894 | 0.6106 | 0.0785 |
| EM-SDAE:200-100-50-20/no dropout | 0.1884 | 0.1687 | 0.3571 | 0.6429 | 0.0933 |
| EM-SDAE:500-200-100-50-20/no dropout | 0.2233 | 0.1604 | 0.3838 | 0.6162 | 0.0745 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, N.; Chen, C.; Shi, W.; Zhang, J.; Ma, J. Weakly Supervised Change Detection Based on Edge Mapping and SDAE Network in High-Resolution Remote Sensing Images. Remote Sens. 2020, 12, 3907. https://doi.org/10.3390/rs12233907
Lu N, Chen C, Shi W, Zhang J, Ma J. Weakly Supervised Change Detection Based on Edge Mapping and SDAE Network in High-Resolution Remote Sensing Images. Remote Sensing. 2020; 12(23):3907. https://doi.org/10.3390/rs12233907
Chicago/Turabian StyleLu, Ning, Can Chen, Wenbo Shi, Junwei Zhang, and Jianfeng Ma. 2020. "Weakly Supervised Change Detection Based on Edge Mapping and SDAE Network in High-Resolution Remote Sensing Images" Remote Sensing 12, no. 23: 3907. https://doi.org/10.3390/rs12233907
APA StyleLu, N., Chen, C., Shi, W., Zhang, J., & Ma, J. (2020). Weakly Supervised Change Detection Based on Edge Mapping and SDAE Network in High-Resolution Remote Sensing Images. Remote Sensing, 12(23), 3907. https://doi.org/10.3390/rs12233907