Abstract
Large infrastructures need continuous maintenance because of materials degradation due to atmospheric agents and their persistent use. This problem makes it imperative to carry out persistent monitoring of infrastructure health conditions in order to guarantee maximum safety at all times. The main issue of early warning infrastructure fault detection is that expensive in-situ distributed monitoring sensor networks have to be installed. On the contrary, the use of satellite data has made it possible to use immediate and low-cost techniques in recent years. In this regard, the potential of spaceborne Synthetic Aperture Radar for the monitoring of critical infrastructures is demonstrated in geographically extended areas, even in the presence of clouds, and in really tough weather. A complete procedure for damage early-warning detection is designed, by using micro-motion (m-m) estimation of critical sites, based on modal proprieties analysis. Particularly, m-m is processed to extract modal features such as natural frequencies and mode shapes generated by vibrations of large infrastructures. Several study cases are here considered and the “Morandi” Bridge (Polcevera Viaduct) in Genoa (Italy) is analyzed in depth highlighting abnormal vibration modes during the period before the bridge collapsed.
1. Introduction
Infrastructure monitoring can be an expensive and complex effort when deployed on a large scale. This is mainly due to the need of having a relatively large number of distributed/networked sensors able to extract displacement and/or vibration information. Structural Health Monitoring (SHM) is a procedure of intensive and persistent health assessment for a structure through an automated system, a key element of cost-effective strategies for maintenance. Generally, the used sensors are constituted by differential global positioning system (GPS) and/or piezoelectric vibration detectors [1].
We demonstrate that an alternative, and, less expensive and much more portable approach can be used through spaceborne synthetic aperture radar (SAR), thanks to its coherent nature capable to accurately measure several parameters [2,3,4,5]. The benefits of SAR for infrastructure monitoring have been already proved in [6,7,8,9] where Differential Interferometry (DInSAR) is applied, and, when the more complex Persistent Scatterers Interferometry (PS-InSAR) is used [10,11]. These techniques are able to estimate structure displacement with millimetric precision, along the acquisition time of long series of interferometric SAR observations, although these methods to be accurate need to preserve a good level of coherence in the images within the acquisition time frame [11]. Moreover, acquiring a long temporal series of interferometric SAR observations, as needed for infrastructure monitoring with the PS-InSAR technique, is not a trivial job and, in any case, a minimum number of observations is needed in order to have a reliable phase screen atmosphere estimation [12].
Even more, observing bridges with PS-InSAR is a difficult task because of their large vibrations, this issue is particularly critical when heavy traffic or strong winds are present [13,14]. All these issues might prejudice the operative SAR products’ employment in infrastructure monitoring. On the contrary, we show that measuring infrastructure vibration using a single SAR image, thus ensuring customers to immediately get the result, is possible through micro-motion (m-m) estimation based on modal proprieties analysis, as also recently shown for dam monitoring [15]. In this paper, we give evidence that this approach also well works for a more challenging situation than that represented by bridges (dams are very large infrastructures, which have very extended surfaces and the Doppler perturbations of the received electromagnetic bursts can be more easily detected). In the present work, we consider several examples and demonstrate that different observation geometries do not affect the effectiveness of the method when the selected cases are considered. And this also foresees well for the robustness of the method because of the recurring geometrical conditions inherent the SAR constellation missions that usually are conceived for the application at hand. Moreover, the technique itself does not require any atmospheric compensation, that is instead mandatory for multitemporal target displacement analysis, since a single image has to be considered in the proposed approach. The complete vibration profile of the infrastructure under analysis is extracted from the satellite SAR data highlighting the presence of any lesions, cracks or other damage (e.g., inaccuracies, singularities, or anomalous vibrations) (Each extended material body is a continuous of material, having the same physical characteristics for each part of it. When there is a crack, which is synonymous with lesion or fissure, or fracture, we mean an interruption in the continuity of the material as a result of tensional or deformation states that are not compatible with its mechanical characteristics.). As a consequence, we highlight the possibility of estimating early-warning cracks by evaluating any anomalies on the vibration maps, resulting in an efficient structural health monitoring and predictive maintenance.
Vibration estimation is a fundamental activity conducted through the modal analysis usually performed using in-situ sensors. Instead of measuring the displacement vector through a conventional measurement tool, the estimated phase shift from a single spaceborne SAR observation can be used. This is done after an appropriate signal processing procedure. Particularly, the vibrations of moving targets are detected by the radar and their positions in a SAR-image are shifted in azimuth and range-azimuth and a defocusing may occur (it is worth to notice that due to the layover all the oscillations in height are spread in the range and azimuth dimensions). This defocusing component can be estimated through a single pass SAR observation and it represent a precious information to be used in a modal analysis. For this reason, the proposed method would have a great impact in infrastructure monitoring and could potentially either replace or work together with the in-situ sensors network, providing additive/complementary infrastructure health data.
Summarizing, in this work, we investigate the main question: can spaceborne single pass SAR data be used to assess critical structural health conditions of Bridges? The purpose of the experimental analysis is to present an initial assessment, answering this question through the observation of various bridges. A complete survey of the “Morandi” bridge is also reported, in order to understand possible causes that led to its collapse. The results have been obtained by processing data observed by the COSMO-SkyMed (CSK) satellite constellation, in the context of the ”Mapitaly” mission. It is important to highlight that the proposed technique can be also applied to the freely distributed Sentinel-1 data ensuring a worldwide coverage.
2. Methodology
In this section the analytical formulation of the proposed micro-motion estimation technique is described. The SAR synthesizes the electromagnetic image through a ”side looking” acquisition, according to the observation geometry shown in Figure 1, where:
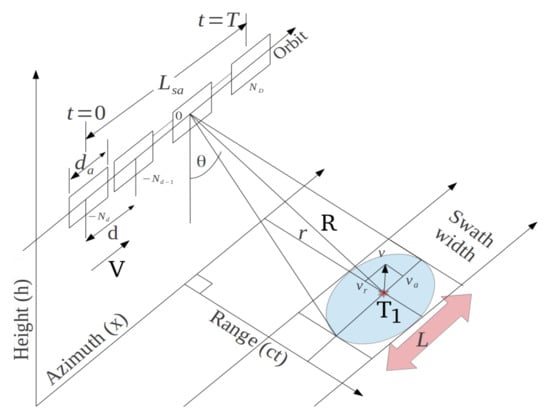
Figure 1.
SAR geometry.
- r is the zero-Doppler distance (constant);
- R is the slant-range;
- is the reference range at ;
- is the physical antenna aperture length;
- V is the platform velocity;
- d is the distance between two range acquisitions;
- is the total synthetic aperture length;
- t is the acquisition time variable;
- T is the observation duration;
- and are the start and stop time acquisition respectively;
- is the azimuth electromagnetic footprint width;
- is the incidence angle of the electromagnetic radiation pattern;
- V is the platform velocity.
All the above parameters are related to the stripmap SAR acquisition that is adopted in this work. The SAR data belonging to the electromagnetic image are formed through the focusing process that involves the application of a two-dimensional matched filter acting in the range direction and in the azimuth direction. The radar transmits the following complex signal
where with the SAR central frequency, is the pulse duration, and is the chirp rate.
The single look complex (SLC) signal resulting from compression is given by [16]:
Equation (2) represents the focused SAR signal generated by the back-scattered electromagnetic energy of a pointing target supposed to be stationary. The terms , and are the total chirp and Doppler bandwidths respectively. The total synthetic aperture is equal to and the azimuth resolution . In (2) the parameter identifies the position in range where the maximum of the sinc function is positioned, while in azimuth it is centered around ”zero”. In the case where the peak of the sinc function has a nozero coordinate along the azimuth dimension, Equation (2) can be recast as:
2.1. Doppler Sub-Apertures Model
The decomposition of the SAR data into Doppler sub apertures is formalized in this subsection, starting from the spectral representation of the focused SAR data. To this end, notice that the 2-dimensional DFT of (3) is given by:
From the last equation, it turns out that a single point stationary target has a two-dimensional rectangular nature with total length proportional to the range-azimuth bandwidths respectively. The term is due to the sinc function dislocation in range and azimuth. In the SAR, the movement of a point target with velocity in both range and azimuth direction is immediately warned by the focusing process, resulting in the following anomalies:
- anomalous azimuth displacement in the presents of target constant range velocity;
- azimuth smearing in the presence of target azimuth velocity or target range accelerations;
- range-walking phenomenon, visible as range defocusing, in the presence of target range speed, backscattered energy is detected over one or more range resolution cells.
In practical cases, the backscattered energy from moving targets is distributed over several range-azimuth resolution cells. As a matter of fact, considering the point-like target (of Figure 1) that is moving with velocity whose range-azimuth and acceleration components are , and , respectively, then we can write
Considering the following Taylor expansion:
and that , and , (5) can be written in the following form:
The term can be neglected and by approximating Equation (8) can be written like:
recasting (9) in terms of , we obtain [17]:
where:
- (due to range velocity);
- (due to range acceleration);
- (due to azimuth velocity).
Thus, the above terms modify the received signal, as shown in [17], and should be taken into account in Equation (4).
2.2. Vibrational Model of Infrastructures
In this subsection, we introduce the model to describe the vibrations generated by a distributed body and show how it relates to the measurable quantities through radar data.
The model of motion for the linear damped forced vibration of a structural dynamic system with a total number of M degrees of freedom can be expressed as [1]
where:
- is the external force vector applied to the system over the time t;
- , and are the nodal displacement, the velocity, and the acceleration vectors, respectively;
- , and are the global mass, damping and stiffness matrices of the dynamic system, respectively.
In forced harmonic vibration, if with a driving frequency , Equation (11) becomes
where is the harmonic displacement vector
with , the frequency response, representing the dynamic flexibility of the structural system. The dynamic stiffness can be defined as the inverse of the frequency response [1]
In a structural dynamic testing, the frequency response function is obtained by measuring the system responses at different locations, and, the displacement vector in (12) is given by an appropriate measurement tool. In this paper, we will use the radar sensor to estimate and the details of the proposed estimation procedure are given in the next subsection.
2.3. Processing Framework
Based on the models and tools described in the previous subsections, here the processing framework to estimate the micro-motion of the infrastructure is introduced. In order to analyze the vibrational anomalies, we use the estimated shifts in conjunction with (13) as follows
Equation (15) gives an operational solution to the vibrational model (13) using SAR data. A flow diagram of the processing framework is represented in Figure 2. As it can be observed, the framework is composed by 8 processing stages: the first two consist in the selection of the single image for the analysis followed by a 2D-DFT of the selected image. The third stage is a band-pass filtering operation generating the sub-images centered at the different Doppler frequencies. These sub-images are the input for the successive stages: the SAR focusing, the coregistration, the Pixel Tracking, and the Modal Analysis which solves (15). In particular, the all stages address the following tasks:
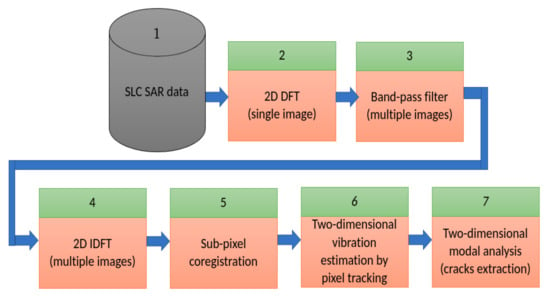
Figure 2.
Computational map.
- Selection of a single SLC-SAR image observing bridges.
- Computation of the bi-dimensional spectrum via 2D-DFT.
- Band-pass filtering according to the small-frequency baseline strategy of Figure 3. The output of the third block consists in multiple images centered at the consecutive different Doppler frequencies.
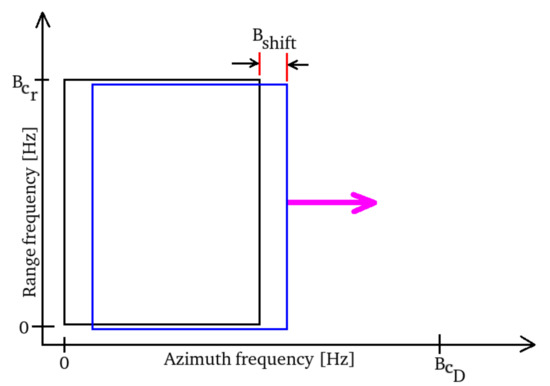 Figure 3. Bandwidth allocation strategy.
Figure 3. Bandwidth allocation strategy. - Computation of the inverse 2D-DFT for retrieving the SLC SAR image with lower azimuth spatial resolution.
- Sub-pixel coregistration;
- Two dimensional vibration estimation by pixel tracking;
- Two-dimensional modal analysis for infrastructure crack extraction.
3. Analyses of Structural Integrity of Bridges from SAR
The experimental results are obtained by processing series of SAR data observed by the Italian CSK satellite constellation. The analysis focuses on the detection, localization, and quantification of vibration trends over five study cases concerning sensible bridges and highway overpasses. In order to achieve this objective, the vibration maps extracted from SAR observations are compared with each other to identify critical points within the structure of the bridge. This is mainly due to the fact that localized areas of fatigue on the bridge structure, such as corrosive phenomena or cracks can generate energy singularities clearly visible on the vibration maps estimated using the proposed technique.
The main characteristics of the SAR acquisition are summarized in Table 1, whereas the detailed list of the performed experiments and data used are shown in Table 2. In particular, the following five cases have been studied:

Table 1.
Characteristics of the SAR acquisitions.

Table 2.
List of data used for experimental results.
- (1)
- “Ponte dell’Industria” is a bridge crossing the Tiber River when it flows through the city of Rome (in the analysis, we consider two opposite geometries, namely, right ascending and right descending, to compare different acquisitions over the same bridge and to prove the repeatability of the procedure);
- (2)
- “Celico” bridge is located in Calabria, a region in southern Italy (it consists of three main spans and two semi-arches);
- (3)
- “Bisantis” bridge is also located in Calabria (both Celico and Bisantis are made of pre-compressed concrete that are very old and still in operation today);
- (4)
- “Italia” of the “SS-119”, an Italian motorway, is also located in Calabria region (the vibration anomalies are analysed);
- (5)
- the last case study investigates the vibration analysis of the the “Morandi” bridge, which collapsed during a strong storm on 14 August 2018 (the “Morandi” bridge crossed the city of Genoa and its collapse caused 43 victims, and, thanks to the proposed method, many critical points have been found on the collapsed stall in a period before the tragic event).
3.1. Study Case 1
“Ponte dell’Industria”, originally known as “Ponte S. Paolo”, has been built in between 1862 and 1863 to connect several railway lines to Rome new central railway station called “Termini”. The bridge, consists of iron and cast iron arches resting on pylons made of cast iron pipes filled with concrete and is higher in the central part to allow steamships and armed ships to freely pass underneath. However, nowadays the bridge is an important junction of the city traffic and therefore it represents a good testbed for SAR monitoring.
In Figure 4a the vibration map of the bridge is shown (SLC and ROI stand for Single Look Complex and Region Of Interest). The map is computed at a fixed frequency of about 10 Hz, with right-ascending observation geometry. Our method provides the spectral analysis in terms of vibrations assumed by the material bodies observed. According to the sampling theorem, spectral observation occurs in the frequency range from a few Hz to the physical limit of half the Doppler frequency, used to synthesise the SAR image at full spatial resolution in azimuth. So the results on a given bridge are given by a tensor where each plane represents the observation space for each frequency. In this case we have chosen only one plane with a frequency equal to 10 Hz. Figure 4b shows the same observation area but using the opposite “right-descending” geometry. It should be noted that the distortion of the observation geometry, which varies from a “right-ascending” to a “right-descending” configuration, does not entail any particular distortion and/or limitation to the analysis. Particularly, the points 1, 2 and 3, shown in both figures, represent three singularities on which high vibration energy is observed. The observed bridges have been also observed through optical images. This is done to find a clue that corresponds to the vibrational behavior observed through the proposed method. Precisely, at each anomalous vibrations position corresponds to a dilation joint that is used to allow an adequate thermal expansion of the road surface constituting the deck of the bridge. The comparison with optical images can be performed considering Figure 5 where the expansion joint 1, corresponding to the vibration singularity 1 of Figure 4, is visible in Figure 5a. The expansion joints 2 and 3, corresponding to the vibration singularities 2 and 3 in Figure 4 are shown in Figure 5b,c, respectively. Thus, the analysis of this first case study allows us to detect the position of all thermal expansion joints in the bridge. This is of fundamental importance because a joint, even if artificial, is built as a real crack (a joint) between two road sections constituting the deck of the bridge. Therefore, we deduce that this technique could be able to detect or, at least, provide a clue for possible cracks and lesions, not specifically designed to discharge the thermal energy of the infrastructure.
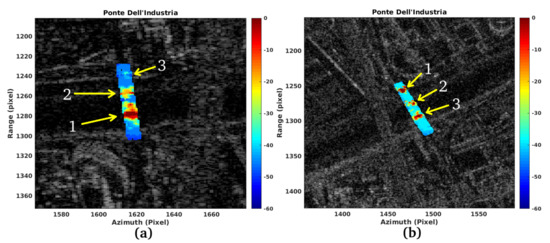
Figure 4.
Vibration maps on SLC image ROI in magnitude: (a) Right ascending, (b) Right descending.

Figure 5.
Optical representation of dilatation joints: (a) Joint number 1, (b) Joint number 2, (c) Joint number 3.
Figure 6 represents the trend over time of the oscillations related to point 1 of Figure 4. Observing this trend, it can be noticed that this point has persistent components at low frequencies and others less marked at higher frequencies. The results of the spectral analysis are shown in Figure 7. Figure 7a shows the overall spectrum, represented on the linear scale. Figure 7b represents a detail of the spectrum corresponding to low frequencies (inside the red box 1 shown in subfigure Figure 7a). The spectral mode 1 presents a maximum in oscillations at about 7 Hz in frequency, while mode 2 is anchored at about 21 Hz and mode number 3 and 4 are standing on about 28 Hz and 35 Hz, respectively. Finally, Figure 7c represents the total spectrum in the logarithmic scale where it is possible to notice an average attenuation level of the low-pass characteristic at near −50 dB.
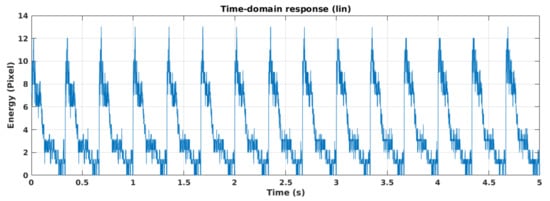
Figure 6.
Temporal trend of vibrations.
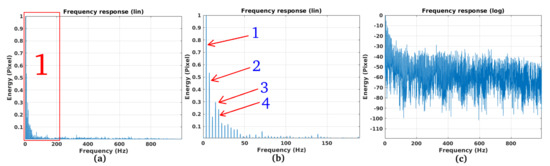
Figure 7.
Vibration trend spectrum (DFT of Figure 6). (a) Spectrum in the linear scale, (b) Particular 1 of the spectrum trend (a), (c) Vibration spectrum in the logarithm scale.
We conclude this case study observing that the Doppler sub-apertures are equal to half the available azimuth band, so the azimuth spatial resolution decreases by a factor 1/2 and we show the effect in discriminating targets selecting a full and a half band in the following. In Figure 8 the optical image of the Ponte dell’Industria is depicted. Points A and B were taken as a test to measure the Rayleigh distance, and therefore the resolution as the Doppler band used during azimuth focusing varies. These points consist of the iron scaffolding that acts as a railing at the bridge, therefore very visible to the SAR. The distance measured ”in-situ” is about 7 m. The CSK product used for processing is a stripmap that guarantees a spatial resolution of 3 m, so points A and B must be displayed separately. In Figure 9a,b the SLC SAR images of the ”Ponte dell’Industria“ observed with full and half Doppler band is depicted, and in Figure 10a,b the reflectivity profiles extrapolated along the red line depicted in Figure 9a,b are depicted. The reflectivity profiles are extrapolated following the red box-profile depicted in Figure 8 and Figure 9a,b. Figure 10a is the full Doppler band image and Figure 10b in the one observed processing only half Doppler band. In Figure 10a is imaged in the linear scale, and the blue function is the imaging function estimated processing the entire Doppler bandwidth and the brown function is the one estimated using only half Doppler band. In Figure 10b is imaged in the log scale, and the blue function is the imaging function estimated processing the entire Doppler bandwidth and the brown function is the one estimated using only half Doppler band. The energy peaks of the iron railing, taken as a test, are correctly separated in distance, in the case of full band, the ”sinc“ is narrower and has a minimum local separation equal to about −7.8 dB, while in the case of half band, the separation is weaker, but always feels, localized at about −2.8 dB. However, the bridge, even if processing half-band Doppler is clearly displayed, and the railings are separated the same in a bit lower energy depth.
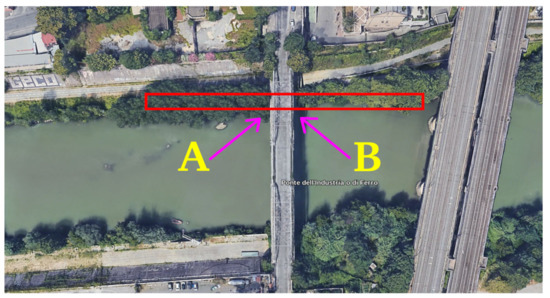
Figure 8.
Optical image.
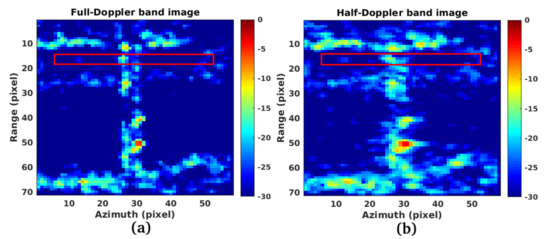
Figure 9.
SAR images: (a): Full resolution. (b): Half resolution.
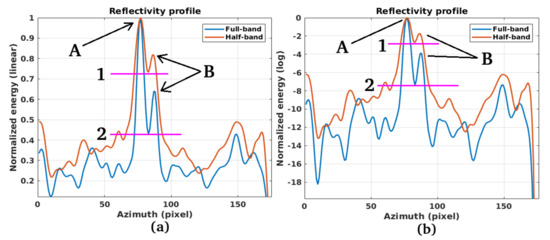
Figure 10.
SAR reflectivity profiles (energy): (a): Full resolution. (b): Half resolution.
As a result of this first analysis, it is possible to state that the proposed methodology is able to extract the position and energy intensity of points along motorway bridges, that could be possible candidates for cracks, even when different acquisition geometries are used.
It is also worth to highlight that the proposed technique has evident band limitations that do not allow for the measurement of very low frequencies, also below Hz, due to the reduced time exposure of the target radiation footprint. In high frequencies, on the other hand, the sensitivity cut is limited by the sampling theorem and limited to half of the maximum Doppler band used to synthesize azimuth resolution.
3.2. Study Case 2
The “Celico” bridge is built in reinforced concrete and has a maximum height of 120 m and a length of 1182 m. The bridge consists of three main spans, and at its ends there are two semi-arches anchored to the ground. In the past the bridge has suffered an accident because one of the three spans collapsed during the renovation work, causing the death of four people. Figure 11a,b show the magnitude of the SLC SAR ROI and the superimposed estimated vibration map, respectively. From Figure 11b, it is possible to observe the joint dilations of the horizontal load-bearing components composing the roadway deck. From this observation geometry, it is possible to count six joints, all numbered and indicated by the yellow arrows drawn on Figure 11b. Joint dilatations from 1 to 3 are confirmed by optical images in Figure 12a–c, respectively, while, joint dilatations from 4 to 6 are confirmed by optical images in Figure 13a–c, respectively.
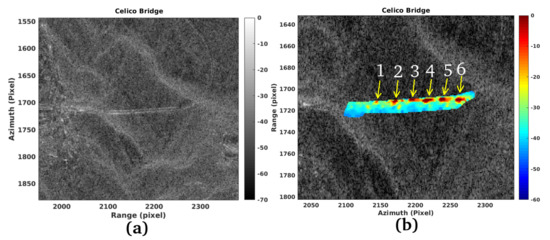
Figure 11.
(a) Celico bridge, SAR SLC magnitude, (b) Vibration map of the Celico bridge.

Figure 12.
Optical representation of dilatation joints: (a) Joint number 1, (b) Joint number 2, (c) Joint number 3.

Figure 13.
Optical representation of dilatation joints: (a) Joint number 4, (b) Joint number 5, (c) Joint number 6.
The time domain vibration plot is reported in Figure 14, where 5 s of observations are reported. Hereafter, the vibration plots are depicted in the time domain. Specifically, the satellite at full spatial resolution in azimuth, takes a certain amount of time for image formation which, for the cases at hand, is 5–6 s. In order to estimate the vibrational micro-motion information of the bodies, it is necessary to synthesize multiple images, with multiple spatial resolution in azimuth, and refocused according to the Doppler sub-aperture strategy of Figure 3. Notice that the rigid sliding of the filters generates the temporal dimension.
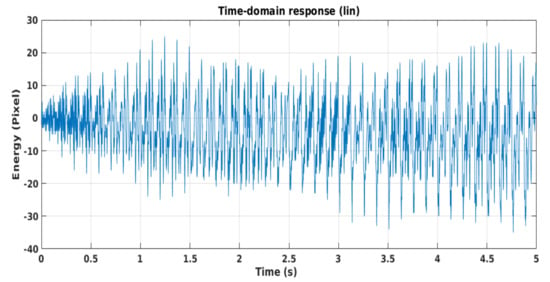
Figure 14.
Temporal trend of vibrations.
Figure 15a,b represent the vibration spectrum in the linear and logarithm scales, respectively. The spectrum has a low-pass characteristic and has three low oscillation energy singularities, the first singularity is located at about 80 Hz, (indicated by the purple arrow (1), the second is located at about 380 Hz, (indicated by the purple arrow (2) the last at about 820 Hz, (indicated by the purple arrow (3). The most energetic harmonics are localized at 75 Hz, then others are present at near 180 Hz. We can also observe sources of vibration harmonics at higher frequencies, localized around 600 Hz.
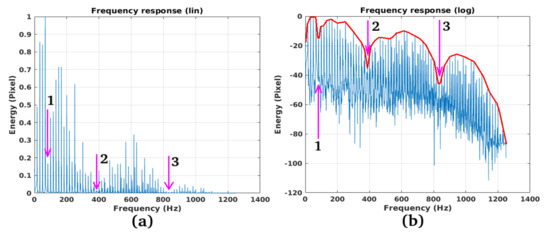
Figure 15.
Vibration spectrum (DFT of Figure 14): (a) Linear scale, (b) Logarithmic scale.
This case study shows the possibility to measure the vibrations of a bridge with a single SAR observation. In particular, we point out that it is possible to monitor the vibrations of the horizontal beams constituting the road surface of the bridge, through the observation of the singularities generated by the cuts constituting the dilation joint.
3.3. Study Case 3
The “Bisantis” bridge is an arched road and pedestrian bridge, consisting of a single carriageway and three lanes, two located in the south west direction and one existing in the north east direction, both built on a single reinforced concrete arch. The “Bisantis” bridge connects the city of Catanzaro with the other cities of the Calabria region. The SLC SAR magnitude representation of the scene is reported in Figure 16a. The vibration map is visible in Figure 17. Looking at this figure, several energy concentration points are clearly visible at one end of the bridge, in the middle and along the arch and the vertical supports. The energy group indicated by the yellow arrow A, are false alarms because the plots are generated by tree canopies, detected by SAR on the street surface due to the layover effect. Energy vibration accumulations 1, 2, 3 and 4 are instead generated by cracks and real deformations that are present on the structure. In particular, vibration anomaly 1 is generated by the strong degradation of the physical characteristics of reinforced concrete visible in Figure 18a and Figure 19a. vibration anomaly 2 is generated by the lesion visible in Figure 19b. The vibrational anomalies indicated by arrows 3 and 4 could be associated with hypothetical damage to the structure. Coincidentally, as in case where significant damage can be observed in Figure 19c,d, every time vibrational anomalies to structures are measured, a visual feedback in terms of joints or material degradation is achieved. The vibration anomaly 5 corresponds to the thermal dilatation joint visible in Figure 18b while vibration anomaly 6 corresponds to the thermal dilatation joint visible in Figure 18c.

Figure 16.
(a): “Bisantis” bridge SLC SAR ROI, (b): “Italia” bridge SLC SAR ROI.
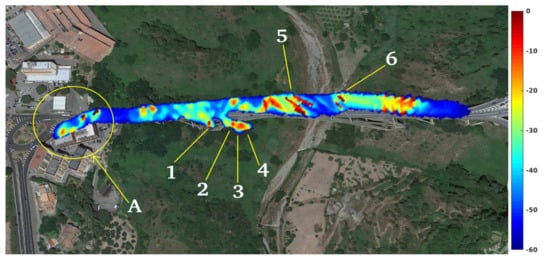
Figure 17.
“Bisantis” bridge vibration map.


Figure 20 represents the trend over time of the oscillations on point 1 of Figure 17. Observing this trend, it can be noticed that this point has persistent components at low frequencies and others less marked at higher frequencies. The results of the spectral analysis are shown in Figure 21. Figure 21a represents the overall spectrum, using the linear scale, whereas, Figure 21b represents the overall spectrum in the logarithmic scale. This result brings out a main mode of oscillation on the frequency of about 5 Hz. Numerous other oscillation modes are visible at frequencies near 80 Hz, and from 180 Hz to 380 Hz. Finally, an abnormal peak around 580 Hz is observed which is probably due to the bridge’s cracks (As reported in [18,19,20] when energy discontinuities are observed, especially at high frequency, an alarm bell should be triggered in order to preserve the health of the infrastructure.)
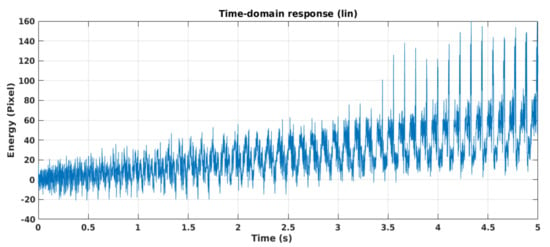
Figure 20.
Time domain vibration trend.
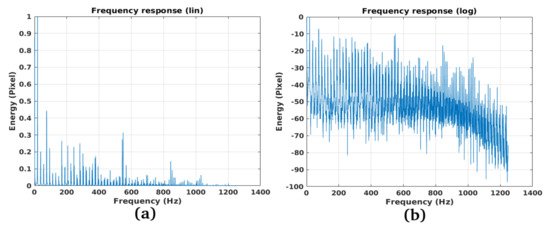
Figure 21.
Vibration spectrum trends (DFT of Figure 20): (a) Linear trend, (b) Logarithmic trend.
Also in this case, the general trend of the frequency response of the infrastructure exhibits a low-pass nature.
3.4. Study Case 4
The viaduct “Italia” is a box shaped viaduct located in the Italian towns of “Laino Borgo” and “Laino Castello”, in the province of Cosenza (Calabria). The construction of the bridge began in October 1966 and ended in November 1969. The result was a viaduct of length 1,161.4 m, resting on 19 spans (16 of which with precompressed reinforced concrete decks, double lane with independent carriageways, three of which are "wide span" with a single metal deck for both roadways). The 18 support piers, independent for both carriageways, are single-column, in reinforced concrete with rectangular structure and vertical reinforcement bar. During the construction of the bridge, the beams were prefabricated on site and laid with the help of a special crane. The highest pile rises 155.3 m from the foundation level. The iron deck has a total length of 425 m and a width of 21.60 m, resting on 4 piles to cover spans of 125 m, 175 m and 125 m respectively. This deck has a box structure made of steel sheet stiffened by ribs. The maximum distance from the street level to the bottom of the valley (the incision of the Lao river) is about 260 m. The “Italia” viaduct was Europe’s highest bridge until 2004 when it was overtaken by the French “Millau” viaduct whose piers reach a height of 343 m from the country floor, with the motorway level at 245 m. In 2016, also as a result of the renovation works started in 2014, the “Italy” bridge remains the highest Italian motorway viaduct, the second highest in Europe and one of the highest in the world.
Figure 22a is the optical representation of the “Italia” bridge. As this viaduct is of recent construction, no structural issues are expected. In Figure 22b we represent the vibration map of the “Italia” viaduct. Through a careful analysis of this result we can observe from the surface of the deck, some square-shaped resonant effect generated by the support pylons, anchored to the ground. These effects are indicated by the yellow arrows 1, 2 and 3. Special magnification boxes (boxes 1, 2 and 3) are visible in the same capture.
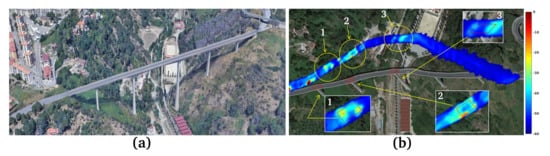
Figure 22.
(a) Optical representation of the “Italia” bridge, (b) vibration map of the “Italia” bridge.
Figure 23 represents the trend in time of the vibrations while Figure 24 is the vibration spectrum, while Figure 24a,b represent linear and logarithmic spectra, respectively. Also in this case anomalous modal peaks are observed, among which one localized at about 250 Hz. We also confirm, in this case, the general low-pass trend of the vibration spectrum.
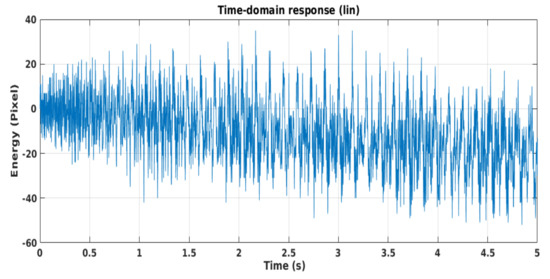
Figure 23.
Temporal trend of vibrations.
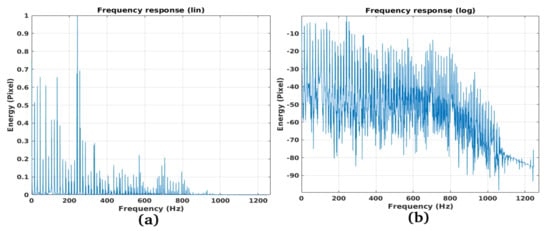
Figure 24.
Vibration spectrum trends (DFT of Figure 23): (a) Linear trend, (b) Logarithmic trend.
3.5. Study Case 5
“Morandi” was one of the world’s longest reinforced concrete bridges when it opened in September 1967. The 1960s were Italy’s economic explosion years. For the first time, many Italians could have a car, but the most of country’s roads needed to be renovated. The “Morandi” Bridge was the fulcrum of a brand-new motorway network connecting heavy traffic from the East to the West of Italy. This was the beginning of the Italian industrial era, for the first time, after World-War Two. The “Morandi” Bridge was very different in other ways with respect also to the “Bisantis” bridge. The deck was entirely made of reinforced concrete, and it had only four cables per tower, instead of the usual dozens. Crucially, the cables were covered in pre-compressed concrete, specifically designed to resist traction. As a result, “Morandi” Bridge was stronger and lighter, with minimal use of steel, than any other bridge of its era and boasted a clean, distinct design that quickly became a symbol of Italian engineering, tangible proof of the country?s technical abilities. On 14 August 2018, the city of Genoa was surrounded by a strong summer storm. At 11.30 a.m., the rain was so heavy that visibility had fallen dramatically. During those severe weather conditions, the third supporting tower and 200 m section of the the “Morandi” Bridge, collapsed. The disaster killed 43 people and left 600 people homeless.
Case Study 5 presents an extended survey of the collapsed bridge. To this end, we resort to the satellite data before the break-down, consisting of a time series of interferometric SAR data observed by the COSMO-SkyMed satellite system. For this case study, we perform the modal analysis, carried out on various points of the bridge and also the bridge axes.
Figure 25a is a schematic representation of the “Morandi” bridge. Pylons 9, 10, and 11 are the largest constituting the main deck arches of the “Morandi” Bridge, while the collapsed pylon is number 9. Figure 26a shows in perspective the “Morandi” bridge where the collapsed pylon (number 9). Point (a) depicts the stall attack which, by falling, probably caused the whole pylon to collapse. Figure 27a,b shows the vibration profile of the “Morandi” bridge. The processed SLC SAR image was acquired before the collapse, on 21 January 2016 and 5 July 2018, respectively. By observing the vibration energy, one can observe interesting energy accumulations in proximity of the pylon 9 stays. Figure 28 depicts the particular of the figure inserted within the red square A of Figure 27. The red spots indicated by the yellow arrows (accumulation points (a)), represent the broken stay indicated in Figure 26a. The frequency analysis is performed on pixel P1 and P2, points belonging to the broken stay. Figure 28 shows the exact position of the measurement points. Figure 29a represents the trend in time of the oscillations observed on point P2, while, Figure 30a,b represent the spectrum in the linear and logarithmic scales, respectively. Looking at the figures, it is possible to observe the presence of a very energetic resonant peak polarized on about 10 Hz and another, of similar strenght, on about 780 Hz. The P2 point has a very different trend. Being the stall attack, the oscillations in the time domain have very high amplitude (Figure 29b). The spectra, in linear and logarithmic scale, represented in Figure 31a,b respectively, have a very particular trend, presenting a maximum at about 210 Hz.

Figure 25.
“Morandi” bridge: (a) Schematic representation, (b) Optical representation.

Figure 26.
(a) Optical representation of the “Morandi” bridge, (b) SAR-SLC in magnitude of the “Morandi” bridge.
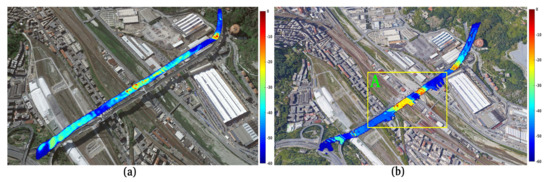
Figure 27.
Vibration maps of the “Morandi” bridge: (a) 21 January 2016, (b) 5 July 2018.
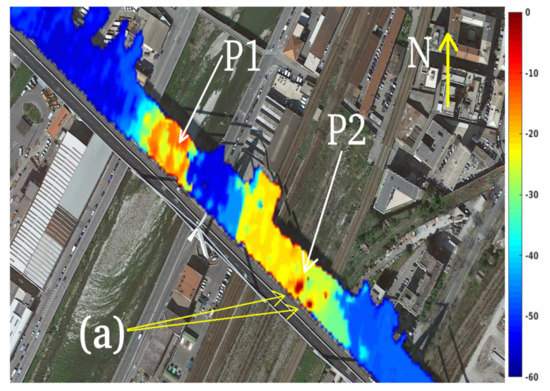
Figure 28.
Vibration map of the “Morandi” bridge (details). 5 July 2018
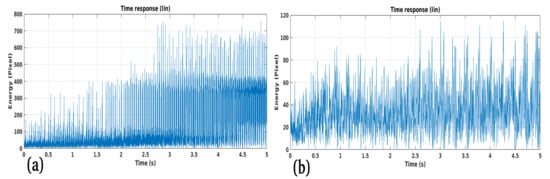
Figure 29.
Temporal trend of vibrations: (a) point P1, (b) point P2.
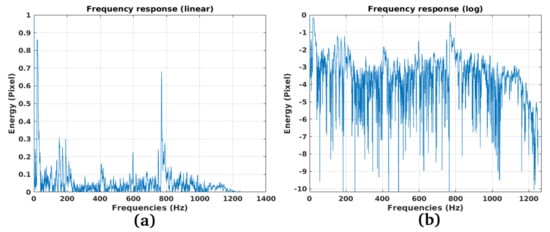
Figure 30.
Vibration spectrum trend of P1 (DFT of Figure 29a): (a) Linear trend, (b) Logarithmic trend.
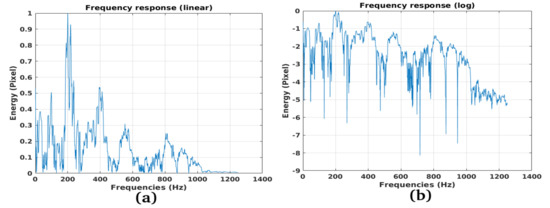
Figure 31.
Vibration spectrum trend of P2 (DFT of Figure 29b): (a) Linear trend, (b) Logarithmic trend.
Figure 32 shows the “Morandi” bridge before the collapse. The vibration energy along the red line positioned longitudinally on the bridge roadway is computed. From the results, numerous abrupt variations of the vibration energy can be observed. Precisely, these anomalies are observed in correspondence of the connection joints shown in Figure 33. These figures are taken a few days before the bridge collapsed. The abrupt variations from 1 to 6 of Figure 34a,b are compared with Figure 33 from a–f, respectively.

Figure 32.
“Morandi” bridge. Satellite image.

Figure 33.
Optical representation of the Morandi bridge, the images were taken from a car crossing the bridge a few days before the collapse. (a–f): The connection joints of the “Morandi” bridge.
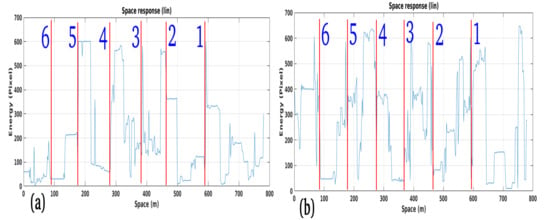
Figure 34.
Longitudinal vibration trend versus space of the “Morandi” bridge: (a) temporal event 1, (b) temporal event 2.
4. Discussion
The results obtained in this work have shown that the use of amplitude information alone from SAR images is enough to estimate the m-m generated by bridges. As a matter of fact, the exploitation of high-resolution SAR data has allowed to appreciate the m-m. The vibrations have been estimated in both time and frequency domains considering different bridges infrastructures. In the first domain, an analysis from the energy point of view can be performed, while in the second domain the main oscillation modes can be identified at frequencies ranging from a few Hz to a several tens of Hz. The case studies we have dealt with have taught us that bridges are highly dynamic structures and are subject to numerous stresses, natural and not. All atmospheric agents such as wind, sea as well as other natural phenomena such as earthquakes are included in natural stresses. In man-made vibration phenomena are mainly those due to car traffic. However, in all cases the oscillating energies and resonance frequencies vary not only according to the shape and materials of the bridge but also according to the season and time of day (day or night) or the particular seasonal period.
We have analyzed various types of bridges, metal and reinforced concrete, all of various shapes and with different construction methods. What we found is that all bridges have different resonance frequencies and various harmonics located in discrete pints of the oscillating mechanical spectrum. It clearly turn out that the bridges have a frequency response to low-pass oscillations and, in most cases, the main resonance harmonic is observed at frequencies below 10 Hz. We have considered the anomalous case of the “Morandi” bridge in Genoa collapsed due to natural causes. In particular, the frequency analysis related to point P2 and presented in Figure 31a,b underline the presence of anomalies that are confirmed through visual inspection (see Figure 35, where longitudinal cracks can be clearly observed). The time-frequency analysis made on the stall has returned the presence of the most resonant harmonic localized at about 210 Hz. In addition, given the high quality of the vibration profiles, we believe that this work opens the way to a new paradigm for large infrastructure monitoring, design of high-performance damage detection, classification, and recognition methods.

Figure 35.
Optical representation of “Morandi” bridge (longitudinal cracks).
5. Conclusions
This research aimed to estimate the m-m of bridges. Large infrastructures need continuous maintenance because of materials degradation due to atmospheric agents and their persistent use. This problem makes it imperative to carry out persistent monitoring of infrastructure health conditions in order to guarantee maximum safety at all times. The main issue of early warning infrastructure fault detection is that expensive in-situ distributed monitoring sensor networks have to be installed. This research proposed a new global infrastructure monitoring paradigm using m-m estimation of critical sites, performing spaceborne SAR data exploitation. We designed a complete procedure for damage early-warning detection, using modal proprieties analysis. m-m is processed to extracted modal features such as natural frequencies and mode shapes generated by vibrations of large infrastructures. Several case studies of bridges are considered in this paper. In addition, the case of the “Morandi” Bridge (Polcevera Viaduct) in Genoa (Italy) is analyzed in depth where the proposed method showed abnormal vibration modes during the period before the bridge collapsed. Finally, estimating cracks, by evaluating any vibration maps anomalies, will permit an efficient structural health monitoring and predictive maintenance.
Author Contributions
Each author dealt with a specific study case and reviewed the other study cases. All authors reviewed the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
No founding is used for this paper.
Acknowledgments
The authors would to thank the Italian Space Agency (ASI) for providing the SAR data. This research used the software SARPROZ: https://www.sarproz.com/, for performing the precise geocoding of the estimated vibration maps.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chen, H.P.; Ni, Y.Q. Structural Health Monitoring of Large Civil Engineering Structures; Wiley Blackwell: Hoboken, NJ, USA, 2018. [Google Scholar]
- Scott, C.P.; Lohman, R.B.; Jordan, T.E. InSAR constraints on soil moisture evolution after the March 2015 extreme precipitation event in Chile. Sci. Rep. 2017, 7, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Bekaert, D.P.S.; Hamlington, B.D.; Buzzanga, B.; Jones, C.E. Spaceborne Synthetic Aperture Radar Survey of Subsidence in Hampton Roads, Virginia (USA). Sci. Rep. 2017, 7, 14752. [Google Scholar] [CrossRef] [PubMed]
- Burnol, A.; Aochi, H.; Raucoules, D.; Veloso, F.M.L.; Koudogbo, F.N.; Fumagalli, A.; Chiquet, P.; Maisons, C. Wavelet-based analysis of ground deformation coupling satellite acquisitions (Sentinel-1, SMOS) and data from shallow and deep wells in Southwestern France. Sci. Rep. 2019, 9, 4903. [Google Scholar] [CrossRef] [PubMed]
- Carlà, T.; Intrieri, E.; Raspini, F.; Bardi, F.; Farina, P.; Ferretti, A.; Colombo, D.; Novali, F.; Casagli, N. Perspectives on the prediction of catastrophic slope failures from satellite InSAR. Sci. Rep. 2019, 9, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Sousa, J.J.; Ruiz, A.M.; Bakoň, M.; Lazecky, M.; Hlaváčová, I.; Patrício, G.; Delgado, J.M.; Perissin, D. Potential of C-Band SAR Interferometry for Dam Monitoring. Procedia Comput. Sci. 2016, 100, 1103–1114. [Google Scholar] [CrossRef]
- Lazecky, M.; Perissin, D.; Bakon, M.; De Sousa, J.M.; Hlavacova, I.; Real, N. Potential of satellite InSAR techniques for monitoring of bridge deformations. In Proceedings of the 2015 Joint Urban Remote Sensing Event (JURSE), Lausanne, Switzerland, 30 March–1 April 2015; pp. 1–4. [Google Scholar]
- Ullo, S.L.; Addabbo, P.; Di Martire, D.; Sica, S.; Fiscante, N.; Cicala, L.; Angelino, C.V. Application of DInSAR Technique to High Coherence Sentinel-1 Images for Dam Monitoring and Result Validation Through In Situ Measurements. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 875–890. [Google Scholar] [CrossRef]
- De Corso, T.; Mignone, L.; Sebastianelli, A.; Del Rosso, M.P.; Yost, C.; Ciampa, E.; Pecce, M.; Sica, S.; Ullo, S.L. Application of DInSAR technique to high coehrence satellite images for strategic infrastructure monitoring. In Proceedings of the 2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 19–24 July 2020. [Google Scholar]
- Ferretti, A.; Prati, C.; Rocca, F. Nonlinear subsidence rate estimation using permanent scatterers in differential SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2202–2212. [Google Scholar] [CrossRef]
- Ferretti, A.; Prati, C.; Rocca, F. Permanent scatterers in SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 8–20. [Google Scholar] [CrossRef]
- Biondi, F.; Clemente, C.; Orlando, D. An Atmospheric Phase Screen Estimation Strategy Based on Multichromatic Analysis for Differential Interferometric Synthetic Aperture Radar. IEEE Trans. Geosci. Remote Sens. 2019, 57, 7269–7280. [Google Scholar] [CrossRef]
- Fujino, Y. Vibration, control and monitoring of long-span bridges—Recent research, developments and practice in Japan. J. Constr. Steel Res. 2002, 58, 71–97. [Google Scholar] [CrossRef]
- Li, H.; Laima, S.; Zhang, Q.; Li, N.; Liu, Z. Field monitoring and validation of vortex-induced vibrations of a long-span suspension bridge. J. Wind Eng. Ind. Aerodyn. 2014, 124, 54–67. [Google Scholar] [CrossRef]
- Biondi, F.; Addabbo, P.; Clemente, C.; Ullo, S.; Orlando, D. Monitoring of Critical Infrastructures by Micro-Motion Estimation: the Mosul Dam Destabilization. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2020, 13, 6337–6351. [Google Scholar] [CrossRef]
- Curlander, J.C.; McDonough, R.N.; Soumekh, M. Synthetic Aperture Radar Signal Processing; Wiley: New York, NY, USA, 1991; Volume 7. [Google Scholar]
- Raney, R.K. Synthetic Aperture Imaging Radar and Moving Targets. IEEE Trans. Aerosp. Electron. Syst. 1971, AES-7, 499–505. [Google Scholar] [CrossRef]
- Ismail, F.; Ibrahim, A.; Martin, H. Identification of fatigue cracks from vibration testing. J. Sound Vib. 1990, 140, 305–317. [Google Scholar] [CrossRef]
- Cheng, S.M.; Swamidas, A.S.J.; Wu, X.J.; Wallace, W. Vibrational Response of a Beam with a Breathing Crack. J. Sound Vib. 1999, 225, 201. [Google Scholar] [CrossRef]
- Ballo, I. Non-linear effects of vibration of a continuous transverse cracked slender shaft. J. Sound Vib. 1998, 217, 321–333. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).