Robust Data Fusion of UAV Navigation Measurements with Application to the Landing System
Abstract
1. Introduction
2. Problem Statement
- Prediction:
- Correction of the state estimate based on current measurements:
3. Robust Filter
3.1. Least Modulus Method
3.2. Chi-Square Test for Failure Detection
3.3. Calculation of the Measurements Covariance Matrix
3.4. Calculating the Predictive Covariance Matrix
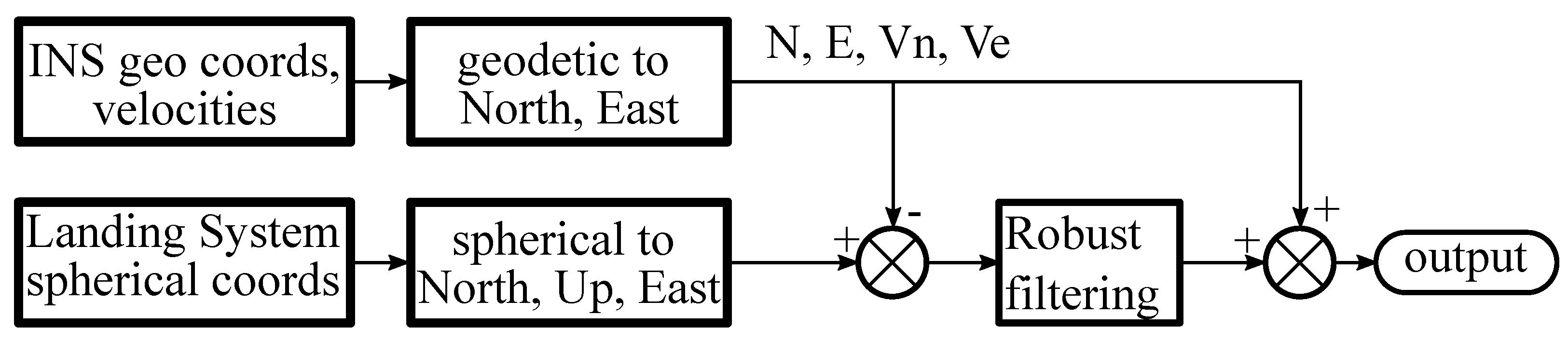
4. Application of the Robust Filter in the Data Fusion Problem
- INS (horizontal coordinates),
- altimeters (radio or barometric) with double redundancy,
- landing systems (as a source of spherical coordinates).
4.1. System Model
- is INS error in the north direction (m),
- is INS speed error in the north direction (m/s),
- is INS error in the eastern direction (m),
- is INS speed error in the east direction (m/s),
- is height according to altimeter data (m),
- is vertical speed according to altimeter data (m/s),
- is height according to the landing system (m),
- is vertical speed according to the indications of the landing system (m/s),
4.2. Measurements Model
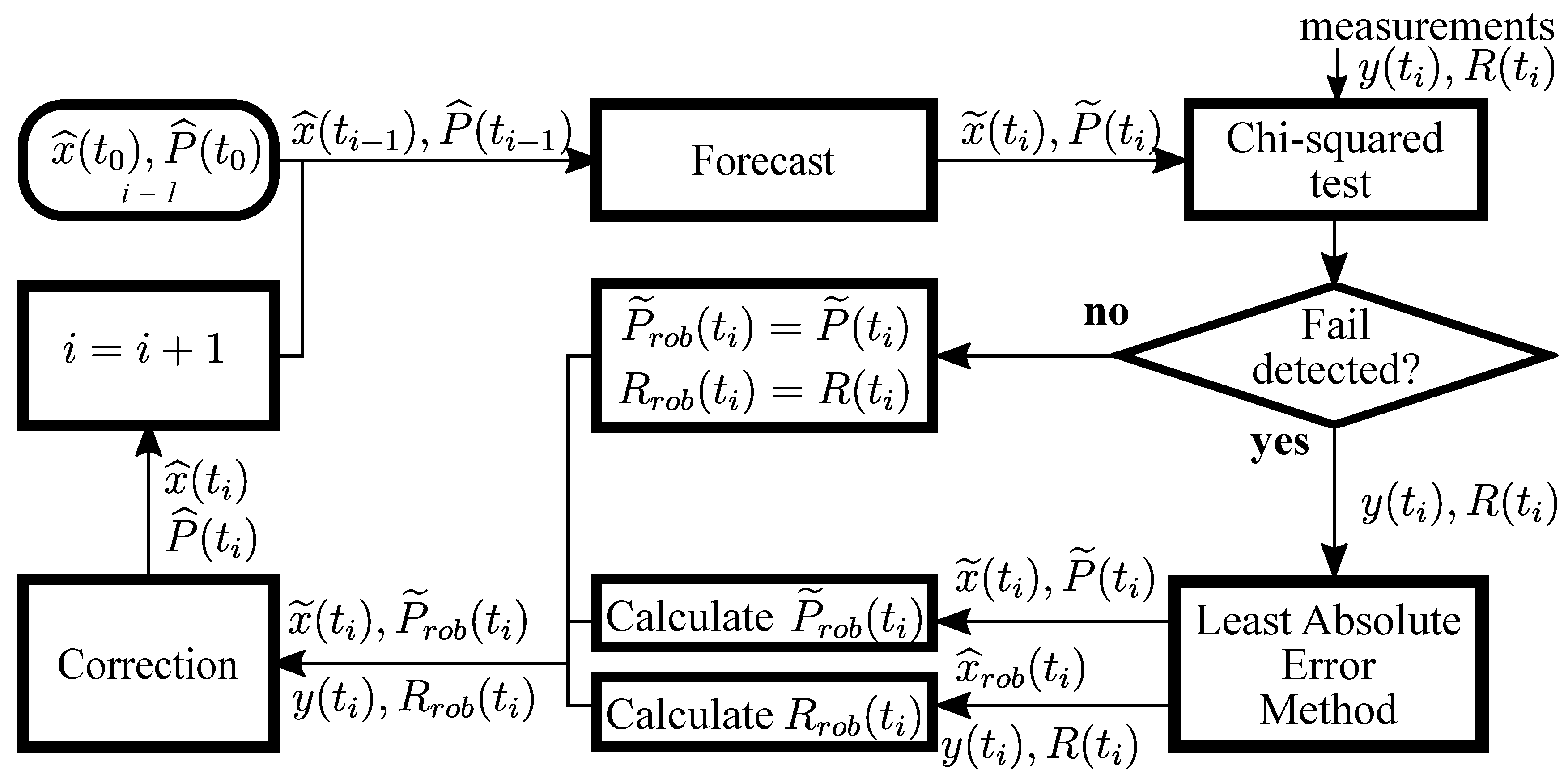
4.3. Data Fusion Algorithm
- Set the initial state of the filter in the horizontal channel and the initial state of the filter in the vertical channel .
- The following steps are repeated as measurements arrive. Calculate state prediction:
- Using residuals and calculate accordingly and by Formula (24).
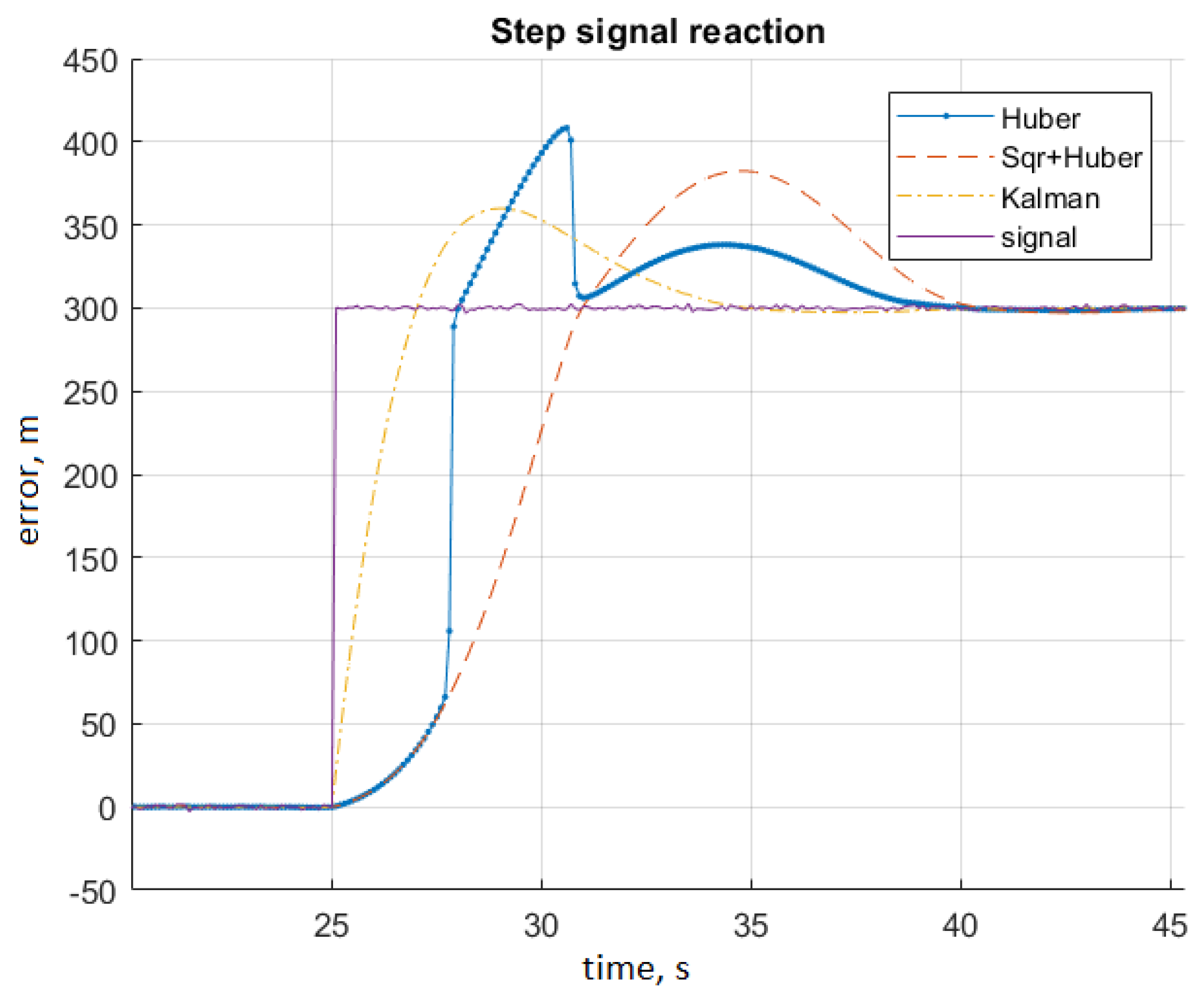
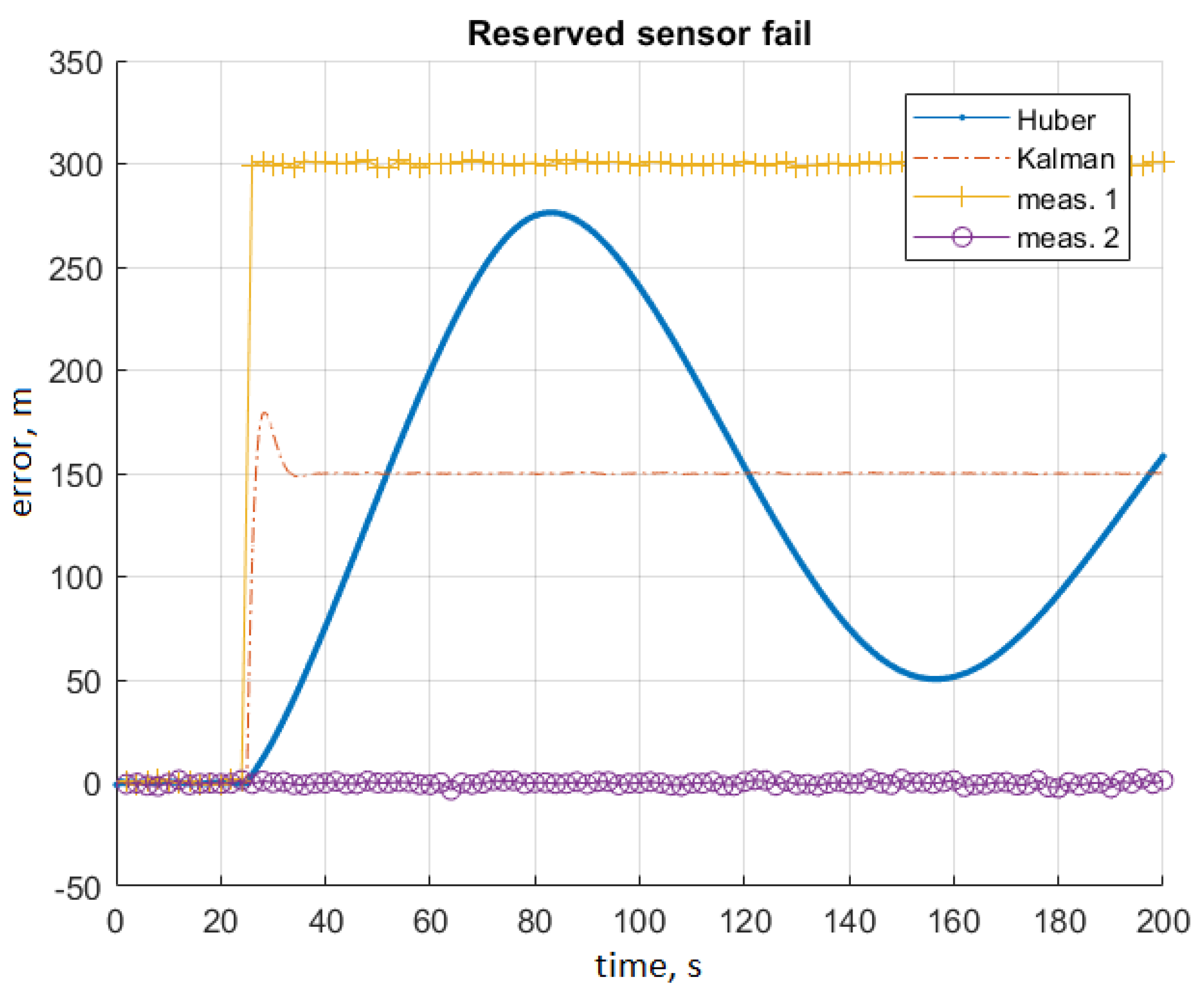
5. Discussion of Test Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| INS | Inertial Navigation System |
| GNSS | Global Navigation Satellite System |
| UKF | Unscented Kalman filter |
| EKF | Extended Kalman Filter |
References
- You, Y.; Cao, J.; Zhou, W. A Survey of Change Detection Methods Based on Remote Sensing Images for Multi-Source and Multi-Objective Scenarios. Remote Sens. 2020, 12, 2460. [Google Scholar] [CrossRef]
- Karpenko, S.; Konovalenko, I.; Miller, A.; Miller, B.; Nikolaev, D. UAV Control on the Basis of 3D Landmark Bearing-Only Observations. Sensors 2015, 15, 29802–29820. [Google Scholar] [CrossRef] [PubMed]
- Konovalenko, I.; Miller, A.; Nikolaev, D.; Miller, B. UAV Navigation On The Basis Of The Feature Points Detection On Underlying Surface. In Proceedings of the 29th European Conference on Modelling and Simulation, ECMS 2015; Valeri, M.M., Ed.; Technical University of Sofia: Sofia, Bulgaria, 2015; pp. 500–505. [Google Scholar]
- Miller, A.B.; Miller, B.M. Stochastic control of light UAV at landing with the aid of bearing-only observations. In Proceedings of the SPIE 9875, Eighth International Conference on Machine Vision (ICMV 2015) (8 December 2015), Barselona, Spain, 19–20 November 2015. [Google Scholar] [CrossRef]
- Tao, F.; Zhou, T. Identification of Urban Functional Areas by Coupling Satellite Images and Taxi GPS Trajectories. Remote Sens. 2020, 12, 2449. [Google Scholar]
- Arce, S.; Cory, A.V.; Hammond, J.; Newell, V.; Janson, J.; Franke, K.W.; Hedengren John, D. Automated 3D Reconstruction Using Optimized View-Planning Algorithms for Iterative Development of Structure-from-Motion Models. Remote Sens. 2020, 12, 2169. [Google Scholar] [CrossRef]
- Farella, E.M.; Torresani, A.; Remondino, F. Refining the Joint 3D Processing of Terrestrial and UAV Images Using Quality Measures. Remote Sens. 2020, 12, 2873. [Google Scholar] [CrossRef]
- Pham, H.X.; La, H.M.; Feil-Seifer, D.; Nguyen, L.V. Autonomous UAV Navigation Using Reinforcement Learning. arXiv 2018, arXiv:1801.05086. [Google Scholar]
- Amer, K.; Samy, M.; Shaker, M.; Elhelw, M. Deep Convolutional Neural Network-Based Autonomous Drone Navigation. arXiv 2019, arXiv:1905.01657. [Google Scholar]
- Hodge, V.J.; Hawkins, R.; Alexander, R. Deep Reinforcement Learning for Drone Navigation Using Sensor Data. Neural Comput. Appl. 2020. [Google Scholar] [CrossRef]
- Maier, A.; Kiesel, S.; Trommer, G.F. Performance analysis of federated filter for SAR/TRN/GPS/INS integration. Gyroscopy Navig. 2011, 2, 293–300. [Google Scholar] [CrossRef]
- Hu, G.; Gao, S.; Zhong, Y.; Gao, B.; Subic, A. Modified federated Kalman filter for INS/GNSS/CNS integration. Proc. IMechE Part G J. Aerosp. Eng. 2016, 230, 30–44. [Google Scholar] [CrossRef]
- Wright, M.A.; Horowitz, R. Particle-filter-enabled real-time sensor fault detection without a model of faults. In Proceedings of the 2017 IEEE 56th Annual Conference on Decision and Control (CDC), Melbourne, VIC, Australia, 12–15 December 2017; pp. 5757–5763. [Google Scholar] [CrossRef]
- Gao, B.; Hu, G.; Gao, S.; Zhong, Y.; Gu, C. Multi-Sensor Optimal Data Fusion Based on the Adaptive Fading Unscented Kalman Filter. Sensors 2018, 18, 488. [Google Scholar] [CrossRef]
- Veremeenko, K.K.; Zheltov, S.Y.; Kim, N.V.; Kozorez, D.A.; Krasil’shchikov, M.N.; Sebryakov, G.G.; Sypalo, K.I.; Chernomorsky, A.I. Modern Information Technologies in the Tasks of Navigation and Guidance of Unmanned Maneuverable Aerial Vehicles; Fizmatlit: Moscow, Russia, 2009. (In Russian) [Google Scholar]
- Salychev, O.S. Mems-Based Inertial Navigation: Expectations and Reality; Bauman Moscow State Technical University: Moscow, Russia, 2012. [Google Scholar]
- Kaplan, E.; Hegarty, C. Understanding GPS: Principles and Applications; ARTECH HOUSE: Boston, MA, USA; London, UK, 2006. [Google Scholar]
- Sierra Nevada Corporation. Tactical Automatic Landing System. Available online: www.sncorp.com (accessed on 20 November 2020).
- Ground-Based Navigation—Instrument Landing System (ILS). Available online: https://www.faa.gov/ (accessed on 20 November 2020).
- OPATS Laser Based Landing Aid for Unmanned Aerial Vehicles. RUAG—Aviation Products Switzerland. Available online: www.ruag.com/aviation (accessed on 20 November 2020).
- Konovalenko, I.; Kuznetsova, E.; Miller, A.; Miller, B.; Popov, A.; Shepelev, D.; Stepanyan, K. New Approaches to the Integration of Navigation Systems for Autonomous Unmanned Vehicles (UAV). Sensors 2018, 18, 3010. [Google Scholar] [CrossRef]
- Sasiadek, J.Z.; Hartana, P. Sensor Fusion for Navigation of an Autonomous Unmanned Aerial Vehicle. In Proceedings of the IEEE lnternational Conference on Robotics and Automation; Program Chair Kimon Valavanis: New Orleans, LA, USA, 2004; Volume 4, pp. 4029–4034. [Google Scholar]
- Titterton, D.; Weston, J.L.; Weston, J. Strapdown Inertial Navigation Technology Stevenage, UK; Institution of Electrical Engineers: Reston, VA, USA, 2004. [Google Scholar]
- Lin, X.; Kirubarajan, T.; Bar–Shalom, Y.; Maskell, S. Comparison of EKF, Pseudomeasurement and Particle Filters for a Bearing-only Target Tracking Problem. Proc. SPIE 2002, 4728, 240–250. [Google Scholar]
- Julier, S.J.; Uhlmann, J.K.; Durrant-Whyte, H.F. A New Approach for Filtering Nonlinear Systems. In Proceedings of the 1995 American Control Conference-ACC’95, Seattle, WA, USA, 21–23 June 1995; pp. 1628–1632. [Google Scholar]
- Miller, A.B.; Miller, B.M. Tracking of the UAV trajectory on the basis of bearing-only observations. In Proceedings of the 53rd IEEE Conference on Decision and Control; Andrew, R.T., Ed.; IEEE: Los Angeles, CA, USA, 2014; pp. 4178–4184. [Google Scholar]
- Huber, P.J. Robust Statistics; Wiley Series in Probability and Mathematical Statistics; John Wiley & Sons: New York, NY, USA, 1981. [Google Scholar]
- Hampel, F.R.; Ronchetti, E.M.; Rousseeuw, P.J.; Stahel, W.A. Robust Statistics: The Approach Based on Influence Function; John Wiley & Sons: New York, NY, USA, 1986. [Google Scholar]
- Bosov, A.V.; Pankov, A.R. Robust Recurrent Estimations of Processes in Stochastic Systems. Autom. Remote Control 1992, 53, 1395–1402. [Google Scholar]
- Pearson, R.K. Outliers in Process Modeling and Identification. IEEE Trans. Control. Syst. Technol. 2002, 10, 55–63. [Google Scholar] [CrossRef]
- Markovich, N. Nonparametric Analysis of Univariate Heavy-Tailed Data: Research and Practice; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Gustafsson, F. Particle filter theory and practice with positioning applications. IEEE Aerosp. Electron. Syst. Mag. 2010, 25, 53–82. [Google Scholar]
- Cao, L.; Qiao, D.; Chen, X. Laplace L1 Huber based cubature Kalman filter for attitude estimation of small satellite. Acta Astronaut. 2018, 148, 48–56. [Google Scholar] [CrossRef]
- Kotz, S.; Kozubowski, T.J.; Podgorski, K. The Laplace Distribution and Generalizations; Springer Science+Business Media: New York, NY, USA, 2001. [Google Scholar]
- Koch, K.R.; Yang, Y. Robust Kalman Filter for Rank Deficient Observation Models. J. Geod. 1998, 72, 436–441. [Google Scholar] [CrossRef]
- Chang, G.; Liu, M. M-estimator-based Robust Kalman Filter for Systems with Process Modeling Errors and Rank Deficient Measurement Models. Nonlinear Dynam. 2015, 80, 1431–1449. [Google Scholar] [CrossRef]
- Abdelmalek, N.N. On the Discrete Linear L1 Approximation and L1 Solutions of Overdetermined Linear Equations. J. Approx. Theory 1974, 11, 38–53. [Google Scholar] [CrossRef]
- Liptser, R.S.; Shiryaev, A.N. Random Process Statistics; Springer: New York, NY, USA, 1978. [Google Scholar]
- Gelb, A. Applied Optimal Estimation; MIT Press: Cambridge, MA, USA, 2001. [Google Scholar]
- Hogben, L. Handbook of Linear Algebra, 2nd ed.; New York Imprint; Chapman and Hall/CRC Press: New York, NY, USA, 2013. [Google Scholar]
- Armstrong, R.D.; Frome, E.L. A Comparison of Two Algorithms for Absolute Deviation Curve Fitting. J. Am. Stat. Assoc. 1976, 71, 328–330. [Google Scholar] [CrossRef]
- Barrodale, I.; Roberts, F. An Improved Algorithm for Discrete L1 Linear Approximation. SIAM J. Numer. Anal. 1973, 10, 839–848. [Google Scholar] [CrossRef]
- Abdelmalek, N.N. An Efficient Method for the Discrete Linear L1 Approximation Problem. Math. Comput. 1975, 29, 844–850. [Google Scholar]
- Teunissen, P.J.G. Distributional Theory for the DIA Method. J. Geod. 2018, 92, 59–80. [Google Scholar] [CrossRef]
- Xu, C.; Rui, X.; Song, X.; Gao, J. Generalized Reliability Measures of Kalman Filtering for Precise Point Positioning. J. Syst. Eng. Electron. 2013, 24, 699–705. [Google Scholar] [CrossRef]
- Popov, A.; Miller, A.; Miller, B.; Stepanyan, K. Optical flow and inertial navigation system fusion in the UAV navigation. In Unmanned/Unattended. Sensors and Sensor Networks XII, Proceedings of the 998606 (2016) SPIE Security + Defence, Edinburgh, UK, 26–29 September 2016; SPIE Digital Library: Bellingham, WA, USA, 2016. [Google Scholar] [CrossRef]
- Miller, B.; Miller, A.; Popov, A.; Stepanyan, K. UAV Landing Based on the Optical Flow Videonavigation. Sensors 2019, 19, 1351. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kolosov, K.; Miller, A.; Miller, B. Robust Data Fusion of UAV Navigation Measurements with Application to the Landing System. Remote Sens. 2020, 12, 3849. https://doi.org/10.3390/rs12233849
Kolosov K, Miller A, Miller B. Robust Data Fusion of UAV Navigation Measurements with Application to the Landing System. Remote Sensing. 2020; 12(23):3849. https://doi.org/10.3390/rs12233849
Chicago/Turabian StyleKolosov, Kirill, Alexander Miller, and Boris Miller. 2020. "Robust Data Fusion of UAV Navigation Measurements with Application to the Landing System" Remote Sensing 12, no. 23: 3849. https://doi.org/10.3390/rs12233849
APA StyleKolosov, K., Miller, A., & Miller, B. (2020). Robust Data Fusion of UAV Navigation Measurements with Application to the Landing System. Remote Sensing, 12(23), 3849. https://doi.org/10.3390/rs12233849






