A Brief Analysis of the Triangle Method and a Proposal for its Operational Implementation

Abstract

The well-known triangle method in optical/thermal remote sensing, its construction, uncertainties, and the significance of its products are first discussed. These topics are then followed by an outline of how the method can be implemented operationally for practical use, including a suggestion for constructing a dynamic crop moisture index.

1. Background

Despite its increasing popularity, evidenced by the plethora of papers on the subject, the triangle method in optical/thermal remote sensing remains an unclear subject, so far lacking any consensus on how to construct the triangle or on a mathematical formalism. Lacking also is a full appreciation for its inherent limitations, the nature of its derivative products, and a clear focus on how it might be used operationally. To briefly summarize, the triangle method allows one to estimate surface soil water content and evapotranspiration fraction EF (here defined as the ratio of transpiration T to net radiation Rn) from remotely sensed optical and thermal measurements. The triangle’s greatest advantage is its mathematical and geometric simplicity and that it requires no ancillary surface or atmospheric data and no detailed land surface model.

In all versions of the triangle method, some sort of mathematical formalism serves as an interface with the input measurements to yield the output: EF and a surface moisture parameter Mo. Input parameters are surface radiant temperature (Tir) and a vegetation index (e.g., NDVI), from which fractional vegetation cover (Fr) is determined. Mo, the surface moisture parameter, is called the surface moisture availability and is loosely defined as the ratio of soil water content to that at field capacity.

Considerable discussion of the triangle method and its application exists in several recent papers (de Tomas et al. [1], Rasmussen et al. [2], Carlson and Petropoulos [3], Silva-Fuzzo et al. [4], Kasim et al. [5], Petropoulos et al. [6]). Many other papers published over the past 25 years have dealt with this subject. In the interest of brevity and to confine the subject to the narrow topic of the triangle, this paper will eschew a lengthy literature review but refer mainly to those papers published on this subject during the past few years. The purpose of this paper is to present the method concisely and to point the way toward its operational implementation, for example for use in the European Space Agency’s Sentinel-3 program [6]. Accordingly, the paper will just briefly outline the mathematical and conceptual basis for the triangle method, discuss some of its inherent uncertainties, precisely describe the nature of its products, and, finally, present steps toward a realization of the triangle method as an operational tool for routinely assessing soil moisture status.

2. Construction of the Triangle

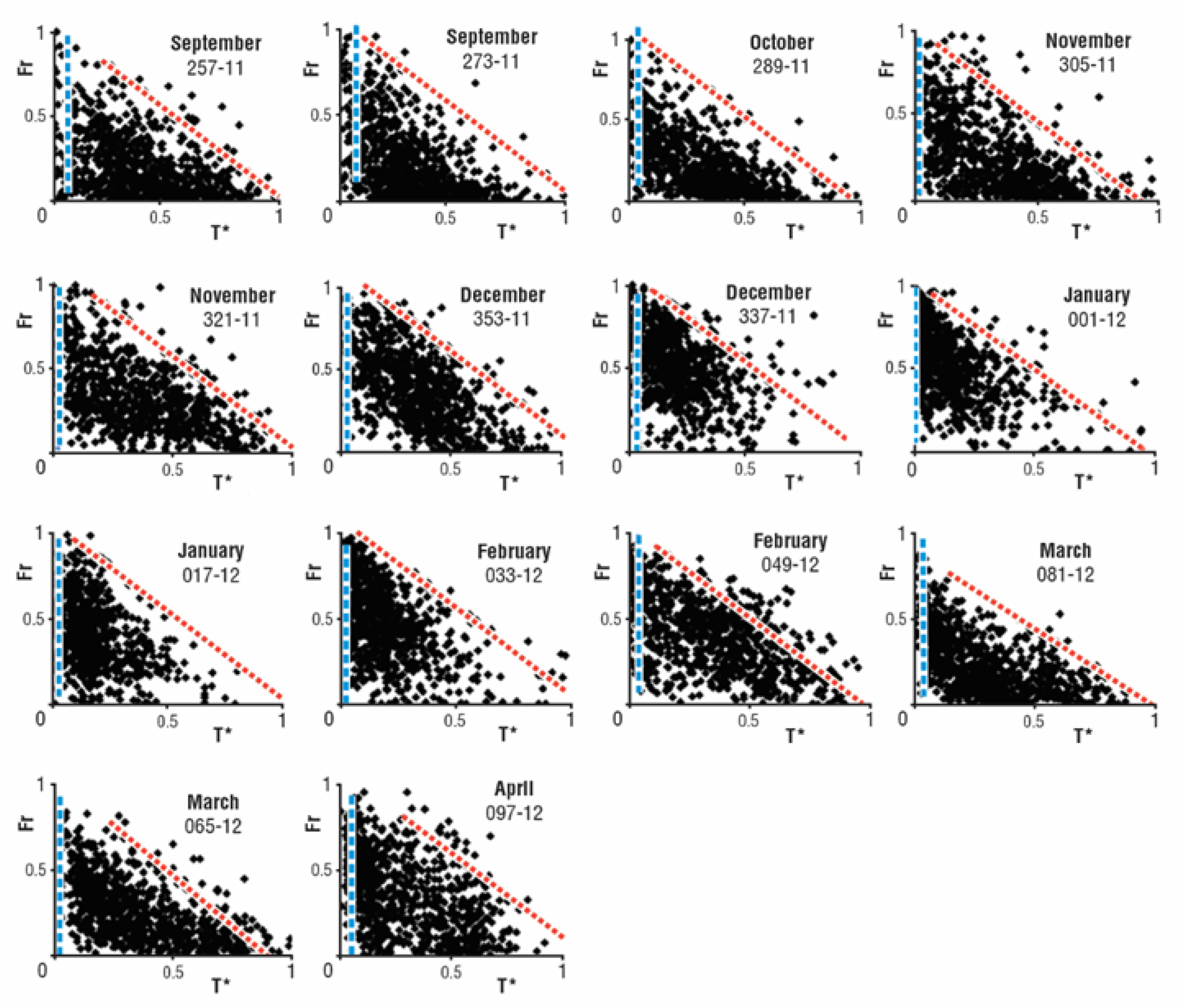
When surface infrared temperature Tir is plotted against vegetation index NDVI or Fr one often finds a triangular patten in the pixel envelope, such as is illustrated in Figure 1. This configuration is most apparent under the following conditions: the image contains a sufficiently large number of pixels with at least some containing both vegetation and bare soil, the surface is not highly inhomogeneous (e.g., a forest aside field of short grass), the surface does not slope by more than about 10%, and standing water and cloud are removed. Its triangular shape represents the fact that, while Tir can vary considerably over bare soil, depending on soil wetness and composition, it does not very spatially by more than a very small amount over vegetation (at least no greater than the error in measuring Tir). While individual leaves can experience a range of temperatures from strong sunlight to shade, it is this author’s experience that large clumps of dense vegetation on scales much larger than individual leaves remains uniformly about 1 °C or so above air temperature at least until severe wilting occurs. The latter observation is consistent with the surface sensible heat flux H being typically small over vegetation. Thus, the triangle shape is determined not by the vegetation but by the bare soil around the plants.

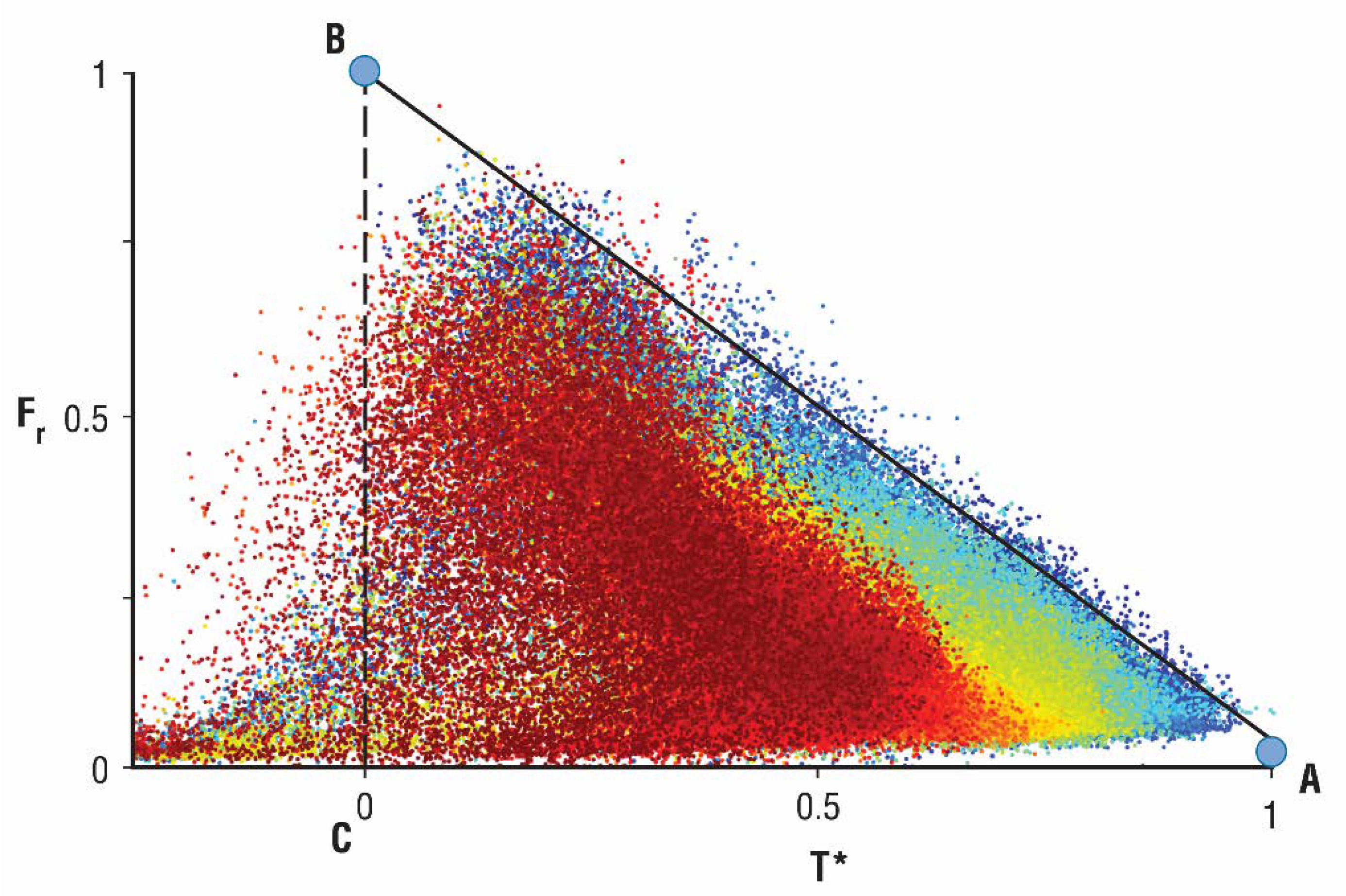
Given the appearance of a triangular shape, the vertical axis can be expressed either as the normalized difference vegetation index (NDVI) or fractional vegetation cover (Fr) and the horizontal as a scaled temperature T*, to be defined below. Two anchor points, A and B, are defined in Figure 2. These points correspond to the lower right-hand vertex (A) where Tir is a maximum over a bare surface, Fr = 0, called Tmax, the vegetation index being defined as NDVIo. The upper vertex (B) corresponds to dense vegetation, Fr = 1.0, where NDVI is defined as NDVIs and Tir is called Tmin, the temperature over dense vegetation, Tmin is also representative of a minimum temperature in the image when all extraneous pixels are removed; the tail of pixels at the lower left-hand corner of Figure 2 are likely due to cloud or standing water. Given these endpoints, a vertical cold edge is drawn down to the soil line from points B to C, defining the boundaries of a right triangle and thereby enclosing almost all the pixels within the triangle. Tir is replaced by the temperature T*, which is scaled between Tmax and Tmin (Equation (2)) and which varies from zero to one. Similarly, NDVI is scaled from its minimum to maximum value and converted to Fr with a simple algorithm (Equation (1)). The segment B–C, the cold edge, forms a right triangle and bounds almost all the pixels on its warm side. Although no fundamental reason exists for the verticality of the cold edge, the data almost always support this assumption, which allows for a more simplified geometry than a slanting one.

In Figure 1 and Figure 2, the warm and cold edges were constructed by eye. Alternately, one can construct the warm edge more objectively. Following Tang et al. [7], the Fr axis is sliced into small segments (e.g., 0.1 wide) and a warm edge is estimated for each slice at the point where, proceeding from the cold edge, a threshold value (e.g., 99%) of the pixels in that slice has been counted. Once all threshold points are made over the full range of Fr, the warm edge is constructed as the least squares straight line through these points extending from the base of the triangle, the soil line at point A, to where it meets the vertical axis, the cold edge, at point B. This procedure is referred to by de Tomas et al. [1] as the ‘Tang dry edge algorithm’.

Scaled variables (T*) and Fr are calculated as follows:

Fr = ((NDVI − NDVIo)/(NDVIs − NDVIo))²

(1)

T* = (Tir − Tmin)/(Tmax − Tmin)

(2)

from which the important moisture variables Mo and EF are calculated. T* is sometimes referred to as the ‘temperature-dryness index’. For a right triangle

Mo = 1 − T* (pixel)/(1 − Fr)

(3)

EF = EF_s (1 − Fr) + EF_veg *Fr

(4)

where Mo pertains only to the bare soil surface and EFveg is the transpiration fraction for vegetation. The latter is assumed to be at potential and therefore it is equal to 1.0.

3. Significance of the Triangle Borders

As shown in Figure 1 and Figure 2, the triangle typically exhibits reasonably well-defined borders, particularly along the bottom of the triangle (the soil line) and its sloping warm side, the warm (or dry) edge. Such sharp edges in nature signify limits of some kind: in this case the limit of no vegetation at its base and the limit of soil dryness along its warm edge. A cold edge, signifying the limit of maximum wetness (field capacity and potential evaporation), is often less well-defined, as is evident in Figure 2.

Two aspects of these triangles are obvious. First, the choice of their warm and cold edges can be somewhat disputed, and, second, the triangles sometimes exhibit small areas with few or no pixels, thereby obscuring somewhat the location of these boundaries. These gaps may occur, for example, because pixels over bare, wet soils are relatively uncommon making the cold edge particularly difficult to locate. Often, what appears to be dense vegetation actually exhibits openings in the plant canopy so that the upper vertex is absent of pixels and the figure resembles a trapezoid, a situation to be addressed in Section 4.

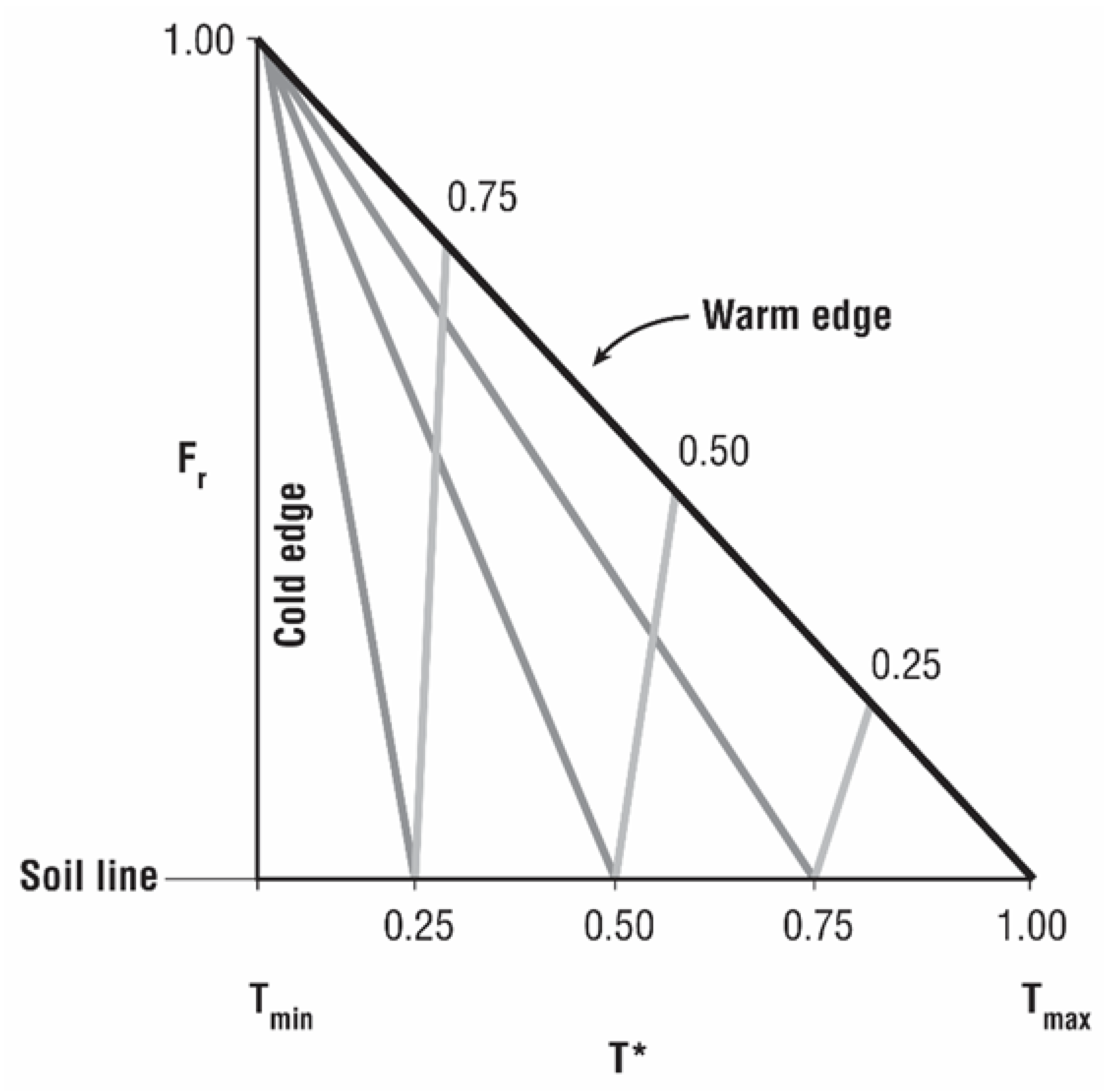
In these types of analyses, one assumes that all the fields internal to the triangle vary linearly across the domain. This enables one to solve for EF and Mo using just a very few simple algebraic formulae. The solution takes the form of the configuration of EF and Mo shown in Figure 3. As the vertical and horizontal axes both vary from 0 to 1.0, all triangles formed with these equations are mathematically congruent, constituting a ‘universal’ triangle. The assumption of linearity is addressed in Section 4.

4. Uncertainties in the Triangle

The triangle approach raises questions concerning the method of assigning its boundaries and the accuracy of the various assumptions. These will now be addressed.

4.1. Errors Arising from the Choice of Anchor Points

An obvious source of uncertainty is the choice of the anchor points that define the vertices of the triangle, A and B in Figure 2. Both points are susceptible to the uncertainty of choice or to the algorithm used to create it, such as a regression line. Some papers have addressed the issue of how much error is engendered by an incorrect location of the warm edge, but this source of error needs to be studied further. Gillies and Carlson [8] thought that it is possible that multiple warm edges might occur in the same image. It seems quite likely that some error in fixing the warm edge can arise from the fact that Tmax and Tmin may have different values within the triangle, the result of differing soil and vegetation types in the image. Addressing uncertainty in choosing these anchor points is further discussed in Section 5. As referred to above, the location of the cold edge is problematic because of the irregular distribution of pixels on that side of the triangle. In practice, nature does not lend itself to simple geometry, so it is necessary to adjust the segment B–C in Figure 2 to intercept the warm edge so as to maintain a right triangle and still include most of the pixels within the triangle.

4.2. The Problem of Scale

Most of us who work with satellite or aircraft imagery believe the higher the resolution is the better. Triangles certainly tend to degrade as the resolution decreases above about 1 km but appear highly satisfactory in the Sentinel image (0.5–1.0 km resolution; Figure 2, see also Gillies and Carlson [8]) and Landsat with its 30–120 resolution (Figure 1). However, extremely high resolution (pixels less than several meters in size) can cause a problem due to small irregularities in the terrain (humps and furrows) and local variations in leaf angles. Such local variations can distort the sun angles, causing significant variations in incident solar flux from those on a horizontal surface, thereby introducing anomalously warm or cold pixels. In such imagery, the triangle edges tend to be fuzzy and less resolvable and so should be composited, as to yield sharper triangle boundaries.

4.3. Triangle or Trapeziod

Many papers on this subject refer to a trapezoid rather than a triangle (e.g., Babaeirian et al. [9]). A trapezoid is just triangle truncated at the top, implying a space void of pixels below the projected vertex. Using a full soil/vegetation/atmosphere/transfer (SVAT) model described by Carlson [10], it was found that a variation of Mo with Tir occurs at full vegetation when the leaf area index (LAI) is not very large (e.g., 3 or less), presumably because the vegetation canopy still exhibits gaps through which radiance from the bare soil beneath can reach the radiometer. When LAI is raised well above 3 in these simulations, the trapezoid collapses to a right triangle, suggesting that the true value of Fr is higher than that originally selected for a full vegetation cover. De Tomas et al. [1] also found the same thing: that the trapezoid reduced to a triangle when LAI was increased to amounts well above 3. Here the full vegetation cover Fr = 1 is defined as that at the triangle’s upper vertex (point B in Figure 2), even if no pixels appear just below it.

4.4. The Assumption of Linearity

A fundamental assumption in the triangle method is that all fields interior to the triangle (or trapezoid) vary linearly. That assumption leads to the interior isopleths of Mo and EF shown in Figure 3.

Solutions for these two variables generated from more complex models, such as the SVAT model referred to in Carlson [10], show very similar nearly straight lines for Mo to those shown in this figure. emanating from the upper vertex to the soil line. EF, on the other hand, is highly nonlinear. Carlson and Petropoulos [3] show that on the average the differences with the linear model are generally less than 20%. Kasim et al. [5] also found close agreement between the fields of Mo and EF generated with the model described above [10] and those represented in Figure 3. Very similar fields of EF to those in Figure 3 are shown by de Tomas et al. [1].

While it might seem useful to determine more accurate values for Mo and EF with a more mathematically complex formalism, it is not clear whether the large number of surface and atmospheric and plant parameters necessary to initialize such models and the mathematical complexity facing the user in operating them would result in more accurate, practical, or cost effective solutions for Mo and EF.

4.5. The Meaning of Mo and EF

Moisture availability Mo is generally equated to the soil water content as the fraction of field capacity or a similar upper value (e.g., saturation). Little evidence exists for assuming a linear relationship, although various studies demonstrate it to be highly correlated with soil water content, albeit generally with low values of correlation, as in Kasim et al. [5].

One problem in equating Mo to soil water content is that comparisons with field measurements are generally rather poor because in situ measurements are usually confined to the top 5 cm, whereas Tir represents a soil skin temperature which is best correlated with water content within the top 1 cm (Capehart and Carlson, [11]). Another problem with Mo is that the accuracy of thermal/optical methods deteriorates with increasing Fr, completely losing any value as Fr approaches 1.0. Consequently, Mo values are essentially valueless near the upper vertex of the triangle (Gillies and Carlson, [8]; Kasim et al. [5]). Conversely, agreement with ground measurements shows a much better correlation when comparisons are limited to pixels with small amounts of vegetation Kasim et al. [5].

Evapotranspiration fraction EF is more useful than transpiration itself, which is highly transient. Depending on its definition (as ET/Rn or ET/(Rn - G), where G is the ground heat flux), EF corresponds approximately or exactly to the Bowen ratio which is defined as H/ET where H is the surface heat flux and ET is the evapotranspiration. As the Bowen ratio is known to remain approximately constant throughout most of the solar day, it can be used to calculate total water lost from the soil during the day by multiplying EF by the total net radiation absorbed at the ground over the length of the solar day. (Note that the ground heat flux G tends toward zero when averaged over a full 24 h.) Both Rasmussen et al. [2] and de Tomas et al. [1], using the triangle method, mapped the value of ϕ (the modifier of the Penman–Monteith evapotranspiration formula), which is essentially identical to EF.

5. Practical Considerations

5.1. Operational Implementation

It is hard to conceive at present that a fully operational system for a practical and systematic implementation of the triangle could be accomplished without a human/machine synergy. The latter is envisaged as the person, interacting with the computer by means of an electronic pen or cursor, whose function would be to insert the two anchor points A and B on an image of pixels plotted in Tir and NDVI space. This would be done according to steps summarized below and illustrated by the image in Figure 2, the latter made over an agricultural site in Spain by Sentinel-3 (Petropoulos et al. [3]). What follows is a roadmap on how this might be accomplished.

• Pixels contaminated by cloud or standing water are first removed. Elimination of these anomalies is accomplished by realizing that the ratio of visible reflectance to Tir is much higher for cloud pixels and the product of NDVI times Tir is much smaller for standing water than for most natural surfaces.
• Remaining pixels are plotted by computer on orthogonal axes as values of Tir and NDVI, as in Figure 2.
• With an electronic pen or cursor, the user inspects the image and visually marks with a dot on the computer monitor the two anchor points, labeled A and B, as in Figure 2. These points correspond, respectively, to Tmax and NDVIo (Fr = 0) and to Tmin and NDVIs (Fr = 1).
• Once points A and B are marked, the computer relabels the axes as Fr and T* (using Equations (1) and (2)) and internally calculates Mo and EF (using Equations (3) and (4)).
• Having marked the two anchor points, the computer immediately draws the warm edge between points A and B and the cold edge between B and C, where the line B–C is drawn vertically from the warm edge line to intersect with the soil line. In so doing, vertical line B–C, the cold edge line, should contain most of the pixels on its warm side.
• The computer then constructs and alternate warm edge line by first determining a series of points in slices of Fr from zero to one corresponding to a threshold percentage of pixels (e.g., 99%) as described above: the ‘Tang dry edge’ (de Tomas et al. [1]).
• An alternate warm edge is constructed by a linear least squares fit to these points and the line extended to the soil line and the vertical cold edge. The user would then have the option of adjusting the visual and analytical warm edges (by moving the anchor points A and B) to achieve a satisfactory and mutually consistent set of borders for the triangle.
• Anchor points A and B may need further adjustment in order to be compatible with the overall pixel distribution and the warm edge. During this process of adjustment, the triangle’s scaling and the internal values of Mo and EF are continually being recalculated.
• When the user is satisfied with the construction, all values of Mo and EF within the triangle are mapped to the surface area over which the image was made.

5.2. A Dynamic Crop Moisture Index

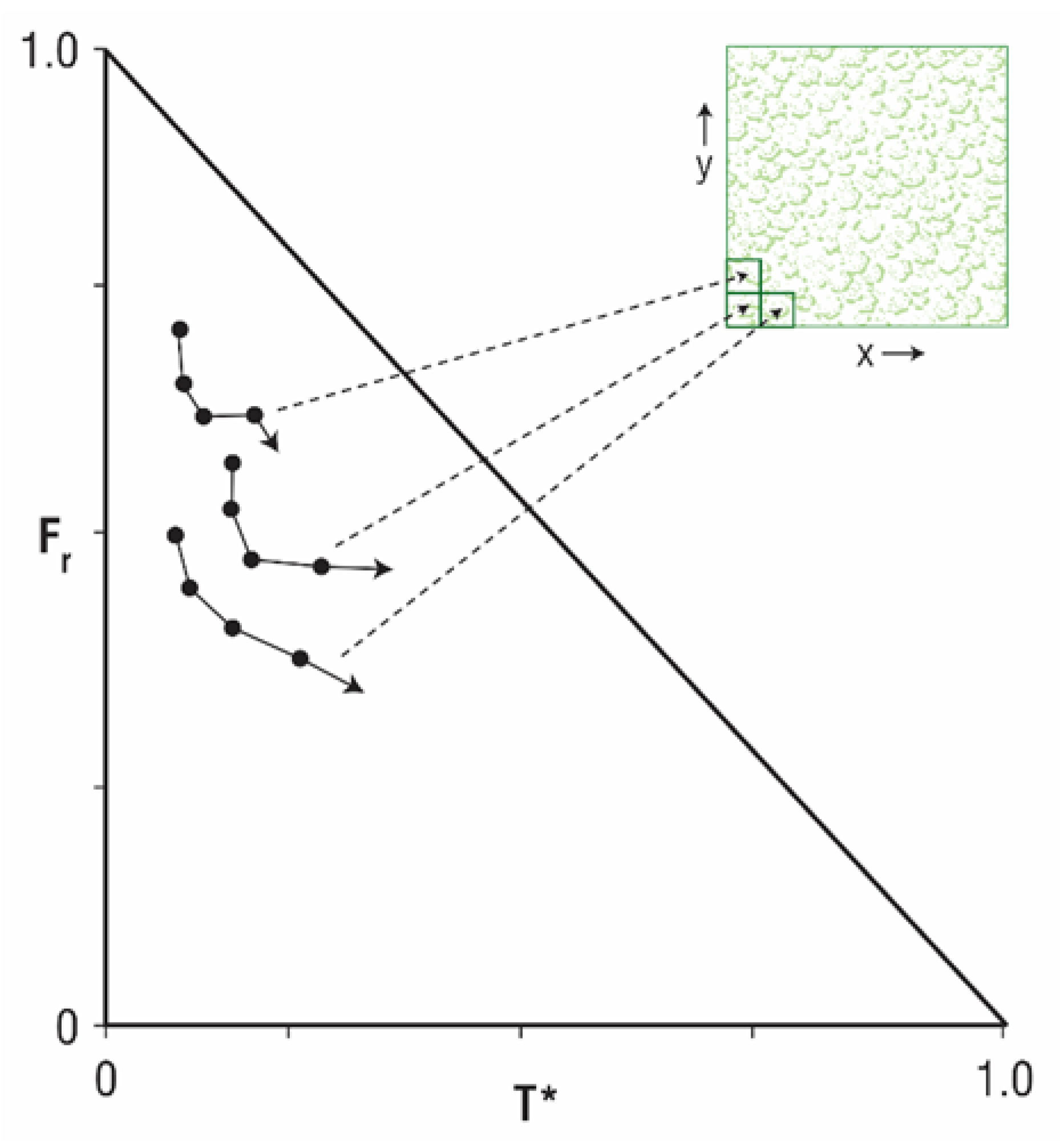
Frequent references haves been made in the literature to a crop moisture index, many of which are virtual transforms of Mo (Jackson et al. [12]). Whether a variation of Mo or as a two-dimensional variable (Fr, T*) within the triangle, a crop moisture index currently represents a single number that does not unambiguously prescribe a level of water stress. A clearer picture of water stress would be achieved by monitoring the changes in the stress parameter over time by including trajectories of points within the triangle for fixed surface locations as represented by the three trajectories in Figure 4.

Each of these three trajectories pertains to values of Mo and EF on five successive days represented by the five dots (including the arrowhead) along the trajectories. Each trajectory pertains to an area in the field represented by one of three squares located the corner of a hypothetical field of vegetation shown to the right of the figure. Illustrated in this figure is a progressive movement toward lower values of EF, Mo and Fr and higher values of T*. (In practice, the fields of Mo and EF will be superimposed on the triangles, as in Figure 3.)

Of course, it would be overwhelming to chart every point in an image containing many hundreds of thousands or millions of pixels. As Figure 4 implies however, fields would be divided into a grid and representative values of Mo and EF determined, each square within the grid, each square initially containing hundreds or thousands of pixels. Averages of Mo and EF for each square would reduce the number of estimates to a viable level that would be displayed on a screen. In such a scenario, the user would be able to scan just a few tens of trajectories and quickly assess the degree of water stress in different parts of the area. More simply, these statistics also could also be tabulated and displayed in each square as numerical changes in Mo and EF.

6. Summary

This paper presents a mathematically and conceptually simple primer for constructing and applying the triangle method, with a view to its operational implementation and practical use, for example, as a crop moisture index. It addresses some uncertainties in triangle construction, notably the uncertainty in fixing its warm and cold edges (anchor points). The paper concludes by presenting a systematic methodology for constructing the triangle in tandem with a computer and displaying a crop moisture index.

Much needs to be explored and clarified in the triangle method. It has not been fully tested and explored when applied in different environmental conditions, for example in tropical or polar regions. Another useful investigation to be undertaken in the future in conjunction with direct field measurements would be to inspect pixels that lie outside the bounds of the triangle so as to determine whether these are truly anomalous or arise from surface irregularities or perhaps constitute some new insight into water stress on vegetation.