Evaporative Fluxes and Surface Soil Moisture Retrievals in a Mediterranean Setting from Sentinel-3 and the “Simplified Triangle”
Abstract
1. Introduction
2. Materials
2.1. Study Sites and In Situ Data
2.2. Sentinels Data: Acquisition and Preprocessing
3. Methods
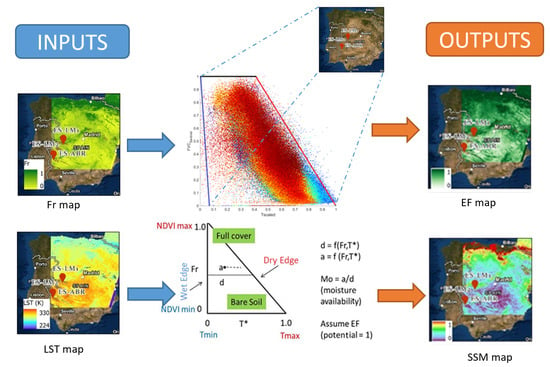
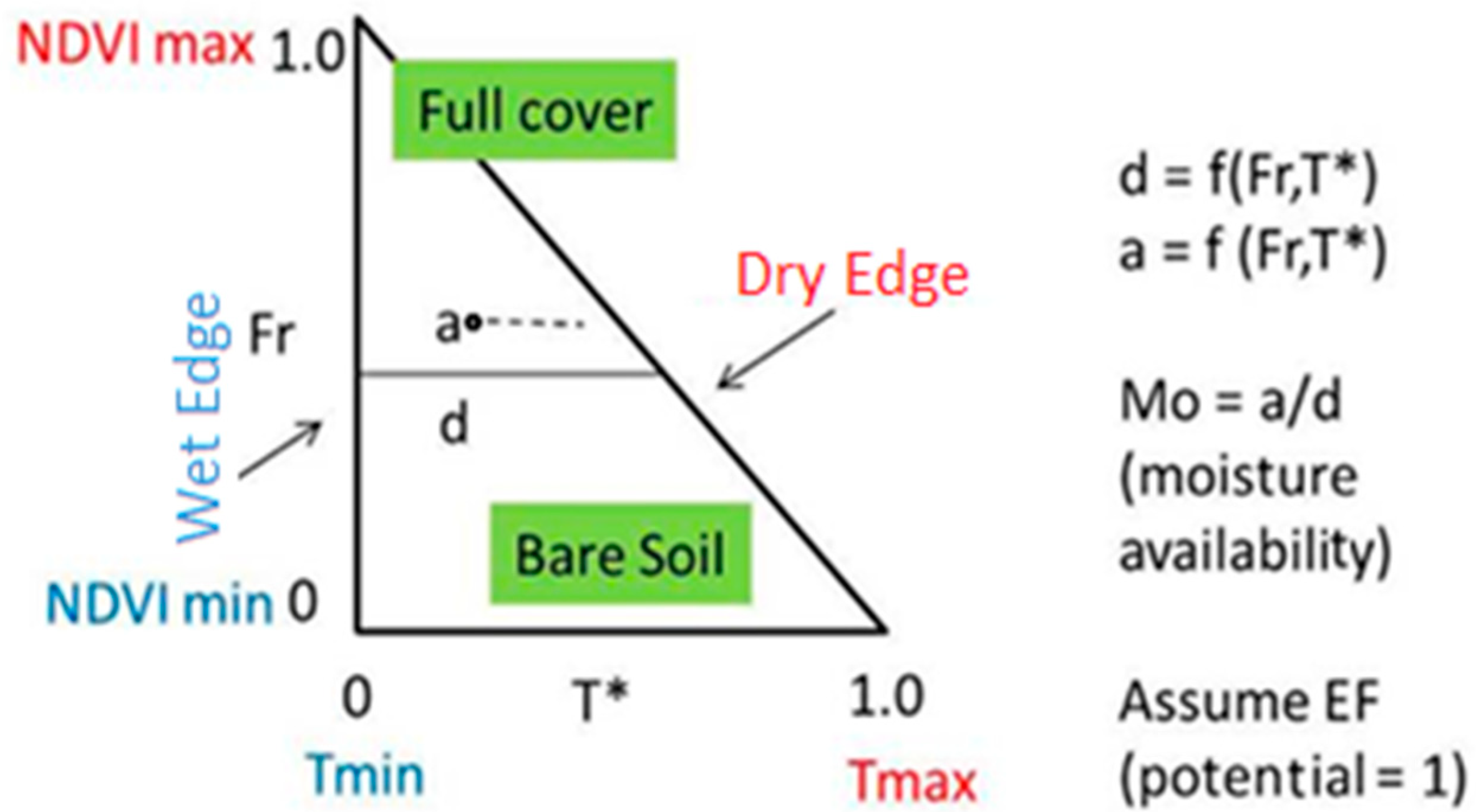
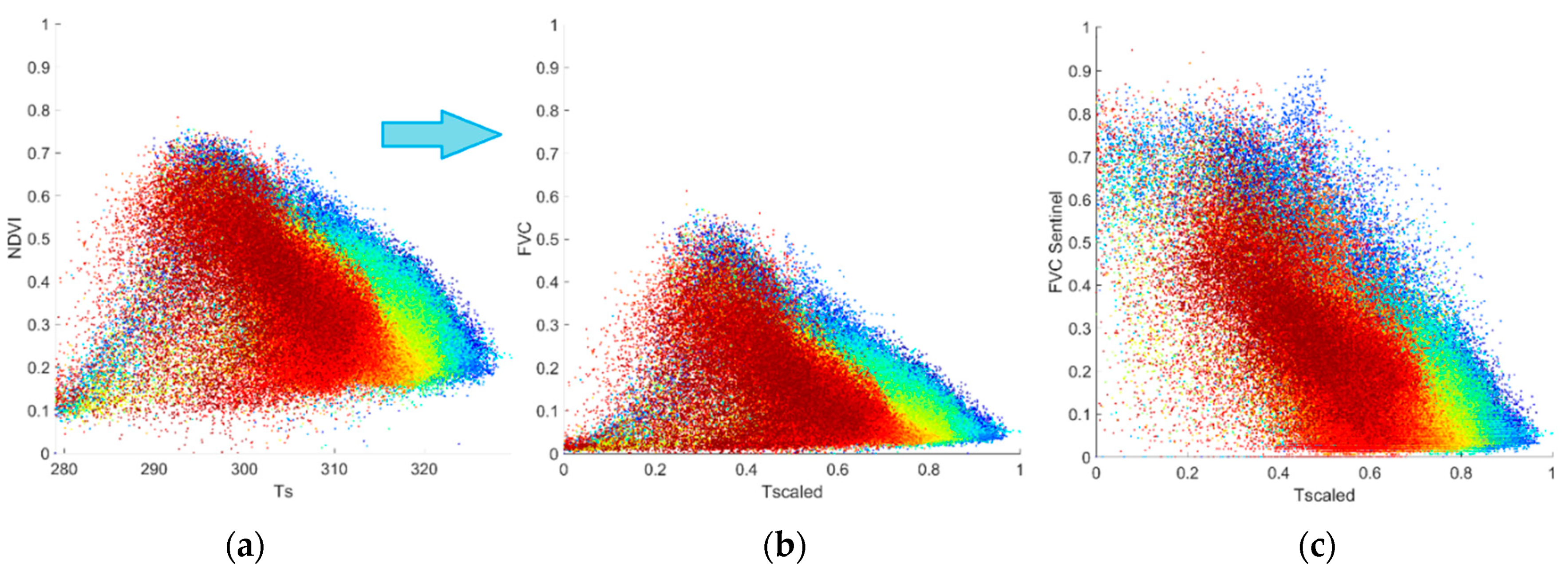
3.1. “Simplified Triangle”
3.2. Statistical Analysis
4. Results
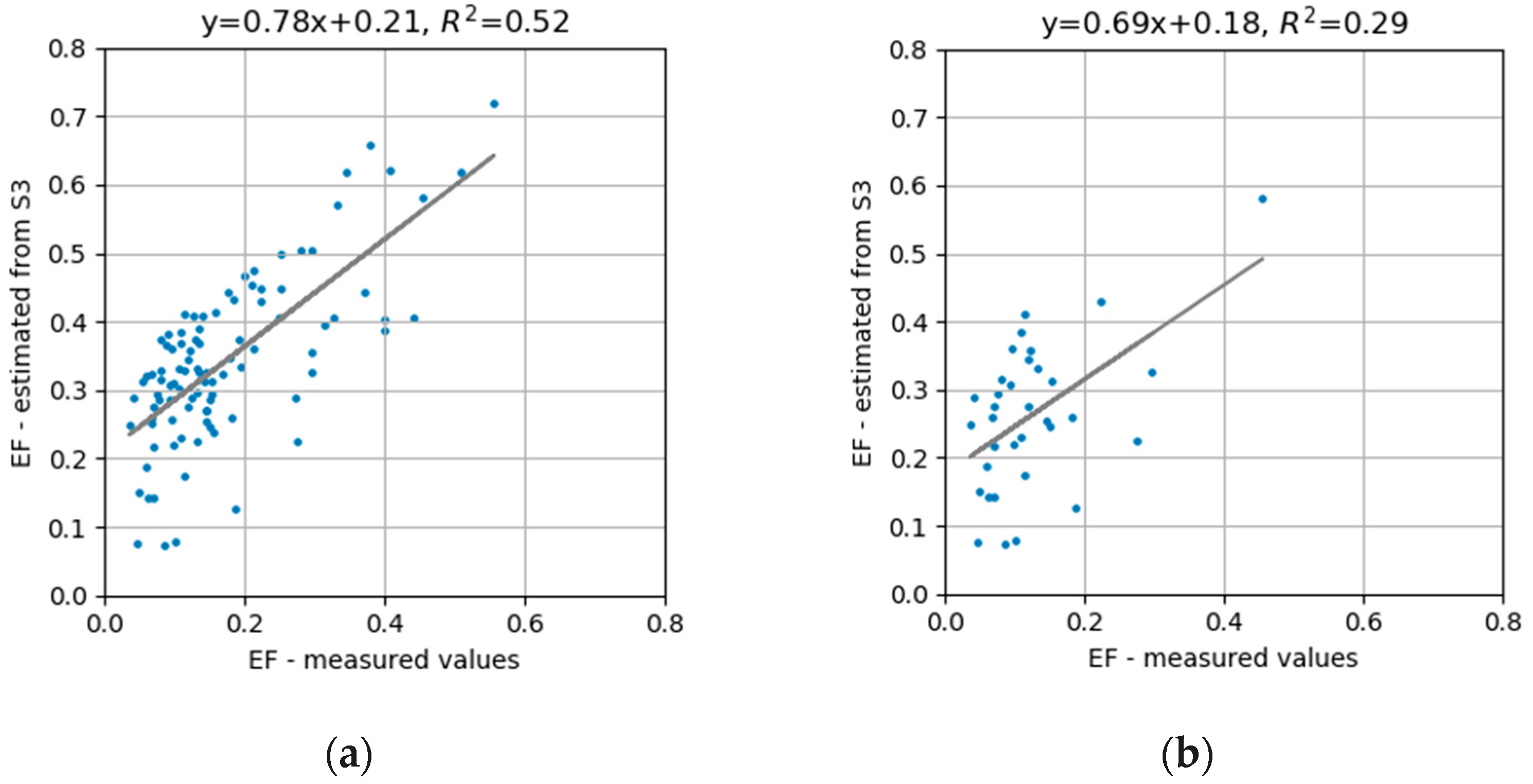
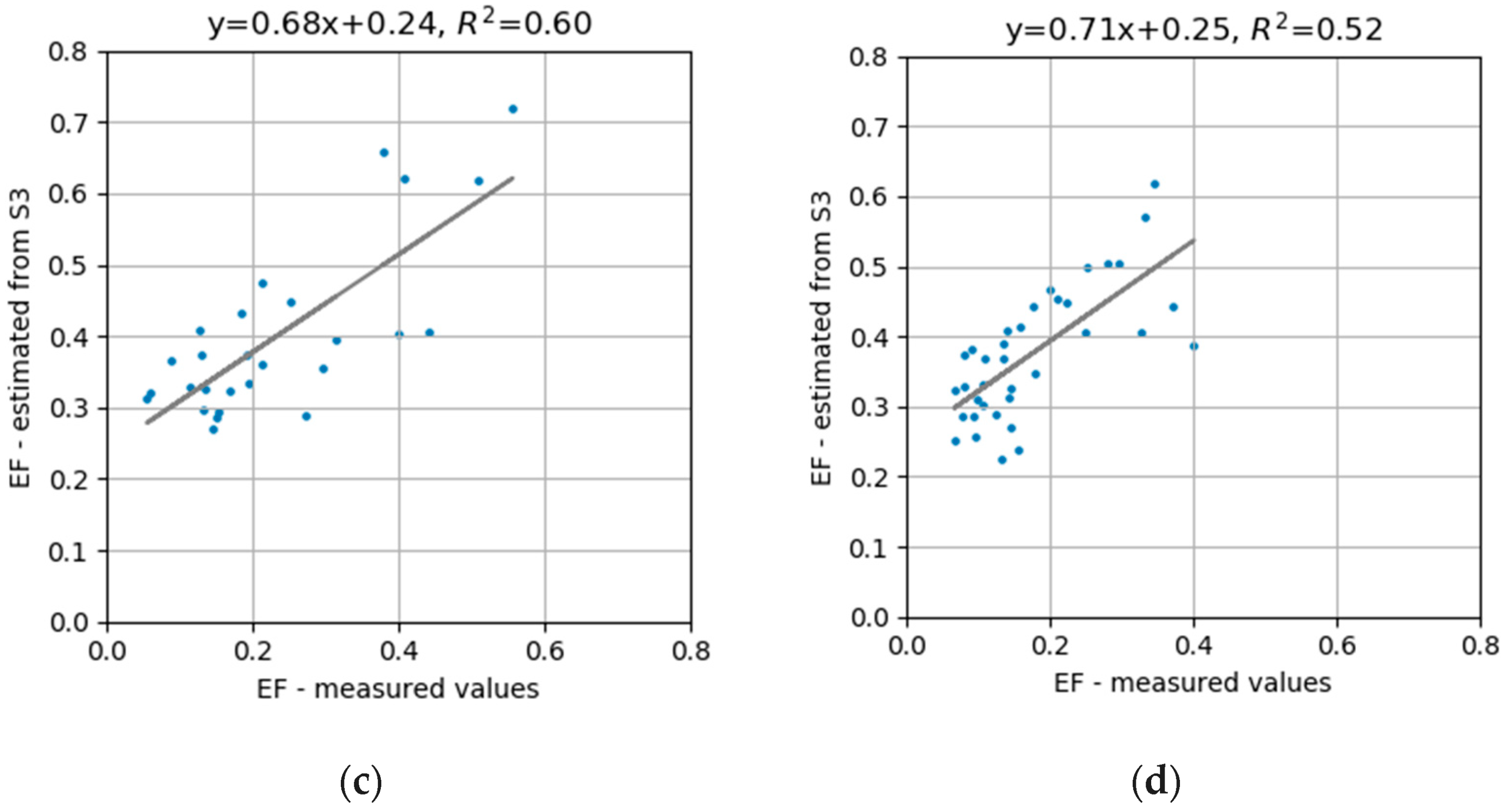
4.1. EF Comparisons
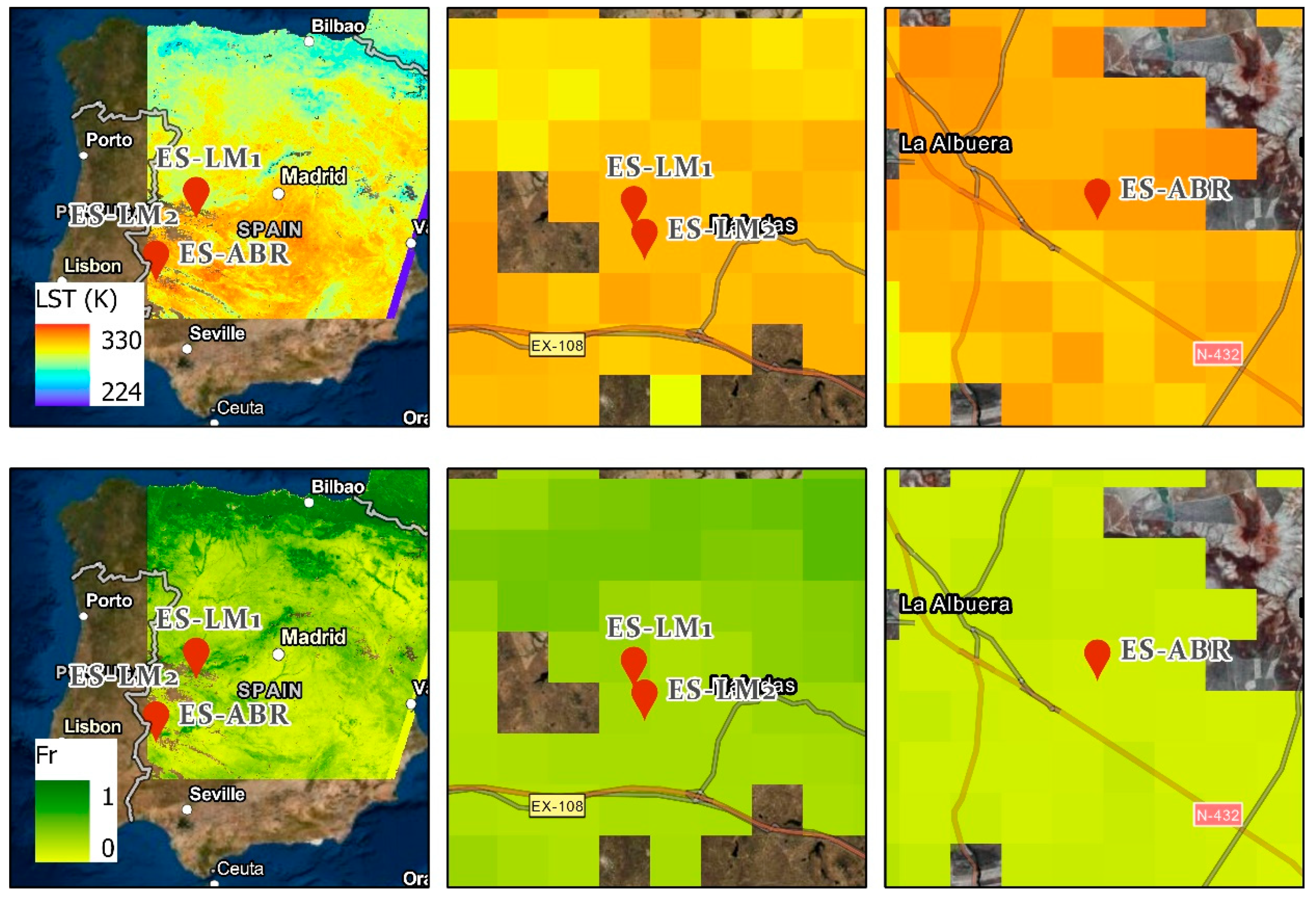
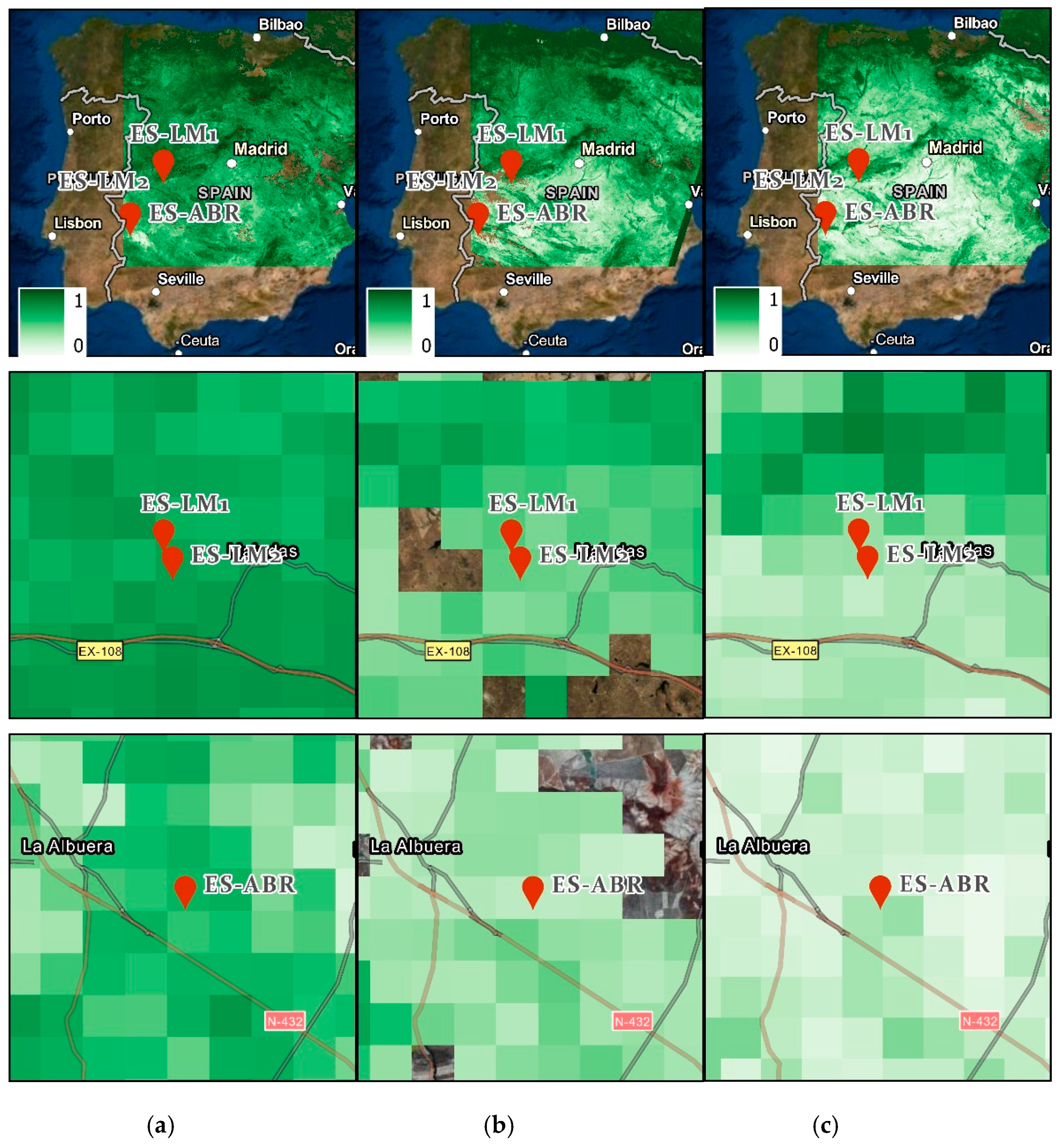
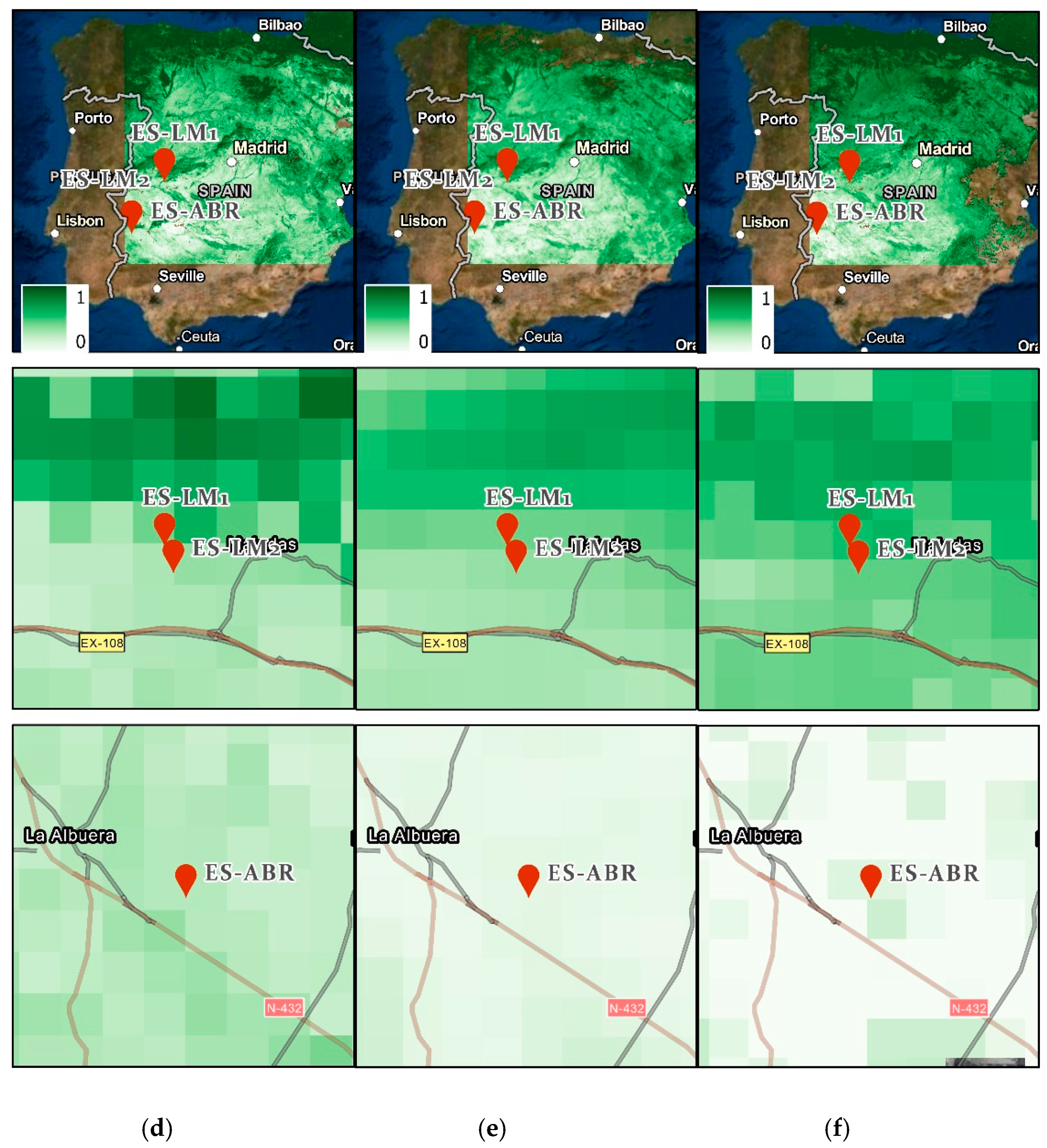
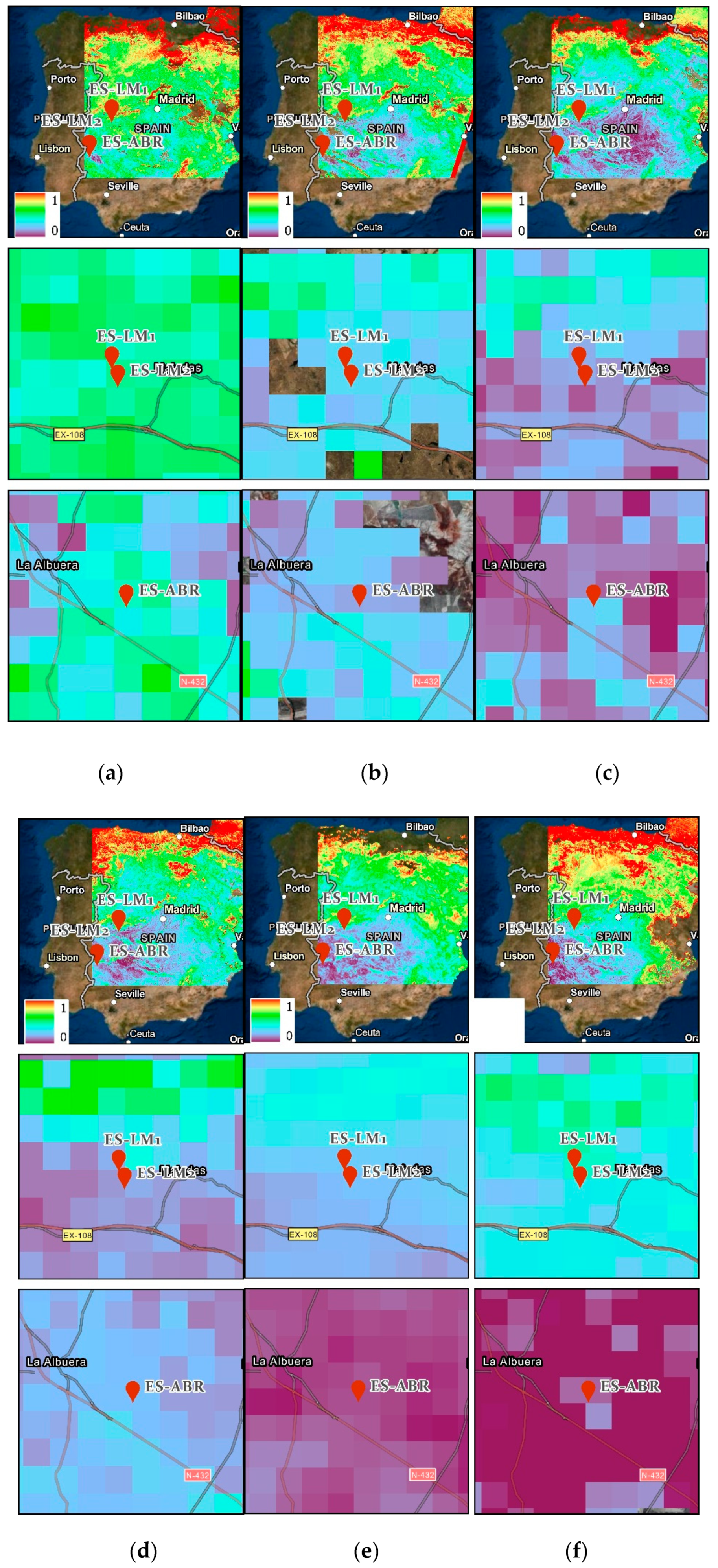
4.1.1. Visual Comparisons
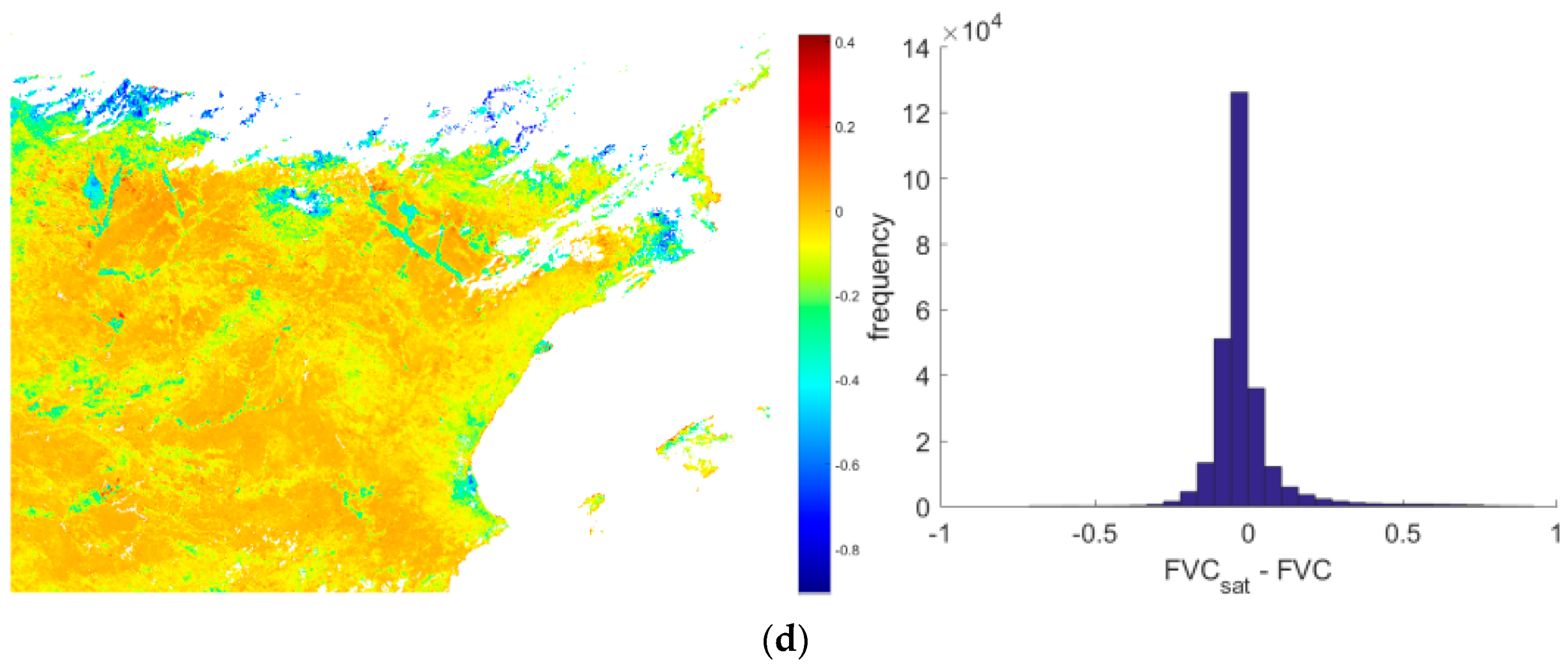
4.1.2. Point Comparisons
4.2. SSM Comparisons
4.2.1. Visual Comparisons
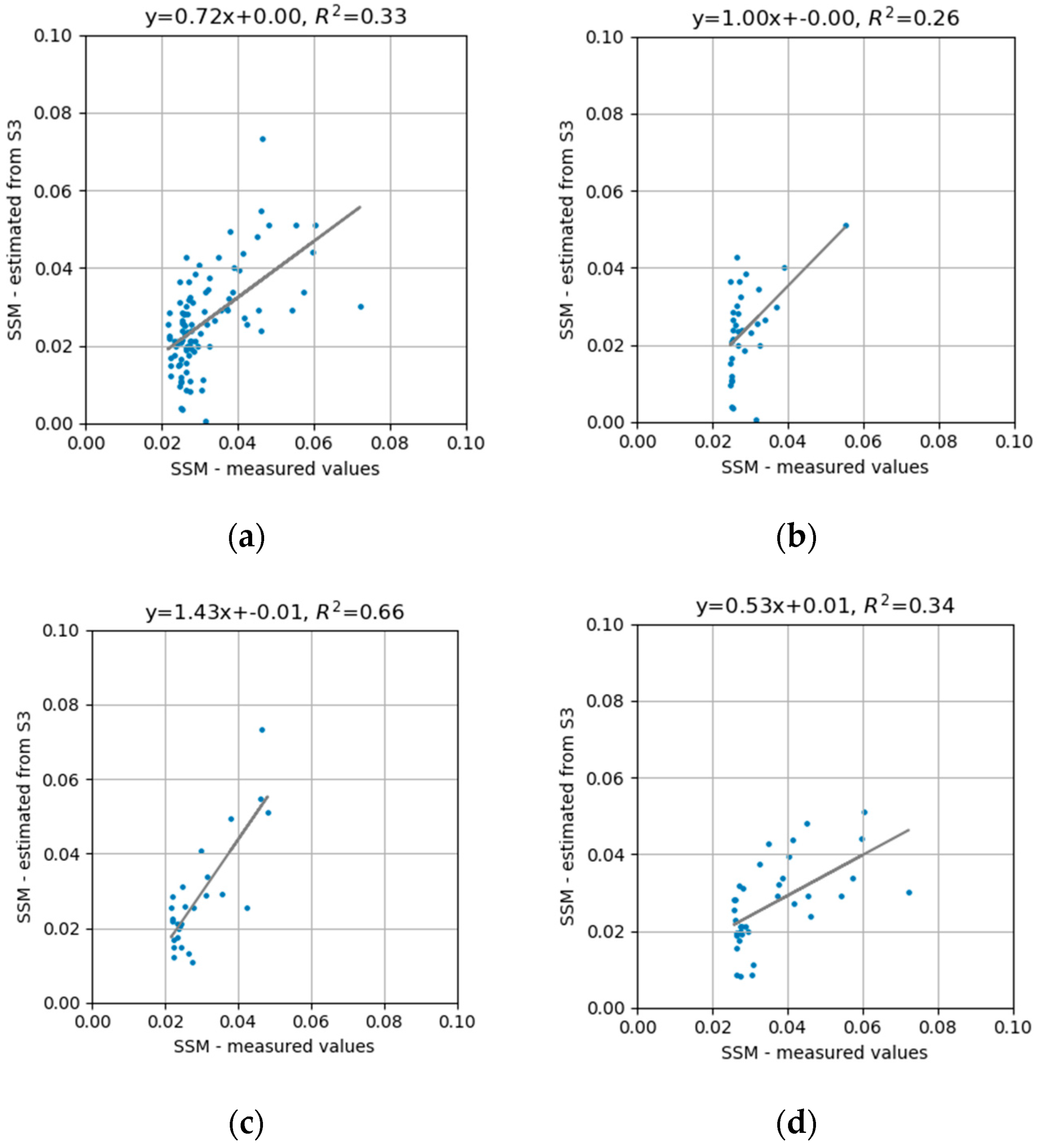
4.2.2. Point Comparisons
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Watts, J.D.; Lawrence, R.L.; Miller, P.R.; Montagne, C. Monitoring of cropland practices for carbon sequestration purposes in north central Montana by Landsat remote sensing. Remote Sens. Environ. 2009, 113, 1843–1852. [Google Scholar] [CrossRef]
- Wang, J.; Chen, Y.; He, T.; Lv, C.; Liu, A. Application of geographic image cognition approach in land type classification using Hyperion image: A case study in China. Int. J. Appl. Earth Obs. Geoinf. 2010, 12, S212–S222. [Google Scholar] [CrossRef]
- Liu, J.-G.; Xie, Z.-H. Improving simulation of soil moisture in China using a multiple meteorological forcing ensemble approach. Hydrol. Earth Syst. Sci. 2013, 17, 3355–3369. [Google Scholar] [CrossRef]
- Anagnostopoulos, V.; Petropoulos, G.P.; Ireland, G.; Carlson, T.N. A modernized version of a 1D soil vegetation atmosphere transfer model for improving its future use in land surface interactions studies. Environ. Model. Softw. 2017, 90, 147–156. [Google Scholar] [CrossRef]
- Deng, K.A.K.; Lamine, S.; Pavlides, A.; Petropoulos, G.P.; Bao, Y.; Srivastava, P.K.; Guan, Y. Large scale operational soil moisture mapping from passive MW radiometry: SMOS product evaluation in Europe & USA. Int. J. Appl. Earth Obs. Geoinf. 2019, 80, 206–217. [Google Scholar]
- Sun, H. A two-source model for estimating evaporative fraction (TMEF) coupling priestley-taylor formula and two-stage trapezoid. Remote Sens. 2016, 8, 248. [Google Scholar] [CrossRef]
- Tang, R.; Li, Z.L.; Huo, X.; Jiang, Y.; Tang, B.; Wu, H. A re-examination of two methods for estimating daily evapotranspiration from remotely sensed instantaneous observations. Int. J. Remote Sens. 2019, 40, 1981–1995. [Google Scholar]
- Bao, Y.; Lin, L.; Wu, S.; Kwal Deng, K.A.; Petropoulos, G.P. Surface soil moisture retrievals over partially vegetated areas from the synergy of Sentinel-1 and Landsat 8 data using a modified water-cloud model. Int. J. Appl. Earth Obs. Geoinf. 2018, 72, 76–85. [Google Scholar] [CrossRef]
- Cui, Y.; Ma, S.; Yao, Z.; Chen, X.; Luo, Z.; Fan, W.J.; Hong, Y. Developing a gap-filling algorithm using DNN for the Ts-VI triangle model to obtain temporally continuous daily actual evapotranspiration in an arid area of China. Remote Sens. 2020, 12, 1121. [Google Scholar] [CrossRef]
- Prentice, I.C.; Liang, X.; Medlyn, B.E.; Wang, Y.-P. Reliable, robust and realistic: The three R’s of next-generation land-surface modelling. Atmos. Chem. Phys. 2015, 15, 5987–6005. [Google Scholar] [CrossRef]
- Yang, T.; Wan, W.; Sun, Z.; Liu, B.; Li, S.; Chen, X. Comprehensive evaluation of using TechDemoSat-1 and CYGNSS data to estimate soil moisture over mainland China. Remote Sens. 2020, 12, 1699. [Google Scholar] [CrossRef]
- Petropoulos, G.P.; Carlson, T.N.; Griffiths, H. Turbulent Fluxes of Heat and Moisture at the Earth’s Land Surface: Importance, Controlling Parameters and Conventional Measurement. In Remote Sensing of Energy Fluxes and Soil Moisture Content; Petropoulos, G.P., Ed.; Taylor and Francis: Boca Raton, FL, USA, 2013; Chapter 1; pp. 3–28. ISBN 978-1-4665-0578-0. [Google Scholar]
- Xu, C.; Qu, J.J.; Hao, X.; Cosh, M.H.; Prueger, J.H.; Zhu, Z.; Gutenberg, L. Downscaling of surface soil moisture retrieval by combining MODIS/Landsat and in situ measurements. Remote Sens. 2018, 10, 210. [Google Scholar] [CrossRef]
- Petropoulos, G.P.; Carlson, T.; Wooster, M.J.; Islam, S. A review of Ts/VI remote sensing based methods for the retrieval of land surface energy fluxes and soil surface moisture. Prog. Phys. Geogr. Earth Environ. 2009, 33, 224–250. [Google Scholar] [CrossRef]
- Gillies, R.R.; Kustas, W.P.; Humes, K.S. A verification of the ‘triangle’ method for obtaining surface soil water content and energy fluxes from remote measurements of the Normalized Difference Vegetation Index (NDVI) and surface e. Int. J. Remote Sens. 1997, 18, 3145–3166. [Google Scholar] [CrossRef]
- De Tomás, A.; Nieto, H.; Guzinski, R.; Salas, J.; Sandholt, I.; Berliner, P. Validation and scale dependencies of the triangle method for the evaporative fraction estimation over heterogeneous areas. Remote Sens. Environ. 2014, 152, 493–511. [Google Scholar] [CrossRef]
- Minacapilli, M.; Consoli, S.; Vanella, D.; Ciraolo, G.; Motisi, A. A time domain triangle method approach to estimate actual evapotranspiration: Application in a Mediterranean region using MODIS and MSG-SEVIRI products. Remote Sens. Environ. 2016, 174, 10–23. [Google Scholar] [CrossRef]
- Zawadzki, J.J.; Przeździecki, K.; Miatkowski, Z. Determining the area of influence of depression cone in the vicinity of lignite mine by means of triangle method and LANDSAT TM/ETM+ satellite images. J. Environ. Manag. 2016, 166, 605–614. [Google Scholar] [CrossRef]
- Piles, M.; Petropoulos, G.P.; Sánchez, N.; González-Zamora, Á.; Ireland, G. Towards improved spatio-temporal resolution soil moisture retrievals from the synergy of SMOS and MSG SEVIRI spaceborne observations. Remote Sens. Environ. 2016, 180, 403–417. [Google Scholar] [CrossRef]
- Amani, M.; Parsian, S.; MirMazloumi, S.M.; Aieneh, O. Two new soil moisture indices based on the NIR-red triangle space of Landsat-8 data. Int. J. Appl. Earth Obs. Geoinform. 2016, 50, 176–186. [Google Scholar] [CrossRef]
- Foucras, M.; Zribi, M.; Albergel, C.; Baghdadi, N.; Calvet, J.-C.; Pellarin, T. Estimating 500-m resolution soil moisture using Sentinel-1 and optical data synergy. Water 2020, 12, 866. [Google Scholar] [CrossRef]
- Bai, J.; Cui, Q.; Zhang, W.; Meng, L. An approach for downscaling SMAP soil moisture by combining Sentinel-1 SAR and MODIS data. Remote Sens. 2019, 11, 2736. [Google Scholar] [CrossRef]
- Wang, K.; Li, Z.; Cribb, M. Estimation of evaporative fraction from a combination of day and night land surface temperatures and NDVI: A new method to determine the Priestley–Taylor parameter. Remote Sens. Environ. 2006, 102, 293–305. [Google Scholar] [CrossRef]
- Chauhan, N.S.; Miller, S.; Ardanuy, P. Spaceborne soil moisture estimation at high resolution: A microwave-optical/IR synergistic approach. Int. J. Remote Sens. 2003, 24, 4599–4622. [Google Scholar] [CrossRef]
- Maltese, A.; Capodici, F.; Ciraolo, G.; La Loggia, G. Soil water content assessment: Critical issues concerning the operational application of the triangle method. Sensors 2015, 15, 6699–6718. [Google Scholar] [CrossRef]
- European Space Agency. A Pathfinder for Innovation in Earth Observation, ESA. Available online: http://due.esrin.esa.int/stse/files/document/STSE_report_121016.pdf (accessed on 10 April 2020).
- Piles, M.; Camps, A.; Vall-Llossera, M.; Corbella, I.; Panciera, R.; Rüdiger, C.; Kerr, Y.H.; Walker, J. Downscaling SMOS-derived soil moisture using MODIS visible/infrared data. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3156–3166. [Google Scholar] [CrossRef]
- Carlson, T.N.; Petropoulos, G.P. A new method for estimating of evapotranspiration and surface soil moisture from optical and thermal infrared measurements: The simplified triangle. Int. J. Remote Sens. 2019, 40, 7716–7729. [Google Scholar] [CrossRef]
- Fuzzo, D.F.S.; Carlson, T.N.; Kourgialas, N.N.; Petropoulos, G.P. Coupling remote sensing with a water balance model for soybean yield predictions over large areas. Earth Sci. Inform. 2019, 13, 345–359. [Google Scholar] [CrossRef]
- Drusch, M.; Del Bello, U.; Carlier, S.; Colin, O.; Fernandez, V.; Gascón, F.; Hoersch, B.; Isola, C.; Laberinti, P.; Martimort, P.; et al. Sentinel-2: ESA’s optical high-resolution mission for GMES operational services. Remote Sens. Environ. 2012, 120, 25–36. [Google Scholar] [CrossRef]
- Guzinski, R.; Nieto, H. Evaluating the feasibility of using Sentinel-2 and Sentinel-3 satellites for high-resolution evapotranspiration estimations. Remote Sens. Environ. 2019, 221, 157–172. [Google Scholar] [CrossRef]
- Baldocchi, D.; Valentini, R.; Running, S.; Oechel, W.C.; Dahlman, R. Strategies for measuring and modelling carbon dioxide and water vapour fluxes over terrestrial ecosystems. Glob. Chang. Biol. 1996, 2, 159–168. [Google Scholar] [CrossRef]
- Aubinet, M.; Grelle, A.; Ibrom, A.; Rannik, Ü.; Moncrieff, J.; Foken, T.; Kowalski, A.; Martin, P.; Berbigier, P.; Bernhofer, C.; et al. Estimates of the annual net carbon and water exchange of forests: The EUROFLUX methodology. Adv. Ecol. Res. 1999, 30, 113–175. [Google Scholar] [CrossRef]
- Wilson, K.; Goldstein, A.H.; Falge, E.; Aubinet, M.; Baldocchi, D.; Berbigier, P.; Bernhofer, C.; Ceulemans, R.; Dolman, H.; Field, C.; et al. Energy balance closure at FLUXNET sites. Agric. For. Meteorol. 2002, 113, 223–243. [Google Scholar] [CrossRef]
- Castellvi, F.; Martínez-Cob, A.; Pérez-Coveta, O. Estimating sensible and latent heat fluxes over rice using surface renewal. Agric. For. Meteorol. 2006, 139, 164–169. [Google Scholar] [CrossRef]
- North, M.R.; Petropoulos, G.P.; Ireland, G.; McCalmont, J. Appraising the capability of a land biosphere model as a tool in modelling land surface interactions: Results from its validation at selected European ecosystems. Earth Syst. Dyn. Discuss. 2015, 6, 217–265. [Google Scholar] [CrossRef]
- Petropoulos, G.P.; Ireland, G.; Griffiths, H.M.; Kennedy, M.C.; Ioannou-Katidis, P.; Kalivas, D. Extending the global sensitivity analysis of the SimSphere model in the context of its future exploitation by the scientific community. Water 2015, 7, 2101–2141. [Google Scholar] [CrossRef]
- Birks, A.; Cox, C. SLSTR: Algorithm Theoretical Basis Definition Document for Level 1 Observables; Science and Technology Facilities Council: Swindon, UK, 2011; p. 173. [Google Scholar]
- Philippe Goryl, E.; Buongiorno, A.; Santella, C.; EUMETSAT Vincent Fournier-Sicre; Santacesaria, V. University of Leicester/NILU Sentinel-3 Optical Products and Algorithm Definition SLSTR ATBD Land Surface Temperature; ESA: Paris, France, 2012. [Google Scholar]
- Carlson, T.N. An overview of the “Triangle Method” for Estimating surface evapotranspiration and soil moisture from satellite imagery. Sensors 2007, 7, 1612–1629. [Google Scholar] [CrossRef]
- Sun, L.; Sun, R.; Li, X.; Liang, S.; Zhang, R. Monitoring surface soil moisture status based on remotely sensed surface temperature and vegetation index information. Agric. For. Meteorol. 2012, 166, 175–187. [Google Scholar] [CrossRef]
- Marshall, M.; Thenkabail, P. Advantage of hyperspectral EO-1 Hyperion over multispectral IKONOS, GeoEye-1, WorldView-2, Landsat ETM+, and MODIS vegetation indices in crop biomass estimation. ISPRS J. Photogramm. Remote Sens. 2015, 108, 205–218. [Google Scholar] [CrossRef]
- Peng, J.; Loew, A. Evaluation of daytime evaporative fraction from MODIS TOA radiances using FLUXNET observations. Remote Sens. 2014, 6, 5959–5975. [Google Scholar] [CrossRef]
- Petropoulos, G.P.; Ireland, G.; Lamine, S.; Griffiths, H.M.; Ghilain, N.; Anagnostopoulos, V.; North, M.R.; Srivastava, P.K.; Georgopoulou, H. Operational evapotranspiration estimates from SEVIRI in support of sustainable water management. Int. J. Appl. Earth Obs. Geoinform. 2016, 49, 175–187. [Google Scholar] [CrossRef]
- Petropoulos, G.P.; Ireland, G.; Srivastava, P.K. Evaluation of the soil moisture operational estimates from smos in europe: Results over diverse ecosystems. IEEE Sens. J. 2015, 15, 5243–5251. [Google Scholar] [CrossRef]
- Lu, J.; Tang, R.; Shao, K.; Li, Z.-L.; Zhou, G. Assessment of two temporal-information-based methods for estimating evaporative fraction over the Southern Great Plains. Int. J. Remote Sens. 2015, 36, 1–17. [Google Scholar] [CrossRef]
- Zhang, H.; Gorelick, S.M.; Avisse, N.; Tilmant, A.; Rajsekhar, D.; Yoon, J. A new temperature-vegetation triangle algorithm with variable edges (TAVE) for satellite-based actual evapotranspiration estimation. Remote Sens. 2016, 8, 735. [Google Scholar] [CrossRef]
- Lu, L.; Luo, G.-P.; Wang, J.-Y. Development of an ATI-NDVI method for estimation of soil moisture from MODIS data. Int. J. Remote Sens. 2014, 35, 3797–3815. [Google Scholar] [CrossRef]
- Petropoulos, G.P.; Ireland, G.; Barrett, B. Surface soil moisture retrievals from remote sensing: Current status, products & future trends. Phys. Chem. Earth Parts A/B/C 2015, 83–84, 36–56. [Google Scholar] [CrossRef]
- Tang, R.; Li, Z.-L.; Tang, B. An application of the Ts–VI triangle method with enhanced edges determination for evapotranspiration estimation from MODIS data in arid and semi-arid regions: Implementation and validation. Remote Sens. Environ. 2010, 114, 540–551. [Google Scholar] [CrossRef]
- Zhang, D.; Tang, R.; Zhao, W.; Tang, B.-H.; Wu, H.; Shao, K.; Li, Z.-L. Surface soil water content estimation from thermal remote sensing based on the temporal variation of land surface temperature. Remote Sens. 2014, 6, 3170–3187. [Google Scholar] [CrossRef]
- Deng, K.A.K.; Lamine, S.; Pavlides, A.; Petropoulos, G.P.; Srivastava, P.K.; Bao, Y.; Hristopulos, D.T.; Anagnostopoulos, V. Operational soil moisture from ASCAT in support of water resources management. Remote Sens. 2019, 11, 579. [Google Scholar] [CrossRef]
- Ghulam, A.; Qin, Q.; Teyip, T.; Li, Z.-L. Modified perpendicular drought index (MPDI): A real-time drought monitoring method. ISPRS J. Photogramm. Remote Sens. 2007, 62, 150–164. [Google Scholar] [CrossRef]
- Finn, M.P.; Lewis, M.; Bosch, D.D.; Giraldo, M.; Yamamoto, K.; Sullivan, D.G.; Kincaid, R.; Luna, R.; Allam, G.K.; Kvien, C.; et al. Remote sensing of soil moisture using airborne hyperspectral data. GISci. Remote Sens. 2011, 48, 522–540. [Google Scholar] [CrossRef]
- Zhang, J.; Zhou, Z.; Yao, F.; Yang, L.; Hao, C. Validating the modified perpendicular drought index in the North China region using in situ soil moisture measurement. IEEE Geosci. Remote Sens. Lett. 2014, 12, 542–546. [Google Scholar] [CrossRef]
- Kasim, A.A.; Carlson, T.N.; Usman, H.S. Limitations in validating derived soil water content from thermal/optical measurements using the simplified triangle method. Remote Sens. 2020, 12, 1155. [Google Scholar] [CrossRef]
- Srivastava, P.K.; Pandey, P.C.; Petropoulos, G.P.; Kourgialas, N.N.; Pandey, V.; Singh, U. GIS and remote sensing aided information for soil moisture estimation: A comparative study of interpolation techniques. Resources 2019, 8, 70. [Google Scholar] [CrossRef]
- Petropoulos, G.; Carlson, T.; Griffiths, H. Turbulent fluxes of heat and moisture at the earth’s land surface. In Remote Sensing of Energy Fluxes and Soil Moisture Content; Informa UK Limited: Colchester, UK, 2013; pp. 3–28. [Google Scholar]
- Crago, R.D. Conservation and variability of the evaporative fraction during the daytime. J. Hydrol. 1996, 180, 173–194. [Google Scholar] [CrossRef]
- Nossent, J.; Elsen, P.; Bauwens, W. Sobol’ sensitivity analysis of a complex environmental model. Environ. Model. Softw. 2011, 26, 1515–1525. [Google Scholar] [CrossRef]

| Site Name | Site Abbreviation | Geographic Coordinates (Lat/Long) | Country | Ecosystem Type/Land Cover | Elevation (m) |
|---|---|---|---|---|---|
| Albuera | Es-Abr | 38.702–6.786 | SPAIN | SAV | 279 |
| Majadas del Tietar North | Es-LM1 | 39.942–5.779 | SPAIN | SAV | 266 |
| Majadas del Tietar South | ES-LM2 | 39.935–5.776 | SPAIN | SAV | 270 |
| Name | Description | Mathematical Definition |
|---|---|---|
| Bias/MBE | Bias (accuracy) or Mean Average Error | |
| Scatter/SD | Scatter (precision) or Standard Deviation | |
| RMSE | Root Mean Square Error | |
| MAE | Mean Absolute Error | |
| R | Pearson’s Correlation Coefficient |
| Country | MAE | MBE | SD | Max Absolute Error | Median Abs Error | R | RMSD | N |
|---|---|---|---|---|---|---|---|---|
| All sites together | 0.174 | 0.170 | 0.088 | 0.298 | 0.192 | 0.721 | 0.191 | 97 |
| ES_Abr | 0.148 | 0.139 | 0.095 | 0.298 | 0.138 | 0.536 | 0.168 | 34 |
| ES-LM1 | 0.170 | 0.167 | 0.086 | 0.281 | 0.167 | 0.775 | 0.188 | 27 |
| ES_LM2 | 0.201 | 0.201 | 0.069 | 0.293 | 0.218 | 0.719 | 0.212 | 36 |
| Fr Ranges | MAE | MBE | SD | Max Absolute Error | Median Abs Error | R | RMSE | N (Number of Days) |
|---|---|---|---|---|---|---|---|---|
| 0.00–20.20 | 0.177 | 0.173 | 0.087 | 0.298 | 0.193 | 0.452 | 0.193 | 79 |
| 0.21–20.40 | 0.147 | 0.143 | 0.087 | 0.274 | 0.153 | 0.671 | 0.167 | 16 |
| 0.41–21.00 | 0.260 | 0.260 | 0.021 | 0.281 | 0.260 | NaN | 0.261 | 2 |
| Country | MAE | MBE | SD | Max Absolute Error | Median Abs Error | R | RMSE | N |
|---|---|---|---|---|---|---|---|---|
| All sites together | 0.009 | −0.005 | 0.010 | 0.042 | 0.007 | 0.577 | 0.012 | 97 |
| ES_Abr | 0.009 | −0.005 | 0.010 | 0.031 | 0.007 | 0.511 | 0.011 | 34 |
| ES-LM1 | 0.007 | −0.001 | 0.009 | 0.027 | 0.006 | 0.809 | 0.009 | 27 |
| ES_LM2 | 0.011 | −0.009 | 0.010 | 0.042 | 0.008 | 0.584 | 0.014 | 36 |
| Fr Ranges | MAE | MBE | SD | Max Absolute Error | Median Abs Error | R | RMSE | N (Number of Days) |
|---|---|---|---|---|---|---|---|---|
| 0.00–0.20 | 0.008 | −0.005 | 0.009 | 0.031 | 0.007 | 0.473 | 0.011 | 79 |
| 0.21–0.04 | 0.010 | −0.004 | 0.012 | 0.027 | 0.008 | 0.656 | 0.013 | 16 |
| 0.41–1.00 | 0.027 | −0.015 | 0.027 | 0.042 | 0.027 | NaN | 0.031 | 2 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Petropoulos, G.P.; Sandric, I.; Hristopulos, D.; Nahum Carlson, T. Evaporative Fluxes and Surface Soil Moisture Retrievals in a Mediterranean Setting from Sentinel-3 and the “Simplified Triangle”. Remote Sens. 2020, 12, 3192. https://doi.org/10.3390/rs12193192
Petropoulos GP, Sandric I, Hristopulos D, Nahum Carlson T. Evaporative Fluxes and Surface Soil Moisture Retrievals in a Mediterranean Setting from Sentinel-3 and the “Simplified Triangle”. Remote Sensing. 2020; 12(19):3192. https://doi.org/10.3390/rs12193192
Chicago/Turabian StylePetropoulos, George P., Ionut Sandric, Dionissios Hristopulos, and Toby Nahum Carlson. 2020. "Evaporative Fluxes and Surface Soil Moisture Retrievals in a Mediterranean Setting from Sentinel-3 and the “Simplified Triangle”" Remote Sensing 12, no. 19: 3192. https://doi.org/10.3390/rs12193192
APA StylePetropoulos, G. P., Sandric, I., Hristopulos, D., & Nahum Carlson, T. (2020). Evaporative Fluxes and Surface Soil Moisture Retrievals in a Mediterranean Setting from Sentinel-3 and the “Simplified Triangle”. Remote Sensing, 12(19), 3192. https://doi.org/10.3390/rs12193192