Developing and Testing Models for Sea Surface Wind Speed Estimation with GNSS-R Delay Doppler Maps and Delay Waveforms
Abstract
1. Introduction
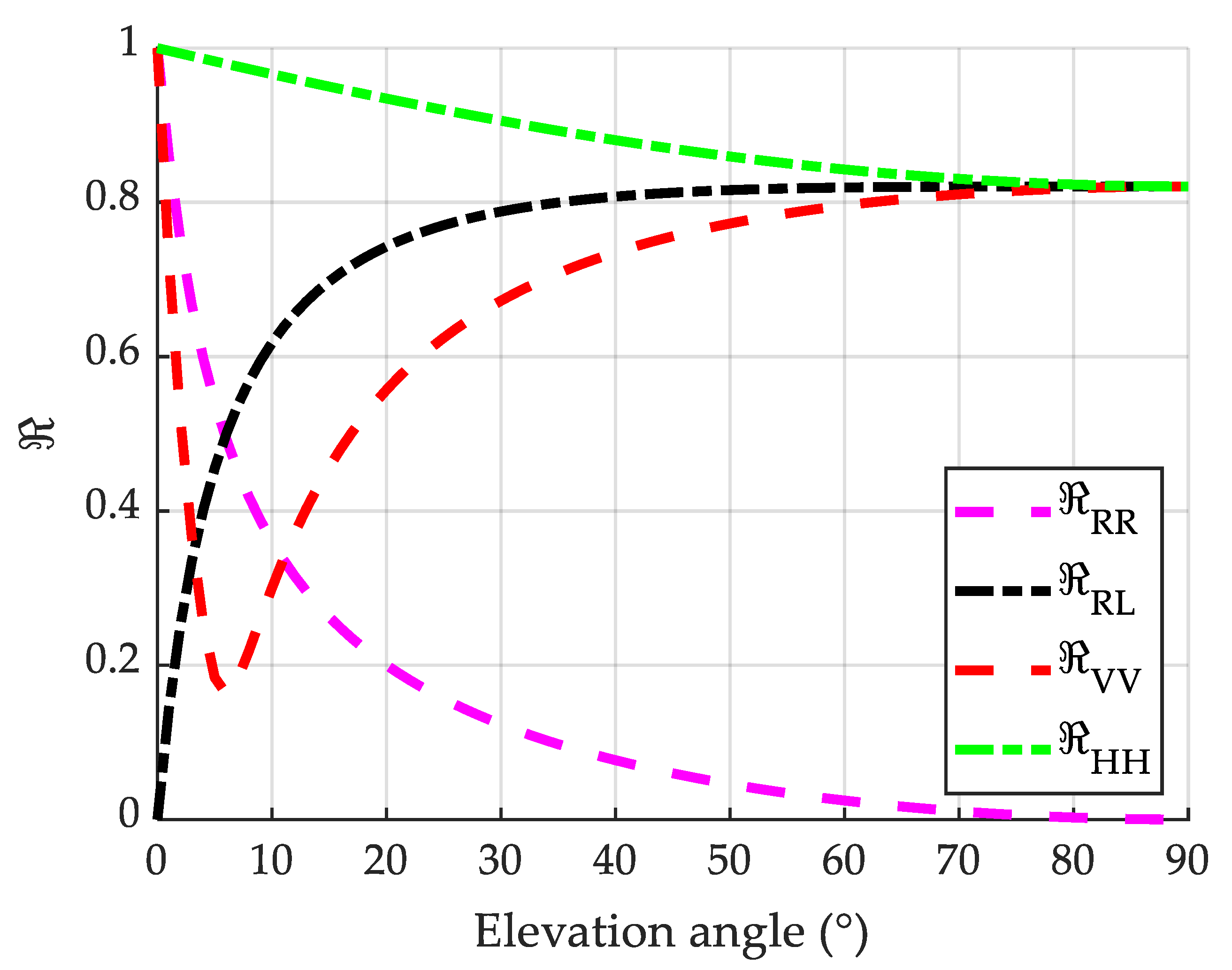
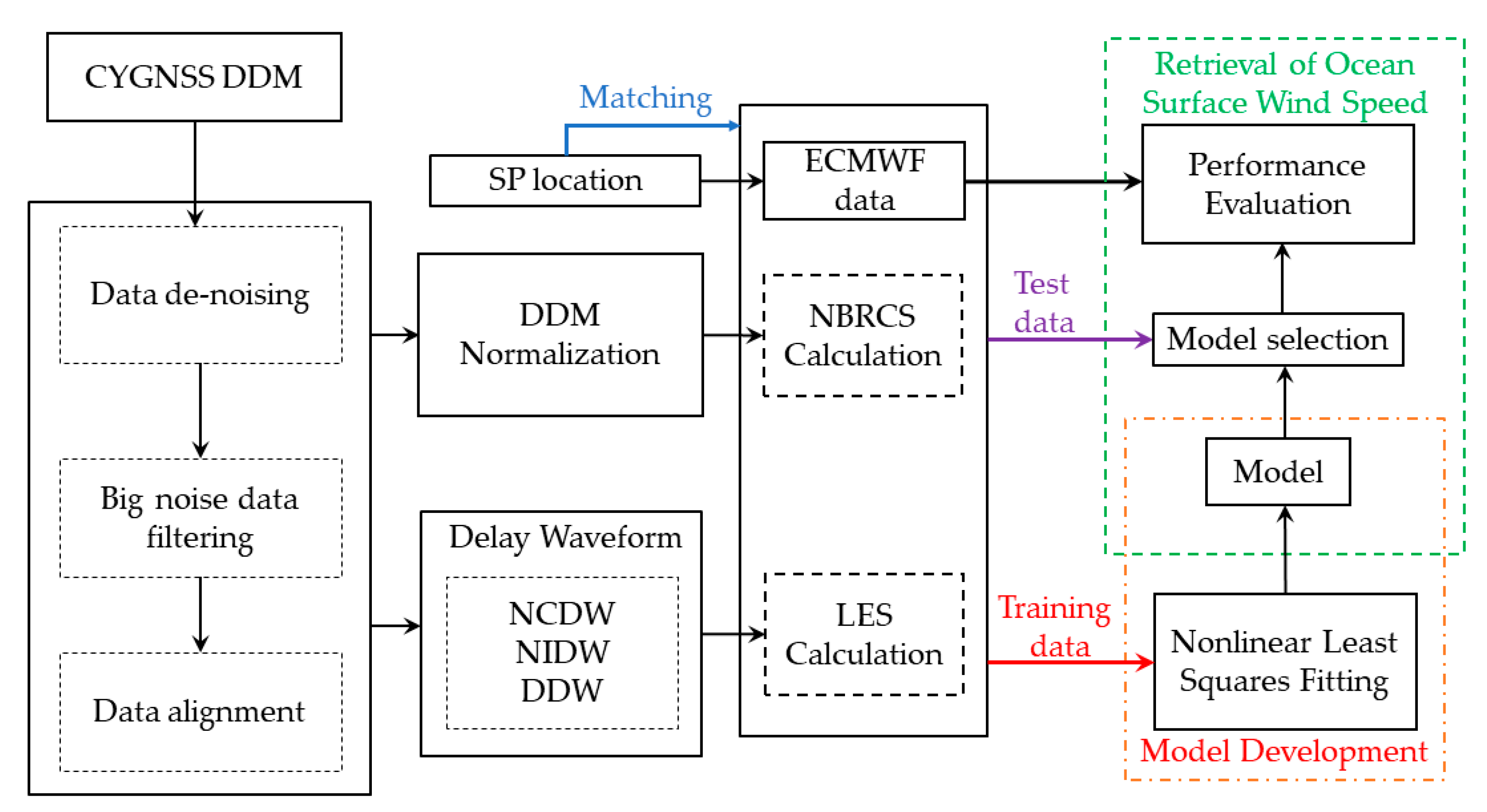
2. Principles, Data, and Methodology
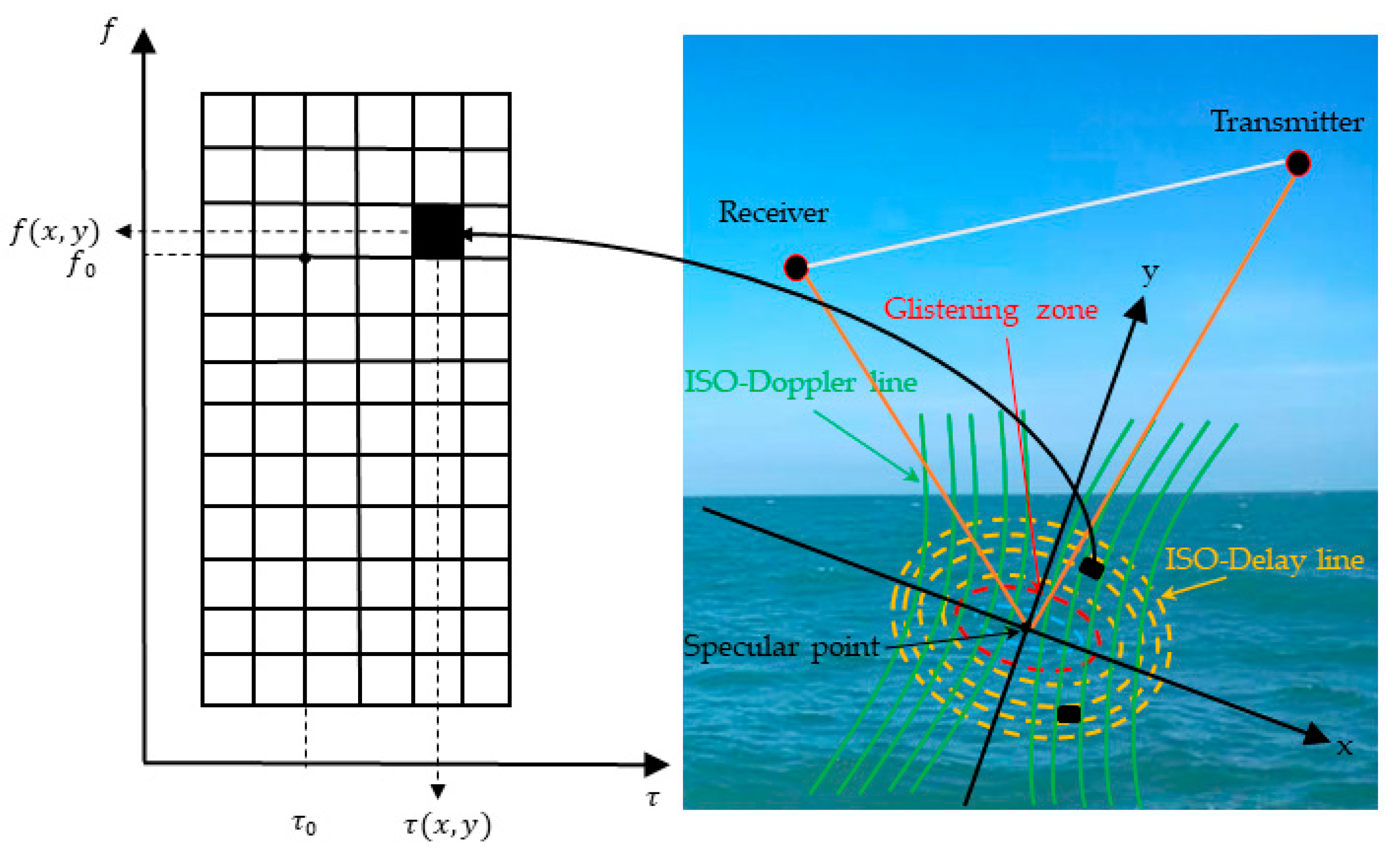
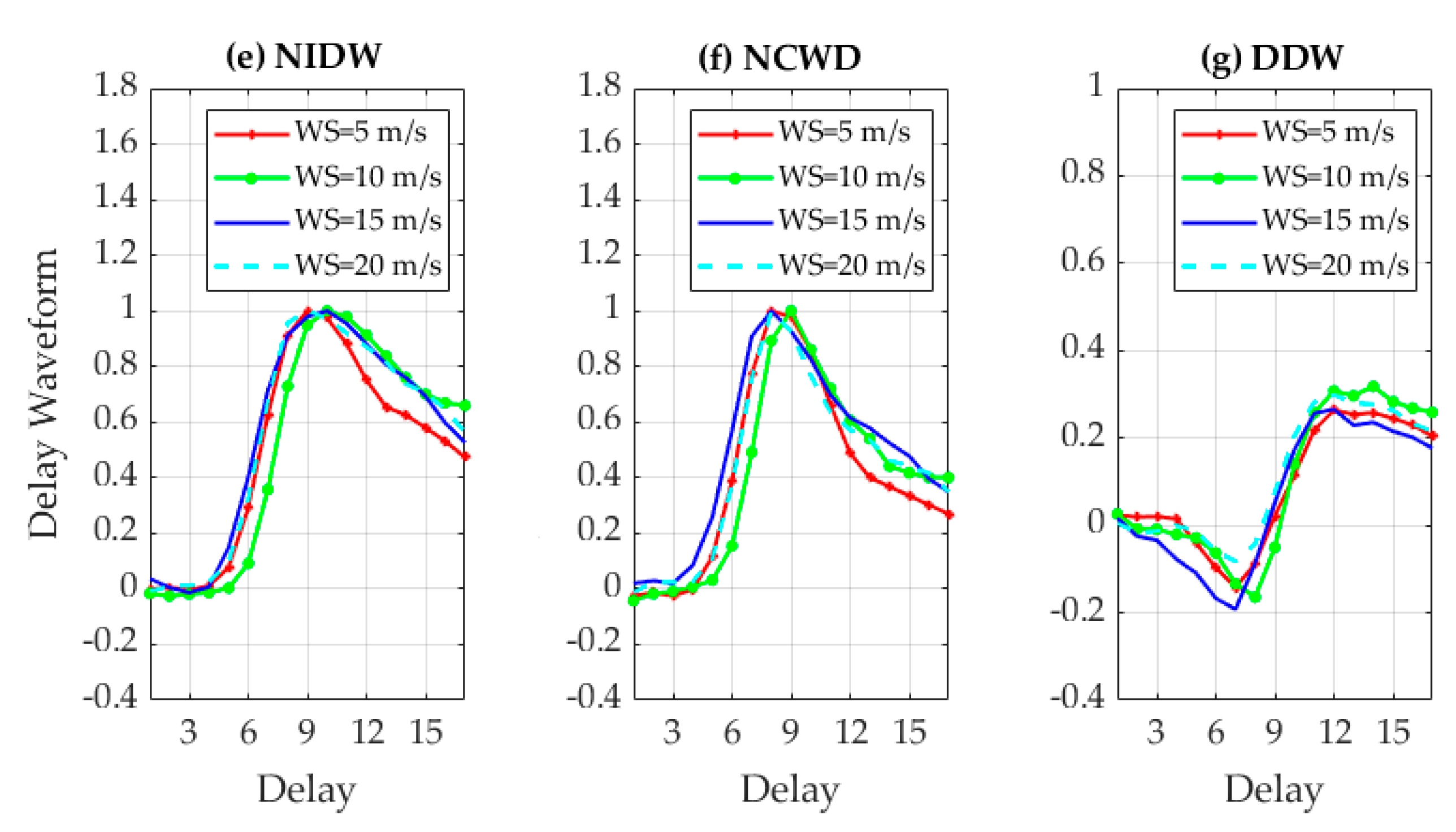
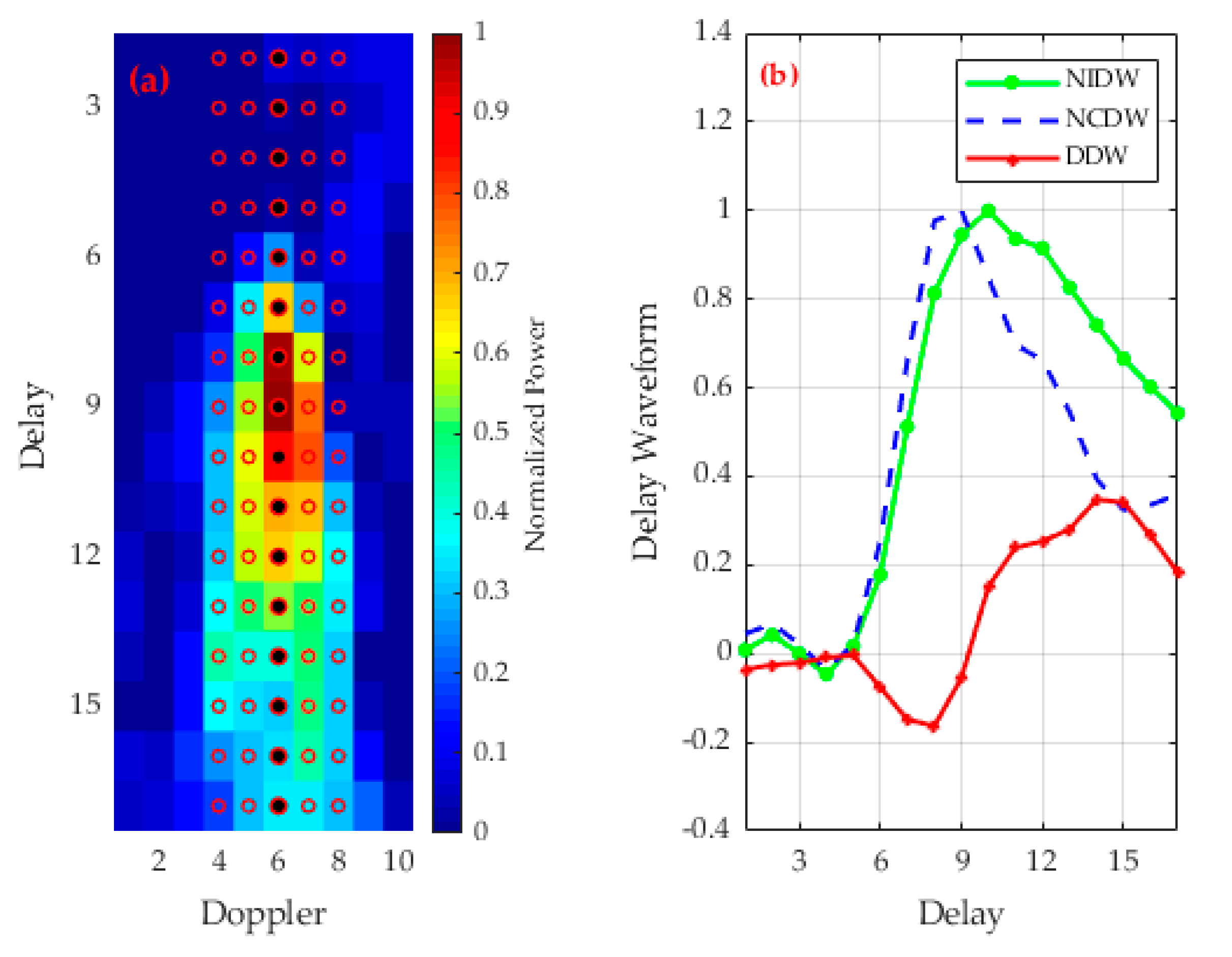
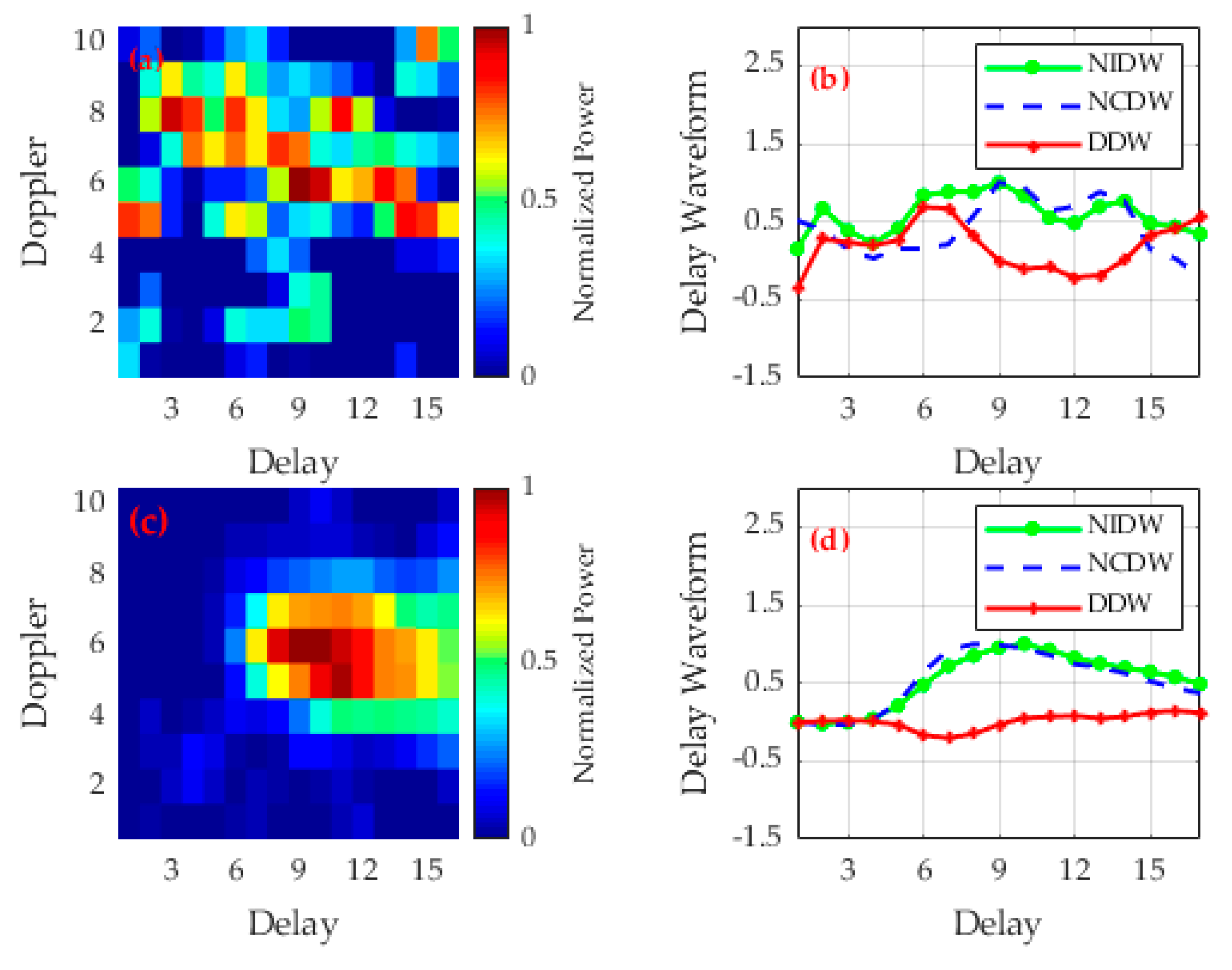
2.1. Spaceborne GNSS-R DDM and Delay Waveforms
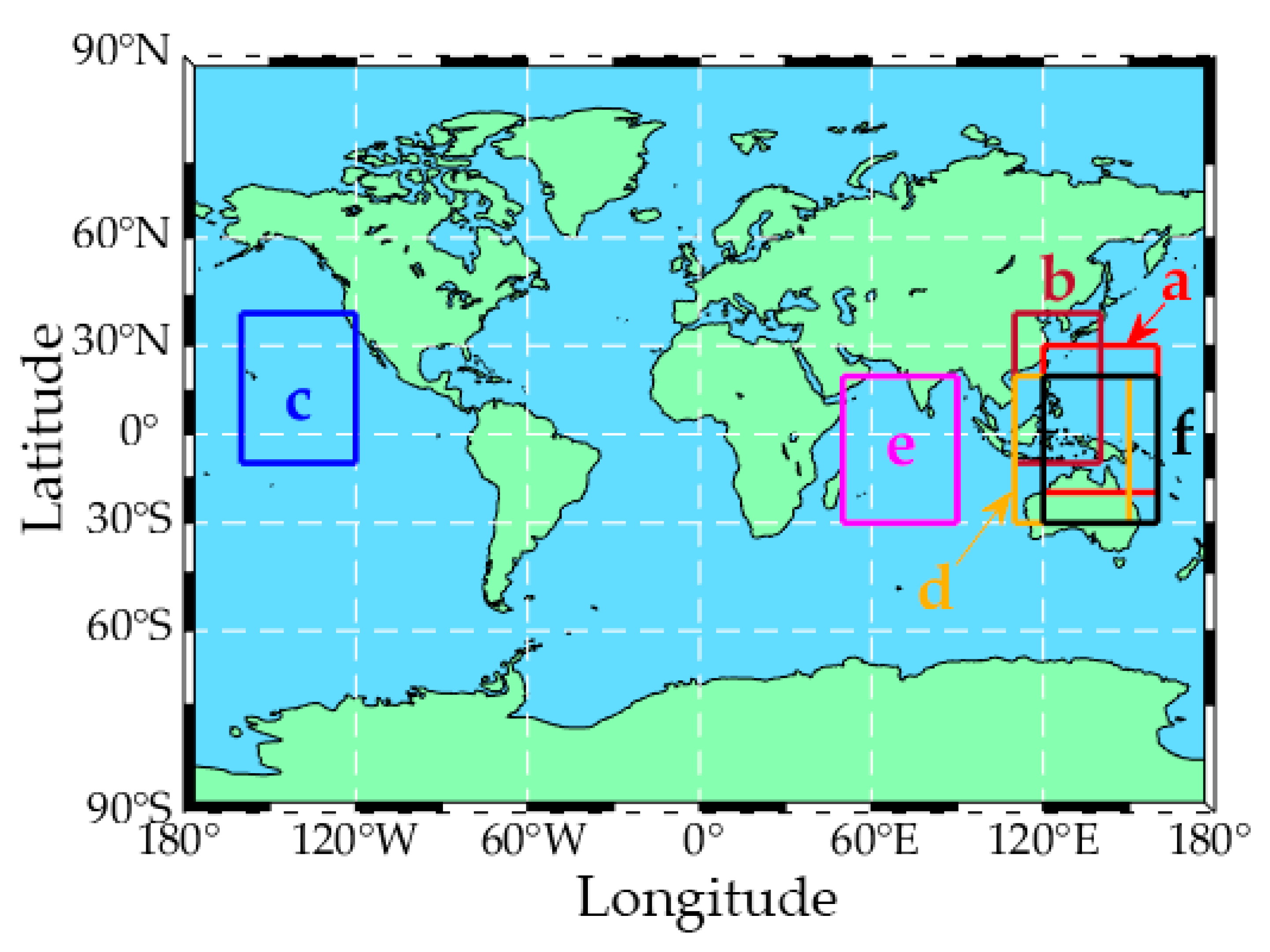
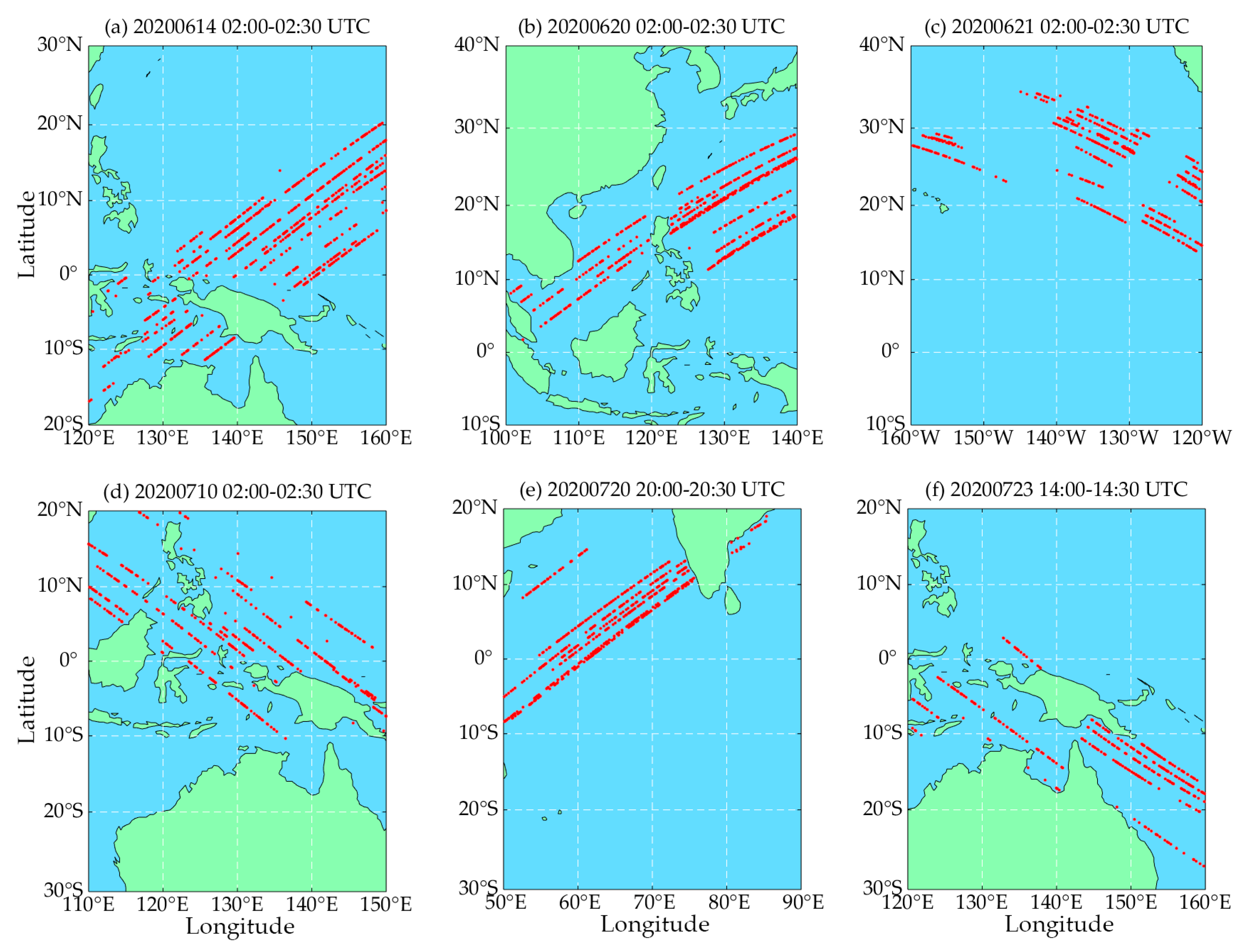
2.2. Data Set
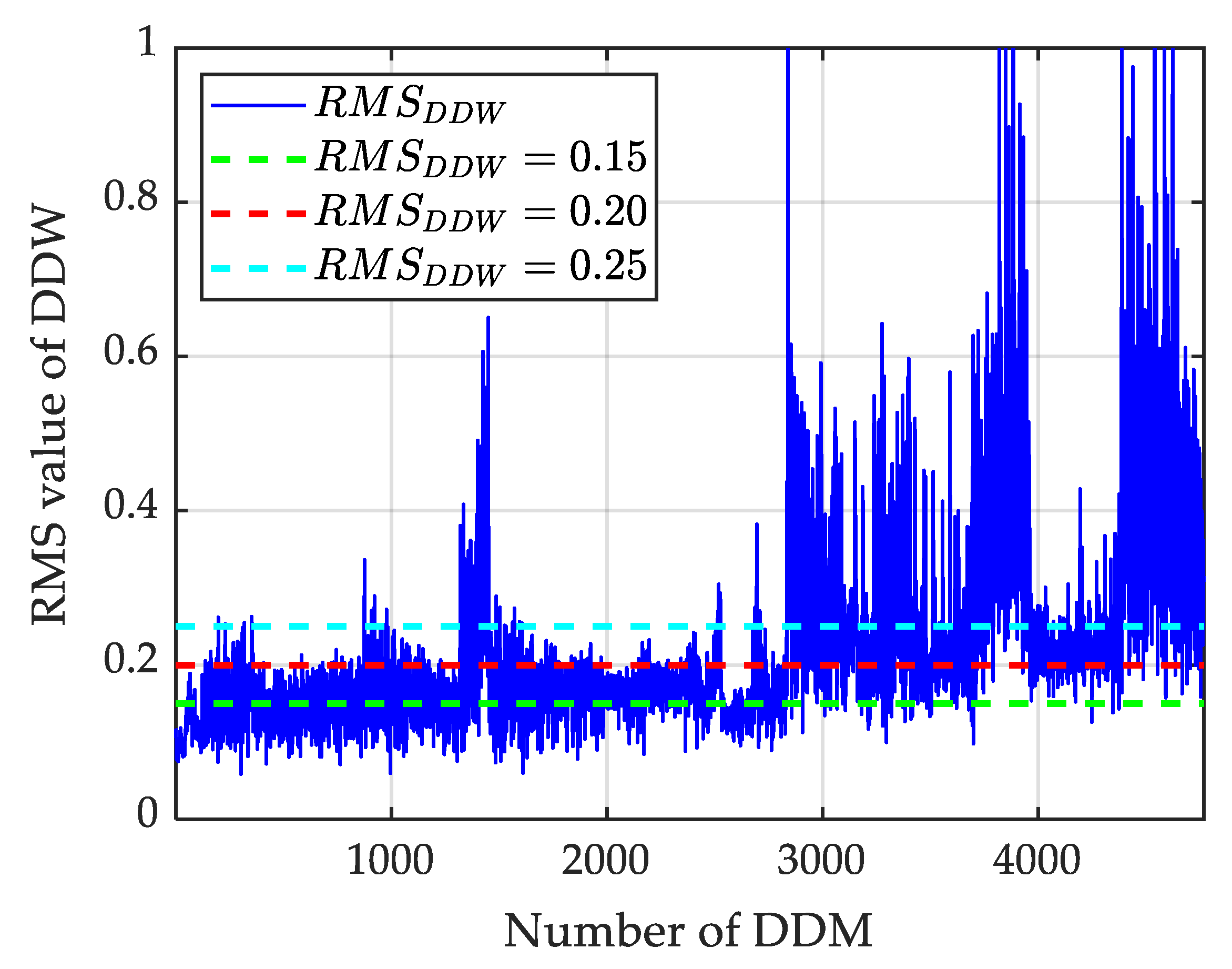
2.3. Methodology
3. Wind Speed Estimation Model
3.1. Modelling Using NBRCS Methods
3.1.1. NBRCS Calculation
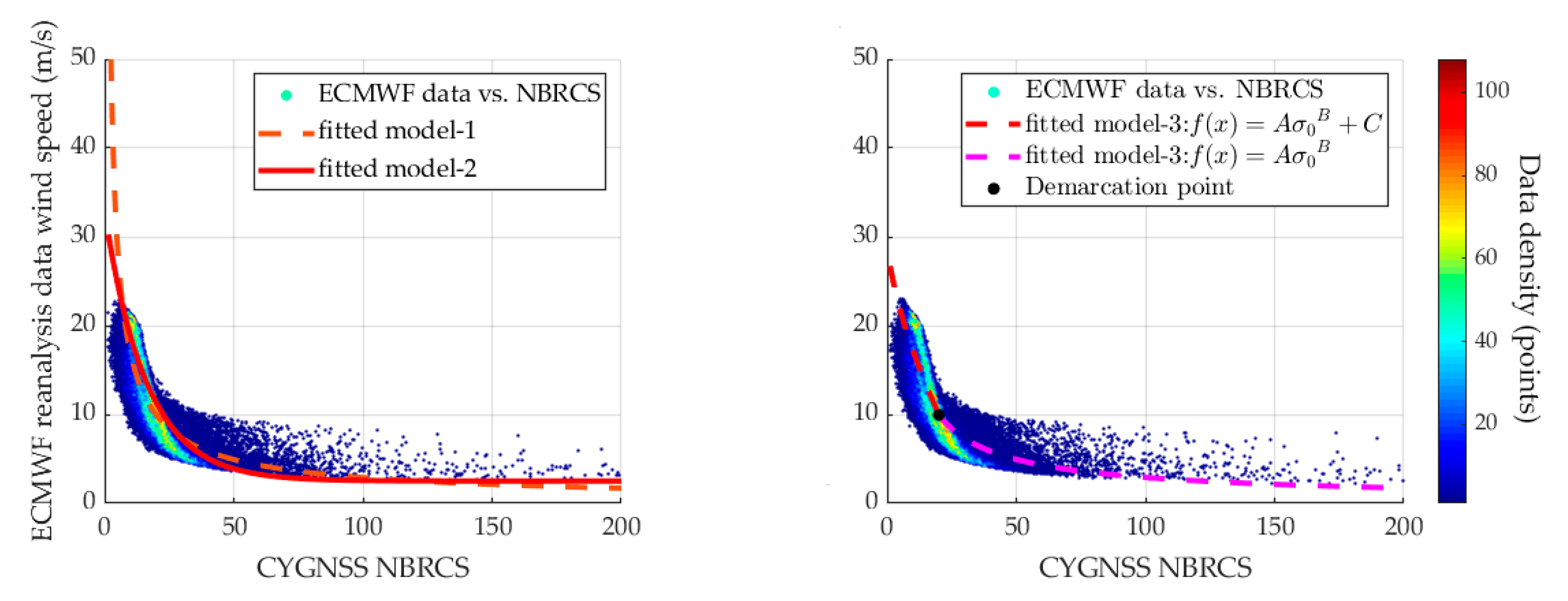
3.1.2. Model-1, Model-2, and Model-3
3.2. Modelling Using LES Methods
3.2.1. LES Calculation
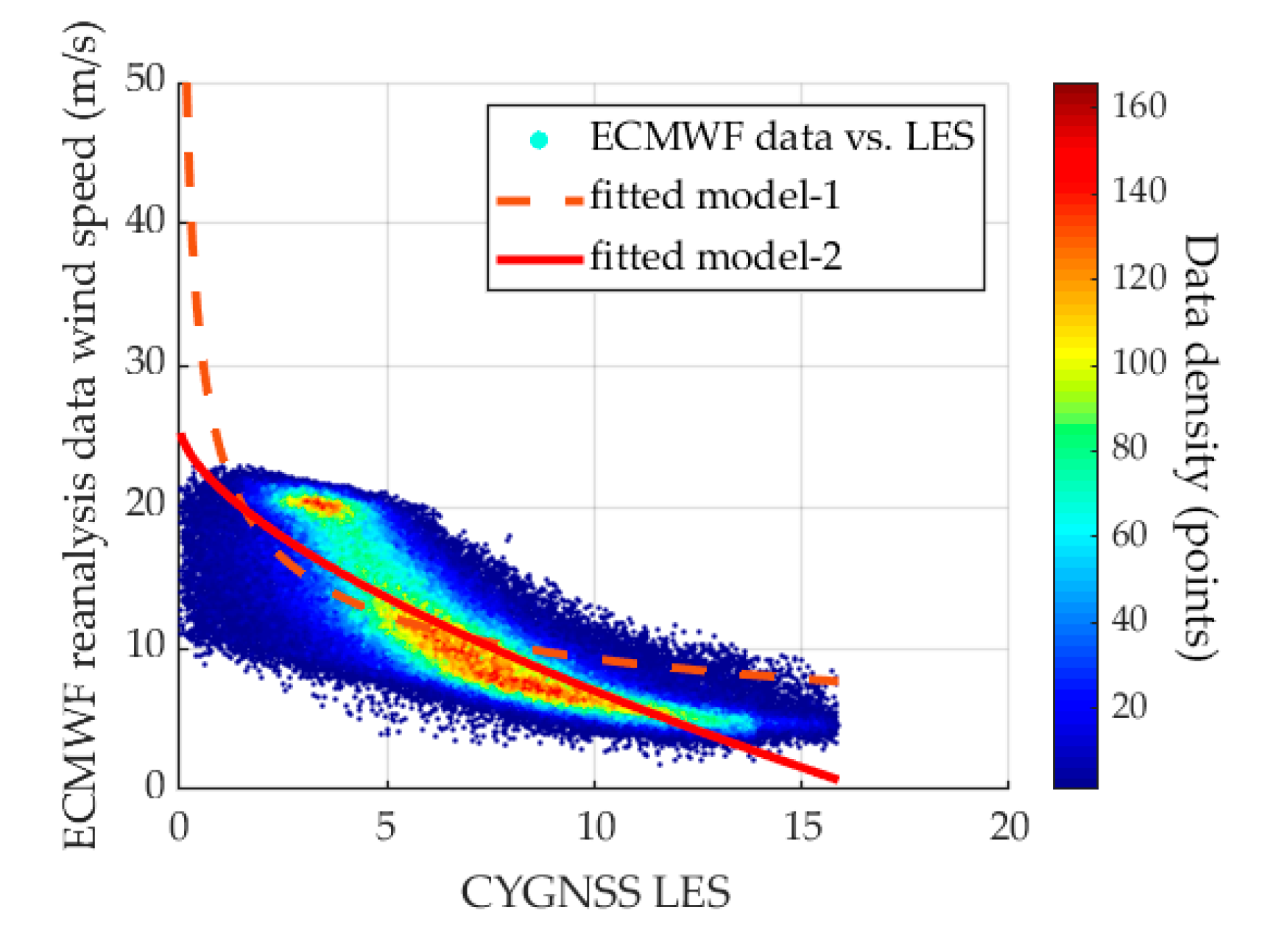
3.2.2. Model-1 and Model-2
3.3. Modeling Using Determination Coefficient-Based Combination
4. Results and Performance Evaluation of Retrieving Wind Speed
4.1. Assessment Method
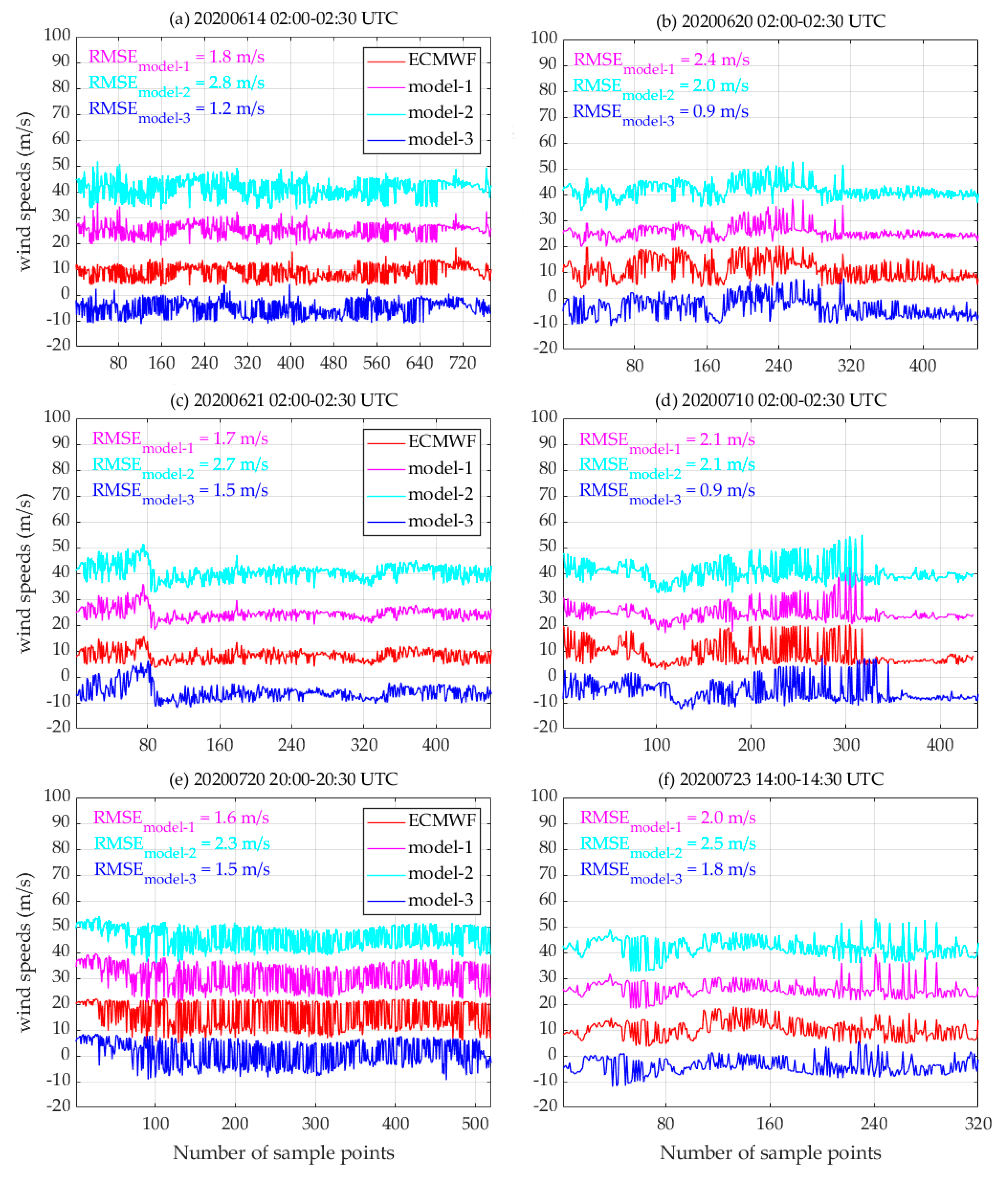
4.2. Performance Assessment of wind Speed Estimation Model Based on NBRCS Method with Double Parameters (Model-1), Triple Parameters (Model-2), and Piecewise Function (Model-3)
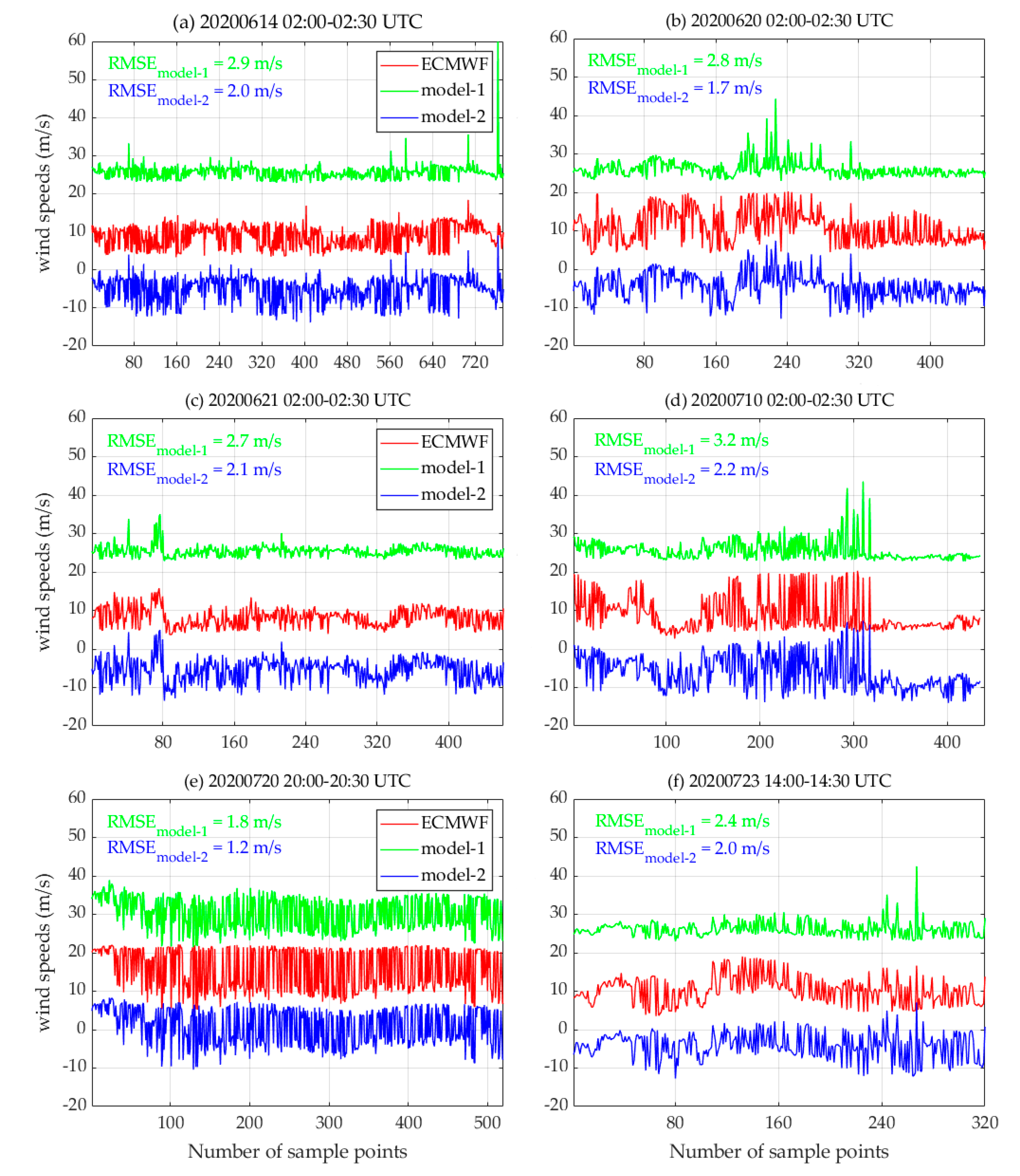
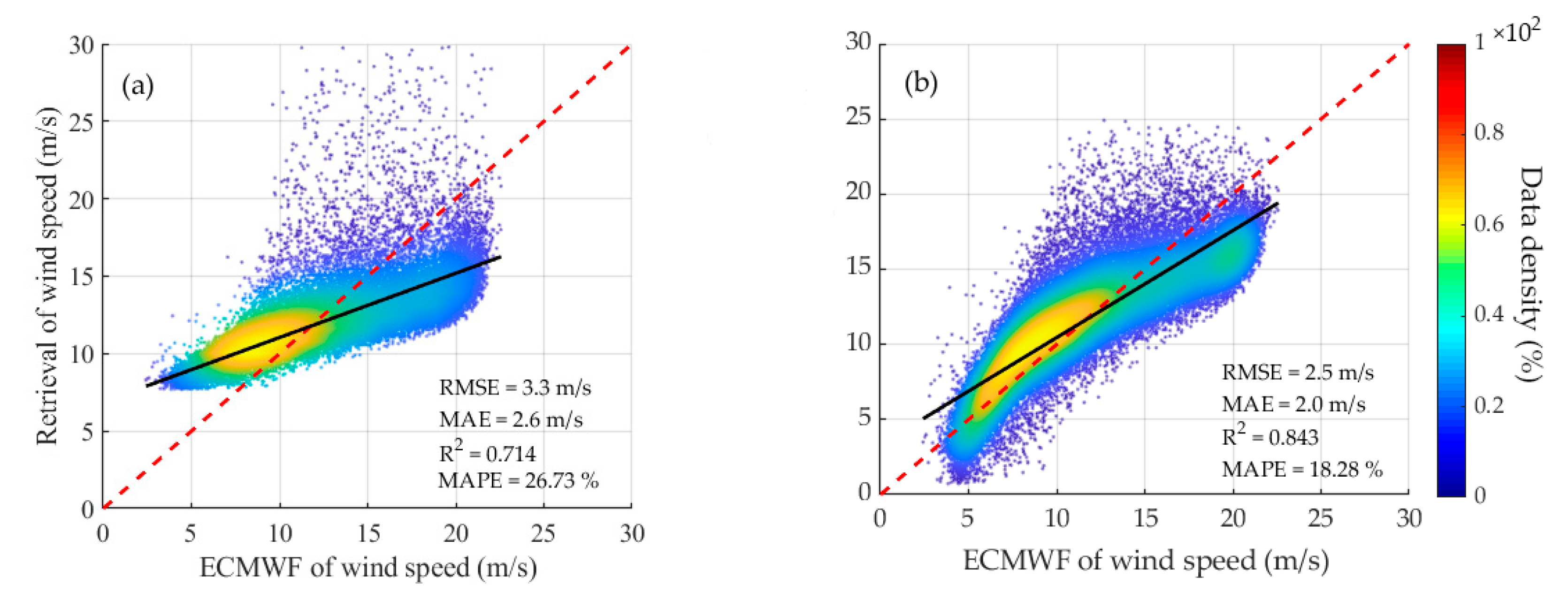
4.3. Double-Parameter (Model-1) and Triple-Parameter (Model-2) Performance Assessment Based on LES Observations
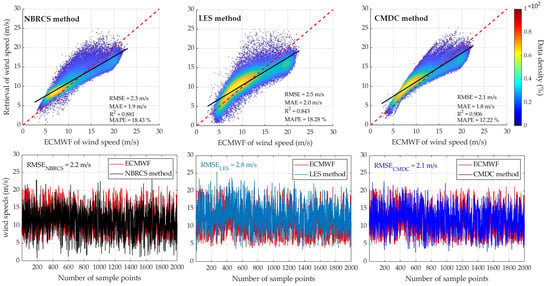
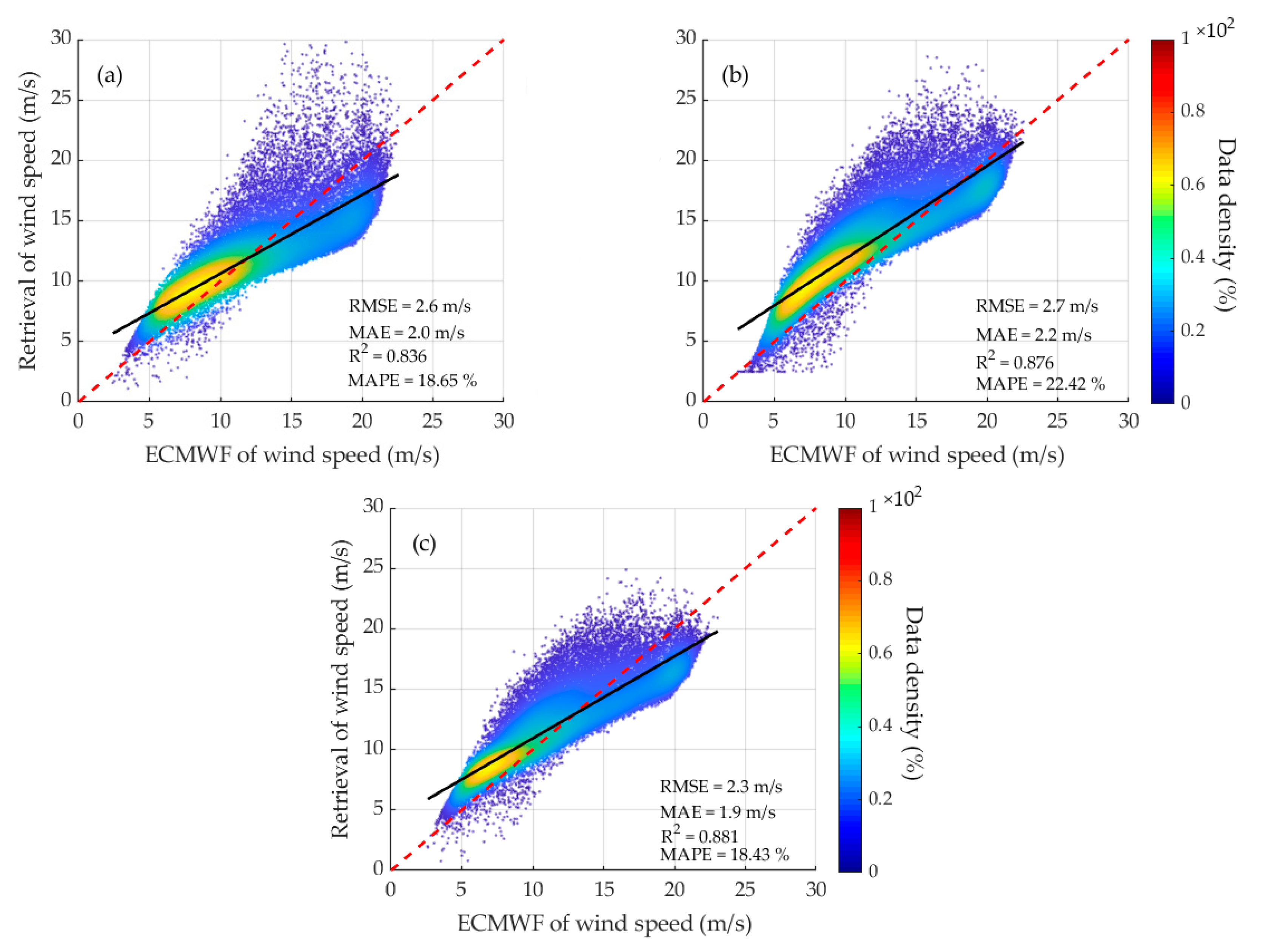
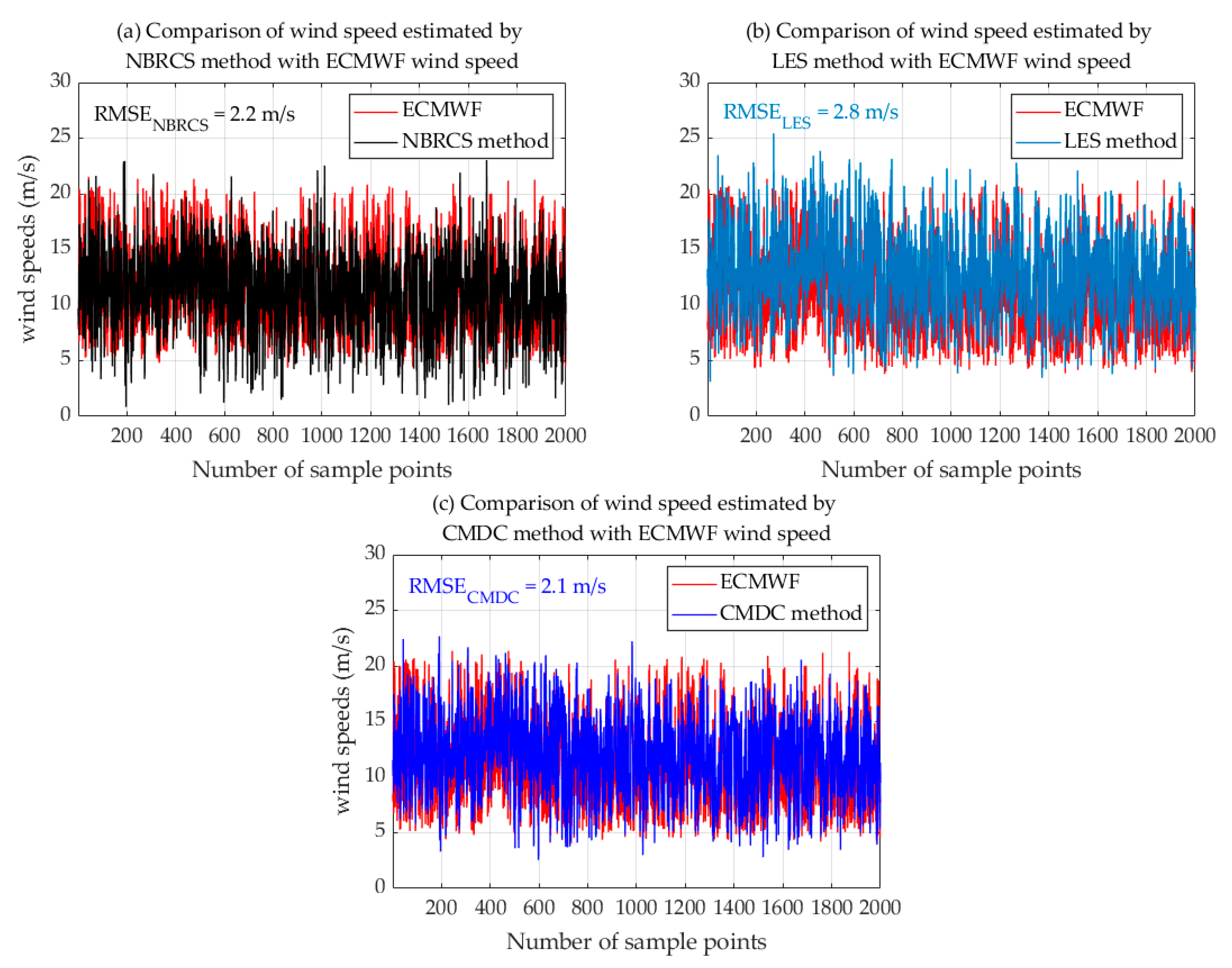
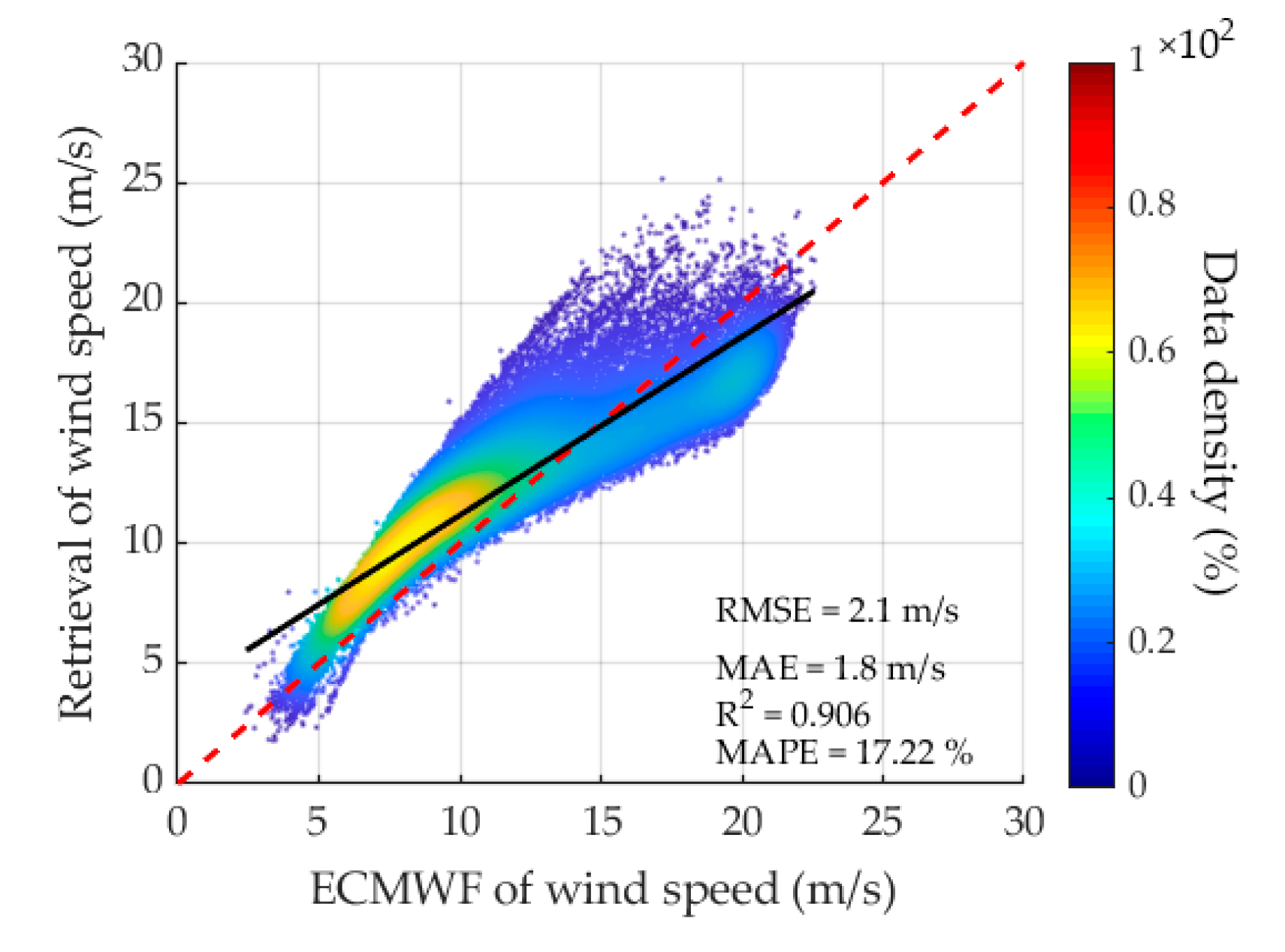
4.4. Performance Assessment of the Combination Model Based on Determination Coefficient (CMDC)
4.5. Discussion
5. Conclusions and Future Opportunities
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Reynolds, J.; Clarizia, M.P.; Santi, E. Wind Speed Estimation from CYGNSS Using Artificial Neural Networks. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 708–716. [Google Scholar] [CrossRef]
- Zhang, G.; Yang, D.; Yu, Y.; Wang, F. Wind Direction Retrieval Using Spaceborne GNSS-R in Nonspecular Geometry. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 649–658. [Google Scholar] [CrossRef]
- Huang, F.; Garrison, J.L.; Rodriguez-Alvarez, N.; O’Brien, A.J.; Schoenfeldt, K.M.; Ho, S.C.; Zhang, H. Sequential Processing of GNSS-R Delay-Doppler Maps to Estimate the Ocean Surface Wind Field. IEEE Trans. Geosci. Remote Sens. 2019, 57, 10202–10217. [Google Scholar] [CrossRef]
- Li, W.; Cardellach, E.; Fabra, F.; Ribo, S.; Rius, A. Assessment of Spaceborne GNSS-R Ocean Altimetry Performance Using CYGNSS Mission Raw Data. IEEE Trans. Geosci. Remote Sens. 2020, 58, 238–250. [Google Scholar] [CrossRef]
- Clarizia, M.P.; Ruf, C.; Cipollini, P.; Zuffada, C. First spaceborne observation of sea surface height using GPS-Reflectometry. Geophys. Res. Lett. 2016, 43, 767–774. [Google Scholar] [CrossRef]
- Zhang, Z.; Guo, F.; Zhang, X. Triple-frequency multi-GNSS reflectometry snow depth retrieval by using clustering and normalization algorithm to compensate terrain variation. GPS Solut. 2020, 24, 52. [Google Scholar] [CrossRef]
- Li, Y.; Chang, X.; Yu, K.; Wang, S.; Li, J. Estimation of snow depth using pseudorange and carrier phase observations of GNSS single-frequency signal. GPS Solut. 2019, 23, 118. [Google Scholar] [CrossRef]
- Yu, K.; Wang, S.; Li, Y.; Chang, X.; Li, J. Snow Depth Estimation with GNSS-R Dual Receiver Observation. Remote Sens. 2019, 11, 2056. [Google Scholar] [CrossRef]
- McCreight, J.L.; Small, E.E.; Larson, K.M. Snow depth, density, and SWE estimates derived from GPS reflection data: Validation in the western U.S. Water Resour. Res. 2014, 50, 6892–6909. [Google Scholar] [CrossRef]
- McCreight, J.L.; Small, E.E. Modeling bulk density and snow water equivalent using daily snow depth observations. Cryosphere 2014, 8, 521–536. [Google Scholar] [CrossRef]
- Cartwright, J.; Banks, C.J.; Srokosz, M. Sea Ice Detection Using GNSS-R Data from TechDemoSat-1. J. Geophys. Res. Oceans 2019, 124, 5801–5810. [Google Scholar] [CrossRef]
- Alonso-Arroyo, A.; Zavorotny, V.U.; Camps, A. Sea Ice Detection Using UK TDS-1 GNSS-R Data. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4989–5001. [Google Scholar] [CrossRef]
- Yan, Q.; Huang, W. Sea Ice Thickness Measurement Using Spaceborne GNSS-R: First Results with TechDemoSat-1 Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 577–587. [Google Scholar] [CrossRef]
- Yan, Q.; Huang, W.; Moloney, C. Neural Networks Based Sea Ice Detection and Concentration Retrieval From GNSS-R Delay-Doppler Maps. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 3789–3798. [Google Scholar] [CrossRef]
- Yan, Q.; Huang, W. Tsunami Detection and Parameter Estimation From GNSS-R Delay-Doppler Map. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4650–4659. [Google Scholar] [CrossRef]
- Yan, Q.; Huang, W.M. GNSS-R Delay-Doppler Map Simulation Based on the 2004 Sumatra-Andaman Tsunami Event. J. Sens. 2016, 2016, 2750862. [Google Scholar] [CrossRef]
- Carreno-Luengo, H.; Luzi, G.; Crosetto, M. Above-Ground Biomass Retrieval over Tropical Forests: A Novel GNSS-R Approach with CyGNSS. Remote Sens. 2020, 12, 1368. [Google Scholar] [CrossRef]
- Chang, X.; Jin, T.; Yu, K.; Li, Y.; Li, J.; Zhang, Q. Soil Moisture Estimation by GNSS Multipath Signal. Remote Sens. 2019, 11, 2559. [Google Scholar] [CrossRef]
- Yan, Q.; Huang, W.; Jin, S.; Jia, Y. Pan-tropical soil moisture mapping based on a three-layer model from CYGNSS GNSS-R data. Remote Sens. Environ. 2020, 247, 111944. [Google Scholar] [CrossRef]
- Martin-Neira, M. A Passive Reflectometry and Interferometry System (PARIS): Application to ocean altimetry. ESA J. 1993, 17, 331–355. [Google Scholar]
- Garrison, J.; Katzberg, S.; Hill, M. Effect of sea roughness on bistatically scattered range coded signals from the Global Positioning System. Geophys. Res. Lett. 1998, 25, 2257–2260. [Google Scholar] [CrossRef]
- Zavorotny, V.; Voronovich, A.G. Scattering of GPS Signals from the Ocean with Wind Remote Sensing Application. IEEE Trans. Geosci. Remote Sens. 2000, 38, 951–964. [Google Scholar] [CrossRef]
- Lowe, S.; Labrecque, J.; Zuffada, C.; Romans, L.; Young, L.; Hajj, G. First spaceborne observation of an Earth-reflected GPS signal. Radio Sci. 2002, 37, 1007. [Google Scholar] [CrossRef]
- Gleason, S.; Hodgart, S.; Yiping, S.; Gommenginger, C.; Mackin, S.; Adjrad, M.; Unwin, M. Detection and Processing of bistatically reflected GPS signals from low Earth orbit for the purpose of ocean remote sensing. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1229–1241. [Google Scholar] [CrossRef]
- Clarizia, M.P.; Ruf, C.S.; Jales, P.; Gommenginger, C. Spaceborne GNSS-R Minimum Variance Wind Speed Estimator. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6829–6843. [Google Scholar] [CrossRef]
- Foti, G.; Gommenginger, C.; Jales, P.; Unwin, M.; Shaw, A.; Robertson, C.; Rosello, J. Spaceborne GNSS reflectometry for ocean winds: First results from the UK TechDemoSat-1 mission. Geophys. Res. Lett. 2015, 42, 5435–5441. [Google Scholar] [CrossRef]
- Hugo, C.L.; Stephen, L.; Cinzia, Z.; Stephan, E.; Shadi, O. Spaceborne GNSS-R from the SMAP Mission: First Assessment of Polarimetric Scatterometry over Land and Cryosphere. Remote Sens. 2017, 9, 362. [Google Scholar]
- Ruf, C.; Atlas, R.; Chang, P.; Clarizia, M.P.; Garrison, J.; Gleason, S.; Katzberg, S.; Jelenak, Z.; Johnson, J.; Majumdar, S.; et al. New Ocean Winds Satellite Mission to Probe Hurricanes and Tropical Convection. Bull. Am. Meteorol. Soc. 2016, 97, 385–395. [Google Scholar] [CrossRef]
- Jing, C.; Niu, X.; Duan, C.; Lu, F.; Di, G.; Yang, X. Sea Surface Wind Speed Retrieval from the First Chinese GNSS-R Mission: Technique and Preliminary Results. Remote Sens. 2019, 11, 3013. [Google Scholar] [CrossRef]
- Wickert, J.; Cardellach, E.; Martín-Neira, M.; Bandeiras, J.; Bertino, L.; Andersen, O.B.; Camps, A.; Catarino, N.; Chapron, B.; Fabra, F.; et al. GEROS-ISS: GNSS REflectometry, Radio Occultation, and Scatterometry Onboard the International Space Station. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4552–4581. [Google Scholar] [CrossRef]
- Wang, F.; Yang, D.; Zhang, B.; Li, W. Waveform-based spaceborne GNSS-R wind speed observation: Demonstration and analysis using UK TechDemoSat-1 data. Adv. Space Res. 2018, 61, 1573–1587. [Google Scholar] [CrossRef]
- Ruf, C.S.; Balasubramaniam, R. Development of the CYGNSS Geophysical Model Function for Wind Speed. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 66–77. [Google Scholar] [CrossRef]
- Ruf, C.S.; Gleason, S.; McKague, D.S. Assessment of CYGNSS Wind Speed Retrieval Uncertainty. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 87–97. [Google Scholar] [CrossRef]
- Clarizia, M.P.; Ruf, C.S. Wind Speed Retrieval Algorithm for the Cyclone Global Navigation Satellite System (CYGNSS) Mission. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4419–4432. [Google Scholar] [CrossRef]
- Rodriguez-Alvarez, N.; Garrison, J.L. Generalized Linear Observables for Ocean Wind Retrieval from Calibrated GNSS-R Delay–Doppler Maps. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1142–1155. [Google Scholar] [CrossRef]
- Liu, Y.; Collett, I.; Morton, Y.J. Application of Neural Network to GNSS-R Wind Speed Retrieval. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9756–9766. [Google Scholar] [CrossRef]
- Gleason, S. Space-Based GNSS Scatterometry: Ocean Wind Sensing Using an Empirically Calibrated Model. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4853–4863. [Google Scholar] [CrossRef]
- Gleason, S.; Ruf, C.S.; Clarizia, M.P.; O’Brien, A.J. Calibration and Unwrapping of the Normalized Scattering Cross Section for the Cyclone Global Navigation Satellite System. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2495–2509. [Google Scholar] [CrossRef]
- Jing, C.; Yang, X.; Ma, W.; Yu, Y.; Dong, D.; Li, Z.; Xu, C. Retrieval of sea surface winds under hurricane conditions from GNSS-R observations. Acta Oceanol. Sin. 2016, 35, 91–97. [Google Scholar] [CrossRef]
- Wang, Q.; Zhu, Y.; Kasantikul, K. A Novel Method for Ocean Wind Speed Detection Based on Energy Distribution of Beidou Reflections. Sensors 2019, 19, 2779. [Google Scholar] [CrossRef]
- Yu, K.; Li, Y.; Chang, X. Snow Depth Estimation Based on Combination of Pseudorange and Carrier Phase of GNSS Dual-Frequency Signals. IEEE Trans. Geosci. Remote Sens. 2019, 57, 1817–1828. [Google Scholar] [CrossRef]
- Ulaby, F.T.; Moore, R.K.; Fung, A.K. Microwave Remote Sensing: Active and Passive; Artech House: Dedham, MA, USA, 1982. [Google Scholar]
- Zhu, Y.; Tao, T.; Yu, K.; Li, Z.; Qu, X.; Ye, Z.; Geng, J.; Zou, J.; Semmling, M.; Wickert, J. Sensing Sea Ice Based on Doppler Spread Analysis of Spaceborne GNSS-R Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 217–226. [Google Scholar] [CrossRef]
- Liu, H.; Jin, S.; Yan, Q. Evaluation of the Ocean Surface Wind Speed Change following the Super Typhoon from Space-Borne GNSS-Reflectometry. Remote Sens. 2020, 12, 2034. [Google Scholar] [CrossRef]
- Ruf, C.S.; Chang, P.; Clarizia, M.P.; Gleason, S.; Jelenak, Z. CYGNSS handbook. In Cyclone Global Navigation Satellite Systems; NASA: Ann Arbor, MI, USA, 2016; Volume 4, pp. 1–155. ISBN 978-1-60785-380-0. [Google Scholar]
- Qiu, H.; Jin, S. Global Mean Sea Surface Height Estimated from Spaceborne Cyclone-GNSS Reflectometry. Remote Sens. 2020, 12, 356. [Google Scholar] [CrossRef]
- Yan, Q.; Huang, W. Spaceborne GNSS-R Sea Ice Detection Using Delay-Doppler Maps: First Results from the UK TechDemoSat-1 Mission. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4795–4801. [Google Scholar] [CrossRef]
- Zhu, Y.; Yu, K.; Zou, J.; Wickert, J. Sea Ice Detection Based on Differential Delay-Doppler Maps from UK TechDemoSat-1. Sensors 2017, 17, 1614. [Google Scholar] [CrossRef]
- Huang, F.; Garrison, J.L.; Leidner, S.M.; Annane, B.; Hoffman, R.N.; Grieco, G.; Stoffelen, A. A Forward Model for Data Assimilation of GNSS Ocean Reflectometry Delay-Doppler Maps. IEEE Trans. Geosci. Remote Sens. 2020. [Google Scholar] [CrossRef]
- Valeriano, T.T.B.; Rolim, G.D.; Bispo, R.C.; de Moraes, J.; Aparecido, L.E.D. Evaluation of air temperature and rainfall from ECMWF and NASA gridded data for southeastern Brazil. Theor. Appl. Climatol. 2019, 137, 1925–1938. [Google Scholar] [CrossRef]
- Qian, N.; Chang, G.; Gao, J. Smoothing for continuous dynamical state space models with sampled system coefficients based on sparse kernel learning. Nonlinear Dyn. 2020, 100, 3597–3610. [Google Scholar] [CrossRef]

| Models | A | B | C |
|---|---|---|---|
| Model-1 | 98.0506 | −0.7641 | |
| Model-2 | 30.2831 | −0.0615 | 2.5 |
| Model-3 Function 1 | −2.8648 | 0.6495 | 29.9137 |
| Model-3 Function 2 | 205.2 | −1.043 |
| Methods | RMSE (m/s) | MAE (m/s) | R2 | MAPE (%) | Improvement (%) |
|---|---|---|---|---|---|
| NBRCS method | 2.3 | 1.9 | 0.881 | 18.43 | 8.69 |
| LES method | 2.5 | 2.0 | 0.843 | 18.28 | 16.0 |
| CMDC method | 2.1 | 1.8 | 0.906 | 17.22 |
| Methods | <15 m/s | >15 m/s | ||||
|---|---|---|---|---|---|---|
| RMSE (m/s) | MAE (m/s) | MAPE (%) | RMSE (m/s) | MAE (m/s) | MAPE (%) | |
| NBRCS method | 1.6 | 1.5 | 11.5 | 2.6 | 1.9 | 16.9 |
| LES method | 1.8 | 1.6 | 14.4 | 3.2 | 2.4 | 18.8 |
| CMDC method | 1.5 | 1.3 | 9.1 | 2.3 | 1.6 | 14.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bu, J.; Yu, K.; Zhu, Y.; Qian, N.; Chang, J. Developing and Testing Models for Sea Surface Wind Speed Estimation with GNSS-R Delay Doppler Maps and Delay Waveforms. Remote Sens. 2020, 12, 3760. https://doi.org/10.3390/rs12223760
Bu J, Yu K, Zhu Y, Qian N, Chang J. Developing and Testing Models for Sea Surface Wind Speed Estimation with GNSS-R Delay Doppler Maps and Delay Waveforms. Remote Sensing. 2020; 12(22):3760. https://doi.org/10.3390/rs12223760
Chicago/Turabian StyleBu, Jinwei, Kegen Yu, Yongchao Zhu, Nijia Qian, and Jun Chang. 2020. "Developing and Testing Models for Sea Surface Wind Speed Estimation with GNSS-R Delay Doppler Maps and Delay Waveforms" Remote Sensing 12, no. 22: 3760. https://doi.org/10.3390/rs12223760
APA StyleBu, J., Yu, K., Zhu, Y., Qian, N., & Chang, J. (2020). Developing and Testing Models for Sea Surface Wind Speed Estimation with GNSS-R Delay Doppler Maps and Delay Waveforms. Remote Sensing, 12(22), 3760. https://doi.org/10.3390/rs12223760