Investigating the Error Propagation from Satellite-Based Input Precipitation to Output Water Quality Indicators Simulated by a Hydrologic Model
Abstract
1. Introduction
2. Materials and Methods
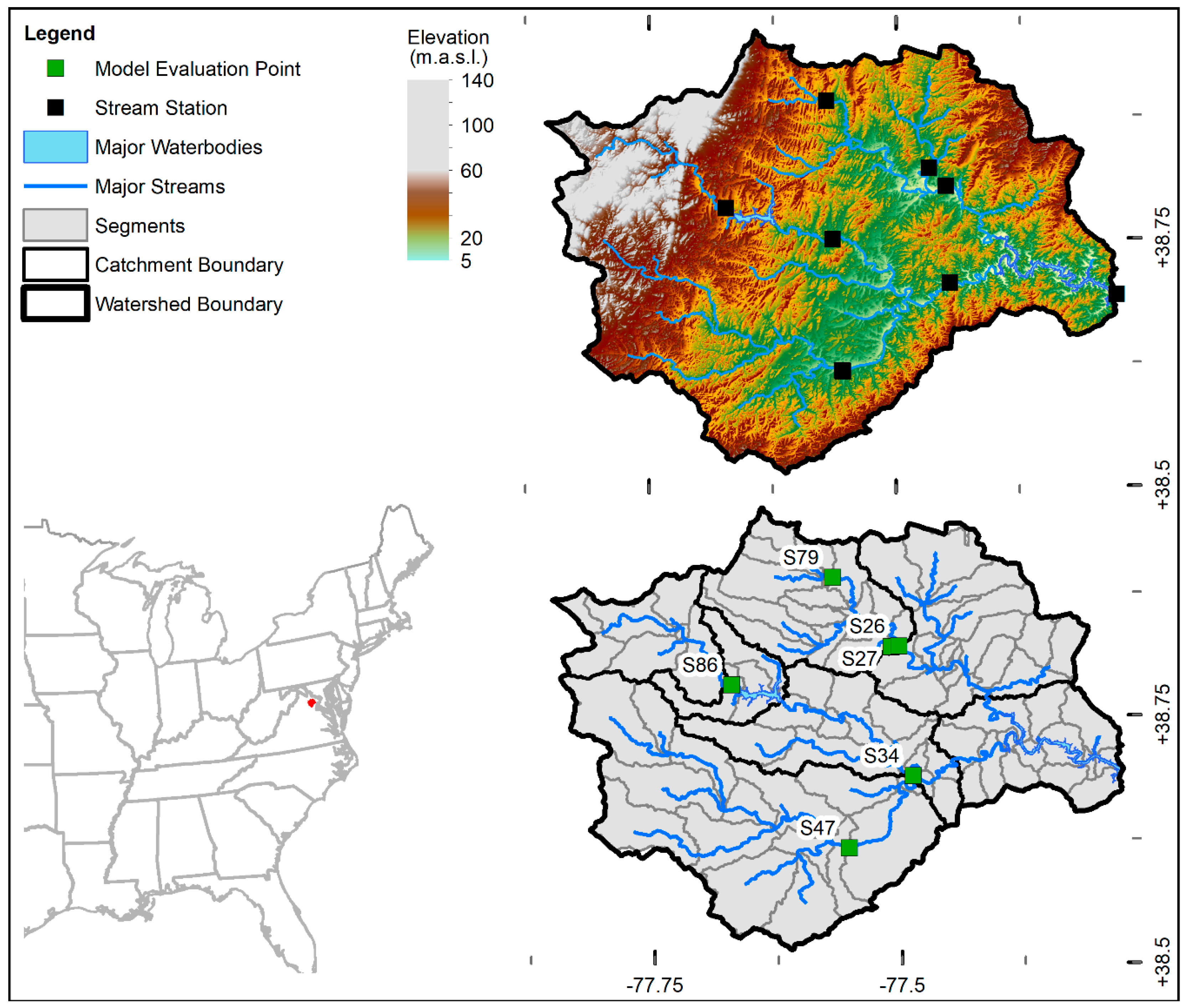
2.1. Study Area
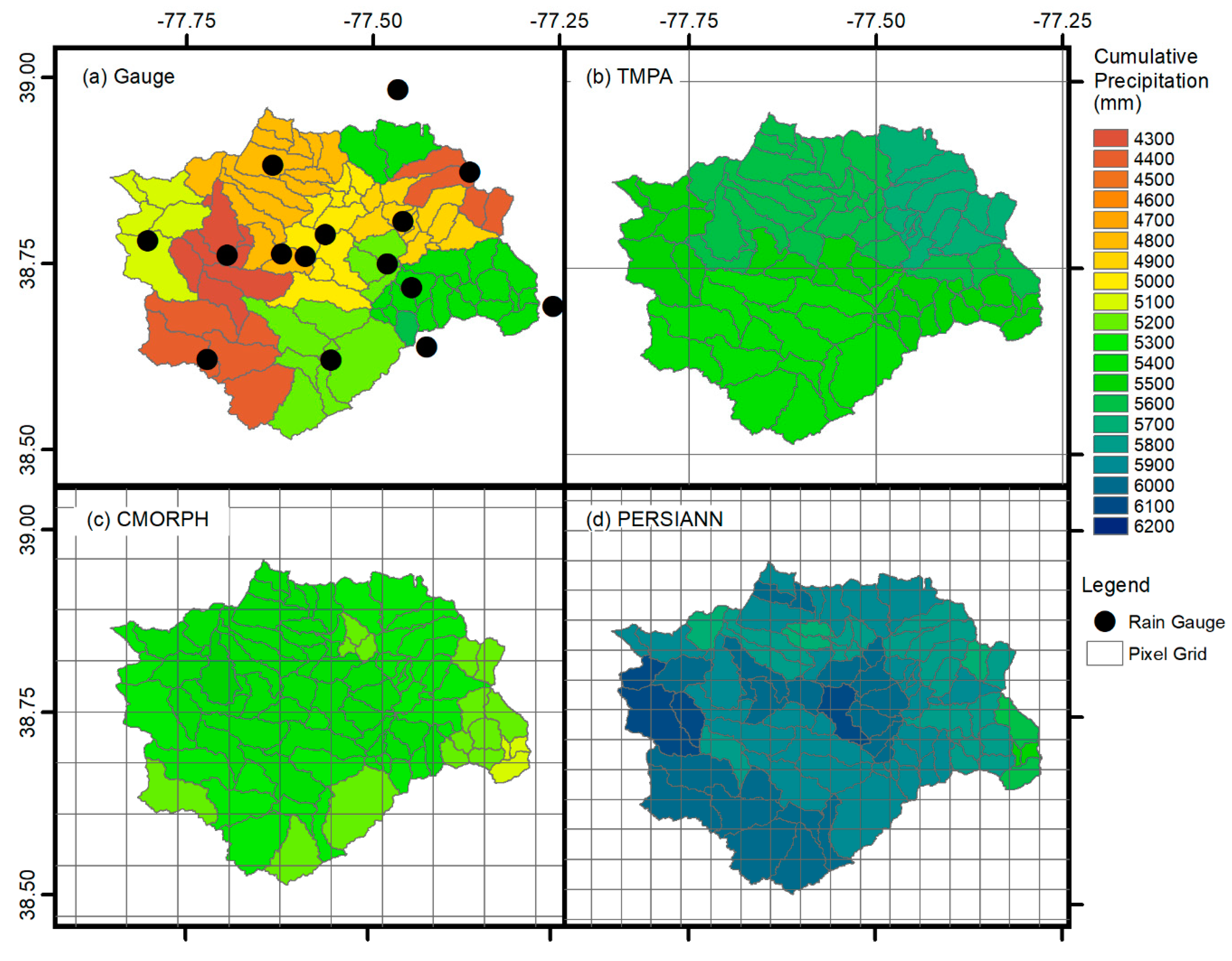
2.2. Precipitation Data
2.3. Hydrologic Model
2.4. Data Processing
2.5. Precipitation Anlaysis
2.6. Output Analysis
3. Results
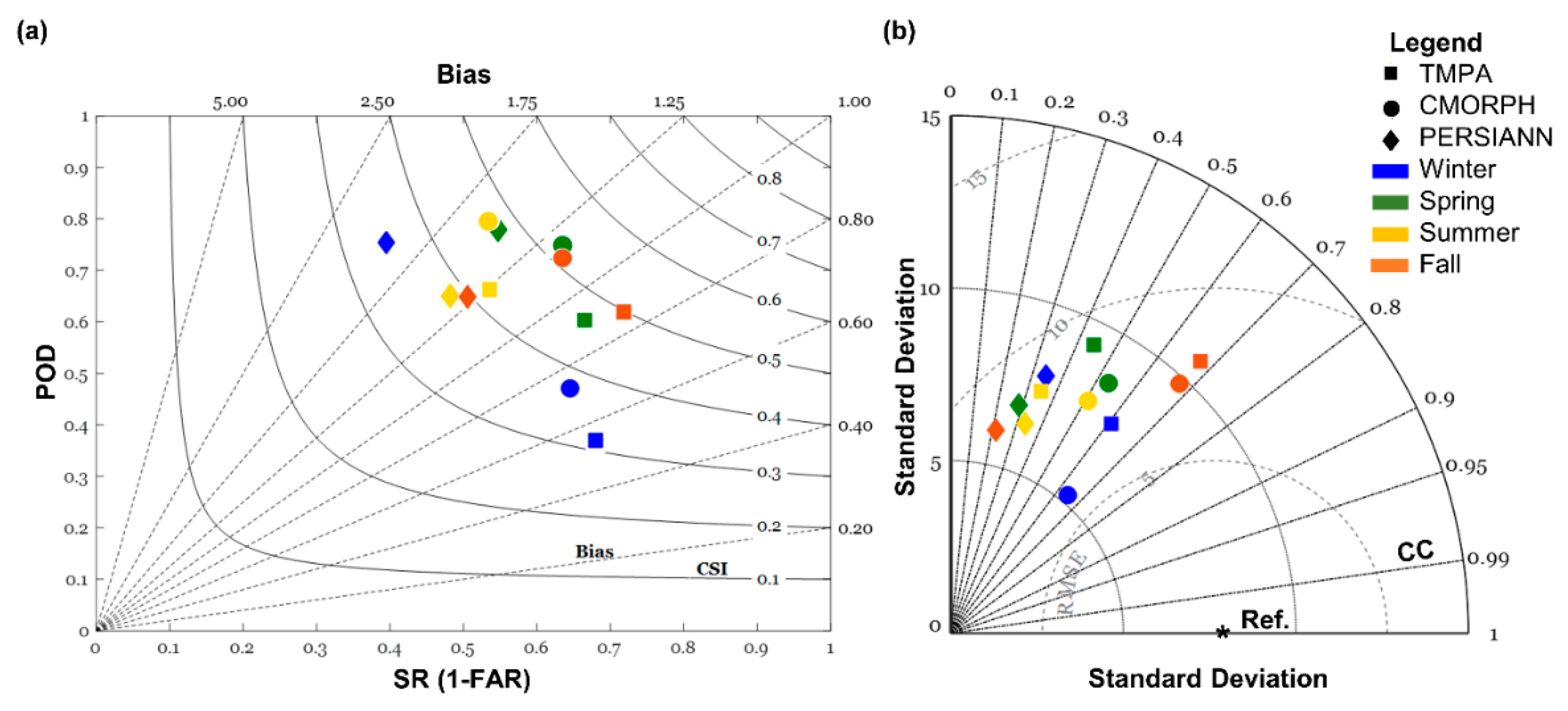
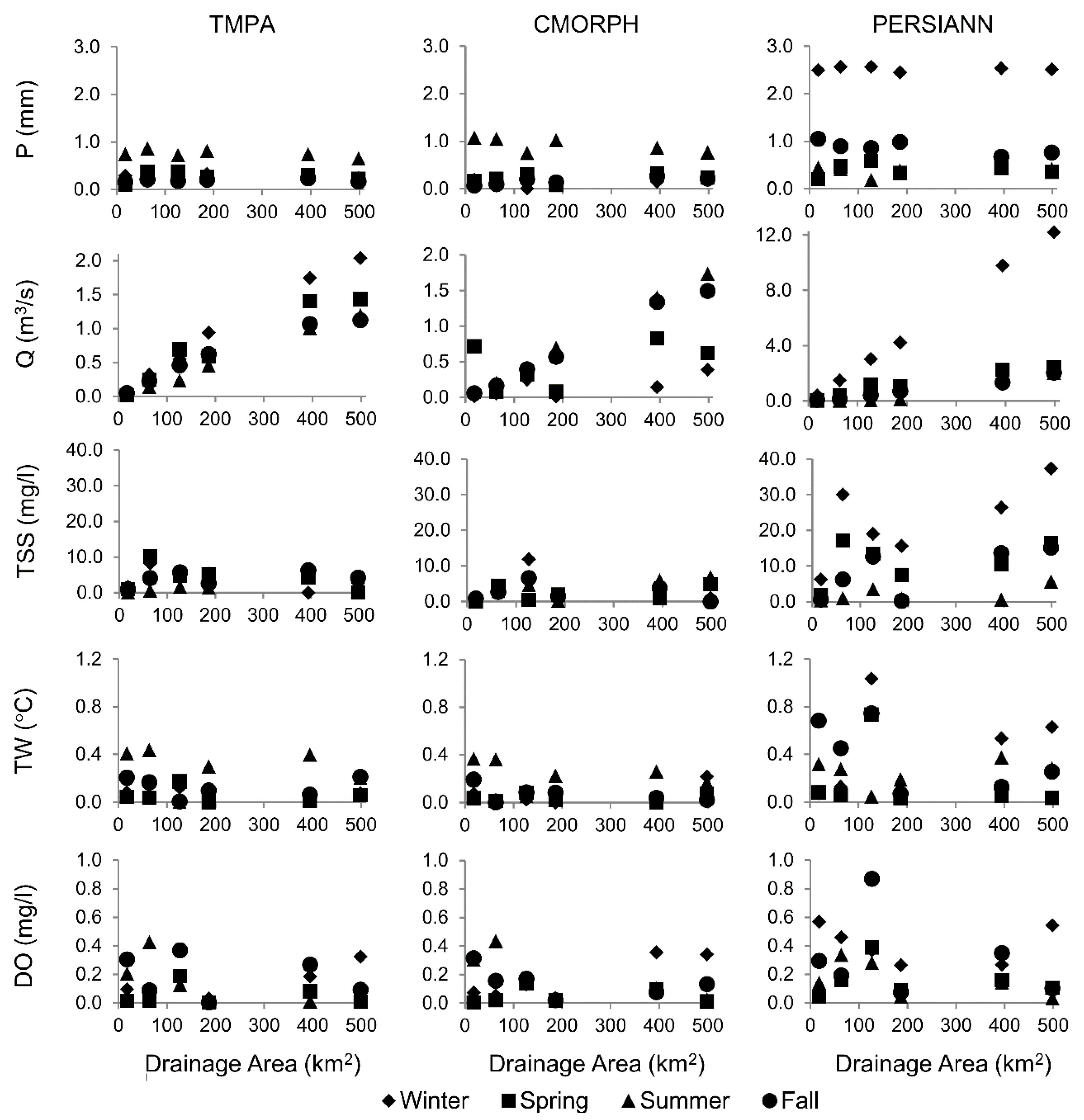
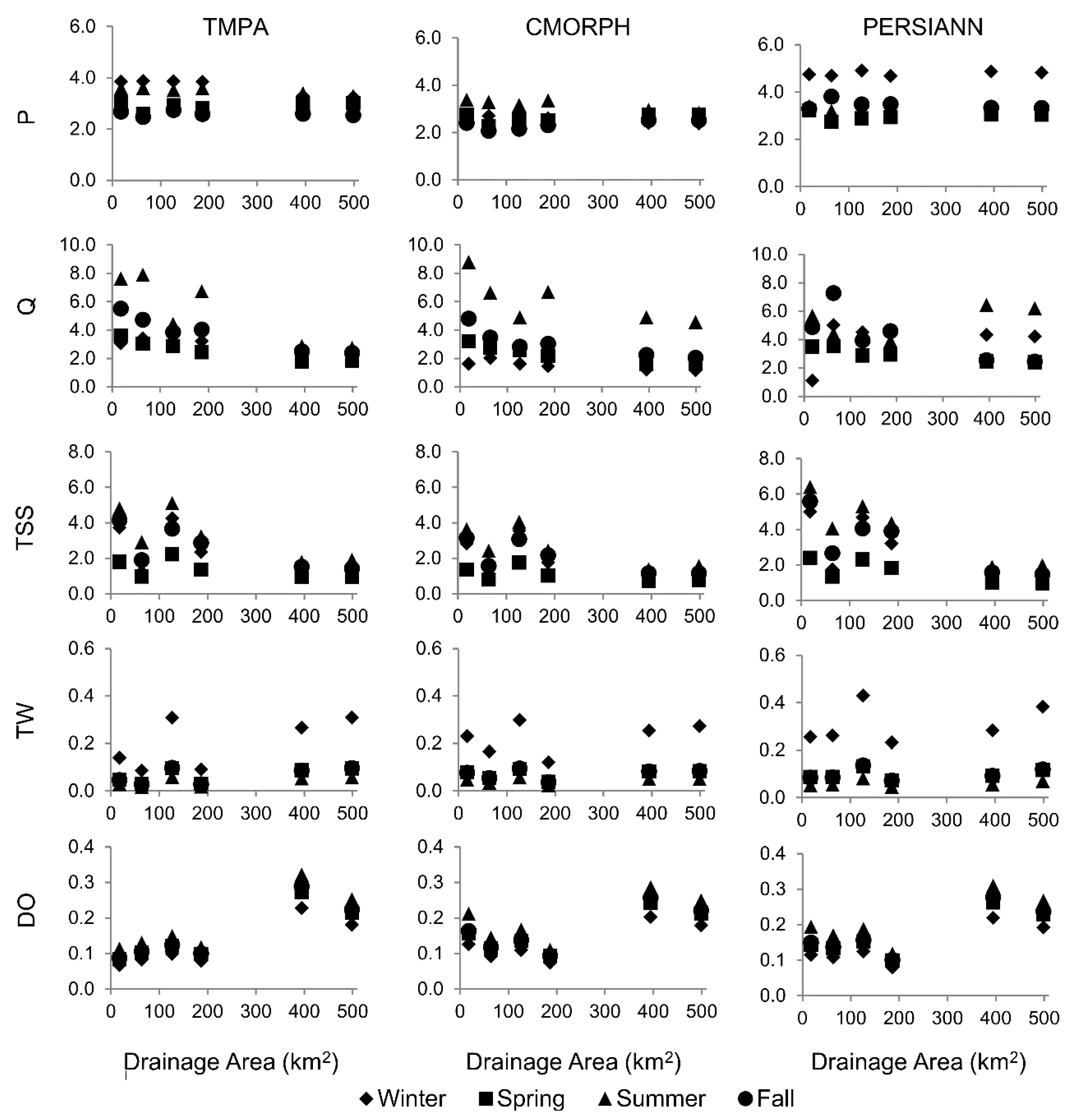
3.1. Seasonal Evaluation of SPPs
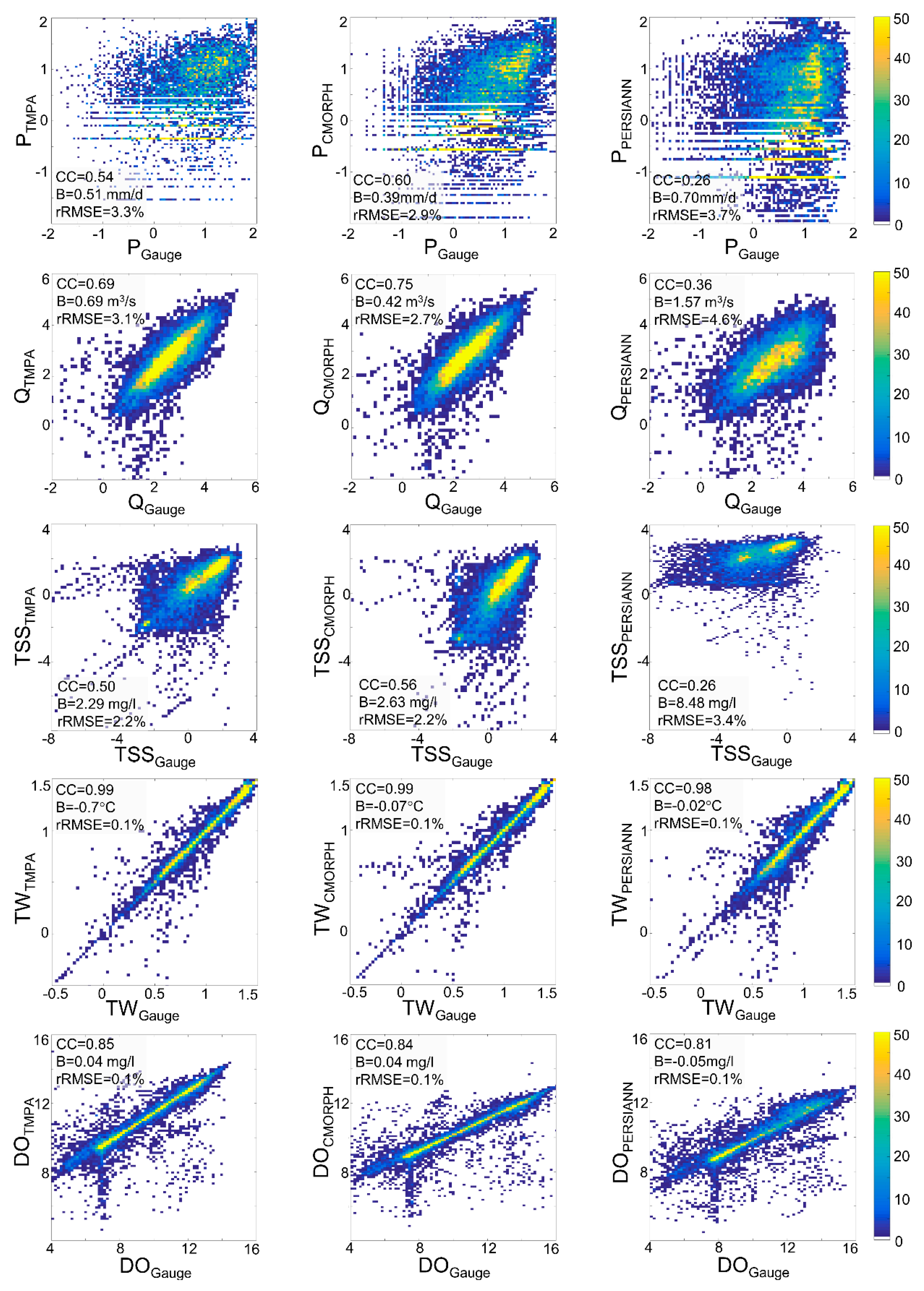
3.2. Model Output Analysis
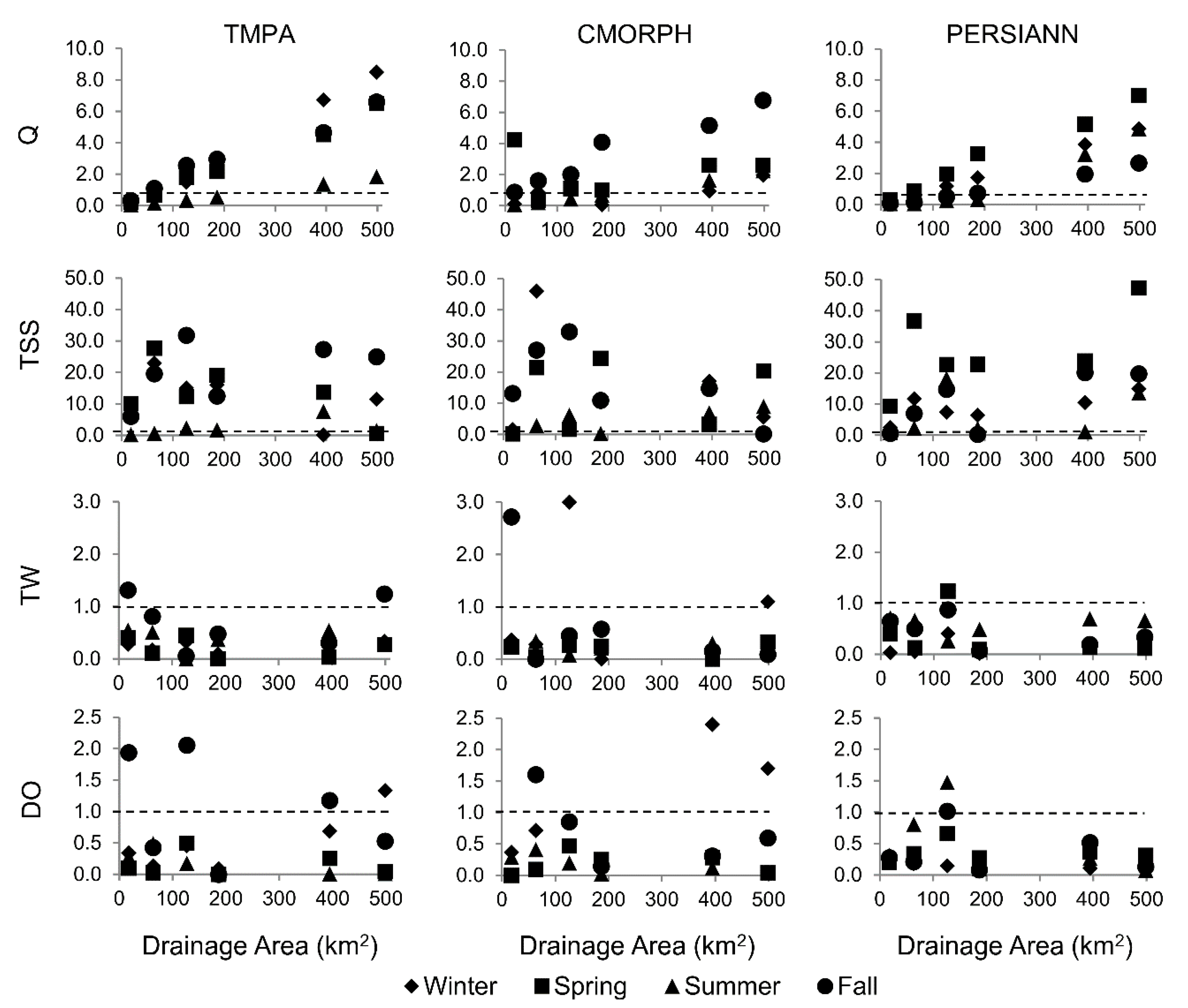
3.3. Error Propagation
4. Discussion
4.1. Seasonal Evaluation of SPPs
4.2. Model Output Analysis
4.3. Error Propagation
5. Conclusions
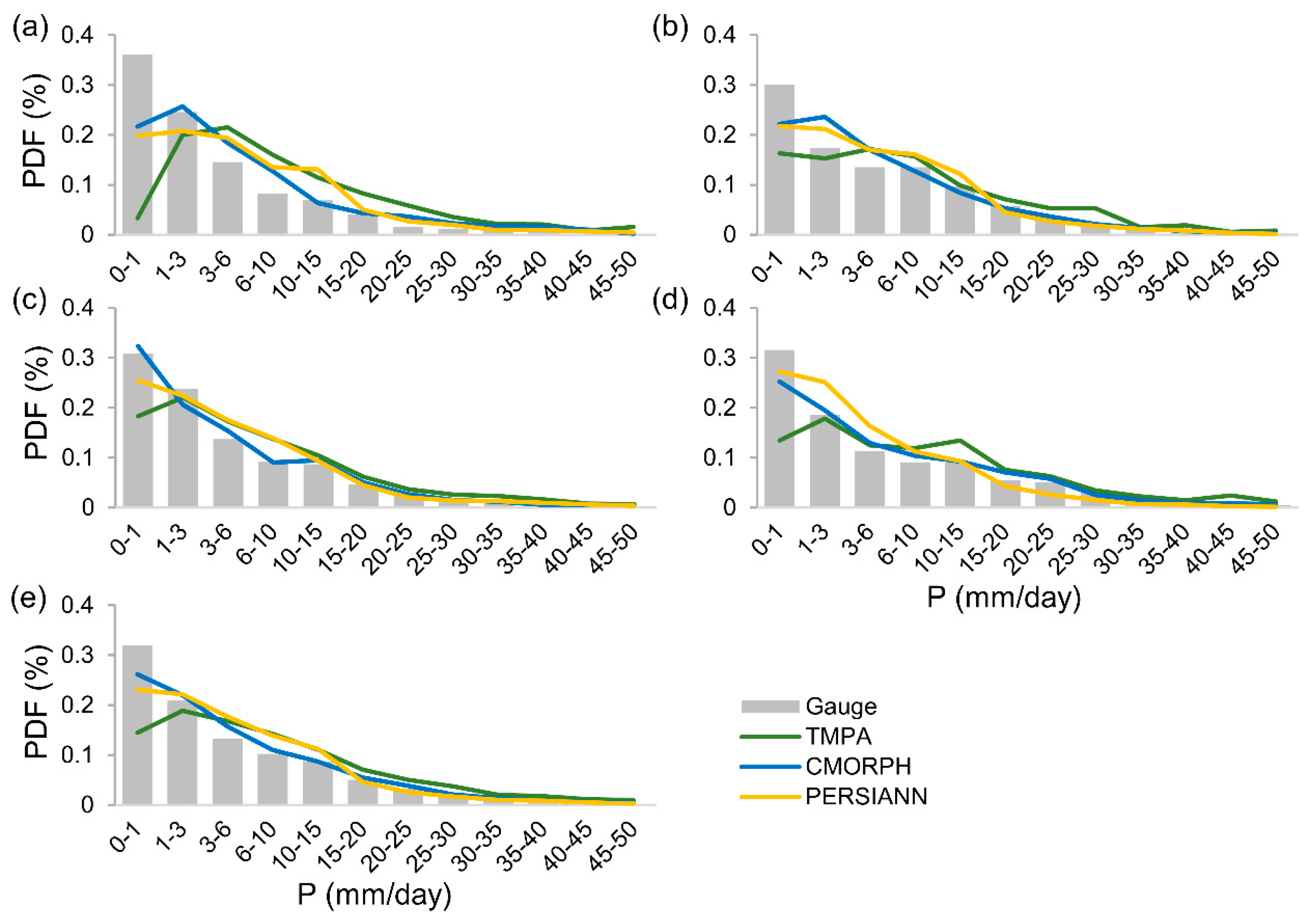
- SPPs show mixed performance skills with a seasonal dependence. Substantial differences are observed with moderate-intensity precipitation events, especially during winter, with both TMPA and PERSIANN grossly overestimating moderate-intensity precipitation. On the other hand, SPP estimates for high-intensity events are well predicted by PERSIANN but overestimated by TMPA. In the spring, all three SPPs tend to under-detect low-intensity precipitation. TMPA tends to under-detect low-intensity events and over-detect moderate- and high-intensity events; however, it is much better able to detect low-intensity events in warmer seasons.
- Correlations between the SPP-simulated streamflow and reference streamflow (simulated by forcing the model with rain gauge observations) are higher with respect to the precipitation ones, although biases are also higher. Generally, random errors for the three SPPs are relatively close between streamflow and precipitation. These results indicate that the HSPF model may have a dampening effect on the streamflow error for both TMPA and CMORPH; however, due to the poor quality of the PERSIANN product, its error is actually amplified through the model, with a positive dependency on basin scale.
- For TSS, TMPA and CMORPH appear to generally outperform PERSIANN during all seasons, which is expected since similar results are noted from streamflow and simulated TSS concentrations are highly dependent on streamflow. Although the systematic error in P is amplified in TSS, the random error is not (and it is actually dampened by the model). It is worthy to mention that while larger TSS errors are generally found in summer for all three SPPs, this seasonal difference is not propagated for TSS.
- The model shows good performance when simulating TW, with TMPA and CMORPH generally outperforming PERSIANN. The error in precipitation is dampened when translated into TW and, as expected, basin scale has no influence on the precipitation-to-TW error propagation.
- Satisfactory model performance is also shown in simulated DO, with TMPA and CMORPH marginally outperforming PERSIANN. The propagation of systematic and random errors from precipitation to DO varies by season, with larger dampening effects in spring and summer for all three SPPs.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hazra, A.; Maggioni, V.; Houser, P.; Antil, H.; Noonan, M. A Monte Carlo-based multi-objective optimization approach to merge different precipitation estimates for land surface modeling. J. Hydrol. 2019, 570, 454–462. [Google Scholar] [CrossRef]
- Sorooshian, S.; AghaKouchak, A.; Arkin, P.; Eylander, J.; Foufoula-Georgiou, E.; Harmon, R.; Hendrickx, J.M.H.; Imam, B.; Kuligowski, R.; Skahill, B.; et al. Advanced Concepts on Remote Sensing of Precipitation at Multiple Scales. Bull. Am. Meteorol. Soc. 2011, 92, 1353–1357. [Google Scholar] [CrossRef]
- Zeng, Q.; Chen, H.; Xu, C.-Y.; Jie, M.-X.; Chen, J.; Guo, S.-L.; Liu, J. The effect of rain gauge density and distribution on runoff simulation using a lumped hydrological modelling approach. J. Hydrol. 2018, 563, 106–122. [Google Scholar] [CrossRef]
- Maggioni, V.; Massari, C. On the performance of satellite precipitation products in riverine flood modeling: A review. J. Hydrol. 2018, 558, 214–224. [Google Scholar] [CrossRef]
- Sun, Q.; Miao, C.; Duan, Q.; Ashouri, H.; Sorooshian, S.; Hsu, K. A Review of Global Precipitation Data Sets: Data Sources, Estimation, and Intercomparisons. Rev. Geophys. 2018, 56, 79–107. [Google Scholar] [CrossRef]
- Nijssen, B.; Lettenmaier, D.P. Effect of precipitation sampling error on simulated hydrological fluxes and states: Anticipating the Global Precipitation Measurement satellites. J. Geophys. Res. 2004, 109. [Google Scholar] [CrossRef]
- Hong, Y.; Gochis, D.; Cheng, J.; Hsu, K.; Sorooshian, S. Evaluation of PERSIANN-CCS Rainfall Measurement Using the NAME Event Rain Gauge Network. J. Hydrometeorol. 2007, 8, 469–482. [Google Scholar] [CrossRef]
- Ebert, E.E.; Janowiak, J.E.; Kidd, C. Comparison of Near-Real-Time Precipitation Estimates from Satellite Observations and Numerical Models. Bull. Am. Meteorol. Soc. 2007, 88, 47–64. [Google Scholar] [CrossRef]
- Li, X.; Zhang, Q.; Xu, C.-Y. Assessing the performance of satellite-based precipitation products and its dependence on topography over Poyang Lake basin. Appl. Clim. 2014, 115, 713–729. [Google Scholar] [CrossRef]
- Falck, A.S.; Maggioni, V.; Tomasella, J.; Vila, D.A.; Diniz, F.L.R. Propagation of satellite precipitation uncertainties through a distributed hydrologic model: A case study in the Tocantins–Araguaia basin in Brazil. J. Hydrol. 2015, 527, 943–957. [Google Scholar] [CrossRef]
- Hossain, F.; Anagnostou, E. Assessment of current passive-microwave- and infrared-based satellite rainfall remote sensing for flood prediction. J. Geophys. Res. 2004, 109, D07102. [Google Scholar] [CrossRef]
- Gebremichael, M.; Liao, G.-Y.; Yan, J. Nonparametric error model for a high resolution satellite rainfall product: NONPARAMETRIC ERROR MODEL. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Guo, H.; Chen, S.; Bao, A.; Hu, J.; Yang, B.; Stepanian, P. Comprehensive Evaluation of High-Resolution Satellite-Based Precipitation Products over China. Atmosphere 2016, 7, 6. [Google Scholar] [CrossRef]
- Hong, Y.; Hsu, K.; Moradkhani, H.; Sorooshian, S. Uncertainty quantification of satellite precipitation estimation and Monte Carlo assessment of the error propagation into hydrologic response: ERROR PROPAGATION FROM SATELLITE RAINFALL. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Maggioni, V.; Vergara, H.J.; Anagnostou, E.N.; Gourley, J.J.; Hong, Y.; Stampoulis, D. Investigating the Applicability of Error Correction Ensembles of Satellite Rainfall Products in River Flow Simulations. J. Hydrometeorol. 2013, 14, 1194–1211. [Google Scholar] [CrossRef]
- Mei, Y.; Nikolopoulos, E.I.; Anagnostou, E.N.; Borga, M. Evaluating Satellite Precipitation Error Propagation in Runoff Simulations of Mountainous Basins. J. Hydrometeorol. 2016, 17, 1407–1423. [Google Scholar] [CrossRef]
- Nikolopoulos, E.I.; Anagnostou, E.N.; Hossain, F.; Gebremichael, M.; Borga, M. Understanding the Scale Relationships of Uncertainty Propagation of Satellite Rainfall through a Distributed Hydrologic Model. J. Hydrometeorol. 2010, 11, 520–532. [Google Scholar] [CrossRef]
- Seyyedi, H.; Anagnostou, E.N.; Beighley, E.; McCollum, J. Hydrologic evaluation of satellite and reanalysis precipitation datasets over a mid-latitude basin. Atmos. Res. 2015, 164–165, 37–48. [Google Scholar] [CrossRef]
- Yu, W.; Nakakita, E.; Kim, S.; Yamaguchi, K. Impact Assessment of Uncertainty Propagation of Ensemble NWP Rainfall to Flood Forecasting with Catchment Scale. Adv. Meteorol. 2016, 2016, 1384302. [Google Scholar] [CrossRef]
- Wang, Z.; Zhong, R.; Lai, C.; Chen, J. Evaluation of the GPM IMERG satellite-based precipitation products and the hydrological utility. Atmos. Res. 2017, 196, 151–163. [Google Scholar] [CrossRef]
- Zhang, J.L.; Li, Y.P.; Huang, G.H.; Wang, C.X.; Cheng, G.H. Evaluation of Uncertainties in Input Data and Parameters of a Hydrological Model Using a Bayesian Framework: A Case Study of a Snowmelt–Precipitation-Driven Watershed. J. Hydrometeorol. 2016, 17, 2333–2350. [Google Scholar] [CrossRef]
- Elsner, M.M.; Gangopadhyay, S.; Pruitt, T.; Brekke, L.D.; Mizukami, N.; Clark, M.P. How Does the Choice of Distributed Meteorological Data Affect Hydrologic Model Calibration and Streamflow Simulations? J. Hydrometeorol. 2014, 15, 1384–1403. [Google Scholar] [CrossRef]
- Raleigh, M.S.; Lundquist, J.D.; Clark, M.P. Exploring the impact of forcing error characteristics on physically based snow simulations within a global sensitivity analysis framework. Hydrol. Earth Syst. Sci. 2015, 19, 3153–3179. [Google Scholar] [CrossRef]
- Yang, Y.; Du, J.; Cheng, L.; Xu, W. Applicability of TRMM satellite precipitation in driving hydrological model for identifying flood events: A case study in the Xiangjiang River Basin, China. Nat. Hazards 2017, 87, 1489–1505. [Google Scholar] [CrossRef]
- Satgé, F.; Ruelland, D.; Bonnet, M.-P.; Molina, J.; Pillco, R. Consistency of satellite-based precipitation products in space and over time compared with gauge observations and snow- hydrological modelling in the Lake Titicaca region. Hydrol. Earth Syst. Sci. 2019, 23, 595–619. [Google Scholar] [CrossRef]
- Riad, P.; Graefe, S.; Hussein, H.; Buerkert, A. Landscape transformation processes in two large and two small cities in Egypt and Jordan over the last five decades using remote sensing data. Landsc. Urban Plan. 2020, 197, 103766. [Google Scholar] [CrossRef]
- Odeh, T.; Mohammad, A.H.; Hussein, H.; Ismail, M.; Almomani, T. Over-pumping of groundwater in Irbid governorate, northern Jordan: A conceptual model to analyze the effects of urbanization and agricultural activities on groundwater levels and salinity. Environ. Earth Sci. 2019, 78, 40. [Google Scholar] [CrossRef]
- Guetter, A.; Georgakakos, K. Are the El Niño and La Niña Predictors of the Iowa River Seasonal Flow? J. Appl. Meteorol. 1996, 35, 690–705. [Google Scholar] [CrossRef]
- Vivoni, E.R.; Entekhabi, D.; Hoffman, R.N. Error Propagation of Radar Rainfall Nowcasting Fields through a Fully Distributed Flood Forecasting Model. J. Appl. Meteor. Clim. 2007, 46, 932–940. [Google Scholar] [CrossRef]
- Vergara, H.; Hong, Y.; Gourley, J.J.; Anagnostou, E.N.; Maggioni, V.; Stampoulis, D.; Kirstetter, P.-E. Effects of Resolution of Satellite-Based Rainfall Estimates on Hydrologic Modeling Skill at Different Scales. J. Hydrometeorol. 2014, 15, 593–613. [Google Scholar] [CrossRef]
- Ehsan Bhuiyan, M.A.; Nikolopoulos, E.I.; Anagnostou, E.N.; Polcher, J.; Albergel, C.; Dutra, E.; Fink, G.; Martínez-de la Torre, A.; Munier, S. Assessment of precipitation error propagation in multi-model global water resource reanalysis. Hydrol. Earth Syst. Sci. 2019, 23, 1973–1994. [Google Scholar] [CrossRef]
- Hostache, R.; Matgen, P.; Montanari, A.; Montanari, M.; Hoffmann, L.; Pfister, L. Propagation of uncertainties in coupled hydro-meteorological forecasting systems: A stochastic approach for the assessment of the total predictive uncertainty. Atmos. Res. 2011, 100, 263–274. [Google Scholar] [CrossRef]
- Zhu, D.; Peng, D.Z.; Cluckie, I.D. Statistical analysis of error propagation from radar rainfall to hydrological models. Hydrol. Earth Syst. Sci. 2013, 17, 1445–1453. [Google Scholar] [CrossRef]
- Gebregiorgis, A.S.; Hossain, F. Understanding the Dependence of Satellite Rainfall Uncertainty on Topography and Climate for Hydrologic Model Simulation. IEEE Trans. Geosci. Remote Sens. 2013, 51, 704–718. [Google Scholar] [CrossRef]
- Neal, C.; Reynolds, B.; Rowland, P.; Norris, D.; Kirchner, J.W.; Neal, M.; Sleep, D.; Lawlor, A.; Woods, C.; Thacker, S.; et al. High-frequency water quality time series in precipitation and streamflow: From fragmentary signals to scientific challenge. Sci. Total Environ. 2012, 434, 3–12. [Google Scholar] [CrossRef]
- Himanshu, S.K.; Pandey, A.; Yadav, B. Assessing the applicability of TMPA-3B42V7 precipitation dataset in wavelet-support vector machine approach for suspended sediment load prediction. J. Hydrol. 2017, 550, 103–117. [Google Scholar] [CrossRef]
- Stryker, J.; Wemple, B.; Bomblies, A. Modeling sediment mobilization using a distributed hydrological model coupled with a bank stability model. Water Resour. Res. 2017, 53, 2051–2073. [Google Scholar] [CrossRef]
- Ma, D.; Xu, Y.-P.; Gu, H.; Zhu, Q.; Sun, Z.; Xuan, W. Role of satellite and reanalysis precipitation products in streamflow and sediment modeling over a typical alpine and gorge region in Southwest China. Sci. Total Environ. 2019, 685, 934–950. [Google Scholar] [CrossRef]
- Bezak, N.; Rusjan, S.; Fijavž, M.K.; Mikoš, M.; Šraj, M. Estimation of Suspended Sediment Loads Using Copula Functions. Water 2017, 9, 628. [Google Scholar] [CrossRef]
- Chang, C.-H.; Cai, L.-Y.; Lin, T.-F.; Chung, C.-L.; van der Linden, L.; Burch, M. Assessment of the Impacts of Climate Change on the Water Quality of a Small Deep Reservoir in a Humid-Subtropical Climatic Region. Water 2015, 7, 1687–1711. [Google Scholar] [CrossRef]
- Gelca, R.; Hayhoe, K.; Scott-Fleming, I.; Crow, C.; Dawson, D.; Patiño, R. Climate-water quality relationships in Texas reservoirs: Climate-Water Quality Relationships in Texas Reservoirs. Hydrol. Process. 2016, 30, 12–29. [Google Scholar] [CrossRef]
- Hayashi, S.; Murakami, S.; Watanabe, M.; Bao-Hua, X. HSPF Simulation of Runoff and Sediment Loads in the Upper Changjiang River Basin, China. J. Environ. Eng. 2004, 130, 801–815. [Google Scholar] [CrossRef]
- Jeznach, L.C.; Hagemann, M.; Park, M.-H.; Tobiason, J.E. Proactive modeling of water quality impacts of extreme precipitation events in a drinking water reservoir. J. Environ. Manag. 2017, 201, 241–251. [Google Scholar] [CrossRef] [PubMed]
- Johnson, T.E.; Butcher, J.B.; Parker, A.; Weaver, C.P. Investigating the Sensitivity of U.S. Streamflow and Water Quality to Climate Change: U.S. EPA Global Change Research Program’s 20 Watersheds Project. J. Water Resour. Plan. Manag. 2012, 138, 453–464. [Google Scholar] [CrossRef]
- Murdoch, P.S.; Baron, J.S.; Miller, T.L. Potential Effects of Climate Change on Surface-Water Quality in North America. J. Am. Water Resour. Assoc. 2000, 36, 347–366. [Google Scholar] [CrossRef]
- Soler, M.; Regüés, D.; Latron, J.; Gallart, F. Frequency–magnitude relationships for precipitation, stream flow and sediment load events in a small Mediterranean basin (Vallcebre basin, Eastern Pyrenees). Catena 2007, 71, 164–171. [Google Scholar] [CrossRef]
- Thorne, O.; Fenner, R.A. The impact of climate change on reservoir water quality and water treatment plant operations: A UK case study: The impact of climate change on reservoir water quality and WTP operations. Water Environ. J. 2011, 25, 74–87. [Google Scholar] [CrossRef]
- Solakian, J.; Maggioni, V.; Lodhi, A.; Godrej, A. Investigating the use of satellite-based precipitation products for monitoring water quality in the Occoquan Watershed. J. Hydrol. Reg. Stud. 2019, 26, 100630. [Google Scholar] [CrossRef]
- U.S. Environmental Protection Agency, Region 3, Water Protection Division. Chesapeake Bay Total Maximum Daily Load for Nitrogen, Phosphorus and Sediment. 2010. Available online: https://www.epa.gov/chesapeake-bay-tmdl/chesapeake-bay-tmdl-document (accessed on 1 November 2020).
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J. The TRMM Multi-Satellite Precipitation Analysis (TMPA). In Satellite Rainfall Applications for Surface Hydrology; Gebremichael, M., Hossain, F., Eds.; Springer: Dordrecht, The Netherlands, 2010; pp. 3–22. [Google Scholar] [CrossRef]
- Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P. CMORPH: A Method that Produces Global Precipitation Estimates from Passive Microwave and Infrared Data at High Spatial and Temporal Resolution. J. Hydrometeorol. 2004, 5, 487–503. [Google Scholar] [CrossRef]
- Hsu, K.; Behrangi, A.; Imam, B.; Sorooshian, S. Extreme Precipitation Estimation Using Satellite-Based PERSIANN-CCS Algorithm. In Satellite Rainfall Applications for Surface Hydrology; Gebremichael, M., Hossain, F., Eds.; Springer: Dordrecht, The Netherlands, 2010. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM Multisatellite Precipitation Analysis (TMPA): Quasi-Global, Multiyear, Combined-Sensor Precipitation Estimates at Fine Scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Tropical Rainfall Measuring Mission (TRMM). TRMM (TMPA) Rainfall Estimate L3 3 Hour 0.25 Degree × 0.25 Degree V7, Greenbelt, MD, Goddard Earth Sciences Data and Information Services Center (GES DISC). 2011. Available online: https://pmm.nasa.gov/data-access/downloads/TRMM (accessed on 22 May 2018). [CrossRef]
- Xie, P.; Joyce, R.; Wu, S.; Yoo, S.-H.; Yarosh, Y.; Sun, F.; Lin, R. Reprocessed, Bias-Corrected CMORPH Global High-Resolution Precipitation Estimates from 1998. J. Hydrometeorol. 2017, 18, 1617–1641. [Google Scholar] [CrossRef]
- Xie, P.; Joyce, R.; Wu, S.; Yoo, S.-H.; Yarosh, Y.; Sun, F.; Lin, R. NOAA CDR Program (2019): NOAA Climate Data Record (CDR) of CPC Morphing Technique (CMORPH) High Resolution Global Precipitation Estimates, Version 1 [8 km × 8 km, 30 min]. NOAA National Centers for Environmental Information. Available online: ftp://ftp.cpc.ncep.noaa.gov/precip/global_CMORPH/30min_8km (accessed on 24 May 2018).
- Hsu, K.; Gao, X.; Sorooshian, S.; Gupta, H.V. Precipitation Estimation from Remotely Sensed Information Using Artificial Neural Networks. J. Appl. Meteorol. 1997, 36, 1176–1190. [Google Scholar] [CrossRef]
- Center for Hydrometeorology and Remote Sensing, PERSIANN-CCS [0.04 × 0.04 degree, 30 min]. Available online: http://chrsdata.eng.uci.edu/ (accessed on 23 April 2018).
- Sorooshian, S.; Hsu, K.; Gao, X.; Gupta, H.V.; Imam, B.; Braithwaite, D. Evaluation of PERSIANN System Satellite-Based Estimates of Tropical Rainfall. Bull. Am. Meteorogogical Soc. 2000, 81, 2035–2046. [Google Scholar] [CrossRef]
- Albek, M.; Bakır Öğütveren, Ü.; Albek, E. Hydrological modeling of Seydi Suyu watershed (Turkey) with HSPF. J. Hydrol. 2004, 285, 260–271. [Google Scholar] [CrossRef]
- Duda, P.; Hummel, P.; Donigian, A.S., Jr.; Imhoff, A.C. BASINS/HSPF: Model Use, Calibration, and Validation. Trans. Asabe 2012, 55, 1523–1547. [Google Scholar] [CrossRef]
- Li, Z.; Liu, H.; Luo, C.; Li, Y.; Li, H.; Pan, J.; Jiang, X.; Zhou, Q.; Xiong, Z. Simulation of runoff and nutrient export from a typical small watershed in China using the Hydrological Simulation Program–Fortran. Environ. Sci. Pollut. Res. 2015, 22, 7954–7966. [Google Scholar] [CrossRef]
- Mishra, A.; Kar, S.; Singh, V.P. Determination of runoff and sediment yield from a small watershed in sub-humid subtropics using the HSPF model. Hydrol. Process. 2007, 21, 3035–3045. [Google Scholar] [CrossRef]
- Huo, S.-C.; Lo, S.-L.; Chiu, C.-H.; Chiueh, P.-T.; Yang, C.-S. Assessing a fuzzy model and HSPF to supplement rainfall data for nonpoint source water quality in the Feitsui reservoir watershed. Environ. Model. Softw. 2015, 72, 110–116. [Google Scholar] [CrossRef]
- Stern, M.; Flint, L.; Minear, J.; Flint, A.; Wright, S. Characterizing Changes in Streamflow and Sediment Supply in the Sacramento River Basin, California, Using Hydrological Simulation Program—FORTRAN (HSPF). Water 2016, 8, 432. [Google Scholar] [CrossRef]
- Diaz-Ramirez, J.; Johnson, B.; McAnally, W.; Martin, J.; Camacho, R. Estimation and Propagation of Parameter Uncertainty in Lumped Hydrological Models: A Case Study of HSPF Model Applied to Luxapallila Creek Watershed in Southeast USA. J. Hydrogeol. Hydrol. Eng. 2013, 2. [Google Scholar] [CrossRef]
- Wu, J.; Yu, S.L.; Zou, R. A Water quality-based approach for watershed wide bmp strategies. JAWRA J. Am. Water Resour. Assoc. 2006, 42, 1193–1204. [Google Scholar] [CrossRef]
- Young, C.B.; Bradley, A.A.; Krajewski, W.F.; Kruger, A.; Morrissey, M.L. Evaluating NEXRAD Multisensor Precipitation Estimates for Operational Hydrologic Forecasting. J. Hydrometeorol. 2000, 1, 14. [Google Scholar] [CrossRef]
- Xu, Z.; Godrej, A.N.; Grizzard, T.J. The hydrological calibration and validation of a complexly-linked watershed–reservoir model for the Occoquan watershed, Virginia. J. Hydrol. 2007, 345, 167–183. [Google Scholar] [CrossRef]
- Schaefer, J.T. The Critical Success Index as an Indicator of Warning Skill. Weather Forecast. 1990, 570–575. [Google Scholar] [CrossRef]
- Roebber, P.J. Visualizing Multiple Measures of Forecast Quality. Weather Forecast. 2009, 24, 601–608. [Google Scholar] [CrossRef]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. Atmos. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Cox, B.A.; Whitehead, P.G. Impacts of climate change scenarios on dissolved oxygen in the River Thames, UK. Hydrol. Res. 2009, 40, 138–152. [Google Scholar] [CrossRef]
- Irby, I.D.; Friedrichs, M.A.M.; Da, F.; Hinson, K.E. The competing impacts of climate change and nutrient reductions on dissolved oxygen in Chesapeake Bay. Biogeosciences 2018, 15, 2649–2668. [Google Scholar] [CrossRef]
- Moreno-Rodenas, A.M.; Tscheikner-Gratl, F.; Langeveld, J.G.; Clemens, F.H.L.R. Uncertainty analysis in a large-scale water quality integrated catchment modelling study. Water Res. 2019, 158, 46–60. [Google Scholar] [CrossRef]

| Metric | Equation | Units | Range | Indicator(s) |
|---|---|---|---|---|
| Probability of Detection | - | 0–1 | P | |
| False Alarm Rate | - | 0–1 | P | |
| Critical Success Index | - | 0–1 | P | |
| Relative Bias | % | 0-∞ | P | |
| Root Mean Square Error | mm/d | 0–∞ | P | |
| Correlation Coefficient | - | −1–1 | P, Q, TSS, TW, DO | |
| Standard Deviation | mm/d, m3/s, °C, mg/L | 0–∞ | P, Q, TSS, TW, DO | |
| Absolute Bias | mm/d, m3/s, °C, mg/L | 0–∞ | P, Q, TSS, TW, DO | |
| Relative Root Mean Square Error | % | 0–∞ | P, Q, TSS, TW, DO | |
| Bias Propagation Factor | - | 0–∞ | P, Q, TSS, TW, DO | |
| rRMSE Propagation Factor | - | 0–∞ | P, Q, TSS, TW, DO |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Solakian, J.; Maggioni, V.; Godrej, A. Investigating the Error Propagation from Satellite-Based Input Precipitation to Output Water Quality Indicators Simulated by a Hydrologic Model. Remote Sens. 2020, 12, 3728. https://doi.org/10.3390/rs12223728
Solakian J, Maggioni V, Godrej A. Investigating the Error Propagation from Satellite-Based Input Precipitation to Output Water Quality Indicators Simulated by a Hydrologic Model. Remote Sensing. 2020; 12(22):3728. https://doi.org/10.3390/rs12223728
Chicago/Turabian StyleSolakian, Jennifer, Viviana Maggioni, and Adil Godrej. 2020. "Investigating the Error Propagation from Satellite-Based Input Precipitation to Output Water Quality Indicators Simulated by a Hydrologic Model" Remote Sensing 12, no. 22: 3728. https://doi.org/10.3390/rs12223728
APA StyleSolakian, J., Maggioni, V., & Godrej, A. (2020). Investigating the Error Propagation from Satellite-Based Input Precipitation to Output Water Quality Indicators Simulated by a Hydrologic Model. Remote Sensing, 12(22), 3728. https://doi.org/10.3390/rs12223728








