Automatic Shoreline Detection from Video Images by Combining Information from Different Methods
Abstract
1. Introduction
2. Methodology
2.1. Study Sites and Video Monitoring Stations
2.2. Manual Shoreline Digitization
2.3. Automatic Shoreline Detection
2.3.1. Raw Shorelines
2.3.2. Weighted Combination of the Raw Shorelines
2.3.3. Filtering of the Combined Shorelines
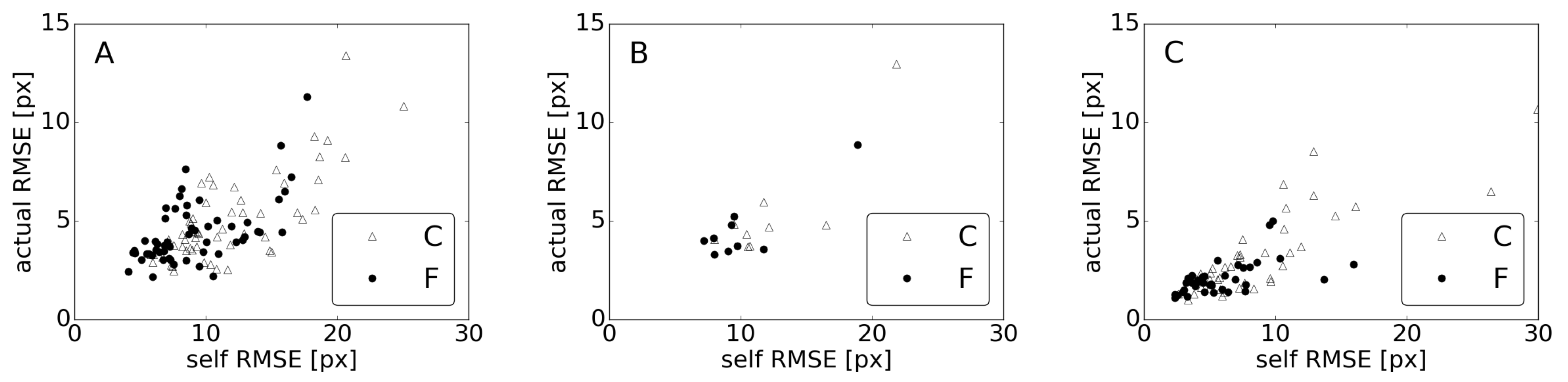
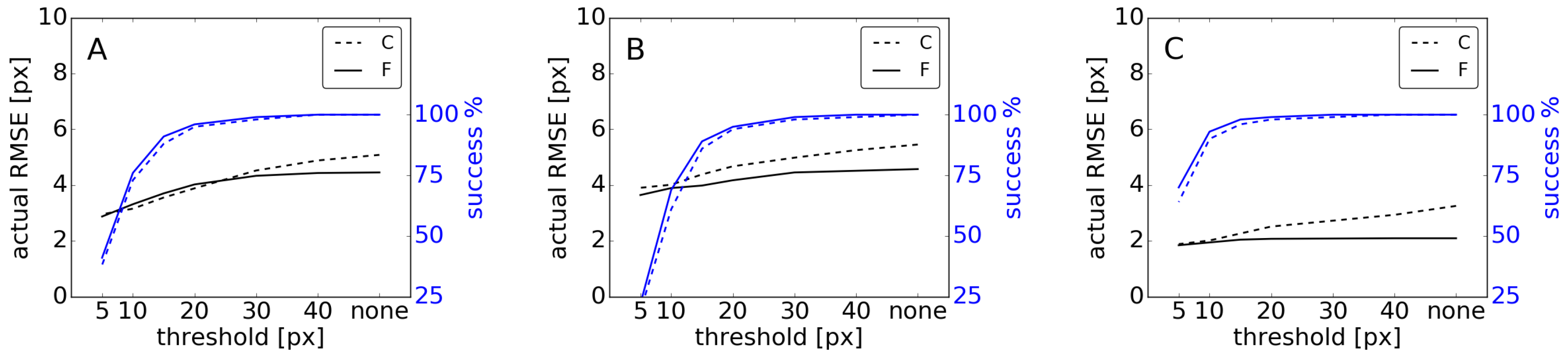
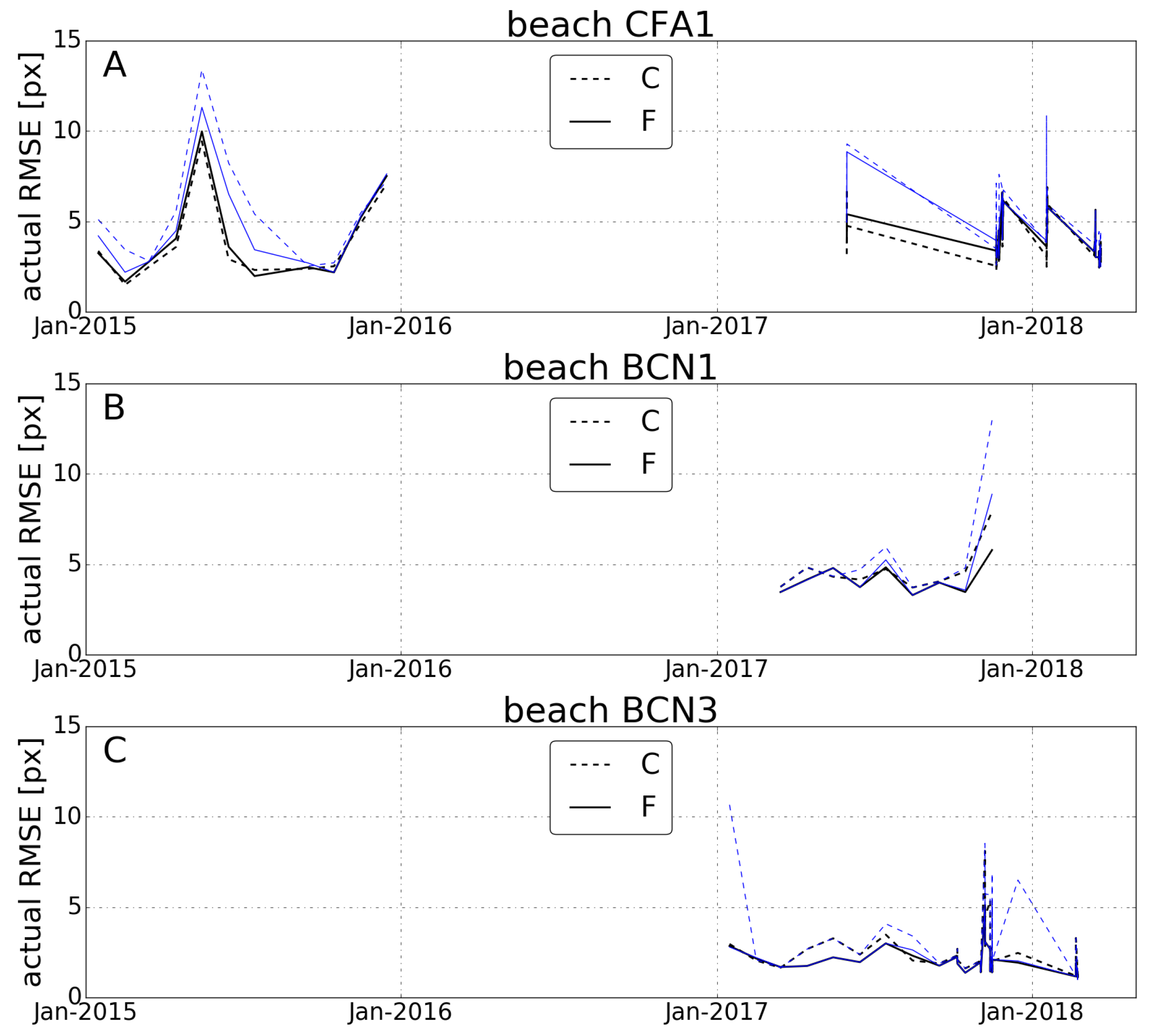
3. Results
3.1. Manual Shorelines
3.2. Automatic Shorelines
4. Discussion
4.1. Sensitivity Analysis
4.2. Interpretation of the Results
4.3. Evaluation of the Raw Methods Used
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Vousdoukas, M.I.; Ranasinghe, R.; Mentaschi, L.; Plomaritis, T.A.; Athanasiou, P.; Luijendijk, A.; Feyen, L. Sandy coastlines under threat of erosion. Nat. Clim. Chang. 2020, 10, 260–263. [Google Scholar] [CrossRef]
- Ojeda, E.; Guillén, J. Shoreline dynamics and beach rotation of artificial embayed beaches. Mar. Geol. 2008, 253, 51–62. [Google Scholar] [CrossRef]
- Kroon, A.; Davidson, M.A.; Aarninkhof, S.G.J.; Archetti, R.; Armaroli, C.; Gonzalez, M.; Medri, S.; Osorio, A.; Aagaard, T.; Holman, R.A.; et al. Application of remote sensing video systems to coastline management problems. Coast. Eng. 2007, 54, 493–505. [Google Scholar] [CrossRef]
- Castelle, B.; Marieu, V.; Bujan, S.; Splinter, K.D.; Robinet, A.; Sénéchal, N.; Ferreira, S. Impact of the winter 2013–2014 series of severe Western Europe storms on a double-barred sandy coast: Beach and dune erosion and megacusp embayments. Geomorphology 2015, 238, 135–148. [Google Scholar] [CrossRef]
- Ribas, F.; Falqués, A.; de Swart, H.E.; Dodd, N.; Garnier, R.; Calvete, D. Understanding coastal morphodynamic patterns from depth-averaged sediment concentration. Rev. Geophys. 2015, 53, 362–410. [Google Scholar] [CrossRef]
- Falqués, A.; Ribas, F.; Idier, D.; Arriaga, J. Formation mechanisms for self-organized km-scale shoreline sand waves. J. Geophys. Res. Earth Surf. 2017, 122, 1121–1138. [Google Scholar] [CrossRef]
- Robinet, A.; Castelle, B.; Idier, D.; Harley, M.D.; Splinter, K.D. Controls of local geology and cross-shore/longshore processes on embayed beach shoreline variability. Mar. Geol. 2020, 422, 106118. [Google Scholar] [CrossRef]
- Roelvink, D.; Huisman, B.; Elghandour, A.; Ghonim, M.; Reyns, J. Efficient Modeling of Complex Sandy Coastal Evolution at Monthly to Century Time Scales. Front. Mar. Sci. 2020, 7, 1121–1138. [Google Scholar] [CrossRef]
- Gibeaut, J. LIDAR: Mapping a shoreline by laser light. Geotimes 2003, 48, 22–27. [Google Scholar]
- Mason, D.; Davenport, L. Accurate and efficient determination of the shoreline in ERS-1 SAR images. IEEE Trans. Geosci. Remote Sens. 1996, 34, 1243–1253. [Google Scholar] [CrossRef]
- Wu, L.; Tajima, Y.; Yamanaka, Y.; Shimozono, T.; Sato, S. Study on characteristics of synthetic aperture radar (SAR) imagery around the coast for shoreline detection. Coast. Eng. J. 2019, 61, 152–170. [Google Scholar] [CrossRef]
- Plant, N.; Holman, R. Intertidal beach profile estimation using video images. Mar. Geol. 1997, 140, 1–24. [Google Scholar] [CrossRef]
- Holman, R.; Stanley, J. The history and technical capabilities of Argus. Coast. Eng. 2007, 54, 477–491. [Google Scholar] [CrossRef]
- Liu, H.; Jezek, K. Automated extraction of coastline from satellite imagery by integrating Canny edge detection and locally adaptive thresholding methods. Int. J. Remote Sens. 2004, 25, 937–958. [Google Scholar] [CrossRef]
- Pardo-Pascual, J.; Almonacid-Caballer, J.; Ruiz, L.; Palomar-Vázquez, J. Automatic extraction of shorelines from Landsat TM and ETM+ multi-temporal images with subpixel precision. Remote Sens. Environ. 2012, 123, 1–11. [Google Scholar] [CrossRef]
- Vos, K.; Splinter, K.; Harley, M.; Simmons, J.; Turner, I. CoastSat: A Google Earth Engine-enabled Python toolkit to extract shorelines from publicly available satellite imagery. Environ. Model. Softw. 2019, 122. [Google Scholar] [CrossRef]
- Pardo-Pascual, J.; Sánchez-García, E.; Almonacid-Caballer, J.; Palomar-Vázquez, J.; de los Santos, E.; Fernández-Sarría, A.; Balaguer-Beser, A. Assessing the accuracy of automatically extracted shorelines on microtidal beaches from landsat 7, landsat 8 and sentinel-2 imagery. Remote Sens. 2018, 10, 326. [Google Scholar] [CrossRef]
- Valentini, N.; Saponieri, A.; Molfetta, M.; Damiani, L. New algorithms for shoreline monitoring from coastal video systems. Earth Sci. Inform. 2017, 10, 495–506. [Google Scholar] [CrossRef]
- Vousdoukas, M.I.; Ferreira, P.M.; Almeida, L.P.; Dodet, G.; Psaros, F.; Andriolo, U.; Taborda, R.; Silva, A.N.; Ruano, A.; Ferreira, Ó.M. Performance of intertidal topography video monitoring of a meso-tidal reflective beach in South Portugal. Ocean Dyn. 2011, 61, 1521–1540. [Google Scholar] [CrossRef]
- Rigos, A.; Andreadis, O.; Andreas, M.; Vousdoukas, M.; Tsekouras, G.; Velegrakis, A. Shoreline extraction from coastal images using Chebyshev polynomials and RBF neural networks. IFIP Adv. Inf. Commun. Technol. 2014, 436, 593–603. [Google Scholar] [CrossRef]
- Simarro, G.; Bryan, K.R.; Guedes, R.M.; Sancho, A.; Guillen, J.; Coco, G. On the use of variance images for runup and shoreline detection. Coast. Eng. 2015, 99, 136–147. [Google Scholar] [CrossRef]
- Aarninkhof, S.; Turner, I.; Dronkers, T.; Caljouw, M.; Nipius, L. A video-based technique for mapping intertidal beach bathymetry. Coast. Eng. 2003, 49, 275–289. [Google Scholar] [CrossRef]
- Kingston, K. Applications of Complex Adaptive Systems, Approaches to Coastal Systems. Ph.D. Thesis, University of Plymouth, Plymouth, UK, 2003. [Google Scholar]
- Plant, N.; Aarninkhof, S.; Turner, I.; Kingston, K. The Performance of Shoreline Detection Models Applied to Video Imagery. J. Coast. Res. 2007, 23, 658–670. [Google Scholar] [CrossRef]
- Turner, I.; Leyden, V.; Symonds, G.; Mcgrath, J.; Jackson, A.; Jancar, T.; Aarninkhof, S.; Elshoff, I. Comparison of observed and predicted coastline changes at the gold coast artificial (surfing) reef. In Proceedings of the International Conference on Coastal Engineering, Sydney, Australia, 16–21 July 2000. [Google Scholar]
- Hoonhout, B.; Radermacher, M.; Baart, F.; van der Maaten, L. An automated method for semantic classification of regions in coastal images. Coast. Eng. 2015, 105, 1–12. [Google Scholar] [CrossRef]
- Rutten, J.; Ruessink, B.G.; Price, T.D. Observations on sandbar behaviour along a man-made curved coast. Earth Surf. Process. Landf. 2018, 43, 134–149. [Google Scholar] [CrossRef]
- Keller, T.; Olkin, I. Combining correlated unbiased estimators of the mean of a normal distribution. In A Festschrift for Herman Rubin; Lecture Notes–Monograph Series; Institute of Mathematical Statistics: Beachwood, OH, USA, 2004; Volume 45, pp. 218–227. [Google Scholar] [CrossRef]
- Khaleghi, B.; Khamis, A.; Karray, F.O.; Razavi, S.N. Multisensor data fusion: A review of the state-of-the-art. Inform. Fusion 2013, 14, 28–44. [Google Scholar] [CrossRef]
- de Swart, R.L.; Ribas, F.; Calvete, D.; Kroon, A.; Orfila, A. Optimal estimations of directional wave conditions for nearshore field studies. Cont. Shelf Res. 2020, in press. [Google Scholar] [CrossRef]
- Nieto, M.; Garau, B.; Balle, S.; Simarro, G.; Zarruk, G.; Ortiz, A.; Tintoré, J.; Álvarez, E.; Gómez-Pujol, L.; Orfila, A. An open source, low cost video-based coastal monitoring system. Earth Surf. Process. Landf. 2010, 35, 1712–1719. [Google Scholar] [CrossRef]
- Simarro, G.; Ribas, F.; Alvarez, A.; Guillén, J.; Chic, O.; Orfila, A. ULISES: An open source code for extrinsic calibrations and planview generations in coastal video monitoring systems. J. Coast. Res. 2017, 33, 1217–1227. [Google Scholar] [CrossRef]
- Xu, H. Modification of normalised difference water index (NDWI) to enhance open water features in remotely sensed imagery. Int. J. Remote Sens. 2006, 27. [Google Scholar] [CrossRef]
- Coco, G.; O’Hare, T.J.; Huntley, D.A. Beach cusps: A comparison of data and theories for their formation. J. Coast. Res. 1999, 15, 741–749. [Google Scholar]




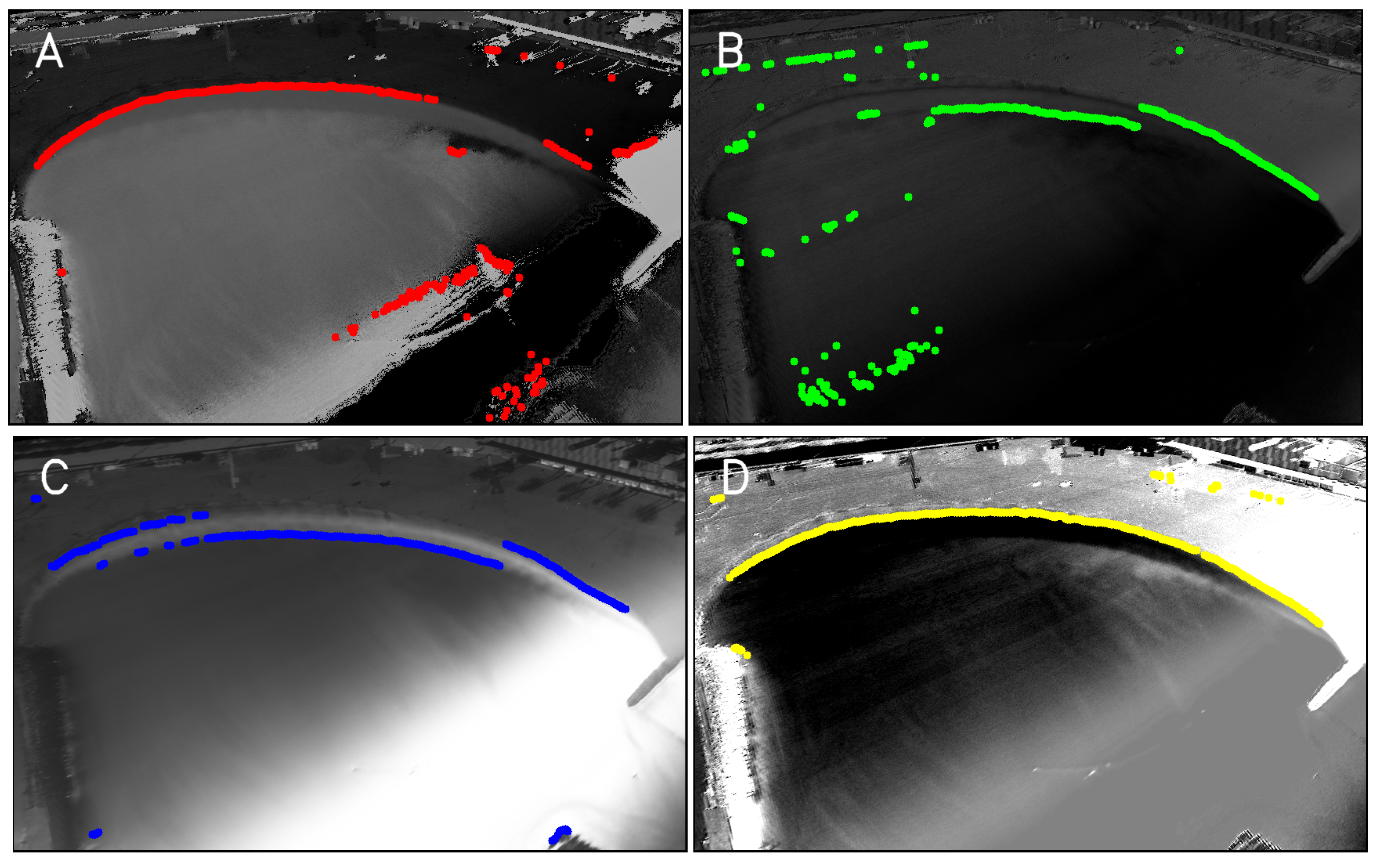
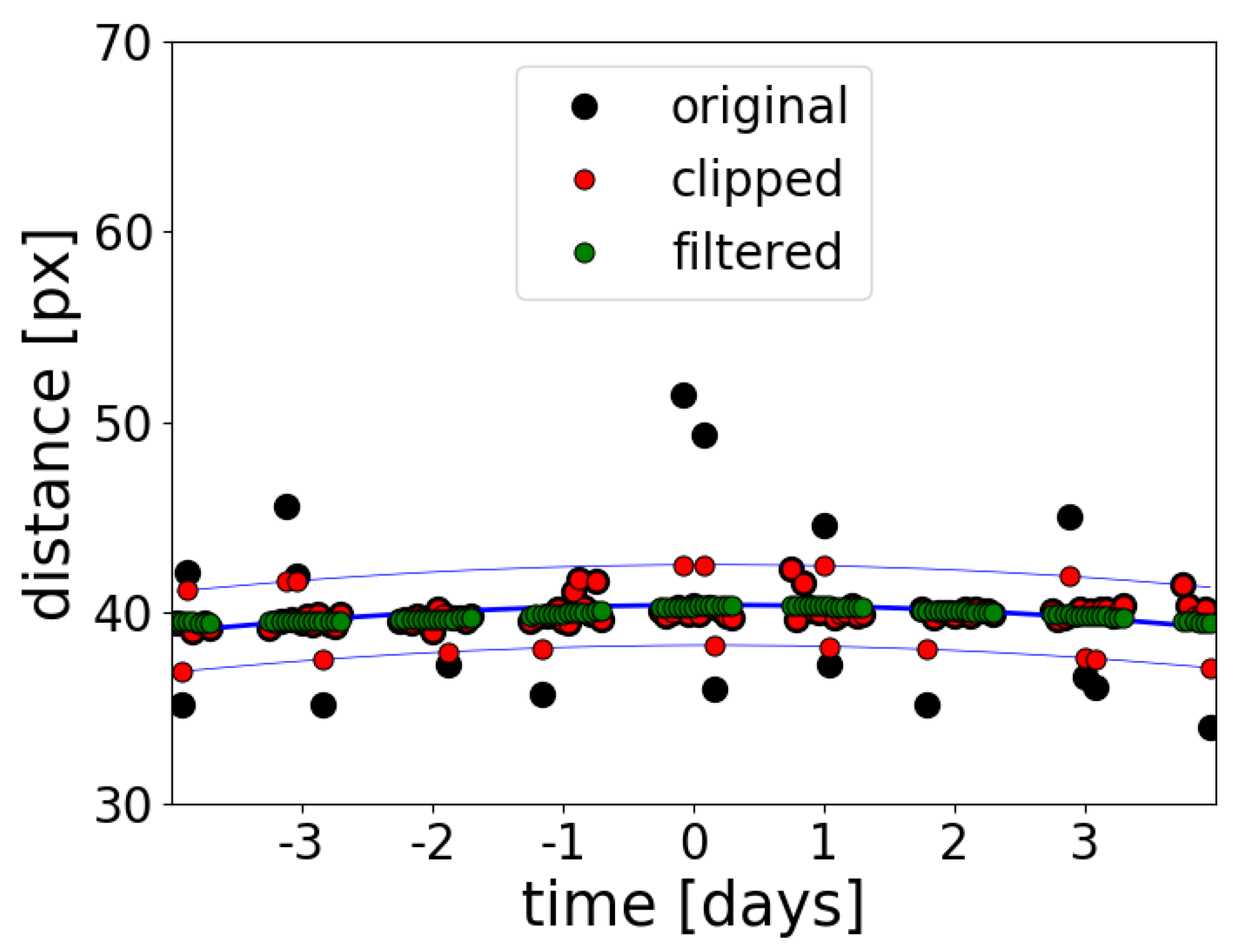
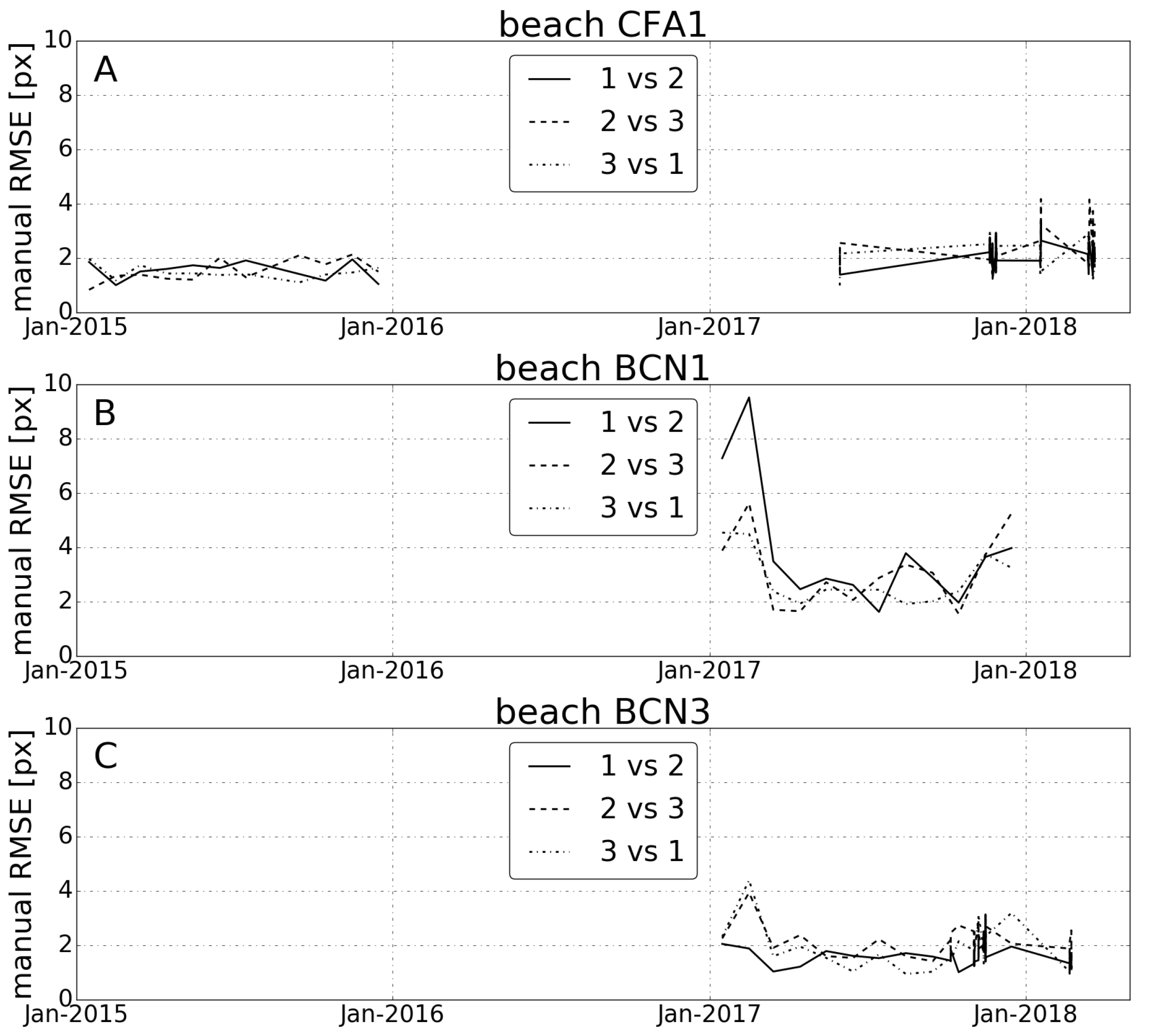


| Beach | Width [px] | Height [px] | # Manual | # Auto |
|---|---|---|---|---|
| CFA1 | 1609 | 359 | 55 | 55 |
| BCN1 | 1461 | 543 | 12 | 9 |
| BCN2 | 923 | 501 | 12 | 10 |
| BCN3 | 857 | 527 | 40 | 40 |
| BCN4 | 749 | 603 | 12 | 12 |
| BCN5 | 1293 | 743 | 12 | 12 |
| total | 143 | 138 |
| Time | Space | Filtering | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Case | ||||||||||
| [days] | [-] | [Days] | [-] | [px] | [-] | [-] | [-] | [-] | [-] | |
| 01 | 15 | 2 | 4 | 4 | 3 | 5 | ||||
| 02 | – | – | – | – | – | – | – | – | – | |
| 03 | – | – | – | – | – | – | – | – | – | |
| 04 | – | 1 | – | – | – | – | – | – | – | – |
| 05 | – | – | – | 2 | – | – | – | – | – | – |
| 06 | – | – | – | – | – | – | – | – | – | |
| 07 | – | – | – | – | – | – | 2 | – | – | – |
| 08 | – | – | – | – | – | – | – | – | – | |
| 09 | – | – | – | – | – | – | – | – | – | |
| 10 | – | – | – | – | – | – | – | – | 1 | – |
| 11 | – | – | – | – | – | – | – | – | 5 | – |
| 12 | – | – | – | – | – | – | – | – | – | 3 |
| 13 | – | – | – | – | – | – | – | – | – | 7 |
| Beach | Threshold [px] | Combined | Filtered | Manual | ||||
|---|---|---|---|---|---|---|---|---|
| RMSE [m] | Bias [m] | Success [%] | RMSE [m] | Bias [m] | Success [%] | RMSE [m] | ||
| CFA1 | none | 2.5 | 0.7 | 100 | 2.2 | 0.9 | 100 | 1.1 |
| 20 | 1.9 | 0.8 | 95 | 2.0 | 0.9 | 96 | ||
| 10 | 1.6 | 0.8 | 73 | 1.7 | 1.0 | 76 | ||
| BCN1 | none | 2.7 | 0.2 | 100 | 2.3 | 0.3 | 100 | 1.4 |
| 20 | 2.3 | 0.4 | 94 | 2.1 | 0.5 | 95 | ||
| 10 | 2.0 | 0.5 | 61 | 1.9 | 0.4 | 79 | ||
| BCN2 | none | 5.2 | −1.4 | 100 | 2.3 | −1.2 | 100 | 1.3 |
| 20 | 1.6 | −0.8 | 95 | 1.7 | −1.1 | 97 | ||
| 10 | 1.6 | −0.8 | 78 | 1.6 | −1.1 | 84 | ||
| BCN3 | none | 1.6 | −0.3 | 100 | 1.0 | −0.2 | 100 | 1.0 |
| 20 | 1.3 | −0.2 | 98 | 1.0 | −0.2 | 99 | ||
| 10 | 1.0 | −0.1 | 90 | 1.0 | −0.1 | 93 | ||
| BCN4 | none | 2.3 | −2.0 | 100 | 2.5 | −2.3 | 100 | 0.7 |
| 20 | 2.3 | −2.0 | 100 | 2.5 | −2.3 | 100 | ||
| 10 | 2.3 | −2.0 | 99 | 2.5 | −2.3 | 100 | ||
| BCN5 | none | 3.9 | −0.1 | 100 | 2.9 | −0.4 | 100 | 0.8 |
| 20 | 1.6 | −0.8 | 93 | 1.5 | −0.9 | 94 | ||
| 10 | 1.6 | −0.9 | 77 | 1.6 | −1.0 | 81 | ||
| Case | Combined | Filtered | ||||
|---|---|---|---|---|---|---|
| RMSE [m] | Bias [m] | Success [%] | RMSE [m] | Bias [m] | Success [%] | |
| 01 | 1.7 | −0.03 | 96 | 1.7 | −0.02 | 97 |
| 02 | 1.7 | −0.04 | 96 | 1.7 | −0.04 | 97 |
| 03 | 1.8 | 0.01 | 96 | 1.7 | 0.06 | 97 |
| 04 | 1.8 | −0.03 | 96 | 1.7 | −0.02 | 97 |
| 05 | 1.7 | −0.01 | 96 | 1.7 | 0.00 | 97 |
| 06 | 1.8 | −0.09 | 86 | 1.8 | −0.05 | 89 |
| 07 | 1.7 | −0.01 | 92 | 1.7 | 0.00 | 94 |
| 08 | 1.7 | −0.03 | 96 | 1.9 | −0.04 | 96 |
| 09 | 1.7 | −0.03 | 96 | 1.7 | −0.01 | 98 |
| 10 | 1.7 | −0.03 | 96 | 1.8 | −0.03 | 96 |
| 11 | 1.7 | −0.03 | 96 | 1.7 | −0.01 | 98 |
| 12 | 1.7 | −0.03 | 96 | 1.7 | −0.02 | 97 |
| 13 | 1.7 | −0.03 | 96 | 1.7 | −0.01 | 97 |
| Beach | RMSE [m] | |||
|---|---|---|---|---|
| H | S | V | R/G | |
| CFA1 | 14 | 31 | 15 | 12 |
| BCN1 | 12 | 78 | 54 | 7 |
| BCN2 | 38 | 53 | 16 | 4 |
| BCN3 | 46 | 14 | 31 | 10 |
| BCN4 | 16 | 15 | 14 | 9 |
| BCN5 | 8 | 15 | 25 | 10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ribas, F.; Simarro, G.; Arriaga, J.; Luque, P. Automatic Shoreline Detection from Video Images by Combining Information from Different Methods. Remote Sens. 2020, 12, 3717. https://doi.org/10.3390/rs12223717
Ribas F, Simarro G, Arriaga J, Luque P. Automatic Shoreline Detection from Video Images by Combining Information from Different Methods. Remote Sensing. 2020; 12(22):3717. https://doi.org/10.3390/rs12223717
Chicago/Turabian StyleRibas, Francesca, Gonzalo Simarro, Jaime Arriaga, and Pau Luque. 2020. "Automatic Shoreline Detection from Video Images by Combining Information from Different Methods" Remote Sensing 12, no. 22: 3717. https://doi.org/10.3390/rs12223717
APA StyleRibas, F., Simarro, G., Arriaga, J., & Luque, P. (2020). Automatic Shoreline Detection from Video Images by Combining Information from Different Methods. Remote Sensing, 12(22), 3717. https://doi.org/10.3390/rs12223717







