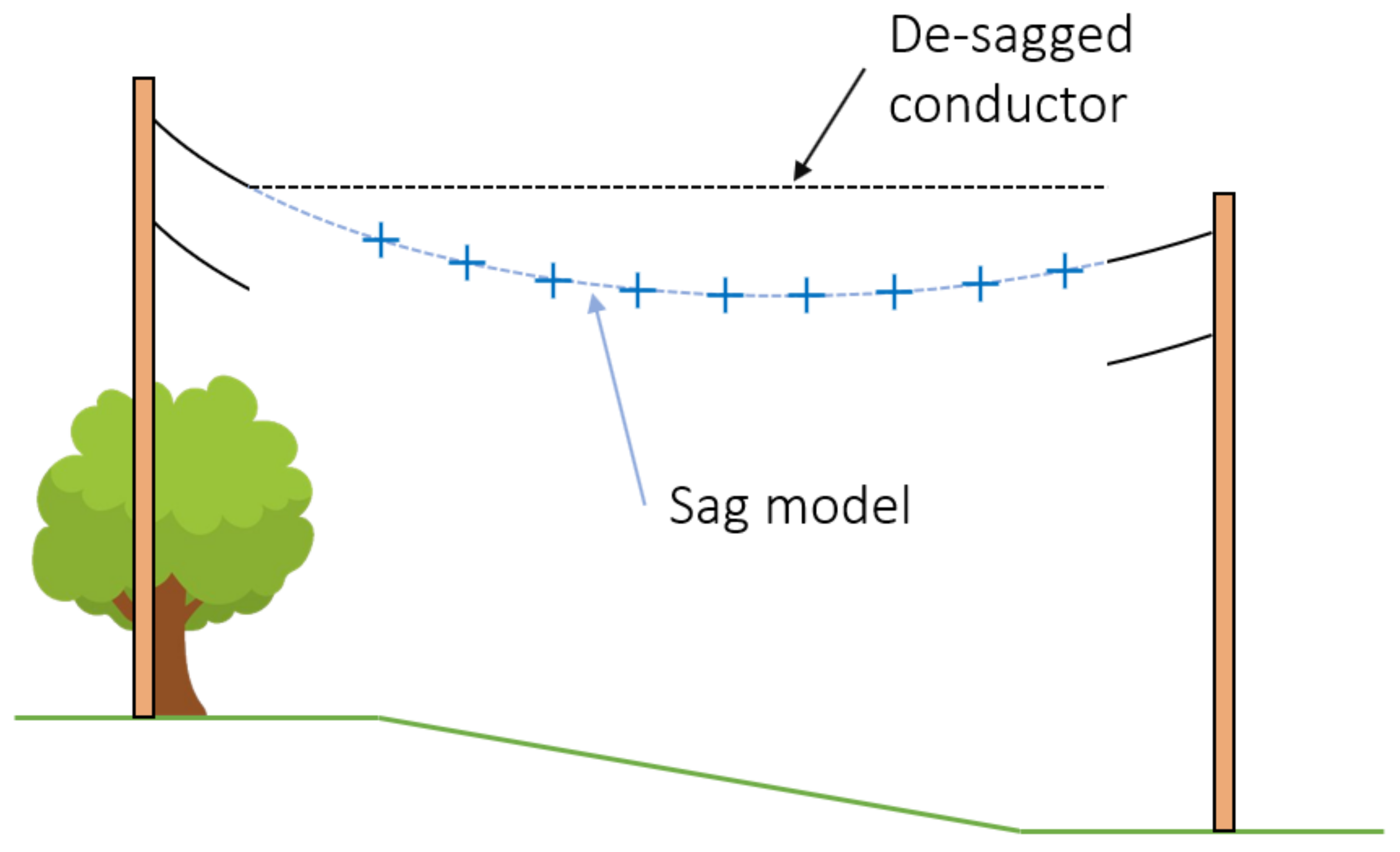
Figure 1.
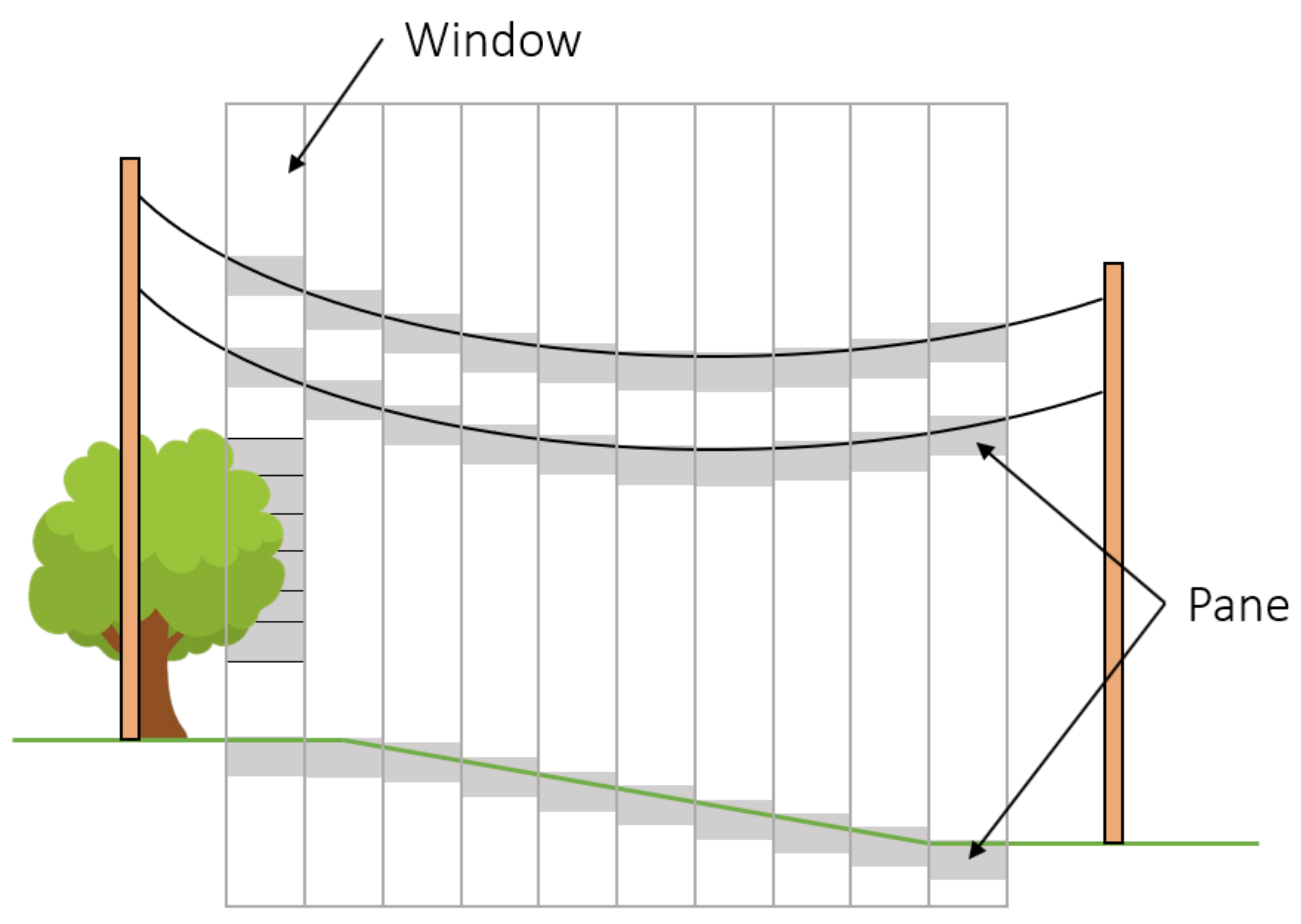
Each window is traversed downwards and new panes are fitted until all points within the window are also included within a pane.
Figure 1.
Each window is traversed downwards and new panes are fitted until all points within the window are also included within a pane.
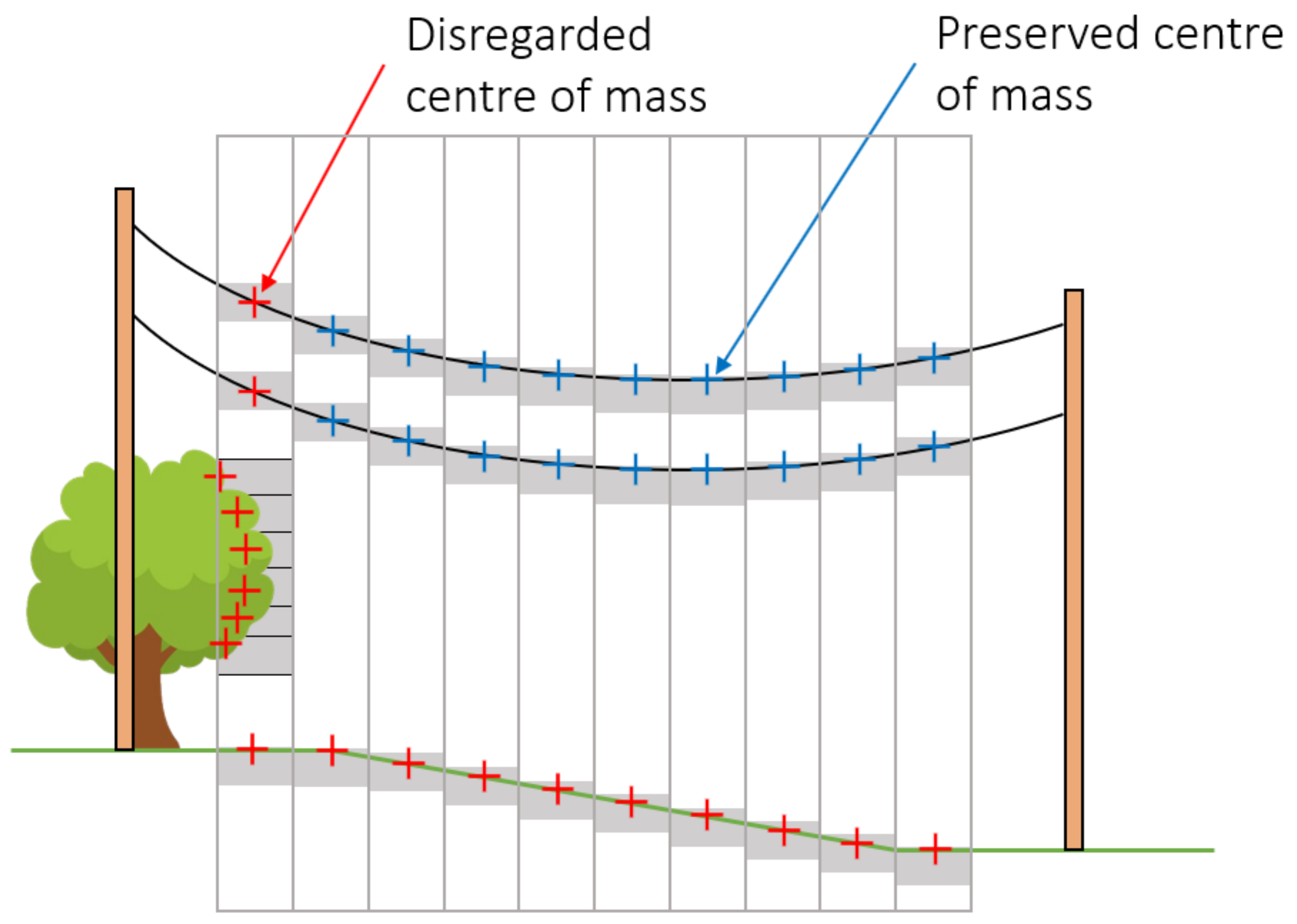
Figure 2.
An example of the multiple centre of masses found for each window. Note the bush in the lower right is partially within the conductor search region and thus has centre of masses associated with it.
Figure 2.
An example of the multiple centre of masses found for each window. Note the bush in the lower right is partially within the conductor search region and thus has centre of masses associated with it.
Figure 3.
An example of filtered centre of masses. COMs along the ground are filtered due to their low height, those belonging to the tree are filtered due to their close proximity to each other. The left most COMs on the conductors are filtered because they belong to a window with the incorrect number of COMs.
Figure 3.
An example of filtered centre of masses. COMs along the ground are filtered due to their low height, those belonging to the tree are filtered due to their close proximity to each other. The left most COMs on the conductors are filtered because they belong to a window with the incorrect number of COMs.
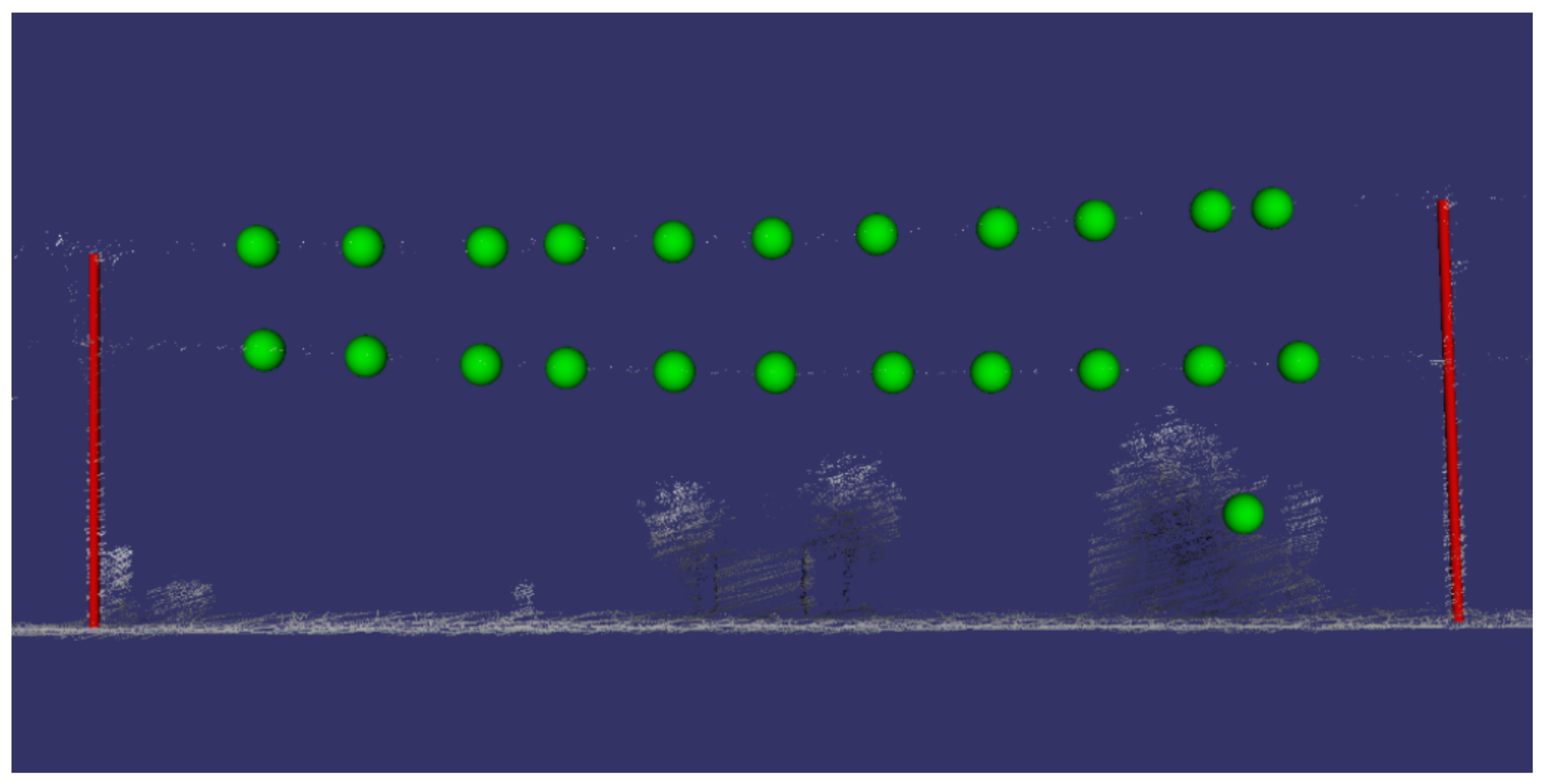
Figure 4.
The remaining centre of masses after filtering. Note all the centre of masses belonging to the ground and the majority of the bush have been removed. The single bush centre of mass remaining fell in a separate window to the rest of the object.
Figure 4.
The remaining centre of masses after filtering. Note all the centre of masses belonging to the ground and the majority of the bush have been removed. The single bush centre of mass remaining fell in a separate window to the rest of the object.
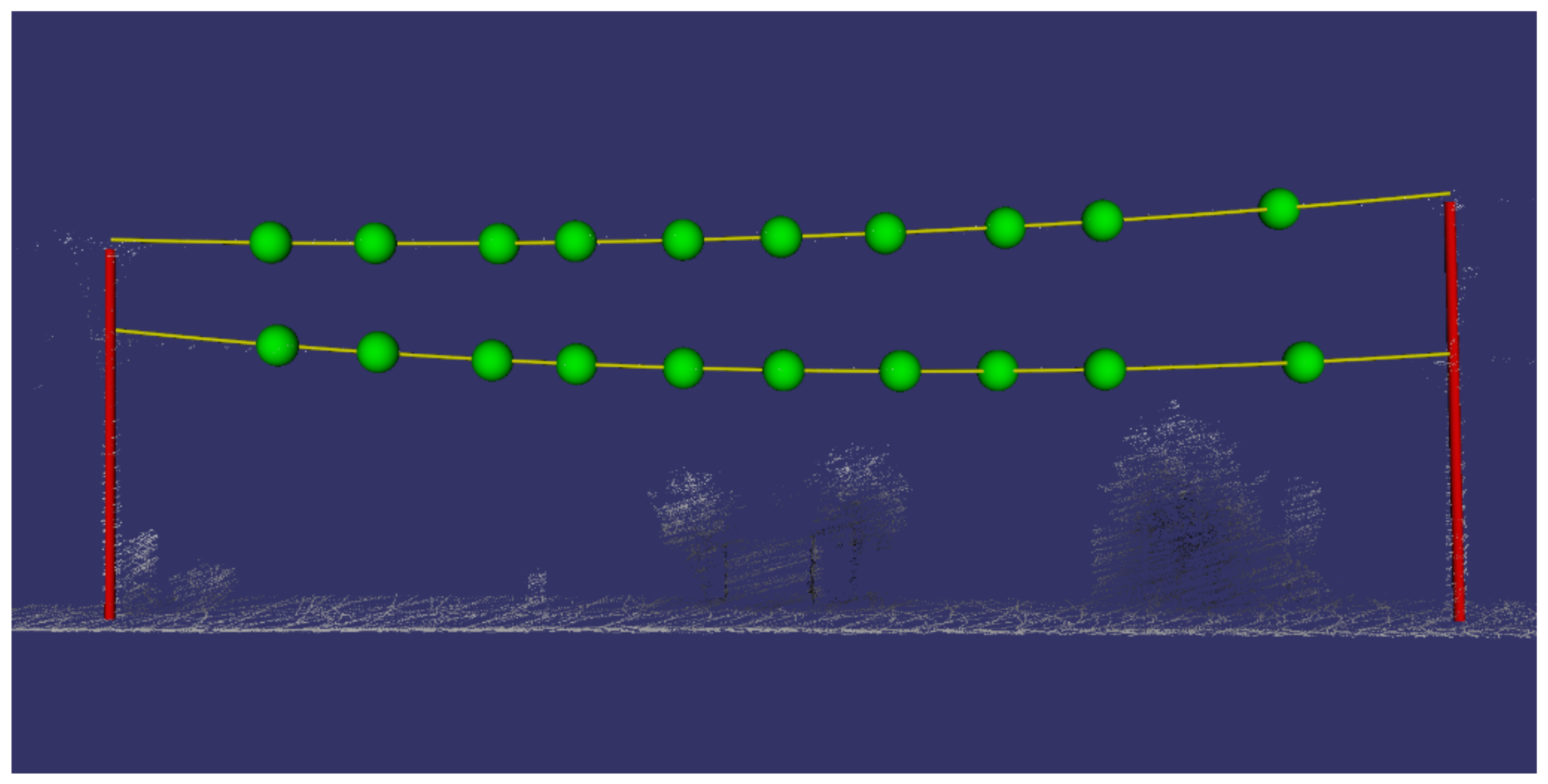
Figure 5.
Example of two fitted sag models and the centre of masses used for fitting. Note the centre of mass that was part of a bush in the lower right along with the two directly above in the same window are no longer present when compared with
Figure 4.
Figure 5.
Example of two fitted sag models and the centre of masses used for fitting. Note the centre of mass that was part of a bush in the lower right along with the two directly above in the same window are no longer present when compared with
Figure 4.
Figure 6.
Using the individual sag models, each level can be individually de-sagged and projected onto the clustering plane. This figure shows the de-sagging process for the upper conductor level; lower levels are each individually processed too.
Figure 6.
Using the individual sag models, each level can be individually de-sagged and projected onto the clustering plane. This figure shows the de-sagging process for the upper conductor level; lower levels are each individually processed too.
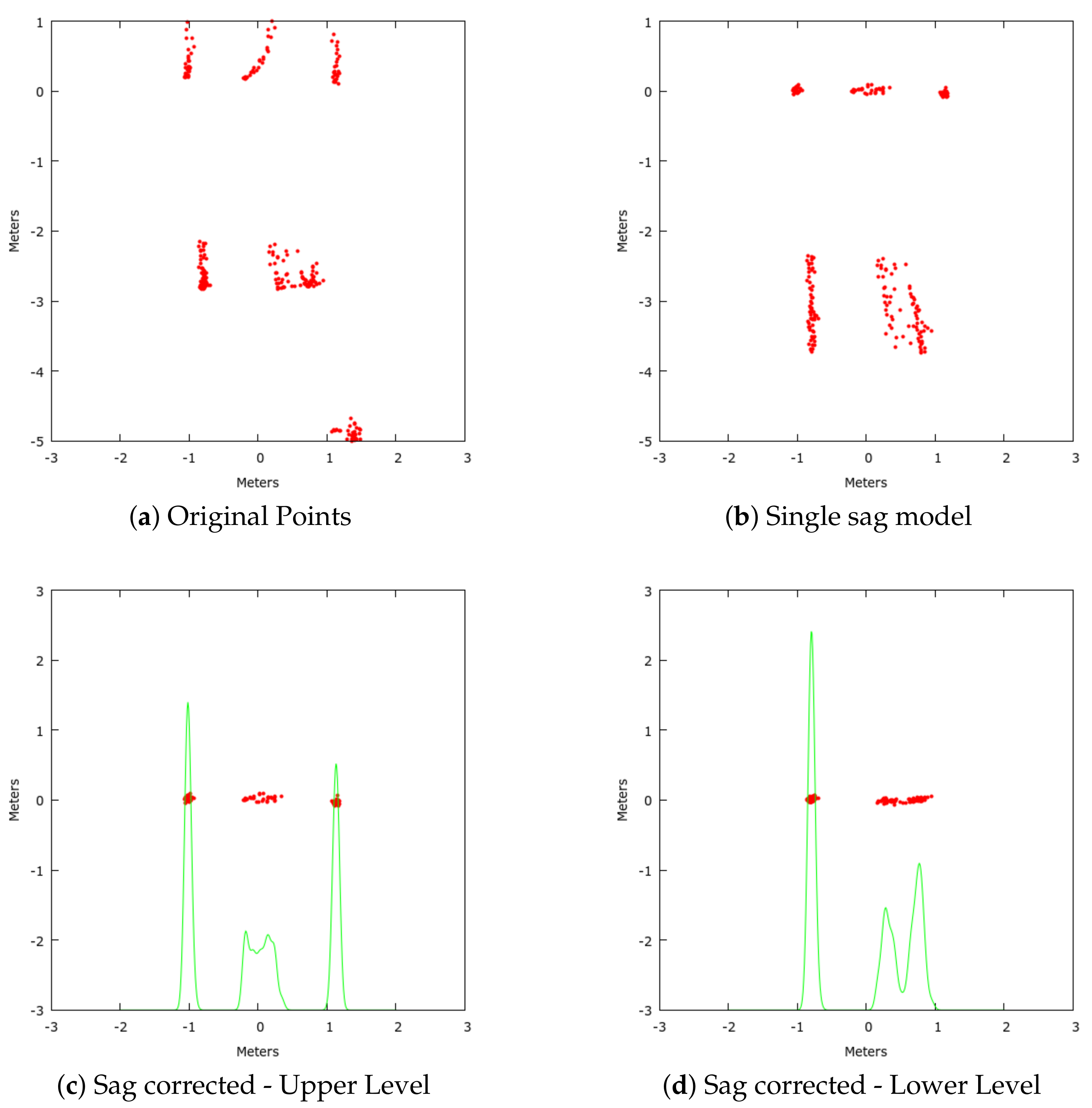
Figure 7.
These figures show the projection of points onto the clustering plane for the span featured in
Figure 4 and
Figure 5. (
a) shows the points projected without sag removal, the points in the lower right belong to a nearby tree. (
b) shows the projected points using a single sag model. Note the spread of the points on the lower level has increased when compared with the original points. (
c,
d) show the upper and lower levels after sag removal using separate sag estimation models. The probability density function is plotted to better show the point density.
Figure 7.
These figures show the projection of points onto the clustering plane for the span featured in
Figure 4 and
Figure 5. (
a) shows the points projected without sag removal, the points in the lower right belong to a nearby tree. (
b) shows the projected points using a single sag model. Note the spread of the points on the lower level has increased when compared with the original points. (
c,
d) show the upper and lower levels after sag removal using separate sag estimation models. The probability density function is plotted to better show the point density.
Figure 8.
Comparison between Cheng’s Nanjing dataset (left), Gilberthorpes (centre), and Hounslow (right). Note the Nanjing image is from 2014 while the LiDAR survey was conducted in 2011.
Figure 8.
Comparison between Cheng’s Nanjing dataset (left), Gilberthorpes (centre), and Hounslow (right). Note the Nanjing image is from 2014 while the LiDAR survey was conducted in 2011.
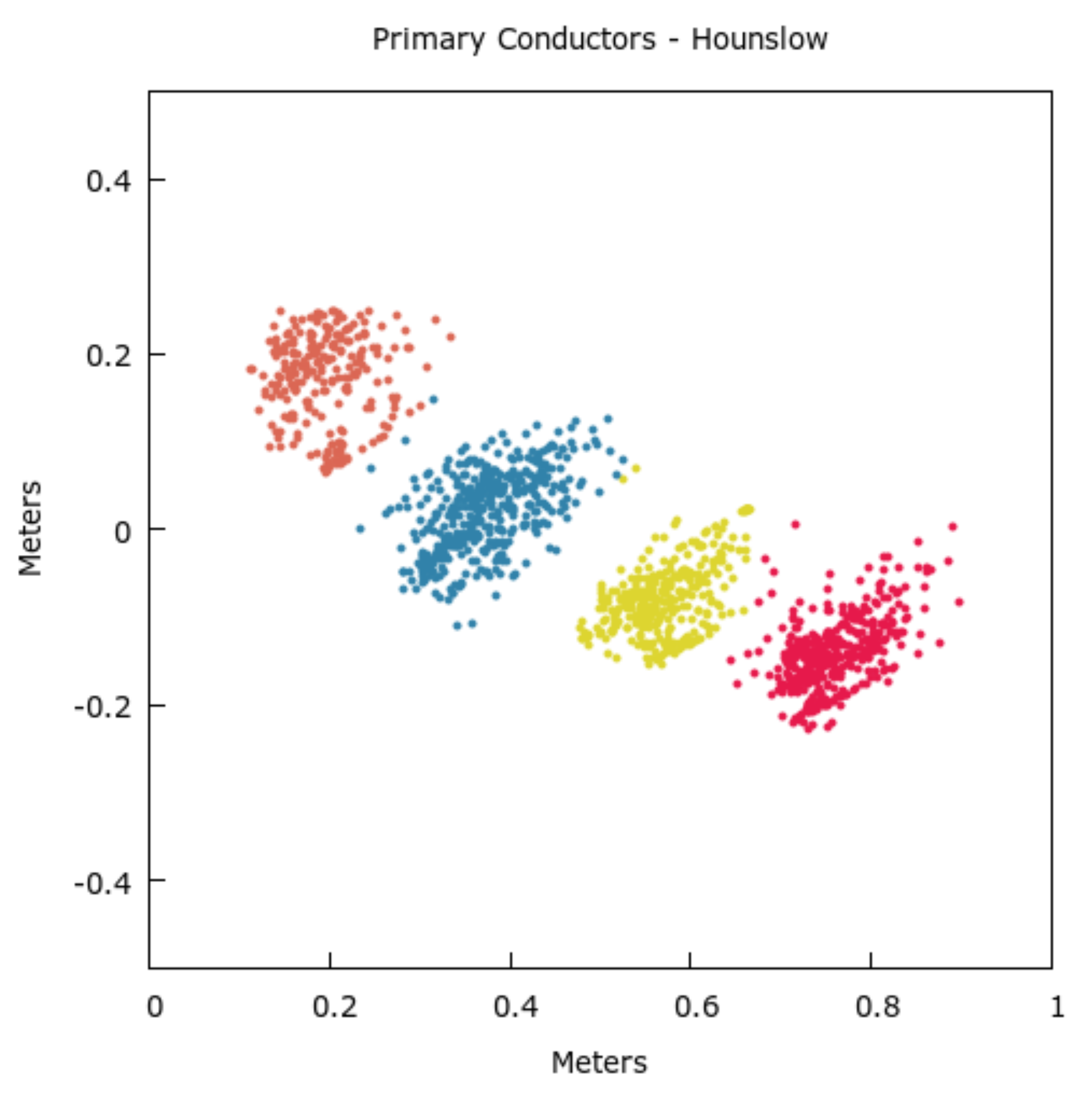
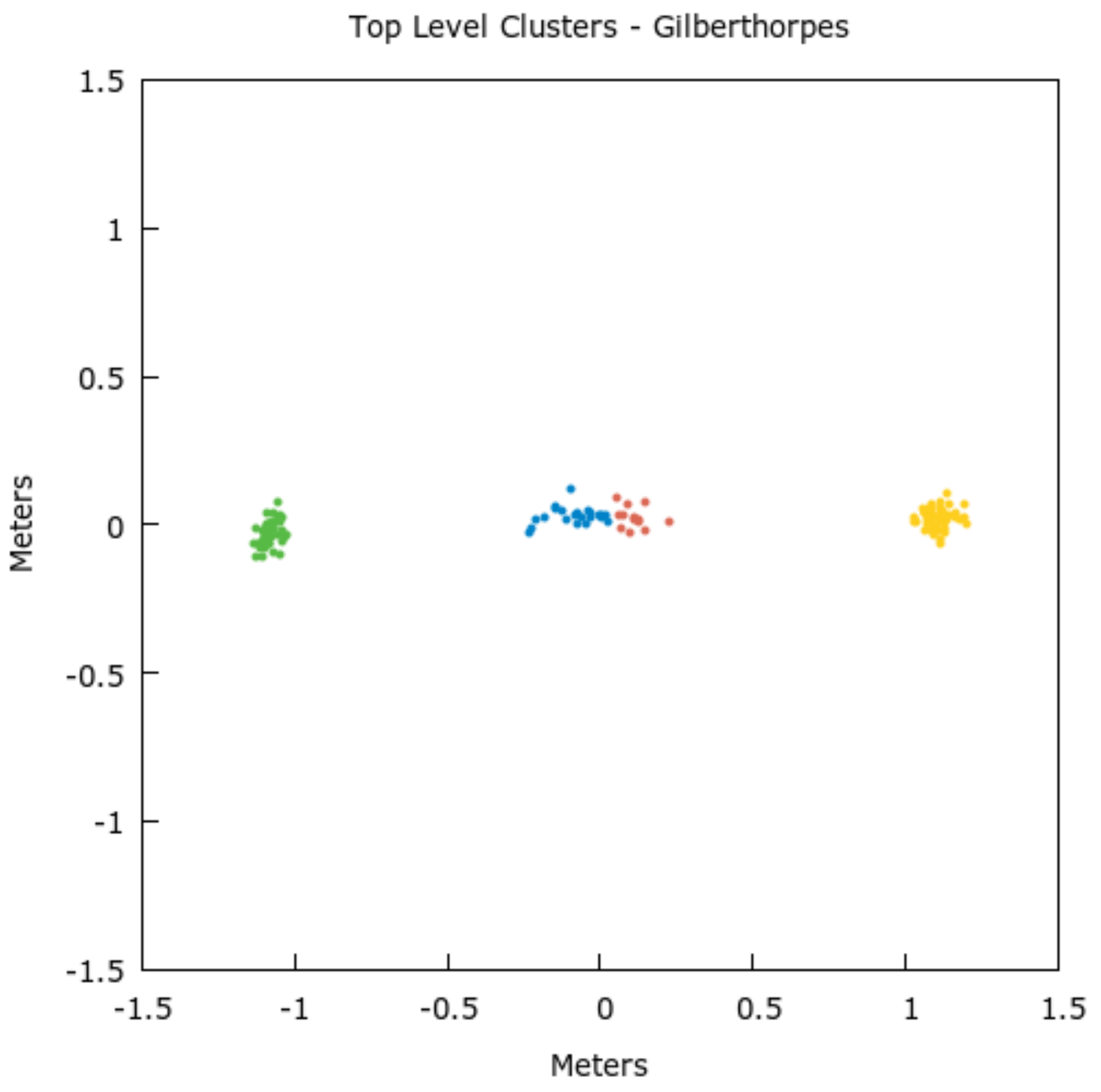
Figure 9.
Example of 2-Dimensional Mean Shift clustering of primary conductors from the Hounslow dataset. Note there is some cross span-wise overlap which results in less defined boundaries if only the cross span-wise component is used.
Figure 9.
Example of 2-Dimensional Mean Shift clustering of primary conductors from the Hounslow dataset. Note there is some cross span-wise overlap which results in less defined boundaries if only the cross span-wise component is used.
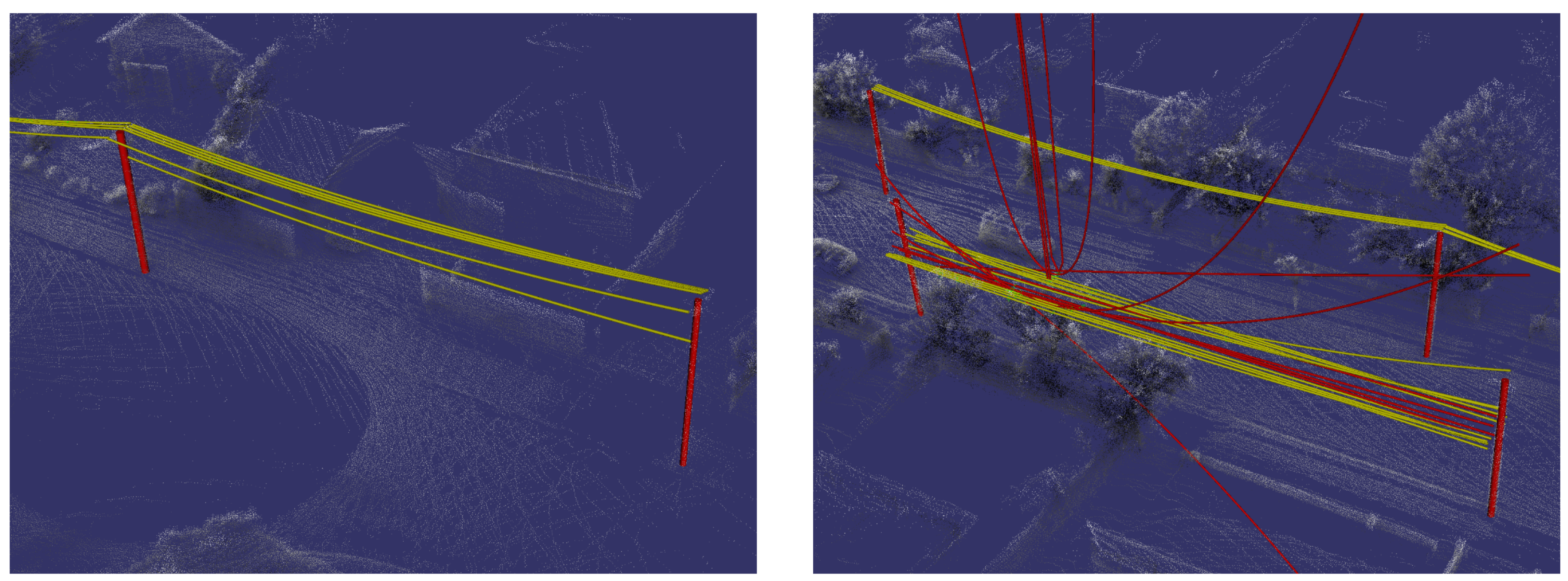
Figure 10.
Example of a poorly observed span which caused a primary conductor to be rejected because it did not contain points along the entire span. Clustered conductor points are rendered green and fitted models are yellow.
Figure 10.
Example of a poorly observed span which caused a primary conductor to be rejected because it did not contain points along the entire span. Clustered conductor points are rendered green and fitted models are yellow.
Figure 11.
Removing the requirement that a conductor cluster must have points distributed along the entire span can increase conductor recovery in less well-observed regions (left) at the cost of less robust rejection of non-conductor objects on the clustering plane (right).
Figure 11.
Removing the requirement that a conductor cluster must have points distributed along the entire span can increase conductor recovery in less well-observed regions (left) at the cost of less robust rejection of non-conductor objects on the clustering plane (right).
Figure 12.
Example of the weaving centre conductor being split into two clusters due to it not being parallel to the span.
Figure 12.
Example of the weaving centre conductor being split into two clusters due to it not being parallel to the span.
Table 1.
Sag model recovery performance on the Hounslow dataset.
Table 1.
Sag model recovery performance on the Hounslow dataset.
| | Correct | Error |
|---|
| Primary | 6 | 0 |
| Secondary | 3 | 0 |
| Crossing | 1 | 3 |
Table 2.
Sag model recovery performance on the Gilberthorpes dataset.
Table 2.
Sag model recovery performance on the Gilberthorpes dataset.
| | Correct | Error |
|---|
| Primary | 18 | 0 |
| Secondary | 7 | 1 |
| Crossing | 10 | 9 |
Table 3.
Sag model rejection performance on the Hounslow dataset.
Table 3.
Sag model rejection performance on the Hounslow dataset.
| | Accepted | Rejected |
|---|
| Valid Sag Model | 11 | 0 |
| Invalid Sag Model | 0 | 5 |
Table 4.
Sag model rejection performance on the extended Gilberthorpes dataset.
Table 4.
Sag model rejection performance on the extended Gilberthorpes dataset.
| | Accepted | Rejected |
|---|
| Valid Sag Model | 54 | 0 |
| Invalid Sag Model | 10 | 8 |
Table 5.
This table shows the number of successfully clustered conductors using 1D Mean Shift Clustering with various bandwidths. All conductor spans from the Hounslow dataset were tested.
Table 5.
This table shows the number of successfully clustered conductors using 1D Mean Shift Clustering with various bandwidths. All conductor spans from the Hounslow dataset were tested.
| Bandwidth | Primary | Secondary |
|---|
| 3 cm | 24 | 7 |
| 4 cm | 24 | 7 |
| 5 cm | 23 | 7 |
| 6 cm | 14 | 7 |
| 7 cm | 6 | 7 |
| 8 cm | 0 | 7 |
Table 6.
This table shows the number of successfully clustered conductors using 1D Mean Shift Clustering with various bandwidths. Conductor spans with two layers from the extended Gilberthorpes dataset were tested.
Table 6.
This table shows the number of successfully clustered conductors using 1D Mean Shift Clustering with various bandwidths. Conductor spans with two layers from the extended Gilberthorpes dataset were tested.
| Bandwidth | Primary | Secondary |
|---|
| 3 cm | 53 | 84 |
| 4 cm | 54 | 78 |
| 5 cm | 54 | 71 |
| 6 cm | 54 | 58 |
| 7 cm | 54 | 46 |
| 8 cm | 54 | 42 |
Table 7.
This table shows the number of successfully clustered conductors using 2-Dimensional Mean Shift Clustering with various bandwidths. All conductor spans from the Hounslow dataset were tested.
Table 7.
This table shows the number of successfully clustered conductors using 2-Dimensional Mean Shift Clustering with various bandwidths. All conductor spans from the Hounslow dataset were tested.
| Bandwidth | Primary | Secondary |
|---|
| 3 cm | 24 | 4 |
| 4 cm | 24 | 4 |
| 5 cm | 24 | 4 |
| 6 cm | 24 | 4 |
| 7 cm | 16 | 6 |
| 8 cm | 6 | 7 |
Table 8.
This table shows the number of successfully clustered conductors from the extended Gilberthorpes dataset using 2-Dimensional Mean Shift Clustering with various bandwidths.
Table 8.
This table shows the number of successfully clustered conductors from the extended Gilberthorpes dataset using 2-Dimensional Mean Shift Clustering with various bandwidths.
| Bandwidth | Top Layer | Bottom Layer |
|---|
| 3 cm | 50 | 78 |
| 4 cm | 52 | 82 |
| 5 cm | 54 | 74 |
| 6 cm | 54 | 63 |
| 7 cm | 54 | 50 |
| 8 cm | 54 | 43 |
Table 9.
Final output on Hounslow dataset using 2-Dimensional Mean Shift Clustering with a bandwidth of 4 cm.
Table 9.
Final output on Hounslow dataset using 2-Dimensional Mean Shift Clustering with a bandwidth of 4 cm.
| | Conductor | Non-Conductor |
|---|
| Modelled Conductors | 26 | 0 |
| Missed Conductors | 5 | |
Table 10.
Final output on extended Gilberthorpes dataset using 2-Dimensional Mean Shift Clustering with a bandwidth of 4 cm.
Table 10.
Final output on extended Gilberthorpes dataset using 2-Dimensional Mean Shift Clustering with a bandwidth of 4 cm.
| | Top | Bottom | Crossing | Secondary |
|---|
| Modelled Conductors | 49 | 74 | 5 | 6 |
| Missed Conductors | 5 | 7 | 14 | 2 |
Table 11.
Completeness and Correctness for primary conductors in Hounslow and Gilberthorpes datasets.
Table 11.
Completeness and Correctness for primary conductors in Hounslow and Gilberthorpes datasets.
| | Completeness | Correctness |
|---|
| Hounslow - Primary | 95.6 % | 100% |
| Gilberthorpes - Top | 90.7% | 98.0% |
| Gilberthorpes - Bottom | 91.4% | 100% |
| Combined | 91.8% | 98.6% |