Self-Organized Model Fitting Method for Railway Structures Monitoring Using LiDAR Point Cloud
Abstract
1. Introduction
2. Materials and Method
2.1. Overview
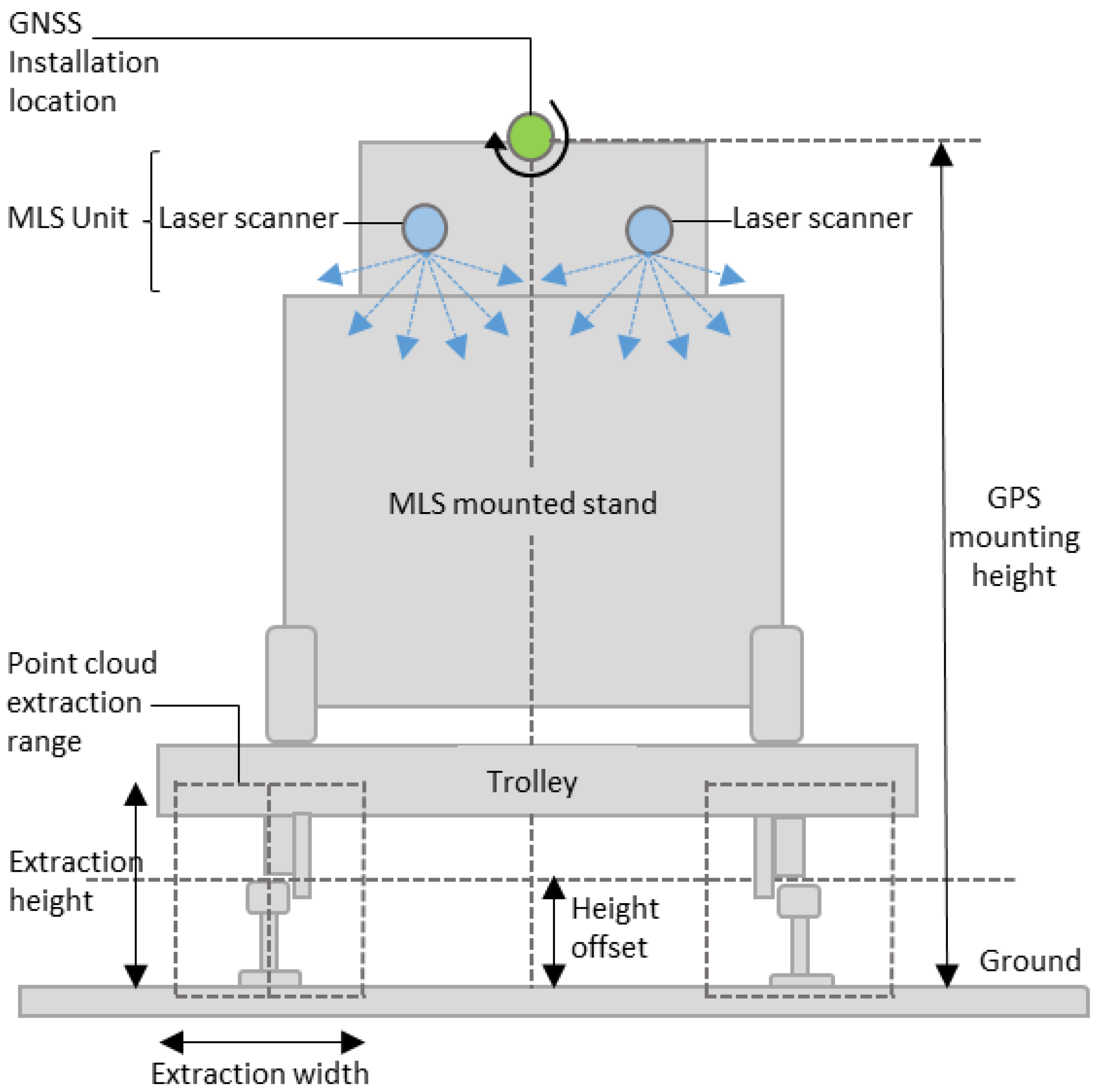
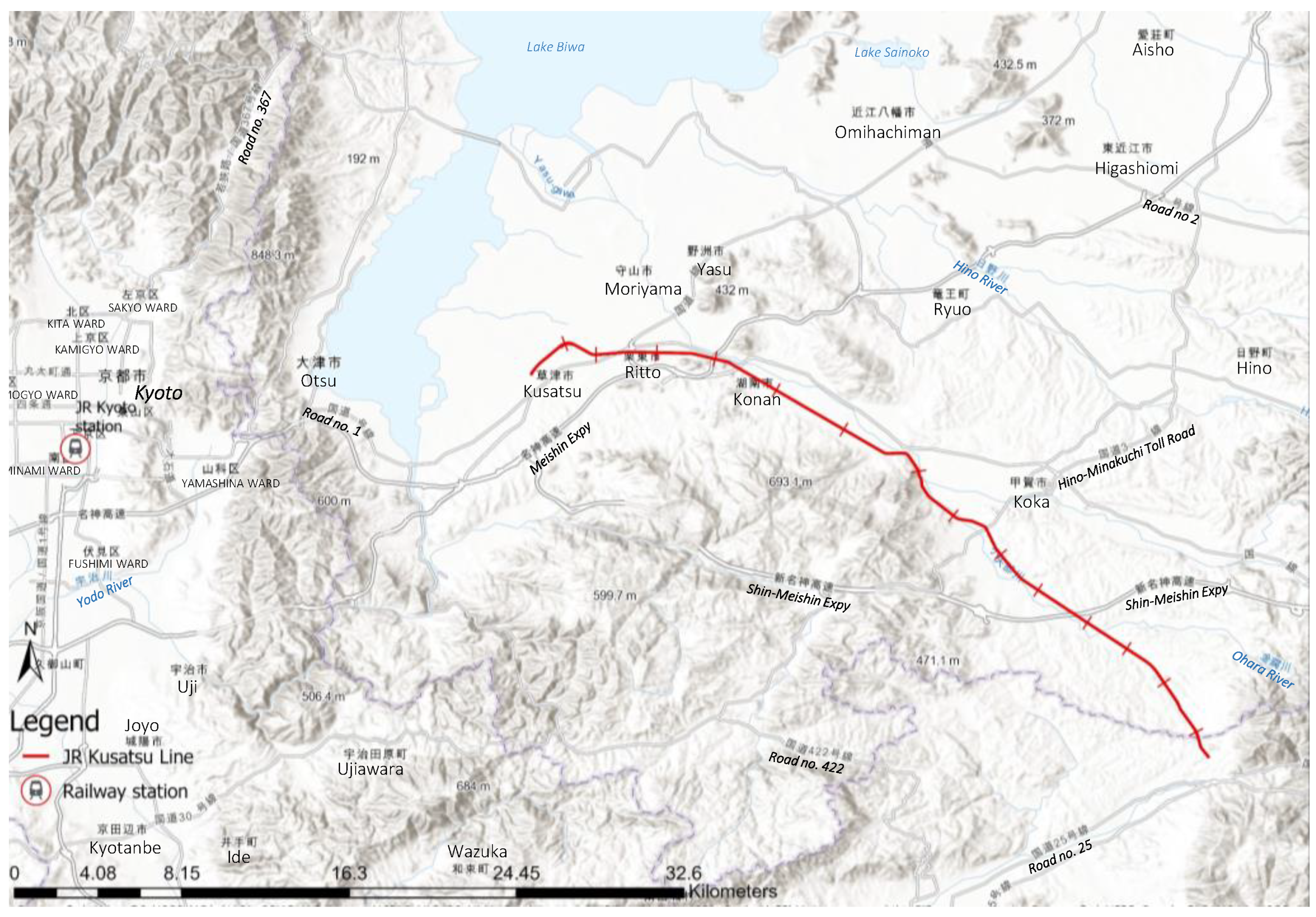
2.2. MLS Sensor and Survey Setup
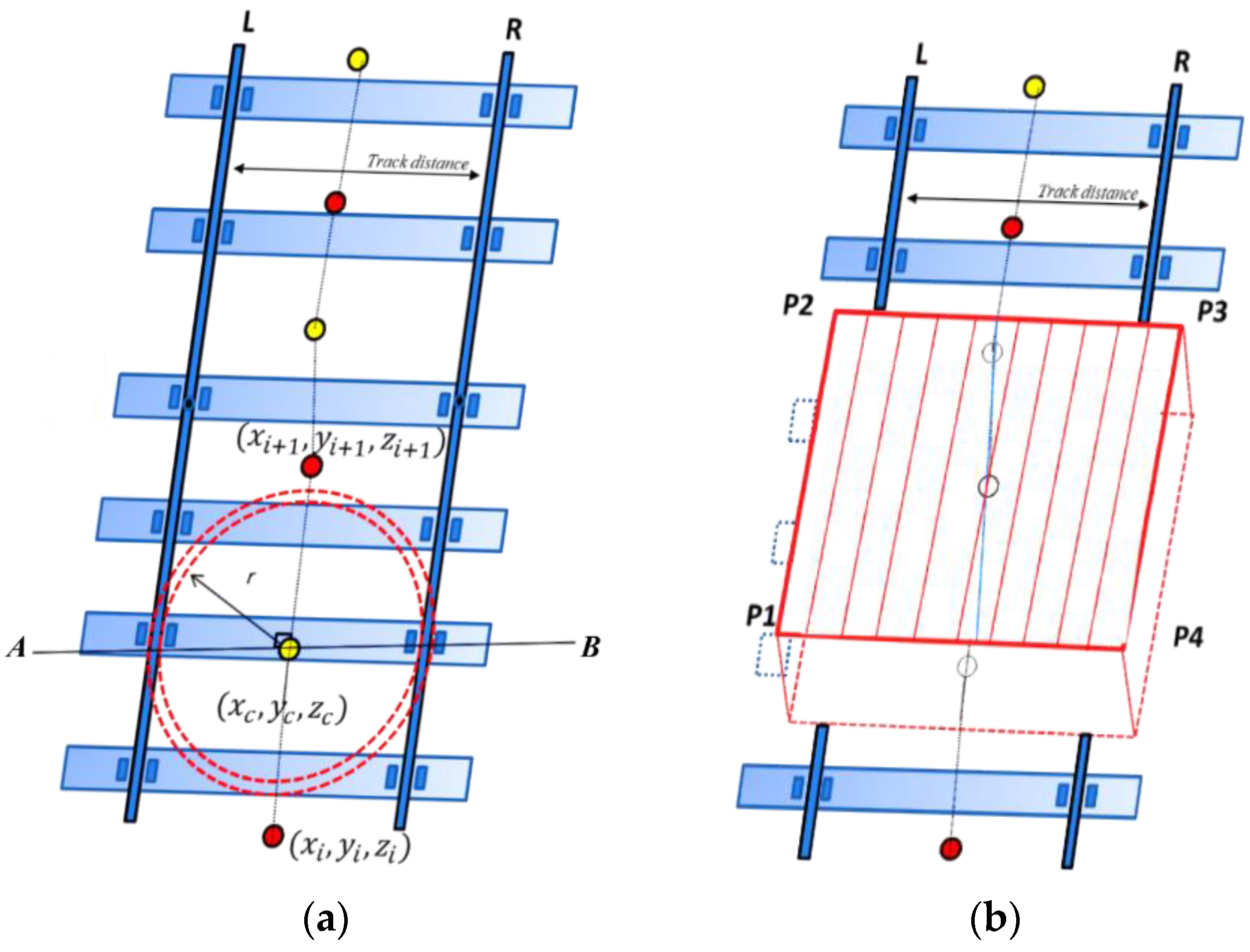
2.3. Vertical Slicing
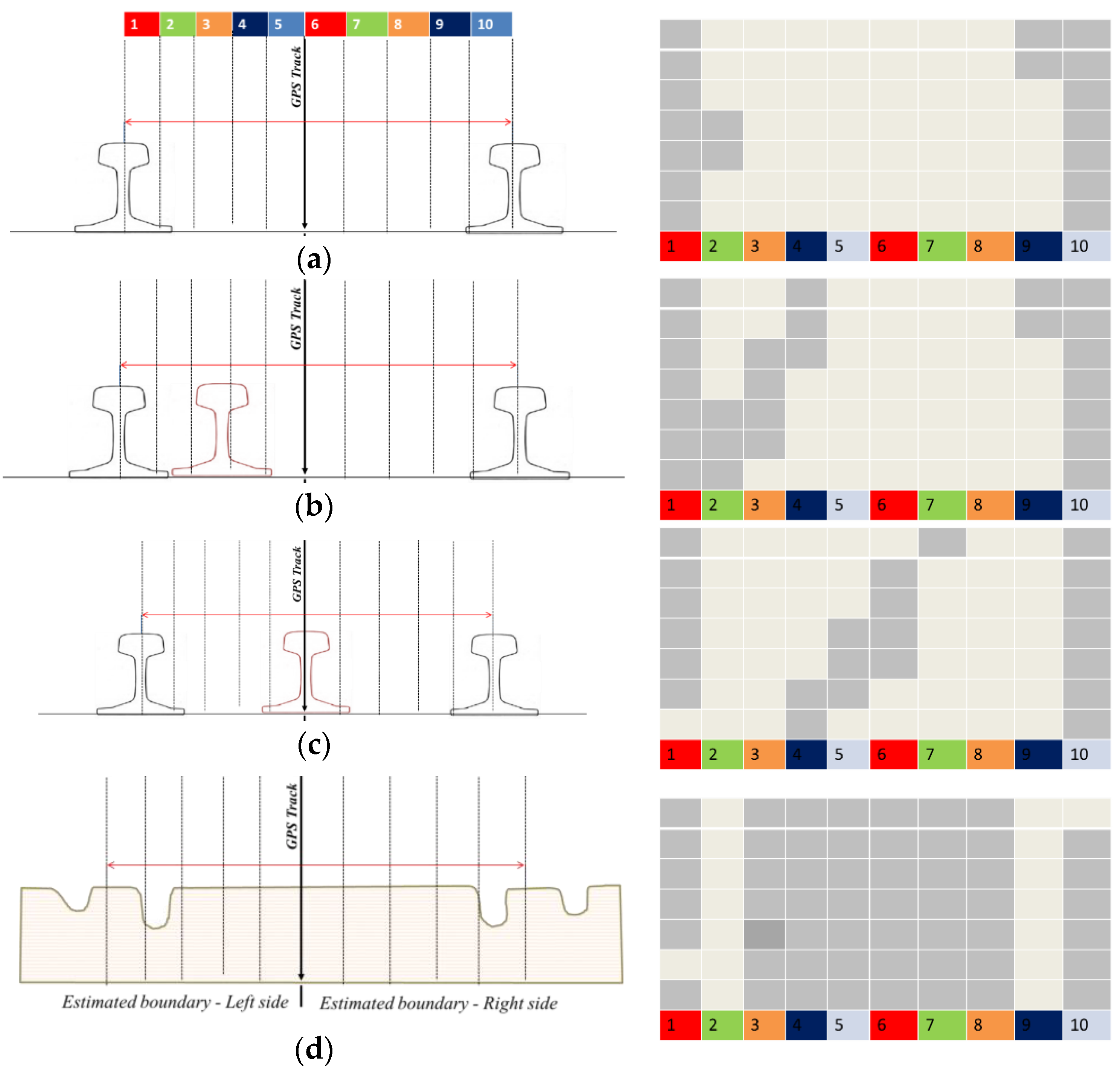
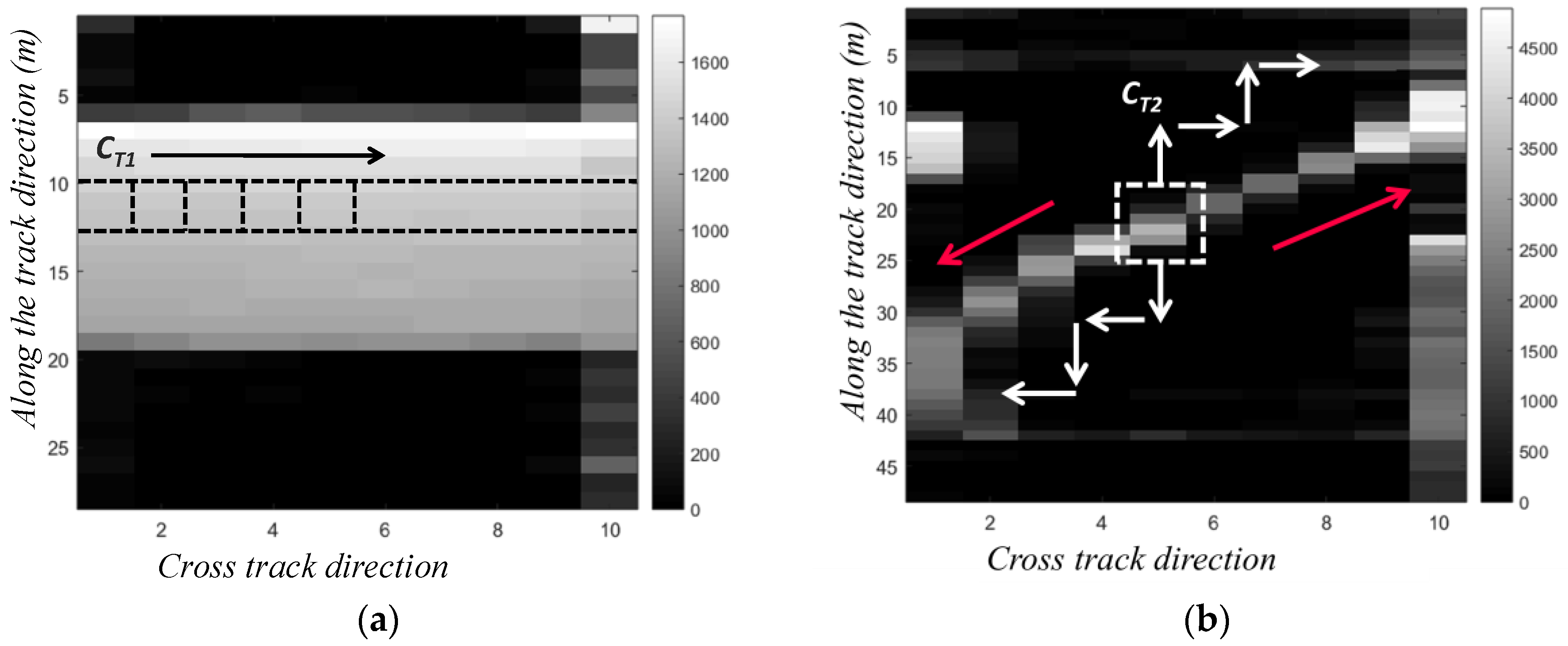
2.4. Structure Detection
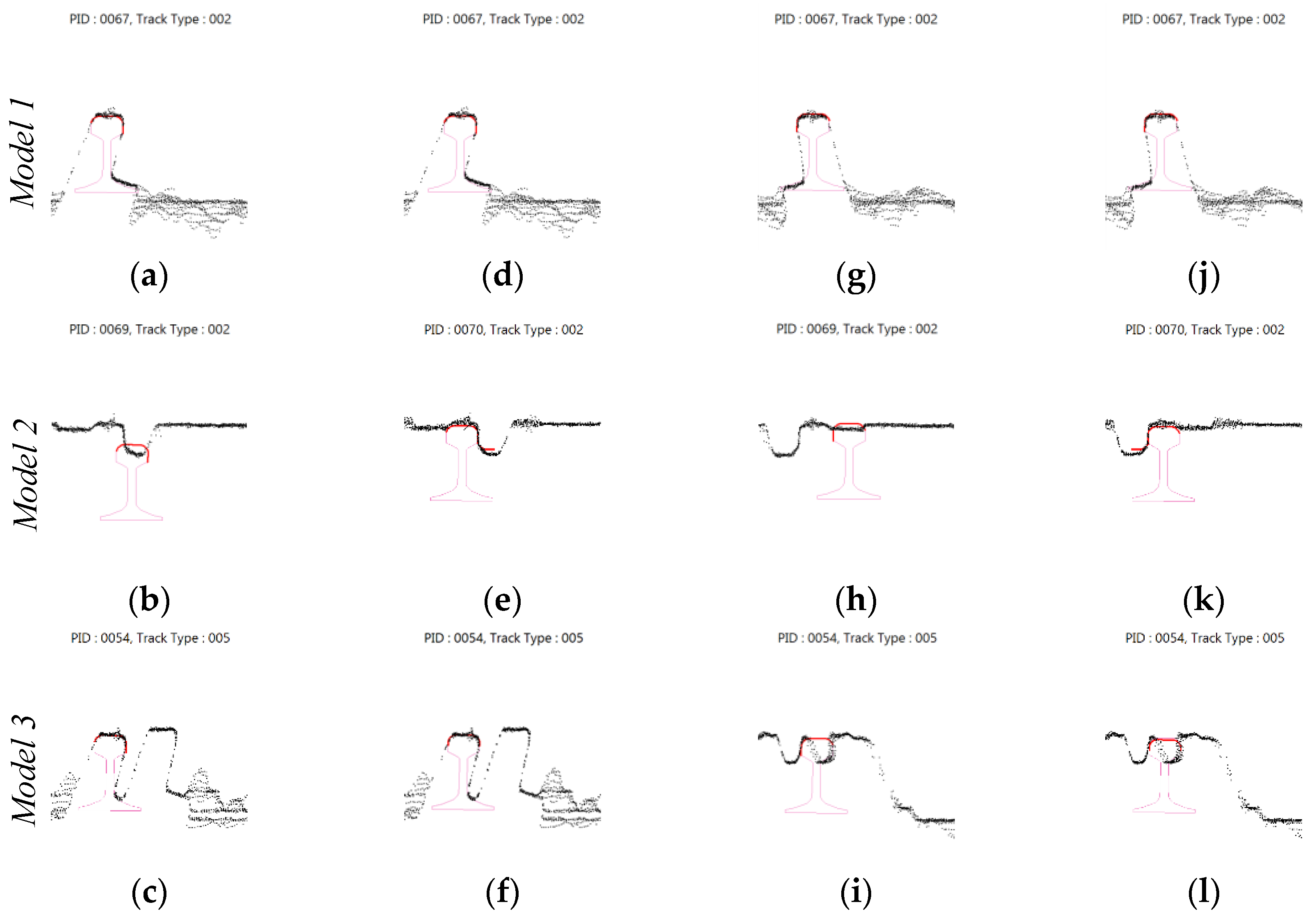
2.5. Model Fitting
3. Experiment and Evaluation
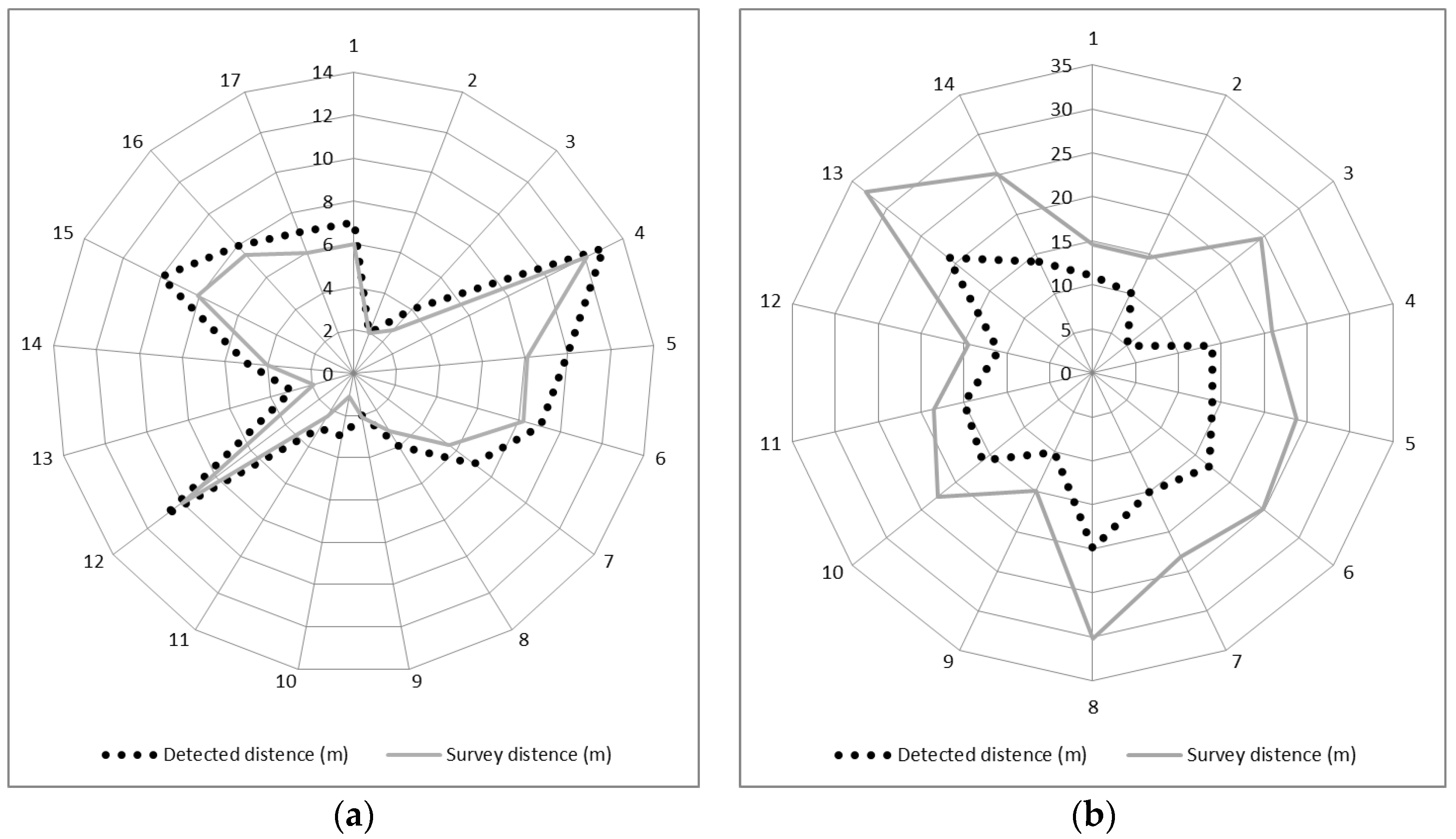
4. Accuracy Estimation
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Niina, Y.; Oketani, E.; Yokouchi, H.; Honma, R.; Tsuji, K.; Kondo, K. Monitoring of railway structures by MMS. J. Jpn. Soc. Photogramm. Remote Sens. 2016, 55, 95–99. [Google Scholar] [CrossRef][Green Version]
- Miao, Z.; Wang, B.; Shi, W.; Wu, H. A Method for Accurate Road Centerline Extraction from a Classified Image. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 4762–4771. [Google Scholar] [CrossRef]
- Miao, Z.; Shi, W.; Zhang, H.; Wang, X. Road Centerline Extraction from High-Resolution Imagery Based on Shape Features and Multivariate Adaptive Regression Splines. IEEE Geosci. Remote Sens. Lett. 2012, 10, 583–587. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, Q.; Zhu, Q.; Liu, L.; Li, C.; Zheng, D. A Survey of Mobile Laser Scanning Applications and Key Techniques over Urban Areas. Remote Sens. 2019, 11, 1540. [Google Scholar] [CrossRef]
- Petrie, G. Mobile mapping systems: An introduction to the technology. GeoInformatics 2010, 13, 32–43. [Google Scholar]
- Puente, I.; González-Jorge, H.; Martínez-Sánchez, J.; Arias, P. Review of mobile mapping and surveying technologies. Measurement 2013, 46, 2127–2145. [Google Scholar] [CrossRef]
- Tang, P.; Huber, D.; Akinci, B.; Lipman, R.; Lytle, A. Automatic reconstruction of as-built building information models from laser-scanned point clouds: A review of related techniques. Autom. Constr. 2010, 19, 829–843. [Google Scholar] [CrossRef]
- Khoshelham, K.; Li, Z. A Model-Based Approach to Semi? Automated Reconstruction of Buildings from Aerial Images. Photogramm. Rec. 2004, 19, 342–359. [Google Scholar] [CrossRef]
- Mikrut, S.; Kohut, P.; Pyka, K.; Tokarczyk, R.; Barszcz, T.; Uhl, T. Mobile Laser Scanning Systems for Measuring the Clearance Gauge of Railways: State of Play, Testing and Outlook. Sensors 2016, 16, 683. [Google Scholar] [CrossRef]
- Soni, A.; Robson, S.; Gleeson, B. Extracting rail track geometry from static terrestrail laser scans for monitoring purposes. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, 45, 553–557. [Google Scholar] [CrossRef]
- Railway ICT Solution “RaiLis” by 3D Laser Measurement, Asia Air Survey Co., LTD. Available online: https://www.ajiko.co.jp/product (accessed on 6 November 2020).
- Soni, A.X. Non-Contact Monitoring of Railway Infrastructure with Terrestrial Laser Scanning and Photogrammetry at Network Rail. Ph.D. Thesis, University College London, London, UK, 2016. [Google Scholar]
- Zou, R.; Fan, X.; Qian, C.; Ye, W.; Zhao, P.; Tang, J.; Liu, H. An Efficient and Accurate Method for Different Configurations Railway Extraction Based on Mobile Laser Scanning. Remote Sens. 2019, 11, 2929. [Google Scholar] [CrossRef]
- Coelho, B.E.Z. Dynamics of Railway Transition Zones in Soft Soil. Master’s Thesis, University of Porto, Porto, Portugal, 2010. [Google Scholar]
- Yang, B.; Fang, L. Automated Extraction of 3-D Railway Tracks from Mobile Laser Scanning Point Clouds. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 4750–4761. [Google Scholar] [CrossRef]
- Besl, P.; McKay, N.D. A method for registration of 3-D shapes. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 239–256. [Google Scholar] [CrossRef]
- Diaz Benito, D. Automatic 3d Modelling of Train Rails in a Lidar Point Cloud. Master’s Thesis, University of Twente, Enschede, The Netherlands, 2012. [Google Scholar]
- Arastounia, M. Automated Recognition of Railroad Infrastructure in Rural Areas from LIDAR Data. Remote Sens. 2015, 7, 14916–14938. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, S.; Mei, X.; Yin, W.; Lin, C.; Hu, Q.; Mao, Q. Railway Tunnel Clearance Inspection Method Based on 3D Point Cloud from Mobile Laser Scanning. Sensors 2017, 17, 2055. [Google Scholar] [CrossRef]
- Elberink, S.O.; Khoshelham, K. Automatic Extraction of Railroad Centerlines from Mobile Laser Scanning Data. Remote Sens. 2015, 7, 5565–5583. [Google Scholar] [CrossRef]
- Niina, Y.; Honma, R.; Honma, Y.; Kondo, K.; Tsuji, K.; Hiramatsu, T.; Oketani, E. Automatic rail extraction and celarance check with a point cloud captured by mls in a railway. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, 767–771. [Google Scholar] [CrossRef]
- Kukko, A.; Kaartinen, H.; Hyyppä, J.; Chen, Y. Multiplatform Mobile Laser Scanning: Usability and Performance. Sensors 2012, 12, 11712–11733. [Google Scholar] [CrossRef]
- Brédif, M.; Vallet, B.; Ferrand, B. Distributed Dimensonality-Based Rendering Of Lidar Point Clouds. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, 40, 559–564. [Google Scholar] [CrossRef]
- Masiero, A.; Fissore, F.; Guarnieri, A.; Yang, B.; Visintini, D.; Vettore, A. Performance Evaluation of Two Indoor Mapping Systems: Low-Cost UWB-Aided Photogrammetry and Backpack Laser Scanning. Appl. Sci. 2018, 8, 416. [Google Scholar] [CrossRef]
- Furitsu, Y.; Deguchi, D.; Kawanishi, Y.; Ide, I.; Murase, H.; Mukojima, H.; Nagamine, N. Semantic Segmentation of Railway Images Considering Temporal Continuity. In Pattern Recognition; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Leica Pegasus: Two Ultimate Mobile Reality Capture, Specification, Leica Geosystems AG 2018. Available online: www.leica-geosystems.com (accessed on 6 November 2020).
- Leica Pegasus: Two Ultimate Mobile Reality Capture, Smart City Applications, Leica Geosystems AG 2018. Available online: www.leica-geosystems.com (accessed on 6 November 2020).
- Leica Pegasus: Map Factory Mobile Reality Capture, Leica Geosystems AG 2018. Available online: www.leica-geosystems.com (accessed on 6 November 2020).
- Leica Pegasus: Manager Complete Work Flows for Reality Capture Projects, Specification, Leica Geosystems AG 2018. Available online: www.leica-geosystems.com (accessed on 6 November 2020).
- Karunathilake, A.; Honma, R.; Niina, Y. Detection of level crossing and turnouts by vertical slicing of railway MLS point cloud. In Proceedings of the Annual Conference of Japan Society of Photogrammetry and Remote Sensing, Tokyo, Japan, 23–24 May 2019. [Google Scholar]
- Gelfand, N.; Ikemoto, L.; Rusinkiewicz, S.; Levoy, M. Geometrically Stable Sampling for the ICP Algorithm. In Proceedings of the Fourth International Conference on 3-D Digital Imaging and Modeling, Banff, AB, Canada, 6–10 October 2003; pp. 260–267. [Google Scholar]
- Yoshimura, R.; Date, H.; Kanai, S.; Honma, R.; Oda, K.; Ikeda, T. Automatic registration of MLS point clouds and SfM meshes of urban area. Geo-Spat. Inf. Sci. 2016, 19, 171–181. [Google Scholar] [CrossRef]
- Lai, K.; Fox, D. Object Recognition in 3D Point Clouds Using Web Data and Domain Adaptation. Int. J. Robot. Res. 2010, 29, 1019–1037. [Google Scholar] [CrossRef]
- Lowe, D.G. Three-dimensional object recognition from single two-dimensional images. Artif. Intell. 1987, 31, 355–395. [Google Scholar] [CrossRef]







| Product Name | Pegasus: Two |
|---|---|
| Manufacture | Leica Geosystems |
| Laser scanner | Z+F PROFILE® 9012 |
| Data acquisition rate | 1.016 million pixel/s (200 Hz) |
| Point density | 1600 pts./m2 (@10 m, 10 m/s) |
| Distances | 0.3–119 m |
| Relative accuracy | About 0.2–0.5 mm (@10 m) |
| Absolute accuracy | 2 cm (Open sky condition) |
| Parameter | Value |
|---|---|
| GPS mounting height | 1500 mm |
| Extraction height | 400 mm |
| Height offset | 200 mm |
| Half width | 1067/2 mm |
| Point cloud extraction range | 1000 mm |
| Height of the trolley from rail head | 500 mm |
| Structure | Height Adjustment (m) | Threshold (points/m2) | By Manual Survey (Number of Structure) | By Algorithm (Number of Structure) |
|---|---|---|---|---|
| Crossing | 1.48 | 200 | 4 | 5 |
| Left-turnout | 1.48 | 400 | 2 | 2 |
| Right-turnout | 1.48 | 400 | 2 | 2 |
| Structure | Height Adjustment (m) | Threshold (points /m2) | By Manual Survey (Number of Structure) | By Algorithm (Number of Structure) |
|---|---|---|---|---|
| Crossing | 1.5 | 200 | 16 | 17 |
| Left-turnout | 1.5 | 400 | 5 | 5 |
| Right-turnout | 1.5 | 400 | 9 | 9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karunathilake, A.; Honma, R.; Niina, Y. Self-Organized Model Fitting Method for Railway Structures Monitoring Using LiDAR Point Cloud. Remote Sens. 2020, 12, 3702. https://doi.org/10.3390/rs12223702
Karunathilake A, Honma R, Niina Y. Self-Organized Model Fitting Method for Railway Structures Monitoring Using LiDAR Point Cloud. Remote Sensing. 2020; 12(22):3702. https://doi.org/10.3390/rs12223702
Chicago/Turabian StyleKarunathilake, Amila, Ryohei Honma, and Yasuhito Niina. 2020. "Self-Organized Model Fitting Method for Railway Structures Monitoring Using LiDAR Point Cloud" Remote Sensing 12, no. 22: 3702. https://doi.org/10.3390/rs12223702
APA StyleKarunathilake, A., Honma, R., & Niina, Y. (2020). Self-Organized Model Fitting Method for Railway Structures Monitoring Using LiDAR Point Cloud. Remote Sensing, 12(22), 3702. https://doi.org/10.3390/rs12223702






