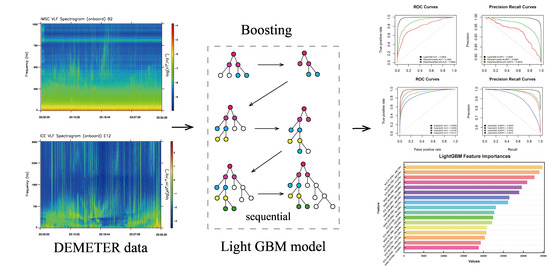
Identification of Electromagnetic Pre-Earthquake Perturbations from the DEMETER Data by Machine Learning
Abstract
1. Introduction
2. Dataset and Preprocessing
2.1. Dataset
2.2. Data Preprocessing
2.3. Frequency Bands Logarithmically Spaced
3. Methodology
3.1. Overview of Our Methodology
3.2. Machine Learning Methods
3.3. Bayesian Hyperparameter Tuning
3.4. Five-Fold Cross-Validation
3.5. Performance Evaluation
3.6. Feature Importance
4. Results and Discussion
4.1. Evaluation of the Model Performance
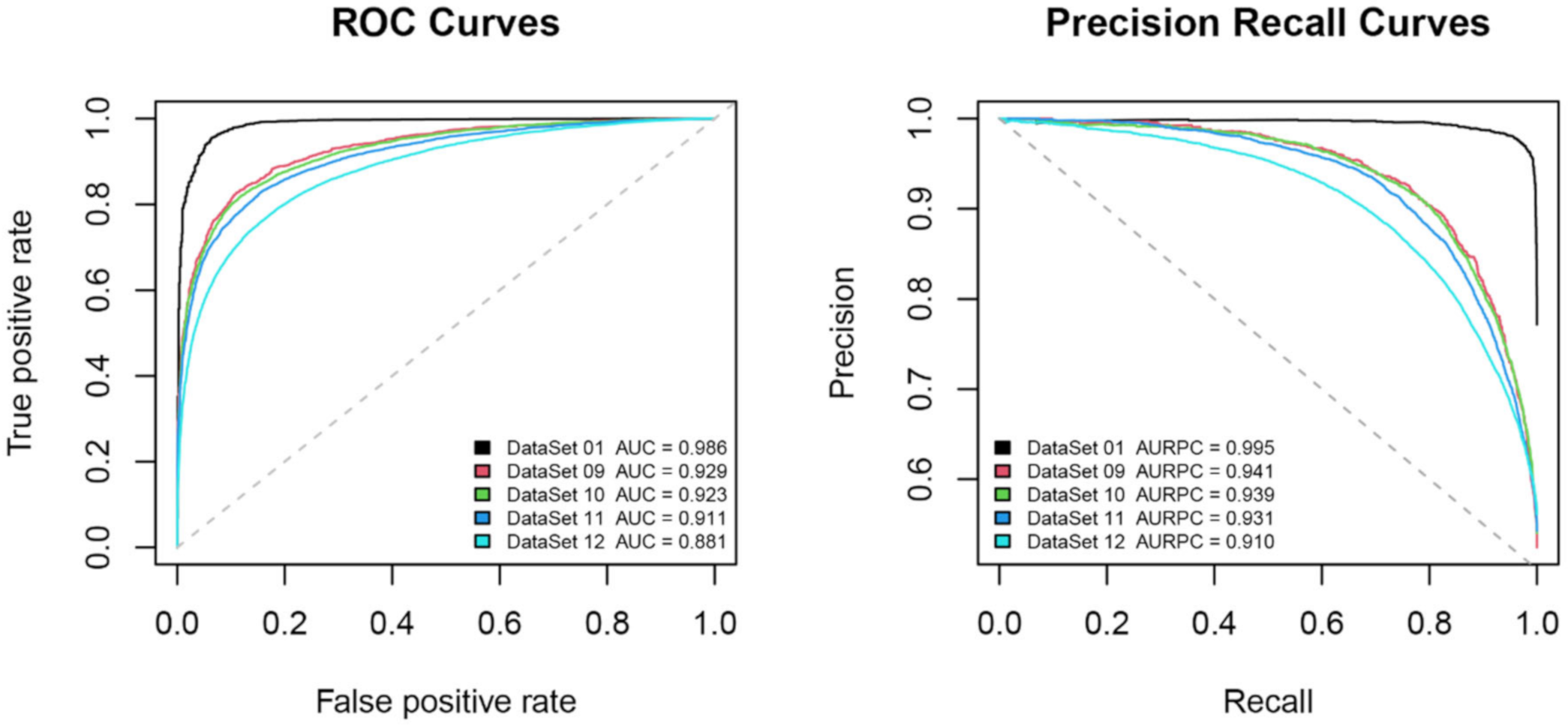
4.2. Considering Different Spatial Windows
4.3. Considering Different Frequency Bands
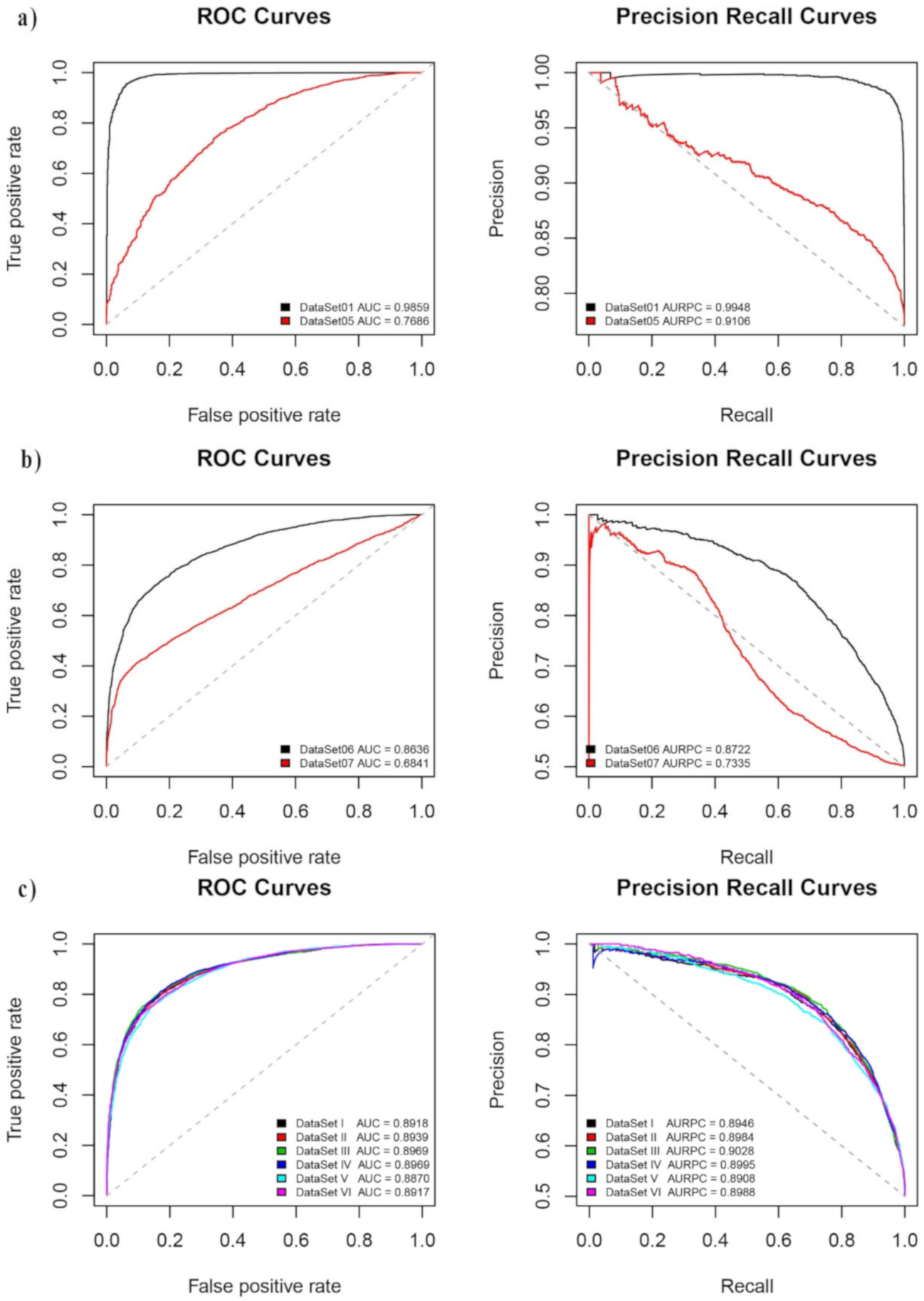
4.4. Considering the Earthquake Geographical Region
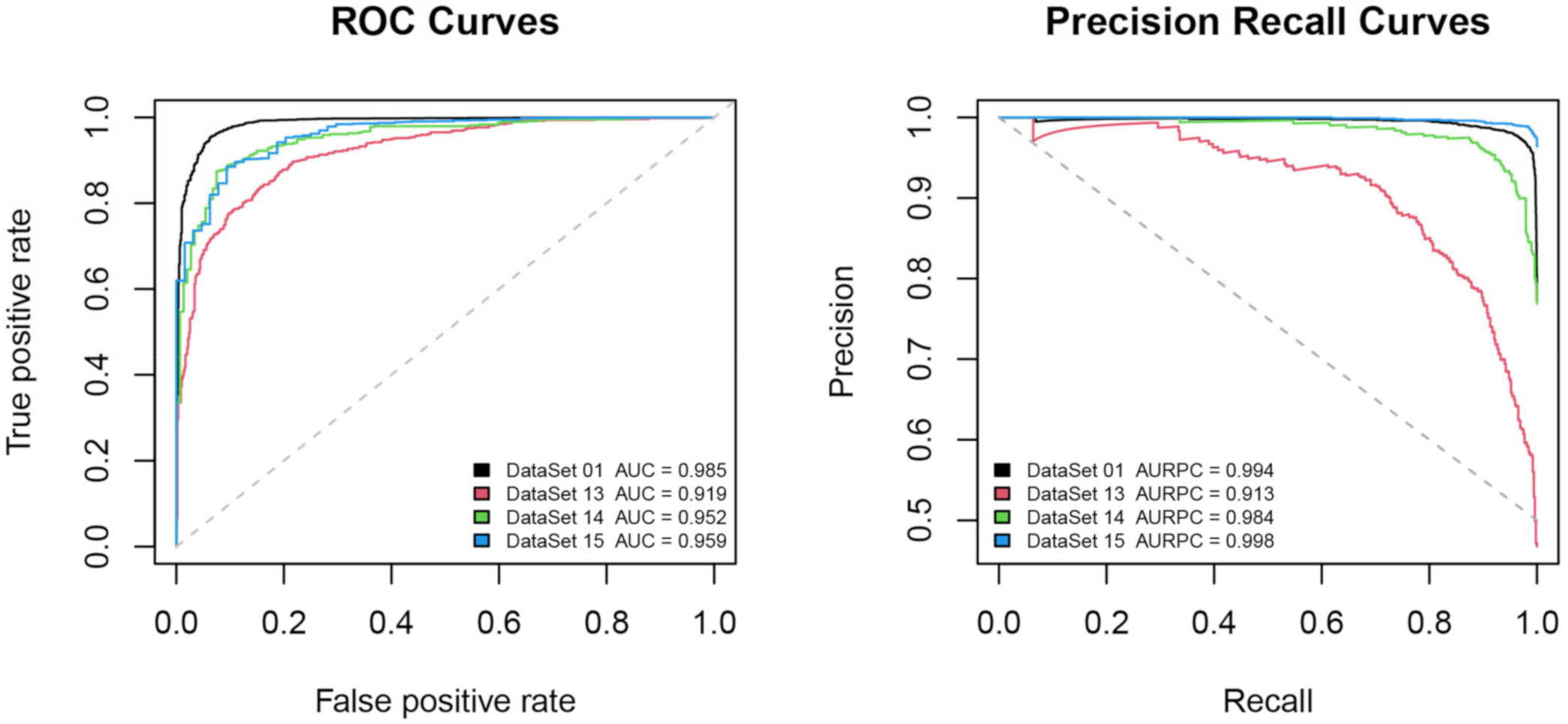
4.5. Considering the Earthquake Mangitude
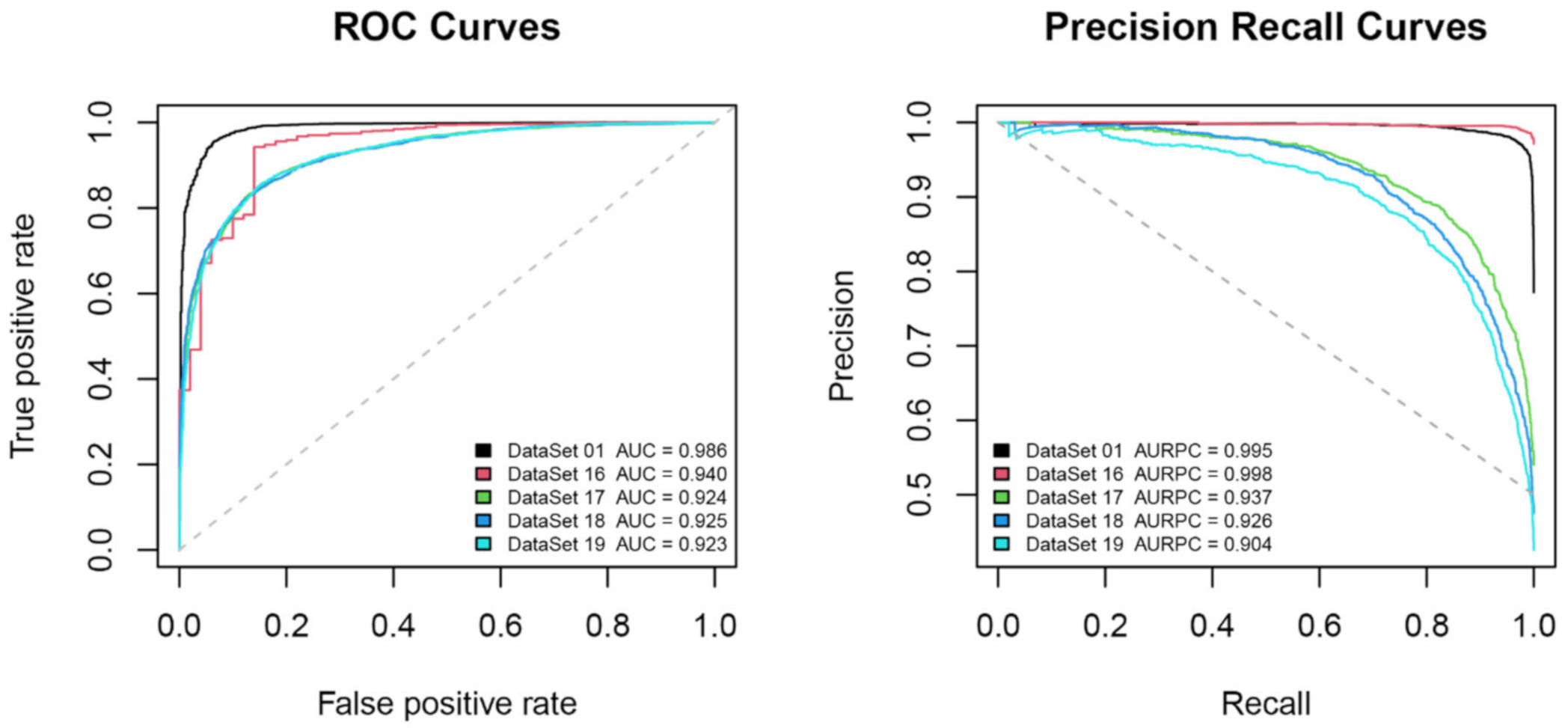
4.6. Considering an Unbalanced Dataset
4.7. Considering Different Temporal Windows
4.8. Dominant Features from LightGBM
4.9. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Shen, X.H.; Zhang, X.M.; Hong, S.Y.; Jing, F.; Zhao, S.F. Progress and development on multi-parameters remote sensing application in earthquake monitoring in China. Earthq. Sci. 2013, 26, 427–437. [Google Scholar] [CrossRef]
- Parrot, M. First results of the DEMETER micro-satellite. Planet. Space Sci. 2006, 54, 411–558. [Google Scholar] [CrossRef]
- Parrot, M.; Berthelier, J.J.; Lebreton, J.P.; Sauvaud, J.A.; Santolik, O.; Blecki, J. Examples of unusual ionospheric observations made by the DEMETER satellite over seismic regions. Phys. Chem. Earth Parts A/B/C 2006, 31, 486–495. [Google Scholar] [CrossRef]
- Zhang, X.; Shen, X.; Liu, J.; Ouyang, X.; Qian, J.; Zhao, S. Analysis of ionospheric plasma perturbations before Wenchuan earthquake. Nat. Hazards Earth Syst. Sci. 2009, 9, 1259–1266. [Google Scholar] [CrossRef]
- Błeçki, J.; Parrot, M.; Wronowski, R. Studies of the electromagnetic field variations in ELF frequency range registered by DEMETER over the Sichuan region prior to the 12 May 2008 earthquake. Int. J. Remote Sens. 2010, 31, 3615–3629. [Google Scholar] [CrossRef]
- Sarkar, S.; Gwal, A.K. Satellite monitoring of anomalous effects in the ionosphere related to the great Wenchuan earthquake of May 12, 2008. Nat. Hazards 2010, 55, 321–332. [Google Scholar] [CrossRef]
- Ryu, K.; Parrot, M.; Kim, S.G.; Jeong, K.S.; Chae, J.S.; Pulinets, S.; Oyama, K.I. Suspected seismo-ionospheric coupling observed by satellite measurements and GPS TEC related to the M7.9 Wenchuan earthquake of 12 May 2008. J. Geophys. Res. Space Phys. 2014, 119, 10305–10323. [Google Scholar] [CrossRef]
- Liu, J.Y.; Chen, Y.I.; Huang, C.C.; Parrot, M.; Shen, X.H.; Pulinets, S.A.; Yang, Q.S.; Ho, Y.Y. A spatial analysis on seismo-ionospheric anomalies observed by DEMETER during the 2008 M8.0 Wenchuan earthquake. J. Asian Earth Sci. 2015, 114, 414–419. [Google Scholar] [CrossRef]
- Walker, S.N.; Kadirkamanathan, V.; Pokhotelov, O.A. Changes in the ultra-low frequency wave field during the precursor phase to the Sichuan earthquake: DEMETER observations. Ann. Geophys. 2013, 31, 1597–1603. [Google Scholar] [CrossRef]
- Píša, D.; Parrot, M.; Santolík, O. Ionospheric density variations recorded before the 2010 Mw 8.8 earthquake in Chile. J. Geophys. Res. Space Phys. 2011, 116. [Google Scholar] [CrossRef]
- Zhang, X.; Qian, J.; Ouyang, X.; Shen, X.; Cai, J.; Zhao, S. Ionospheric electromagnetic perturbations observed on DEMETER satellite before Chile M7.9 earthquake. Earthq. Sci. 2009, 22, 251–255. [Google Scholar] [CrossRef][Green Version]
- Ho, Y.Y.; Liu, J.Y.; Parrot, M.; Pinçon, J.L. Temporal and spatial analyses on seismo-electric anomalies associated with the 27 February 2010 M=8.8 Chile earthquake observed by DEMETER satellite. Nat. Hazards Earth Syst. Sci. 2013, 13, 3281–3289. [Google Scholar] [CrossRef]
- Ho, Y.Y.; Jhuang, H.K.; Su, Y.C.; Liu, J.Y. Seismo-ionospheric anomalies in total electron content of the GIM and electron density of DEMETER before the 27 February 2010 M8.8 Chile earthquake. Adv. Space Res. 2013, 51, 2309–2315. [Google Scholar] [CrossRef]
- Louerguioui, S.; Gaci, S.; Zaourar, N. Irregularities of the ionospheric plasma and the ULF electric components obtained from DEMETER satellite experiments above Chile earthquake (27 February 2010). Arab. J. Geosci. 2014, 8, 2433–2441. [Google Scholar] [CrossRef][Green Version]
- Mofiz, U.A.; Battiston, R. Possible ion-acoustic soliton formation in the ionospheric perturbations observed on DEMETER before the 2007 Pu’er earthquake. Earthq. Sci. 2009, 22, 257–262. [Google Scholar] [CrossRef][Green Version]
- He, Y.; Yang, D.; Qian, J.; Parrot, M. Anomaly of the ionospheric electron density close to earthquakes: Case studies of Pu’er and Wenchuan earthquakes. Earthq. Sci. 2011, 24, 549–555. [Google Scholar] [CrossRef][Green Version]
- Shen, X.H.; Zhang, X.; Liu, J.; Zhao, S.F.; Yuan, G.P. Analysis of the enhanced negative correlation between electron density and electron temperature related to earthquakes. Ann. Geophys. 2015, 33, 471–479. [Google Scholar] [CrossRef]
- Stangl, G.; Boudjada, M.Y.; Biagi, P.F.; Krauss, S.; Maier, A.; Schwingenschuh, K.; Al-Haddad, E.; Parrot, M.; Voller, W. Investigation of TEC and VLF space measurements associated to L’Aquila (Italy) earthquakes. Nat. Hazards Earth Syst. Sci. 2011, 11, 1019–1024. [Google Scholar] [CrossRef][Green Version]
- Bertello, I.; Piersanti, M.; Candidi, M.; Diego, P.; Ubertini, P. Electromagnetic field observations by the DEMETER satellite in connection with the 2009 L’Aquila earthquake. Ann. Geophys. 2018, 36, 1483–1493. [Google Scholar] [CrossRef]
- Athanasiou, M.A.; Anagnostopoulos, G.C.; Iliopoulos, A.C.; Pavlos, G.P.; David, C.N. Enhanced ULF radiation observed by DEMETER two months around the strong 2010 Haiti earthquake. Nat. Hazards Earth Syst. Sci. 2011, 11, 1091–1098. [Google Scholar] [CrossRef]
- Němec, F.; Santolík, O.; Parrot, M.; Berthelier, J.J. Spacecraft observations of electromagnetic perturbations connected with seismic activity. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Němec, F.; Santolík, O.; Parrot, M. Decrease of intensity of ELF/VLF waves observed in the upper ionosphere close to earthquakes: A statistical study. J. Geophys. Res. Space Phys. 2009, 114. [Google Scholar] [CrossRef]
- Píša, D.; Němec, F.; Parrot, M.; Santolík, O. Attenuation of electromagnetic waves at the frequency ~1.7 kHz in the upper ionosphere observed by the DEMETER satellite in the vicinity of earthquakes. Ann. Geophys. 2012, 55. [Google Scholar] [CrossRef]
- Píša, D.; Němec, F.; Santolík, O.; Parrot, M.; Rycroft, M. Additional attenuation of natural VLF electromagnetic waves observed by the DEMETER spacecraft resulting from preseismic activity. J. Geophys. Res. Space Phys. 2013, 118, 5286–5295. [Google Scholar] [CrossRef]
- Hobara, Y.; Nakamura, R.; Suzuki, M.; Hayakawa, M.; Parrot, M. Ionospheric perturbations observed by the low altitude satellite DEMETER and possible relation with seismicity. J. Atmos. Electr. 2013, 33, 21–29. [Google Scholar] [CrossRef]
- Ryu, K.; Lee, E.; Chae, J.S.; Parrot, M.; Pulinets, S. Seismo-ionospheric coupling appearing as equatorial electron density enhancements observed via DEMETER electron density measurements. J. Geophys. Res. Space Phys. 2014, 119, 8524–8542. [Google Scholar] [CrossRef]
- He, Y.; Yang, D.; Zhu, R.; Qian, J.; Parrot, M. Variations of electron density and temperature in ionosphere based on the DEMETER ISL data. Earthq. Sci. 2010, 23, 349–355. [Google Scholar] [CrossRef]
- He, Y.; Yang, D.; Qian, J.; Parrot, M. Response of the ionospheric electron density to different types of seismic events. Nat. Hazards Earth Syst. Sci. 2011, 11, 2173–2180. [Google Scholar] [CrossRef]
- Yan, R.; Parrot, M.; Pinçon, J.-L. Statistical Study on Variations of the Ionospheric Ion Density Observed by DEMETER and Related to Seismic Activities. J. Geophys. Res. Space Phys. 2017, 122, 412–421. [Google Scholar] [CrossRef]
- Parrot, M. Statistical analysis of the ion density measured by the satellite DEMETER in relation with the seismic activity. Earthq. Sci. 2011, 24, 513–521. [Google Scholar] [CrossRef]
- Li, M.; Parrot, M. “Real time analysis” of the ion density measured by the satellite DEMETER in relation with the seismic activity. Nat. Hazards Earth Syst. Sci. 2012, 12, 2957–2963. [Google Scholar] [CrossRef]
- Parrot, M. Statistical analysis of automatically detected ion density variations recorded by DEMETER and their relation to seismic activity. Ann. Geophys. 2012, 55. [Google Scholar] [CrossRef]
- Li, M.; Parrot, M. Statistical analysis of an ionospheric parameter as a base for earthquake prediction. J. Geophys. Res. Space Phys. 2013, 118, 3731–3739. [Google Scholar] [CrossRef]
- Parrot, M.; Li, M. Statistical analysis of the ionospheric density recorded by the demeter satellite during seismic activity. Pre-Earthq. Process. 2018. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, P.; Zhang, F.; Song, Q. CloudNet: Ground-based cloud classification with deep convolutional neural network. Geophys. Res. Lett. 2018. [Google Scholar] [CrossRef]
- Bergen, K.J.; Johnson, P.A.; de Hoop, M.V.; Beroza, G.C. Machine learning for data-driven discovery in solid Earth geoscience. Science 2019, 363. [Google Scholar] [CrossRef] [PubMed]
- Rouet-Leduc, B.; Hulbert, C.; Johnson, P.A. Continuous chatter of the Cascadia subduction zone revealed by machine learning. Nat. Geosci. 2018, 12, 75–79. [Google Scholar] [CrossRef]
- Hulbert, C.; Rouet-Leduc, B.; Johnson, P.A.; Ren, C.X.; Rivière, J.; Bolton, D.C.; Marone, C. Similarity of fast and slow earthquakes illuminated by machine learning. Nat. Geosci. 2018, 12, 69–74. [Google Scholar] [CrossRef]
- Perol, T.; Gharbi, M.; Denolle, M. Convolutional neural network for earthquake detection and location. Sci. Adv. 2018, 4, e1700578. [Google Scholar] [CrossRef]
- Yoon, C.E.; O’Reilly, O.; Bergen, K.J.; Beroza, G.C. Earthquake detection through computationally efficient similarity search. Sci. Adv. 2015, 1, e1501057. [Google Scholar] [CrossRef] [PubMed]
- Berthelier, J.J.; Godefroy, M.; Leblanc, F.; Malingre, M.; Menvielle, M.; Lagoutte, D.; Brochot, J.Y.; Colin, F.; Elie, F.; Legendre, C.; et al. ICE, the electric field experiment on DEMETER. Planet. Space Sci. 2006, 54, 456–471. [Google Scholar] [CrossRef]
- Parrot, M.; Benoist, D.; Berthelier, J.J.; Błęcki, J.; Chapuis, Y.; Colin, F.; Elie, F.; Fergeau, P.; Lagoutte, D.; Lefeuvre, F.; et al. The magnetic field experiment IMSC and its data processing onboard DEMETER: Scientific objectives, description and first results. Planet. Space Sci. 2006, 54, 441–455. [Google Scholar] [CrossRef]
- Parrot, M.; Berthelier, J.J.; Blecki, J.; Brochot, J.Y.; Hobara, Y.; Lagoutte, D.; Lebreton, J.P.; Němec, F.; Onishi, T.; Pinçon, J.L.; et al. Unexpected very low frequency (VLF) radio events recorded by the ionospheric satellite DEMETER. Surv. Geophys. 2015, 36, 483–511. [Google Scholar] [CrossRef]
- Parrot, M.; Buzzi, A.; Santolík, O.; Berthelier, J.J.; Sauvaud, J.A.; Lebreton, J.P. New observations of electromagnetic harmonic ELF emissions in the ionosphere by the DEMETER satellite during large magnetic storms. J. Geophys. Res. 2006, 111. [Google Scholar] [CrossRef]
- Dobrovolsky, I.; Zubkov, S.; Miachkin, V. Estimation of the size of earthquake preparation zones. Pure Appl. Geophys. 1979, 117, 1025–1044. [Google Scholar] [CrossRef]
- Snoek, J.; Larochelle, H.; Adams, R.P. Practical bayesian optimization of machine learning algorithms. In Advances in Neural Information Processing Systems; Curran Associates Inc.: Lake Tahoe, NV, USA, 2012; pp. 2951–2959. [Google Scholar]
- Rodriguez, J.D.; Perez, A.; Lozano, J.A. Sensitivity analysis of k-fold cross validation in prediction error estimation. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 32, 569–575. [Google Scholar] [CrossRef] [PubMed]
- Michie, D.; Spiegelhalter, D.J.; Taylor, C.C.; Campbell, J. (Eds.) Machine Learning, Neural and Statistical Classification; Ellis Horwood: Upper Saddle River, NJ, USA, 1994; p. 289. [Google Scholar]
- Cox, D.R. The regression analysis of binary sequences. J. R. Stat. Soc. Ser. B 1958, 20, 215–232. [Google Scholar] [CrossRef]
- Gruber, M. Improving Efficiency by Shrinkage: The James–Stein and Ridge Regression Estimators; Routledge: New York, NY, USA, 2017. [Google Scholar]
- Bottou, L. Stochastic gradient descent tricks. In Neural Networks: Tricks of the Trade; Springer: Berlin/Heidelberg, Germany, 2012; pp. 421–436. [Google Scholar]
- Crammer, K.; Dekel, O.; Keshet, J.; Shalev-Shwartz, S.; Singer, Y. Online passive-aggressive algorithms. J. Mach. Learn. Res. 2006, 7, 551–585. [Google Scholar]
- Fisher, R.A. The Use of Multiple Measurements in Taxonomic Problems. Ann. Eugen. 1936, 7, 179–188. [Google Scholar] [CrossRef]
- Friedman, J.; Hastie, T.; Tibshirani, R. The Elements of Statistical Learning; Springer Series in Statistics New York: New York, NY, USA, 2001; Volume 1. [Google Scholar]
- Breiman, L. Classification and Regression Trees; Routledge: New York, NY, USA, 2017. [Google Scholar]
- Geurts, P.; Ernst, D.; Wehenkel, L. Extremely randomized trees. Mach. Learn. 2006, 63, 3–42. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Maron, M.E. Automatic indexing: An experimental inquiry. J. ACM 1961, 8, 404–417. [Google Scholar] [CrossRef]
- Kégl, B. The return of AdaBoost. MH: Multi-class Hamming trees. arXiv 2013, arXiv:1312.6086. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.-Y. LightGBM: A highly efficient gradient boosting decision tree. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 3149–3157. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Meng, Q.; Ke, G.; Wang, T.; Chen, W.; Ye, Q.; Ma, Z.-M.; Liu, T.-Y. A communication-efficient parallel algorithm for decision tree. In Proceedings of the 30th International Conference on Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; pp. 1279–1287. [Google Scholar]
- Ranka, S.; Singh, V. CLOUDS: A decision tree classifier for large datasets. In Proceedings of the 4th Knowledge Discovery and Data Mining Conference, New York, NY, USA, 27–31 August 1998; pp. 2–8. [Google Scholar]
- Jin, R.; Agrawal, G. Communication and memory efficient parallel decision tree construction. In Proceedings of the 2003 SIAM International Conference on Data Mining, San Francisco, CA, USA, 1–3 May 2003; pp. 119–129. [Google Scholar]
- Bergstra, J.; Yamins, D.; Cox, D.D. Making a science of model search: Hyperparameter optimization in hundreds of dimensions for vision architectures. In Proceedings of the 30th International Conference on International Conference on Machine Learning—Volume 28, Atlanta, GA, USA, 16–21 June 2013; pp. I-115–I-123. [Google Scholar]
- Kohavi, R. A study of cross-validation and bootstrap for accuracy estimation and model selection. In Proceedings of the 14th International Joint Conference on Artificial Intelligence, Montreal, QC, Canada, 20–25 August 1995; pp. 1137–1145. [Google Scholar]
- Davis, J.; Goadrich, M. The relationship between Precision-Recall and ROC curves. In Proceedings of the 23rd International Conference on Machine Learning, Pittsburgh, PA, USA, 25–29 June 2006; pp. 233–240. [Google Scholar]
- Iwata, S. Weights and measures in the indus valley. In ENCYCLOPAEDIA of the History of Science, Technology, and Medicine in Non-Western Cultures, 2nd ed.; Selin, H., Ed.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 2254–2255. [Google Scholar]
- Sing, T.; Sander, O.; Beerenwinkel, N.; Lengauer, T.J.B. ROCR: Visualizing classifier performance in R. Bioinformatics 2005, 21, 3940–3941. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Sarkar, S.; Gwal, A.K.; Parrot, M. Electric and magnetic field perturbations recorded by DEMETER satellite before seismic events of the 17th July 2006 M 7.7 earthquake in Indonesia. J. Asian Earth Sci. 2009, 34, 634–644. [Google Scholar] [CrossRef]
- Eppelbaum, L.; Finkelstein, M. Radon Emanation, Magnetic and VLF Temporary Variations: Removing Components not Associated with Dynamic Processes. 1998. Available online: https://www.researchgate.net/publication/231817102_Radon_emanation_magnetic_and_VLF_temporary_variations_removing_components_not_associated_with_dynamic_processes (accessed on 4 November 2020).
- Wang, Y.D.; Pi, D.C.; Zhang, X.M.; Shen, X.H. Seismo-ionospheric precursory anomalies detection from DEMETER satellite data based on data mining. Nat. Hazards 2014, 76, 823–837. [Google Scholar] [CrossRef]
- Xu, F.; Song, X.; Wang, X.; Su, J. Neural network model for earthquake prediction using DMETER data and seismic belt information. In Proceedings of the 2010 Second WRI Global Congress on Intelligent Systems, Wuhan, China, 16–17 December 2010; pp. 180–183. [Google Scholar]
- Zang, S.; Pi, D.; Zhang, X.; Shen, X. Recognizing methods for epicenter-neighboring orbits with ionospheric information from DEMETER satellite data. Adv. Space Res. 2017, 60, 980–990. [Google Scholar] [CrossRef]
- Zang, S.; Pi, D.; Zhang, X.; Shen, X. Seismic classification-based method for recognizing epicenter-neighboring orbits. Adv. Space Res. 2017, 59, 1886–1894. [Google Scholar] [CrossRef]
- Santolík, O.; Parrot, M. Case studies on the wave propagation and polarization of ELF emissions observed by Freja around the local proton gyrofrequency. J. Geophys. Res. Space Phys. 1999, 104, 2459–2475. [Google Scholar] [CrossRef]
- Santolík, O.; Parrot, M. Application of wave distribution function methods to an ELF hiss event at high latitudes. J. Geophys. Res. Space Phys. 2000, 105, 18885–18894. [Google Scholar] [CrossRef]
- Santolík, O.; Chum, J.; Parrot, M.; Gurnett, D.; Pickett, J.; Cornilleau-Wehrlin, N. Propagation of whistler mode chorus to low altitudes: Spacecraft observations of structured ELF hiss. J. Geophys. Res. Space Phys. 2006, 111. [Google Scholar] [CrossRef]
- Chen, L.; Santolík, O.; Hajoš, M.; Zheng, L.; Zhima, Z.; Heelis, R.; Hanzelka, M.; Horne, R.B.; Parrot, M. Source of the low-altitude hiss in the ionosphere. Geophys. Res. Lett. 2017, 44, 2060–2069. [Google Scholar] [CrossRef]
- Xia, Z.; Chen, L.; Zhima, Z.; Santolík, O.; Horne, R.B.; Parrot, M. Statistical characteristics of ionospheric hiss waves. Geophys. Res. Lett. 2019, 46, 7147–7156. [Google Scholar] [CrossRef]
- Pulinets, S.A.; Morozova, L.I.; Yudin, I.A. Synchronization of atmospheric indicators at the last stage of earthquake preparation cycle. Res. Geophys. 2015, 4. [Google Scholar] [CrossRef]
- Pulinets, S.; Davidenko, D. Ionospheric precursors of earthquakes and Global Electric Circuit. Adv. Space Res. 2014, 53, 709–723. [Google Scholar] [CrossRef]
- Kuo, C.L.; Lee, L.C.; Huba, J.D. An improved coupling model for the lithosphere-atmosphere-ionosphere system. J. Geophys. Res. Space Phys. 2014, 119, 3189–3205. [Google Scholar] [CrossRef]
- Harrison, R.G.; Aplin, K.L.; Rycroft, M.J. Atmospheric electricity coupling between earthquake regions and the ionosphere. J. Atmos. Sol.-Terr. Phys. 2010, 72, 376–381. [Google Scholar] [CrossRef]
- Pulinets, S.; Ouzounov, D. Lithosphere–Atmosphere–Ionosphere Coupling (LAIC) model—An unified concept for earthquake precursors validation. J. Asian Earth Sci. 2011, 41, 371–382. [Google Scholar] [CrossRef]

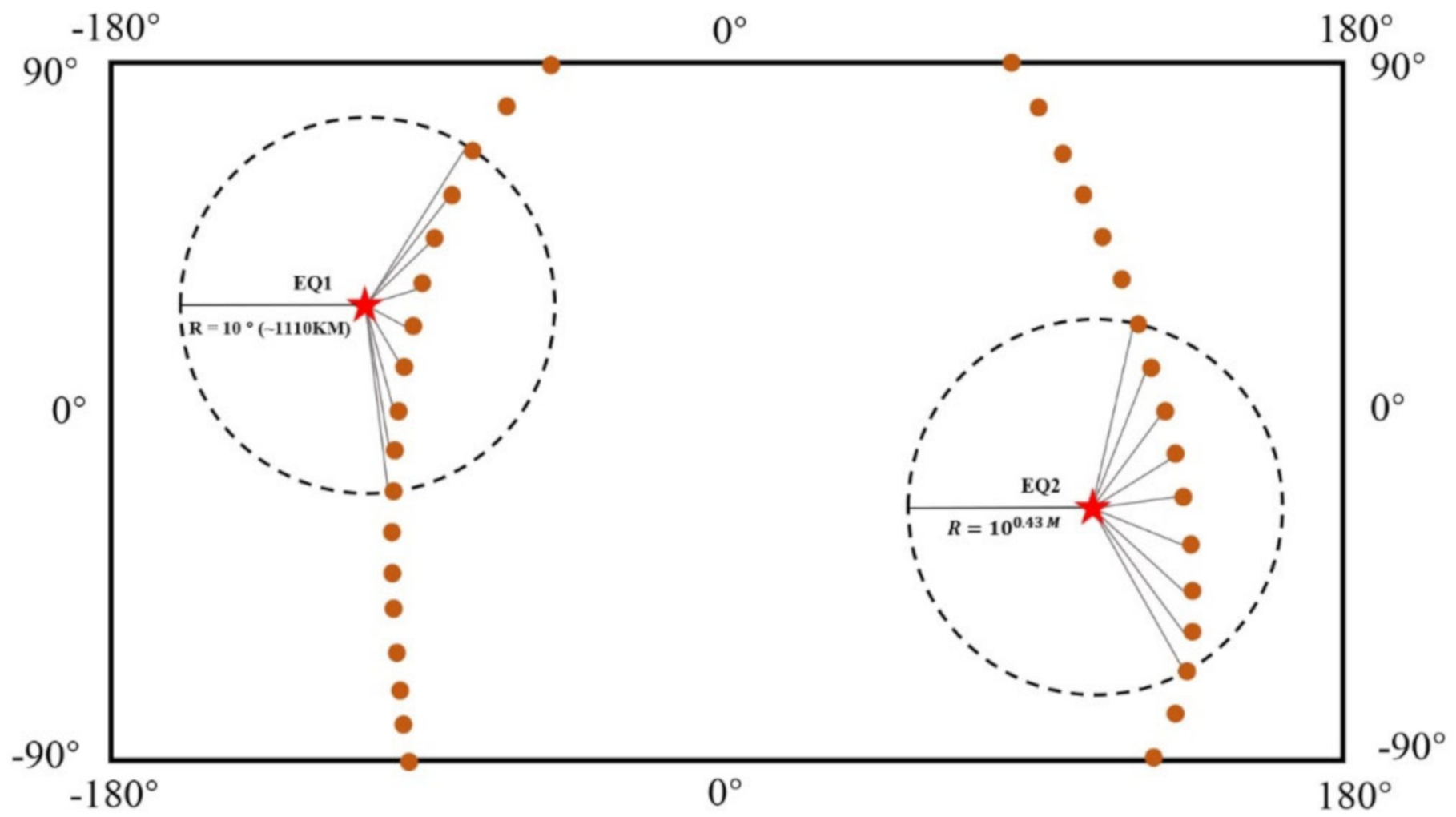








| Night/Daytime | Spatial Feature (with Its Center at the Epicenter and the Dobrovolsky Radius/a Deviation of 10°) | Temporal Feature | Frequency Feature | Artificial Non-Seismic Events/Data Generation | |
|---|---|---|---|---|---|
| DataSet 01 | Nighttime | the Dobrovolsky radius | 48 h | low frequencies | stagger the time and place |
| DataSet 02 | Nighttime | a deviation of 10° | 7 days | low frequencies | stagger the time and place |
| DataSet 03 | Daytime | the Dobrovolsky radius | 48 h | low frequencies | stagger the time and place |
| DataSet 04 | Daytime | a deviation of 10° | 7 days | low frequencies | stagger the time and place |
| DataSet 05 | Nighttime | the Dobrovolsky radius | 48 h | high frequencies | stagger the time and place |
| DataSet 06 | Nighttime | the Dobrovolsky radius | 48 h | low frequencies | only stagger the time |
| DataSet 07 | Nighttime | the Dobrovolsky radius | 48 h | high frequencies | only stagger the time |
| DataSet 20 | Nighttime | the Dobrovolsky radius | 7 days | low frequencies | stagger the time and place |
| DataSet 21 | Nighttime | the Dobrovolsky radius | 10 days | low frequencies | stagger the time and place |
| DataSet 22 | Nighttime | the Dobrovolsky radius | 20 days | low frequencies | stagger the time and place |
| DataSet 23 | Nighttime | the Dobrovolsky radius | 30 days | low frequencies | stagger the time and place |
| DataSet I | Nighttime | the Dobrovolsky radius | 48 h | low frequencies | 10–20 days before/after real earthquakes |
| DataSet II | Nighttime | the Dobrovolsky radius | 48 h | low frequencies | 20–30 days before/after real earthquakes |
| DataSet III | Nighttime | the Dobrovolsky radius | 48 h | low frequencies | 30–40 days before/after real earthquakes |
| DataSet IV | Nighttime | the Dobrovolsky radius | 48 h | low frequencies | 40–50 days before/after real earthquakes |
| DataSet V | Nighttime | the Dobrovolsky radius | 48 h | low frequencies | 50–60 days before/after real earthquakes |
| DataSet VI | Nighttime | the Dobrovolsky radius | 48 h | low frequencies | 60–70 days before/after real earthquakes |
| Method | DataSet 01 | ||||
|---|---|---|---|---|---|
| Specificity | Sensitivity | Accuracy | Precision | AUC | |
| lgb | 0.941 | 0.948 | 0.947 | 0.981 | 0.985 |
| rf | 0.909 | 0.948 | 0.939 | 0.971 | 0.98 |
| svm | 0.833 | 0.861 | 0.855 | 0.944 | 0.913 |
| xgb | 0.821 | 0.814 | 0.816 | 0.937 | 0.897 |
| gbm | 0.813 | 0.818 | 0.817 | 0.935 | 0.895 |
| dnn | 0.812 | 0.836 | 0.830 | 0.936 | 0.894 |
| ada | 0.786 | 0.767 | 0.772 | 0.922 | 0.852 |
| cart | 0.768 | 0.922 | 0.886 | 0.929 | 0.845 |
| qda | 0.829 | 0.718 | 0.744 | 0.933 | 0.834 |
| lda | 0.771 | 0.763 | 0.764 | 0.916 | 0.833 |
| logistic | 0.771 | 0.765 | 0.766 | 0.916 | 0.832 |
| extra | 0.730 | 0.915 | 0.872 | 0.918 | 0.823 |
| bayes | 0.685 | 0.648 | 0.657 | 0.872 | 0.727 |
| sgd | 0.611 | 0.766 | 0.730 | 0.879 | 0.688 |
| ridge | 0.321 | 0.954 | 0.807 | 0.822 | 0.638 |
| pa | 0.363 | 0.789 | 0.690 | 0.833 | 0.576 |
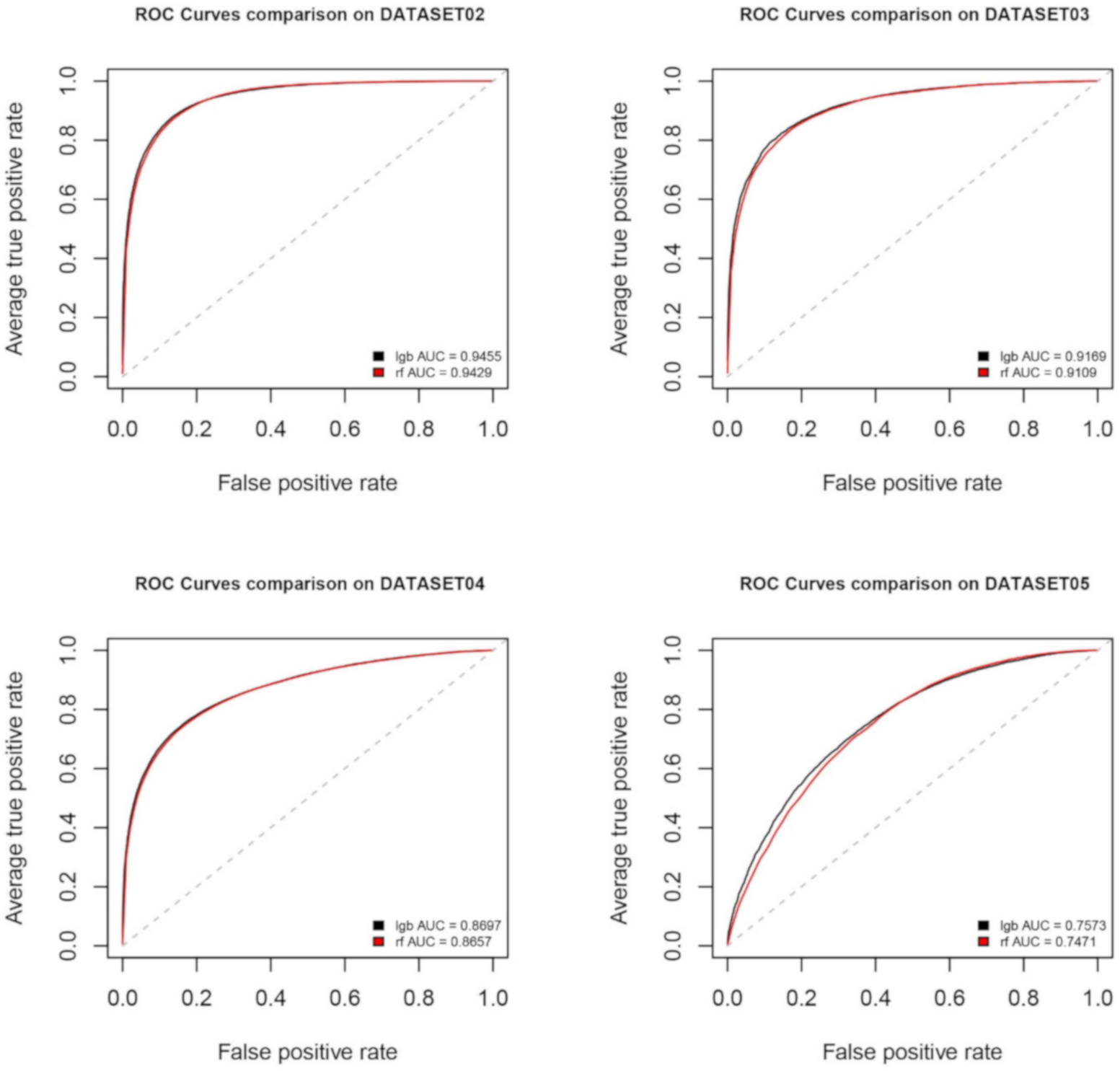
| Method | DataSet 02 | ||||
| Specificity | Sensitivity | Accuracy | Precision | AUC | |
| LightGBM | 0.870 | 0.874 | 0.872 | 0.880 | 0.945 |
| Random Forest | 0.855 | 0.879 | 0.868 | 0.869 | 0.942 |
| Method | DataSet 03 | ||||
| Specificity | Sensitivity | Accuracy | Precision | AUC | |
| LightGBM | 0.870 | 0.811 | 0.834 | 0.955 | 0.916 |
| Random Forest | 0.832 | 0.833 | 0.832 | 0.944 | 0.910 |
| Method | DataSet 04 | ||||
| Specificity | Sensitivity | Accuracy | Precision | AUC | |
| LightGBM | 0.836 | 0.752 | 0.789 | 0.851 | 0.869 |
| Random Forest | 0.832 | 0.747 | 0.785 | 0.847 | 0.865 |
| Method | DataSet 05 | ||||
| Specificity | Sensitivity | Accuracy | Precision | AUC | |
| LightGBM | 0.656 | 0.725 | 0.719 | 0.875 | 0.757 |
| Random Forest | 0.631 | 0.738 | 0.713 | 0.869 | 0.747 |
| Dataset | LightGBM | |||||
|---|---|---|---|---|---|---|
| Specificity | Sensitivity | Accuracy | Precision | AUC | AURPC | |
| DataSet 01 | 0.887 | 0.980 | 0.959 | 0.967 | 0.986 | 0.995 |
| DataSet 02 | 0.895 | 0.893 | 0.894 | 0.907 | 0.960 | 0.965 |
| DataSet 03 | 0.862 | 0.835 | 0.841 | 0.954 | 0.919 | 0.974 |
| DataSet 04 | 0.848 | 0.743 | 0.79 | 0.856 | 0.873 | 0.903 |
| DataSet 05 | 0.638 | 0.760 | 0.732 | 0.877 | 0.768 | 0.910 |
| DataSet 06 | 0.848 | 0.717 | 0.782 | 0.826 | 0.863 | 0.872 |
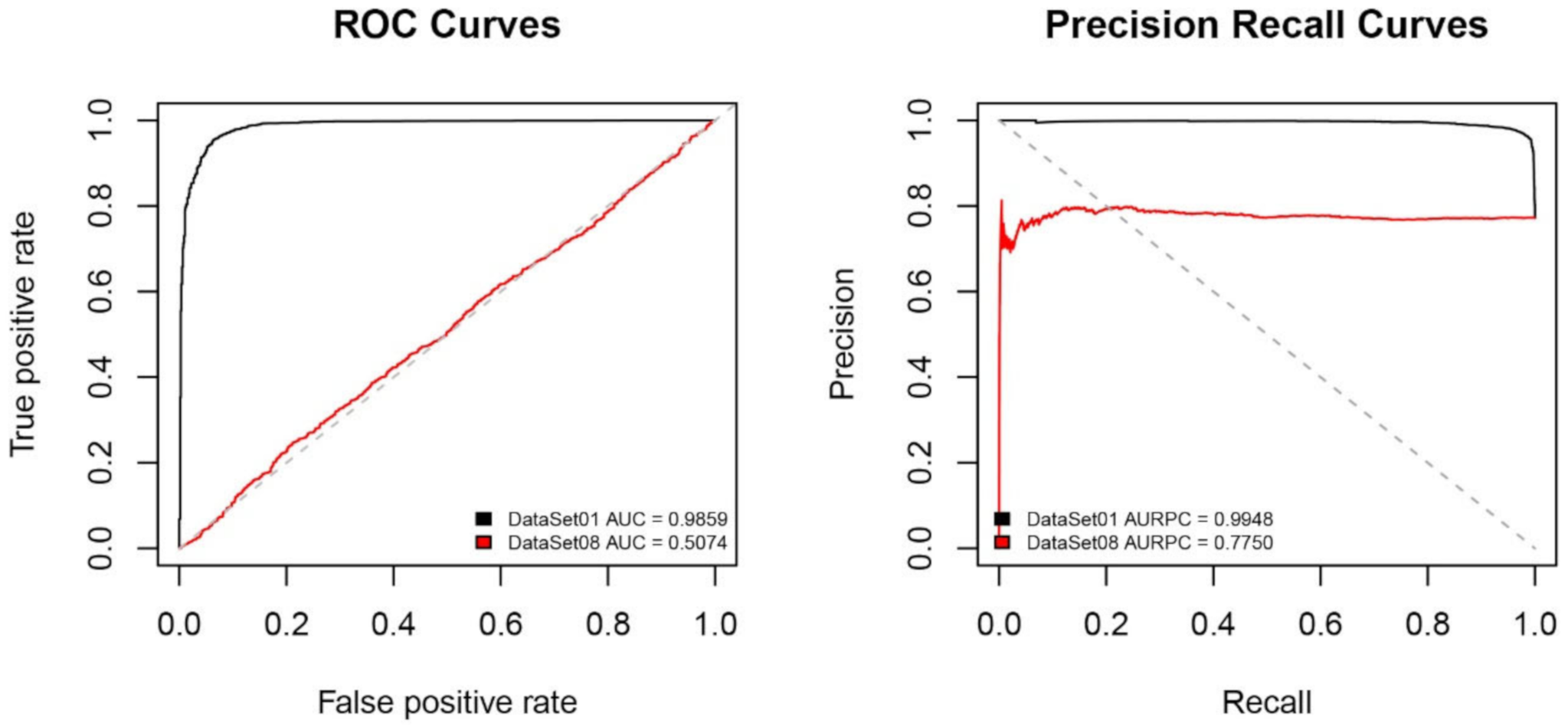
| DataSet 07 | 0.904 | 0.411 | 0.657 | 0.811 | 0.684 | 0.733 |
| DataSet 08 | 0.788 | 0.246 | 0.370 | 0.798 | 0.507 | 0.775 |
| DataSet I | 0.819 | 0.811 | 0.815 | 0.818 | 0.891 | 0.896 |
| DataSet II | 0.852 | 0.784 | 0.818 | 0.842 | 0.894 | 0.898 |
| DataSet III | 0.833 | 0.807 | 0.820 | 0.829 | 0.896 | 0.902 |
| DataSet IV | 0.828 | 0.811 | 0.820 | 0.826 | 0.896 | 0.899 |
| DataSet V | 0.852 | 0.759 | 0.805 | 0.837 | 0.887 | 0.890 |
| DataSet VI | 0.827 | 0.785 | 0.806 | 0.821 | 0.891 | 0.898 |
| Night/Daytime | Spatial Feature | Temporal Feature | Earthquake Magnitude/Number of Earthquakes | Number of Data Used for Training | |
|---|---|---|---|---|---|
| DataSet 09 | Nighttime | with its center at the epicenter and a deviation of 3° | 48 h | all/8760 | 444,772 |
| DataSet 10 | Nighttime | with its center at the epicenter and a deviation of 5° | 48 h | all/8760 | 1,243,216 |
| DataSet 11 | Nighttime | with its center at the epicenter and a deviation of 7° | 48 h | all/8760 | 2,360,36 |
| DataSet 12 | Nighttime | with its center at the epicenter and a deviation of 12° | 48 h | all/8760 | 6,517,967 |
| DataSet 13 | Nighttime | with its center at the epicenter and the Dobrovolsky radius | 48 h | 5.0~5.5/6818 | 110,839 |
| DataSet 14 | Nighttime | with its center at the epicenter and the Dobrovolsky radius | 48 h | 5.5~6.0/1813 | 63,584 |
| DataSet 15 | Nighttime | with its center at the epicenter and the Dobrovolsky radius | 48 h | above 6.0/589 | 176,945 |
| DataSet 16 | Nighttime | with its center at the epicenter and the Dobrovolsky radius | 48 h | 1:2 | 176,943 |
| DataSet 17 | Nighttime | with its center at the epicenter and the Dobrovolsky radius | 48 h | 1:3 | 462,642 |
| DataSet 18 | Nighttime | with its center at the epicenter and the Dobrovolsky radius | 48 h | 1:4 | 535,777 |
| DataSet 19 | Nighttime | with its center at the epicenter and the Dobrovolsky radius | 48 h | 1:5 | 603,208 |
| Testing Set | Training Set | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| AUC | AURPC | FP | FN | Specificity | Precision | Sensitivity | Accuracy | Accuracy | |
| DataSet 01 | 0.986 | 0.995 | 90 | 54 | 0.887 | 0.967 | 0.980 | 0.959 | 1.000 |
| DataSet 09 | 0.929 | 0.941 | 286 | 358 | 0.865 | 0.873 | 0.846 | 0.855 | 0.995 |
| DataSet 10 | 0.923 | 0.939 | 724 | 1170 | 0.873 | 0.885 | 0.826 | 0.848 | 0.985 |
| DataSet 11 | 0.911 | 0.931 | 1502 | 2455 | 0.861 | 0.873 | 0.808 | 0.832 | 0.962 |
| DataSet 12 | 0.881 | 0.910 | 4657 | 8559 | 0.837 | 0.858 | 0.766 | 0.797 | 0.943 |
| DataSet 13 | 0.919 | 0.913 | 69 | 109 | 0.883 | 0.856 | 0.790 | 0.839 | 1.000 |
| DataSet 14 | 0.952 | 0.984 | 29 | 32 | 0.803 | 0.940 | 0.935 | 0.904 | 1.000 |
| DataSet 15 | 0.959 | 0.998 | 33 | 12 | 0.484 | 0.981 | 0.993 | 0.975 | 1.000 |
| DataSet 16 | 0.940 | 0.998 | 27 | 9 | 0.460 | 0.984 | 0.995 | 0.980 | 1.000 |
| DataSet 17 | 0.924 | 0.937 | 330 | 377 | 0.845 | 0.865 | 0.849 | 0.847 | 1.000 |
| DataSet 18 | 0.925 | 0.926 | 332 | 469 | 0.882 | 0.862 | 0.816 | 0.851 | 1.000 |
| DataSet 19 | 0.923 | 0.904 | 322 | 566 | 0.907 | 0.861 | 0.780 | 0.853 | 1.000 |
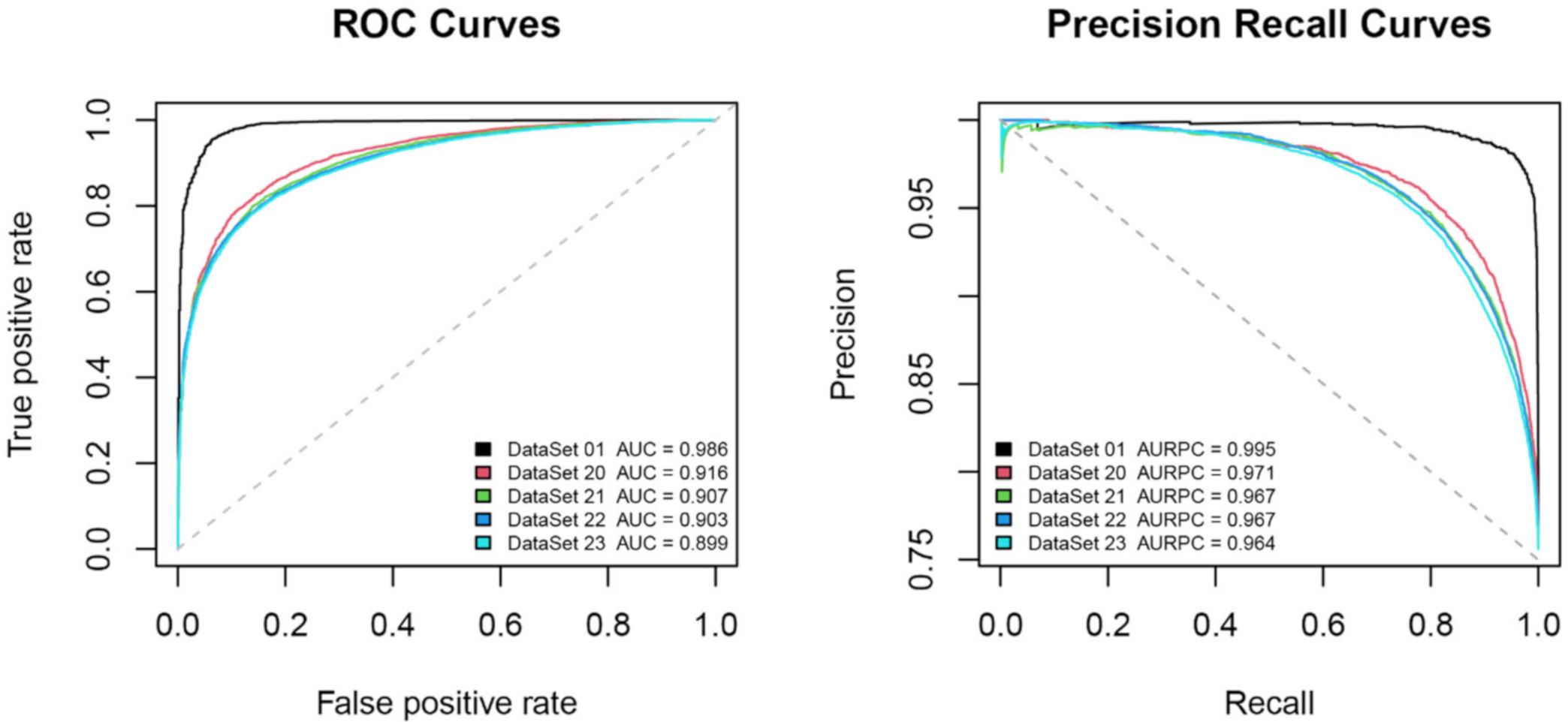
| DataSet 20 | 0.916 | 0.971 | 1003 | 512 | 0.619 | 0.888 | 0.939 | 0.864 | 1 |
| DataSet 21 | 0.907 | 0.967 | 922 | 1574 | 0.758 | 0.918 | 0.868 | 0.841 | 0.967 |
| DataSet 22 | 0.903 | 0.967 | 1549 | 3463 | 0.780 | 0.926 | 0.849 | 0.832 | 0.938 |
| DataSet 23 | 0.899 | 0.964 | 1994 | 5618 | 0.809 | 0.930 | 0.826 | 0.822 | 0.909 |
| Study | Study Area | Study Period | Input Data | Model | Objective and Performance |
|---|---|---|---|---|---|
| Xu et al. [77] | The globe | 2007–2008 | Ne, Te, Ti, NO+, H+ and He+ from IAP and ISL | BPNN | predict seismic events in 2008. Accuracy: 69.96%. |
| Li and Parrot [33] | The globe | June 2004–December 2010 | Total ion density (the sum of H+, He+ and O+)) from IAP | Statistics model | statistics of data perturbation. Sensitivity: 65.25% Specificity: 71.95% |
| Wang, Pi, Zhang and Shen [76] | Taiwan, China | January 2008–June 2008 | Ne, Ni, Te, Ti, NO+, H+, He+ and O+ from IAP and ISL | MARBDP | predict earthquakes of Ms >5.0 from January 2008 to June 2008. sensitivity: 70.01% |
| Zang et al. [78] | The globe | June 2004–December 2010 | Ne, Ni, Te, Ti, NO+, H+, He+ and O+ from IAP and ISL | calculate asymmetry and stability using DTW distance | recognizing epicenter-neighboring orbits during strong seismic Sensitivity: 65.03% |
| Zang et al. [79] | The globe | June 2004–December 2010 | Ne, Te, Ti, O+, plasma potential | S4VMs with kernel combination | seismic classification-based method for recognizing epicenter-neighboring orbit. Sensitivity: 79.36% Specificity: 98.34% |
| Our proposed method | The globe | June 2004–December 2010 | Low-frequency power spectra from IMSC and ICE | LightGBM | discriminate electromagnetic pre-earthquake perturbations Sensitivity: 95.41% Specificity: 93.69% Accuracy: 95.01% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiong, P.; Long, C.; Zhou, H.; Battiston, R.; Zhang, X.; Shen, X. Identification of Electromagnetic Pre-Earthquake Perturbations from the DEMETER Data by Machine Learning. Remote Sens. 2020, 12, 3643. https://doi.org/10.3390/rs12213643
Xiong P, Long C, Zhou H, Battiston R, Zhang X, Shen X. Identification of Electromagnetic Pre-Earthquake Perturbations from the DEMETER Data by Machine Learning. Remote Sensing. 2020; 12(21):3643. https://doi.org/10.3390/rs12213643
Chicago/Turabian StyleXiong, Pan, Cheng Long, Huiyu Zhou, Roberto Battiston, Xuemin Zhang, and Xuhui Shen. 2020. "Identification of Electromagnetic Pre-Earthquake Perturbations from the DEMETER Data by Machine Learning" Remote Sensing 12, no. 21: 3643. https://doi.org/10.3390/rs12213643
APA StyleXiong, P., Long, C., Zhou, H., Battiston, R., Zhang, X., & Shen, X. (2020). Identification of Electromagnetic Pre-Earthquake Perturbations from the DEMETER Data by Machine Learning. Remote Sensing, 12(21), 3643. https://doi.org/10.3390/rs12213643