Abstract
During the past years, unmanned aerial vehicles (UAVs) gained importance as a tool to quickly collect high-resolution imagery as base data for cadastral mapping. However, the fact that UAV-derived geospatial information supports decision-making processes involving people’s land rights ultimately raises questions about data quality and accuracy. In this vein, this paper investigates different flight configurations to give guidance for efficient and reliable UAV data acquisition. Imagery from six study areas across Europe and Africa provide the basis for an integrated quality assessment including three main aspects: (1) the impact of land cover on the number of tie-points as an indication on how well bundle block adjustment can be performed, (2) the impact of the number of ground control points (GCPs) on the final geometric accuracy, and (3) the impact of different flight plans on the extractability of cadastral features. The results suggest that scene context, flight configuration, and GCP setup significantly impact the final data quality and subsequent automatic delineation of visual cadastral boundaries. Moreover, even though the root mean square error of checkpoint residuals as a commonly accepted error measure is within a range of few centimeters in all datasets, this study reveals large discrepancies of the accuracy and the completeness of automatically detected cadastral features for orthophotos generated from different flight plans. With its unique combination of methods and integration of various study sites, the results and recommendations presented in this paper can help land professionals and bottom-up initiatives alike to optimize existing and future UAV data collection workflows.
1. Introduction
Harnessing disruptive technologies is crucial to achieving the Sustainable Development Goals. Amongst others, unmanned aerial vehicles (UAVs) play a significant role in the so-called Fourth Industrial Revolution. They are being referred to as mature technologies for remote delivery, geospatial mapping, and land use detection and management [1]. In the domain of land administration, UAV technology gained in importance as a promising technique that can bridge the gap between time-consuming but accurate field surveys and the fast pace of conventional aerial surveys [2,3]. Various publications tested UAV-based workflows for cadastral applications, covering formal cadastral systems such as in Albania [4] Poland [5], The Netherlands [6], or Switzerland [7] as well as less formal systems in Namibia [8], Kenya [9], or Rwanda [10]. Findings examine vast opportunities, especially with the additional information of textured 3D models and high-resolution orthophotos that ease public participation in boundary delineation [4,8,11]. Benefitting from the advantages of UAV data, various authors utilized approaches in artificial intelligence and developed (semi-) automatic scene understanding procedures to extract cadastral boundaries [12,13,14,15].
The fact that UAV-derived geospatial information can support decision-making processes involving people’s land rights raises questions about the quality of UAV data. In this context, the concept of quality is closely linked to spatial accuracy, which can be defined as absolute (external) or relative (internal) accuracy. According to [16], absolute accuracy refers to the closeness of reported coordinate values to values accepted as or being true. In contrast, relative accuracy describes the similarity of relative positions of features in the scope to their respective relative positions accepted as or being true. Both measures are equally crucial in land administration contexts (c.f. [17]), firstly, the correct representation of image objects such as houses or walls (relative accuracy) as well as the correct position of corner points (absolute accuracy) [16]. Generally speaking, the spatial accuracy depends on configurations of the UAV flight mission such as sensor specifications, UAV itself, mode of georeferencing, flight pattern, flight height, photogrammetric processing, image overlap, but also on external factors such as weather, illumination, or terrain.
During the past decades, remote sensing, as well as computer vision communities alike, studied those impacting parameters emphasizing image matching algorithms, different means of georeferencing, and various flight planning parameters, among others. Finding accurate and reliable image correspondences is the basis for a successful image-based 3D reconstruction. Numerous authors investigated this fundamental part of the photogrammetric pipeline while trying to increase the precision of image correspondences and to optimize computational costs [18,19,20,21]. The quantity of tie-points derived during feature matching mainly depends on the type and the content of the image signal. Deficient success rates negatively impact the spatial accuracy and overall reliability of the 3D reconstruction and ultimately worsen the quality of the digital surface model (DSM) and orthophoto [22].
Next to the aspect of feature matching, georeferencing refers to one of the most practice-relevant yet most discussed topics when utilizing UAV imagery for surveying and mapping applications. More than 60 studies examined various methods of sensor orientation for terrestrial applications, as outlined by [23]. The choice for a georeferencing approach typically represents trade-offs between spatial accuracy and operational efficiency [24]. Even though direct sensor orientation or integrated sensor orientation brings significant time-savings for the data collection operation, planimetric accuracies usually range between 0.5 and 1 m due to the low accuracy and reliability of directly measured attitude and positional parameters by onboard navigational units without a reference station [25,26,27]. Due to inaccurate scale estimation of those insufficient methods, not only the absolute but also the relative accuracy might be not suitable for a particular application. In contrast, the use of real-time kinematic (RTK) or post-processing kinematic (PPK) enabled GNSS devices allows to improve the spatial accuracy to a range of several centimeters [28,29,30,31,32]. However, issues of sensor synchronization, as well as insufficient lever-arm and boresight calibration, remain challenging [29,33], particularly for off-the-shelf UAVs.
In addition to positional or full aerial control, integrated sensor orientation offers the option to include ground observations, known as ground control points (GCPs). This has proven to be beneficial to mitigate systematic lateral and vertical deformations in the resulting data products [34]. Various studies addressed the impact of the survey design of GCPs in terms of quantity and distribution. In their meta-study, [23] did not find a clear relationship between the number of GCPs and the size of the study area, but investigated a weak negative relationship between statistics of the residuals and the number of GCPs collected per hectare. Data from several sources confirm that the distribution of GCPs strongly impacts the spatial accuracy, and an equal distribution is recommended [35,36,37]. However, looking at the results of the optimal number of GCPs, different conclusions are evident. Results from relatively small study sites suggest that the vertical error stabilizes after 5 or 6 GCPs [35,38] and the horizontal error after 5 GCPs [35,36]. In contrast, [39] obtained a low spatial quality with 5 GCP and recommended to use a medium to a high number of GCPs to reconstruct large image blocks accurately. In [40,41] the authors achieved similar results with a concluding recommendation to integrate 15 or 20 GCPs in the image processing workflow, respectively. Aside from GCPs, higher spatial accuracy can be achieved by additionally including oblique imagery [42] or perpendicular flight strips [30]. In most cases, checkpoint residuals were measured in the point cloud or obtained directly after the bundle block adjustment and, thus, do not necessarily represent the displacement of image points in the final data product, as potential offsets during the orthophoto generation were not taken into consideration. However, particularly for the application in cadastral mapping, the correct estimation of the spatial accuracy is of vital importance.
Even though weak dependencies between several impacting factors on the data quality are evident, the results of existing studies are very heterogeneous. Furthermore, most studies remain narrow in focus, dealing mainly with only one study site situated in non-populated areas, and it is questionable whether recommendations can be transferred to the cadastral context. To the best of the authors’ knowledge, existing studies on UAV-based cadastral mapping only highlight the usability of UAVs without assessing different flight configurations or the impact on the final absolute or relative accuracy. To this end, a comprehensive analysis of varying data quality measures should provide a factual basis for clear recommendations that ensure data quality for UAV-based cadastral mapping. Thus, this paper seeks to conclude on best practice guidance for optimal flight configurations by integrating results of a detailed quality assessment including three main aspects: (1) feature matching, (2) ground-truthing, and (3) reconstruction of cadastral features. Whereas the first two approaches target the evaluation of the data quality during and after photogrammetric processing, the latter method focusses on the implications of different orthophoto qualities for the automated extraction of cadastral features. Similar to diverse practices of quality assessment, research data are also manifold and are drawn from six study sites located in Africa and Europe.
In many low- and middle-income countries, conditions for flying, controlling, and referencing respective data are more complex than in Western-oriented countries, a situation which is often underestimated. Primarily spatial and radiometric accuracy can be negatively influenced by poor flight planning and adverse meteorological conditions. Moreover, ground control measurements can be problematic due to a lack of reference stations, the availability of professional surveying equipment, or capacity. In the field of land administration in general and cadastral mapping in particular, incorrect geometries of the orthophoto might cause negative consequences to civil society as the subject deals with a spatial representation of land parcels and attached rights and responsibilities. As an example, erroneous localization and estimations of parcel sizes might imply inadequate tax charges, problems with land compensation funds, or challenges to merge existing databases spatially. With its unique combination of methods and integration of various study sites, it is hoped that the results and recommendations presented in this paper help land administration professionals and bottom-up initiatives alike to optimize existing and future data collection workflows.
The remainder of the paper is structured as follows. Section two provides background information on data collection, data processing, and quality assessment methods. The results section is divided into three separate subsections with (1) findings showing the impact of land use on the number of tie-points, (2) a comprehensive comparison of different ground control setups and its effect on the final absolute accuracy, and (3) an evaluation of qualitative and quantitative characteristics of extracted cadastral features. The discussion critically reflects on the results based on existing literature and outlines best practice guidance for UAV-based data collection workflows in land administration contexts.
2. Materials and Methods
The study setup foresaw three different means of quality assessment targeting at absolute as well as relative accuracy as outlined in the conceptual framework in Figure 1. Well-known methods as the statistical evaluation of checkpoint residuals were combined with quantitative measures of image matching results as well as characteristics of automatically delineated cadastral features. Different clues on the spatial accuracy substantiate the results to provide best practice guidance. Detailed workflows and specifications of the analysis are outlined below.
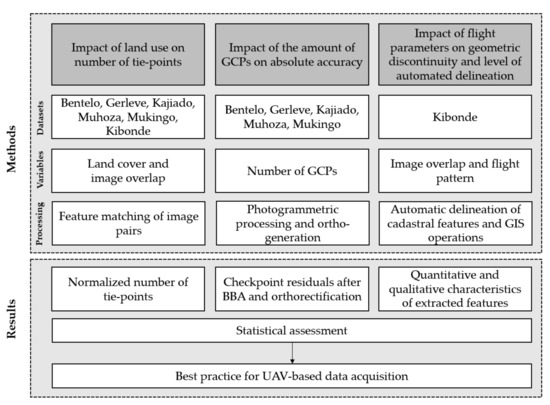
Figure 1.
Conceptual framework.
2.1. UAV and GNSS Data Collection
To test the transferability of the findings and to ultimately claim best-practice recommendations, methods were applied to different datasets collected with diverse UAVs and sensor equipment. This includes, in total, six study areas across Europe (Gerleve, Bentelo) and Africa (Kajiado, Kibonde, Muhoza, Mukingo) ranging from 0.14 to 8.7 km2 (Figure 2). UAV equipment as well as sensor specifications are outlined in Table 1 and included two fixed-wing UAVs (Ebee Plus, DT18), one hybrid UAV (FireFly6), and two rotary-wing UAV (DJI Inspire 2, DJI Phantom 4) equipped with an RGB sensor. Two out of the five UAVs worked with a PPK. Prices for the platforms and sensors range from 1000 to 40,000 €. Flights in Gerleve, Bentelo, Muhoza, Kajiado, and Mukingo were carried out according to a classical flight pattern without cross-flights and an overlap of 80% forward overlap and 70% side lap for all datasets. Additionally, the study in Kibonde foresaw several flights that were repeatedly carried out with varying image overlap (60%, 70%, and 80% side lap) to assess the impact of flight parameters on the characteristics of extracted cadastral features. Following existing literature that proves the benefit of cross flight patterns [16], three perpendicular strips in a different flight height were added to the regular flight and are part of the accuracy evaluation in Kibonde as well.

Figure 2.
Overview of all datasets presented as orthomosaics (a) Bentelo, (b) Gerleve, (c) Mukingo, (d) Kajiado, (e) Kibonde, and (f) Muhoza (scales vary).

Table 1.
Unmanned Aerial Vehicles (UAVs) and technical specifications of the sensor. GSD refers to ground sampling distance.
To allow the inclusion of external reference points into the bundle block adjustment (BBA) as well as for means of independent quality assessment, GCPs were deployed. Due to different contexts and time delays between marking and the data collection flights [17], different shapes and methods to mark control points were used. In Musanze, Mukingo, Bentelo, and Kibonde quadratic plastic tiles with two equally sized black and white squares were fixed with iron pegs. Crosses marked with permanent white paint were used in Kajiado, as the flight missions took several days. For Gerleve, white sprayed Compact Disks were deployed and fixed with survey pins. Three-dimensional coordinates of the central point were determined with survey-grade GNSS devices. As Continuous Operating Reference Stations (CORS) are only available at a few locations in Africa, different modes were used to achieve a measurement accuracy of less than 2 cm. Real-time CORS corrections could be harnessed in Europe, while a base-rover setting over a known survey point and either radio-transmitted real-time corrections or a classical post-processing approach was the preferred surveying operation for the African missions. All GCPs were measured twice, before and after the UAV flight. The average of both measurements was converted from the local geodetic datum to WGS84 or ETRF89. A detailed list of specifications about the GNSS device, number of measured control points, as well as original and target geodetic datums are given in Table 2.

Table 2.
Specifications of GCP measurements.
2.2. Estimating the Impact of Land Cover on the Number of Automatic Tie Points
The establishment of image correspondences is a crucial component of image orientation. In the first step, primitives are extracted and defined by a unique description. Secondly, the descriptors of overlapping pictures are compared, and correspondences determined. With a low number of automatic tie-points, the image orientation is less reliable and negatively impacts the quality of subsequent image matching processes. Different land use classes were defined (cf. Table 3) to evaluate the impact of land cover on the number of automatic tie-points. If a particular land use was present in a dataset, representative image pairs were manually selected and processed as described below.

Table 3.
Land use classes and representation in datasets (Bentelo, Gerleve, Kajiado, Kibonde, Muhoza, Mukingo). Digits indicate the number of image pairs used for the experiment. Percentage, as outlined in the definition, refers to pixel representing specific land cover.
Most commercial photogrammetric software packages do not provide information on their image matching techniques, and respective code might be subject to frequent changes. Instead of using such a black-box software, we chose three state-of-the-art feature matching approaches which were selected, reflecting the variety of blob and corner detectors with binary and string descriptors: SIFT [43], SURF [44], and AKAZE [45]. The open-source photogrammetric software PhotoMatch [46] was utilized to carry out the tests. Before the feature matching process, all images were pre-processed by a contrast-preserving decolorization tool [47], maintaining the full image resolution. The feature matching was conducted with a brute-force method and supported by RANSAC for filtering wrong matches. Thus, image correspondences are searched by comparing each key-point with all key-points in the overlapping image. Settings for feature extraction and description were kept to default values as this analysis is meant to detect relative changes of feature matching rates according to the type of land cover instead of performance evaluation of different approaches. Resulting tie-points (i.e., inlier of key-point matches) were normalized according to the image resolution to reach comparability between various sensor specifications within one land use class. To enable an evaluation of matching quality and variation in different land use classes and feature extraction/matching technique, the number of matches per image pair was normalized with respect to the number of matches within a specific matching algorithm, see equation below for the so-called z-score. Here ATP indicates the normalized number of automatic tie-points per image pair, the mean of all matches of the respective feature extraction approach, and the standard deviation of all matches of the respective matching approach. The z-score provides insights on how many standard deviations below or above the mean the quantity of tie-points in comparison to the other algorithms, within a land use class, is.
To also visualize absolute quantities, the mean value of ATP for all different datasets in the same land use class was calculated. Furthermore, the overlap of image pairs was added as an additional variable. For this analysis, data from Kibonde and Bentelo served as input image pairs as both datasets offered various overlap configurations.
2.3. Estimating the Impact of the Number of GCPs on the Final Geometric Accuracy
All images were processed using Pix4D, keeping the original image resolution. Point clouds were created with an optimal point density, and DSMs as well as the orthomosaics were produced with a resolution of 1 GSD. To allow the comparability of the spatial accuracy of different datasets, uniformly distributed GCPs were included in the processing pipeline according to a standard pattern (Figure 3). Ground markers were identified and linked to at least six images. Depending on the specific number of GCPs (0–10), the remaining points were used as independent checkpoints to estimate the vertical and horizontal accuracy of the final data products.
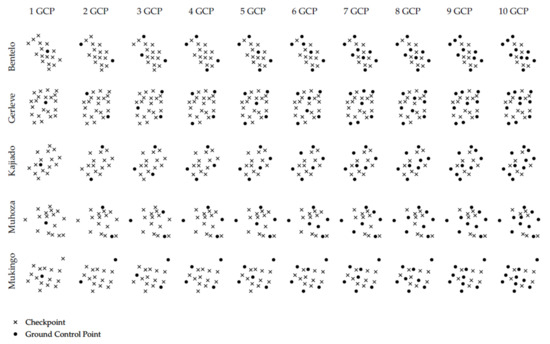
Figure 3.
Distribution of GCPs for experimental assessment of the spatial accuracy.
The spatial accuracy was calculated at two different stages of the photogrammetric processing. Firstly, the geometric error was determined after the BBA, as outlined in the quality report of Pix4D. The horizontal error of a checkpoint was calculated using the Euclidean distance of the residuals in X and Y directions. The residuals of the Z coordinate represented the vertical offset. Secondly, this study also foresaw an accuracy assessment of checkpoint residuals in the final data product as the absolute accuracy of points in the orthophoto is of vital importance for cadastral surveying. This measure reveals information about displacement errors introduced during the orthorectification. The center of checkpoints was visually identified and marked in the orthomosaic using QGIS. Horizontal errors were derived by X and Y residuals, whereas the vertical error was extracted based on the raster value of the DSM. To describe the overall planimetric and vertical error of a particular processing scenario, the root mean square error (RMSE) was calculated following the ISO standard [16]. In this context, the GNSS measurement of the checkpoint coordinate was treated as true value and the extracted coordinates from the orthophoto as the predicted value.
2.4. Estimating the Impact of Different Flight Plans on the Characteristics of Extracted Cadastral Features
In contrast to the other two methods, the third quality evaluation utilizes only data from one regional context. Following basic photogrammetric principles, it is clear that the amount of image overlap significantly impacts the quality of the reconstructed scene. Thus, different flight pattern (with and without cross-flight), as well as multiple image overlap (50% and 75% forward overlap as well as 60%, 70%, and 80% side lap) configurations, were exemplified for the study area Kibonde to ultimately show the impact of various flight configurations on the reconstruction quality of cadastral features and subsequent automatic delineation results. Orthophotos were processed. Subsequently, a quadratic shape of 500 × 500 m was extracted as required by the image segmentation algorithm [48]. To ultimately analyze geometric features and line discontinuities, this paper foresaw a workflow including image segmentation algorithms as well as raster and vector operations, as shown in Figure 4 and Figure 5. The first step was the establishment of reference lines and the creation of a mask to clip all candidate lines subject to this analysis. Reference lines were based on independently captured UAV images (80% forward overlap and side lap, cross-flight at a different altitude) and a resulting orthomosaic with 1.5 cm resolution. Two distinct features, namely building rooftops and concrete walls, were selected as representative visible objects that are important for cadastral applications. Both feature types were manually digitized and served as reference lines for subsequent analyses.

Figure 4.
Workflow to define reference lines and a search mask for lines representing concrete walls and rooftops.
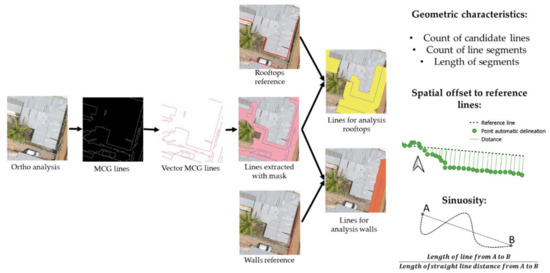
Figure 5.
Workflow to compute and select MCG lines representing rooftops or walls and analytical tools to describe geometric characteristics of selected MCG lines.
A uniform vector mask representing the vicinity of concrete walls and rooftops was created to minimize the number of candidate boundary lines. A slope layer served as the basis to select a 1 m buffer of all raster cells of the DSM representing >75% of the height gradient. Additionally, a vegetation mask was created to remove vegetated areas as those would negatively impact the straightness of selected cadastral features independent of the quality of the orthomosaic and thus would introduce unintended noise to the analysis of geometric discontinuities. The vegetation mask was based on the Gree-Red Difference Index (GRDI). Raster cells above a GRDI of 0.02 were classified as vegetation and polygonized to calculate a buffer of 1 m. Finally, the slope-based mask was clipped with the buffer of the GRDI to exclude vegetation from the samples.
In the second step, multiscale combinatorial grouping (MCG) [49] was applied to all orthophotos to ultimately derive closed contour lines of visible objects, as suggested by [50]. The segmentation threshold was set to k = 0.6 as this has proven to limit over-segmentation while still maintaining relevant cadastral objects in the context of this study. As shown in Figure 5, resulting lines were polygonized and simplified according to [48]. Once the lines were clipped with the reference mask, several geometric and spatial characteristics were queried (c.f. Figure 5). Candidate lines were selected by overlaying the MCG lines with a 0.5 m buffer of reference lines. From those candidate lines, actual lines representing rooftops and walls were chosen manually. To calculate the correspondence as well as the spatial difference to reference lines, the MCG lines representing walls and rooftops were split to segments of 10 cm and subsequently converted to points. Afterwards the distance from each point in the MCG line to the closest point of the reference line was calculated to derive statistical values for the spatial offset. To describe the amount of MCG lines that could automatically be extracted (i.e., correspondence with reference lines), a neighborhood analysis was carried out to estimate the percentage of reference lines that could be reproduced by the MCG algorithm. As a last characteristic, this study calculated the sinuosity as a measure of the straightness of MCG lines to reflect on inconsistencies of critical features in the orthomosaics. Similar to the spatial offset, the sinuosity was calculated based on summed length of the MCG lines for one object in relation to the length of a virtual straight line (Figure 5).
3. Results
3.1. Image Matching: Image Correspondences
The number of pairwise image correspondences was derived from comparing feature matching success rates representing certain land use classes prevalent in the images. The diagram in Figure 6 depicts standardized z-scores as well as mean values of automatic tie-points for SIFT, SURF, and AKAZE. At first glance, the results of various matching algorithms demonstrate a similar distribution, whereas apparent differences between land use classes are evident.
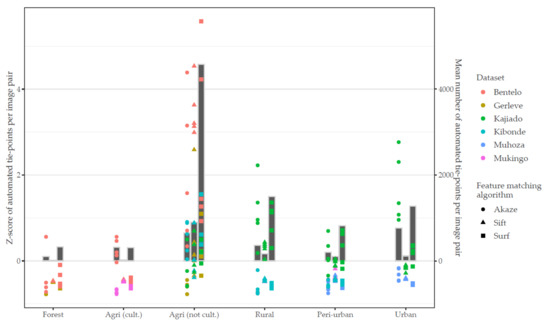
Figure 6.
Standardized values of automatic tie-points using SIFT, AKAZE, and SURF as feature extraction, detection, and matching algorithm. The mean number of automatic tie-points per algorithm and land use class is reflected as bars. The x-axis represents land use classes as defined in Table 3.
Image pairs characterized by forest and cultivated agricultural fields show significantly low numbers of automatic tie-points. In some cases, no matches could be found. Images, displaying non-cultivated agricultural field plots stick out by a broad range of images correspondences for all three feature matching approaches. Here, the dataset Bentelo reaches the highest z-scores and results are multiple standard deviations above the mean. However, also insufficient numbers of automatic tie-points are evident in this land use class, particularly for Gerleve. This can be ascribed to poor illumination conditions and little contrast in the images. The remaining datasets are clustered in a range between −0.5 and 1.5 of the z-score.
For image scenes showing human-made structures, two different trends are visible. The first trend describes the following correlation: on average Kibonde, Muhoza, and Mukingo indicate more key-point matches if less vegetation and more structures are prevalent. Thus, for Kibonde and Mukingo, a higher z-score was achieved with the peri-urban scene context compared to the rural context. The same applies to Muhoza with the land uses peri-urban and urban, respectively. In contrast, Kajiado does not follow this trend and represents the dataset with the highest z-scores for all three land use classes (rural, peri-urban, urban). The same applies for all three image matching algorithms. A possible explanation for this may be the climate zone. As indicated above, high vegetation presents an adverse condition for finding tie-points. In contrast to the humid climate in Kibonde, Mukingo, and Muhoza, Kajiado is located in a semiarid region characterized by a sparse shrub and bush vegetation. Thus, the impact of vegetation is almost not visible and rural as well as urban scenes achieve similar z-scores. Secondly, next to the climate zone, also the GSD might have an impact on the above-average z-score of Kajiado for the rural, peri-urban, and urban land use class.
Looking at the impact of image overlap on the automatic tie-points in Table 4, it becomes clear that the poor feature matching results of forest can only be overcome with 90% image overlap while the other land use classes already show sufficient matches with less overlap. Similar to Figure 6, non-cultivated agricultural areas present the highest rate of image correspondences for all image overlap scenarios. Two adverse conditions could explain the low rate of automatic tie-points in the forest. Firstly, although the flight is configured with a high image overlap, the difference in the viewing angle is larger between image points showing the crown of the tree than for image objects on the ground. Thus, we observe that key-points show insufficient similarity to be determined as image correspondence. This challenge can only be overcome by 80–90% image overlap. However, at the same time, the descriptors of leaves could also be too similar, leading to ambiguities during the feature matching process. Both effects are visible and could explain the comparatively low number of automatic tie-points for all four image overlap configurations. In addition, and more or less independently from that, high vegetation cannot be regarded “static”, which is, however, an indispensable requirement for mono-camera bundle adjustment. It should be emphasized that those results were derived with single image pairs. It is expected that a priori location and alignment information of images in an image block ease the feature matching process compared to the brute-force approach used in this analysis.

Table 4.
Mean of automatic tie-points of image pairs using SURF showing different land use classes and overlap.
3.2. Absolute Accuracy: Checkpoint Residuals in DSM and Orthophotos
The absolute accuracy was determined after the bundle block adjustment as well as after the orthophoto generation. Figure 7 presents the RMSE of horizontal and vertical checkpoint residuals of all datasets. Looking at the results, it is evident that, in general, all datasets show a similar pattern. For photogrammetric processing with less than 5 GCPs, resulting RMSE of the datasets differ widely, whereas, for results with more than 5 GCPs, the final RMSE seems to stabilize at a certain level.
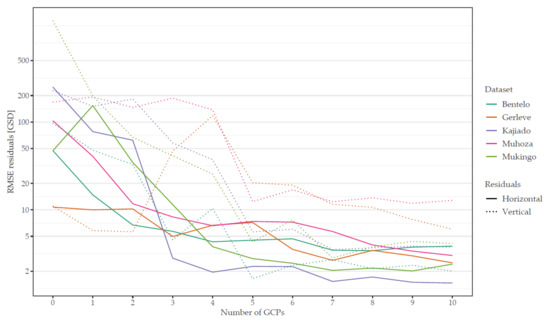
Figure 7.
RMSE of checkpoint residuals measured in the DSM (vertical) and orthophoto (horizontal).
Looking at the horizontal RMSE, the large variance of the datasets for processing scenarios from 0 to 5 GCPs can be explained by the different quality of positional sensors. If no ground truth is included (0 GCPs), the BBA solely uses image geotags to estimate the absolute position of the reconstructed scene. Here, Gerleve was the only dataset with a professional PPK enabled GNSS device and attained the lowest RMSE (10 GSD) for all datasets processed with 0 GCP. In contrast, Kajiado was flown with a consumer-grade UAV showing a large horizontal offset of more than 200 GSD. Bentelo, Mukingo, and Muhoza achieve an RMSE between 50 and 100 GSD without GCPs, which is considered a typical error range of GNSS positioning without enhancement methods. Except for the dataset Mukingo, the RMSE drops significantly with including 1 GCP which corrects systematic lateral shifts. For the scenario with 3 GCP, all datasets achieve a horizontal RMSE between 10 and 20 cm. Gerleve and Bentelo reach an RMSE of less than 10 cm after 6 GCPs and are followed by Kajiado and Muhoza after 7 GCPs. Subsequently, almost all datasets keep the same level alternating within a range of 1 GSD. In this aspect, Mukingo achieves the most accurate results with less than 5 cm RMSE after 5 GCPs. Muhoza is the only dataset which nearly improves its RMSE for each scenario that adds one more GCP.
Looking at the vertical residuals, Figure 7 suggests a higher dynamic compared to horizontal residuals. In general, residuals are larger than the values of the horizontal RMSE and start to level only after 7 GCPs. With a height offset of more than 1000 GSD, which corresponds to approximately 30 m, the dataset Mukingo shows the maximum value without including GCPs. This can be attributed to a general definition problem of the height model used by DJI and can be corrected by adding at least 1 GCP. Similar to the horizontal residuals, Gerleve achieves the highest accuracy with an RMSE of only 10 GSD. However, after 2 GCPs, the height residuals abruptly increase before decreasing again after 4 GCP, indicating that this dataset requires a checkpoint in the center of the scene to correct severe height deformations. At 5 GCPs, all datasets demonstrate a significant improvement of the vertical RMSE. Independent from the size of the area, five evenly distributed GCPs can be considered as the minimum number of GCPs which efficiently fixes cushion and dome deformations during scene reconstruction. After 7 GCPs the vertical residuals of Bentelo, Kajiado, and Mukingo stabilize within the range of 1 GSD whereas Muhoza and Gerleve continue to lower its RMSE.
Additional to the absolute accuracy, the difference of the RMSE after BBA to the RMSE after DSM and orthophoto generation are shown in Table 5. The presented values reveal insights about the share of the overall error, which accumulates after the BBA during the 3D-reconstruction and ortho-generation process, independent of horizontal or vertical displacement indicated during the BBA. Negative values suggest that the RMSE after the BBA is higher than the RMSE of the residuals taken from the DSM/orthophoto. On average, variations between the error measures remain very low (below 1 GSD) and do not show a clear trend of an overestimation of one or the other, as well as no relation to the number of GCPs. However, for Gerleve and Muhoza, horizontal residuals range up to 3 GSD, and for vertical residuals we observe differences up to 5 GSD in two cases. For both datasets, significantly higher differences in the RMSE of checkpoint residuals could be explained by the challenging conditions for the 3D-reconstruction and orthophoto-generation processes. For Muhoza, difficulties could arise from considerable height (i.e., land surface) dynamics of the densely populated urbanized center. Gerleve stands out for its poor illumination conditions and subsequent problems to reliably reconstruct the image scenes.

Table 5.
Differences of RMSE of checkpoint residuals measured after the BBA and in the orthophoto/DSM. Values are normalized, according to GSD. Horizontal (h) and vertical (v) errors are treated separately. Differences >1 GSD are indicated bold.
3.3. Relative Accuracy: Characteristics of Automatically Extracted Cadastral Features
Various line geometry measures present the quality of the scene reconstruction and subsequent feature extraction. For the chosen quadratic scene in the center of the Kibonde dataset, houses are predominantly covered by corrugated iron roofs and parcels are usually separated by concrete walls or bushes. To minimize external noise to our statistical assessment, only walls and rooftops without the interference of vegetation were delineated as reference (Figure 8). This adds up to a total of 692.3 m of lines referring to rooftops and 196.4 m of lines representing walls. As presented in Table 6, this relation is also expressed by candidate lines counted in a 0.5 m buffer of all reference lines. Interestingly, the impact of the flight pattern (cross-flight or no cross-flight) is more evident for rooftops than for walls, shown by the difference of line counts for different flight pattern scenarios. Concerning reference walls, marginally (within 10% range) fewer candidate lines were selected compared to the same scenario without a cross-flight pattern. In contrast, for rooftops, differences range from 10% to 40%.
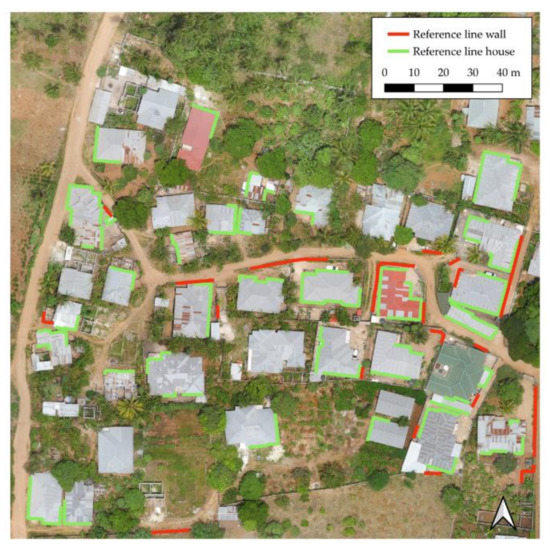
Figure 8.
Selected reference lines representing rooftops (green) and walls (red) for the area of interest in Kibonde.

Table 6.
Qualitative and quantitative characteristics of line geometries representing rooftops (R) and walls (W) separated according to flight configuration (forward overlap (f), side lap (s)) and flight pattern (CF = cross flight pattern, no CF = no cross-flight pattern). Minimum and maximum values are presented in bold.
Looking at the count of selected line segments, a more homogenous picture can be drawn. In all cases, the line count for the cross-flight pattern is lower than for the same image overlap scenario without a cross-flight. The mean length of line segments shows no significant difference between walls and rooftops. However, an important observation can be made concerning the image overlap. On average, line segments are shorter for scenarios with only 50% forward overlap compared to flight plans with 75% overlap. The combination of a higher count of line segments and a smaller average line length proves a higher fragmentation of boundary features for orthophotos without a cross flight pattern, as well as for lower image overlap scenarios. This result becomes even more apparent concerning the correlation of selected MCG lines with the reference dataset. Here, the improvement of the correlation with reference lines is more significant for walls than for rooftops. In this aspect, walls demonstrate a range between 71.5% and 93% and steadily increase with higher image overlap (both, forward and side lap). This means, the MCG algorithm applied to the orthophoto generated with a poor flight plan, produces contours for only 71.5% of the walls. In contrast, an orthophoto based on a favorable flight plan achieves an object detection rate of 93%. Hence, the detection range of contour lines for rooftops is comparatively small with maximal 2.9% variance between different flight plan scenarios.
A similar observation is evident for the sinuosity. Here, rooftops do not differ much, and lines of rooftops are on average 1.5 times longer than a perfectly straight line from the start to the endpoint. MCG lines representing walls are on average more curved and show a clear trend concerning the flight parameters reaching a minimal curviness with a cross flight pattern and 75% forward overlap and 80% side lap. Particularly for lines representing rooftops, it should be noted that the sinuosity values are relatively high due to the origin of the MCG lines, which were created based on a raster dataset and consequently still show undulations at the pixel level.
Aside from line feature characteristics, the spatial correlation was also investigated in terms of distance measurements of MCG lines to reference lines. Figure 9 visualizes the results and exemplifies the spatial correlation with a small sample of the entire dataset. Rooftops are mainly delineated close to the reference line, whereas walls show considerable variability. As an example, we included the orthophoto generated with the poorest image overlap at the bottom of Figure 9. The visual interpretation reveals a significant deformation and poor orthorectification of the wall, which ultimately leads to the displacement of MCG lines for the dataset with 50%/60% overlap and without a cross-flight.

Figure 9.
Example showing the differences of automatically extracted rooftops and walls separated according to flight configuration (forward overlap (%), side lap (%)) and flight pattern (CF = cross flight, noCF = no cross flight).
This variability is also apparent in the statistics of the point-to-line distances, presented as box-whisker plots in Figure 10. The interquartile range of rooftops is significantly smaller than the one of the walls. It should be noted that the distances of reference walls are subject to a systematic offset of 15 cm as the reference line was placed in the center of the wall, whereas the MCG algorithm produced lines on the right or left edge.
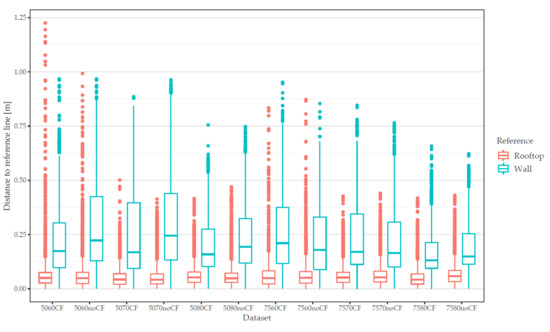
Figure 10.
Box-whisker plot of point distances to reference lines separated according to the reference wall and rooftop. Box represents the interquartile range (IQR) with the median; whisker represent 1.5 IQR, points represent outliers. x-axes label refers to flight parameter, e.g., 5060CF means 50% forward overlap, 60% side lap and cross-flight (CF) pattern. Distances reflect the length of perpendicular lines from points to reference lines. Points were created every 10 cm from a line geometry that was derived by feature extraction with the MCG algorithm.
For two flight scenarios with low overlap, outliers of point distances of rooftops exceed the outliers of walls. In general, the share of outliers is higher for rooftops than for walls indicating that almost all rooftops are delineated in a range of approximately 20 cm with a few extreme variations. For wall features, the statistical analysis confirms the observations from the line characteristics, showing that the overall quality of delineated walls differs highly with respect to the image overlap and flight plan settings. Best results represented by the lowest five-number values of the box-whisker plot were returned for flight scenarios with 75% forward overlap, 80% side lap, and a cross flight pattern.
As evident in Figure 11, the RMSE of horizontal checkpoint residuals of the orthophoto stays between 0.8 and 1.5 GSD for all flight configurations, which corresponds to 2.5–4 cm. Similar to Figure 9, the statistics of the offset of detected line features show a noticeable discrepancy between rooftops (<10 cm) and walls (20–40 cm).
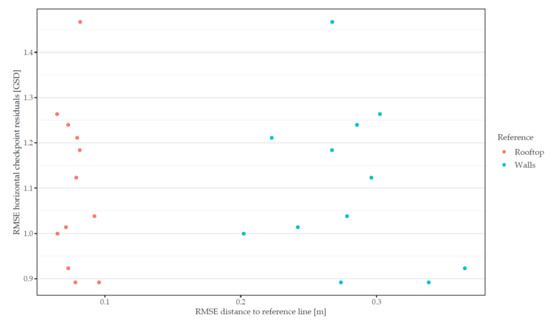
Figure 11.
Scatterplot of error metrics for delineated rooftops and walls of orthophotos captured with different flight configurations. Absolute accuracy of the orthophoto is given on the y-axis with the RMSE of horizontal checkpoint residuals. Relative accuracy is shown on the x-axis displayed by the RMSE of point distances to reference lines. Note that both axes have different scales.
In contrast to checkpoint residuals of the orthophoto, which do not show a correlation with the error metrics, Figure 12 reveals that the flight pattern has implications on the relative accuracy of extracted features. Walls directed perpendicular to the flight direction show almost the same statistics for both scenarios, with a cross-flight or without a cross-flight pattern. However, for walls parallel to the flight direction, a cross-flight pattern improves the results indicated by a lower median and a smaller IQR. This result could be attributed to the fact that geometries of features parallel to epipolar lines imply more challenges to correctly estimate the 3D position and subsequent image matching and ortho-generation.
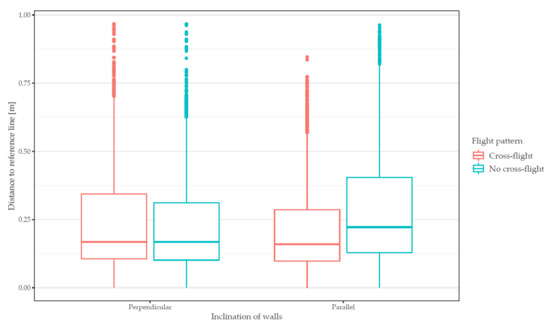
Figure 12.
Box-whisker plot of distances to reference lines separated according to the direction of walls (parallel or perpendicular to the flight direction). Box represents the interquartile range (IQR) with the median; whisker represent 1.5 IQR, points represent outliers.
4. Discussion
Even though UAV can collect images with a resolution of a few centimeters, results in this paper show that the absolute and relative accuracy can differ from some centimeters up to several meters depending on the chosen flight configuration. To exploit the full potential of UAV-based workflows for land administration tasks, careful decisions on efficient mission planning are essential. This holds true for both sides: collecting as many images and GCPs as needed to meet the expected survey accuracy, but also for collecting just as many images and GCPs as necessary to minimize computational costs in favor of time constraints or potential hardware limitations.
Several reports have shown that the quantity of automatic tie-points impacts the quality of the photogrammetric 3D reconstruction as image correspondences are fundamental for the correct estimation of image orientation parameters. Even though different sensors, UAV, scenes, and flight conditions were analyzed in this paper, a homogenous picture can be drawn when looking at generated tie-points in relation to land use classes. In image scenes showing trees or crops significantly lower rates of tie-points could be extracted compared to scenes with human-made structures or grassland. In the former case, only a high image overlap of at least 80–90% is sufficient to achieve an adequate number of image correspondences. These results match those reported in [51]. In tropical or subtropical regions, most rural and peri-urban scenes are also characterized by vegetated areas subject to subsistence farming side-by-side to residential buildings. Thus, an optimal flight mission might need to be configured with higher image overlap compared to a flight mission in arid or semiarid regions.
Although a clear correlation of generated tie-points and land use can be shown, the results suggest that the optimal number of GCPs seems to be independent of the climate zone or land cover, as all datasets in this analysis reveal a similar pattern and indicate no significant changes of the RMSE after seven equally distributed GCPs. This result reflects those of [36,38,40] who also observed no significant differences in the final vertical or horizontal RMSE after 5 or 6 GCPs, respectively. In contrast to earlier findings [39], no evidence of the impact of the GCPs density was detected. In terms of GSD and despite considerably different extents of the study areas, all datasets in this analysis reach a similar error level with 10 GCPs, 2–3 GSD for the horizontal accuracy, and 2–4 GSD for the vertical accuracy. Thus, the number and distribution of GCPs might play a more critical role than the density of GCPs. This is particularly interesting for the mission planning and calculation of costs as placing, marking, and measuring of GCPs is one of the most time-consuming and consequently, most costly aspects of the entire UAV-based data collection campaign. In the case of Mukingo, we observed a substantial offset of the vertical error in the scenario without GCPs. This magnitude of height offset was already reported before [35] and seemed to be specific to DJI UAV.
Contrary to most other studies that investigate checkpoint residuals, this analysis presents the absolute accuracy with regard to the residuals after the BBA and in the final DSM and orthophoto. For two out of six datasets, our results show significant discrepancies between the checkpoint residuals with a magnitude of up to 5 GSD. In both cases, challenging conditions were present, i.e., poor illumination conditions for Gerleve and a densely populated built-up area in Muhoza. We observe that particular the height component could be strongly impacted. Consequently, the consideration of checkpoint residuals measured in the orthophoto is indispensable for the evaluation of the final accuracy, as additional offsets might be introduced during the 3D reconstruction and orthophoto-generation process.
As a third central aspect, this study reveals yet another perspective on the orthophoto quality: success rates of the automatic extraction of cadastral features. Here, our findings point on a clear difference between the delineation of rooftops and walls. Whereas various flight configurations showed less impact on the extractability of rooftops, the automatic extraction of walls achieves more accurate and complete lines with large image overlaps and a cross-flight pattern. Even though the absolute difference of the correlation seems minor in our example, values of either 70% correlation or 93% correlation with reference lines are significant for scaled applications. A smaller percentage would entail a lot more manual work of delineating respective walls that were not represented by MCG lines. Furthermore, the MCG algorithm applied on an orthophoto of a weak image block—as described by lower image overlap—produces shorter line segments which also implies more manual effort to receive a complete delineation finally. Thus, thoughts should also be given to characteristics of extractable features when designing a UAV flight mission. Our findings suggest that planar cadastral features are less sensitive to differences in flight configurations than thin image objects such as walls or fences. Consequently, the latter necessitates a higher percentage of image overlap to be reliably reconstructed and detectable during subsequent automatic delineation processing. Additionally, when thin cadastral objects are oriented towards different cardinal directions, a cross-flight pattern is clearly recommendable.
In combination, the results are significant in at least two aspects. Firstly, although this study investigated very different study sites, common trends are evident. Thus, some general recommendations can be drawn. Independent of the sensor or feature matching algorithm, vegetated spaces, and forests or cultivated agricultural areas, still present challenges to the establishment of image correspondences. However, findings of checkpoint residuals suggest that the impact on the overall accuracy is only marginal when looking at scenes with multiple land use classes.
Secondly, the research investigations reveal large discrepancies between the spatial accuracy and the completeness of automatically detected cadastral features, even though the RMSE of the orthophoto as commonly accepted error measure is low. According to these data, we can infer that the flight configurations play a crucial role in achieving high data quality, particularly for cadastral features characterized by height differences and thin shape as exemplified for concrete walls. Moreover, in most cases, checkpoints are put out in open and visible spaces which do not necessarily reflect objects subject to manual or automatic cadastral delineation. Consequently, it should be emphasized that context-driven error analysis is essential to assess the overall accuracy of UAV-based data products.
Finally, a multifactorial analysis, as presented in this paper includes shortcomings on various ends. The study design foresaw various UAV and sensor configurations to mimic a variety of different contexts and real-world applications, focusing on the quality of final data products. Despite various camera specifications, common trends and characteristics are evident throughout all datasets. However, as a limitation of this study, the impact of hardware differences on the final data quality could not be estimated. Next to this, it cannot be ruled out that the GSD affects the quantity of generated tie-points. Further investigations are needed to evaluate this nexus. Lastly, it should be emphasized that all datasets were collected following flight plans as specified in the methods of this paper and the transferability of our findings to other flight configurations or other contexts cannot be guaranteed.
5. Conclusions
This paper provides recommendations on optimal UAV data collection workflows for cadastral mapping based on a comprehensive analysis of data quality measures applied to numerous orthophotos generated from various flight configurations. Methods covered several aspects ranging from statistics of automatic tie-points and an evaluation of the geometric accuracy to characteristics of automatically delineated cadastral features. The results highlight that scene context, flight configuration, and GCP setup significantly impact the final data quality of resulting orthophotos and subsequent automatic extraction of relevant cadastral features.
In a nutshell, the following recommendations can be drawn:
- Land use has a significant impact on the generation of tie-points. Image scenes characterized by a high percentage of vegetated areas and especially trees or forest require image overlap settings of at least 80–90% to establish sufficient image correspondences.
- Independent of the size of the study area, the error level of planimetric and vertical residuals remains steady after seven equally distributed GCPs (according to the scheme presented in Figure 3), given at least 70% forward overlap and 70% side lap. As the absolute accuracy does not increase significantly with adding more GCPs, 7 GCPs can be recommended as optimal survey design.
- The quality of reconstructed thin cadastral objects, as exemplified for concrete walls, is highly variable to the flight configuration. A large image overlap, as well as a cross-flight pattern, has proven to enhance the reliability of the generated orthophoto as quantified by the increased accuracy and completeness of automatically delineated walls. In contrast, the delineation results of rooftops showed less sensitivity to the flight configuration.
- Even though checkpoint residuals indicate high absolute accuracy of an orthophoto, the reliability of reconstructed scene objects could vary, particularly in adverse conditions with large variations in the height component. We furthermore recommend measuring checkpoint residuals in the generated orthophoto in addition to after the BBA.
Generally, these findings have important implications for developing UAV-based workflows for land administration tasks. This fact that the data quality can significantly change depending on the flight configurations involves risks and opportunities. The risk is that UAVs are used as off the shelf products with little knowledge of photogrammetric principles and options to customize flight configurations. Consequently, even though the end-product appears to be of good quality, spatial offsets, deformations, or poor reconstruction results of relevant features might be present but remain undetected. However, at the same time, we also realize immense opportunities in the customization of UAV workflows. The results in this analysis show that different flight configurations and various ground-truthing measures offer a wide range of options to tailor the data collection task to financial, personnel, and time capacities and optimally align it to customer needs and requirements in the land sector. This equips UAV workflows as a viable and sustainable tool to deliver reliable and cost-efficient information to cope with current and future cadastral challenges.
Future research building upon our results could follow different pathways. Firstly, although our study foresaw six different contexts, the terrain was mostly flat or slightly undulated and showed only minor surface variations. It would be interesting to explore if data of hilly and larger study areas could substantiate our recommendations. Secondly, this study neglects the ground sampling distance as a variable in our assessment. It is expected that next to the orthophoto quality also variations in the resolution might impact the feature matching process as well as completeness and accuracy of automatically extracted line geometries. Clues on this correlation could expand best-practice examples by adding recommendations on camera specifications and flight heights.
Author Contributions
Conceptualization, C.S., F.N., M.G., M.K.; Methodology, C.S., F.N., M.G.; Data Curation, C.S.; Writing—Original Draft Preparation, C.S.; Writing—Review and Editing, C.S., F.N., M.G., M.K.; Visualization, C.S.; Supervision, F.N., M.K.; Project Administration, M.K. All authors have read and agreed to the published version of the manuscript.
Funding
The research described in this paper was funded by the research project “its4land”, which is part of the Horizon 2020 program of the European Union, project number 687828.
Acknowledgments
We acknowledge the support of all its4land project partners and local stakeholders in facilitating the UAV flight missions in Europe and Africa.
Conflicts of Interest
The authors declare no conflict of interest.
References
- World Economic Forum. Unlocking Technology for the Global Goals; World Economic Forum: Geneva, Switzerland, 2020. [Google Scholar]
- Jazayeri, I.; Rajabifard, A.; Kalantari, M. A geometric and semantic evaluation of 3D data sourcing methods for land and property information. Land Use Policy 2014, 36, 219–230. [Google Scholar] [CrossRef]
- Shakhatreh, H.; Sawalmeh, A.H.; Al-Fuqaha, A.; Dou, Z.; Almaita, E.; Khalil, I.; Othman, N.S.; Khreishah, A.; Guizani, M. Unmanned Aerial Vehicles (UAVs): A Survey on civil applications and key research challenges. IEEE Access 2019, 7, 48572–48634. [Google Scholar] [CrossRef]
- Barnes, G.; Volkmann, W. High-resolution mapping with unmanned aerial systems. Surv. L. Inf. Sci. 2015, 74, 5–13. [Google Scholar]
- Kurczynski, Z.; Bakuła, K.; Karabin, M.; Markiewicz, J.S.; Ostrowski, W.; Podlasiak, P.; Zawieska, D. The possibility of using images obtained from the uas in cadastral works. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci.-ISPRS Arch. 2016, 41, 909–915. [Google Scholar] [CrossRef]
- Rijsdijk, M.; Van Hinsbergh, W.H.M.; Witteveen, W.; Buuren, G.H.M.; Schakelaar, G.A.; Poppinga, G.; Van Persie, M.; Ladiges, R. Unmanned aerial systems in the process of juridical verification of cadastral border. Int. Arch. Photogramm. Remote Sens. 2013, 40, 4–6. [Google Scholar] [CrossRef]
- Manyoky, M.; Theiler, P.; Steudler, D.; Eisenbeiss, H. Unmanned aerial vehicle in cadastral applications. ISPRS-Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, 38, 57–62. [Google Scholar] [CrossRef]
- Mumbone, M.; Bennett, R.M.; Gerke, M.; Volkmann, W. Innovations in boundary mapping: Namibia, customary lands and UAVs. In Proceedings of the Land and Poverty Conference 2015: Linking Land Tenure and Use for Shared Prosperity, Washington, DC, USA, 23–27 March 2015. [Google Scholar]
- Koeva, M.; Stöcker, C.; Crommelinck, S.; Ho, S.; Chipofya, M.; Sahib, J.; Bennett, R.; Zevenbergen, J.; Vosselman, G.; Lemmen, C.; et al. Innovative remote sensing methodologies for Kenyan land tenure mapping. Remote Sens. 2020, 12, 273. [Google Scholar] [CrossRef]
- Koeva, M.; Muneza, M.; Gevaert, C.; Gerke, M.; Nex, F. Using UAVs for map creation and updating. A case study in Rwanda. Surv. Rev. 2016, 50, 1–14. [Google Scholar] [CrossRef]
- Ramadhani, S.A.; Bennett, R.M.; Nex, F.C. Exploring UAV in Indonesian cadastral boundary data acquisition. Earth Sci. Informatics 2018, 11, 129–146. [Google Scholar] [CrossRef]
- Crommelinck, S.; Koeva, M.N.; Yang, M.Y.; Vosselman, G. Interactive cadastral boundary delineation from UAV data. In Proceedings of the ISPRS Annals of Photogrammetry, Remote Sensing and Spatial Information Sciences, Riva del Garda, Italy, 4–7 June 2018; Volume 4, pp. 4–7. [Google Scholar]
- Yu, X.; Zhang, Y. Sense and avoid technologies with applications to unmanned aircraft systems: Review and prospects. Prog. Aerosp. Sci. 2015, 74, 152–166. [Google Scholar] [CrossRef]
- Fetai, B.; Oštir, K.; Fras, M.K.; Lisec, A. Extraction of visible boundaries for cadastral mapping based on UAV imagery. Remote Sens. 2019, 11, 1510. [Google Scholar] [CrossRef]
- Xia, X.; Persello, C.; Koeva, M. Deep fully convolutional networks for cadastral boundary detection from UAV images. Remote Sens. 2019, 11, 1725. [Google Scholar] [CrossRef]
- International Standardization Organization (ISO). ISO 19157: 2013 Geographic Information-Data Quality; European Committee for Standardization: Brussels, Belgium, 2013. [Google Scholar]
- Grant, D.; Enemark, S.; Zevenbergen, J.; Mitchell, D.; McCamley, G. The Cadastral triangular model. Land Use Policy 2020, 97, 104758. [Google Scholar] [CrossRef]
- Förstner, W.; Gülch, E. A Fast Operator for Detection and Precise Location of Distinct Points, Corners and Centres of Circular Features. In Proceedings of the ISPRS Intercommission Conference on Fast Processing of Photogrammetric Data, Interlaken, Switzerland, 2–4 June 1987; pp. 281–305. [Google Scholar]
- Lowe, G. SIFT—The Scale Invariant Feature Transform. Int. J. 2004, 2, 91–110. [Google Scholar]
- Snavely, N.; Seitz, S.M.; Szeliski, R. Photo tourism: Exploring image collections in 3D. Proc. SIGGRAPH 2006 2006, 1, 835–846. [Google Scholar]
- Remondino, F.; Spera, M.G.; Nocerino, E.; Menna, F.; Nex, F. State of the art in high density image matching. Photogramm. Rec. 2014, 29, 144–166. [Google Scholar] [CrossRef]
- Gruen, A. Development and status of image matching in photogrammetry. Photogramm. Rec. 2012, 27, 36–57. [Google Scholar] [CrossRef]
- Singh, K.K.; Frazier, A.E. A meta-analysis and review of unmanned aircraft system (UAS) imagery for terrestrial applications. Int. J. Remote Sens. 2018, 39, 5078–5098. [Google Scholar] [CrossRef]
- Rehak, M.; Skaloud, J. Applicability of new approaches of sensor orientation to micro aerial vehicles. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 3, 441–447. [Google Scholar] [CrossRef]
- Pfeifer, N.; Glira, P.; Briese, C. Direct georeferencing with on board navigation components of light weight UAV platforms. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci.-ISPRS Arch. 2012, 39, 487–492. [Google Scholar] [CrossRef]
- Turner, D.; Lucieer, A.; Wallace, L. Direct georeferencing of ultrahigh-resolution UAV imagery. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2738–2745. [Google Scholar] [CrossRef]
- Haala, N.; Cramer, M.; Weimer, F.; Trittler, M. Performance test on UAV-based photogrammetric data collection. ISPRS-Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, 38, 7–12. [Google Scholar] [CrossRef]
- Eling, C.; Klingbeil, L.; Kuhlmann, H. Development of an RTK-GPS System for Precise Real-time Positioning of Lightweight UAVs. In Ingenieurvermessung 14, Proceedings of the 17. Ingenieurvermessungskurs, Zürich, Switzerland, 14–17 January 2014; Wieser, A., Ed.; S. Wichmann Verlag: Berlin, Germang, 2014; pp. 111–123. [Google Scholar]
- Stöcker, C.; Nex, F.; Koeva, M.; Gerke, M. Quality assessment of combined IMU/GNSS data for direct georeferencing in the context of UAV-based mapping. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences—ISPRS Archives, Colone, Germany, 4–7 September 2017; Volume 42. [Google Scholar]
- Gerke, M.; Przybilla, H.J. Accuracy analysis of photogrammetric UAV image blocks: Influence of onboard RTK-GNSS and cross flight patterns. Photogramm.-Fernerkundung-Geoinf. 2016, 2016, 17–30. [Google Scholar] [CrossRef]
- Hugenholtz, C.; Brown, O.; Walker, J.; Barchyn, T.; Nesbit, P.; Kucharczyk, M.; Myshak, S. Spatial accuracy of UAV-derived orthoimagery and topography: Comparing photogrammetric models processed with direct georeferencing and ground control points. Geomatica 2016, 70, 21–30. [Google Scholar] [CrossRef]
- Forlani, G.; Dall’Asta, E.; Diotri, F.; di Cella, U.M.; Roncella, R.; Santise, M. Quality assessment of DSMs produced from UAV flights georeferenced with onboard RTK positioning. Remote Sens. 2018, 10, 311. [Google Scholar] [CrossRef]
- Ekaso, D.; Nex, F.; Kerle, N. Accuracy assessment of real-time kinematics (RTK) measurements on unmanned aerial vehicles (UAV) for direct georeferencing. Geo-Spatial Inf. Sci. 2020, 23, 165–181. [Google Scholar] [CrossRef]
- James, M.R.; Robson, S.; Centre, L.E.; Engineering, G. Mitigating systematic error in topographic models derived from UAV and ground-based image networks. Earth Surf. Process. Landf. 2014, 1420, 1413–1420. [Google Scholar] [CrossRef]
- Manfreda, S.; Dvorak, P.; Mullerova, J.; Herban, S.; Vuono, P.; Arranz Justel, J.; Perks, M. Assessing the accuracy of digital surface models derived from optical imagery acquired with unmanned aerial systems. Drones 2019, 3, 15. [Google Scholar] [CrossRef]
- Mesas-Carrascosa, F.J.; Torres-Sánchez, J.; Clavero-Rumbao, I.; García-Ferrer, A.; Peña, J.M.; Borra-Serrano, I.; López-Granados, F. Assessing optimal flight parameters for generating accurate multispectral orthomosaicks by uav to support site-specific crop management. Remote Sens. 2015, 7, 12793–12814. [Google Scholar] [CrossRef]
- Villanueva, J.K.S.; Blanco, A.C. Optimization of ground control point (GCP) configuration for unmanned aerial vehicle (UAV) survey using structure from motion (SFM). Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci.-ISPRS Arch. 2019, 42, 167–174. [Google Scholar] [CrossRef]
- Tonkin, T.N.; Midgley, N.G. Ground-control networks for image based surface reconstruction: An investigation of optimum survey designs using UAV derived imagery and structure-from-motion photogrammetry. Remote Sens. 2016, 8, 786. [Google Scholar] [CrossRef]
- Sanz-Ablanedo, E.; Chandler, J.H.; Rodríguez-Pérez, J.R.; Ordóñez, C. Accuracy of Unmanned Aerial Vehicle (UAV) and SfM photogrammetry survey as a function of the number and location of ground control points used. Remote Sens. 2018, 10, 1606. [Google Scholar] [CrossRef]
- Agüera-Vega, F.; Carvajal-Ramírez, F.; Martínez-Carricondo, P. Assessment of photogrammetric mapping accuracy based on variation ground control points number using unmanned aerial vehicle. Measurement 2017, 98, 221–227. [Google Scholar] [CrossRef]
- Oniga, V.E.; Breaban, A.I.; Pfeifer, N.; Chirila, C. Determining the suitable number of ground control points for UAS images georeferencing by varying number and spatial distribution. Remote Sens. 2020, 12, 876. [Google Scholar] [CrossRef]
- James, M.R.; Robson, S.; d’Oleire-Oltmanns, S.; Niethammer, U. Optimising UAV topographic surveys processed with structure-from-motion: Ground control quality, quantity and bundle adjustment. Geomorphology 2017, 280, 51–66. [Google Scholar] [CrossRef]
- Lowe, D.G. Object recognition from local scale-invariant features. Proc. IEEE Int. Conf. Comput. Vis. 1999, 2, 1150–1157. [Google Scholar]
- Bay, H.; Ess, A.; Tuytelaars, T.; Van Gool, L. Speeded-up robust features (SURF). Comput. Vis. Image Underst. 2008, 110, 346–359. [Google Scholar] [CrossRef]
- Alcantarilla, P.F.; Nuevo, J.; Bartoli, A. Fast explicit diffusion for accelerated features in nonlinear scale spaces. In Proceedings of the BMVC 2013-Electronic Proceedings of the British Machine Vision Conference, Bristol, UK, 9–13 September 2013. [Google Scholar]
- Gonzales-Aguilera, D.; Ruiz de Ona, E.; Lopez-Fernandez, L.; Farella, E.M.; Stathopoulou, E.; Toschi, I.; Remondino, F.; Fusiello, A.; Nex, F. Photomatch: An open-source multi-view and multi-modal feature matching tool for photogrammetric applications. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, 43, 213–219. [Google Scholar] [CrossRef]
- Lu, C.; Xu, L.; Jia, J. Contrast preserving decolorization. In Proceedings of the 2012 IEEE International Conference on Computational Photography (ICCP), Seattle, WA, USA, 28–29 April 2012. [Google Scholar]
- Crommelinck, S. Delineation Tool. Available online: https://github.com/SCrommelinck/delineation-tool (accessed on 10 July 2020).
- Pont-Tuset, J.; Arbelaez, P.; Barron, J.T.; Marques, F.; Malik, J. Multiscale combinatorial grouping for image segmentation and object proposal generation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 128–140. [Google Scholar] [CrossRef]
- Crommelinck, S.; Koeva, M.; Yang, M.Y.; Vosselman, G. Application of deep learning for delineation of visible cadastral boundaries from remote sensing imagery. Remote Sens. 2019, 11, 2505. [Google Scholar] [CrossRef]
- Seifert, E.; Seifert, S.; Vogt, H.; Drew, D.; van Aardt, J.; Kunneke, A.; Seifert, T. Influence of drone altitude, image overlap, and optical sensor resolution on multi-view reconstruction of forest images. Remote Sens. 2019, 11, 1252. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).