Experimental Fire Measurement with UAV Multimodal Stereovision
Abstract
1. Introduction
2. Materials and Methods
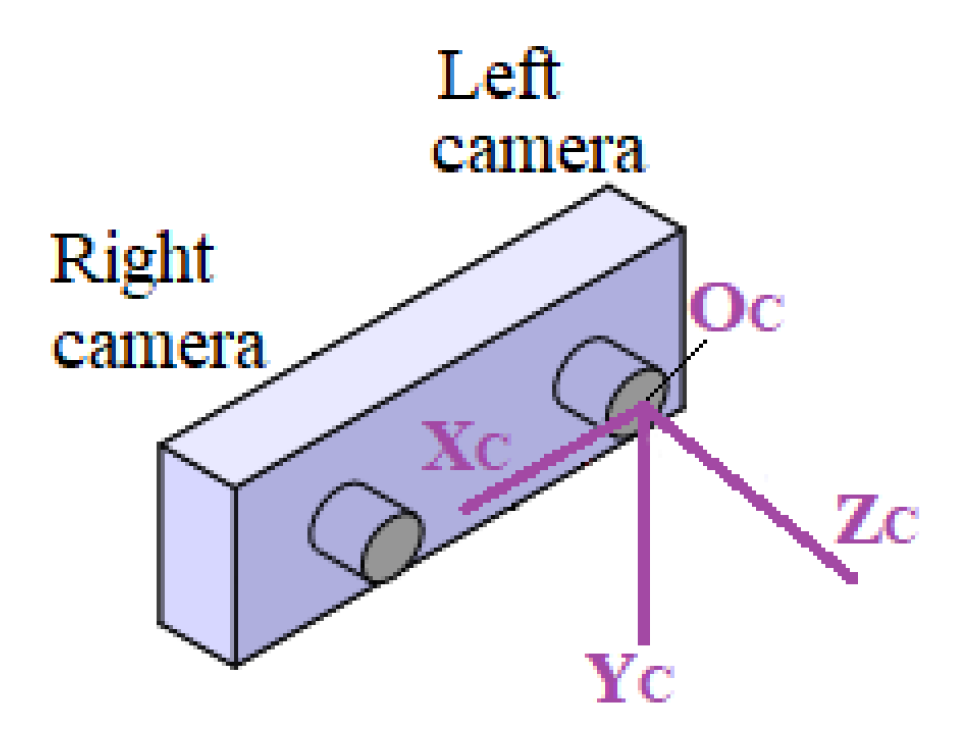
2.1. Multimodal Stereovision System
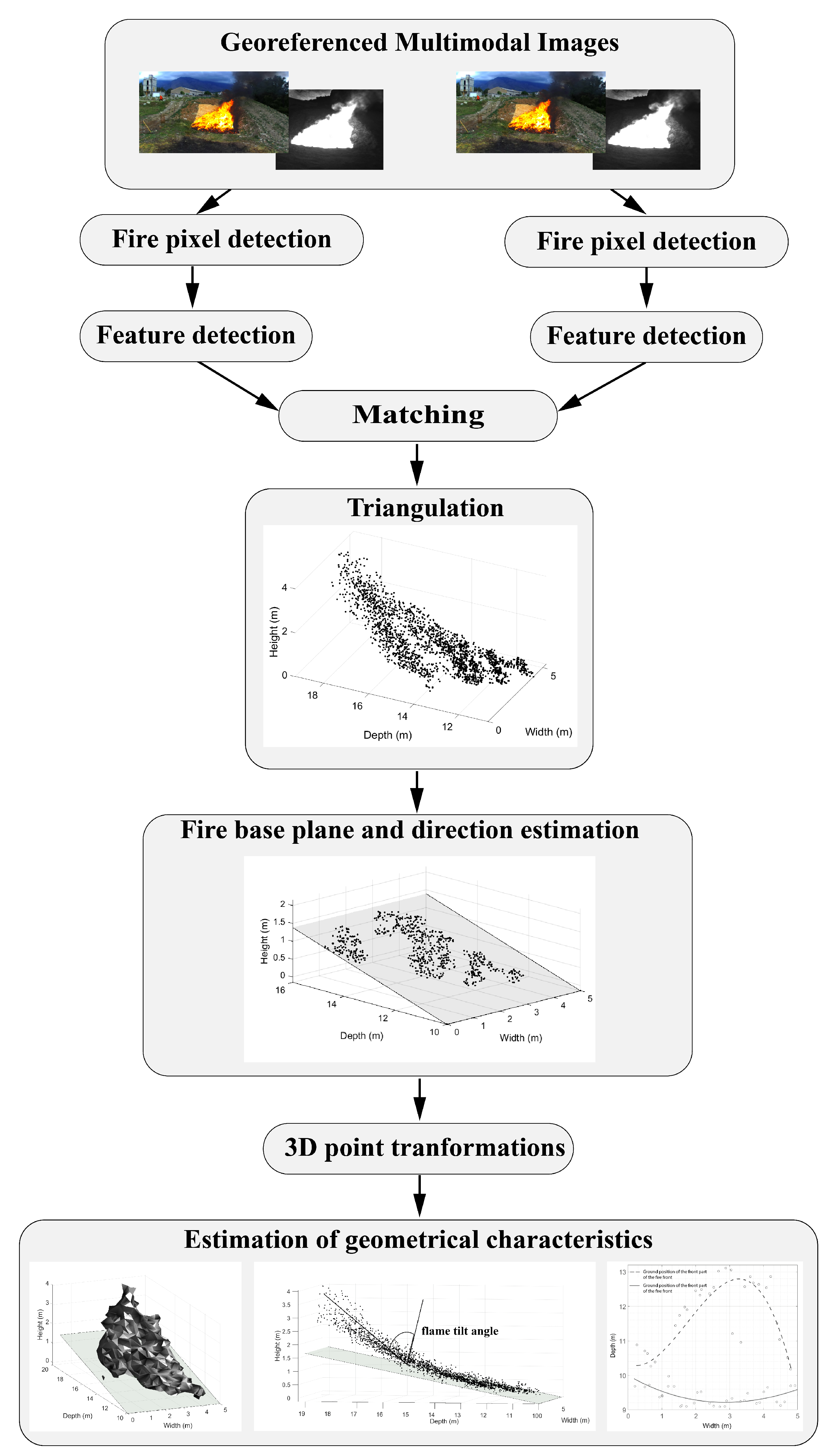
2.2. Methodology
2.2.1. Multimodal Fire Pixel Detection
2.2.2. Feature Detection, Matching, and Triangulation
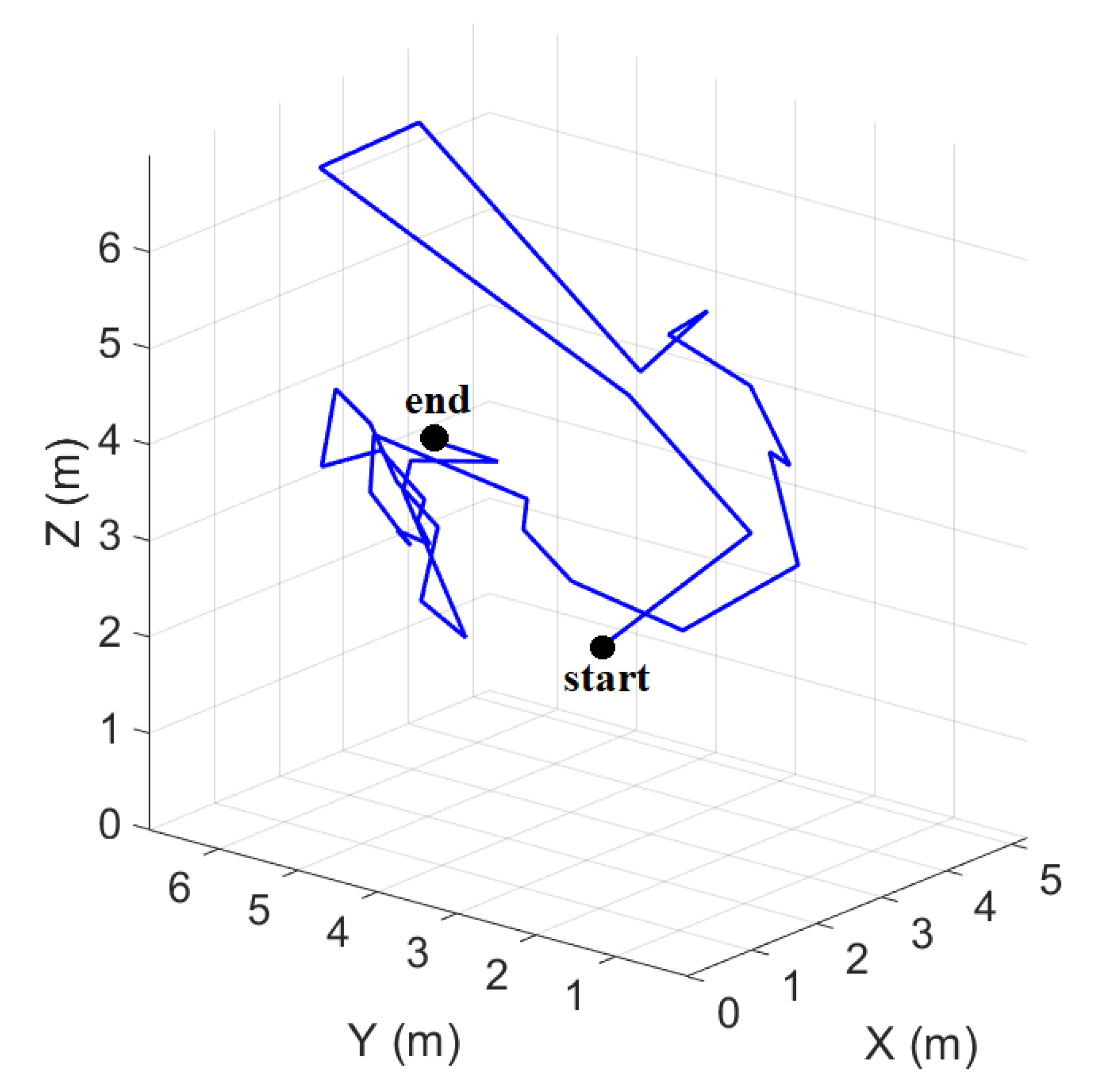
2.2.3. Fire Local Propagation Plane and Principal Direction Estimation
Fire Local Propagation Plane
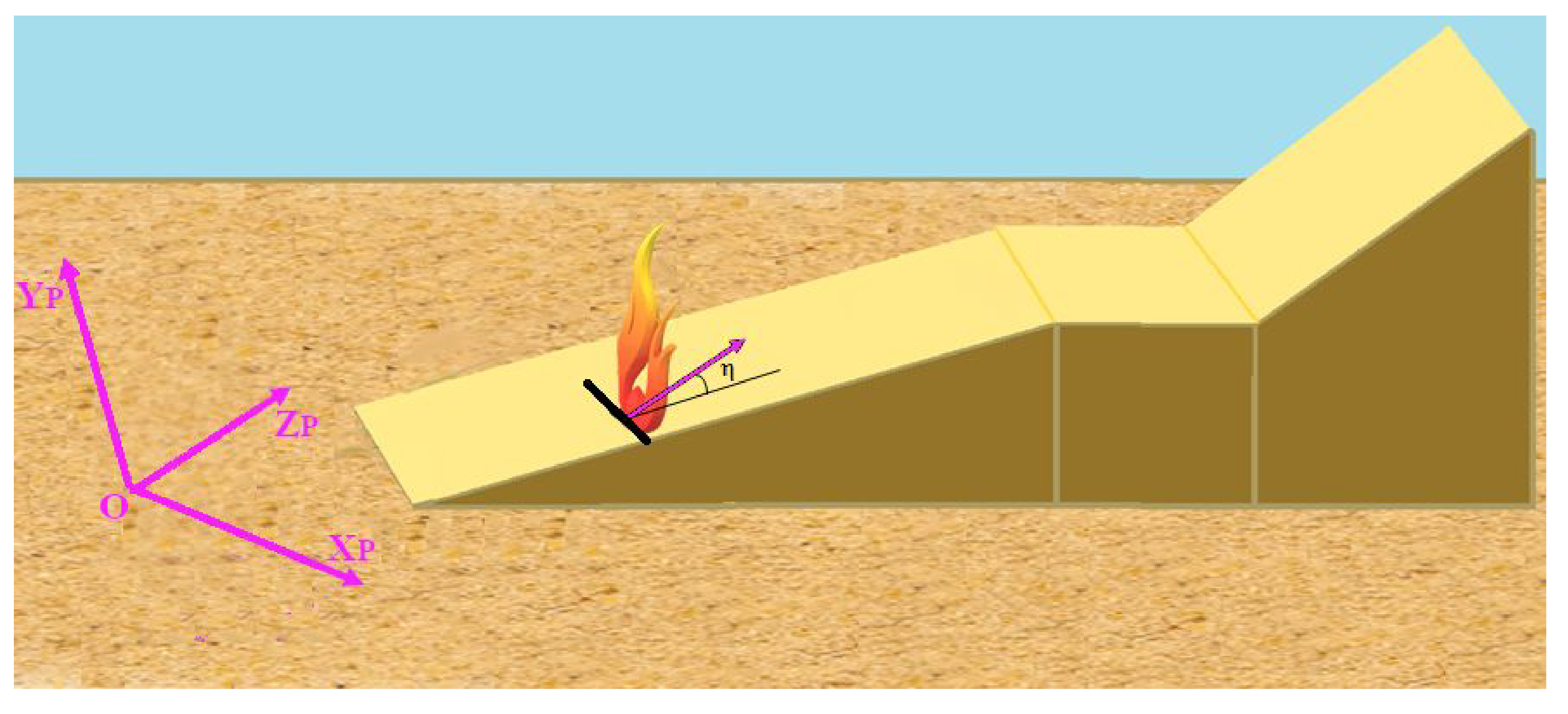
Principal Direction
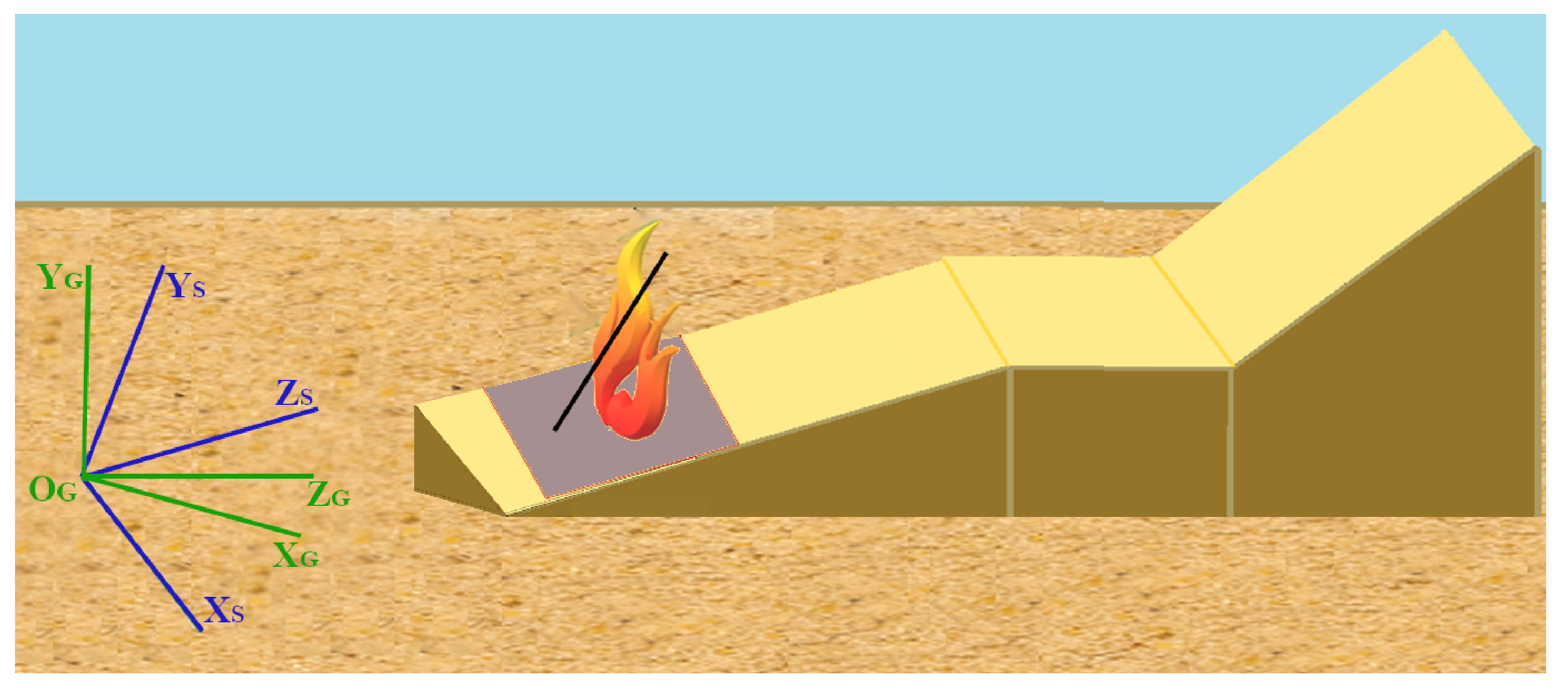
2.2.4. 3D Fire Points Transformations
2.2.5. Fire Geometric Characteristics Estimation
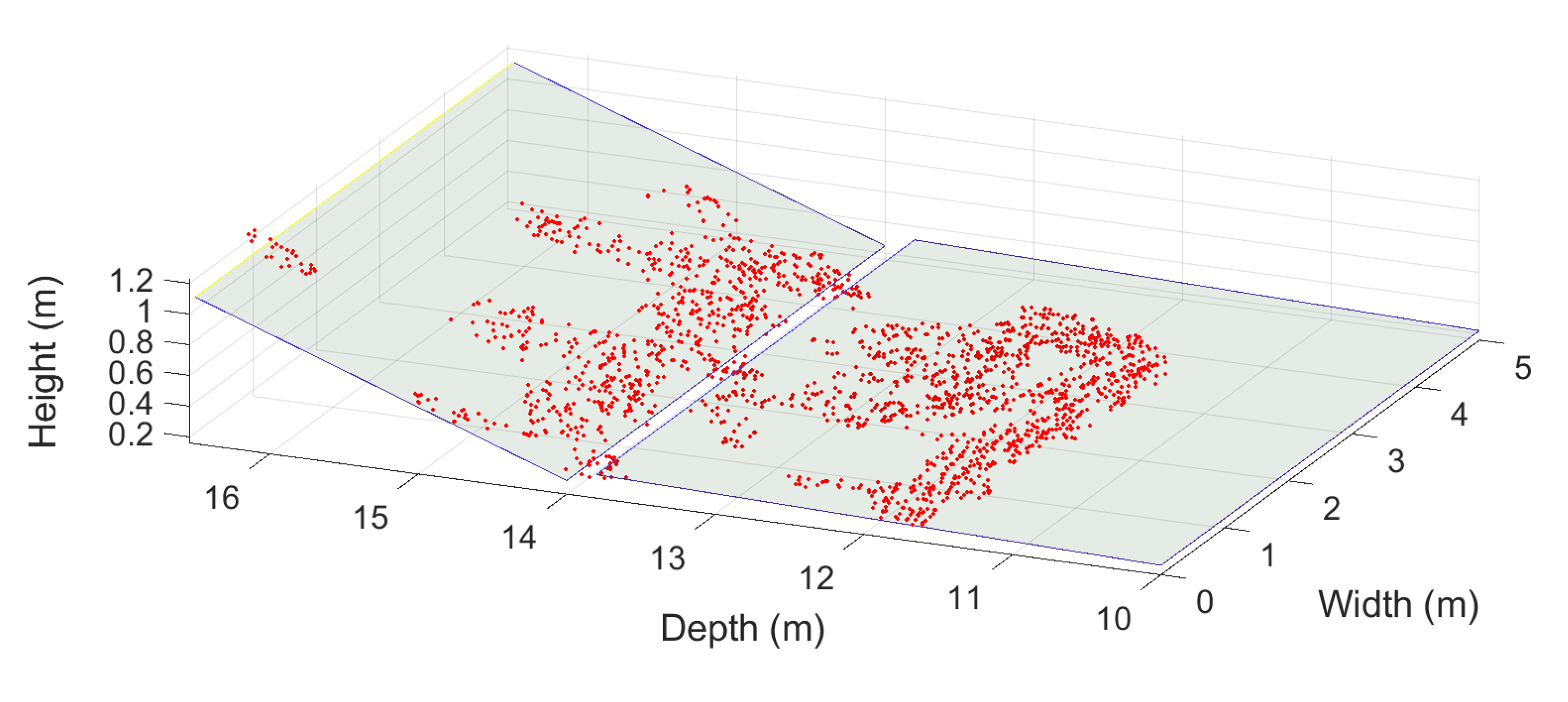
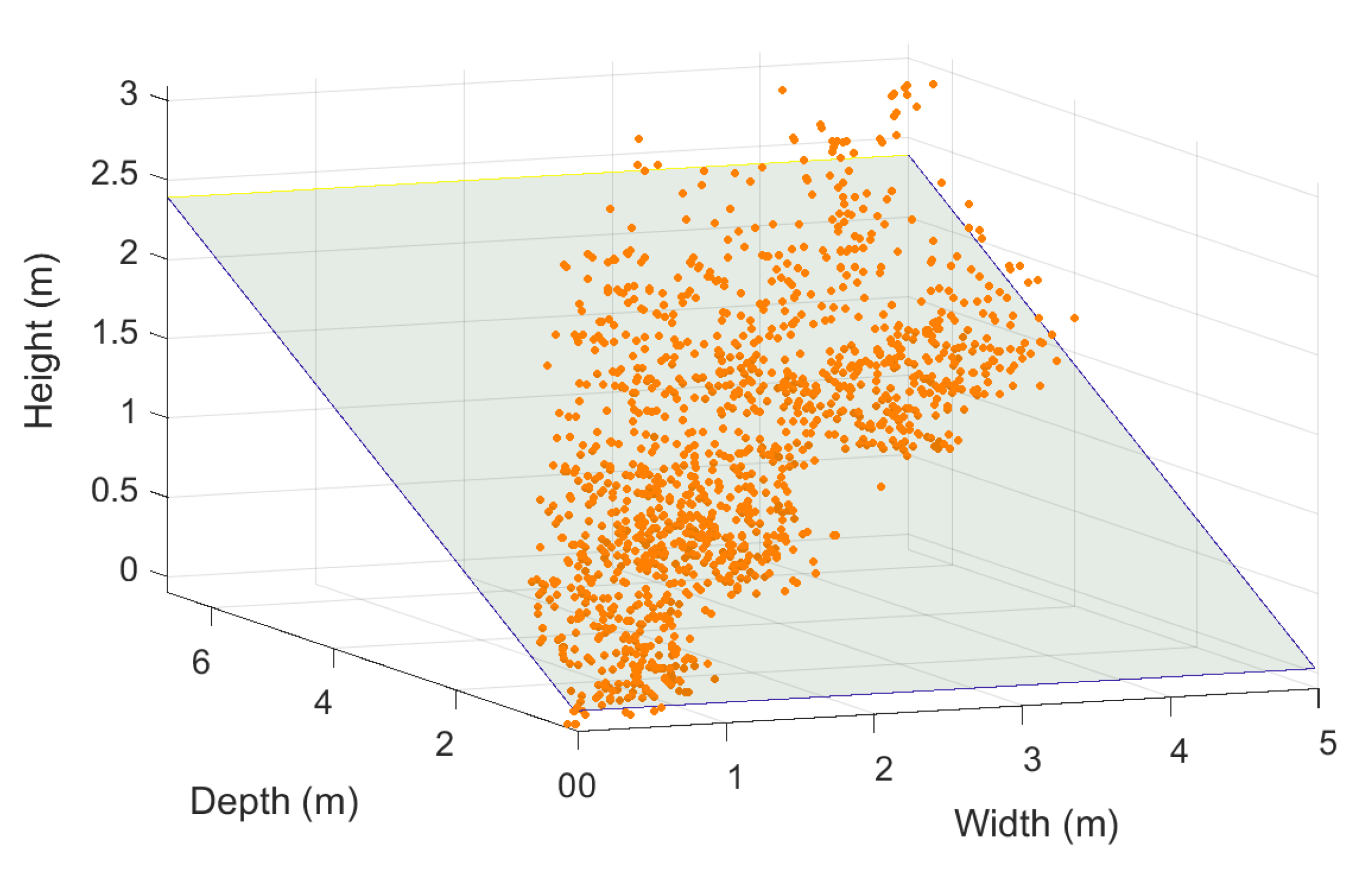
Shape and Volume
Surface and View Factor
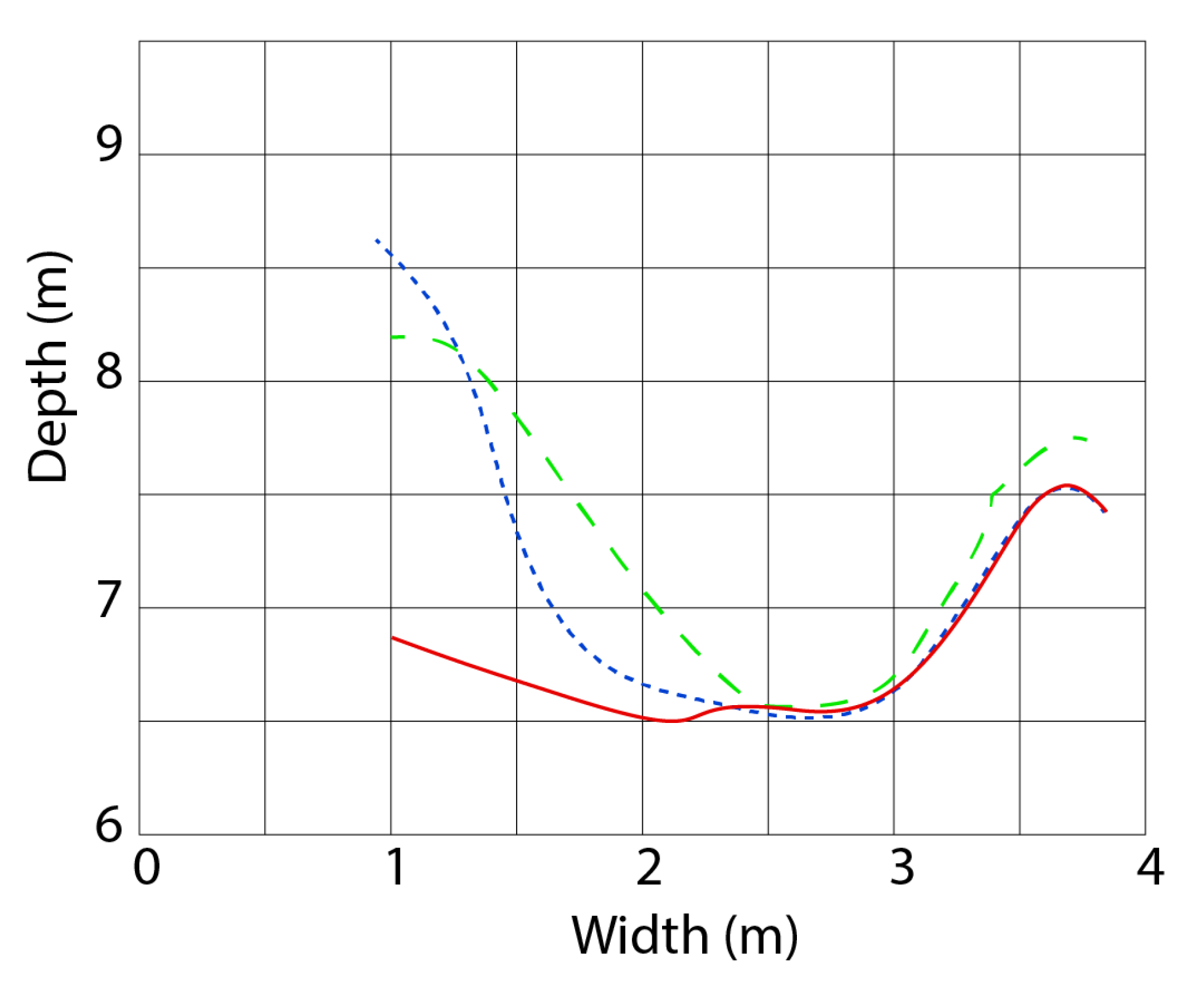
Position, Rate of Spread and Depth
Combustion Surface
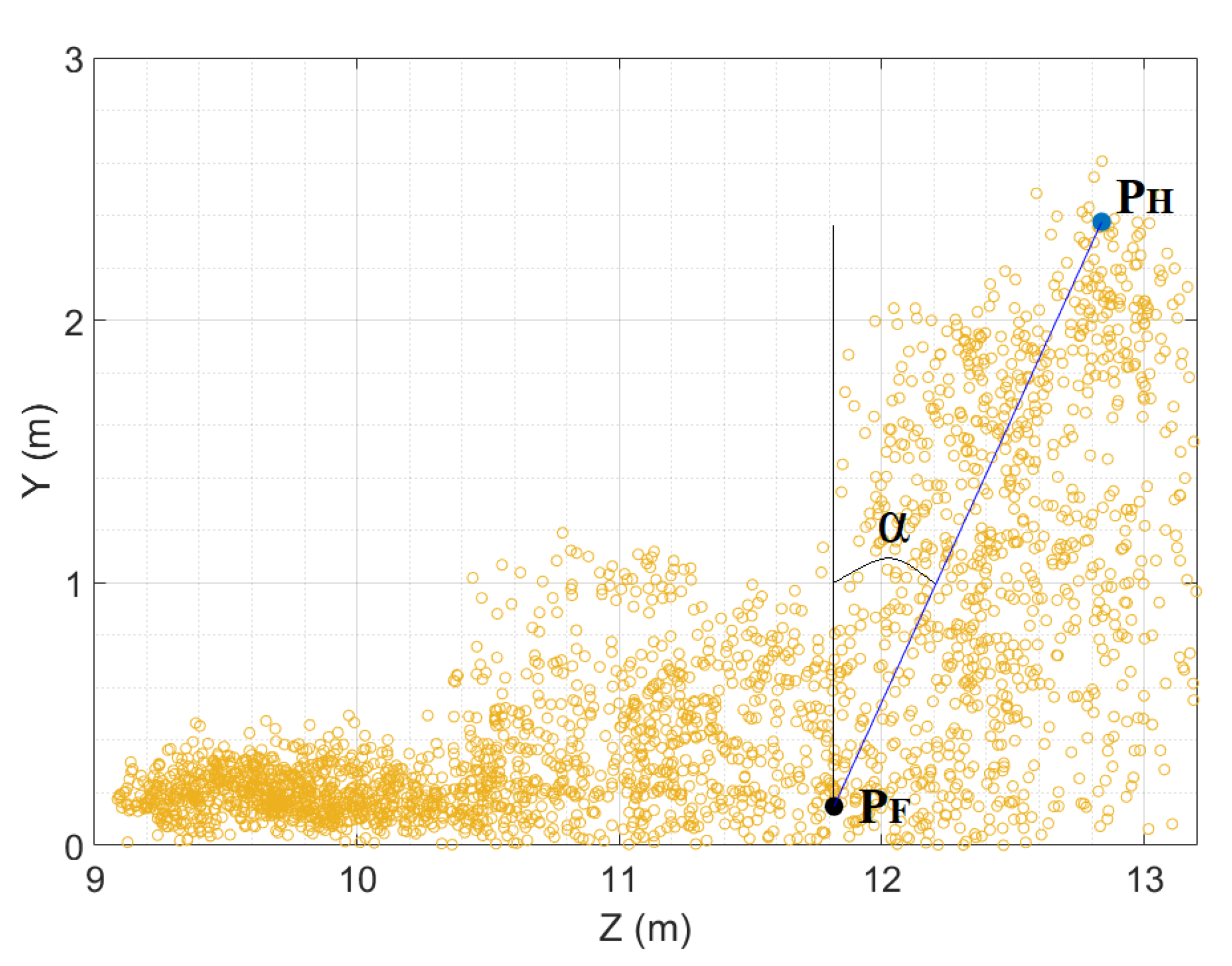
Width, Height, Length and Inclination Angle
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- European Science & Technology Advisory Group (E-STAG). Evolving Risk of Wildfires in Europe—The Changing Nature of Wildfire Risk Calls for a Shift in Policy Focus from Suppression to Prevention; United Nations for Disaster Risk Reduction–Regional Office for Europe: Brussels, Belgium, 2020; Available online: https://www.undrr.org/publication/evolving-risk-wildfires-europe-thematic-paper-european-science-technology-advisory (accessed on 29 October 2020).
- European Commission. Forest Fires—Sparking Firesmart Policies in the EU; Research & Publications Office of the European Union: Brussels, Belgium, 2018; Available online: https://ec.europa.eu/info/publications/forest-fires-sparking-firesmart-policies-eu_en (accessed on 29 October 2020).
- Tedim, F.; Leone, V.; Amraoui, M.; Bouillon, C.; Coughlan, M.; Delogu, G.; Fernandes, P.; Ferreira, C.; McCaffrey, S.; McGee, T.; et al. Defining extreme wildfire events: Difficulties, challenges, and impacts. Fire 2018, 1, 9. [Google Scholar] [CrossRef]
- Global Land Cover Change—Wildfires. Available online: http://stateoftheworldsplants.org/2017/report/SOTWP_2017_8_global_land_cover_change_wildfires.pdf (accessed on 25 March 2020).
- Jolly, M.; Cochrane, P.; Freeborn, Z.; Holden, W.; Brown, T.; Williamson, G.; Bowman, D. Climate-induced variations in global wildfire danger from 1979 to 2013. Nat. Commun. 2015, 6, 7537. [Google Scholar] [CrossRef] [PubMed]
- Ganteaume, A.; Jappiot, M. What causes large fires in Southern France. For. Ecol. Manag. 2013, 294, 76–85. [Google Scholar] [CrossRef]
- McArthur, A.G. Weather and Grassland Fire Behaviour; Australian Forest and Timber Bureau Leaflet, Forest Research Institute: Canberra, Australia, 1966. [Google Scholar]
- Rothermel, R.C. A Mathematical Model for Predicting Fire Spread in Wildland Fuels; United States Department of Agriculture: Ogden, UT, USA, 1972. [Google Scholar]
- Morvan, D.; Dupuy, J.L. Modeling the propagation of a wildfire through a Mediterranean shrub using the multiphase formulation. Combust. Flame 2004, 138, 199–210. [Google Scholar] [CrossRef]
- Balbi, J.H.; Rossi, J.L.; Marcelli, T.; Chatelon, F.J. Physical modeling of surface fire under nonparallel wind and slope conditions. Combust. Sci. Technol. 2010, 182, 922–939. [Google Scholar] [CrossRef]
- Balbi, J.H.; Chatelon, F.J.; Rossi, J.L.; Simeoni, A.; Viegas, D.X.; Rossa, C. Modelling of eruptive fire occurrence and behaviour. J. Environ. Sci. Eng. 2014, 3, 115–132. [Google Scholar]
- Sacadura, J. Radiative heat transfer in fire safety science. J. Quant. Spectrosc. Radiat. Transf. 2005, 93, 5–24. [Google Scholar] [CrossRef]
- Rossi, J.L.; Chetehouna, K.; Collin, A.; Moretti, B.; Balbi, J.H. Simplified flame models and prediction of the thermal radiation emitted by a flame front in an outdoor fire. Combust. Sci. Technol. 2010, 182, 1457–1477. [Google Scholar] [CrossRef]
- Chatelon, F.J.; Balbi, J.H.; Morvan, D.; Rossi, J.L.; Marcelli, T. A convective model for laboratory fires with well-ordered vertically-oriented. Fire Saf. J. 2017, 90, 54–61. [Google Scholar] [CrossRef]
- Finney, M.A. FARSITE: Fire Area Simulator-Model Development and Evaluation; Rocky Mountain Research Station: Ogden, UT, USA, 1998. [Google Scholar]
- Linn, R.; Reisner, J.; Colman, J.J.; Winterkamp, J. Studying wildfire behavior using FIRETEC. Int. J. Wildland Fire 2002, 11, 233–246. [Google Scholar] [CrossRef]
- Tymstra, C.; Bryce, R.W.; Wotton, B.M.; Taylor, S.W.; Armitage, O.B. Development and Structure of Prometheus: The Canadian Wildland Fire Growth Simulation Model; Natural Resources Canada: Ottawa, ON, Canada; Canadian Forest Service: Ottawa, ON, Canada; Northern Forestry Centre: Edmonton, AB, Canada, 2009. [Google Scholar]
- Bisgambiglia, P.A.; Rossi, J.L.; Franceschini, R.; Chatelon, F.J.; Bisgambiglia, P.A.; Rossi, L.; Marcelli, T. DIMZAL: A software tool to compute acceptable safety distance. Open J. For. 2017, A, 11–33. [Google Scholar] [CrossRef][Green Version]
- Rossi, J.L.; Chatelon, F.J.; Marcelli, T. Encyclopedia of Wildfires and Wildland-Urban Interface (WUI) Fires; Springer: Cham, Switzerland, 2018. [Google Scholar] [CrossRef]
- Siegel, R. Howell, J. Thermal Radiation Heat Transfer; Hemisphere Publishing Corporation: Washington, DC, USA, 1994. [Google Scholar] [CrossRef]
- Toulouse, T.; Rossi, L.; Akhloufi, M.; Turgay, C.; Maldague, X. Benchmarking of wildland fire colour segmentation algorithms. IET Image Process. 2015, 9, 1–9. [Google Scholar] [CrossRef]
- Phillips, W., III; Shah, M.; da Vitoria Lobo, N. Flame recognition in video. Pattern Recognit. Lett. 2002, 23, 319–327. [Google Scholar] [CrossRef]
- Chen, T.H.; Wu, P.H.; Chiou, Y.C. An early fire-detection method based on image processing. In Proceedings of the IEEE International Conference on Image Processing (ICIP), Singapore, 24–27 October 2004; pp. 1707–1710. [Google Scholar]
- Horng, W.B.; Peng, J.W.; Chen, C.Y. A new image-based real-time flame detection method using color analysis. In Proceedings of the IEEE Networking, Sensing and Control Proceddings, Tucson, AZ, USA, 19–22 March 2005; pp. 100–105. [Google Scholar]
- Celik, T.; Demirel, H.; Ozkaramanli, H.; Uyguroǧlu, M. Fire detection using statistical color model in video sequences. J. Vis. Commun. Image Represent. 2007, 18, 176–185. [Google Scholar] [CrossRef]
- Ko, B.C.; Cheong, K.H.; Nam, J.Y. Fire detection based on vision sensor and support vector machines. Fire Saf. J. 2009, 44, 322–329. [Google Scholar] [CrossRef]
- Celik, T.; Demirel, H. Fire detection in video sequences using a generic color model. Fire Saf. J. 2009, 44, 147–158. [Google Scholar] [CrossRef]
- Celik, T. Fast and efficient method for fire detection using image processing. ETRI J. 2010, 32, 881–890. [Google Scholar] [CrossRef]
- Chitade, A.Z.; Katiyar, S. Colour based image segmentation using k-means clustering. Int. J. Eng. Sci. Technol. 2010, 2, 5319–5325. [Google Scholar]
- Collumeau, J.F.; Laurent, H.; Hafiane, A.; Chetehouna, K. Fire scene segmentations for forest fire characterization: A comparative study. In Proceedings of the 18th IEEE International Conference on Image Processing (ICIP), Brussels, Belgium, 11–14 September 2011; pp. 2973–2976. [Google Scholar]
- Rossi, L.; Akhloufi, M.; Tison, Y. On the use of stereovision to develop a novel instrumentation system to extract geometric fire fronts characteristics. Fire Saf. J. 2011, 46, 9–20. [Google Scholar] [CrossRef]
- Rudz, S.; Chetehouna, K.; Hafiane, A.; Laurent, H.; Séro-Guillaume, O. Investigation of a novel image segmentation method dedicated to forest fire applications. Meas. Sci. Technol. 2013, 24, 075403. [Google Scholar] [CrossRef]
- Toulouse, T.; Rossi, L.; Celik, T.; Campana, A.; Akhloufi, M. Computer vision for wildfire research: An evolving image dataset for processing and analysis. Fire Saf. J. 2017, 92, 188–194. [Google Scholar] [CrossRef]
- Gouverneur, B.; Verstockt, S.; Pauwels, E.; Han, J.; de Zeeuw, P.M.; Vermeiren, J. Archeological treasures protection based on early forest wildfire multi-band imaging detection system. In Proceedings of the Electro-Optical and Infrared Systems: Technology and Applications IX, Edinburgh, UK, 24 October 2012; p. 85410J. [Google Scholar] [CrossRef]
- Billaud, Y.; Boulet, P.; Pizzo, Y.; Parent, G.; Acem, Z.; Kaiss, A.; Collin, A.; Porterie, B. Determination of woody fuel flame properties by means of emission spectroscopy using a genetic algorithm. Combust. Sci. Technol. 2013, 185, 579–599. [Google Scholar] [CrossRef]
- Verstockt, S.; Vanoosthuyse, A.; Van Hoecke, S.; Lambert, P.; Van de Walle, R. Multi-sensor fire detection by fusing visual and non-visual flame features. In Proceedings of the International Conference on Image and Signal Processing, Quebec, QC, Canada, 30 June–2 July 2010; pp. 333–341. [Google Scholar] [CrossRef]
- Verstockt, S.; Van Hoecke, S.; Beji, T.; Merci, B.; Gouverneur, B.; Cetin, A.; De Potter, P.; Van de Walle, R. A multimodal video analysis approach for car park fire detection. Fire Saf. J. 2013, 57, 9–20. [Google Scholar] [CrossRef]
- Clements, H.B. Measuring fire behavior with photography. Photogram. Eng. Remote Sens. 1983, 49, 213–219. [Google Scholar]
- Pastor, E.; Águeda, A.; Andrade-Cetto, J.; Muñoz, M.; Pérez, Y.; Planas, E. Computing the rate of spread of linear flame fronts by thermal image processing. Fire Saf. J. 2006, 41, 569–579. [Google Scholar] [CrossRef]
- De Dios, J.R.M.; André, J.C.; Gonçalves, J.C.; Arrue, B.C.; Ollero, A.; Viegas, D. Laboratory fire spread analysis using visual and infrared images. Int. J. Wildland Fire 2006, 15, 179–186. [Google Scholar] [CrossRef]
- Verstockt, S.; Van Hoecke, S.; Tilley, N.; Merci, B.; Lambert, P.; Hollemeersch, C.; Van de Walle, R. FireCube: A multi-view localization framework for 3D fire analysis. Fire Saf. J. 2011, 46, 262–275. [Google Scholar] [CrossRef]
- Martinez-de Dios, J.R.; Arrue, B.C.; Ollero, A.; Merino, L.; Gómez-Rodríguez, F. Computer vision techniques for forest fire perception. Image Vis. Comput. 2008, 26, 550–562. [Google Scholar] [CrossRef]
- Martínez-de Dios, J.R.; Merino, L.; Caballero, F.; Ollero, A. Automatic forest-fire measuring using ground stations and unmanned aerial systems. Sensors 2011, 11, 6328–6353. [Google Scholar] [CrossRef]
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Ng, W.B.; Zhang, Y. Stereoscopic imaging and reconstruction of the 3D geometry of flame surfaces. Exp. Fluids 2003, 34, 484–493. [Google Scholar] [CrossRef]
- Rossi, L.; Molinier, T.; Akhloufi, M.; Tison, Y.; Pieri, A. Estimating the surface and the volume of laboratory-scale wildfire fuel using computer vision. IET Image Process. 2013, 6, 1031–1040. [Google Scholar] [CrossRef]
- Toulouse, T.; Rossi, L.; Akhloufi, M.; Pieri, A.; Maldague, X. A multimodal 3D framework for fire characteristics estimation. Meas. Sci. Technol. 2018, 29, 025404. [Google Scholar] [CrossRef]
- Trucco, E.; Verri, A. Introductory Techniques for 3-D Computer Vision; Prentice Hall: Englewood Cliffs, NJ, USA, 1998. [Google Scholar]
- Ciullo, V.; Rossi, L.; Toulouse, T.; Pieri, A. Fire geometrical characteristics estimation using a visible stereovision system carried by unmanned aerial vehicle. In Proceedings of the 15th International Conference on Control, Automation, Robotics and Vision (ICARCV), Singapore, 18–21 November 2018; pp. 1216–1221. [Google Scholar] [CrossRef]
- FLIR Duo Pro R Specifications. Available online: Https://www.flir.com/products/duo-pro-r/ (accessed on 14 October 2020).
- Camera Calibration Toolbox for Matlab. Available online: Http://www.vision.caltech.edu/bouguetj/calib_doc/ (accessed on 14 October 2020).
- Balcilar, M. Stereo Camera Calibration under Different Resolution. 2019. Available online: https://github.com/balcilar/Calibration-Under_Different-Resolution (accessed on 14 October 2020).
- Otsu, N. A threshold selection method from gray-level histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Harris, C.G.; Stephens, M. A combined corner and edge detector. In Proceedings of the Alvey Vision Conference, Manchester, UK, 31 August–2 September 1988; pp. 147–151. [Google Scholar]
- Bay, H.; Tuytelaars, T.; Van Gool, L. Surf: Speeded up Robust Features; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Brown, M.; Szeliski, R.; Winder, S. Multi-Image Matching Using Multi-Scale Oriented Patches. In Proceedings of the IEEE Computer Vision and Pattern Recognition Conference (CVPR), San Diego, CA, USA, 20–25 June 2005; pp. 510–517. [Google Scholar]
- Delaunay, B. Sur la sphere vide. Izv. Akad. Nauk SSSR Otd. Mat. I Estestv. Nauk 1934, 7, 793–800. [Google Scholar]
- Rossi, L.; Molinier, T.; Pieri, A.; Tison, Y.; Bosseur, F. Measurement of the geometrical characteristics of a fire front by stereovision techniques on field experiments. Meas. Sci. Technol. 2011, 22, 125504. [Google Scholar] [CrossRef]
- Moretti, B. Modélisation du Comportement des Feux de Forêt pour des Outils d’aide à la Décision. Ph.D. Thesis, University of Corsica, Corte, France, 2015. [Google Scholar]
- Edelsbrunner, H.; Kirkpatrick, D.; Seidel, R. On the shape of a set of points in the plane. IEEE Trans. Inf. Theory 1983, 29, 551–559. [Google Scholar] [CrossRef]






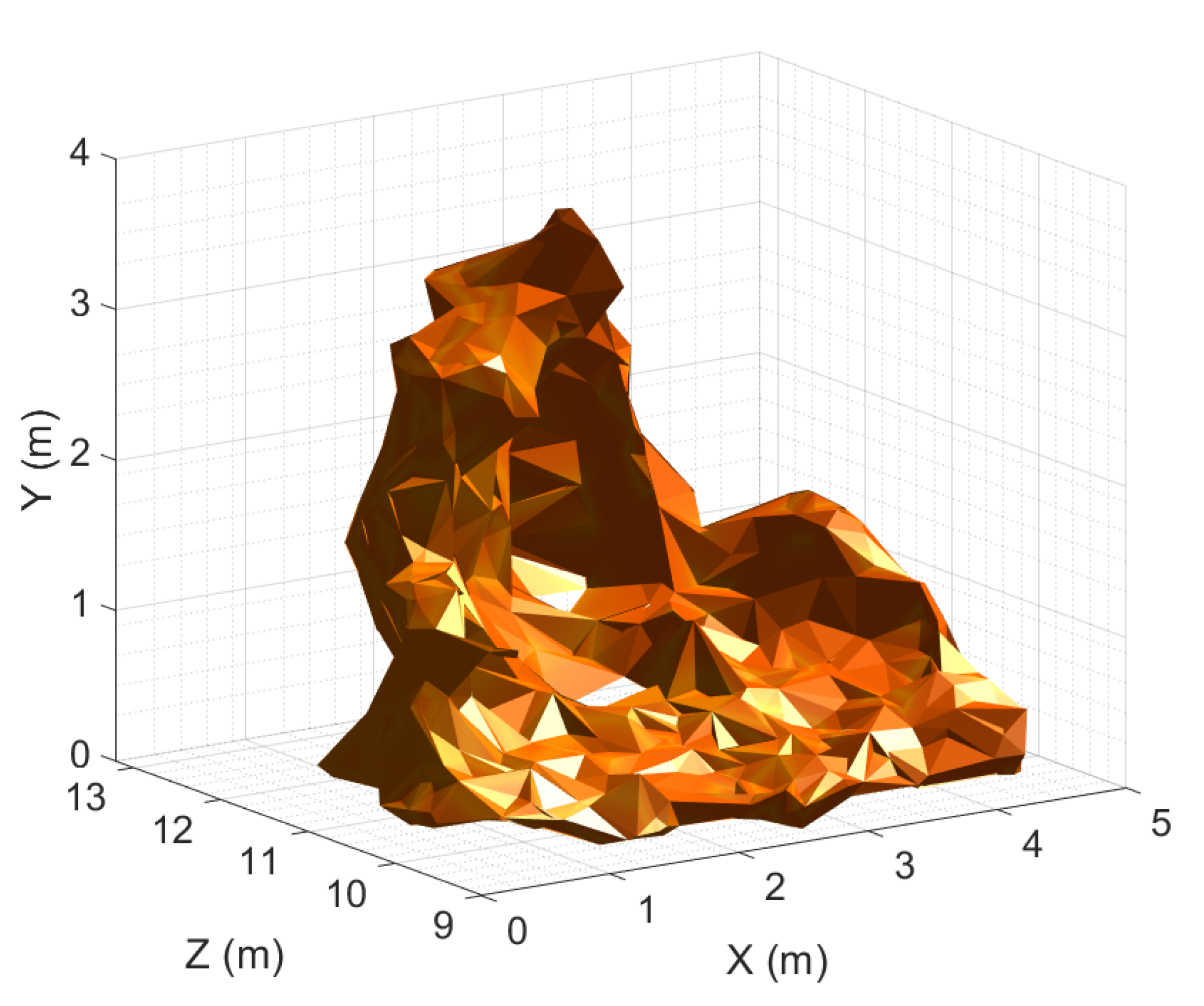

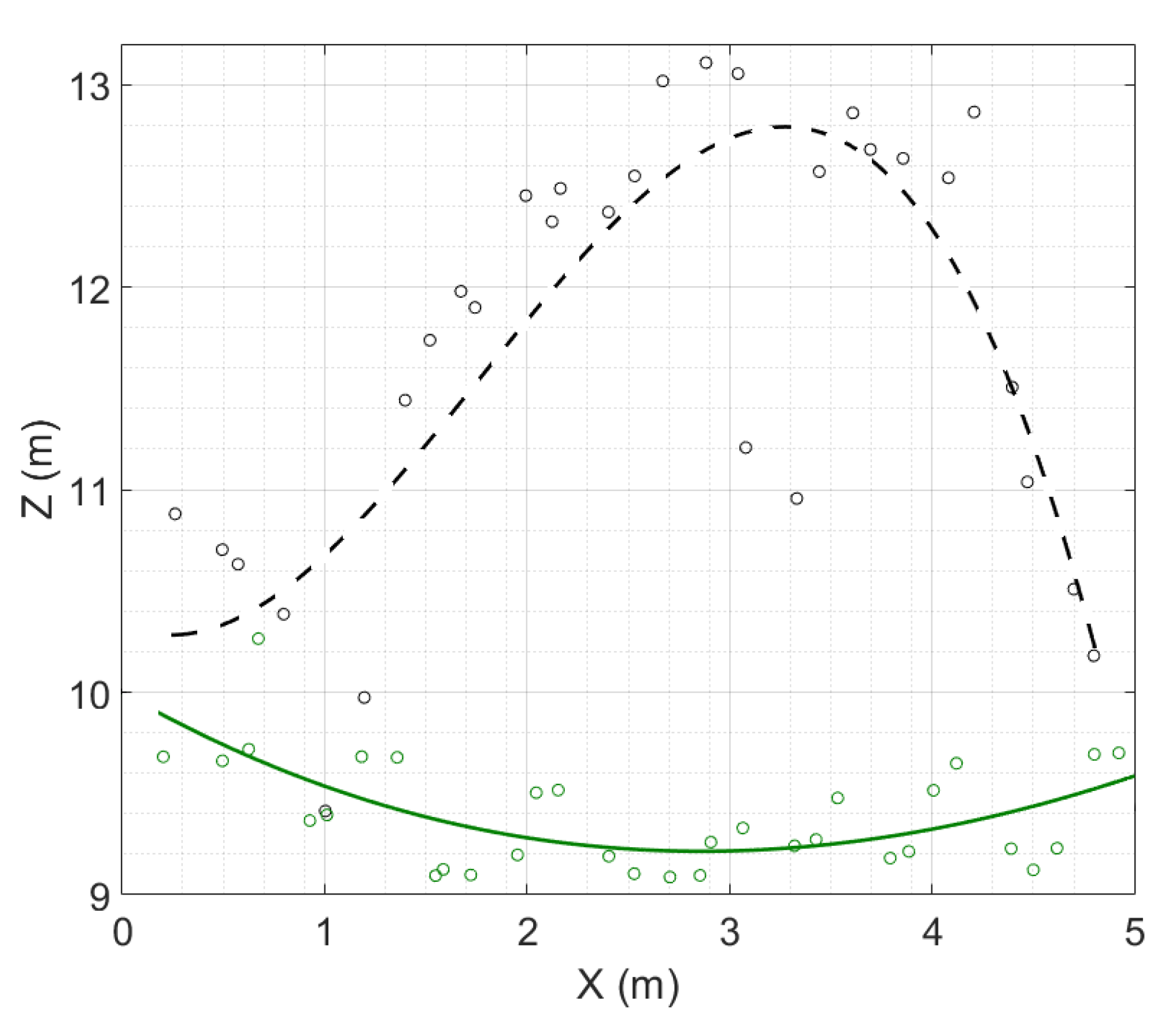
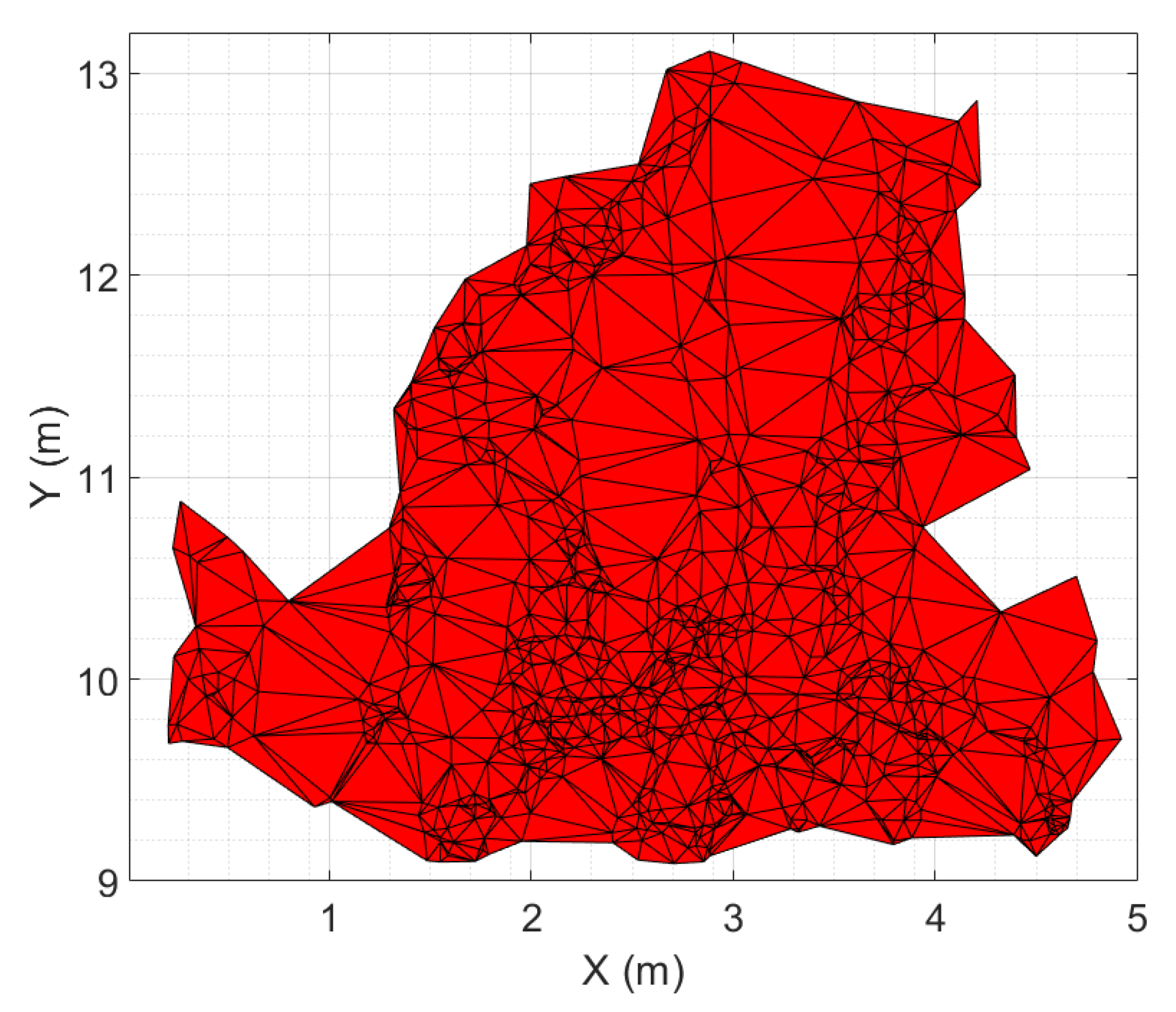
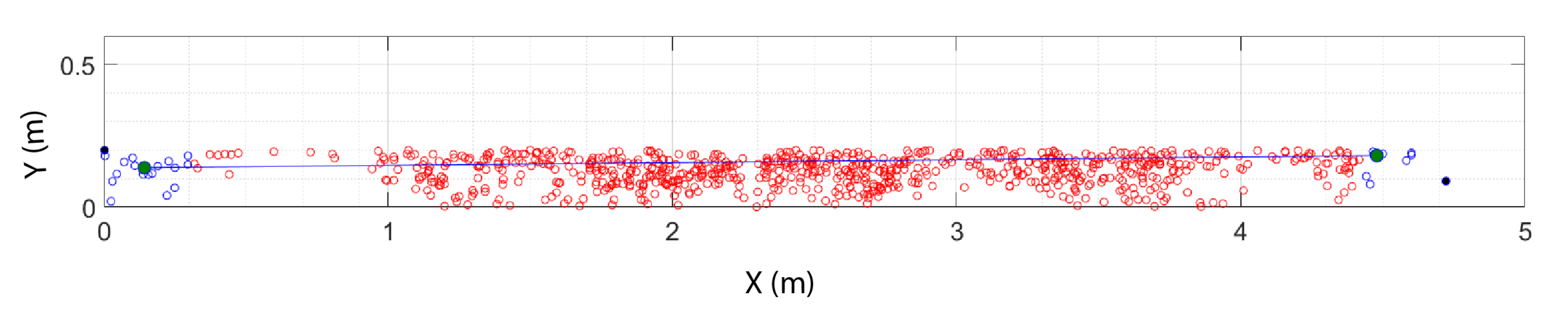



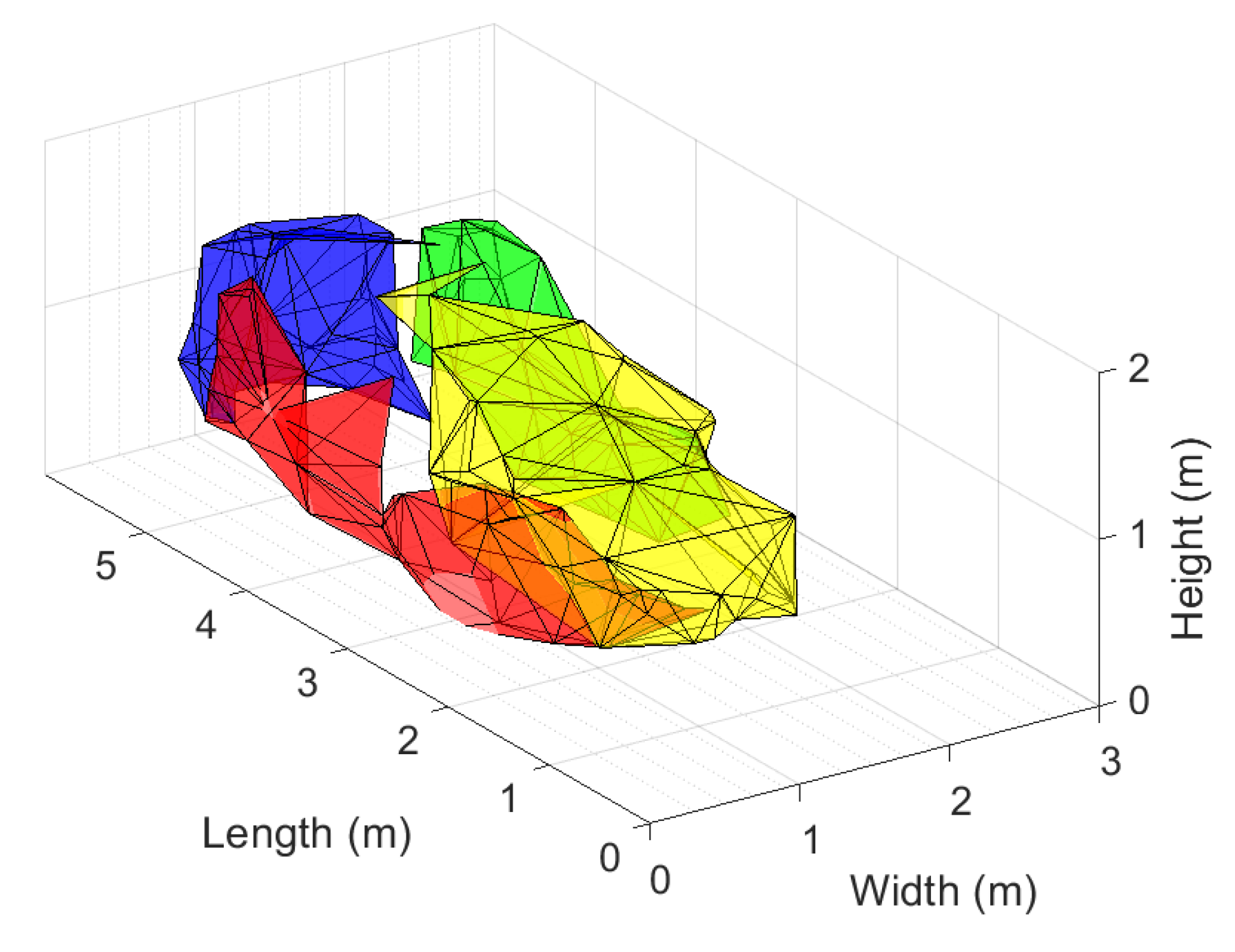
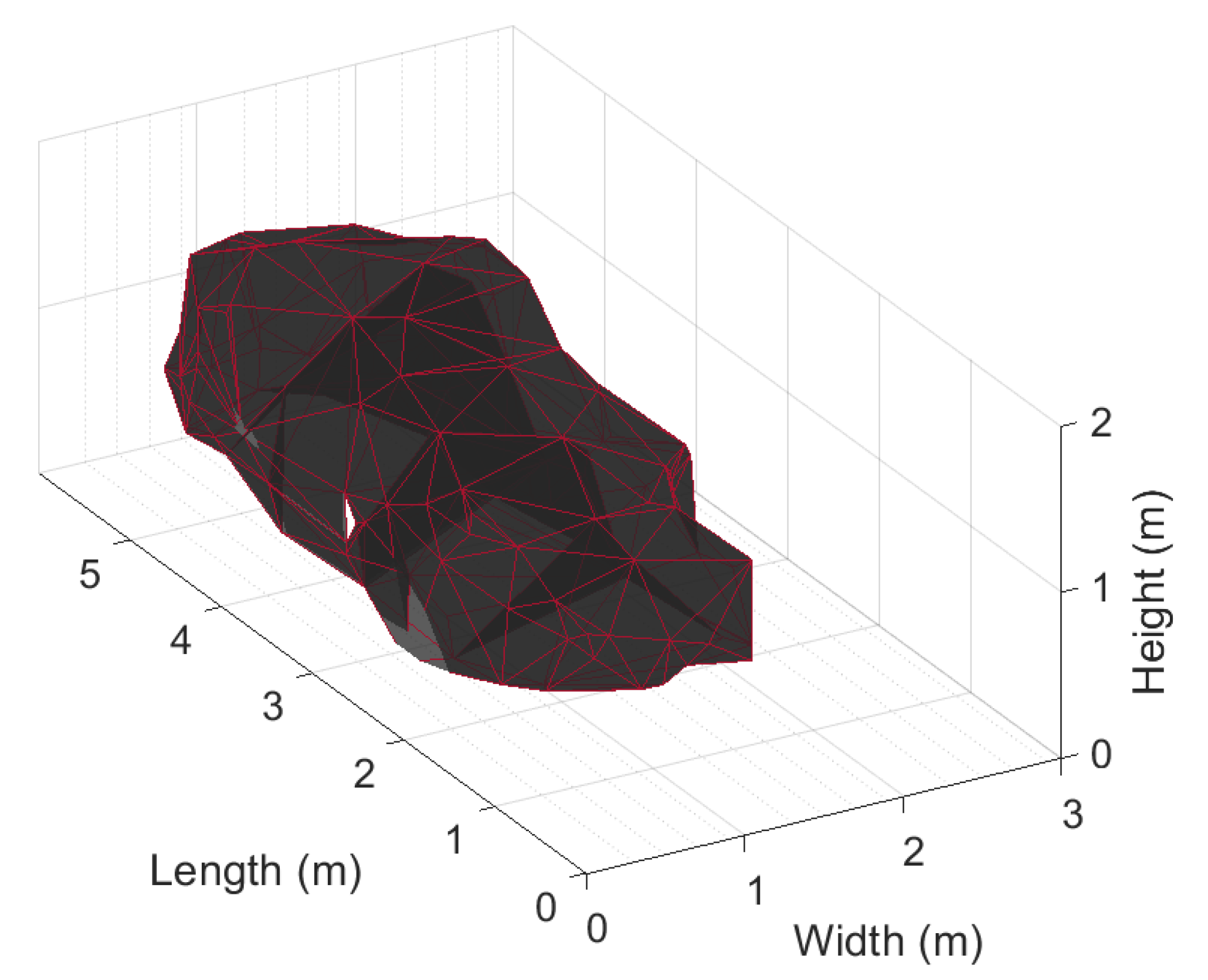

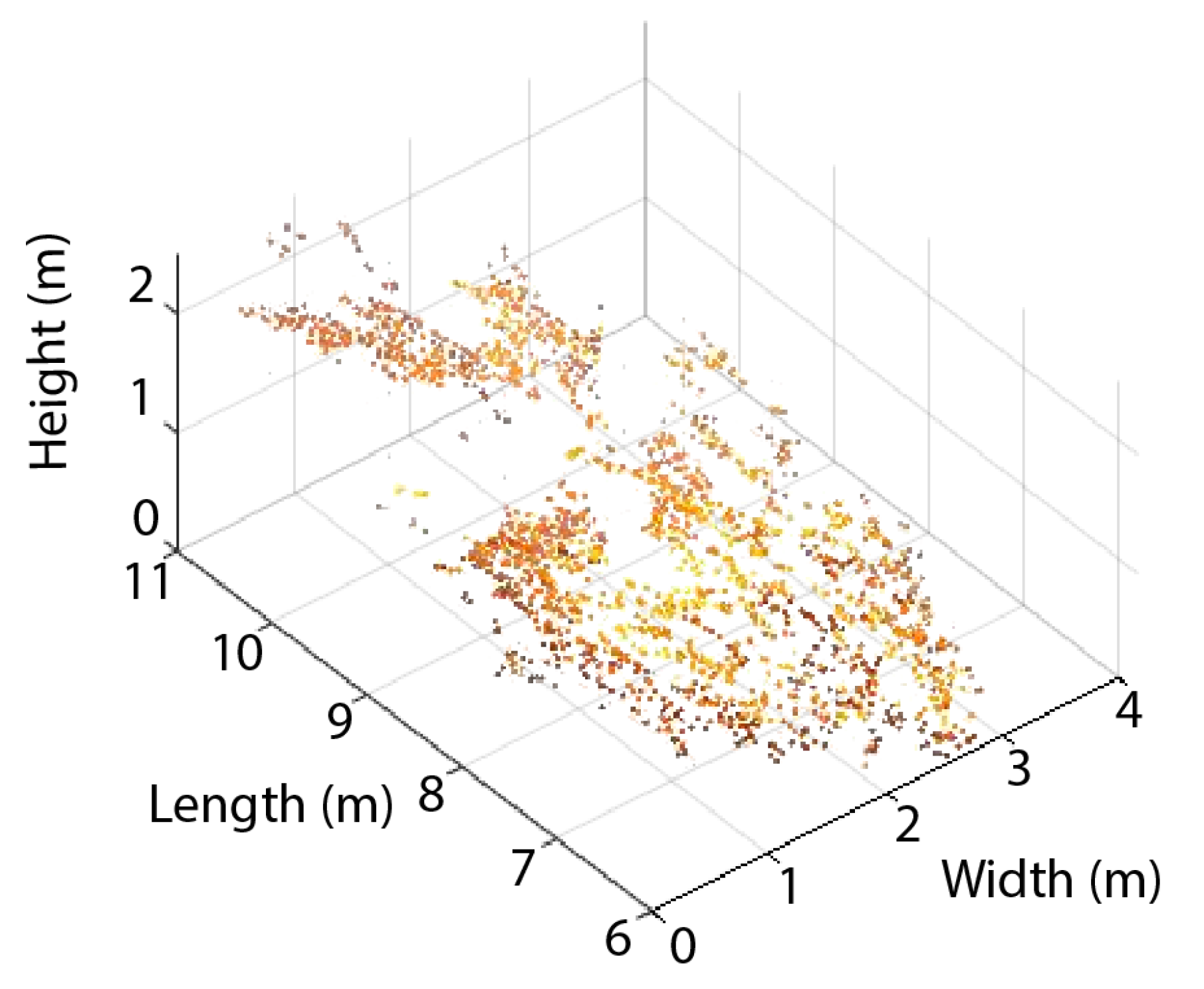




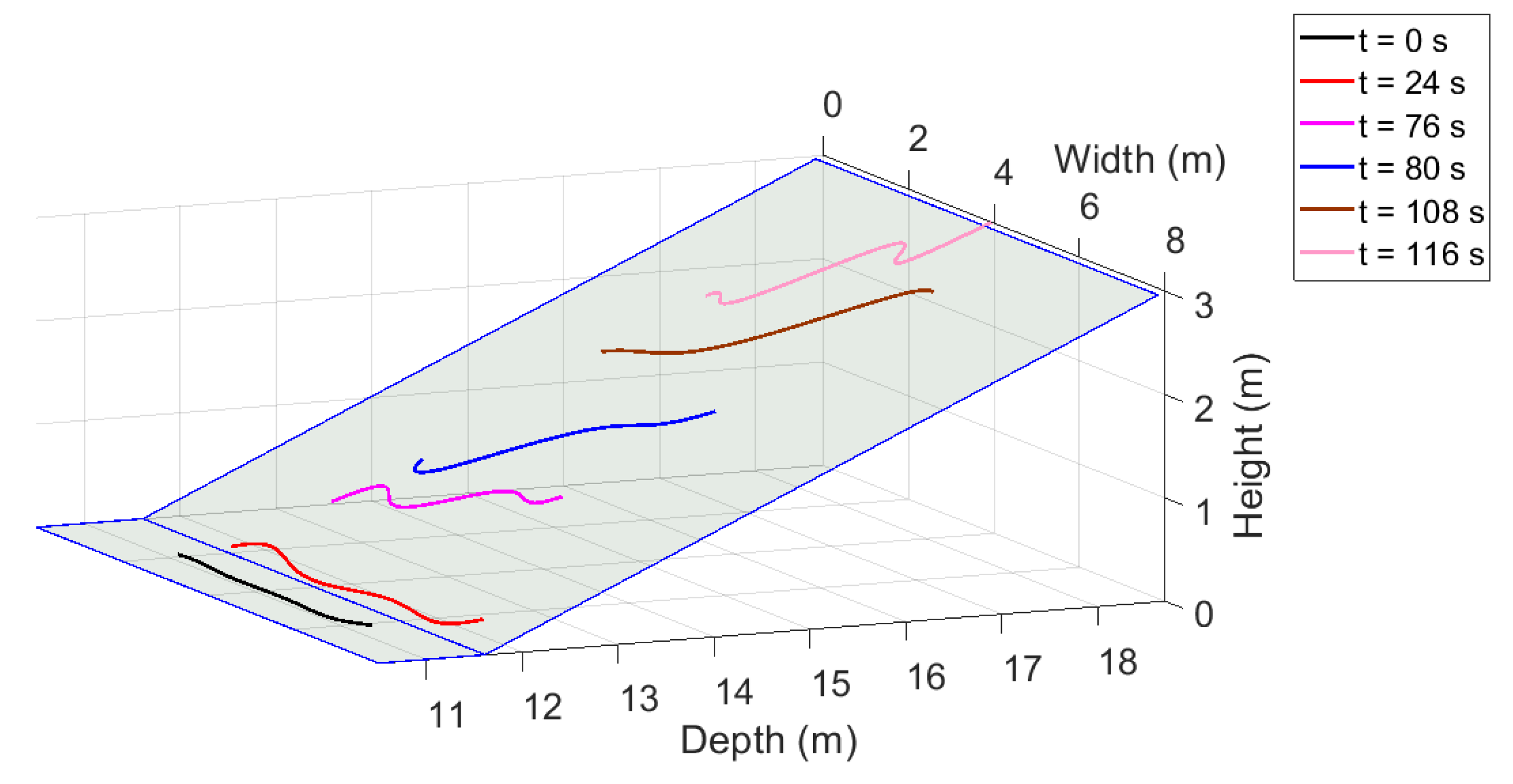
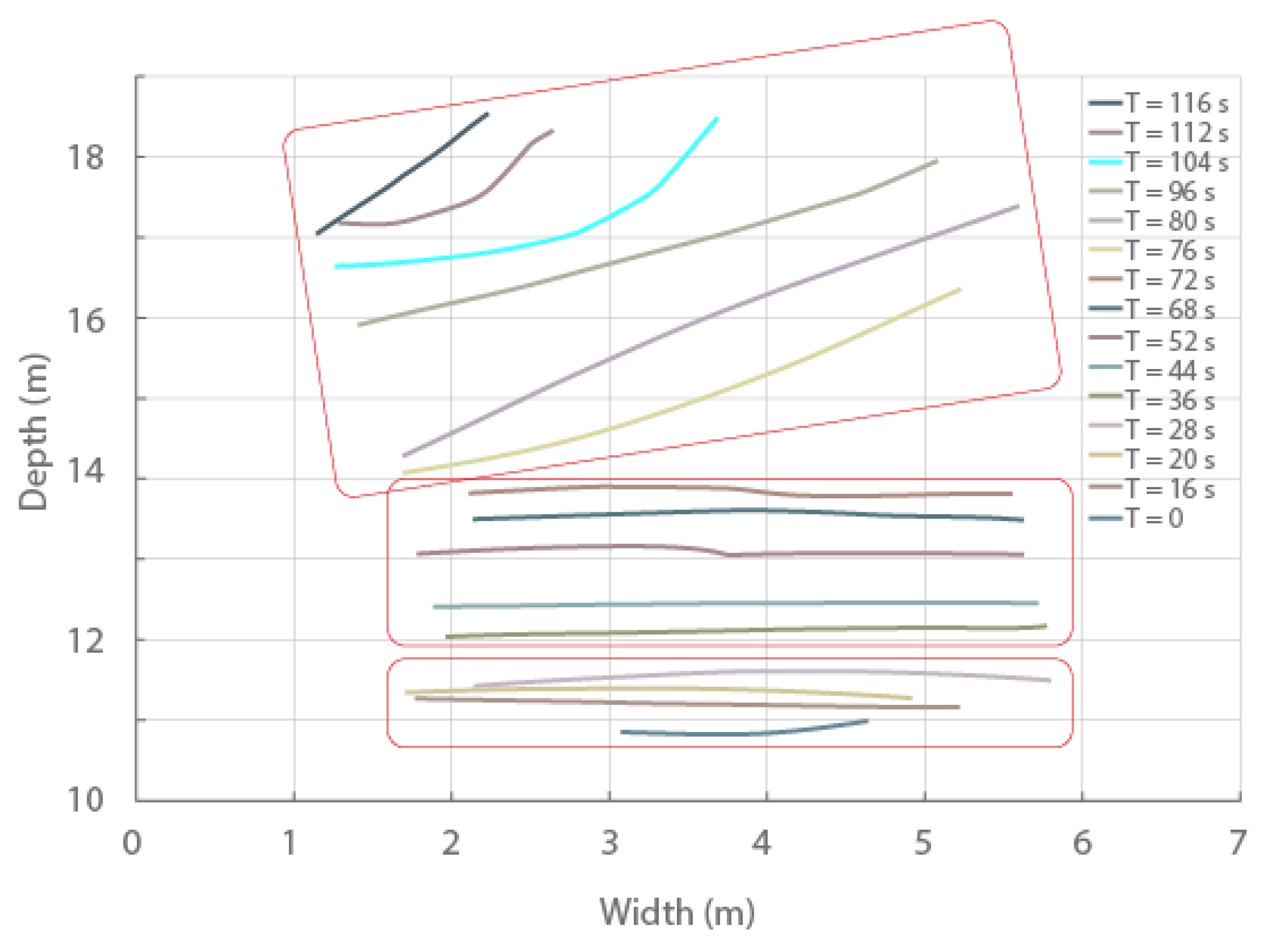
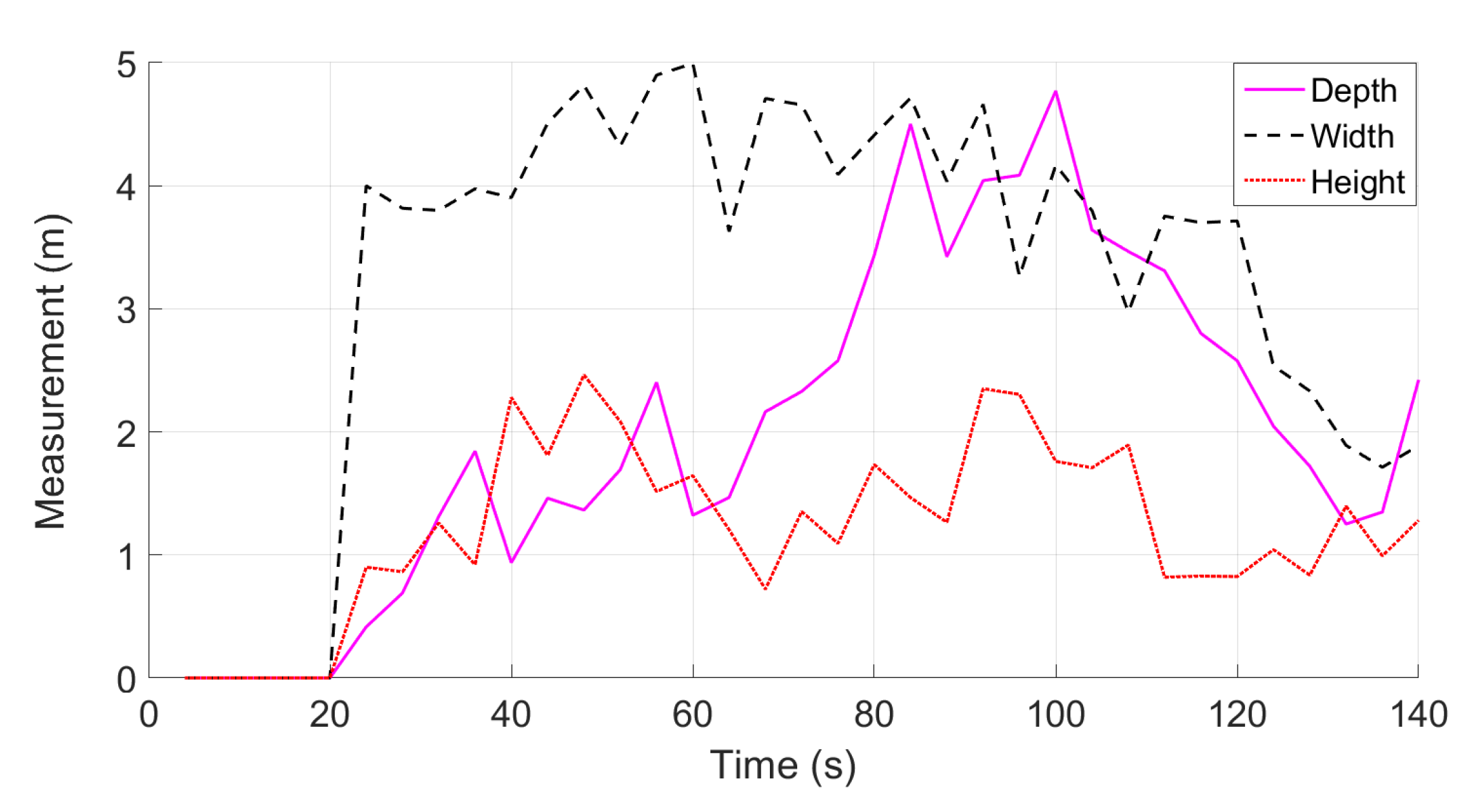
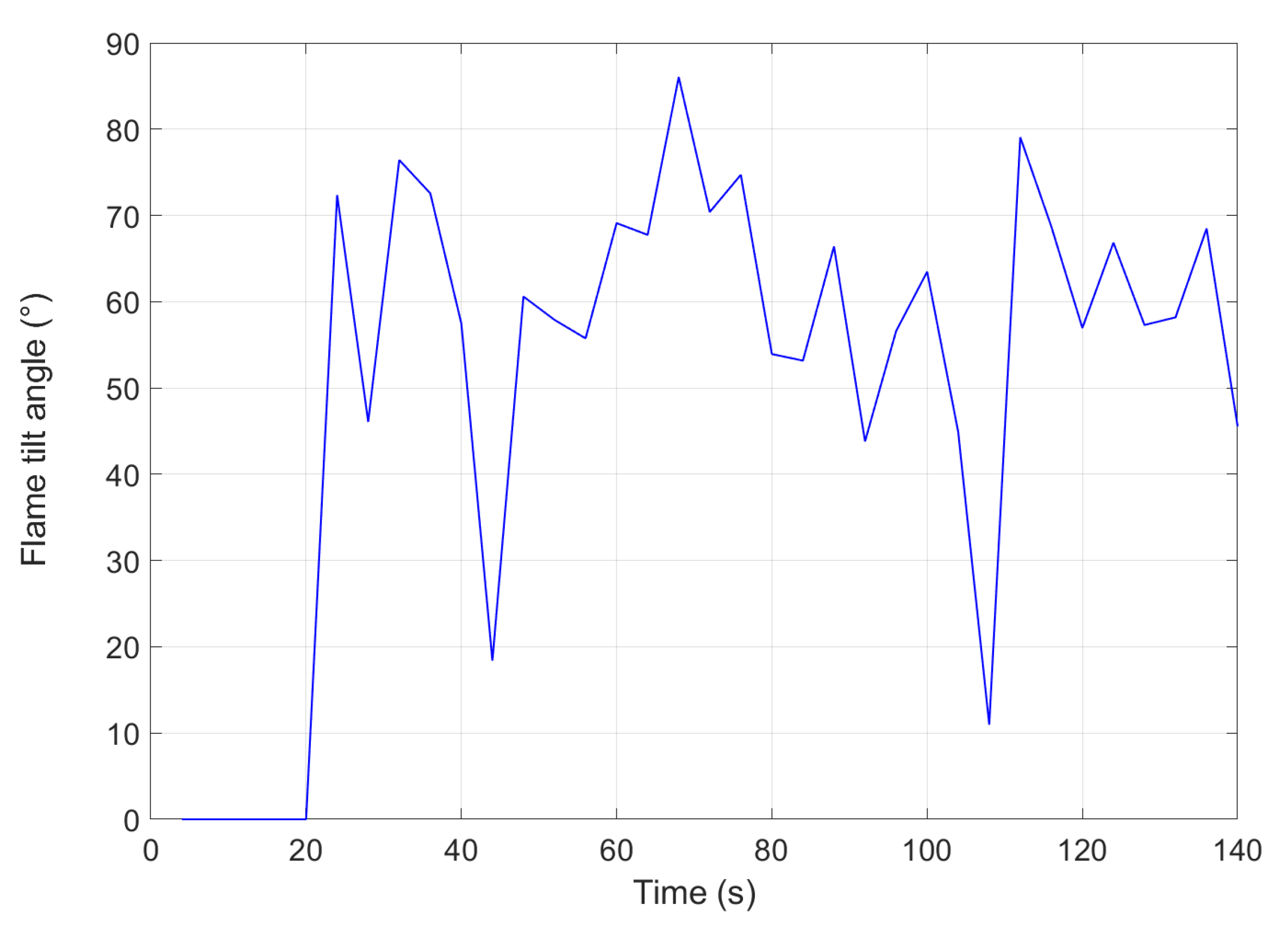
| Length (m) | Width (m) | Height (m) | Position (lat, lon) | |
|---|---|---|---|---|
| Real | 3.99 | 1.64 | 1.50 | (42.2999911, 9.1755291) |
| Estimated | 3.96 | 1.62 | 1.48 | (42.2999923, 9.1755259) |
| Error | 0.7% | 1.2% | 1.1% | 0.26 m |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ciullo, V.; Rossi, L.; Pieri, A. Experimental Fire Measurement with UAV Multimodal Stereovision. Remote Sens. 2020, 12, 3546. https://doi.org/10.3390/rs12213546
Ciullo V, Rossi L, Pieri A. Experimental Fire Measurement with UAV Multimodal Stereovision. Remote Sensing. 2020; 12(21):3546. https://doi.org/10.3390/rs12213546
Chicago/Turabian StyleCiullo, Vito, Lucile Rossi, and Antoine Pieri. 2020. "Experimental Fire Measurement with UAV Multimodal Stereovision" Remote Sensing 12, no. 21: 3546. https://doi.org/10.3390/rs12213546
APA StyleCiullo, V., Rossi, L., & Pieri, A. (2020). Experimental Fire Measurement with UAV Multimodal Stereovision. Remote Sensing, 12(21), 3546. https://doi.org/10.3390/rs12213546







