Digital Elevation Model Quality Assessment Methods: A Critical Review
Abstract
1. Introduction
- New platforms extended the capabilities of the aircraft: satellites covering larger areas (first TIROS observation satellite in 1960, across-track stereoscopy from different orbits with SPOT-1 in 1986, along-track stereoscopy with SPOT-5 in 2002), UAVs (fixed-wing for large area surveys, multirotor for small area surveys requiring agility and precision), and mobile mapping systems on land vehicles.
- New processing methods were developed, such as aerotriangulation and automatic image matching that made it possible to process large quantities of images for the industrial production of orthophoto mosaics and altimetric databases with few ground control points [5], and the synergy between digital photogrammetry and computer vision led to very powerful 3D reconstruction methods such as SfM (structure from motion).
- DEM is multi-user information, so that multiple quality criteria must be met, and although a particular user may specify application-driven requirements, the case of multi-user databases is obviously more complex.
- The Earth’s surface is a material object that speaks to our senses, so that one can complain about unrealistic relief modelling even in an unknown region; this leads to strong requirements including aesthetic ones.
2. Prerequisite: Definition of the Nominal Terrain
3. DEM as a Cartographic Product
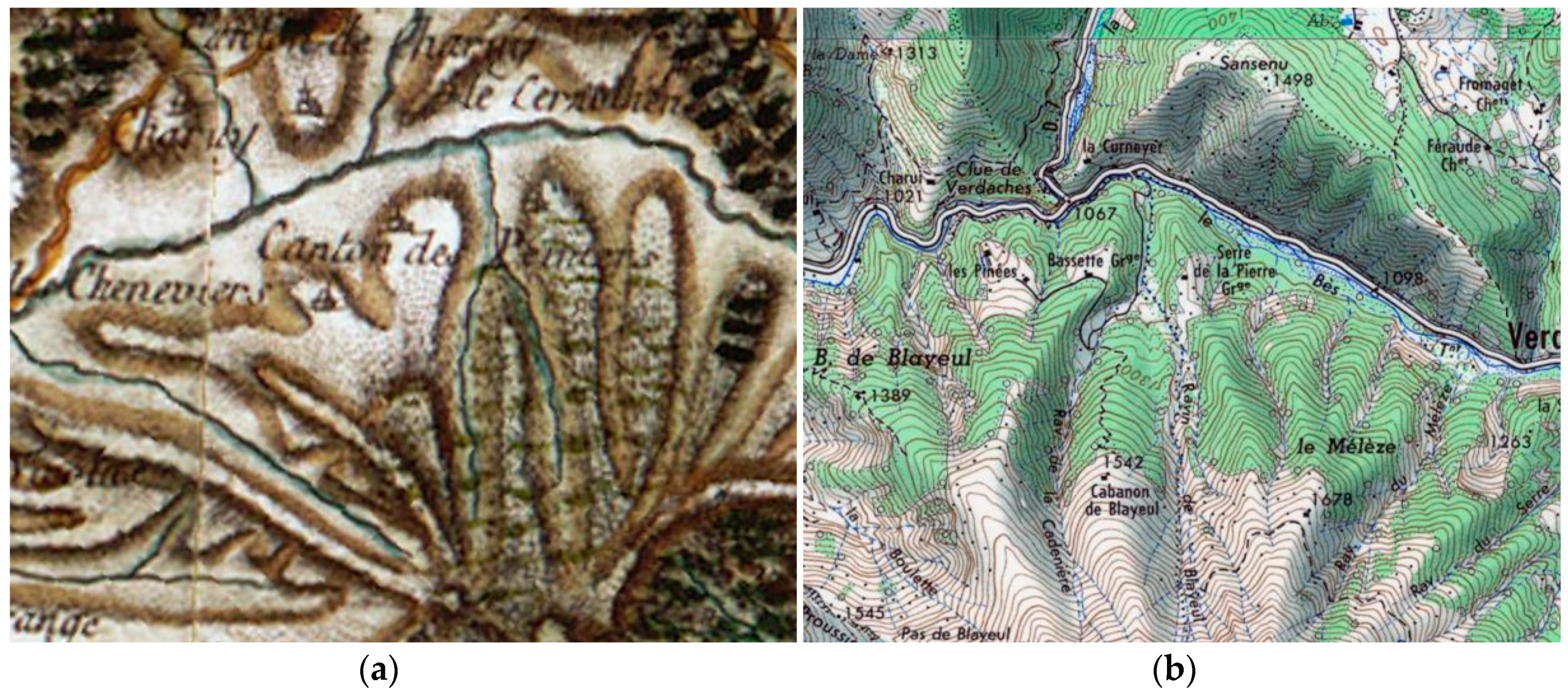
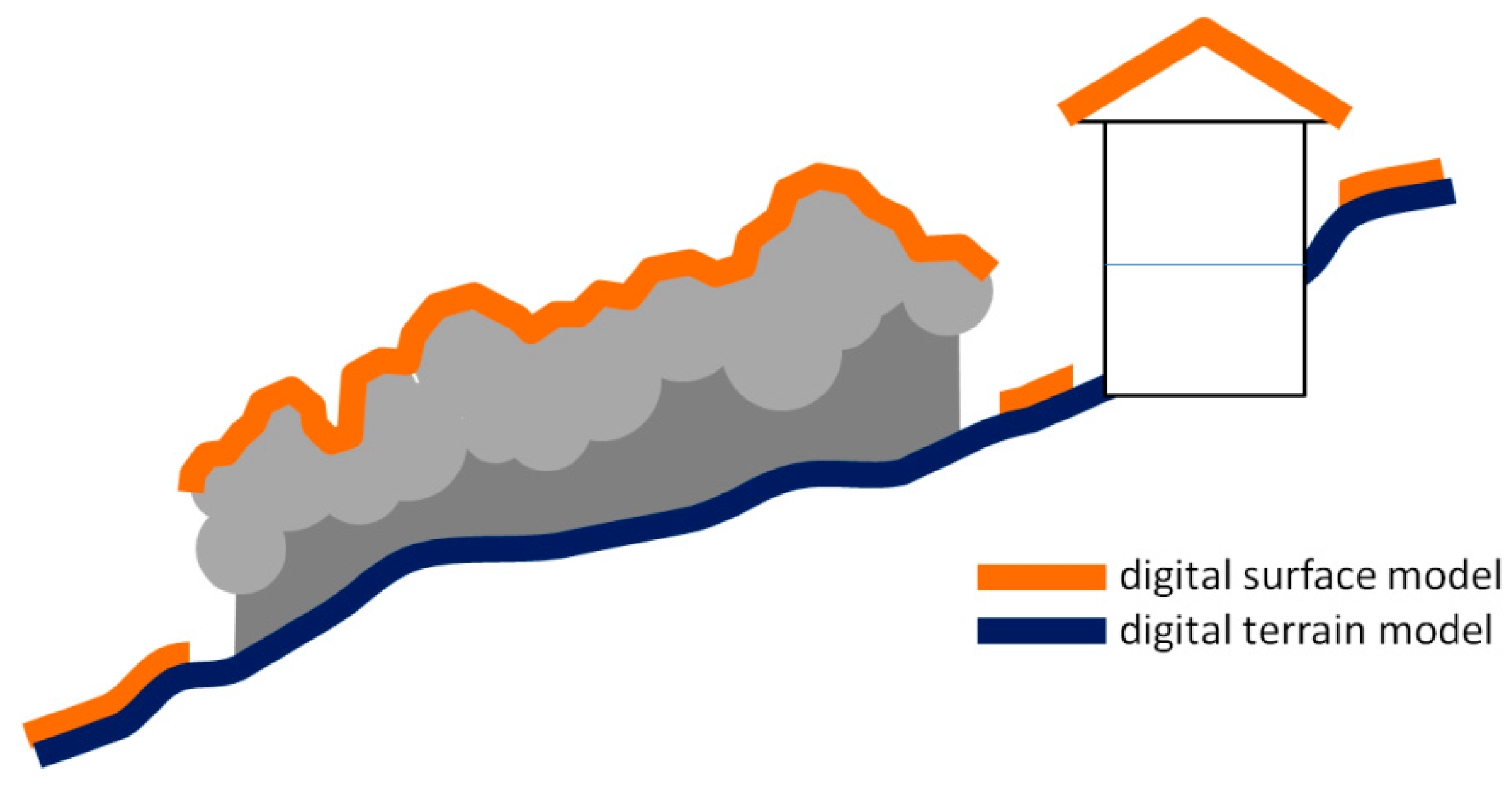
3.1. A Very Peculiar Surface
3.2. Planimetric Grid Sructure
3.2.1. Grid Structure
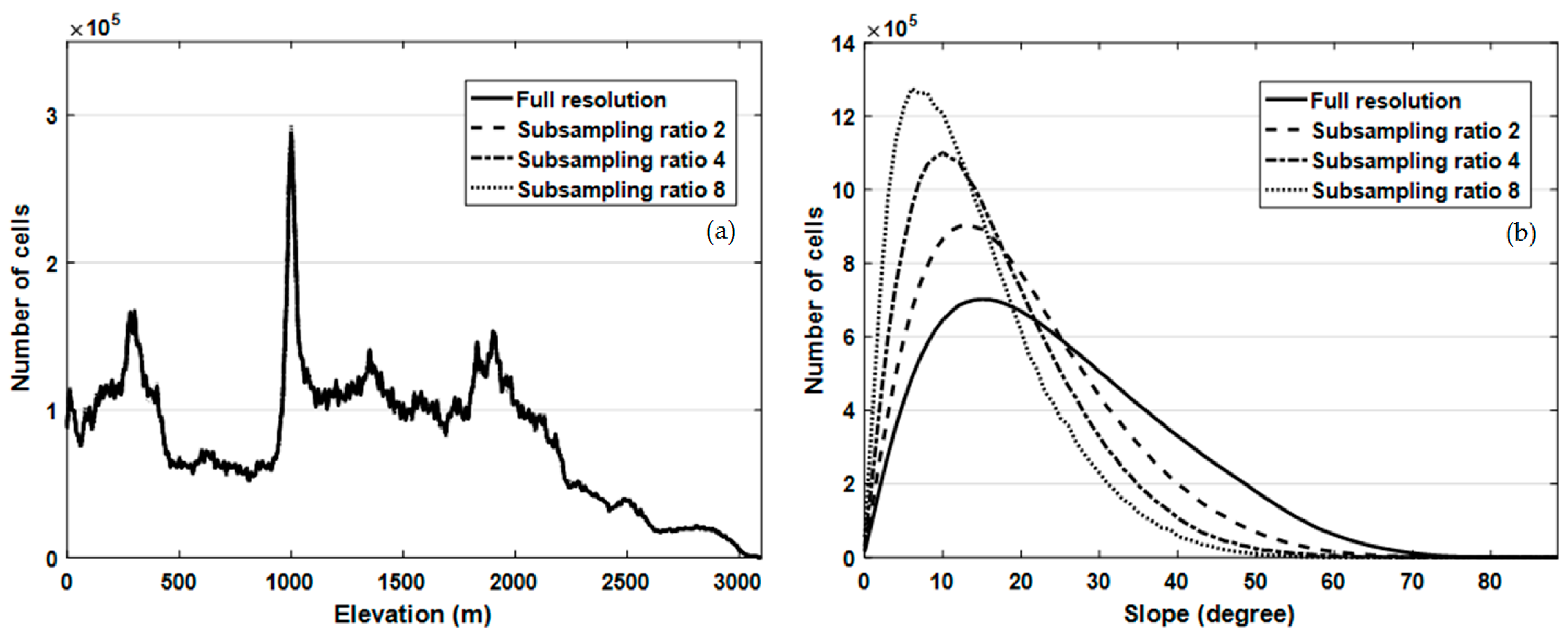
- The mesh size (and therefore the grid density) has an impact on the DEM absolute accuracy, but also on the ability of the DEM to describe landforms as shown below in Section 4.2. This ability is intuitive, since a smaller mesh is expected to allow a better rendering of small topographic objects, but a signal processing approach may also provide criteria to optimize resampling and to detect DEM errors [50]. The link between mesh size and resolution, and the way DEM quality assessment should consider these concepts, are addressed in Section 6.
- The mesh shape has an influence on the adequacy of the surface modelling to local landforms. Between the two most common grid structures, namely constant size squares and variable size triangles, the latter is clearly better suited to describe a surface morphology in which drainages, ridges and other slope breaks have variable orientations. However, there are several solutions to build a network of triangles from a given point cloud. For example, the Delaunay triangulation is advantageous to avoid very elongated triangles (which are less suitable for spatial analysis), but it does not necessarily give the most accurate DEM nor the most respectful one of terrain shapes: it must therefore be constrained so that the edges of the triangles are placed along slope discontinuities such as drainages or other slope break lines. This is an advantage of triangle networks, which are able to adapt to the topography.
3.2.2. Interpolation Algorithm
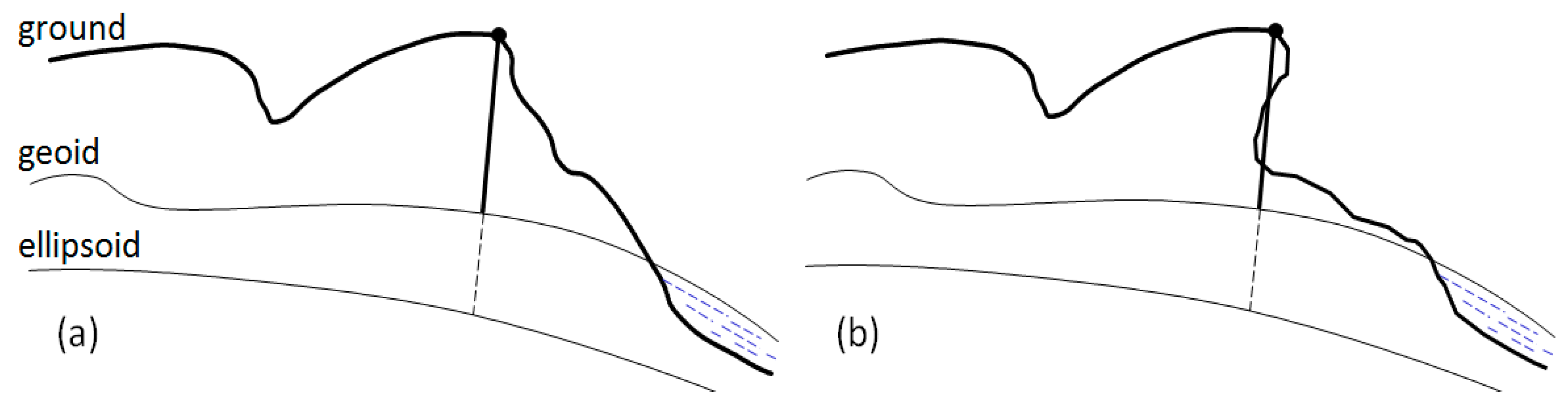
3.3. Numerical Representation of Elevation Values
4. Main DEM Quality Assessment Approaches
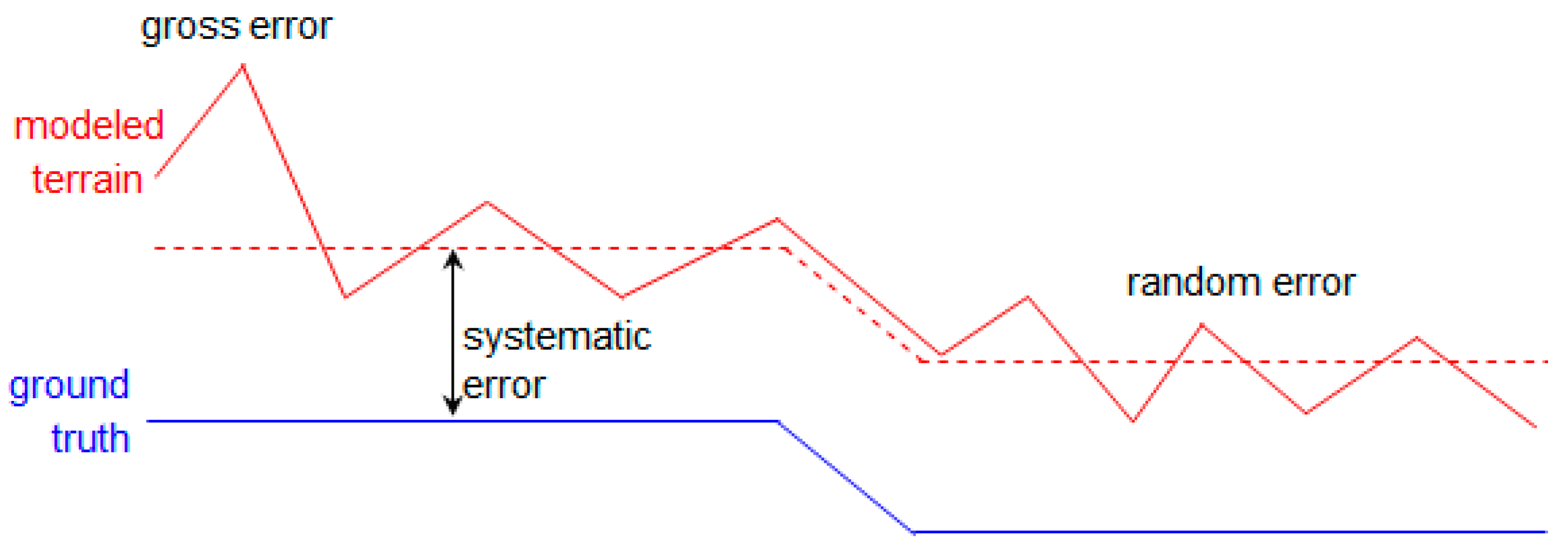
4.1. External Quality Assessment
4.1.1. Comparison with Ground Control Data
- It must be much more accurate than the evaluated DEM.
- It must be dense enough and well distributed over the area to allow meaningful statistical analysis, and even a spatial analysis of the error.
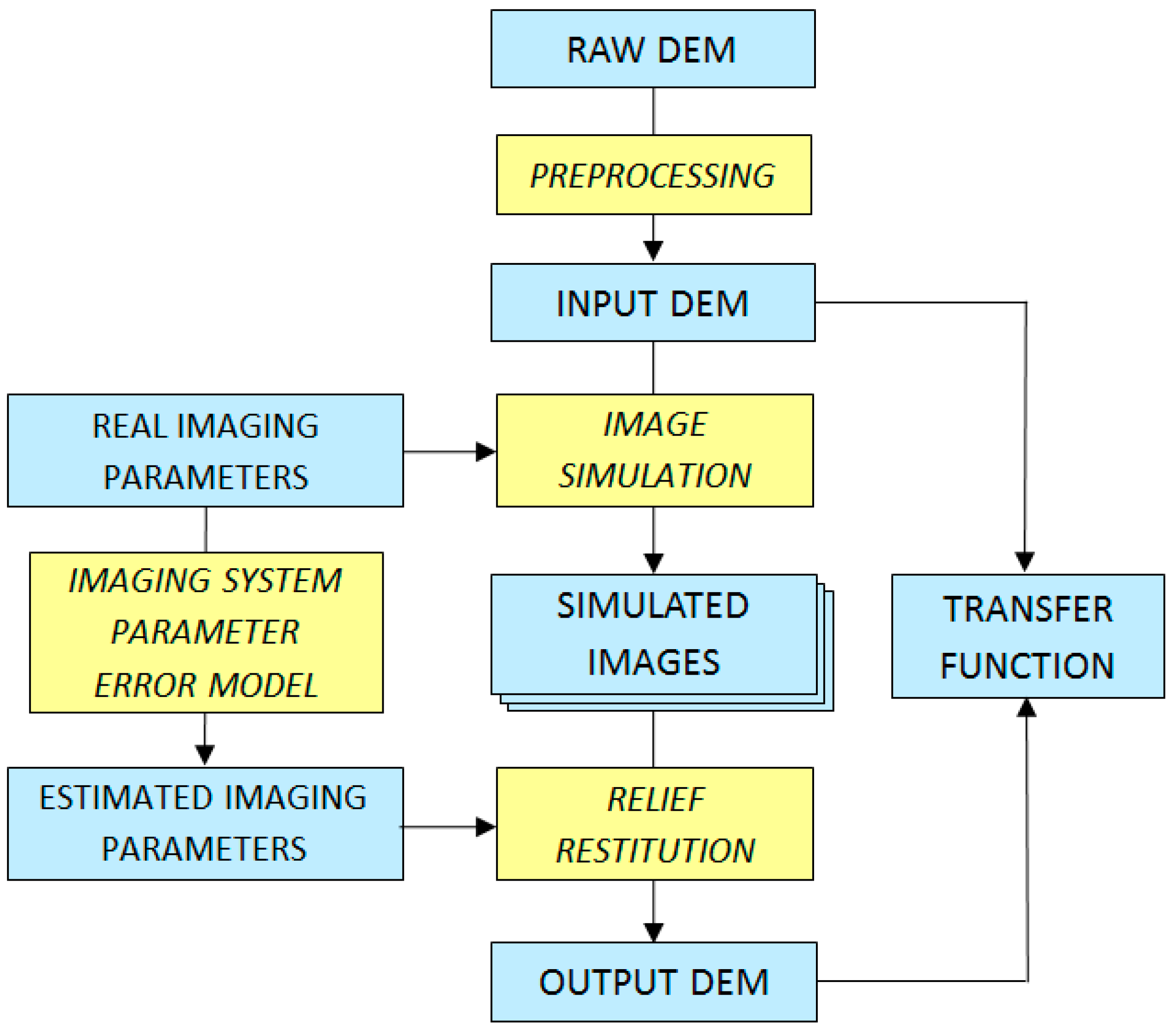
4.1.2. Simulation-Based DEM Production Method Validation
- The topographic restitution method can be tested over a variety of landscapes, leading to more comprehensive conclusions than over a particular DEM.
- It can also be tested with a variety of sensor parameters and orbit configurations, leading to recommendations for optimum image acquisition conditions if the images are to be processed for DEM production.
- The input DEM can be reprocessed, either to exaggerate the elevation amplitude, or to introduce topographic details such as microrelief or buildings (note that all these changes in the input DEM can be parametrically controlled, allowing analytical sensitivity studies). Fractal resampling can be implemented to produce a more realistic input DEM [102], and geomorphology provides criteria to verify this realism requirement in accordance with the principles of internal validation which we will see further [103].
- Sensor parameter uncertainties can be introduced to consider the fact that the DEM production method always uses an approximation of the exact parameters.
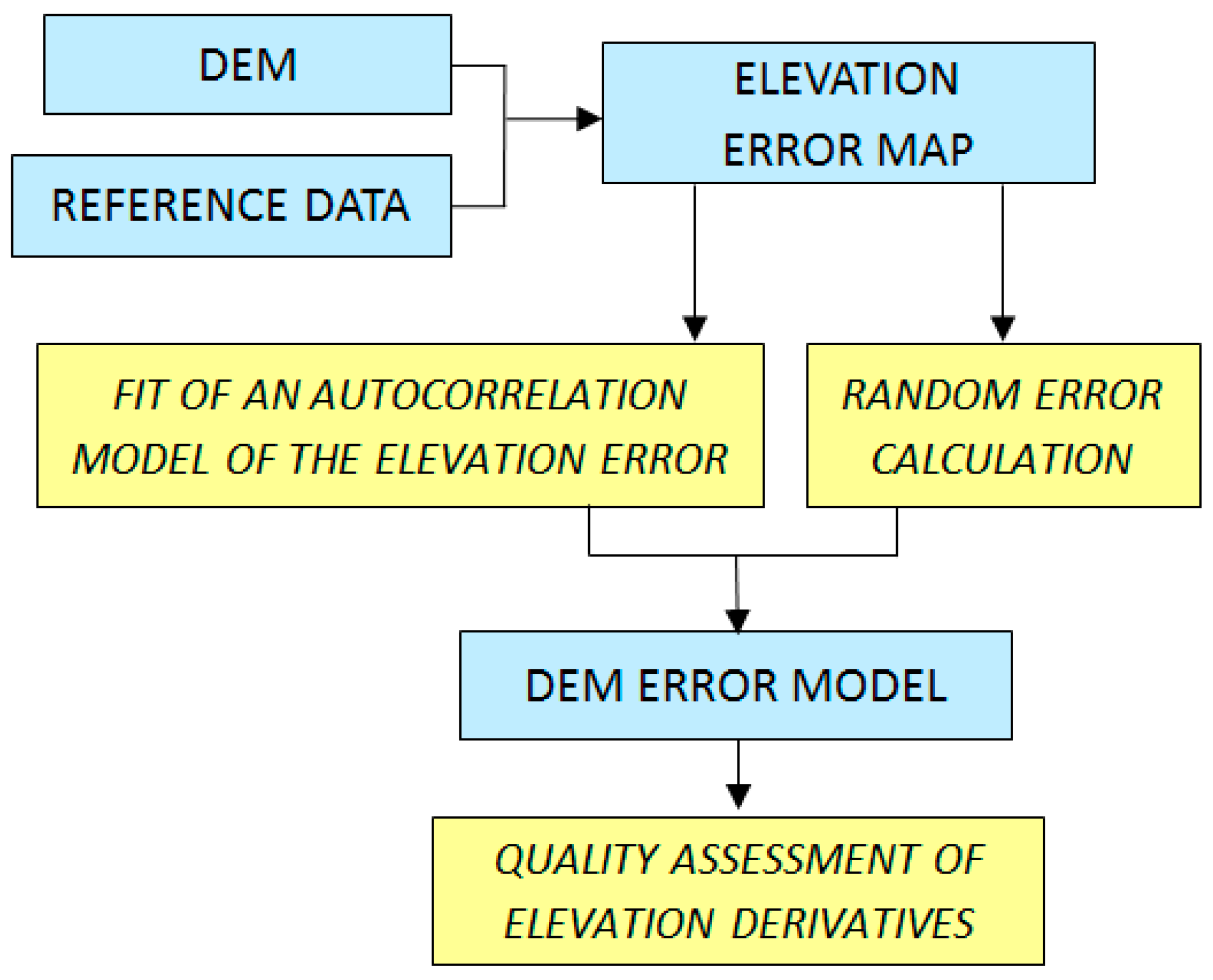
4.2. Internal Quality Assessment
4.2.1. Visual Control
4.2.2. Quantitative Internal Quality Assessment
5. DEM Validation at Different Levels
5.1. From Point Cloud to Grid Surface Model
- In terms of absolute vertical accuracy, the input data are essential: the errors of the input point cloud are generally autocorrelated (due to orbit, relief…) so that they remain in the resampled DEM whatever the selected interpolation method.
- In terms of shape realism, the interpolation plays a major role since it can remove or create artifacts (noise, stripe, pixelation, etc.). The resampling step may filter the noise of the input point cloud and therefore improve the quality in terms of elevation accuracy. In contrast, the interpolation implemented for resampling may produce an exaggerated smoothing effect or a raster grid effect, resulting in a quality degradation in terms of shape rendering. Indeed, the choice of an interpolation algorithm affects not only the elevation absolute accuracy but also the geomorphometric indices [150], and this effect depends on the local terrain morphology [151,152,153,154]. The effect of an interpolator on the DEM quality depends on both the DEM production technique and the application-oriented user requirements [43,155,156]. Hengl and Evans [70] distinguish three aspects for classifying interpolation methods, namely, the smoothing effect (exact or approximate interpolation), the proximity effect (local or global interpolation) and the stochastic hypothesis. For example, an exact interpolation method, such as linear interpolation, is recommended if the data are very dense and accurate, while a smoothing method should be used if the data are noisy. Mitas and Mitasova [157] state that the description of the smoothing and tension effects and the consideration of ridges and streams are the most important evaluation criteria for an interpolation method.
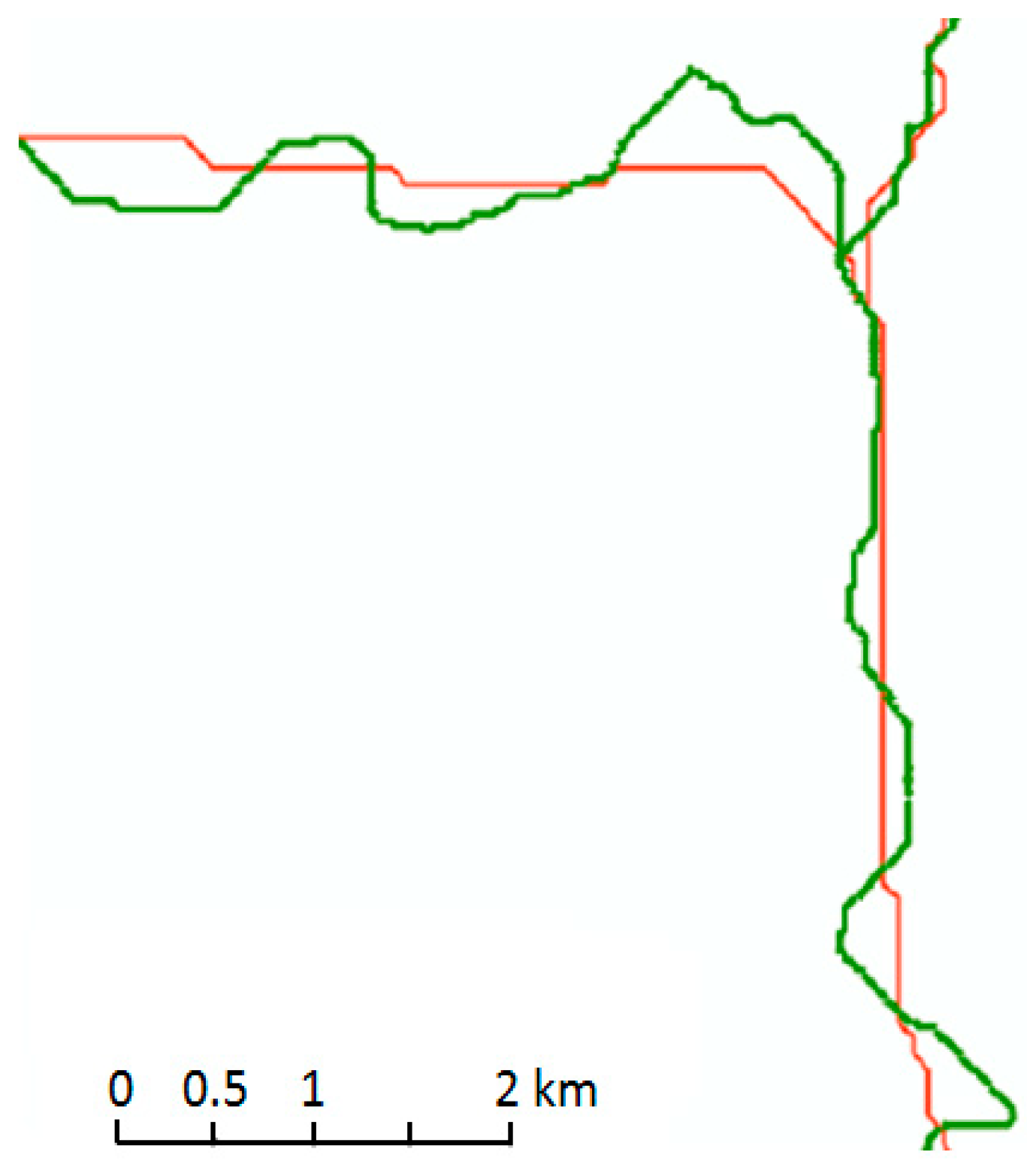
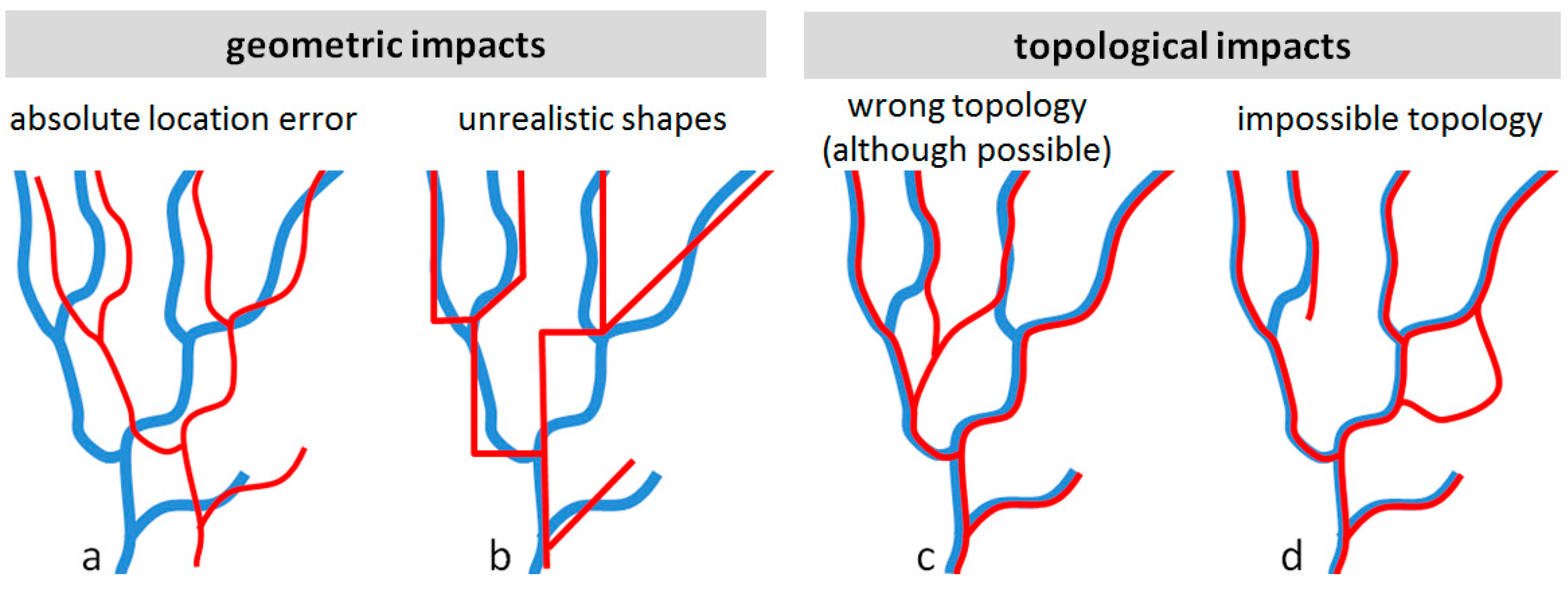
5.2. From Grid Surface Model to Derived Topographic Features
- The accuracy of the thickness, which can be estimated through the RMSE of the DEM difference, is:which in the case of two DEMs having the same quality can be written:hence a very strong requirement in terms of DEM accuracy.
- whatever the accuracy of the two DEMs, any horizontal registration error Δx between them will lead to a vertical error Δz on the thickness, which is a function of the slope θ:
5.3. Challenge of Global DEM Quality Assessment
- Allow a user to predict the quality of the DEM on a given site for a given application.
- Guide product improvements by post-processing or by merging data from different sources.
- Consider the variety of geographic conditions as we have just seen, to guarantee that the conclusions on the global DEM quality do not depend on particular conditions, or to limit the scope of the conclusions to a particular landscape.
- Consider different quality criteria as suggested in Section 4 (including the artifacts produced by resampling, which have been shown to also have a significant impact on the geomorphometric quality of the final DEM), so that a variety of user needs is considered. Indeed, a global DEM is typically a multi-user database, for which it is difficult to define quality standards that are suitable for all potential users.
6. Resolution Dependency in DEM Validation
6.1. From Scale to Resolution
- The point cloud generally has a variable density, with low density areas due to physical reasons (e.g., airborne lidar point clouds have a lower density under forests than on bare ground); moreover, a cloud (for photogrammetry) or a forest (for repeat-pass SAR interferometry) can prevent the calculation of elevations and create holes in the DEM so that the resolution is locally lost.
- Whatever the input point cloud, the interpolator imposes its form to some extent, mainly in low density areas.
6.2. Stability of Topographic Indices with Regards to Resolution
6.3. Relevant Resolution for Landform Modelling
7. Discussion
- σz is a very optimistic indicator and it may give the illusion that the accuracy of a global DEM is the same all over the world. σz is a very limited indicator as we have shown, excellent for predicting the vertical accuracy of the DEM but unsuitable for guaranteeing a realistic shape rendering.
- σz also depends on slope and landcover, and this double influence cannot be predicted quantitatively because the slope is not necessarily known before the DEM is calculated and the landcover can be described qualitatively at best.
- The interpolation, which is applied to resample the DEM in the required grid structure, also has an impact on the quality by creating artifacts.
- Mathematical modelling of the error expected for different DEM production techniques as a function of landscape characteristics and acquisition/processing parameters.
- Definition of invariant properties of the Earth’s surface to support internal quality assessment methods, based on the advances of geoscience and even comparative planetology.
- Analysis of scale effects, which has become a challenging research issue with the development of very high-resolution products, leading to increased needs for gigantic data volumes management and for the characterization of extremely complex phenomena.
8. Conclusions
- The quality of a DEM makes sense for a given application, i.e., depends on user needs.
- The nominal terrain, i.e., the physical surface, which is supposed to be modelled, must be explicitly defined for the quality to make sense.
- The quality of a DEM can be assessed using different methods, with or without ground control data, according to quantitative criteria.
- Artifact detection can be carried out with no ground control data, by revealing the non-compliance of the DEM with physical or statistical characteristics of the Earth’s surface.
- Visual analysis can complement quality control provided that the DEM is visualized appropriately.
- Testing mapping methods on simulated images allows a more in-depth validation of these methods.
- The quality must be considered at a given scale. However, the concept of scale is an abuse of language that comes from the paper map and must be replaced by equivalent concepts adapted to the digital world.
- The quality of a global DEM cannot be easily deduced from an analysis of local data nor from a theoretical approach only: it also requires a great deal of experience based on the analysis of many DEMs on a variety of landscapes, or on simulation-based studies.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Goldthwaite, R.P.; Matsch, C.L. Glossary of Geology, 4th ed.; American Geological Institute: Alexandria, VA, USA, 1997. [Google Scholar]
- Huggett, R.J. What is Geomorphology? In Fundamentals of Geomorphology, 3rd ed.; Routledge: London, UK, 2011; pp. 3–18. [Google Scholar]
- Laussedat, A. Mémoire Sur L’Emploi de la Photographie Dans la Levée Des Plans par M. Laussedat. Comptes Rendus Séances Académie Sci. 1859, 49, 732–734. [Google Scholar]
- Li, W. Digital Photogrammetry: A Practical Course; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006; ISBN 978-3-540-29153-4. [Google Scholar]
- Kasser, M.; Egels, Y. Digital Photogrammetry; Taylor & Francis: London, UK; New York, NY, USA, 2002. [Google Scholar]
- Graham, L. Synthetic Interferometer Radar for Topographic Mapping. Proc. IEEE 1974, 62, 763–768. [Google Scholar] [CrossRef]
- Toutin, T.; Gray, L. State-of-the-Art of Elevation Extraction from Satellite SAR Data. ISPRS J. Photogramm. Remote Sens. 2000, 55, 13–33. [Google Scholar] [CrossRef]
- Leberl, F. Radargrammetric Image Processing; Artech House: London, UK, 1989; ISBN 978-0-89006-273-9. [Google Scholar]
- Baltsavias, E. Airborne Laser Scanning: Existing Systems and Firms and Other Resources. ISPRS J. Photogramm. Remote Sens. 1999, 54, 164–198. [Google Scholar] [CrossRef]
- Hodgson, M.E.; Bresnahan, P. Accuracy of Airborne Lidar-Derived Elevation. Photogramm. Eng. Remote Sens. 2004, 70, 331–339. [Google Scholar] [CrossRef]
- Moore, I.D.; Grayson, R.B.; Ladson, A.R. Digital Terrain Modelling: A Review of Hydrological, Geomorphological, and Biological Applications. Hydrol. Process. 1991, 5, 3–30. [Google Scholar] [CrossRef]
- Hengl, T.; Reuter, H.I. Geomorphometry: Concepts, Software, Applications; Elsevier Science: Amsterdam, The Netherlands, 2009; ISBN 978-0-12-374345-9. [Google Scholar]
- Park, S.; McSweeney, K.; Lowery, B. Identification of the Spatial Distribution of Soils Using a Process-Based Terrain Characterization. Geoderma 2001, 103, 249–272. [Google Scholar] [CrossRef]
- Zhang, J.; Xu, W.; Qin, L.; Tian, Y. Spatial Distribution Estimates of the Urban Population Using DSM and DEM Data in China. ISPRS Int. J. Geo-Inf. 2018, 7, 435. [Google Scholar] [CrossRef]
- Shimada, M. Ortho-Rectification and Slope Correction of SAR Data Using DEM and Its Accuracy Evaluation. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2010, 3, 657–671. [Google Scholar] [CrossRef]
- Reinartz, P.; Müller, R.; Schwind, P.; Suri, S.; Bamler, R. Orthorectification of VHR Optical Satellite Data Exploiting the Geometric Accuracy of TerraSAR-X data. ISPRS J. Photogramm. Remote Sens. 2011, 66, 124–132. [Google Scholar] [CrossRef]
- Pike, R.J. Geomorphometry-Diversity in Quantitative Surface Analysis. Prog. Phys. Geogr. Earth Environ. 2000, 24, 1–20. [Google Scholar] [CrossRef]
- Rasemann, S.; Schmidt, J.; Schrott, L.; Dikau, R. Geomorphometry in Mountain Terrain. In GIS & Mountain Geomorphology; Bishop, M.P., Shroder, J.F., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 101–145. [Google Scholar]
- Pike, R.; Evans, I.; Hengl, T. Geomorphometry: A Brief Guide. In Developments in Soil Organic Matter; Hengl, T., Reuter, H.I., Eds.; Elsevier BV: Amsterdam, The Netherlands, 2009; Volume 33, pp. 3–30. [Google Scholar]
- Macmillan, R.; Shary, P. Landforms and Landform Elements in Geomorphometry. In Developments in Soil Science; Hengl, T., Reuter, H.I., Eds.; Elsevier BV: Amsterdam, The Netherlands, 2009; Volume 33, pp. 227–254. [Google Scholar]
- Hengl, T.; MacMillan, R.A. Geomorphometry—A Key to Landscape Mapping and Modelling. In Developments in Soil Science; Hengl, T., Reuter, H.I., Eds.; Elsevier: Amsterdam, The Netherlands, 2009; Volume 33, pp. 433–460. [Google Scholar]
- Olaya, V. Basic Land-Surface Parameters. In Developments Soil Organic Matter; Hengl, T., Reuter, H.I., Eds.; Elsevier BV: Amsterdam, The Netherlands, 2009; Volume 33, pp. 141–169. [Google Scholar]
- Wilson, J.P.; Gallant, J.C. Terrain Analysis: Principles and Applications; John Wiley & Sons: Hoboke, NJ, USA, 2000; ISBN 978-0-471-32188-0. [Google Scholar]
- Schneider, B. On the Uncertainty of Local Shape of Lines and Surfaces. Cartogr. Geogr. Inf. Sci. 2001, 28, 237–247. [Google Scholar] [CrossRef]
- Holmes, K.; Chadwick, O.; Kyriakidis, P. Error in a USGS 30- Meter Digital Elevation Model and Its Impact on Terrain Modeling. J. Hydrol. 2000, 233, 154–173. [Google Scholar] [CrossRef]
- Shary, P.A.; Sharaya, L.S.; Mitusov, A.V. Fundamental Quantitative Methods of Land Surface Analysis. Geoderma 2002, 107, 1–32. [Google Scholar] [CrossRef]
- Heuvelink, G.B.M. Analysing Uncertainty Propagation in GIS: Why is it not that Simple? In Uncertainty in Remote Sensing and GIS; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2002; pp. 155–165. [Google Scholar]
- Heuvelink, G.B. Error Propagation in Environmental Modelling with GIS; CRC Press: Boca Raton, FL, USA, 1998. [Google Scholar]
- Polidori, L.; El Hage, M.; Villard, L.; Koleck, T.; Le Toan, T. Potential of P-Band Sar Topographic Products Over Forested Areas in Terms of Terrain Morphological Description: A Preliminary Study in the Framework of the Biomass Mission. In Proceedings of the Simposio Latinoamericano de Percepción Remota y Sistemas de Información Espacial, La Havana, Cuba, 6–9 November 2018. [Google Scholar]
- D’Alessandro, M.M.; Tebaldini, S. Digital Terrain Model Retrieval in Tropical Forests Through P-Band SAR Tomography. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6774–6781. [Google Scholar] [CrossRef]
- Le Toan, T.; Quegan, S.; Davidson, M.; Balzter, H.; Paillou, P.; Papathanassiou, K.; Plummer, S.; Rocca, F.; Saatchi, S.; Shugart, H.; et al. The BIOMASS Mission: Mapping Global Forest Biomass to Better Understand the Terrestrial Carbon Cycle. Remote Sens. Environ. 2011, 115, 2850–2860. [Google Scholar] [CrossRef]
- Fryer, J.G. A Simple System for Photogrammetric Mapping in Shallow Water. Photogramm. Rec. 2006, 11, 203–208. [Google Scholar] [CrossRef]
- Allouis, T.; Bailly, J.-S.; Feurer, D. Assessing Water Surface Effects on Lidar Bathymetry Measurements in Very Shallow Rivers: A Theoretical Study. In Proceedings of the Second ESA Space for Hydrology Workshop, Geneva, Switzerland, 12–14 November 2007; pp. 12–14. [Google Scholar]
- Gratiot, N.; Gardel, A.; Polidori, L. Remote Sensing Based Bathymetry on the Highly Dynamic Amazonian Coast. In Proceedings of the 9th International Coastal Symposium, Hornafjörður, Island, 5–8 June 2005; pp. 5–8. [Google Scholar]
- Dai, W.; Li, H.; Zhou, Z.; Cybele, S.; Lu, C.; Zhao, K.; Zhang, X.; Yang, H.; Li, D. UAV Photogrammetry for Elevation Monitoring of Intertidal Mudflats. J. Coast. Res. 2018, 85, 236–240. [Google Scholar] [CrossRef]
- Smith, L.C. Emerging Applications of Interferometric Synthetic Aperture Radar in Geomorphology and Hydrology. Ann. Assoc. Am. Geogr. 2002, 92, 385–398. [Google Scholar] [CrossRef]
- Catani, F.; Farina, P.; Moretti, S.; Nico, G.; Strozzi, T. On the Application of SAR Interferometry to Geomorphological Studies: Estimation of Landform Attributes and Mass Movements. Geomorphology 2005, 66, 119–131. [Google Scholar] [CrossRef]
- Toutin, T. ASTER DEMs for Geomatic and Geoscientific Applications: A Review. Int. J. Remote Sens. 2008, 29, 1855–1875. [Google Scholar] [CrossRef]
- Biljecki, F.; LeDoux, H.; Stoter, J.; Zhao, J. Formalisation of the Level of Detail in 3D City Modelling. Comput. Environ. Urban Syst. 2014, 48, 1–15. [Google Scholar] [CrossRef]
- Biljecki, F.; LeDoux, H.; Stoter, J. An Improved LOD Specification for 3D Building Models. Comput. Environ. Urban Syst. 2016, 59, 25–37. [Google Scholar] [CrossRef]
- Longley, P.; Goodchild, M.F. Geographic Information Science and Systems; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Poiker, T.K.; Fowler, R.J.; Little, J.J.; Mark, D.M. The Triangulated Irregular Network. In Proceedings of the Digital Terrain Models Symposium, Missouri, MO, USA, 9–11 May 1978; pp. 516–540. [Google Scholar]
- Li, Z.; Zhu, C.; Gold, C. Accuracy of Digital Terrain Models. In Digital Terrain Modeling Principles and Methodology; Taylor and Francis: New York, NY, USA, 2005; pp. 158–190. [Google Scholar]
- Hutchinson, M.F. Calculation of Hydrologically Sound Digital Elevation Models. In Proceedings of the Third International Symposium on Spatial Data Handling, Sydney, Australia, 17–19 August 1988; pp. 117–133. [Google Scholar]
- Hutchinson, M. A New Procedure for Gridding Elevation and Stream Line Data with Automatic Removal of Spurious Pits. J. Hydrol. 1989, 106, 211–232. [Google Scholar] [CrossRef]
- Makarovic, B. Progressive Sampling for Digital Terrain Models. ITC J. 1973, 3, 397–416. [Google Scholar]
- Makarovic, B. Composite Sampling for Digital Terrain Models. ITC J. 1977, 3, 406–433. [Google Scholar]
- Charif, M.; Makarovic, B. Optimizing Progressive and Composite Sampling for DTMs. ITC J. 1989, 2, 104–111. [Google Scholar]
- Pajarola, R.; Gobbetti, E. Survey of Semi-Regular Multiresolution Models for Interactive Terrain Rendering. Vis. Comput. 2007, 23, 583–605. [Google Scholar] [CrossRef]
- Florinsky, I.V. Errors of Signal Processing in Digital Terrain Modelling. Int. J. Geogr. Inf. Sci. 2002, 16, 475–501. [Google Scholar] [CrossRef]
- Heritage, G.L.; Milan, D.J.; Large, A.R.; Fuller, I. Influence of Survey Strategy and Interpolation Model on DEM Quality. Geomorphology 2009, 112, 334–344. [Google Scholar] [CrossRef]
- Weber, D.; Englund, E. Evaluation and Comparison of Spatial Interpolators. Math. Geol. 1992, 24, 381–391. [Google Scholar] [CrossRef]
- Zheng, X.; Chen, Z.; Han, Q.; Deng, X.; Sun, X.; Yin, Q. Self-similarity Based Multi-layer DEM Image Up-Sampling. In Advances in Intelligent Systems and Computing; Springer Science and Business Media LLC: Cham, Switzerland, 2019; pp. 533–545. [Google Scholar]
- Polidori, L.; Chorowicz, J. Comparison of Bilinear and Brownian Interpolation for Digital Elevation Models. ISPRS J. Photogramm. Remote Sens. 1993, 48, 18–23. [Google Scholar] [CrossRef]
- Featherstone, W.; Dentith, M.; Kirby, J. Strategies for the Accurate Determination of Orthometric Heights From Gps. Surv. Rev. 1998, 34, 278–296. [Google Scholar] [CrossRef]
- Erol, B.; Erol, S.; Celik, R.N. Height Transformation Using Regional Geoids and GPS/Levelling in Turkey. Surv. Rev. 2008, 40, 2–18. [Google Scholar] [CrossRef]
- Durland, N.H. Defining Mean Sea Level in Military Simulations with DTED. In Proceedings of the 2009 Spring Simulation Multiconference, San Diego, CA, USA, 22–27 March 2009; Society for Computer Simulation International: San Diego, CA, USA, 2009; pp. 1–3. [Google Scholar]
- Paparoditis, N.; Dissard, O. 3D Data Acquisition from Visible Images. In Digital Photogrammetry; Kasser, M., Egels, Y., Eds.; Taylor & Francis: London, UK; New York, NY, USA, 2002; Volume 48, pp. 168–220. [Google Scholar]
- Rabus, B.; Eineder, M.; Roth, A.; Bamler, R. The Shuttle Radar Topography Mission—A New Class of Digital Elevation Models Acquired by Spaceborne Radar. ISPRS J. Photogramm. Remote Sens. 2003, 57, 241–262. [Google Scholar] [CrossRef]
- Jarvis, A.; Rubiano, J.; Nelson, A.; Farrow, A.; Mulligan, M. Practical Use of SRTM Data in the Tropics: Comparisons with Digital Elevation Models Generated from Cartographic Data; International Centre for Tropical Agriculture: Cali, Columbia, 2004; Volume 198, pp. 1–35. [Google Scholar]
- Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L.; et al. The Shuttle Radar Topography Mission. Rev. Geophys. 2007, 45. [Google Scholar] [CrossRef]
- Reuter, H.I.; Hengl, T.; Gessler, P.; Soille, P. Preparation of DEMs for Geomorphometric Analysis. In Developments in Soil Organic Matter; Elsevier BV: Amsterdam, The Netherlands, 2009; Volume 33, pp. 87–120. [Google Scholar]
- Höhle, J.; Potuckova, M. Assessment of the Quality of Digital Terrain Models. Eur. Spat. Data Res. 2011, 60, 91. [Google Scholar]
- Cooper, M.A.R. Datums, Coordinates and Differences. In Landform Monitoring, Modelling and Analysis; Lane, S., Richards, K., Chandler, J., Eds.; Wiley: Chichester, UK, 1998; pp. 21–36. [Google Scholar]
- Wise, S. Assessing the Quality for Hydrological Applications of Digital Elevation Models Derived from Contours. Hydrol. Process. 2000, 14, 1909–1929. [Google Scholar] [CrossRef]
- Hu, P.; Liu, X.; Hu, H. Accuracy Assessment of Digital Elevation Models based on Approximation Theory. Photogramm. Eng. Remote Sens. 2009, 75, 49–56. [Google Scholar] [CrossRef]
- Fisher, P.F.; Tate, N.J. Causes and Consequences of Error in Digital Elevation Models. Prog. Phys. Geogr. Earth Environ. 2006, 30, 467–489. [Google Scholar] [CrossRef]
- Hunter, G.J.; Goodchild, M.F. Modeling the Uncertainty of Slope and Aspect Estimates Derived from Spatial Databases. Geogr. Anal. 2010, 29, 35–49. [Google Scholar] [CrossRef]
- Temme, A.; Heuvelink, G.; Schoorl, J.; Claessens, L. Geostatistical Simulation and Error Propagation in Geomorphometry. In Developments in Soil Organic Matter; Hengl, T., Reuter, H.I., Eds.; Elsevier BV: Amsterdam, The Netherlands, 2009; Volume 33, pp. 121–140. [Google Scholar]
- Hengl, T.; Evans, I. Mathematical and Digital Models of the Land Surface. In Developments in Soil Organic Matter; Hengl, T., Reuter, H.I., Eds.; Elsevier BV: Amsterdam, The Netherlands, 2009; Volume 33, pp. 31–63. [Google Scholar]
- Hebeler, F.; Purves, R.S. The Influence of Elevation Uncertainty on Derivation of Topographic Indices. Geomorphology 2009, 111, 4–16. [Google Scholar] [CrossRef]
- Devillers, R.; Stein, A.; Bédard, Y.; Chrisman, N.; Fisher, P.; Shi, W. Thirty Years of Research on Spatial Data Quality: Achievements, Failures, and Opportunities. Trans. GIS 2010, 14, 387–400. [Google Scholar] [CrossRef]
- Granshaw, S.I. Photogrammetric Terminology: Third Edition. Photogramm. Rec. 2016, 31, 210–252. [Google Scholar] [CrossRef]
- Newby, P.R.T. Accuracy, Precision, Extraction, Citation and Valediction. Photogramm. Rec. 2011, 26, 149–153. [Google Scholar] [CrossRef]
- Höhle, J.; Höhle, M. Accuracy Assessment of Digital Elevation Models by Means of Robust Statistical Methods. ISPRS J. Photogramm. Remote Sens. 2009, 64, 398–406. [Google Scholar] [CrossRef]
- Wechsler, S.P. Uncertainties Associated with Digital Elevation Models for Hydrologic Applications: A Review. Hydrol. Earth Syst. Sci. 2007, 11, 1481–1500. [Google Scholar] [CrossRef]
- Hengl, T.; Heuvelink, G.B.M.; Van Loon, E.E. On the Uncertainty of Stream Networks Derived from Elevation Data: The Error Propagation Approach. Hydrol. Earth Syst. Sci. 2010, 14, 1153–1165. [Google Scholar] [CrossRef]
- Snyder, M.W. A Comparison of Four Techniques for the Calculation of Slope and Aspect from Digital Terrain Matrices. Master’s Thesis, University of Illinois at Urbana-Champaign, Champaign, IL, USA, 1983. [Google Scholar]
- Skidmore, A.K. A Comparison of Techniques for Calculating Gradient and Aspect from a Gridded Digital Elevation Model. Int. J. Geogr. Inf. Syst. 1989, 3, 323–334. [Google Scholar] [CrossRef]
- Srinivasan, R.; Engel, B.A. Effect of Slope Prediction Methods on Slope and Erosion Estimates. Appl. Eng. Agric. 1991, 7, 779–783. [Google Scholar] [CrossRef]
- Zhou, Q.; Liu, X. Error Analysis on Grid-Based Slope and Aspect Algorithms. Photogramm. Eng. Remote. Sens. 2004, 70, 957–962. [Google Scholar] [CrossRef]
- Zhou, Q.; Liu, X. Analysis of Errors of Derived Slope and Aspect Related to DEM Data Properties. Comput. Geosci. 2004, 30, 369–378. [Google Scholar] [CrossRef]
- Bolstad, P.V.; Stowe, T. An Evaluation of DEM Accuracy: Elevation, Slope, and Aspect. Photogram. Eng. Remote Sens. 1994, 60, 1327–1332. [Google Scholar]
- El Hage, M.; Simonetto, E.; Faour, G.; Polidori, L. Evaluation of Elevation, Slope and Stream Network Quality of SPOT DEMs. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, 2, 63–67. [Google Scholar] [CrossRef]
- Oksanen, J.; Sarjakoski, T. Error Propagation of DEM-Based Surface Derivatives. Comput. Geosci. 2005, 31, 1015–1027. [Google Scholar] [CrossRef]
- Aguilar, F.J.; Mills, J.P.; Delgado, J.; Aguilar, M.A.; Negreiros, J.; Pérez, J.L. Modelling Vertical Error in LiDAR-Derived Digital Elevation Models. ISPRS J. Photogramm. Remote Sens. 2010, 65, 103–110. [Google Scholar] [CrossRef]
- Florinsky, I.V. Accuracy of Local Topographic Variables Derived from Digital Elevation Models. Int. J. Geogr. Inf. Sci. 1998, 12, 47–62. [Google Scholar] [CrossRef]
- Wilson, J.P. Digital Terrain Modeling. Geomorphology 2012, 137, 107–121. [Google Scholar] [CrossRef]
- Evans, I.S. General Geomorphometry, Derivatives of Altitude, and Descriptive Statistics. In Spatial Analysis in Geomorphology; Chorley, R.J., Ed.; Methuen & Co., Ltd.: London, UK, 1972; pp. 17–90. [Google Scholar]
- El Hage, M. Etude de la Qualité Géomorphologique de Modèles Numériques de Terrain Issus de L’Imagerie Spatiale. Ph.D. Thesis, Conservatoire National des Arts et Metiers, Paris, France, 2012. [Google Scholar]
- Warren, S.; Hohmann, M.; Auerswald, K.; Mitasova, H. An Evaluation of Methods to Determine Slope Using Digital Elevation Data. Catena 2004, 58, 215–233. [Google Scholar] [CrossRef]
- Horn, B. Hill Shading and the Reflectance Map. Proc. IEEE 1981, 69, 14–47. [Google Scholar] [CrossRef]
- Burrough, P.A.; McDonnell, R.; McDonnell, R.A.; Lloyd, C.D. Principles of Geographical Information Systems; OUP: Oxford, UK, 2015; ISBN 978-0-19-874284-5. [Google Scholar]
- Liu, X.; Bian, L. Accuracy Assessment of DEM Slope Algorithms Related to Spatial Autocorrelation of DEM Errors. In Advances in Digital Terrain Analysis; Zhou, Q., Lees, B., Tang, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 307–322. ISBN 978-3-540-77800-4. [Google Scholar]
- Gastellu-Etchegorry, J.-P.; Grau, E.; Lauret, N.A. A 3D Model for Remote Sensing Images and Radiative Budget of Earth Surfaces. In Modeling and Simulation in Engineering; Alexandru, C., Ed.; IntechOpen: London, UK, 2012. [Google Scholar]
- Gastellu-Etchegorry, J.-P.; Yin, T.; Lauret, N.; Cajgfinger, T.; Gregoire, T.; Grau, E.; Feret, J.-B.; Lopes, M.; Guilleux, J.; Dedieu, G.; et al. Discrete Anisotropic Radiative Transfer for Modeling Airborne and Satellite Spectroradiometer and LIDAR Acquisitions of Natural and Urban Landscapes. Remote Sens. 2015, 7, 1667–1701. [Google Scholar] [CrossRef]
- Paparoditis, N.; Polidori, L.; Savaria, E. Parametric Simulation-Based Evaluation of 3D Mapping Techniques on Optical Remote Sensing Images. Satell. Remote Sens. II 1995, 2579, 423–435. [Google Scholar] [CrossRef]
- Chu, H.-J.; Chen, R.-A.; Tseng, V.S.; Wang, C.-K. Identifying LiDAR Sample Uncertainty on Terrain Features from DEM Simulation. Geomorphology 2014, 204, 325–333. [Google Scholar] [CrossRef]
- Guindon, B. Application of SAR Simulation Techniques to Improve the Understanding of Spaceborne Sar Scenes of Moderate to Rugged Terrain. Proc. EARSeL I 1991, 9, 100–109. [Google Scholar]
- Polidori, L.; Armand, P. On the use of SAR Image Simulation for the Validation of Relief Mapping Techniques. EARSeL Adv. Remote Sens. 1995, 4, 40–48. [Google Scholar]
- Taglioretti, C.; Manzino, A.M. Terrestrial Mobile Mapping: Photogrammetric simulator. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, 3, 333–339. [Google Scholar] [CrossRef]
- Polidori, L. Fractal-Based Evaluation of Relief Mapping Techniques. In Proceedings of the Joint EC-EARSeL Expert Meeting on Fractals in Geosciences and Remote Sensing, Ispra, Italy, 14–15 April 1994; pp. 277–297. [Google Scholar]
- Griffin, M.W. Terrain Synthesis: The Creation, Management, Presentation and Validation of Artificial Landscapes. Ph.D. Thesis, University of Nottingham, Nottingham, UK, 2001. [Google Scholar]
- Podobnikar, T. Methods for Visual Quality Assessment of a Digital Terrain Model. SAPIENS 2009, 2, 1–10. [Google Scholar]
- Borchia, R.; Nesci, O.; Codice, P. Atlante Illustrato Del Reale Paesaggio Della Gioconda; Mondadori Electa: Florence, Italy, 2012; pp. 1–144. ISBN 978-88-370-9422-5. [Google Scholar]
- Oksanen, J. Tracing the Gross Errors of DEM-Visualisation Techniques for Preliminary Quality Analysis. In Proceedings of the 21st International Cartographic Conference, Durban, South Africa, 10–16 August 2003; pp. 2410–2415. [Google Scholar]
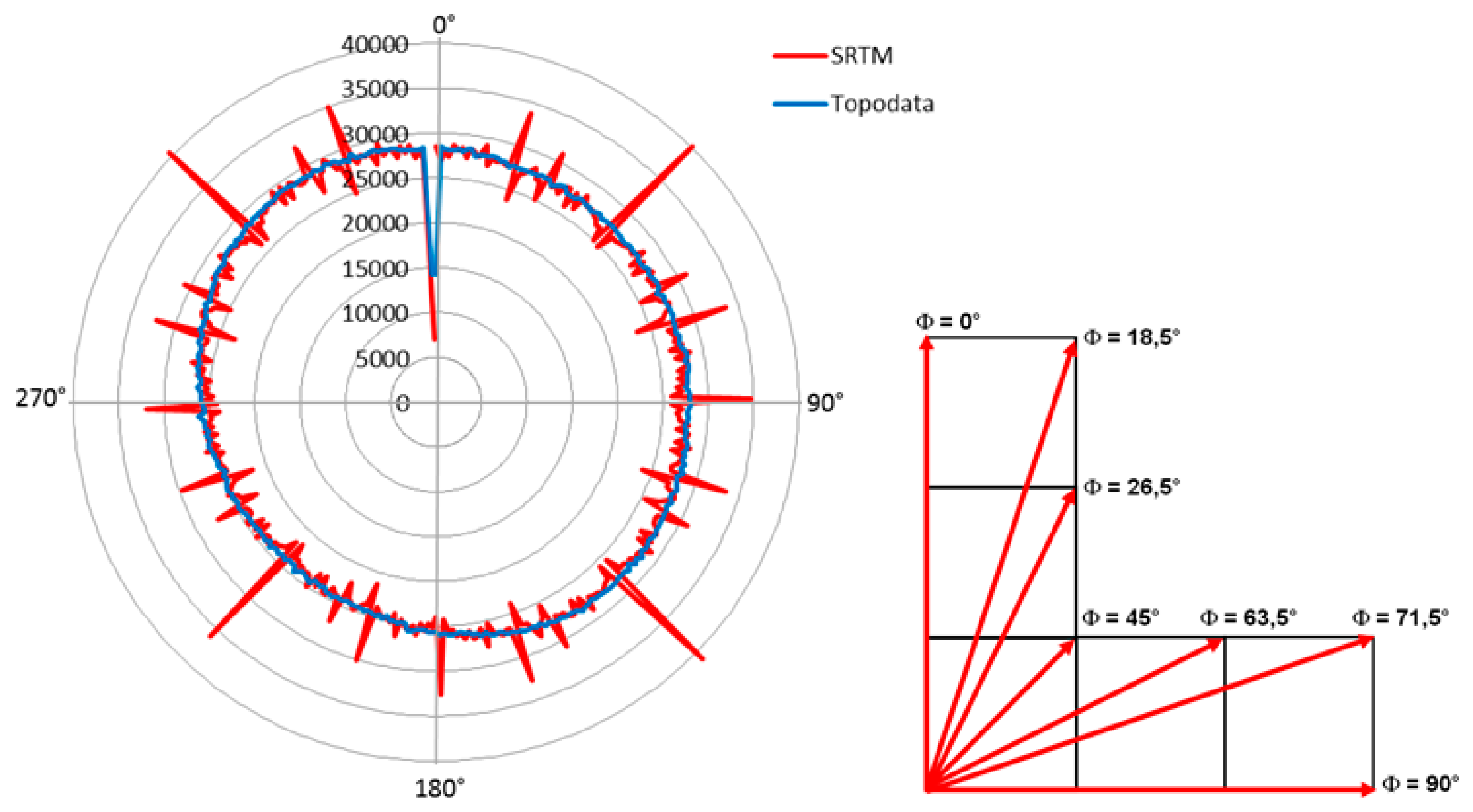
- Arrell, K.; Wise, S.; Wood, J.; Donoghue, D.; Donoghue, D.N. Spectral Filtering as a Method of Visualising and Removing Striped Artefacts in Digital Elevation Data. Earth Surf. Process. Landf. 2008, 33, 943–961. [Google Scholar] [CrossRef]
- Polidori, L.; El Hage, M.; Valeriano, M.D.M. Digital Elevation Model Validation with No Ground Control: Application to the Topodata Dem in Brazil. Bol. Ciências Geodésicas 2014, 20, 467–479. [Google Scholar] [CrossRef]
- Shary, P.A.; Sharaya, L.S.; Mitusov, A.V. The Problem of Scale-Specific and Scale-Free Approaches in Geomorphometry. Geogr. Fis. Din. Quat. 2005, 28, 81–101. [Google Scholar]
- El Hage, M.; Simonetto, E.; Faour, G.; Polidori, L. Impact of DEM Reconstruction Parameters on Topographic Indices. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Paris, France, 1–2 September 2010; Volume 38, pp. 40–44. [Google Scholar]
- Santos, V.; El Hage, M.; Polidori, L.; Stevaux, J.C. Effect of Digital Elevation Model Mesh Size on Geomorphic Indices: A Case Study of the Ivaí River Watershed-State of Paraná, Brazil. Bol. Ciências Geodésicas 2017, 23, 684–699. [Google Scholar] [CrossRef]
- Hutchinson, M.; Gallant, J.C. Digital Elevation Eodel and Representation of Terrain Shape. In Terrain Analysis: Principles and Applications; Wilson, J.P., Gallant, J.C., Eds.; John Wiley & Sons: Hoboke, NJ, USA, 2000; ISBN 978-0-471-32188-0. [Google Scholar]
- Hirt, C. Artefact Detection in Global Digital Elevation Models (DEMs): The Maximum Slope Approach and Its Application for Complete Screening of the SRTM v4.1 and MERIT DEMs. Remote Sens. Environ. 2018, 207, 27–41. [Google Scholar] [CrossRef]
- Tobler, W.R. A Computer Movie Simulating Urban Growth in the Detroit Region. Econ. Geogr. 1970, 46, 234. [Google Scholar] [CrossRef]
- Miller, H.J. Tobler’s First Law and Spatial Analysis. Ann. Assoc. Am. Geogr. 2004, 94, 284–289. [Google Scholar] [CrossRef]
- Rodriguez-Iturbe, I.; Rinaldo, A.; Levy, O. Fractal River Basins: Chance and Self-Organization; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Gaucherel, C.; Salomon, L.; LaBonne, J. Variable Self-Similar Sinuosity Properties Within Simulated River Networks. Earth Surf. Process. Landf. 2011, 36, 1313–1320. [Google Scholar] [CrossRef]
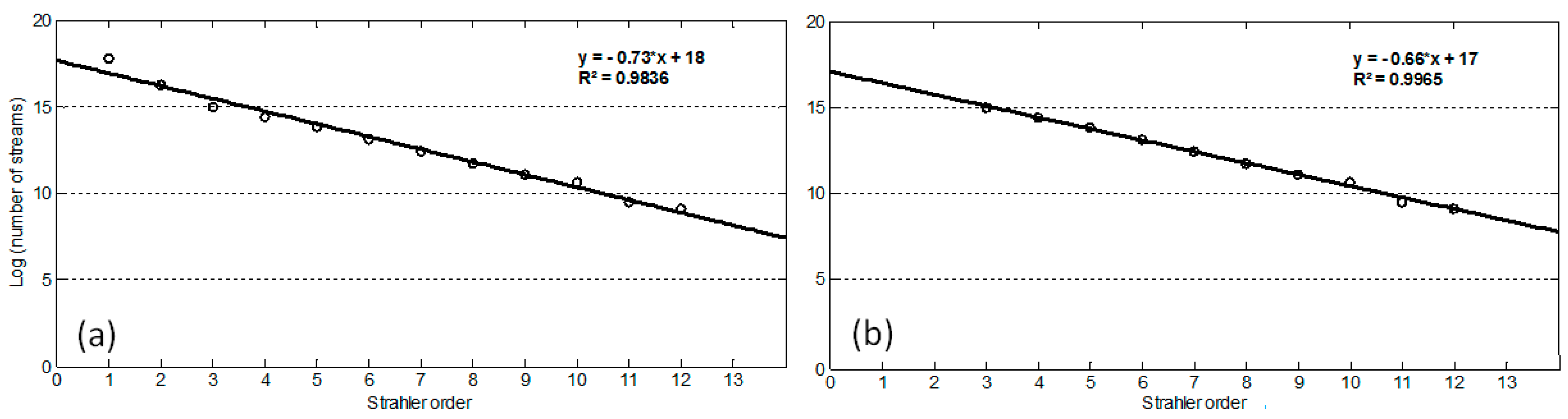
- Strahler, A.N. Quantitative Analysis of Watershed Geomorphology. Trans. Am. Geophys. Union 1957, 38, 913–920. [Google Scholar] [CrossRef]
- Gaucherel, C.; Frelat, R.; Salomon, L.; Rouy, B.; Pandey, N.; Cudennec, C. Regional Watershed Characterization and Classification with River Network Analyses. Earth Surf. Process. Landf. 2017, 42, 2068–2081. [Google Scholar] [CrossRef]
- Valeriano, M.D.M.; Rossetti, D.F. Topodata: Brazilian Full Coverage Refinement of SRTM Data. Appl. Geogr. 2012, 32, 300–309. [Google Scholar] [CrossRef]
- Fernández, D.C.J. Evaluation of Algorithms and Digital Elevation Models for Drainage Extraction. Master’s Thesis, Instituto Nacional de Pesquisas Espaciais, Sao Jose dos Campos, Brazil, 2011. [Google Scholar]
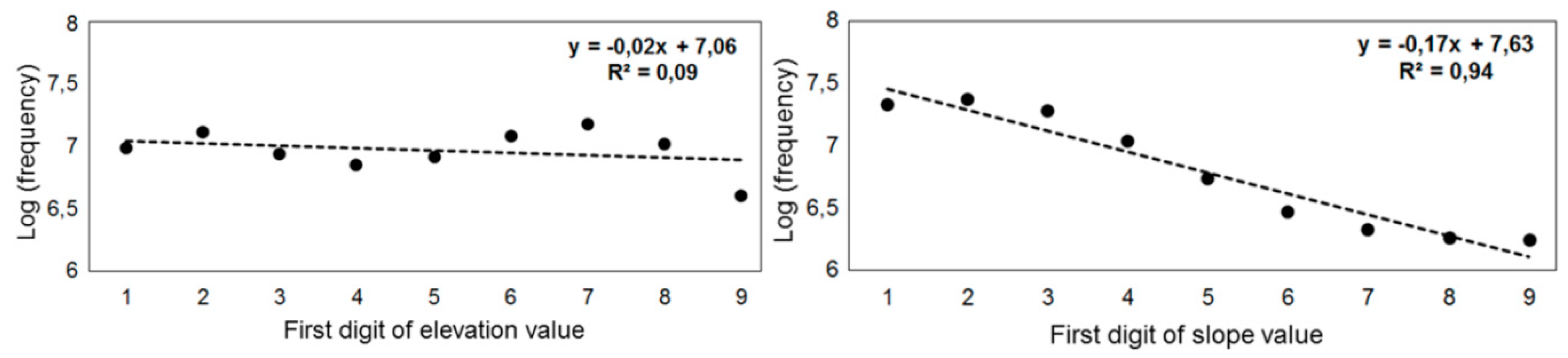
- Benford, F. The Law of Anomalous Numbers. Proc. Am. Philos. Soc. 1938, 78, 551–572. [Google Scholar]
- Berger, A.; Hill, T.P. An Introduction to Benford’s Law; Princeton University Press: Princeton, NJ, USA, 2015. [Google Scholar]
- Nigrini, M.J. Benford’s Law: Applications for Forensic Accounting, Auditing, and Fraud Detection; John Wiley & Sons: Hoboken, NJ, USA, 2012; ISBN 978-1-118-15285-0. [Google Scholar]
- Polidori, L.; El Hage, M. Application de la Loi de Benford AU Contrôle de Qualité Des Modèles Numériques de Terrain. Revue XYZ 2019, 158, 19–22. [Google Scholar]
- Polidori, L.; Chorowicz, J.; Guillande, R. Description of Terrain as a Fractal Surface, and Application to Digital Elevation Model Quality Assessment. Photogramm. Eng. Remote Sens. 1991, 57, 1329–1332. [Google Scholar]
- Wise, S. Information Entropy as a Measure of DEM Quality. Comput. Geosci. 2012, 48, 102–110. [Google Scholar] [CrossRef]
- Renouard, L. Extraction Automatique de Mnt à Différentes Résolutions. Int. Arch. Photogramm. Remote Sens. 1993, 29, 886. [Google Scholar]
- Krupnik, A. Accuracy Assessment of Automatically Derived Digital Elevation Models from SPOT Images. Photogramm. Eng. Remote Sens. 2000, 66, 1017–1023. [Google Scholar]
- Hashemian, M.S.; Abootalebi, A.; Kianifar, F. Accuracy Evaluation of Dem Generated from Spot 5 Hrs Imageries. In Proceedings of the XXth ISPRS Congress, Commission I, Istanbul, Turkey, 12–23 July 2004; pp. 12–23. [Google Scholar]
- Cuartero, A.; Felicísimo, A.M.; Ariza, F.J. Accuracy of DEM Generation from TERRA-ASTER Stereo Data. Int. Arch. Photogramm. Remote Sens. 2004, 35, 559–563. [Google Scholar]
- Cuartero, A.; Felicísimo, A.M.; Ariza, F. Accuracy, Reliability, and Depuration of SPOT HRV and Terra ASTER Digital Elevation Models. IEEE Trans. Geosci. Remote Sens. 2005, 43, 404–407. [Google Scholar] [CrossRef]
- Poon, J.; Fraser, C.S.; Zhang, C.; Zhang, L.; Gruen, A. Quality Assessment of Digital Surface Models Generated from IKONOS Imagery. Photogramm. Rec. 2005, 20, 162–171. [Google Scholar] [CrossRef]
- Evans, G.; Ramachandran, B.; Zhang, Z.; Bailey, B.; Cheng, P. An Accuracy Assessment of Cartosat-1 Stereo Image Data-Derived Digital Elevation Models: A Case Study of the Drum Mountains, Utah. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2008, 37, 1161–1164. [Google Scholar]
- Bignone, F.; Umakawa, H. Assessment of ALOS PRISM Digital Elevation Model Extraction over Japan. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2008, 37, 1135–1138. [Google Scholar]
- Gooch, M.J.; Chandler, J.H.; Stojić, M. Accuracy Assessment of Digital Elevation Models Generated Using the Erdas Imagine Orthomax Digital Photogrammetric System. Photogramm. Rec. 1999, 16, 519–531. [Google Scholar] [CrossRef]
- Lane, S.N.; James, T.D.; Crowell, M.D. Application of Digital Photogrammetry to Complex Topography for Geomorphological Research. Photogramm. Rec. 2000, 16, 793–821. [Google Scholar] [CrossRef]
- Hanssen, R.; Bamler, R. Evaluation of interpolation kernels for SAR interferometry. IEEE Trans. Geosci. Remote Sens. 1999, 37, 318–321. [Google Scholar] [CrossRef]
- Slacikova, J.; Potuckova, M. Evaluation of Interpolation Methods in InSAR DEM Derivation from ERS Tandem Data. In Proceedings of the 31st EARSeL Symposium, Prague, Czech Republic, 30 May–2 June 2011; pp. 544–551. [Google Scholar]
- El Hage, M.; Simonetto, E.; Faour, G.; Polidori, L. Effect of Image-Matching Parameters and Local Morphology on the Geomorphological Quality of SPOT DEMs. Photogramm. Rec. 2017, 32, 255–275. [Google Scholar] [CrossRef]
- Li, Z. Variation of the Accuracy of Digital Terrain Models with Sampling Interval. Photogramm. Rec. 2006, 14, 113–128. [Google Scholar] [CrossRef]
- Gao, J. Comparison of Sampling Schemes in Constructing Tdms From Topographic Maps. ITC J. 1995, 1, 18–22. [Google Scholar]
- Gao, J. Resolution and Accuracy of Terrain Representation by Grid DEMs at a Micro-Scale. Int. J. Geogr. Inf. Sci. 1997, 11, 199–212. [Google Scholar] [CrossRef]
- Weng, Q. Quantifying Uncertainty of Digital Elevation Models Derived from Topographic Maps. In Proceedings of the Open Source Approaches in Spatial Data Handling; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 2002; pp. 403–418. [Google Scholar]
- Su, J.; Bork, E. Influence of Vegetation, Slope, and Lidar Sampling Angle on DEM Accuracy. Photogramm. Eng. Remote Sens. 2006, 72, 1265–1274. [Google Scholar] [CrossRef]
- Toutin, T. Impact of Terrain Slope and Aspect on Radargrammetric DEM Accuracy. ISPRS J. Photogramm. Remote Sens. 2002, 57, 228–240. [Google Scholar] [CrossRef]
- Toutin, T. Generation of DSMs from SPOT-5 in-Track HRS and across-Track HRG Stereo Data Using Spatiotriangulation and Autocalibration. ISPRS J. Photogramm. Remote Sens. 2006, 60, 170–181. [Google Scholar] [CrossRef]
- Felicísimo, A.M. Digital Terrain Models and their Application to Environmental Sciences. Ph.D. Thesis, University of Oviedo, Asturias, Spain, 1992. [Google Scholar]
- Papasaika, H.; Baltsavias, E. Investigations on the Relation of Geomorphological Parameters to DEM Accuracy. In Geomorphometry 2009, Proceedings of the Geomorphometry Conference, Zurich, Switzerland, 31 August–2 September 2009; Purves, R., Gruber, S., Straumann, R., Hengl, T., Eds.; University of Zurich: Zurich, Switzerland, 2009; pp. 162–168. [Google Scholar]
- Schwendel, A.C.; Fuller, I.C.; Death, R.G. Assessing DEM Interpolation Methods for Effective Representation of Upland Stream Morphology for Rapid Appraisal of Bed Stability. River Res. Appl. 2010, 28, 567–584. [Google Scholar] [CrossRef]
- Aguilar, F.J.; Agüera, F.; Aguilar, M.A.; Carvajal, F. Effects of Terrain Morphology, Sampling Density, and Interpolation Methods on Grid DEM Accuracy. Photogramm. Eng. Remote Sens. 2005, 71, 805–816. [Google Scholar] [CrossRef]
- Chaplot, V.; Darboux, F.; Bourennane, H.; Leguédois, S.; Silvera, N.; Phachomphon, K. Accuracy of Interpolation Techniques for the Derivation of Digital Elevation Models in Relation to Landform Types and Data Density. Geomorphology 2006, 77, 126–141. [Google Scholar] [CrossRef]
- Binh, T.Q.; Thuy, N.T. Assessment of the Influence of Interpolation Techniques on the Accuracy of Digital Elevation Model. VNU J. Sci. Earth Sci. 2008, 24, 176–183. [Google Scholar]
- Bater, C.W.; Coops, N.C. Evaluating Error Associated with Lidar-Derived Dem Interpolation. Comput. Geosci. 2009, 35, 289–300. [Google Scholar] [CrossRef]
- Weibel, R.; Heller, M. Digital terrain modelling. In Geographical Information Systems; Maguire, D.J., Goodchild, M.F., Rhind, D.W., Eds.; Longman: London, UK, 1991; Volume 1, pp. 269–297. [Google Scholar]
- Pain, C.F. Size Does Matter: Relationships Between Image Pixel Size and Landscape Process Scales. In International Congress of Modelling and Simulation, Proceedings of the MODSIM, Sydney, Australia, 12–15 December 2005; Modelling and Simulation Society of Australia and New Zealand Inc.: Sydney, Australia, 2005; pp. 1430–1436. [Google Scholar]
- Mitas, L.; Mitasova, H. Spatial interpolation. In Geographical Information Systems: Principles, Techniques, Management and Applications; Longley, P., Goodchild, M.F., Maguire, D.J., Rhind, D.W., Eds.; Wiley: Hoboken, NJ, USA, 1999; Volume 1, pp. 481–492. [Google Scholar]
- Tarboton, D.G.; Ames, D.P. Advances in the Mapping of Flow Networks from Digital Elevation Data. Bridg. Gap 2001, 1–10. [Google Scholar] [CrossRef]
- Hancock, G.R. The Use of Digital Elevation Models in the Identification and Characterization of Catchments Over Different Grid Scales. Hydrol. Process. 2005, 19, 1727–1749. [Google Scholar] [CrossRef]
- Hancock, G.R.; Martinez, C.; Evans, K.G.; Moliere, D.R. A Comparison of SRTM and High-Resolution Digital Elevation Models and Their Use in Catchment Geomorphology and Hydrology: Australian Examples. Earth Surf. Process. Landf. 2006, 31, 1394–1412. [Google Scholar] [CrossRef]
- Murphy, P.N.C.; Ogilvie, J.; Meng, F.-R.; Arp, P. Stream Network Modelling Using Lidar and Photogrammetric Digital Elevation Models: A Comparison and Field Verification. Hydrol. Process. 2008, 22, 1747–1754. [Google Scholar] [CrossRef]
- Trofaier, A.M.; Rees, W.G. The Suitability of Using ASTER GDEM2 for Terrain-Based Extraction of Stream Channel Networks in a Lowland Arctic Permafrost Catchment. Fenn. Int. J. Geogr. 2015, 193, 66–82. [Google Scholar]
- Veregin, H. The Effects of Vertical Error in Digital Elevation Models on the Determination of Flow-path Direction. Cartogr. Geogr. Inf. Syst. 1997, 24, 67–79. [Google Scholar] [CrossRef]
- Raaflaub, L.D.; Collins, M.J. The Effect of Error in Gridded Digital Elevation Models on the Estimation of Topographic Parameters. Environ. Model. Softw. 2006, 21, 710–732. [Google Scholar] [CrossRef]
- Khan, A.; Richards, K.S.; Parker, G.T.; McRobie, A.; Mukhopadhyay, B. How large is the Upper Indus Basin? The Pitfalls of Auto-Delineation Using DEMs. J. Hydrol. 2014, 509, 442–453. [Google Scholar] [CrossRef]
- Chakra, C.A.; Gascoin, S.; Somma, J.; Fanise, P.; Drapeau, L.; Chakra, A. Monitoring the Snowpack Volume in a Sinkhole on Mount Lebanon using Time Lapse Photogrammetry. Sensors 2019, 19, 3890. [Google Scholar] [CrossRef] [PubMed]
- Shaw, T.E.; Gascoin, S.; Mendoza, P.A.; Pellicciotti, F.; McPhee, J. Snow Depth Patterns in a High Mountain Andean Catchment from Satellite Optical Tristereoscopic Remote Sensing. Water Resour. Res. 2020, 56. [Google Scholar] [CrossRef]
- Bubenzer, O.; Bolten, A. The Use of New Elevation Data (SRTM/ASTER) for the Detection and Morphometric Quantification of Pleistocene Megadunes (Draa) in the Eastern Sahara and the Southern Namib. Geomorphology 2008, 102, 221–231. [Google Scholar] [CrossRef]
- Pipaud, I.; Loibl, D.; Lehmkuhl, F. Evaluation of TanDEM-X Elevation Data for Geomorphological Mapping and Interpretation in High Mountain Environments—A Case Study from SE Tibet, China. Geomorphology 2015, 246, 232–254. [Google Scholar] [CrossRef]
- Domeneghetti, A. On the Use of SRTM and Altimetry Data for Flood Modeling in Data-Sparse Regions. Water Resour. Res. 2016, 52, 2901–2918. [Google Scholar] [CrossRef]
- Du, X.; Guo, H.; Fan, X.; Zhu, J.; Yan, Z.; Zhan, Q. Vertical Accuracy Assessment of Freely Available Digital Elevation Models Over Low-Lying Coastal Plains. Int. J. Digit. Earth 2015, 9, 252–271. [Google Scholar] [CrossRef]
- Böhme, R. Inventory of World Topographic Mapping; International Cartographic Association by Elsevier Applied Science Publishers: New York, NY, USA, 1993; ISBN 978-1-85166-357-6. [Google Scholar]
- Weydahl, D.J.; Sagstuen, J.; Dick, Ø.B.; Rønning, H. SRTM DEM Accuracy Assessment Over Vegetated Areas in Norway. Int. J. Remote Sens. 2007, 28, 3513–3527. [Google Scholar] [CrossRef]
- Hawker, L.; Neal, J.; Bates, P. Accuracy Assessment of the TanDEM-X 90 Digital Elevation Model for Selected Floodplain Sites. Remote Sens. Environ. 2019, 232, 111319. [Google Scholar] [CrossRef]
- Zhao, S.-M.; Cheng, W.; Zhou, C.; Chen, X.; Zhang, S.; Zhou, Z.; Liu, H.; Chai, H. Accuracy Assessment of the ASTER GDEM and SRTM3 DEM: An Example in the Loess Plateau and North China Plain of China. Int. J. Remote Sens. 2011, 32, 8081–8093. [Google Scholar] [CrossRef]
- Gómez, M.F.; Lencinas, J.D.; Siebert, A.; Díaz, G.M. Accuracy Assessment of ASTER and SRTM DEMs: A Case Study in Andean Patagonia. GISci. Remote Sens. 2012, 49, 71–91. [Google Scholar] [CrossRef]
- Satgé, F.; Bonnet, M.; Timouk, F.; Calmant, S.; Pillco, R.; Molina, J.; Lavado-Casimiro, W.; Arsen, A.; Crétaux, J.; Garnier, J. Accuracy Assessment of SRTM v4 and ASTER GDEM v2 over the Altiplano Watershed Using ICESat/GLAS Data. Int. J. Remote Sens. 2015, 36, 465–488. [Google Scholar] [CrossRef]
- Toutin, T.; Cheng, P. DEM Generation with ASTER Stereo Data. Earth Obs. Mag. 2001, 10, 10–13. [Google Scholar] [CrossRef]
- Hasegawa, H.; Matsuo, K.; Koarai, M.; Watanabe, N.; Masaharu, H.; Fukushima, Y. DEM Accuracy and the Base to Height (B/H) Ratio of Stereo Images. Int. Arch. Photogramm. Remote Sens. 2000, 33, 356–359. [Google Scholar]
- Gallant, J.C.; Read, A.M.; Dowling, T. Removal of Tree Offsets from SRTM and Other Digital Surface Models. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, 39, 275–280. [Google Scholar] [CrossRef]
- Yamazaki, D.; Ikeshima, D.; Tawatari, R.; Yamaguchi, T.; O’Loughlin, F.; Neal, J.C.; Sampson, C.C.; Kanae, S.; Bates, P.D. A High-Accuracy Map of Global Terrain Elevations. Geophys. Res. Lett. 2017, 44, 5844–5853. [Google Scholar] [CrossRef]
- EUROSTAT. Manual of Concepts on Land Cover and Land Use Information Systems; European Communities: Luxembourg, 2001. [Google Scholar]
- McBratney, A.; Santos, M.M.; Minasny, B. On Digital Soil Mapping. Geoderma 2003, 117, 3–52. [Google Scholar] [CrossRef]
- NGA. Performance Specification Digital Terrain Elevation Data (DTED); Report MILPRF-89020A; NGA: Springfield, VA, USA, 1996; pp. 1–45. [Google Scholar]
- Heady, B.; Kroenung, G.; Rodarmel, C. High Resolution Elevation Data (HRE) Specification Overview. In Proceedings of the ASPRS/MAPPS 2009 Conference, San Antonio, TX, USA, 16–19 November 2009. [Google Scholar]
- Takagi, M.; Asano, H.; Kikuchi, Y. Optimum Spatial Resolution of Digital Elevation Model for Topographical Analysis. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Ottawa, ON, Canada, 1–5 October 2002; Volume 34, pp. 442–446. [Google Scholar]
- Hengl, T. Finding the Right Pixel Size. Comput. Geosci. 2006, 32, 1283–1298. [Google Scholar] [CrossRef]
- Shary, P.A. Models of Topography. In Advances in Digital Terrain Analysis; Zhou, Q., Lees, B., Tang, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 29–57. ISBN 978-3-540-77800-4. [Google Scholar]
- Eco, U. On the Impossibility of Drawing a Map of the Empire on a Scale of 1 to 1. In How Travel Salmon Other Essays; Houghton Mifflin: Boston, MA, USA, 1994; pp. 95–106. [Google Scholar]
- Charif, M. Optimum Sampling for Digital Terrain Modelling. Int. Arch. Photogramm. Remote Sens. 1992, 29, 77–78. [Google Scholar]
- Evans, I.; Hengl, T.; Gorsevski, P.V. Chapter 22 Applications in Geomorphology. In Developments in Soil Organic Matter; Hengl, T., Reuter, H.I., Eds.; Elsevier BV: Amsterdam, The Netherlands, 2009; Volume 33, pp. 497–525. [Google Scholar]
- Erskine, R.H.; Green, T.; Ramirez, J.A.; Macdonald, L.H. Digital Elevation Accuracy and Grid Cell Size: Effects on Estimated Terrain Attributes. Soil Sci. Soc. Am. J. 2007, 71, 1371–1380. [Google Scholar] [CrossRef]
- Kienzle, S. The Effect of DEM Raster Resolution on First Order, Second Order and Compound Terrain Derivatives. Trans. GIS 2003, 8, 83–111. [Google Scholar] [CrossRef]
- Guoan, T.; Mudan, Z.; Tianwen, L.; Yongmei, L.; Ting, Z. Simulation on Slope Uncertainty Derived from DEMs at Different Resolution Levels: A Case Study in the Loess Plateau. J. Geogr. Sci. 2003, 13, 387–394. [Google Scholar] [CrossRef]
- Thompson, J.A.; Bell, J.C.; Butler, C.A. Digital Elevation Model Resolution: Effects on Terrain Attribute Calculation and Quantitative Soil-Landscape Modeling. Geoderma 2001, 100, 67–89. [Google Scholar] [CrossRef]
- Vaze, J.; Teng, J. Impact of DEM Resolution on Topographic Indices and Hydrological Modelling Results. In Proceedings of the MODSIM 2007 International Congress on Modelling and Simulation, Christchurch, New Zealand, 10–13 December 2007. [Google Scholar]
- Vaze, J.; Teng, J.; Spencer, G. Impact of DEM Accuracy and Resolution on Topographic Indices. Environ. Model. Softw. 2010, 25, 1086–1098. [Google Scholar] [CrossRef]
- Wu, S.; Li, J.; Huang, G. Modeling the Effects of Elevation Data Resolution on the Performance of Topography-Based Watershed Runoff Simulation. Environ. Model. Softw. 2007, 22, 1250–1260. [Google Scholar] [CrossRef]
- Gravelius, H. Grundrifi der Gesamten Gewcisserkunde. Compend. Hydrol. 1914, I, 265–278. [Google Scholar]
- Mandelbrot, B.B. The Fractal Geometry of Nature, Revised ed.; W.H. Freeman: San Francisco, CA, USA, 1982. [Google Scholar]
- Polidori, L.; Simonetto, E. Effect of Scale on the Correlation Between Topography and Canopy Elevations in an Airborne InSAR Product Over Amazonia. Procedia Technol. 2014, 16, 180–185. [Google Scholar] [CrossRef]
- Wechsler, S.P. Perceptions of Digital Elevation Model Uncertainty by DEM Users. URISA J. 2003, 15, 57–64. [Google Scholar]
- Lopez, C. Improving the Elevation Accuracy of Digital Elevation Models: A Comparison of Some Error Detection Procedures. Trans. GIS 2000, 4, 43–64. [Google Scholar] [CrossRef]
- Milledge, D.; Lane, S.N.; Warburton, J. The Potential of Digital Filtering of Generic Topographic Data for Geomorphological Research. Earth Surf. Process. Landf. 2009, 34, 63–74. [Google Scholar] [CrossRef]
- Monti-Guarnieri, A. Topographic Statistics for Phase Unwrapping. In Proceedings of the EUSAR, Cologne, Germany, 4–6 June 2002; pp. 1–4. [Google Scholar]
- Guarnieri, A.M. Using Topography Statistics to Help Phase Unwrapping. Sonar Navig. IEE Proc. Radar 2003, 150, 144. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Polidori, L.; El Hage, M. Digital Elevation Model Quality Assessment Methods: A Critical Review. Remote Sens. 2020, 12, 3522. https://doi.org/10.3390/rs12213522
Polidori L, El Hage M. Digital Elevation Model Quality Assessment Methods: A Critical Review. Remote Sensing. 2020; 12(21):3522. https://doi.org/10.3390/rs12213522
Chicago/Turabian StylePolidori, Laurent, and Mhamad El Hage. 2020. "Digital Elevation Model Quality Assessment Methods: A Critical Review" Remote Sensing 12, no. 21: 3522. https://doi.org/10.3390/rs12213522
APA StylePolidori, L., & El Hage, M. (2020). Digital Elevation Model Quality Assessment Methods: A Critical Review. Remote Sensing, 12(21), 3522. https://doi.org/10.3390/rs12213522




