Abstract
Stand-level maps of past forest disturbances (expressed as time since disturbance, TSD) are needed to model forest ecosystem processes, but the conventional approaches based on remotely sensed satellite data can only extend as far back as the first available satellite observations. Stand-level analysis of airborne LiDAR data has been demonstrated to accurately estimate long-term TSD (~100 years), but large-scale coverage of airborne LiDAR remains costly. NASA’s spaceborne LiDAR Global Ecosystem Dynamics Investigation (GEDI) instrument, launched in December 2018, is providing billions of measurements of tropical and temperate forest canopies around the globe. GEDI is a spatial sampling instrument and, as such, does not provide wall-to-wall data. GEDI’s lasers illuminate ground footprints, which are separated by ~600 m across-track and ~60 m along-track, so new approaches are needed to generate wall-to-wall maps from the discrete measurements. In this paper, we studied the feasibility of a data fusion approach between GEDI and Landsat for wall-to-wall mapping of TSD. We tested the methodology on a ~52,500-ha area located in central Idaho (USA), where an extensive record of stand-replacing disturbances is available, starting in 1870. GEDI data were simulated over the nominal two-year planned mission lifetime from airborne LiDAR data and used for TSD estimation using a random forest (RF) classifier. Image segmentation was performed on Landsat-8 data, obtaining image-objects representing forest stands needed for the spatial extrapolation of estimated TSD from the discrete GEDI locations. We quantified the influence of (1) the forest stand map delineation, (2) the sample size of the training dataset, and (3) the number of GEDI footprints per stand on the accuracy of estimated TSD. The results show that GEDI-Landsat data fusion would allow for TSD estimation in stands covering ~95% of the study area, having the potential to reconstruct the long-term disturbance history of temperate even-aged forests with accuracy (median root mean square deviation = 22.14 years, median BIAS = 1.70 years, 60.13% of stands classified within 10 years of the reference disturbance date) comparable to the results obtained in the same study area with airborne LiDAR.
1. Introduction
Global and regional maps of forest stand age are required to improve carbon pools and flux estimates, and to understand the impact of forest disturbances on net carbon accumulation [1,2,3,4]. Available stand age datasets can be obtained from several sources, such as field inventory and remotely sensed data. Forest inventories provide accurate ground-based measurements of forest age, but these are limited to discrete sample locations [1]. Optical satellite sensor data, in particular Landsat data, have so far been the best alternative to generate records of stand age (expressed as time since disturbance, TSD) through change detection and multi-temporal time series analysis (e.g., [5,6,7,8,9,10,11]). While these methods can provide spatially explicit information on disturbances at high temporal frequency (i.e., every 16 days in the case of a Landsat satellite), they can only detect disturbances that have happened since the beginning of the Earth Observation satellite data record in 1972 with Landsat 1 [12].
Active remotely sensed data, which are sensitive to the three-dimensional (3-D) structure of the forest canopy, are increasingly used to estimate forest age as it is strongly correlated to forest structure and height growth [13,14,15,16,17]. Light Detection and Ranging (LiDAR) sensors directly record the distribution of forest canopy elements, making it the most powerful current remote sensing technology to describe forest structure [18]. LiDAR data are suitable to estimate a wide variety of stand structure attributes, such as height, basal area, tree density, leaf area index, and biomass (e.g., [19,20,21,22,23,24,25,26]). More recent studies have demonstrated that canopy structure attributes characterized by LiDAR also have explanatory power and can be used as a proxy to estimate stand temporal attributes, such as age, forest regrowth, forest succession, and long-term TSD (~100 years) [12,13,27,28].
The deployment of LiDAR is currently dominated by commercial airborne platforms, but wide area systematic LiDAR coverage is only attainable through satellite systems. The Geoscience Laser Altimeter System (GLAS), onboard the Ice Cloud and Land Elevation Satellite (ICESat), was the first sensor providing global LiDAR measurements from space [29]. GLAS collected ~250 million observations over forest regions from 2003 to 2009 [30], which were used in a variety of forest-related studies [30,31,32,33,34,35,36]. Succeeding this pioneering mission are two recently launched and complementary LiDAR spaceborne missions, ICESat-2 and the Global Ecosystem Dynamics Investigations (GEDI), which are collecting billions of measurements of forest structure globally. GEDI is the first spaceborne instrument specifically designed to monitor forest ecosystems and improve the understanding of global forest carbon dynamics [37]. With a two-year mission design, GEDI is recording data from tropical and temperate forests between ~51.6°N and 51.6°S latitudes as constrained by the orbit of the International Space Station (ISS), where GEDI was mounted in December 2018.
The sampling configuration of the GEDI instrument is a multi-beam large-footprint waveform LiDAR composed of three laser transmitters that generate eight ground tracks; GEDI footprints have a nominal 25-m diameter (actual diameter 19-25 m depending on elevation, viewing angle, and orbit), spaced ~600 m across-track, and ~60 m along-track [37]. This makes it necessary to develop approaches that extend the forest structural information collected at discrete sensor footprints across synoptic spatial scales. Pioneering work using ICESat data have clustered footprint observations into cells of constant resolution (e.g., [31,32]). GEDI products, such as the L3 or L4B, will respectively provide gridded canopy metrics and biomass density at a 1-km spatial resolution [37]. However, the grid cell does not represent by itself a true geographical unit of analysis [38], and its use might introduce large uncertainties into the analysis depending on cell size and landscape heterogeneity. Alternatively, footprint observations can be combined with ancillary wall-to-wall remotely sensed datasets and be scaled up to image-objects that represents a forest patch [30,33]. Geographic Object-Based Image Analysis (GEOBIA) carries out the delineation of image-objects through semi-automated image segmentation procedures [39], for which spatially contiguous remotely sensed data are required. Lefsky [30], for instance, used object-based image analysis to delineate forest patches using MODIS data to generate wall-to-wall canopy height maps from spaceborne GLAS data. GEDI will provide a denser sampling of LiDAR data for tropical and temperate forests during its shorter planned two-year programmed mission compared to the ICESat missions. Therefore, object-based data fusion strategies between GEDI, passive optical, radar, or other image data of moderate spatial resolution, such as Landsat, are worth exploring. Landsat provides global coverage—ideal for vegetation landscape mapping—and has an adequate spatial resolution (i.e., 30 m) for stand-level analysis at regional scales. Moreover, Landsat data have been used for image segmentation in studies related to the estimation of stand structure attributes, such as height, biomass, and TSD [33,40,41,42,43].
We hypothesized that the fusion of GEDI and Landsat data could be suitable to map TSD wall-to-wall at the stand level, by implementing a GEOBIA approach to delineate the stands. However, the feasibility of the object-based data fusion approach would depend on the combined effects of the GEDI sampling grid, the delineation of the forest stands, and the size and spatial pattern of stand-level disturbances. These considerations are directly related to the number of GEDI footprints available to estimate TSD per stand. In this study, we used GEDI data simulated over the two-year programmed mission [44] to estimate TSD in forest stands delineated from Landsat data. The main goals were to assess whether (1) Landsat data can be used to delineate even-aged forest patches to generate wall-to-wall TSD maps, and (2) the GEDI sampling configuration is a limiting factor to map stand-level TSD.
2. Datasets and Data Processing
2.1. Study Area
The study area is in the Nez Perce-Clearwater National Forest in Idaho, USA (Figure 1). It is a temperate mixed-conifer forest covering ~52,500 ha of the Clear Creek, Selway River, and Elk Creek watersheds. The study area is mountainous, with elevation ranging from ~400 to 2000 m, and steep, with slopes often higher than 30%. Predominant tree species are Douglas fir (Pseudotsuga menziesii (Mirb.) Franco.) and grand fir (Abies grandis (Dougl. Ex D. Don) Lindl.), often accompanied by ponderosa pine (Pinus ponderosa C. Lawson) and western red cedar (Thuja plicata Donn ex D.Don).
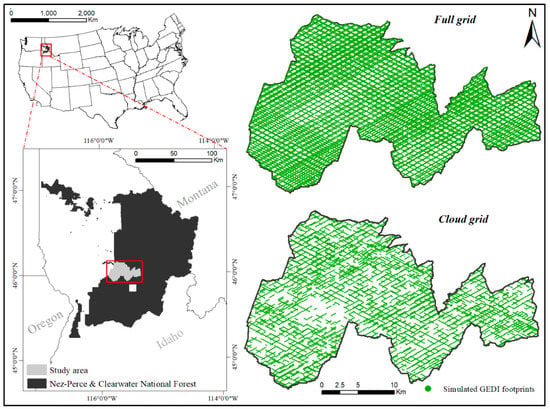
Figure 1.
Study area in the Nez-Perce and Clearwater National Forest (Idaho, USA) and distribution of the simulated GEDI footprints.
The landscape is largely characterized by the presence of even-aged stands resulting primarily from (1) stand-replacing wildfires that have disturbed the study area since the 19th century and (2) clearcut harvests during the latter half of the 20th century [45,46]. Other anthropogenic disturbances shaping the landscape of the study area include commercial thinning, seed tree, and shelterwood cuts [46].
2.2. LiDAR Data and GEDI Simulated Data
Small-footprint discrete return airborne LiDAR data were acquired in October 2009 and June-July 2012 on the Clear Creek watershed and the Selway River and Elk Creek watersheds, respectively. A Leica ALS60 instrument in multi-pulse mode and at a pulse rate of 69,400 Hz was used in the Clear Creek area and another at 88,000 Hz in the Selway area. The average pulse density was greater than 4 points/m2 in both datasets.
Large-footprint LiDAR waveforms were simulated from the airborne LiDAR point clouds using the GEDI simulator, developed for the calibration of algorithms and assessment of GEDI mission accuracy [44,47]. The waveforms were simulated on 22-m-diameter footprints (i.e., the mean expected GEDI footprint diameter), the location of which is determined by the nominal ISS orbits, combined with the GEDI sampling configuration.
Two grids of simulated GEDI footprints were generated over the study area:
- 66,177 simulated footprints; the simulation assumes that the GEDI instrument will be firing 60% of the time over the two-year programmed mission (henceforth, ‘full grid’).
- 28,602 simulated footprints; the simulation assumes that, besides the 60% firing rate, an additional data loss of approximately 50% of the footprints is expected due to snow and cloud cover (henceforth, ‘cloud grid’).
From the waveforms simulated for each footprint, 57 summary metrics were calculated (Table 1). There are several ground finding algorithms being tested by the GEDI mission. We mainly used a set of simulated waveform metrics where the ground is estimated from the center of gravity of the waveform intensity between the lowest two inflection points on a denoised and smoothed waveform. Default GEDI calibration database settings were used, with a smoothing width at 0.7 m and minimum feature width at 3 bins, and no noise was selected for the simulations.

Table 1.
List of the 57 derived metrics from simulated GEDI waveforms [44], calculated on each footprint of the two grids (Figure 1).
Topographic aspect has an important influence on microclimate gradients that constrain forest productivity and composition; therefore, the solar radiation aspect index ‘SRAI’ [49], defined as a linear transformation of the topographic aspect, was calculated for each GEDI simulated footprint. The SRAI ranges between 0 and 1 and relates to solar insolation: lower values represent cooler and moister areas that are north-northeast oriented, and higher values represent warmer and drier areas that are south-southwest oriented. SRAI was calculated on a 30-m raster grid (Equation (1)) and for each simulated GEDI footprint location, the SRAI value at the footprint center was extracted as:
where is the topographic aspect that was obtained from the digital terrain model (DTM) interpolated at a 30-m resolution from the ground returns of the airborne LiDAR point cloud using FUSION software [50]. Note that SRAI was only used for stratification and selection of the training dataset, i.e., it was not included as a predictor variable to estimate TSD (see Section 3.2).
2.3. Landsat Data
A cloud-free Landsat 8 Operational Land Imager (OLI) image (path 42, row 28) close in time (23 July 2013) to the airborne LiDAR surveys was downloaded from the USGS Earth Explorer (https://earthexplorer.usgs.gov). Landsat 8 was preferred over Landsat 5 or 7, both overlapping in time with the airborne LiDAR acquisitions, because of the poor radiometric resolution of the TM instrument on Landsat 5, and the failure in 2003 of the Scan Line Corrector (SLC) of the ETM+ sensor on Landsat 7.
The Landsat top of atmosphere reflectance multispectral data were pan-sharpened using the panchromatic band and the near neighbor diffusion (NNDiffuse) algorithm implemented in ENVI software [51]. Tasseled cap (TC) indices of brightness (TCB), greenness (TCG), and wetness (TCW) were then calculated using the coefficients published in Baig et al. [52] for the TC transformation based on Landsat 8 top of atmosphere reflectance. The three indices were rescaled between 0–100 applying a 2% linear stretch to be used as input data for image segmentation (see Section 2.4).
2.4. Landsat Image Segmentation
Landsat segmentation was performed using the multiresolution segmentation (MRS) algorithm [53] implemented in eCognition 9.1 software. The MRS segmentation output is adjusted through the specification and weighting of input data, and three parameters: scale (unitless, unbounded), compactness, and shape (both unitless, values defined between 0 and 1). The parameters control the spectral homogeneity, size, border smoothness, and compactness of the image-objects. TC indices were the input data for segmentation since they are more correlated to successional stages and recent disturbances (particularly the TCW) compared to other Landsat-derived indices [54,55,56]. Additionally, they have been previously used for the segmentation of forest patches in studies related to the estimation of forest structural parameters, such as biomass or TSD [33,40]. The three TC indices were included as input for segmentation and four combinations assigning different layer weights in the MRS algorithm were tested (one combination assigning equal weight to the three TC layers and another three combinations assigning double weight to one of the layers). For each combination of input data layers and weights, a set of 135 segmentations were obtained varying the values of the scale parameter (between 10 and 100 in increments of 2 units) and the compactness parameter (values of 0.1, 0.5, and 0.9). The shape parameter was kept constant at a low value (0.1) as recommended in Kavzoglu and Yildiz [57].
Subsequently, a two-stage object-based evaluation strategy was followed to identify an optimal segmentation [58]. Area-based dissimilarity metrics of oversegmentation and undersegmentation were used to identify the best combination of input layer weights [58,59]. Subsequently, measures of spatial autocorrelation [58,60,61,62] were used to identify, out of the 135 segmentations generated, the one with the maximum degree of intra-segment homogeneity and inter-segment heterogeneity. The optimal segmentation was obtained, giving the TCB and TCG equal weights in the MRS segmentation algorithm, while TCW was given double weight, and setting compactness = 0.1, shape = 0.1, and scale parameter = 46. For a more detailed explanation of the selection workflow, which combines both unsupervised and supervised object-based evaluation methods, refer to Sanchez-Lopez et al. [58]. The segmentation resulted in 2098 image-objects. Of these, 39 were smaller than 2 ha, which is commonly used as a threshold between stand and patch forest management units in areas of the Pacific Northwest [46], and were therefore merged with the most spectrally similar neighboring image-object, applying the ’remove’ eCognition algorithm. Figure 2 shows the resulting segmentation composed of 2059 image-objects.
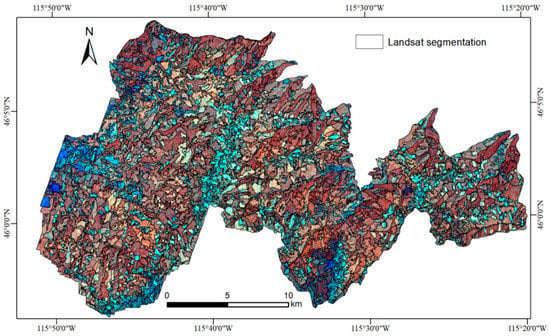
Figure 2.
Optimal Landsat segmentation (grey vectors) overlaid on the Tasseled Cap Brightness (TCB), Greenness (TCG), and Wetness (TCW) indices shown as an RGB color composite (R = TCW, G = TCG, B = TCB).
2.5. Airborne LiDAR Segmentation
An airborne LiDAR-based map of even-aged forest stands was used as a baseline. The airborne LiDAR datasets are described in Section 2.2 (for more details on the processing steps, see Sanchez-Lopez et al. [12]). The map of even-aged forest stands, described and validated in Sanchez-Lopez et al. [12,58], was generated through the segmentation of the gridded 95th percentile summary metric of the airborne LiDAR canopy height returns binned at a 30-m resolution, identified as the optimal LiDAR metric for the delineation of even-aged forest stands. The map defines 1470 forest stands with an average size of 35.6 ha and a median size of 29 ha (Figure 3).
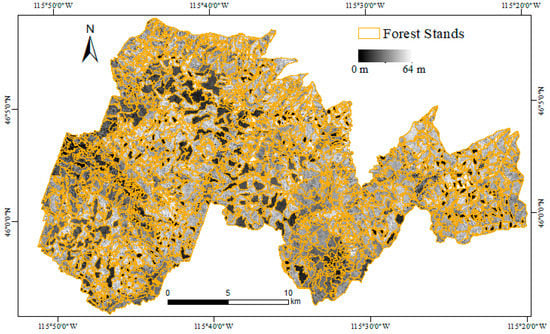
Figure 3.
Airborne LiDAR segmentation. The outline of even-aged forest stands (orange vectors) is overlaid on airborne LiDAR data (95th percentile of heights summary metric) displayed in grayscale.
2.6. Ancillary Reference Data
Records of stand-replacing disturbances that occurred in the study area between 1870 and 2005 were available from two different data sources:
- (1)
- A dataset of burned area perimeters of historical wildfires that occurred from 1870 to 2000, photo-interpreted using fire atlas data and historical aerial photographs [45]. The dataset includes a classification of fire severity classes of unburned, low, moderate, and high severity. We kept for analysis the areas labeled as moderate and high severity, which equate to stand-replacing fire. The dataset includes 166 fires, the greater majority recorded prior to 1940 (157 fires, representing 99.95% of the area burned).
- (2)
- The FACTS (Forest ACtivity Tracking System) timber harvest dataset, which is maintained by the U.S. Forest Service and contains spatial and temporal records of planned and accomplished forest management activities, such as clearcuts. It consists of polygon features with embedded metadata that include the fiscal year in which the activity was done. The dataset contained harvest records since 1956 for the study area [46].
The two datasets were harmonized, merged, and manually refined to amend potential unreported post-disturbances (e.g., small areas with evident biomass removal and other post-logging activity, especially within fire perimeters) as described in Sanchez Lopez et al. [12]. TSD was assigned to each polygon, as the number of years between the stand-replacing disturbance and 2012, used as the reference year based on the acquisition dates of the airborne LiDAR (used to simulate the GEDI data) (Section 2.2).
To ensure that the reference dataset included stands of both categories, i.e., disturbed after 1870 and undisturbed since 1870, 20 additional undisturbed forest stands (i.e., not disturbed since before 1870) were digitized and visually interpreted from the 2011 National Agriculture Imagery Program (NAIP) digital imagery (1-m spatial resolution using the closest available date to the LiDAR data) and the airborne LiDAR point clouds. The stands were characterized by dense canopy closure and relatively tall height of the dominant cohort of the forest canopy [12]. The reference dataset covered 29,154 ha (55.5% of the study area) (Figure 4).
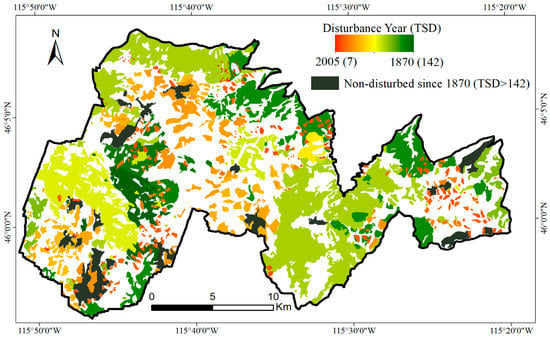
Figure 4.
Reference map of stand-replacing disturbances reported in the study area between 1870 and 2005. The dataset was compiled from records of historical burns digitized from aerial photographs [45] and digitized perimeters of the clearcut management units reported in the FACTs (Forest Service Activity Track System) harvest dataset [46]. Twenty forest stands undisturbed since before 1870 were delineated through visual interpretation of 1-m 2011 NAIP (National Agriculture Imagery Program) imagery and added to the dataset.
3. Methods
3.1. GEDI Coverage Analysis
A preliminary assessment was conducted to establish whether the GEDI footprint grid was sufficiently dense, relative to the size of the forest stands, to allow for the implementation of an object-oriented data fusion approach. The simulated GEDI footprints were combined with the stand map obtained from image segmentation, to compute the distribution of the number of GEDI footprints per stand. A parameter of particular importance is the number of forest stands not intersected by any GEDI footprints, i.e., the stands where no direct TSD estimation from GEDI would be possible.
The analysis was performed by considering the six possible combinations of the two stand maps derived from image segmentation (i.e., the Landsat segmentation described in Section 2.4, and the LiDAR segmentation described in Section 2.5) and three subsets of the GEDI simulated footprints, namely (a) the ‘full grid’ defined in Section 2.2; (b) the subset of the ‘full grid’ obtained by selecting only the footprints that are fully enclosed in a single forest stand, i.e., omitting footprints on stand edges (henceforth ‘full grid–within stand’); and (c) the subset of the ‘cloud grid’ obtained by selecting only the footprints that are fully enclosed in a single forest stand (henceforth ‘cloud grid—within stand’). Both image segmentations were considered because, as discussed in Section 1 and Section 2.4, it is reasonable to expect the Landsat segmentation to be a sub-optimal stand map. Therefore, the use of the optimal LiDAR segmentation, already validated in Sanchez-Lopez et al. [58], allows verification of whether any limitations of this study are to be attributed to the GEDI sampling, or to the use of Landsat data. Similarly, it is expected that eliminating from the subsequent steps of the analysis the footprints that straddle stand boundaries might increase the accuracy of the TSD estimation but at the cost of a reduced number of available measurements.
3.2. Estimation of Time Since Disturbance
The TSD estimation was performed by adapting to GEDI simulated waveforms the object-oriented methodology introduced by Sanchez-Lopez et al. [12] for airborne LiDAR data. TSD was estimated through (a) the selection of a training set of GEDI footprints belonging to forest stands with known TSD, used to train a random forest classifier; (b) the imputation of TSD to the entire set of GEDI footprints covering the study area; (c) the subsequent extrapolation to the stand level by using the stand polygons to calculate median TSD from the footprint-level estimations; and finally (d) accuracy assessment comparing the estimated TSD to the ancillary reference dataset.
The TSD estimation was performed independently using the six combinations of segmentation-derived stand maps (i.e., Landsat and LiDAR segmentation) and GEDI footprint grids defined above (i.e., ‘full grid’, ‘full grid–within stand’, and ‘cloud grid–within stand’). The six resulting scenarios ranged from a conservative scenario in the study area (i.e., ‘cloud grid–within stand’ for the footprint-level imputation, extrapolated to the sub-optimal Landsat-derived stand map) to the baseline representing ideal conditions (i.e., ‘full grid’ of GEDI footprints, extrapolated to the optimal LiDAR-derived stand map).
For each of the six combinations, a sensitivity analysis was performed, to determine the sensitivity of the accuracy metrics to the size of the training sample, i.e., the number of forest stands with known TSD used to locate the training set of GEDI footprints. The training sample was extracted through random sampling using a GEDI-assisted stratification. Ten sample sizes were tested, and the random extraction was repeated 100 times for each defined sample size. The entire classification procedure was performed for each instance of the random extraction (6 grid/segmentation combinations, 10 sample sizes, 100 random extractions resulting in 6000 total classifications), the accuracy of each classification was assessed, and summary nonparametric statistics (median, 25th, and 75th percentiles) of the accuracy metrics were calculated for each grid/segmentation combination and for each sample size. Section 3.2.1 describes in detail the experimental design of the sensitivity analysis and the stratified random sampling, and Section 3.2.2 reports the accuracy metrics used.
3.2.1. Experimental Design: Sensitivity Analysis
For each combination of GEDI footprint grid and segmentation-derived stand maps, a sample of forest stands of known TSD was extracted through stratified random sampling from the total population of candidate stands, defined as all the stands that (1) overlapped at least 75% of their area with the ancillary reference dataset (Figure 4); and (2) enclosed at least one GEDI footprint.
Topographic and canopy height-related metrics were used as stratification variables, adapting the stand-level stratification defined in Sanchez-Lopez et al. [12]. LiDAR-assisted stratification for forest inventories is cost-effective to reduce the amount of data required for model calibration in comparison to random sampling [63,64]. Our GEDI-assisted stratification was used to ensure the representativeness of the training set and minimize the number of required stands with known TSD. In practice, the time of the disturbance may only be known for a small percentage of stands that comprise the landscape and that potentially can be used to locate training GEDI footprints.
The topographic aspect-derived metric ‘SRAI’ was adopted as the first stratification variable, and the 98% relative height GEDI metric (‘rhInfl98′, Table 1) was selected as a second stratification variable. For each candidate stand, the mean ‘SRAI’ and mean ‘rhInfl98′ were calculated considering all the footprints belonging to the stand. Two ‘SRAI’ strata (mesic/xeric) of equal size were defined, using the median ‘SRAI’ of the candidate stands as a threshold. Within each ‘SRAI’ stratum, five ‘rhInfl98′ strata were defined, corresponding to the quintiles of the ‘rhInfl98′ distribution. As a result, 10 strata of equal size were identified and used for the selection of training data (Figure 5).
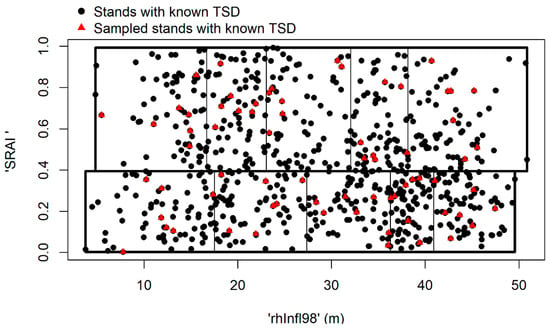
Figure 5.
Scheme of the stratified random sampling to extract the training set of stands of known TSD. The mean topographic solar-radiation aspect index (‘SRAI’) and the mean GEDI 98% relative height (from inflection points) (‘rhInfl98′) were used as stratification variables. This is a specific example with sample size = 7 (seven stands per stratum, reported as red triangles), resulting in a total of 70 stands sampled to create the training dataset, for the Landsat segmentation and ‘full grid-within stand’ scenario. In this case, the quintiles of the GEDI 98% relative height are 17.5, 27.4, 36.3, 40.9, and 49.6 m (SRAI < 0.39) and 16.7, 23.0, 32.0, 38.1, and 50.8 m (SRAI > 0.39). The extraction was replicated 100 times per sample size (varying from 1 to 10 in each stratum) for each of the studied scenarios.
The extraction was replicated 100 times for each sample size, with the sample size varying from 1 to 10 in each stratum (i.e., 10 to 100 training stands in total). Therefore, for each scenario, 1000 random extractions were performed. Note that, onwards, we refer to the sample size as the number of stands sampled in each stratum.
The R ‘yaImpute’ package [65] was used to train an RF classifier and predict TSD for each GEDI footprint. The training data used in the RF consisted of the GEDI footprint observations enclosed within the perimeters of the sampled stands. TSD, as observed in the ancillary reference data, was the dependent variable and the 57 GEDI derived metrics of the simulated GEDI waveforms were the predictor variables (Table 1). The number of decision trees was left at the default value (i.e., 500), as well as the number of predictor variables available to split at each tree node, which was seven. Once the RF classifier was trained, TSD was imputed to the grid of GEDI simulated footprints.
TSD at the stand level was calculated as the median value of the TSD predictions of the GEDI footprints intersecting or fully enclosed within each forest stand.
3.2.2. Accuracy Assessment Metrics
The accuracy of the predictions was assessed at the stand level using three accuracy metrics, defined as follows:
The root mean square difference between the estimated and observed TSD of the stands ():
The bias ():
The percentage of stands with absolute TSD error of less than 10 years (Perct.10). Ten years was selected as a benchmark to compute this accuracy metric given (1) the complexity of accurately estimating stand age using structural and topography-related derived indicators [13], (2) the analysis performed in the same study area using airborne LiDAR [12], and the potential suitability of decadal maps of stand-replacing TSD disturbance to categorize successional forest stages:
In Equations (2)–(4), n is the number of stands, and and are respectively the estimated and observed TSD of stand i.
The validation dataset used to compute these metrics comprised all the stands of known TSD that were not used for training. The stands overlapping with the manually interpreted undisturbed forest stands (i.e., not disturbed since 1870) were also excluded because their age was unknown.
4. Results
4.1. GEDI Coverage Analysis
The cumulative distribution of the percentage of stands and percentage of the study area, reported as a function of the minimum number of footprints per stand, is shown in Figure 6 for the six combinations of forest stand segmentation and GEDI footprint grids. The representative parameters of the distributions (total number of GEDI footprints, 95th, 75th, 50th, and 25th percentiles, and number of stands with no GEDI footprints) are reported in Table 2.
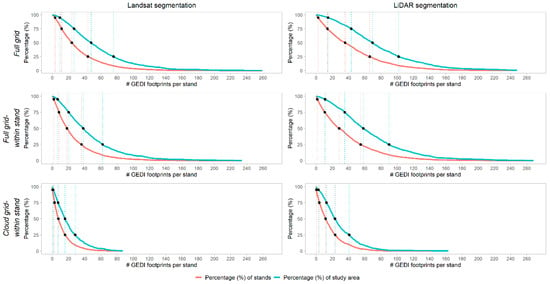
Figure 6.
Cumulative distribution of the number of footprints per stand expressed as a percentage of the number of stands (red), and percentage of the study area (blue). Black dots and dotted vertical lines mark the 95th, 75th, 50th, and 25th percentiles of the distribution.

Table 2.
Summary parameters of the cumulative distributions of the number of footprints per stand, expressed as a percentage of the number of stands (i.e., red curves in Figure 6), and percentage of the study area (i.e., blue curves in Figure 6), for the six combinations of segmentation-derived stand maps and subsets of the GEDI simulated footprints.
Comparison between the Landsat and the equivalent LiDAR-based scenarios confirms that oversegmentation translates into fewer footprints per stand available to estimate TSD (Figure 6). The increase in the number of stands costs a reduction in the average stand size and the number of intersecting footprints. The effect is accentuated when only fully enclosed footprints are considered (i.e., ‘full grid-within stand’ and ‘cloud grid-within stand’) because there are more segment boundaries for GEDI footprints to straddle.
Both the ‘full grid’ and the ‘full grid–within stand’ scenarios have good overall coverage of GEDI footprints per stand. Stands intersecting 20 footprints or more represent 75% of the study area regardless of the segmentation. The ‘cloud grid – within stand’ scenario, on the other hand, is the most restrictive case. Note that the ‘cloud grid’ had approximately 50% fewer footprints than the ‘full grid’ (Section 2.2). Notwithstanding this, stands with more than 7 and 12 GEDI footprints observations represented 75% of the study area in the Landsat and LiDAR segmentations, respectively.
The number of stands not intersected by any GEDI footprint is always lower than 15%, and represent less than 5% of the study area in all considered scenarios (Table 2); direct estimation of TSD and associated uncertainties with the current approach is not possible in these stands.
4.2. Sensitivity Analysis of the Estimated Time Since Disturbance
The experimental design detailed in Section 3.2 resulted in 6000 separate TSD estimations, which are discussed in detail in Section 4.2.1 through Section 4.2.3. The number of stands and GEDI footprints with known TSD available for training the RF and validating the proposed methodology is displayed in Table 3. Figure 7 shows, as an illustrative example, one of the instances of the TSD estimation obtained using the Landsat segmentation and the ‘full grid—within stand’ GEDI footprints.

Table 3.
Dataset of stands with known TSD available for training and validation of the proposed methodology for the six combinations of segmentation-derived stand map and GEDI footprint grid. All these stands overlapped at least 75% of their area with the ancillary reference dataset (Figure 4), and enclosed at least one GEDI footprint.
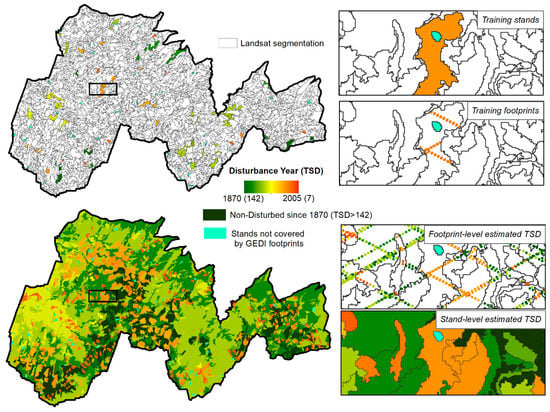
Figure 7.
Illustrative example of the methodology for the stand-level TSD estimation, showing the results of one of the 100 instances generated using the Landsat segmentation, the ‘full grid – within stand’ GEDI subset of footprints, and a sample size of 7 training stands per stratum. Top row: location of the randomly selected training stands, with on the right a detail of the GEDI footprints intersecting the training stands (i.e., the footprints used to train the imputation). Bottom row: estimated TSD for the whole study area, with on the right a detail of the footprint—level estimations, which were then aggregated to generate the stand-level estimation. In this specific case, RMSD was 18.9 years, BIAS was 0.4 years, and Perct.10 was 67.0% (71.4% when considering only the stands disturbed since 1910).
Even-aged stands are relatively homogenous, but there is inherent within-stand variability of the vegetation in terms of age and attributes, such as canopy cover and height. This variability increases with TSD, which translates into increased variability in the GEDI footprint-level observations, as illustrated by the distribution of the ´rhInfl98´ GEDI metric (Figure 8). The metric shows a relatively strong correlation with observed TSD—higher at the stand-level (R = 0.768)–represented by the median value of estimates of the enclosed GEDI footprints–than at the individual footprint level (R = 0.674).
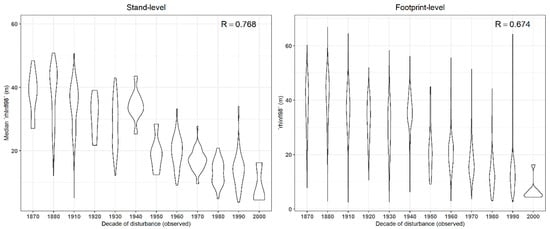
Figure 8.
Violin plots (i.e., combination of a box plot and a density plot) displaying the relationship between canopy height (´rhInfl98´GEDI metric) by decade for the illustrative example displayed in Figure 7. At left, values at the stand level, calculated as the median value of the enclosed GEDI footprints; at right, values at the GEDI footprints. R: Pairwise Pearson correlation coefficient between TSD and the canopy height metric.
4.2.1. Sensitivity to Training Sample Size
Figure 9 shows RMSD, BIAS, and Perct.10 boxplots of the TSD estimations obtained from the 100 random extractions of training stands for each sample size (i.e., from 1 to 10 training stands per stratum). In all six combinations of segmentation and footprint grids, the accuracy metrics show a similar monotonic pattern, with increasing accuracy as the number of training stands and GEDI footprints increases. As expected, there is a linear relationship between the number of training sampled stands and the number of GEDI footprints used to train the RF. In all cases, the sensitivity of the accuracy metrics to the sample size is initially high, and then steeply declines for sample sizes ≥ 4 stands per stratum. For instance, with the most conservative ‘cloud grid-within stand’ and Landsat segmentation, at sample size = 4, the median Perct.10 is 55.77% (i.e., 55.77% of the stands are classified within 10 years of the reference disturbance date), whereas at sample size = 10, Perct.10 is 60.56%. The interquartile range of all the accuracy metrics also decreases monotonically, with the greatest decrease observed for sample sizes ≤ 6.
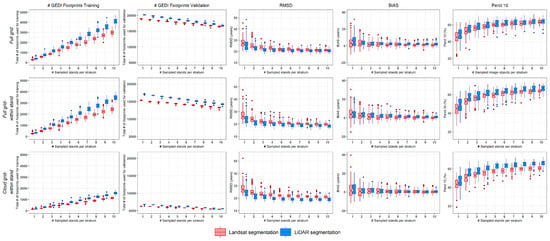
Figure 9.
Total number of footprints used for training the RF, total number of footprints available for validation, and accuracy (RMSD, BIAS, Perct.10) of the estimated TSD as a function of the training sample size (1 to 10 stands per stratum) and for the six combinations of segmentation-derived stand map and GEDI footprint grid. For each sample size and segmentation/grid combination, the training sample was extracted 100 times: the boxplots summarize the distribution of the accuracy metrics of the resulting 100 TSD estimations. The boxes report the median (thick central line) and the interquartile range of the distribution, the whiskers are 1.5 times the range of the upper and lower quartiles, and the dots show the outliers.
As a consequence, a training sample size of 6 stands per stratum was identified as the best compromise between the cost of generating training data and the reduction in classification errors.
Figure 10 shows for sample size = 6, the accuracy metrics stratified by stand height (i.e., the ‘rhInfl98’ GEDI metric).
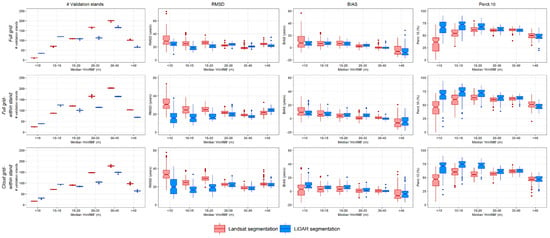
Figure 10.
Histogram of the distribution of the median ‘rhInfl98’ (m) of the stands in the validation dataset (left column), and boxplots of , , and Perct.10 stratified by stand height represented by the ‘rhInfl98’ GEDI metric (rightmost three columns); results of the 100 replicates obtained with training sample size = 6 stands for each scenario. The thick central line represents the median, the edges of the box are the first (i.e., the 25th percentile) and third (i.e., 75th percentile) quartiles, and the whiskers are 1.5 times the range of the upper and lower quartiles.
4.2.2. Sensitivity to the Stand Map
Comparison of the results obtained using the Landsat segmentation (red in Figure 9) and the LiDAR segmentation (blue in Figure 9) shows, with all grids and all sample sizes, that the former had a slightly worse performance as measured by RMSD and Perc.10, and slightly better performance as measured by the BIAS. The difference is relatively small, indicating that despite the oversegmentation discussed in Section 2.4 and Section 4.1, the Landsat segmentation can provide a suitable stand map. At a sample size = 6, the largest difference between the two segmentations was observed in the most conservative ‘cloud grid-within stand’ scenario, where median RMSD, median BIAS, and median Perc.10 were, respectively, 22.01 years, 0.01 years, and 57.77% for the Landsat segmentation, and 19.13 years, 0.42 years, and 63.53% for the LiDAR segmentation (Table 4). Nevertheless, and as expected, the LiDAR segmentation depicts overall higher accuracies compared to the Landsat segmentation when analyzing stratified stand heights (Figure 10), which is accentuated on stands with median ‘rhInfl98’ lower than 10 m.

Table 4.
RMSD, BIAS, and Perct.10 for the six combinations of segmentation-derived stand map and GEDI footprint grid for the 100 replicates obtained for a sample size of 6 stands per stratum.
A second-order effect of the stand oversegmentation using Landsat is that more footprints are discarded when only footprints fully enclosed within a stand are considered. Using the Landsat segmentation, 13,731 footprints (21% of the total) were discarded when considering the ‘full grid-within stand’ scenario instead of the ‘full grid’ scenario, whereas 10,417 (15% of the total) were discarded with the LiDAR segmentation (Table 2). In both cases, however, accuracy was higher with the ‘full grid-within stand’ than the ‘full grid’ scenario, indicating that eliminating footprints straddling two or more stands increases the accuracy even though fewer observations are available to estimate TSD. This was confirmed by extracting the training set from the ‘full grid-within stand’ to train the RF, and then applying the same RF to the ‘full grid’ and ‘full grid–within stand’. The accuracy metrics (Figure 11) indicate that, in all cases, the exclusion of the footprints straddling stands leads to a small increase in accuracy.
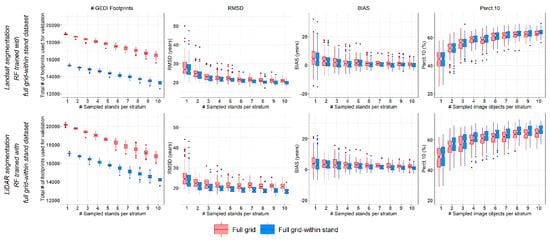
Figure 11.
Accuracy metrics (, , and Perct.10) stratified by training sample size (1 to 10 stands per stratum) of the TSD estimations obtained by extracting the training set from the ‘Full grid-within stand’ to train the RF, and then applying it to the ‘full grid-within stand’ (in blue) and the ‘full grid’ (in red). The thick central line represents the median, the edges of the box are the first (i.e., the 25th percentile), and third (i.e., 75th percentile) quartiles, and the whiskers are 1.5 times the range of the upper and lower quartiles.
4.2.3. Sensitivity to the Number of Footprints per Stand
The absolute number of available footprints per stand, and the density of footprints relative to the stand area, are in principle critical factors in evaluating the feasibility of the proposed object-based approach for the generation of a wall-to-wall TSD map. Comparison of the results obtained with the three grids (i.e., comparison of the three rows of Figure 9 and Table 4) shows that despite the large difference in available footprints, the three grids yielded very similar results, with the ‘cloud grid-within stand’ scenario only slightly less accurate than the ‘full grid–within stand’ scenario but more accurate than the ‘full grid’ scenario, due to the benefit of removing footprints that straddle stand edges.
In Figure 12, the accuracy of the TSD classifications obtained with sample size = 6 is stratified by the number of footprints available in each stand, and in Figure 13, the same results are reported as a function of the density of footprints per unit area. As expected, the accuracy of the TSD predictions increases with the number of footprints per stand, but the results are stable with about 15 footprints per stand (Figure 12), which translates to a density of more than 0.5 footprint per ha (Figure 13).
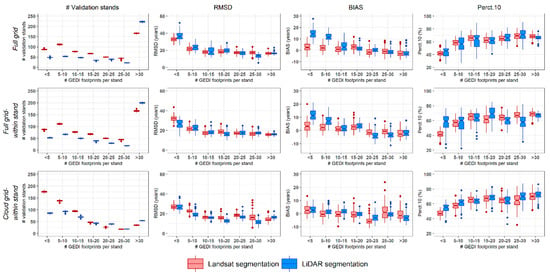
Figure 12.
Histogram of the distribution of the number of GEDI footprints per stand in the validation dataset (left column), and boxplots of , , and Perct.10 stratified by the number of available GEDI footprints per stand (rightmost three columns); all results are obtained with training sample size = 6 stands. The thick central line represents the median, the edges of the box are the first (i.e., the 25th percentile) and the third (i.e., 75th percentile) quartiles, and the whiskers are 1.5 times the range of the upper and lower quartile.
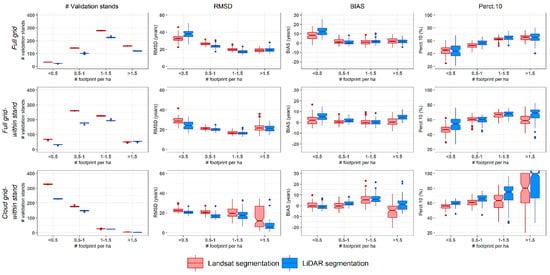
Figure 13.
Histogram of the distribution of the density of GEDI footprints per unit area in the validation dataset (left column), and boxplots of , , and Perct.10 stratified by the density of available GEDI footprints per ha within stands (rightmost three columns); all results are obtained with training sample size = 6 stands. The thick central line represents the median, the edges of the box are the first (i.e., the 25th percentile) and third (i.e., 75th percentile) quartiles, and the whiskers are 1.5 times the range of the upper and lower quartiles.
5. Discussion
The GEDI spaceborne LiDAR instrument is providing unprecedented observations of global vegetation structure. Its sampling configuration makes it a priority to develop approaches for the spatial extrapolation of footprint-level observations to generate wall-to-wall maps of vegetation characteristics. In this research, we studied the feasibility of an object-oriented fusion of GEDI footprints and Landsat data for the estimation of time since disturbance at the stand level; the analysis was conducted using simulated GEDI data generated from a small-footprint airborne LiDAR dataset.
We adapted to GEDI the approach for TSD estimation developed for airborne LiDAR in Sanchez-Lopez et al. [12]. The resulting methodology involves the extraction of a training set of stands with known TSD, followed by RF classification to obtain footprint-level TSD estimates, and finally object-oriented fusion with a Landsat-derived stand map.
The proposed stratification for the selection of the training set is based solely on topography and GEDI-observed height. In the present study, ´SRAI´ was derived from the DEM generated from the airborne LiDAR acquisition, but in principle, it could be generated from any globally available surface elevation data (e.g., SRTM); thus, it is not expected to limit the findings or future application of this research since it was only used for stratification and selection of the training data. A minimum of six stands per stratum (60 stands in total) was needed to obtain acceptable accuracies, and to constrain the standard errors of the accuracy metrics. The ‘rhInfl98′ metric, representing the height of the upper layer of the canopy, was selected for stratification based on the expected high correlation between canopy height and TSD [12], which was confirmed in the present analysis (Figure 8); nevertheless, alternative metrics accounting also for canopy cover might be well suited as stratification variables, especially when considering relatively old stands (i.e., TSD > 100 years).
The stratification ensures that the full range of forest conditions is sampled, while requiring the collection of TSD training data (usually expensive and time-consuming to gather in the field) only on the sampled stands. In other study sites where information on TSD is not available, forest change maps [66] and available optical remotely sensed imagery could be used to identify recent disturbances. In areas where clearcut harvesting is commonly practiced and field data records of forest operations are available (e.g., in the U.S.A, Canada, or the Scandinavian countries), those can be in a TSD reference dataset, as well as information from national forest inventories that often include dendrochronology records of specific stands. If none of these records exist, the proposed methods could still be implemented, by estimating TSD from tree age cores on the sampled stands.
Landsat data have an adequate spatial resolution (i.e., 30 m) to detect typical forest management units, such as forest stands. However, a few limitations should be considered. It is well established that the sensitivity of Landsat reflectance to forest structure is low in dense canopies [54,67]. In particular, there is an asymptotic relationship between optical reflectance and stand age, with low separability of mature forest stands since the signal saturates above intermediate biomass levels [68]. As expected, a degree of mismatch was observed between the perimeters of the Landsat image-objects and the actual forest stands, especially in stands disturbed many decades ago (i.e., TSD>80 years). Overall, the Landsat-based stand map was oversegmented in comparison to the airborne LiDAR-based one. While oversegmentation is considered less problematic compared to undersegmentation in object-based image analysis, in the specific case of data fusion with a sampling instrument, oversegmentation has the undesirable effect of reducing the number of GEDI footprints available to estimate TSD within each stand. The 25-m diameter of the GEDI footprints results in a number of observations straddling the boundaries between of stands of different TSD. The results indicate that using only footprints fully enclosed within a single forest stand increased accuracy, despite the tradeoff with the reduced number of available observations (e.g., Figure 9 and Figure 11). It therefore is important to ensure an optimal delineation of the forest stands, to avoid oversegmentation, thus minimizing the number of discarded GEDI footprints.
The total number of footprints used for training the RF had, overall, less effect on accuracy than the number of training stands sampled in each stratum (as noted above, the gain in accuracy is very considerable for small sample sizes of up to six stands per stratum). This is demonstrated in Figure 9: the accuracy of the results obtained using the three grids is substantially identical at each given sample size, even though the total number of footprints used for training (Figure 9, left column) varies greatly across grids. This is not unexpected, as a larger number of training stands would ensure that the training dataset better represents the full range of forest conditions in the study area.
The spatial distribution of GEDI footprints, with regularly spaced observations along and across the orbits of the International Space Station, effectively ensures that larger stands will include more footprints than smaller stands. The accuracy of the results monotonically increases with the number of footprints per stand, but our results indicate that the accuracy improves only marginally above 15 footprints per stand (corresponding to a density of 0.5 footprints per ha).
The number of footprints available to estimate TSD in each stand at the end of the two-year programmed mission will depend, among other factors, on cloud coverage. We observed only a very modest decrease in accuracy when comparing the results obtained with the full grid of simulated observations to the grid with 50% cloud cover; and our analysis suggests that only 5% of the study area will be represented by stands unsampled by a GEDI footprint. When considering the present results for future studies, note should be taken that footprint density is also a function of latitude. The study area is located on ~46N, where a higher track density is expected compared to lower latitudes nearer the tropics [37]. Additionally, the size and shape of the forest stands will differ in other ecosystems, due to different stand-replacing disturbance dynamics and harvesting practices. As a result, the number of stands not intersected by any GEDI footprint might increase or decrease, and wall-to-wall mapping of TSD with the proposed methodology might require more complex data fusion strategies with alternative sources of remotely sensed data.
This research builds upon the study of Sanchez-Lopez et al. [12], who used airborne LiDAR data to predict stand-level TSD in the same study area. When accounting for clouds, two years of GEDI footprints are expected to cover only ~4% of the study area, whereas the airborne LiDAR point clouds provided complete coverage with a return density of >4 points/m2. Even so, the change in accuracy between the two studies was not pronounced. The overall accuracy obtained using the LiDAR segmentation and the ‘cloud grid-within stand’ scenario (median = 19.13 years, median = 0.42 years, and median Perct.10 = 63.53% (Table 4)) was comparable to the results obtained from airborne LiDAR in the former study: = 17.5 years, = 0.8 years, and Perct.10 = 72.8%.
Even-aged stands are structurally homogenous, but there exists an intrinsic degree of heterogeneity driven by, among other things, regeneration and regrowth patterns, micro-site conditions, and competition, which becomes accentuated with age as an uneven-aged distribution of the trees comprising the stand develops. Sanchez-Lopez et al. [12] argued that the introduction of meaningful spatial units of analysis in the form of stand boundaries reduced the inherent variability of cell-level analyses, to improve estimates of forest attributes (such as TSD) such that they vary less within stands than between stands. Similarly, here, the use of stand perimeters provided contextual information to aggregate TSD at the stand level, reducing the variability observed by individual GEDI footprints (Figure 8). It should be noted that part of the variability observed in the footprint-level GEDI metrics might be attributed to the ground filtering algorithm used to retrieve the GEDI metrics. Default settings, such as the smoothing width, could be adjusted for this specific biome to make ground detection more precise.
Thanks to the availability of the burn history dataset [45] and clearcut harvest records (i.e., FACTs dataset) [46], our analysis considered TSD up to 140 years. Some limitation of the reference dataset ought, however, to be discussed. The distribution of disturbances changed through time, with a very large number of disturbed stands in some decades (e.g., 1910s) and no disturbed stands in others (e.g., 1900s, 1890s). Moreover, most of the older disturbed stands (TSD > 60 years) resulted from large fires that occurred in the 1910s and 1930s, whereas younger disturbed stands (TSD < 60 years) resulted from smaller clearcuts. It should also be considered that the reference dataset included fires of medium to high severity [12,45]. Stand regeneration and regrowth patterns might significantly vary as a function of fire severity, especially when combined with other factors, such as topography and micro-climate conditions. It is expected that that the incorporation of additional variables in the RF, linked to the type and magnitude of disturbance, or to climate and topography, would increase the accuracy of the TSD predictions [12]. It is also likely that the FACTs dataset has omission errors (i.e., additional clearcuts and some post-fire logging that might not have been recorded), but these would not affect the accuracy metrics.
The validation results (RMSD ~20 years and Perct.10 ~60% on TSD up to 140 years) indicate that the TSD estimation is sufficiently precise for a broad characterization of stand age (old-growth, primary forest from non-disturbed and industrial areas), and to identify successional states (e.g., open, stand initiation, young multistory, mature multistory, old multistory) [27] but not for providing the exact decade of the disturbance.
Overall, the present study indicates that GEDI will provide a relatively dense grid of measurements after its two-year programmed mission and its combination with a stand delineation provides a means to map stand-level TSD synoptically, at least in areas with similar disturbance dynamics and at relatively high latitudes. The method has been specifically designed for stand-replacing disturbances. Further research would be required to address the suitability of the method including more subtle disturbances, such as partial harvests, low-severity fires, droughts, or insect outbreaks.
6. Conclusions
Upscaling footprint estimates to objects that represent even-aged forest stands overcomes the limitations of the GEDI sampling configuration and allows for the estimation of stand-level TSD. In contrast to the use of cells of constant size for data fusion with spaceborne LiDAR data (e.g., 1 km, 500 m) [31,32,69], the use of image-objects is preferable to map forest attributes, such as TSD, in managed forests that vary less within stands than between stands even decades after stand-replacing disturbance events. Thus, footprints enclosed within the same stand likely represent canopy structures of similar TSD.
Datasets of the stand-level disturbance history of forest ecosystems are required to fully understand global carbon cycle dynamics and assess the actual role of forests in the mitigation of climate change. Forest vertical structure data provide the information needed to accurately reconstruct the long-term disturbance history of forests typified by stand-replacing disturbance regimes, and data fusion between GEDI and Landsat, as proposed in this study, can be used to map TSD at the stand level, especially in areas disturbed within the last 100 years. GEDI–Landsat data fusion is a promising strategy to develop TSD maps and could be exploited to map other temporal stand attributes, such as forest succession and regrowth, or stand structure attributes, such as height, basal area, or biomass.
Author Contributions
N.S.-L., L.B., and A.T.H. conceived the overall approach of the paper and define the methodology. N.S.-L. refined the methods, analyzed the data, and wrote the draft of the paper with assistance from L.B. and A.T.H.; S.H. simulated GEDI data from airborne LiDAR; S.H. and L.I.D. provided comments, edits and feedback while finalizing drafting the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
The project is supported by NASA’s Land-Cover/Land-Use Change (LCLUC) program (award number NHX14AD92G); the Carbon Monitoring System (CMS) projects (award numbers: NNH15AZ06I and 80HQTR20T0002); and by the United States Department of Agriculture (USDA) under award USDA NIFA 2011-32100-06016.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Pan, Y.; Chen, J.M.; Birdsey, R.; McCullough, K.; He, L.; Deng, F. Age structure and disturbance legacy of North American forests. Biogeosciences 2011, 8, 715–732. [Google Scholar] [CrossRef]
- Pregitzer, K.S.; Euskirchen, E.S. Carbon cycling and storage in world forests: Biome patterns related to forest age. Glob. Chang. Biol. 2004, 10, 2052–2077. [Google Scholar] [CrossRef]
- Pugh, T.A.; Lindeskog, M.; Smith, B.; Poulter, B.; Arneth, A.; Haverd, V.; Calle, L. Role of forest regrowth in global carbon sink dynamics. Proc. Natl. Acad. Sci. USA 2019, 116, 4382–4387. [Google Scholar] [CrossRef] [PubMed]
- Bradford, J.B.; Birdsey, R.A.; Joyce, L.A.; Ryan, M.G. Tree age, disturbance history, and carbon stocks and fluxes in subalpine Rocky Mountain forests. Glob. Chang. Biol. 2008, 14, 2882–2897. [Google Scholar] [CrossRef]
- Hansen, M.C.; Stehman, S.V.; Potapov, P.V.; Loveland, T.R.; Townshend, J.R.G.; DeFries, R.S.; Pittman, K.W.; Arunarwati, B.; Stolle, F.; Steininger, M.K.; et al. Humid tropical forest clearing from 2000 to 2005 quantified by using multitemporal and multiresolution remotely sensed data. Proc. Natl. Acad. Sci. USA 2008, 105, 9439–9444. [Google Scholar] [CrossRef]
- Huang, C.; Goward, S.N.; Masek, J.G.; Gao, F.; Vermote, E.F.; Thomas, N.; Schleeweis, K.; Kennedy, R.E.; Zhu, Z.; Eidenshink, J.C.; et al. Development of time series stacks of Landsat images for reconstructing forest disturbance history. Int. J. Digit. Earth 2009, 2, 195–218. [Google Scholar] [CrossRef]
- Huo, L.-Z.; Boschetti, L.; Sparks, A.M. Object-Based Classification of Forest Disturbance Types in the Conterminous United States. Remote Sens. 2019, 11, 477. [Google Scholar] [CrossRef]
- Kennedy, R.E.; Yang, Z.; Cohen, W.B. Detecting trends in forest disturbance and recovery using yearly Landsat time series: 1. LandTrendr—Temporal segmentation algorithms. Remote Sens. Environ. 2010, 114, 2897–2910. [Google Scholar] [CrossRef]
- Lu, D.; Mausel, P.; Brondízio, E.; Moran, E. Change detection techniques. Int. J. Remote Sens. 2004, 25, 2365–2401. [Google Scholar] [CrossRef]
- Masek, J.G.; Huang, C.; Wolfe, R.; Cohen, W.; Hall, F.; Kutler, J.; Nelson, P. North American forest disturbance mapped from a decadal Landsat record. Remote Sens. Environ. 2008, 112, 2914–2926. [Google Scholar] [CrossRef]
- Schroeder, T.A.; Cohen, W.B.; Yang, Z. Patterns of forest regrowth following clearcutting in western Oregon as determined from a Landsat time-series. For. Ecol. Manag. 2007, 243, 259–273. [Google Scholar] [CrossRef]
- Sanchez-Lopez, N.; Boschetti, L.; Hudak, A.T. Reconstruction of the disturbance history of a temperate coniferous forest through stand-level analysis of airborne LiDAR data. For. Int. J. For. Res. 2020, 93, 38–55. [Google Scholar] [CrossRef]
- Racine, E.B.; Coops, N.C.; St-Onge, B.; Bégin, J. Estimating Forest Stand Age from LiDAR-Derived Predictors and Nearest Neighbor Imputation. For. Sci. 2014, 60, 128–136. [Google Scholar] [CrossRef]
- Poulter, B.; Aragão, L.; Andela, N.; Bellassen, V.; Ciais, P.; Kato, T.; Lin, X.; Nachin, B.; Luyssaert, S.; Pederson, N.; et al. The global forest age dataset and its uncertainties (GFADv1.1). NASA Natl. Aeronaut. Space Adm. 2019. [Google Scholar] [CrossRef]
- Monserud, R.A. Height Growth and Site Index Curves for Inland Douglas-fir Based on Stem Analysis Data and Forest Habitat Type. For. Sci. 1984, 30, 943–965. [Google Scholar] [CrossRef]
- Oliver, C.D.; Larson, B.C. Forest Stand Dynamics: Updated Edition; John Wiley and Sons: Hoboken, NJ, USA, 1996. [Google Scholar]
- Ryan, M.G.; Binkley, D.; Fownes, J.H.; Giardina, C.P.; Senock, R.S. An Experimental Test of the Causes of Forest Growth Decline with Stand Age. Ecol. Monogr. 2004, 74, 393–414. [Google Scholar] [CrossRef]
- Goetz, S.; Dubayah, R. Advances in remote sensing technology and implications for measuring and monitoring forest carbon stocks and change. Carbon Manag. 2011, 2, 231–244. [Google Scholar] [CrossRef]
- Andersen, H.-E.; McGaughey, R.J.; Reutebuch, S.E. Estimating forest canopy fuel parameters using LIDAR data. Remote Sens. Environ. 2005, 94, 441–449. [Google Scholar] [CrossRef]
- Boudreau, J.; Nelson, R.F.; Margolis, H.A.; Beaudoin, A.; Guindon, L.; Kimes, D.S. Regional aboveground forest biomass using airborne and spaceborne LiDAR in Québec. Remote Sens. Environ. 2008, 112, 3876–3890. [Google Scholar] [CrossRef]
- Hudak, A.T.; Crookston, N.L.; Evans, J.S.; Falkowski, M.J.; Smith, A.M.; Gessler, P.E.; Morgan, P. Regression modeling and mapping of coniferous forest basal area and tree density from discrete-return lidar and multispectral satellite data. Can. J. Remote Sens. 2006, 32, 126–138. [Google Scholar] [CrossRef]
- Lefsky, M.A.; Cohen, W.B.; Acker, S.A.; Parker, G.G.; Spies, T.A.; Harding, D. Lidar Remote Sensing of the Canopy Structure and Biophysical Properties of Douglas-Fir Western Hemlock Forests. Remote Sens. Environ. 1999, 70, 339–361. [Google Scholar] [CrossRef]
- Lefsky, M.A.; Hudak, A.T.; Cohen, W.B.; Acker, S.A. Patterns of covariance between forest stand and canopy structure in the Pacific Northwest. Remote Sens. Environ. 2005, 95, 517–531. [Google Scholar] [CrossRef]
- Næesset, E. Determination of mean tree height of forest stands using airborne laser scanner data. ISPRS J. Photogramm. Remote Sens. 1997, 52, 49–56. [Google Scholar] [CrossRef]
- Nelson, R.; Krabill, W.; Tonelli, J. Estimating forest biomass and volume using airborne laser data. Remote Sens. Environ. 1988, 24, 247–267. [Google Scholar] [CrossRef]
- Zhao, K.; Popescu, S. Lidar-based mapping of leaf area index and its use for validating globcarbon satellite LAI product in a temperate forest of the southern USA. Remote Sens. Environ. 2009, 113, 1628–1645. [Google Scholar] [CrossRef]
- Falkowski, M.J.; Evans, J.S.; Martinuzzi, S.; Gessler, P.E.; Hudak, A.T. Characterizing forest succession with lidar data: An evaluation for the Inland Northwest, USA. Remote Sens. Environ. 2009, 113, 946–956. [Google Scholar] [CrossRef]
- Zhang, C.; Ju, W.; Chen, J.M.; Li, D.; Wang, X.; Fan, W.; Li, M.; Zan, M. Mapping forest stand age in China using remotely sensed forest height and observation data. J. Geophys. Res. Biogeosci. 2014, 119, 1163–1179. [Google Scholar] [CrossRef]
- Zwally, H.J.; Schutz, B.; Abdalati, W.; Abshire, J.; Bentley, C.; Brenner, A.; Bufton, J.; Dezio, J.; Hancock, D.; Harding, D. ICESat’s laser measurements of polar ice, atmosphere, ocean, and land. J. Geodyn. 2002, 34, 405–445. [Google Scholar] [CrossRef]
- Lefsky, M.A. A global forest canopy height map from the Moderate Resolution Imaging Spectroradiometer and the Geoscience Laser Altimeter System. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Baccini, A.; Goetz, S.J.; Walker, W.S.; Laporte, N.T.; Sun, M.; Sulla-Menashe, D.; Hackler, J.; Beck, P.S.A.; Dubayah, R.; Friedl, M.A. Estimated carbon dioxide emissions from tropical deforestation improved by carbon-density maps. Nat. Clim. Chang. 2012, 2, 182–185. [Google Scholar] [CrossRef]
- Simard, M.; Pinto, N.; Fisher, J.B.; Baccini, A. Mapping forest canopy height globally with spaceborne lidar. J. Geophys. Res. Biogeosci. 2011, 116. [Google Scholar] [CrossRef]
- Montesano, P.M.; Cook, B.D.; Sun, G.; Simard, M.; Nelson, R.F.; Ranson, K.J.; Zhang, Z.; Luthcke, S. Achieving accuracy requirements for forest biomass mapping: A spaceborne data fusion method for estimating forest biomass and LiDAR sampling error. Remote Sens. Environ. 2013, 130, 153–170. [Google Scholar] [CrossRef]
- Duncanson, L.I.; Niemann, K.O.; Wulder, M.A. Estimating forest canopy height and terrain relief from GLAS waveform metrics. Remote Sens. Environ. 2010, 114, 138–154. [Google Scholar] [CrossRef]
- Peterson, B.; Nelson, K.J. Mapping forest height in Alaska using GLAS, Landsat composites, and airborne LiDAR. Remote Sens. 2014, 6, 12409–12426. [Google Scholar] [CrossRef]
- Peterson, B.; Nelson, K.; Wylie, B. Towards integration of GLAS into a national fuel mapping program. Photogramm. Eng. Remote Sens. 2013, 79, 175–183. [Google Scholar] [CrossRef]
- Dubayah, R.; Blair, J.B.; Goetz, S.; Fatoyinbo, L.; Hansen, M.; Healey, S.; Hofton, M.; Hurtt, G.; Kellner, J.; Luthcke, S.; et al. The Global Ecosystem Dynamics Investigation: High-resolution laser ranging of the Earth’s forests and topography. Sci. Remote Sens. 2020, 1, 100002. [Google Scholar] [CrossRef]
- Fisher, P. The pixel: A snare and a delusion. Int. J. Remote Sens. 1997, 18, 679–685. [Google Scholar] [CrossRef]
- Blaschke, T.; Lang, S.; Hay, G. Object-Based Image Analysis: Spatial Concepts for Knowledge-Driven Remote Sensing Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008; ISBN 978-3-540-77058-9. [Google Scholar]
- Wulder, M.A.; Skakun, R.S.; Kurz, W.A.; White, J.C. Estimating time since forest harvest using segmented Landsat ETM+ imagery. Remote Sens. Environ. 2004, 93, 179–187. [Google Scholar] [CrossRef]
- Wulder, M.A.; Seemann, D. Forest inventory height update through the integration of lidar data with segmented Landsat imagery. Can. J. Remote Sens. 2003, 29, 536–543. [Google Scholar] [CrossRef]
- Wulder, M.A.; Han, T.; White, J.C.; Sweda, T.; Tsuzuki, H. Integrating profiling LIDAR with Landsat data for regional boreal forest canopy attribute estimation and change characterization. Remote Sens. Environ. 2007, 110, 123–137. [Google Scholar] [CrossRef]
- Wulder, M.A.; White, J.C.; Alvarez, F.; Han, T.; Rogan, J.; Hawkes, B. Characterizing boreal forest wildfire with multi-temporal Landsat and LIDAR data. Remote Sens. Environ. 2009, 113, 1540–1555. [Google Scholar] [CrossRef]
- Hancock, S.; Armston, J.; Hofton, M.; Sun, X.; Tang, H.; Duncanson, L.I.; Kellner, J.R.; Dubayah, R. The GEDI simulator: A large-footprint waveform lidar simulator for calibration and validation of spaceborne missions. Earth Space Sci. 2019. [Google Scholar] [CrossRef] [PubMed]
- Morgan, P.; Hudak, A.T.; Wells, A.; Parks, S.A.; Baggett, L.S.; Bright, B.C.; Green, P. Multidecadal trends in area burned with high severity in the Selway-Bitterroot Wilderness Area 1880–2012. Int. J. Wildland Fire 2017, 26, 930–943. [Google Scholar] [CrossRef]
- USDA, Forest Service Forest Service Activity Tracking System (FACTs) Harvest Database. Available online: http://data.fs.usda.gov/geodata/edw/datasets.php (accessed on 28 February 2018).
- Blair, J.B.; Hofton, M.A. Modeling laser altimeter return waveforms over complex vegetation using high-resolution elevation data. Geophys. Res. Lett. 1999, 26, 2509–2512. [Google Scholar] [CrossRef]
- Lefsky, M.A.; Keller, M.; Pang, Y.; Camargo, P.B.d.; Hunter, M.O. Revised method for forest canopy height estimation from Geoscience Laser Altimeter System waveforms. J. Appl. Remote Sens. 2007, 1, 013537. [Google Scholar] [CrossRef]
- Roberts, D.W.U.S.U.; Cooper, S.V. Concepts and Techniques of Vegetation Mapping; Food and agriculture Organization of the United Nation: Rome, Italy, 1989. [Google Scholar]
- McGaughey, R.J. FUSION/LDV: Software for LIDAR Data Analysis and Visualization; US Department of Agriculture, Forest Service, Pacific Northwest Research Station: Seattle, WA, USA, 2009.
- Sun, W.; Chen, B.; Messinger, D. Nearest-neighbor diffusion-based pan-sharpening algorithm for spectral images. Opt. Eng. 2014, 53, 013107. [Google Scholar] [CrossRef]
- Baig, M.H.A.; Zhang, L.; Shuai, T.; Tong, Q. Derivation of a tasselled cap transformation based on Landsat 8 at-satellite reflectance. Remote Sens. Lett. 2014, 5, 423–431. [Google Scholar] [CrossRef]
- Baatz, M.; Schape, A. Multiresolution Segmentation–an optimization approach for high quality multi-scale image segmentation. AGIT Symp. Salzbg. 2000, 2000, 12–23. [Google Scholar]
- Cohen, W.B.; Spies, T.A.; Fiorella, M. Estimating the age and structure of forests in a multi-ownership landscape of western Oregon, USA. Int. J. Remote Sens. 1995, 16, 721–746. [Google Scholar] [CrossRef]
- Cohen, W.B.; Spies, T.A. Estimating structural attributes of Douglas-fir/western hemlock forest stands from Landsat and SPOT imagery. Remote Sens. Environ. 1992, 41, 1–17. [Google Scholar] [CrossRef]
- Jin, S.; Sader, S.A. Comparison of time series tasseled cap wetness and the normalized difference moisture index in detecting forest disturbances. Remote Sens. Environ. 2005, 94, 364–372. [Google Scholar] [CrossRef]
- Kavzoglu, T.; Yildiz, M. Parameter-based performance analysis of object-based image analysis using aerial and QuikBird-2 images. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, 2, 31. [Google Scholar] [CrossRef]
- Sanchez-Lopez, N.; Boschetti, L.; Hudak, A. Semi-Automated Delineation of Stands in an Even-Age Dominated Forest: A LiDAR-GEOBIA Two-Stage Evaluation Strategy. Remote Sens. 2018, 10, 1622. [Google Scholar] [CrossRef]
- Clinton, N.; Holt, A.; Scarborough, J.; Yan, L.I.; Gong, P. Others Accuracy assessment measures for object-based image segmentation goodness. Photogramm. Eng. Remote Sens. 2010, 76, 289–299. [Google Scholar] [CrossRef]
- Böck, S.; Immitzer, M.; Atzberger, C. On the Objectivity of the Objective Function—Problems with Unsupervised Segmentation Evaluation Based on Global Score and a Possible Remedy. Remote Sens. 2017, 9, 769. [Google Scholar] [CrossRef]
- Espindola, G.M.; Camara, G.; Reis, I.A.; Bins, L.S.; Monteiro, A.M. Parameter selection for region-growing image segmentation algorithms using spatial autocorrelation. Int. J. Remote Sens. 2006, 27, 3035–3040. [Google Scholar] [CrossRef]
- Johnson, B.; Xie, Z. Unsupervised image segmentation evaluation and refinement using a multi-scale approach. ISPRS J. Photogramm. Remote Sens. 2011, 66, 473–483. [Google Scholar] [CrossRef]
- Gobakken, T.; Korhonen, L.; Næsset, E. Laser-assisted selection of field plots for an area-based forest inventory. Silva Fenn. 2013, 47, 943. [Google Scholar] [CrossRef]
- Hawbaker, T.J.; Keuler, N.S.; Lesak, A.A.; Gobakken, T.; Contrucci, K.; Radeloff, V.C. Improved estimates of forest vegetation structure and biomass with a LiDAR-optimized sampling design. J. Geophys. Res. Biogeosci. 2009, 114, G00E04. [Google Scholar] [CrossRef]
- Crookston, N.L.; Finley, A.O. yaImpute: An R package for kNN imputation. J. Stat. Softw. 2008, 23, 16. [Google Scholar] [CrossRef]
- Hansen, M.C.; Potapov, P.V.; Moore, R.; Hancher, M.; Turubanova, S.A.; Tyukavina, A.; Thau, D.; Stehman, S.V.; Goetz, S.J.; Loveland, T.R.; et al. High-Resolution Global Maps of 21st-Century Forest Cover Change. Science 2013, 342, 850–853. [Google Scholar] [CrossRef] [PubMed]
- Turner, D.P.; Cohen, W.B.; Kennedy, R.E.; Fassnacht, K.S.; Briggs, J.M. Relationships between Leaf Area Index and Landsat TM Spectral Vegetation Indices across Three Temperate Zone Sites. Remote Sens. Environ. 1999, 70, 52–68. [Google Scholar] [CrossRef]
- Zhao, P.; Lu, D.; Wang, G.; Wu, C.; Huang, Y.; Yu, S. Examining Spectral Reflectance Saturation in Landsat Imagery and Corresponding Solutions to Improve Forest Aboveground Biomass Estimation. Remote Sens. 2016, 8, 469. [Google Scholar] [CrossRef]
- Baccini, A.; Laporte, N.; Goetz, S.J.; Sun, M.; Dong, H. A first map of tropical Africa’s above-ground biomass derived from satellite imagery. Environ. Res. Lett. 2008, 3, 045011. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).