Depth-Wise Separable Convolution Neural Network with Residual Connection for Hyperspectral Image Classification
Abstract
1. Introduction
2. Model Design
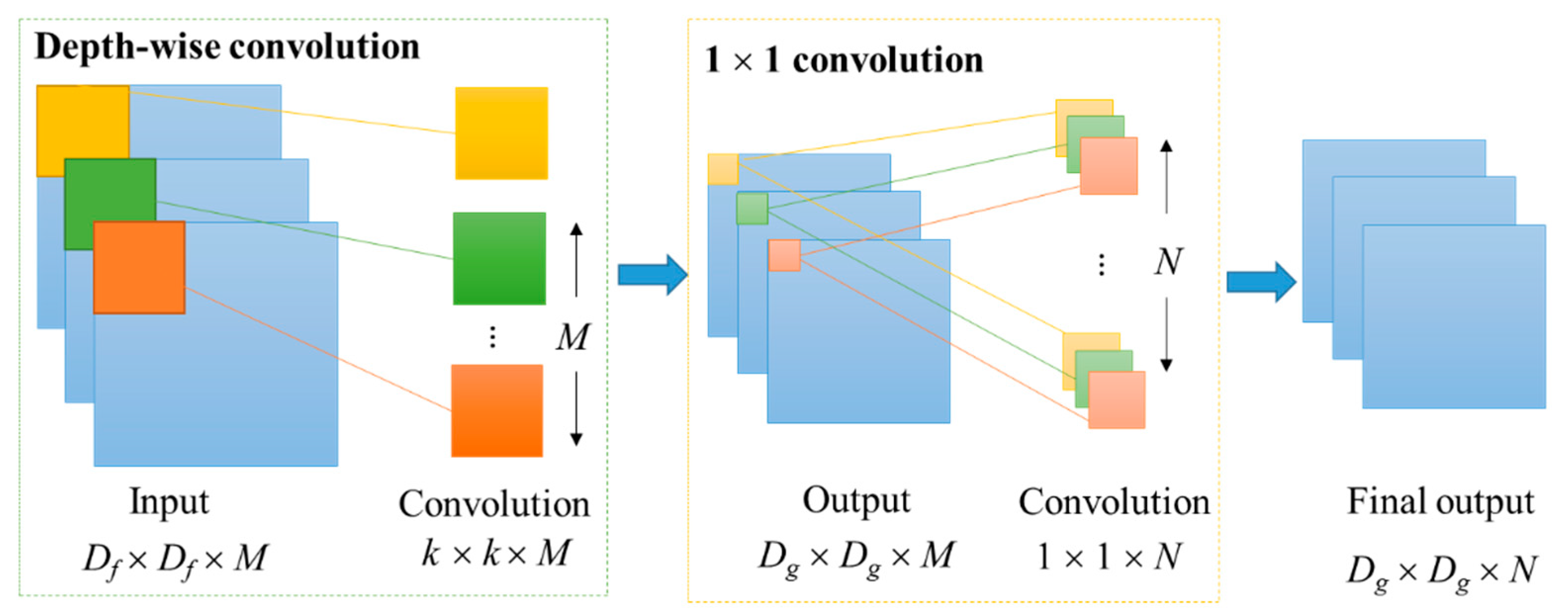
2.1. Depth-Wise Separable Convolution
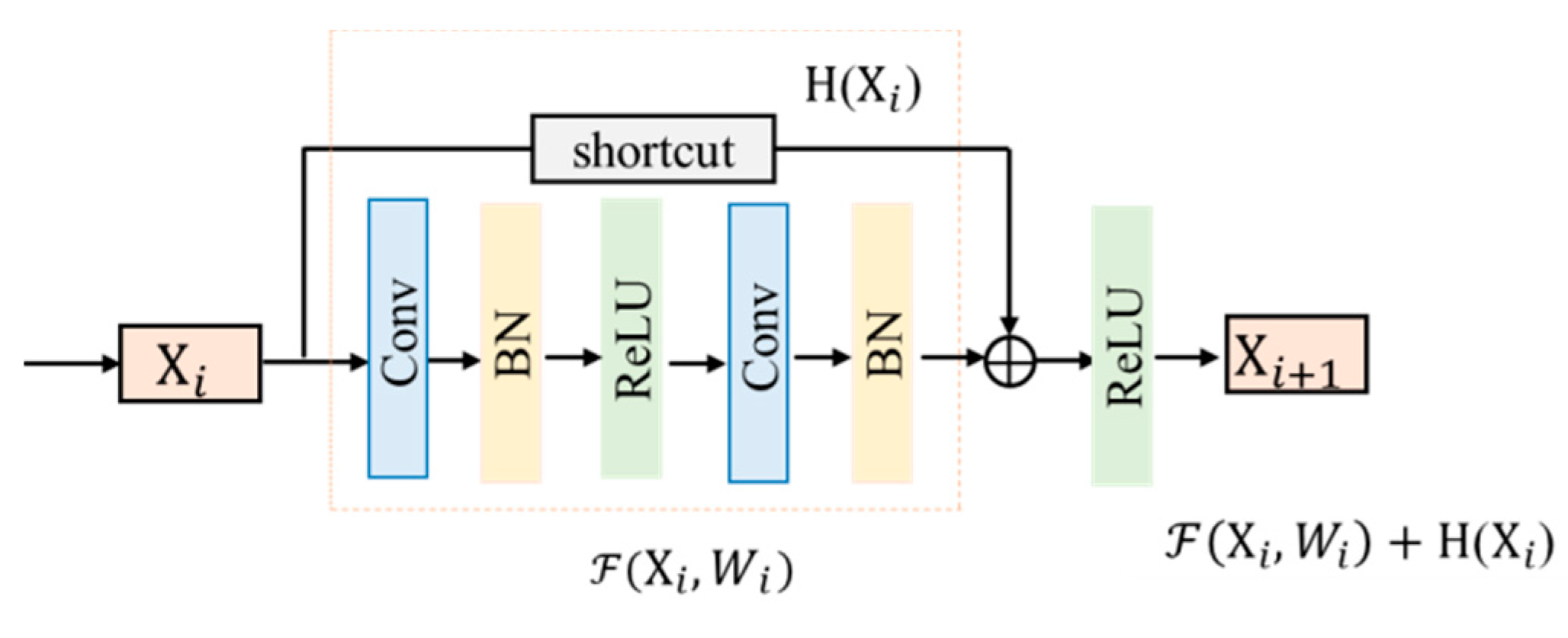
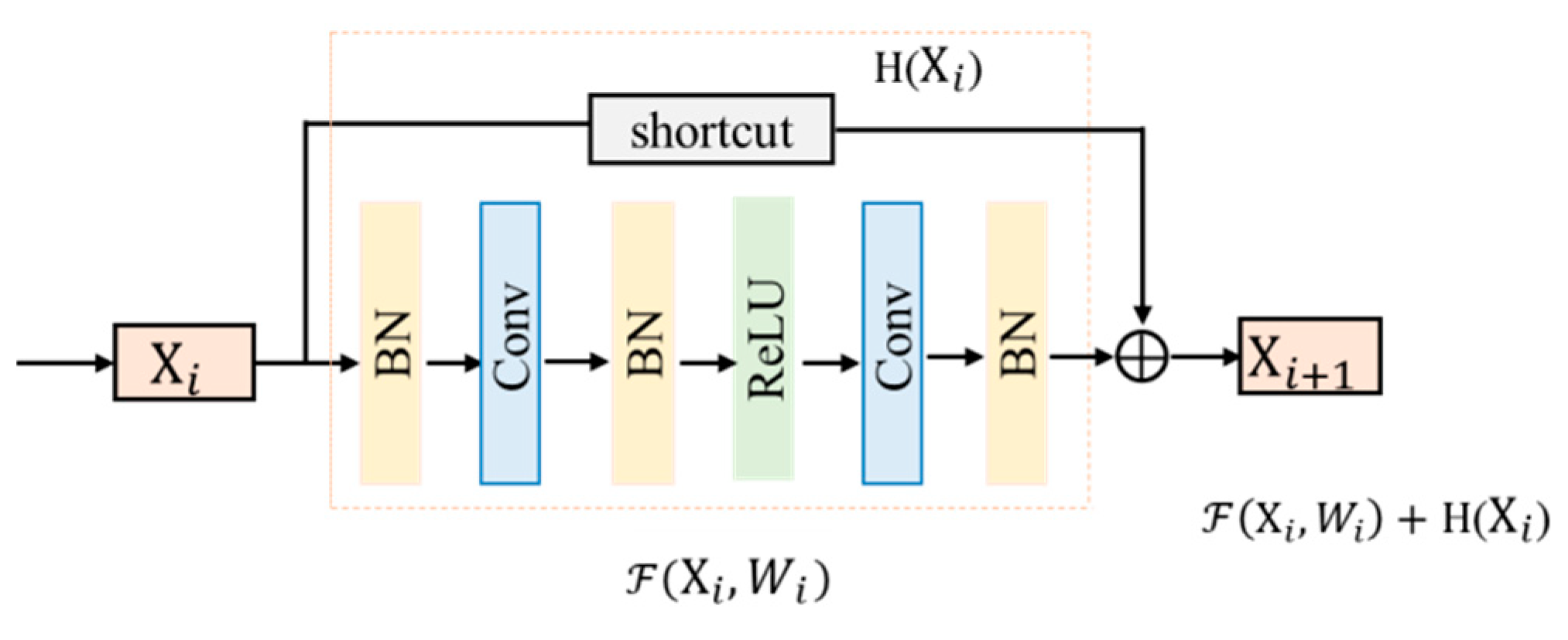
2.2. Residual Unit
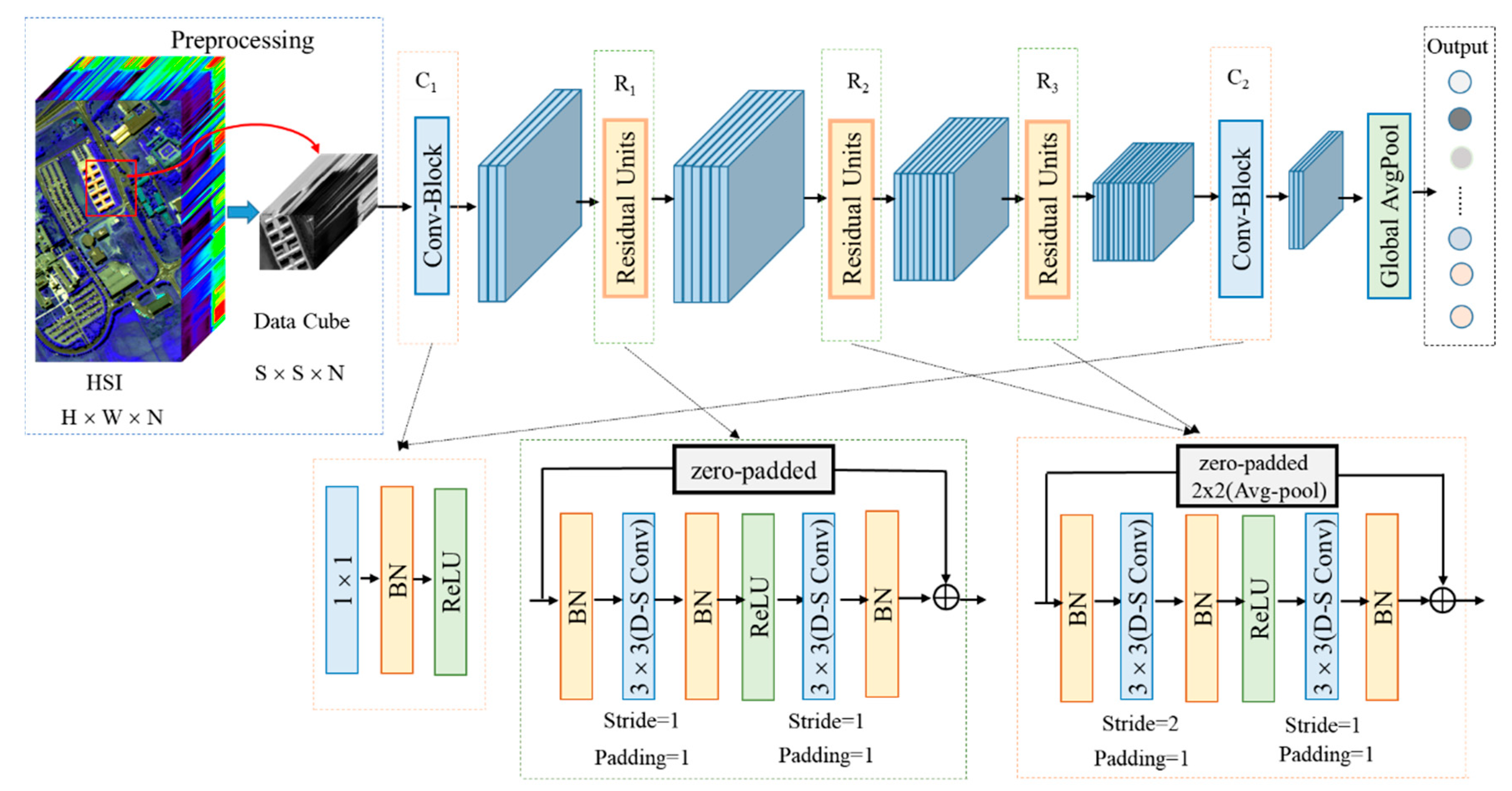
2.3. Proposed Model for HSI Classification
2.4. Detailed Design of the Model
3. Experimental Setup and Parameter Discussion
3.1. Datasets Description
3.2. Experimental Setup
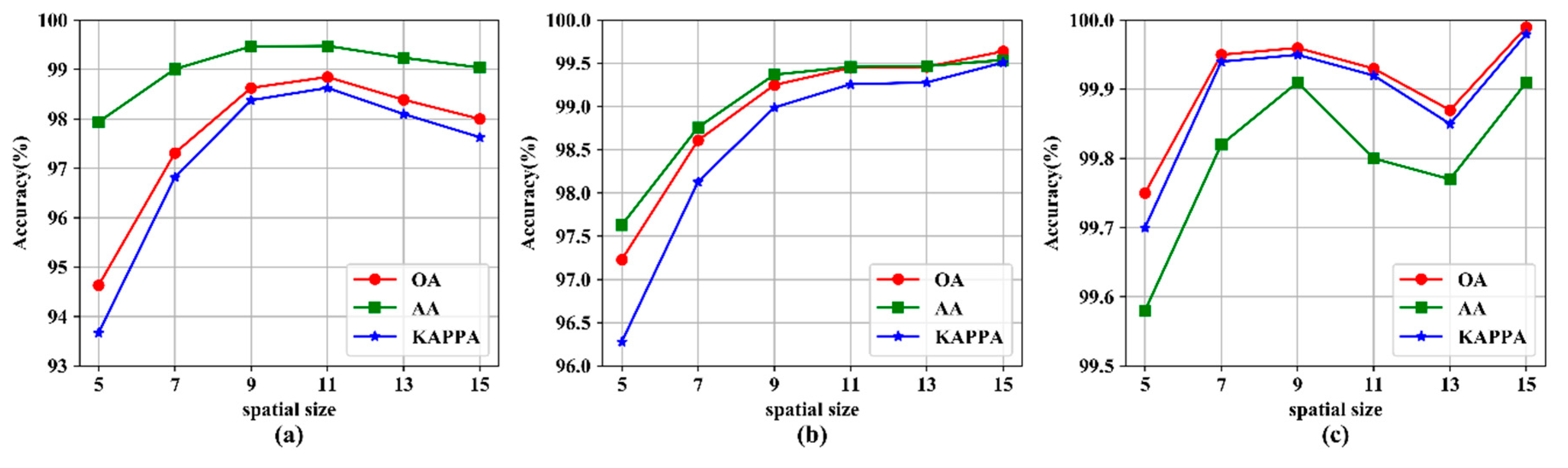
3.3. The Impact of Spatial Size
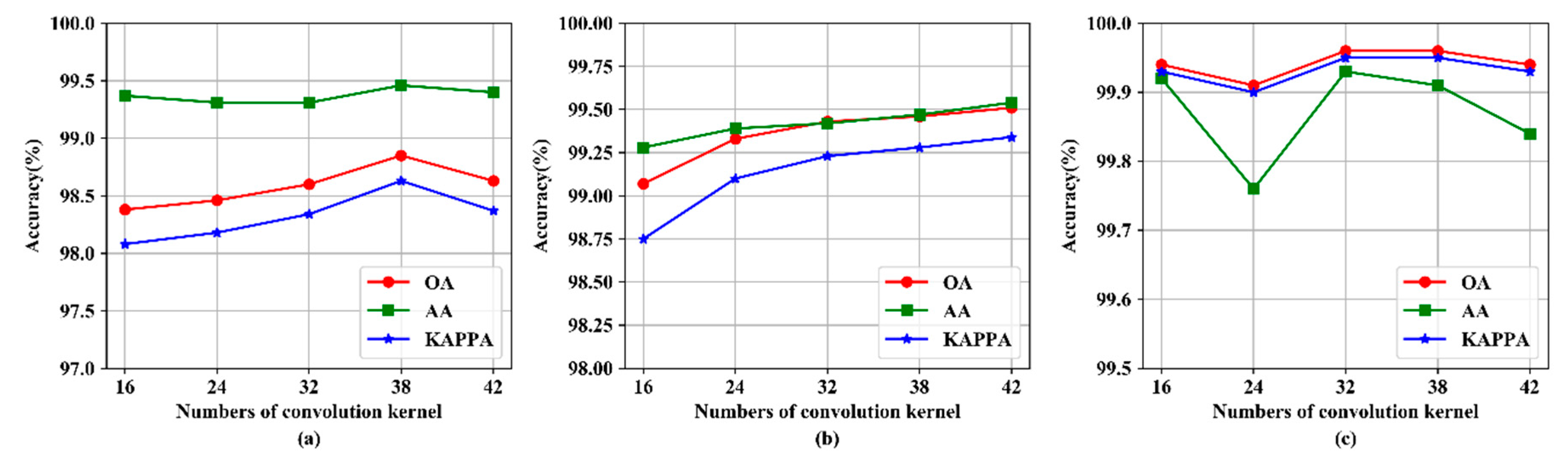
3.4. The Impact of Initial Convolution Kernels Number
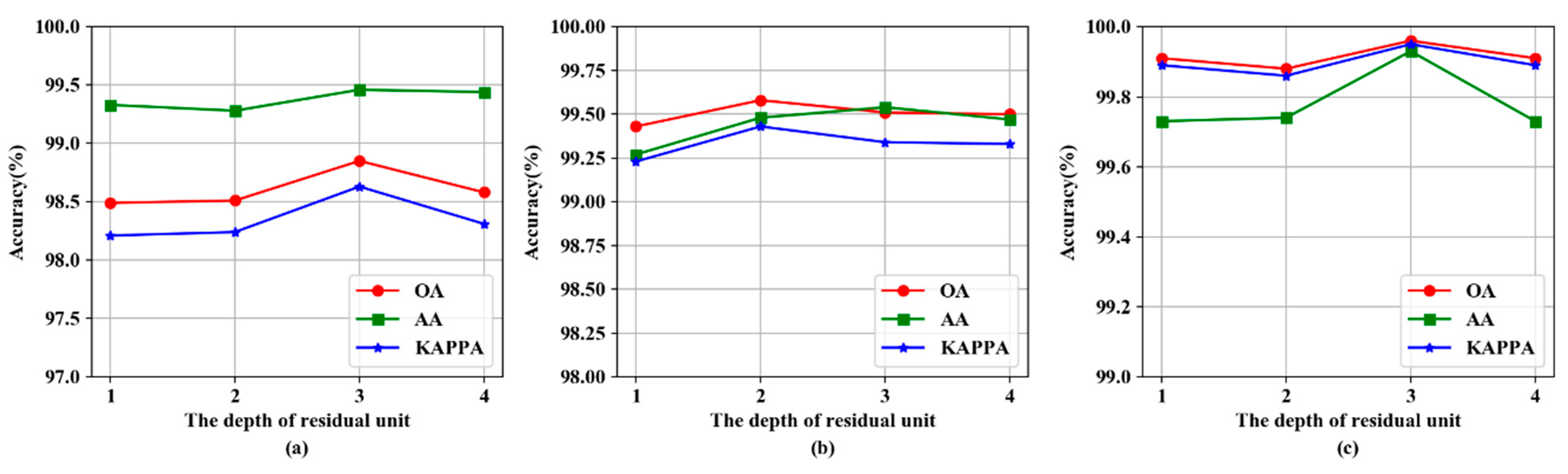
3.5. The Impact of Residual Unit Depth
4. Results and Discussion
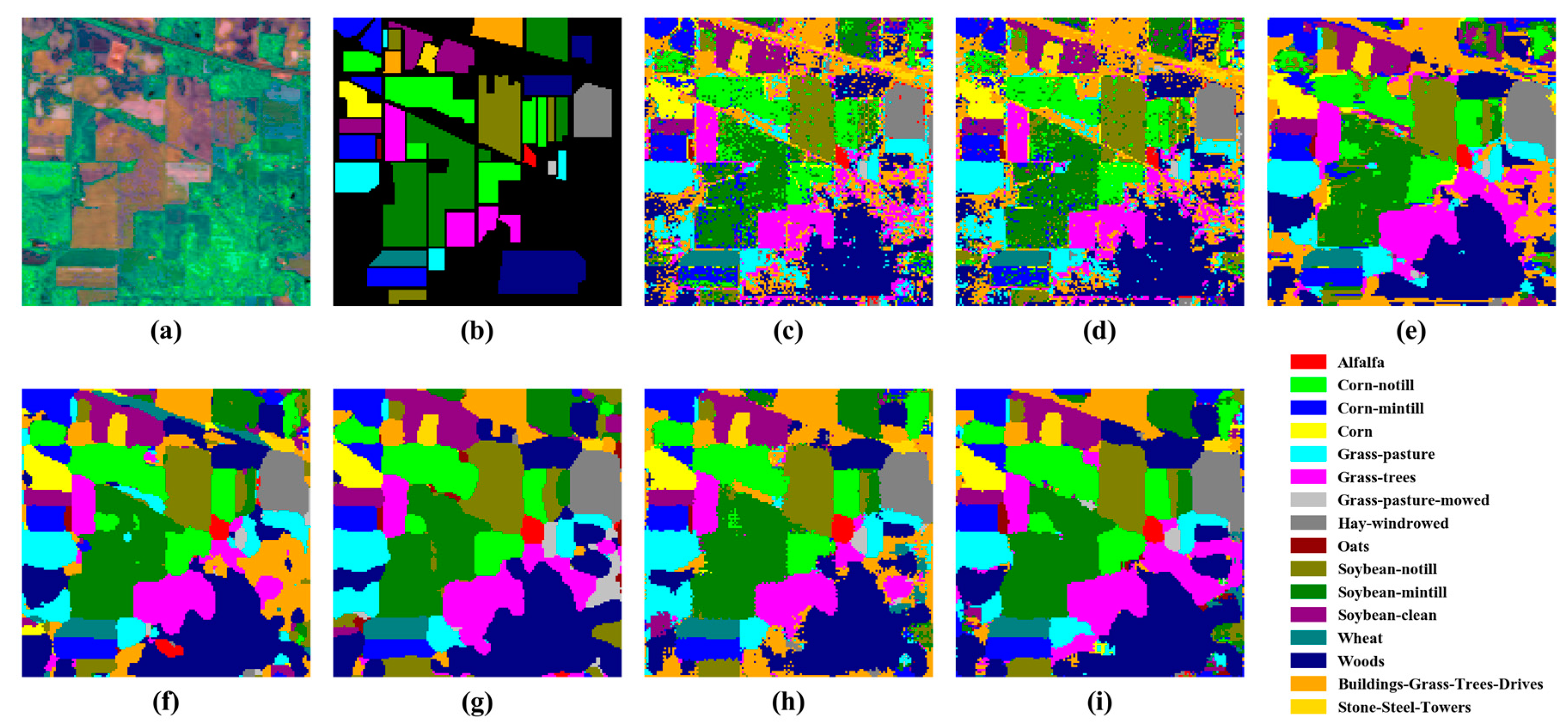
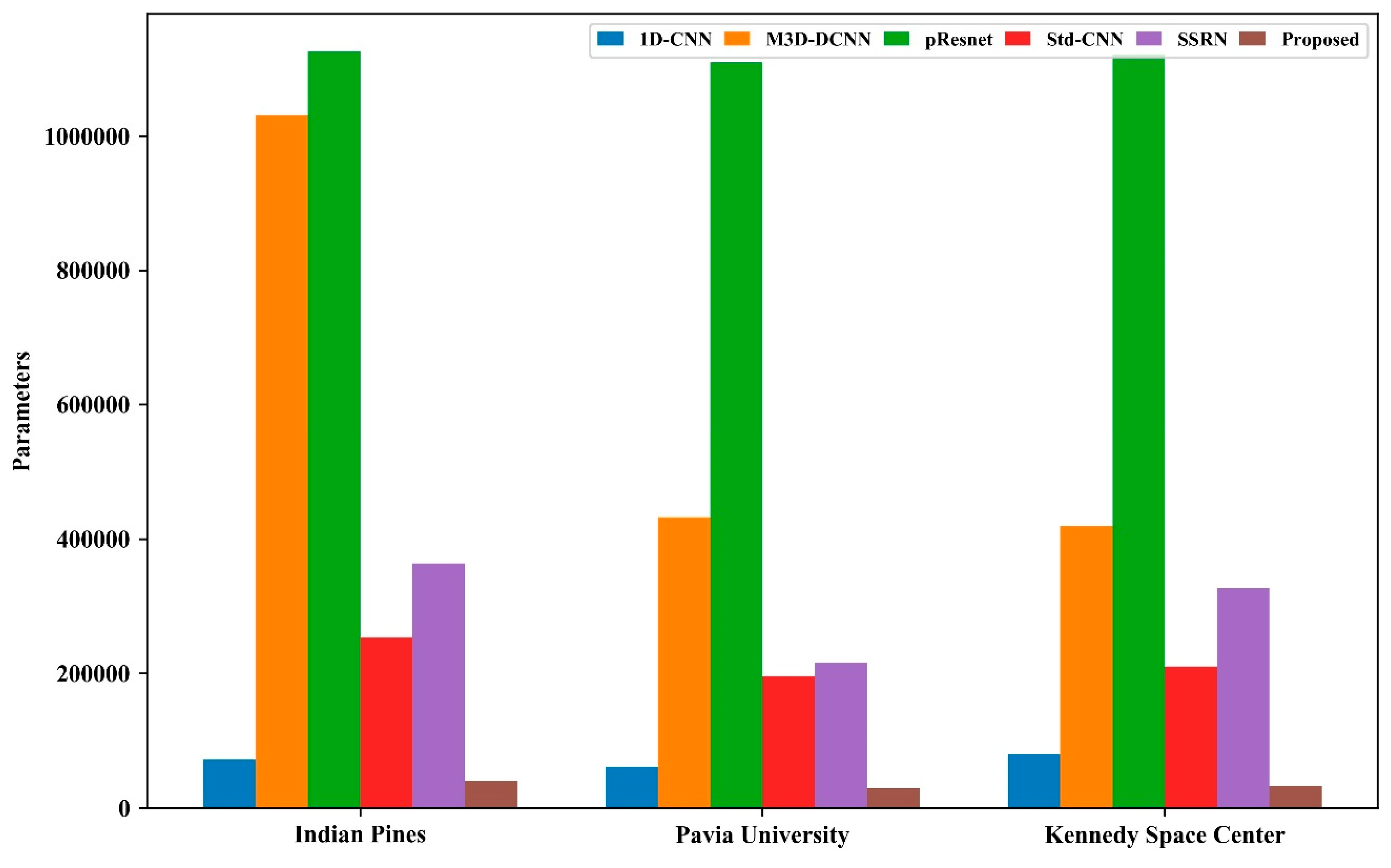
4.1. Comparison with Other Methods
4.2. Effectiveness Analysis to Depth-Separable Convolution
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Nakhostin, S.; Clenet, H.; Corpetti, T.; Courty, N. Joint anomaly detection and spectral unmixing for planetary Hyperspectral Images. IEEE Geosci. Remote Sens. 2016, 54, 6879–6894. [Google Scholar] [CrossRef]
- Torrecilla, E.; Stramski, D.; Reynolds, R.A.; Millán-Núñez, E.; Piera, J. Cluster analysis of hyperspectral optical data for discriminating phytoplankton pigment assemblages in the open ocean. Remote Sens. Environ. 2011, 115, 2578–2593. [Google Scholar] [CrossRef]
- Pan, Z.; Glennie, C.L.; Fernandez-Diaz, J.C.; Legleiter, C.J.; Overstreet, B. Fusion of LiDAR orthowaveforms and hyperspectral imagery for shallow river bathymetry and turbidity estimation. IEEE Geosci. Remote Sens. 2016, 54, 4165–4177. [Google Scholar] [CrossRef]
- Li, C.H.; Hun, C.C.; Taur, J.S. An effective feature selection method for hyperspectral image classification based on genetic algorithm and support vector machine. Knowl. Based Syst. 2011, 24, 40–48. [Google Scholar] [CrossRef]
- Kuo, B.C.; Ho, H.H.; Li, C.H. A kernel-based feature selection method for SVM with RBF kernel for hyperspectral image classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 7, 317–326. [Google Scholar]
- Zhu, Z.; Jia, S.; He, S.; Sun, Y.; Ji, Z.; Shen, L. Three-dimensional gabor feature extraction for hyperspectral imagery classification using a memetic framework. Inf. Sci. 2015, 298, 274–287. [Google Scholar] [CrossRef]
- Fauvel, M.; Dechesne, C.; Zullo, A.; Ferraty, F. Fast forward feature selection of hyperspectral images for classification with gaussian mixture models. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 2824–2831. [Google Scholar] [CrossRef]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE Inst. Electr. Electron Eng. 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2015, arXiv:1409.1556. [Google Scholar]
- Howard, A.G.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Adam, H. MobileNets: Efficient convolutional neural networks for mobile vision applications. arXiv 2015, arXiv:1704.04861. [Google Scholar]
- Abdel-Hamid, O.; Mohamed, A.R.; Jiang, H.; Penn, G. Applying Convolutional Neural Networks Concepts to Hybrid NN-HMM Model for Speech Recognition. In Proceedings of the International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Kyoto, Japan, 25–30 March 2012; pp. 4277–4280. [Google Scholar]
- Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Rich feature hierarchies for accurate object detection and semantic segmentation. Proc. IEEE Conf. Comput. Vis. Pattern Recognit. 2014, 580–587. [Google Scholar] [CrossRef]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 39, 640–651. [Google Scholar]
- Hu, W.; Huang, Y.; Wei, L.; Zhang, F.; Li, H. Deep convolutional neural networks for hyperspectral image classification. J. Sens. 2015, 2015, 258619. [Google Scholar] [CrossRef]
- Makantasis, K.; Karantzalos, K.; Doulamis, A.; Doulamis, N. Deep supervised learning for hyperspectral data classification through convolutional neural networks. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 4959–4962. [Google Scholar]
- Zhang, H.; Li, Y.; Zhang, Y.; Shen, Q. Spectral-spatial classification of hyperspectral imagery using a dual-channel convolutional neural network. Remote Sens. Lett. 2017, 8, 438–447. [Google Scholar] [CrossRef]
- Yu, S.; Jia, S.; Xu, C. Convolutional neural networks for hyperspectral image classification. Neurocomputing 2017, 219, 88–89. [Google Scholar] [CrossRef]
- Lee, H.; Kwon, H. Contextual deep CNN based hyperspectral classification. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 3322–3325. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Rabinovich, A. Going deeper with convolutions. Proc. IEEE Conf. Comput. Vis. Pattern Recognit. 2015, 1–9. [Google Scholar] [CrossRef]
- He, M.; Li, B.; Chen, H. Multi-scale 3D deep convolutional neural network for hyperspectral image classification. Proc. IEEE Int. Conf. Image Process. 2017, 3904–3908. [Google Scholar] [CrossRef]
- Zhong, Z.; Li, J.; Luo, Z.; Chapman, M. Spectral–spatial residual network for hyperspectral image classification: A 3-D deep learning framework. IEEE Trans. Geosci. Remote Sens. 2018, 56, 847–858. [Google Scholar] [CrossRef]
- Wang, W.; Dou, S.; Jiang, Z.; Sun, L. A fast dense spectral spatial convolution network framework for hyperspectral images classification. Remote Sens. 2018, 10, 1068. [Google Scholar] [CrossRef]
- Gao, H.; Yang, Y.; Li, C.; Zhang, X.; Zhao, J.; Yao, D. Convolutional neural network for spectral–spatial classification of hyperspectral images. Neural. Comput. 2018, 31, 8997–9012. [Google Scholar] [CrossRef]
- Paoletti, M.E.; Haut, J.M.; Fernandez-Beltran, R.; Plaza, J.; Plaza, A.J.; Pla, F. Deep pyramidal residual networks for spectral–Spatial hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 740–754. [Google Scholar] [CrossRef]
- Han, D.; Kim, J.; Kim, J. Deep pyramidal residual networks. Proc. IEEE Conf. Comput. Vis. Pattern Recognit. 2017, 6307–6315. [Google Scholar] [CrossRef]
- Chollet, F. Xception: Deep Learning with depthwise separable convolutions. arXiv 2017, arXiv:1610.02357. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. Proc. IEEE Conf. Comput. Vis. Pattern Recognit. 2016, 770–778. [Google Scholar]
- Nair, V.; Hinton, G.E. Rectified linear units improve restricted Boltzmann machines. In Proceedings of the 27th International Conference on International Conference on Machine Learning (ICML), Haifa, Israel, 21–24 June 2010; Omnipress: Madison, WI, USA, 2010; pp. 807–814. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Proceedings of the 32nd International Conference on International Conference on Machine Learning, Paris, France, 6–11 July 2015; pp. 448–456. [Google Scholar]
- Donoho, D.L. High-dimensional data analysis: The curses and blessings of dimensionality. AMS Math Chall. Lect. 2000, 1, 32. [Google Scholar]
- Lin, M.; Chen, Q.; Yan, S. Network in network. arXiv 2013, arXiv:1312.4400. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving deep into rectifiers: Surpassing human-level performance on ImageNet classification. In Proceedings of the International Conference on Computer Vision (ICCV), Santiago, Chile, 13–16 December 2015; pp. 1026–1034. [Google Scholar] [CrossRef]


| Layer | Output Size | Kernel Size | Stride | Padding |
|---|---|---|---|---|
| Input | 11 × 11 × 200 | |||
| C1 | 11 × 11 × 38 | 1 × 1 | 1 | 0 |
| R1 | 11 × 11 × 54 | 3 × 3(DS-Conv) | 1 | 1 |
| 11 × 11 × 54 | 3 × 3(DS-Conv) | 1 | 1 | |
| R2 | 6 × 6 × 70 | 3 × 3(DS-Conv) | 2 | 1 |
| 6 × 6 × 70 | 3 × 3(DS-Conv) | 1 | 1 | |
| R3 | 3 × 3 × 86 | 3 × 3(DS-Conv) | 2 | 1 |
| 3 × 3 × 86 | 3 × 3(DS-Conv) | 1 | 1 | |
| C2 | 3 × 3 × 16 | 1 × 1 | 1 | 0 |
| GAP | 1 × 16 |
| IP | PU | KSC | |
|---|---|---|---|
| Type of Sensor | AVIRIS | ROSIS | AVIRIS |
| Spatial Size | 145 × 145 | 610 × 340 | 512 × 614 |
| Spectral Range | 0.4–2.5 µm | 0.43–0.86 µm | 0.4–2.5 µm |
| Spatial Resolution | 20 m | 1.3 m | 18 m |
| Bands | 200 | 103 | 176 |
| Num. of Classes | 16 | 9 | 13 |
| No | Class | Total | Train | Test |
|---|---|---|---|---|
| 1 | Alfalfa | 46 | 37 | 9 |
| 2 | Corn-notill | 1428 | 200 | 1228 |
| 3 | Corn-mintill | 830 | 200 | 630 |
| 4 | Corn | 237 | 200 | 37 |
| 5 | Grass-pasture | 483 | 200 | 283 |
| 6 | Grass-trees | 730 | 200 | 530 |
| 7 | Grass-pasture-mowed | 28 | 23 | 5 |
| 8 | Hay-windowed | 478 | 200 | 278 |
| 9 | Oats | 20 | 16 | 4 |
| 10 | Soybean-notill | 972 | 200 | 772 |
| 11 | Soybean-mintill | 2455 | 200 | 2255 |
| 12 | Soybean-clean | 593 | 200 | 393 |
| 13 | Wheat | 205 | 200 | 5 |
| 14 | Woods | 1265 | 200 | 1065 |
| 15 | Buildings-Grass-Trees | 386 | 200 | 186 |
| 16 | Stone-Steel-Towers | 93 | 75 | 18 |
| Total | 10,249 | 2551 | 7698 | |
| No | Class | Total | Train | Test |
|---|---|---|---|---|
| 1 | Asphalt | 6631 | 200 | 6431 |
| 2 | Meadows | 18,649 | 200 | 18,449 |
| 3 | Gravel | 2099 | 200 | 1899 |
| 4 | Trees | 3064 | 200 | 2864 |
| 5 | Sheets | 1345 | 200 | 1145 |
| 6 | Bare soils | 5029 | 200 | 4829 |
| 7 | Bitumen | 1330 | 200 | 1130 |
| 8 | Bricks | 3682 | 200 | 3482 |
| 9 | Shadows | 947 | 200 | 747 |
| Total | 42,776 | 1800 | 40,976 | |
| No | Class | Total | Train | Test |
|---|---|---|---|---|
| 1 | Scrub | 761 | 200 | 561 |
| 2 | Willow swamp | 243 | 200 | 43 |
| 3 | CP hammock | 256 | 200 | 56 |
| 4 | Slash pine | 252 | 200 | 52 |
| 5 | Oak/Broadleaf | 161 | 129 | 32 |
| 6 | Hardwood | 229 | 200 | 29 |
| 7 | Swamp | 105 | 84 | 21 |
| 8 | Graminoid marsh | 431 | 200 | 231 |
| 9 | Spartina marsh | 520 | 200 | 320 |
| 10 | Cattail marsh | 404 | 200 | 204 |
| 11 | Salt marsh | 419 | 200 | 219 |
| 12 | Mud flats | 503 | 200 | 303 |
| 13 | Water | 527 | 200 | 727 |
| Total | 5211 | 2413 | 2798 | |
| Spatial Size | Indian Pines | Pavia University | Kennedy Space Center | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Training Time(s) | Test Time(s) | OA (%) | Training Time(s) | Test Time(s) | OA (%) | Training Time(s) | Test Time(s) | OA (%) | |
| 5 × 5 | 576.32 ± 19.84 | 2.07 ± 0.03 | 94.63 ± 0.97 | 519.46 ± 14.22 | 3.67 ± 0.05 | 97.23 ± 0.69 | 787.59 ± 15.14 | 1.90 ± 0.02 | 99.75 ± 0.12 |
| 7 × 7 | 593.70 ± 15.06 | 2.54 ± 0.05 | 97.31 ± 0.55 | 579.74 ± 44.64 | 5.25 ± 0.09 | 98.61 ± 0.31 | 776.79 ± 22.03 | 2.08 ± 0.07 | 99.95 ± 0.05 |
| 9 × 9 | 640.74 ± 27.28 | 3.32 ± 0.03 | 98.63 ± 0.38 | 591.55 ± 34.47 | 7.30 ± 0.09 | 99.25 ± 0.41 | 806.58 ± 26.58 | 2.28 ± 0.04 | 99.96 ± 0.08 |
| 11 × 11 | 714.28 ± 16.92 | 4.57 ± 0.03 | 98.85 ± 0.23 | 616.49 ± 22.25 | 10.62 ± 0.06 | 99.45 ± 0.19 | 871.04 ± 23.12 | 2.59 ± 0.02 | 99.93 ± 0.07 |
| 13 × 13 | 796.30 ± 16.75 | 6.22 ± 0.73 | 98.39 ± 0.36 | 666.41 ± 39.68 | 14.33 ± 0.22 | 99.46 ± 0.19 | 900.05 ± 0.95 | 2.90 ± 0.01 | 99.87 ± 0.28 |
| 15 × 15 | 1017.71 ± 8.19 | 8.15 ± 0.95 | 98.00 ± 0.44 | 748.43 ± 42.31 | 18.47 ± 0.09 | 99.64 ± 0.13 | 980.50 ± 13.08 | 3.39 ± 0.05 | 99.99 ± 0.03 |
| C | Indian Pines | Pavia University | Kennedy Space Center | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Training Time(s) | Test Time(s) | OA (%) | Training Time(s) | Test Time(s) | OA (%) | Training Time(s) | Test Time(s) | OA (%) | |
| 16 | 708.97 ± 15.58 | 4.60 ± 0.06 | 98.38 ± 0.65 | 739.87 ± 22.69 | 14.18 ± 0.06 | 99.07 ± 0.47 | 816.49 ± 12.83 | 2.29 ± 0.03 | 99.94 ± 0.09 |
| 24 | 715.34 ± 39.67 | 4.57 ± 0.03 | 98.46 ± 0.53 | 749.73 ± 40.44 | 14.24 ± 0.07 | 99.33 ± 0.42 | 814.42 ± 21.80 | 2.28 ± 0.02 | 99.91 ± 0.07 |
| 32 | 708.66 ± 15.27 | 4.56 ± 0.05 | 98.60 ± 0.40 | 719.52 ± 1.15 | 14.21 ± 0.05 | 99.43 ± 0.27 | 850.34 ± 74.70 | 2.31 ± 0.01 | 99.96± 0.05 |
| 38 | 714.28 ± 16.92 | 4.57 ± 0.03 | 98.85 ± 0.23 | 666.41 ± 39.68 | 14.33 ± 0.22 | 99.46 ± 0.19 | 806.58 ± 25.68 | 2.28 ± 0.04 | 99.96 ± 0.08 |
| 42 | 722.69 ± 20.08 | 4.57 ± 0.04 | 98.63 ± 0.29 | 729.48 ± 5.88 | 14.26 ± 0.16 | 99.51 ± 0.20 | 799.62 ± 5.93 | 2.27 ± 0.02 | 99.94 ± 0.04 |
| R | Indian Pines | Pavia University | Kennedy Space Center |
|---|---|---|---|
| 1 | 21284 | 18750 | 17114 |
| 2 | 31036 | 29622 | 25306 |
| 3 | 40660 | 40366 | 33370 |
| 4 | 50252 | 51078 | 41402 |
| R | Indian Pines | Pavia University | Kennedy Space Center | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Training Time(s) | Test Time(s) | OA (%) | Training Time(s) | Test Time(s) | OA (%) | Training Time(s) | Test Time(s) | OA (%) | |
| 1 | 725.25 ± 66.24 | 4.60 ± 0.04 | 98.49 ± 0.23 | 655.02 ± 50.04 | 14.13 ± 0.11 | 99.43 ± 0.25 | 755.43 ± 16.10 | 2.21 ± 0.03 | 99.91 ± 0.11 |
| 2 | 712.27 ± 24.13 | 4.59 ± 0.07 | 98.51 ± 0.28 | 739.40 ± 20.06 | 14.24 ± 0.05 | 99.58 ± 0.12 | 863.41 ± 13.49 | 2.25 ± 0.03 | 99.88 ± 0.12 |
| 3 | 714.28 ± 16.92 | 4.57 ± 0.03 | 98.85 ± 0.23 | 729.48 ± 5.88 | 14.26 ± 0.16 | 99.51 ± 0.20 | 850.34 ± 74.70 | 2.31 ± 0.01 | 99.96 ± 0.05 |
| 4 | 735.02 ± 28.17 | 5.74 ± 3.45 | 98.58 ± 0.36 | 638.42 ± 33.87 | 13.90 ± 0.08 | 99.50 ± 0.17 | 874.02 ± 55.47 | 2.34 ± 0.04 | 99.91 ± 0.08 |
| Class | SVM-RBF | 1D-CNN | M3D-DCNN | pResNet | SSRN | Std-CNN | Proposed |
|---|---|---|---|---|---|---|---|
| 1 | 85.56 | 90.00 | 97.78 | 100.00 | 98.89 | 100.00 | 100.00 |
| 2 | 77.02 | 82.15 | 86.29 | 97.29 | 98.20 | 96.51 | 98.22 |
| 3 | 76.35 | 78.57 | 92.21 | 99.13 | 99.27 | 99.1 | 99.16 |
| 4 | 91.62 | 90.27 | 100.00 | 100.00 | 100.00 | 100.00 | 99.73 |
| 5 | 94.63 | 94.98 | 99.12 | 99.89 | 99.96 | 99.93 | 99.86 |
| 6 | 96.96 | 97.89 | 99.36 | 99.74 | 99.89 | 99.77 | 99.85 |
| 7 | 86.00 | 94.00 | 98.00 | 100.00 | 100.00 | 100.00 | 100.00 |
| 8 | 98.17 | 99.06 | 99.86 | 100.00 | 100.00 | 100.00 | 100.00 |
| 9 | 82.5 | 97.50 | 95.00 | 100.00 | 95.00 | 100.00 | 100.00 |
| 10 | 83.06 | 87.66 | 92.51 | 98.94 | 98.81 | 97.67 | 98.60 |
| 11 | 66.82 | 70.52 | 80.15 | 96.12 | 97.99 | 95.60 | 98.22 |
| 12 | 86.39 | 89.92 | 96.95 | 98.63 | 99.54 | 98.47 | 98.78 |
| 13 | 98.00 | 98.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 |
| 14 | 89.25 | 91.62 | 96.03 | 98.61 | 99.88 | 96.51 | 99.58 |
| 15 | 80.16 | 82.53 | 99.19 | 99.84 | 100.00 | 99.10 | 100.00 |
| 16 | 97.22 | 96.11 | 100.00 | 99.44 | 97.22 | 100.00 | 99.44 |
| OA (%) | 79.76 ± 0.68 | 82.99 ± 0.85 | 89.80 ± 1.36 | 98.09 ± 1.11 | 98.89± 0.44 | 97.67 ± 0.52 | 98.85 ± 0.23 |
| AA (%) | 86.86 ± 2.07 | 90.05 ± 0.92 | 95.78 ± 1.09 | 99.10 ± 0.55 | 99.04 ± 0.93 | 99.12 ± 0.15 | 99.46 ± 0.14 |
| Kappa × 100 | 76.46 ± 0.78 | 80.17 ± 0.95 | 88.05 ± 1.57 | 97.59 ± 1.24 | 98.68± 0.52 | 97.24 ± 0.62 | 98.63 ± 0.27 |
| F1-score × 100 | 76.41 ± 1.91 | 78.32± 1.70 | 90.66 ± 1.68 | 97.67 ± 1.01 | 97.47 ± 1.98 | 96.11 ± 1.21 | 97.79 ± 1.17 |
| Class | SVM-RBF | 1D-CNN | M3D-DCNN | pResNet | SSRN | Std-CNN | Proposed |
|---|---|---|---|---|---|---|---|
| 1 | 86.01 | 87.48 | 90.84 | 98.86 | 99.56 | 99.81 | 99.83 |
| 2 | 90.25 | 89.87 | 96.01 | 99.55 | 99.68 | 99.64 | 99.71 |
| 3 | 84.47 | 84.92 | 91.72 | 98.58 | 99.02 | 99.71 | 99.67 |
| 4 | 95.10 | 95.93 | 98.01 | 98.84 | 98.20 | 97.92 | 97.74 |
| 5 | 99.42 | 99.78 | 99.92 | 99.94 | 99.87 | 99.79 | 99.83 |
| 6 | 89.96 | 88.66 | 97.84 | 99.69 | 99.99 | 100.00 | 99.90 |
| 7 | 93.19 | 92.27 | 96.65 | 99.51 | 100.00 | 100.00 | 100.00 |
| 8 | 85.11 | 81.92 | 93.27 | 99.15 | 99.16 | 99.35 | 99.22 |
| 9 | 99.92 | 99.79 | 99.57 | 99.92 | 99.42 | 99.45 | 99.41 |
| OA (%) | 89.70 ± 0.95 | 89.40 ± 0.98 | 95.31 ± 2.10 | 99.35 ± 0.17 | 99.53 ± 0.14 | 99.58 ± 0.29 | 99.58 ± 0.12 |
| AA (%) | 91.49 ± 0.45 | 91.18 ± 0.43 | 95.98 ± 1.31 | 99.34 ± 0.21 | 99.43 ± 0.16 | 99.52± 0.13 | 99.48 ± 0.15 |
| Kappa × 100 | 86.36 ± 1.22 | 85.97 ± 1.23 | 93.76 ± 2.73 | 99.12 ± 0.23 | 99.37 ± 0.19 | 99.43 ± 0.39 | 99.43 ± 0.16 |
| F1-score × 100 | 88.62 ± 0.68 | 88.24 ± 0.86 | 94.26 ± 1.96 | 99.16 ± 0.25 | 99.33 ± 0.25 | 99.44 ± 0.21 | 99.38 ± 0.16 |
| Class | SVM-RBF | 1D-CNN | M3D-DCNN | pResNet | SSRN | Std-CNN | Proposed |
|---|---|---|---|---|---|---|---|
| 1 | 92.23 | 90.71 | 99.18 | 99.63 | 99.57 | 99.93 | 99.89 |
| 2 | 95.81 | 90.70 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 |
| 3 | 93.39 | 88.39 | 98.39 | 99.64 | 99.46 | 99.82 | 100.00 |
| 4 | 86.54 | 77.69 | 95.00 | 99.23 | 99.81 | 98.85 | 99.23 |
| 5 | 77.50 | 70.00 | 93.44 | 99.06 | 99.38 | 98.75 | 100.00 |
| 6 | 89.66 | 87.93 | 99.66 | 100.00 | 100.00 | 100.00 | 100.00 |
| 7 | 92.86 | 87.14 | 100.00 | 99.52 | 100.00 | 99.52 | 100.00 |
| 8 | 95.93 | 94.89 | 99.48 | 100.00 | 100.00 | 100.00 | 100.00 |
| 9 | 97.72 | 97.72 | 99.69 | 99.91 | 99.84 | 99.94 | 100.00 |
| 10 | 99.02 | 99.61 | 99.56 | 99.90 | 100.00 | 100.00 | 99.90 |
| 11 | 98.63 | 98.54 | 99.77 | 100.00 | 100.00 | 100.00 | 100.00 |
| 12 | 96.53 | 97.33 | 99.9 | 100.00 | 100.00 | 99.93 | 100.00 |
| 13 | 99.93 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 |
| OA (%) | 96.41 ± 0.30 | 95.67 ± 0.85 | 99.49 ± 0.26 | 99.87 ± 0.25 | 99.87 ± 0.10 | 99.93 ± 0.06 | 99.96 ± 0.05 |
| AA (%) | 93.52 ± 0.90 | 90.82 ± 0.85 | 98.77 ± 0.81 | 99.76 ± 0.35 | 99.85 ± 0.13 | 99.75 ± 0.21 | 99.93 ± 0.09 |
| Kappa × 100 | 95.78 ± 0.35 | 94.91 ± 0.98 | 99.40 ± 0.31 | 99.85 ± 0.29 | 99.85 ± 0.12 | 99.92 ± 0.08 | 99.95 ± 0.06 |
| F1-score × 100 | 90.53 ± 0.71 | 87.82 ± 1.14 | 98.32 ± 0.89 | 99.57± 0.80 | 99.59 ± 0.36 | 99.71 ± 0.29 | 99.85 ± 0.19 |
| 1D-CNN | M3D-DCNN | pResNet | SSRN | Std-CNN | Proposed | ||
|---|---|---|---|---|---|---|---|
| Indian Pines | FLOPs(×106) | 0.16 | 75.31 | 30.09 | 234.68 | 10.34 | 2.20 |
| Training time(s) | 511.25 | 3380.23 | 1040.36 | 3519.76 | 772.93 | 714.28 | |
| Test time(s) | 1.29 | 8.49 | 8.01 | 16.75 | 4.62 | 4.57 | |
| Pavia University | FLOPs(×106) | 0.08 | 54.26 | 42.16 | 168.71 | 17.95 | 3.01 |
| Training time(s) | 541.52 | 1975.36 | 908.99 | 1759.32 | 684.71 | 739.40 | |
| Test time(s) | 1.81 | 29.72 | 26.52 | 60.46 | 14.11 | 14.24 | |
| Kennedy Space Center | FLOPs(×106) | 0.15 | 39.25 | 20.44 | 137.74 | 5.87 | 1.20 |
| Training time(s) | 509.26 | 2008.18 | 1396.61 | 2117.42 | 715.60 | 668.25 | |
| Test time(s) | 1.31 | 2.66 | 3.31 | 4.01 | 2.06 | 1.91 |
| Indian Pines | Pavia University | Kennedy Space Center | |||||
|---|---|---|---|---|---|---|---|
| Std-CNN | Des-CNN | Std-CNN | Des-CNN | Std-CNN | Des-CNN | ||
| Spatial Size | 5 × 5 | 89.04 ± 0.81 | 94.63 ± 0.97 | 96.48 ± 0.99 | 97.23 ± 0.69 | 99.54 ± 0.24 | 99.75 ± 0.12 |
| 7 × 7 | 94.36 ± 0.94 | 97.31 ± 0.55 | 98.33 ± 0.44 | 98.61 ± 0.31 | 99.80 ± 0.11 | 99.95 ± 0.05 | |
| 9 × 9 | 97.42 ± 0.57 | 98.63 ± 0.38 | 99.48 ± 0.11 | 99.25 ± 0.41 | 99.96 ± 0.05 | 99.96 ± 0.08 | |
| 11 × 11 | 97.87 ± 0.39 | 98.85 ± 0.23 | 99.46 ± 0.25 | 99.45 ± 0.19 | 99.97 ± 0.06 | 99.93 ± 0.07 | |
| 13 × 13 | 98.01 ± 0.46 | 98.39 ± 0.36 | 99.54 ± 0.25 | 99.46 ± 0.19 | 99.96 ± 0.05 | 99.87 ± 0.28 | |
| 15 × 15 | 97.68 ± 0.34 | 98.00 ± 0.44 | 99.57 ± 0.16 | 99.64 ± 0.13 | 99.99 ± 0.02 | 99.99 ± 0.03 | |
| Initial Convolution Kernels Number | 16 | 97.37 ± 0.42 | 98.38 ± 0.65 | 99.36 ± 0.24 | 99.07 ± 0.47 | 99.93 ± 0.09 | 99.94 ± 0.09 |
| 24 | 97.63 ± 0.50 | 98.46 ± 0.53 | 99.50 ± 0.39 | 99.33 ± 0.42 | 99.95 ± 0.04 | 99.91 ± 0.07 | |
| 32 | 97.79 ± 0.43 | 98.60 ± 0.40 | 99.51 ± 0.26 | 99.43 ± 0.27 | 99.89 ± 0.11 | 99.96± 0.05 | |
| 38 | 97.87 ± 0.39 | 98.85± 0.23 | 99.54 ± 0.25 | 99.46 ± 0.19 | 99.96 ± 0.05 | 99.96 ± 0.08 | |
| 42 | 97.68 ± 0.48 | 98.63 ± 0.29 | 99.36 ± 0.64 | 99.51± 0.20 | 99.96 ± 0.05 | 99.94 ± 0.04 | |
| Residual Unit Depth | 1 | 98.74 ± 0.44 | 98.49 ± 0.23 | 99.57 ± 0.13 | 99.43 ± 0.25 | 99.92 ± 0.08 | 99.91 ± 0.11 |
| 2 | 98.29 ± 0.24 | 98.51 ± 0.28 | 99.44 ± 0.53 | 99.58 ± 0.12 | 99.94 ± 0.06 | 99.88 ± 0.12 | |
| 3 | 97.87 ± 0.39 | 98.85 ± 0.23 | 99.54 ± 0.25 | 99.51 ± 0.20 | 99.89 ± 0.11 | 99.96 ± 0.05 | |
| 4 | 96.58 ± 0.67 | 98.58 ± 0.36 | 99.37 ± 0.28 | 99.50 ± 0.17 | 99.87 ± 0.10 | 99.91 ± 0.08 | |
| Indian Pines | Pavia University | Kennedy Space Center | |||||
|---|---|---|---|---|---|---|---|
| Std-CNN | Des-CNN | Std-CNN | Des-CNN | Std-CNN | Des-CNN | ||
| Spatial size | 5 × 5 | 91.24 ± 1.21 | 94.45 ± 1.14 | 96.31 ± 0.73 | 96.95 ± 0.90 | 98.67 ± 0.70 | 99.75 ± 0.12 |
| 7 × 7 | 94.91 ± 0.92 | 96.91 ± 1.01 | 97.95 ± 0.42 | 98.29 ± 0.39 | 99.33 ± 0.41 | 99.80 ± 0.14 | |
| 9 × 9 | 97.19 ± 0.96 | 98.35 ± 0.85 | 99.30 ± 0.17 | 99.13 ± 0.35 | 99.88 ± 0.12 | 99.84 ± 0.31 | |
| 11 × 11 | 96.11 ± 1.21 | 97.79 ± 1.17 | 99.35 ± 0.25 | 99.31 ± 0.21 | 99.92 ± 0.19 | 99.78 ± 0.17 | |
| 13 × 13 | 96.19 ± 1.57 | 96.20 ± 1.56 | 99.41 ± 0.20 | 99.31 ± 0.23 | 99.96 ± 0.05 | 99.57 ± 0.79 | |
| 15 × 15 | 94.81 ± 1.95 | 96.04 ± 1.36 | 99.40 ± 0.16 | 99.47 ± 0.11 | 99.94 ± 0.12 | 99.93 ± 0.18 | |
| Initial Convolution Kernels Number | 16 | 96.68 ± 1.32 | 97.87 ± 1.23 | 99.20 ± 0.20 | 98.99 ± 0.38 | 99.71 ± 0.40 | 99.81 ± 0.37 |
| 24 | 96.96 ± 0.96 | 97.44 ± 1.01 | 99.39 ± 0.33 | 99.22 ± 0.31 | 99.79 ± 0.19 | 99.91 ± 0.07 | |
| 32 | 96.93 ± 0.99 | 96.84 ± 1.76 | 99.51 ± 0.26 | 99.26 ± 0.32 | 99.61 ± 0.32 | 99.85 ± 0.19 | |
| 38 | 96.11 ± 1.21 | 97.79 ± 1.17 | 99.41 ± 0.20 | 99.31 ± 0.23 | 99.88 ± 0.12 | 99.84 ± 0.31 | |
| 42 | 96.51 ± 0.91 | 97.52 ± 1.79 | 99.24 ± 0.61 | 99.42 ± 0.17 | 99.82 ± 0.21 | 99.76 ± 0.16 | |
| Residual Unit Depth | 1 | 97.04 ± 1.41 | 96.02 ± 1.90 | 99.34 ± 0.18 | 99.14 ± 0.24 | 99.76 ± 0.25 | 99.59 ± 0.57 |
| 2 | 96.04 ± 1.77 | 96.28 ± 1.68 | 99.30 ± 0.39 | 99.58 ± 0.12 | 99.94 ± 0.06 | 99.88 ± 0.12 | |
| 3 | 96.11 ± 1.21 | 97.79 ± 1.17 | 99.41 ± 0.20 | 99.42 ± 0.17 | 99.89 ± 0.11 | 99.85 ± 0.19 | |
| 4 | 96.25 ± 1.39 | 98.00 ± 0.79 | 99.39 ± 0.24 | 99.34 ± 0.36 | 99.49 ± 0.39 | 99.91 ± 0.08 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dang, L.; Pang, P.; Lee, J. Depth-Wise Separable Convolution Neural Network with Residual Connection for Hyperspectral Image Classification. Remote Sens. 2020, 12, 3408. https://doi.org/10.3390/rs12203408
Dang L, Pang P, Lee J. Depth-Wise Separable Convolution Neural Network with Residual Connection for Hyperspectral Image Classification. Remote Sensing. 2020; 12(20):3408. https://doi.org/10.3390/rs12203408
Chicago/Turabian StyleDang, Lanxue, Peidong Pang, and Jay Lee. 2020. "Depth-Wise Separable Convolution Neural Network with Residual Connection for Hyperspectral Image Classification" Remote Sensing 12, no. 20: 3408. https://doi.org/10.3390/rs12203408
APA StyleDang, L., Pang, P., & Lee, J. (2020). Depth-Wise Separable Convolution Neural Network with Residual Connection for Hyperspectral Image Classification. Remote Sensing, 12(20), 3408. https://doi.org/10.3390/rs12203408






