A Robust Algorithm Based on Phase Congruency for Optical and SAR Image Registration in Suburban Areas
Abstract
1. Introduction
- Several methods detect keypoints directly from a PC map (PCM) or the moment of the PCM for feature matching. However, because of SAR speckle noise, some unreasonable points are detected in the SAR image; further, because of significant nonlinear intensity differences, the feature detection result of one image generally has no corresponding feature points in the other image. Several classical methods are tested using a pair of optical and SAR images, as shown in Figure 1. These limitations lead to the low repeatability of the feature point, which is not conducive to feature matching.
- The extracted points are not uniformly distributed. When calculating the PC of a whole image, the noise threshold is estimated using the Rayleigh distribution mode, which is a fixed value. This leads to a noise threshold larger than the actual noise in the dark region. The feature information is drowned by the noise. As shown in Figure 1, the features are always concentrated in the bright region, especially in the SAR image. The nonuniform distribution of feature points leads to limited registration accuracy on large images or high-contrast images.
- Because of the different imaging mechanisms for optical and SAR sensors, the acquired images have different expressions for the same objects, thereby resulting in large radiation differences between image pairs. Such nonlinear radiation differences reduce the correlation between corresponding points, which often leads to difficulties in feature description.
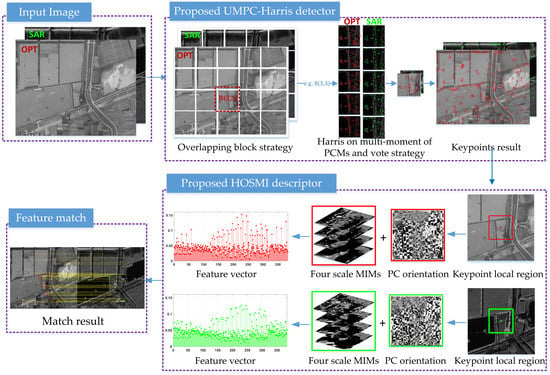
- The UMPC-Harris feature detection method is proposed based on the multi-moment of the PCM, a voting strategy, and an overlapping block strategy. The detector can obtain enough reliable and uniformly distributed feature points.
- The HOSMI feature description method is proposed based on the histograms of phase congruency orientation on multi-scale max amplitude index maps. The descriptor is more robust against nonlinear radiation variation and speckle noise.
2. Methodology
2.1. Review of PC Theory
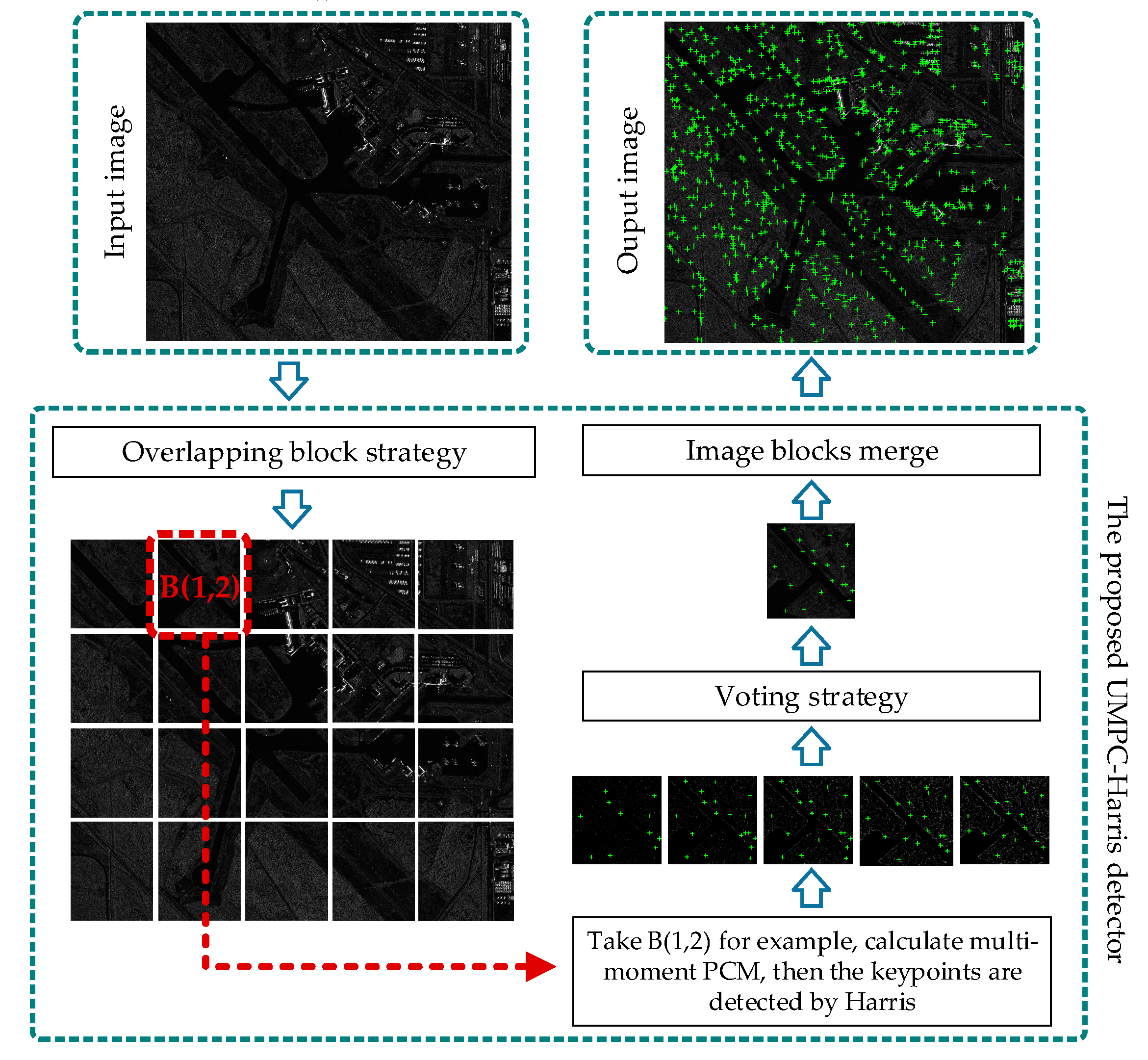
2.2. The Proposed UMPC-Harris Feature Detector
2.3. Feature Description
2.3.1. Multi-Scale Max Index Maps
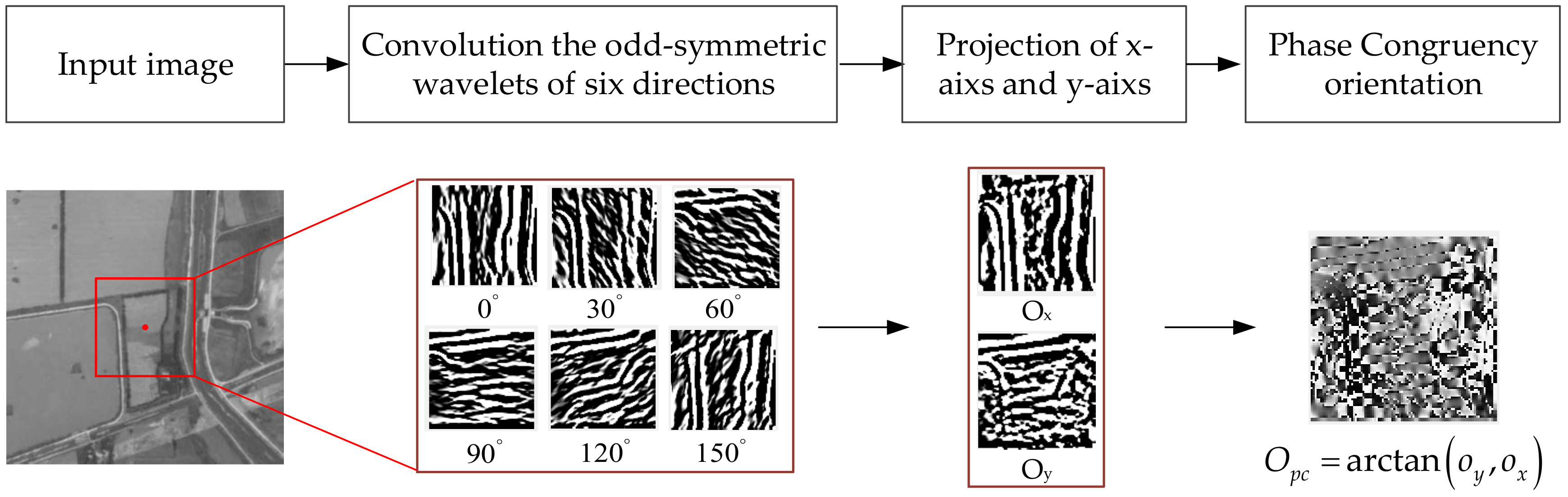
2.3.2. Orientation of Phase Congruency
2.3.3. The Proposed HOSMI Feature Descriptor
- Apply the LGF to the local region of each keypoint, and then, calculate the odd and even convolution results of four scales and six orientations.
- Calculate the amplitude map over four scales and six orientations. In each scale, the corresponding orientation to the maximum amplitude forms the multi-scale MIMs; the detailed calculation process is shown in Figure 3.
- Obtain the PC orientation using the odd convolution results; the detailed calculation process is shown in Figure 4. The PC orientation is restricted to an interval , which can handle gradient inversion in optical and SAR images, and large intensity differences between the optical and SAR images can be reduced.
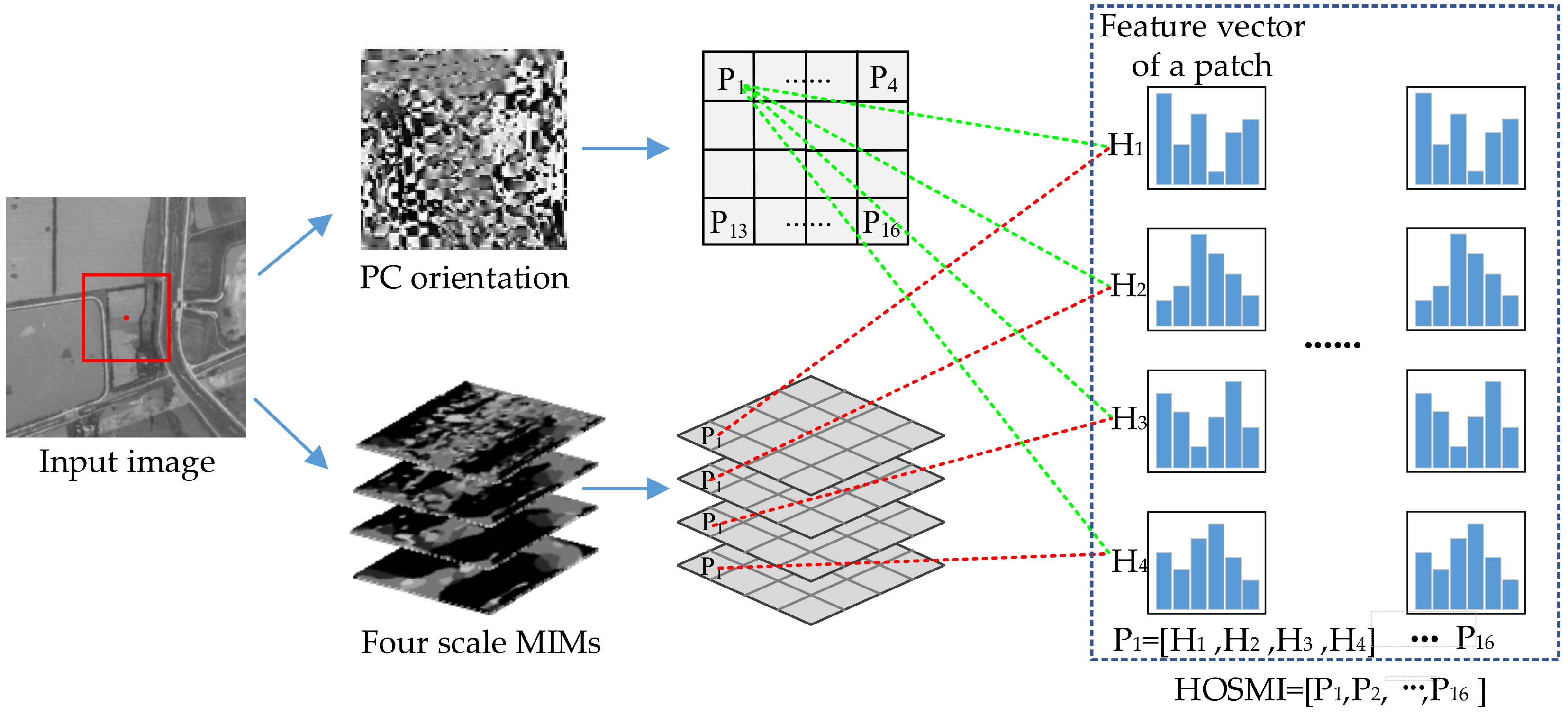
- Divide the PC orientation map and the multi-scale MIMs of each keypoint into patches. If the local region is selected with a size of pixels, the size of the patch is pixels. The feature vector of each patch is calculated in order, and then a descriptor is constructed by combining the feature vectors of all patches.
- To calculate the feature vector of a patch, PC orientation is formed using bins covering the 180 degrees range of orientations. The sample added to the histogram is the element of the corresponding location on the MIM. To interpolate the peak position for better accuracy, a parabola is fitted to the three histogram values closest to each peak. The feature vector of patch is calculated on four scales; therefore, the dimension of the feature vector of a patch is . In Figure 5, we take the first patch as an example. The scale used in the PC method is set to 4, and the feature vector of the patch is constructed as , where ~ are the histograms of the four scales.
- To obtain the feature descriptor of a keypoint, the feature vectors of all patches are combined into one feature vector. The feature descriptor is normalized by the norm to achieve better invariance to illumination and shadowing. The dimension of the feature descriptor of a keypoint is . As shown in Figure 5, if the local region of a keypoint is divided into 4 4 patches, the feature descriptor is constructed by the 16 patches, as in .
- Construct a local feature descriptor HOSMI for optical and SAR image registration.
3. Experimental Results and Discussion
3.1. Performance Experiments of Proposed UMPC-Harris Detector
3.1.1. Evaluation Criteria of Feature Detector
3.1.2. Experimental Data and Parameter Settings of Feature Detector
- Experimental Data
- b.
- Parameter Settings
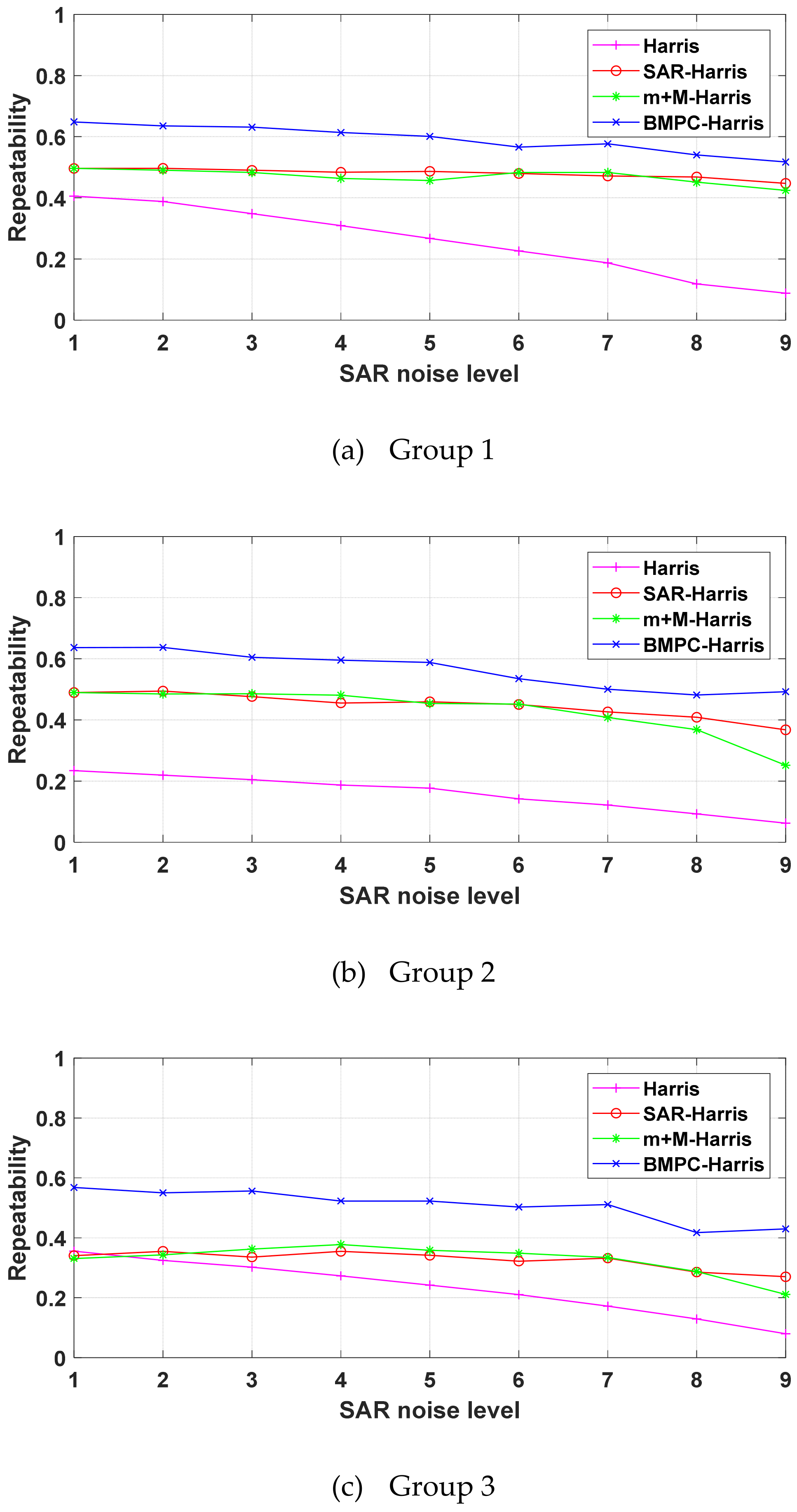
3.1.3. Influence of Noise Level on Proposed UMPC-Harris Detector
3.1.4. Influence of Radiometric Changes on Proposed UMPC-Harris Detector
3.1.5. Results and Discussion of the Proposed UMPC-Harris Detector
- The UMPC-Harris aims to extract feature points on the multi-moment of the PCM. Stable and valuable keypoints are selected by voting on the Harris corner, which appears repeatedly on the PCM. The combination of the effective corners and edge points not only ensures the high repeatability of the features, but also a large number of features, which lays a foundation for subsequent feature matching.
- Keypoints are well-distributed in the entire image, further points with obvious local features in the dark regions can be detected. This ensures that the keypoints are not limited to the bright region, thereby improving the accuracy of image registration.
3.2. Performance Experiments of Proposed ROS-PC Registration Algorithm
3.2.1. Evaluation Criteria of the Registration Algorithm
3.2.2. Datasets and Parameter Settings of the Registration Algorithm
- Datasets
- b.
- Parameter Settings
3.2.3. Comparison of Experimental Results and Discussion
- The UMPC-Harris can obtain a higher repeatability rate of keypoints than SAR-Harris and m + M-Harris between SAR and optical images.
- The HOSMI descriptor uses four-scale and six-orientation LGFs to capture the multi-scale max index and orientation feature information of PC, which is robust to nonlinear radiation variations of optical and SAR images. Further, it can effectively overcome the noise and scattering of SAR images.
3.3. Influence of Rotation and Scale Variations on the Proposed ROS-PC
3.3.1. Rotation Experiments of the Proposed ROS-PC
3.3.2. Scale Experiments of the Proposed ROS-PC
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhang, Q.; Liu, Y.; Blum, R.S.; Han, J.G.; Tao, D.C. Sparse representation based multi-sensor image fusion for multi-focus and multi-modality images: A review. Inf. Fusion 2018, 40, 57–75. [Google Scholar] [CrossRef]
- Kulkarni, S.C.; Rege, P.P. Pixel level fusion techniques for SAR and optical images: A review. Inf. Fusion 2020, 59, 13–29. [Google Scholar] [CrossRef]
- Tapete, D.; Cigna, F. Detection of archaeological looting from space: Methods, achievements, and challenges. Remote Sens. 2019, 11, 2389. [Google Scholar] [CrossRef]
- Song, S.L.; Jin, K.; Zuo, B.; Yang, J. A novel change detection method combined with registration for SAR images. Remote Sens. Lett. 2019, 10, 669–678. [Google Scholar] [CrossRef]
- Zhang, S.L.; Chen, J.Q.; Liu, X.; Li, J. Change Detection of Huangqi Lake Based on Modified Active Contour Using Sentinel-1 SAR Image. In Proceedings of the 2018 Progress in Electromagnetics Research Symposium (PIERS), Toyama, Japan, 1–4 August 2018; pp. 2291–2295. [Google Scholar]
- Li, K.; Zhang, X.Q. Review of Research on Registration of SAR and Optical Remote Sensing Image Based on Feature. In Proceedings of the 2018 IEEE 3rd International Conference on Signal and Image Processing (ICSIP 2018), Shenzhen, China, 13–15 July 2018; pp. 111–115. [Google Scholar]
- Wang, F.; You, H.J. Robust registration method of SAR and optical remote sensing images based on cascade. J. Infrared Millim. Waves 2015, 34, 486–492. [Google Scholar]
- Zitova, B.; Flusser, J. Image registration methods: A survey. Image Vis. Comput. 2003, 21, 977–1000. [Google Scholar] [CrossRef]
- Suri, S.; Reinartz, P. Mutual-information-based registration of TerraSAR-X and Ikonos imagery in urban areas. IEEE Trans. Geosci. Remote Sens. 2010, 48, 939–949. [Google Scholar] [CrossRef]
- Shu, L.X.; Tan, T.N. SAR and SPOT Image Registration Based on Mutual Information with Contrast Measure. In Proceedings of the 2007 IEEE International Conference on Image Processing, San Antonio, TX, USA, 16 September–19 October 2007; pp. 2681–2684. [Google Scholar]
- Shi, W.; Su, F.Z.; Wang, R.R.; Fan, J.F. A Visual Circle Based Image Registration Algorithm for Optical and SAR Imagery. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium (IGARSS 2012), Munich, Germany, 22–27 July 2012; pp. 2109–2112. [Google Scholar]
- Wang, F.; Vemuri, B.C. Non-rigid multi-modal image registration using cross-cumulative residual entropy. Int. J. Comput. Vis. 2007, 74, 201–215. [Google Scholar] [CrossRef]
- Yu, L.; Zhang, D.R.; Holden, E.J. A fast and fully automatic registration approach based on point features for multi-source remote-sensing images. Comput. Geosci. 2008, 34, 838–848. [Google Scholar] [CrossRef]
- Liu, S.Y.; Jiang, J. Registration algorithm based on line-intersection-line for satellite remote sensing images of urban areas. Remote Sens. 2019, 11, 26. [Google Scholar] [CrossRef]
- Sui, H.G.; Xu, C.; Liu, J.Y.; Hua, F. Automatic optical-to-SAR image registration by iterative line extraction and Voronoi integrated spectral point matching. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6058–6072. [Google Scholar] [CrossRef]
- Li, H.; Manjunath, B.S.; Mitra, S.K. Contour-Based Multisensor Image Registration. In Proceedings of the Conference Record of the Twenty-Sixth Asilomar Conference on Signals, Systems & Computers, Pacific Grove, CA, USA, 26–28 October 1992; pp. 182–186. [Google Scholar]
- Lowe, D. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 20, 91–110. [Google Scholar] [CrossRef]
- Ke, Y.; Sukthankar, R.; Society, I.C. PCA-SIFT: A More Distinctive Representation for Local Image Descriptors. In Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR 2004), Washington, DC, USA, 27 June–2 July 2004; pp. 506–513. [Google Scholar]
- Bay, H.; Tuytelaars, T.; Gool, L.V. SURF: Speeded Up Robust Features. In Proceedings of the 9th European Conference on Computer Vision (ECCV 2006), Graz, Austria, 7–13 May 2006; pp. 404–417. [Google Scholar]
- Morel, J.M.; Yu, G. ASIFT: A new framework for fully affine invariant image comparison. SIAM J. Imaging Sci. 2009, 2, 438–469. [Google Scholar] [CrossRef]
- Sedaghat, A.; Mokhtarzade, M.; Ebadi, H. Uniform robust scale-invariant feature matching for optical remote sensing images. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4516–4527. [Google Scholar] [CrossRef]
- Sedaghat, A.; Ebadi, H. Remote sensing image matching based on adaptive binning SIFT descriptor. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5283–5293. [Google Scholar] [CrossRef]
- Fan, B.; Huo, C.L.; Pan, C.H.; Kong, Q.Q. Registration of optical and SAR satellite images by exploring the spatial relationship of the improved SIFT. IEEE Trans. Geosci. Remote Sens. Lett. 2013, 10, 657–661. [Google Scholar] [CrossRef]
- Gong, M.; Zhao, S.; Jiao, L.; Tian, D.; Wang, S. A novel coarse-to-fine scheme for automatic image registration based on SIFT and mutual information. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4328–4338. [Google Scholar] [CrossRef]
- Dellinger, F.; Delon, J.; Gousseau, Y.; Michel, J.; Tupin, F. SAR-SIFT: A SIFT-like algorithm for SAR images. IEEE Trans. Geosci. Remote Sens. 2015, 53, 453–466. [Google Scholar] [CrossRef]
- Ma, W.; Wen, Z.; Wu, Y.; Jiao, L.; Gong, M.; Zheng, Y.; Liu, L. Remote sensing image registration with modified SIFT and enhanced feature matching. IEEE Geosci. Remote Sens. Lett. 2017, 14, 3–7. [Google Scholar] [CrossRef]
- Paul, S.; Pati, U.C. A Gabor odd filter-based ratio operator for SAR image matching. IEEE Trans. Geosci. Remote Sens. Lett. 2019, 16, 397–401. [Google Scholar] [CrossRef]
- Xiang, Y.; Wang, F.; You, H. OS-SIFT: A robust SIFT-like algorithm for high-resolution optical-to-SAR image registration in suburban areas. IEEE Trans. Geosci. Remote Sens. 2018, 56, 3078–3090. [Google Scholar] [CrossRef]
- Govindaraj, P.; Sudhakar, M.S. A new 2D shape retrieval scheme based on phase congruency and histogram of oriented gradients. Sig. Image Video Process. 2019, 13, 771–778. [Google Scholar] [CrossRef]
- Jiang, S.; Wang, B.N.; Zhu, X.Y.; Xiang, M.S.; Fu, X.K.; Sun, X.F. Registration of SAR and Optical Images by Weighted SIFT Based on Phase Congruency. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS 2018), Valencia, Spain, 22–27 July 2018; pp. 8885–8888. [Google Scholar]
- Cui, S.; Zhong, Y.F. Multi-Modal Remote Sensing Image Registration Based on Multi-Scale Phase Congruency. In Proceedings of the 10th IAPR Workshop on Pattern Recognition in Remote Sensing (PRRS 2018), Beijing, China, 19–20 August 2018; pp. 1–5. [Google Scholar]
- Ragb, H.K.; Asari, V.K. Histogram of oriented phase (HOP): A new descriptor based on phase congruency. In Mobile Multimedia/Image Processing, Security, and Applications 2016; SPIE: Bellingham, WA, USA, 19 May 2016; p. 98690V1-10. [Google Scholar]
- Ye, Y.; Shan, J.; Bruzzone, L.; Shen, L. Robust registration of multimodal remote sensing images based on structural similarity. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2941–2958. [Google Scholar] [CrossRef]
- Ye, Y.; Shan, J.; Hao, S.; Bruzzone, L.; Qin, Y. A local phase based invariant feature for remote sensing image matching. ISPRS J. Photogramm. Remote Sens. 2018, 142, 205–221. [Google Scholar] [CrossRef]
- Chen, M.; Habib, A.; He, H.Q.; Zhu, Q.; Zhang, W. Robust feature matching method for SAR and optical images by using Gaussian-gamma-shaped Bi-windows-based descriptor and geometric constraint. Remote Sens. 2017, 9, 25. [Google Scholar] [CrossRef]
- Paul, S.; Pati, U.C. Automatic optical-to-SAR image registration using a structural descriptor. IET Image Process. 2020, 14, 62–73. [Google Scholar] [CrossRef]
- Fu, Z.; Qin, Q.; Luo, B.; Sun, H.; Wu, C. HOMPC: A local feature descriptor based on the combination of magnitude and phase congruency information for multi-sensor remote sensing images. Remote Sens. 2018, 10, 1234. [Google Scholar] [CrossRef]
- Fan, J.W.; Wu, Y.; Li, M.; Liang, W.K.; Cao, Y.C. SAR and optical image registration using nonlinear diffusion and phase congruency structural descriptor. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5368–5379. [Google Scholar] [CrossRef]
- Li, J.; Hu, Q.; Ai, M. RIFT: Multi-modal image matching based on radiation-variation insensitive feature transform. IEEE Trans. Image Process. 2020, 29, 3296–3310. [Google Scholar] [CrossRef]
- Ye, Y.; Li, S. HOPC: A Novel Similarity Metric Based on Geometric Structural Properties for Multi-Modal Remote Sensing Image Matching. In Proceedings of the ISPRS Annals of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Prague, Czech Republic, 12–19 July 2016; pp. 1–18. [Google Scholar]
- Kovesi, P. Image features from phase congruency. J. Comput. Vis. Res. 1999, 1, 1–26. [Google Scholar]
- Kovesi, P. Phase Congruency Detects Corners and Edges. In Proceedings of the International Conference on Digital Image Computing: Techniques and Applications (DICTA 2003), Macquarie University, Sydney, Australia, 10–12 December 2003; pp. 309–318. [Google Scholar]
- Wu, Y.; Ma, W.; Gong, M.; Su, L.; Jiao, L. A novel point-matching algorithm based on fast sample consensus for image registration. IEEE Geosci. Remote Sens. 2015, 12, 43–47. [Google Scholar] [CrossRef]


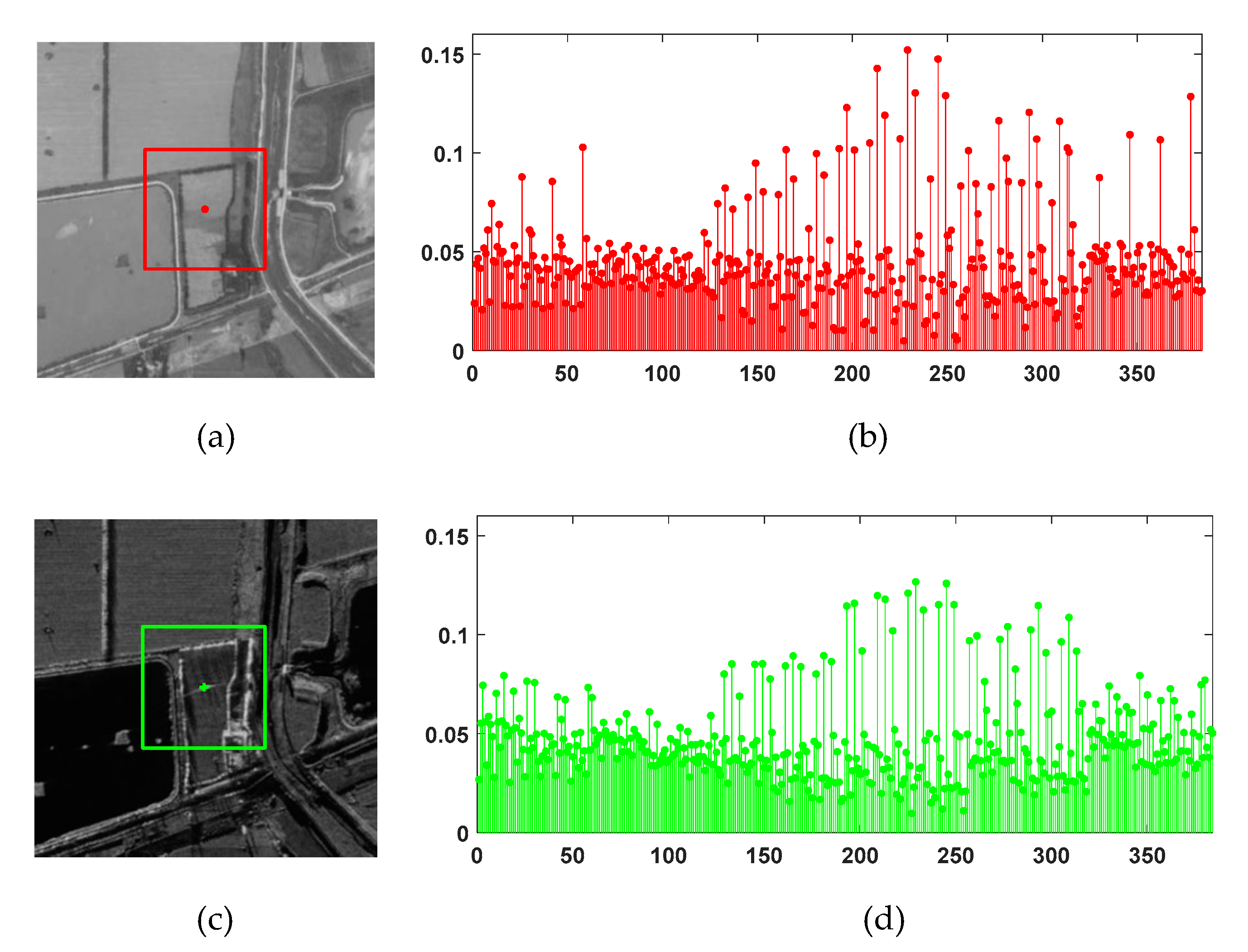


















| Method | Harris | SAR-Harris | m+M-Harris | UMPC-Harris |
|---|---|---|---|---|
| Repeatability (%) | 59.98 | 71.83 | 68.80 | 90.96 |
| Pair | Sensor | Resolution | Date | Size (Pixel) |
|---|---|---|---|---|
| A | Google Earth | 1 m | 9 October 2012 | 923 × 704 |
| TerraSAR-X | 1 m | 23 December 2010 | 900 × 795 | |
| B | Google Earth | 1 m | 27 March 2020 | 932 × 684 |
| Airborne SAR | 1 m | June 2020 | 867 × 740 | |
| C | Google Earth | 3 m | 24 June 2020 | 1019 × 699 |
| Airborne SAR | 3 m | April 2018 | 1016 × 697 | |
| D | Google Earth | 3 m | 1 July 2017 | 1741 × 1075 |
| Airborne SAR | 3 m | April 2018 | 1744 × 1078 | |
| E | Google Earth | 3.2 m | 25 April 2020 | 874 × 768 |
| Airborne SAR | 4 m | April 2018 | 692 × 612 | |
| F | Google Earth | 2.5 m | 19 February 2020 | 1019 × 701 |
| Airborne SAR | 2.5 m | April 2018 | 1020 × 711 | |
| G | Google Earth | 2.2 m | 19 February 2020 | 968 × 662 |
| Airborne SAR | 2.2 m | April 2018 | 1010 × 676 | |
| H | Google Earth | 2.5 m | 19 February 2020 | 858 × 758 |
| Airborne SAR | 2.5 m | April 2018 | 863 × 761 |
| Method | OS-SIFT | RIFT | ROS-PC | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Pair | RMSE | NCM | Time(s) | RMSE | NCM | Time(s) | RMSE | NCM | Time(s) | |
| A | 1.8507 | 30 | 52.84 | 2.2953 | 39 | 10.4 | 1.9326 | 41 | 73.46 | |
| B | 16.1443 | 6 | 65.74 | --- | --- | --- | 2.8296 | 17 | 77.36 | |
| C | --- | --- | --- | 5.6334 | 17 | 11.94 | 2.6961 | 31 | 74.45 | |
| D | 4.8541 | 9 | 81.12 | 2.6507 | 33 | 24.33 | 1.6741 | 58 | 97.49 | |
| E | 20.7450 | 4 | 52.90 | 2.7754 | 38 | 9.93 | 1.9116 | 38 | 75.56 | |
| F | 22.2591 | 5 | 67.62 | 4.6117 | 19 | 13.58 | 1.7773 | 30 | 74.12 | |
| G | 5.6215 | 5 | 57.6 | 2.9563 | 23 | 12.25 | 1.5264 | 35 | 71.26 | |
| H | --- | --- | --- | --- | --- | --- | 1.7612 | 33 | 70.59 | |
| Rotation Angle | −12° | −9° | −6° | −3° | 0° | 4° | 8° | 12° | 16° |
| NCM | 8 | 19 | 28 | 35 | 58 | 32 | 31 | 20 | 15 |
| Scale | 0.6 | 0.7 | 0.8 | 0.9 | 1 | 1.1 | 1.2 | 1.3 | 1.4 |
| NCM | 16 | 27 | 39 | 55 | 58 | 39 | 23 | 13 | 13 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Sun, M.; Liu, J.; Cao, L.; Ma, G. A Robust Algorithm Based on Phase Congruency for Optical and SAR Image Registration in Suburban Areas. Remote Sens. 2020, 12, 3339. https://doi.org/10.3390/rs12203339
Wang L, Sun M, Liu J, Cao L, Ma G. A Robust Algorithm Based on Phase Congruency for Optical and SAR Image Registration in Suburban Areas. Remote Sensing. 2020; 12(20):3339. https://doi.org/10.3390/rs12203339
Chicago/Turabian StyleWang, Lina, Mingchao Sun, Jinghong Liu, Lihua Cao, and Guoqing Ma. 2020. "A Robust Algorithm Based on Phase Congruency for Optical and SAR Image Registration in Suburban Areas" Remote Sensing 12, no. 20: 3339. https://doi.org/10.3390/rs12203339
APA StyleWang, L., Sun, M., Liu, J., Cao, L., & Ma, G. (2020). A Robust Algorithm Based on Phase Congruency for Optical and SAR Image Registration in Suburban Areas. Remote Sensing, 12(20), 3339. https://doi.org/10.3390/rs12203339