4.1. Completeness and Correctness of Stem Detection
In this section, we present the tree detection results for the different methods based on the measurements conducted on the two test sites. A summary of the completeness and correctness rates can be found in
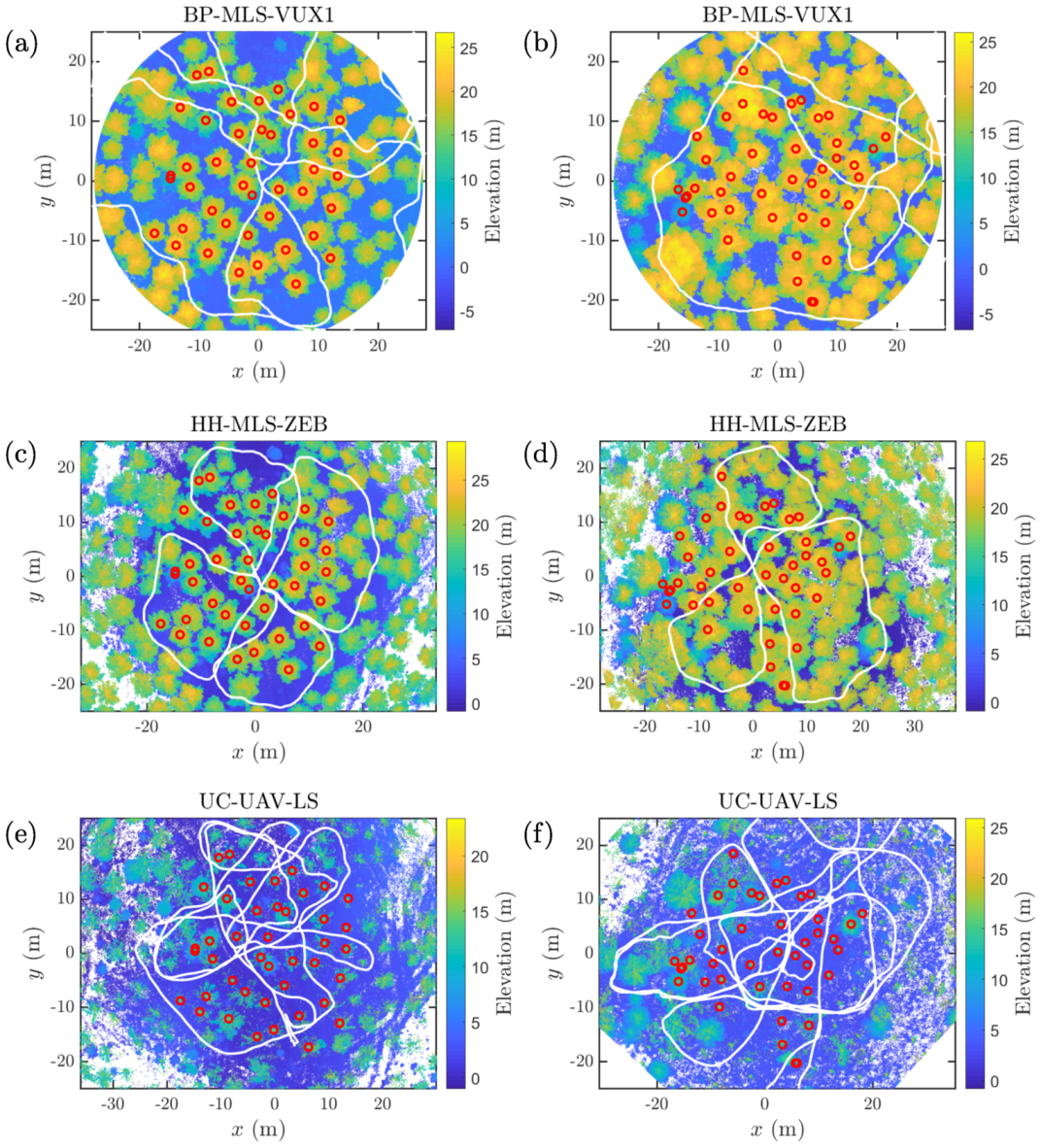
Table 6. Overall, the differences in the completeness of stem detection were rather small between the ground-based MLS methods and the above-canopy UAV methods when it comes to detecting dominant pines and birches. In the sparse plot, the overall completeness of tree detection varied between 88.1% (UAV-LS-VQ480U) and 95.2% (BP-MLS-VUX1 A1), and the backpack laser scanning provided the best stem detection accuracy. In the obstructed plot, the completeness of tree detection varied between 76.7% (HH-MLS-ZEB) and 88.4% (BP-MLS-VUX1 A1). Importantly, the number of false observations, i.e., commission errors was low for all of the measurements, which can be attributed to good-quality point cloud data, and algorithms suitable for boreal forest surveys. The only commission error occurred for the backpack MLS method, which detected a dead tree that was not included in the set of reference trees in both of the test sites.
Note that all of the methods detected only a small fraction of the spruces (0.0–37.5%) present on the test sites, whereas the detection rate of pines was close to 100% for all of the measurements. Even though the detection rates for the ground-based mobile measurements and the above-canopy measurements were similar, the underlying factors determining the detection rates are quite different for these two classes of methods. For the ground-based/under-canopy MLS measurements, the most important factors limiting the detection of a particular tree are a small stem diameter and a poor stem visibility due to, e.g., branches. The pines on the test sites were dominant trees with visible and straight stems (see
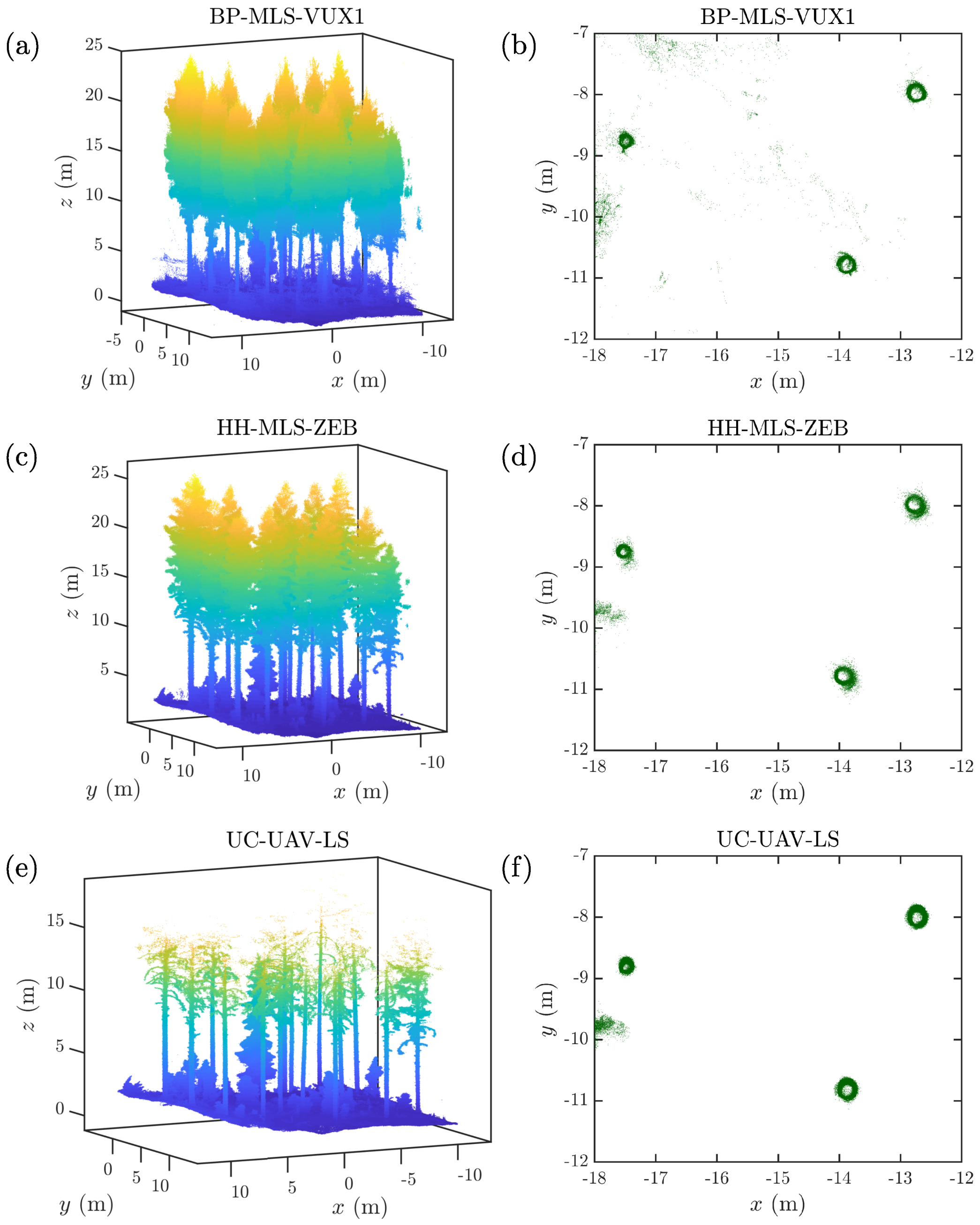
Figure 2a), and thus their detection rate was close to 100% based on the ground-based/under-canopy MLS measurements. On the other hand, basically all of the spruces on the test sites had an occluded stem and a small DBH (average 10 cm) as illustrated in
Figure 2b. Therefore, it was difficult for the algorithms to detect the spruce stems and estimate their diameter using the stem detection-based approach employed in this study. However, if one is interested in detecting the spruces and not their stems, the completeness of spruce detection can be improved by using, e.g., methods based on vertical line fitting [
14]. It is also noteworthy that it is most often the young spruces that tend to suffer from the stem occlusion problem. Typically, mature spruces relevant for the forest industry have visible stems at least close to the ground level, and thus stem-detection-based methods should work with a reasonable accuracy.
For the above-canopy UAV measurements, the high completeness of pine detection can be attributed to the fact that pines were mostly dominant trees whose tree tops were easily detectable from the canopy height model. On the other hand, the low completeness of spruce detection was due to the fact that most of the spruces on the test sites were shadowed by nearby located taller pines or birches. Thus, the canopy height model did not have a local maximum at the location of many of the spruces resulting in omission errors.
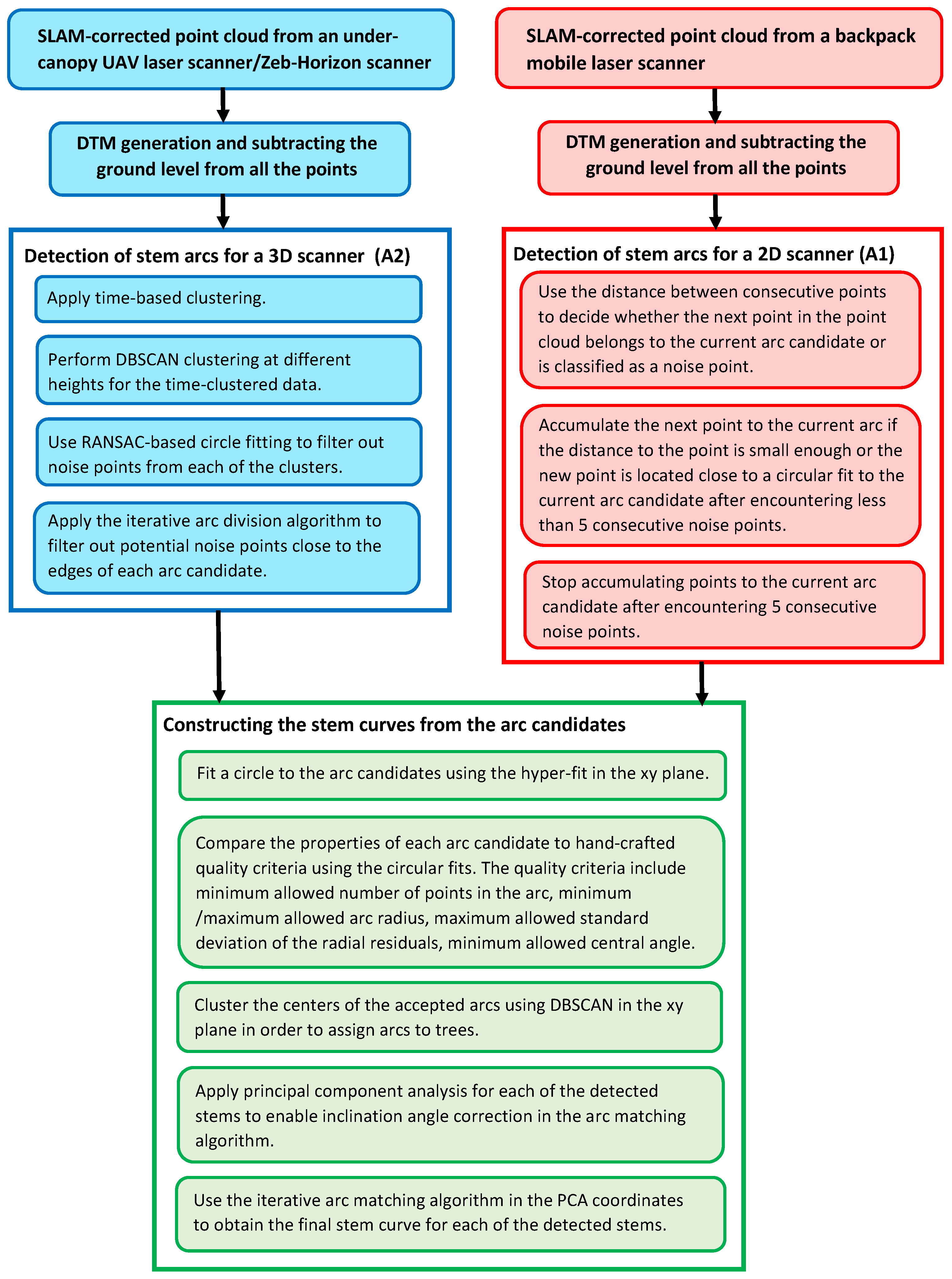
As an interesting note, the method based on backpack MLS resulted in the highest completeness rates, which was mainly due to the fact that the method was able to detect approximately one-third of the spruces, whereas the spruce detection rate was lower for the other methods. Importantly, the best results were obtained by using the arc detection algorithm that had been specifically designed for 2D laser scanners. As the arc finding algorithm for 2D scanners is based on scan line arc detection, it can apparently detect partly occluded stems with a better success rate as compared with the more general method designed for 3D scanners despite of the filtering steps in the more general algorithm.
4.2. Accuracy Comparison: DBH, Stem Curve, Tree Height, and Stem Volume
In this section, we present and discuss the results of stem diameter, tree height, and stem volume estimation for the different MLS measurements. The obtained values for bias and RMSE are summarized in
Table 7. In
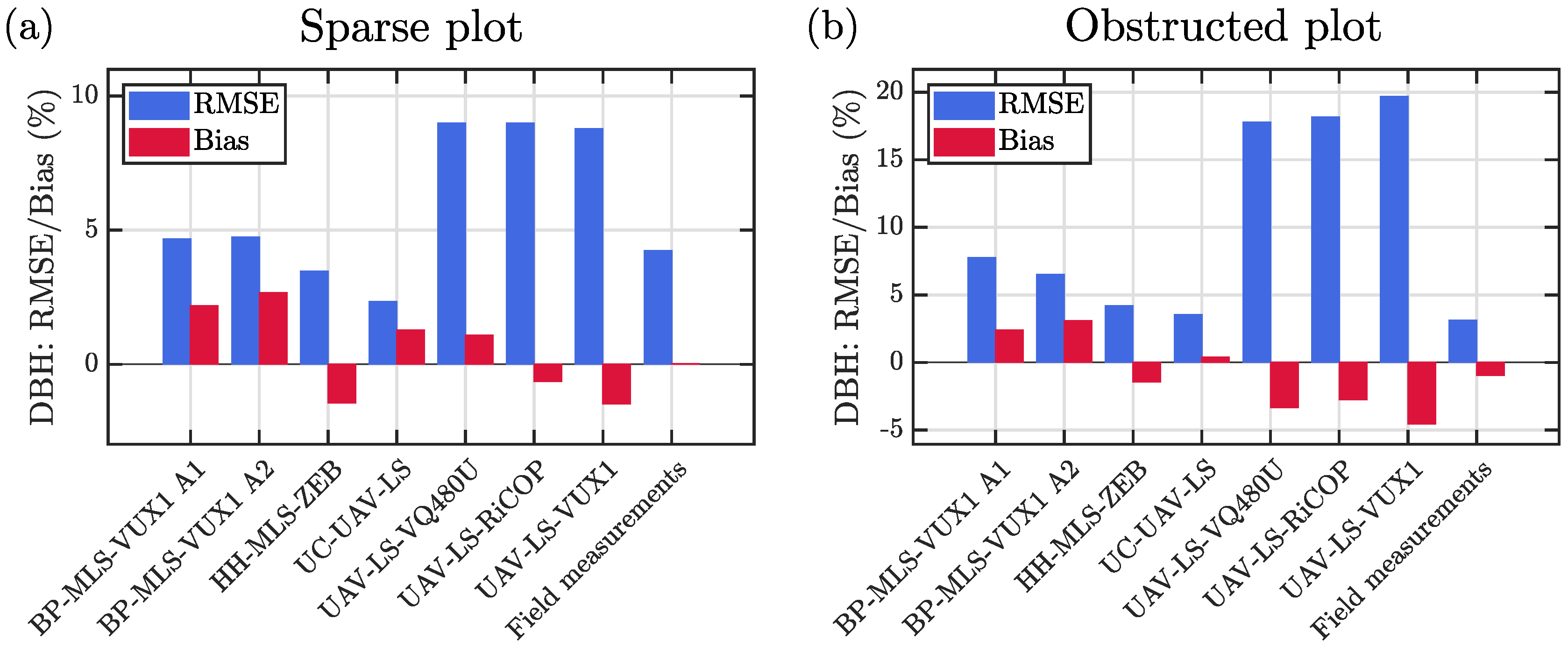
Figure 9, we show the relative bias and RMSE of the DBH estimates for the different methods in both the sparse and the obstructed plot. For each of the methods, the bias and RMSE were computed based on the trees that were detected with the particular method. In the sparse plot, the relative RMSE of DBH estimates varied between 2% and 5% for the ground-based/under-canopy MLS measurements, and the best results were obtained with the under-canopy UAV laser scanning system. In the obstructed plot, the relative RMSE of DBH estimation ranged between 4% and 8% for the ground-based/under-canopy MLS measurements, and again the best results were obtained with the under-canopy UAV system. Rather surprisingly, the RMSE of DBH estimation was higher for the backpack MLS system than for either the handheld laser scanner or the under-canopy UAV laser scanning system despite of the better ranging accuracy of the backpack laser scanner (see
Figure 7). Importantly, the ground-based/under-canopy MLS measurements allowed us to estimate the DBH with an RMSE that was of similar magnitude as the error based on ordinary field measurements. For the ordinary field measurements, we obtained 4% for the relative RMSE of DBH estimation in the sparse plot, and 3% in the obstructed plot.
For the above-canopy UAV measurements, the RMSE of DBH estimation was significantly higher. In the sparse plot, all these three airborne laser scanning methods resulted in a relative RMSE of close to 10%, whereas the corresponding relative RMSE in the obstructed plot was close to 20%. The much higher error in the obstructed plot was due to the higher variation in the sizes of trees. Namely, the random forest model used in this study was observed to underestimate the diameters of large trees and overestimate the diameters of small trees. In general, the point density and season (leaf-off or leaf-on) had a small effect on the overall results.
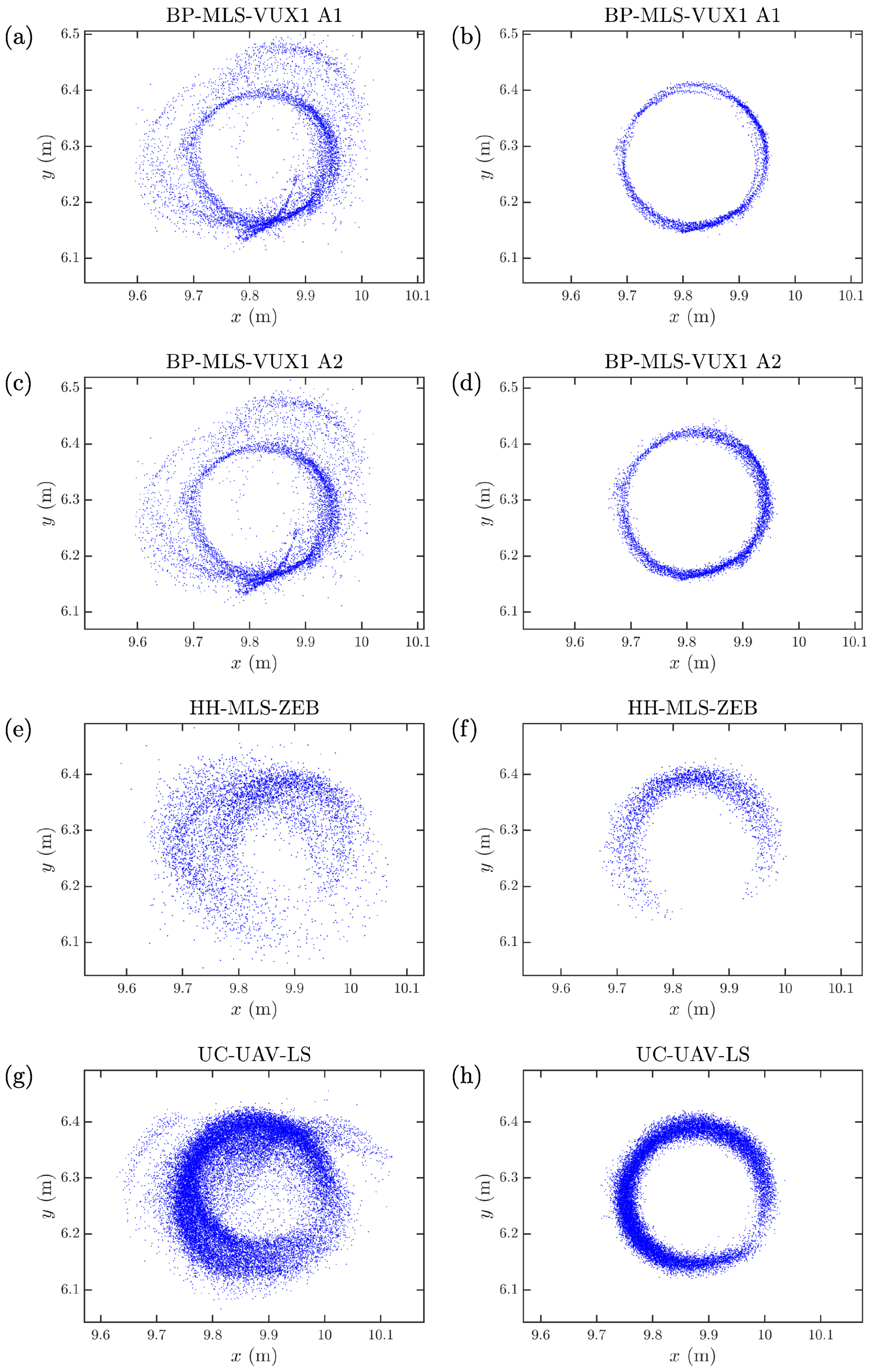
In
Figure 10, we show the relative bias and RMSE for the stem curves estimated with the backpack MLS method, the handheld MLS method, and the under-canopy UAV method. When the backpack MLS data was processed using the stem arc detection algorithm for 2D scanners (A1), the bias of stem curve estimation was found to be close to zero and independent of measurement height. If we instead analyzed the same backpack MLS data using the stem arc detection algorithm for 3D scanners (A2), we observed that the bias of the estimated stem curves increased with increasing height. The same kind of behavior was also observed for the methods based on handheld MLS and under-canopy UAV LS, for which we also used the stem arc detection algorithm for 3D scanners. For the handheld MLS method, the bias and RMSE of the estimated stem curves increased the most rapidly as a function of height: even though the bias (RMSE) was essentially 0% (5%) at the breast height, the bias (RMSE) approached 10% (15%) already at the height of 7 m.
There are a few reasons that could potentially explain the height dependent bias and RMSE of the stem curve estimates. First, the average distance between the scanner and the reflected stem points increased as a function of the height of the stem arcs. This increased distance might have resulted in an increased transverse width of the laser pulse. Previously, it has been shown that the finite transverse width of the laser pulse can result in an overestimated diameter of the circular fit (see [
49]). Interestingly, the bias of the stem curves extracted with the under-canopy UAV method attained its minimum value at the height of 3–4 m corresponding to a typical flying altitude of the UAV, whereas the smallest bias was recorded at the height of 1–2 m for the handheld Zeb-horizon system. This notion seems to support our hypothesis that the increased distance between the scanner and the stem arc is one major reason for the diameter overestimation at higher altitudes.
Second, the number of branches in a tree typically increased as a function of height, and thus noise points corresponding to the tree branches may have resulted in an overestimation of the stem diameter. We presume that the stem arc detection algorithm for 2D scanners was more robust against these effects since the point number threshold for an acceptable scan-line arc was set rather high. This helped to automatically filter out those stem arcs, for which the distance between the scanner and the arc was large. Additionally, we explicitly removed the two outermost points in each arc to mitigate edge effects as explained in
Section 3.4.
Despite of the height dependent bias and RMSE, the accuracy of the MLS-based stem curve measurements is at the state-of-the-art level. We presume that the high accuracy of the stem curve measurements can be attributed to the arc-based approach utilized in the stem detection algorithm. When using this approach, the positional drift of the scanner hardly distorts individual arcs since the stem points in a single arc are obtained during a short period of time. Thus, the arc-based approach can be used to eliminate the positional drift of the scanner and to obtain high-quality stem diameter estimates by matching the individual stem arcs together.
We suspect that the arc matching process itself is actually not vital for obtaining accurate diameter estimates. One could probably obtain relatively good results by, e.g., computing the median of the arc diameters within each height interval for each stem model. However, the arc matching algorithm allows one to visualize the results of the stem curve extraction algorithm in an efficient fashion. This is of utmost importance in practical applications, where one must be able to assess the quality of the automatic measurements. Note also that the laser scanner must be clearly tilted with respect to the vertical plane, contrary to a TLS scanner, in order to ensure that the arc-based approach works efficiently.
In
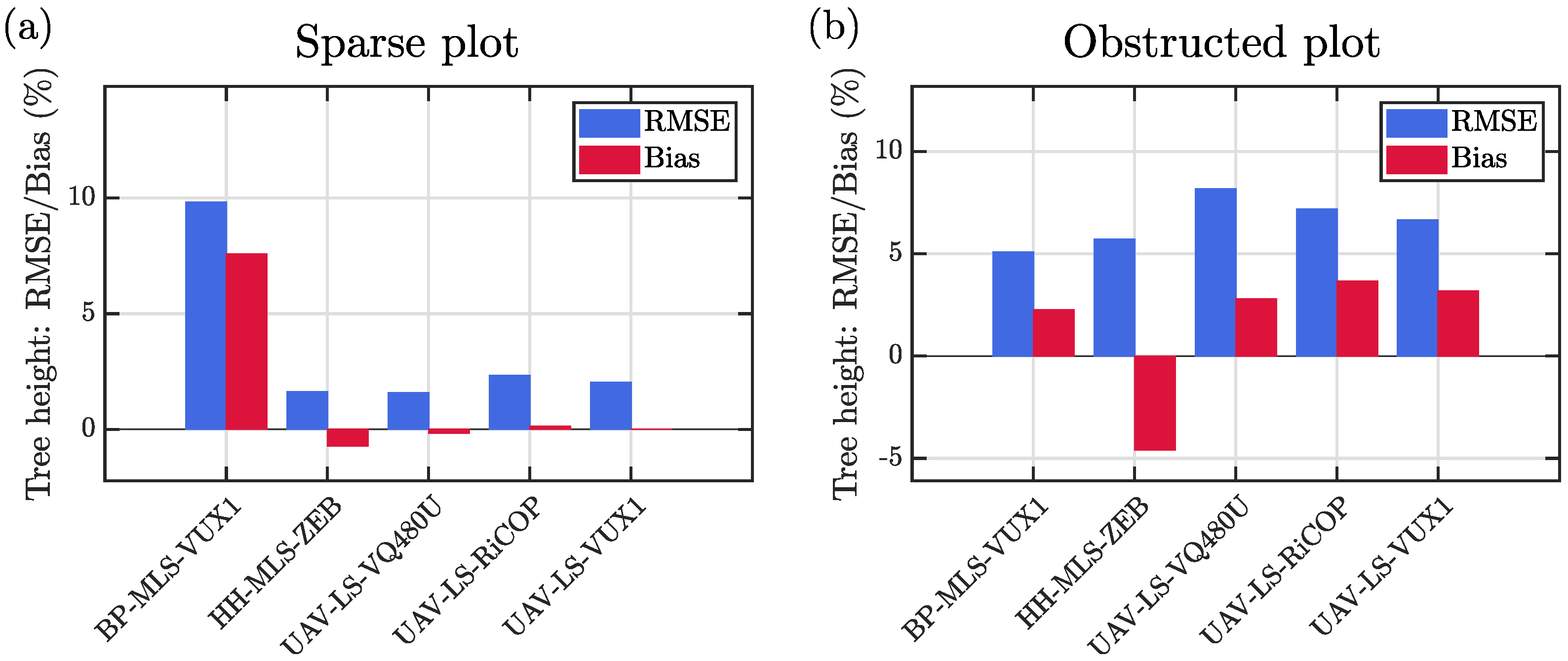
Figure 11, we illustrate the bias and RMSE of the estimated tree heights for the backpack MLS method, the handheld MLS method and the three above-canopy UAV systems. In the sparse plot, the backpack laser scanner method overestimated tree heights by 1.6 m (7.6%), whereas the handheld laser scanner achieved a similar accuracy as the above-canopy UAV methods (
). In the obstructed plot, the RMSE of height estimation was of similar magnitude for all the five methods (
), and actually the ground-based methods outperformed the methods based on above-canopy flying UAVs.
We presume that the severe overestimation of the tree heights by the backpack MLS method in the sparse plot was due to a failure of the graph-SLAM algorithm to perform matching in the vertical direction as discussed in [
13]. This hypothesis is supported by the fact that the bias of the tree heights was observed to vary systematically with the tree location in the sparse plot. Additional support for this claim is provided by the fact that a similar overestimation of tree heights was not observed in the obstructed plot.
It is rather surprising that the accuracy of tree height estimation in the obstructed plot was slightly better for the ground-based mobile methods as compared with the methods based on above-canopy flying UAVs. The larger error in the above-canopy-based tree heights was mainly due to the fact that these methods severely overestimated the heights of those spruces that were detected from the canopy height model (see species-wise statistics in
Table 8). These spruces were, namely, located close to taller pines, which made it difficult to obtain accurate height estimates for them. This observation suggests that it is fairly difficult to estimate accurately the tree heights of suppressed trees using above-canopy collected point clouds. This problem could potentially be alleviated if the above-canopy point clouds were dense enough to enable locating the stems of trees. In this case, the stem locations could be used to guide the tree height estimation.
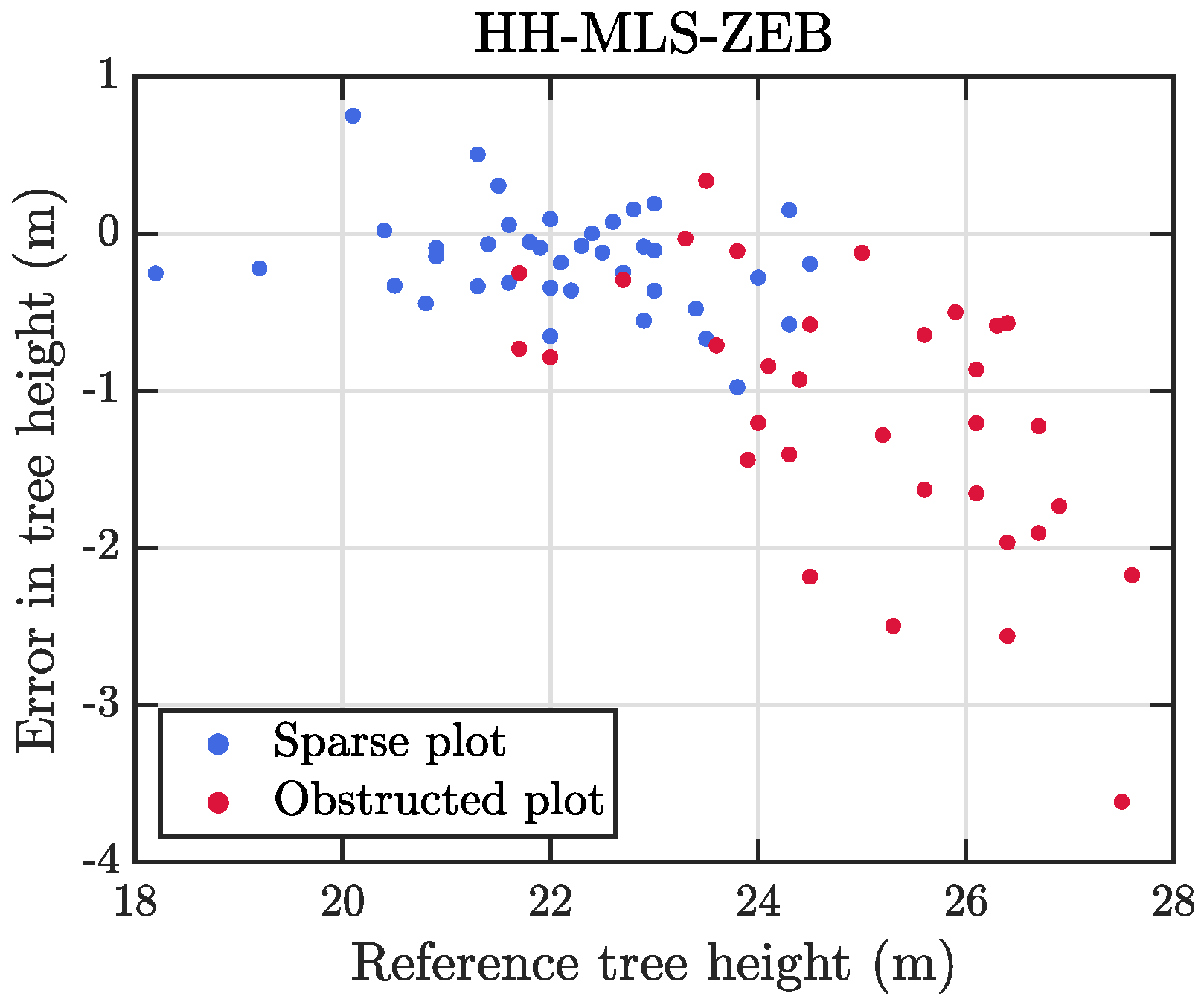
Additionally, we observed that the handheld Zeb-Horizon system systematically underestimated the heights of trees taller than 25 m as illustrated in
Figure 12. Importantly, the systematic underestimation increased linearly with increasing height above the height of 25 m, which means that the range of the scanner is sufficient for measuring the tree heights up to the height of approximately 25 m in boreal forest conditions.
In
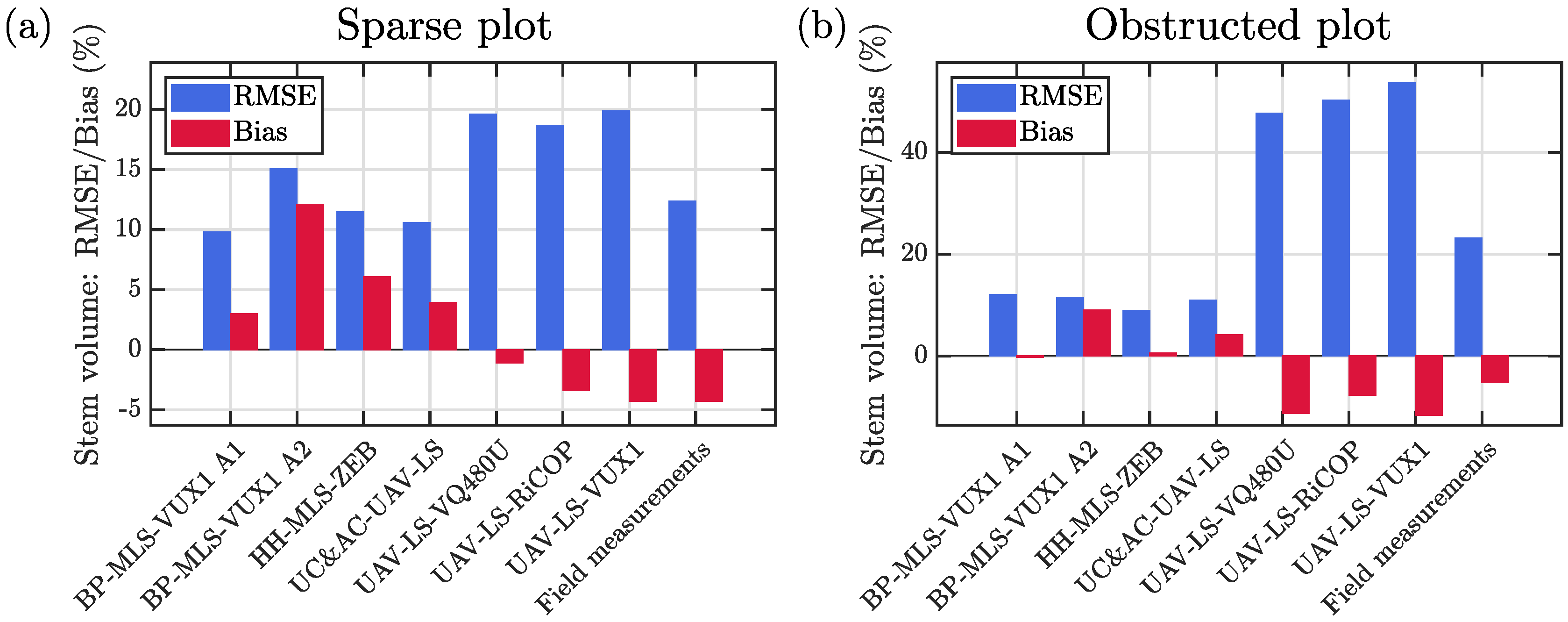
Figure 13, we illustrate the bias and RMSE of stem volume estimates for the different methods. We can observe that the ground-based/under-canopy MLS methods slightly overestimated the stem volumes on average since these methods tended to overestimate the stem diameters as discussed above. For all of the ground-based/under-canopy MLS methods, the RMSE of the stem volume estimation was approximately 10–15% in both of the test sites. Note that the results for the handheld Zeb-Horizon scanner are perhaps deceptively good (
) in the obstructed plot since the underestimation of tree heights was compensated by the overestimation of stem diameters. Note that the differences in the stem volume estimation accuracy were fairly small for the three ground-based/under-canopy MLS methods, and thus it is not possible to construct a conclusive ranking of these methods. One should also remember that the parameters of the algorithms were chosen heuristically meaning that it is possible that the parameters of the different methods might not be equally close to the optimal working point. Nevertheless, the errors in the stem volume estimates were of similar magnitude as results obtained with multi-scan TLS measurements in equivalent forest conditions [
32].
Importantly, the errors in the stem volumes estimated with the ground-based/under-canopy MLS methods were at the same level or lower as the errors based on conventional stem volume measurements that had been conducted on the same test sites. In this study, the conventional volume measurements were carried out by inputting the field measured DBH, tree height and tree species into the Finnish national allometric model [
57]. Importantly, the allometric model often tended to underestimate the volumes of large trees. For example, the volume of a large birch (DBH = 58 cm, V = 2.9 m
3) in the obstructed plot was greatly underestimated by the allometric model (V = 2.0 m
3). Note that this observation seems to suggest that it is beneficial to predict the stem volume using stem curve information from a wide height interval instead of using only the diameter at the breast height in the prediction of the stem volume. Naturally, this claim is true only if the stem curve can be extracted with a sufficient accuracy.
For the above-canopy laser scanning methods, the RMSE of stem volume estimation was approximately 20% in the sparse plot and close to 50% in the obstructed plot. The high error in the estimated stem volumes means that the above-canopy UAV LS methods cannot be used to derive the stem volume with a sufficient accuracy for individual tree level inventories unlike the ground-based/under-canopy MLS measurements. For these methods, the bias of the stem volume estimation was approximately % to 0%, which means that above-canopy UAV methods can, however, be used for collecting reference data for plot level forest inventories.
Additionally, it should be noted that the training data used for the above-canopy UAV methods was based on volumes computed with the Finnish national allometric model from field measured DBHs and tree heights on nearby plots. Therefore, the errors in the field estimated volumes propagated to the model. Nevertheless, the conclusions made in this section would not change had we used stem volumes extracted semi-manually from multi-scan TLS data to train the random forest models. Overall, we can conclude that the stem curve information is vital for estimating the stem volumes with a high accuracy at the individual tree level. Therefore, ground-based/under-canopy MLS methods have a clear advantage over methods based on above-canopy flying UAVs.
In
Table 8, we further present the species-wise bias and RMSE of DBH, tree height, and stem volume estimation. As already discussed above, the results were the best for pines, as the pines were dominant trees with visible, straight, and circular stems. The worst results were obtained for spruces that were all relatively young and thus had an occluded stem with a DBH of approximately 10 cm. Since the spruces were located nearby taller pines and birches, the algorithms used for the tree height estimation often tended to overestimate their heights by several meters regardless of whether ground-based or above-canopy systems were used. Note that the relative bias and RMSE values for the spruce trees are inflated by the fact that the spruces were on average relatively small. For the birch trees, the ground-based/under-canopy MLS methods managed to extract the stem volume with a good accuracy (RMSE = 7–17%), whereas the above-canopy LS measurements failed to provide accurate information of their DBH or stem volume. However, it is noteworthy that the results for the birch trees depended largely on how accurately the methods managed to model the very large birch located in the obstructed test site.
Overall, the number of spruces and birches on the test sites was relatively low, and therefore, one should not draw too far-reaching conclusions based on the data provided in
Table 8. Importantly, the spruces on the test sites did not include any mature trees with a partly visible stem. Therefore, the results presented in
Table 8 probably give a too pessimistic view of the performance of the methods when it comes to detecting and modeling mature spruces that are relevant for the forest industry.
In
Table 9, we present statistics of the trees that were not detected by the different MLS methods. Importantly, the omitted trees were relatively small with a mean DBH in the range of 8 to 14 cm depending on the method. Importantly, the total volume of the omitted trees varied between 0.6% and 3.6% of the total stem volume present on the test sites. The best result (0.6%) was obtained for the backpack laser scanning system, whereas the worst result (3.6%) was obtained for the handheld scanner. Nevertheless, the total volume of the omitted trees was small for all the different methods meaning that all of them were able to detect the trees that were relevant from the point of view of forest industry.