1. Introduction
A large-aperture densely-populated coherent hydrophone array system typically detects hundreds of thousands to millions of acoustic signals in the 10 Hz to 4000 Hz frequency range for each day of observation in a continental shelf ocean via the passive ocean acoustic waveguide remote sensing (POAWRS) technique [
1,
2]. The acoustic signal detections include both broadband transient and narrowband tonal signals from a wide range of natural and man-made sound sources [
3,
4,
5,
6,
7], such as marine mammal vocalizations [
1,
2,
8,
9,
10,
11], fish grunts, ship radiated sound [
12,
13], and seismic airgun signals [
14]. Here, we focus our efforts on developing automatic classifers for fin whale vocalizations detected in the Norwegian and Barents Seas during our Norwegian Sea 2014 Experiment (NorEx14) [
1]. The fin whale vocalization signals have been previously detected, identified and manually labeled via semiautomatic analysis followed by visual inspection.
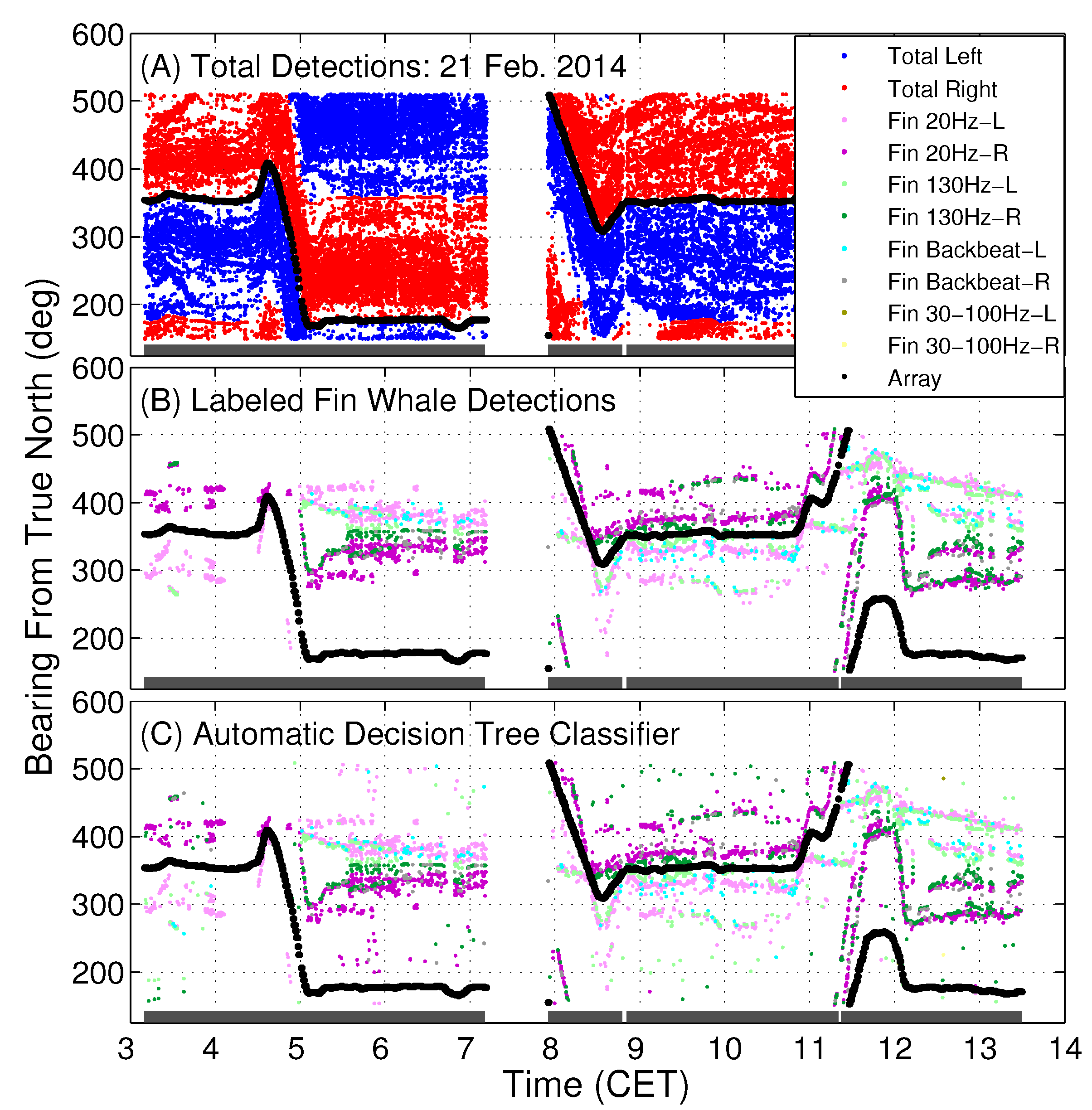
A total of approximately 170,000 fin whale vocalizations have been identified and extracted from the coherent hydrophone array recordings of NorEx14 [
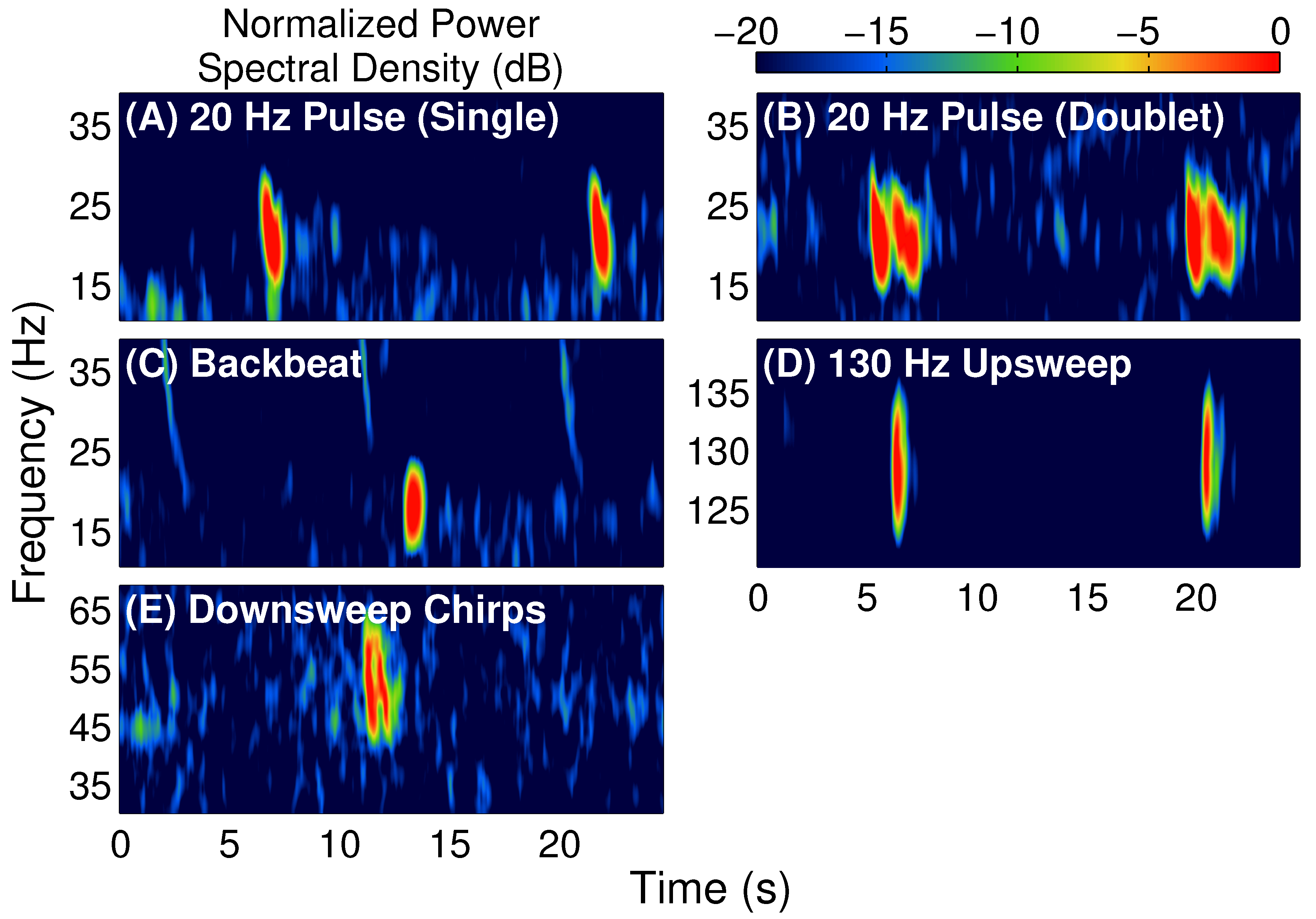
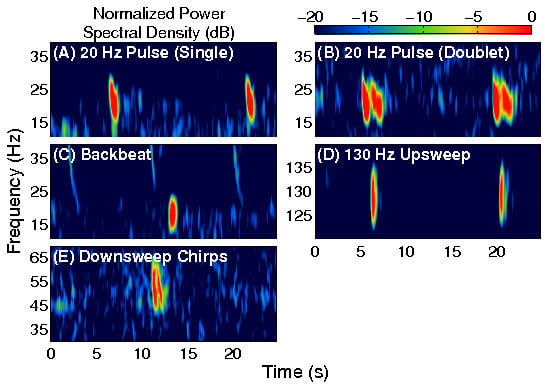
1]. The main types of fin whale vocalizations observed were the 20 Hz pulse, the 18–19 Hz backbeat pulse, the 130 Hz upsweep pulse, and the 30–100 Hz downsweep chirp [
1,
15,
16,
17,
18]. Typical spectrograms for each of these fin whale vocalizations are displayed in
Figure 1.
One of the challenges of developing an automatic classifier for near real-time fin whale vocalization detection from acoustic spectrograms, is the ability to differentiate fin whale vocalizations from other biological and man-made acoustic sound sources.
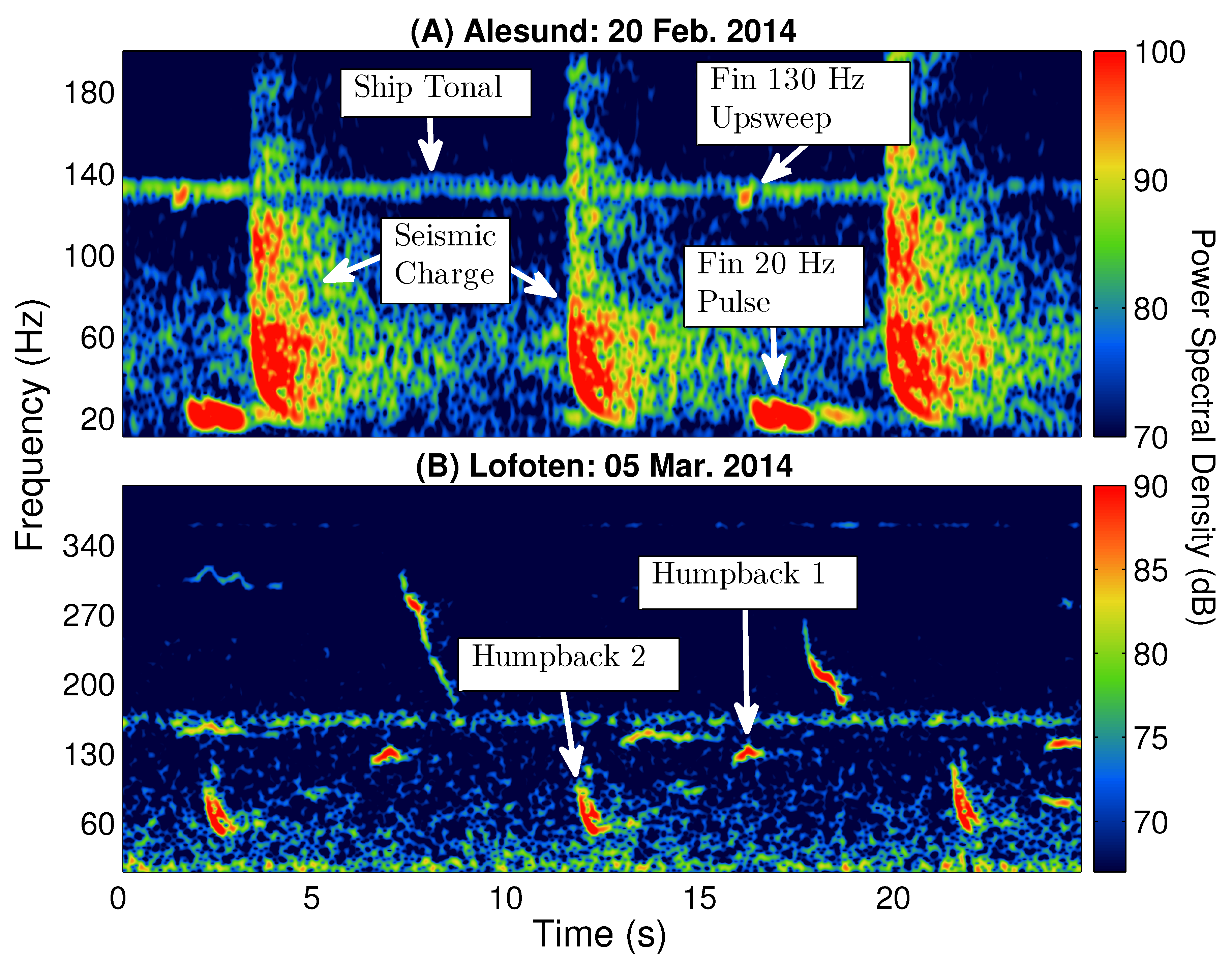
Figure 2 displays examples of several common acoustic signals and sound sources observed during the Norwegian Sea Experiment 2014 (NorEx14) [
1] in the frequency range of fin whale vocalizations, which include seismic airgun, ship tonal, and humpback whale vocalization signals. Unfortunately, many of these signals have overlapping features, such as bandwidth, with specific types of fin whale vocalizations that may cause ambiguity in identification. As an example,
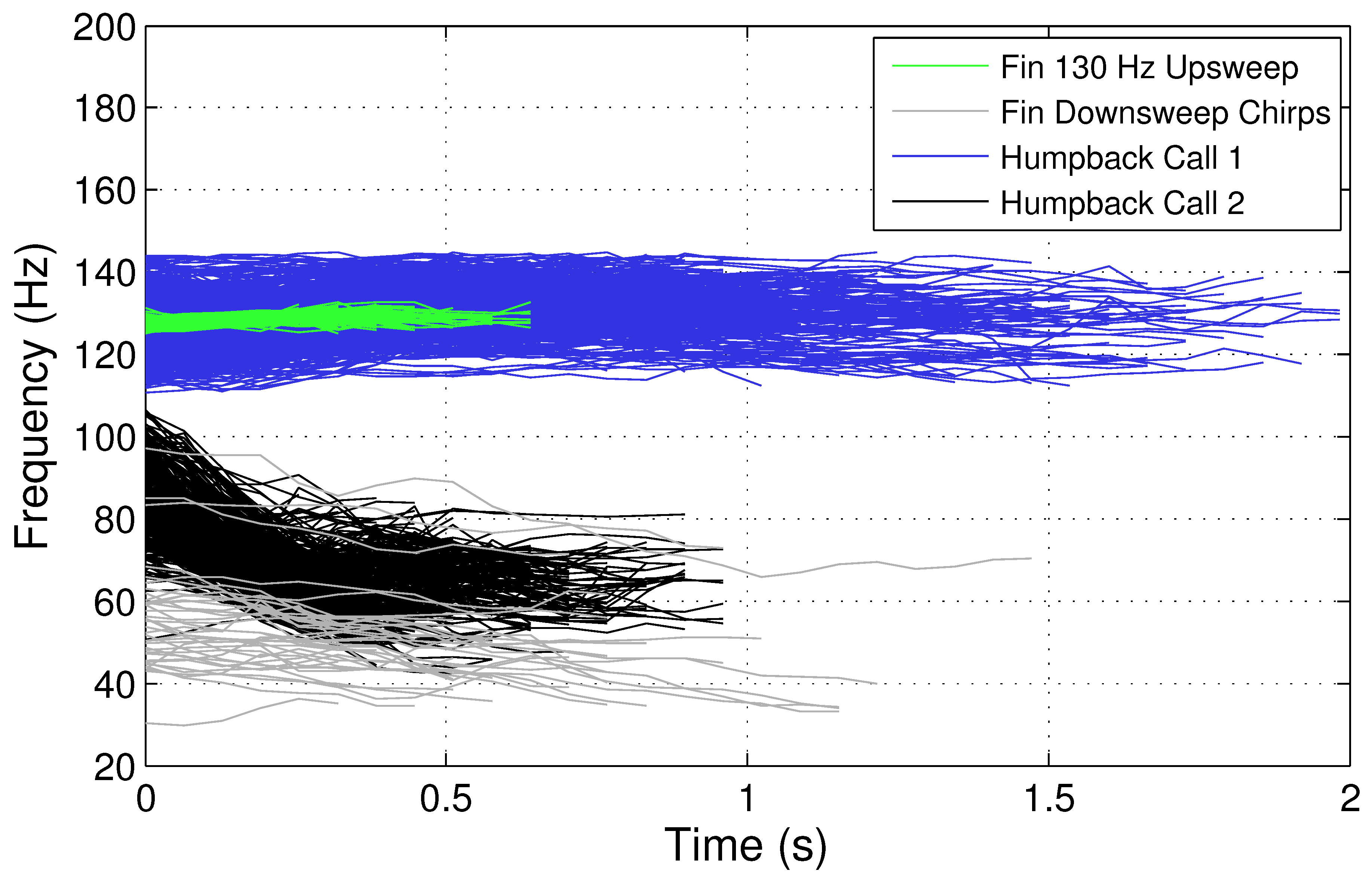
Figure 3 compares the pitch-tracks for two types of humpback whale vocalizations with the fin whale 130 Hz upsweep and 30–100 Hz downsweeps. As indicated in
Figure 3, the humpback whale vocalizations appear to have some similar time–frequency characteristics as the fin whale 130 Hz upsweep and 30–100 Hz downsweeps, and it may be challenging to correctly classify these two types of fin whale vocalizations from humpback whales vocalizing in the same region, depending on the classification method utilized. Therefore, a robust classification system is necessary to enable the fin whale 20 Hz pulse, 130 Hz upsweep, backbeat pulse, and 30–100 downsweep chirp vocalizations to be recognized and differentiated from other acoustic sound sources.
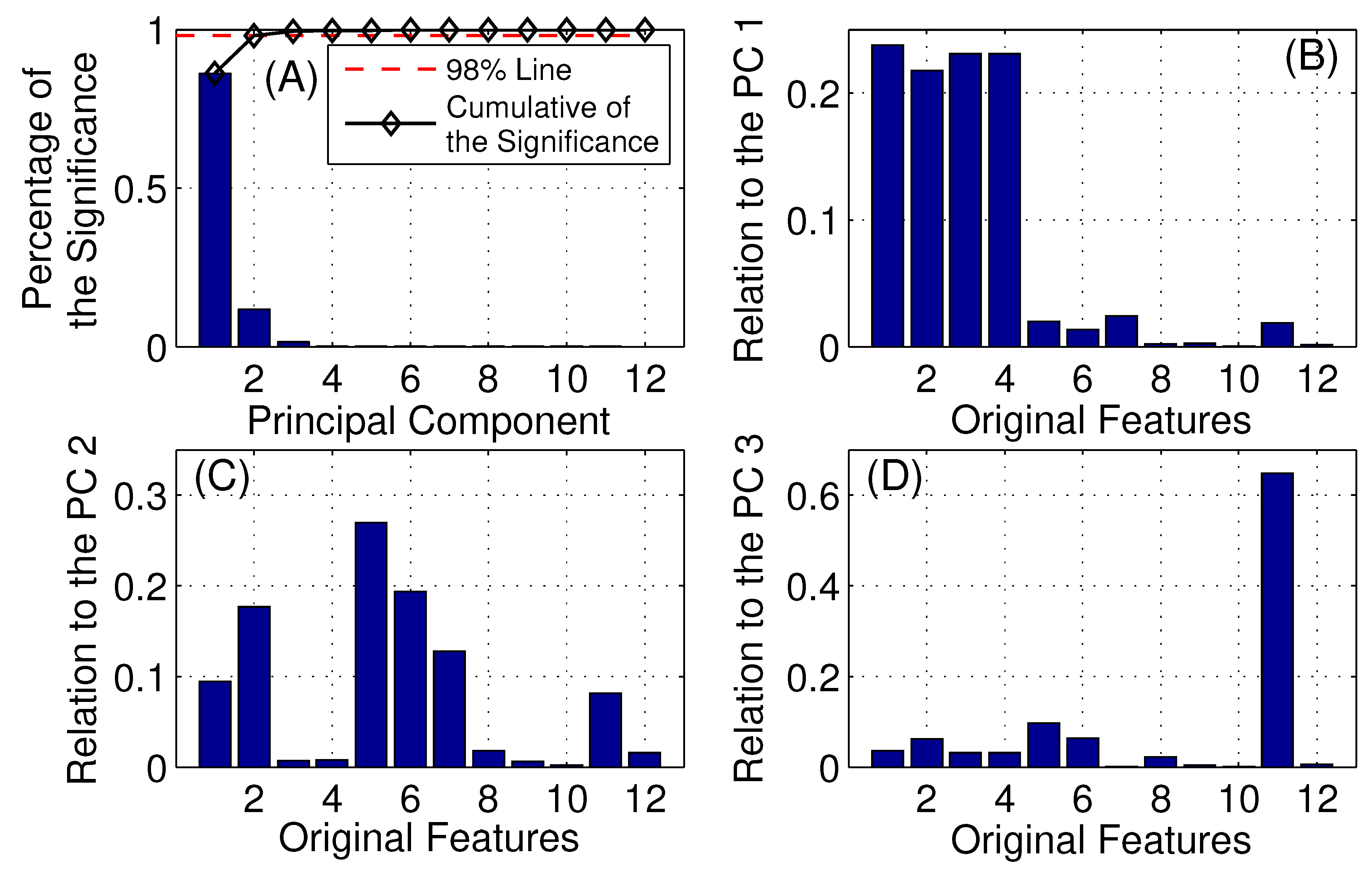
Here, a large training data set of fin whale vocalization and other acoustic signal detections are gathered after manual inspection and labeling. The fin whale vocalizations were identified by first clustering all the detected acoustic signals, on a specific observation day, using various time–frequency features and unsupervised clustering algorithms described in
Section 2.2. Each cluster was then manually inspected to positively label a cluster as containing fin whale vocalization detections. This was accomplished by visually reviewing the spectrograms and time–frequency characteristics associated with the detected acoustic signals from each cluster. As a final step, each cluster identified as containing fin whale vocalization detections was filtered manually to eliminate non-fin whale vocalization detections [
1]. This approach gave us the capability to analyze and identify marine mammal vocalizations that have not been previously documented or observed, by associating bearing-time trajectories of unknown acoustic sound sources with known acoustic sound sources. However, manual filtering is not a viable method of identifying fin whale vocalizations for real-time applications given the long time duration needed for the analysis and limited number of trained individuals with experience to visually identify different types of fin whale vocalizations from spectrograms. Therefore, it is essential to develop an automatic classifier for real-time fin whale vocalization detection applications.
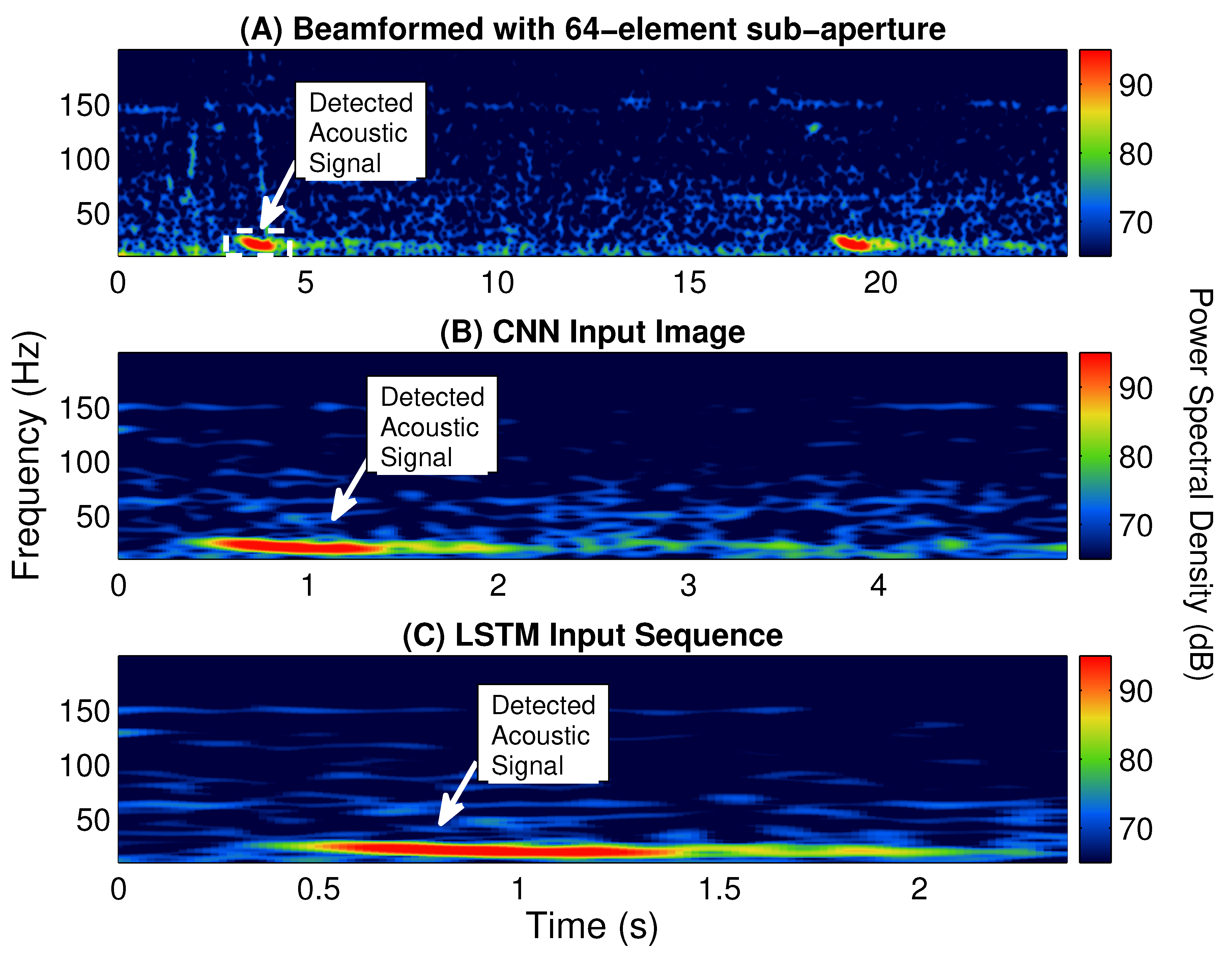
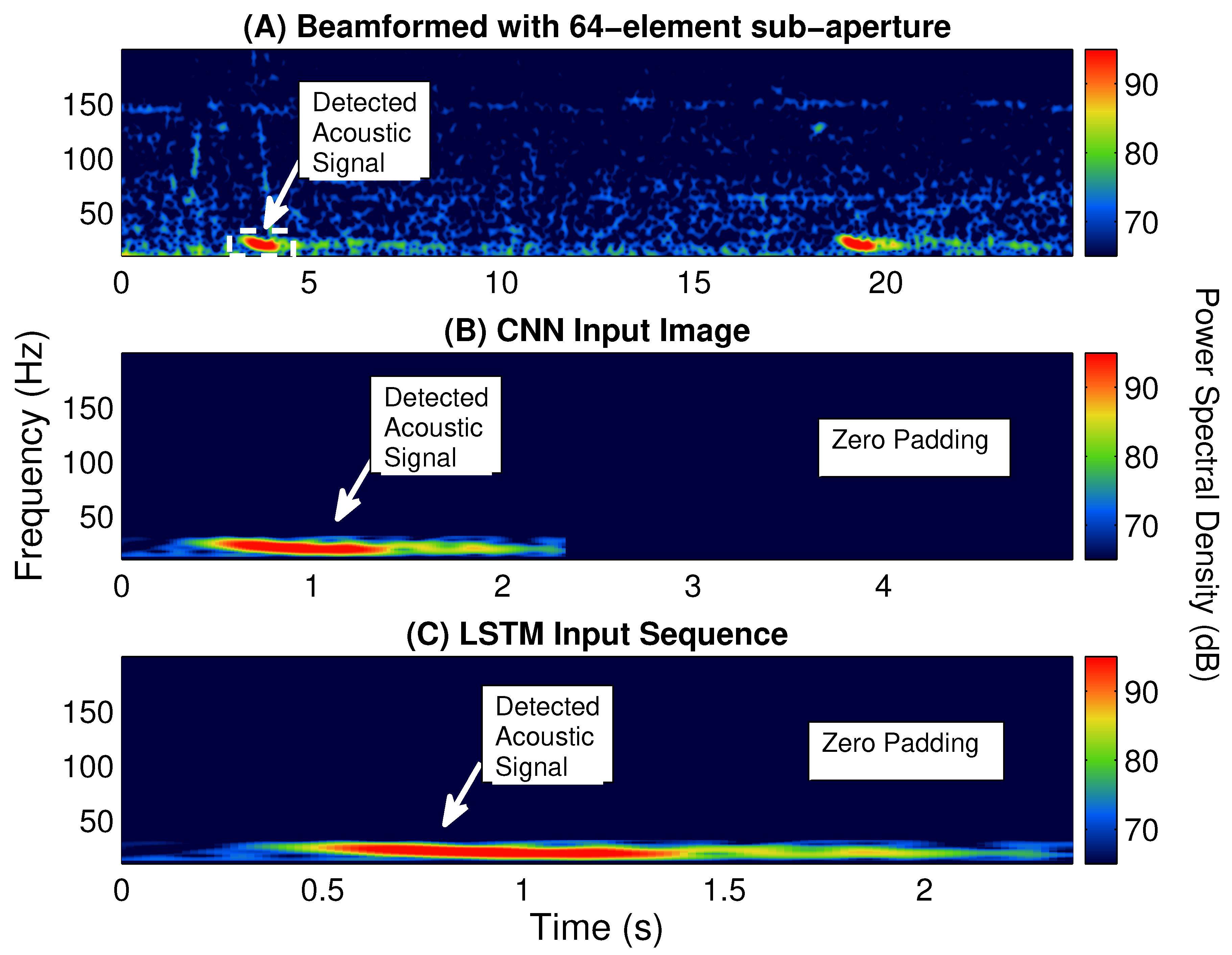
Multiple classifiers, including a logistic regression, SVM, decision tree [
19], CNN [
20,
21,
22], and LSTM network [
23], are built and tested for identifying fin whale vocalizations from the enormous amount of acoustic signals detected by POAWRS per day. Here, the CNN and LSTM classifiers are trained using beamformed spectrogram images as inputs to classify each detected acoustic signal, while logistic regression, SVM and decision tree classifiers are trained using 12 features extracted from each detected acoustic signal in a beamformed spectrogram. The performance of the classifiers are evaluated and compared using multiple metrics including accuracy, precision, recall and F1-score. The last step includes integrating one of the classifiers into the existing POAWRS array and signal processing software to provide an automatic classifier for near real-time fin whale monitoring applications. The classifiers developed here can enable near real-time identification of fin whale vocalization signal types since the classification run time is found to be on the order of seconds, given tens to hundreds of thousands of input signals received by the coherent hydrophone array. The fin whale vocalization classifier presented, here, will lay the foundation for building an automatic classifier for near real-time detection and identification of various other biological, geophysical, and man-made sound sources in the ocean.
Automatic classification approaches, including machine learning, can help to efficiently and rapidly classify ocean acoustic signals according to sound sources in ocean acoustic data sets within significantly reduced time frames. Various automatic classification techniques have been applied for ocean biological sensing from animal vocalizations and sounds received on both single hydrophone and coherent hydrophone arrays [
9,
24,
25]. In [
26], the performance of Mel Frequency Cepstrum Coefficients (MFCC), the linear prediction coding (LPC) coefficients, and Cepstral coefficients for representing humpback whale vocalizations were explored, and then K-means clustering was used to cluster units and subunits of humpback whale vocalizations into 21 and 18 clusters, respectively. The temporal and spatial statistics of humpback whales song and non-song calls in the Gulf of Maine, observed using a large-aperture coherent hydrophone array, were quantified over instantaneous continental shelf scale regions in [
9]. Subclassification of humpback whale downsweep moan calls into 13 sub-groups were accomplished using K-means clustering after beamformed spectrogram analysis, pitch-tracking and time–frequency feature extraction. Automatic classifiers were further developed in [
24] to distinguish humpback whale song sequences from nonsong calls in the Gulf of Maine by first applying Bag of Words to build feature vectors from beamformed time-series signals, calculating both power spectral density and MFCC features, and then employing and comparing the performances of Support Vector Machine (SVM), Neural Networks, and Naive Bayes in the classification. Identification of individual male humpback whales from their song units was investigated in [
27], via extracting Cepstral coefficients for features and then applying SVM for classification. In [
28], blue whale calls were classified using neural network with features derived from short-time Fourier and wavelet transforms. In [
29], an automatic detection and classification system for baleen whale calls was developed using pitch tracking and quadratic discriminant function analysis. Echolocation clicks of odontocetes were classified by exploiting cepstral features and Gaussian mixture models in [
30], while in [
31], whale call classification was accomplished using CNNs and transfer learning on time–frequency features. Fish sounds were classified using random forest and SVM in [
32].
Here, the automatic classification and machine learning algorithms are applied to large-aperture coherent hydrophone array data, where the input to the classifiers are beamformed data in the form of beamformed frequency-time spectrograms or extracted features, or beamformed time-series, spanning all 360 degrees horizontal azimuth about the coherent hydrophone array. The output of the classifier therefore provides identification of fin whale call types spatially distributed across multiple bearings from the receiver array. The identified fin whale vocalization bearing-time trajectories are required for spatial localization and horizontal positioning of fin whales [
1].
5. Conclusions
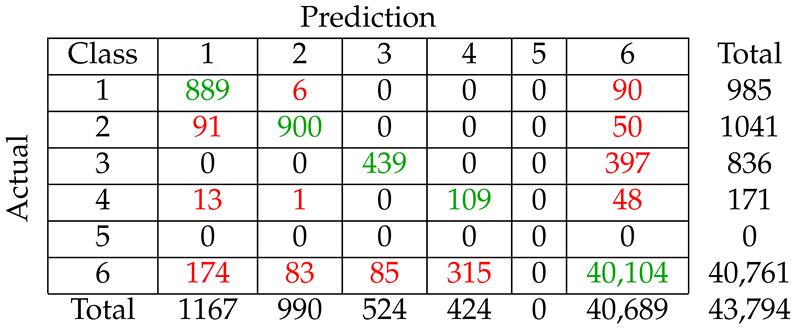
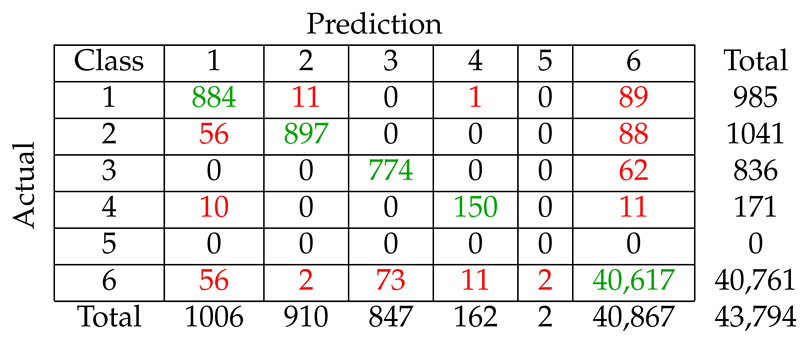
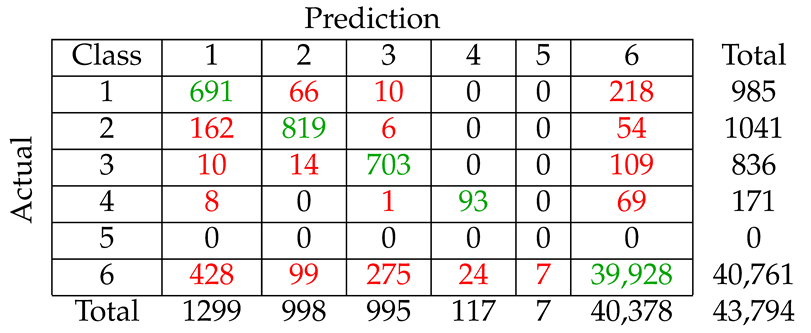
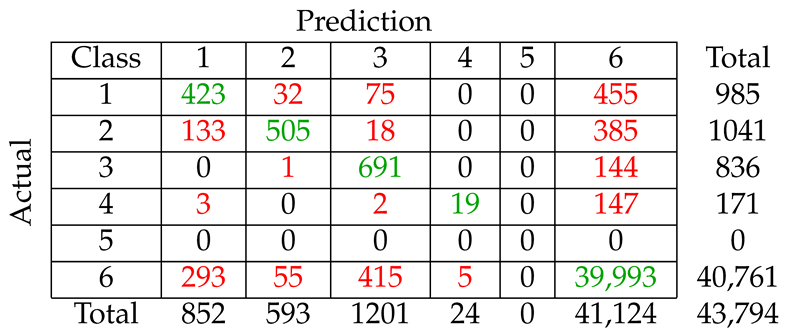
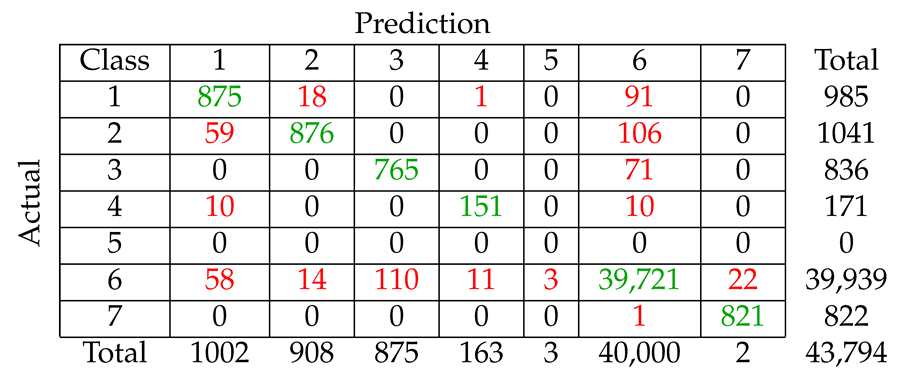
We considered five different types of classification algorithms to identify fin whale vocalizations: logistic regression, SVM, decision tree, CNN, and LSTM. The goal was to develop a fin whale classifier for near real-time fin whale detection applications. Each classifier was trained and tested using POAWRS detections from the NorEX14 data set. Each detection was categorized as either a specific type of fin whale vocalization or a non-fin whale vocalization. Further analysis will be required to identify the best classification approach for fin whale vocalizations due to challenges such as the limited size of the data set, which does not include the seasonal and regional differences in the acoustic signals detected. However, the decision tree classifier was ranked number 1 out of the five classifiers and has F1-score results all greater than from the current data set used.
The demonstrated performance of the decision tree classifier suggest that it is an excellent candidate to be applied for near-real time classification of fin whale detections for the Norwegian and Barents Seas. Ultimately, the fin whale classifier developed in this journal article will provide a framework for future development, such as incorporating new classes of acoustic signals from future collections of training data, as was shown here by incorporating detections of seismic airgun signals.