Ground Based Hyperspectral Imaging to Characterize Canopy-Level Photosynthetic Activities
Abstract
1. Introduction
2. Materials and Methods
2.1. Plant Materials and Experimental Design
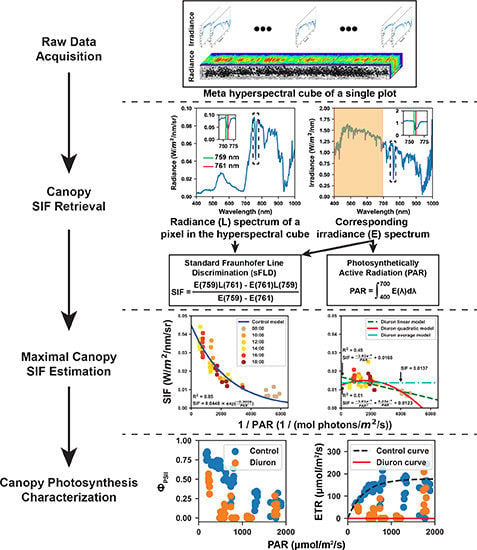
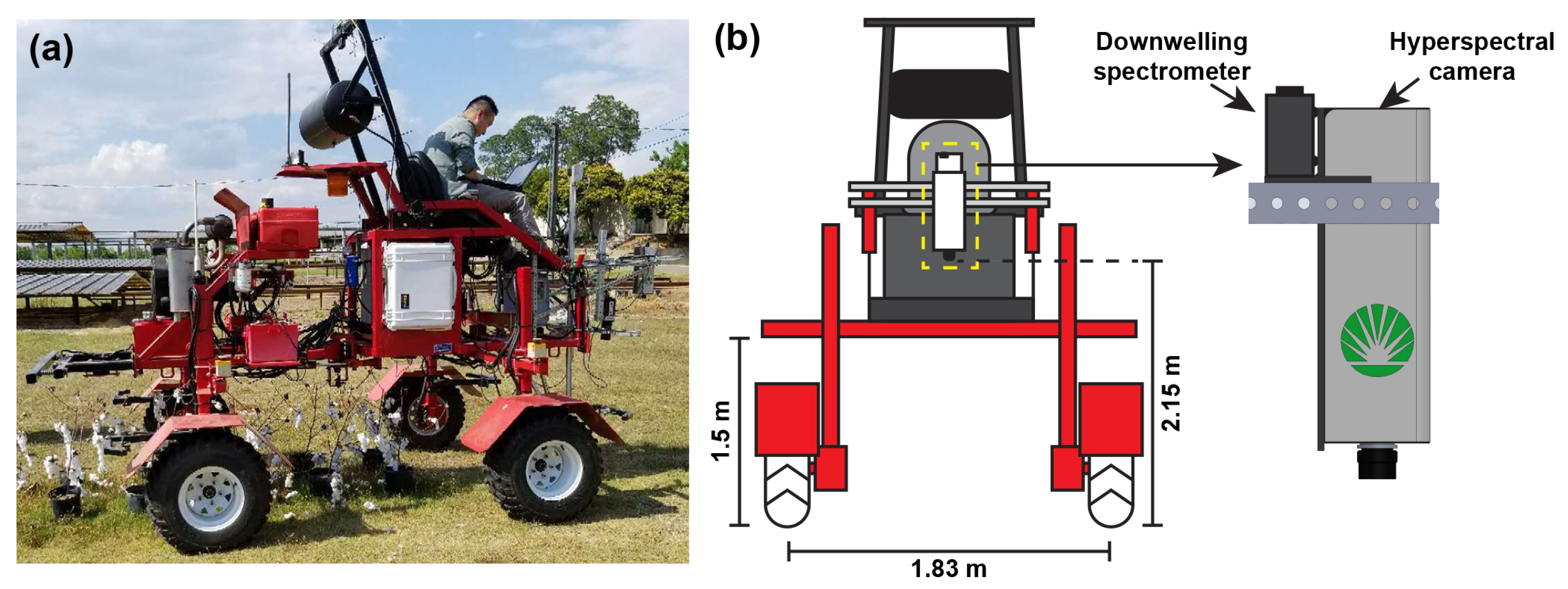
2.2. Data Acquisition
2.2.1. Hyperspectral Data Acquisition
2.2.2. Fluorometry Measurement
2.3. Characterization of Canopy-Level Photosynthetic Efficiency
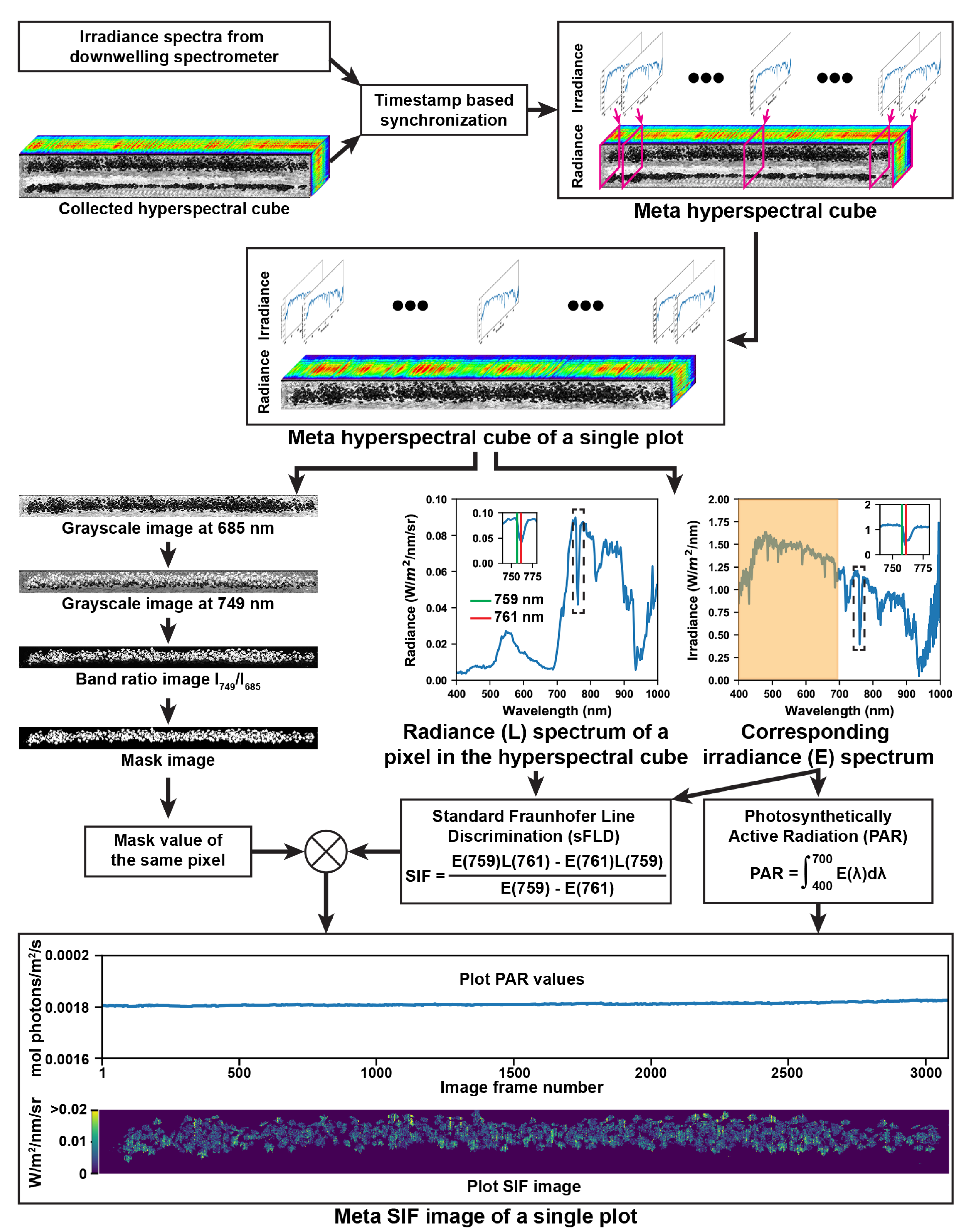
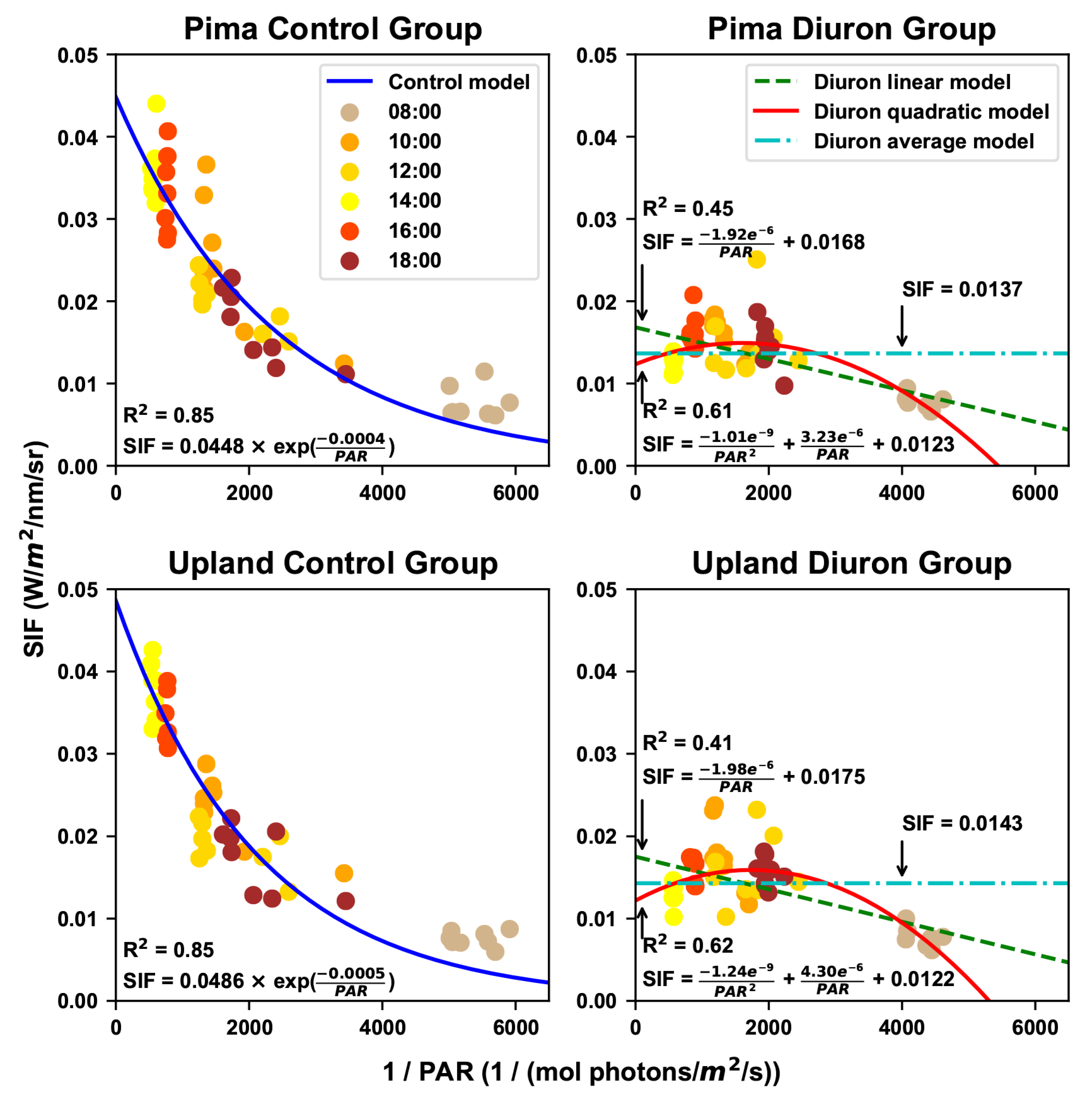
2.3.1. Retrieval of Solar Induced Fluorescence
2.3.2. Calculation of Effective Quantum Yield and Electron Transport Rate
2.3.3. Rapid Light Curve and Standardized ETR
2.4. Calculation of Standardized Photochemical Reflectance Index
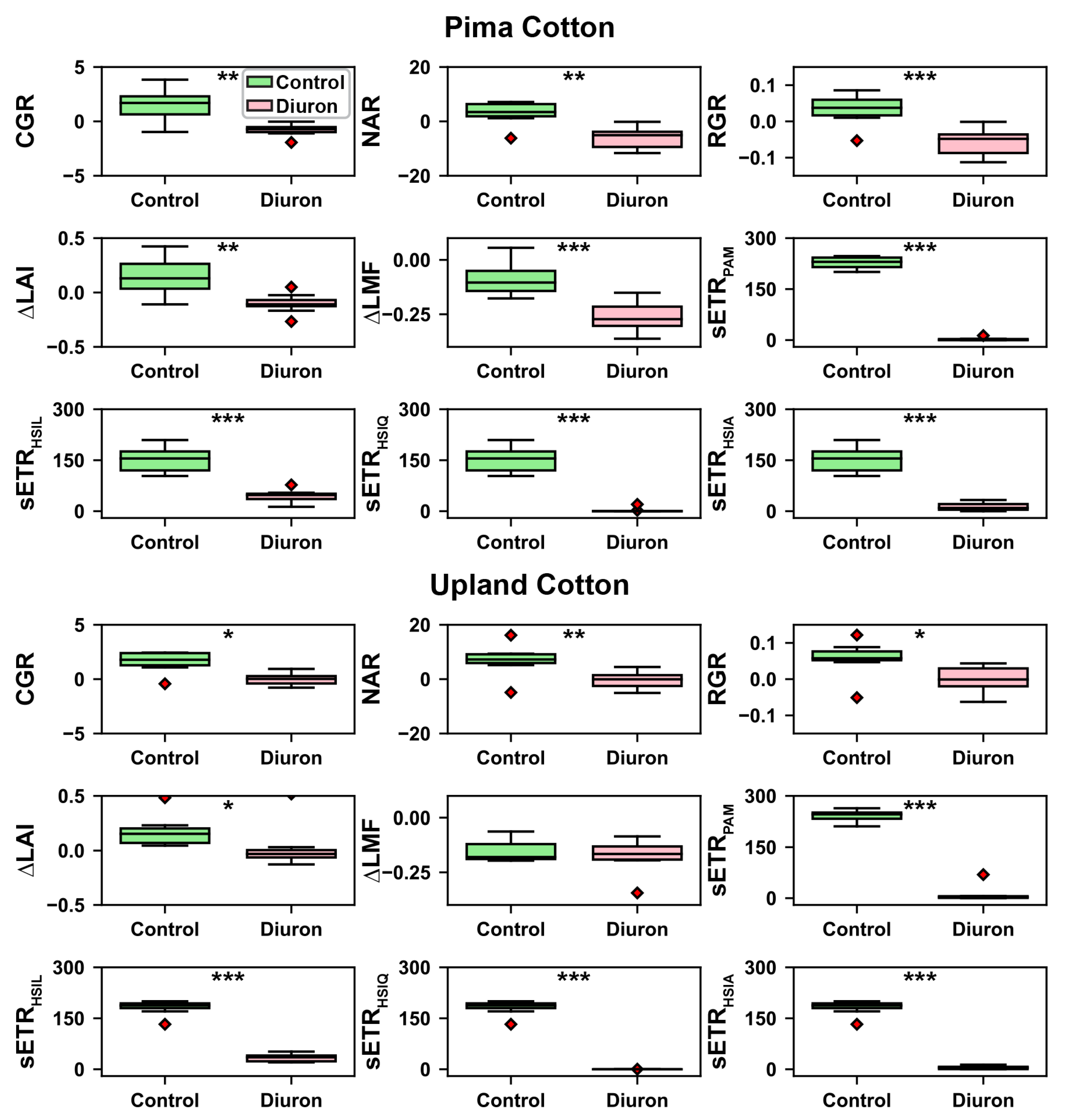
2.5. Growth Analysis
2.6. Statistical Analysis
3. Results
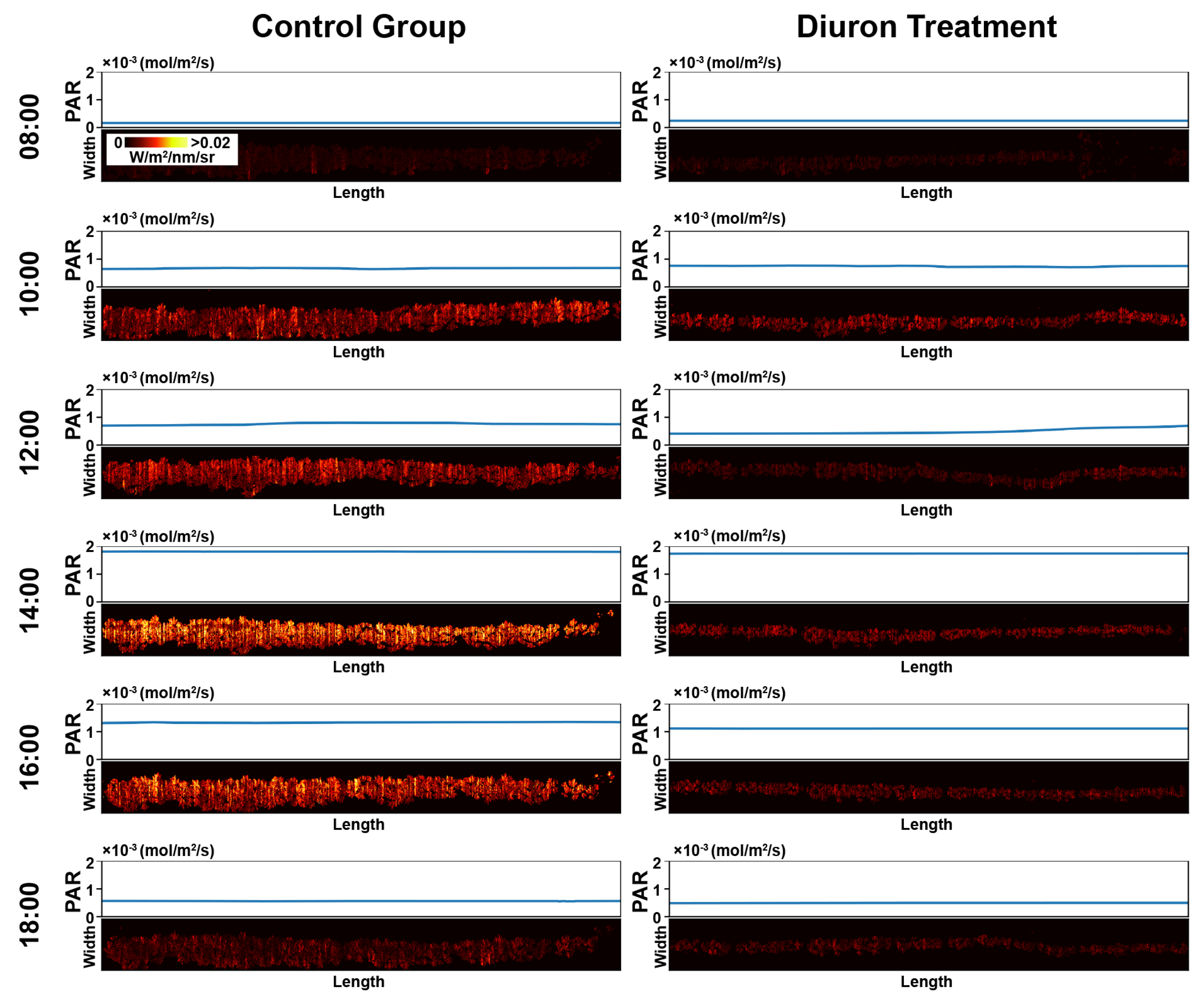
3.1. Representative Meta-SIF Images
3.2. Estimated Maximal Fluorescence
3.3. Calculated Effective Quantum Yield and RLCs
3.4. ANOVA Test Results
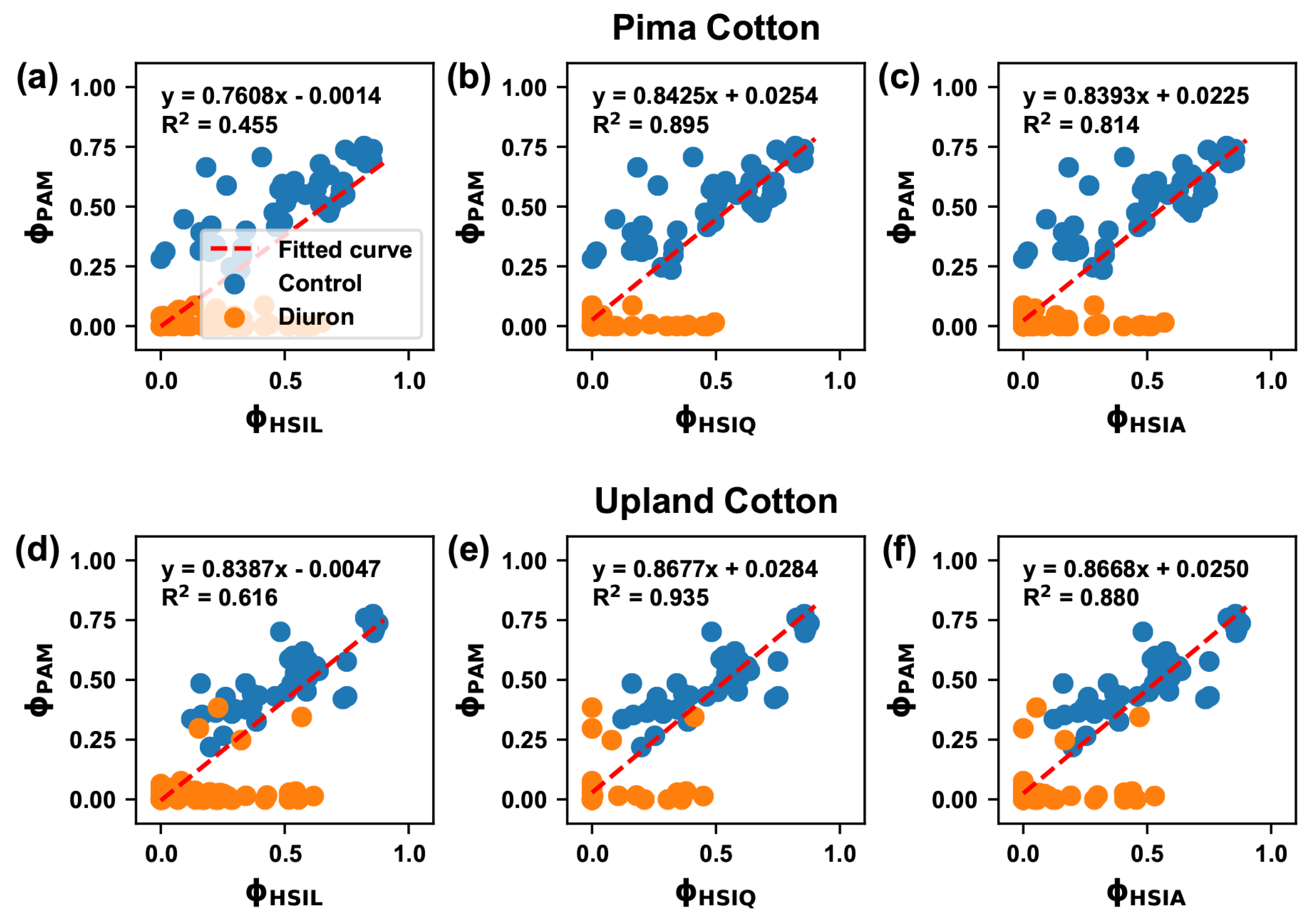
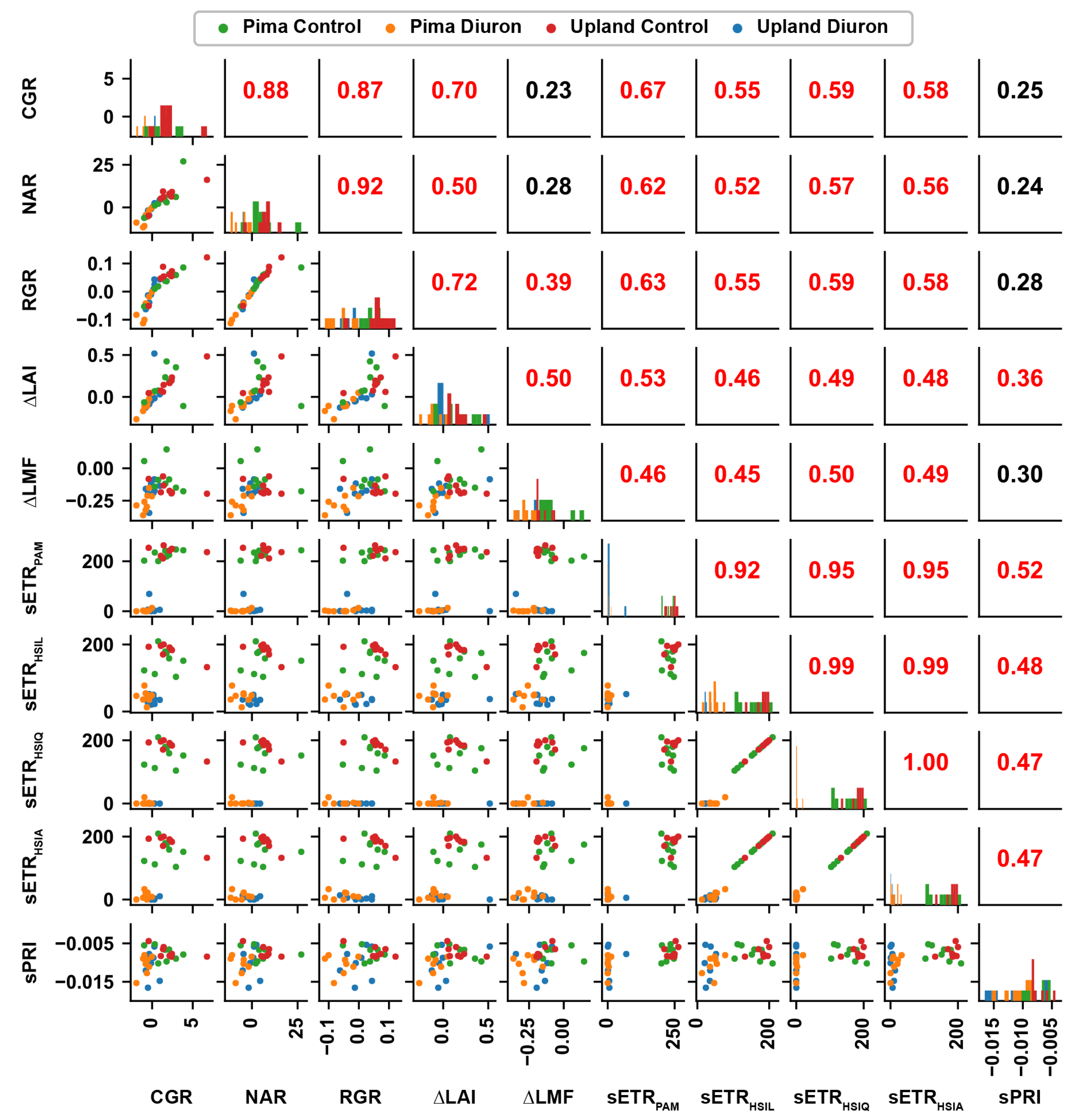
3.5. Correlation between Traits
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| MDPI | Multidisciplinary Digital Publishing Institute |
| DOAJ | Directory of open access journals |
| TLA | Three letter acronym |
| LD | linear dichroism |
References
- Tilman, D.; Balzer, C.; Hill, J.; Befort, B.L. Global food demand and the sustainable intensification of agriculture. Proc. Natl. Acad. Sci. USA 2011, 108, 20260–20264. [Google Scholar] [CrossRef]
- Steensland, A.; Zeigler, M. 2018 Global Agricultural Productivity Report. 2018. Available online: https://globalagriculturalproductivity.org/ (accessed on 7 April 2019).
- USDA-ERS. Cotton and Wool: Overview. 2017. Available online: https://www.ers.usda.gov/topics/crops/cotton-wool/ (accessed on 7 April 2019).
- Reynolds, M.; Langridge, P. Physiological breeding. Curr. Opin. Plant Biol. 2016, 31, 162–171. [Google Scholar] [CrossRef] [PubMed]
- Monteith, J. Solar radiation and productivity in tropical ecosystems. J. Appl. Ecol. 1972, 9, 747–766. [Google Scholar] [CrossRef]
- Hedden, P. The genes of the Green Revolution. Trends Genet. 2003, 19, 5–9. [Google Scholar] [CrossRef]
- Fischer, R.; Edmeades, G.O. Breeding and cereal yield progress. Crop Sci. 2010, 50, S-85–S-98. [Google Scholar] [CrossRef]
- Meredith, W.R.; Wells, R. Potential for increasing cotton yields through enhanced partitioning to reproductive structures. Crop Sci. 1989, 29, 636–639. [Google Scholar] [CrossRef]
- Wells, R. The Use of Obsolete and Modern Cultivars to Examine Advances in Yield and Dry Matter Partitioning. J. Cotton Sci. 2016, 20, 246–252. [Google Scholar]
- Constable, G.A.; Bange, M.P. The yield potential of cotton (Gossypium hirsutum L.). Field Crop. Res. 2015, 182, 98–106. [Google Scholar] [CrossRef]
- Murchie, E.H.; Lawson, T. Chlorophyll fluorescence analysis: A guide to good practice and understanding some new applications. J. Exp. Bot. 2013, 64, 3983–3998. [Google Scholar] [CrossRef]
- Damm, A.; Elbers, J.; Erler, A.; Gioli, B.; Hamdi, K.; Hutjes, R.; Kosvancova, M.; Meroni, M.; Miglietta, F.; Moersch, A. Remote sensing of sun-induced fluorescence to improve modeling of diurnal courses of gross primary production (GPP). Glob. Chang. Biol. 2010, 16, 171–186. [Google Scholar] [CrossRef]
- Baker, N.R. Chlorophyll fluorescence: A probe of photosynthesis in vivo. Annu. Rev. Plant Biol. 2008, 59, 89–113. [Google Scholar] [CrossRef] [PubMed]
- Van der Tol, C.; Verhoef, W.; Rosema, A. A model for chlorophyll fluorescence and photosynthesis at leaf scale. Agric. For. Meteorol. 2009, 149, 96–105. [Google Scholar] [CrossRef]
- Bolhar-Nordenkampf, H.; Long, S.; Baker, N.; Oquist, G.; Schreiber, U.; Lechner, E. Chlorophyll fluorescence as a probe of the photosynthetic competence of leaves in the field: A review of current instrumentation. Funct. Ecol. 1989, 3, 497–514. [Google Scholar] [CrossRef]
- Kolber, Z.; Klimov, D.; Ananyev, G.; Rascher, U.; Berry, J.; Osmond, B. Measuring photosynthetic parameters at a distance: Laser induced fluorescence transient (LIFT) method for remote measurements of photosynthesis in terrestrial vegetation. Photosynth. Res. 2005, 84, 121–129. [Google Scholar] [CrossRef]
- Schreiber, U.; Kühl, M.; Klimant, I.; Reising, H. Measurement of chlorophyll fluorescence within leaves using a modified PAM fluorometer with a fiber-optic microprobe. Photosynth. Res. 1996, 47, 103–109. [Google Scholar] [CrossRef]
- Beer, S.; Björk, M. Measuring rates of photosynthesis of two tropical seagrasses by pulse amplitude modulated (PAM) fluorometry. Aquat. Bot. 2000, 66, 69–76. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; Miller, J.R.; Mohammed, G.H.; Noland, T.L. Chlorophyll fluorescence effects on vegetation apparent reflectance: I. Leaf-level measurements and model simulation. Remote Sens. Environ. 2000, 74, 582–595. [Google Scholar] [CrossRef]
- Sakowska, K.; Alberti, G.; Genesio, L.; Peressotti, A.; Delle Vedove, G.; Gianelle, D.; Colombo, R.; Rodeghiero, M.; Panigada, C.; Juszczak, R. Leaf and canopy photosynthesis of a chlorophyll deficient soybean mutant. Plant Cell Environ. 2018, 41, 1427–1437. [Google Scholar] [CrossRef]
- Campbell, P.K.E.; Huemmrich, K.F.; Middleton, E.M.; Ward, L.A.; Julitta, T.; Daughtry, C.S.T.; Burkart, A.; Russ, A.L.; Kustas, W.P. Diurnal and Seasonal Variations in Chlorophyll Fluorescence Associated with Photosynthesis at Leaf and Canopy Scales. Remote Sens. 2019, 11, 488. [Google Scholar] [CrossRef]
- Vilfan, N.; van der Tol, C.; Verhoef, W. Estimating photosynthetic capacity from leaf reflectance and chlorophyll fluorescence by coupling radiative transfer to a model for photosynthesis. New Phytol. 2019, 223, 487–500. [Google Scholar] [CrossRef]
- Cendrero-Mateo, M.P.; Moran, M.S.; Papuga, S.A.; Thorp, K.; Alonso, L.; Moreno, J.; Ponce-Campos, G.; Rascher, U.; Wang, G. Plant chlorophyll fluorescence: Active and passive measurements at canopy and leaf scales with different nitrogen treatments. J. Exp. Bot. 2015, 67, 275–286. [Google Scholar] [CrossRef] [PubMed]
- Meroni, M.; Rossini, M.; Guanter, L.; Alonso, L.; Rascher, U.; Colombo, R.; Moreno, J. Remote sensing of solar-induced chlorophyll fluorescence: Review of methods and applications. Remote Sens. Environ. 2009, 113, 2037–2051. [Google Scholar] [CrossRef]
- Ustin, S.L.; Gitelson, A.A.; Jacquemoud, S.; Schaepman, M.; Asner, G.P.; Gamon, J.A.; Zarco-Tejada, P. Retrieval of foliar information about plant pigment systems from high resolution spectroscopy. Remote Sens. Environ. 2009, 113, S67–S77. [Google Scholar] [CrossRef]
- Süß, A.; Hank, T.; Mauser, W. Deriving diurnal variations in sun-induced chlorophyll-a fluorescence in winter wheat canopies and maize leaves from ground-based hyperspectral measurements. Int. J. Remote Sens. 2016, 37, 60–77. [Google Scholar] [CrossRef]
- Xu, S.; Liu, Z.; Zhao, L.; Zhao, H.; Ren, S. Diurnal Response of Sun-Induced Fluorescence and PRI to Water Stress in Maize Using a Near-Surface Remote Sensing Platform. Remote Sens. 2018, 10, 1510. [Google Scholar] [CrossRef]
- Sun, Y.; Frankenberg, C.; Wood, J.D.; Schimel, D.S.; Jung, M.; Guanter, L.; Drewry, D.; Verma, M.; Porcar-Castell, A.; Griffis, T.J. OCO-2 advances photosynthesis observation from space via solar-induced chlorophyll fluorescence. Science 2017, 358, eaam5747. [Google Scholar] [CrossRef]
- Guan, K.; Berry, J.A.; Zhang, Y.; Joiner, J.; Guanter, L.; Badgley, G.; Lobell, D.B. Improving the monitoring of crop productivity using spaceborne solar-induced fluorescence. Glob. Chang. Biol. 2016, 22, 716–726. [Google Scholar] [CrossRef]
- Wohlfahrt, G.; Gerdel, K.; Migliavacca, M.; Rotenberg, E.; Tatarinov, F.; Müller, J.; Hammerle, A.; Julitta, T.; Spielmann, F.M.; Yakir, D. Sun-induced fluorescence and gross primary productivity during a heat wave. Sci. Rep. 2018, 8, 14169. [Google Scholar] [CrossRef]
- Guanter, L.; Zhang, Y.G.; Jung, M.; Joiner, J.; Voigt, M.; Berry, J.A.; Frankenberg, C.; Huete, A.R.; Zarco-Tejada, P.; Lee, J.E.; et al. Global and time-resolved monitoring of crop photosynthesis with chlorophyll fluorescence. Proc. Natl. Acad. Sci. USA 2014, 111, E1327–E1333. [Google Scholar] [CrossRef]
- Liu, J.; Bowman, K.W.; Schimel, D.S.; Parazoo, N.C.; Jiang, Z.; Lee, M.; Bloom, A.A.; Wunch, D.; Frankenberg, C.; Sun, Y. Contrasting carbon cycle responses of the tropical continents to the 2015–2016 El Niño. Science 2017, 358, eaam5690. [Google Scholar] [CrossRef]
- Moreno, J.; Colombo, R.; Damm, A.; Goulas, Y.; Middleton, E.; Miglietta, F.; Mohammed, G.; Möttus, M.; North, P.; Rascher, U.; et al. Quantitative global mapping of terrestrial vegetation photosynthesis: The Fluorescence Explorer (FLEX) mission. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 435–438. [Google Scholar] [CrossRef]
- Yao, X.; Si, H.; Cheng, T.; Jia, M.; Chen, Q.; Tian, Y.; Zhu, Y.; Cao, W.; Chen, C.; Cai, J. Hyperspectral estimation of canopy leaf biomass phenotype per ground area using a continuous wavelet analysis in wheat. Front. Plant Sci. 2018, 9. [Google Scholar] [CrossRef] [PubMed]
- Din, M.; Zheng, W.; Rashid, M.; Wang, S.; Shi, Z. Evaluating hyperspectral vegetation indices for leaf area index estimation of Oryza sativa L. at diverse phenological stages. Front. Plant Sci. 2017, 8, 820. [Google Scholar] [CrossRef] [PubMed]
- Blackburn, G.A. Hyperspectral remote sensing of plant pigments. J. Exp. Bot. 2006, 58, 855–867. [Google Scholar] [CrossRef] [PubMed]
- Rossini, M.; Nedbal, L.; Guanter, L.; Ač, A.; Alonso, L.; Burkart, A.; Cogliati, S.; Colombo, R.; Damm, A.; Drusch, M. Red and far red Sun-induced chlorophyll fluorescence as a measure of plant photosynthesis. Geophys. Res. Lett. 2015, 42, 1632–1639. [Google Scholar] [CrossRef]
- Pinto, F.; Damm, A.; Schickling, A.; Panigada, C.; Cogliati, S.; Müller-Linow, M.; Balvora, A.; Rascher, U. Sun-induced chlorophyll fluorescence from high-resolution imaging spectroscopy data to quantify spatio-temporal patterns of photosynthetic function in crop canopies. Plant Cell Environ. 2016, 39, 1500–1512. [Google Scholar] [CrossRef]
- Gamon, J.A.; Peñuelas, J.; Field, C.B. A narrow-waveband spectral index that tracks diurnal changes in photosynthetic efficiency. Remote Sens. Environ. 1992, 41, 35–44. [Google Scholar] [CrossRef]
- Peñuelas, J.; Filella, I.; Gamon, J.A. Assessment of photosynthetic radiation-use efficiency with spectral reflectance. New Phytol. 1995, 131, 291–296. [Google Scholar] [CrossRef]
- Barton, C.V.M.; North, P.R.J. Remote sensing of canopy light use efficiency using the photochemical reflectance index: Model and sensitivity analysis. Remote Sens. Environ. 2001, 78, 264–273. [Google Scholar] [CrossRef]
- Soudani, K.; Hmimina, G.; Dufrêne, E.; Berveiller, D.; Delpierre, N.; Ourcival, J.M.; Rambal, S.; Joffre, R. Relationships between photochemical reflectance index and light-use efficiency in deciduous and evergreen broadleaf forests. Remote Sens. Environ. 2014, 144, 73–84. [Google Scholar] [CrossRef]
- Méthy, M. Analysis of Photosynthetic Activity at the Leaf and Canopy Levels from Reflectance Measurements: A Case Study. Photosynthetica 2000, 38, 505–512. [Google Scholar] [CrossRef]
- Van der Tol, C.; Berry, J.; Campbell, P.; Rascher, U. Models of fluorescence and photosynthesis for interpreting measurements of solar-induced chlorophyll fluorescence. J. Geophys. Res. Biogeosci. 2014, 119, 2312–2327. [Google Scholar] [PubMed]
- Earl, H.J.; Ennahli, S. Estimating photosynthetic electron transport via chlorophyll fluorometry without Photosystem II light saturation. Photosynth. Res. 2004, 82, 177–186. [Google Scholar] [CrossRef] [PubMed]
- Wise, R.R.; Sassenrath-Cole, G.F.; Percy, R.G. A Comparison of Leaf Anatomy in Field-grown Gossypium hirsutum and G. barbadense. Ann. Bot. 2000, 86, 731–738. [Google Scholar] [CrossRef]
- Whitaker, J. Cotton Irrigation, Defoliation, Contamination. 2016. Available online: https://extension.uga.edu/content/dam/extension-county-offices/webster-county/anr/Cotton%20Irrigation%2C%20Defoliation%2C%20and%20Contamination.pdf (accessed on 28 March 2019).
- Jiang, Y.; Li, C.; Robertson, J.S.; Sun, S.; Xu, R.; Paterson, A.H. Gphenovision: A ground mobile system with multi-modal imaging for field-based high throughput phenotyping of cotton. Sci. Rep. 2018, 8, 1213. [Google Scholar] [CrossRef] [PubMed]
- Plascyk, J.A. The MK II Fraunhofer line discriminator (FLD-II) for airborne and orbital remote sensing of solar-stimulated luminescence. Opt. Eng. 1975, 14, 144339. [Google Scholar] [CrossRef]
- Flexas, J.; Escalona, J.; Medrano, H. Down-regulation of photosynthesis by drought under field conditions in grapevine leaves. Funct. Plant Biol. 1998, 25, 893–900. [Google Scholar] [CrossRef]
- Yin, X.; Struik, P. C3 and C4 photosynthesis models: An overview from the perspective of crop modelling. NJAS-Wagening. J. Life Sci. 2009, 57, 27–38. [Google Scholar] [CrossRef]
- Flexas, J.; Badger, M.; Chow, W.S.; Medrano, H.; Osmond, C.B. Analysis of the relative increase in photosynthetic O2 uptake when photosynthesis in grapevine leaves is inhibited following low night temperatures and/or water stress. Plant Physiol. 1999, 121, 675–684. [Google Scholar] [CrossRef]
- Maxwell, K.; Johnson, G.N. Chlorophyll fluorescence—A practical guide. J. Exp. Bot. 2000, 51, 659–668. [Google Scholar] [CrossRef]
- White, A.J.; Critchley, C. Rapid light curves: A new fluorescence method to assess the state of the photosynthetic apparatus. Photosynth. Res. 1999, 59, 63–72. [Google Scholar] [CrossRef]
- Ralph, P.J.; Gademann, R. Rapid light curves: A powerful tool to assess photosynthetic activity. Aquat. Bot. 2005, 82, 222–237. [Google Scholar] [CrossRef]
- Ehleringer, J.R.; Hammond, S.D. Solar Tracking and Photosynthesis in Cotton Leaves. Agric. For. Meteorol. 1987, 39, 25–35. [Google Scholar] [CrossRef]
- R Development Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2008; ISBN 3-900051-07-0. [Google Scholar]
- Henley, W.J. Measurement and interpretation of photosynthetic light-response curves in algae in the context of photoinhibition and diel changes. J. Phycol. 1993, 29, 729–739. [Google Scholar] [CrossRef]
- Merlier, E.; Hmimina, G.; Dufrêne, E.; Soudani, K. Explaining the variability of the photochemical reflectance index (PRI) at the canopy-scale: Disentangling the effects of phenological and physiological changes. J. Photochem. Photobiol. B Biol. 2015, 151, 161–171. [Google Scholar] [CrossRef]
- Yang, X.; Tang, J.W.; Mustard, J.F.; Lee, J.E.; Rossini, M.; Joiner, J.; Munger, J.W.; Kornfeld, A.; Richardson, A.D. Solar-induced chlorophyll fluorescence that correlates with canopy photosynthesis on diurnal and seasonal scales in a temperate deciduous forest. Geophys. Res. Lett. 2015, 42, 2977–2987. [Google Scholar] [CrossRef]
- Liu, Z.J.; Wu, C.Y.; Peng, D.L.; Wang, S.S.; Gonsamo, A.; Fang, B.; Yuan, W.P. Improved modeling of gross primary production from a better representation of photosynthetic components in vegetation canopy. Agric. For. Meteorol. 2017, 233, 222–234. [Google Scholar] [CrossRef]
- Scholes, J.D.; Rolfe, S.A. Chlorophyll fluorescence imaging as tool for understanding the impact of fungal diseases on plant performance: A phenomics perspective. Funct. Plant Biol. 2009, 36, 880–892. [Google Scholar] [CrossRef]
- Atta, B.M.; Saleem, M.; Ali, H.; Arshad, H.M.I.; Ahmed, M. Chlorophyll as a biomarker for early disease diagnosis. Laser Phys. 2018, 28, 065607. [Google Scholar] [CrossRef]
- Cen, H.Y.; Weng, H.Y.; Yao, J.N.; He, M.B.; Lv, J.W.; Hua, S.J.; Li, H.Y.; He, Y. Chlorophyll Fluorescence Imaging Uncovers Photosynthetic Fingerprint of Citrus Huanglongbing. Front. Plant Sci. 2017, 8, 1509. [Google Scholar] [CrossRef]
- Corp, L.; Middleton, E.M.; Cheng, Y.B.; Campbell, P.E.; Huemmrich, K.F. Impact of spectral resolution on solar induced fluorescence and reflectance indices for monitoring vegetation. In Proceedings of the IGARSS 2008–2008 IEEE International Geoscience and Remote Sensing Symposium, Boston, MA, USA, 6–11 July 2008; Volume 4, pp. 1387–1390. [Google Scholar]
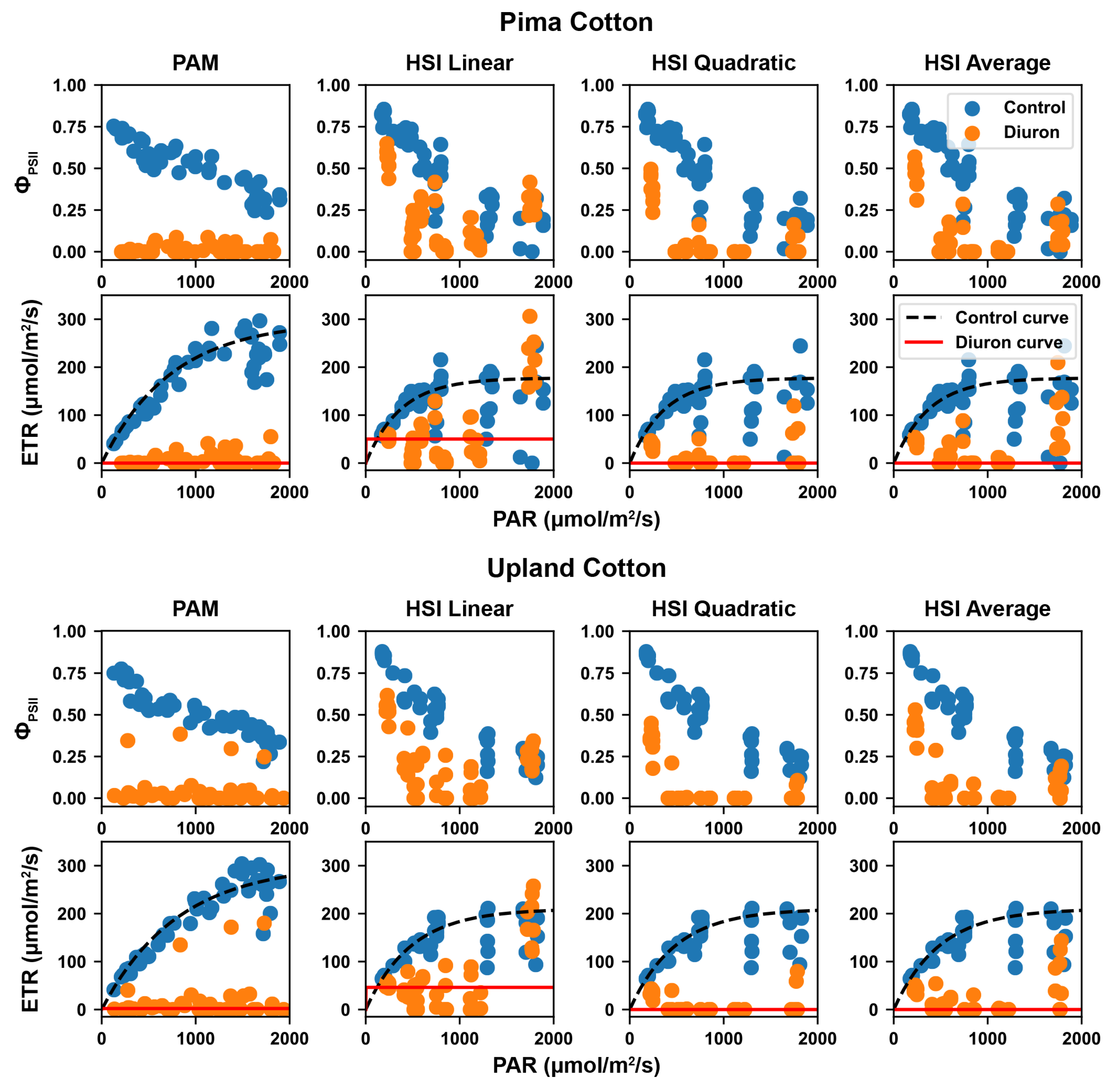
| Method | Cultivar | Treatment | mETR | R2 | ||
|---|---|---|---|---|---|---|
| PAM | Pima | Control | 296.70 | 0.3989 | 743.73 | 0.94 |
| PAM | Pima | Diuron | 0.00 | 0.5000 | 0.00 | |
| PAM | Upland | Control | 303.90 | 0.3771 | 805.98 | 0.99 |
| PAM | Upland | Diuron | 2.12 | 0.5000 | 4.24 | |
| HSI_Linear | Pima | Control | 177.51 | 0.4780 | 371.33 | 0.92 |
| HSI_Linear | Pima | Diuron | 50.13 | 77.0580 | 0.65 | |
| HSI_Linear | Upland | Control | 210.07 | 0.4348 | 483.13 | 0.99 |
| HSI_Linear | Upland | Diuron | 46.19 | 93.9418 | 0.49 | |
| HSI_Quadratic | Pima | Control | 177.51 | 0.4780 | 371.33 | 0.92 |
| HSI_Quadratic | Pima | Diuron | 0.00 | 0.5000 | 0.00 | |
| HSI_Quadratic | Upland | Control | 210.07 | 0.4348 | 483.13 | 0.99 |
| HSI_Quadratic | Upland | Diuron | 0.00 | 0.5000 | 0.00 | |
| HSI_Avg | Pima | Control | 177.51 | 0.4780 | 371.33 | 0.92 |
| HSI_Avg | Pima | Diuron | 0.00 | 95.0250 | 0.00 | |
| HSI_Avg | Upland | Control | 210.07 | 0.4348 | 483.13 | 0.99 |
| HSI_Avg | Upland | Diuron | 0.00 | 0.5000 | 0.00 |
| Trait | Cultivar | Treatment | Interaction between Cultivar and Treatment |
|---|---|---|---|
| CGR | 0.1568 | 0.0001 | 0.8406 |
| NAR | 0.1229 | 0.0002 | 0.3513 |
| RGR | 0.0128 | 0 | 0.2899 |
| 0.1801 | 0.0018 | 0.3906 | |
| 0.9069 | 0.0008 | 0.006 | |
| 0.0792 | 0 | 0.65 | |
| 0.2661 | 0 | 0.0237 | |
| 0.0864 | 0 | 0.0411 | |
| 0.1663 | 0 | 0.0241 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, Y.; Snider, J.L.; Li, C.; Rains, G.C.; Paterson, A.H. Ground Based Hyperspectral Imaging to Characterize Canopy-Level Photosynthetic Activities. Remote Sens. 2020, 12, 315. https://doi.org/10.3390/rs12020315
Jiang Y, Snider JL, Li C, Rains GC, Paterson AH. Ground Based Hyperspectral Imaging to Characterize Canopy-Level Photosynthetic Activities. Remote Sensing. 2020; 12(2):315. https://doi.org/10.3390/rs12020315
Chicago/Turabian StyleJiang, Yu, John L. Snider, Changying Li, Glen C. Rains, and Andrew H. Paterson. 2020. "Ground Based Hyperspectral Imaging to Characterize Canopy-Level Photosynthetic Activities" Remote Sensing 12, no. 2: 315. https://doi.org/10.3390/rs12020315
APA StyleJiang, Y., Snider, J. L., Li, C., Rains, G. C., & Paterson, A. H. (2020). Ground Based Hyperspectral Imaging to Characterize Canopy-Level Photosynthetic Activities. Remote Sensing, 12(2), 315. https://doi.org/10.3390/rs12020315