Sentinel-2 Sharpening via Parallel Residual Network
Abstract
1. Introduction
- We propose a Sentinel-2 sharpening method to raise the spatial resolution of both 20 m and 60 m bands with the help of 10 m bands, which can produce the HR image with all bands at 10 m resolution.
- We develop a parallel network structure for extracting feature from different resolution bands by separate branches. This idea enables to improve the spatial resolution of LR bands while keeping spectral fidelity simultaneously.
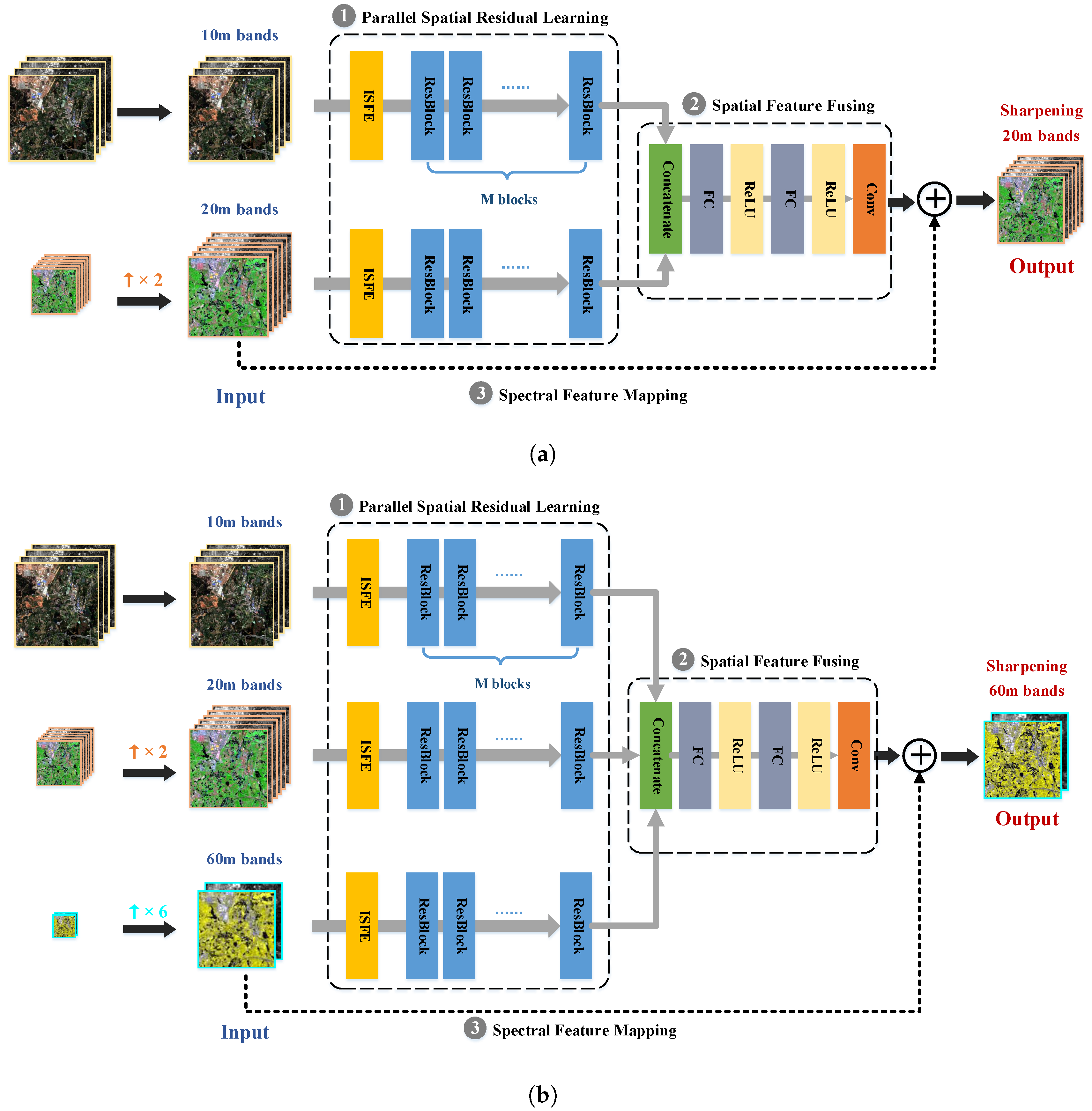
2. Proposed Method
2.1. Network Architecture
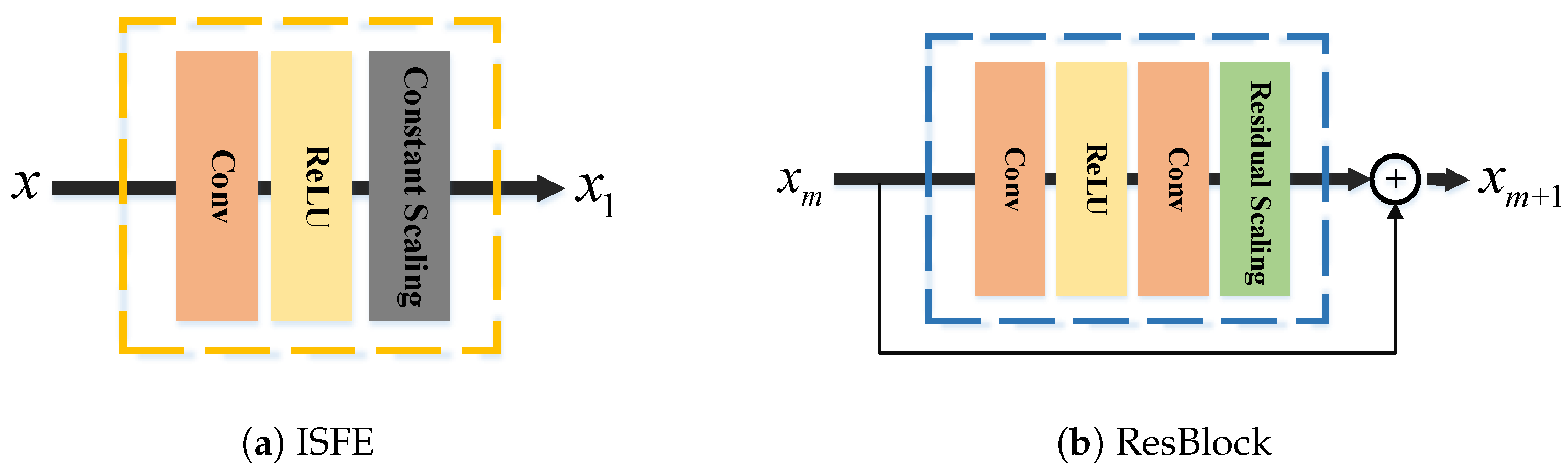
2.2. Parallel Spatial Residual Learning
2.3. Spatial Feature Fusing
2.4. Spectral Feature Mapping
2.5. Training and Applying
3. Experiments
3.1. Data
3.2. Experimental Details
3.3. Baselines and Quantitative Evaluation Metrics
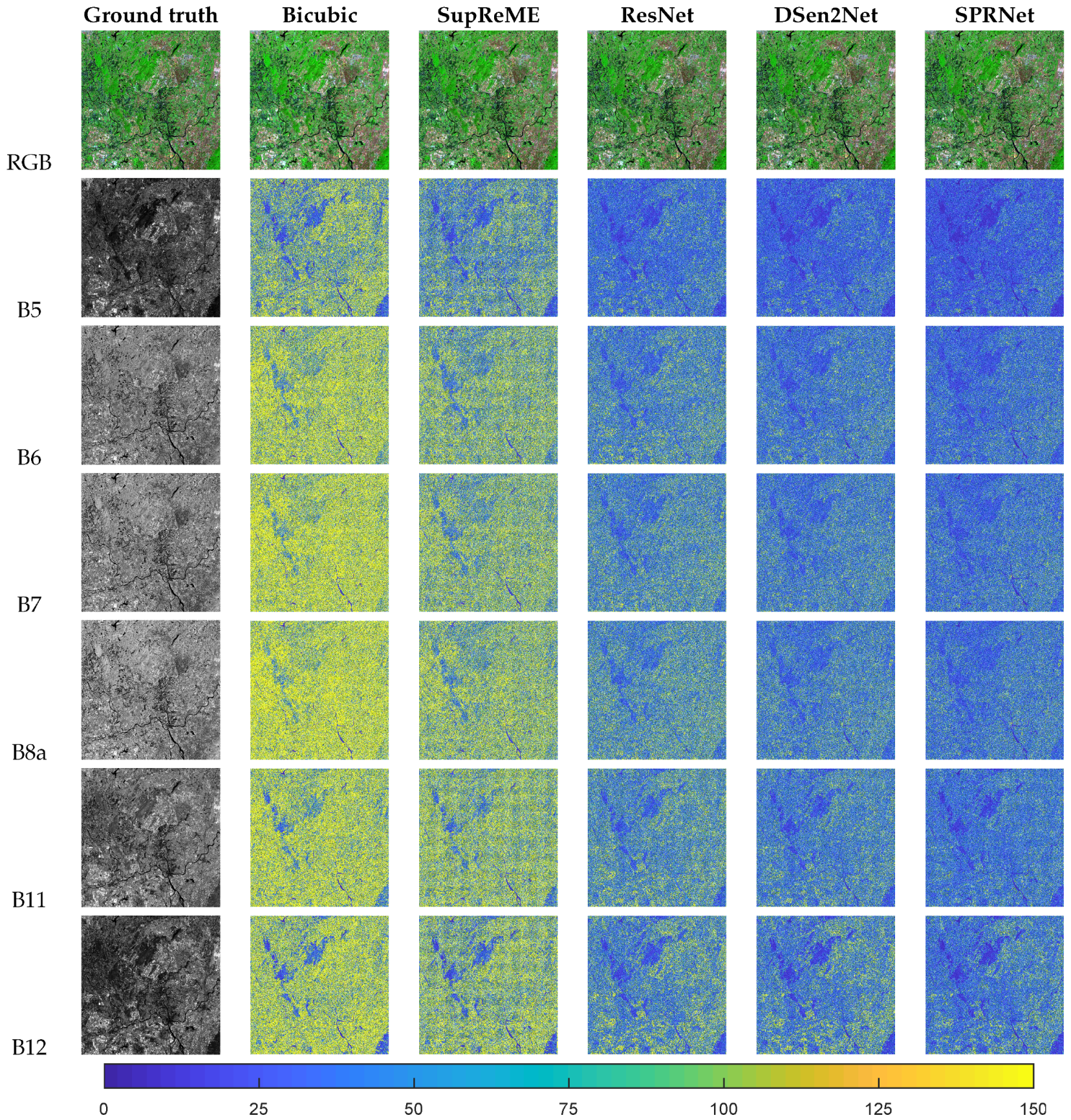
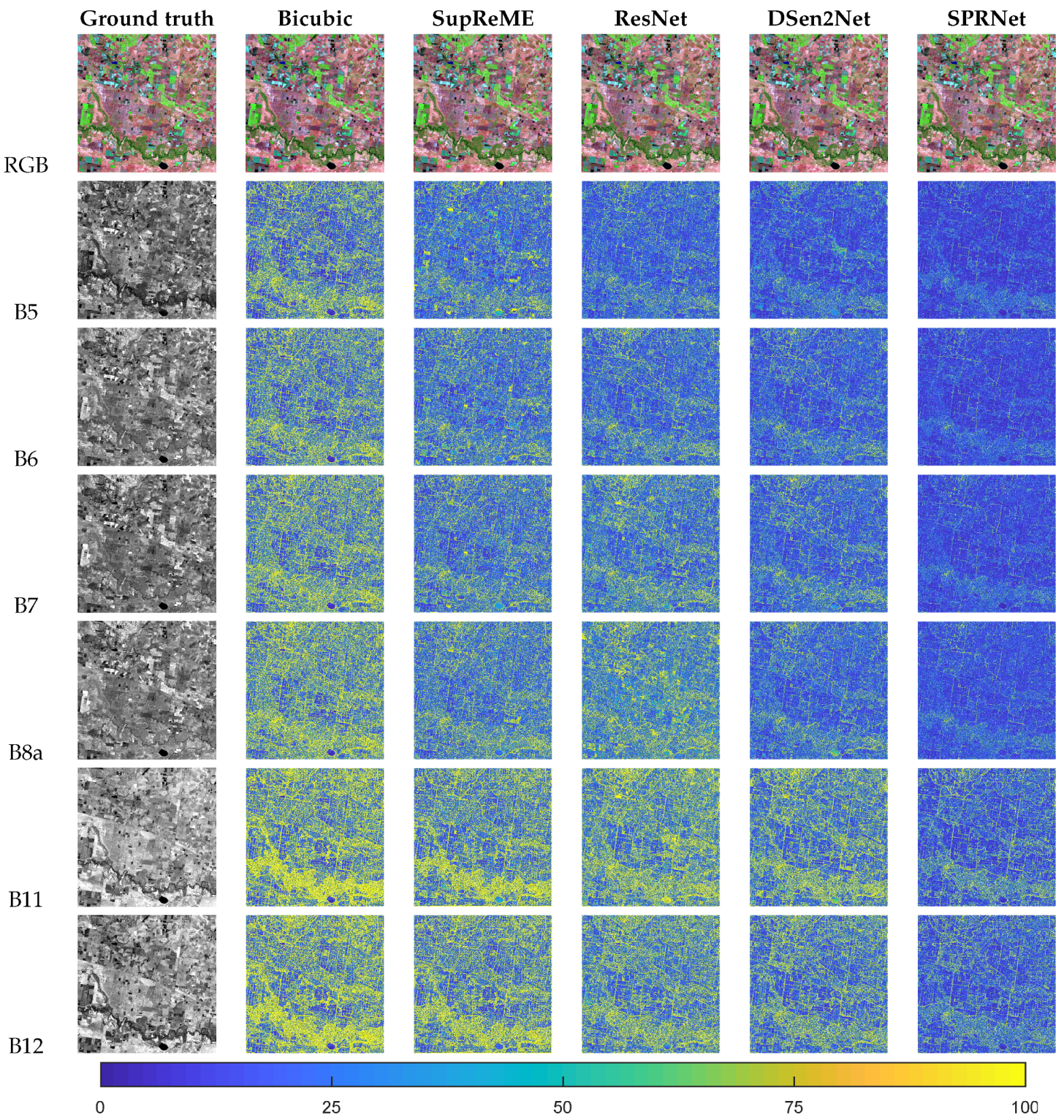
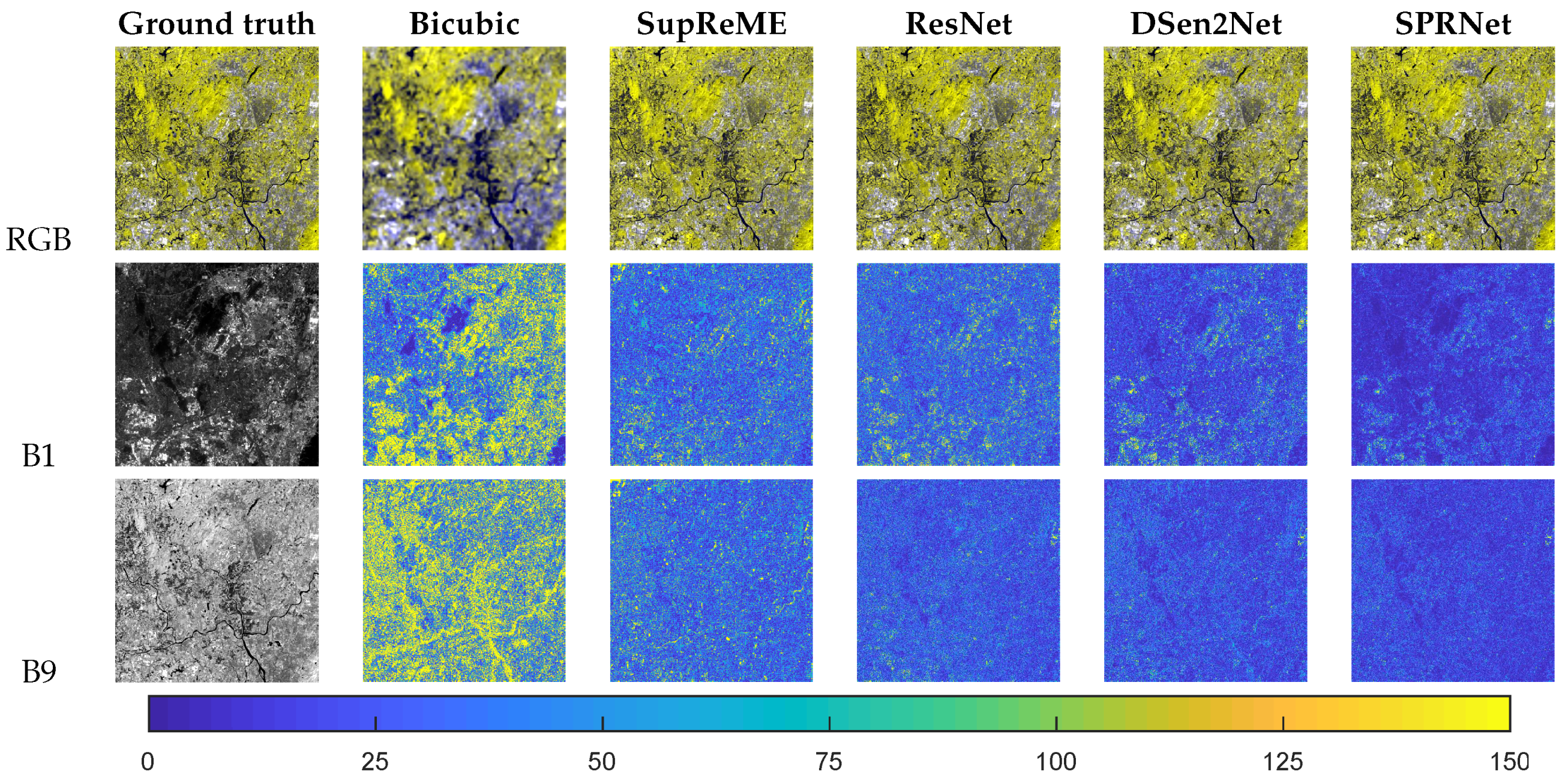
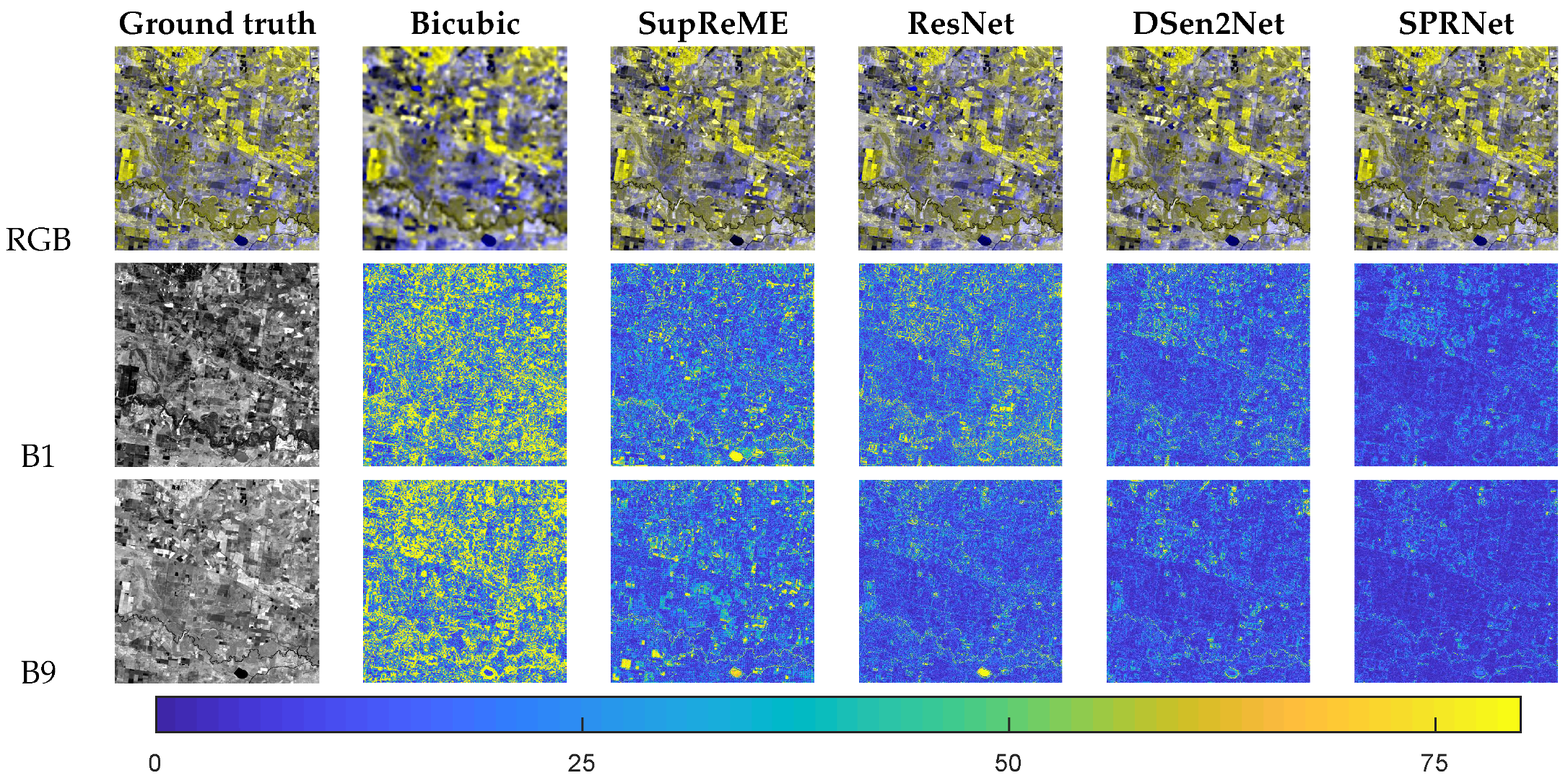
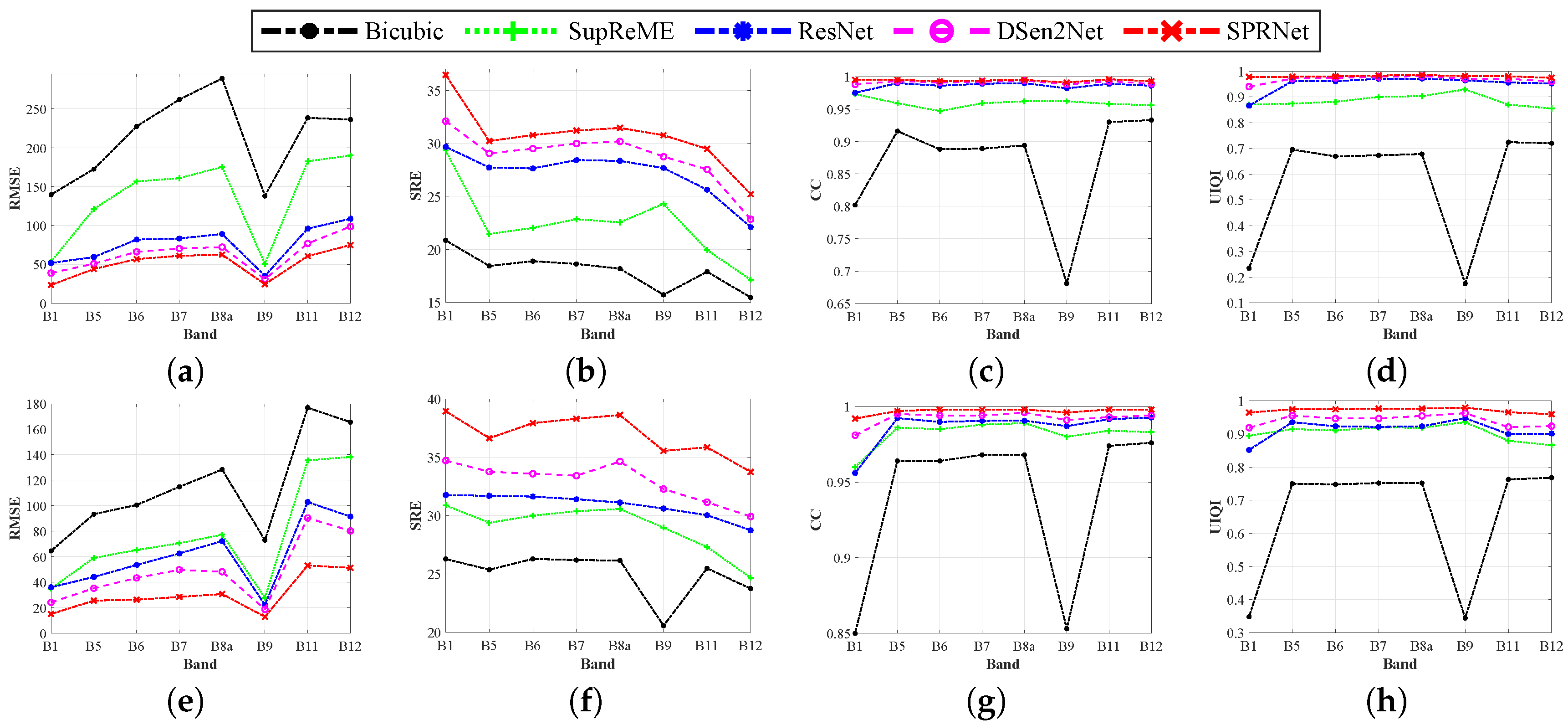
3.4. Experimental Results
3.4.1. Evaluation at Lower Scale
3.4.2. Evaluation at the Original Scale
4. Discussions
4.1. Effect of Combining Various-Resolution Bands
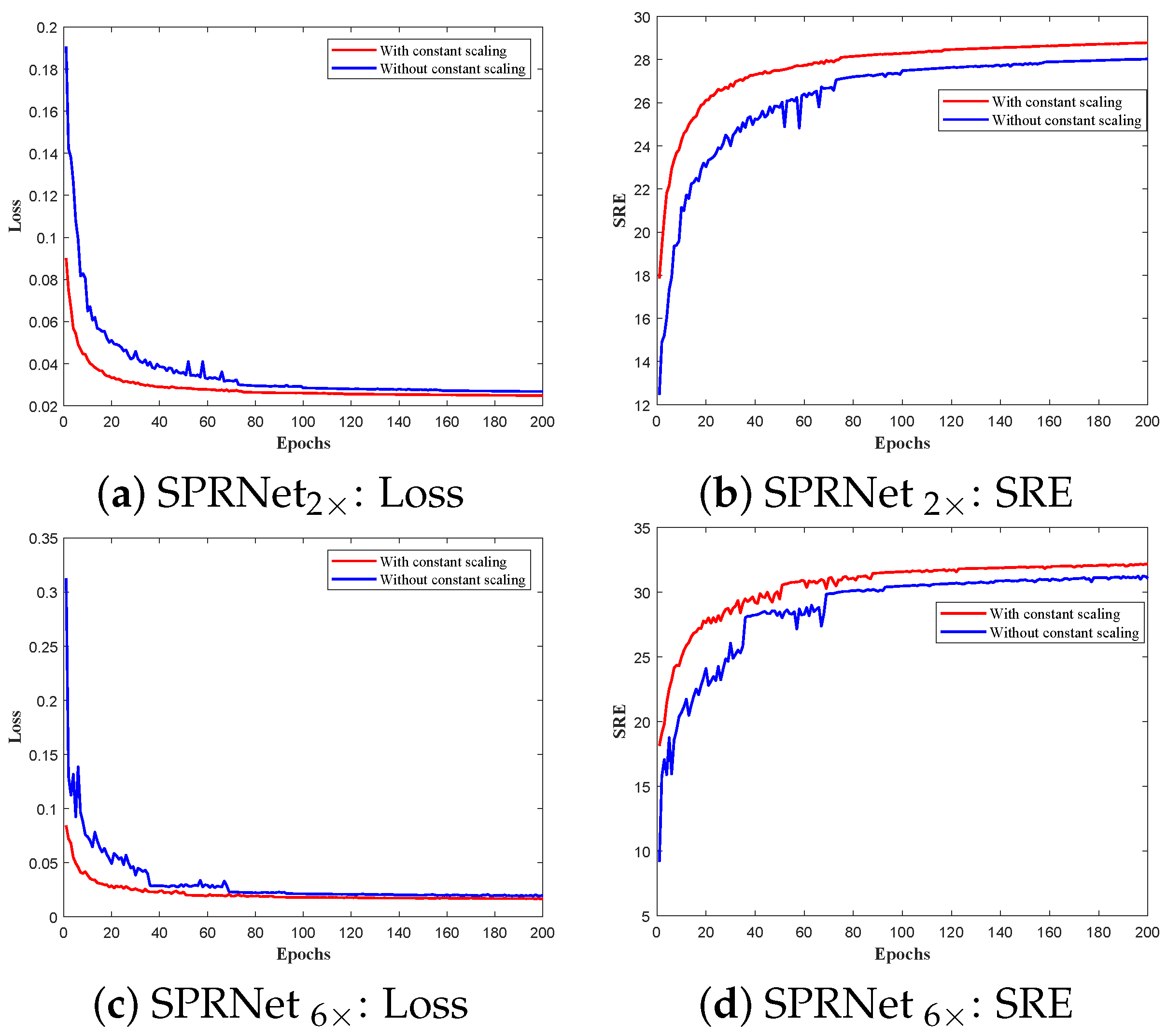
4.2. Effect of Constant Scaling in ISFE
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Schmitt, M.; Hughes, L.H.; Zhu, X.X. The SEN1-2 Dataset for Deep Learning in SAR-Optical Data Fusion. arXiv 2018, arXiv:1807.01569. [Google Scholar] [CrossRef]
- Frampton, W.J.; Dash, J.; Watmough, G.; Milton, E.J. Evaluating the capabilities of Sentinel-2 for quantitative estimation of biophysical variables in vegetation. ISPRS J. Photogramm. Remote Sens. 2013, 82, 83–92. [Google Scholar] [CrossRef]
- Castillo, J.A.A.; Apan, A.A.; Maraseni, T.N.; Salmo, S.G., III. Estimation and mapping of above-ground biomass of mangrove forests and their replacement land uses in the Philippines using Sentinel imagery. ISPRS J. Photogramm. Remote Sens. 2017, 134, 70–85. [Google Scholar] [CrossRef]
- Delloye, C.; Weiss, M.; Defourny, P. Retrieval of the canopy chlorophyll content from Sentinel-2 spectral bands to estimate nitrogen uptake in intensive winter wheat cropping systems. Remote Sens. Environ. 2018, 216, 245–261. [Google Scholar] [CrossRef]
- Mura, M.; Bottalico, F.; Giannetti, F.; Bertani, R.; Giannini, R.; Mancini, M.; Orlandini, S.; Travaglini, D.; Chirici, G. Exploiting the capabilities of the Sentinel-2 multi spectral instrument for predicting growing stock volume in forest ecosystems. Int. J. Appl. Earth Obs. Geoinf. 2018, 66, 126–134. [Google Scholar] [CrossRef]
- Vrabel, J. Multispectral imagery band sharpening study. Photogramm. Eng. Remote Sens. 1996, 62, 1075–1084. [Google Scholar]
- Matteoli, S.; Diani, M.; Corsini, G. Automatic target recognition within anomalous regions of interest in hyperspectral images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 1056–1069. [Google Scholar] [CrossRef]
- Murray, N.J.; Keith, D.A.; Simpson, D.; Wilshire, J.H.; Lucas, R.M. REMAP: An online remote sensing application for land cover classification and monitoring. Methods. Ecol. Evol. 2018, 9, 2019–2027. [Google Scholar] [CrossRef]
- Liu, Z.; Li, G.; Mercier, G.; He, Y.; Pan, Q. Change detection in heterogenous remote sensing images via homogeneous pixel transformation. IEEE Trans. Image Process. 2017, 27, 1822–1834. [Google Scholar] [CrossRef]
- Sirguey, P.; Mathieu, R.; Arnaud, Y.; Khan, M.M.; Chanussot, J. Improving MODIS spatial resolution for snow mapping using wavelet fusion and ARSIS concept. IEEE Geosci. Remote Sens. Lett. 2008, 5, 78–82. [Google Scholar] [CrossRef]
- Aiazzi, B.; Alparone, L.; Baronti, S.; Santurri, L.; Selva, M. Spatial resolution enhancement of ASTER thermal bands. In Image Signal Processing Remote Sensing XI; International Society for Optics and Photonics: Bellingham, WA, USA, 2005; Volume 5982, p. 59821G. [Google Scholar]
- Maglione, P.; Parente, C.; Vallario, A. Pan-sharpening Worldview-2: IHS, Brovey and Zhang methods in comparison. Int. J. Eng. Technol 2016, 8, 673–679. [Google Scholar]
- Picaro, G.; Addesso, P.; Restaino, R.; Vivone, G.; Picone, D.; Dalla Mura, M. Thermal sharpening of VIIRS data. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 7260–7263. [Google Scholar]
- Carper, W.; Lillesand, T.; Kiefer, R. The use of intensity-hue-saturation transformations for merging SPOT panchromatic and multispectral image data. Photogramm. Eng. Remote Sens. 1990, 56, 459–467. [Google Scholar]
- Aiazzi, B.; Baronti, S.; Selva, M. Improving component substitution pansharpening through multivariate regression of MS + Pan data. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3230–3239. [Google Scholar] [CrossRef]
- Shensa, M.J. The discrete wavelet transform: Wedding the à trous and Mallat algorithms. IEEE Trans. Signal Process. 1992, 40, 2464–2482. [Google Scholar] [CrossRef]
- Wang, Q.; Shi, W.; Li, Z.; Atkinson, P.M. Fusion of Sentinel-2 images. Remote Sens. Environ. 2016, 187, 241–252. [Google Scholar] [CrossRef]
- Vaiopoulos, A.; Karantzalos, K. Pansharpening on the narrow VNIR and SWIR spectral bands of Sentinel-2. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 41, 723. [Google Scholar] [CrossRef]
- Park, H.; Choi, J.; Park, N.; Choi, S. Sharpening the VNIR and SWIR bands of Sentinel-2A imagery through modified selected and synthesized band schemes. Remote Sens. 2017, 9, 1080. [Google Scholar] [CrossRef]
- Kaplan, G. Sentinel-2 Pan Sharpening-Comparative Analysis. MDPI Proc. 2018, 2, 345. [Google Scholar] [CrossRef]
- Du, Y.; Zhang, Y.; Ling, F.; Wang, Q.; Li, W.; Li, X. Water bodies’ mapping from Sentinel-2 imagery with modified normalized difference water index at 10-m spatial resolution produced by sharpening the SWIR band. Remote Sens. 2016, 8, 354. [Google Scholar] [CrossRef]
- Gašparović, M.; Jogun, T. The effect of fusing Sentinel-2 bands on land-cover classification. Int. J. Remote Sens. 2018, 39, 822–841. [Google Scholar] [CrossRef]
- Lanaras, C.; Bioucas-Dias, J.; Galliani, S.; Baltsavias, E.; Schindler, K. Super-resolution of Sentinel-2 images: Learning a globally applicable deep neural network. ISPRS J. Photogramm. Remote Sens. 2018, 146, 305–319. [Google Scholar] [CrossRef]
- Simões, M.; Bioucas-Dias, J.; Almeida, L.B.; Chanussot, J. A convex formulation for hyperspectral image superresolution via subspace-based regularization. IEEE Trans. Geosci. Remote Sens. 2014, 53, 3373–3388. [Google Scholar] [CrossRef]
- Khademi, G.; Ghassemian, H. Incorporating an adaptive image prior model into Bayesian fusion of multispectral and panchromatic images. IEEE Geosci. Remote Sens. Lett. 2018, 15, 917–921. [Google Scholar] [CrossRef]
- Cheng, M.; Wang, C.; Li, J. Sparse representation based pansharpening using trained dictionary. IEEE Geosci. Remote Sens. Lett. 2013, 11, 293–297. [Google Scholar] [CrossRef]
- Lanaras, C.; Bioucas-Dias, J.; Baltsavias, E.; Schindler, K. Super-resolution of multispectral multiresolution images from a single sensor. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Honolulu, HI, USA, 21–26 July 2017; pp. 20–28. [Google Scholar]
- Ulfarsson, M.O.; Dalla Mura, M. A low-rank method for sentinel-2 sharpening using cyclic descent. In Proceedings of the IGARSS 2018–2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 8857–8860. [Google Scholar]
- Paris, C.; Bioucas-Dias, J.; Bruzzone, L. A hierarchical approach to superresolution of multispectral images with different spatial resolutions. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 2589–2592. [Google Scholar]
- Brodu, N. Super-resolving multiresolution images with band-independent geometry of multispectral pixels. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4610–4617. [Google Scholar] [CrossRef]
- Ulfarsson, M.O.; Palsson, F.; Dalla Mura, M.; Sveinsson, J.R. Sentinel-2 Sharpening Using a Reduced-Rank Method. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6408–6420. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436. [Google Scholar] [CrossRef]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Learning a deep convolutional network for image super-resolution. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; pp. 184–199. [Google Scholar]
- Masi, G.; Cozzolino, D.; Verdoliva, L.; Scarpa, G. Pansharpening by convolutional neural networks. Remote Sens. 2016, 8, 594. [Google Scholar] [CrossRef]
- Palsson, F.; Sveinsson, J.R.; Ulfarsson, M.O. Multispectral and hyperspectral image fusion using a 3-D-convolutional neural network. IEEE Geosci. Remote Sens. Lett. 2017, 14, 639–643. [Google Scholar] [CrossRef]
- Yang, J.; Zhao, Y.Q.; Chan, J. Hyperspectral and multispectral image fusion via deep two-branches convolutional neural network. Remote Sens. 2018, 10, 800. [Google Scholar] [CrossRef]
- Huang, W.; Xiao, L.; Wei, Z.; Liu, H.; Tang, S. A new pan-sharpening method with deep neural networks. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1037–1041. [Google Scholar] [CrossRef]
- Yang, J.; Fu, X.; Hu, Y.; Huang, Y.; Ding, X.; Paisley, J. PanNet: A deep network architecture for pan-sharpening. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 5449–5457. [Google Scholar]
- Yuan, Q.; Wei, Y.; Meng, X.; Shen, H.; Zhang, L. A multiscale and multidepth convolutional neural network for remote sensing imagery pan-sharpening. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 978–989. [Google Scholar] [CrossRef]
- Gargiulo, M.; Mazza, A.; Gaetano, R.; Ruello, G.; Scarpa, G. A CNN-based fusion method for super-resolution of sentinel-2 data. In Proceedings of the IGARSS 2018-2018 IEEE International Geoscience and Remote Sensing Symposium, Seoul, Korea, 25–29 July 2018; pp. 4713–4716. [Google Scholar]
- Gargiulo, M.; Mazza, A.; Gaetano, R.; Ruello, G.; Scarpa, G. Fast Super-Resolution of 20 m Sentinel-2 Bands Using Convolutional Neural Networks. Remote Sens. 2019, 11, 2635. [Google Scholar] [CrossRef]
- Palsson, F.; Sveinsson, J.; Ulfarsson, M. Sentinel-2 image fusion using a deep residual network. Remote Sens. 2018, 10, 1290. [Google Scholar] [CrossRef]
- Lim, B.; Son, S.; Kim, H.; Nah, S.; Mu Lee, K. Enhanced deep residual networks for single image super-resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Honolulu, HI, USA, 21 July 2017; pp. 136–144. [Google Scholar]
- Loncan, L.; De Almeida, L.B.; Bioucas-Dias, J.M.; Briottet, X.; Chanussot, J.; Dobigeon, N.; Fabre, S.; Liao, W.; Licciardi, G.A.; Simoes, M.; et al. Hyperspectral pansharpening: A review. IEEE Geosci. Remote Sens. Mag. 2015, 3, 27–46. [Google Scholar] [CrossRef]
- Drusch, M.; Del Bello, U.; Carlier, S.; Colin, O.; Fernandez, V.; Gascon, F.; Hoersch, B.; Isola, C.; Laberinti, P.; Martimort, P.; et al. Sentinel-2: ESA’s optical high-resolution mission for GMES operational services. Remote Sens. Environ. 2012, 120, 25–36. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Dozat, T. Incorporating Nesterov Momentum into Adam. 2016. Available online: https://openreview.net/pdf?id=OM0jvwB8jIp57ZJjtNEZ (accessed on 6 February 2018).
- Yuan, Y.; Zheng, X.; Lu, X. Hyperspectral image superresolution by transfer learning. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 1963–1974. [Google Scholar] [CrossRef]




| Resolution | 10 m | 20 m | 60 m | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Band index | B2 | B3 | B4 | B8 | B5 | B6 | B7 | B8a | B11 | B12 | B1 | B9 | B10 |
| Center Wavelength (nm) | 490 | 560 | 665 | 842 | 705 | 740 | 783 | 865 | 1610 | 2190 | 443 | 945 | 1375 |
| Ideal | Band | Bicubic | SupReME | ResNet | DSen2Net | SPRNet | |
|---|---|---|---|---|---|---|---|
| RMSE | 0 | B5 | 172.571 | 121.093 | 59.363 | 50.719 | 44.007 |
| B6 | 227.449 | 156.636 | 81.834 | 66.152 | 56.708 | ||
| B7 | 262.031 | 160.877 | 83.242 | 70.331 | 60.983 | ||
| B8a | 289.247 | 175.351 | 89.080 | 72.175 | 62.439 | ||
| B11 | 238.489 | 182.597 | 95.896 | 76.858 | 60.541 | ||
| B12 | 236.283 | 189.993 | 108.664 | 98.661 | 74.780 | ||
| Mean | 237.678 | 164.424 | 86.347 | 72.483 | 59.910 | ||
| SRE (dB) | ∞ | B5 | 18.443 | 21.454 | 27.716 | 29.051 | 30.213 |
| B6 | 18.899 | 22.034 | 27.632 | 29.501 | 30.776 | ||
| B7 | 18.634 | 22.852 | 28.425 | 29.980 | 31.199 | ||
| B8a | 18.187 | 22.550 | 28.343 | 30.177 | 31.451 | ||
| B11 | 17.899 | 19.943 | 25.623 | 27.541 | 29.475 | ||
| B12 | 15.483 | 17.152 | 22.118 | 22.847 | 25.212 | ||
| Mean | 17.924 | 20.998 | 26.643 | 28.183 | 29.721 | ||
| CC | 1 | B5 | 0.916 | 0.959 | 0.990 | 0.993 | 0.995 |
| B6 | 0.888 | 0.947 | 0.986 | 0.991 | 0.993 | ||
| B7 | 0.889 | 0.959 | 0.989 | 0.992 | 0.994 | ||
| B8a | 0.894 | 0.962 | 0.990 | 0.994 | 0.995 | ||
| B11 | 0.930 | 0.958 | 0.989 | 0.993 | 0.996 | ||
| B12 | 0.933 | 0.956 | 0.986 | 0.989 | 0.993 | ||
| Mean | 0.908 | 0.957 | 0.988 | 0.992 | 0.994 | ||
| UIQI | 1 | B5 | 0.695 | 0.874 | 0.961 | 0.971 | 0.978 |
| B6 | 0.669 | 0.881 | 0.961 | 0.974 | 0.980 | ||
| B7 | 0.673 | 0.900 | 0.970 | 0.978 | 0.983 | ||
| B8a | 0.678 | 0.903 | 0.971 | 0.981 | 0.985 | ||
| B11 | 0.724 | 0.870 | 0.956 | 0.970 | 0.980 | ||
| B12 | 0.720 | 0.855 | 0.952 | 0.960 | 0.974 | ||
| Mean | 0.693 | 0.881 | 0.962 | 0.972 | 0.980 | ||
| ERGAS | 0 | 2.262 | 1.636 | 0.879 | 0.756 | 0.606 | |
| SAM | 0 | 2.845 | 2.347 | 2.006 | 1.666 | 1.384 |
| Ideal | Band | Bicubic | SupReME | ResNet | DSen2Net | SPRNet | |
|---|---|---|---|---|---|---|---|
| RMSE | 0 | B5 | 93.332 | 58.979 | 44.042 | 35.161 | 25.443 |
| B6 | 100.533 | 65.210 | 53.416 | 43.207 | 26.161 | ||
| B7 | 114.797 | 70.440 | 62.458 | 49.627 | 28.337 | ||
| B8a | 128.315 | 77.231 | 72.154 | 48.098 | 30.561 | ||
| B11 | 176.907 | 135.533 | 102.824 | 90.342 | 53.017 | ||
| B12 | 165.544 | 138.220 | 91.405 | 80.193 | 51.161 | ||
| Mean | 129.905 | 90.935 | 71.050 | 57.771 | 35.780 | ||
| SRE (dB) | ∞ | B5 | 25.366 | 29.386 | 31.694 | 33.761 | 36.636 |
| B6 | 26.286 | 29.999 | 31.630 | 33.584 | 37.922 | ||
| B7 | 26.190 | 30.376 | 31.403 | 33.417 | 38.295 | ||
| B8a | 26.151 | 30.564 | 31.116 | 34.635 | 38.612 | ||
| B11 | 25.477 | 27.309 | 30.034 | 31.145 | 35.849 | ||
| B12 | 23.752 | 24.680 | 28.745 | 29.918 | 33.740 | ||
| Mean | 25.537 | 28.719 | 30.770 | 32.744 | 36.842 | ||
| CC | 1 | B5 | 0.964 | 0.986 | 0.992 | 0.995 | 0.997 |
| B6 | 0.964 | 0.985 | 0.990 | 0.994 | 0.998 | ||
| B7 | 0.968 | 0.988 | 0.991 | 0.994 | 0.998 | ||
| B8a | 0.968 | 0.989 | 0.991 | 0.996 | 0.998 | ||
| B11 | 0.974 | 0.984 | 0.992 | 0.993 | 0.998 | ||
| B12 | 0.976 | 0.983 | 0.993 | 0.994 | 0.998 | ||
| Mean | 0.969 | 0.986 | 0.991 | 0.994 | 0.998 | ||
| UIQI | 1 | B5 | 0.750 | 0.915 | 0.936 | 0.956 | 0.975 |
| B6 | 0.748 | 0.911 | 0.924 | 0.947 | 0.975 | ||
| B7 | 0.752 | 0.920 | 0.922 | 0.947 | 0.977 | ||
| B8a | 0.752 | 0.919 | 0.924 | 0.955 | 0.977 | ||
| B11 | 0.763 | 0.880 | 0.900 | 0.921 | 0.966 | ||
| B12 | 0.768 | 0.866 | 0.901 | 0.924 | 0.960 | ||
| Mean | 0.755 | 0.902 | 0.918 | 0.942 | 0.972 | ||
| ERGAS | 0 | 0.893 | 0.637 | 0.486 | 0.398 | 0.249 | |
| SAM | 0 | 1.173 | 1.071 | 1.239 | 0.945 | 0.586 |
| Ideal | Band | Bicubic | SupReME | ResNet | DSen2Net | SPRNet | |
|---|---|---|---|---|---|---|---|
| RMSE | 0 | B1 | 139.703 | 53.456 | 51.702 | 38.833 | 23.473 |
| B9 | 137.938 | 50.511 | 35.213 | 30.847 | 24.437 | ||
| Mean | 138.821 | 51.984 | 43.457 | 34.840 | 23.955 | ||
| SRE (dB) | ∞ | B1 | 20.855 | 29.319 | 29.674 | 32.086 | 36.446 |
| B9 | 15.728 | 24.300 | 27.672 | 28.746 | 30.762 | ||
| Mean | 18.292 | 26.810 | 28.673 | 30.416 | 33.604 | ||
| CC | 1 | B1 | 0.802 | 0.973 | 0.975 | 0.988 | 0.995 |
| B9 | 0.681 | 0.962 | 0.982 | 0.988 | 0.991 | ||
| Mean | 0.742 | 0.968 | 0.979 | 0.988 | 0.993 | ||
| UIQI | 1 | B1 | 0.234 | 0.870 | 0.866 | 0.940 | 0.978 |
| B9 | 0.175 | 0.929 | 0.964 | 0.971 | 0.981 | ||
| Mean | 0.205 | 0.900 | 0.915 | 0.955 | 0.980 | ||
| ERGAS | 0 | 2.167 | 0.807 | 0.622 | 0.515 | 0.381 | |
| SAM | 0 | 3.039 | 1.228 | 0.937 | 0.704 | 0.542 |
| Ideal | Band | Bicubic | SupReME | ResNet | DSen2Net | SPRNet | |
|---|---|---|---|---|---|---|---|
| RMSE | 0 | B1 | 64.444 | 34.835 | 35.902 | 24.026 | 14.919 |
| B9 | 72.906 | 27.764 | 22.113 | 18.561 | 12.750 | ||
| Mean | 68.675 | 31.299 | 29.007 | 21.293 | 13.835 | ||
| SRE (dB) | ∞ | B1 | 26.281 | 30.884 | 31.758 | 34.707 | 38.938 |
| B9 | 20.569 | 28.971 | 30.608 | 32.268 | 35.546 | ||
| Mean | 23.425 | 29.928 | 31.183 | 33.488 | 37.242 | ||
| CC | 1 | B1 | 0.850 | 0.960 | 0.956 | 0.981 | 0.992 |
| B9 | 0.853 | 0.980 | 0.987 | 0.991 | 0.996 | ||
| Mean | 0.852 | 0.970 | 0.971 | 0.986 | 0.994 | ||
| UIQI | 1 | B1 | 0.348 | 0.895 | 0.852 | 0.919 | 0.965 |
| B9 | 0.344 | 0.936 | 0.948 | 0.963 | 0.980 | ||
| Mean | 0.346 | 0.916 | 0.900 | 0.941 | 0.972 | ||
| ERGAS | 0 | 1.203 | 0.503 | 0.442 | 0.341 | 0.227 | |
| SAM | 0 | 1.521 | 0.728 | 0.659 | 0.504 | 0.342 |
| Model | SPRNet | SPRNet | ||||
|---|---|---|---|---|---|---|
| SPRNet-1 | SPRNet-2 | SPRNet-3 | SPRNet-1 | SPRNet-2 | SPRNet-3 | |
| 10 m | ✗ | ✓ | ✓ | ✗ | ✓ | ✓ |
| 20 m | ✓ | ✓ | ✓ | ✗ | ✗ | ✓ |
| 60 m | ✗ | ✗ | ✓ | ✓ | ✓ | ✓ |
| RMSE | 144.934/85.833 | 59.910/35.780 | 67.260/40.917 | 131.115/62.107 | 27.021/17.578 | 23.955/13.835 |
| SRE | 21.939/28.895 | 29.721/36.842 | 28.810/36.074 | 18.772/24.220 | 32.616/35.155 | 33.604/37.242 |
| CC | 0.965/0.986 | 0.994/0.998 | 0.993/0.997 | 0.772/0.875 | 0.991/0.990 | 0.993/0.994 |
| UIQI | 0.889/0.878 | 0.980/0.972 | 0.976/0.964 | 0.299/0.444 | 0.973/0.958 | 0.980/0.972 |
| ERGAS | 1.356/0.594 | 0.606/0.249 | 0.698/0.291 | 2.038/1.082 | 0.425/0.289 | 0.381/0.227 |
| SAM | 2.022/0.987 | 1.384/0.586 | 1.539/0.685 | 2.812/1.342 | 0.609/0.419 | 0.542/0.342 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, J.; He, Z.; Hu, J. Sentinel-2 Sharpening via Parallel Residual Network. Remote Sens. 2020, 12, 279. https://doi.org/10.3390/rs12020279
Wu J, He Z, Hu J. Sentinel-2 Sharpening via Parallel Residual Network. Remote Sensing. 2020; 12(2):279. https://doi.org/10.3390/rs12020279
Chicago/Turabian StyleWu, Jiemin, Zhi He, and Jie Hu. 2020. "Sentinel-2 Sharpening via Parallel Residual Network" Remote Sensing 12, no. 2: 279. https://doi.org/10.3390/rs12020279
APA StyleWu, J., He, Z., & Hu, J. (2020). Sentinel-2 Sharpening via Parallel Residual Network. Remote Sensing, 12(2), 279. https://doi.org/10.3390/rs12020279






