Characterisation of Terrain Variations of an Underwater Ancient Town in Qiandao Lake
Abstract
1. Introduction
2. Methods
2.1. Topographical Change Monitoring of Underwater Ancient Town with Multibeam Echo Sounder System (MBES)
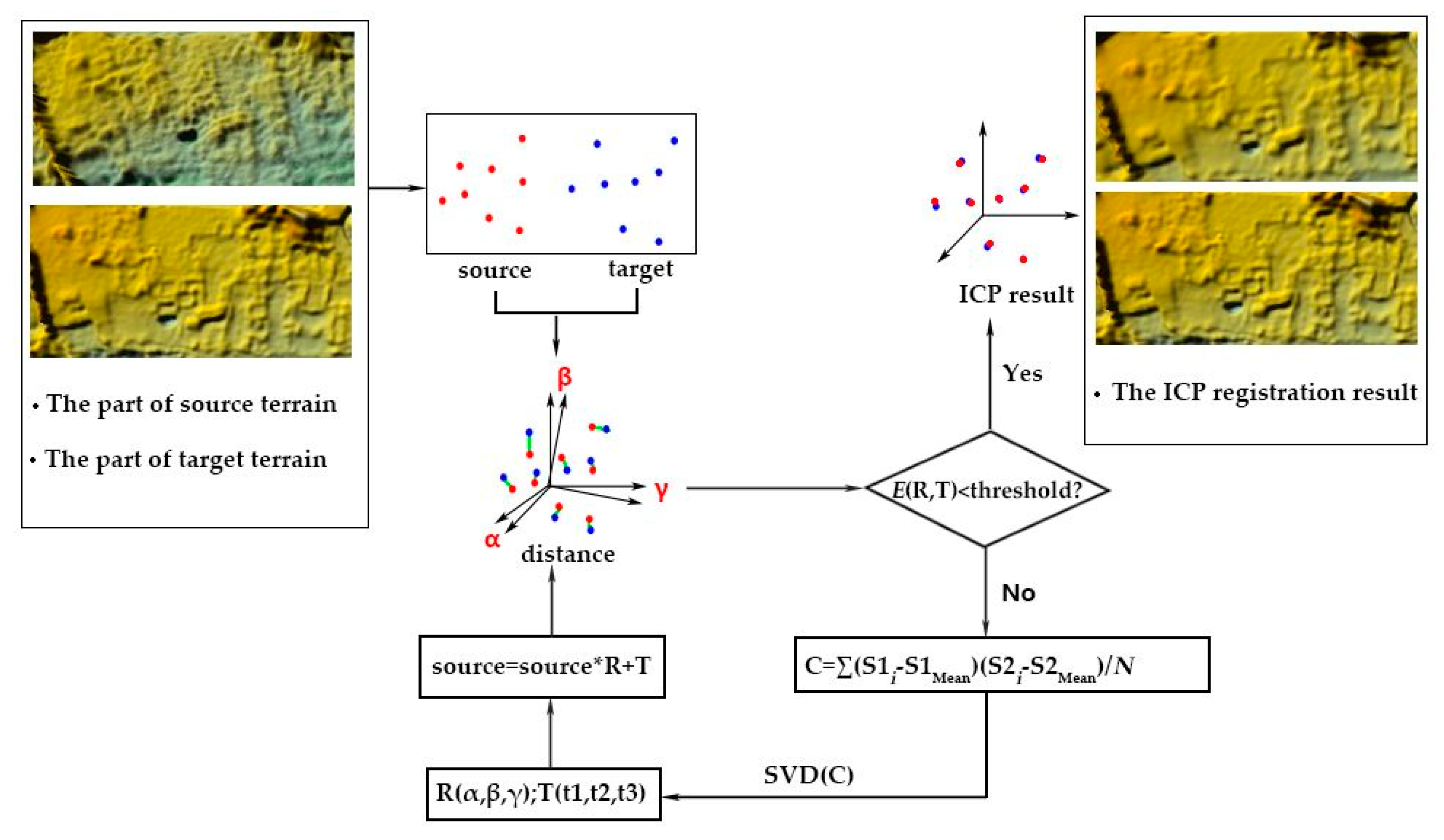
2.2. Coordinate Frame Registration
2.3. Detection of Terrain Variations
3. Experiment and Results
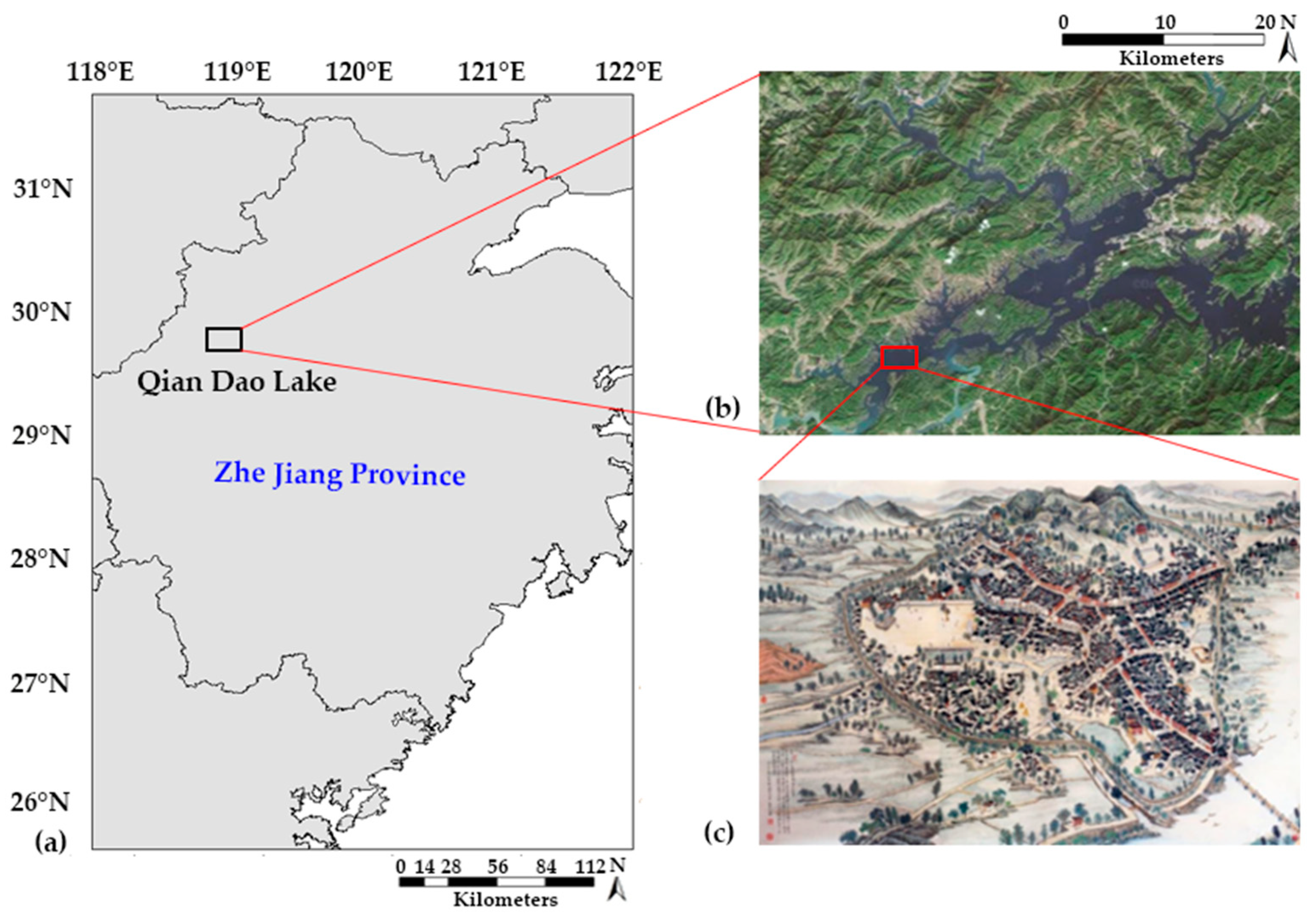
3.1. Study Area and Data Collection
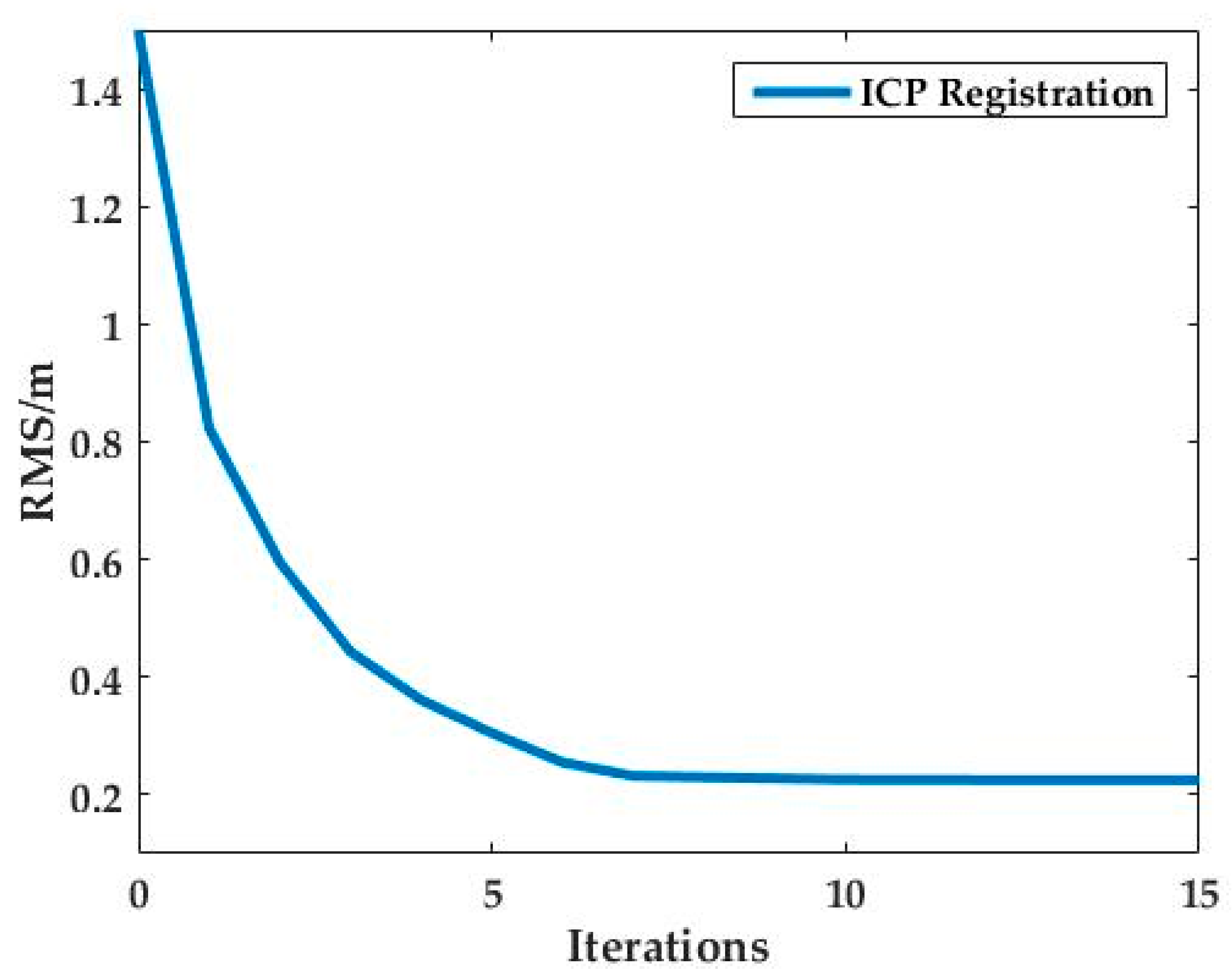
3.2. Registration of Point Sets
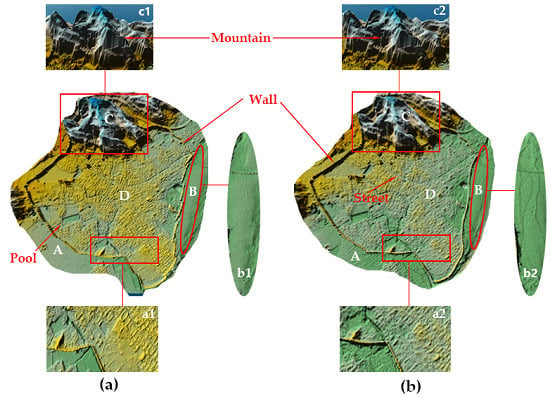
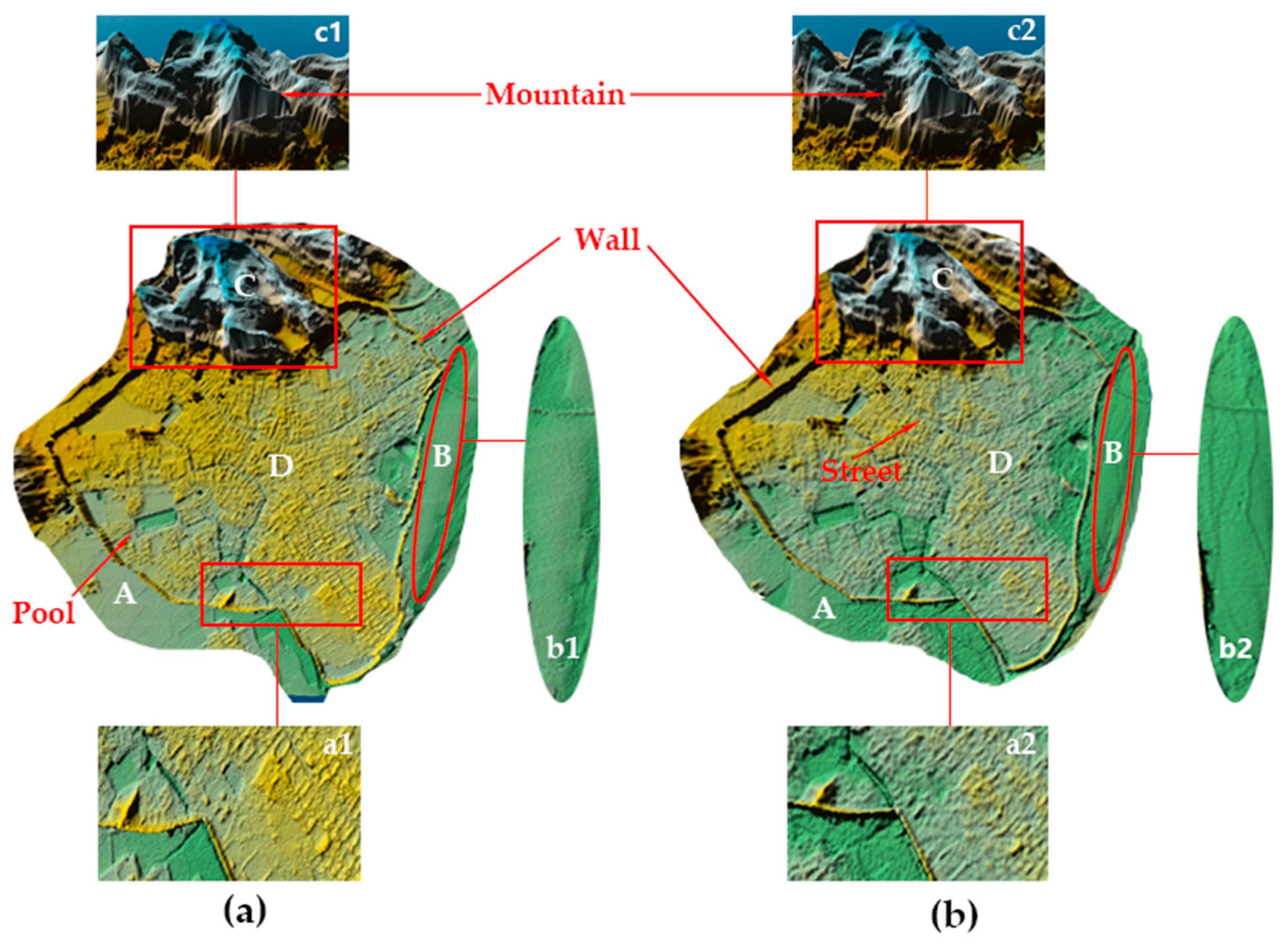
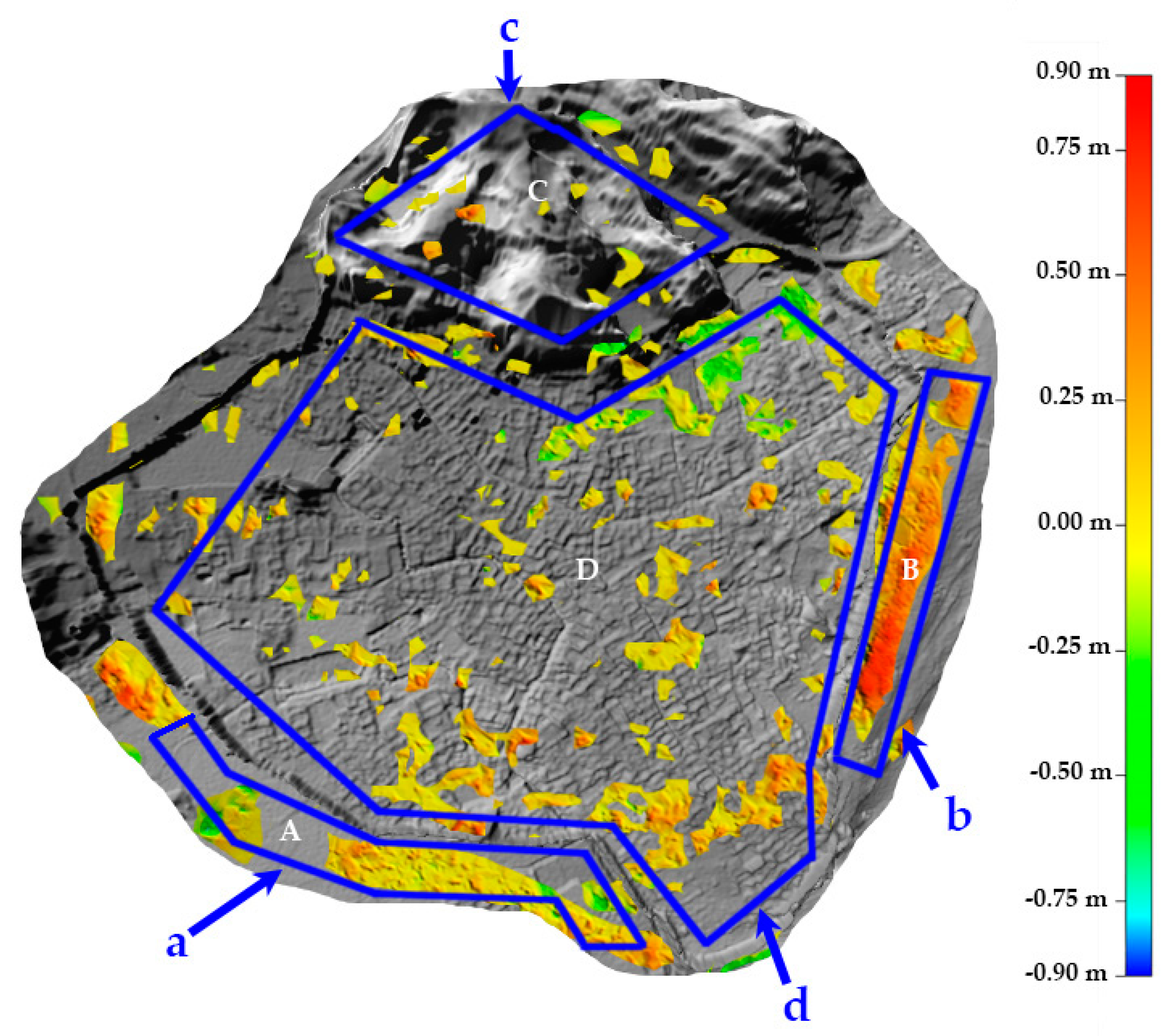
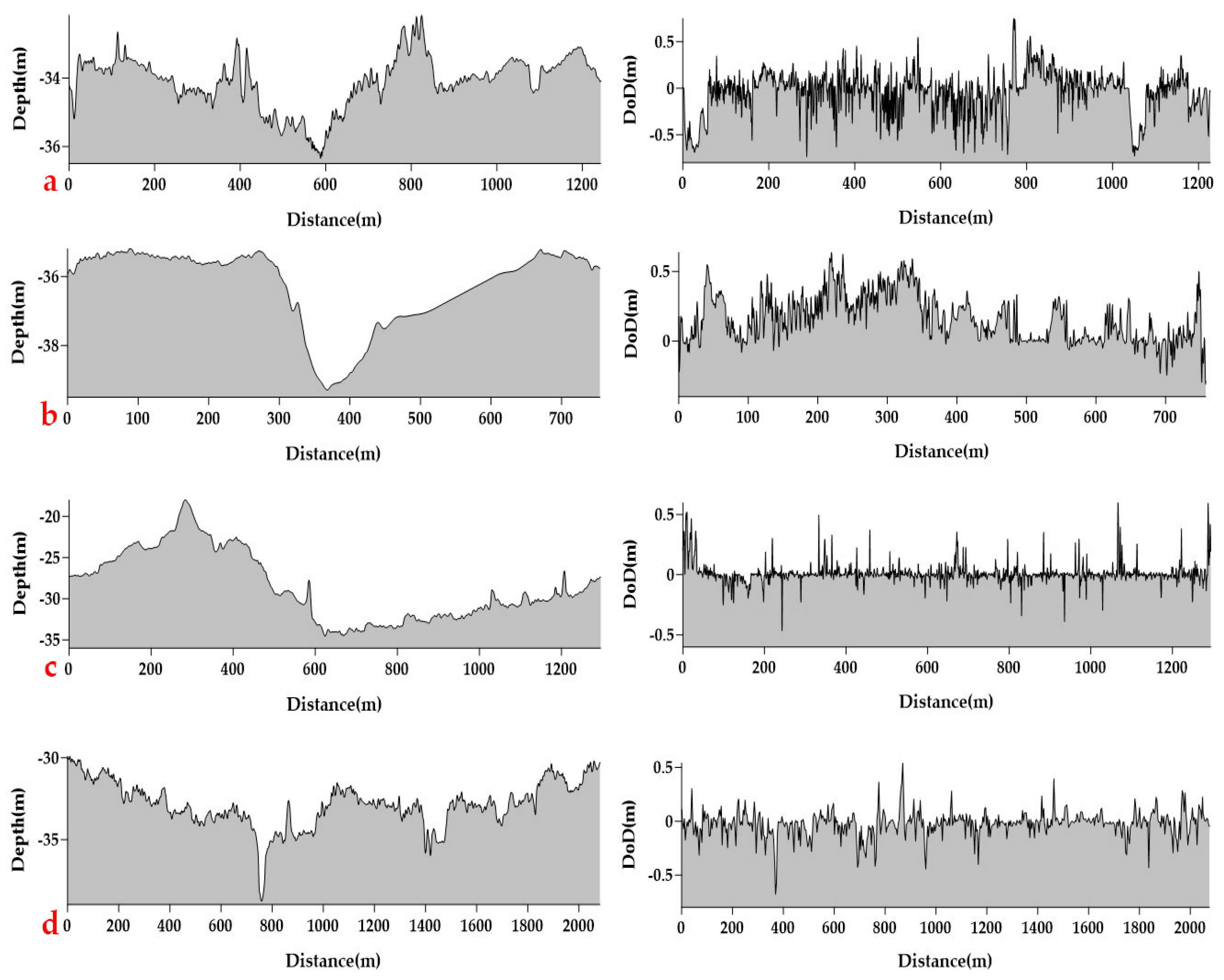
3.3. Regional Analysis
4. Discussion
4.1. Various Threats to the Ancient Town
4.2. Validation of Analysis
4.3. Monitoring Suggestions for Ancient Town
4.4. Conservation Suggestion of Ancient Towns
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bailey, G.N.; Flemming, N.C. Archaeology of the continental shelf: Marine resources, submerged landscapes and underwater archaeology. Quat. Sci. Rev. 2008, 27, 2153–2165. [Google Scholar] [CrossRef]
- Halligan, J.J.; Waters, M.R.; Angelina, P.; Owens, I.J.; Feinberg, J.M.; Bourne, M.D.; Fenerty, B.; Winsborough, B.; Carlson, D.; Fisher, D.C.; et al. Pre-Clovis occupation 14, 550 years ago at the Page-Ladson site, Florida, and the peopling of the Americas. Sci. Adv. 2016, 2, e1600375. [Google Scholar] [CrossRef] [PubMed]
- Eriksson, N.; Rönnby, J. Mars (1564): The initial archaeological investigations of a great 16th-century Swedish warship. Int. J. Naut. Archaeol. 2017, 46, 92–107. [Google Scholar] [CrossRef]
- Auer, J.; Firth, A. The ‘gresham ship’: An interim report on a 16th-century wreck from princes channel, thames estuary. Post Mediev. Archaeol. 2007, 41, 222–241. [Google Scholar] [CrossRef]
- Ono, R.; Katagiri, C.; Kan, H.; Nagao, M.; Sakagami, N. Discovery of iron grapnel anchors in early modern ryukyu and management of underwater cultural heritage in okinawa, japan. Int. J. Naut. Archaeol. 2016, 45, 77–93. [Google Scholar] [CrossRef]
- McCawley, J.C.; Pearson, C. Conservation of Marine Archaeological Objects. Stud. Conserv. 1991, 36, 121. [Google Scholar] [CrossRef]
- Anderson, D.G.; Bissett, T.G.; Yerka, S.J.; Wells, J.J.; Kansa, E.C.; Kansa, S.W.; Myers, K.N.; DeMuth, R.C.; White, D.A. Sea-level rise and archaeological site destruction: An example from the southeastern United States using DINAA (Digital Index of North American Archaeology). PLOS ONE 2017, 12, e0188142. [Google Scholar] [CrossRef]
- Stevenson, P. A titanic struggle: One possible resolution of the conflict between preservation for the public good and private law property rights. Art Antiq. Law Leic. 2011, 16, 53–66. [Google Scholar]
- Petriaggi, R. The role of the italian central institute of restoration in the field of underwater archaeology. Int. J. Naut. Archaeol. 2002, 31, 74–82. [Google Scholar] [CrossRef]
- Gregory, J.D. Formation Processes in Underwater Archaeology: A Study of Chemical and Biological Deterioration. Ph.D. Thesis, University of Leicester, Leicester, UK, 1996. [Google Scholar]
- Crisci, G.M.; Russa, M.F.L.; Macchione, M.; Malagodi, M.; Palermo, A.M.; Ruffolo, S.A.; La Russa, M.F. Study of archaeological underwater finds: Deterioration and conservation. Appl. Phys. A 2010, 100, 855–863. [Google Scholar] [CrossRef]
- Harmsen, H.; Hollesen, J.; Madsen, C.K.; Albrechtsen, B.; Myrup, M.; Matthiesen, H. A Ticking Clock? Preservation and Management of Greenland’s Archaeological Heritage in the Twenty-First Century. Conserv. Manag. Archaeol. Sites 2018, 20, 175–198. [Google Scholar] [CrossRef]
- Stewart, W.K. Multisensor Visualization for Underwater Archaeology. IEEE Comput. Soc. Press 1991, 11, 13–18. [Google Scholar] [CrossRef]
- Bass, G.F.; Pulak, C.; Collon, D.; Weinstein, J. The Bronze Age Shipwreck at Ulu Burun: 1986 Campaign. Am. J. Archaeol. 1989, 93, 1–29. [Google Scholar] [CrossRef]
- Mccarthy, J.K.; Benjamin, J.; Winton, T.; Van Duivenvoorde, W. The Rise of 3D in Maritime Archaeology. In 3D Recording and Interpretation for Maritime Archaeology; Springer: New York, NY, USA, 2019. [Google Scholar]
- Pacheco-Ruiz, R.; Adams, J.; Pedrotti, F. 4D modelling of low visibility Underwater Archaeological excavations using multi-source photogrammetry in the Bulgarian Black Sea. J. Archaeol. Sci. 2018, 100, 120–129. [Google Scholar] [CrossRef]
- Westley, K.; Mcneary, R. Archaeological Applications of Low-Cost Integrated Sidescan Sonar/Single-Beam Echosounder Systems in Irish Inland Waterways. Archaeol. Prospect. 2016, 24, 37–57. [Google Scholar] [CrossRef]
- Doneus, M.; Doneus, N.; Briese, C.; Pregesbauer, M.; Mandlburger, G.; Verhoeven, G. Airborne laser bathymetry—Detecting and recording submerged archaeological sites from the air. J. Archaeol. Sci. 2013, 40, 2136–2151. [Google Scholar] [CrossRef]
- Bates, C.R.; Lawrence, M.; Dean, M.; Robertson, P. Geophysical Methods for Wreck-Site Monitoring: The Rapid Archaeological Site Surveying and Evaluation (RASSE) programme. Int. J. Naut. Archaeol. 2010, 40, 404–416. [Google Scholar] [CrossRef]
- Poglajen, S. Acoustic Data in Underwater Archaeology. In Proceedings of the Computer Applications & Quantitative Methods in Archaeology (CAA) 2012 Conference, University of Southampton, Southampton, UK, 26–30 March 2012. [Google Scholar]
- Plets, R.; Quinn, R.; Forsythe, W.; Westley, K.; Bell, T.; Benetti, S.; Robinson, R. Using multi-beam Echo-Sounder Data to Identify Shipwreck Sites: Archaeological assessment of the Joint Irish Bathymetric Survey data. Int. J. Naut. Archaeol. 2011, 40, 87–98. [Google Scholar] [CrossRef]
- Ernstsen, V.B.; Noormets, R.; Winter, C.; Hebbeln, D.; Bartholomä, A.; Flemming, B.W.; Bartholdy, J. Development of subaqueous barchanoid-shaped dunes due to lateral grain size variability in a tidal inlet channel of the Danish Wadden Sea. J. Geophys. Res. Space Phys. 2005, 110. [Google Scholar] [CrossRef]
- Tassetti, A.N.; Malaspina, S.; Fabi, G. Using a multi-beam Echosounder to Monitor AN Artificial Reef. ISPRS. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, XL-5/W5, 207–213. [Google Scholar] [CrossRef]
- Clarke, J.E.H.; Mayer, L.A.; Wells, D.E. Shallow-water imaging multi-beam sonars: A new tool for investigating seafloor processes in the coastal zone and on the continental shelf. Mar. Geophys. Res. 1996, 18, 607–629. [Google Scholar] [CrossRef]
- Bu, X.; Yang, F.; Ma, Y.; Wu, D.; Zhang, K.; Xu, F. Simplified calibration method for multibeam footprint displacements due to non-concentric arrays. Ocean Eng. 2020, 197, 106862. [Google Scholar] [CrossRef]
- Jian-Lin, M.A.; Jing, J.; Xiang-Hua, L. The Construction of Seafloor Digital Terrain Model Based on multi-beam Soundings. Hydrogr. Surv. Charting 2005, 25, 15–17. [Google Scholar]
- Schimel, A.C.G.; Ierodiaconou, D.; Hulands, L.; Kennedy, D.M. Accounting for uncertainty in volumes of seabed change measured with repeat multi-beam sonar surveys. Cont. Shelf Res. 2015, 111, 52–68. [Google Scholar] [CrossRef]
- Zhu, W.Q.; Wei, J.J.; Li, M.W.; Yin, D.Y. Random error model of multi-beam echo-sounding sonar. J. Mar. Technol. 1986, 2, 98–105. [Google Scholar]
- Guériot, D.; Chèdru, J.; Daniel, S.; Maillard, E. The patch test: A comprehensive calibration tool for multi-beam echosounders. In Proceedings of the OCEANS 2000 MTS/IEEE Conference and Exhibition, Providence, RI, USA, 11–14 September 2000. [Google Scholar]
- Smith, D.P.; Kvitek, R.; Iampietro, P.J.; Wong, K. Twenty-nine months of geomorphic change in upper Monterey Canyon (2002–2005). Mar. Geol. 2007, 236, 79–94. [Google Scholar] [CrossRef]
- Brothers, L.L.; Kelley, J.T.; Belknap, D.F.; Barnhardt, W.A.; Andrews, B.D.; Maynard, M.L. More than a century of bathymetric observations and present-day shallow sediment characterization in Belfast Bay, Maine, USA: Implications for pockmark field longevity. Geophys. Mar. Lett. 2011, 31, 237–248. [Google Scholar] [CrossRef][Green Version]
- Zhang, K.; Yang, F.L.; Zhao, C.; Feng, C. Using robust correlation matching to estimate sand-wave migration in Monterey Submarine Canyon, California. Mar. Geol. 2016, 376, 102–108. [Google Scholar] [CrossRef]
- Nygren, I.; Jansson, M. Terrain navigation for underwater vehicles using the correlator method. IEEE J. Ocean. Eng. 2004, 29, 906–915. [Google Scholar] [CrossRef]
- Blas, L.; Valero, G.; Navas, A.; Javier, M.; Walling, D. Sediment sources and siltation in mountain reservoirs: A case study from the central spanish pyrenees. Geomorphology 1999, 28, 23–41. [Google Scholar]
- Abraham, J. Spatial distribution of major and trace elements in shallow reservoir sediments: An example from lake waco, texas. Environ. Geol. 1998, 36, 349–363. [Google Scholar] [CrossRef]
- Zhang, W. Crustal Deformation Monitoring Based on D-InSAR Technology in Hangzhou Area and Study on Deformation Mechanism. Ph.D. Thesis, Zhejiang University, Zhejiang, China, 2008. [Google Scholar]
- Clarke, J.E.H. Dynamic motion residuals in swath sonar data: Ironing out the creases. Int. Hydrogr. Rev. 2003, 4, 6–23. [Google Scholar]
- Dorst, L.L.; Roos, P.C.; Hulscher, S.; Lindenbergh, R.C. The estimation of sea floor dynamics from bathymetric surveys of a sand wave area. J. Appl. Geodesy 2009, 3, 97–120. [Google Scholar] [CrossRef]
- Dorst, L.L.; Roos, P.C.; Hulscher, S. Spatial differences in sand wave dynamics between the Amsterdam and the Rotterdam region in the Southern North Sea. Cont. Shelf Res. 2011, 31, 1096–1105. [Google Scholar] [CrossRef]
- Cherlet, J.; Besio, G.; Blondeaux, P.; Van Lancker, V.; Verfaillie, E.; Vittori, G. Modeling sand wave characteristics on the Belgian Continental Shelf and in the Calais-Dover Strait. J. Geophys. Res. 2007, 112. [Google Scholar] [CrossRef]
- Van Dijk, T.A.; Kleinhans, M.G. Processes controlling the dynamics of compound sandwaves in the North Sea, Netherlands. J. Geophys. Res. 2005, 110. [Google Scholar] [CrossRef]


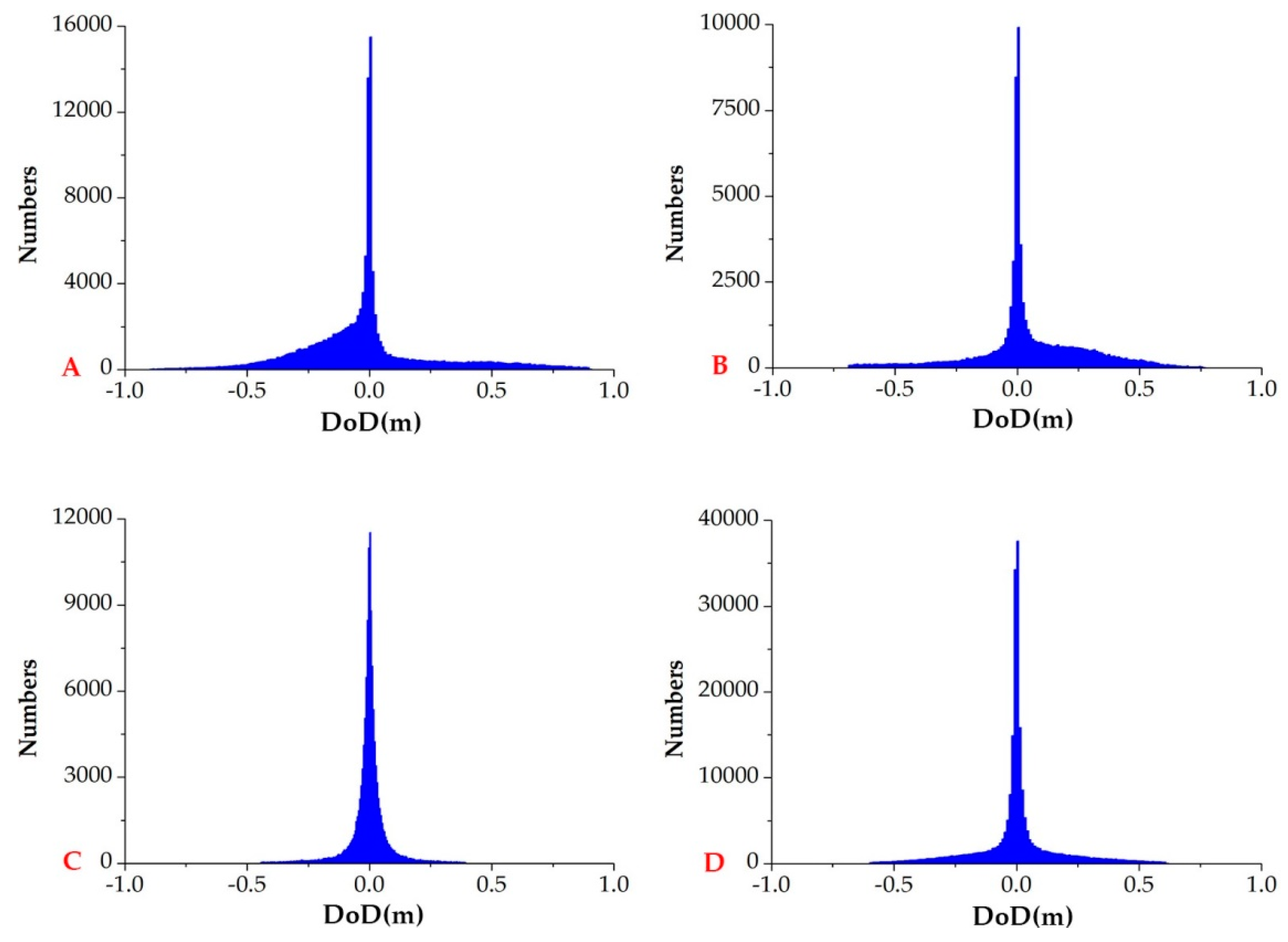
| Region | Minimum (m) | Maximum (m) | Mean (m) | MAV (m) | RMS (m) |
|---|---|---|---|---|---|
| Global | −0.89 | 0.88 | 0 | 0.12 | 0.21 |
| A | −0.89 | 0.88 | −0.01 | 0.18 | 0.27 |
| B | −0.76 | 0.69 | 0.04 | 0.16 | 0.25 |
| C | −0.41 | 0.39 | 0 | 0.06 | 0.13 |
| D | −0.61 | 0.60 | 0 | 0.10 | 0.19 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, F.; Xu, F.; Zhang, K.; Bu, X.; Hu, H.; Anokye, M. Characterisation of Terrain Variations of an Underwater Ancient Town in Qiandao Lake. Remote Sens. 2020, 12, 268. https://doi.org/10.3390/rs12020268
Yang F, Xu F, Zhang K, Bu X, Hu H, Anokye M. Characterisation of Terrain Variations of an Underwater Ancient Town in Qiandao Lake. Remote Sensing. 2020; 12(2):268. https://doi.org/10.3390/rs12020268
Chicago/Turabian StyleYang, Fanlin, Fangzheng Xu, Kai Zhang, Xianhai Bu, Hao Hu, and Michael Anokye. 2020. "Characterisation of Terrain Variations of an Underwater Ancient Town in Qiandao Lake" Remote Sensing 12, no. 2: 268. https://doi.org/10.3390/rs12020268
APA StyleYang, F., Xu, F., Zhang, K., Bu, X., Hu, H., & Anokye, M. (2020). Characterisation of Terrain Variations of an Underwater Ancient Town in Qiandao Lake. Remote Sensing, 12(2), 268. https://doi.org/10.3390/rs12020268