The Applicability of SWOT’s Non-Uniform Space–Time Sampling in Hydrologic Model Calibration
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Used to Simulate SWOT Mission Discharge
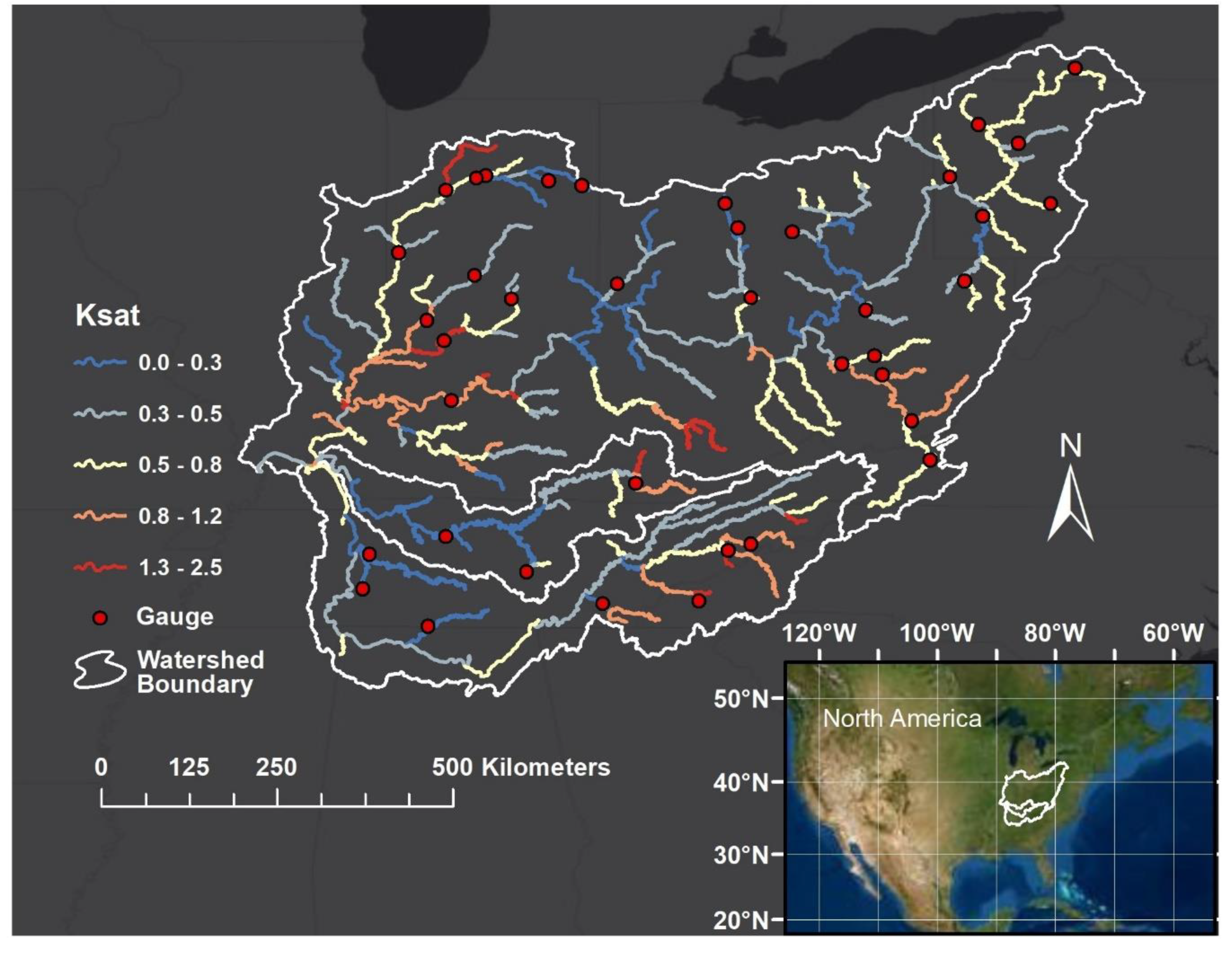
2.2. HRR-VIC Model and Input Data
2.3. Model Calibration
2.3.1. Variables and Spatial Variation
2.3.2. Calibration and Sensitivity Analysis
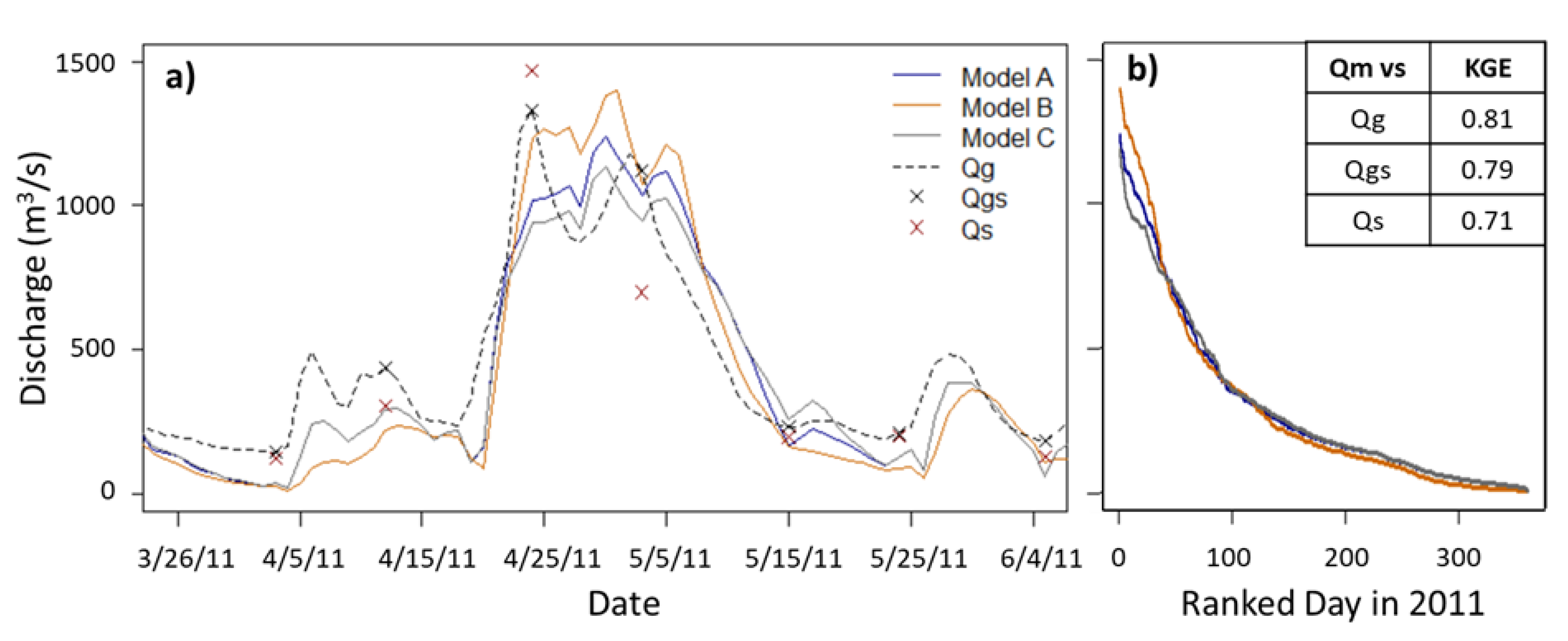
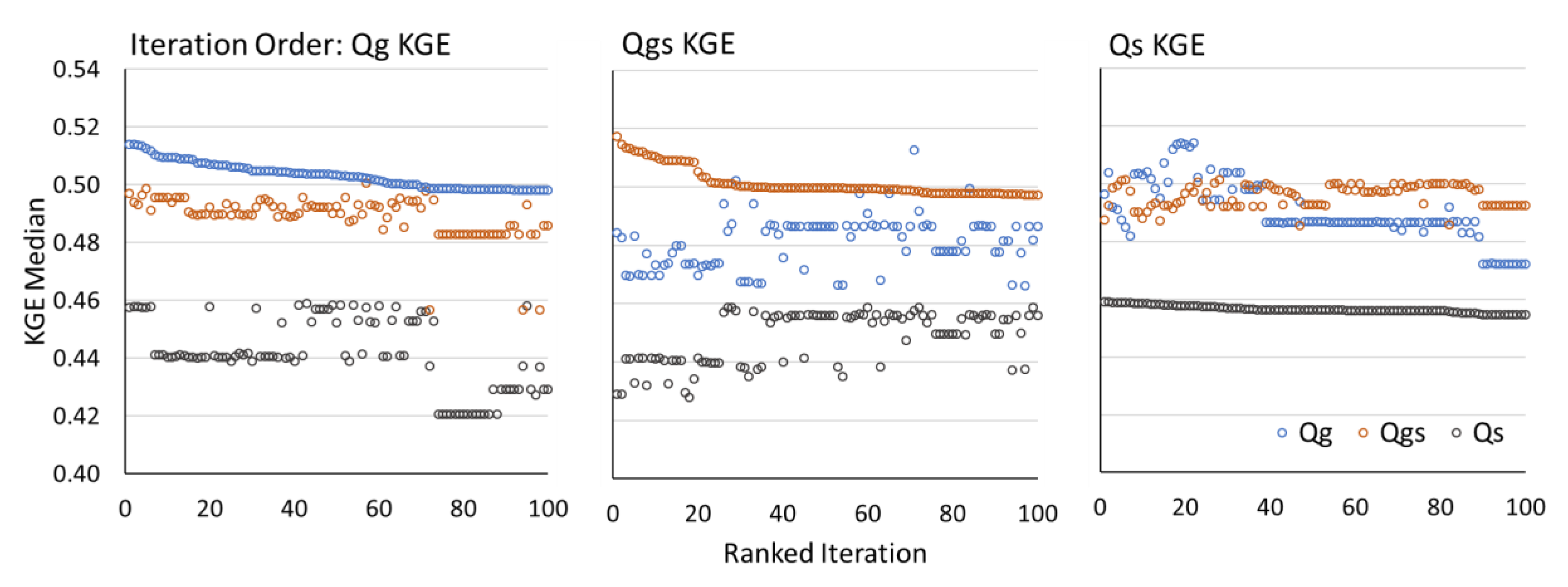
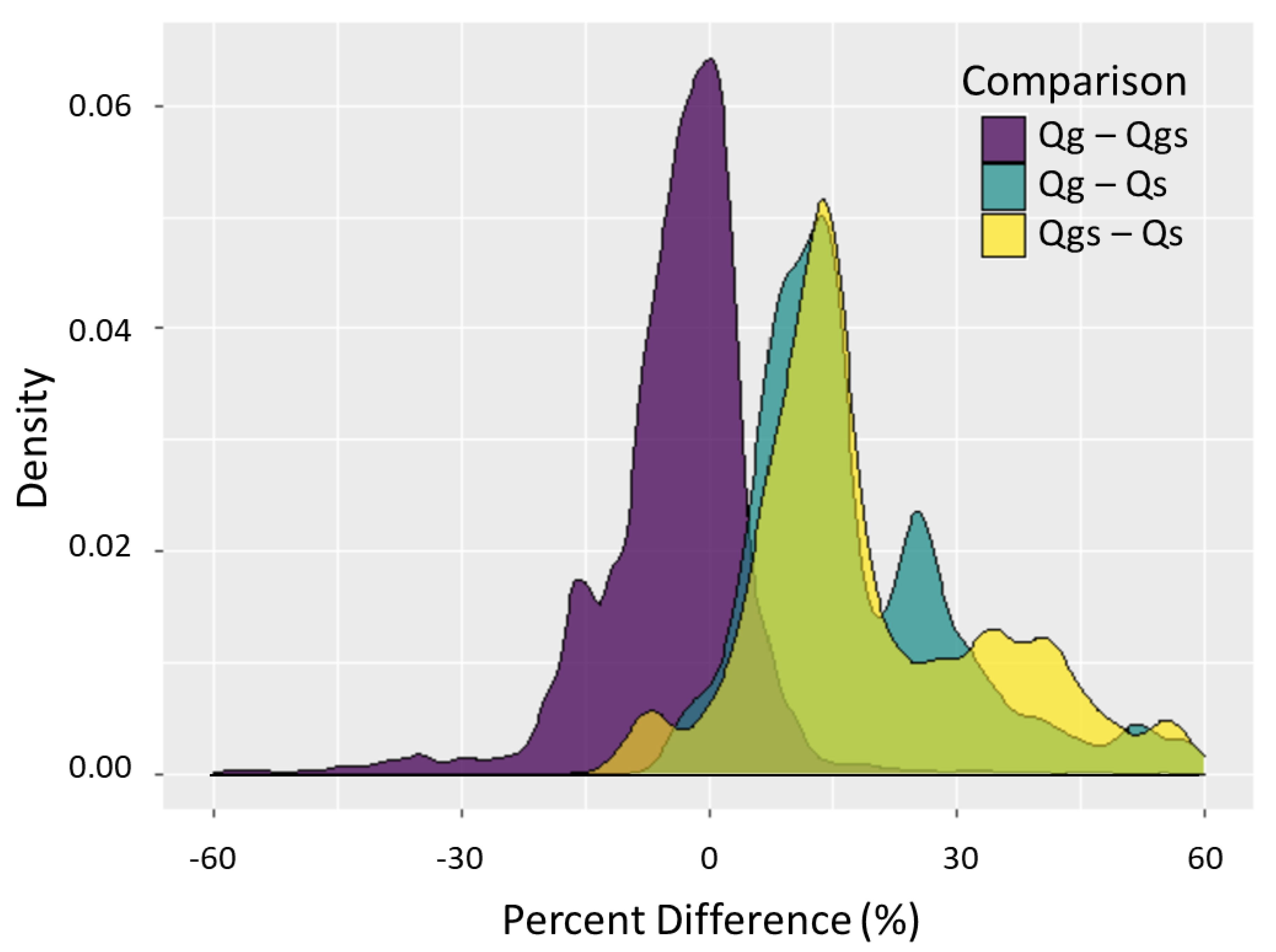
3. Results
3.1. VIC Parameter Trends and Relationships
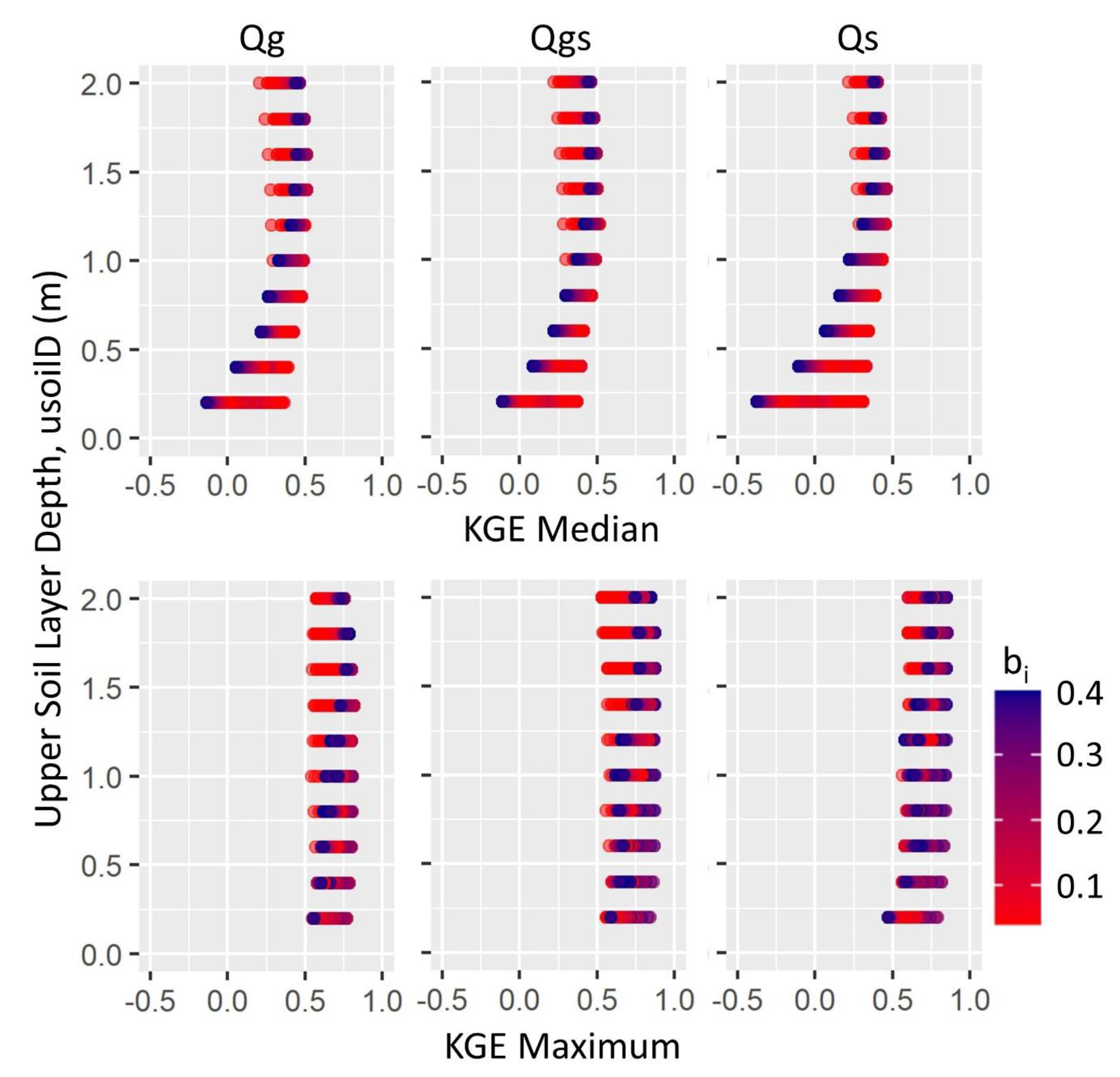
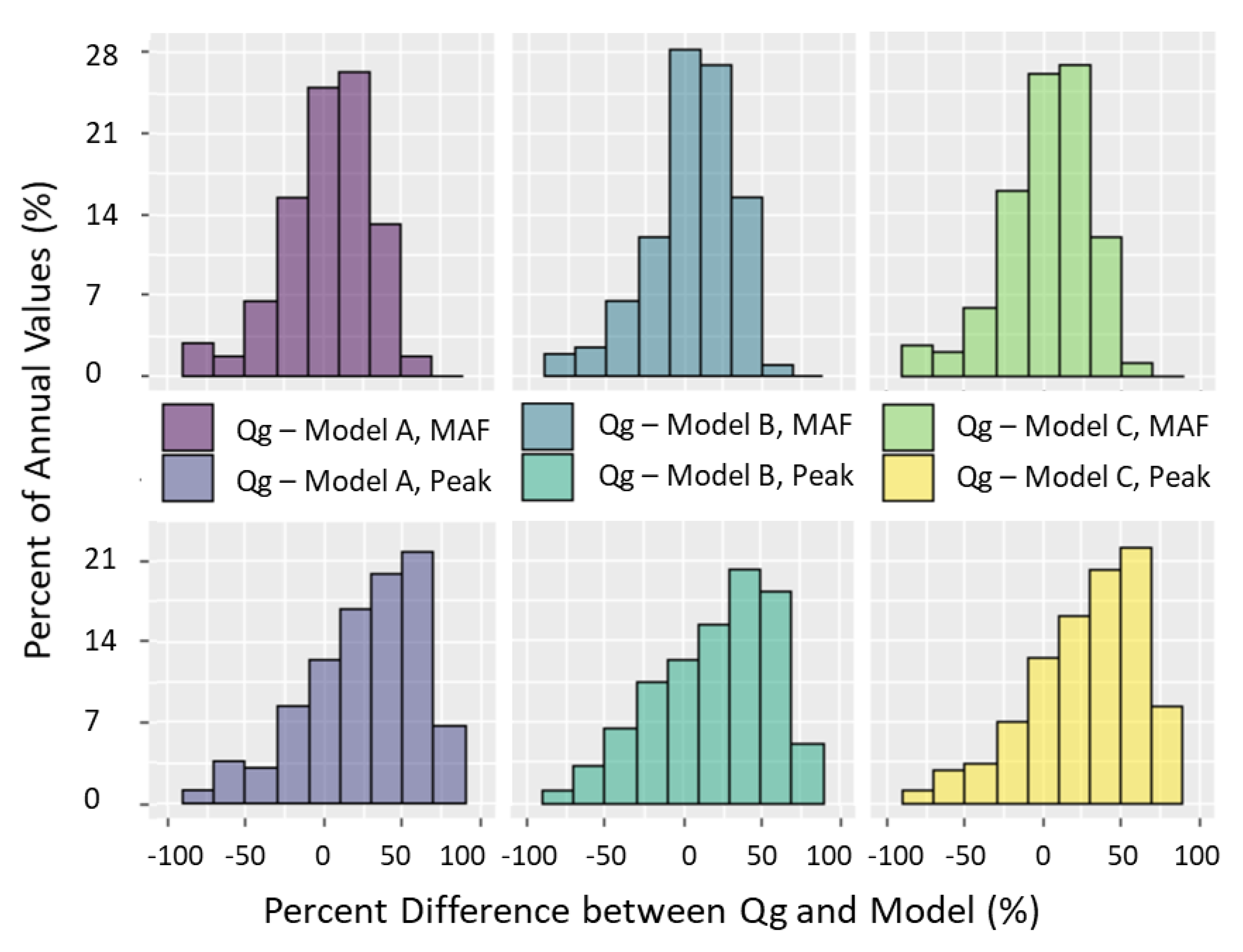
3.2. Iteration Comparisons among Timeseries
3.3. Sensitivity and Validation Analysis
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Feng, D.; Beighley, E. Identifying uncertainties in hydrologic fluxes and seasonality from hydrologic model components for climate change impact assessments. Hydrol. Earth Syst. Sci. 2020, 24, 2253–2267. [Google Scholar] [CrossRef]
- Andreadis, K.M.; Schumann, G.J.P. Estimating the impact of satellite observations on the predictability of large-scale hydraulic models. Adv. Water Resour. 2014, 73, 44–54. [Google Scholar] [CrossRef]
- Beighley, R.E.; Eggert, K.G.; Dunne, T.; He, Y.; Gummadi, V.; Verdin, K.L. Simulating hydrologic and hydraulic processes throughout the Amazon River Basin. Hydrol. Process. 2009, 23, 1221–1235. [Google Scholar] [CrossRef]
- Chawla, I.; Karthikeyan, L.; Mishra, A.K. A review of remote sensing applications for water security: Quantity, quality, and extremes. J. Hydrol. 2020, 585, 124826. [Google Scholar] [CrossRef]
- Brêda, J.P.L.F.; Paiva, R.C.D.; Bravo, J.M.; Passaia, O.A.; Moreira, D.M. Assimilation of Satellite Altimetry Data for Effective River Bathymetry. Water Resour. Res. 2019, 55, 7441–7463. [Google Scholar] [CrossRef]
- Domeneghetti, A.; Tarpanelli, A.; Grimaldi, L.; Brath, A.; Schumann, G. Flow Duration Curve from Satellite: Potential of a Lifetime SWOT Mission. Remote Sens. 2018, 10, 1107. [Google Scholar] [CrossRef]
- Gleason, C.J.; Wada, Y.; Wang, J. A Hybrid of Optical Remote Sensing and Hydrological Modeling Improves Water Balance Estimation. J. Adv. Modeling Earth Syst. 2018, 10, 2–17. [Google Scholar] [CrossRef]
- Liu, G.; Schwartz, F.W.; Tseng, K.-H.; Shum, C.K. Discharge and water-depth estimates for ungauged rivers: Combining hydrologic, hydraulic, and inverse modeling with stage and water-area measurements from satellites. Water Resour. Res. 2015, 51, 6017–6035. [Google Scholar] [CrossRef]
- Pedinotti, V.; Boone, A.; Ricci, S.; Biancamaria, S.; Mognard, N. Assimilation of satellite data to optimize large-scale hydrological model parameters: A case study for the SWOT mission. Hydrol. Earth Syst. Sci. 2014, 18, 4485–4507. [Google Scholar] [CrossRef]
- Demaria, E.M.; Nijssen, B.; Wagener, T. Monte Carlo sensitivity analysis of land surface parameters using the Variable Infiltration Capacity model. J. Geophys. Res. Atmos. 2007, 112, D11113. [Google Scholar] [CrossRef]
- Huang, M.; Liang, X. On the assessment of the impact of reducing parameters and identification of parameter uncertainties for a hydrologic model with applications to ungauged basins. J. Hydrol. 2006, 320, 37–61. [Google Scholar] [CrossRef]
- Oubeidillah, A.A.; Kao, S.C.; Ashfaq, M.; Naz, B.S.; Tootle, G. A large-scale, high-resolution hydrological model parameter data set for climate change impact assessment for the conterminous US. Hydrol. Earth Syst. Sci. 2014, 18, 67–84. [Google Scholar] [CrossRef]
- Troy, T.J.; Wood, E.F.; Sheffield, J. An efficient calibration method for continental-scale land surface modeling. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Yang, Y.; Pan, M.; Beck, H.E.; Fisher, C.K.; Beighley, R.E.; Kao, S.-C.; Hong, Y.; Wood, E.F. In Quest of Calibration Density and Consistency in Hydrologic Modeling: Distributed Parameter Calibration against Streamflow Characteristics. Water Resour. Res. 2019, 55, 7784–7803. [Google Scholar] [CrossRef]
- Biancamaria, S.; Lettenmaier, D.P.; Pavelsky, T.M. The SWOT Mission and Its Capabilities for Land Hydrology. Surv. Geophys. 2016, 37, 307–337. [Google Scholar] [CrossRef]
- Durand, M.; Gleason, C.J.; Garambois, P.A.; Bjerklie, D.; Smith, L.C.; Roux, H.; Rodriguez, E.; Bates, P.D.; Pavelsky, T.M.; Monnier, J.; et al. An intercomparison of remote sensing river discharge estimation algorithms from measurements of river height, width, and slope. Water Resour. Res. 2016, 52, 4527–4549. [Google Scholar] [CrossRef]
- Hagemann, M.W.; Gleason, C.J.; Durand, M.T. BAM: Bayesian AMHG-Manning Inference of Discharge Using Remotely Sensed Stream Width, Slope, and Height. Water Resour. Res. 2017, 53, 9692–9707. [Google Scholar] [CrossRef]
- Pavelsky, T.M.; Durand, M.T.; Andreadis, K.M.; Beighley, R.E.; Paiva, R.C.D.; Allen, G.H.; Miller, Z.F. Assessing the potential global extent of SWOT river discharge observations. J. Hydrol. 2014, 519, 1516–1525. [Google Scholar] [CrossRef]
- Nickles, C.; Beighley, E.; Zhao, Y.; Durand, M.; David, C.; Lee, H. How does the unique space-time sampling of the SWOT mission influence river discharge series characteristics? Geophys. Res. Lett. 2019, 46, 8154–8161. [Google Scholar] [CrossRef]
- Baratelli, F.; Flipo, N.; Rivière, A.; Biancamaria, S. Retrieving river baseflow from SWOT spaceborne mission. Remote Sens. Environ. 2018, 218, 44–54. [Google Scholar] [CrossRef]
- Solander, K.C.; Reager, J.T.; Famiglietti, J.S. How well will the Surface Water and Ocean Topography (SWOT) mission observe global reservoirs? Water Resour. Res. 2016, 52, 2123–2140. [Google Scholar] [CrossRef]
- Frasson, R.P.D.M.; Schumann, G.J.-P.; Kettner, A.J.; Brakenridge, G.R.; Krajewski, W.F. Will the Surface Water and Ocean Topography (SWOT) satellite mission observe floods? Geophys. Res. Lett. 2019, 46. [Google Scholar] [CrossRef]
- Getirana, A.C.V. Integrating spatial altimetry data into the automatic calibration of hydrological models. J. Hydrol. 2010, 387, 244–255. [Google Scholar] [CrossRef]
- Sun, W.; Fan, J.; Wang, G.; Ishidaira, H.; Bastola, S.; Yu, J.; Fu, Y.H.; Kiem, A.S.; Zuo, D.; Xu, Z. Calibrating a hydrological model in a regional river of the Qinghai–Tibet plateau using river water width determined from high spatial resolution satellite images. Remote Sens. Environ. 2018, 214, 100–114. [Google Scholar] [CrossRef]
- Wongchuig-Correa, S.; Cauduro Dias de Paiva, R.; Biancamaria, S.; Collischonn, W. Assimilation of future SWOT-based river elevations, surface extent observations and discharge estimations into uncertain global hydrological models. J. Hydrol. 2020, 590, 125473. [Google Scholar] [CrossRef]
- Huang, Q.; Long, D.; Du, M.; Han, Z.; Han, P. Daily Continuous River Discharge Estimation for Ungauged Basins Using a Hydrologic Model Calibrated by Satellite Altimetry: Implications for the SWOT Mission. Water Resour. Res. 2020, 56, e2020WR027309. [Google Scholar] [CrossRef]
- Liang, X.; Lettenmaier, D.P.; Wood, E.F.; Burges, S.J. A simple hydrologically based model of land surface water and energy fluxes for general circulation models. J. Geophys. Res. Atmos. 1994, 99, 14415–14428. [Google Scholar] [CrossRef]
- Allen, G.H.; Pavelsky, T.M. Global extent of rivers and streams. Science 2018, 361, 585–588. [Google Scholar] [CrossRef]
- Centre National d’Etudes Spatiales. SWOT Orbit: Ground Track and Swath Files. 2018. Available online: https://www.aviso.altimetry.fr/en/missions/future-missions/swot/orbit.html (accessed on 1 May 2018).
- Ray, R.L.; Beighley, R.E.; Yoon, Y. Integrating Runoff Generation and Flow Routing in Susquehanna River Basin to Characterize Key Hydrologic Processes Contributing to Maximum Annual Flood Events. J. Hydrol. Eng. 2016, 21, 04016026. [Google Scholar] [CrossRef]
- Shangguan, W.; Dai, Y.; Duan, Q.; Liu, B.; Yuan, H. A global soil data set for earth system modeling. J. Adv. Modeling Earth Syst. 2014, 6, 249–263. [Google Scholar] [CrossRef]
- Xia, Y. NCEP/EMC, NLDAS Primary Forcing Data L4 Hourly 0.125 × 0.125 degree V002, Edited by David Mocko, NASA/GSFC/HSL, Greenbelt, Maryland, USA, Goddard Earth Sciences Data and Information Services Center (GES DISC). 2009. Available online: https://disc.gsfc.nasa.gov/datasets/NLDAS_FORA0125_H_002/summary (accessed on 1 October 2019). [CrossRef]
- Xia, Y.; Mitchell, K.; Ek, M.; Sheffield, J.; Cosgrove, B.; Wood, E.; Luo, L.; Alonge, C.; Wei, H.; Meng, J.; et al. Continental-scale water and energy flux analysis and validation for the North American Land Data Assimilation System project phase 2 (NLDAS-2): 1. Intercomparison and application of model products. J. Geophys. Res. Atmos. 2012, 117, D03109. [Google Scholar] [CrossRef]
- Qin, Y.; Abatzoglou, J.T.; Siebert, S.; Huning, L.S.; AghaKouchak, A.; Mankin, J.S.; Hong, C.; Tong, D.; Davis, S.J.; Mueller, N.D. Agricultural risks from changing snowmelt. Nat. Clim. Chang. 2020, 10, 459–465. [Google Scholar] [CrossRef]
- US Department of Agriculture (USDA). National Engineering Handbook. Snowmelt. 2004. Available online: https://directives.sc.egov.usda.gov/OpenNonWebContent.aspx?content=17753.wba (accessed on 1 April 2020).
- Anderson, E. National Weather Service River Forecast System—Snow Accumulation and Ablation Model; NOAA Tech. Memo. NWS HYDRO-17; U.S. Dep. Commerce: Silver Springs, MD, USA, 1973; 217p.
- Barnhart, T.B.; Molotch, N.P.; Livneh, B.; Harpold, A.A.; Knowles, J.F.; Schneider, D. Snowmelt rate dictates streamflow. Geophys. Res. Lett. 2016, 43, 8006–8016. [Google Scholar] [CrossRef]
- Rango, A.; Martinec, J. Revisiting the degree-day method for snowmelt computations. J. Am. Water Resour. Assoc. 1995, 31, 657–669. [Google Scholar] [CrossRef]
- Nickles, C.; Beighley, E.; Feng, D. Hillslope River Routing Variable Infiltration Capacity Model (HRR-VIC) and Calibration Results. Available online: http://www.hydroshare.org/resource/172bf3533b1d46ea8d89feea51d44fb7 (accessed on 21 September 2020). [CrossRef]
- Clapp, R.B.; Hornberger, G.M. Empirical equations for some soil hydraulic properties. Water Resour. Res. 1978, 14, 601–604. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Knoben, W.J.M.; Freer, J.E.; Woods, R.A. Technical note: Inherent benchmark or not? Comparing Nash–Sutcliffe and Kling–Gupta efficiency scores. Hydrol. Earth Syst. Sci. 2019, 23, 4323–4331. [Google Scholar] [CrossRef]
- Dang, T.D.; Kamal Chowdhury, A.F.M.; Galelli, S. On the representation of water reservoir storage and operations in large-scale hydrological models: Implications on model parameterization and climate change impact assessments. Hydrol. Earth Syst. Sci. 2020, 24, 397–426. [Google Scholar] [CrossRef]
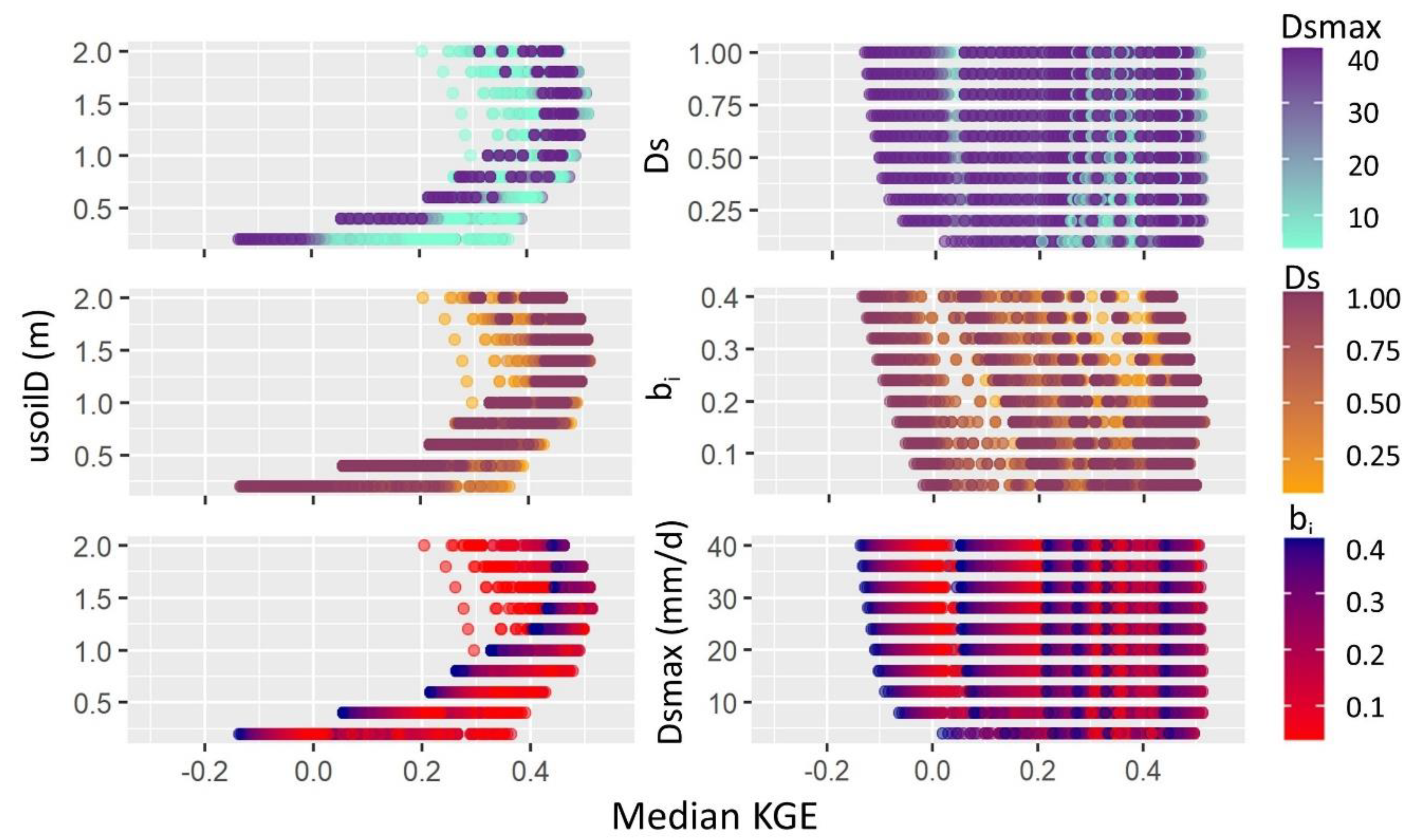
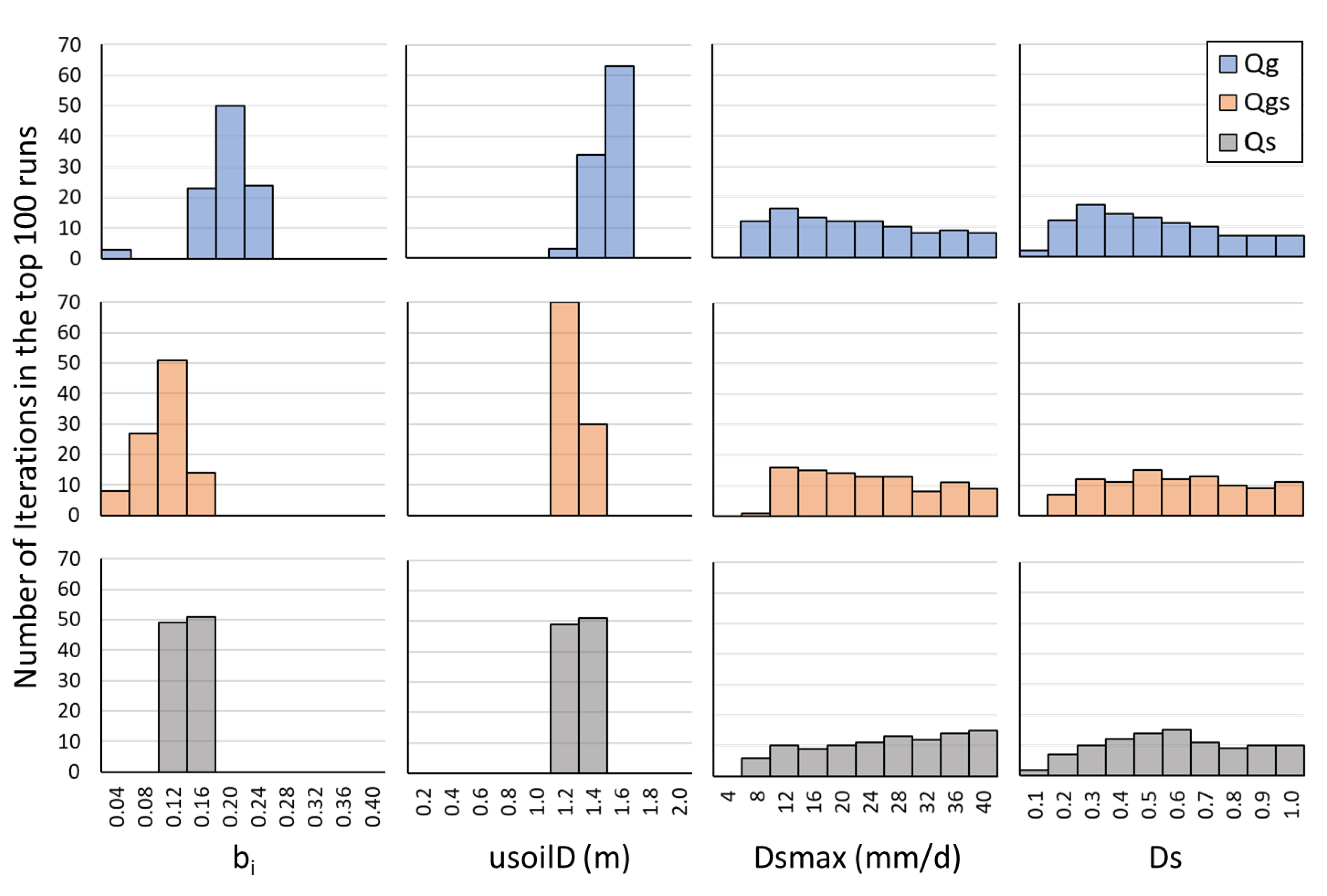
| VIC Parameter | Range Tested | Step By | Units | Description |
|---|---|---|---|---|
| bi | 0.04–0.4 | +0.04 | - | Variable infiltration curve parameter |
| usoilD | 0.2–2.0 | +0.2 | m | Upper soil layer depth |
| Dsmax | 4.0–40.0 | +4.0 | mm/d | Maximum velocity of baseflow |
| Ds | 0.1–1.0 | +0.1 | - | Fraction of Dsmax where nonlinear baseflow begins |
| Parameter Set | Timeseries vs. Qm | bi | usoilD (m) | Dsmax (mm/d) | Ds | Median KGE | Maximum KGE |
|---|---|---|---|---|---|---|---|
| A | Qg | 0.16 | 1.4 | 20 | 0.3 | 0.51 | 0.81 |
| B | Qgs | 0.04 | 1.2 | 12 | 1.0 | 0.52 | 0.79 |
| C | Qs | 0.16 | 1.4 | 40 | 0.1 | 0.46 | 0.71 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nickles, C.; Beighley, E.; Feng, D. The Applicability of SWOT’s Non-Uniform Space–Time Sampling in Hydrologic Model Calibration. Remote Sens. 2020, 12, 3241. https://doi.org/10.3390/rs12193241
Nickles C, Beighley E, Feng D. The Applicability of SWOT’s Non-Uniform Space–Time Sampling in Hydrologic Model Calibration. Remote Sensing. 2020; 12(19):3241. https://doi.org/10.3390/rs12193241
Chicago/Turabian StyleNickles, Cassandra, Edward Beighley, and Dongmei Feng. 2020. "The Applicability of SWOT’s Non-Uniform Space–Time Sampling in Hydrologic Model Calibration" Remote Sensing 12, no. 19: 3241. https://doi.org/10.3390/rs12193241
APA StyleNickles, C., Beighley, E., & Feng, D. (2020). The Applicability of SWOT’s Non-Uniform Space–Time Sampling in Hydrologic Model Calibration. Remote Sensing, 12(19), 3241. https://doi.org/10.3390/rs12193241








