1. Introduction
The majority of today’s global population lives in close proximity to a river, as they are a crucial resource for fresh water, agriculture, or industrial development, as well as being the source of religious and cultural values [
1,
2,
3,
4]. Although the majority of people are directly or indirectly affected by rivers, most river basins are poorly monitored or lack any hydrological information [
5]. Moreover, the number of gauging stations has decreased in the past on a global scale, which is particularly severe in front of hydrological regimes that have changed considerably in recent years or will do so in the future as a result of climate change [
6,
7]. In this regard, new ways and technologies need to be found and applied for measuring hydrological parameters [
8]. Here, with the growing number of earth observation satellites and their temporal and spatial resolution continuously improving, spaceborne sensors can be used to address this situation on a global scale.
As discharge is one of the most important characteristics of a river basin, many concepts for estimating discharge using remote sensing data have already been developed and applied. One basic concept is using satellite-derived information as input data for hydrological models [
9,
10,
11,
12,
13]. Laiolo et al. [
10] analyzed the impact of different remotely sensed soil moisture data on the discharge simulation of their distributed hydrological model, and Li et al. [
13] used remotely sensed soil moisture to improve their hydrological model calibration. Using multiple earth-observation data sources, Stisen et al. [
9] proposed a distributed hydrological model, driven solely by remote sensing data. Another way is to obtain hydraulic river parameters (e.g., river width, slope and stage) from satellite images in order to estimate the discharge [
14,
15,
16,
17,
18,
19,
20]. Using TOPEX/Poseidon altimetry, Kouarev et al. [
21] estimated discharge using rating curves based on in situ discharge and river level measured in their study region. Birkinshaw et al. [
16] used ENVISAT and ERS-2 altimetry data to improve the discharge estimation of an ungauged river site, using available in situ data at a 200 km away river. Birkinshaw et al. [
22] proposed a method using ENVISAT, ERS-2, and Landsat for river level, longitudinal channel slope, and width measurements for estimating river discharge based on the Manning equation, using solely one in situ reference discharge for the unknown bathymetric depth. By repeatedly measuring river width from satellite images, Gleason and Smith [
18] presented an approach estimating discharge based on at-a-station hydraulic geometry (AHG) by Leopold and Maddock [
23]. Here, the river discharge can be related to the river width for a cross section using a power-law function, derived empirically from in situ observations [
18]. For river cross sections within a mass-conserved river reach, the coefficients of this function can be in turn described by a log-linear function. This so called at-many-stations hydraulic geometry (AMHG) relationship can be used to estimate the river discharge from repeated measurements of the river width by minimizing simulated estimated discharge between the river cross sections [
1]. The method was tested for multiple rivers with up to 20 Landsat-5 TM images with RRMSE ranging between 20% to 30% and they proposed to use a proxy of −0.3 for the slope and −0.3 times the mean of all observed river widths as the intercept for the AMHG function to estimate the discharge without using any in situ data [
18,
24].
With the upcoming satellite mission Surface Water and Ocean Topography (SWOT), scheduled for September 2021, simultaneous measurements of river level, channel slope, and width will become available for rivers wider than 100 m, taking remotely sensed discharge estimation a great step further [
25]. Still, as the SWOT mission has a repeat cycle of 21 days, the temporal coverage will not be suitable for daily discharge estimation or monitoring at local sites [
19]. Here, additional satellite missions should be considered to fill this gap. In preparation for this mission, Durand et al. analyzed the AMHG discharge estimation method as well as four methods (Garambois and Monier, Metropolis Manning, Mean Flow and Geomorphology, and Mean Flow and Constant Roughness) based on the Manning flow resistance equation by using 365 synthetical generated measurements [
19]. As a result, no method was considered to be the best approach, as they all showed mixed performance. Nevertheless, the AMHG method showed a significantly lower error as in previous studies, with RRMSE between 11% and 176%, due to the increased number of observations, which leads the proposed proxy to generate incorrect AHG relationships [
19]. The AMHG method furthermore has its greatest deviations in the discharge estimation during the rainy season [
26]. This is especially true for the estimation of flood peaks with overbank-flows and floodplain inundation, as other hydraulic conditions apply [
19,
27]. In summary, the AMHG method proposed in Gleason and Wang [
24] to calculate discharge solely from remote sensing river width measurements has great potential to improve both the estimation of discharge in the rainy season and to overcome the deterioration in performance caused by a large number of measurements.
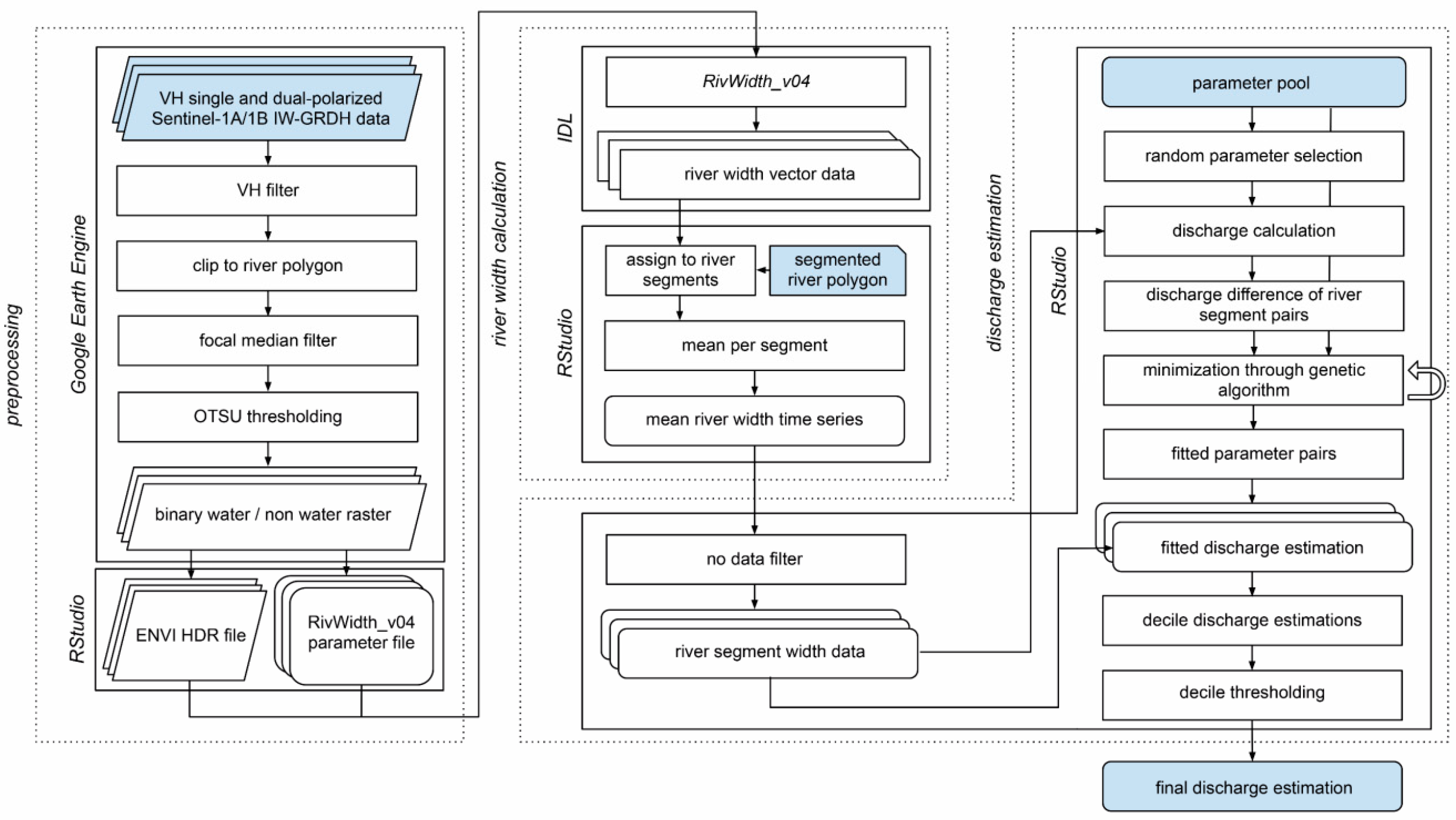
In this study, a novel approach for estimating river discharge is applied using river width measurements derived from Sentinel-1A and 1B time series, improving the AMHG discharge estimation method of Gleason and Wang [
24], without using any a priori information or proxy assumptions on the AMHG function. The key element of our approach is a decile thresholding method, which groups the estimated discharge values into discharge time series related to specific discharge ranges. In a next step, the so-called decile discharge simulations are stacked, using variable thresholds, to filter out discharge values from over- or underestimating simulations. By using Sentinel-1 SAR data, a cloud- and weather-independent measurement of continuous river widths is possible, which is necessary to create a coherent time series. This spaceborne radar data differ from optical satellite data, which, especially in tropical and subtropical areas, do not allow coherent observations due to the heavy cloud cover during the rainy season. To enable a global application of this spaceborne discharge estimation, the decile thresholding method is embedded into an automated workflow, incorporating well established processing steps as well as novel steps, using the Google Earth Engine (GEE) platform [
28], and programs written in the Interactive Data Language (IDL) and R programming languages. We propose an applicable, step-by-step processing approach, which holds the potential for global application as well as making a contribution to the upcoming SWOT mission. The study was carried out on a 28 km river reach of the Mekong River near the capital city of Laos, Vientiane, for the period 2015 to 2018.
2. Study Area
Starting on the Tibetan Plateau at 5200 m above sea level, the Mekong River flows about 4800 km southeast into the South China Sea, crossing China, Myanmar, Laos, Thailand, Cambodia, and Vietnam. With a total area of 795,000 km², the Mekong River Basin has a mean annual runoff of over 475 billion cubic meters, with up to 85% of it occurring in the wet season between June and November [
29,
30]. The hydrological regime is mainly dominated by the southwest monsoon during May to September and to a smaller proportion by the northeast monsoon from November to February, resulting in a regular single flood peak pattern [
31].
The basin can be divided into three main regions, the upper basin, the lower basin, and the delta region. Ranging from its source in Qinghai Province in China to the tri-border corner of Myanmar, Laos, and Thailand, 24% of the total basin area, the Upper Mekong Basin is characterized by its deep gorges and small tributary catchments. Due to the high altitude and snow melt in the headwater region, the Upper Mekong River Basin provides more than 75% of the rivers low-flow as well as more than 50% of the peak flow of the upper part of the downstream Lower Mekong River Basin [
29]. The hydrological regime in the lower part of the Lower Mekong Basin is mainly influenced by the left-bank tributaries in Laos. The Lower Mekong Basin, which reaches as far as Phnom Penh, has less steep slopes and the Mekong riverbed is generally wider here and often shows braided river segments during the low-flow period [
29,
31]. The Mekong Delta region is mainly dominated by artificial canals and dykes, which make the floodplains usable for the cultivation of rice, vegetables, and shrimp. Although the hydrological regime of the Mekong is strongly influenced by both the upstream discharge as well as the tidal interactions with the South China Sea, the inundation of floodplains is mostly cut-off from its natural pattern due to sluice management practices [
32].
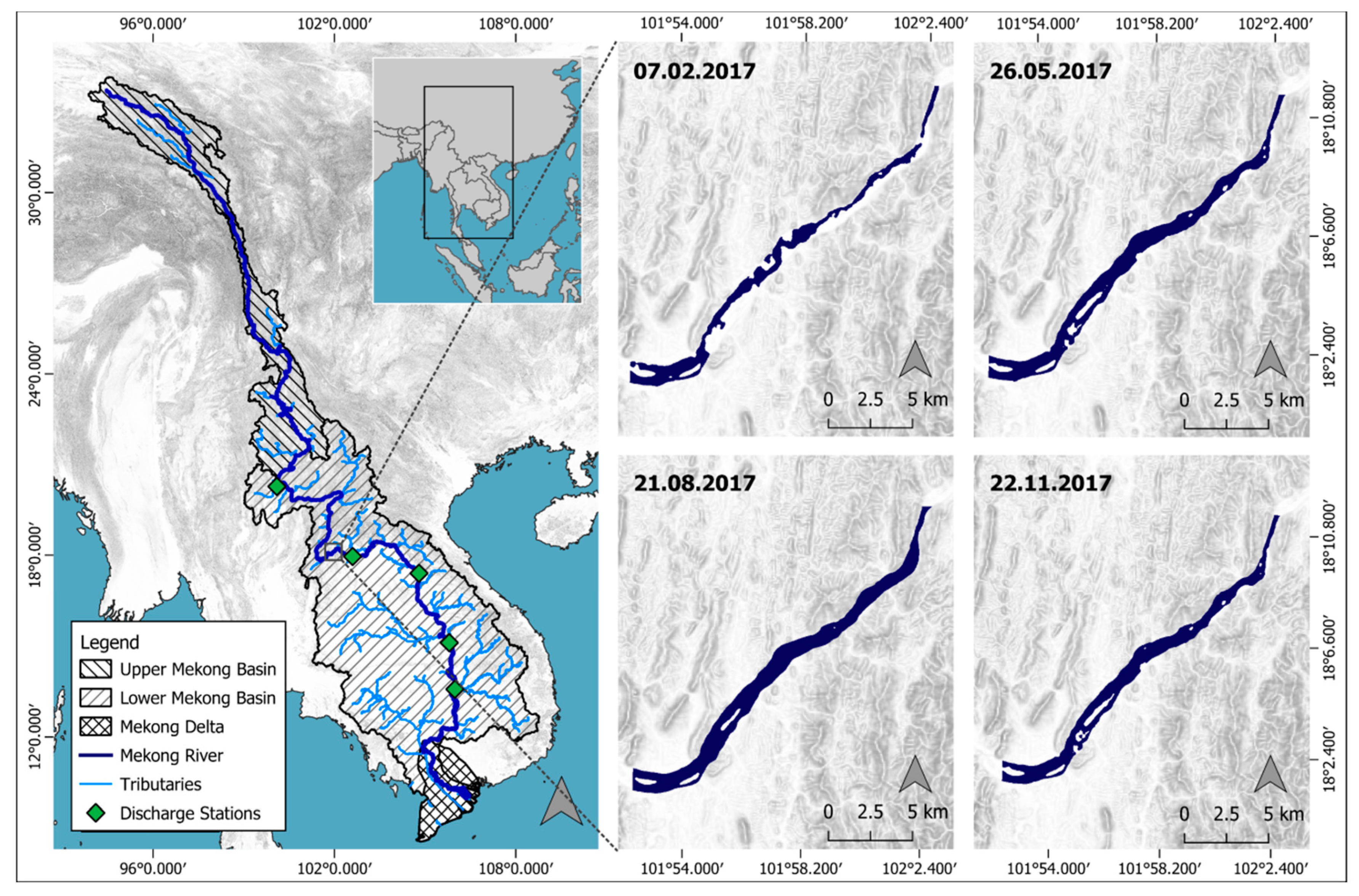
A 28 km long river section located in the Lower Mekong River Basin, 70 km west of Laos’ capital city Vientiane, was selected for estimating the discharge in this study (
Figure 1). This area was chosen because the river shows a great variety in width within this section throughout the year and because it is in closer proximity to a discharge station compared to similar sites. During the dry season, the riverbed has a braided character, with a perennial main channel and several intermittent side channels, partly cut off by islands and vegetation as observed using optical satellite images. During the wet season, the riverbed is completely inundated. Throughout the year, the Mekong River shows a highly dynamic flood pattern at this location with an average width of around 500 m during the dry season and around 700 m during the wet season. In this regard, Sentinel-1 image data with its 10 m pixel spacing is capable of detecting even slight river width changes. The average widths are calculated using RivWidth_v04 software tool from Pavelsky and Smith applied on water masks derived from Sentinel-1 SAR images and the Otsu thresholding method [
33,
34]. The drainage area of this river location is around 4815 km², the mean annual discharge is around 4500 m³/s, based on the values of the nearest gauging station, and the slope along the river section is ~0.05%. Along the selected river section there are no major in- or outflows, fulfilling the criteria of mass-conservancy required for the applied method. The nearest in situ measuring station we had access to is located about 100 km downstream in Vientiane and is used for validation data.
4. Results
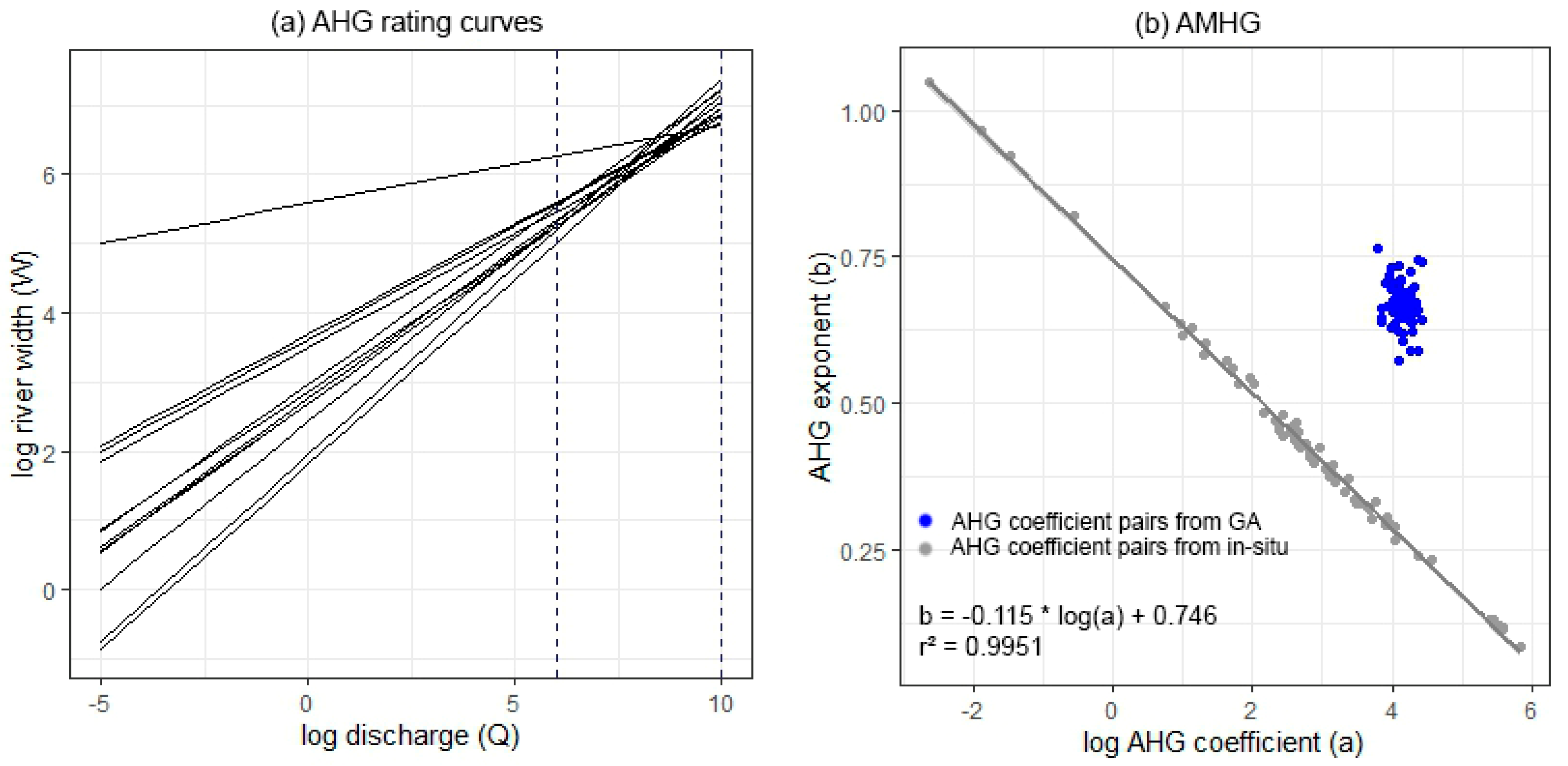
Based on the in situ discharge measurements, the river segments within the observed river reach exhibit distinct AMHG behavior. Correlating the in situ discharge data to the corresponding river width measurements, the AHG rating curves intersect around the same log(Q) – log(W) values (
Figure 13a). As shown in
Figure 13b, the AHG parameters (gray points) of the investigated river reach can therefore be described by a log-linear AMHG function (gray line) with b = −0.115 *log(a) + 0.746, which has an r² of 0.9951. The parameters log(a) and b are between −2.6 to 5.8 and between 0.08 to 1.05, respectively. In comparison, the AMHG parameters derived from the genetic algorithm (blue points) are between 3.7 to 4.4 for parameter log(a) and 0.57 to 0.76 for parameter b. With a root mean square error (RMSE) of 0.405, the parameter pairs are not in close proximity to the AMHG function. Furthermore, they do not tend to show an AMHG relationship by themselves, as they appear to be quite clustered. In this regard, the genetic algorithm using completely randomly drawn initial parameters from the parameter pool was not able to generate AHG parameters comparable to the ones observed from in situ data.
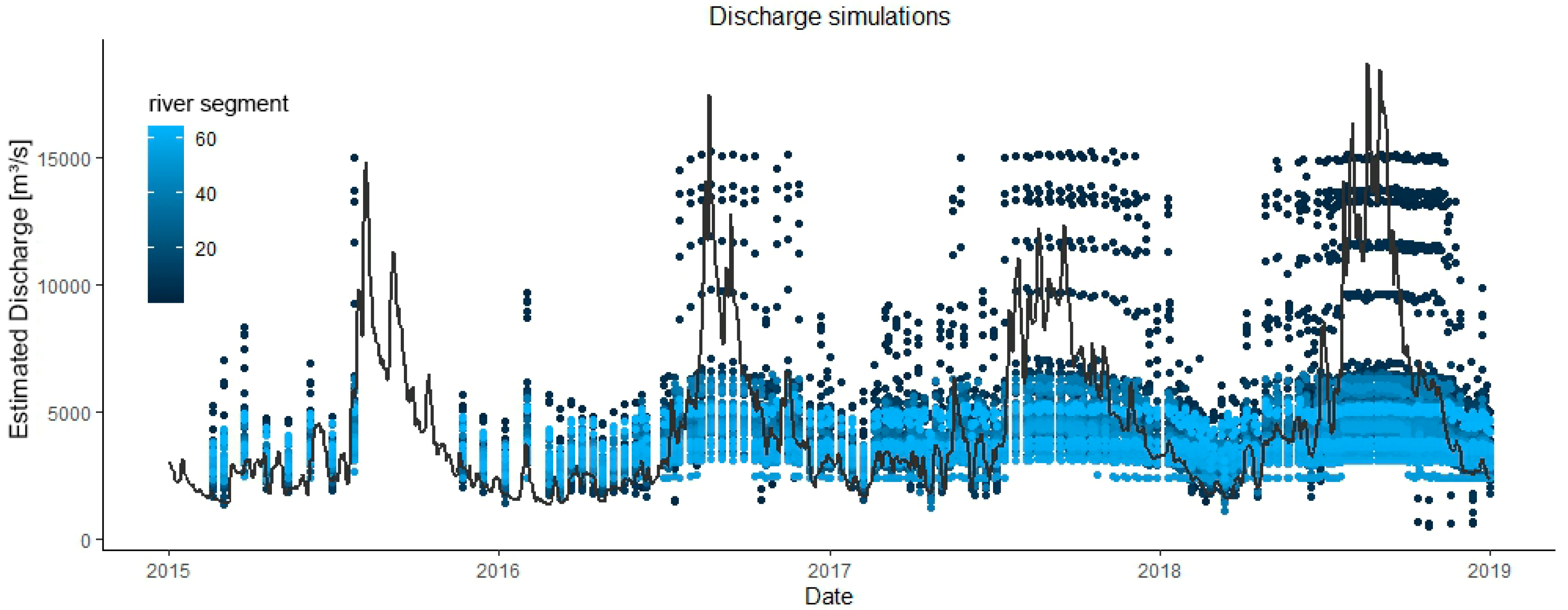
The discharge estimations derived from the AHG optimization show great variability for each day, even though the genetic algorithm decreases the difference in discharge between the river segments (
Figure 14). They do not tend to draw a consistent discharge behavior of the river but rather form a daily discharge interval. With an average difference of 5000 m³/s between the highest and lowest simulation value, the simulations are closer together during the dry season than during the rainy season, with a difference of around 10,000 m³/s. The minimal discharge is 473 m³/s, whereas the maximal discharge is 15,237 m³/s; both underestimate the minimum and maximum in situ discharge. Nevertheless, a seasonal pattern can be observed in all simulations, with some simulations having a wider range between minimum and maximum discharge and a larger variance in their discharge values.
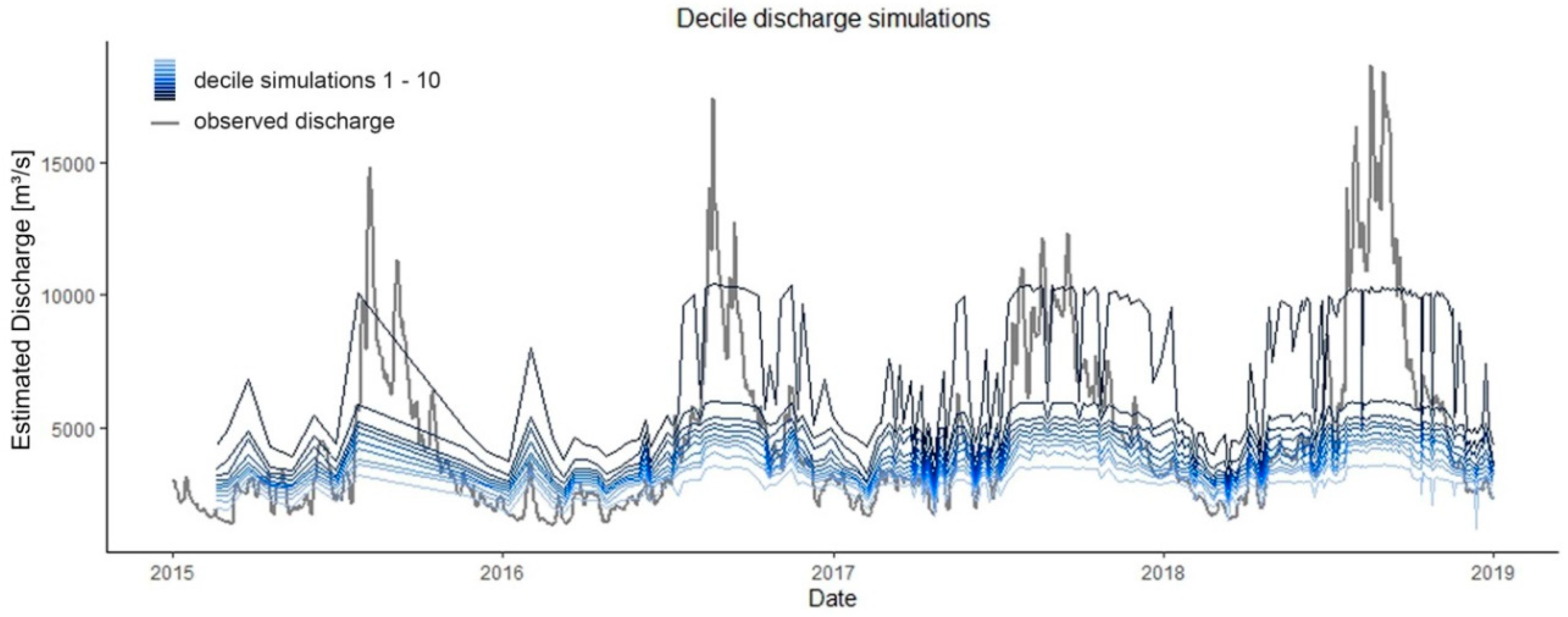
The calculation of the mean decile simulations results in ten simulations which have a certain discharge range, where the difference between estimated and observed discharge is smallest, compared to the other simulations within the same range (
Figure 15). The simulations follow a similar pattern and are superimposed, with the lowest decile simulation having the lowest discharge values and the highest decile simulation having the highest values. The difference between the single simulations is not equal but tends to be larger for the lowest and the highest decile simulations, especially during the high discharge periods. The mean difference between the first and second simulation, as well as between the eighth and ninth simulation, is around 400 m³/s, whereas the difference between the second to eight simulation is around 170 m³/s to 300 m³/s. The greatest difference is between the ninth and tenth simulation with around 2200 m³/s and a maximum difference of 4450 m³/s.
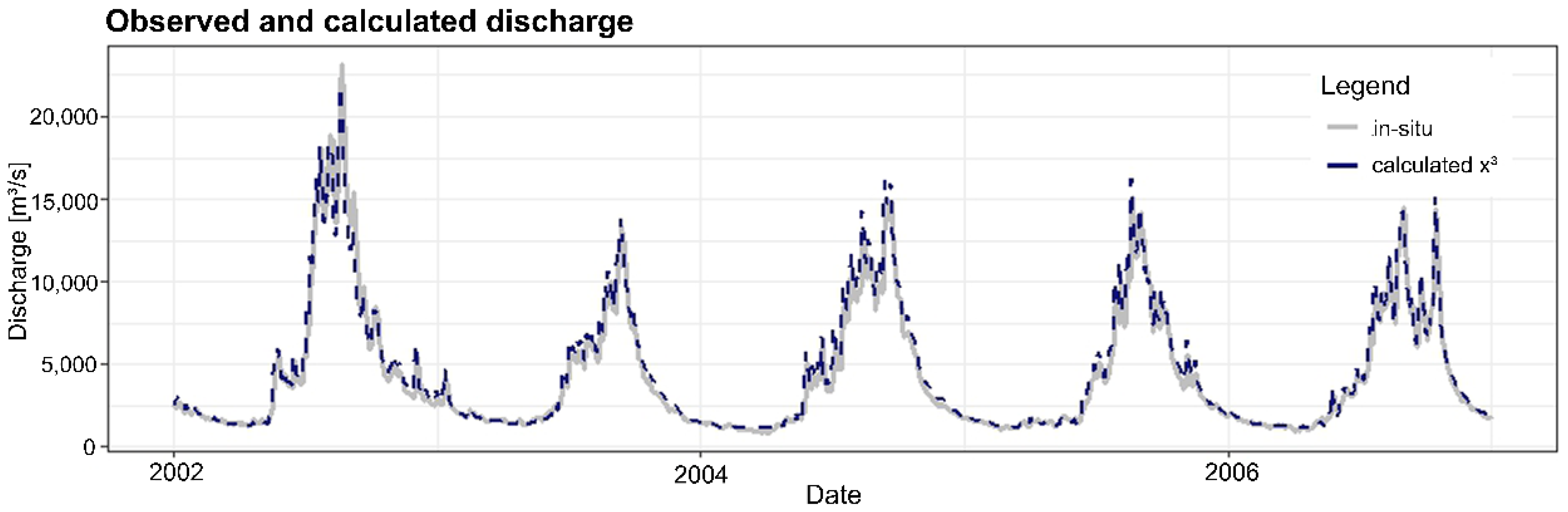
By combining the decile discharge simulations into a single final simulation, the estimated discharge largely corresponds to the observed discharge values, significantly improving the estimation of low flow and peak flow compared to the optimized AMHG method (
Figure 16). The minimum discharge is 1197 m³/s, the maximum discharge is 10,439 m³/s as well as the overall mean is 4485 m³/s. Comparing the simulation to the observed discharge, it is about 8236 m³/s below the maximum observed discharge value, 147 m³/s below the minimum observed discharge value and just 73 m³/s below the observed mean discharge. Regarding the optimized AMHG discharge estimation derived from the method of Gleason and Wang [
24], it shows greater deviations to the validation data, underestimating the high flow discharges as well overestimating the low flow discharges to a far greater extent (
Figure 16). Here, the minimum discharge is 2558 m³/s, the maximum discharge is 5488 m³/s and the mean discharge is 4260 m³/s, resulting in a respective deviation of 1213 m³/s, −13,188 m³/s and −298 m³/s to the minimum, maximum and mean of the validation data.
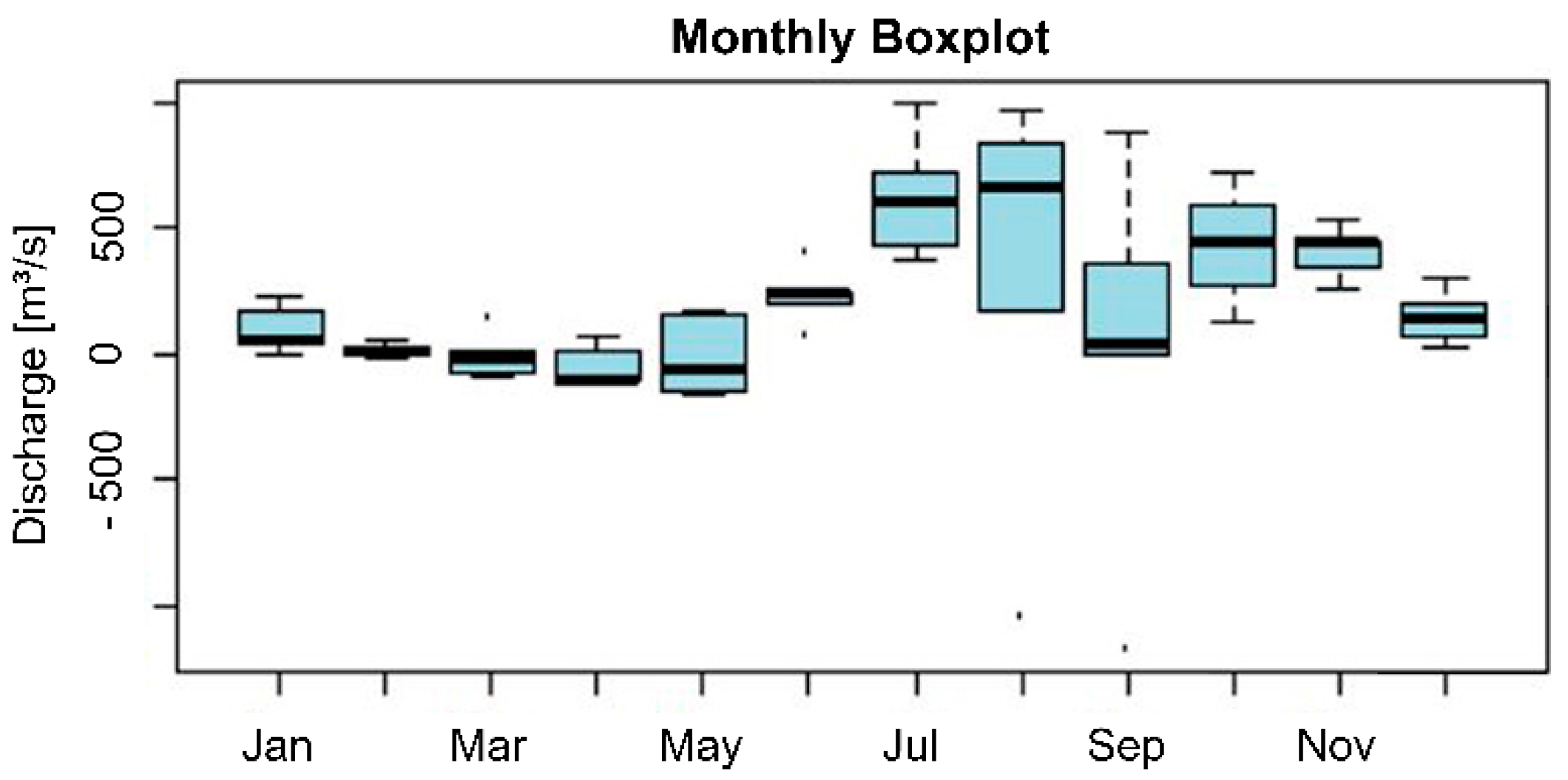
Comparing the discharge values of the simulations with the observed values on the respective day of recording, the decile thresholding method shows a root mean square error (RMSE) and relative root mean square error (RRMSE) almost half as large as the optimized AMHG method, with 1706 m³/s versus 3074 m³/s and 19.5 % versus 38.5%. The median error of the decile thresholding method is 152 m³/s, which is more than three times smaller than the median error of the optimized AMHG method with 538 m³/s. Looking more closely at the performance of the simulation grouped by months, for the dry season months, both simulations have much lower errors than during the wet season (
Figure 17). For the months November to June, both methods show here in general smaller interquartile ranges, less extreme outliers, and smaller median errors, while the discharge is always overestimated. The best results from the decile thresholding method are obtained for the months of May and June with RRMSE of 10.9% and 10.8%. The optimized AMHG method achieves its best results in the months of June and November with a RRMSE of 21.9% and 17.0%.
Looking at the months of July to October, which are characterized by the occurrence of monsoon-related flood peaks, the differences between estimated and observed discharge are greatest in both discharge estimations. In these months, both methods have far greater interquartile ranges and more extreme outliers, while always underestimating the observed discharge. For August and September, the months with the greatest discrepancy between simulation and observed discharge values, the decile thresholding method has a RRMSE of 28.8% and 26.5%. The optimized AMHG method has a RRMSE of 53.7% and 50.0% in the same months, which is almost twice as high. A complete overview about the performance of both methods is displayed in
Table 1.
5. Discussion
With an overall RRMSE of 19.5%, the decile thresholding method achieves a level of performance almost a twice as good at the study region as the optimized AMHG method, with an RRMSE of 38.5%. As both methods have comparable mean discharge values of 4485 m³/s and 4260 m³/s, and are therefore close to the observed mean of 4558 m³/s, their main difference can be found in the estimation in low and high discharge ranges. With minimum discharge of 2558 m³/s and a maximum discharge of 5488 m³/s, the optimized AMHG method is not able to represent the full range of observed discharge values, ranging between 1345 m³/s and 18,676 m³/s. In this way, it systematically overestimates both the low flow discharges and underestimates the flood discharges, which is clearly visible in
Figure 16 and
Figure 17. In comparison, the decile thresholding method is able to improve the estimation of both the low flow discharge as well as the peak discharge. With a minimum estimated discharge of 1197 m³/s and a maximum estimated discharge of 10,439 m³/s, it can cover the observed discharge range comparably better. For the distribution of discharge deviations, a decrease of around 70% can be seen regarding the mean error (152 m³/s to 538 m³/s) as well as the interquartile range is decreasing around 53% (−663 m³/s to 387 m³/s and −1354 m³/s to 891 m³/s).
Even though the methods are site specific, the results of the decile thresholding, using 272 observations, are comparable to the optimized AMHG discharge estimations in Gleason and Smith, with RRMSE of 20%, 23%, and 30% for respective river sites at Athabasca River, Mississippi River, and Yangtze River using up to 20 observations [
18]. Using our novel proposed method, high numbers of observations do not lead to relatively inferior performances as described in Durand et al. [
19], which tested the optimized AMHG method with up to 365 observations for 16 different river sites, achieving RRMSE ranging between 11% to 176.6% with a mean RRMSE of 80.9%. The weaker performance of the optimized AMHG method is caused by the increasing number of observations, which leads to several issues with the AMHG. On the one hand, the proposed AMHG proxy by Gleason and Wang [
24] leads to an ineffective AHG optimization. On the other hand, as an increasing number of observations cover a yearly or greater period, the different AHG behavior of wet and dry season becomes a problem within the optimization process [
19]. Both problems can be observed as well on the discharge estimation derived from optimized AMHG method in our study region. Using the AMHG proxy function with a slope of −0.3 and 1.91 as intercept, it significantly differs from the AMHG function with a slope of −0.115 and intercept of 0.746 derived from the in situ measurements. In this regard, the proxy AMHG function is not representative for the study site and therefore gives misleading discharge estimates. Furthermore, by taking the mean of all discharge estimations derived from each river segment, the different AHG behavior of wet and dry seasons cannot be coped, resulting in both an overestimation of the low flow discharge as well as an underestimation of peak flow discharge. Even though the later problem also applies to the decile thresholding method, as both use the same initial AHG parameters derived by the genetic algorithm optimization, the decile thresholding method can mitigate this problem. By grouping the discharge estimations into discharge ranges, dry and wet season discharge is represented by different river segments. The calculation of the decile simulations and their combination into a final discharge estimation uses therefore discharge estimations from river segments whose AHG parameters are more fitting for the related discharge range. By this, a decrease of 60% of RRMSE for the dry season months and 39% of RRMSE for the wet season months can be achieved using the decile thresholding method compared to the optimized AMHG method. In this regard, the method can further be incorporated into the upcoming SWOT satellite mission. As river width, stage, and slope measurements will be available, Hagemann et al. [
51] proposed novel approach estimating river discharge by using both Manning equation and adding the AMHG method, if the river reach has a high percentage of intersecting AHG curves. Following the same idea, the decile thresholding method can be incorporated into a SWOT adapted method based on Manning equation, if the AMHG behavior is strong in a river reach.
Looking at the dry and wet seasons, there is a clear difference in performance of the discharge estimates, especially regarding the flood peaks. Considering only the months where no flood peak discharge is occurring (Oct–Jun), the accuracy of the decile threshold discharge estimation increases to a RRMSE of 16.0%, while the optimized AMHG method follows the same trend, with an increased accuracy with a RRMSE of 34.5%. This is in line with the trend observed in Gleason and Hamdan [
26], reducing the RRMSE from 56% to 28% for an AMHG discharge estimate of the Ganges River considering only the dry season months.
While the decile thresholding method achieves good results in the low-flow range, the peak flows are almost always underestimated with both methods. Looking at the flood peak maxima, the estimated discharge values of the decile thresholding method do not exceed a certain level at around 10,000 m³/s. This is particularly evident in 2018, when the observed discharge exceeded this level in the months of July, August and September. While the observed values vary, the estimated values remain mostly constant around 10,000 m³/s. This characteristic also occurs in the optimized AMHG method, where it reaches its limit at ~5500 m³/s. Due to a lack of correlation between discharge and river width at this discharge level within the corresponding river segments, the estimated discharge is not increasing. The reason for this is found in the underlying shape of the riverbed. If there is no river width change, the method for estimating the river discharge reaches its physical limits. Another related issue is that AHG only describes inbank flow conditions, as overbank flow is driven by other physical parameters [
27]. Therefore, the estimation of peak flood discharges causing overbank flow must be managed with other methods. Using floodplain hydraulic geometry, the extent of floodplains along a river course for specific peak discharges can be modeled based on a digital elevation model (DEM) and historic discharge records [
27,
52]. Reversing this method, measuring the width of floodplain segments can be used to estimate the related peak discharge. Here, future research combining both methods for estimating discharge could be a promising way coping with the underestimation of flood peak discharge.
While the overall accuracy can be increased due to the calculation and combination of decile simulations, in some cases this method does not give the best result possible. This limitation is evident in particular in July 2015, where the final discharge estimation shows a low value derived from the ninth decile simulation, although the discharge estimation from the tenth decile simulation is more consistent to the observed discharge (
Figure 16). To avoid these errors, the thresholding should be more closely adapted to the individual hydrological pattern, e.g., for each hydrological year and not just based on data from the total discharge.
The AHG parameters derived from the genetic algorithm do not match the AHG parameters derived from in situ discharge observations. The estimates from the genetic algorithm are all in the range from 3.7 < log(a) < 4.4 and 0.57 < b < 0.76 while the range of the AHG parameters from the in situ measurements range from −2.6 < log(a) < 5.8 and 0.08 < b < 1.05 (
Figure 13). In addition, the a and b parameter pairs do not show the linear correlation of the AMHG function. Thus, the genetic algorithm is not able to correctly calculate the respective AHG parameters of the segments, but rather provides adjusted, very similar parameters. As the genetic algorithm only reduces the difference in discharge between the river segments, the optimum does not necessarily result in AHG parameters comparable to the in situ measured ones. Furthermore, the genetic algorithm could have also fallen into a local optimum, even though this issue was addressed using the random mutation of AHG pairs. Using the bayesian inference method for AMHG-based discharge estimation as proposed in Hagemann et al. could improve the calculation of AHG parameters, as it tends to show lower maximum RRMSE values as well as fewer outliers [
51]. Nevertheless, as this method also tends to have higher minimum RRMSE values, further research on both optimization methods should be performed, as it could improve the related discharge estimation. Nevertheless, the estimated AHG parameters for each river segment generally provide suitable results for a specific discharge range. As the AHG parameters differ for the wet and dry season, the approach of considering individual river segment simulations for different discharge ranges gives better results than using all river segment simulations for the entire range of discharge.
Strength and Limitations
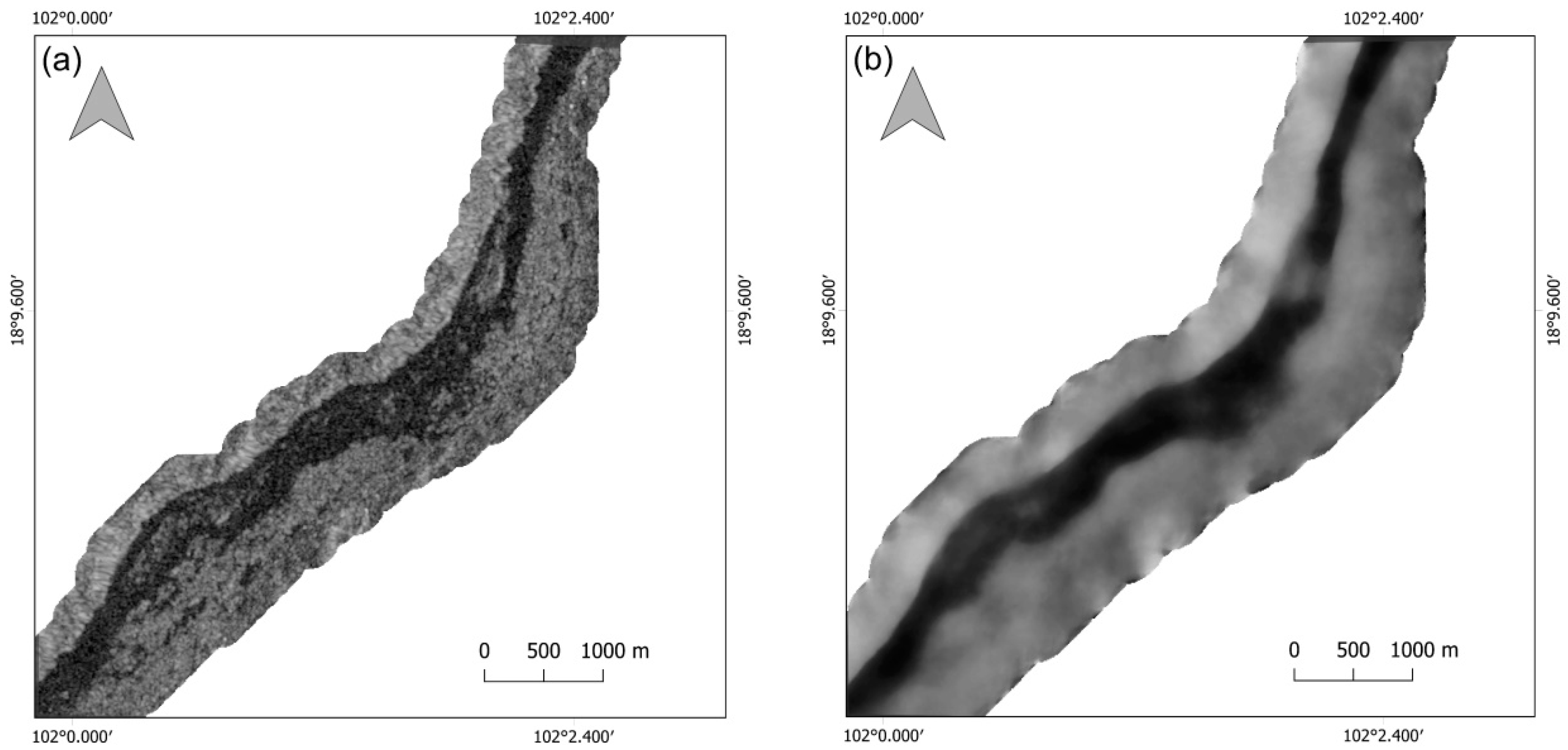
This paper mainly deals with the evaluation of river discharge estimations from river width time series. Nevertheless, the measurement of the river width using remote sensing methods on Sentinel-1 SAR data has a significant influence on the results of the discharge estimation. Starting with the mapping of highly dynamic river regions, the segment length for calculating the seasonality percentage is highly affecting the identification of these regions. In this study, the river region was selected due to its high seasonality percentage for both 25 km and 5 km segments and its proximity to an in situ discharge station. Developing a systematic approach for identifying suitable river regions with an adaptive segment length for calculating the seasonality percentage would be necessary for applying the method on a global scale. In this regard, also the minimum seasonality percentage for which the discharge estimation method yields good results should be defined. The same is true for the length of the investigated river reach and the number of individual river segments used in the genetic algorithm. As shown in this paper, the use of 65 river segments, with a width of 100 m and within a 28 km long river reach is able to give reasonable results for the discharge estimation. As this number is based on the limitations of Sentinel-1 images and the output of the RivWidth_v04 software, it does not necessarily give optimal results. More detailed studies, on how the number of river segments and the chosen river reach affects discharge estimation could therefore further improve the discharge estimation. Regarding the remote sensing of river width using Sentinel-1 images, speckle has a major impact on the water classification. Especially if the boundary between water and river bank is not clear but is ambiguous due to bank vegetation, partial flooding or abandoned river channels, the speckle can lead to major misinterpretations of the actual river width. Using the focal median filter, the speckle could be efficiently reduced, still losing information by blurring the river boundaries (
Figure 10). As different methods for speckle filtering are developed and applied in remote sensing, a detailed consideration of the most suitable filtering method for the purpose of river width measurements should be made. Furthermore, as our method is applied on a single river reach, further research is needed to apply the decile thresholding method on various river reaches worldwide and comparing it to existing spaceborne discharge estimation methods to verify our results.
6. Conclusions and Outlook
We present a novel framework for estimating river discharge using river width measurements, Sentinel-1 SAR time series data and a priori knowledge on minimum and maximum discharge. By using exclusively remotely sensed information about the river width, the discharge estimation method shown in this study requires the least amount of input data, compared to other methods which apply spaceborne earth observation data [
38]. Using weather-independent Copernicus Sentinel-1 data with a revisit time of 6 days, which enables observations also during the highly-clouded rainy season, a continuous river width and discharge time series could be created over the whole observation period from 2015 to 2018.
With an RRMSE of 19.5% for the entire investigated period and a RRMSE of 16% for just the dry-season months, the decile thresholding discharge estimation performed well compared to the optimized AMHG method proposed by Gleason and Wang [
24], with RRMSE of 38.5% and 34.5% respectively. As shown, our novel decile thresholding method can reduce the error both in the low flow as well as peak flow discharge range, resulting in a decrease of 60% in RRMSE for the dry season and a decrease of 39% in RRMSE for the wet season. Compared to global runoff products with a mean RRMSE of 40%, the decile thresholding method can lead to a significant improvement in discharge estimation, whereas the optimized AMHG method just gives a marginal improvement [
38]. An increased error between observed and estimated discharge caused by a high number of observations, as described in Durand et al. [
19], could be partly addressed using the decile thresholding method, whereas it can be observed in the optimized AMHG method. To validate our results, the decile thresholding method should be applied on a global scale at various river reaches and compared to existing methods in further research.
As our proposed method depends on a strong correlation between river width and river discharge, which becomes weaker at higher discharge and overbank flow rates [
19], the capacity for improving on the discharge is rather limited with our method. Incorporating other remote sensed data (e.g., river level), can be therefore a promising way to extend the approach for flood peak discharge conditions. Here, also the incorporation of floodplain hydraulic geometry methods for estimating peak discharge from floodplain width measurements should be researched in more detail to overcome this issue.
To further improve the result of the presented method and its applicability on a global scale, a closer look on the individual processing steps should be taken. Developing a methodological approach for selecting appropriate, highly dynamic river regions as well as investigating the necessary amount of river segments for discharge estimation would help to further automate the method and apply it to other river systems. Requiring just river width measurements, the method can be easily applied to other spaceborne data, besides Copernicus Sentinel-1 SAR. By combining multiple spaceborne data sources, optical as well as radar, an almost daily observation interval can be achieved. Furthermore, with the upcoming earth observation satellites with increased spatial resolution, the method can be also applied on smaller rivers as well as it will further improve the detectable correlation between river width and river discharge.
As presented, the described framework has great potential for an automated estimation of discharge on an almost daily basis for river systems worldwide. Especially for large, ungauged basins in remote areas, this method can help provide valuable information for both scientific as well as operational use. Using only a short, highly dynamic river reach to estimate the discharge and runoff from the upstream catchment, this method could be applied on multiple locations along the river. By this, not only the total runoff can be estimated but also the runoff between two highly dynamic locations.