Background Tropospheric Delay in Geosynchronous Synthetic Aperture Radar
Abstract
1. Introduction
2. Decorrelation Problems of Spatial Variation and BTD Error in the GEO SAR Configuration
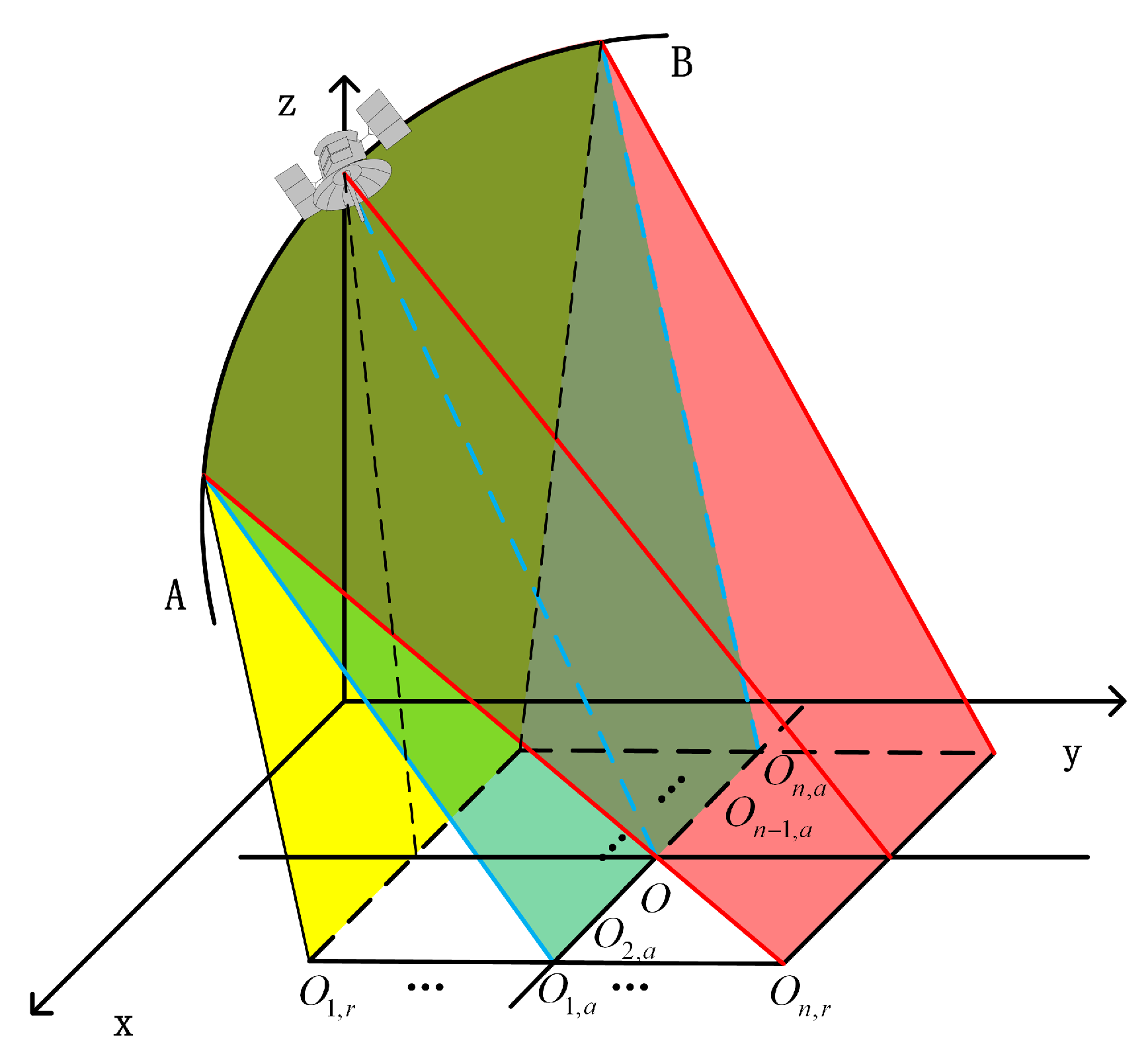
2.1. Geometric Distance Model
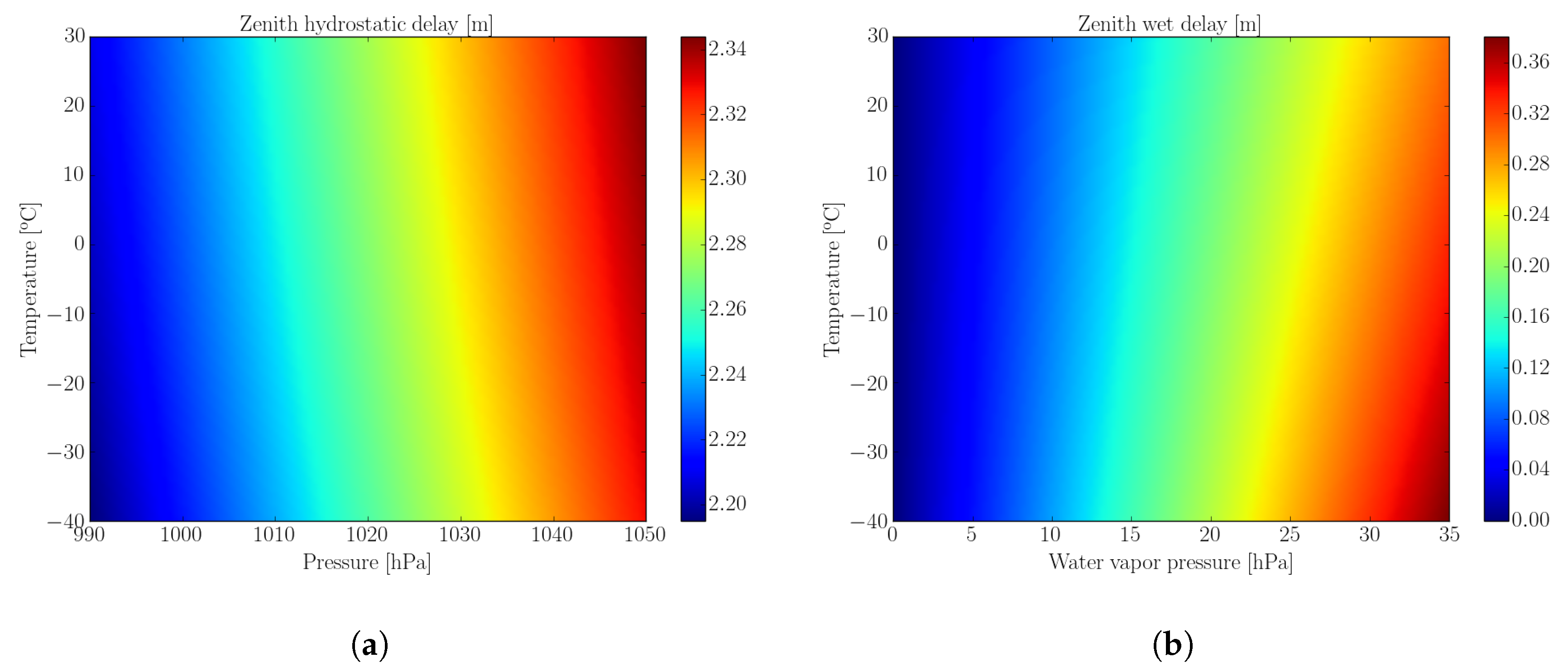
2.2. BTD Error Model
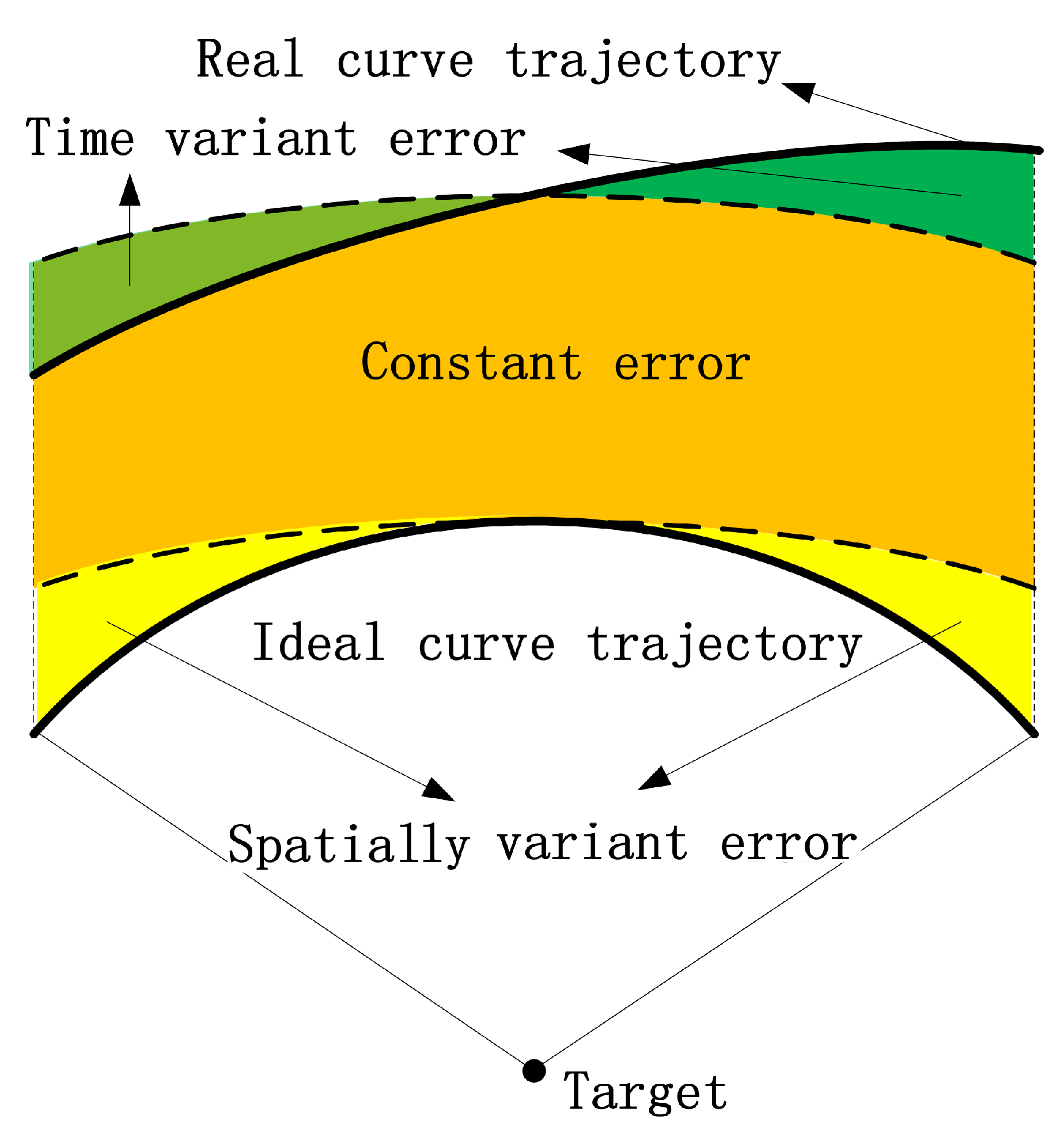
3. Error Analysis of Background Tropospheric Delay
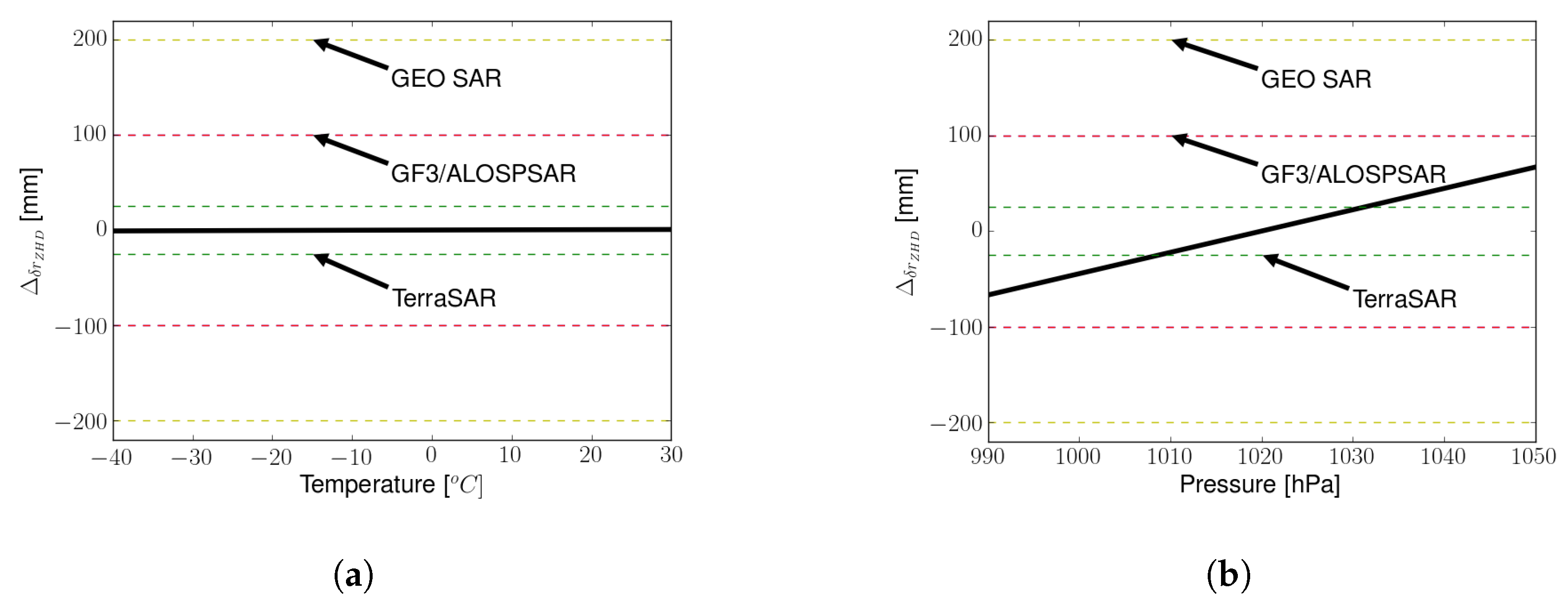
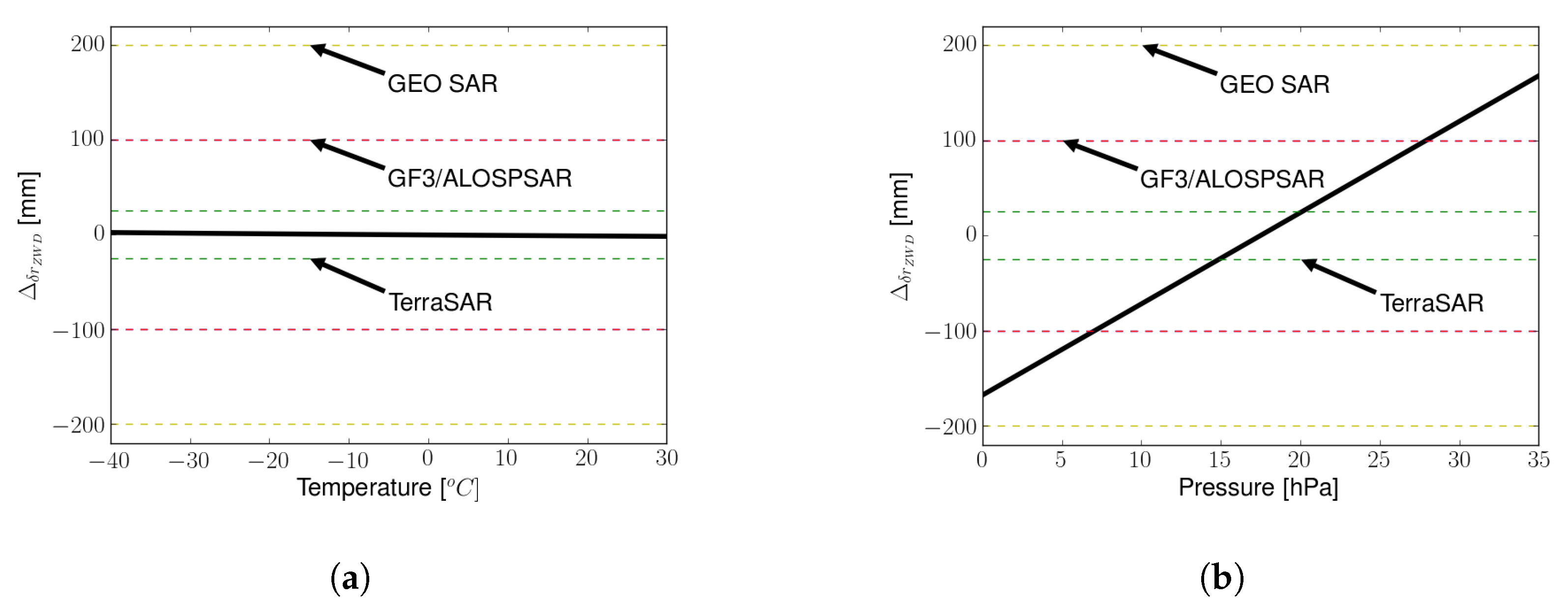
3.1. Constant Error
3.2. Spatially Variant Error
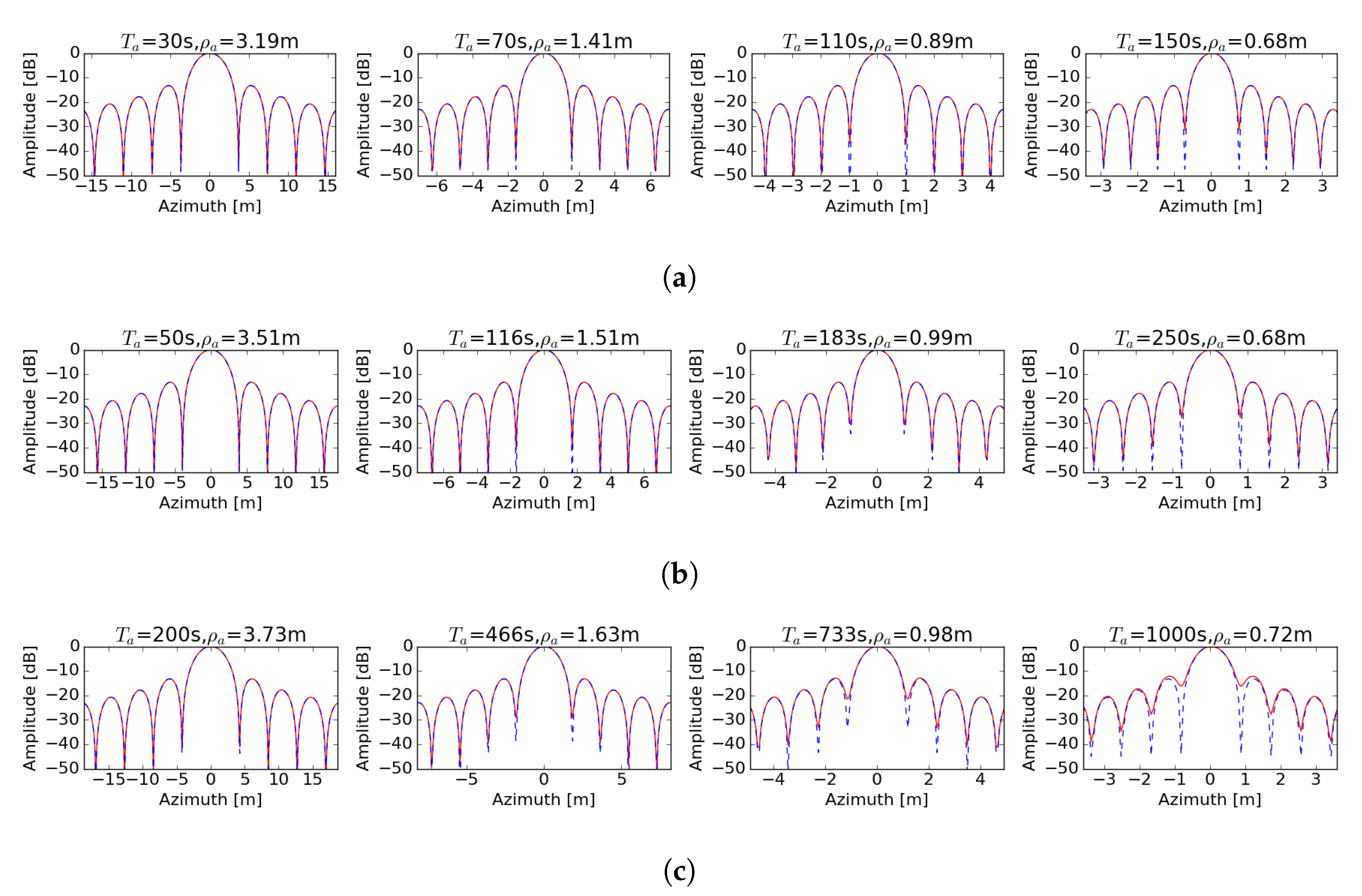
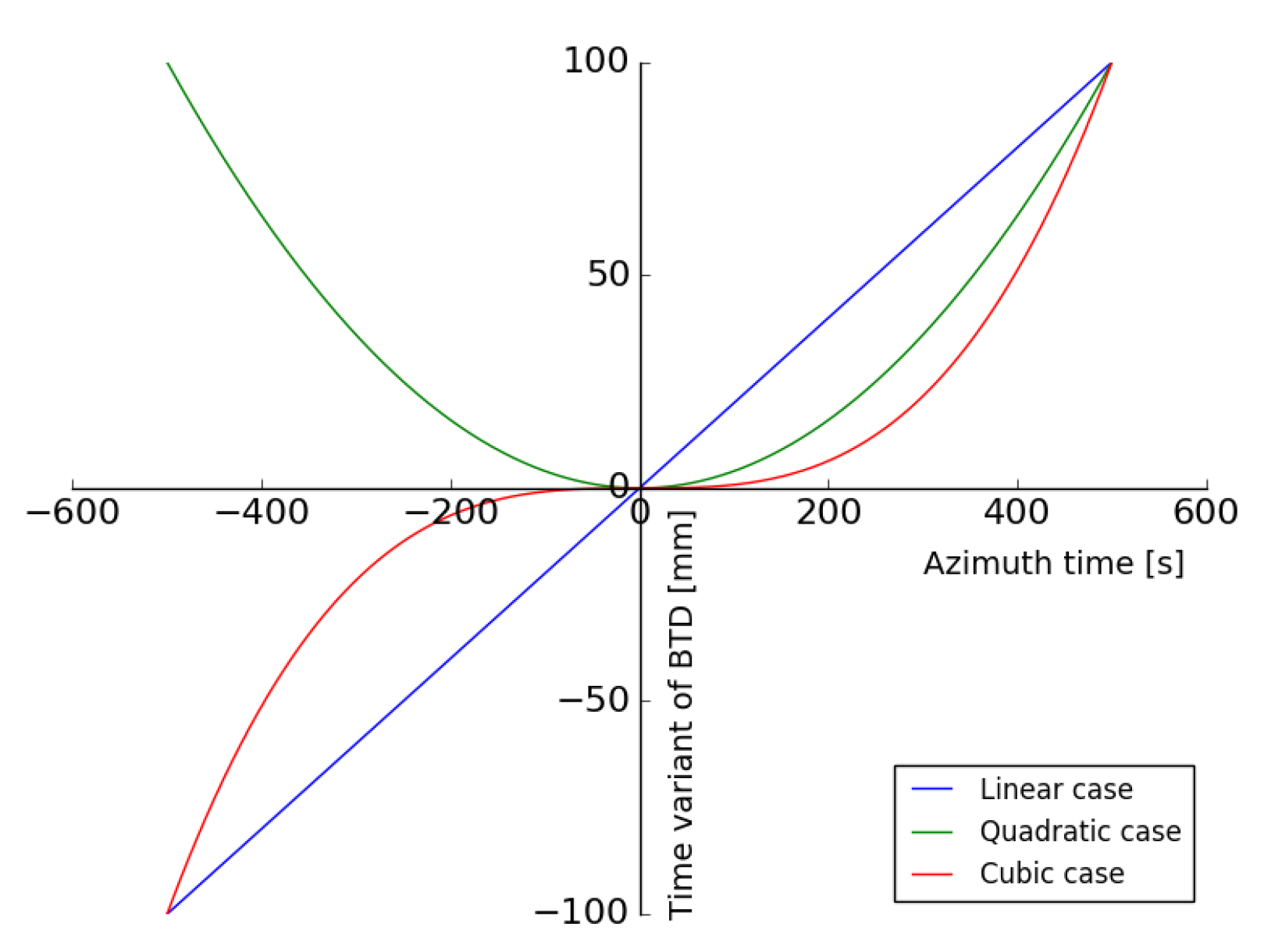
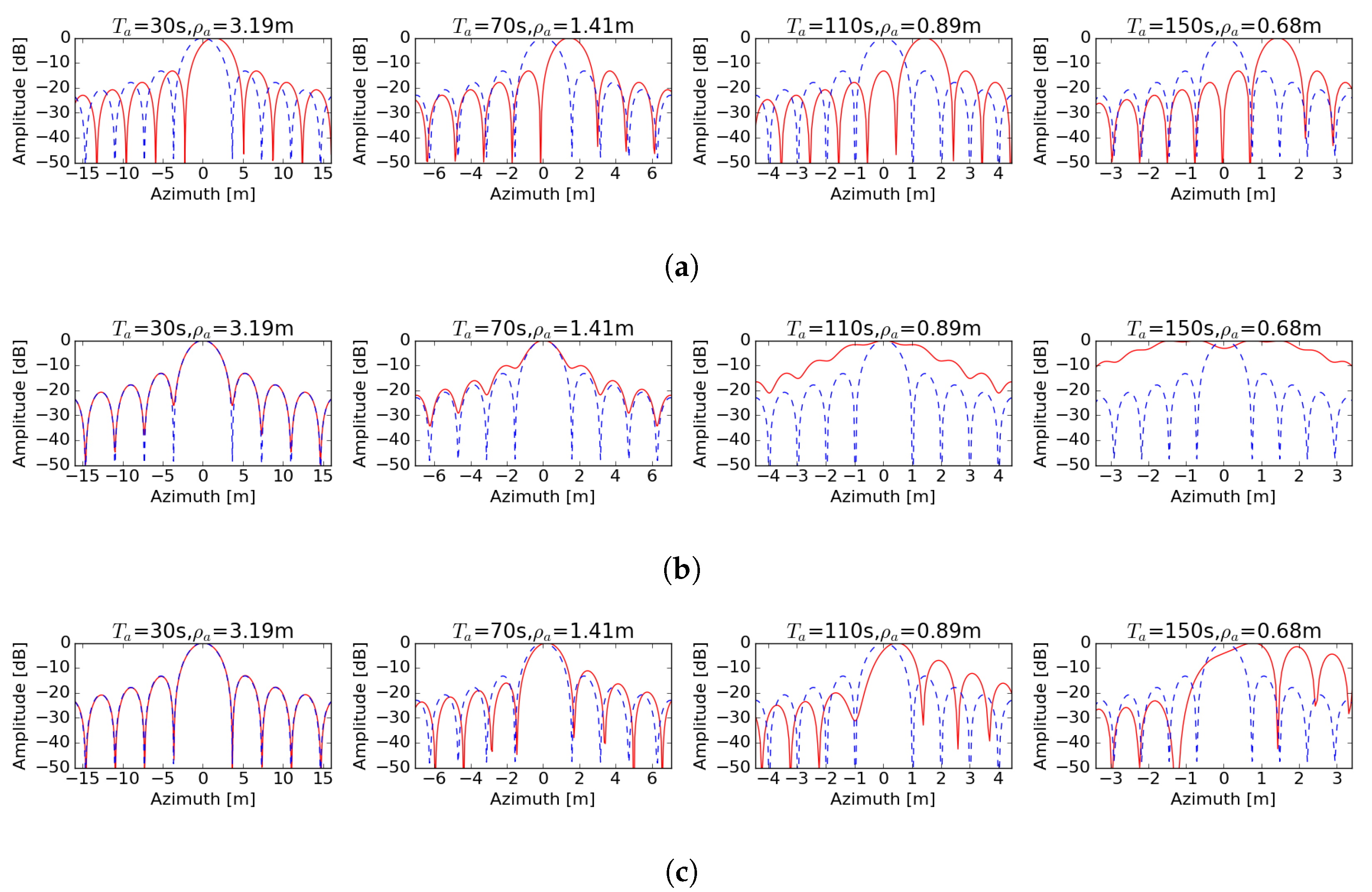
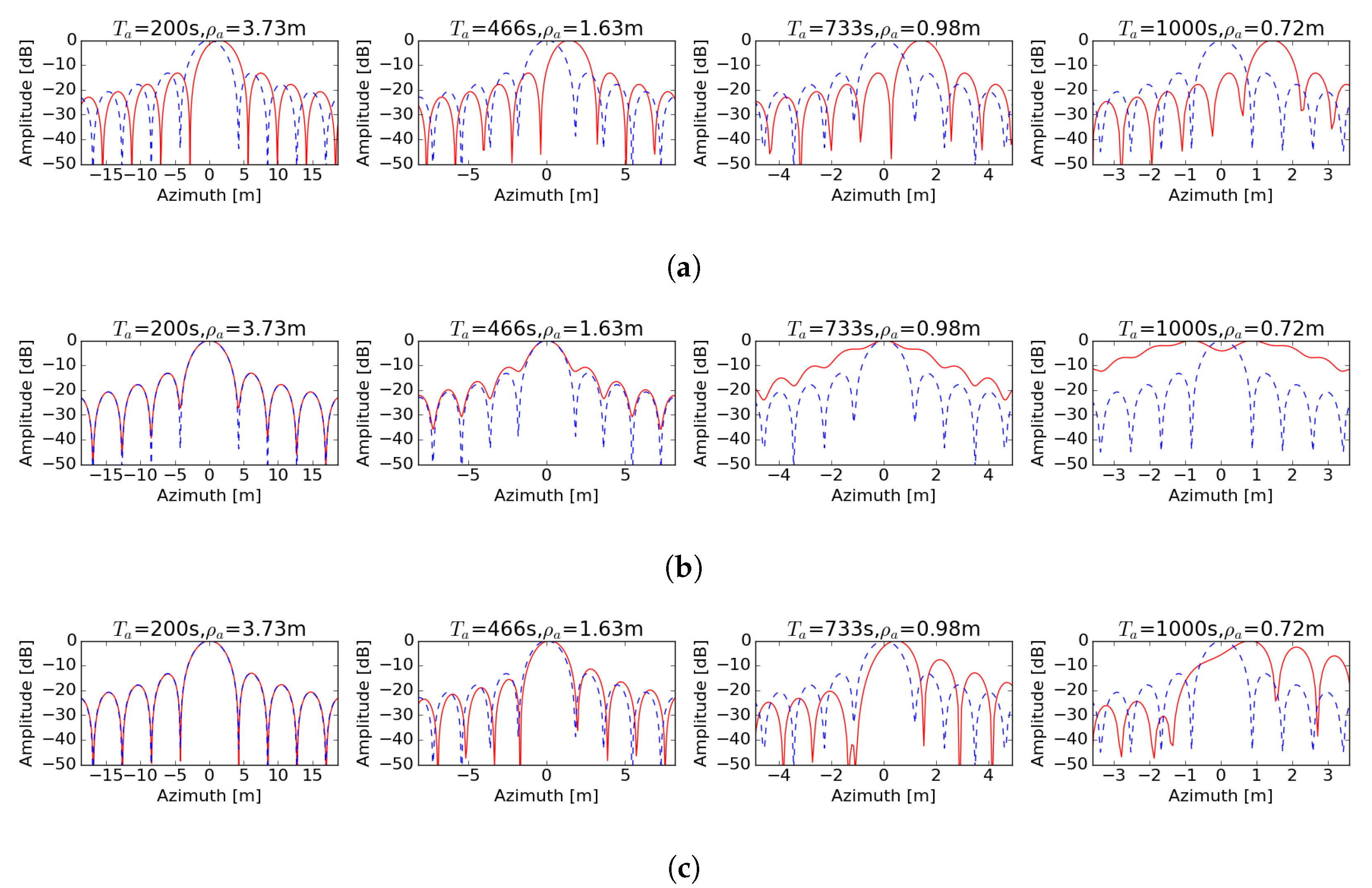
3.3. Time Variant Error
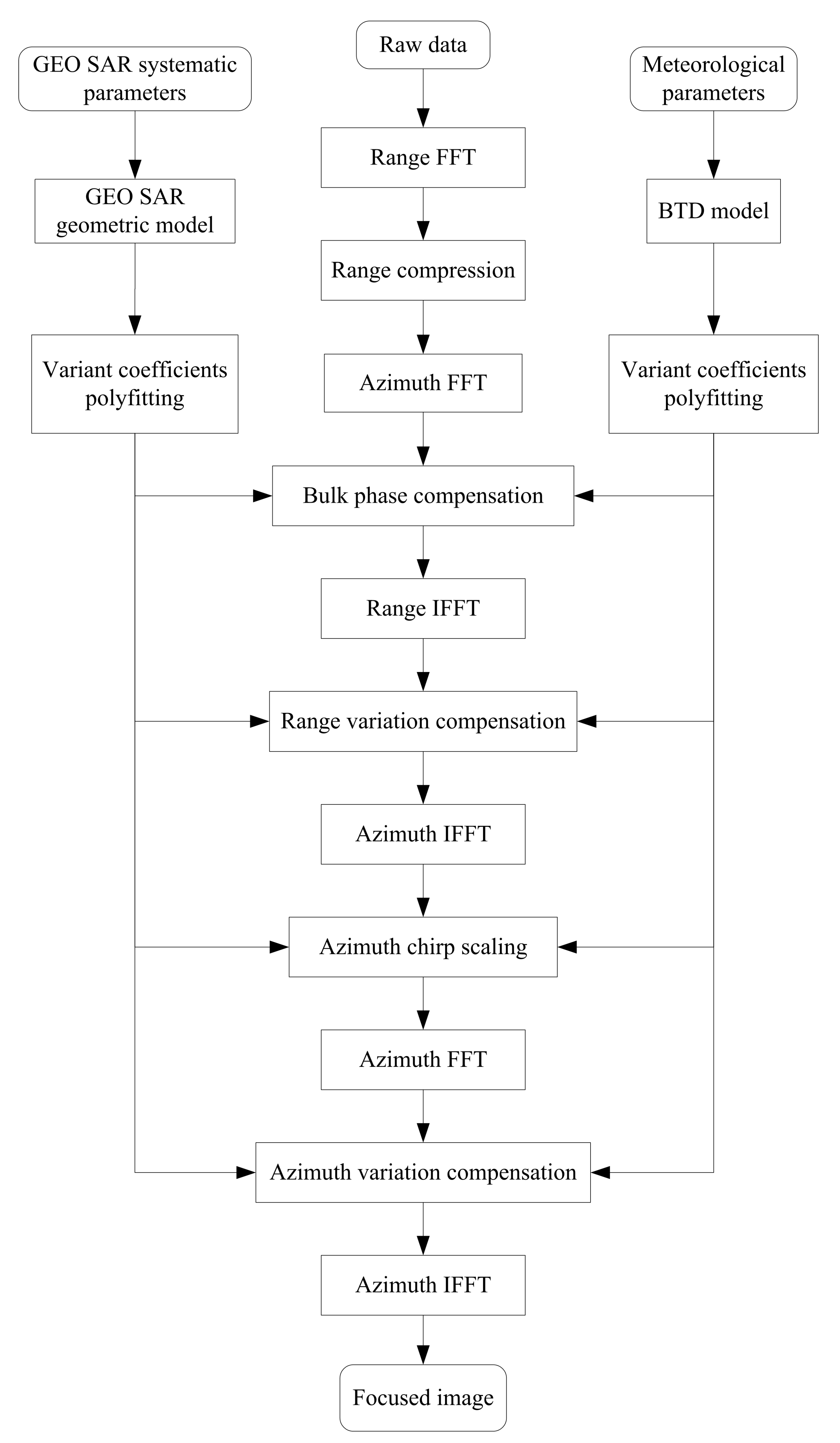
4. Decorrelation Compensation in GEO SAR Image Formation
4.1. GEO SAR Signal Model
4.2. Bulk Phase Compensation
4.3. Range Variant Compensation
4.4. Azimuth Variant Compensation
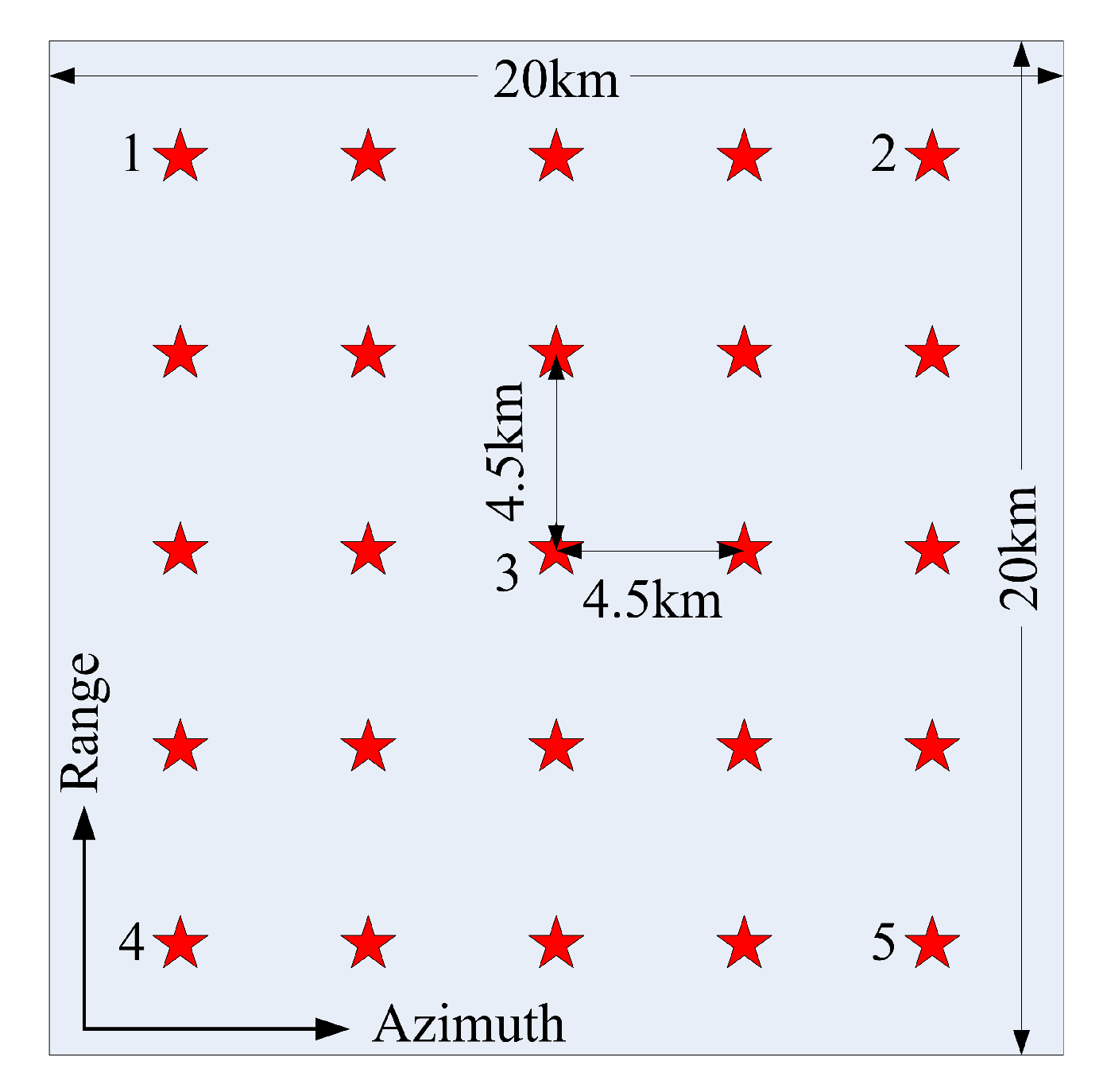
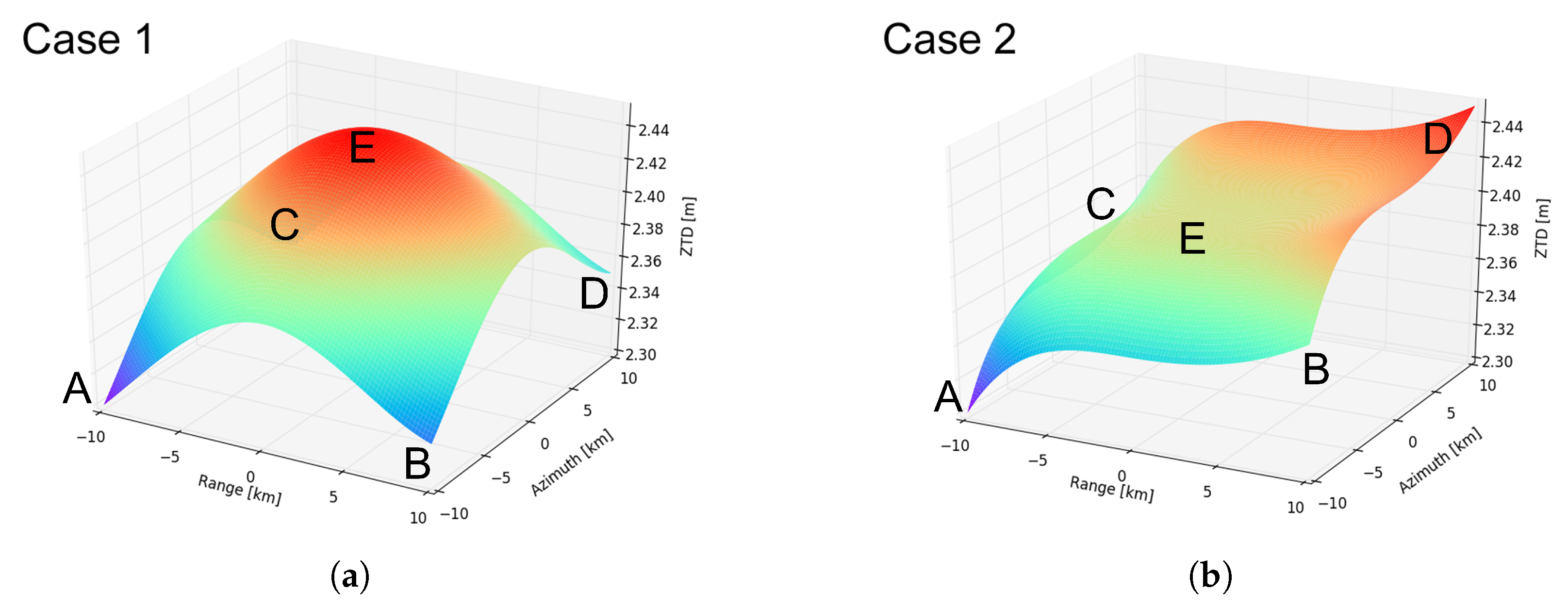
5. Experiments
6. Summary
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Rodon, J.R.; Broquetas, A.; Guarnieri, A.M.; Rocca, F. Geosynchronous SAR Focusing with Atmospheric Phase Screen Retrieval and Compensation. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4397–4404. [Google Scholar] [CrossRef]
- Tomiyasu, K. Synthetic aperture radar in geosynchronous orbit. In Proceedings of the Synthetic Aperture Radar Technology Conference, Washington, DC, USA, 15–19 March 1978. [Google Scholar]
- Kou, L.; Xiang, M.; Wang, X.; Zhu, M. Tropospheric effects on L-band geosynchronous circular SAR imaging. IET Radar Sonar Navig. 2013, 7, 693–701. [Google Scholar] [CrossRef]
- Hobbs, S.E.; Guarnieri, A.M.; Broquetas, A.; Calvet, J.C.; Casagli, N.; Chini, M.; Ferretti, R.; Nagler, T.; Pierdicca, N.; Prudhomme, C.; et al. G-CLASS: Geosynchronous radar for water cycle science— Orbit selection and system design. J. Eng. 2019, 21, 7534–7537. [Google Scholar] [CrossRef]
- Hanssen, R. Radar Interferometry: Data Interpretation and Error Analysis; Kluwer: Dordrecht, The Netherlands, 2001. [Google Scholar]
- Li, D.; Dong, Z.; Yu, A.; Zhang, Y.; Zhang, Q.; He, F.; Wu, M. Estimation and Compensation of turbulent tropospheric delay in High-resolution SAR Image. IEEE Trans. Geosci. Remote Sens. 2020. [Google Scholar] [CrossRef]
- Ji, Y.; Zhang, Q.; Zhang, Y.; Dong, Z.; Yao, B. Spaceborne P-band SAR imaging degradation by anisotropic ionospheric irregularities: A comprehensive numerical study. IEEE Trans. Geosci. Remote Sens. 2020, 58, 5516–5526. [Google Scholar] [CrossRef]
- Ji, Y.; Zhang, Y.; Dong, Z.; Zhang, Q.; Li, D.; Yao, B. Impacts of ionospheric irregularities on L-band geosynchronous synthetic aperture radar. IEEE Trans. Geosci. Remote Sens. 2020, 58, 3941–3954. [Google Scholar] [CrossRef]
- Ishimaru, A.; Kuga, Y.; Liu, J.; Kim, Y.; Freeman, T. Ionospheric effects on synthetic aperture radar at 100 MHz to 2 GHz. Radio Sci. 1999, 34, 257–268. [Google Scholar] [CrossRef]
- Breit, H.; Fritz, T.; Balss, U.; Lachaise, M.; Niedermeier, A.; Vonavka, M. TerraSAR-X SAR Processing and Products. IEEE Trans. Geosci. Remote Sens. 2010, 48, 727–740. [Google Scholar] [CrossRef]
- Prats-Iraola, P.; Scheiber, R.; Rodriguez-Cassola, M.; Mittermayer, J.; Wollstadt, S.; Zan, F.D.; Bräutigam, B.; Schwerdt, M.; Reigber, A.; Moreira, A. On the Processing of Very High Resolution Spaceborne SAR Data. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6003–6016. [Google Scholar] [CrossRef]
- Yu, Z.; Li, Z.; Wang, S. An imaging compensation algorithm for correcting the impact of tropospheric delay on spaceborne high-resolution SAR. IEEE Trans. Geosci. Remote Sens. 2015, 53, 4825–4836. [Google Scholar] [CrossRef]
- Guarnieri, A.M.; Leanza, A.; Recchia, A.; Tebaldini, S.; Venuti, G. Atmospheric Phase Screen in GEO-SAR:Estimation and Compensation. IEEE Trans. Geosci. Remote Sens. 2018, 56, 1668–1679. [Google Scholar] [CrossRef]
- Saastamoinen, J. Atmospheric correction for the troposphere and stratospherein radio ranging of satellites. Geophys. Monogr. Ser. 1972, 15, 247–251. [Google Scholar]
- Davis, J.L.; Herring, T.A.; Shapiro, I.I.; Rogers, A.E.E.; Elgered, G. Geodesy by radio interferometry: Effects of atmospheric modeling errors on estimates of baseline length. Radio Sci. 1985, 20, 1593–1607. [Google Scholar] [CrossRef]
- Askne, J.; Nordius, H. Estimation of tropospheric delay for microwaves from surface weather data. Radio Sci. 1987, 22, 379–386. [Google Scholar] [CrossRef]
- Böhm, J.; Werl, B.; Schuh, H. Troposphere mapping functions for GPS and very long baseline interferometry from European Centre for Medium-Range Weather Forecasts operational analysis data. J. Geophys. Res. 2006, 111. [Google Scholar] [CrossRef]
- Rasmussen, C.E.; Williams, C.K. Gaussian Processes for Machine Learning; The MIT Press: Cambridge, MA, USA, 2006. [Google Scholar]
- George, W.K. Lectures in Turbulence for the 21st Century; Imperial College of London: London, UK, 2013. [Google Scholar]
- Li, D.; Rodriguez-Cassola, M.; Prats-Iraola, P.; Dong, Z.; Wu, M.; Moreira, A. Modeling of Tropospheric Delays in Geosynchronous Synthetic Aperture Radar. China Sci. Inform. Sci. 2017, 60, 81–98. [Google Scholar] [CrossRef]
- Hu, C.; Liu, Z.; Long, T. An Improved CS Algorithm Based on the Curved Trajectory in Geosynchronous SAR. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 795–808. [Google Scholar] [CrossRef]
- Sun, G.C.; Xing, M.; Wang, Y.; Yang, J.; Bao, Z. A 2-D Space-Variant Chirp Scaling Algorithm Based on the RCM Equalization and Subband Synthesis to Process Geosynchronous SAR Data. IEEE Tran. Geosci. Remote Sens. 2014, 52, 4868–4880. [Google Scholar]
- Li, D.; Wu, M.; Sun, Z.; He, F.; Dong, Z. Modeling and Processing of Two-Dimensional Spatial-Variant Geosynchronous SAR Data. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 2015, 8, 3999–4009. [Google Scholar] [CrossRef]
- Wong, F.H.; Cumming, I.G.; Neo, Y.L. Focusing Bistatic SAR Data Using the Nonlinear Chirp Scaling Algorithm. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2493–2505. [Google Scholar] [CrossRef]
- Smith, E.K.; Weintraub, S. The Constants in the Equation for Atmospheric Refractive Index at Radio Frequencies. Proc. IRE 1953, 41, 1035–1037. [Google Scholar] [CrossRef]
- Boehm, J.; Heinkelmann, R.; Schuh, H. Short Note: A global model of pressure and temperature for geodetic applications. J. Geod. 2007, 81, 679–683. [Google Scholar] [CrossRef]
- Lagler, K.; Schindelegger, M.; Boehm, J.; Krásná, H.; Nilsson, T. GPT2: Empirical slant delay model for radio space geodetic techniques. Geophys. Res. Lett. 2013, 40, 1069–1073. [Google Scholar] [CrossRef] [PubMed]
- Böhm, J.; Möller, G.; Schindelegger, M.; Pain, G.; Weber, R. Development of an improved empirical model for slant delays in the troposphere (GPT2w). GPS Solut. 2015, 19, 433–441. [Google Scholar] [CrossRef]
- Cumming, I.G.; Wong, F.H. Digital Processing of Synthetic Aperture Radar; Artech House: Boston, MA, USA, 2005. [Google Scholar]

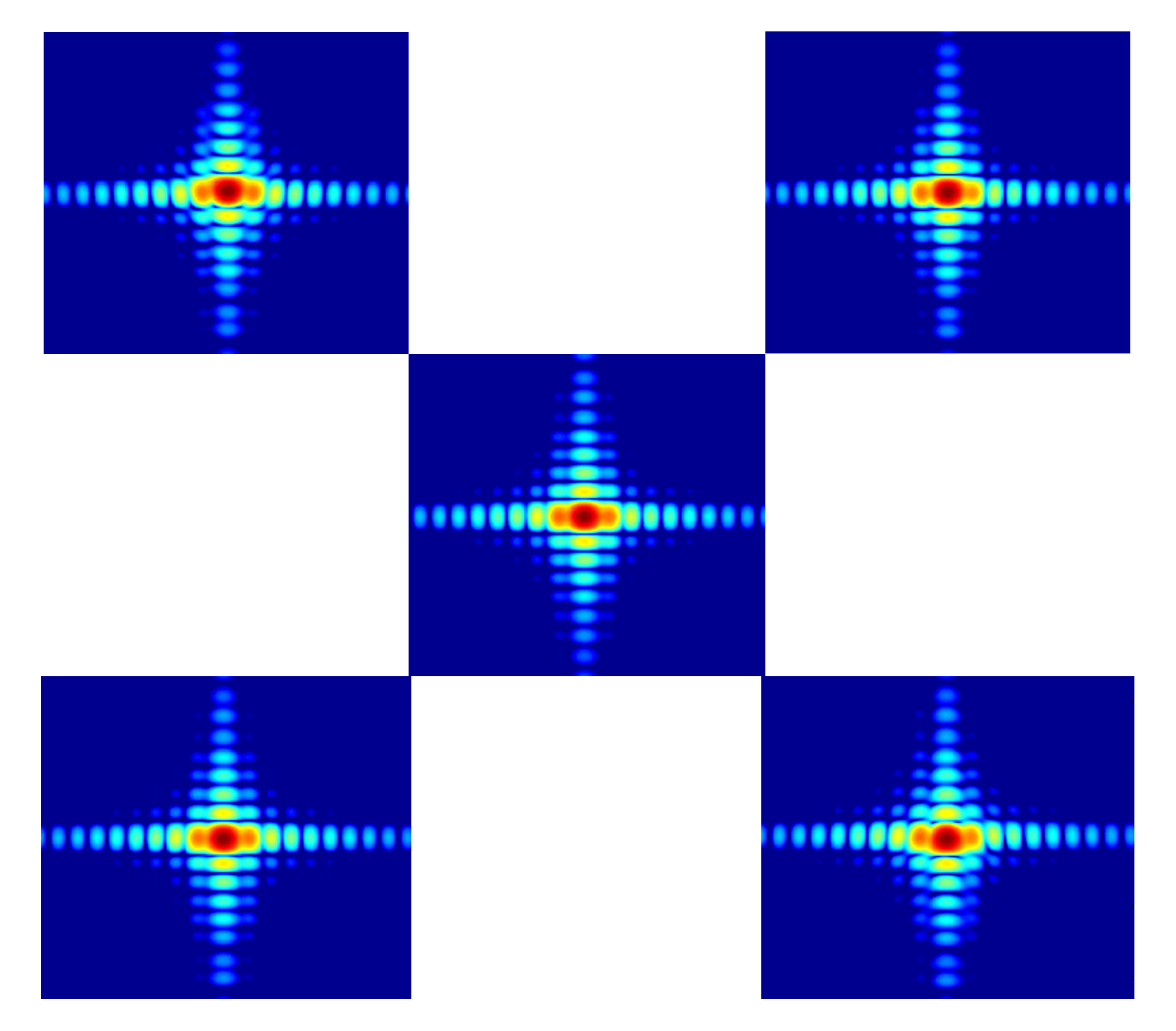


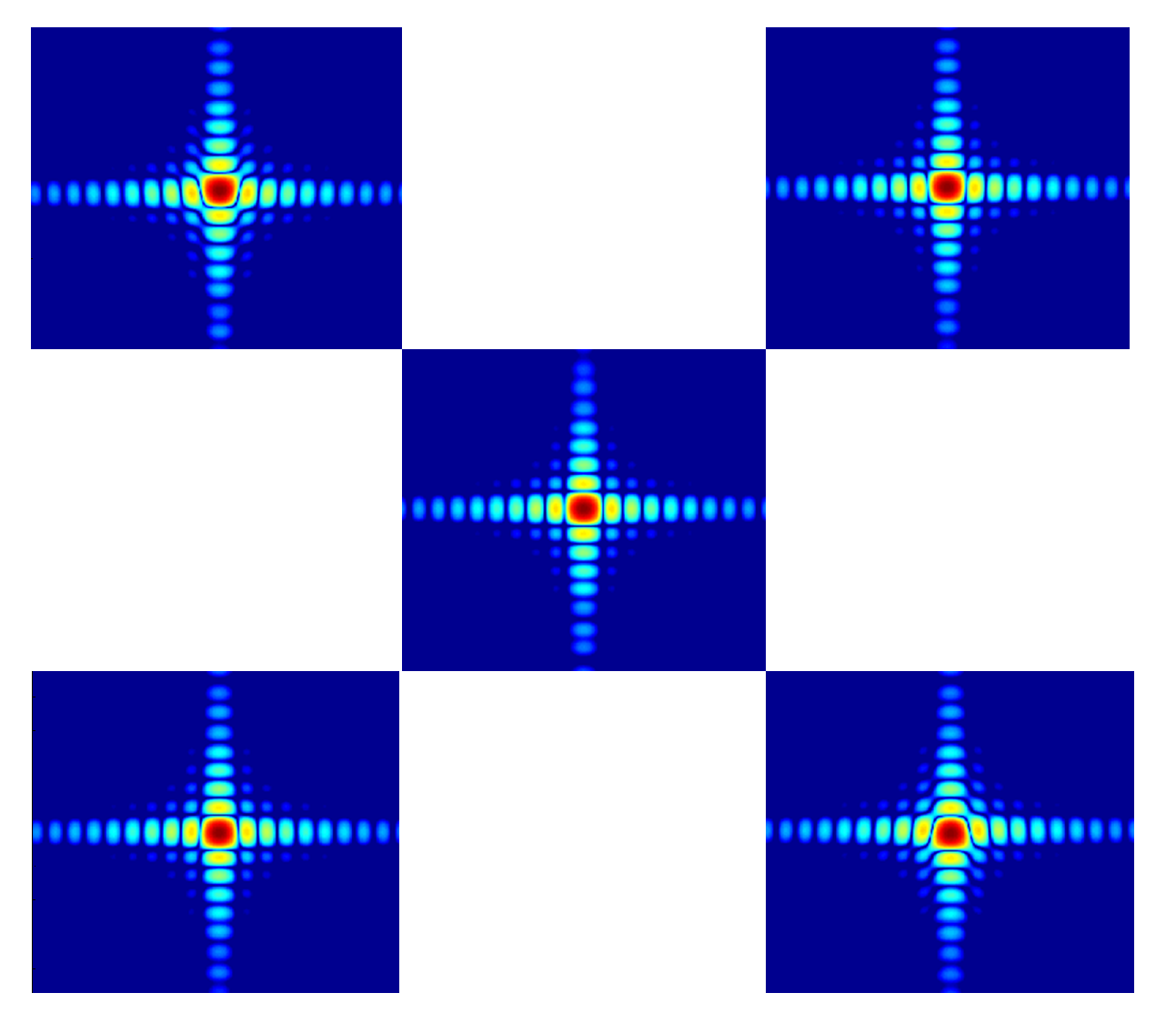
| Parameters | Values | Parameters | Values |
|---|---|---|---|
| 0.0029 | 0.062 | ||
| (, 0) | (0.007, 0.005) | ||
| (0.002, 0.001) | 0.0000253 | ||
| 0.00549 | 0.00114 | ||
| 0.00146 | 0.04391 |
| Parameters (Units) | TerraSAR | ALOS-PSAR | GF3 | GEO SAR |
|---|---|---|---|---|
| Orbital height (km) | 514 | 691.65 | 755 | 36,000 |
| Eccentricity (-) | 0 | 0 | 0 | 0 |
| Orbital inclination (deg) | 97.44 | 98.16 | 97 | 60 |
| Incident angle (deg) | 15∼60 | 8∼60 | 10∼60 | 25 |
| Antenna size (m × m) | 0.7 × 4.78 | 3.1 × 8.9 | 1.5 × 15 | 30 × 30 |
| Waveband | X | L | C | L |
| Parameters | Values | Units |
|---|---|---|
| Semi-major axis | 42,164.17 | km |
| Eccentricity | 1 × 10−8 | |
| Orbital inclination | 60 | deg |
| Right ascension of ascending (RAAN) | 0 | deg |
| Perigee | 0 | deg |
| True anomaly | 0 | deg |
| Carrier frequency | 1.25 | GHz |
| Antenna size | 30 × 30 | m × m |
| Squint angle | 0 | deg |
| Incident angle | 30.28 | deg |
| Pulse repetition frequency (PRF) | 200 | Hz |
| Chirp duration | 1 | s |
| Chirp bandwidth | 30 | MHz |
| Cases | Point | A | B | C | D | E |
|---|---|---|---|---|---|---|
| Case 1 | 1008.1 | 1008.44 | 1008.4 | 1008.92 | 1009.29 | |
| 28 | 29.5 | 30 | 29 | 30 | ||
| 5.79 | 8.59 | 8.6 | 11.38 | 22.95 | ||
| Case 2 | 1008.1 | 1008.44 | 1008.47 | 1009.29 | 1008.9 | |
| 28 | 29.5 | 29 | 30 | 29.3 | ||
| 5.79 | 14.28 | 14.26 | 22.95 | 17.21 |
| Targets | 1 | 2 | 3 | 4 | 5 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Cases | Azimuth | Range | Azimuth | Range | Azimuth | Range | Azimuth | Range | Azimuth | Range | |
| Case 1 without BTD compensation | IRW | 2.14 | 4.44 | 2.10 | 4.41 | 2.14 | 4.45 | 2.13 | 4.41 | 2.12 | 4.45 |
| PSLR | −8.95 | −14.23 | −8.88 | −13.99 | −8.32 | −13.85 | −8.96 | −13.90 | −8.60 | −13.90 | |
| ISLR | −6.21 | −11.09 | −7.22 | −10.96 | −6.20 | −10.60 | −6.22 | −10.88 | −6.96 | −10.83 | |
| Case 1 with BTD compensation | IRW | 2.04 | 4.45 | 2.03 | 4.45 | 2.04 | 4.41 | 2.04 | 4.45 | 2.04 | 4.48 |
| PSLR | −13.06 | −13.89 | −13.22 | −13.71 | −13.26 | −14.07 | −13.25 | −13.72 | −13.14 | −13.90 | |
| ISLR | −9.78 | −10.93 | −9.77 | −10.74 | −9.84 | −10.98 | −9.89 | −10.69 | −9.81 | −10.82 | |
| Case 2 without BTD compensation | IRW | 2.08 | 4.47 | 2.04 | 4.45 | 2.06 | 4.41 | 2.09 | 4.47 | 2.05 | 4.48 |
| PSLR | −8.48 | −13.95 | −9.48 | −13.71 | −9.07 | −14.08 | −8.47 | −13.72 | −9.40 | −13.90 | |
| ISLR | −12.21 | −10.93 | −12.97 | −10.74 | −12.99 | −10.96 | −12.28 | −10.67 | −13.31 | −10.81 | |
| Case 2 with BTD compensation | IRW | 2.04 | 4.47 | 2.04 | 4.45 | 2.04 | 4.41 | 2.05 | 4.45 | 2.04 | 4.48 |
| PSLR | −13.05 | −13.90 | −13.19 | −13.71 | −13.27 | −14.07 | −13.21 | −13.72 | −13.12 | −13.90 | |
| ISLR | −9.71 | −10.93 | −9.82 | −10.74 | −9.85 | −10.98 | −9.85 | −10.70 | −9.90 | −10.82 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, D.; Zhu, X.; Dong, Z.; Yu, A.; Zhang, Y. Background Tropospheric Delay in Geosynchronous Synthetic Aperture Radar. Remote Sens. 2020, 12, 3081. https://doi.org/10.3390/rs12183081
Li D, Zhu X, Dong Z, Yu A, Zhang Y. Background Tropospheric Delay in Geosynchronous Synthetic Aperture Radar. Remote Sensing. 2020; 12(18):3081. https://doi.org/10.3390/rs12183081
Chicago/Turabian StyleLi, Dexin, Xiaoxiang Zhu, Zhen Dong, Anxi Yu, and Yongsheng Zhang. 2020. "Background Tropospheric Delay in Geosynchronous Synthetic Aperture Radar" Remote Sensing 12, no. 18: 3081. https://doi.org/10.3390/rs12183081
APA StyleLi, D., Zhu, X., Dong, Z., Yu, A., & Zhang, Y. (2020). Background Tropospheric Delay in Geosynchronous Synthetic Aperture Radar. Remote Sensing, 12(18), 3081. https://doi.org/10.3390/rs12183081





