Detection of Italian Ryegrass in Wheat and Prediction of Competitive Interactions Using Remote-Sensing and Machine-Learning Techniques
Abstract
1. Introduction
2. Materials and Methods
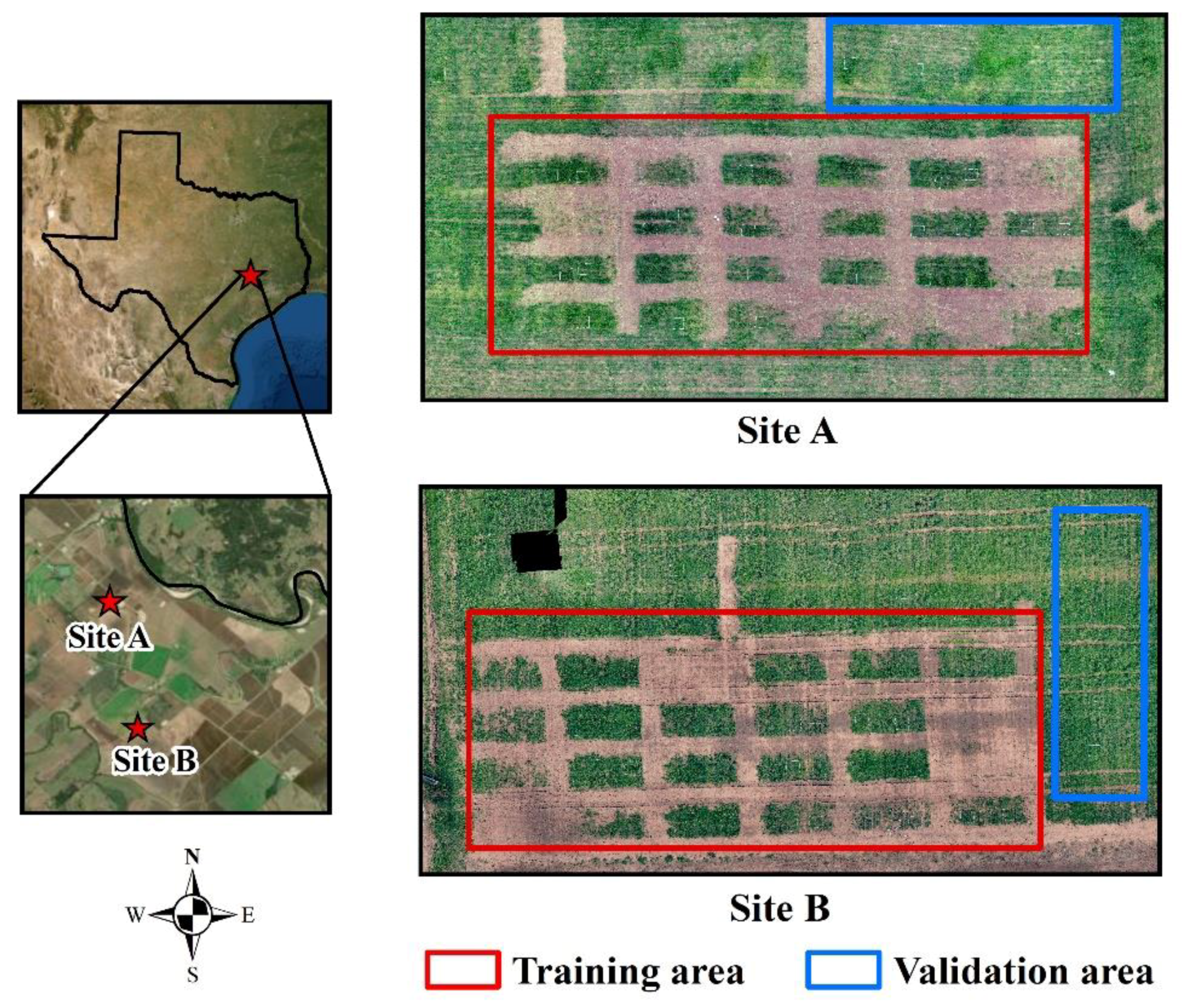
2.1. Location and Experimental Setup
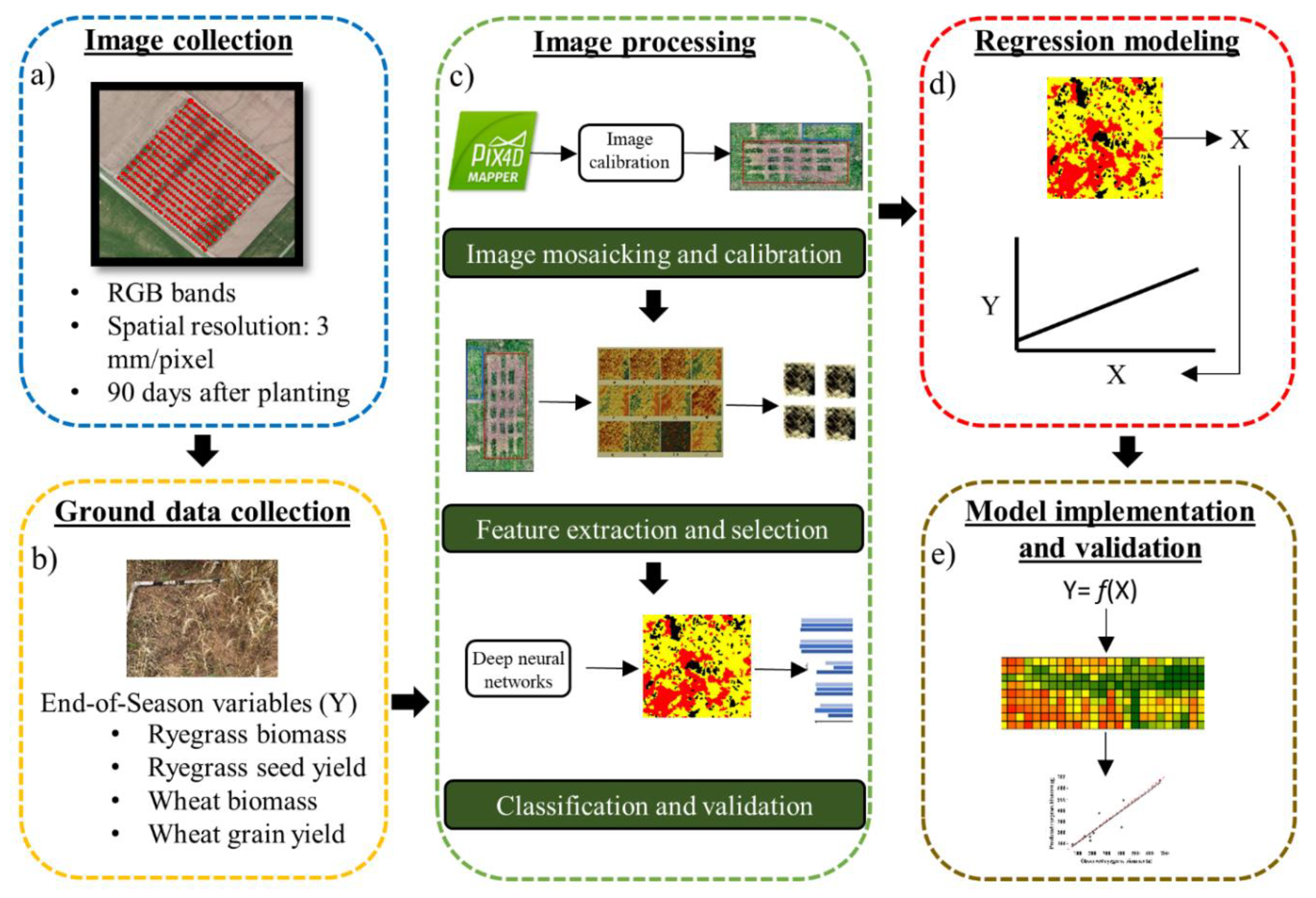
2.2. General Workflow
2.3. Data Collection
2.3.1. Image Collection
2.3.2. Ground-Truth Data Collection
2.4. Image Processing
2.4.1. Image Mosaicking and Calibration
2.4.2. Feature Extraction and Selection
2.4.3. Image Classification and Validation
2.5. Regression Modeling
2.6. Predictive Model Implementation and Validation
3. Results
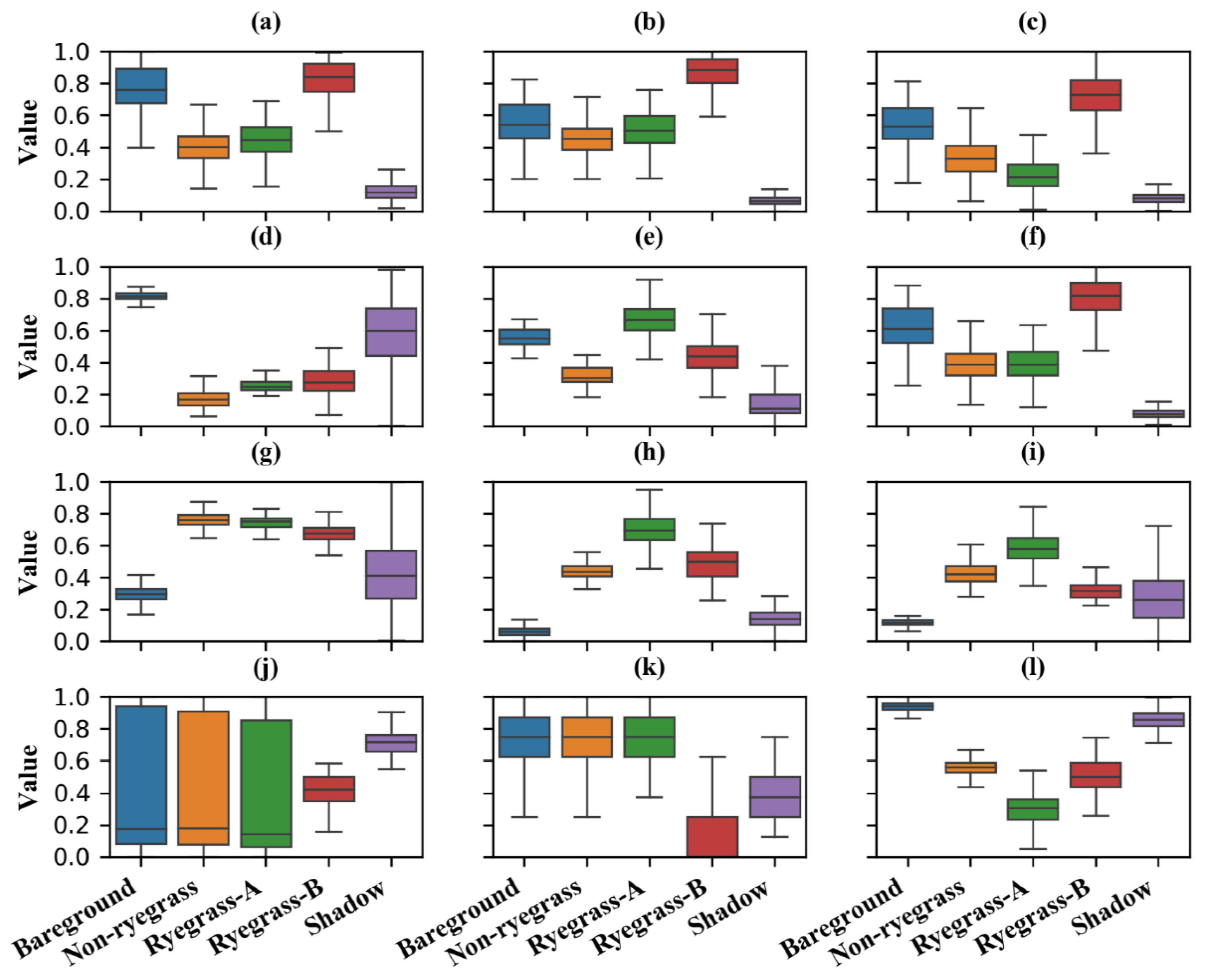
3.1. Ryegrass Detection Using Feature Combinations
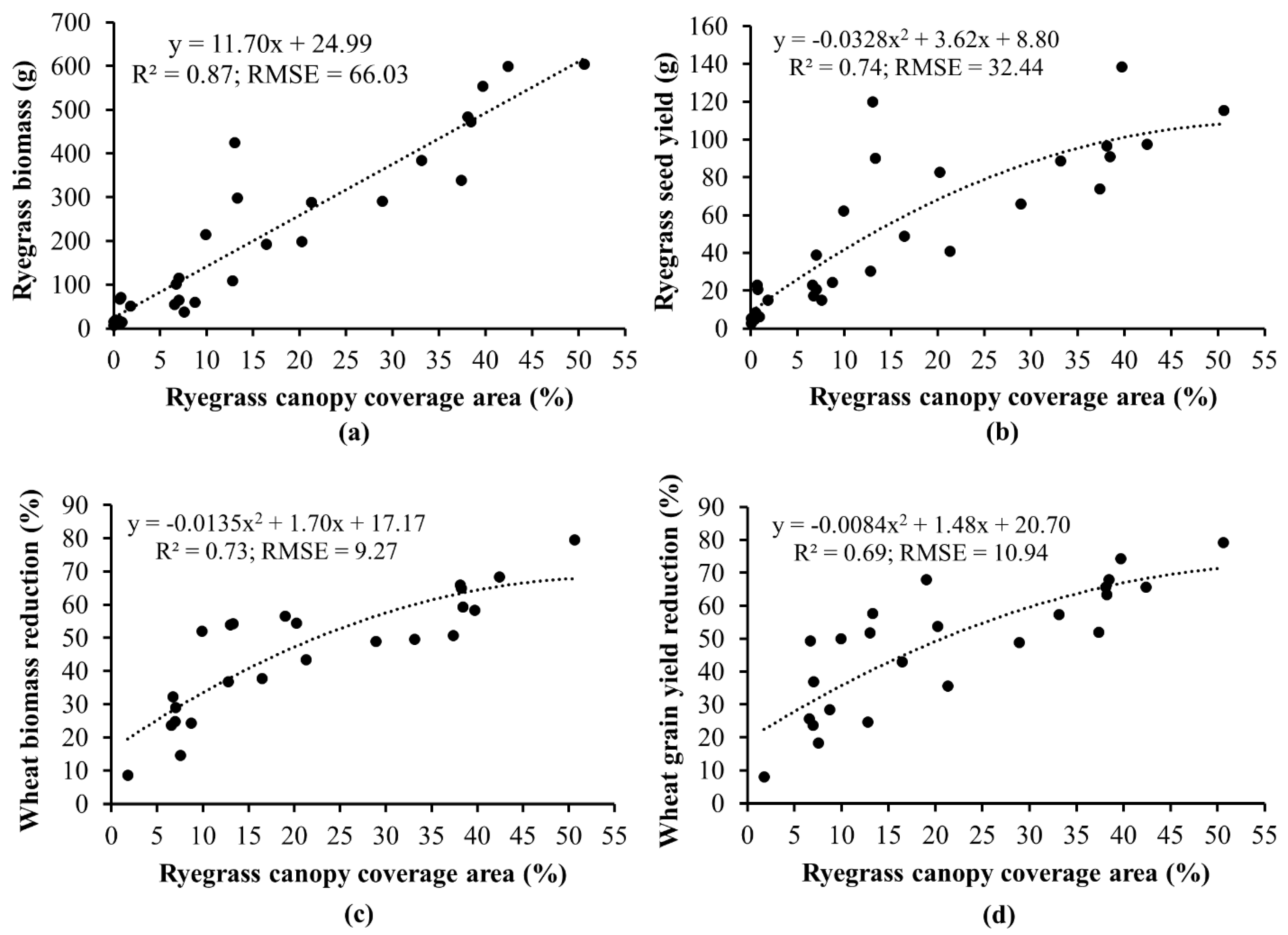
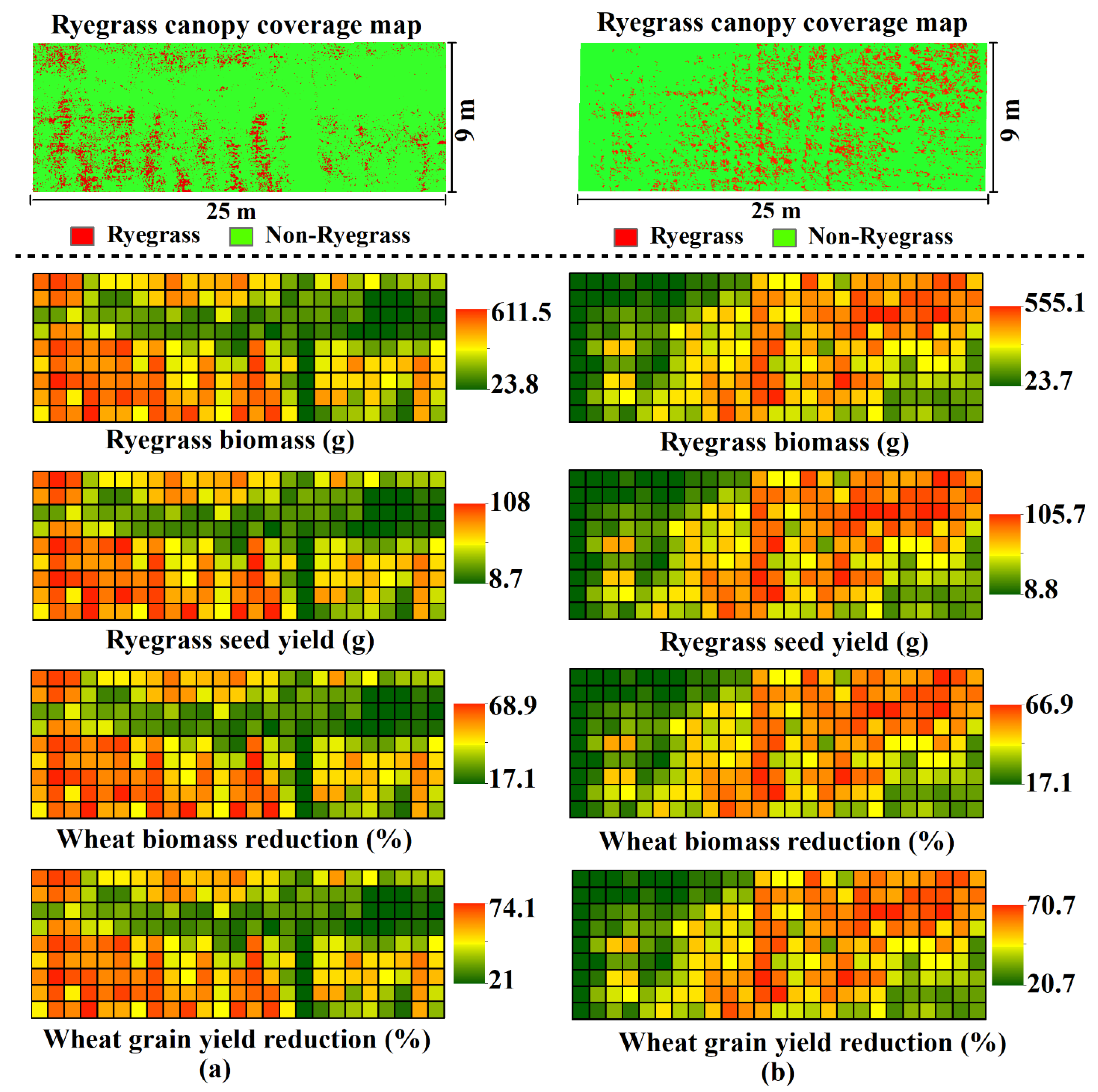
3.2. Prediction of Competitive Outcomes between Italian Ryegrass and Wheat
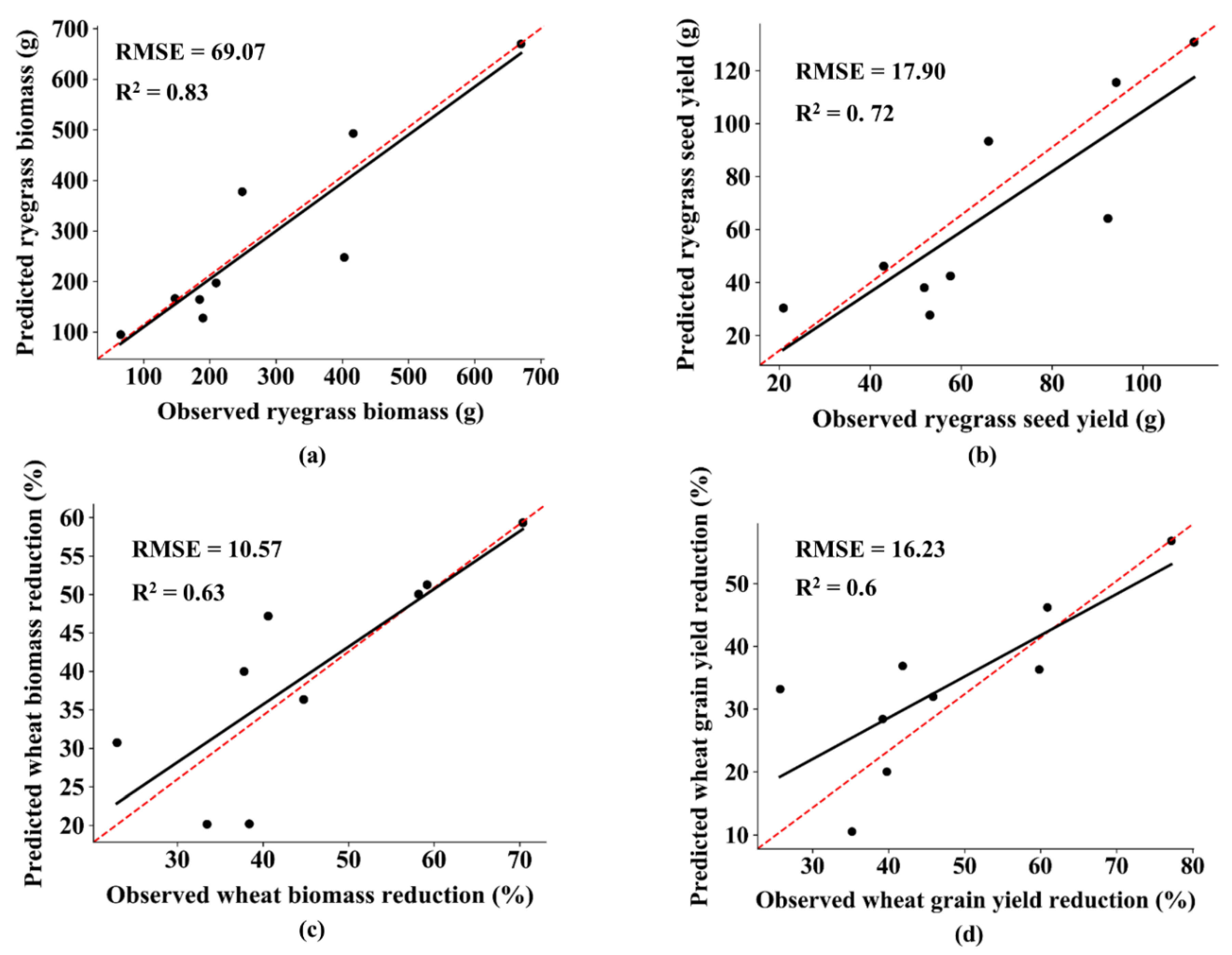
3.3. Model Validation
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Tucker, K.P.; Morgan, G.D.; Senseman, S.A.; Miller, T.D.; Baumann, P.A. Identification, distribution, and control of Italian ryegrass (Lolium multiflorum) ecotypes with varying levels of sensitivity to triasulfuron in Texas. Weed Technol. 2006, 20, 745–750. [Google Scholar] [CrossRef]
- Stone, M.J.; Cralle, H.T.; Chandler, J.M.; Miller, T.D.; Bovey, R.W.; Carson, K.H. Above-and belowground interference of wheat (Triticum aestivum) by Italian ryegrass (Lolium multiflorum). Weed Sci. 1998, 46, 438–441. [Google Scholar] [CrossRef]
- Carson, K.H.; Cralle, H.T.; Chandler, J.M.; Miller, T.D.; Bovey, R.W.; Senseman, S.A.; Stone, M.J. Triticum aestivum and Lolium multiflorum interaction during drought. Weed Sci. 1999, 47, 440–445. [Google Scholar] [CrossRef]
- Liebl, R.; Worsham, A.D. Interference of Italian ryegrass (Lolium multiflorum) in wheat (Triticum aestivum). Weed Sci. 1987, 35, 819–823. [Google Scholar] [CrossRef]
- Singh, V.; Rana, A.; Bishop, M.; Filippi, A.M.; Cope, D.; Rajan, N.; Bagavathiannan, M. Chapter three-unmanned aircraft systems for precision weed detection and management: Prospects and challenges. In Advances in Agronomy; Sparks, D.L., Ed.; Academic Press: Cambridge, MA, USA, 2020; Volume 159, pp. 93–134. [Google Scholar]
- Thompson, J.F.; Stafford, J.V.; Miller, P.C.H. Potential for automatic weed detection and selective herbicide application. Crop Prot. 1991, 10, 254–259. [Google Scholar] [CrossRef]
- Mingyang, L.; Andrew, G.H.; Carol, M.-S. Characterization of multiple herbicide-resistant Italian Ryegrass [Lolium perenne L. ssp. multiflorum (Lam.)] populations from winter wheat fields in Oregon. Weed Sci. 2016, 64, 331–338. [Google Scholar]
- Caio, A.C.G.B.; Bradley, D.H. Multiple herbicide–resistant Italian Ryegrass [Lolium perenne L. spp. multiflorum (Lam.) Husnot] in California perennial crops: Characterization, mechanism of resistance, and chemical management. Weed Sci. 2018, 66, 696–701. [Google Scholar]
- Shaner, D.L.; Beckie, H.J. The future for weed control and technology. Pest Manag. Sci. 2014, 70, 1329–1339. [Google Scholar] [CrossRef] [PubMed]
- Ali, A.; Streibig, J.C.; Andreasen, C. Yield loss prediction models based on early estimation of weed pressure. Crop Protect. 2013, 53, 125–131. [Google Scholar] [CrossRef]
- López-Granados, F.; Peña-Barragán, J.M.; Jurado-Expósito, M.; Francisco-Fernández, M.; Cao, R.; Alonso-Betanzos, A.; Fontenla-Romero, O. Multispectral classification of grass weeds and wheat (Triticum durum) using linear and nonparametric functional discriminant analysis and neural networks. Weed Res. 2008, 48, 28–37. [Google Scholar] [CrossRef]
- Gómez-Casero, M.T.; Castillejo-González, I.L.; García-Ferrer, A.; Peña-Barragán, J.M.; Jurado-Expósito, M.; García-Torres, L.; López-Granados, F. Spectral discrimination of wild oat and canary grass in wheat fields for less herbicide application. Agron. Sustain. Dev. 2010, 30, 689–699. [Google Scholar] [CrossRef]
- Kodagoda, S.; Zhang, Z.; Ruiz, D.; Dissanayake, G. Weed detection and classification for autonomous farming. In Intelligent Production Machines and Systems, Proceedings of the 4th International Virtual Conference on Intelligent Production Machines and Systems, Amsterdam, The Netherlands, 3–14 July 2008; Elesevier: Amsterdam, The Netherlands, 2008. [Google Scholar]
- Golzarian, M.R.; Frick, R.A. Classification of images of wheat, ryegrass and brome grass species at early growth stages using principal component analysis. Plant Methods 2011, 7, 28. [Google Scholar] [CrossRef] [PubMed]
- Singh, G.; Kumar, E. Input data scale impacts on modeling output results: A review. J. Spat. Hydrol. 2017, 13, 1. [Google Scholar]
- Cotter, A.S.; Chaubey, I.; Costello, T.A.; Soerens, T.S.; Nelson, M.A. Water quality model output uncertainty as affected by spatial resolution of input data. J. Am. Water Res. Assoc. 2003, 39, 977–986. [Google Scholar] [CrossRef]
- Gao, J.; Liao, W.; Nuyttens, D.; Lootens, P.; Vangeyte, J.; Pižurica, A.; He, Y.; Pieters, J.G. Fusion of pixel and object-based features for weed mapping using unmanned aerial vehicle imagery. Int. J. Appl. Earth Obs. 2018, 67, 43–53. [Google Scholar] [CrossRef]
- Peña, J.M.; Torres-Sánchez, J.; de Castro, A.I.; Kelly, M.; López-Granados, F. Weed mapping in early-season maize fields using object-based analysis of unmanned aerial vehicle (UAV) images. PLoS ONE 2013, 8, e77151. [Google Scholar] [CrossRef]
- López-Granados, F.; Torres-Sánchez, J.; Serrano-Pérez, A.; de Castro, A.I.; Mesas-Carrascosa, F.J.; Peña, J.-M. Early season weed mapping in sunflower using UAV technology: Variability of herbicide treatment maps against weed thresholds. Precis. Agric. 2016, 17, 183–199. [Google Scholar] [CrossRef]
- Tamouridou, A.; Alexandridis, T.; Pantazi, X.; Lagopodi, A.; Kashefi, J.; Moshou, D. Evaluation of UAV imagery for mapping Silybum marianum weed patches. Int. J. Remote Sens. 2017, 38, 2246–2259. [Google Scholar] [CrossRef]
- De Castro, A.I.; Torres-Sánchez, J.; Peña, J.M.; Jiménez-Brenes, F.M.; Csillik, O.; López-Granados, F. An automatic random forest-OBIA algorithm for early weed mapping between and within crop rows using UAV imagery. Remote Sens. 2018, 10, 285. [Google Scholar] [CrossRef]
- Sapkota, B.; Singh, V.; Cope, D.; Valasek, J.; Bagavathiannan, M. Mapping and estimating weeds in cotton using unmanned aerial systems-borne imagery. AgriEngineering 2020, 2, 350–366. [Google Scholar] [CrossRef]
- Yang, M.-D.; Huang, K.-S.; Kuo, Y.-H.; Tsai, H.P.; Lin, L.-M. Spatial and spectral hybrid image classification for rice lodging assessment through UAV imagery. Remote Sens. 2017, 9, 583. [Google Scholar] [CrossRef]
- Gašparović, M.; Zrinjski, M.; Barković, Đ.; Radočaj, D. An automatic method for weed mapping in oat fields based on UAV imagery. Comput. Electron. Agric. 2020, 173, 105385. [Google Scholar] [CrossRef]
- Kanellopoulos, I.; Wilkinson, G.G. Strategies and best practice for neural network image classification. Int. J. Remote Sens. 1997, 18, 711–725. [Google Scholar] [CrossRef]
- Yang, C.C.; Prasher, S.O.; Landry, J.A.; Ramaswamy, H.S. Development of a herbicide application map using artificial neural networks and fuzzy logic. Agric. Syst. 2003, 76, 561–574. [Google Scholar] [CrossRef]
- Gutiérrez, P.A.; López-Granados, F.; Peña-Barragán, J.M.; Jurado-Expósito, M.; Hervás-Martínez, C. Logistic regression product-unit neural networks for mapping Ridolfia segetum infestations in sunflower crop using multitemporal remote sensed data. Comput. Electron. Agric. 2008, 64, 293–306. [Google Scholar] [CrossRef]
- Li, Z.; An, Q.; Ji, C. Classification of weed species using artificial neural networks based on color leaf texture feature. In Proceedings of the International Conference on Computer and Computing Technologies in Agriculture, Beijing, China, 18–20 October 2008; pp. 1217–1225. [Google Scholar]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Soil Survey Staff, Natural Resources Conservation Service, United States Department of Agriculture. Web Soil Survey. Available online: http://websoilsurvey.sc.egov.usda.gov/ (accessed on 6 January 2020).
- Pérez, M.; Agüera, F.; Carvajal, F. Low cost surveying using an unmanned aerial vehicle. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci 2013, 40, 311–315. [Google Scholar] [CrossRef]
- Conte, P.; Girelli, V.A.; Mandanici, E. Structure from Motion for aerial thermal imagery at city scale: Pre-processing, camera calibration, accuracy assessment. ISPRS J. Photogramm. Remote Sens. 2018, 146, 320–333. [Google Scholar] [CrossRef]
- Xue, B.; Zhang, M.; Browne, W.N. Particle swarm optimization for feature selection in classification: A multi-objective approach. IEEE Trans. Cybern. 2013, 43, 1656–1671. [Google Scholar] [CrossRef]
- Woebbecke, D.M.; Meyer, G.E.; Von Bargen, K.; Mortensen, D.A. Color indices for weed identification under various soil, residue, and lighting conditions. Trans. ASAE 1995, 38, 259–269. [Google Scholar] [CrossRef]
- Hunt, E.R., Jr.; Daughtry, C.S.T.; Eitel, J.U.H.; Long, D.S. Remote sensing leaf chlorophyll content using a visible band index. Agron. J. 2011, 103, 1090–1099. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Kaufman, Y.J.; Stark, R.; Rundquist, D. Novel algorithms for remote estimation of vegetation fraction. Remote Sens. Environ. 2002, 80, 76–87. [Google Scholar] [CrossRef]
- Shapiro, L.; Stockman, G. Computer Vision; Prentice Hall Inc.: Upper Saddle River, NJ, USA, 2001. [Google Scholar]
- Stanković, R.S.; Falkowski, B.J. The Haar wavelet transform: Its status and achievements. Comput. Electron. Eng. 2003, 29, 25–44. [Google Scholar] [CrossRef]
- Pearson, K. On lines and planes of closest fit to systems of points in space. Lond. Edinb. Dublin Phil. Mag. J. Sci. 1901, 2, 559–572. [Google Scholar] [CrossRef]
- Atkinson, P.M.; Tatnall, A.R.L. Introduction neural networks in remote sensing. Int. J. Remote Sens. 1997, 18, 699–709. [Google Scholar] [CrossRef]
- Keras, F.C. The Python Deep Learning Library, 2015. Available online: https://keras.io/ (accessed on 20 September 2019).
- Chaves-González, J.M.; Vega-Rodríguez, M.A.; Gómez-Pulido, J.A.; Sánchez-Pérez, J.M. Detecting skin in face recognition systems: A colour spaces study. DSP 2010, 20, 806–823. [Google Scholar] [CrossRef]
- Hemming, J.; Rath, T. PA—Precision agriculture: Computer-vision-based weed identification under field conditions using controlled lighting. J. Agric. Eng. Res. 2001, 78, 233–243. [Google Scholar] [CrossRef]
- Burks, T.F.; Shearer, S.A.; Green, J.D.; Heath, J.R. Influence of weed maturity levels on species classification using machine vision. Weed Sci. 2002, 50, 802–811. [Google Scholar] [CrossRef]
- Yang, W.; Wang, S.; Zhao, X.; Zhang, J.; Feng, J. Greenness identification based on HSV decision tree. Inf. Process. Agric. 2015, 2, 149–160. [Google Scholar] [CrossRef]
- Milas, A.S.; Arend, K.; Mayer, C.; Simonson, M.A.; Mackey, S. Different colours of shadows: Classification of UAV images. Int. J. Remote Sens. 2017, 38, 3084–3100. [Google Scholar] [CrossRef]
- Huang, H.; Deng, J.; Lan, Y.; Yang, A.; Deng, X.; Zhang, L. A fully convolutional network for weed mapping of unmanned aerial vehicle (UAV) imagery. PLoS ONE 2018, 13, e0196302. [Google Scholar] [CrossRef] [PubMed]
- Sa, I.; Popović, M.; Khanna, R.; Chen, Z.; Lottes, P.; Liebisch, F.; Nieto, J.; Stachniss, C.; Walter, A.; Siegwart, R. WeedMap: A large-scale semantic weed mapping framework using aerial multispectral imaging and deep neural network for precision farming. Remote Sens. 2018, 10, 1423. [Google Scholar] [CrossRef]
- Gao, J.; French, A.P.; Pound, M.P.; He, Y.; Pridmore, T.P.; Pieters, J.G. Deep convolutional neural networks for image-based Convolvulus sepium detection in sugar beet fields. Plant Methods 2020, 16, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Shanahan, J.F.; Schepers, J.S.; Francis, D.D.; Varvel, G.E.; Wilhelm, W.W.; Tringe, J.M.; Schlemmer, M.R.; Major, D.J. Use of remote-sensing imagery to estimate corn grain yield. Agron. J. 2001, 93, 583–589. [Google Scholar] [CrossRef]
- Xue, L.-H.; Cao, W.-X.; Yang, L.-Z. Predicting grain yield and protein content in winter wheat at different N supply levels using canopy reflectance spectra. Pedosphere 2007, 17, 646–653. [Google Scholar] [CrossRef]
- Zhou, X.; Zheng, H.B.; Xu, X.Q.; He, J.Y.; Ge, X.K.; Yao, X.; Cheng, T.; Zhu, Y.; Cao, W.X.; Tian, Y.C. Predicting grain yield in rice using multi-temporal vegetation indices from UAV-based multispectral and digital imagery. ISPRS J. Photogramm. Remote Sens. 2017, 130, 246–255. [Google Scholar] [CrossRef]
- Fassnacht, K.S.; Gower, S.T.; MacKenzie, M.D.; Nordheim, E.V.; Lillesand, T.M. Estimating the leaf area index of North Central Wisconsin forests using the landsat thematic mapper. Remote Sens. Environ. 1997, 61, 229–245. [Google Scholar] [CrossRef]
- Turner, D.P.; Cohen, W.B.; Kennedy, R.E.; Fassnacht, K.S.; Briggs, J.M. Relationships between leaf area index and landsat TM spectral vegetation indices across three temperate zone sites. Remote Sens. Environ. 1999, 70, 52–68. [Google Scholar] [CrossRef]
- Yagbasanlar, T.; Özkan, H.; Genç, I. Relationships of growth periods, harvest index and grain yield in common wheat under Mediterranean climatic conditions. Cereal Res. Commun. 1995, 23, 59–62. [Google Scholar]
- Slafer, G.; Calderini, D.; Miralles, D. Yield components and compensation in wheat: Opportunities for further increasing yield potential. In Increasing Yield Potential in Wheat: Breaking the Barriers; Reynolds, M.P., Rajaram, S., McNab, A., Eds.; CIMMYT: El Batan, Mexico, 1996; pp. 101–133. [Google Scholar]
- Heather, J.G.; Bennett, K.A.; Ralph, B.B.; Tardif, F.J. Evaluation of site-specific weed management using a direct-injection sprayer. Weed Sci. 2001, 49, 359–366. [Google Scholar]
- Swanton, C.J.; Weaver, S.; Cowan, P.; Acker, R.V.; Deen, W.; Shrestha, A. Weed thresholds. J. Crop Prod. 1999, 2, 9–29. [Google Scholar] [CrossRef]
- Cousens, R. A simple model relating yield loss to weed density. Ann. Appl. Biol. 1985, 107, 239–252. [Google Scholar] [CrossRef]
- Christensen, S. Crop weed competition and herbicide performance in cereal species and varieties. Weed Res. 1994, 34, 29–36. [Google Scholar] [CrossRef]
- Colbach, N.; Collard, A.; Guyot, S.H.M.; Meziere, D.; Munier-Jolain, N. Assessing innovative sowing patterns for integrated weed management with a 3D crop:weed competition model. Eur. J. Agron. 2014, 53, 74–89. [Google Scholar] [CrossRef]
- Kropff, M.J.; Spitters, J.T. A simple model of crop loss by weed competition from early observations on relative leaf area of the weeds. Weed Res. 1991, 31, 97–105. [Google Scholar] [CrossRef]

| Category | Features | Description/Formula ** | Reference |
|---|---|---|---|
| Original bands (3) | Blue | - | - |
| Green | |||
| Red | |||
| Vegetation indices (3) | Excess Green Index (ExG) | [35] | |
| Triangular Greenness Index (TGI) | [36] | ||
| Visible Atmospheric Resistant Index (VARI) | [37] | ||
| Color space transformed features (3) | Hue | A gradation or variety of a color | [38] |
| Saturation | Depth, purity, or shades of the color | ||
| Value | Brightness intensity of the color tone | ||
| Wavelet transformed coefficients (2) | Wavelet coefficient mean | Mean value calculated for a pixel using discrete wavelet transformation | [39] |
| Wavelet coefficient standard deviation | Standard deviation calculated for a pixel using discrete wavelet transformation | ||
| Principal components (1) | Principal component 1 | Principal component analysis-derived component accounting maximum amount of variance | [40] |
| Hyperparameter | Values | Selected Value(s) |
|---|---|---|
| Number of hidden layers | 1,2,3,4,5 | 5 |
| Nodes in hidden layers * | (20) (40, 20) (60, 40, 20) (80, 60, 40, 20) (100, 80, 60, 40, 20) | (100, 80, 60, 40, 20) |
| Activation function | “Rectified linear unit” “Sigmoid function” | “Rectified linear unit” |
| Batch size | 10, 20, 30, 40, 50 | 20 |
| Number of epochs | 100, 300, 500 | 100 |
| Feature Model # | Features Used ** | Precision (%) * | Recall (%) * | F-score (%) * |
|---|---|---|---|---|
| 1 | Green, Blue, Hue, Sat, Value, TGI, ExG, PC-1 | 94.28 ± 4.86 | 94.28 ± 5.24 | 94.27 ± 4.96 |
| 2 | Hue, Value, VARI, ExG | 94.28 ± 4.50 | 94.28 ± 7.94 | 94.27 ± 5.26 |
| 3 | Red, Hue, Sat, VARI, ExG, Wavelet_Mean | 94.95 ± 4.58 | 94.91 ± 4.98 | 94.91 ± 4.43 |
| 4 | Hue, VARI, TGI, ExG | 91.53 ± 6.75 | 90.63 + 8.93 | 90.54 + 2.29 |
| 5 | Green, Blue, Hue, Sat, Value, ExG, Wavelet_Mean, PC-1 | 95.33 ± 4.23 | 95.38 ± 5.07 | 95.36 ± 4.14 |
| 6 | Red, Green, Hue, Sat, ExG, Wavelet_Std | 94.45 ± 4.67 | 94.44 ± 5.83 | 94.41 ± 4.98 |
| 7 | Red, Green, Hue, Sat, TGI, Wavelet_Std | 95.01 ± 4.31 | 94.94 ± 5.5 | 94.91 ± 4.25 |
| 8 | Sat, Value, VARI, ExG | 91.74 ± 8.14 | 91.59 ± 9.48 | 91.54 ± 8.21 |
| 9 | Red, Blue, Sat, VARI, ExG, Wavelet_Mean | 95.01 ± 4.71 | 94.97 ± 5.36 | 94.96 ± 4.67 |
| 10 | Hue, Sat, VARI, ExG | 95.34 ± 4.27 | 95.68 ± 5.05 | 95.56 ± 4.11 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sapkota, B.; Singh, V.; Neely, C.; Rajan, N.; Bagavathiannan, M. Detection of Italian Ryegrass in Wheat and Prediction of Competitive Interactions Using Remote-Sensing and Machine-Learning Techniques. Remote Sens. 2020, 12, 2977. https://doi.org/10.3390/rs12182977
Sapkota B, Singh V, Neely C, Rajan N, Bagavathiannan M. Detection of Italian Ryegrass in Wheat and Prediction of Competitive Interactions Using Remote-Sensing and Machine-Learning Techniques. Remote Sensing. 2020; 12(18):2977. https://doi.org/10.3390/rs12182977
Chicago/Turabian StyleSapkota, Bishwa, Vijay Singh, Clark Neely, Nithya Rajan, and Muthukumar Bagavathiannan. 2020. "Detection of Italian Ryegrass in Wheat and Prediction of Competitive Interactions Using Remote-Sensing and Machine-Learning Techniques" Remote Sensing 12, no. 18: 2977. https://doi.org/10.3390/rs12182977
APA StyleSapkota, B., Singh, V., Neely, C., Rajan, N., & Bagavathiannan, M. (2020). Detection of Italian Ryegrass in Wheat and Prediction of Competitive Interactions Using Remote-Sensing and Machine-Learning Techniques. Remote Sensing, 12(18), 2977. https://doi.org/10.3390/rs12182977







