High-Performance Lossless Compression of Hyperspectral Remote Sensing Scenes Based on Spectral Decorrelation
Abstract
1. Introduction
2. Methods and Materials
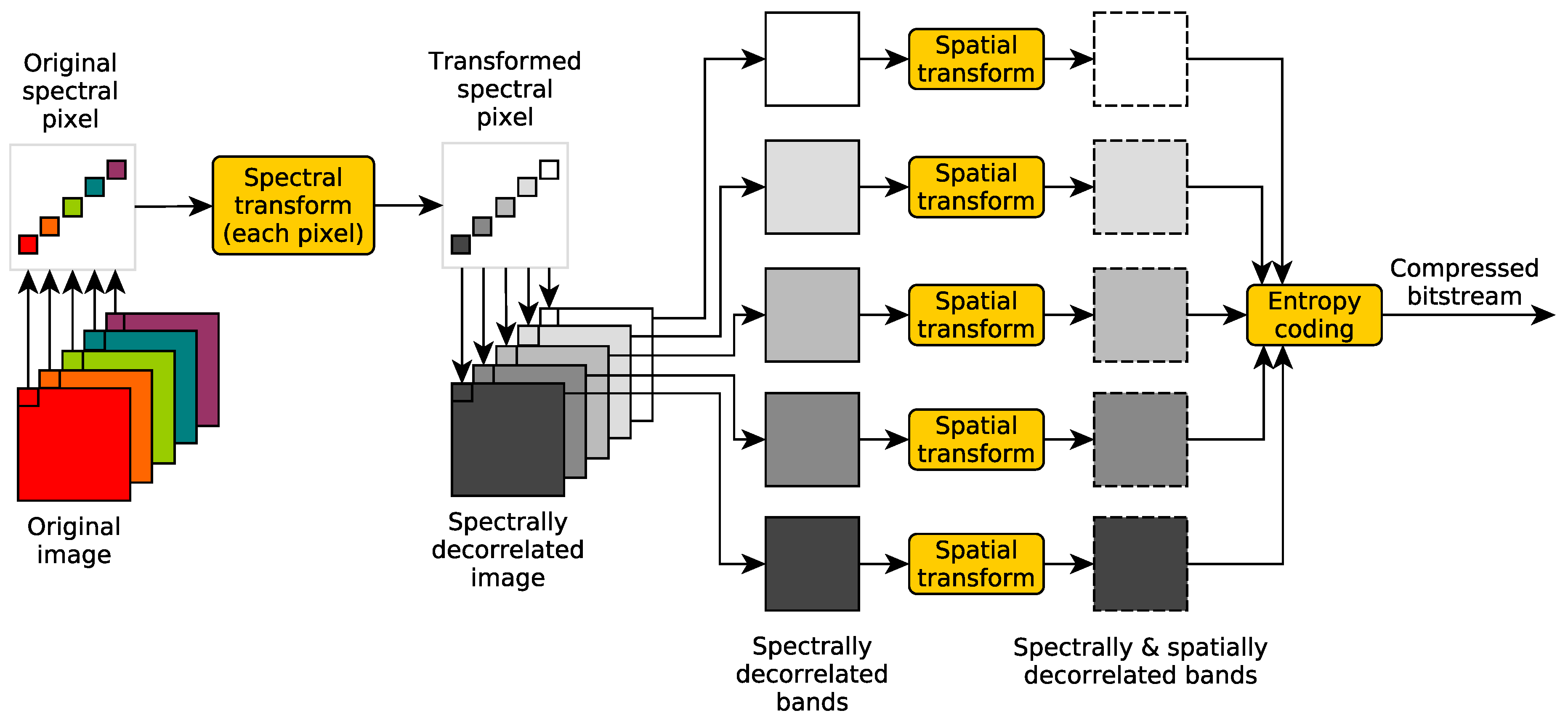
2.1. Spectral Decorrelation Methods
2.2. Low-Complexity Compression Methods
2.3. Test Corpus
3. Experimental Results
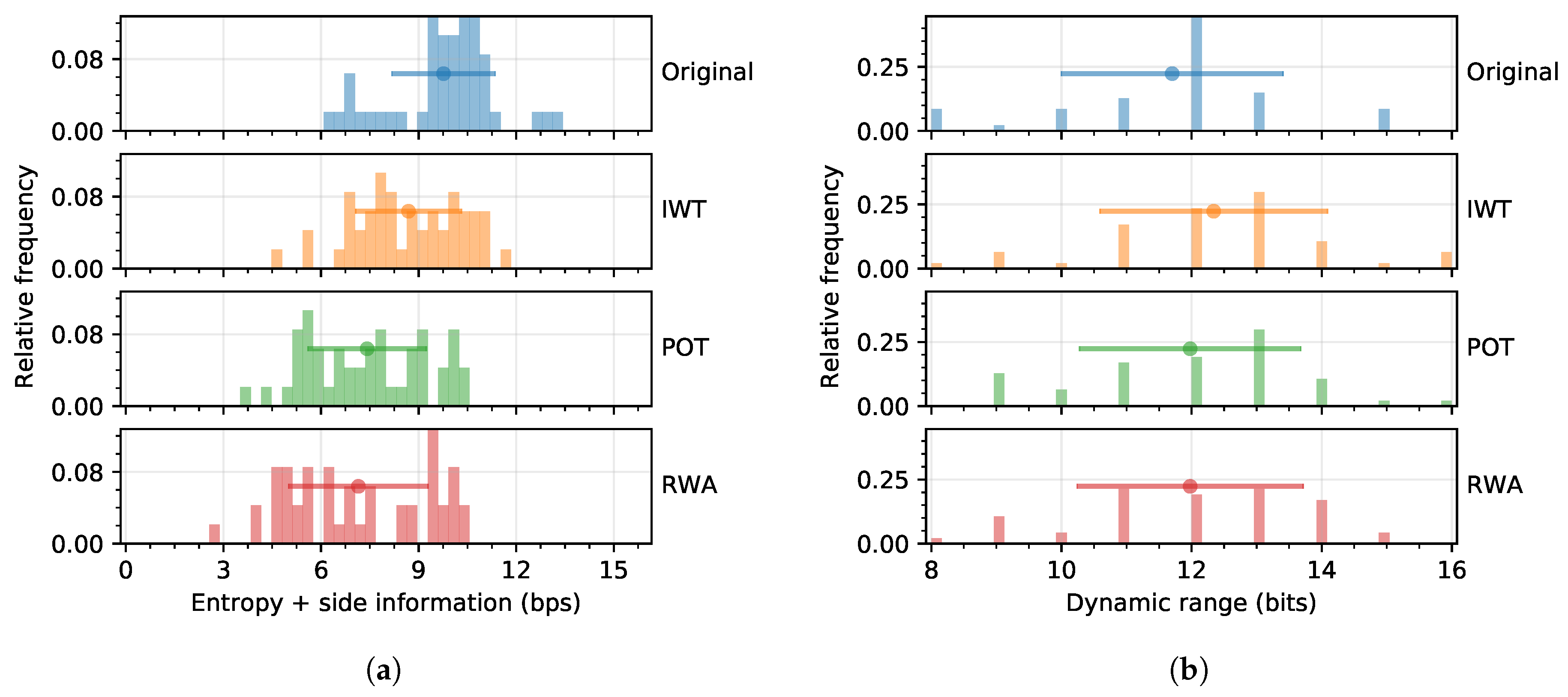
3.1. Spectral Transforms
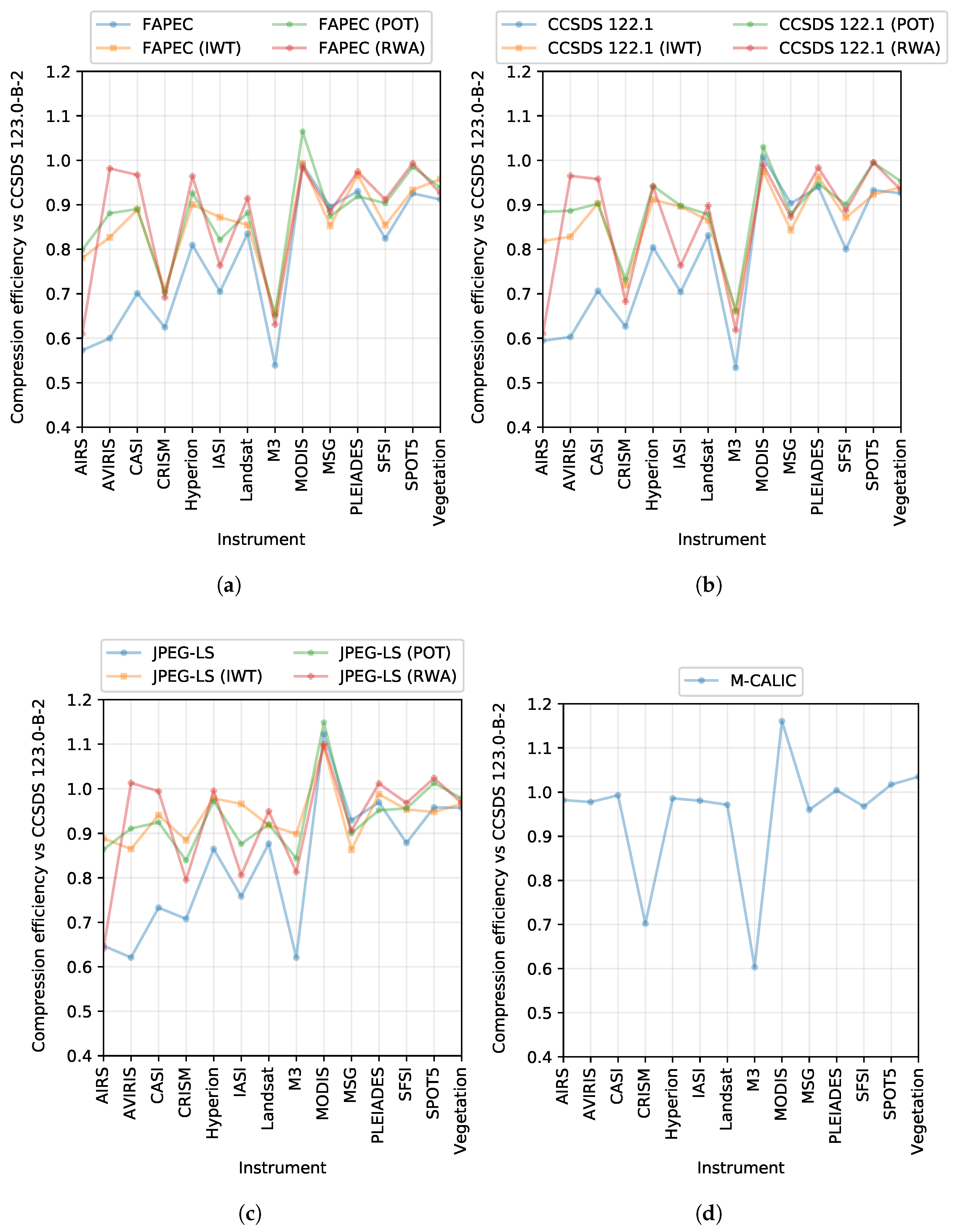
3.2. Lossless Compression Rates
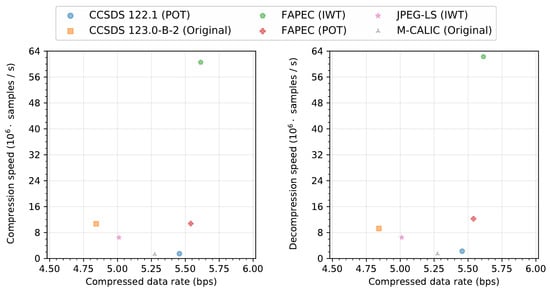
3.3. Throughput Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| bps | Bits per sample |
| CALIC | Context-based, Adaptive, Lossless Image Coder |
| CCSDS | Consultative Committee for Space Data Systems |
| DWT | Discrete Wavelet Transform |
| FAPEC | Fully Adaptive Prediction Error Coder |
| HSI | HyperSpectral Imagery |
| IWT | Integer Wavelet Transform |
| POT | Pair-Orthogonal Transform |
| RWA | Regression Wavelet Analysis |
References
- Parente, M.; Kerekes, J.; Heylen, R. A Special Issue on Hyperspectral Imaging [From the Guest Editors]. IEEE Geosci. Remote Sens. Mag. 2019, 7, 6–7. [Google Scholar] [CrossRef]
- Malyy, M.; Tekic, Z.; Golkar, A. What Drives Technology Innovation in New Space? A Preliminary Analysis of Venture Capital Investments in Earth Observation Start-Ups. IEEE Geosci. Remote Sens. Mag. 2019, 7, 59–73. [Google Scholar]
- Denis, G.; Claverie, A.; Pasco, X.; Darnis, J.P.; de Maupeou, B.; Lafaye, M.; Morel, E. Towards disruptions in Earth observation? New Earth Observation systems and markets evolution: Possible scenarios and impacts. Acta Astronaut. 2017, 137, 415–433. [Google Scholar]
- Sun, W.; Du, Q. Hyperspectral Band Selection: A Review. IEEE Geosci. Remote Sens. Mag. 2019, 7, 118–139. [Google Scholar] [CrossRef]
- Li, S.; Song, W.; Fang, L.; Chen, Y.; Ghamisi, P.; Benediktsson, J.A. Deep Learning for Hyperspectral Image Classification: An Overview. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6690–6709. [Google Scholar] [CrossRef]
- Duan, P.; Kang, X.; Li, S.; Ghamisi, P.; Benediktsson, J.A. Fusion of Multiple Edge-Preserving Operations for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 10336–10349. [Google Scholar] [CrossRef]
- Su, Y.; Li, J.; Plaza, A.; Marinoni, A.; Gamba, P.; Chakravortty, S. DAEN: Deep Autoencoder Networks for Hyperspectral Unmixing. IEEE Trans. Geosci. Remote Sens. 2019, 57, 4309–4321. [Google Scholar] [CrossRef]
- Chen, Y.; Zhu, K.; Zhu, L.; He, X.; Ghamisi, P.; Benediktsson, J.A. Automatic Design of Convolutional Neural Network for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 7048–7066. [Google Scholar] [CrossRef]
- Haut, J.M.; Gallardo, J.A.; Paoletti, M.E.; Cavallaro, G.; Plaza, J.; Plaza, A.; Riedel, M. Cloud Deep Networks for Hyperspectral Image Analysis. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9832–9848. [Google Scholar] [CrossRef]
- Tu, B.; Zhang, X.; Kang, X.; Wang, J.; Benediktsson, J.A. Spatial Density Peak Clustering for Hyperspectral Image Classification With Noisy Labels. IEEE Trans. Geosci. Remote Sens. 2019, 57, 5085–5097. [Google Scholar] [CrossRef]
- Bhardwaj, K.; Patra, S.; Bruzzone, L. Threshold-Free Attribute Profile for Classification of Hyperspectral Images. IEEE Trans. Geosci. Remote Sens. 2019, 57, 7731–7742. [Google Scholar] [CrossRef]
- Lu, X.; Dong, L.; Yuan, Y. Subspace Clustering Constrained Sparse NMF for Hyperspectral Unmixing. IEEE Trans. Geosci. Remote Sens. 2020, 58, 3007–3019. [Google Scholar] [CrossRef]
- Della Porta, C.J.; Bekit, A.A.; Lampe, B.H.; Chang, C. Hyperspectral Image Classification via Compressive Sensing. IEEE Trans. Geosci. Remote Sens. 2019, 57, 8290–8303. [Google Scholar] [CrossRef]
- Nalepa, J.; Myller, M.; Kawulok, M. Validating Hyperspectral Image Segmentation. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1264–1268. [Google Scholar] [CrossRef]
- Hong, D.; Wu, X.; Ghamisi, P.; Chanussot, J.; Yokoya, N.; Zhu, X.X. Invariant Attribute Profiles: A Spatial-Frequency Joint Feature Extractor for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2020, 58, 3791–3808. [Google Scholar] [CrossRef]
- Theiler, J.; Ziemann, A.; Matteoli, S.; Diani, M. Spectral Variability of Remotely Sensed Target Materials: Causes, Models, and Strategies for Mitigation and Robust Exploitation. IEEE Geosci. Remote Sens. Mag. 2019, 7, 8–30. [Google Scholar] [CrossRef]
- Zhong, Y.; Wang, X.; Xu, Y.; Wang, S.; Jia, T.; Hu, X.; Zhao, J.; Wei, L.; Zhang, L. Mini-UAV-Borne Hyperspectral Remote Sensing: From Observation and Processing to Applications. IEEE Geosci. Remote Sens. Mag. 2018, 6, 46–62. [Google Scholar] [CrossRef]
- Khan, M.J.; Khan, H.S.; Yousaf, A.; Khurshid, K.; Abbas, A. Modern Trends in Hyperspectral Image Analysis: A Review. IEEE Access 2018, 6, 14118–14129. [Google Scholar] [CrossRef]
- Qian, S.E. Optical Satellite Data Compression and Implementation; SPIE: Bellingham, WA, USA, 2013. [Google Scholar]
- Turpie, K.; Veraverbeke, S.; Wright, R.; Anderson, M.; Quattrochi, D. NASA 2014 The Hyperspectral Infrared Imager (HyspIRI)—Science Impact of Deploying Instruments on Separate Platforms; Techreport JPL-Publ-14-13; Jet Propulsion Lab: Pasadena, CA, USA, 2014.
- Qian, S.E. Optical Satellite Signal Processing and Enhancement; SPIE: Bellingham, WA, USA, 2013. [Google Scholar]
- Calderbank, A.R.; Daubechies, I.; Sweldens, W.; Yeo, B.-L. Lossless image compression using integer to integer wavelet transforms. In Proceedings of the International Conference on Image Processing, Santa Barbara, CA, USA, 26–29 October 1997; Volume 1, pp. 596–599. [Google Scholar]
- Blanes, I.; Serra-Sagristà, J. Pairwise Orthogonal Transform for Spectral Image Coding. IEEE Trans. Geosci. Remote Sens. 2011, 49, 961–972. [Google Scholar] [CrossRef]
- Amrani, N.; Serra-Sagristà, J.; Laparra, V.; Marcellin, M.W.; Malo, J. Regression Wavelet Analysis for Lossless Coding of Remote-Sensing Data. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5616–5627. [Google Scholar] [CrossRef]
- Portell, J.; Iudica, R.; García-Berro, E.; Villafranca, A.; Artigues, G. FAPEC, a versatile and efficient data compressor for space missions. Int. J. Remote Sens. 2018, 39, 2022–2042. [Google Scholar] [CrossRef]
- Consultative Committee for Space Data Systems (CCSDS). Spectral Preprocessing Transform for Multispectral and Hyperspectral Image Compression. In Blue Book; Issue 1, Number CCSDS 122.1-B-1; CCSDS: Washington, DC, USA, 2017. [Google Scholar]
- Weinberger, M.J.; Seroussi, G.; Sapiro, G. The LOCO-I lossless image compression algorithm: Principles and standardization into JPEG-LS. IEEE Trans. Image Process. 2000, 9, 1309–1324. [Google Scholar] [CrossRef] [PubMed]
- Consultative Committee for Space Data Systems (CCSDS). Low-Complexity Lossless and Near-Lossless Multispectral and Hyperspectral Image Compression. In Blue Book; Issue 2, Number CCSDS 123.0-B-2; CCSDS: Washington, DC, USA, 2019. [Google Scholar]
- Magli, E.; Olmo, G.; Quacchio, E. Optimized onboard lossless and near-lossless compression of hyperspectral data using CALIC. IEEE Geosci. Remote Sens. Lett. 2004, 1, 21–25. [Google Scholar] [CrossRef]
- Portell, J.; Blanes, I.; Hernández-Cabronero, M.; Serra-Sagristà, J.; Iudica, R.; Villafranca, A.G. Prepending spectral decorrelating transforms to FAPEC: A competitive high-performance approach for remote sensing data compression. In Proceedings of the On-Board Payload Data Compression (OBPDC), Matera, Italy, 20–21 September 2018. [Google Scholar]
- Tsigkanos, A.; Kranitis, N.; Theodorou, G.A.; Paschalis, A. A 3.3 Gbps CCSDS 123.0-B-1 Multispectral Hyperspectral Image Compression Hardware Accelerator on a Space-Grade SRAM FPGA. IEEE Trans. Emerg. Top. Comput. 2018, 1. [Google Scholar] [CrossRef]
- Keymeulen, D.; Shin, S.; Riddley, J.; Klimesh, M.; Kiely, A.; Liggett, E.; Sullivan, P.; Bernas, M.; Ghossemi, H.; Flesch, G.; et al. High Performance Space Computing with System-on-Chip Instrument Avionics for Space-based Next Generation Imaging Spectrometers (NGIS). In Proceedings of the 2018 NASA/ESA Conference on Adaptive Hardware and Systems (AHS), Edinburgh, UK, 6–9 August 2018; pp. 33–36. [Google Scholar]
- Santos, L.; Gomez, A.; Sarmiento, R. Implementation of CCSDS Standards for Lossless Multispectral and Hyperspectral Satellite Image Compression. IEEE Trans. Aerosp. Electron. Syst. 2019, 56, 1120–1138. [Google Scholar] [CrossRef]
- Daubechies, I.; Sweldens, W. Factoring wavelet transforms into lifting steps. J. Fourier Anal. Appl. 1998, 4, 247–269. [Google Scholar] [CrossRef]
- Artigues, G.; Portell, J.; Villafranca, A.G.; Ahmadloo, H.; García-Berro, E. Discrete wavelet transform fully adaptive prediction error coder: Image data compression based on CCSDS 122.0 and fully adaptive prediction error coder. J. Appl. Remote Sens. 2013, 7, 074592. [Google Scholar]
- Blanes, I.; Kiely, A.; Hernández-Cabronero, M.; Serra-Sagristà, J. Performance Impact of Parameter Tuning on the CCSDS-123.0-B-2 Low-Complexity Lossless and Near-Lossless Multispectral and Hyperspectral Image Compression Standard. Remote Sens. 2019, 11, 1390. [Google Scholar] [CrossRef]



| Instrument | Scene Type | Dynamic Range (bits) | #Bands | Width | Height | #Scenes |
|---|---|---|---|---|---|---|
| AIRS | raw | 12 | 1501 | 90 | 135 | 1 |
| AVIRIS | raw | 15 | 224 | 680 | 512 | 1 |
| raw | 10 | 224 | 614 | 512 | 1 | |
| calibrated | 13 | 224 | 677 | 512 | 1 | |
| CASI | raw | 12, 13, 15 | 72 | 406 | 1225 | 3 |
| CRISM | raw | 11 | 107 | 640 | 510 | 2 |
| raw | 12, 13 | 438 | 640 | 510 | 2 | |
| raw | 12, 13 | 545 | 640 | 510 | 2 | |
| raw | 13 | 545 | 320 | 450 | 2 | |
| calibrated | 11 | 74 | 64 | 2700 | 2 | |
| Hyperion | raw | 12 | 242 | 256 | 1024 | 3 |
| IASI L1C | calibrated | 15 | 8461 | 60 | 1530 | 1 |
| Landsat | raw | 8 | 6 | 1024 | 1024 | 3 |
| M3 | raw | 12 | 260 | 640 | 512 | 2 |
| raw | 11, 12 | 86 | 320 | 512 | 2 | |
| MODIS | raw | 12 | 17 | 1354 | 2030 | 2 |
| raw | 12, 13 | 14 | 1354 | 2030 | 2 | |
| raw | 12, 13 | 5 | 2708 | 4060 | 2 | |
| raw | 12 | 2 | 5416 | 8120 | 2 | |
| MSG | calibrated | 10 | 11 | 3712 | 3712 | 1 |
| PLEIADES | calibrated | 12 | 4 | 224 | 2465 | 1 |
| calibrated | 12 | 4 | 224 | 2448 | 3 | |
| SFSI | calibrated | 15 | 240 | 452 | 140 | 1 |
| raw | 9, 11 | 240 | 496 | 140 | 2 | |
| SPOT5 | calibrated | 8 | 3 | 1024 | 1024 | 1 |
| Vegetation | raw | 10 | 4 | 1728 | 10,080 | 2 |
| FAPEC | CCSDS 122.1 | JPEG-LS | CCSDS 123.0-B-2 | M- CALIC | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Corpus | No | IWT | POT | RWA | No | IWT | POT | RWA | No | IWT | POT | RWA | No | No | ||||
| AIRS | 7.18 | 5.27 | 5.15 | 6.75 | 6.92 | 5.03 | 4.65 | 6.74 | 6.35 | 4.63 | 4.76 | 6.43 | 4.11 | 4.19 | ||||
| AVIRIS | 7.12 | 5.20 | 4.88 | 4.40 | 7.08 | 5.18 | 4.84 | 4.46 | 6.89 | 4.98 | 4.73 | 4.27 | 4.36 | 4.43 | ||||
| CASI | 8.53 | 6.76 | 6.75 | 6.24 | 8.46 | 6.66 | 6.67 | 6.29 | 8.17 | 6.40 | 6.51 | 6.07 | 6.06 | 6.10 | ||||
| CRISM | 6.19 | 5.48 | 5.57 | 5.69 | 6.17 | 5.41 | 5.33 | 5.76 | 5.44 | 4.36 | 4.60 | 4.92 | 3.89 | 5.69 | ||||
| Hyperion | 5.25 | 4.72 | 4.59 | 4.41 | 5.28 | 4.66 | 4.51 | 4.52 | 4.91 | 4.34 | 4.37 | 4.27 | 4.25 | 4.31 | ||||
| IASI | 9.56 | 7.73 | 8.20 | 8.83 | 9.57 | 7.52 | 7.50 | 8.83 | 8.88 | 6.97 | 7.69 | 8.36 | 6.74 | 6.87 | ||||
| Landsat | 4.02 | 3.92 | 3.80 | 3.66 | 4.04 | 3.88 | 3.81 | 3.73 | 3.83 | 3.66 | 3.64 | 3.53 | 3.36 | 3.47 | ||||
| M3 | 5.04 | 4.05 | 4.10 | 4.23 | 5.07 | 4.04 | 4.03 | 4.31 | 4.38 | 2.93 | 3.12 | 3.24 | 2.65 | 4.51 | ||||
| MODIS | 6.77 | 6.71 | 6.25 | 6.77 | 6.67 | 6.83 | 6.46 | 6.73 | 6.03 | 6.06 | 5.77 | 6.04 | 6.66 | 5.90 | ||||
| MSG | 3.93 | 4.13 | 4.03 | 3.98 | 3.90 | 4.18 | 4.00 | 4.04 | 3.79 | 4.08 | 3.91 | 3.89 | 3.52 | 3.67 | ||||
| PLEIADES– | 7.74 | 7.45 | 7.83 | 7.39 | 7.66 | 7.48 | 7.60 | 7.32 | 7.43 | 7.28 | 7.56 | 7.11 | 7.20 | 7.17 | ||||
| SFSI | 4.88 | 4.70 | 4.43 | 4.39 | 5.02 | 4.59 | 4.45 | 4.52 | 4.56 | 4.21 | 4.21 | 4.17 | 4.02 | 4.13 | ||||
| SPOT5 | 5.70 | 5.65 | 5.35 | 5.31 | 5.66 | 5.72 | 5.30 | 5.30 | 5.51 | 5.56 | 5.21 | 5.15 | 5.28 | 5.19 | ||||
| Vegetation | 5.60 | 5.33 | 5.44 | 5.52 | 5.52 | 5.44 | 5.36 | 5.48 | 5.33 | 5.28 | 5.22 | 5.27 | 5.11 | 4.93 | ||||
| All scenes | 6.26 | 5.61 | 5.54 | 5.59 | 6.23 | 5.60 | 5.46 | 5.62 | 5.75 | 5.01 | 5.05 | 5.11 | 4.84 | 5.27 | ||||
| FAPEC | CCSDS 122.1 | JPEG-LS | CCSDS 123.0-B-2 | M- CALIC | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Corpus | No | IWT | POT | RWA | No | IWT | POT | RWA | No | IWT | POT | RWA | No | No | ||||
| AIRS | 0.81 | 0.25 | 2.67 | 2.26 | 14.28 | 11.66 | 11.39 | 11.32 | 2.48 | 4.59 | 5.17 | 4.61 | 1.55 | 15.46 | ||||
| AVIRIS | 2.44 | 1.16 | 7.20 | 6.71 | 55.32 | 45.17 | 46.56 | 42.93 | 9.97 | 11.43 | 13.76 | 13.08 | 7.32 | 61.33 | ||||
| CASI | 1.08 | 0.56 | 3.48 | 2.88 | 30.31 | 25.77 | 27.60 | 25.87 | 4.97 | 5.69 | 7.00 | 6.30 | 3.53 | 30.55 | ||||
| CRISM | 3.25 | 1.30 | 9.28 | 9.57 | 66.32 | 63.61 | 67.18 | 69.52 | 11.51 | 14.21 | 17.18 | 17.47 | 7.11 | 77.90 | ||||
| Hyperion | 2.15 | 0.87 | 6.97 | 6.05 | 39.14 | 36.16 | 38.14 | 38.33 | 7.63 | 9.76 | 12.11 | 11.22 | 6.36 | 52.33 | ||||
| IASI | 9.87 | 14.73 | 120.43 | 208.01 | 723.38 | 615.70 | 623.41 | 751.97 | 117.99 | 175.99 | 217.58 | 301.01 | 82.63 | 724.83 | ||||
| Landsat | 0.16 | 0.09 | 0.49 | 0.38 | 3.43 | 3.34 | 3.57 | 3.38 | 0.71 | 0.87 | 1.03 | 0.91 | 0.65 | 4.39 | ||||
| M3 | 1.54 | 0.71 | 4.79 | 4.62 | 31.53 | 29.18 | 31.34 | 32.12 | 5.67 | 7.16 | 8.79 | 8.74 | 4.00 | 40.89 | ||||
| MODIS | 1.82 | 1.63 | 4.48 | 4.00 | 42.26 | 42.50 | 42.85 | 42.53 | 6.99 | 8.58 | 9.66 | 9.16 | 5.69 | 39.55 | ||||
| MSG | 4.85 | 4.38 | 12.78 | 11.74 | 81.68 | 86.69 | 91.35 | 87.04 | 16.38 | 21.41 | 24.84 | 23.96 | 15.33 | 114.45 | ||||
| PLEIADES– | 0.07 | 0.05 | 0.23 | 0.13 | 2.22 | 2.19 | 2.30 | 2.20 | 0.38 | 0.46 | 0.53 | 0.43 | 0.29 | 2.05 | ||||
| SFSI | 0.44 | 0.21 | 1.53 | 1.37 | 9.94 | 8.99 | 9.66 | 9.48 | 1.79 | 2.30 | 2.87 | 2.69 | 1.62 | 13.18 | ||||
| SPOT5 | 0.07 | 0.05 | 0.22 | 0.16 | 2.12 | 2.17 | 2.16 | 2.10 | 0.39 | 0.48 | 0.53 | 0.47 | 0.32 | 2.04 | ||||
| Vegetation | 2.23 | 2.02 | 5.48 | 4.46 | 47.40 | 46.51 | 49.74 | 47.38 | 8.66 | 10.58 | 11.95 | 10.98 | 7.06 | 47.86 | ||||
| All scenes | 1.97 | 1.30 | 7.55 | 9.15 | 52.49 | 48.28 | 50.08 | 52.76 | 9.04 | 11.81 | 14.23 | 15.73 | 6.51 | 57.55 | ||||
| FAPEC | CCSDS 122.1 | JPEG-LS | CCSDS 123.0-B-2 | M- CALIC | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Corpus | No | IWT | POT | RWA | No | IWT | POT | RWA | No | IWT | POT | RWA | No | No | ||||
| AIRS | 0.74 | 0.27 | 2.38 | 1.14 | 10.05 | 8.07 | 7.58 | 7.19 | 2.43 | 4.34 | 4.73 | 3.40 | 1.86 | 13.62 | ||||
| AVIRIS | 2.35 | 1.11 | 6.35 | 3.81 | 38.27 | 30.76 | 31.11 | 27.77 | 9.91 | 11.04 | 12.62 | 9.82 | 8.56 | 55.63 | ||||
| CASI | 1.02 | 0.52 | 3.00 | 1.70 | 21.04 | 17.65 | 18.49 | 17.10 | 5.01 | 5.60 | 6.51 | 5.06 | 4.10 | 27.99 | ||||
| CRISM | 3.18 | 1.28 | 8.11 | 5.01 | 44.05 | 42.32 | 43.79 | 44.78 | 11.30 | 13.76 | 15.59 | 12.68 | 8.51 | 71.52 | ||||
| Hyperion | 2.20 | 0.91 | 6.22 | 3.45 | 26.63 | 24.96 | 25.62 | 24.95 | 7.30 | 9.39 | 10.89 | 8.15 | 7.49 | 46.73 | ||||
| IASI | 12.43 | 18.24 | 106.99 | 176.51 | 522.67 | 445.48 | 429.82 | 568.51 | 118.92 | 168.05 | 200.70 | 265.14 | 95.24 | 682.36 | ||||
| Landsat | 0.16 | 0.09 | 0.45 | 0.27 | 2.19 | 2.21 | 2.29 | 2.11 | 0.67 | 0.89 | 0.94 | 0.76 | 0.72 | 4.05 | ||||
| M3 | 1.56 | 0.71 | 4.20 | 2.54 | 19.34 | 18.12 | 19.13 | 19.48 | 5.41 | 6.93 | 7.96 | 6.40 | 4.81 | 36.87 | ||||
| MODIS | 1.72 | 1.53 | 3.97 | 2.81 | 28.74 | 29.96 | 29.05 | 28.80 | 6.95 | 9.21 | 9.09 | 7.93 | 6.49 | 37.32 | ||||
| MSG | 4.80 | 4.26 | 11.40 | 8.21 | 52.00 | 57.06 | 58.33 | 53.58 | 15.76 | 21.24 | 22.80 | 19.54 | 17.64 | 102.83 | ||||
| PLEIADES– | 0.06 | 0.04 | 0.19 | 0.10 | 1.52 | 1.55 | 1.58 | 1.51 | 0.38 | 0.48 | 0.51 | 0.40 | 0.31 | 1.92 | ||||
| SFSI | 0.45 | 0.22 | 1.34 | 0.78 | 6.38 | 6.15 | 6.35 | 6.04 | 1.72 | 2.21 | 2.59 | 1.99 | 1.85 | 11.78 | ||||
| SPOT5 | 0.07 | 0.04 | 0.19 | 0.13 | 1.42 | 1.53 | 1.42 | 1.41 | 0.37 | 0.52 | 0.48 | 0.42 | 0.34 | 1.87 | ||||
| Vegetation | 2.11 | 1.96 | 4.94 | 3.41 | 31.12 | 31.53 | 31.65 | 31.08 | 8.31 | 10.99 | 11.08 | 9.62 | 8.04 | 44.01 | ||||
| All scenes | 1.98 | 1.35 | 6.67 | 6.51 | 35.87 | 33.23 | 33.30 | 35.93 | 8.93 | 11.58 | 13.06 | 12.82 | 7.59 | 53.11 | ||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hernández-Cabronero, M.; Portell, J.; Blanes, I.; Serra-Sagristà, J. High-Performance Lossless Compression of Hyperspectral Remote Sensing Scenes Based on Spectral Decorrelation. Remote Sens. 2020, 12, 2955. https://doi.org/10.3390/rs12182955
Hernández-Cabronero M, Portell J, Blanes I, Serra-Sagristà J. High-Performance Lossless Compression of Hyperspectral Remote Sensing Scenes Based on Spectral Decorrelation. Remote Sensing. 2020; 12(18):2955. https://doi.org/10.3390/rs12182955
Chicago/Turabian StyleHernández-Cabronero, Miguel, Jordi Portell, Ian Blanes, and Joan Serra-Sagristà. 2020. "High-Performance Lossless Compression of Hyperspectral Remote Sensing Scenes Based on Spectral Decorrelation" Remote Sensing 12, no. 18: 2955. https://doi.org/10.3390/rs12182955
APA StyleHernández-Cabronero, M., Portell, J., Blanes, I., & Serra-Sagristà, J. (2020). High-Performance Lossless Compression of Hyperspectral Remote Sensing Scenes Based on Spectral Decorrelation. Remote Sensing, 12(18), 2955. https://doi.org/10.3390/rs12182955