Abstract
The knowledge of tree characteristics, especially the shape of standing trees, is important for living tree volume estimation, the computation of a wide range of forest stand features, and the evaluation of stand stability. Nowadays, nondestructive and accurate approaches to data collection in the forest environment are required. Therefore, the implementation of accurate point cloud-based information in the field of forest inventory has become increasingly required. We evaluated the stem curves of the lower part of standing trees (diameters at heights of 0.3 m to 8 m). The experimental data were acquired from three point cloud datasets, which were created through different approaches to three-dimensional (3D) environment modeling (varying in terms of data acquisition and processing time, acquisition costs, and processing complexity): terrestrial laser scanning (TLS), close-range photogrammetry (CRP), and handheld mobile laser scanning (HMLS) with a simultaneous localization and mapping algorithm (SLAM). Diameter estimation errors varied across heights of cross sections and methods. The average root mean squared error (RMSE) of all cross sections for the specific methods was 1.03 cm (TLS), 1.26 cm (HMLS), and 1.90 cm (CRP). TLS and CRP reached the lowest RMSE at a height of 1.3 m, while for HMLS, it was at the height of 8 m. Our findings demonstrated that the accuracy of measurements of the standing tree stem curve was comparable for the usability of all three devices in forestry practices.
1. Introduction
Forest management, inventory, and planning require precise information about several tree parameters. The basic tree characteristics, e.g., diameter at breast height (DBH) and tree height, are easy to measure. However, more complicated tree parameters, like stem profiles, stem ovality, open stem height, and damage, are often needed [1]. Such parameters are hard to measure and often require destructive methods. Thus, easy-to-use terrestrial remote sensing methods are becoming important and they have many applications in forest inventory [2].
Terrestrial laser scanning (TLS) has been proven to be a fast and accurate method of high-density three-dimensional point cloud acquisition. The main advantage of TLS application in forestry inventory and practice lies in the possibilities of visualization and digital modeling of forest environment and the estimation of various tree-level and plot-level attributes [2]. As the understanding of TLS performance grows, more complex forest attributes that normally are not measurable with nondestructive methods might be estimated. For example, there is no suitable measuring tool for a stem curve of living trees, even though it is essential to determine the proportions of saw-wood and pulpwood [3]. TLS provides a nondestructive alternative through a localized tapering function. Taper functions determine the change in diameter in relation to the height of the tree; therefore, they are generally used for the volume estimation [4]. Volume estimation by the TLS single-scan method was compared with the volume of harvested trees [5]. Different applications of TLS methods for tree stem and tree canopy biomass estimation were presented in studies conducted by Dassot et al. [6] and Olofsson and Holmgren [7].
TLS point clouds are commonly based on single-scan or multi-scan (a co-registered combination of individual scans) methods and diameters are calculated from registered point clouds, usually by a cylinder- or the circle-fitting method. In the first step, stems are detected by surface norms and the cylinder-fitting method, and cutting the stems into horizontal slices to assess diameters at exact points. Diameters of slices are then used to create spline-based taper curve models for each tree [8]. Liang et al. [9] evaluated the stem curve estimation accuracy while using averages of the tree-wise RMSEs and biases. For the purpose of this work, we adopted the explanation of stem curve by Hyyppä et al. [10], who refer to trunk diameters at different heights with the term stem curve.
TLS is understood to be a data collection method with the possibility to acquire dense point clouds of forest environment with a millimeter level of precision. Despite the high precision, there are limitations, such as the high occlusion effect of the single-scan method, which can be partly reduced by the use of several scanner stations (the multi-scan method). However, the multi-scan method requires more time for the preparation of the scanning area (placement of reference spheres, scanning scheme determination) and a longer time for the acquisition of multiple scans [11,12]. Among other things, this resulted in the installation of a laser scanning devices on a variety of platforms [13], such as a mobile laser scanner (MLS) on a car [14] or tractor [15], a personal laser scanner (PLS) on a backpack [16,17], on unmanned airborne vehicles (UAV) [10], or handheld mobile phone devices [18,19], and handheld mobile laser scanners [11,20,21,22].
The mobile laser scanning systems, with all of their advantages, may compete with static TLS methods; however, a complex forest environment might be challenging because of terrain conditions and, more importantly, due to the necessity of Global Navigation Satellite Systems (GNSS) signal reception, which is significantly limited under the dense forest canopy [11]. Handheld mobile laser scanning (HMLS) devices typically consist of a laser scanner and a low-cost Inertial Measurement Unit (IMU) and the use the technology of Simultaneous Localization and Mapping (SLAM). Some devices, like ZEB1, use, instead of GNSS navigation, SLAM technology taken from the robotics field for precise positioning under the forest canopy [23]. A ZEB-Horizon (GeoSLAM Inc., Sterling, VA, USA) device applied in our research used the SLAM algorithm for the localization and mapping. The applicability of HMLS in different environments was tested, e.g., building interiors [23], outdoor open spaces [24], and a forest environment [13].
The potential of handheld mobile laser scanning devices for forest inventory lies in DBH (diameter at breast height) estimation and tree identification; however, the tree height estimation is highly affected by the low scanning range [20]. Nevertheless, tree height estimation from point clouds that are derived from terrestrial devices is still under study, and it is related to the occlusion effect and problems with the determination of an exact treetop position [25].
Advances in the computational capacity of personal computers and the development of image-matching algorithms brought about the possibility of applying close-range photogrammetry (CRP) to create high-density 3D point clouds from the series of overleaping images acquired by a camera [12]. The main advantages of CRP over TLS are the low hardware costs and efficiency: TLS is almost six-fold more time-consuming than CRP [26]. Cabo et al. [20] reached high data acquisition efficiency, when comparing TLS with HMLS. However, the cost of a device is still several times higher than that of a camera for CRP. These reasons led the authors to calculate the single tree attributes [27,28] or plot-level parameters [19,29,30] by image-matching algorithms from datasets created from CRP. Iglhaut et al. [31] published a comprehensive overview of forestry-related studies that are applying terrestrial Structure-from-Motion (SfM) CRP workflow, e.g., biospheric variables, like height, biomass, crown profiles from aerial or diameter at breast height, and tree position.
The use of CRP offers various data acquisition methods and settings, including camera orientation (vertical, horizontal), shooting mode (mobile, stop and go), shooting path pattern (waves, outside, outside/inside, strips), camera holding method (handheld pole, gimbal), and camera settings (aperture, ISO, shutter speed, focus). A different combination of the mentioned methods may be appropriate, depending on the intended purpose. However, the most suitable method for forest data collection with the aim of estimating DBH is a vertically oriented camera held by hand with an outside/inside path and in stop and go shooting mode [32].
The demand for precise forest environment information using nondestructive remote sensing methods is growing in terms of national forest inventory, biomass storage, and CO2 sequestration in the tree biomass. The estimation of the diameter at different heights on the standing tree is crucial for the estimation of living tree volume. However, to our knowledge, the statistics of stem curve estimation from point cloud data were compared at the tree-level and the influence of the height, in which the diameter was estimated, has not been studied sufficiently.
The aim of the article was to compare the accuracy of stem curve models using three terrestrial remote sensing devices. Highly precise models of tree stems were used for the evaluation of the diameter estimation accuracy with changing height. The accuracy was calculated and tested on 11 cross sections of a lower part of a tree stem up to a height of 8 m. Diameters of the lower part of the tree (the most valuable part of the tree from the wood stock and wood quality point of view) were compared. Differences in diameter estimations and their errors that were related to different height sections were statistically tested to demonstrate the suitability of the applied device for the mapping of a forest stand, when considering the height level of the tree stem. Finally, we concluded whether the achieved accuracy of the tested devices would be sufficient for the collection of environmental data on forest stands.
2. Materials and Methods
2.1. Research Plot and Field Measurements
The study was conducted on the research plot established in the Sessile oak (Quercus petraea (Matt.) Liebl.) forest stand in the area of the University Forest Enterprise of the Technical University in Zvolen in central Slovakia (48°36′17.269 N; 19°5′7.239 E) (Figure 1). The circular research plot, with a radius of 16 m, included 43 oak trees of an average age of 115 years. Two European hornbeams (Carpinus betulus L.) were located in the understory and, thus, were excluded from the measurement and data processing. Experimental measurements were done on a windless day to eliminate the wind’s influence on the accuracy of the gathered data.
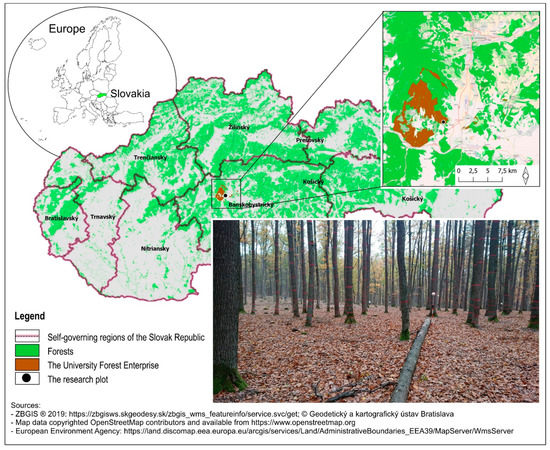
Figure 1.
Location of the research plot.
The diameters of oak trees were measured in 11 cross sections from 0.3 m up to 8 m above the ground on all 43 oak trees (Table 1) by a diameter tape (Ben Meadows Co.). In this research, a nondestructive measurement method was the only acceptable solution; hence, a lifting platform (PKP 14-7) was used for the measurement of diameter at inaccessible heights. The sections were marked by a color ring at the place where the diameter tape was attached. Colorized 5 cm wide rings were used to mark the f exact position of the measurement that was further processed, and a point cloud was created.

Table 1.
Reference diameters in height sections on the research plot.
2.2. Experimental Data Acquisition
The research plot was scanned by Trimble TX8 terrestrial laser scanner (Trimble, Inc., Sunnyvale, CA, USA). The scanner works on the principle of a vertically rotating mirror on a horizontally rotating base, providing an angular field of view of 360° horizontally and 317° vertically. The maximum scanning range was 120 m (11.3 mm point spacing at 30 m, 138 Mpts), while using ultra-high-speed time-of-flight ranging principle.
The research plot (Figure 2A) was scanned from 13 positions with the use of 18 reference spheres with a diameter of 14.4 cm. Reference spheres were placed 1 m to 2 m above the ground and used for the point cloud registration along with the central scan. A project that was created by a scanner Trimble TX8 that contained 13 scans was imported to the software of Trimble RealWorks version 11.1 (Trimble, Inc.) for the registration of the point cloud. Reference spheres were automatically identified and placed by the software, and visually validated. Misplaced reference spheres were deleted (shaded and incompletely scanned spheres with a small number of reflected points), and a point cloud was automatically created using a local coordinate system. The research plot with nearby surroundings was selected by the limit box and exported for further processing to reduce the time consumption.
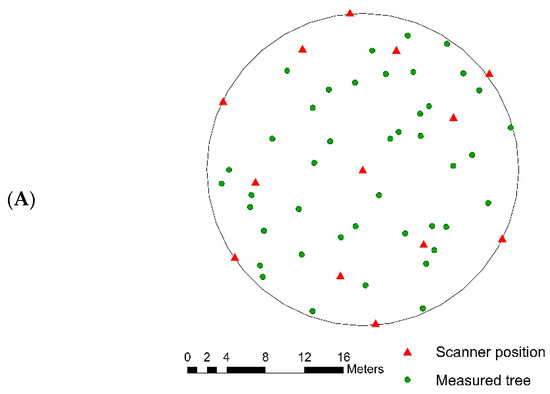
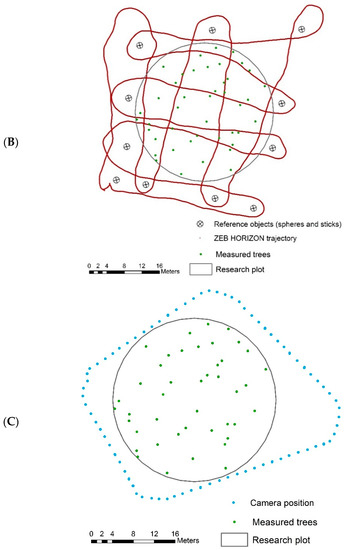
Figure 2.
Scanning schemes of the research plot with a 16 m radius: (A) terrestrial laser scanning (TLS); (B) handheld mobile laser scanning (HMLS); and, (C) close-range photogrammetry (CRP).
The HMLS dataset was acquired by the SLAM device ZEB-Horizon. For the survey, a closed-loop, free walking method, and specific scan path were used [33] (Figure 2B). The HMLS ZEB-Horizon is a personal device, so it was carried around reference spheres. Positioning marks on wooden sticks were placed on the research plot to facilitate the operator’s orientation during the data acquisition. The trajectory was a wavy line, with approximately 10 m wide spaces between single lines. The three-dimensional (3D)s point cloud was generated in GeoSLAM Hub & Draw software (GeoSLAM Inc., Sterling, VA, USA), applying the principles of the SLAM algorithm, whereby a model of the environment and a navigation solution are produced concurrently [34]. The position and orientation of the device in relation to the surrounding recorded objects defined the position and more precise model [35]. The maximum range of ZEB-Horizon was 100 m and the data acquisition rate was 300,000 points/s. First, a dense 3D point cloud of a broader area was generated. Subsequently, the research plot and close surroundings were clipped in respect to the aim of research and the computational capacity of the workstations. The clipped 3D point cloud was exported in a suitable format (*.LAS) and processed in DendroCloud 1.50 (gis.tuzvo.sk/dendrocloud).
The close-range photogrammetric dataset was compiled by the stop-and-go method. A Canon EOS 5D Mark II (35 mm) digital single-lens reflectance (DSLR) camera with 5.616 × 3.744 resolution was used, fixed on a telescopic pole. Manual focus was set up during the image collection. The images were taken at three different heights, 1.5, 2.0, and 2.5 m, on each image shooting position. With this approach, the circular area of the research plot was walked around in approximately 1.5 m long steps (Figure 2C). The photographer was moving on the four connected lines around the outside border of the plot. The four range poles and paper positioning targets were placed on the research plot for orientation purposes and scaling. The dataset was processed in Agisoft Photoscan Professional 1.2.0 (Agisoft LLC., St. Petersburg, Russia) software, where a high-quality dense point cloud was generated as a result of the image alignment. We used the alignment settings as follows: pair selection—generic; accuracy—high; key point limit (default)—40,000; and, tie points (default)—4000. The point cloud was scaled and oriented using four positioning markers, and XYZ coordinates were set up for each of the four markers. The total transformation error was 0.002 m. Subsequently, the point cloud was recalculated, and the accuracy of transformation was checked by four scale bars. The lengths were added and evaluated with a total error of 0.009 m.
In the next step of the research, point clouds were filtered, a digital terrain model (DTM) was created individually from each of the datasets that were acquired by TLS, HMLS, and CRP, trees were identified, cross sections were extracted, and diameters in the 11 sections were estimated by the software DendroCloud 1.50 (gis.tuzvo.sk/dendrocloud).
Point clouds were imported and clipped by a box filter in the first step. The size of the box filter (44 × 44 × 34 m) ensured that false laser beam reflections and distant noise points were omitted. Point clouds of specified sizes were slightly larger than the diameter of the research plot. Therefore, all parts of the trees in question, also beyond the diameter of the research plot, were captured.
The vertical projection method [36] was used for DTM creation of the research plot with an output raster resolution of 0.5 m. This resolution was suitable for primary cross section extraction from the point clouds due to the flatness of the terrain and almost no depressions or elevations.
As the positions of trees were measured 1.3 m above the terrain, primary cross sections were also extracted at this height for tree identification purposes and trunk position extraction. Based on our previous experience, 10 cm wide cross sections (1.25‒1.35 m above DTM) were used. Subsequently, spatial clusters of points contained in cross sections were created. Each point belongs to the spatial cluster group if the distance between points was less than 2 cm and the group contained at least 200 points. Points that did not meet the limits were automatically deleted. Spatial clusters were manually revised, and diameters and positions were only calculated from those representing the trees.
The procedures of tree diameter estimation are based on the geometrical properties of points in the horizontal cross section. Circle-fitting algorithms are methods for the calculation of tree diameter; in other words, they are mathematical functions fitting the best circle to a set of points. The optimal circle method was used for the initial estimation of tree diameters and positions. The optimal circle method is finding a circle with a minimal RMSE value while using a multidimensional mathematical optimization algorithm. The optimal circle method enhances the diameter and position of circle with the last square algorithm. For a specific cluster of points the method uses steep descendent algorithm to search for a local minimum of the optimization function [36]. Tree positions were used to calculate the elevations of tree base, and points that were contained in the annulus cylinder with a center at a tree position were selected. The inner and outer annulus diameters were 40 cm and 120 cm larger than the tree diameters, respectively. The base of the annular cylinder was placed at the lowest elevation of the selected points. The annulus cylinder height was 50 cm. To avoid terrain extremes and noise, the tree base elevation was calculated as the arithmetic mean of point elevations in the range 30−70% above the annulus base.
Multiple cross sections at heights of 0.3 m, 0.7 m, 1 m, 1.3 m, 2 m, 3 m, 4 m, 5 m, 6 m, 7 m, and 8 m above the calculated tree base were extracted automatically. All of the cross sections at all heights were manually validated and cross sections containing noise, branches, leaves, etc. were filtered out manually. Finally, the diameters of multiple cross sections were estimated by the optimal circle method. The high density of points in cross sections and especially on the surface of every tree section created by TLS resulted in a long computation time (usually several hours). A random subsampling of cross section points was used to reduce the computation time. A randomly selected subsample of a maximum of 20,000 points was used in the circle-fitting algorithm for each tree diameter estimation.
The diameters at different heights were evaluated by Equations (1)–(3). The diameter estimation error ei was computed as the difference between the estimated diameter (xest) and the reference diameter (xref), as follows:
Bias, the measure of the systematic component of error, was calculated as the arithmetic mean of diameter estimation errors:
The RMSE of diameter estimation is an indicator of the dataset accuracy:
The significance of diameter estimation errors was tested by one-way ANOVA with a post hoc Tukey HSD test in Statistica software (Statsoft Inc., Tulsa, OK, USA).
3. Results
3.1. Experimental Data Acquisition
Point clouds were created by three different methods (TLS, HMLS, and CRP) and stem curves (diameters from 0.3 m to 8 m in 11 cross sections) were estimated. The data acquisition time varied between the methods; the fastest data collection method at the circular research plot (r = 16 m; a research area of 804 m2) was HMLS, which finished the process in 12 min. CRP was slightly slower with tree stripes at different heights of image shooting (32 min), while TLS data collection and reference sphere placement took 64 min. All of the times were measured for one operator doing all operations that were related to data collection.
All of the devices were able to acquire the data quality necessary to generate a point cloud with density adequate to identify all 43 trees; however, the density varied between point clouds. Trimble TX 8 (TLS) acquired a higher number of points (1264 million) as compared to ZEB-Horizon (HMLS) (47 million) and Canon EOS 5D Mark II (CRP) (366,000). TLS and HMLS were able to model all trees with a high level of detail, even exceeding the height of the last cross section (8 m). The CRP method was not able to reconstruct the stem at heights over ~9 m. This is related to the cross section height and the number of points in the cross sections that are available for diameter estimation. The number of points in cross sections in TLS was approximately 10 times higher than in CRP and nine times higher than in HMLS (Figure 3). In the case of TLS and CRP devices, there was a descending trend in the number of points, related to the increasing height of the tree stem in cross sections. TLS exhibited two peaks on the curve in the graph, while HMLS and CRP only exhibited one peak. The HMLS device had the densest point clouds at a height of 2 m above the ground, which necessitated the free-walking scanning method. The operator held the scanner, combining the functionality of device and ergonomic grip, while walking around the trees. The lower parts of the closest trees were outside of the field of view of the device. On the other hand, CRP and TLS had the highest number of points in the lowest sections of tree stems, which was caused by, e.g., their irregular shapes and larger diameter providing a more extensive reflective surface. The point density of TLS decreased rapidly after 3 m, while for HMLS and CRP it decreased slightly (Figure 3).
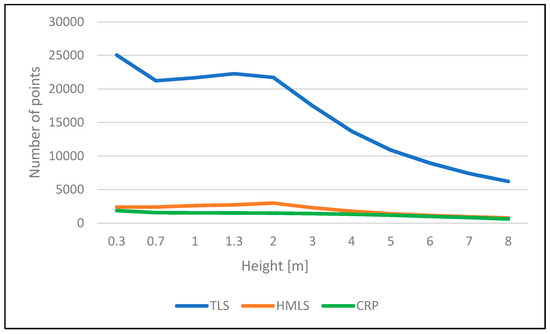
Figure 3.
Number of points in the cross sections.
3.2. Diameter at Breast Height (DBH) Estimation
Diameters at breast height were estimated by a circle-fitting method from point clouds that were created by all three data acquisition methods. Estimated diameters were statistically tested using analysis of variance (ANOVA), which proved the significant influence of different data collection approaches on DBH estimation error (Table A1). All three methods underestimated the diameters: TLS by 0.63 cm, HMLS by 1.57 cm, and CRP by 1.11 cm. The diameters estimated from the TLS-based point cloud reached the lowest RMSE (0.80 cm); CRP errors had the largest variance (−3.26 cm to 1.74 cm), while HMLS with the smallest variance of error (−2.41 cm to −0.11 cm), reaching a slightly worse RMSE (1.62 cm) than CRP (Figure 4).
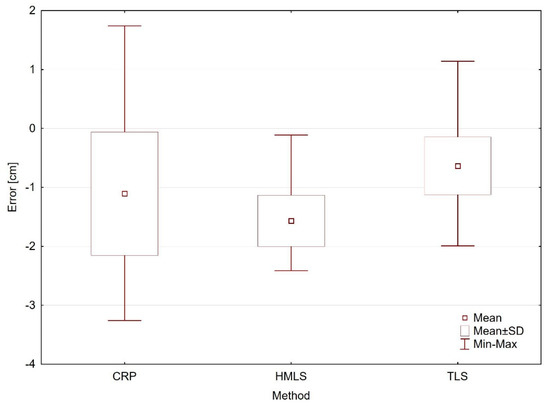
Figure 4.
DBH estimation errors.
3.3. Cross Section Height
The tree diameters at different cross section heights estimated from the TLS, HMLS, and CRP point clouds were statistically tested against the reference data that were collected with the nondestructive method by a diameter tape. The diameter estimation errors from the point cloud generated by the TLS multi-scan method were tested using one-way ANOVA with a post hoc Tukey HSD test (Table A2), which proved a significant impact of cross section height on the diameter estimation errors. The estimation error of diameter at 0.3 m above the ground was significantly different from all other estimation errors. The average tree diameter estimation error in this cross section was only overestimated in the TLS point cloud. All other section biases were between −1.08 cm and −0.63 cm (Figure 5).
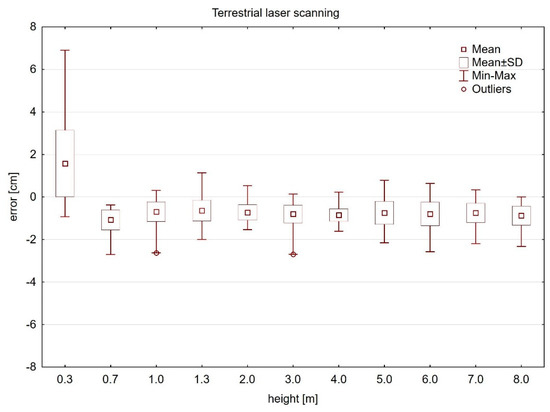
Figure 5.
Diameter estimation errors in TLS point cloud cross sections.
In the case of the point cloud generated by a handheld mobile laser scanner, an ANOVA test proved a significant influence of cross section height on estimation error for almost all cross sections. There was no statistically significant difference between the diameter estimation errors that were closest to the height of the HMLS device (1.0–2.0 m) (Table A3). The diameter estimation error decreased with increasing height and the DBHs were underestimated in all cross sections up to the 7 m high cross section (Figure 6).
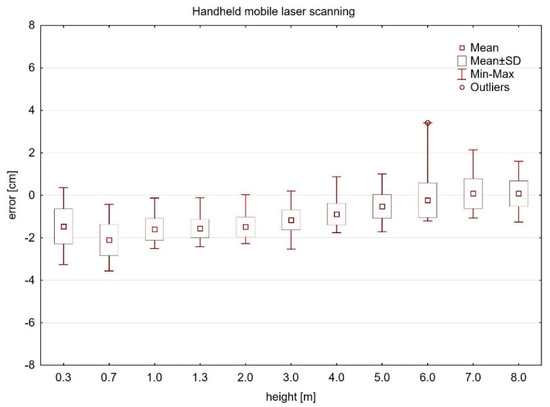
Figure 6.
Diameter estimation errors in HMLS point cloud cross sections.
During the determination of the diameters at different heights, we faced a problem with the CRP point cloud, which did not sufficiently cover the surface of all trunks at the different heights to estimate the diameters with the circle-fitting methods. We evaluated all of the diameters that we were able to estimate from the point cloud (Table 2).

Table 2.
Number of trees identified from CRP point cloud cross sections.
The estimated diameters from CRP were statistically tested and, in the CRP point clouds, the influence of cross section height was proven. The diameter estimation error at 0.7 m of the cross section height is significantly different from errors in other cross section heights (Table A4). We assume that the significant influence in this cross section was caused by the reduction of points in this section, as low parts of trees were further from the camera placed on a handheld pole. Influence was not proven for the cross section 0.3 m above the ground. However, in relation to the TLS point cloud (which is considered the most accurate) and the significant overestimation of the reference data, we assume that the low number of points was not sufficient to cover the surface of trunks in some cases. Figure 7 shows the diameter estimation errors in different CRP point clouds cross section heights. The variability and extent of errors, as well as the standard deviation of errors, are the largest of all used methods.
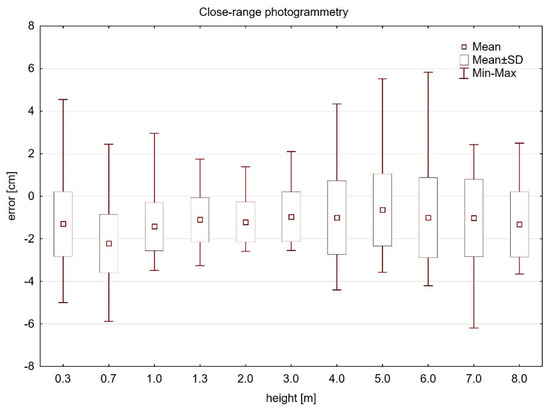
Figure 7.
Diameter estimation errors in CRP point cloud cross sections.
Diameter estimation errors varied across cross section heights and methods; the average RMSE for all cross sections was 1.03 cm for TLS, 1.26 cm for HMLS, and 1.90 cm for CRP method. TLS and CRP reached the lowest RMSE (Figure 8) in the cross section 1.3 m above the ground, while HMLS had its lowest RMSE at the height of 8 m with values of 0.80 cm, 1.67 cm, and 0.60 cm, respectively. The highest TLS RMSE was caused by the overestimation of measured data by circle-fitting algorithms, which are sensitive to noncircular shapes. We assume that the CRP and HMLS methods did not acquire sufficient point density to cover the trunk surface in detail, which would raise the RMSE due to the influence of the irregular shape.
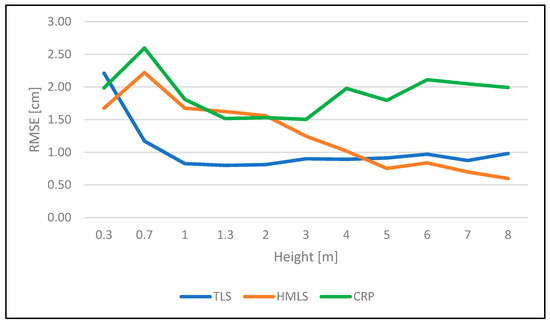
Figure 8.
Root mean squared error of diameter estimation at different heights.
4. Discussion
Forest inventory that is performed with conventional measurement technologies is time-consuming, with a high demand for qualified personnel and many specific forestry-related measuring tools, which leads to high costs of acquired data. At the same time, the data do not include as high level of detail as TLS-, HMLS-, or CRP-based point clouds, or the possibility to repeatedly measure the same variables or correct possible error. James and Quinton [24] claim that HMLS is expected to be approximately six times faster than SfM CRP and 40 times faster compared to TLS. In our case, HMLS showed to be the fastest of all the methods used, but only 2.7 times faster than CRP and 5.3 times faster than TLS. However, our research plot was relatively small (804 m2) and the point cloud generated by CRP was slightly larger. The point clouds from the TLS and HMLS data were a few times larger than the research plot. This article has an experimental character and, at the beginning of an experiment, there are always going to be many questions about how to increase the research performance and minimize time and money consumption. According to our findings, demonstrated in Figure 2, we suggest ways for optimizing the workflow in future field research. On the one hand, a slower walk with HMLS and adding more CRP stations may increase the point density of these devices. On the other hand, the reducing of stations of TLS may decrease the number of points, which would mean that it differs markedly in density from the HMLS and CRP point clouds.
When comparing the data collection time from authors who applied different methods, it is helpful to calculate the area (m2) versus time (min) per surveyor. In this context, HMLS devices (depending on the author) had the best results, from 20 m2 to 277.78 m2 per min. per surveyor [20,22,24,37]. CRP also demonstrated to be a potentially fast data acquisition method, with an area from 30.63 m2 to 136 m2 per min. per surveyor [32]. The TLS data acquisition rate was lower, as in the two previous methods (0.85–72.46 m2 per min. per surveyor) [20,22]. Data acquisition time is directly related to the costs of the acquired data and it is also necessary to take into account the acquisition costs of the device. Therefore, it is necessary to prepare a precise plan of the potential use of data which corresponds with application of an appropriate device and methods accordingly.
Diameter at breast height is one of the most important variables for forestry; therefore, it is often estimated from point clouds created by different data acquisition methods. Before the process of DBH estimation itself, it is important to identify trees in the research plot. Low DBH estimation error will be useless for forest inventory if only a small percentage of trees is identified. The number of trees identified varies across studies, ranging from 76% identified by CRP [29] up to 100% identified by multi-scan TLS [12,38] or HMLS [39].
In our study, the diameters at breast height but also the diameters estimated at different heights, were underestimated, except the diameters at 0.3 m with TLS and 7 m and 8 m with HMLS. On average, DBH estimated by a circle-fitting method was underestimated by 0.63 cm, 1.57 cm, and 1.11 cm with TLS, HMLS, and CRP, respectively, which is in line with our previous experience. DBH underestimation is also common for other authors when using the circle-fitting algorithms. Koreň et al. [36] compared five circle-fitting methods in both single-scan and multi-scan approaches and, in nine out of 10 cases, the diameters were underestimated. Similarly underestimated results were reported for three different circle-fitting methods with the MLS approach by Čerňava et al. [40], for three different research plots with the TLS approach by Cabo et al. [38], and for four different image-shooting methods with CRP by Mokroš et al. [32].
Relatively good DBH estimation RMS errors were acquired by the authors focused on the estimation of single tree parameters’ the RMSE of DBH estimation from CRP was 0.59 cm [28] or 0.96 cm [27]. For TLS point cloud and simulated diameter tape path on the tree, an RMSE of 0.09 cm was acquired by You et al. [41]. The estimated RMS errors on the plot-level typically produce higher values of RMSE, e.g., 4.41–5.98 cm [9] or 7.2 cm [29] by CRP, 2.65–5.57 cm by MLS [40], 1.58–1.65 cm by HMLS [37,39], and 0.77–4.27 cm by TLS [12,36]. Comparison of the mentioned publications is hard, because there are many differences in terms of the materials and methods used; therefore, it is always necessary to learn about the specific workflow and keep differences in mind when comparing results.
In this study, we estimated tree diameters at different heights up to 8 m and statistically tested the influence of the cross section height on the diameter estimation error. Point clouds and reference data were nondestructively collected. To describe the shape of standing trees, authors commonly consider the stem curve or the taper curve as the stem diameter is the function of height [9,42]. In other cases, tree shape is characterized by diameters 1.3 and 6 m above the ground and height; altogether, it is used in allometric equations to estimate the standing tree volume [8,43]. Hyyppä et al. [10] used the term stem curve, referring to the tree diameter at different heights.
Manual data processing is time-consuming, so a comparison of manual and automated methods of diameter estimation at different heights (DBH and d6—6 m above the ground) was conducted by Liang et al. [44]. In the case of DBH estimation, automated processing shows lower RMS error (0.82 cm) than manual (1.26 cm); in the case of d6, the results of manual estimation were slightly better (1.03 cm) than automated (1.13 cm). The authors state that it is possible to automatically estimate diameters at different heights and the estimation accuracy is satisfactory for the use of forest inventory. Additionally, Pitkänen et al. [8] estimated DBH and d6 as characteristics of trunk shape. They used 505 trees as the sample dataset. In this case, the RMS errors were under 1 cm for both DBH (0.73 cm) and d6 (0.84 cm); the biggest estimation errors were observed in the lowest and highest parts of the trees. Errors in the lowest parts were assigned to irregularities of the trunk that were caused by root crown, while errors in the upper part were assigned to the occlusion effect and trunk movement caused by the wind. The influence of wind on diameter in different heights’ estimation was studied by Vaaja et al. [45], who stated that the lower parts of the trunk (<28%) are not influenced by wind with a speed less than 9 m/s. In our study, we observed the influence of the low part of trees, which was proven in ANOVA tests at 0.3 m (TLS point cloud) and 0.7 m (CRP) above the ground, but we can reject the influence of wind in our data, as the weather during data acquisition by all three methods was without wind. However, we observed the influence of rests of fallen branches or nodes on diameter estimation error in some specific cases presented on TLS point cloud cross sections in Figure 9.
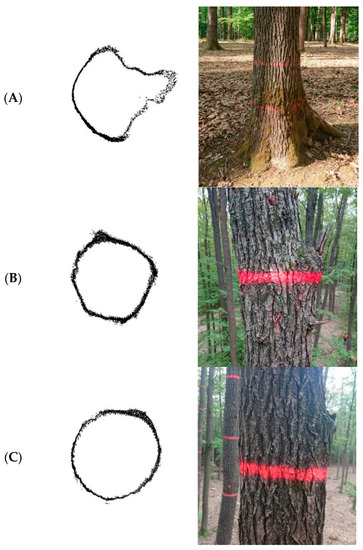
Figure 9.
Examples of irregular shape caused by (A) root crown; (B) rest of fallen branch; and, (C) node.
Liang et al. [9] published a benchmark of TLS approaches for forest inventories, where one of the researched variables was the tree stem curve. The diameters were estimated at heights of 0.65 m, 1.3 m, 2 m, and 3 m and up the trunk with a 1-m step until the uppermost measurable diameter. Stem curves were estimated by RMS error for the whole trunk, and differences between heights were not measured. The acquired results had a wide range of RMSE values with the single-scan method (1.3 cm to 6.0 cm) as well as with the multi-scan method (0.9 cm to 5.0 cm). Our results for the average of stem curves RMSE were the lowest for the TLS multi-scan method (1.03 cm), followed by HMLS (1.26 cm) and CRP (1.90 cm). However, the lowest section (0.3 m above the ground) was influenced by irregularities in the trunk. The shape of cross sections was not circular and, therefore, influenced the estimation errors of the circle-fitting algorithm, especially for the TLS method (Figure 10).

Figure 10.
The irregular shape of trunk cross sections, visualized on representative trees.
The backpack-carried MLS system was tested at easy- and medium-difficulty research plots and the RMSE of stem curve estimation was 1.2 cm and 1.7 cm, respectively [16]. The results in the mentioned study were compared against TLS estimated diameters; therefore, it is hard to compare this study with the results of our study, which involved manually measured reference data.
ZEB-Horizon uses the SLAM algorithm for the spatial navigation. Its usability is mainly limited by the sensor used, the environmental conditions, and the visibility of objects during real-time mapping [46]. SLAM solutions in modern mapping devices are expected to improve the measurement accuracy in case the satellite signal is weak [47]. The experiment presented in this paper showed that HMLS performed with ZEB-Horizon had the accuracy, comparable to TLS and CRP devices in terms of their usability in forestry practice in which diameters are often measured in 2 cm intervals. The research was conducted at a small research plot (about 804 m2) with ideal terrain, because it has an experimental character. The mapping of more extensive areas in forest stands on steep slopes and rugged terrain is challenging with terrestrial remote sensing devices.
5. Conclusions
In this study, we evaluated the stem curve of the lower part of standing trees (0.3 m to 8 m) with three different data acquisition methods (TLS, HMLS, and CRP). When considering the results of our study, and the advantages and disadvantages of the methods used, we consider TLS to be the most precise method; however, its acquisition costs are high. Therefore, this method might be used for scientific purposes that require high precision. However, diameters that are estimated by circle-fitting methods are generally underestimated and diameters of noncircular trees show higher error. Therefore, it will be crucial to find a method with the potential to follow the shape of the point cloud cross section to improve the accuracy of diameter estimation at various heights by the TLS method. The HMLS method acquired slightly higher RMSEs. On the other hand, it was proven to be the fastest data acquisition method with a low postprocessing time and the possibility of acquiring information not only about the trunk shape, but also about the crown of the tree. Therefore, it is a suitable method for a larger data collection range. We suggest choosing a higher distance for the free-walking method from the border of the area of interest to ensure that low parts of trunks close to the border will also be scanned sufficiently in order to improve the number of points in lower parts of point clouds. Future improvement of SLAM may reduce the point cloud noise and related estimation error. Close-range photogrammetry acquired a better average RMSE than HMLS, but the variability of error was noticeable higher. Additionally, the tree crowns were not visible in the point cloud, so the method must be adjusted if higher parts of the trees are to be investigated. CRP showed similar problems to HMLS in that the lower parts of the trunks were not sufficiently covered by points. We suggest choosing a higher distance for a scanning or image-shooting device from the area of interest and adjusting the camera parameters to improve the height of the created point cloud, but also refine the point coverage of low trunk parts. The acquisition costs of the camera are several times lower than for TLS or HMLS devices. Therefore, we believe that CRP might be a great asset for small forest owners.
Author Contributions
Conceptualization, M.H., J.C., M.K., and F.C.; software, M.K.; formal analysis, M.H. and J.C.; investigation, M.H. and J.C.; data curation, M.H., J.C., and J.T.; writing—original draft preparation, M.H. and J.C.; writing—review and editing, J.T. and M.S.; supervision, F.C. and M.K.; project administration, F.C.; funding acquisition, F.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Scientific Grant Agency (VEGA) of the Ministry of Education, Science, Research and Sport of the Slovak Republic and the Slovak Academy of Sciences (grant number 1/0868/18) (Innovative techniques for mapping of anthropogenic and natural landforms applicable in survey of landscape status).
Acknowledgments
Thanks for the equipment support provided by 3GON Slovakia s.r.o.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Appendix A

Table A1.
Results of one-way ANOVA post hoc Tukey HSD test for different methods of DBH estimation.
Table A1.
Results of one-way ANOVA post hoc Tukey HSD test for different methods of DBH estimation.
| Error: Between MS = 0.50797, df = 126.00 | |||
|---|---|---|---|
| Method | CRP | HMLS | TLS |
| CRP | 0.007832 | 0.006134 | |
| HMLS | 0.007832 | 0.000022 | |
| TLS | 0.006134 | 0.000022 | |
Note: Marked values represent significant differences (significance level α = 0.05).

Table A2.
Results of one-way ANOVA post hoc Tukey HSD test for TLS data.
Table A2.
Results of one-way ANOVA post hoc Tukey HSD test for TLS data.
| Error: Between MS = 0.41190, df = 462.00 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Height [m] | 0.3 | 0.7 | 1.0 | 1.3 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 | 7.0 | 8.0 |
| 0.3 | 0.000015 | 0.000015 | 0.000015 | 0.000015 | 0.000015 | 0.000015 | 0.000015 | 0.000015 | 0.000015 | 0.000015 | |
| 0.7 | 0.000015 | 0.153022 | 0.052261 | 0.276182 | 0.641138 | 0.838445 | 0.341074 | 0.627986 | 0.373420 | 0.929709 | |
| 1.0 | 0.000015 | 0.153022 | 0.999999 | 1.000000 | 0.999362 | 0.989910 | 1.000000 | 0.999481 | 0.999998 | 0.961369 | |
| 1.3 | 0.000015 | 0.052261 | 0.999999 | 0.999896 | 0.983411 | 0.917372 | 0.999580 | 0.985240 | 0.999262 | 0.818133 | |
| 2.0 | 0.000015 | 0.276182 | 1.000000 | 0.999896 | 0.999984 | 0.998897 | 1.000000 | 0.999988 | 1.000000 | 0.992334 | |
| 3.0 | 0.000015 | 0.641138 | 0.999362 | 0.983411 | 0.999984 | 1.000000 | 0.999998 | 1.000000 | 0.999999 | 0.999983 | |
| 4.0 | 0.000015 | 0.838445 | 0.989910 | 0.917372 | 0.998897 | 1.000000 | 0.999669 | 1.000000 | 0.999824 | 1.000000 | |
| 5.0 | 0.000015 | 0.341074 | 1.000000 | 0.999580 | 1.000000 | 0.999998 | 0.999669 | 0.999999 | 1.000000 | 0.996762 | |
| 6.0 | 0.000015 | 0.627986 | 0.999481 | 0.985240 | 0.999988 | 1.000000 | 1.000000 | 0.999999 | 1.000000 | 0.999976 | |
| 7.0 | 0.000015 | 0.373420 | 0.999998 | 0.999262 | 1.000000 | 0.999999 | 0.999824 | 1.000000 | 1.000000 | 0.997926 | |
| 8.0 | 0.000015 | 0.929709 | 0.961369 | 0.818133 | 0.992334 | 0.999983 | 1.000000 | 0.996762 | 0.999976 | 0.997926 | |
Note: Marked values represent significant differences (significance level α = 0.05).

Table A3.
Results of one-way ANOVA post hoc Tukey HSD test for HMLS data.
Table A3.
Results of one-way ANOVA post hoc Tukey HSD test for HMLS data.
| Error: Between MS = 0.38048, df = 462.00 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Height [m] | 0.3 | 0.7 | 1.0 | 1.3 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 | 7.0 | 8.0 |
| 0.3 | 0.000103 | 0.996114 | 0.999547 | 1.000000 | 0.440629 | 0.000704 | 0.000015 | 0.000015 | 0.000015 | 0.000015 | |
| 0.7 | 0.000103 | 0.007040 | 0.002972 | 0.000233 | 0.000015 | 0.000015 | 0.000015 | 0.000015 | 0.000015 | 0.000015 | |
| 1.0 | 0.996114 | 0.007040 | 1.000000 | 0.999318 | 0.041190 | 0.000019 | 0.000015 | 0.000015 | 0.000015 | 0.000015 | |
| 1.3 | 0.999547 | 0.002972 | 1.000000 | 0.999962 | 0.079448 | 0.000030 | 0.000015 | 0.000015 | 0.000015 | 0.000015 | |
| 2.0 | 1.000000 | 0.000233 | 0.999318 | 0.999962 | 0.320051 | 0.000311 | 0.000015 | 0.000015 | 0.000015 | 0.000015 | |
| 3.0 | 0.440629 | 0.000015 | 0.041190 | 0.079448 | 0.320051 | 0.606685 | 0.000089 | 0.000015 | 0.000015 | 0.000015 | |
| 4.0 | 0.000704 | 0.000015 | 0.000019 | 0.000030 | 0.000311 | 0.606685 | 0.174987 | 0.000053 | 0.000015 | 0.000015 | |
| 5.0 | 0.000015 | 0.000015 | 0.000015 | 0.000015 | 0.000015 | 0.000089 | 0.174987 | 0.514141 | 0.000352 | 0.000352 | |
| 6.0 | 0.000015 | 0.000015 | 0.000015 | 0.000015 | 0.000015 | 0.000015 | 0.000053 | 0.514141 | 0.421240 | 0.421240 | |
| 7.0 | 0.000015 | 0.000015 | 0.000015 | 0.000015 | 0.000015 | 0.000015 | 0.000015 | 0.000352 | 0.421240 | 1.000000 | |
| 8.0 | 0.000015 | 0.000015 | 0.000015 | 0.000015 | 0.000015 | 0.000015 | 0.000015 | 0.000352 | 0.421240 | 1.000000 | |
Note: Marked values represent significant differences (significance level α = 0.05).

Table A4.
Results of one-way ANOVA post hoc Tukey HSD test for CRP data.
Table A4.
Results of one-way ANOVA post hoc Tukey HSD test for CRP data.
| Error: Between MS = 2.0546, df = 393.00 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Height [m] | 0.3 | 0.7 | 1.0 | 1.3 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 | 7.0 | 8.0 |
| 0.3 | 0.130692 | 0.999999 | 0.999939 | 1.000000 | 0.992947 | 0.997608 | 0.646144 | 0.998865 | 0.999498 | 1.000000 | |
| 0.7 | 0.130692 | 0.288665 | 0.016889 | 0.052073 | 0.003072 | 0.006837 | 0.000090 | 0.015730 | 0.034956 | 0.456800 | |
| 1.0 | 0.999999 | 0.288665 | 0.995288 | 0.999876 | 0.929862 | 0.964634 | 0.367331 | 0.979806 | 0.989325 | 1.000000 | |
| 1.3 | 0.999939 | 0.016889 | 0.995288 | 1.000000 | 0.999996 | 1.000000 | 0.939284 | 1.000000 | 1.000000 | 0.999986 | |
| 2.0 | 1.000000 | 0.052073 | 0.999876 | 1.000000 | 0.999327 | 0.999859 | 0.798004 | 0.999946 | 0.999981 | 1.000000 | |
| 3.0 | 0.992947 | 0.003072 | 0.929862 | 0.999996 | 0.999327 | 1.000000 | 0.995818 | 1.000000 | 1.000000 | 0.998462 | |
| 4.0 | 0.997608 | 0.006837 | 0.964634 | 1.000000 | 0.999859 | 1.000000 | 0.992153 | 1.000000 | 1.000000 | 0.999454 | |
| 5.0 | 0.646144 | 0.000090 | 0.367331 | 0.939284 | 0.798004 | 0.995818 | 0.992153 | 0.993370 | 0.994880 | 0.856477 | |
| 6.0 | 0.998865 | 0.015730 | 0.979806 | 1.000000 | 0.999946 | 1.000000 | 1.000000 | 0.993370 | 1.000000 | 0.999702 | |
| 7.0 | 0.999498 | 0.034956 | 0.989325 | 1.000000 | 0.999981 | 1.000000 | 1.000000 | 0.994880 | 1.000000 | 0.999846 | |
| 8.0 | 1.000000 | 0.456800 | 1.000000 | 0.999986 | 1.000000 | 0.998462 | 0.999454 | 0.856477 | 0.999702 | 0.999846 | |
Note: Marked values represent significant differences (significance level α = 0.05).
References
- Maas, H.G.; Bienert, A.; Scheller, S.; Keane, E. Automatic forest inventory parameter determination from terrestrial laser scanner data. Int. J. Remote Sens. 2008, 29, 1579–1593. [Google Scholar] [CrossRef]
- Liang, X.; Kankare, V.; Hyyppä, J.; Wang, Y.; Kukko, A.; Haggrén, H.; Yu, X.; Kaartinen, H.; Jaakkola, A.; Guan, F.; et al. Terrestrial laser scanning in forest inventories. ISPRS J. Photogramm. Remote Sens. 2016, 115, 63–77. [Google Scholar] [CrossRef]
- Liang, X.; Hyyppä, J.; Kankare, V.; Holopainen, M. Stem curve measurement using terrestrial laser scanning. In Proceedings of the 11th International Conference on LiDAR Applications for Assessing Forest Ecosystems, SilviLaser 2011, Hobart, Australia, 16–20 October 2011; Available online: http://www.locuscor.net/silvilaser2011/papers/059_Liang.pdf (accessed on 6 May 2020).
- Sun, Y.; Liang, X.; Liang, Z.; Welham, C.; Li, W. Deriving merchantable volume in poplar through a localized tapering function from non-destructive terrestrial laser scanning. Forests 2016, 7, 87. [Google Scholar] [CrossRef]
- Astrup, R.; Ducey, M.J.; Granhus, A.; Ritter, T.; von Lüpke, N. Approaches for estimating stand-level volume using terrestrial laser scanning in a single-scan mode. Can. J. For. Res. 2014, 44, 666–676. [Google Scholar] [CrossRef]
- Dassot, M.; Colin, A.; Santenoise, P.; Fournier, M.; Constant, T. Terrestrial laser scanning for measuring the solid wood volume, including branches, of adult standing trees in the forest environment. Comput. Electron. Agric. 2012, 89, 86–93. [Google Scholar] [CrossRef]
- Olofsson, K.; Holmgren, J. Tree stem and canopy biomass estimates from terrestrial laser scanning data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. ISPRS Arch. 2017, 42, 157–160. [Google Scholar] [CrossRef]
- Pitkänen, T.P.; Raumonen, P.; Kangas, A. Measuring stem diameters with TLS in boreal forests by complementary fitting procedure. ISPRS J. Photogramm. Remote Sens. 2019, 147, 294–306. [Google Scholar] [CrossRef]
- Liang, X.; Hyyppä, J.; Kaartinen, H.; Lehtomäki, M.; Pyörälä, J.; Pfeifer, N.; Holopainen, M.; Brolly, G.; Francesco, P.; Hackenberg, J.; et al. International benchmarking of terrestrial laser scanning approaches for forest inventories. ISPRS J. Photogramm. Remote Sens. 2018, 144, 137–179. [Google Scholar] [CrossRef]
- Hyyppä, E.; Hyyppä, J.; Hakala, T.; Kukko, A.; Wulder, M.A.; White, J.C.; Pyörälä, J.; Yu, X.; Wang, Y.; Virtanen, J.P.; et al. Under-canopy UAV laser scanning for accurate forest field measurements. ISPRS J. Photogramm. Remote Sens. 2020, 164, 41–60. [Google Scholar] [CrossRef]
- Bauwens, S.; Bartholomeus, H.; Calders, K.; Lejeune, P. Forest inventory with terrestrial LiDAR: A comparison of static and hand-held mobile laser scanning. Forests 2016, 7, 127. [Google Scholar] [CrossRef]
- Liang, X.; Wang, Y.; Jaakkola, A.; Kukko, A.; Kaartinen, H.; Hyyppä, J.; Honkavaara, E.; Liu, J. Forest data collection using terrestrial image-based point clouds from a handheld camera compared to terrestrial and personal laser scanning. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5117–5132. [Google Scholar] [CrossRef]
- Del Perugia, B.; Giannetti, F.; Chirici, G.; Travaglini, D. Influence of scan density on the estimation of single-tree attributes by hand-held mobile laser scanning. Forests 2019, 10, 277. [Google Scholar] [CrossRef]
- Kaartinen, H.; Hyyppä, J.; Kukko, A.; Jaakkola, A.; Hyyppä, H. Benchmarking the performance of mobile laser scanning systems using a permanent test field. Sensors 2012, 12, 12814–12835. [Google Scholar] [CrossRef]
- Čerňava, J.; Mokroš, M.; Tuček, J.; Antal, M.; Slatkovská, Z. Processing chain for estimation of tree diameter from GNSS-IMU-based mobile laser scanning Data. Remote Sens. 2019, 11, 615. [Google Scholar] [CrossRef]
- Hyyppä, E.; Kukko, A.; Kaijaluoto, R.; White, J.C.; Wulder, M.A.; Pyörälä, J.; Liang, X.; Yu, X.; Wang, Y.; Kaartinen, H.; et al. Accurate derivation of stem curve and volume using backpack mobile laser scanning. ISPRS J. Photogramm. Remote Sens. 2020, 161, 246–262. [Google Scholar] [CrossRef]
- Williams, R.D.; Lamy, M.L.; Maniatis, G.; Stott, E. Three-dimensional reconstruction of fluvial surface sedimentology and topography using personal mobile laser scanning. Earth Surf. Process. Landforms 2020, 45, 251–261. [Google Scholar] [CrossRef]
- Hyyppä, J.; Virtanen, J.P.; Jaakkola, A.; Yu, X.; Hyyppä, H.; Liang, X. Feasibility of google tango and kinect for crowdsourcing forestry information. Forests 2017, 9, 6. [Google Scholar] [CrossRef]
- Tomaštík, J.; Saloň, Š.; Tunák, D.; Chudý, F.; Kardoš, M. Tango in forests–An initial experience of the use of the new google technology in connection with forest inventory tasks. Comput. Electron. Agric. 2017, 141, 109–117. [Google Scholar] [CrossRef]
- Cabo, C.; del Pozo, S.; Rodríguez-Gonzálvez, P.; Ordóñez, C.; González-Aguilera, D. Comparing terrestrial laser scanning (TLS) and wearable laser scanning (WLS) for individual tree modeling at plot level. Remote Sens. 2018, 10, 540. [Google Scholar] [CrossRef]
- Chiabrando, F.; Della Coletta, C.; Sammartano, G.; Spanò, A.; Spreafico, A. TORINO 1911 project: A contribution of a SLAM-based survey to extensive 3D heritage modeling. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. ISPRS Arch. 2018, 42, 225–234. [Google Scholar] [CrossRef]
- Ryding, J.; Williams, E.; Smith, M.J.; Eichhorn, M.P. Assessing handheld mobile laser scanners for forest surveys. Remote Sens. 2015, 7, 1095–1111. [Google Scholar] [CrossRef]
- Sirmacek, B.; Shen, Y.; Lindenbergh, R.; Zlatanova, S.; Diakite, A. Comparison of Zeb1 and leica C10 indoor laser scanning point clouds. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 1, 143–149. [Google Scholar] [CrossRef]
- James, M.R.; Quinton, J.N. Ultra-rapid topographic surveying for complex environments: The hand-held mobile laser scanner (HMLS). Earth Surf. Process. Landforms 2014, 39, 138–142. [Google Scholar] [CrossRef]
- Wang, Y.; Lehtomäki, M.; Liang, X.; Pyörälä, J.; Kukko, A.; Jaakkola, A.; Liu, J.; Feng, Z.; Chen, R.; Hyyppä, J.; et al. Is field-measured tree height as reliable as believed—A comparison study of tree height estimates from field measurement, airborne laser scanning and terrestrial laser scanning in a boreal forest. ISPRS J. Photogramm. Remote Sens. 2019, 147, 132–145. [Google Scholar] [CrossRef]
- Liu, J.; Feng, Z.; Yang, L.; Mannan, A.; Khan, T.U.; Zhao, Z.; Cheng, Z. Extraction of sample plot parameters from 3D point cloud reconstruction based on combined RTK and CCD continuous photography. Remote Sens. 2018, 10, 1299. [Google Scholar] [CrossRef]
- Miller, J.; Morgenroth, J.; Gomez, C. 3D modelling of individual trees using a handheld camera: Accuracy of height, diameter and volume estimates. Urban For. Urban Green. 2015, 14, 932–940. [Google Scholar] [CrossRef]
- Surový, P.; Yoshimoto, A.; Panagiotidis, D. Accuracy of reconstruction of the tree stem surface using terrestrial close-range photogrammetry. Remote Sens. 2016, 8, 123. [Google Scholar] [CrossRef]
- Forsman, M.; Börlin, N.; Holmgren, J. Estimation of tree stem attributes using terrestrial photogrammetry with a camera rig. Forests 2016, 7, 61. [Google Scholar] [CrossRef]
- Panagiotidis, D.; Surový, P.; Kuželka, K. Accuracy of structure from motion models in comparison with terrestrial laser scanner for the analysis of DBH and height influence on error behaviour. J. For. Sci. 2016, 62, 357–365. [Google Scholar] [CrossRef]
- Iglhaut, J.; Cabo, C.; Puliti, S.; Piermattei, L.; O’Connor, J.; Rosette, J. Structure from motion photogrammetry in forestry: A review. Curr. For. Rep. 2019, 5, 155–168. [Google Scholar] [CrossRef]
- Mokroš, M.; Liang, X.; Surový, P.; Valent, P.; Čerňava, J.; Chudý, F.; Tunák, D.; Saloň, I.; Merganič, J. Evaluation of close-Range photogrammetry image collection methods for estimating tree diameters. ISPRS Int. J. Geo. Inf. 2018, 7, 93. [Google Scholar] [CrossRef]
- Gollob, C.; Ritter, T.; Nothdurft, A. Forest inventory with long range and high-speed personal laser scanning (PLS) and simultaneous localization and mapping (SLAM) technology. Remote Sens. 2020, 12, 1509. [Google Scholar] [CrossRef]
- Kurian, A.; Morin, K.W. A fast and flexible method for meta-map building for ICP based slam. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. ISPRS Arch. 2016, 41, 273–278. [Google Scholar] [CrossRef]
- Cadena, C.; Carlone, L.; Carrillo, H.; Latif, Y.; Scaramuzza, D.; Neira, J.; Reid, I.; Leonard, J.J. Past, present, and future of simultaneous localization and mapping: Toward the robust-perception age. IEEE Trans. Robot. 2016, 32, 1309–1332. [Google Scholar] [CrossRef]
- Koreň, M.; Mokroš, M.; Bucha, T. Accuracy of tree diameter estimation from terrestrial laser scanning by circle-fitting methods. Int. J. Appl. Earth Obs. Geoinf. 2017, 63, 122–128. [Google Scholar] [CrossRef]
- Chen, S.; Liu, H.; Feng, Z.; Shen, C.; Chen, P. Applicability of personal laser scanning in forestry inventory. PLoS ONE 2019, 14, e0211392. [Google Scholar] [CrossRef]
- Cabo, C.; Ordóñez, C.; López-Sánchez, C.A.; Armesto, J. Automatic dendrometry: Tree detection, tree height and diameter estimation using terrestrial laser scanning. Int. J. Appl. Earth Obs. Geoinf. 2018, 69, 164–174. [Google Scholar] [CrossRef]
- Chudá, J.; Hunčaga, M.; Tuček, J.; Mokroš, M. The handheld mobile laser scanners as a tool for accurate positioning under forest canopy. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, 2, 211–218. [Google Scholar] [CrossRef]
- Čerňava, J.; Tuček, J.; Koreň, M.; Mokroš, M. Estimation of diameter at breast height from mobile laser scanning data collected under a heavy forest canopy. J. For. Sci. 2017, 63, 433–441. [Google Scholar] [CrossRef]
- You, L.; Tang, S.; Song, X.; Lei, Y.; Zang, H.; Lou, M.; Zhuang, C. Precise measurement of stem diameter by simulating the path of diameter tape from terrestrial laser scanning data. Remote Sens. 2016, 8, 717. [Google Scholar] [CrossRef]
- Piermattei, L.; Karel, W.; Wang, D.; Wieser, M.; Mokroš, M.; Surový, P.; Koreň, M.; Tomaštík, J.; Pfeifer, N.; Hollaus, M.; et al. Terrestrial structure from motion photogrammetry for deriving forest inventory data. Remote Sens. 2019, 11, 950. [Google Scholar] [CrossRef]
- Liang, X.; Hyyppä, J. Automatic stem mapping by merging several terrestrial laser scans at the feature and decision levels. Sensors 2013, 13, 1614–1634. [Google Scholar] [CrossRef]
- Liang, X.; Kankare, V.; Yu, X.; Hyyppä, J.; Holopainen, M. Automated stem curve measurement using terrestrial laser scanning. IEEE Trans. Geosci. Remote Sens. 2014, 52, 1739–1748. [Google Scholar] [CrossRef]
- Vaaja, M.T.; Virtanen, J.P.; Kurkela, M.; Lehtola, V.; Hyyppä, J.; Hyyppä, H. The effect of wind on tree stem parameter estimation using terrestrial laser scanning. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 8, 117–122. [Google Scholar] [CrossRef]
- Van Brummelen, J.; O’Brien, M.; Gruyer, D.; Najjaran, H. Autonomous vehicle perception: The technology of today and tomorrow. Transp. Res. Part C Emerg. Technol. 2018, 89, 384–406. [Google Scholar] [CrossRef]
- Qian, C.; Liu, H.; Tang, J.; Chen, Y.; Kaartinen, H.; Kukko, A.; Zhu, L.; Liang, X.; Chen, L.; Hyyppä, J.; et al. An integrated GNSS/INS/LiDAR-SLAM positioning method for highly accurate forest stem mapping. Remote Sens. 2017, 9, 3. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).