Abstract
High-resolution precipitation field has been widely used in hydrological and meteorological modeling. This paper establishes the spatial and temporal distribution model of precipitation in Hubei Province from 2006 through 2014, based on the data of 75 meteorological stations. This paper applies a geographically and temporally weighted regression kriging (GTWRK) model to precipitation and assesses the effects of timescales and a time-weighted function on precipitation interpolation. This work’s results indicate that: (1) the optimal timescale of the geographically and temporally weighted regression (GTWR) precipitation model is daily. The fitting accuracy is improved when the timescale is converted from months and years to days. The average mean absolute error (MAE), mean relative error (MRE), and the root mean square error (RMSE) decrease with scaling from monthly to daily time steps by 36%, 56%, and 35%, respectively, and the same statistical indexes decrease by 13%, 15%, and 14%, respectively, when scaling from annual to daily steps; (2) the time weight function based on an exponential function improves the predictive skill of the GTWR model by 3% when compared to geographically weighted regression (GWR) using a monthly time step; and (3) the GTWRK has the highest accuracy, and improves the MAE, MRE and RMSE by 3%, 10% and 1% with respect to monthly precipitation predictions, respectively, and by 3%, 10% and 5% concerning annual precipitation predictions, respectively, compared with the GWR results.
1. Introduction
Precipitation is a critical flux in the water cycle [,]. It is, for this reason, imperative to study the spatial–temporal features of precipitation [,]. Precipitation data are usually derived from meteorological sites with limited spatial coverage and sensor-gathered data, such as remote sensing satellites and rainfall radars []. Meteorological site location observations yield local, discrete, and limited spatial data points, which cannot account for the spatial precipitation variability accurately [,]. The general spatial resolution of remote sensing precipitation data products is generally low, which does capture the precipitation distribution in small areas []. These problems constrain the application of precipitation data for multiple practical purposes. Thus, there is a need for further study on how to obtain continuous and accurate distributions of precipitation at regional scales.
Spatial interpolation of precipitation data falls into two categories: deterministic interpolation and spatial–temporal interpolation. Deterministic interpolation is further divided into two categories: global interpolation and local interpolation [,,]. Spatial–temporal interpolation includes two categories: subtraction and extension []. Spatial–temporal interpolation methods for spatial–temporal irregular dataset interpolation and missing data patching include the spatial–temporal inverse distance weighting method, the spatial–temporal kriging method, and collaborative spatial-temporal kriging, among the main ones [,,]. It has become a common practice to explore the distribution of precipitation employing spatial statistical analysis to cope with the spatial-temporal non-smoothness of precipitation. The geographically weighted regression (GWR) model was proposed for the study of spatial relations and spatial correlation, based on the common linear regression model by Fotheringham et al. []. The GWR model prescribes parameter estimation based on the location function expressing the non-stationary spatial features of precipitation. The regression coefficients in the GWR model capture the locational attribute. They can, therefore, take into account the influence of spatial heterogeneity, thus significantly improving the ability to analyze the variation in spatiotemporal characteristics of precipitation. This means the GWR model has attracted wide attention regarding quantitative precipitation estimation, as well as other spatial variables [,]. However, the GWR model only considers the spatial characteristics of precipitation data, while ignoring time characteristics of precipitation. The geographically and temporally weighted regression (GTWR) model was proposed in 2010 by Huang et al., and incorporates the time dimension into the model formulation []. On the one hand, the GTWR model has the basic characteristics of a general variable coefficient model and exhibits the high fitting skill of the local regression model, which captures the differences in spatial position and takes into account the spatial heterogeneity of precipitation. On the other hand, the model adds the time series traits, synthesizes the time dimension distribution information of the sample points, and embeds the spatial–temporal characteristics into the model [].
GTWR performs wells in predicting spatial–temporal heterogeneity, and many studies in a variety of fields of science have proven the effectiveness of the GTWR model in spatial economic analysis, atmospheric sciences, population analysis, and other social and economic fields. The GTWR model was applied to model housing price data in London by Fotheringham et al. [], which validated the proposed method and its superiority over the traditional GWR method while highlighting the importance of time explicit spatial modeling. The GTWR model was applied to assess the spatial–temporal differences in the influence of each driving factor on the scale of carbon emissions and the intensity of carbon emissions in China by Xiao et al. []. Liu et al. studied housing price data and related factors in Beijing from 1980 to 2016 [], to propose a calculation method for travel distance, applying the GWR. The GTWR model was employed to study the influencing factors on housing prices, and it was concluded that the GTWR model is suitable for identifying effective real estate management policies. The fire record data from 2002 to 2010 in Hefei, China, was reviewed by Song et al. [], using the linear model (LM), GWR, and GTWR to model urban fire risk. The latter authors concluded that road density and commercial spatial distribution have the most significant influence on fire risk. GTWR can detect small changes in variable spatial–temporal heterogeneity of diverse phenomena. The performance of the GTWR model was verified with particulate matter ≤2.5 μm (PM2.5) concentration data in the Xuzhou area, China, and compared with ordinary least squares (OLS), GWR, and time-weighted regression (TWR) models by Bai et al. []. The results indicate that the regression coefficient of the GTWR model was the highest, and its interpolation skill was optimal. The GTWR model was applied to estimate the ground concentration of nitrogen dioxide (NO2) in central China by Qin et al. [], and cross-validation results proved that the fitting results of the GTWR model were better than those of the OLS, GWR, and TWR models. Five models, including GTWR, were implemented to analyze the relationships between PM2.5 and other criteria of air pollutants by Wei et al. [], and GTWR showed great advantages over the other three models in terms of higher model R2 and more desirable model residuals, and only slightly less than TWR.
Precipitation has a high causal correlation both in space and time. Therefore, it is intuitively logical to use the GTWR model to fit precipitation data. At present, the use of spatial statistical analysis to fit precipitation interpolation is mainly represented by the GWR model. Brunsdon et al. [] reported a study of the relation between total annual precipitation and elevation in the UK by employing the GWR model. Their results revealed that the rate of precipitation increased with elevation, and that the predicted sea level precipitation varied between 600 mm and 1250 mm. The precipitation data from the Tropical Rainfall Measuring Mission (TRMM) 3B43 products were fitted with a multi-variable GWR reduction method to obtain 1 km × 1 km precipitation data by Chen et al. []. The GWR method was compared with two other downscaling methods (single variable regression (UR) and multivariate regression (MR)). Chen et al. (29) concluded that the GWR method could predict annual and monthly TRMM 1 km x 1 km precipitation with high precision. The accuracy of TRMM precipitation products at the daily and monthly scales in the Qaidam Basin of China was evaluated by Lv et al. [] with the GWR model. Their results indicate that the precipitation GWR model based on ground and satellite data reduced the error of TRMM products, which was of significance in the fields of hydrology and climate change. The vegetation and climate data (Normalized Vegetation Difference Index (NVDI) and rainfall) from 2002 through 2012 for the growing season (June–September) in the Sahel region of Africa was relied upon in the GWR model by Georganos et al. []. The results showed that the spatial pattern of the NDVI–rainfall relationship is characterized when selecting the appropriate scale. Their GWR model performs better than the OLS in terms of predictive skill, accuracy, and residual autocorrelations. With the further research of scholars, geographically weighted regression kriging (GWRK) [], as an extension of the GWR model, appears in the spatial interpolation of temperature and soil properties. It has also been explored in the field of precipitation and prediction research, achieving excellent results. The GWRK model combines the GWR with the kriging method, and uses the kriging method to interpolate the residual part of the GWR model, which eliminates the influence of the spatial correlation of the residual on the model fit, and shows that it is masked by spatial non-stationary local variation.
The GTWR model focuses primarily on the time dimension, although it accounts for the characterization of spatial heterogeneity []. At a particular timescale, the GTWR handles the distribution of the time dimension in a manner dissimilar to that described by the first law of geography (Tobler []), and, thus, it can be improved. Ge et al. proposed the seasonal differential geographically and temporally weighted regression (seasonal-difference GTWR, SD-GTWR) []. The latter authors applied the SD-GTWR model to data for hemorrhagic fever with renal syndromes from Hubei Province to show that the SD-GTWR model is superior to the ordinary GTWR model. The SD-GTWR model relied on the results of incremental spatial autocorrelation when balancing the roles of space and time. Data from the Zhejiang coast (China) from 2012 through 2016 was employed by Du et al. [] to propose a geographical and periodic time-weighted regression model (GcTWR) that unifies spatial distance and temporal distance. The results confirmed that the seasonal effects on coastal areas are related to an interannual effect.
Although the GWR model performs well in the spatial interpolation, precipitation not only has continuity in space, but also has strong continuity in time. However, few kinds of research have been carried out on the spatial–temporal interpolation of precipitation. Fortunately, the application of the GTWR model in different fields has gradually become mature, and it is possible to introduce it into precipitation interpolation. Therefore, to better understand the temporal and spatial heterogeneity of precipitation, this paper interpolates the spatial distribution from 2006 through 2014 of the monthly and annual rainfall in Hubei Province, based on the GTWR model. Then, this work adjusts the spatial and temporal weight, according to the temporal characteristics of precipitation. The Gaussian kernel model is selected as the spatial weight, and the exponential function model is chosen as the temporal weight. Meanwhile, this work introduces the kriging model to eliminate the influence of residual spatial correlation on model fitting, which can improve the interpolation accuracy.
2. Materials and Methods
2.1. Methodology
2.1.1. Geographically and Temporally Weighted Regression Model
The GTWR model is expressed as Equation (1) [,]:
where denotes the spatial–temporal coordinates of the observed location , which contains the location and temporal information; k denotes the index k = 1, 2… n. represents a set of values for the number n of parameters at point i, and represents the random error of the predicted variable yi. The estimates of are given by Formula (2):
The spatial–temporal weight matrix is based on the definition of the spatial–temporal distance and its decay functions. Generally, the weight functions include the distance threshold method, distance inverse ratio method, Gaussian (Gauss) function method, and double square root (bi-square) kernel function method. The Gaussian and bi-square kernel function methods are commonly used in the GTWR model []. The Gaussian kernel function is given by Equation (3):
where the element of the weighting matrix is determined by the spatial–temporal distance and spatial–temporal bandwidth . The GTWR model sets the spatial–temporal distance as a function of the temporal distance and the spatial distance, as expressed in Equation (4):
and denote the spatial distance factor and the temporal distance factor, respectively, which balance the effect of the space and time dimension on parameter estimation. The wij element of the spatial–temporal weight matrix is expressed by Equation (5):
It is seen in Equation (5) that the spatial–temporal element or kernel function equals the spatial kernel function multiplied by the temporal kernel function . and are the spatial and temporal bandwidths, respectively. One can determine the weight of the observed variable at a given location to the regressed variable at the same location at a specific time by the spatial–temporal kernel function. The spatial bandwidth and temporal bandwidth are decided by cross-validation (CV), and they are obtained by minimizing the expression on the right-hand side of Equation (6):
when is minimized, it yields the optimal spatial bandwidth and temporal bandwidth of the model. A method for determining spatial and temporal bandwidth in steps was proposed by Fotheringham et al. []. The principle of this method is that GTWR can be regarded as GWR for a period of time. In each time period of data, the spatial bandwidth is determined by the GWR model by minimizing , and then determining the time bandwidth that minimizes CV ().
One obtains the optimal spatial bandwidth and temporal bandwidth when the CV is minimized. This paper relies on a step-by-step approach [] to calculate the bandwidth. This approach considers the data at a specific time or a period at first. The GTWR became similar to the GWR model in this manner. One minimize the spatial data of each period, and then obtain the appropriate time bandwidth by minimizing the CV ().
2.1.2. Comparison Models with Different Spatial–Temporal Parameters
The spatial–temporal distance calculation method of the GTWR model is similar to the extension method, which adds the temporal distance as the third dimension to the distance calculation. Previous studies have generally neglected the shortcomings of the extension method, whereby the uncertainty of the units (say, m or km for spatial units) introduces uncertainty of the spatial–temporal interpolation results when calculating the spatial–temporal distance []. The calculated results differ substantially depending on the adopted units, such as the unit of spatial distance being in meters or kilometers, and the time unit being the year, month, day, minute, or second. This paper chooses km as the spatial distance unit, whereas the timescale may be annual, monthly, and daily, according to the experimental data scale.
The temporal weighting formulas may be inconsistent with the spatial weighting formulas whenever the spatial–temporal weight is decomposed into the product of the spatial weight and the temporal weight. This work proposes a time weight in the form of an exponential function, as shown in Formula (7), in agreement with the last line on the right-hand side of Equation (5):
Furthermore, the distribution of variables or objects in the time dimension is not entirely governed by the previously cited first law of geography. There are apparent cyclical changes in the four seasons of the year. The physical characteristics of the climate at a location differ in the winter compared with summer, but they have statistical similarities for the same season in different years. Concerning monthly precipitation it is known that there may be statistical similarities between a given month’s precipitation and non-adjacent month precipitation in the same quarter. Thus, it is necessary to improve the calculation method of the spatial–temporal distance to capture such similarities. The temporal distribution of precipitation exhibits periodicity, therefore, this paper relies on the sinusoidal function to calculate the temporal distance. It selects the exponential function model as a temporal weight formula. The calculation formula of the periodic temporal distance is given by Equation (8), where denotes the period of the function:
2.1.3. Geographically and Temporally Weighted Regression Kriging
It is a spatial interpolation method based on geostatistics of the kriging method which fully considers the characteristics of the spatial variability of the sample points. It has the advantages of strong applicability and high prediction accuracy, and is currently most widely used in the fields of meteorology, ecology, and soil. The kriging algorithm can achieve optimal linear unbiased values, improving the accuracy of estimation to a certain extent. Moreover, for regionalized variables, it reveals its spatial structure well.
The GTWR model embeds temporal information and geographic location into the model, making full use of the spatial and temporal characteristics of data, and has a useful application in regional regression analysis. Geographically and temporally weighted regression kriging (GTWRK) is a hybrid method based on the GTWR model. First, we use the GTWR method to establish the regression relationship between precipitation and auxiliary information. Second, we use the kriging method to interpolate the residuals ε of the GTWR model. Finally, we add the interpolation result of residuals and the GTWR regression estimation value to obtain the GTWRK estimation result. Therefore, the GTWRK method considers the relationship between precipitation and influencing factors and the spatial autocorrelation of precipitation. The GTWR model is given by Equation (9):
where: is the estimated value of GTWRK; denotes the estimated value of GTWR; and represents the residual interpolation result of GTWR regression obtained by ordinary kriging (OK) interpolation. The variogram must be selected when the kriging method is used to interpolate the residuals. This work chooses an exponential variogram for ordinary kriging interpolation based on exploratory analysis of the precipitation data.
The flow chart of the GTWRK model is shown in Figure 1.
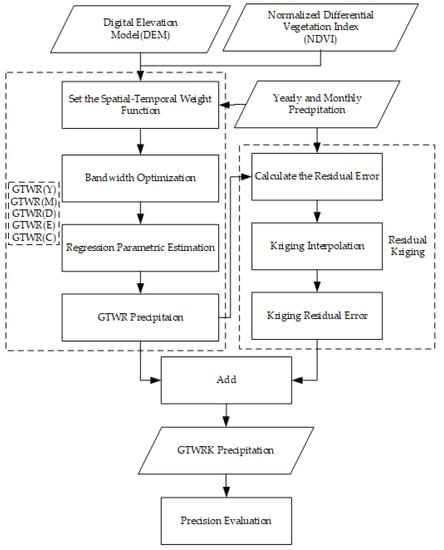
Figure 1.
The flow chart of the geographically and temporally weighted regression kriging (GTWRK) model.
2.1.4. Precision Evaluation
Because of the large amount of data generated in the interpolation comparison, it would be burdensome to display all the results. The results corresponding to precipitation fitting in July 2008 and May 2013 are representative of the monthly scale data, and the results of precipitation fitting in 2010 and 2012 are representative of the annual scale data. The evaluation of the interpolation models relied on several performance indices, namely the mean absolute error (MAE), mean relative error (MRE), and the root mean square error (RMSE). The smaller the values of MAE, MRE, and RMSE, the better the interpolation effect.
in which n denotes the sample size, Yi represents the ith a sample value, denots the sample estimates.
2.2. Study Area and Data
Hubei Province is located between northern latitudes 29°05′ and 33°20′ and eastern latitudes 108°21′ and 116°07′ within China. The province covers an area of 185,900 square kilometers, and includes a variety of topographical regions, including mountains, plains, and transitional topographic zones. The topography of Hubei Province exhibits the highest elevation of 3090 m in its western region, and lowest towards its eastern area, with a lowest elevation of −142 m []. Hubei Province lies within a north–south transitional climatic zone, belonging to the northeastern Asian monsoonal region, except for the higher elevations of the western mountainous areas. Most of the province features a subtropical monsoonal, humid climate. The warm temperature coincides with the rainy period, providing abundant rainfall to support agroforest production []. The spatial distribution of meteorological sites and the digital elevation model (DEM) are shown in Figure 2.
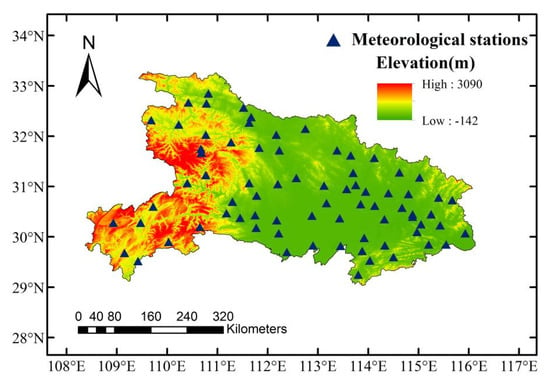
Figure 2.
The spatial distribution of meteorological sites and digital elevation model (DEM) data representation.
The Hubei Meteorological Bureau provided annual and monthly precipitation data from 75 meteorological stations from 2006 through 2014 in Hubei Province. Figure 3 displays the average monthly precipitation distribution for the period of record.
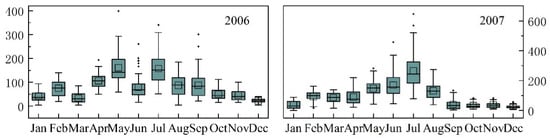
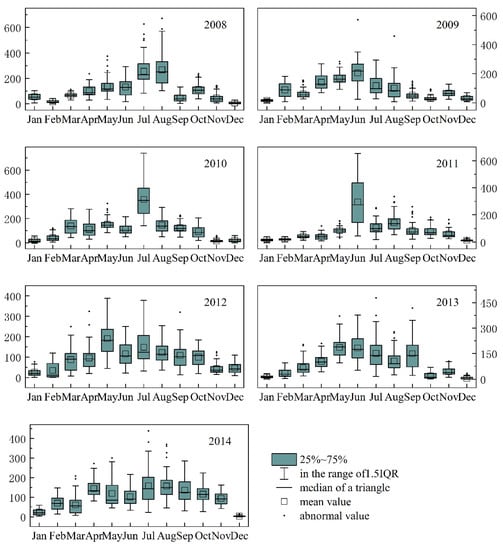
Figure 3.
The monthly precipitation distribution from 2006 to 2014.
Many factors influence the spatial distribution of precipitation. Previous studies have demonstrated that topographic characteristics are the main controlling factor [,]. The Normalized Differential Vegetation Index (NDVI) is influenced by precipitation, and vice versa [,]. This work employs the Digital Elevation Model (DEM) Shuttle Radar Topography Mission (SRTM) data with 90 m resolution. The NDVI data are the MODND1M for China with 500 m resolution NDVI monthly synthesis products. All of the above data are available from the Geospatial Data Cloud website (http://www.gscloud.cn).
2.3. Data Preprocessing
All data were consolidated under the WGS-84 geographic coordinate system. The grid resolution employed was 0.1° × 0.1°. Precipitation constitutes the dependent variable; longitude, latitude, DEM, and the NDVI are the independent variables. The timescale of precipitation data is divided into monthly and annual categories. The monthly data represent the time series data from January 2006 through December 2014. The yearly data denote the time series data from 2006 through 2014.
The interpolation accuracy of the GTWR models was evaluated by cross-verification (CV). The 75 meteorological sites were randomly divided into 60 sites (80% of the total number of sites) as the modeling set for interpolation; the remaining 15 sites (20% of the total number of sites) were chosen as the validation set, which was used to evaluate the models’ accuracies. This paper employs the GTWR models corresponding to several timescales listed in Table 1.

Table 1.
Listing of the geographically and temporally weighted regression (GTWR) models.
3. Results and Analysis
3.1. Monthly Data
The fitting interpolation distribution maps for July 2008 and May 2013 are shown in Figure 4 and Figure 5, respectively.
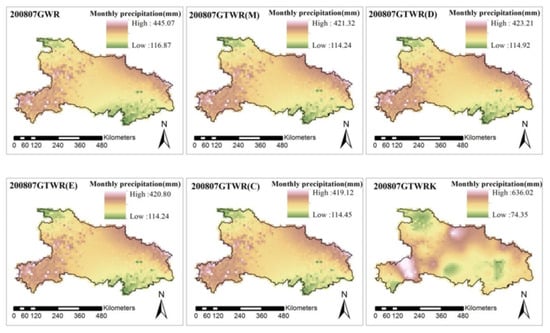
Figure 4.
The fitting interpolation distribution map for geographically weighted regression (GWR), GTWR(M), GTWR(D), GTWR(E), and GTWR(C) corresponding to July 2008.
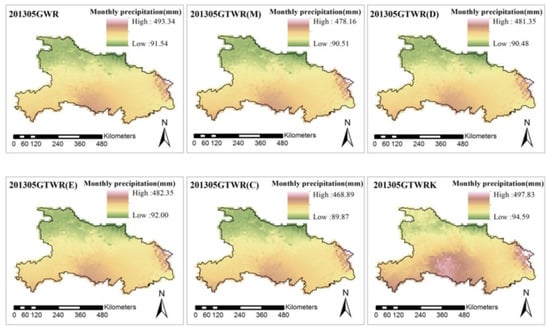
Figure 5.
The interpolation distribution maps for GWR, GTWR(M), GTWR(D), GTWR(E), and GTWR(C) corresponding to May 2013.
The average error maps of MAE, MRE, and RMSE for monthly scale data are shown in Figure 6.
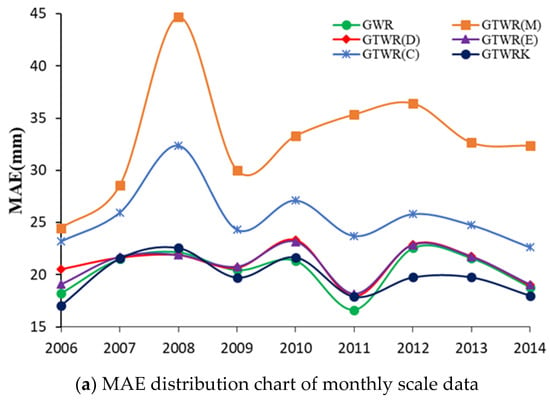
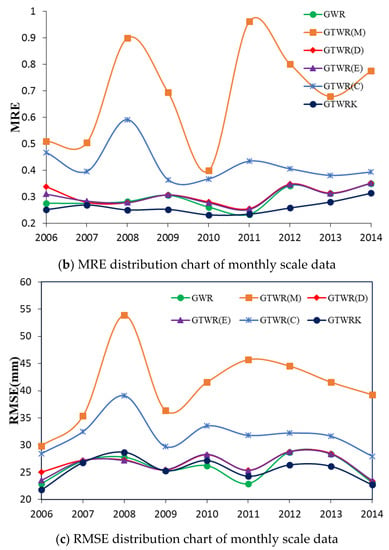
Figure 6.
The average error maps for monthly scale data from 2006 through 2014. (a–c) represent the average distribution chart of mean average error (MAE), mean root error (MRE), and root mean square error (RMSE), respectively.
It can be seen in Figure 6 and Table 2 that the optimal timescale of the GTWR model is daily for the monthly scale data. The MAE, MRE, and RMSE decrease by 36%, 56%, and 35%, respectively, when choosing GTWR(D) instead of GTWR(M). The GTWR(E) improves the accuracy of the results compared to GTWR(D), by reducing the MAE, MRE, and RMSE by 0.7%, 1.1%, and 0.6%, respectively. The fitting accuracy of GTWR(E) and GWR are similar, with a difference of about 3% for the monthly scale data results shown in Table 2. The GTWR(C) has a lower accuracy compared with GWR, and increased MAE, MRE, and RMSE by 25%, 45%, and 24%. The GTWRK has the highest accuracy compared with GWR, and decreased MAE, MRE, and RMSE by 3%, 10%, and 1%, respectively.

Table 2.
The average MAE, MRE, and RMSE for the monthly scale data.
Figure 7 shows the MAE, MRE, and RMSE of monthly GWR and GTWRK models in different seasons. According to the character, the fitting accuracy of the GTWRK model is higher than that of the GWR model as a whole, especially in spring, autumn, and winter.
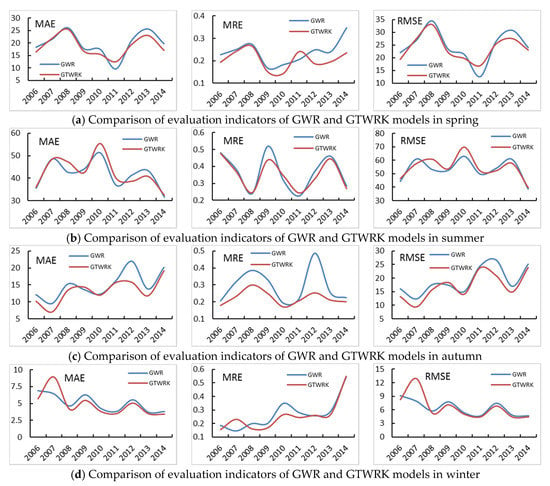
Figure 7.
Applicability of GWR and GTWRK models in different seasons. (a–d) represent the distribution chart of MAE (Units: mm), MRE, and RMSE (Units: mm) in the four seasons, respectively.
3.2. Annual Data
The interpolation distribution maps corresponding to 2010 and 2012 are shown in Figure 8 and Figure 9, respectively.
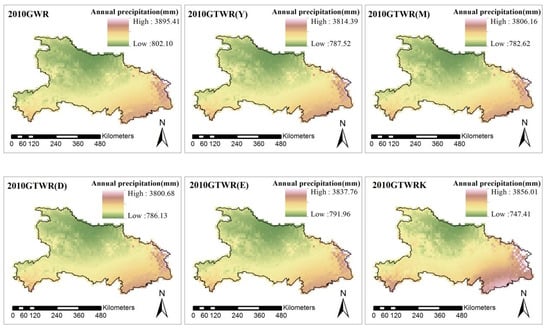
Figure 8.
The interpolation distribution maps for GWR, GTWR(Y), GTWR(M), GTWR(D), and GTWR(E) corresponding to 2010.
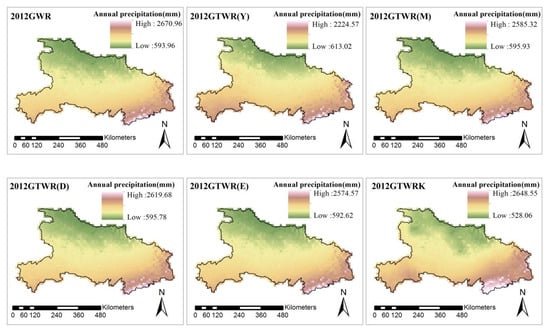
Figure 9.
The interpolation distribution maps for GWR, GTWR(Y), GTWR(M), GTWR(D), and GTWR(E) corresponding to 2012.
It is seen in Figure 10 and Table 3 that the optimal timescale of the GTWR model is daily for the annual scale data. The MAE, MRE, RMSE decrease by 13%, 15%, and 14%, respectively, when choosing the GTWR(Y) over the GTWR(D). In the results, the accuracy error of GTWR(E) can be reduced by about 0.2%, compared to GTWR(D). When the GTWRK is compared to the GWR model, MAE, MRE, and RMSE decrease by 3%, 10%, and 5%, respectively.
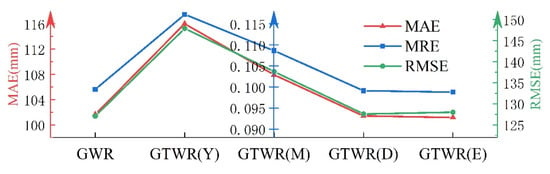
Figure 10.
The average error for annual data.

Table 3.
The average MAE, MRE, and RMSE for the annual data.
4. Discussion
The performances of GWR and GTWR models are relatively similar at the annual and monthly scales according to the reductions in average MAE, MRE, and RMSE. However the application of the GTWR model is not effective with respect to all the indicators, which reflects the extreme uncertainties of rainfall in time.
It is preferable to use a daily time scale to calculate spatial weights. Precipitation is formed by precipitation processes, and the duration of each process is usually several days. Therefore, as the timescale goes from yearly to daily the fine temporal details of precipitation gradually become prominent. Figure 11 shows the precipitation process in August 2008. The average monthly precipitation stands for the rainfall of the whole month. Consequently, the performance of the GTWR(D) model with a daily time scale is much better than the GTWR(M) and GTWR(Y) models’ at the monthly (Table 2) and annual (Table 3) scales.
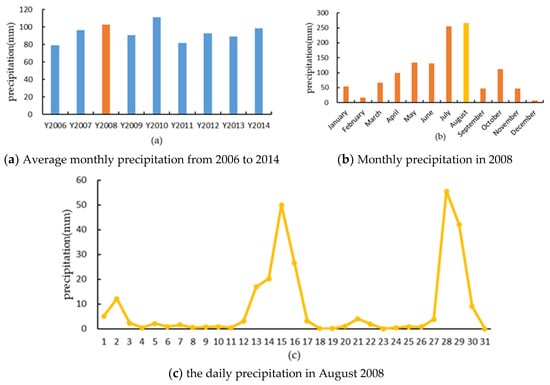
Figure 11.
The average precipitation of Hubei.
The periodicity of precipitation has some impact on improving the accuracy of interpolation. As shown in Figure 6 shows the GTWR(C) model performs better than GTWR(M). However, the frequency and amplitude of each precipitation cycle are very different, as shown in Figure 3 and Figure 11. The calculation of the periodic function needs further study.
The introduction of kriging is reasonable in the improvement of interpolation accuracy. Table 4 shows the normality test of residuals between the results of the GTWR model and the actual precipitation. The residuals of most months fitted normal distribution (significance > 0.05), while other months, such as May, June, September, and December, fitted approximate normal distribution (kurtosis < 10 and skewness < 3). Compared with the GTWR model, the GTWRK model performed well in terms of average MAE, MRE, and RMSE (Table 2 and Table 3). The GTWRK model produces a more accurate spatio-temporal precipitation. The GTWRK model’s performance varies performs through the seasons. This work represent summer as June, July, and August. It seen in Table 4, the residuals in these months all fitted the approximately normal distribution, which affects the accuracy of the GTWRK model to some extent.

Table 4.
The normality test of residuals between GTWR and the actual precipitation.
5. Conclusions
In this work, a GTWRK model combined with the GTWR and kriging model was introduced to interpolate the spatial distribution of monthly and annual precipitation from 2006 through 2014 in Hubei Province. The main conclusions are as follows:
- (1)
- GTWRK obtains a better average interpolation accuracy, compared to the GWR model. In the comparison between the GTWRK and GWR, the MAE decreased from 101.64 to 98.27. Consequently, we conclude that it is an improvement to extend GTWR with kriging.
- (2)
- The optimal timescale for interpolating precipitation data with the GTWR model is daily. The fitting accuracy is improved when the timescale is converted from yearly to daily. Compared with the GTWR(M) model, the average MAE, MRE, and RMSE of the monthly scale data decreased by 36%, 56%, and 35%, respectively, when using daily data. The same indices for the annual data reduced by 13%, 15%, and 14% when using daily data, respectively.
- (3)
- The temporal weight based on an exponential function improved the GTWR model at the monthly and annual data. It reduced the accuracy difference of the monthly scale between GTWR and GWR by about 3%. For the yearly scale data, the years with improved accuracy account for about 55%. Especially in 2008, 2009, 2010, 2011, and 2013, the accuracy was improved significantly. Meanwhile, the GTWRK improves the accuracy as measured by the MAE, MRE, and RMSE by 3%, 10%, and 1%, respectively, of monthly precipitation prediction, and by 3%, 10%, and 5%, respectively, of annual precipitation predictions.
- (4)
- The proposed model could be applied to manage similar phenomena with a large historical dataset. Meanwhile, the GTWR model takes into account the spatial and temporal heterogeneity of precipitation and produces better estimates of the residuals.
- (5)
- This work explored the annual, monthly, and daily scales to adjust the optimal time scale, while other time scales should be explored in future work. Additionally, the influence of the periodic characteristics of precipitation on the GTWR model needs further study.
Author Contributions
W.Z. proposed the theme and method of the article, conducted the initial analysis, provided the financial support for the project leading to this publication and provided the creation of the revision and published work; D.L. conducted the research and investigation process, performed the experiment of the thesis, and write the original draft; S.Z. provided and processed the source of the data, and participated the investigation process; S.L. provided the presentation of the revision and published work; H.A.L. provided critical review, data interpretation and presentation of results, and English editing in the revision and publication stages; W.L. took part in the presentation of the published work on revision and publication stages. All authors have read and agreed to the published version of the manuscript.
Funding
This study was partially supported by the National Natural Science Foundation of China under Grant No. 41501584, and Grant No. 41871304.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bhattacharya, A.; Adhikari, A.; Maitra, A. Multi-technique observations on precipitation and other related phenomena during cyclone Aila at a tropical location. Int. J. Remote Sens. 2013, 34, 1965–1980. [Google Scholar] [CrossRef]
- Goovaerts, P. Geostatistical approaches for incorporating elevation into the spatial interpolation of rainfall. J. Hydrol. 2000, 228, 113–129. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A multiscalar drought index sensitive to global warming: The standardized precipitation evapotranspiration index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Plouffe, C.C.F.; Robertson, C.; Chandrapala, L. Comparing interpolation techniques for monthly rainfall mapping using multiple evaluation criteria and auxiliary data sources: A case study of Sri Lanka. Environ. Model. Softw. 2015, 67, 57–71. [Google Scholar] [CrossRef]
- Collischonn, B.; Collischonn, W.; Tucci, C.E.M. Daily hydrological modeling in the Amazon basin using TRMM rainfall estimates. J. Hydrol. 2008, 360, 207–216. [Google Scholar] [CrossRef]
- Lin, Z.; Mo, X.; Li, H.; Li, H. Comparison of Three Spatial Interpolation Methods for Climate Variables in China. Acta Geogr. Sin. 2002, 57, 47–56. [Google Scholar]
- Feng, Z.; Yang, Y.; Ding, X.; Lin, Z. Optimization of the spatiaI interpolation methods for climate resources. Geogr. Res. 2004, 23, 357–364. [Google Scholar]
- Liu, J.-F.; Chen, R.-S.; Han, C.-T.; Tan, C.-P. Evaluating TRMM multi-satellite precipitation analysis using gauge precipitation and MODIS snow-cover products. Adv. Water Sci. 2010, 21, 343–348. [Google Scholar]
- Zhu, L.; Huang, J. Comparis on of spatial interpolation m ethod for precipitation of mountain areas in county scale. Trans. CSAE 2007, 23, 80–85. [Google Scholar]
- Li, C.; Chen, L.; Wang, Y. Research on spatial interpolation of rainfall distribution-A case study of Idaho State in the USA. Miner. Resour. Geol. 2007, 21, 684–687. [Google Scholar]
- Lam, N.S.-N. Spatial Interpolation Methods: A Review. Am. Cartogr. 1983, 10, 129–150. [Google Scholar] [CrossRef]
- Li, L.; Revesz, P. Interpolation methods for spatio-temporal geographic data. Comput. Environ. Urban. Syst. 2004, 28, 201–227. [Google Scholar] [CrossRef]
- Peng, S. Developments of Spatio-temporal Interpolation Methods for Meteorological Elements. Master’s Thesis, Central South University, Changsha, China, 2010. [Google Scholar]
- Li, S.; Shu, H.; Xu, Z. Interpolation of temperature based on spatial-temporal Kriging. Geomatics Inf. Sci. Wuhan Univ. 2012, 37, 237–241. [Google Scholar]
- Lu, Y. Spatio-Temporal Cokriging Interpolation for Air Pollution Index Analysis. Master’s Thesis, Chinese Academy of Surveying & Mapping, Beijing, China, 2018. [Google Scholar]
- Fotheringham, A.S.; Brunsdon, C.; Charlton, M.E. Geographically Weighted Regression: A Method for Exploring Spatial Nonstationarity. Geogr. Anal. 1996, 28, 281–298. [Google Scholar]
- Hu, Q.; Li, Z.; Wang, L.; Huang, Y.; Wang, Y.; Li, L. Rainfall Spatial Estimations: A Review from Spatial Interpolation to Multi-Source Data Merging. Water 2019, 11, 579. [Google Scholar] [CrossRef]
- Wang, M.; He, G.; Zhang, Z.; Wang, G.; Zhang, Z.; Cao, X.; Wu, Z.; Liu, X. Comparison of Spatial Interpolation and Regression Analysis Models for an Estimation of Monthly Near Surface Air Temperature in China. Remote. Sens. 2017, 9, 1278. [Google Scholar] [CrossRef]
- Huang, B.; Wu, B.; Barry, M. Geographically and temporally weighted regression for modeling spatio-temporal variation in house prices. Int. J. Geogr. Inf. Sci. 2010, 24, 383–401. [Google Scholar] [CrossRef]
- Wu, B.; Li, R.; Huang, B. A geographically and temporally weighted autoregressive model with application to housing prices. Int. J. Geogr. Inf. Sci. 2014, 28, 1186–1204. [Google Scholar] [CrossRef]
- Fotheringham, A.S.; Crespo, R.; Yao, J. Geographical and Temporal Weighted Regression (GTWR). Geogr. Anal. 2015, 47, 431–452. [Google Scholar] [CrossRef]
- Xiao, H.; Yi, D. Empirical study of carbon emission drivers based on Geographically time weighted regression model. Stat. Inf. Forum 2014, 29, 83–89. [Google Scholar]
- Liu, J.; Yang, Y.; Xu, S.; Zhao, Y.; Wang, Y.; Zhang, F. A geographically temporal weighted regression approach with travel distance for house price estimation. Entropy 2016, 18, 303. [Google Scholar] [CrossRef]
- Song, C.; Kwan, M.P.; Zhu, J. Modeling fire occurrence at the city scale: A comparison between geographically weighted regression and global linear regression. Int. J. Environ. Res. Public Health 2017, 14, 396. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Wu, L.; Zhang, Y.; Shen, Y.; Qin, K.; Bai, Y. A Geographically and Temporally Weighted Regression Model for Ground-Level PM2.5 Estimation from Satellite-Derived 500 m Resolution AOD. Remote Sens. 2016, 8, 262. [Google Scholar]
- Qin, K.; Rao, L.; Xu, J.; Bai, Y.; Zou, J.; Hao, N.; Li, S.; Yu, C. Estimating ground level NO2 concentrations over central-eastern China using a satellite-based geographically and temporally weighted regression model. Remote Sens. 2017, 9, 950. [Google Scholar] [CrossRef]
- Wei, Q.; Zhang, L.; Duan, W.; Zhen, Z. Global and Geographically and Temporally Weighted Regression Models for Modeling PM2.5 in Heilongjiang, China from 2015 to 2018. Int. J. Environ. Res. Public Health 2019, 16, 5107. [Google Scholar] [CrossRef] [PubMed]
- Brunsdon, C.; McClatchey, J.; Unwin, D.J. Spatial variations in the average rainfall-altitude relationship in Great Britain: An approach using geographically weighted regression. Int. J. Climatol. 2001, 21, 455–466. [Google Scholar] [CrossRef]
- Chen, C.; Zhao, S.; Duan, Z.; Qin, Z. An Improved Spatial Downscaling Procedure for TRMM 3B43 Precipitation Product Using Geographically Weighted Regression. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 4592–4604. [Google Scholar] [CrossRef]
- Lv, A.; Zhou, L. A rainfall model based on a Geographically Weighted Regression algorithm for rainfall estimations over the arid Qaidam Basin in China. Remote Sens. 2016, 8, 311. [Google Scholar] [CrossRef]
- Georganos, S.; Abdi, A.M.; Tenenbaum, D.E.; Kalogirou, S. Examining the NDVI-rainfall relationship in the semi-arid Sahel using geographically weighted regression. J. Arid Environ. 2017, 146, 64–74. [Google Scholar] [CrossRef]
- Li, Y.; Xiong, L.; Yan, L.A. Geographically Weighted Regression Krigin Approach for TRMM-Rain Gauge Data Merging and its Application in Hydrological Forecasting. Resour. Environ. Yangtze Basin 2017, 26, 1359–1368. [Google Scholar]
- Liu, J.; Zhao, Y.; Yang, Y.; Xu, S.; Zhang, F.; Zhang, X.; Shi, L.; Qiu, A. A mixed geographically and temporallyweighted regression: Exploring spatial-temporal variations from global and local perspectives. Entropy 2017, 19, 53. [Google Scholar] [CrossRef]
- Tobler, W. A computer movie simulating urban growth in the Detroit region. Econ. Geogr. 1970, 46 (Suppl. 46), 234–240. [Google Scholar] [CrossRef]
- Ge, L.; Zhao, Y.; Sheng, Z.; Wang, N.; Zhou, K.; Mu, X.; Guo, L.; Wang, T.; Yang, Z.; Huo, X. Construction of a seasonal difference-geographically and temporally weighted regression (SD-GTWR) model and comparative analysis with GWR-based models for hemorrhagic fever with renal syndrome (HFRS) in Hubei Province (China). Int. J. Environ. Res. Public Health 2016, 13, 1062. [Google Scholar] [CrossRef] [PubMed]
- Du, Z.; Wu, S.; Zhang, F.; Liu, R.; Zhou, Y. Extending geographically and temporally weighted regression to account for both spatiotemporal heterogeneity and seasonal variations in coastal seas. Ecol. Inform. 2018, 43, 185–199. [Google Scholar] [CrossRef]
- Dong, F.; Wang, Y.; Zhang, X. Can Environmental Quality Improvement and Emission Reduction Targets Be Realized Simultaneously? Evidence from China and A Geographically and Temporally Weighted Regression Model. Int. J. Environ. Res. Public Health 2018, 15, 2343. [Google Scholar] [CrossRef] [PubMed]
- Qin, W. The Basic Theoretics and Application Research on Geographically Weighted Regression. Ph.D. Thesis, Tongji University, Shanghai, China, 2007. [Google Scholar]
- Yuan, M. Dynamic Change of Vegetation and Phenology Response to Climate Change in Hubei Province. Master’s Thesis, Wuhan University, Wuhan, China, 2017. [Google Scholar]
- Spreen, W.C. A determination of the effect of topography upon precipitation. Trans. Am. Geophys. Union 1947, 28, 285–290. [Google Scholar] [CrossRef]
- Smith, R.B. The influence of mountains on the atmosphere. Adv. Geophys. 1979, 21, 87–230. [Google Scholar]
- Kang, L.; Di, L.; Shao, Y.; Yu, E.; Zhang, B.; Shrestha, R. Study of the NDVI-precipitation correlation stratified by crop type and soil permeability. In Proceedings of the 2013 2nd International Conference on Agro-Geoinformatics: Information for Sustainable Agriculture, Agro-Geoinformatics, Fairfax, VA, USA, 12–16 August 2013; pp. 194–199. [Google Scholar]
- Feng, J.; Zhang, H.; Hu, X.; Shi, Q.; Zubaidai, M. Spatial non-stationarity characteristics of the impacts of precipitation and temperature on vegetation coverage index: A case study in Yili River Valley, Xinjiang. Acta Ecol. Sin. 2016, 36, 4626–4634. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).