Prediction of Individual Tree Diameter and Height to Crown Base Using Nonlinear Simultaneous Regression and Airborne LiDAR Data
Abstract
1. Introduction
2. Methods
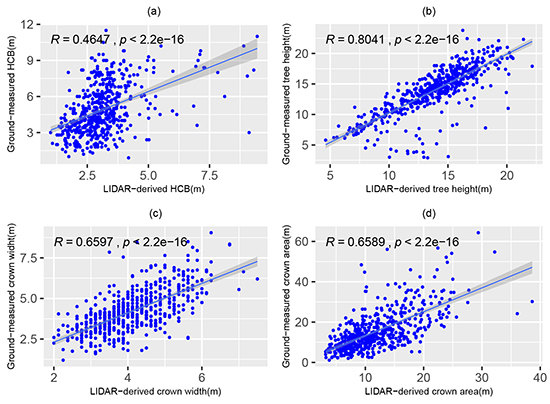
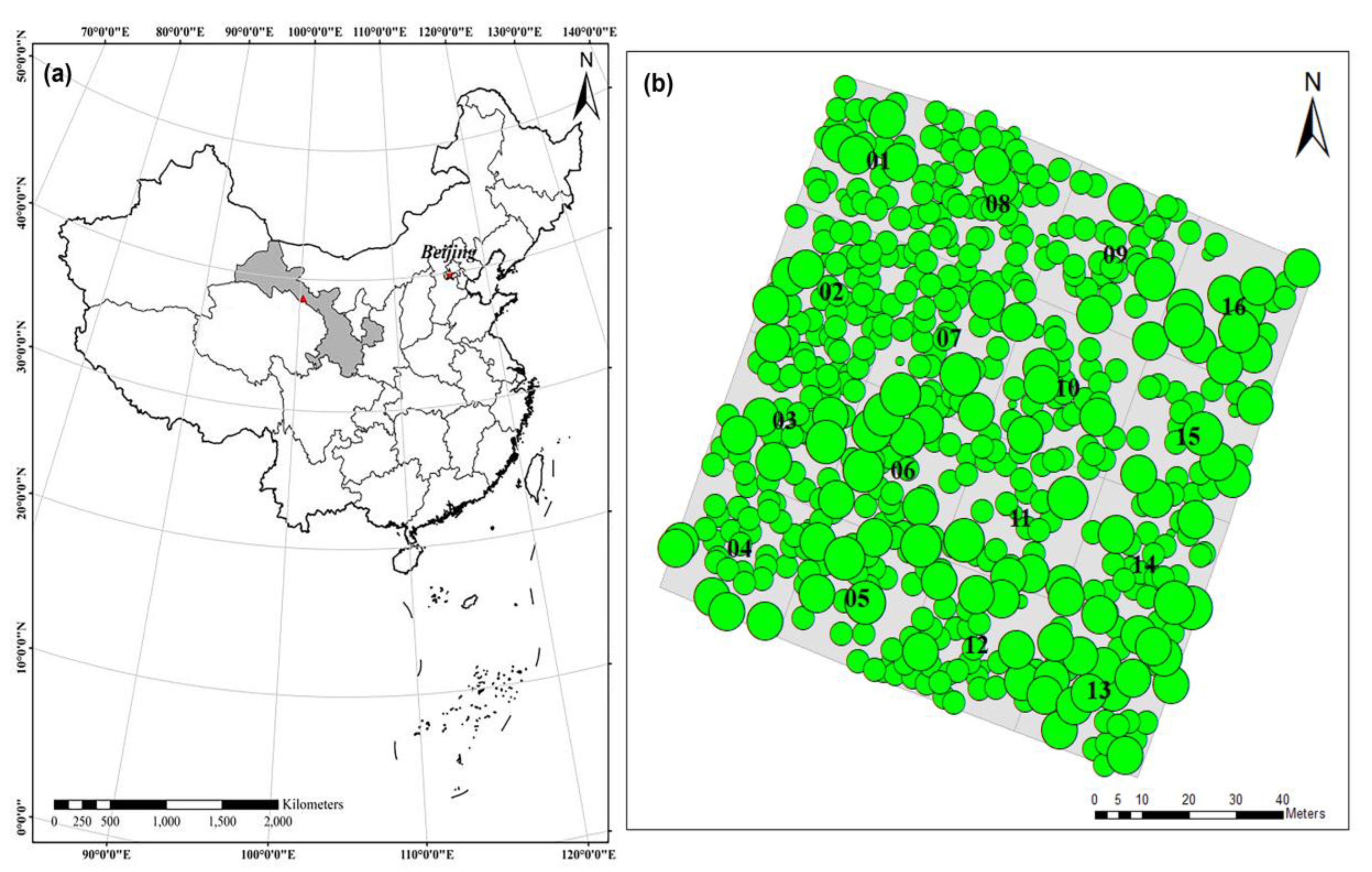
2.1. Data Collection
2.2. Base Model
2.2.1. LiDAR–DBH Base Model
2.2.2. LiDAR–HCB Base Model
2.3. A Compatible Individual Tree DBH and HCB EIV Equation System
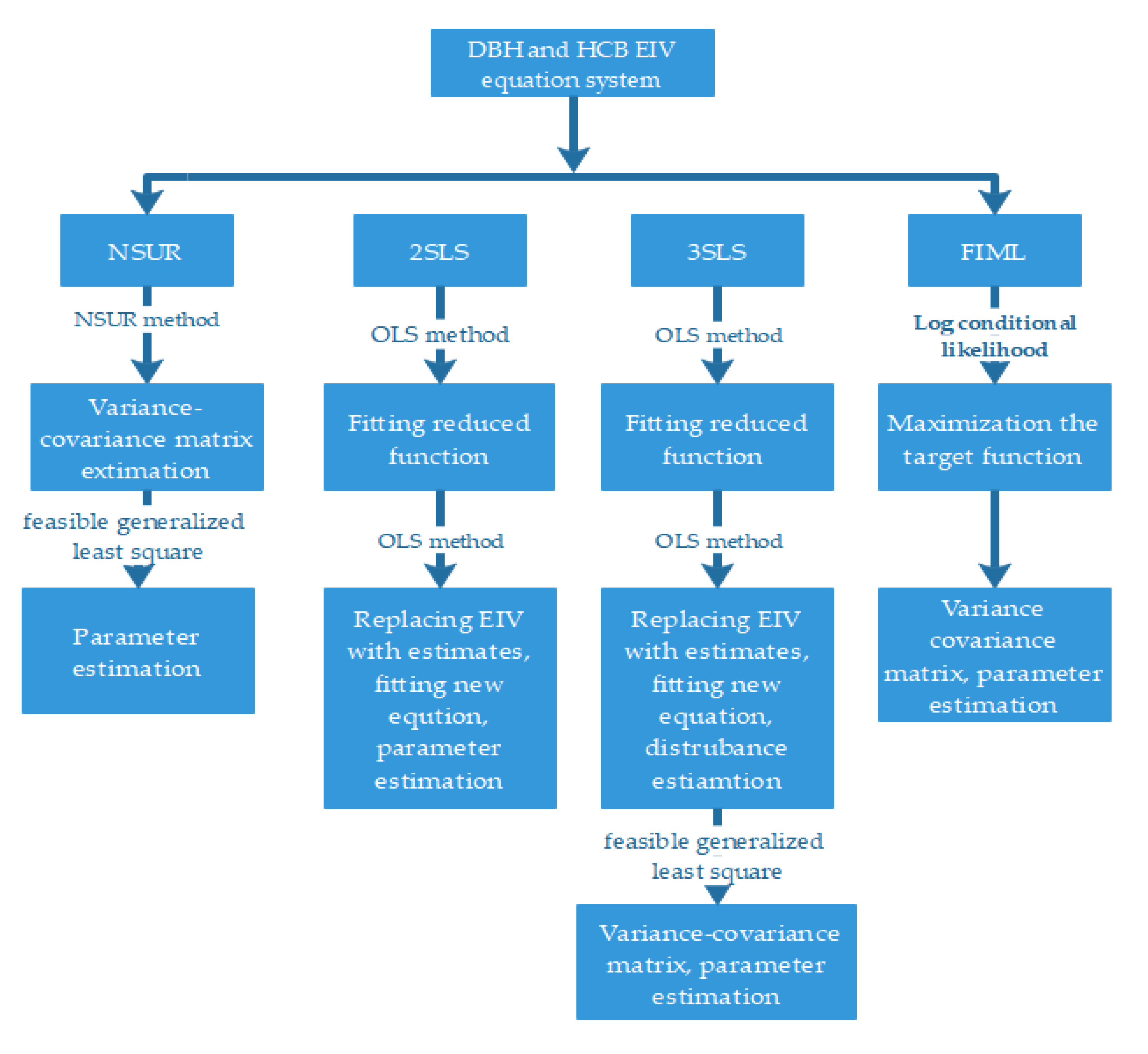
2.4. Parameter Estimation
2.5. Other Model Structures for Comparison
2.5.1. Nonlinear Least Squares with HCB Estimation not Based on DBH (NLS and NBD)
2.5.2. Nonlinear Least Squares with HCB Estimation Based on DBH (NLS and BD)
2.6. Comparison and Evaluation of Models
3. Results
3.1. Parameters Estimation
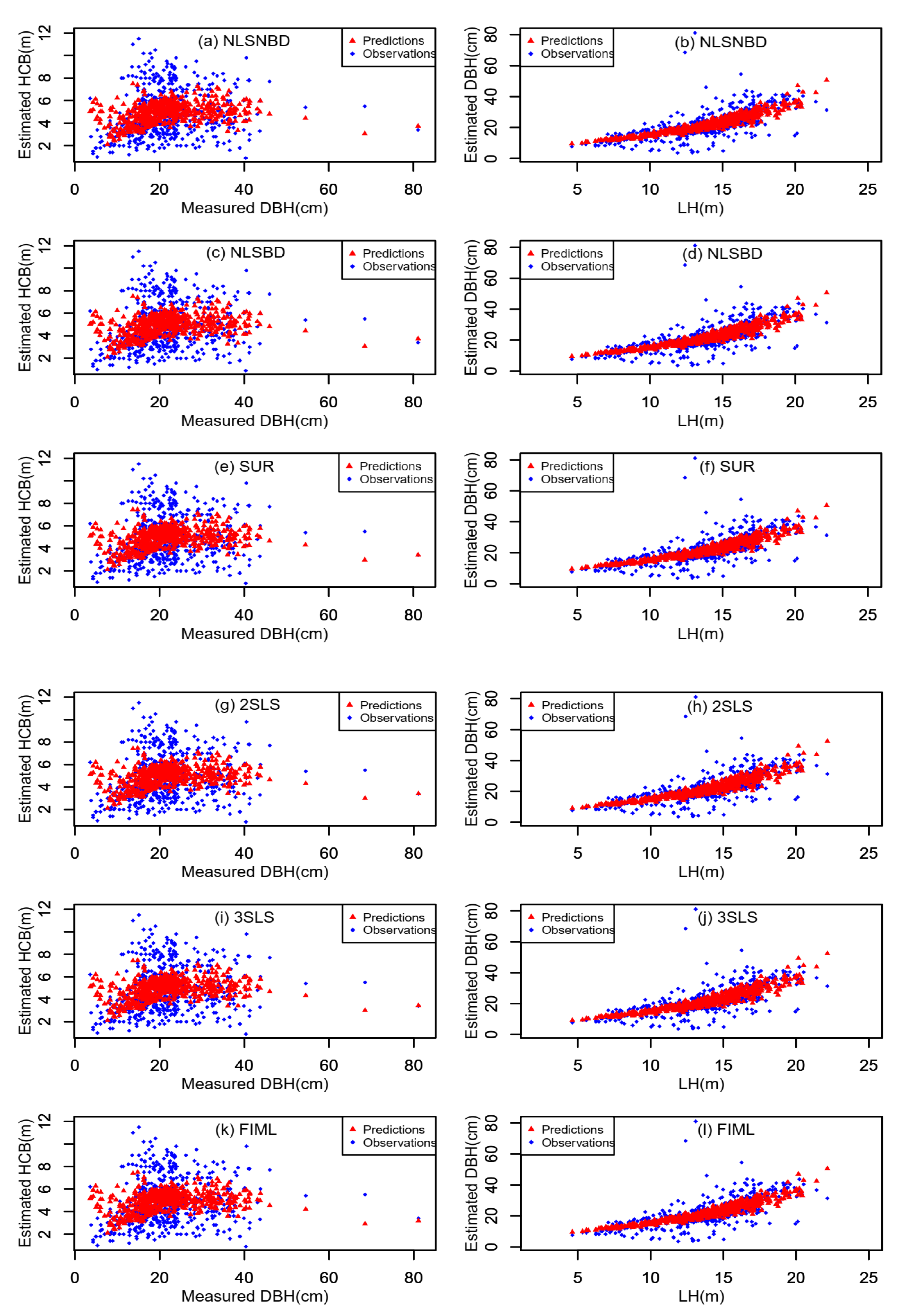
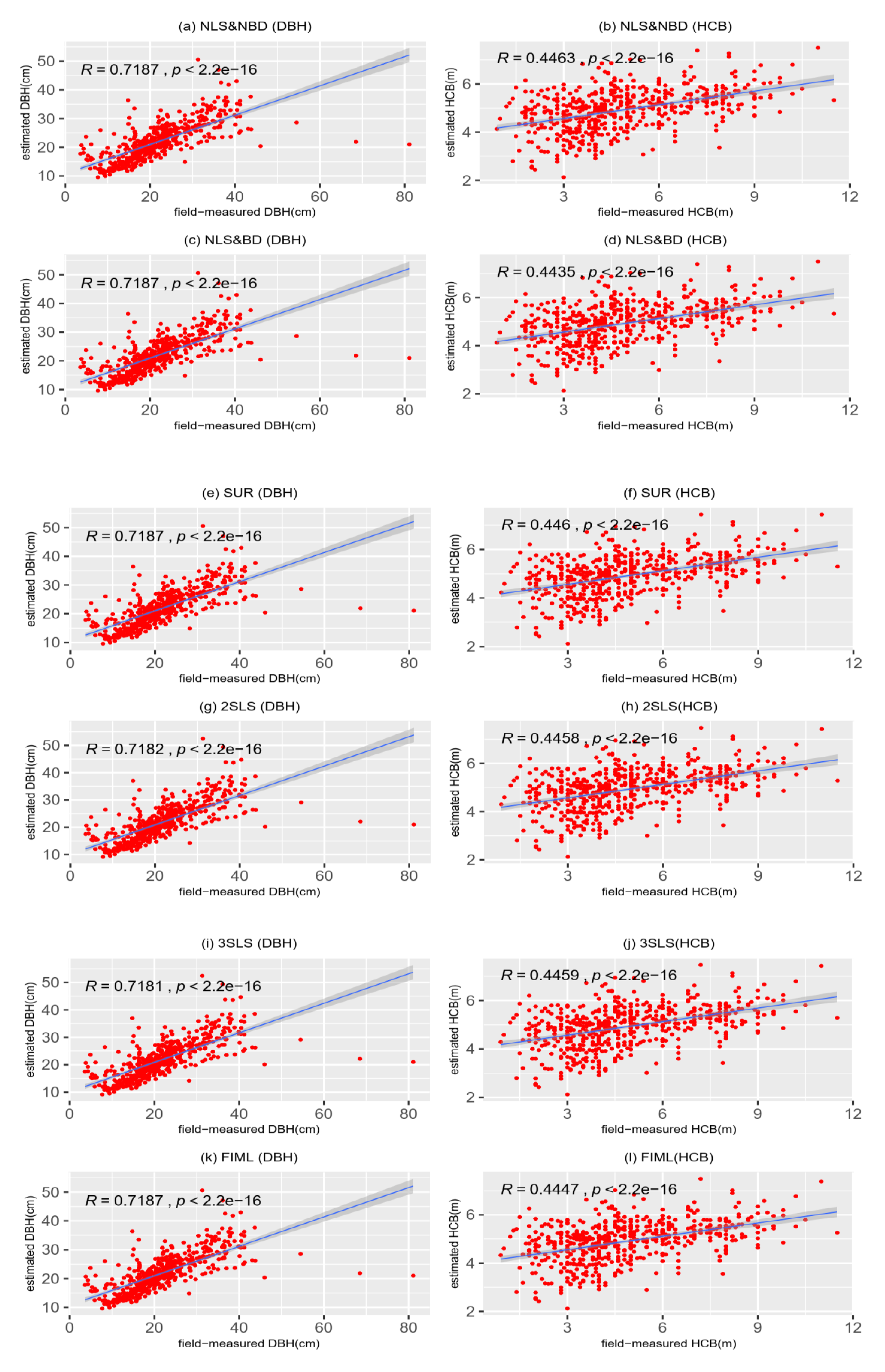
3.2. Model Prediction
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Daniels, R.F.; Burkhart, H.E. Simulation of Individual Tree Growth and Stand Development in Managed Loblolly Pine Plantations; FWS-5-75; Division of Forestry and Wildlife Resources, Virginia Polytechnic and State University: Blacksburg, VA, USA, 1975; 69p. [Google Scholar]
- Navratil, S. Wind damage in thinned stands. In Proceedings of the A Commercial Thinning Workshop, Whitecourt, AB, Canada, 17–18 October 1997; pp. 29–36. [Google Scholar]
- Ancelin, P.; Courbaud, B.; Fourcaud, T. Development of an individual tree-based mechanical model to predict wind damage within forest stands. For. Ecol. Manag. 2004, 203, 101–121. [Google Scholar] [CrossRef]
- Dean, T.J.; Cao, Q.V.; Roberts, S.D.; Evans, D.L. MeaNSURing heights to crown base and crown median with LiDAR in a mature, even-aged loblolly pine stand. For. Ecol. Manag. 2009, 257, 126–133. [Google Scholar] [CrossRef]
- Scott, J.H.; Reinhardt, D. Assessing Crown Fire Potential by Linking Models of Surface and Crown Fire Potential; USDA Forest Service, Rocky Mountain Research: Washington, WA, USA, 2001.
- Hynynen, J. Predicting tree crown ratio model for Austrian forests. Can. J. For. Res. 1995, 25, 57–62. [Google Scholar] [CrossRef]
- Vauhkonen, J. Estimating crown base height for Scots pine by means of the 3D geometry of airborne laser scanning data. Int. J. Remote Sens. 2010, 31, 1213–1226. [Google Scholar] [CrossRef]
- Michael, E.D.; Burkhart, H.E. Compatible crown ratio and crown height models. Can. J. For. Res. 1987, 17, 572–574. [Google Scholar]
- Ritchie, M.W.; Hann, D.W. Equations for Predicting Height to Crown Base for Fourteen Tree Species in Southwest Oregon; Research Paper; Oregon State University, Forestry Research Laboratory: Corvallis, OR, USA, 1987. [Google Scholar]
- Baburam, R.; Aaron, R.; Weiskittel, J.A.; Kershaw, J. Development of height to crown base models for thirteen tree species of the North American Acadian Region. For. Chron. 2012, 88, 60–73. [Google Scholar] [CrossRef]
- Sharma, R.P.; Vacek, Z.; Vacek, S.; Podrázský, V.; Jansa, V. Modelling individual tree height to crown base of Norway spruce (Picea abies (L.) Karst.) and European beech (Fagus sylvatica L.). PLoS ONE 2017, 12, e0186394. [Google Scholar] [CrossRef] [PubMed]
- Fu, L.Y.; Sharma, R.P.; Hao, K.J.; Tang, S.Z. A generalized interregional nonlinear mixed-effects crown width model for Prince Rupprecht larch in northern China. For. Ecol. Manag. 2017, 389, 364–373. [Google Scholar] [CrossRef]
- Popescu, S.C. Estimating biomass of individual pine trees using airborne LiDAR. Biomass Bioenergy 2007, 31, 646–655. [Google Scholar] [CrossRef]
- Broadbent, E.N.; Asner, G.P.; Peña-Claros, M.; Palace, M.; Soriano, M. Spatial partitioning of biomass and diversity in a lowland Bolivian forest: Linking field and remote sensing measurements. For. Ecol. Manag. 2008, 255, 2602–2616. [Google Scholar] [CrossRef]
- Heurich, M. Automatic recognition and measurement of single trees based on data from airborne laser scanning over the richly structured natural forests of the Bavarian Forest National Park. For. Ecol. Manag. 2008, 255, 2416–2433. [Google Scholar] [CrossRef]
- Bi, H.; Fox, J.C.; Li, Y.; Lei, Y.; Pang, Y. Evaluation of nonlinear equations for predicting diameter from tree height. Can. J. Remote Sens. 2012, 42, 789–806. [Google Scholar] [CrossRef]
- Lefsky, M.A.; Cohen, W.B.; Acker, S.A.; Parker, G.G.; Spies, T.A.; Harding, D. LiDAR Remote Sensing of the Canopy Structure and Biophysical Properties of Douglas-Fir Western Hemlock Forests. Remote Sens. Environ. 1999, 70, 339–361. [Google Scholar] [CrossRef]
- Næsset, E. Predicting forest stand characteristics with airborne scanning laser using a practical two-stage procedure and field data. Remote Sens. Environ. 2002, 80, 88–99. [Google Scholar] [CrossRef]
- Pyysalo, U.; Hyyppä, H. Reconstructing tree crowns from laser scanner data for feature extraction. Int. Archives of Photogram. Remote Sens. Spat. Inf. Sci. XXXIV Part 3B 2002, 34, 218–221. [Google Scholar]
- Holmgren, J.; Persson, Å.; Söderman, U. Species identification of individual trees by combining high resolution LIDAR data with multi-spectral images. Int. J. Remote Sens. 2008, 29, 1537–1552. [Google Scholar] [CrossRef]
- Popescu, S.C.; Zhao, K. A voxel-based LiDAR method for estimating crown base height for deciduous and pine trees. Remote Sens. Environ. 2008, 112, 767–781. [Google Scholar] [CrossRef]
- Maltamo, M.; Bollandsås, O.M.; Vauhkonen, J.; Breidenbach, J.; Gobakken, T.; Næsset, E. Comparing different methods for prediction of mean crown height in Norway spruce stands using airborne laser scanner data. Forestry 2010, 83, 257–268. [Google Scholar] [CrossRef]
- Luo, L.; Zhai, Q.; Su, Y.; Ma, Q.; Kelly, M.; Guo, Q. Simple method for direct crown base height estimation of individual conifer trees using airborne LiDAR data. Opt. Express. 2018, 26, A562–A578. [Google Scholar] [CrossRef]
- Solberg, S.; Næsset, E.; Bollandsås, O.M. Single tree segmentation using airborne laser scanning data in a structurally heterogeneous spruce forest. Photogramm. Eng. Remote Sens. 2006, 72, 1369–1378. [Google Scholar] [CrossRef]
- Næsset, E.; Økland, T. Estimating tree height and tree crown properties using airborne scanning laser in a boreal nature reserve. Remote Sens. Environ. 2002, 79, 105–115. [Google Scholar] [CrossRef]
- Andersen, H.E.; McGaughey, R.J.; Reutebuch, S.E. Estimating forest canopy fuel parameters using LiDAR data. Remote Sens. Environ. 2005, 94, 441–449. [Google Scholar] [CrossRef]
- Maltamo, M.; Hyyppä, J.; Malinen, J. A comparative study of the use of laser scanner data and field measurements in the prediction of crown height in boreal forests. Scand. J. Forest Res. 2006, 21, 231–238. [Google Scholar] [CrossRef]
- Maltamo, M.; Karjalainen, T.; Repola, J.; Vauhkonen, J. Incorporating tree- and stand-level information on crown base height into multivariate forest management inventories based on airborne laser scanning. Silva Fennica 2018, 52, 1–18. [Google Scholar] [CrossRef]
- Zhang, W.; Ke, Y.; Quackenbush, L.J.; Zhang, L. Using error-in-variable (EIV) regression to predict tree diameter and crown width from remotely sensed imagery. Can. J. For. Res. 2010, 40, 1095–1108. [Google Scholar] [CrossRef]
- Rechenr, A.C.; Schaalje, G.B. Linear Models in Statistics, 2nd ed.; Woley: New York, NY, USA, 2008. [Google Scholar]
- Kangas, A.S. Effect of errors-in-variables on coefficients of a growth model and on prediction of growth. For. Ecol. Manag. 1998, 102, 203–212. [Google Scholar] [CrossRef]
- Carroll, R.J.; Ruppert, D.; Stefanski, L.A.; Crainiceanu, C.M. Measurement Error in Nonlinear Models: A Modern Perspective; Taylor & Francis Group LLC: New York, NY, USA, 2006; p. 438. [Google Scholar]
- Fu, L.Y.; Liu, Q.W.; Sun, H.; Wang, Q.Y.; Li, Z.Y.; Chen, E.X.; Pang, Y.; Song, X.Y.; Wang, G.X. Development of a system of compatible individual tree diameter and aboveground biomass prediction models using error-in-variable regression and airborne LiDAR data. Remote Sens. 2018, 10, 325. [Google Scholar] [CrossRef]
- Tang, S.; Li, Y.; Fu, L.Y. Statistical Foundation for Biomathematical Models, 2nd ed.; Higher Education Press: Beijing, China, 2015; p. 435. ISBN 978-7-04-042303-7. [Google Scholar]
- Fuller, W.A. Meansureement Error Models; John Wiley and Sons: New York, NY, USA, 1987. [Google Scholar]
- Tang, S.; Zhang, S. Measurement error models and their applications. J. Biomath. 1998, 13, 161–166. [Google Scholar]
- Tang, S.; Li, Y.; Wang, Y. Simultaneous equations, errors-invariable models, and model integration in systems ecology. Ecol. Model. 2001, 142, 285–294. [Google Scholar] [CrossRef]
- Lindley, D.V. Regression lines and the linear functional relationship. J. R. Stat. Soc. B 1947, 9, 218–244. [Google Scholar] [CrossRef]
- Tang, S.; Wang, Y. A parameter estimation program for the errors-in-variable model. Ecol. Model. 2002, 156, 225–236. [Google Scholar] [CrossRef]
- Walters, D.K.; Hann, D.W. Taper Equations for Six Conifer Species in Southwest Oregon; Forest Research Laboratory, Oregon State University: Corvallis, OR, USA, 1986; p. 41. [Google Scholar]
- Pang, Y.; Chen, E.; Liu, Q.; Xiao, Q.; Zhong, K.; Li, X.; Ma, M. WATER: Dataset of airborne LiDAR mission at the super site in the Dayekou watershed flight zone on Jun. 23, 2008. In Chinese Academy of Forestry; Institute of Remote Sensing Applications, Chinese Academy of Sciences; Cold and Arid Regions Environmental and Engineering Research Institute, Chinese Academy of Sciences; Heihe Plan Science Data Center: Lanzhou, China, 2008. [Google Scholar]
- Koch, B.; Heyder, U.; Weinacker, H. Detection of Individual Tree Crowns in Airborne Lidar Data. Photogramm. Eng. Remote Sens. 2006, 72, 357–363. [Google Scholar] [CrossRef]
- Parent, J.R.; Volin, J.C. Assessing the potential for leaf–off LiDAR data to model canopy closure in temperate deciduous forests. Photogramm. Eng. Remote Sens. 2014, 95, 134–145. [Google Scholar] [CrossRef]
- Liu, Q.; Fu, L.; Wang, G.; Li, S.; Li, Z.; Chen, E.; Pang, Y.; Hu, K. Improving estimation of forest canopy cover by introducing loss ratio of laser pulses using airborne LiDAR. IEEE Trans. Geosci. Remote. 2020, 58, 567–584. [Google Scholar] [CrossRef]
- Liu, Q. Study on the Estimation Method of Forest Parameters Using Airborne Lidar. Ph.D. Thesis, Chinese Academy of Forestry, Beijing, China, 2009. (In Chinese). [Google Scholar]
- Liu, Q.; Li, Z.; Chen, E.; Pang, Y.; Wu, H. Extracting individual tree heights and crowns using airborne LIDAR data. J. Beijing For. Univ. 2008, 30, 83–89. [Google Scholar]
- Fu, L.; Lei, Y.; Wang, G.; Bi, H.; Tang, S.; Song, X. Comparison of seemingly unrelated regressions with multivariate errors-in-variables models for developing a system of nonlinear additive biomass equations. Trees 2016, 30, 839–857. [Google Scholar] [CrossRef]
- Parresol, B.R. Assessing tree and stand biomass: A review with examples and critical comparisons. For. Sci. 1999, 45, 573–593. [Google Scholar]
- Parresol, B.R. Additivity of nonlinear biomass equations. Can. J. For. Res. 2011, 31, 865–878. [Google Scholar] [CrossRef]
- Judge, G.G.; Hill, R.C.; Griffifiths, W.E.; Lutkepohl, H.; Lee, T.C. Introduction to the Theory and Ractice of Econometrics, 2nd ed.; Wiley: New York, NY, USA, 1988. [Google Scholar]
- Zellner, A.; Theil, H. Three Stage Least Squares: Simultaneous Estimation of Simultaneous Equations. Econometrica 1962, 30, 54–78. [Google Scholar] [CrossRef]
- Fumio, H. Econometrics; Shanghai University of Finance and Economics Press: Shanghai, China, 2005; p. 536. ISBN 7-81098-499-3. [Google Scholar]
- Nord-Larsen, T.; Meilby, H.; Skovsgaard, J.P. Site-specific height growth models for six common tree species in Denmark. Scand. J. For. Res. 2009, 24, 194–204. [Google Scholar] [CrossRef]
- Timilsina, N.; Staudhammer, C.L. Individual tree-based diameter growth model of slash pine in Florida using nonlinear mixed modeling. For. Sci. 2013, 59, 27–31. [Google Scholar] [CrossRef]
- Zhao, D.; Lynch, T.B.; Westfall, J.; Coulston, J.; Kane, M.; Adams, D.E. Compatibility, development and estimation of taper and volume equation systems. For. Sci. 2019, 65, 1–13. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2018; Available online: https://www.R-project.org/ (accessed on 15 March 2020).
- Greene, W.J. Econometric Analysis, 7th ed.; Pearson Education, Inc.: New York, NY, USA, 2001; p. 1188. ISBN 0-13-139538-6. [Google Scholar]
- Curran, P.J.; Hay, A.M. The importance of mesauement error for certain procedures in remote sensing at optical wavelengths. Photogramm. Eng. Remote Sens. 1986, 52, 229–241. [Google Scholar]
- Wykoff, W.R. A basal area increment model for individual conifers in the northern Rocky Mountains. For. Sci. 1990, 136, 1077–1104. [Google Scholar]
- Van Deusen, P.C.; Biging, G.S. STAG, A Stand Generator for Mixed Species Stands; Research Note; Northern 55 California Forest Yield Cooperative, Department of Forestry and Resource Management, University of California: Berkeley, CA, USA, 1985; Volume 11, 25p. [Google Scholar]
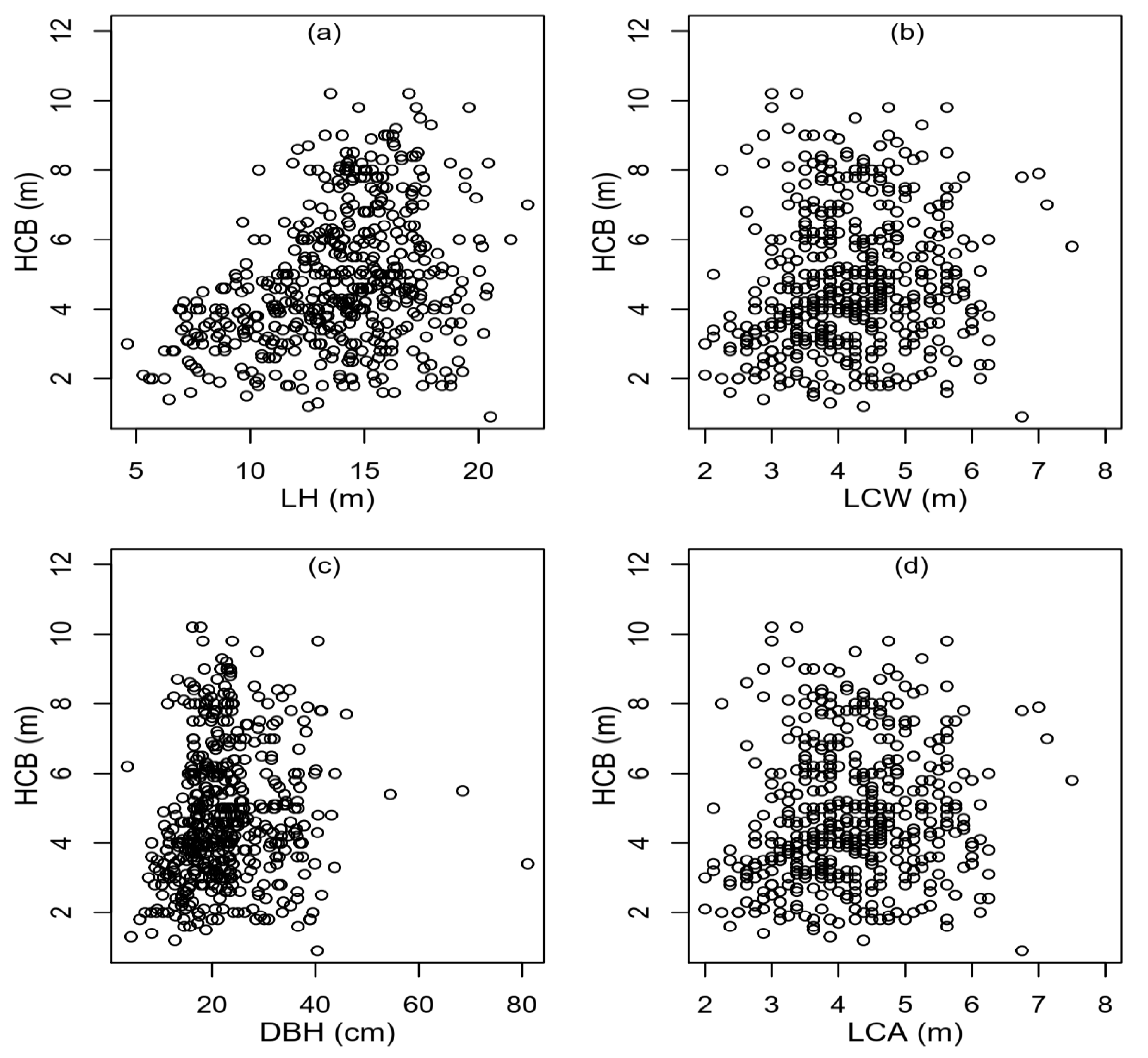
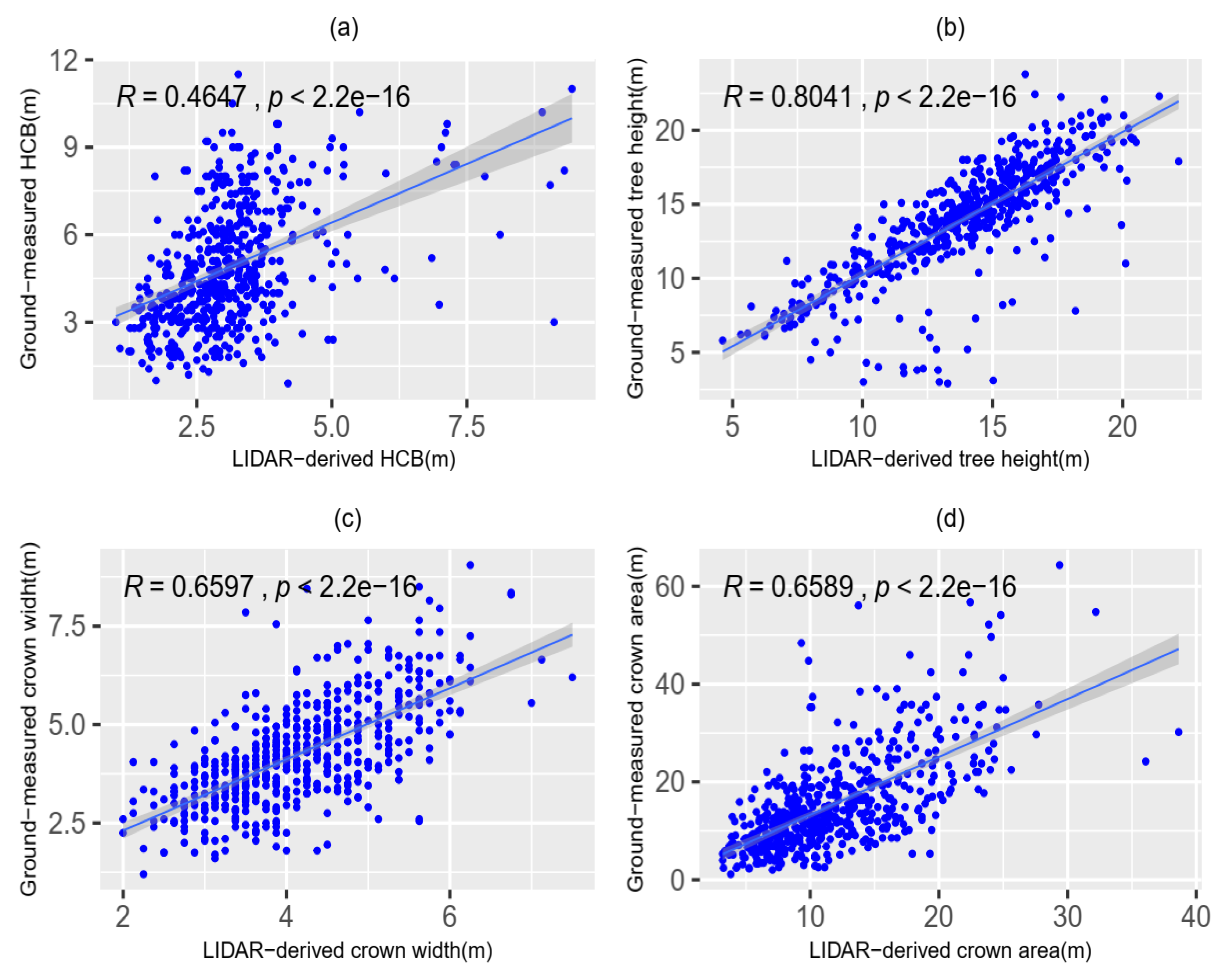
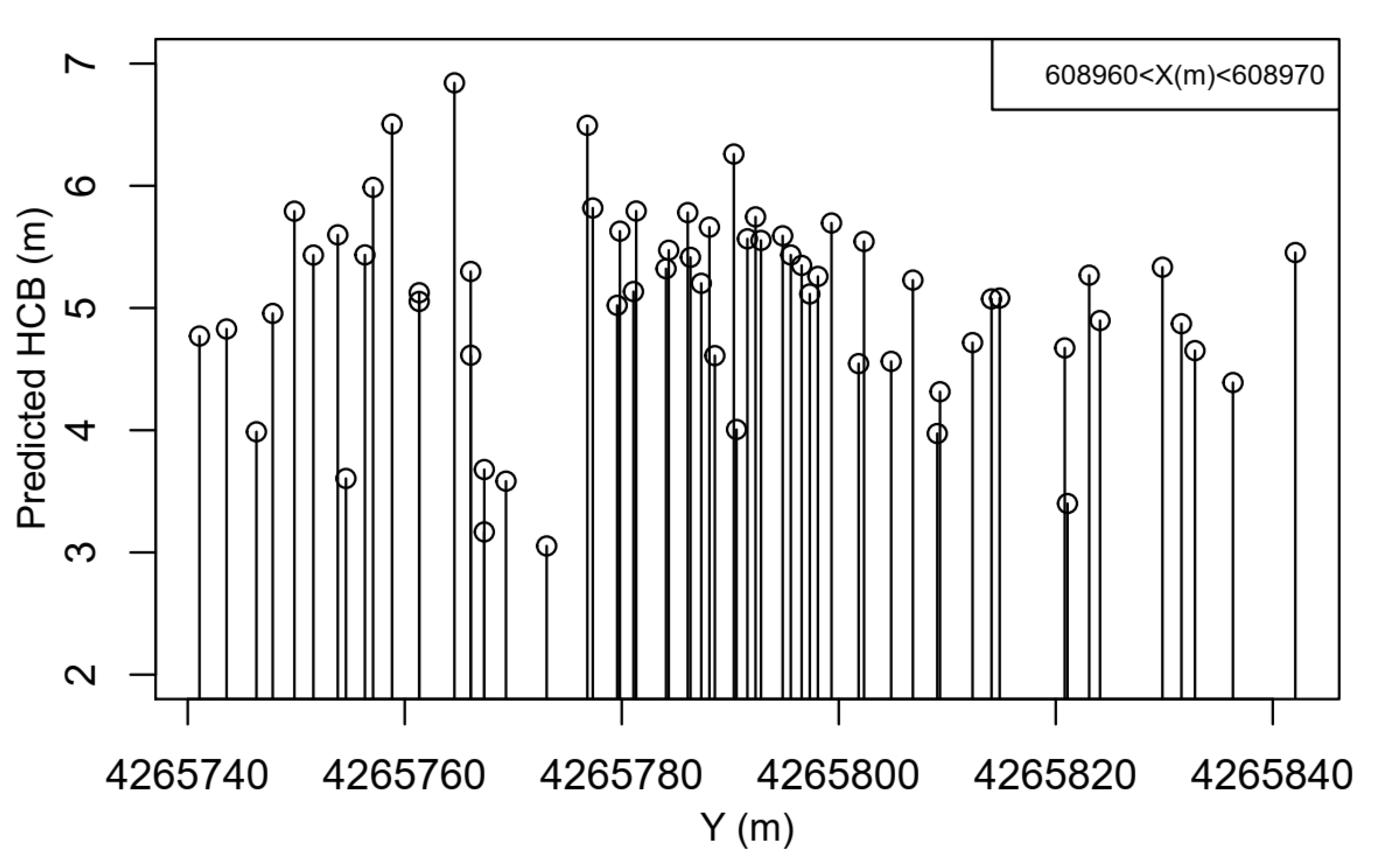
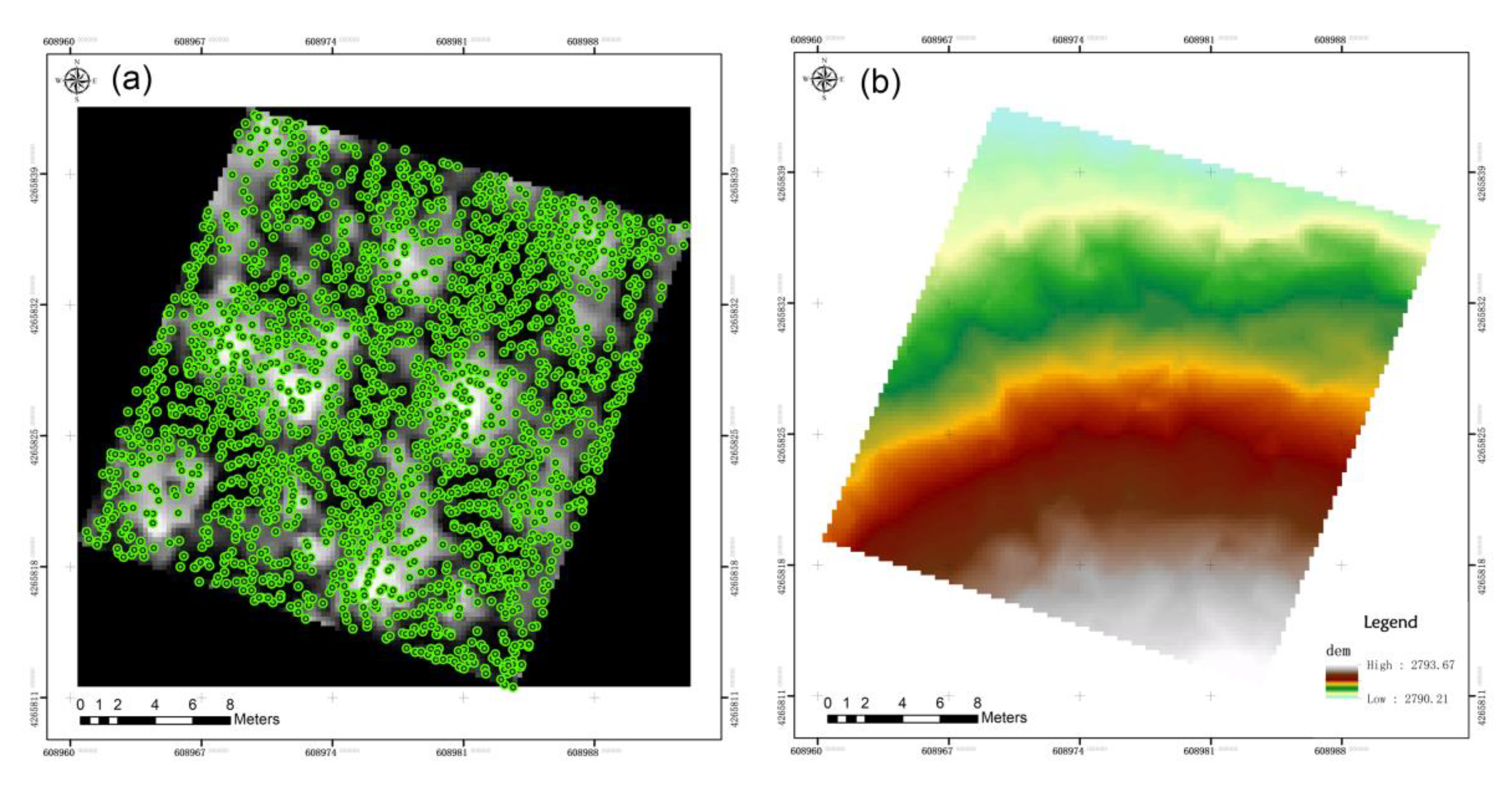
| Variable | Min. | Max. | Mean | SD |
|---|---|---|---|---|
| LH (m) | 4.62 | 22.15 | 13.84 | 3.20 |
| HCB (m) | 0.90 | 10.20 | 4.80 | 3.52 |
| LCW (m) | 2.00 | 7.50 | 4.20 | 0.95 |
| DBH (cm) | 3.60 | 81.10 | 22.57 | 8.54 |
| LCA (m) | 3.19 | 38.63 | 12.21 | 5.47 |
| Model | Method | Parameters | Estimates | Standard Error | t-Value |
|---|---|---|---|---|---|
| LiDAR–DBH base model (Equation (1)) | NLS | 5.7161 | 0.3599 | 15.882 | |
| −0.0567 | 0.0061 | −9.344 | |||
| −0.1264 | 0.0178 | −7.108 | |||
| 37.22 | |||||
| LiDAR–HCB base model (Equation (2)) | NLS | 0.0053 | 0.0031 | 1.68 | |
| 0.0367 | 0.0057 | 6.4340 | |||
| 3.37 | |||||
| HCB based on DBH model (Equation (13)) | NLS | −0.0003 | 0.0547 | −0.00 | |
| NLS and BD | 0.2472 | 0.1987 | −1.24 | ||
| 0.0800 | 0.0520 | 1.54 | |||
| 0.0283 | 0.0137 | 2.07 | |||
| 3.33 | |||||
| Simultaneous equation system (Equation (3)) | NSUR | 5.6992 | 0.3615 | 15.77 | |
| −0.0563 | 0.0061 | −9.27 | |||
| −0.1283 | 0.0180 | −7.12 | |||
| 0.0059 | 0.0032 | 1.87 | |||
| 0.0361 | 0.0058 | 6.26 | |||
| 37.22 | |||||
| 3.32 | |||||
| 0.608 | |||||
| Simultaneous equation system (Equation (3)) | 2SLS | 5.2496 | 0.3586 | 14.64 | |
| −0.0567 | 0.0064 | −8.83 | |||
| −0.1451 | 0.0186 | −7.80 | |||
| 0.0054 | 0.0051 | 1.04 | |||
| 0.0370 | 0.0091 | 4.08 | |||
| 37.93 | |||||
| 3.32 | |||||
| 0.551 | |||||
| Simultaneous equation system (Equation (3)) | 3SLS | 5.2641 | 0.3590 | 14.66 | |
| −0.0564 | 0.0064 | −8.78 | |||
| −0.1457 | 0.0186 | −7.83 | |||
| 0.0052 | 0.0051 | 1.01 | |||
| 0.0373 | 0.0091 | 4.12 | |||
| 37.88 | |||||
| 3.32 | |||||
| 0.553 | |||||
| Simultaneous equation system (Equation (3)) | FIML | 5.7036 | 0.3469 | 16.44 | |
| −0.0561 | 0.0047 | −11.84 | |||
| −0.1289 | 0.0149 | −8.66 | |||
| 0.0074 | 0.0042 | 1.76 | |||
| 0.0335 | 0.0076 | 4.39 | |||
| 37.72 | |||||
| 3.31 | |||||
| 0.65 |
| Fitting Method | Variables | RMSE | MAE | ||
|---|---|---|---|---|---|
| NLS and NBD | DBH | −0.0426 | 37.6572 | 6.1367 | 3.6998 |
| HCB | −0.0367 | 3.3387 | 1.8276 | 1.4619 | |
| NLS and BD | HCB | −0.4186 | 3.3530 | 1.8784 | 1.4619 |
| NSUR | DBH | −0.0458 | 37.6577 | 6.1368 | 3.7008 |
| HCB | −0.0276 | 3.3414 | 1.8281 | 1.4606 | |
| 2SLS | DBH | 0.0093 | 37.7985 | 6.1481 | 3.6984 |
| HCB | −0.0336 | 3.3421 | 1.8285 | 1.4612 | |
| 3SLS | DBH | 0.0026 | 37.7977 | 6.1480 | 3.7004 |
| HCB | −0.0341 | 3.3416 | 1.8283 | 1.4613 | |
| FIML | DBH | −0.0457 | 37.6598 | 6.1369 | 3.7012 |
| HCB | −0.0195 | 3.3470 | 1.8296 | 1.4613 |
| Model | Method | Response Variable | Min. of Residuals | Max. of Residuals | Mean of Residuals | SD of Residuals |
|---|---|---|---|---|---|---|
| LiDAR–DBH base model (Equation (1)) | NLS | DBH | −60.0992 | 21.6027 | 0.0423 | 6.1365 |
| LiDAR–HCB base model (Equation (2)) | NLS | HCB | −6.1705 | 4.3487 | 0.0367 | 1.8272 |
| HCB based on DBH model, NLS and BD (Equation (13)) | NLS | HCB | −6.1708 | 4.3495 | 0.0342 | 1.8300 |
| Simultaneous equation system (Equation (3)) | NSUR | DBH | −60.0883 | 21.5831 | 0.0458 | 6.1366 |
| HCB | −6.2068 | 4.4099 | 0.0276 | 1.8279 | ||
| Simultaneous equation system (Equation (3)) | 2SLS | DBH | −60.1132 | 22.2219 | −0.0093 | 6.1481 |
| HCB | −6.2193 | 4.4061 | 0.0336 | 1.8282 | ||
| Simultaneous equation system (Equation (3)) | 3SLS | DBH | −60.0874 | 22.1638 | −0.0026 | 6.1480 |
| HCB | −6.2150 | 4.3999 | 0.0341 | 1.8280 | ||
| Simultaneous equation system (Equation (3)) | FIML | DBH | −60.0819 | 21.5710 | 0.0457 | 6.1368 |
| HCB | −6.2407 | 4.4668 | 0.0295 | 1.8295 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Z.; Liu, Q.; Luo, P.; Ye, Q.; Duan, G.; Sharma, R.P.; Zhang, H.; Wang, G.; Fu, L. Prediction of Individual Tree Diameter and Height to Crown Base Using Nonlinear Simultaneous Regression and Airborne LiDAR Data. Remote Sens. 2020, 12, 2238. https://doi.org/10.3390/rs12142238
Yang Z, Liu Q, Luo P, Ye Q, Duan G, Sharma RP, Zhang H, Wang G, Fu L. Prediction of Individual Tree Diameter and Height to Crown Base Using Nonlinear Simultaneous Regression and Airborne LiDAR Data. Remote Sensing. 2020; 12(14):2238. https://doi.org/10.3390/rs12142238
Chicago/Turabian StyleYang, Zhaohui, Qingwang Liu, Peng Luo, Qiaolin Ye, Guangshuang Duan, Ram P. Sharma, Huiru Zhang, Guangxing Wang, and Liyong Fu. 2020. "Prediction of Individual Tree Diameter and Height to Crown Base Using Nonlinear Simultaneous Regression and Airborne LiDAR Data" Remote Sensing 12, no. 14: 2238. https://doi.org/10.3390/rs12142238
APA StyleYang, Z., Liu, Q., Luo, P., Ye, Q., Duan, G., Sharma, R. P., Zhang, H., Wang, G., & Fu, L. (2020). Prediction of Individual Tree Diameter and Height to Crown Base Using Nonlinear Simultaneous Regression and Airborne LiDAR Data. Remote Sensing, 12(14), 2238. https://doi.org/10.3390/rs12142238