A Combined Use of TSVD and Tikhonov Regularization for Mass Flux Solution in Tibetan Plateau
Abstract
:1. Introduction
2. Data and Methods
2.1. GRACE Data
2.2. Mascon Modeling
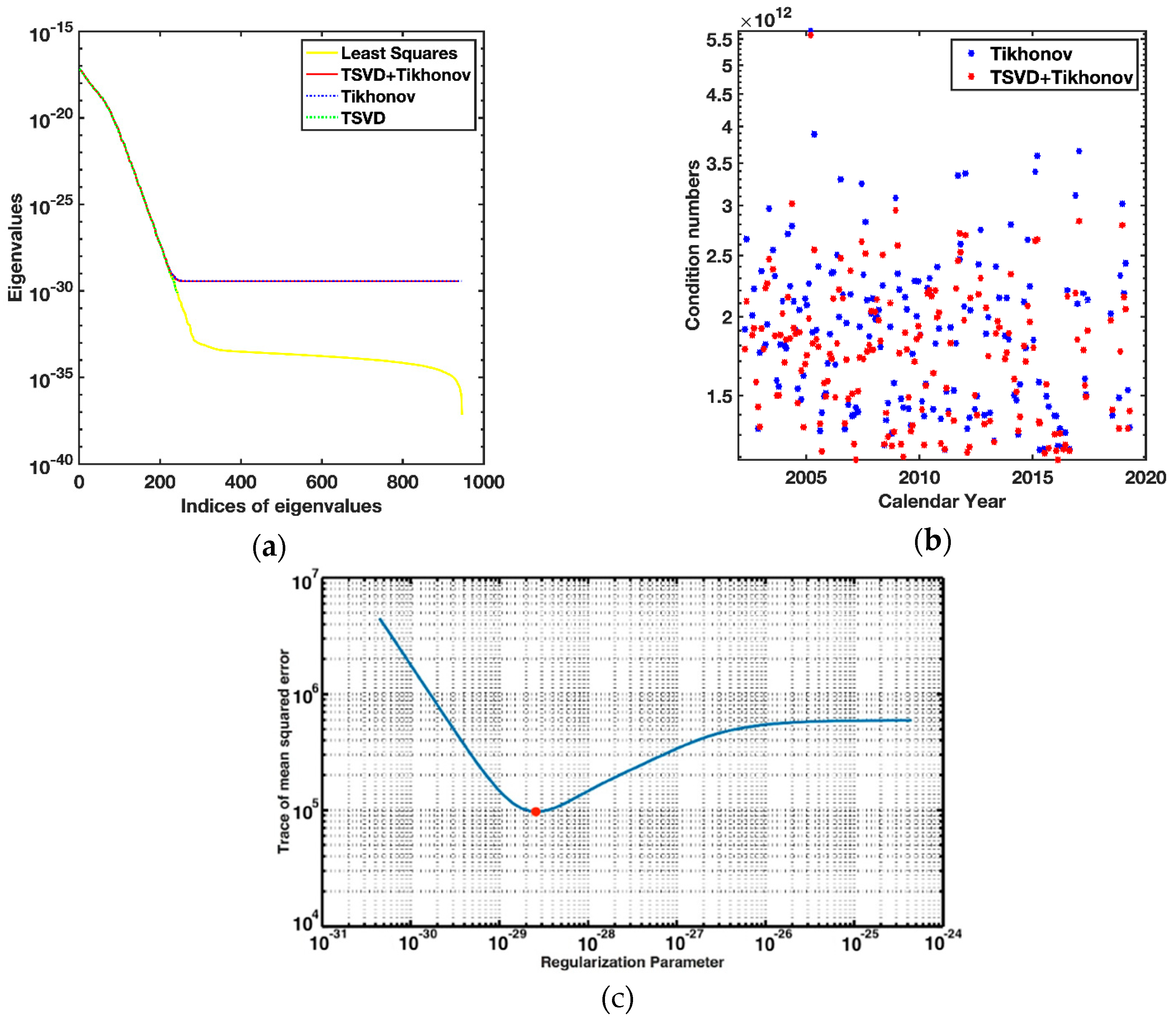
2.3. Combined Use of TSVD and Tikhonov Regularization
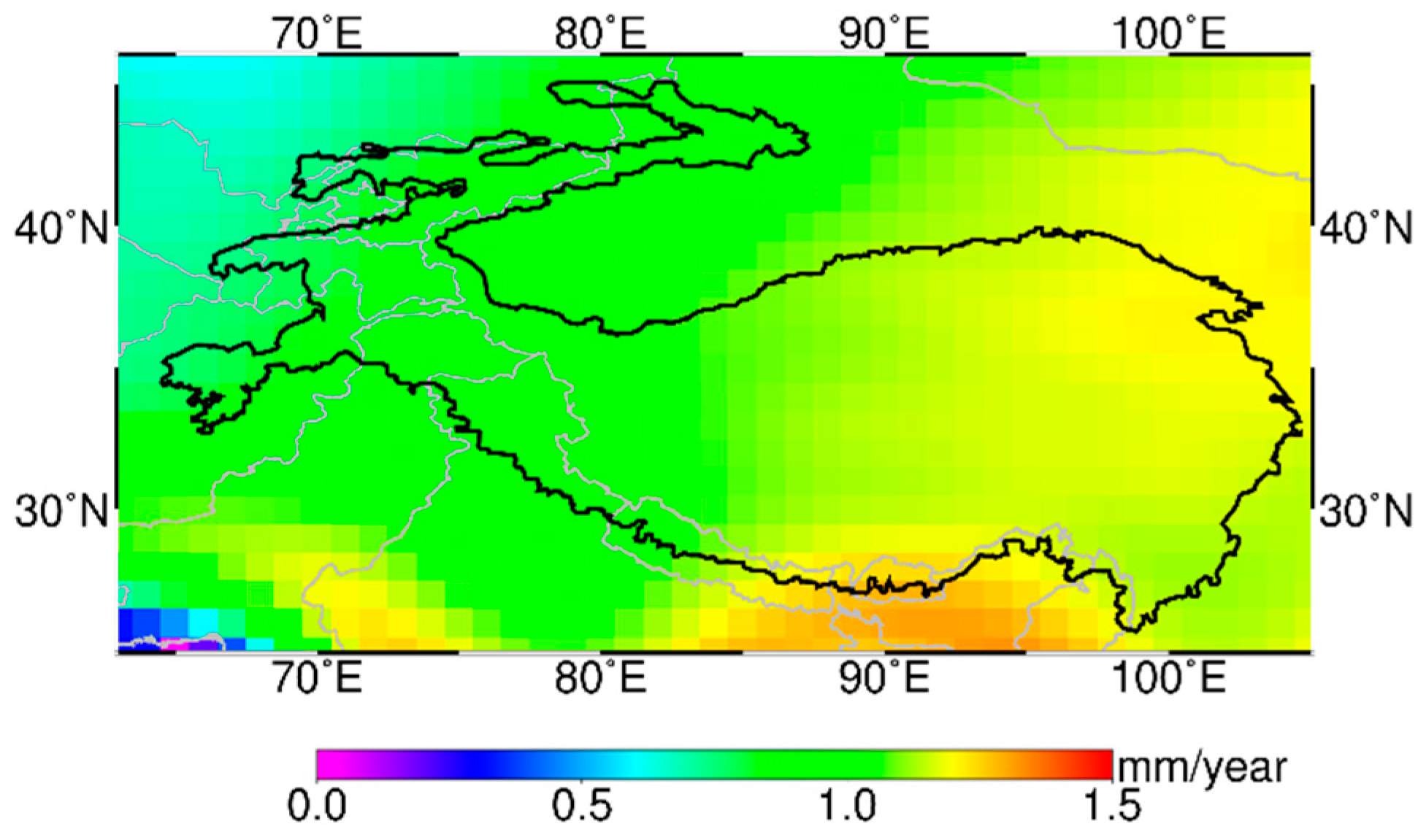
2.4. Leakage Correction
3. Results and Discussion
3.1. MSE Roots
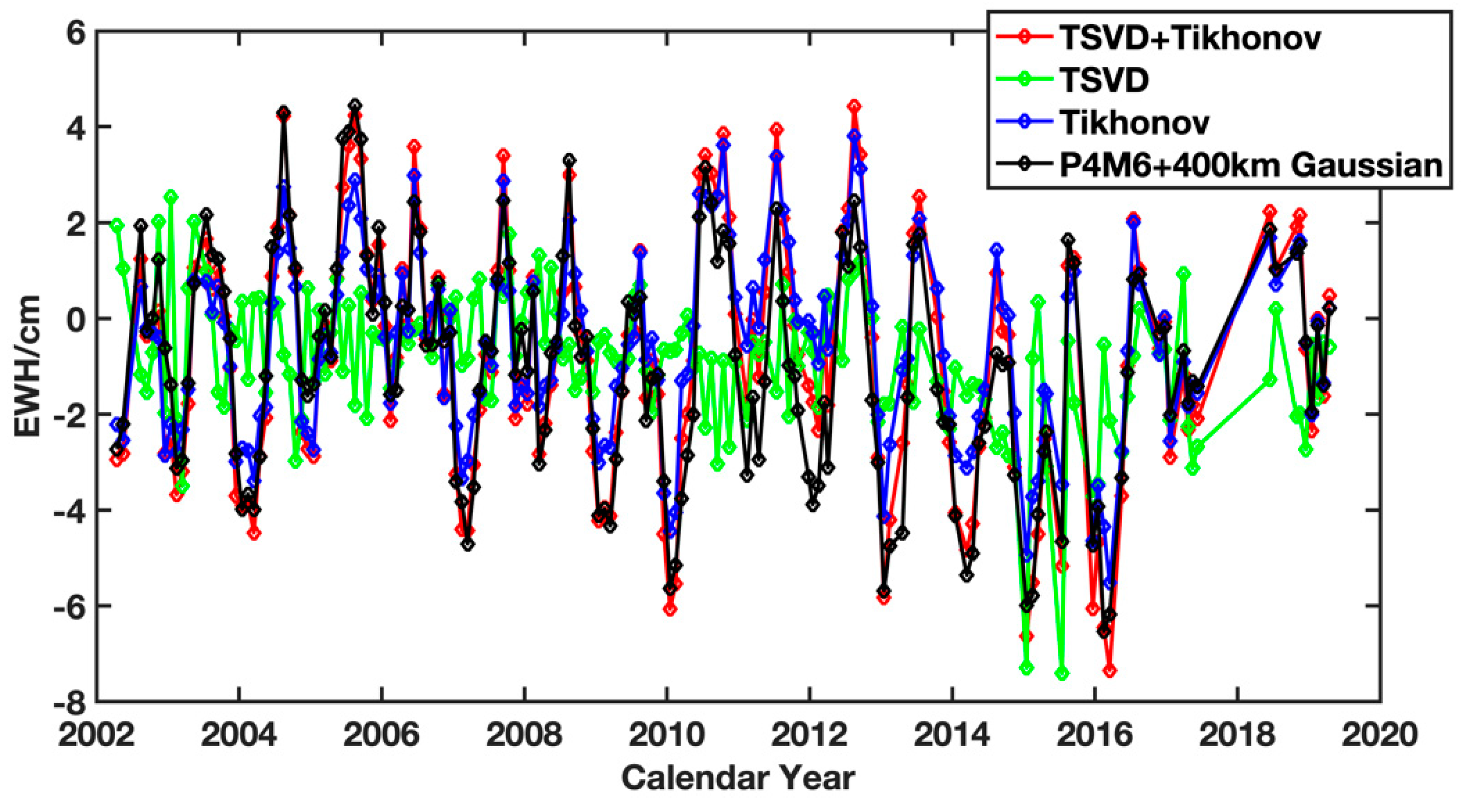
3.2. Total Mass Variations
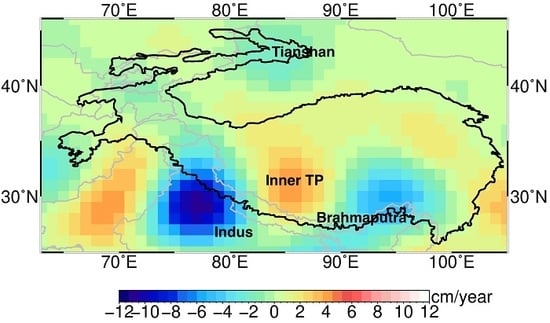
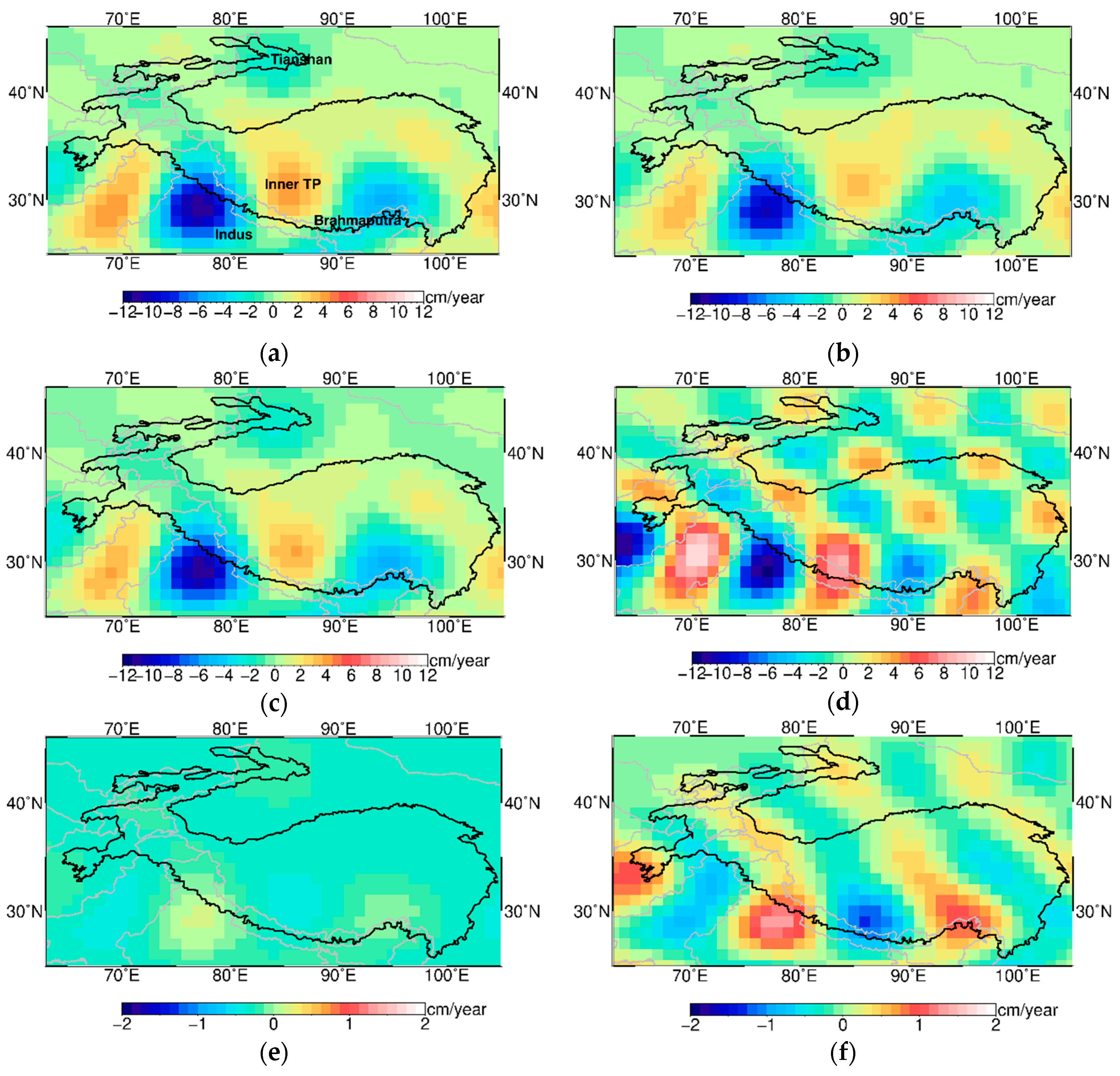
3.3. Mass Variations Distribution
4. Summary
Author Contributions
Funding
Conflicts of Interest
References
- Flechtner, F.; Neumayer, K.-H.; Dahle, C.; Dobslaw, H.; Fagiolini, E.; Raimondo, J.-C.; Güntner, A. What can be expected from the GRACE-FO laser ranging interferometer for earth science applications? Surv. Geophys. 2016, 37, 453–470. [Google Scholar] [CrossRef] [Green Version]
- Luthcke, S.B.; Sabaka, T.J.; Loomis, B.D.; Arendt, A.A.; McCarthy, J.J.; Camp, J. Antarctica, Greenland and Gulf of Alaska land-ice evolution from an iterated GRACE global mascon solution. J. Glaciol. 2013, 59, 613–631. [Google Scholar] [CrossRef]
- Rignot, E.; Velicogna, I.; van den Broeke, M.R.; Monaghan, A.; Lenaerts, J.T.M. Acceleration of the contribution of the Greenland and Antarctic ice sheets to sea level rise: Acceleration of ice sheet loss. Geophys. Res. Lett. 2011, 38, L05503. [Google Scholar] [CrossRef] [Green Version]
- Chambers, D.P. Observing seasonal steric sea level variations with GRACE and satellite altimetry. J. Geophys. Res. 2006, 111. [Google Scholar] [CrossRef]
- Qiu, J. China: The third pole. Nature 2008, 454, 393–396. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Krause, P.; Biskop, S.; Helmschrot, J.; Flügel, W.-A.; Kang, S.; Gao, T. Hydrological system analysis and modelling of the Nam Co basin in Tibet. Adv. Geosci. 2010, 27, 29–36. [Google Scholar] [CrossRef] [Green Version]
- Brun, F.; Berthier, E.; Wagnon, P.; Kääb, A.; Treichler, D. A spatially resolved estimate of High Mountain Asia glacier mass balances, 2000–2016. Nat. Geosci. 2017, 10, 668–673. [Google Scholar] [CrossRef]
- Jacob, T.; Wahr, J.; Pfeffer, W.T.; Swenson, S. Recent contributions of glaciers and ice caps to sea level rise. Nature 2012, 482, 514–518. [Google Scholar] [CrossRef]
- Tapley, B.D.; Schutz, B.E.; Born, G.H. Statistical Orbit Determination; Elsevier Academic Press: Amsterdam, The Netherlands; Boston, MA, USA, 2004; ISBN 978-0-12-683630-1. [Google Scholar]
- Jekeli, C. Alternative Methods to Smooth the Earth’s Gravity Field; Report 327 of Geodetic Science and Surveying; Ohio Ohio State University: Columbus, OH, USA, 1981. [Google Scholar]
- Wahr, J.; Molenaar, M.; Bryan, F. Time variability of the Earth’s gravity field: Hydrological and oceanic effects and their possible detection using GRACE. J. Geophys. Res. Solid Earth 1998, 103, 30205–30229. [Google Scholar] [CrossRef]
- Swenson, S.; Wahr, J. Post-processing removal of correlated errors in GRACE data. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Kusche, J. Approximate decorrelation and non-isotropic smoothing of time-variable GRACE-type gravity field models. J. Geod. 2007, 81, 733–749. [Google Scholar] [CrossRef] [Green Version]
- Kusche, J.; Schmidt, R.; Petrovic, S.; Rietbroek, R. Decorrelated GRACE time-variable gravity solutions by GFZ, and their validation using a hydrological model. J. Geod. 2009, 83, 903–913. [Google Scholar] [CrossRef] [Green Version]
- Tapley, B.D.; Watkins, M.M.; Flechtner, F.; Reigber, C.; Bettadpur, S.; Rodell, M.; Sasgen, I.; Famiglietti, J.S.; Landerer, F.W.; Chambers, D.P.; et al. Contributions of GRACE to understanding climate change. Nat. Clim. Chang. 2019, 9, 358–369. [Google Scholar] [CrossRef] [PubMed]
- Watkins, M.M.; Wiese, D.N.; Yuan, D.-N.; Boening, C.; Landerer, F.W. Improved methods for observing Earth’s time variable mass distribution with GRACE using spherical cap mascons: Improved Gravity Observations from GRACE. J. Geophys. Res. Solid Earth 2015, 120, 2648–2671. [Google Scholar] [CrossRef]
- Sabaka, T.J.; Rowlands, D.D.; Luthcke, S.B.; Boy, J.-P. Improving global mass flux solutions from Gravity Recovery and Climate Experiment (GRACE) through forward modeling and continuous time correlation. J. Geophys. Res. 2010, 115. [Google Scholar] [CrossRef]
- Baur, O.; Sneeuw, N. Assessing Greenland ice mass loss by means of point-mass modeling: A viable methodology. J. Geod. 2011, 85, 607–615. [Google Scholar] [CrossRef]
- Vishwakarma, B.D.; Devaraju, B.; Sneeuw, N. What is the spatial resolution of grace satellite products for hydrology? Remote Sens. 2018, 10, 852. [Google Scholar] [CrossRef] [Green Version]
- Eicker, A.; Schall, J.; Kusche, J. Regional gravity modelling from spaceborne data: Case studies with GOCE. Geophys. J. Int. 2014, 196, 1431–1440. [Google Scholar] [CrossRef] [Green Version]
- Sakumura, C.; Bettadpur, S.; Bruinsma, S. Ensemble prediction and intercomparison analysis of GRACE time-variable gravity field models. Geophys. Res. Lett. 2014, 41, 1389–1397. [Google Scholar] [CrossRef]
- University Of Texas Center For Space Research (UTCSR). GRACE Static Field Geopotential Coefficients CSR Release 6.0 2018. Available online: https://podaac.jpl.nasa.gov/dataset/GRACE_GSM_L2_GRAV_CSR_RL06 (accessed on 24 August 2019). [CrossRef]
- Hofmann-Wellenhof, B.; Moritz, H. Physical Geodesy, 2nd corrected ed.; Springer: Wien, Austria; New York, NY, USA, 2006; ISBN 978-3-211-33544-4. [Google Scholar]
- Cheng, M.; Tapley, B.D.; Ries, J.C. Deceleration in the Earth’s oblateness: J2 VARIATIONS. J. Geophys. Res. Solid Earth 2013, 118, 740–747. [Google Scholar] [CrossRef]
- Loomis, B.D.; Rachlin, K.E.; Wiese, D.N.; Landerer, F.W.; Luthcke, S.B. Replacing GRACE/GRACE-FO with satellite laser ranging: Impacts on Antarctic ice sheet mass change. Geophys. Res. Lett. 2020, 47. [Google Scholar] [CrossRef]
- Wahr, J.; Zhong, S. Computations of the viscoelastic response of a 3-D compressible Earth to surface loading: An application to Glacial Isostatic Adjustment in Antarctica and Canada. Geophys. J. Int. 2013, 192, 557–572. [Google Scholar] [CrossRef]
- Zhang, T.Y.; Jin, S.G. Estimate of glacial isostatic adjustment uplift rate in the Tibetan Plateau from GRACE and GIA models. J. Geodyn. 2013, 72, 59–66. [Google Scholar] [CrossRef]
- Chen, T.; Shen, Y.; Chen, Q. Mass flux solution in the Tibetan Plateau using mascon modeling. Remote Sens 2016, 8, 439. [Google Scholar] [CrossRef] [Green Version]
- Ran, J.; Ditmar, P.; Klees, R.; Farahani, H.H. Statistically optimal estimation of Greenland Ice Sheet mass variations from GRACE monthly solutions using an improved mascon approach. J. Geod. 2017. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Save, H.V. Using Regularization for Error Reduction in GRACE Gravity Estimation. Ph.D. Thesis, The University of Texas at Austin, Austin, TX, USA, 2009. [Google Scholar]
- Hansen, P.C. Truncated singular value decomposition solutions to discrete Ill-posed problems with Ill-determined numerical rank. SIAM J. Sci. Stat. Comput. 1990, 11, 503–518. [Google Scholar] [CrossRef]
- Xu, P. Truncated SVD methods for discrete linear ill-posed problems. Geophys. J. Int. 1998, 135, 505–514. [Google Scholar] [CrossRef]
- Shen, Y.; Xu, P.; Li, B. Bias-corrected regularized solution to inverse ill-posed models. J. Geod. 2012, 86, 597–608. [Google Scholar] [CrossRef]
- Xu, P.; Shen, Y.; Fukuda, Y.; Liu, Y. Variance component estimation in linear inverse Ill-posed models. J. Geod. 2006, 80, 69–81. [Google Scholar] [CrossRef]
- Reichel, L.; Shyshkov, A. A new zero-finder for Tikhonov regularization. BIT Numer. Math. 2008, 48, 627–643. [Google Scholar] [CrossRef]
- Kusche, J.; Klees, R. Regularization of gravity field estimation from satellite gravity gradients. J. Geod. 2002, 76, 359–368. [Google Scholar] [CrossRef]
- Yi, S.; Sun, W. Evaluation of glacier changes in high-mountain Asia based on 10 year GRACE RL05 models: Evaluation of glacier changes. J. Geophys. Res. Solid Earth 2014, 119, 2504–2517. [Google Scholar] [CrossRef]
- Pan, Y.; Shen, W.-B.; Hwang, C.; Liao, C.; Zhang, T.; Zhang, G. Seasonal mass changes and crustal vertical deformations constrained by GPS and GRACE in Northeastern Tibet. Sensors 2016, 16, 1211. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zou, F.; Tenzer, R.; Jin, S. Water storage variations in Tibet from GRACE, ICESat, and hydrological data. Remote Sens. 2019, 11, 1103. [Google Scholar] [CrossRef] [Green Version]
- Jiang, W.; Yuan, P.; Chen, H.; Cai, J.; Li, Z.; Chao, N.; Sneeuw, N. Annual variations of monsoon and drought detected by GPS: A case study in Yunnan, China. Sci. Rep. 2017, 7. [Google Scholar] [CrossRef] [PubMed]
- Long, D.; Chen, X.; Scanlon, B.R.; Wada, Y.; Hong, Y.; Singh, V.P.; Chen, Y.; Wang, C.; Han, Z.; Yang, W. Have GRACE satellites overestimated groundwater depletion in the Northwest India Aquifer? Sci. Rep. 2016, 6. [Google Scholar] [CrossRef] [PubMed]
- Bettinelli, P.; Avouac, J.-P.; Flouzat, M.; Jouanne, F.; Bollinger, L.; Willis, P.; Chitrakar, G.R. Plate motion of india and interseismic strain in the Nepal Himalaya from GPS and DORIS measurements. J. Geod. 2006, 80, 567–589. [Google Scholar] [CrossRef]
- Gardner, A.S.; Moholdt, G.; Wouters, B.; Wolken, G.J.; Burgess, D.O.; Sharp, M.J.; Cogley, J.G.; Braun, C.; Labine, C. Sharply increased mass loss from glaciers and ice caps in the Canadian Arctic Archipelago. Nature 2011, 473, 357–360. [Google Scholar] [CrossRef]
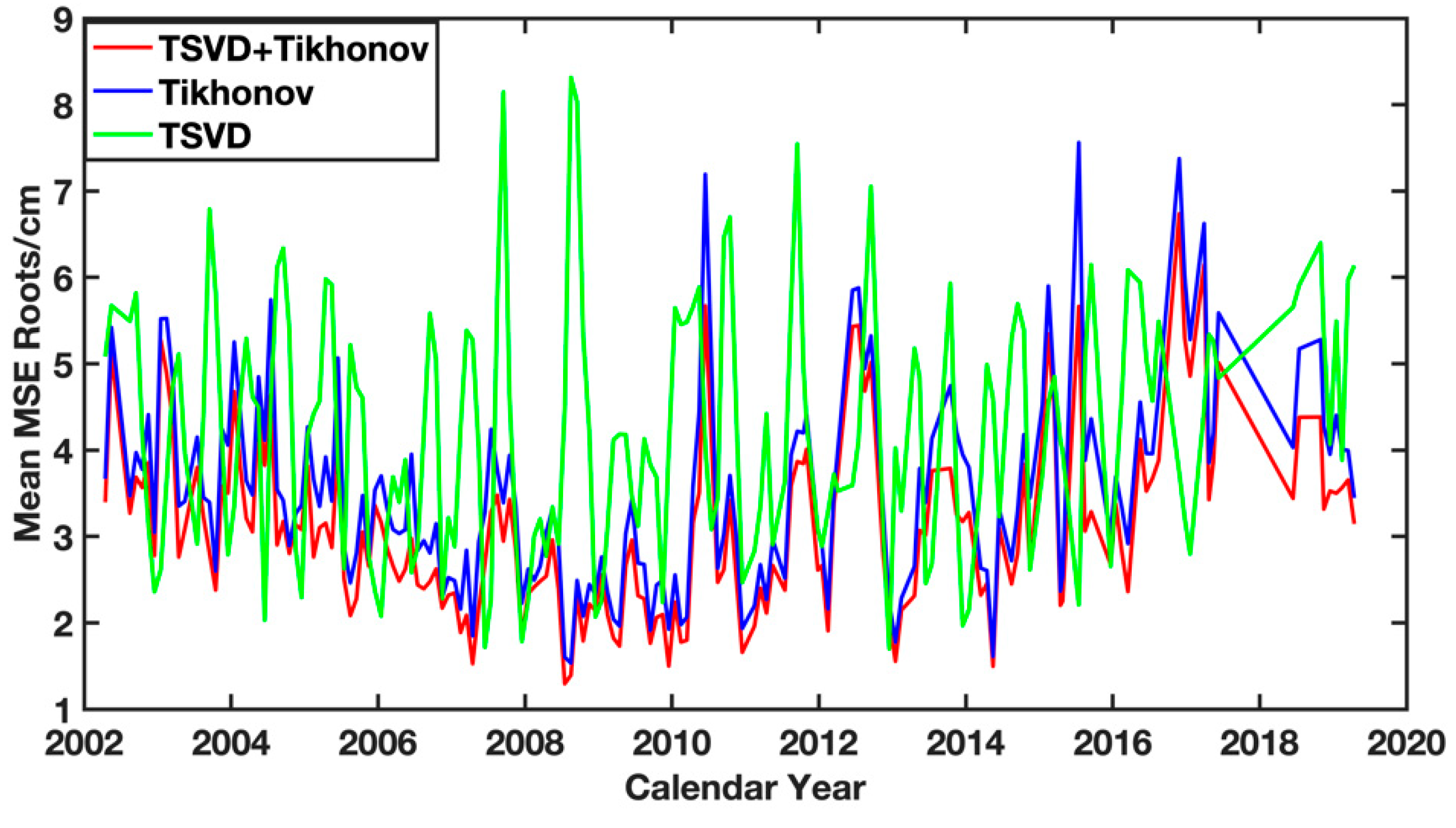
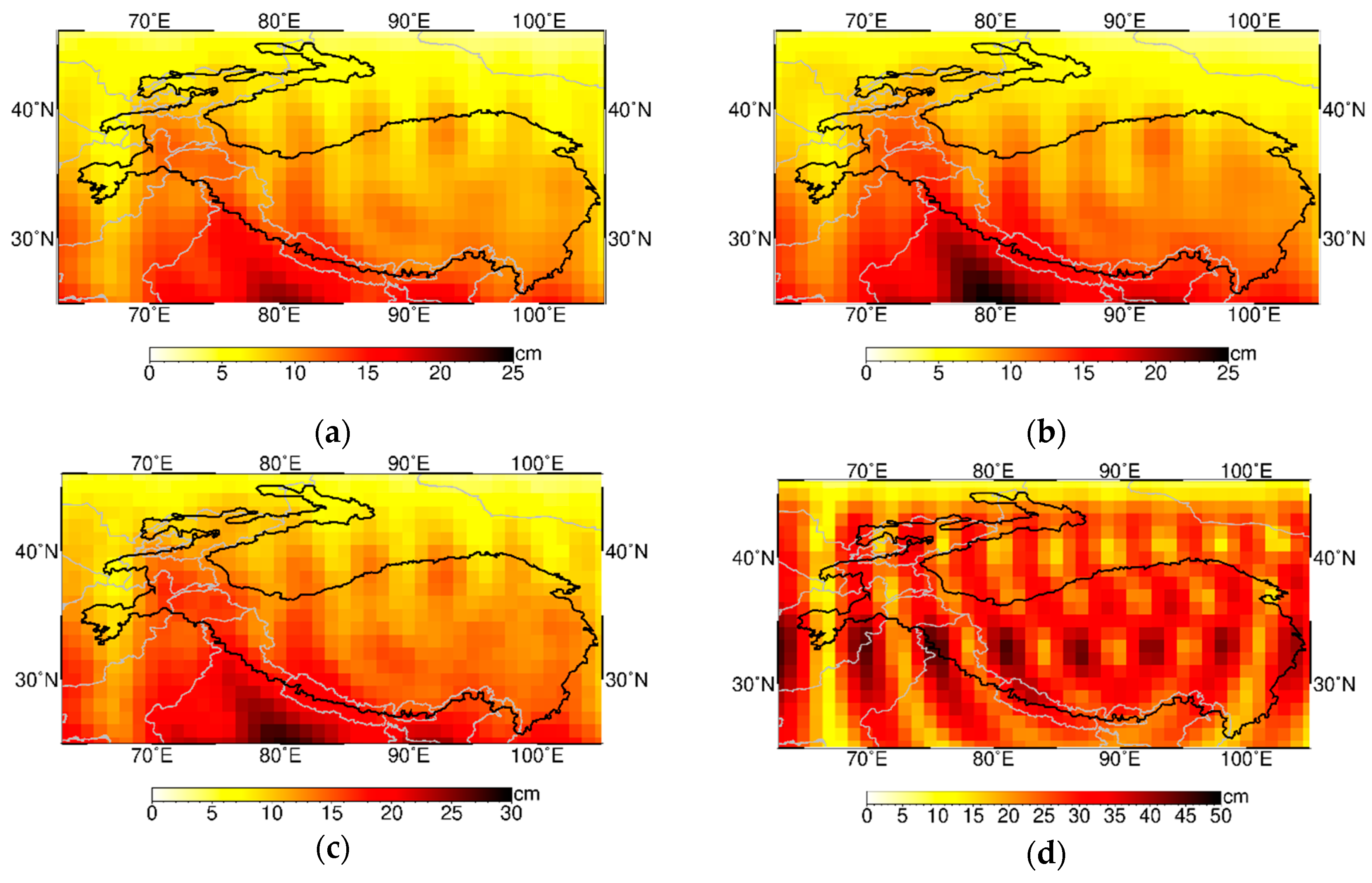
| MSE Roots | Maximum | Minimum | Mean |
|---|---|---|---|
| Tikhonov + TSVD | 6.74 | 1.29 | 3.08 |
| TSVD | 8.31 | 1.70 | 4.23 |
| Tikhonov | 7.56 | 1.53 | 3.53 |
| Method | Trend (Gt/year) | Annual | RMSE (cm) | RMS Ratio | |
|---|---|---|---|---|---|
| Amplitude(cm) | Phase (°) | ||||
| Tikhonov + TSVD | −5.6 ± 4.2 | 2.8 ± 0.5 | 226.8 ± 14.4 | 1.9 | 1.21 |
| TSVD | −8.9 ± 5.9 | 2.2 ± 1.9 | 262.6 ± 34.3 | 1.6 | 0.45 |
| Tikhonov | −6.8 ± 5.2 | 2.3 ± 0.5 | 220.2 ± 26.4 | 2.2 | 0.78 |
| P4M6 + 400 km | −8.6 ± 5.8 | 2.3 ± 0.6 | 223.1 ± 23.5 | 1.8 | 1.16 |
| Method | Time Intervals | GRACE Data | Trend (Gt/year) | Trend of Combined Method (Gt/year) |
|---|---|---|---|---|
| TSVD + Tikhonov | Apr 2002–Apr 2019 | GFZ Release 06 | −5.9 ± 4.3 | −5.6 ± 4.2 |
| Jacob et al. [8] | Jan 2003–Dec 2010 | CSR Release 04 | −4 ± 20 | −2.3 ± 5.7 |
| Yi and Sun [35] | Jan 2003–Dec 2012 | CSR Release 05 | −7.8 ± 5.7 | −4.6 ± 5.3 |
| Zou et al. [37] | Aug 2002–Dec 2016 | CSR Release 05 | −6.2 ± 1.7 | −7.6 ± 3.8 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, T.; Kusche, J.; Shen, Y.; Chen, Q. A Combined Use of TSVD and Tikhonov Regularization for Mass Flux Solution in Tibetan Plateau. Remote Sens. 2020, 12, 2045. https://doi.org/10.3390/rs12122045
Chen T, Kusche J, Shen Y, Chen Q. A Combined Use of TSVD and Tikhonov Regularization for Mass Flux Solution in Tibetan Plateau. Remote Sensing. 2020; 12(12):2045. https://doi.org/10.3390/rs12122045
Chicago/Turabian StyleChen, Tianyi, Jürgen Kusche, Yunzhong Shen, and Qiujie Chen. 2020. "A Combined Use of TSVD and Tikhonov Regularization for Mass Flux Solution in Tibetan Plateau" Remote Sensing 12, no. 12: 2045. https://doi.org/10.3390/rs12122045
APA StyleChen, T., Kusche, J., Shen, Y., & Chen, Q. (2020). A Combined Use of TSVD and Tikhonov Regularization for Mass Flux Solution in Tibetan Plateau. Remote Sensing, 12(12), 2045. https://doi.org/10.3390/rs12122045