Deep Learning and Adaptive Graph-Based Growing Contours for Agricultural Field Extraction
Abstract
1. Introduction
2. Data and Materials
2.1. Study Areas
2.2. Satellite Imagery
2.3. Reference Data
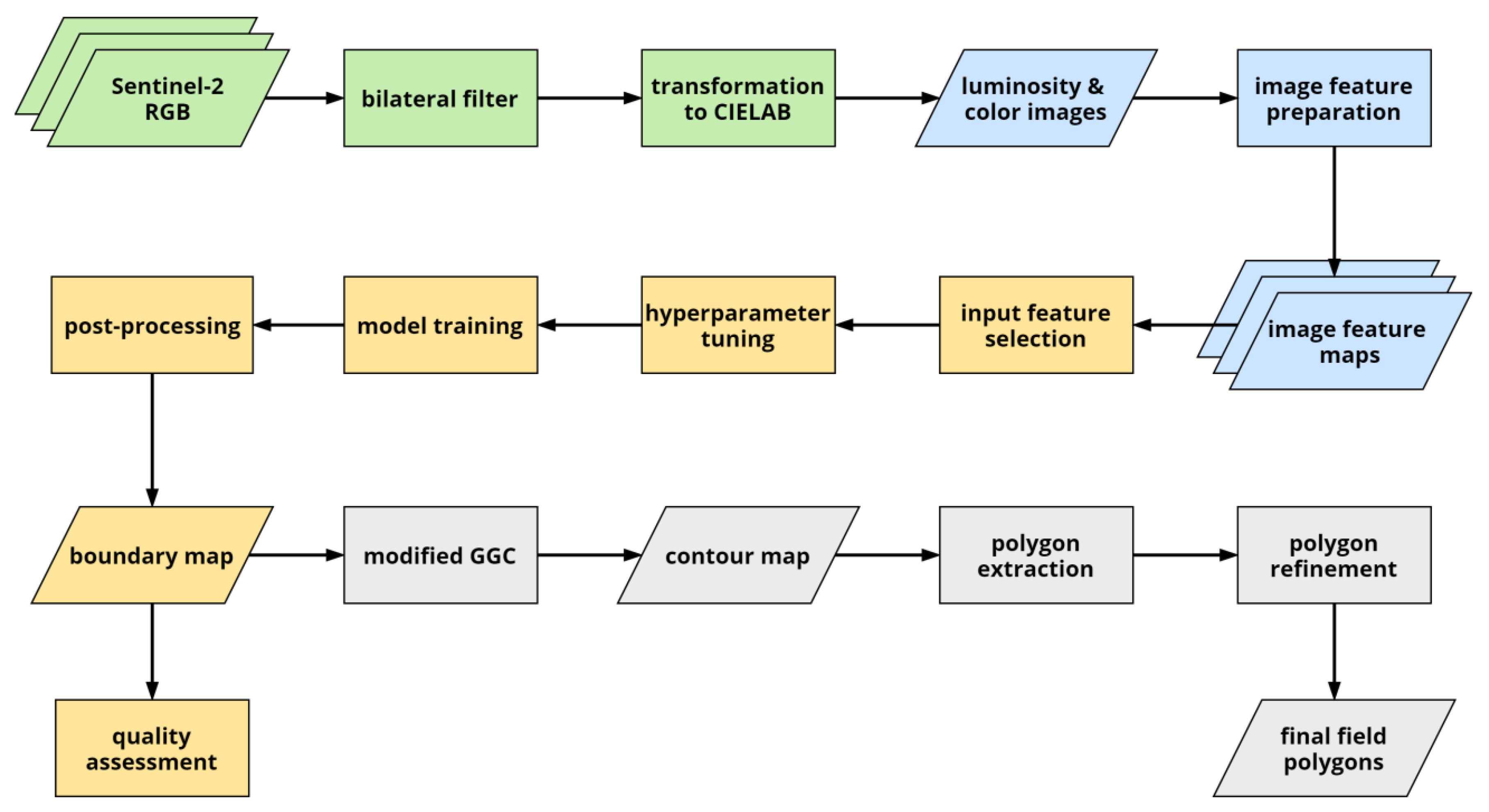
3. Methodology
3.1. Image Feature Preparation
3.1.1. Image Gradient
3.1.2. Local Statistics
3.1.3. Hessian Matrix
3.1.4. Second-Order texture Metrics
3.1.5. Angular Dispersion
3.1.6. Homogeneity Measures
3.1.7. Local Cues
3.2. Boundary Detection
3.2.1. Dataset Preparation
3.2.2. Model Development Setup
3.2.3. Input Feature Selection
3.2.4. Hyperparameter Tuning and Model Training
3.2.5. Boundary Map Post-Processing
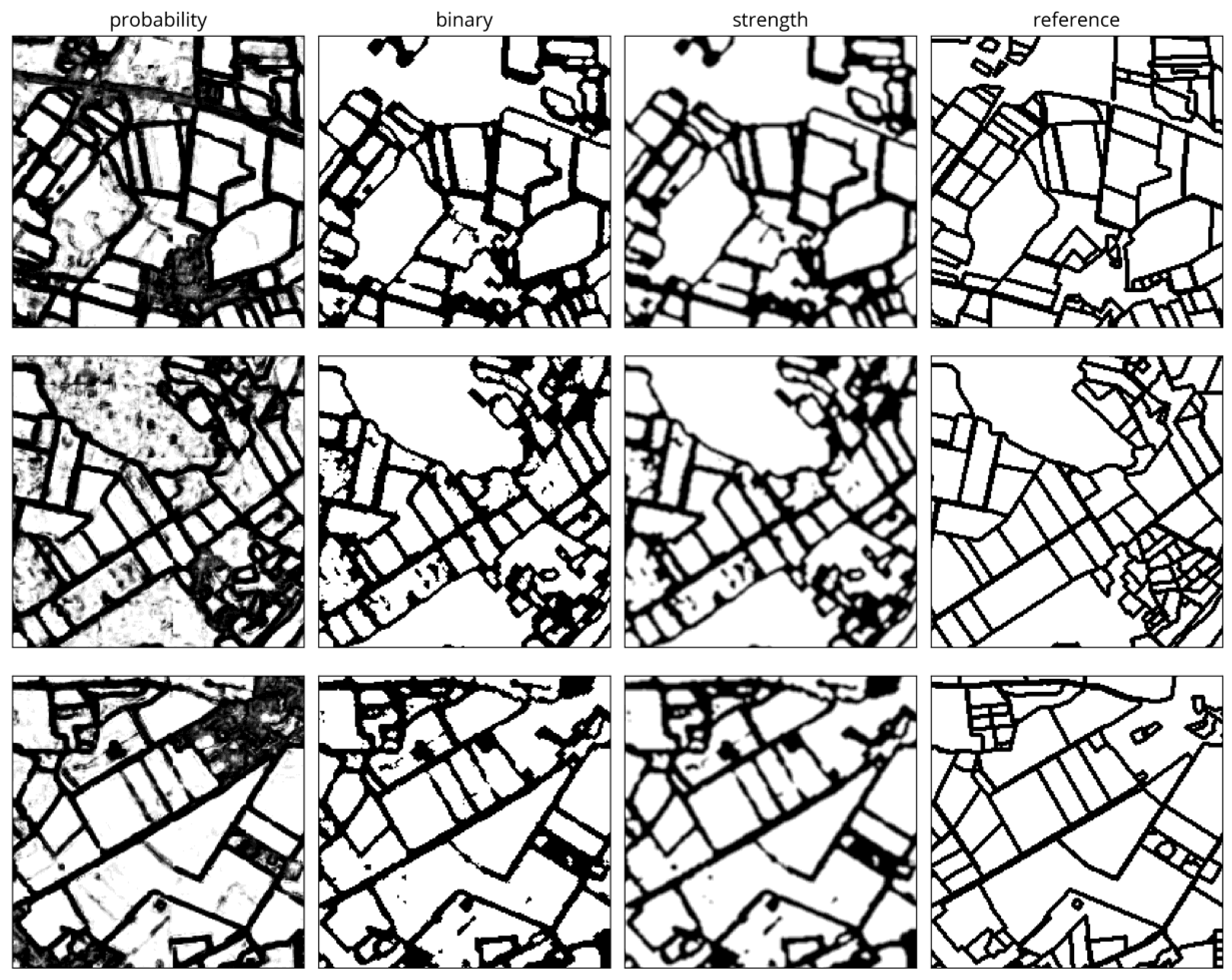
3.2.6. Quality Assessment
3.3. Field Extraction
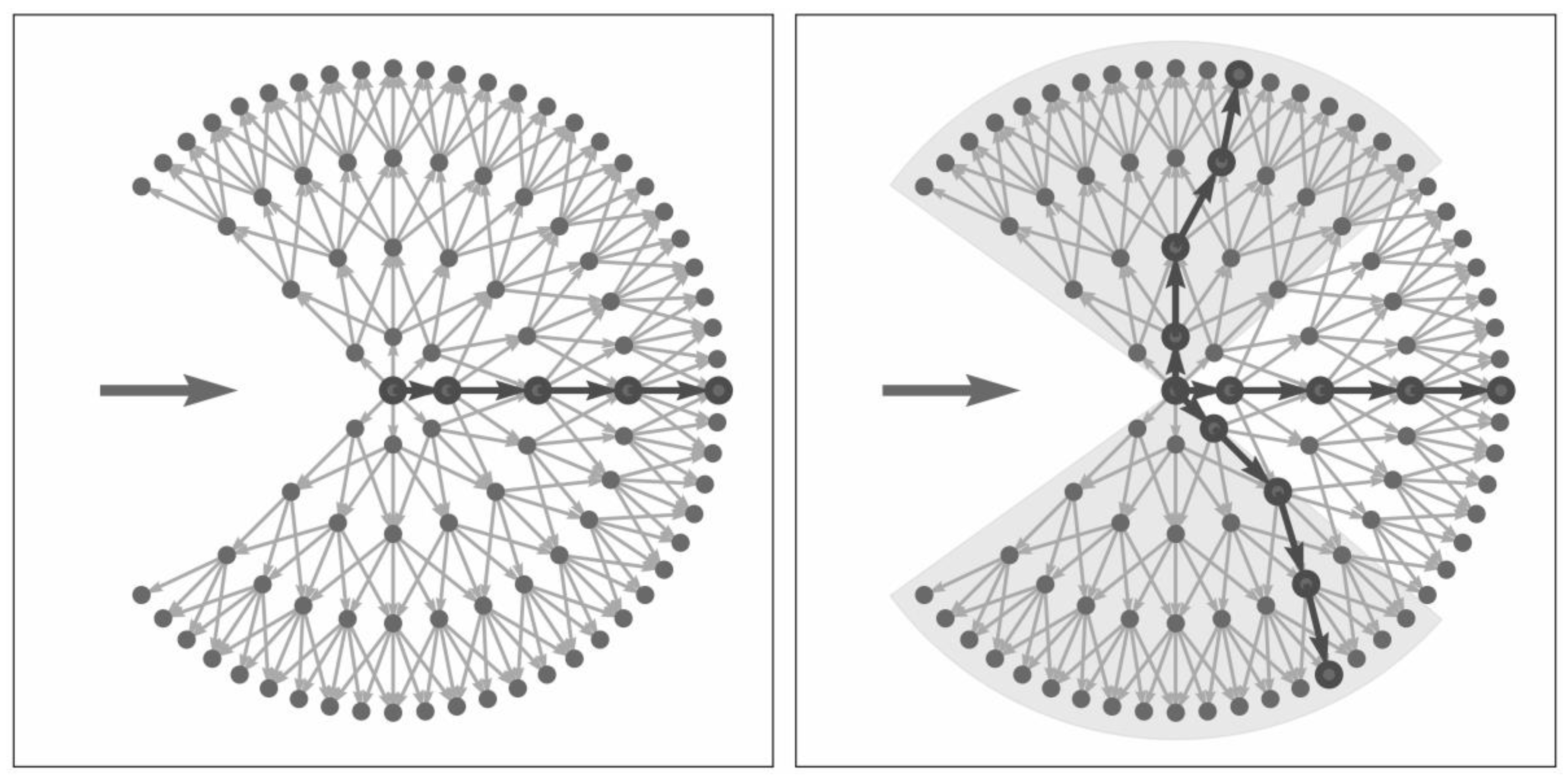
3.3.1. The Graph-Based Growing Contours Method
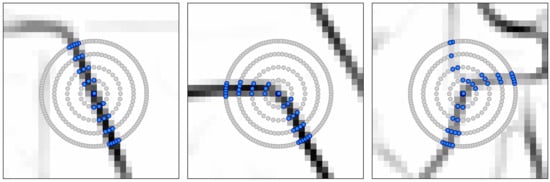
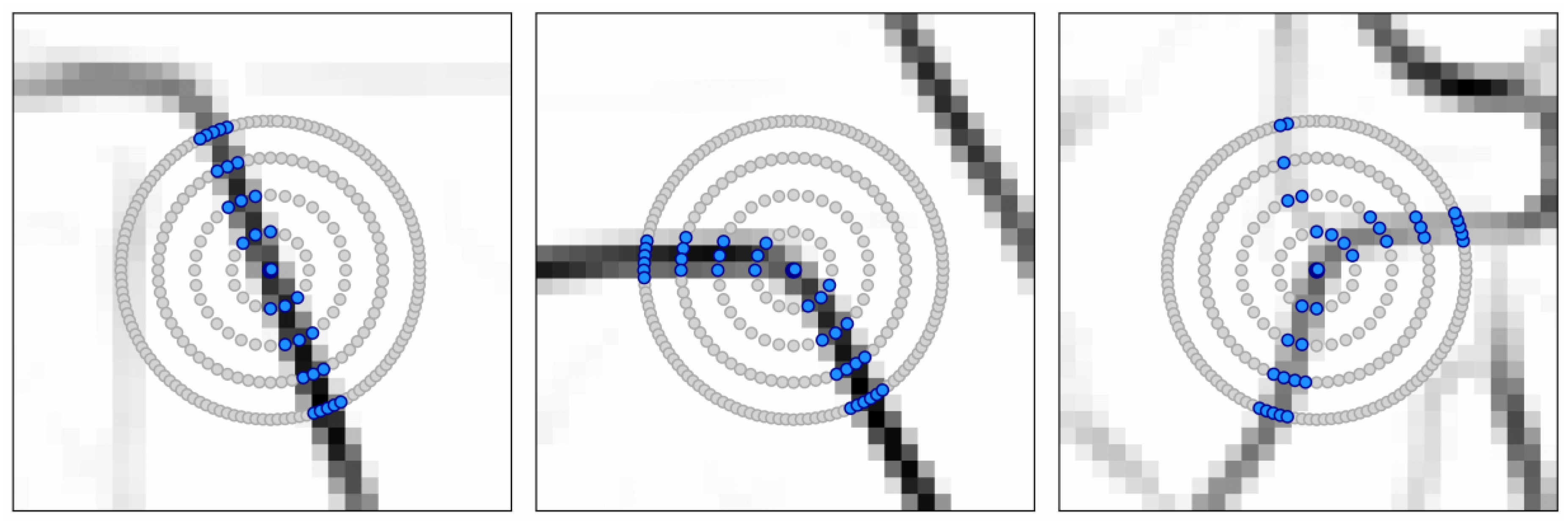
3.3.2. Modifications and Adaptive Masking
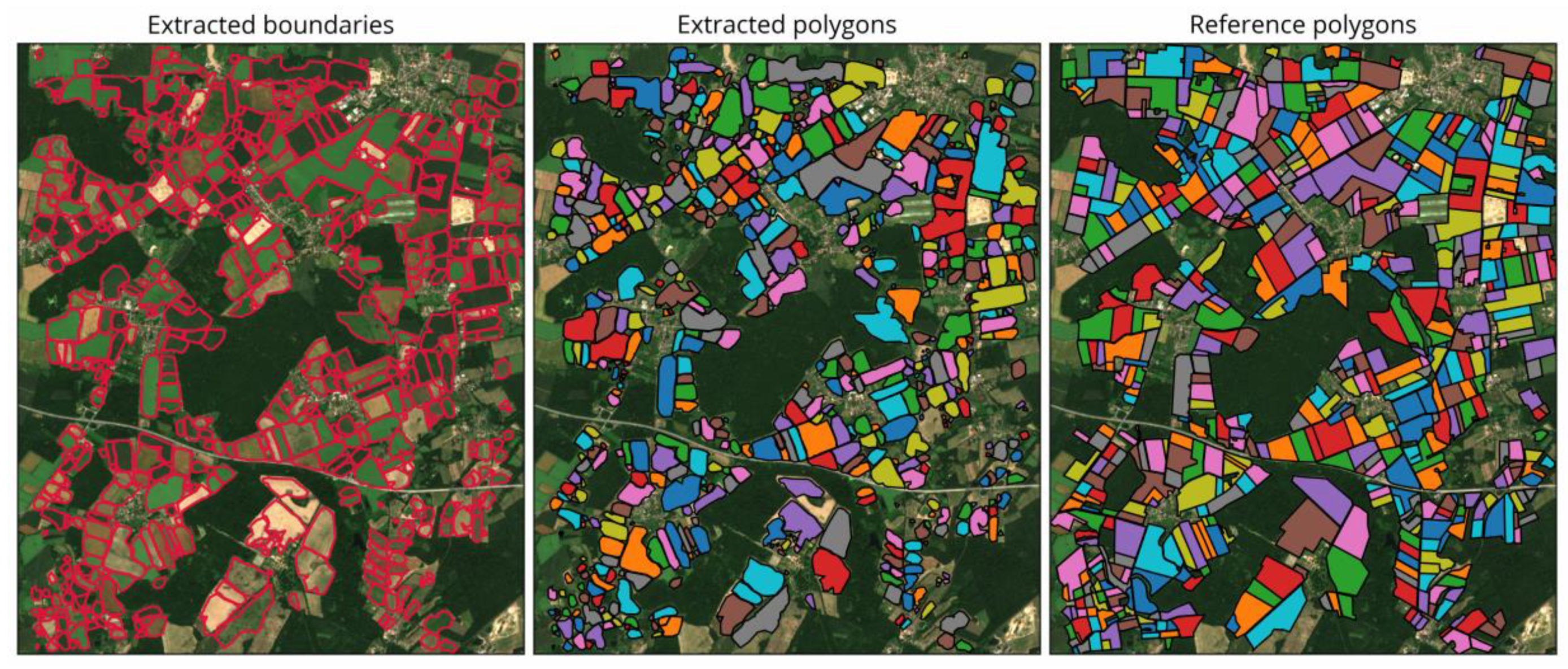
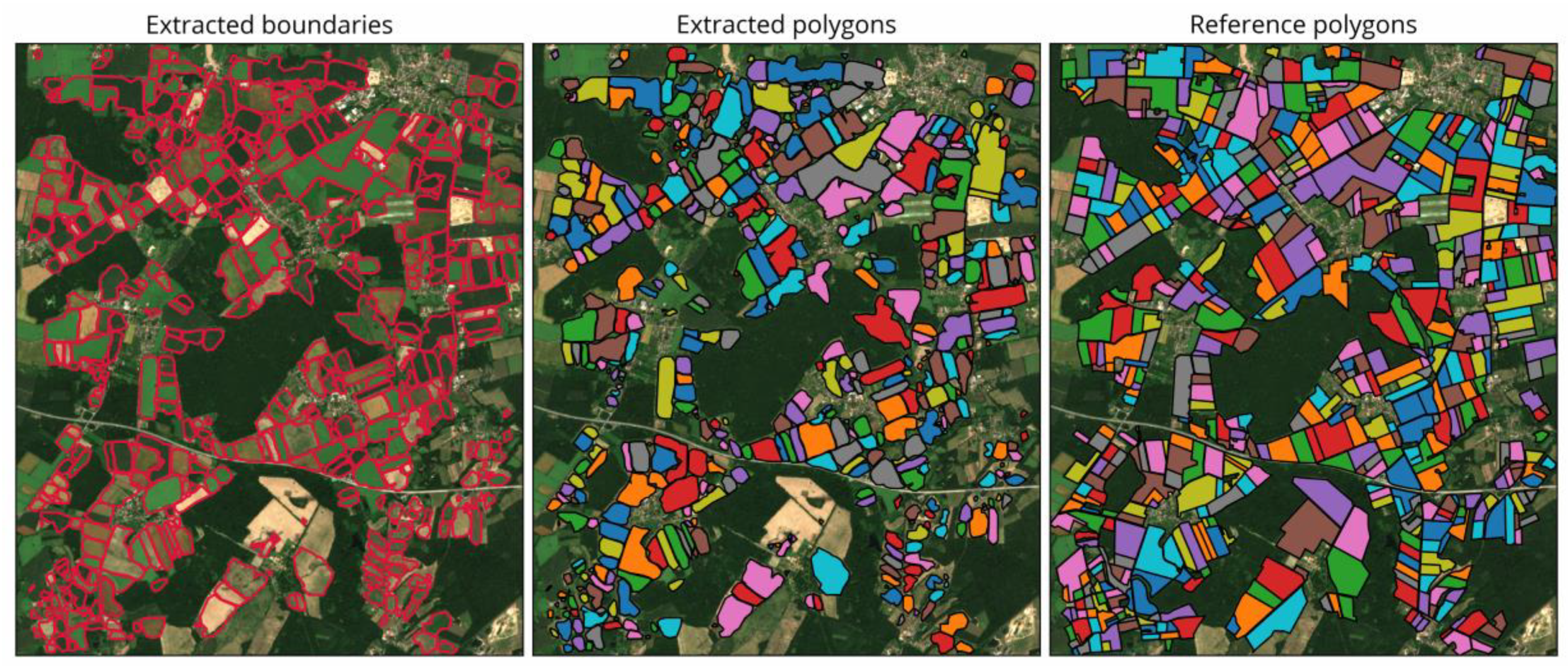
3.3.3. Field Polygon Extraction
4. Results
4.1. Boundary Detection
4.1.1. Input Feature Importance
4.1.2. Performance Metrics
4.1.3. Visual Comparison
4.2. Field Extraction Results
4.2.1. Visual Comparison
4.2.2. Processing Speed and Upscaling
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- García-Pedrero, A.; Gonzalo-Martín, C.; Lillo-Saavedra, M. A machine learning approach for agricultural parcel delineation through agglomerative segmentation. Int. J. Remote Sens. 2017, 38, 1809–1819. [Google Scholar] [CrossRef]
- Rahman, M.S.; Di, L.; Yu, Z.; Yu, E.G.; Tang, J.; Lin, L.; Zhang, C.; Gaigalas, J. Crop Field Boundary Delineation using Historical Crop Rotation Pattern. In Proceedings of the 8th International Conference on Agro-Geoinformatics (Agro-Geoinformatics), Istanbul, Turkey, 16–19 June 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Turker, M.; Kok, E.H. Field-based sub-boundary extraction from remote sensing imagery using perceptual grouping. ISPRS J. Photogramm. Remote Sens. 2013, 79, 106–121. [Google Scholar] [CrossRef]
- Sagris, V.; Devos, W. LPIS Core Conceptual Model: Methodology for Feature Catalogue and Application Schema; OPOCE: Luxembourg, 2008. [Google Scholar]
- Inan, H.I.; Sagris, V.; Devos, W.; Milenov, P.; van Oosterom, P.; Zevenbergen, J. Data model for the collaboration between land administration systems and agricultural land parcel identification systems. J. Environ. Manag. 2010, 91, 2440–2454. [Google Scholar] [CrossRef]
- European Court of Auditors. The Land Parcel Identification System: A Useful Tool to Determine the Eligibility of Agricultural Land—But Its Management Could Be further Improved; European Union: Luxembourg, 2016; ISBN 9789287259677. [Google Scholar]
- Jégo, G.; Pattey, E.; Liu, J. Using Leaf Area Index, retrieved from optical imagery, in the STICS crop model for predicting yield and biomass of field crops. F. Crop. Res. 2012, 131, 63–74. [Google Scholar] [CrossRef]
- Verrelst, J.; Rivera, J.P.; Leonenko, G.; Alonso, L.; Moreno, J. Optimizing LUT-based RTM inversion for semiautomatic mapping of crop biophysical parameters from sentinel-2 and -3 data: Role of cost functions. IEEE Trans. Geosci. Remote Sens. 2014, 52, 257–269. [Google Scholar] [CrossRef]
- Liu, J.; Pattey, E.; Miller, J.R.; McNairn, H.; Smith, A.; Hu, B. Estimating crop stresses, aboveground dry biomass and yield of corn using multi-temporal optical data combined with a radiation use efficiency model. Remote Sens. Environ. 2010, 114, 1167–1177. [Google Scholar] [CrossRef]
- Belgiu, M.; Csillik, O. Sentinel-2 cropland mapping using pixel-based and object-based time-weighted dynamic time warping analysis. Remote Sens. Environ. 2018, 204, 509–523. [Google Scholar] [CrossRef]
- Kussul, N.; Lemoine, G.; Gallego, F.J.; Skakun, S.V.; Lavreniuk, M.; Shelestov, A.Y. Parcel-Based Crop Classification in Ukraine Using Landsat-8 Data and Sentinel-1A Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 2500–2508. [Google Scholar] [CrossRef]
- Peña, J.M.; Gutiérrez, P.A.; Hervás-Martínez, C.; Six, J.; Plant, R.E.; López-Granados, F. Object-based image classification of summer crops with machine learning methods. Remote Sens. 2014, 6, 5019–5041. [Google Scholar] [CrossRef]
- Watkins, B.; van Niekerk, A. A comparison of object-based image analysis approaches for field boundary delineation using multi-temporal Sentinel-2 imagery. Comput. Electron. Agric. 2019, 158, 294–302. [Google Scholar] [CrossRef]
- Yan, L.; Roy, D.P. Automated crop field extraction from multi-temporal Web Enabled Landsat Data. Remote Sens. Environ. 2014, 144, 42–64. [Google Scholar] [CrossRef]
- Tiwari, P.S.; Pande, H.; Kumar, M.; Dadhwal, V.K. Potential of IRS P-6 LISS IV for agriculture field boundary delineation. J. Appl. Remote Sens. 2009, 3, 033528. [Google Scholar] [CrossRef]
- Debats, S.R.; Luo, D.; Estes, L.D.; Fuchs, T.J.; Caylor, K.K. A generalized computer vision approach to mapping crop fields in heterogeneous agricultural landscapes. Remote Sens. Environ. 2016, 179, 210–221. [Google Scholar] [CrossRef]
- Da Costa, J.P.; Michelet, F.; Germain, C.; Lavialle, O.; Grenier, G. Delineation of vine parcels by segmentation of high resolution remote sensed images. Precis. Agric. 2007, 8, 95–110. [Google Scholar] [CrossRef]
- El-Sayed, M.A.; Estaitia, Y.A.; Khafagy, M.A. Automated Edge Detection Using Convolutional Neural Network. Int. J. Adv. Comput. Sci. Appl. 2013, 4, 11–17. [Google Scholar] [CrossRef]
- Kemker, R.; Salvaggio, C.; Kanan, C. Algorithms for semantic segmentation of multispectral remote sensing imagery using deep learning. ISPRS J. Photogramm. Remote Sens. 2018, 145, 60–77. [Google Scholar] [CrossRef]
- Längkvist, M.; Kiselev, A.; Alirezaie, M.; Loutfi, A. Classification and segmentation of satellite orthoimagery using convolutional neural networks. Remote Sens. 2016, 8, 329. [Google Scholar] [CrossRef]
- Masoud, K.M.; Persello, C.; Tolpekin, V.A. Delineation of Agricultural Field Boundaries from Sentinel-2 Images Using a Novel Super-Resolution Contour Detector Based on Fully Convolutional Networks. Remote Sens. 2019, 12, 59. [Google Scholar] [CrossRef]
- Waldner, F.; Diakogiannis, F.I. Deep learning on edge: Extracting field boundaries from satellite images with a convolutional neural network. Remote Sens. Environ. 2020, 245, 111741. [Google Scholar] [CrossRef]
- Persello, C.; Tolpekin, V.A.; Bergado, J.R.; de By, R.A. Delineation of agricultural fields in smallholder farms from satellite images using fully convolutional networks and combinatorial grouping. Remote Sens. Environ. 2019, 231. [Google Scholar] [CrossRef]
- Kamilaris, A.; Prenafeta-Boldú, F.X. Deep learning in agriculture: A survey. Comput. Electron. Agric. 2018, 147, 70–90. [Google Scholar] [CrossRef]
- Wagner, M.P.; Oppelt, N. Extracting Agricultural Fields from Remote Sensing Imagery Using Graph-Based Growing Contours. Remote Sens. 2020, 12, 1205. [Google Scholar] [CrossRef]
- Bishop, C. Pattern Recognition and Machine Learning, 1st ed.; Joran, M., Kleinberg, J., Schölkopf, B., Eds.; Springer: New York, NY, USA, 2006; ISBN 9780387310732. [Google Scholar]
- Kottek, M.; Grieser, J.; Beck, C.; Rudolf, B.; Rubel, F. World Map of the Köppen-Geiger climate classification updated. Meteorol. Zeitschrift 2006, 15, 259–263. [Google Scholar] [CrossRef]
- Statistisches Amt für Hamburg und Schleswig-Holstein. Die Bodennutzung in Schleswig-Holstein; Statistisches Amt für Hamburg und Schleswig-Holstein: Hamburg, Germany, 2019. [Google Scholar]
- Tomasi, C.; Manduchi, R. Bilateral filtering for gray and color images. In Proceedings of the Sixth International Conference on Computer Vision, Bombay, India, 4–7 January 1998; pp. 839–846. [Google Scholar] [CrossRef]
- Arbeitsgemeinschaft der Vermessungsverwaltungen der Länder der Bundesrepublik Deutschland (AdV). Produktspezifikation für ALKIS-Daten im Format Shape; AdV: Berlin, Germany, 2016. [Google Scholar]
- NIST. NIST/SEMATECH e-Handbook of Statistical Methods. Available online: http://www.itl.nist.gov/div898/handbook/ (accessed on 15 May 2020).
- Meijering, E.; Jacob, M.; Sarria, J.-C.F.; Steiner, P.; Hirling, H.; Unser, M. Design and validation of a tool for neurite tracing and analysis in fluorescence microscopy images. Cytometry 2004, 58A, 167–176. [Google Scholar] [CrossRef] [PubMed]
- Ando, S. Image field categorization and edge/corner detection from gradient covariance. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 179–190. [Google Scholar] [CrossRef]
- Sato, Y.; Nakajima, S.; Shiraga, N.; Atsumi, H.; Yoshida, S.; Koller, T.; Gerig, G.; Kikinis, R. Three-dimensional multi-scale line filter for segmentation and visualization of curvilinear structures in medical images. Med. Image Anal. 1998, 2, 143–168. [Google Scholar] [CrossRef]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I. Textural Features for Image Classification. IEEE Trans. Syst. Man. Cybern. 1973, SMC-3, 610–621. [Google Scholar] [CrossRef]
- Gregson, P.H. Using Angular Dispersion of Gradient Direction for Detecting Edge Ribbons. IEEE Trans. Pattern Anal. Mach. Intell. 1993, 15, 682–696. [Google Scholar] [CrossRef]
- Aganj, I.; Lenglet, C.; Jahanshad, N.; Yacoub, E.; Harel, N.; Thompson, P.M.; Sapiro, G. A Hough transform global probabilistic approach to multiple-subject diffusion MRI tractography. Med. Image Anal. 2011, 15, 414–425. [Google Scholar] [CrossRef]
- Martin, D.R.; Fowlkes, C.C.; Malik, J. Learning to detect natural image boundaries using brightness and texture. IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 530–549. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning, 2nd ed.; Springer Science+Business Media: New York, NY, USA, 2009. [Google Scholar]
- Robbins, H.; Monro, S. A Stochastic Approximation Method. Ann. Math. Stat. 1951, 22, 400–407. [Google Scholar] [CrossRef]
- Nair, V.; Hinton, G.E. Rectified Linear Units Improve Restricted Boltzmann Machines. In Proceedings of the 27th International Conference on Machine Learning, Haifa, Israel, 21–24 June 2010. [Google Scholar]
- Weigand, M.; Staab, J.; Wurm, M.; Taubenböck, H. Spatial and semantic effects of LUCAS samples on fully automated land use/land cover classification in high-resolution Sentinel-2 data. Int. J. Appl. Earth Obs. Geoinf. 2020, 88, 102065. [Google Scholar] [CrossRef]
- Büttner, G.; Kosztra, B.; Soukup, T.; Sousa, A.; Langanke, T. CLC2018 Technical Guidelines; European Environment Agency: Vienna, Austria, 2017. [Google Scholar]
- Velasco, F.A.; Marroquin, J.L. Growing snakes: Active contours for complex topologies. Pattern Recognit. 2003, 36, 475–482. [Google Scholar] [CrossRef]
- Kass, M.; Witkin, A.; Terzopoulos, D. Snakes: Active contour models. Int. J. Comput. Vis. 1988, 1, 321–331. [Google Scholar] [CrossRef]
- Yiu, P. The uses of homogeneous barycentric coordinates in plane Euclidean geometry. Int. J. Math. Educ. Sci. Technol. 2000, 31, 569–578. [Google Scholar] [CrossRef]
- Otsu, N. A Threshold Selection Method from Gray-Level Histograms. IEEE Trans. Syst. Man Cybernet. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Deng, G.; Cahill, L.W. An Adaptive Gaussian Filter For Noise Reduction and Edge Detection. In Proceedings of the IEEE Conference Record Nuclear Science Symposium and Medical Imaging Conference, 31 October–6 November 1993, San Francisco, CA, USA; pp. 1615–1619.
- Douglas, D.H.; Peucker, T.K. Algorithms for the Reduction of the Number of Points Required to Represent a Digitized Line or Its Caricature. Cartogr. Int. J. Geogr. Inf. Geovisualization 1973, 10, 112–122. [Google Scholar] [CrossRef]
- Ramer, U. An iterative procedure for the polygonal approximation of plane curves. Comput. Graph. Image Process. 1972, 1, 244–256. [Google Scholar] [CrossRef]


| Study Area | Total Extent | Field Sizes | Field Count |
|---|---|---|---|
| 1 | ~13.5 × 12.4 km2 | ~0.9 to 75 ha | ~1400 |
| 2 | ~9.2 × 7.5 km2 | ~0.8 to 50 ha | ~600 |
| Feature Group | Feature | ||
|---|---|---|---|
| G1 | image gradient (l) | F1 | gradient magnitude (l) |
| G2 | image gradient (a, b) | F2 | gradient magnitude (a, b) |
| G3 | local statistics (l) | F3 | variance (l) |
| F4 | skewness (l) | ||
| F5 | kurtosis (l) | ||
| G4 | local statistics (a, b) | F6 | variance (a, b) |
| F7 | skewness (a, b) | ||
| F8 | kurtosis (a, b) | ||
| G5 | Hessian matrix (l) | F9 | eigenvalue along ridge (l) |
| F10 | eigenvalue across ridge (l) | ||
| G6 | Hessian matrix (a, b) | F11 | eigenvalue along ridge (a, b) |
| F12 | eigenvalue across ridge (a, b) | ||
| G7 | texture metrics (l) | F13 | contrast (l) |
| F14 | correlation (l) | ||
| F15 | asm (l) | ||
| F16 | homogeneity (l) | ||
| G8 | texture metrics (a, b) | F17 | contrast (a, b) |
| F18 | correlation (a, b) | ||
| F19 | asm (a, b) | ||
| F20 | homogeneity (a, b) | ||
| G9 | angular dispersion (l) | F21 | modified angular dispersion (l) |
| G10 | angular dispersion (a, b) | F22 | modified angular dispersion (a, b) |
| G11 | homogeneity measures (l) | F23 | PEG (l) |
| F24 | QEG (l) | ||
| G12 | homogeneity measures (a, b) | F25 | PEG (a, b) |
| F26 | QEG (a, b) | ||
| G13 | local cues (l) | F27 | brightness gradient (l) |
| F28 | texture gradient (l) | ||
| G14 | local cues color (a, b) | F29 | color gradient (a, b) |
| Hyperparameter | Considered Values |
|---|---|
| Number of hidden layers | 2, 3, 4, 5 |
| Number of nodes per hidden layer | 15, 20, 25, 30, 35, 40, 45, 50 |
| Type of activation function | Sigmoid, ReLU |
| Learning rate | 0.01, 0.001, 0.0001, 0.00001 |
| Dropout rate per hidden layer | 20%, 30%, 40%, 50%, 60%, 70%, 80%, 90% |
| Round 1 | Round 2 | Round 3 | Round 4 | Round 5 | |
|---|---|---|---|---|---|
| G1 | 0.20 | 0.19 | 0.30 | 0.49 | 0.83 |
| G2 | 0.17 | 0.19 | 0.29 | 0.47 | - |
| G3 | 0.25 | 0.19 | 0.28 | - | - |
| G4 | 1.00 | 0.54 | 0.48 | 0.69 | 0.94 |
| G5 | 0.33 | 0.22 | 0.29 | 0.51 | 0.75 |
| G6 | 0.50 | 0.35 | 0.39 | 0.53 | 0.79 |
| G7 | 0.10 | 0.18 | - | - | - |
| G8 | 0.11 | 1.00 | 1.00 | 1.00 | 1.00 |
| G9 | 0.07 | - | - | - | - |
| G10 | 0.08 | - | - | - | - |
| G11 | 0.09 | 0.18 | 0.26 | - | - |
| G12 | 0.13 | 0.22 | 0.30 | 0.48 | - |
| G13 | 0.08 | 0.17 | - | - | - |
| G14 | 0.14 | 0.20 | 0.28 | 0.55 | 0.88 |
| Full Dataset | Only Non-Agricultural Areas | |||||
|---|---|---|---|---|---|---|
| Study area | 1 & 2 | 1 | 2 | 1 & 2 | 1 | 2 |
| Sensitivity | 77.9% | 77.3% | 79.1% | 81.6% | 81.3% | 82.5% |
| Specificity | 92.1% | 92.9% | 93.2% | 93.5% | 93.2% | 94.4% |
| Accuracy | 83.8% | 83.4% | 84.8% | 87.2% | 87.8% | 88.2% |
| F1 | 0.85 | 0.85 | 0.86 | 0.87 | 0.87 | 0.88 |
| AUC | 0.92 | 0.92 | 0.93 | 0.94 | 0.94 | 0.94 |
| Settings | ||||
|---|---|---|---|---|
| Acceleration | Points extracted | Acceleration | Points extracted | |
| 2.5 × 2.5 km2 subset | 1.3× | ~5500 | 2.2× | ~3800 |
| 5.0 × 5.0 km2 subset | 1.3× | ~20,000 | 2.2× | ~14,000 |
| 10.2 × 7.5 km2 scene | 1.3× | ~55,000 | 2.3× | ~40,000 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wagner, M.P.; Oppelt, N. Deep Learning and Adaptive Graph-Based Growing Contours for Agricultural Field Extraction. Remote Sens. 2020, 12, 1990. https://doi.org/10.3390/rs12121990
Wagner MP, Oppelt N. Deep Learning and Adaptive Graph-Based Growing Contours for Agricultural Field Extraction. Remote Sensing. 2020; 12(12):1990. https://doi.org/10.3390/rs12121990
Chicago/Turabian StyleWagner, Matthias P., and Natascha Oppelt. 2020. "Deep Learning and Adaptive Graph-Based Growing Contours for Agricultural Field Extraction" Remote Sensing 12, no. 12: 1990. https://doi.org/10.3390/rs12121990
APA StyleWagner, M. P., & Oppelt, N. (2020). Deep Learning and Adaptive Graph-Based Growing Contours for Agricultural Field Extraction. Remote Sensing, 12(12), 1990. https://doi.org/10.3390/rs12121990