A New Algorithm for Daily Sea Ice Lead Identification in the Arctic and Antarctic Winter from Thermal-Infrared Satellite Imagery

Abstract

The presence of sea ice leads in the sea ice cover represents a key feature in polar regions by controlling the heat exchange between the relatively warm ocean and cold atmosphere due to increased fluxes of turbulent sensible and latent heat. Sea ice leads contribute to the sea ice production and are sources for the formation of dense water which affects the ocean circulation. Atmospheric and ocean models strongly rely on observational data to describe the respective state of the sea ice since numerical models are not able to produce sea ice leads explicitly. For the Arctic, some lead datasets are available, but for the Antarctic, no such data yet exist. Our study presents a new algorithm with which leads are automatically identified in satellite thermal infrared images. A variety of lead metrics is used to distinguish between true leads and detection artefacts with the use of fuzzy logic. We evaluate the outputs and provide pixel-wise uncertainties. Our data yield daily sea ice lead maps at a resolution of 1 km² for the winter months November– April 2002/03–2018/19 (Arctic) and April–September 2003–2019 (Antarctic), respectively. The long-term average of the lead frequency distributions show distinct features related to bathymetric structures in both hemispheres.

Dataset: 10.1594/PANGAEA.917588

Dataset License: CC-BY

1. Introduction

Sea ice leads are a key feature in the closed pack ice, which represent elongated cracks covering up to hundreds of kilometers in length where open water and thin ice is present. Thereby, they influence the ocean/sea-ice/atmosphere interactions dramatically. Leads are predominantly induced by mechanical stress, namely wind stress and ocean currents [1] and they significantly increase the turbulent heat fluxes between the relatively warm ocean and cold atmosphere during wintertime [2,3]. Sea ice leads influence the lower atmosphere by reducing the overall sea ice concentration and thereby warming the regional atmospheric boundary layer [4,5]. In an idealized model study, Reference [6] show that small decreases in the sea ice fraction by 1% at ice concentrations larger than 90% cause a rise of the near-surface temperature by up to 3.5 K. According to Reference [7], the heat flux at constant sea ice concentration is increased when multiple leads are present compared to a single and equal area of open water. Because of the associated ocean heat loss in leads, new sea ice is produced, causing significant salt rejection, which in turn affects dense water formation and the ocean circulation [1,8,9,10].

Ice-free areas including sea ice leads were also identified as sources for methane emissions [11,12]. The relevance of leads, polynyas and the sea ice edge for marine species is shown in Reference [13]. Weather prediction, climate, and ocean models rely strongly on detailed information on the respective state of the sea ice. The majority of numerical models, however, cannot produce sea ice leads explicitly and sea ice concentrations from passive microwave data are too coarse to resolve leads [14,15].

Thus there is a need to develop and provide new algorithms to retrieve daily maps of sea ice leads on circum-polar scales in both hemispheres. So far, no dataset exists which describes a climatology of the daily distribution of sea ice leads in both polar regions in a consistent way. Almost all of the previously published studies are conducted for the Arctic and focus on smaller regions and time scales or have coarser geometric resolutions.

The potential of thermal infrared satellite data for the detection of sea ice leads is shown in References [8,16]. However, lead detections then there rely on clear-sky situations and on winter months only to make use of a high temperature contrast between open water and sea ice. Leads in the Arctic are manually identified based on thermal imagery in Reference [17] with a 5-year climatology of wintertime leads derived for the years of 1979/1980 to 1984/1985. Data from the Moderate-Resolution Imaging Spectroradiometer (MODIS) are used in References [18,19] to derive maps of potential open water per pixel and they furthermore evaluate the potential of this approach as a sea ice concentration retrieval method. The differentiation between thick and thin sea ice, including polynyas and leads, was successfully demonstrated in Reference [20], where a polarization ratio of two frequencies of the Advanced Microwave Scanning Radiometer-EOS (AMSR-E) was used. Due to the footprint of the sensor, they identify only leads broader than 3 km and produce daily wintertime lead maps for the Arctic for the winters 2002–2012. The follow-up study from Reference [21] presents a 9-year lead climatology in the Arctic Ocean, revealing multiple hot spots with increased lead observations in the Beaufort Gyre and close to the Fram Strait.

Leads in the Arctic are identified in SAR images from CryoSat-2 and lead fractions and lead width distributions are derived by optimizing the threshold applied on the backscattered waveforms [22]. However, data are presented only for the winters 2011 and 2013 and the derived sea ice products have a comparably low spatial resolution of around 100 km × 100 km. Another approach uses thermal imagery from MODIS, where sea ice leads are identified based on their positive surface temperature anomaly [23]. The authors produce daily maps of sea ice leads with a spatial resolution of 1.5 km × 1.5 km for the months of January to April in the Arctic from 2002 to 2015 [24]. Remaining cloud artefacts that usually represented an obstacle for an automatic lead detection are removed with a fuzzy inference system.

The available lead fractions from AMSR-E [20] are evaluated in Reference [25] by using lead observations in SAR data as a reference, and show that AMSR-E overestimates the lead fraction compared to the SAR data, particularly the lead fraction classes near 100%. A further lead retrieval algorithm for CryoSat-2 data was developed by Reference [26] making use of the specific waveform of the backscattered signal to identify leads as in Reference [22]. They present monthly averages for lead fractions in the Arctic on a 10 km grid covering the years 2011 to 2016 and compare their results with the products from Reference [20] (AMSR-E), Reference [23] (MODIS), and Reference [22] (CryoSat-2) for the respective period. They reveal differences in the data sets due to differences in the spatial and temporal resolution of the used satellite sensors. A study by Reference [27] uses MODIS thermal infrared data with an approach similar to References [23,24] using a fixed threshold and a sequence of multiple tests to produce daily Arctic lead maps.

Since no lead fraction data set exists at this time for the Antarctic, this study aims at presenting a new and robust lead retrieval algorithm that is applicable in both polar regions. Furthermore, we present long-term average lead frequencies for wintertime sea ice in the Arctic (November–April 2002/03–2018/19) and the Southern Ocean (April–September 2003–2019). The algorithm expands upon the work of Reference [23], including major improvements and an adaption to the Southern Hemisphere. Therefore, not only a new lead dataset for the Antarctic is obtained, but also the existing lead dataset for the Arctic [24] receives an extension and update. We use satellite thermal infrared data from MODIS to derive daily maps of leads for the winter months, that is, November to April for Arctic sea ice and April to September for Antarctic sea ice, respectively, including pixel-based retrieval uncertainties. In Section 2, we present the used data and applied methods in detail, which comprise the tile-based processing, the fuzzy filtering and manual quality control for both hemispheres. In Section 3, we show example results of the new lead retrieval approach and go ahead with a discussion of the implemented methods, showing strengths and potential shortcomings of the algorithm in Section 4.

2. Data and Methods

We use collection 6 of MYD/MOD29 ice surface temperature (IST) data [28] to infer daily sea ice leads for both polar regions. MODIS, onboard the two satellites Terra and Aqua (NASA-EOS), provides data since 2000 (Terra) and 2002 (Aqua) and acquisitions are stored in 5-min tiles with a 1 km spatial resolution at nadir. The product includes the MODIS land and cloud mask. An overview of the most important information on both polar regions is presented in

Table 1. Key facts about the data used for both hemispheres.

Hemisphere	Grid	Observation Period	Geographical Coverage	Number of Tiles	Cloud Fraction %, Overall
Arctic	EPSG:3413	2002/03–2018/19, Nov–Apr	north of 60°	421,953	44
Antarctic	EPSG:3412	2003–2019, Apr–Sep	south of 50°	514,950	61

. The cloud fraction for sea ice areas in both hemispheres is defined as the long-term average of daily cloud fractions. The cloud fraction is derived from the MODIS cloud mask and represents the fraction of cloud observations in relation to the maximum number of tiles per pixel.

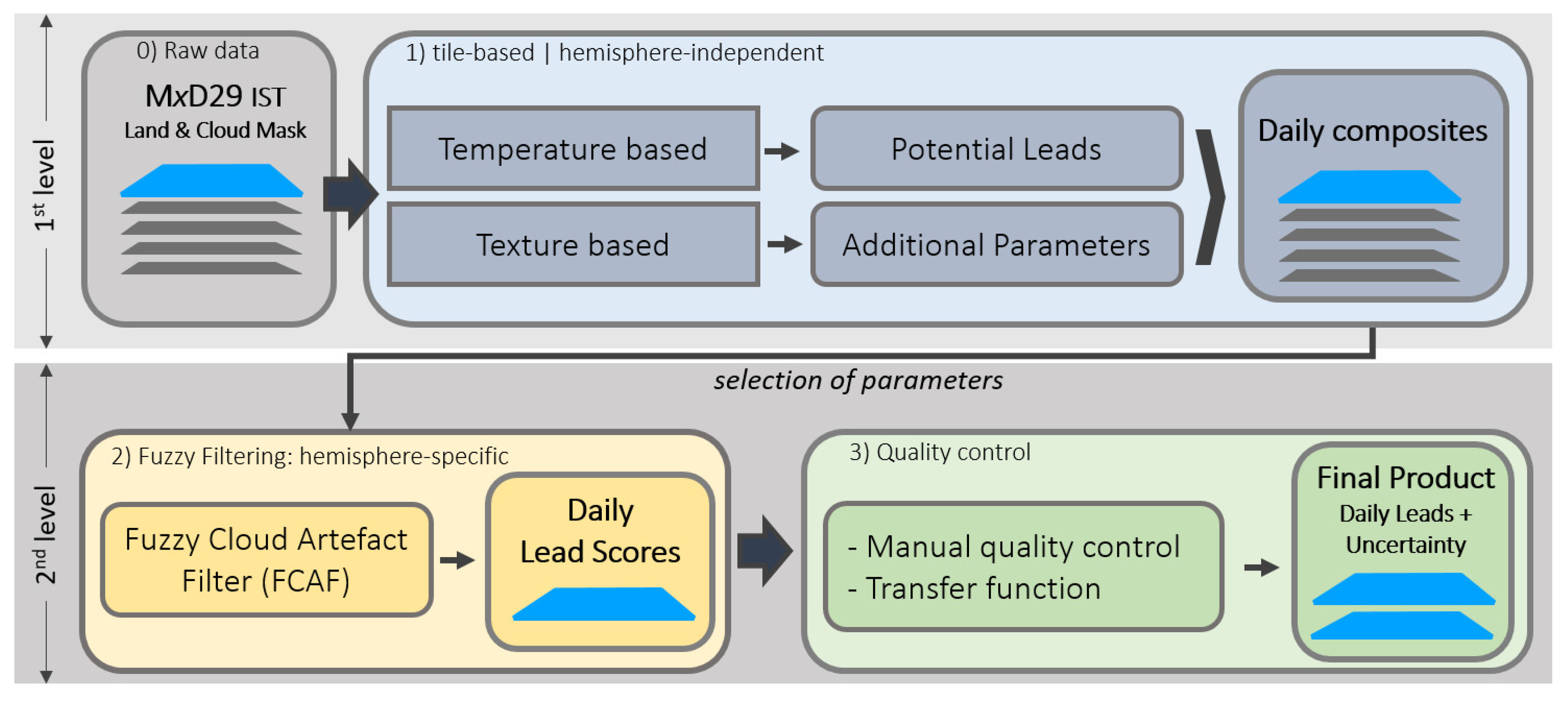
Due to the open water or thin ice present in leads, these can be identified as a warm temperature anomaly, surrounded by cold sea ice. Although the MODIS cloud mask is applied to select clear-sky pixels, the satellite image may be partially covered by clouds or fog that is not included in the mask. A significant fraction of unidentified clouds appear as warm features, which are consequently misinterpreted as leads by unsupervised algorithms. Therefore, a two-stage processing chain is applied, consisting of (1) lead detection, where potential leads are retrieved from the IST data and (2) filtering, where a fuzzy filter is applied to remove false detections. An overview of the processing is provided in Figure 1.

The tile displayed in Figure 2 shows the IST from the MYD29 product (Aqua) for a region in the central Arctic on January 21, 2008. The presented data type corresponds to the 0-th processing step (raw data) in Figure 1. The warm signature of sea ice leads is clearly visible (arrow 1). The MODIS land and cloud mask are also shown. Undetected clouds are visible in the satellite image and can appear as warm features (arrow 2) and represent the major source of errors and noise in automatically derived lead maps. For the preparation of daily maps we make use of multiple daily satellite overpasses and an associated stacking to fill data gaps that result from the MODIS cloud mask.

First, potential leads are identified from the local surface temperature anomalies. To support the subsequent filtering, additional metrics are derived. This step is identical for both the Northern and Southern Hemispheres (Figure 1, box 1). A selection of derived parameters is provided in Figure 3, where the IST is shown as reference (Figure 3a). Based on the IST, local thresholding with a 51 × 51 kernel is applied on the tiles to identify pixels that are significantly warmer than the local neighborhood (Figure 3a, arrow 2). By this, large-scale temperature gradients due to different air masses are omitted while the relative surface temperature contrast is preserved. From this, we obtain potential leads (Figure 3b). This parameter also includes other warm temperature anomalies, which are not associated to sea ice leads, namely cloud artefacts (top arrow 1). Therefore, we derive a set of additional metrics that will allow for a better differentiation between true leads and artefacts. The potential open water POTOWA is based on the IST and describes the fraction of a pixel covered by open water [16,18], which is the inverse of sea-ice concentration (Figure 3c). This concept assumes that a pixel is composed of a mixture of different surface types, namely open water and sea ice. For leads (arrow 2), the POTOWA values are higher than in the surrounding. Warm features arising from clouds, for example arrow 1, have low to medium POTOWA values. By applying a Canny filter [29] on the POTOWA, strong gradients are detected, which are indicative of sea ice lead edges (Figure 3d). By this, most of the features with low to medium POTOWA are excluded.

We derive additionally a linearity measure of potential lead objects by calculating two-dimensional angular variability similar to a Hough transform (Figure 3e). Consequently, leads have the highest linearity values combined with medium to high POTOWA (arrow 2), while cloud artefacts are characterized by low linearity scores combined with low to medium POTOWA (arrow 1). We furthermore derive a predicted lead indicator for every pixel based on different input parameters, for example, the linearity, Canny edges, and other texture parameters derived from gray-level co-occurrence analysis namely the dissimilarity, homogeneity, and correlation (Figure 3f). For this purpose, a universal logistic regression model is set up and trained with manually classified IST tiles. The output of the logistic regression is binary, where 1 (yellow pixels) represents predicted true leads. Here, cloud artefacts (arrow 1, Figure 3f) are classified as ‘no leads’.

After all parameters are derived, the tiles are combined to daily stacks by reprojecting them to the respective reference grid (ARC: EPSG:3413, ANT: EPSG:3412) by calculating the sum or average for the respective parameter (see also Figure 1 box 1c). As an example for one of the obtained daily stacks, Figure 4 shows the potential lead count as the daily sum of potential lead detections for the Arctic (left, 26 November 2007) and the Antarctic (right, 23 May 2018), with the sea ice cover (>15% concentration) derived from AMSR-E/AMSR-2 in the background (blue). Areas that were permanently covered by clouds during the respective day are colored black. The potential lead count indicates the presence of leads, where the maximum value varies around 12 daily observations, depending on the number of tiles per day and on the cloud coverage during a day. High values show rather persistent lead objects (yellow arrows), while lower values indicate the presence of less frequently identified leads or artefacts (red arrows), that is, remaining warm cloud features that fulfilled the criteria of being identified as a potential lead. Due to the faster movement of clouds compared to the sea ice cover, a false lead detection from cloud artefacts generally receives low counts. Some real leads may receive low counts (e.g., yellow arrow 1 in the Fram Strait) due to clouds, which reduce the total number of observations per day, or due to closing of the leads during the day because of changes in the sea ice drift, which makes the count parameter by itself insufficient to separate leads from artefacts. For this reason, we prepare additional daily stacks from the metrics that are described above, for example, linearity and texture parameters. For the day shown in Figure 4, sea ice leads indicated by yellow arrows are mainly visible in the Beaufort Gyre and the Fram Strait (left, Arctic) and in the Antarctic in the southeastern Weddell Sea and Ross Sea (right, Antarctic).

To further differentiate between true leads and warm temperature artefacts, we use an extended version of the fuzzy filter introduced by Reference [23] and use two different set ups for each hemisphere. With fuzzy logic a multi-layer input data set can be processed and translated into a combined, single-layer result by using a set of membership functions and rules [30]. The great advantage over black-box algorithms where the transfer functions are not directly accessible (e.g., neural networks, clustering algorithms) is that the user is able to modify the system by selecting specific membership functions and rules. The defined rules are of linguistic format, hence they can be interpreted easily and expert knowledge can be included in a straightforward manner. The output data is continuous and determines the degree to which a certain pixel belongs to the output membership, hereafter called Lead Score (LS). It can be understood as an indirect measure of uncertainty and is re-calculated into uncertainty by conducting a manual quality control in the subsequent processing step. The selection of input parameters, definition of membership functions and rules involves user knowledge and has the aim to maximize both the true positive classification of sea ice leads and the obtained LS range. In the following we refer to this filtering as the Fuzzy Cloud Artefact Filter (FCAF). For further processing, we defined two different FCAFs to compensate for hemisphere-specific requirements, which are mainly caused by the different spatial coverage and mobility of the sea ice extent. In the Antarctic, sea ice extends further north, and is therefore more frequently influenced by warm air advection from mid-latitudes. Associated to the warm air advection are clouds, which is shown by the higher average cloud fraction compared to the Arctic (Table 1). The temperature contrast is also reduced when warm air is advected, thus increasing the uncertainty for the identification of leads based on their temperature anomaly. The input parameters for the FCAFs for the Northern and Southern Hemispheres are listed in

Table 2. List of parameters used for both FCAFs with the input parameters coming from the daily stacks.

FCAF Input Parameter	Originating From	Description
potential leads	IST	positive local temperature anomaly
predicted leads	linearity, edges, texture parameters	logistic regression, binary output (leads | no leads)
combined texture	hough-derived parameters	combination of hough-parameters: e.g., dissimilarity
linearity	edges, POTOWA	linearity of potential lead objects. High = lead
background temperature anomaly	IST	climatological mean of IST—daily IST. Indicative for warm air advection
clear sky ratio	MODIS cloudmask	number of clear sky observations per day in relation to number of tiles per day and pixel
POTOWA	IST	potential open water: fraction a pixel is covered by open water
white tophat POTOWA	POTOWA	filtered POTOWA, keeps small objects with high POTOWA
edges	POTOWA	Canny filtered image

. Two additional parameters are calculated for the FCAF, namely the background temperature anomaly and the clear sky ratio. The first represents the daily averaged regional surface temperature minus its climatological mean. It turns out, that large-scale positive surface temperature anomalies are particularly associated with the formation of clouds and reduce the IST contrast over leads, making the background temperature anomaly a valuable additional metric for the FCAF. The clear sky ratio is the fraction of clear-sky observations per day in relation to the maximum possible number of observations, that is, number of tiles per day and pixel and represents a useful metric to address confidence to a lead retrieval.

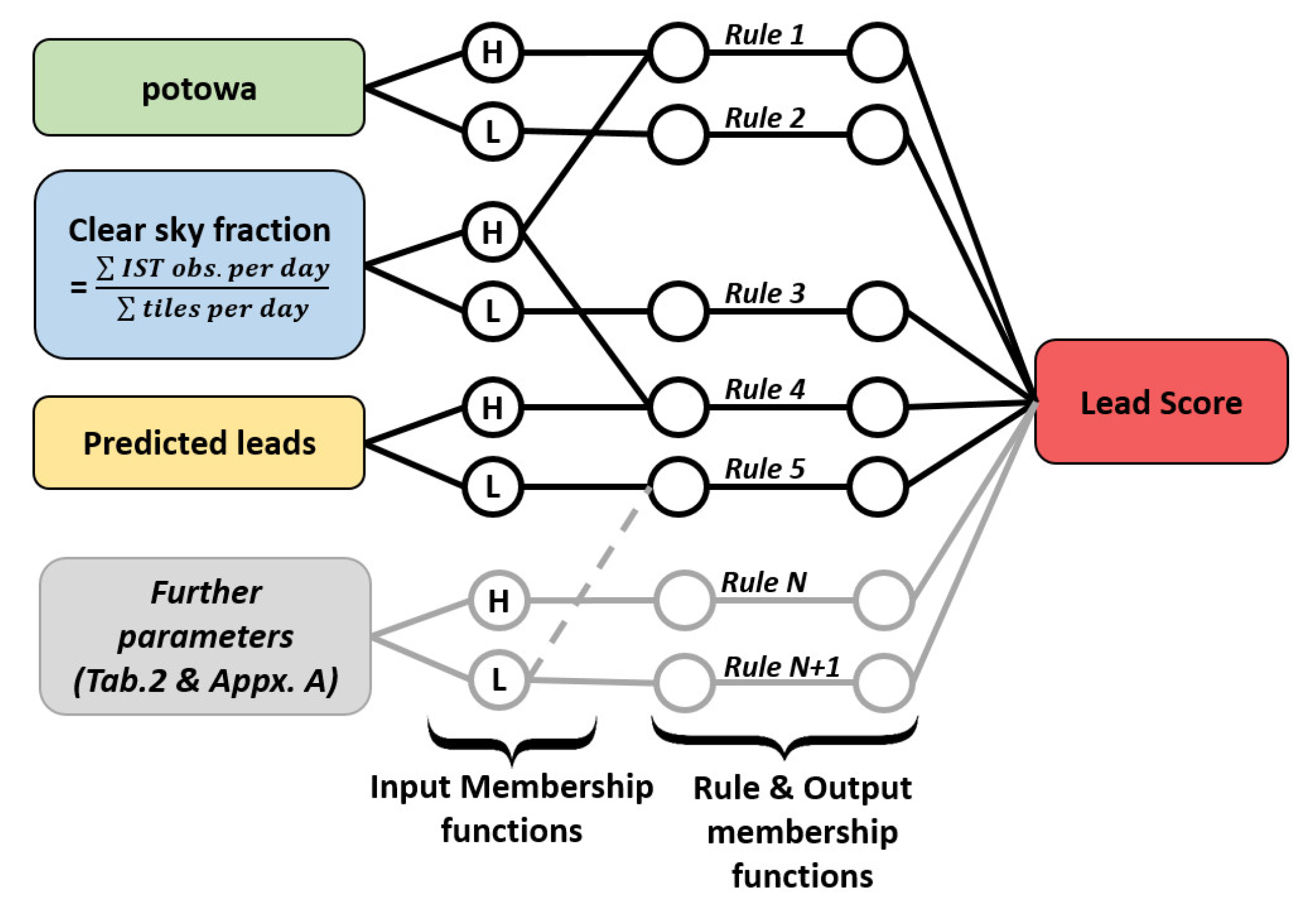
In Figure 5 an outline of the FCAF is shown, indicating that all input parameters are combined by internal fuzzy variables and membership functions, processed accordingly and the final LS is thereby calculated for every day. For instance, the POTOWA is combined with the clear sky ratio by formulating the rule, that both must have high values for the LS to be high. An overview of the fuzzy rules for both polar regions is given in

Table A1. Fuzzy rules for the Arctic (top) and the Antarctic (bottom) with high input variables corresponding to high LS (left column) and low input variables corresponding to low LS (right column). Multiple input variables for one rule are combined by the operation and. The parameters are described in Table 2 in Section 2.

	input ’high’ → LS ’high’	input ’low’ → LS ’low’
ARCTIC	potential leads	potential leads
	predicted leads
	edges
	combined texture
	POTOWA
	backgr.t-anomaly
		clear sky ratio
ANTARCTIC	potential leads	potential leads
	predicted leads
	clear sky ratio	clear sky ratio
	linearity
	combined texture
	white tophat POTOWA
	backgr. t-anomaly

, respectively. An example of the retrieved daily LS maps for the Arctic and Antarctic is presented in Figure 6. As indicated by yellow arrows, high LS values are present in the Beaufort Gyre and Fram Strait (left, Arctic), or in the Weddell Sea and Ross Sea (right, Antarctic) and indicate the presence of sea ice leads with high confidence. Red arrows, however, are rather indicative of lead detection with lower confidence or artefacts.

3. Results

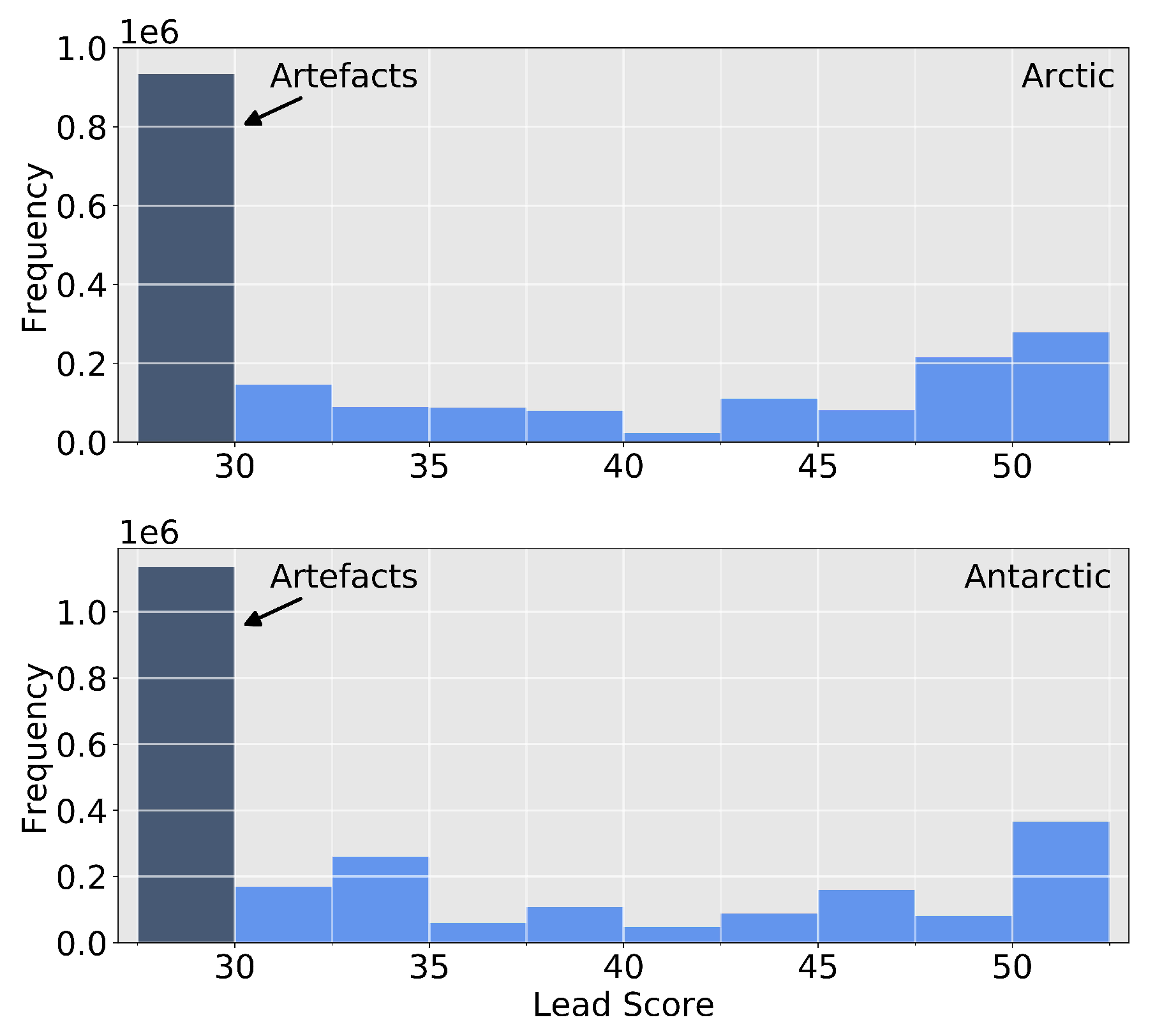
The LS histograms for both hemispheres are presented in Figure 7. Both distributions show a large mode of LS values smaller than 30 and lower but increasing frequencies for higher LS values. The large class of LS values below 30 contains pixels that are prone to a low probability for a true lead, which emerges from the fuzzy rules and emberships applied. However, true leads may be included in the artefact class but with a high retrieval uncertainty. In contrast, the LS exceeding a value of 30 provides increasing confidence for the presence of a true lead. The LS is not a direct measure for uncertainty, but rather an indicator that a respective pixel belongs gradually to either artefacts or leads. Therefore, we performed a manual quality control to associate LS values with the probability of false detections and to derive the associated transfer function, with which we can then obtain pixel-wise uncertainties.

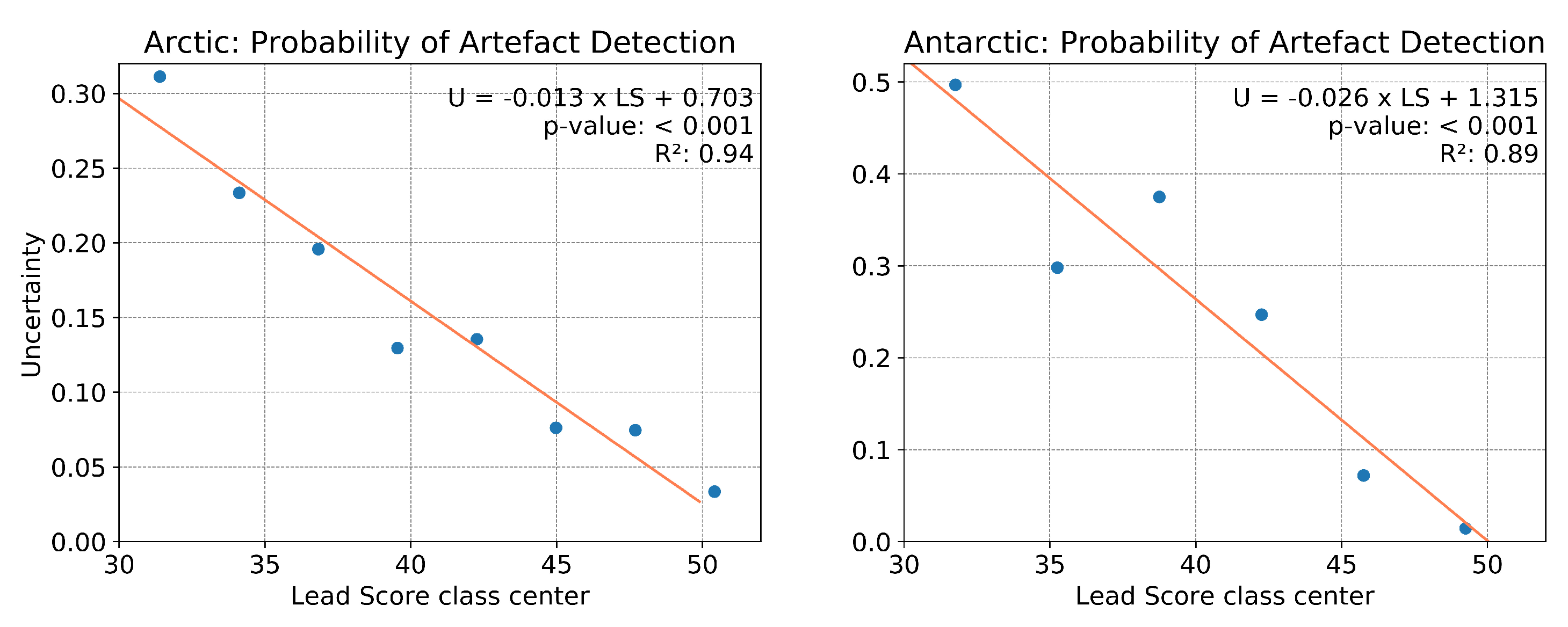
We conduct a manual quality control (MQC) for each hemisphere yielding two different transfer functions for the calculation of detection uncertainty from LS. Within a set of 6 representative LS maps for each hemisphere, areas containing true sea ice leads and artefacts were visually identified and classified, respectively. Subsequently, the probability of artefact detection is calculated for each of the applied LS classes. Afterwards, a linear regression model describing the relation between probability of artefact detection and LS class yields the transfer function, which is used to calculate pixel-wise uncertainties (Figure 8). The previously identified artefact class (LS < 30) is not included in the linear regression, but obviously corresponds to uncertainties larger than 30% (Arctic) and 50% (Antarctic). The slope of the transfer function for the Arctic is smaller compared to the Antarctic, indicating that the uncertainty is higher for most areas in the Antarctic. However, for LS larger than 45 the uncertainty decreases to less than 10% in both hemispheres.

Figure 9 shows the resulting lead uncertainties for the Arctic and Antarctic for one day with a detailed view corresponding to the red rectangle. White arrows indicate the location of identified leads with low uncertainties, while dark-gray colored areas correspond to artefacts and black colored areas represent the MODIS cloudmask. The artefact class can be used as an additional cloud mask, meaning that no information about surface features is available. For the presented day in the Arctic, leads with high confidence can be seen throughout the entire hemisphere with pronounced leads in the Beaufort Gyre, Fram Strait, Baffin Bay, and Kara Sea. In the Antarctic, leads are predominantly present in the Weddell Sea and in the Ross Sea. The influence of clouds and large-scale temperature gradients is visible in the smooth gradient of uncertainties indicated by the blue arrow (Figure 9d). The uncertainty increases in the neighborhood of clouds due to the associated warm air advection in this case, which in turn evokes a positive temperature anomaly weakening the local temperature contrast.

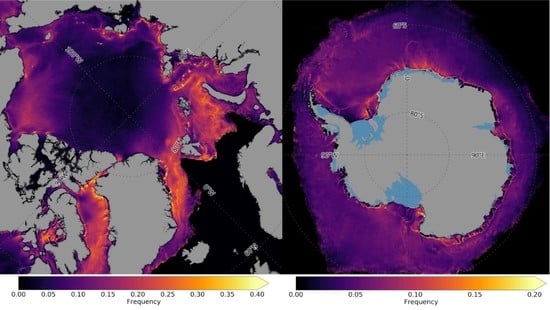
Based on the obtained daily lead data we can derive long-term average lead frequencies for both hemispheres. Figure 10 shows the relative lead frequency for the Arctic (2002/03 to 2018/19, November to April) and the Antarctic (2003 to 2019, April to September) as derived from the daily lead observations. For this purpose, all daily lead maps were averaged over the respective time-period, with artefacts (LS < 30) being excluded. For both hemispheres, increased lead frequencies can be seen along the shelf break. In the Arctic, lead frequencies are also increased in the Beaufort Gyre, Baffin Bay, the Greenland, and the Barents Seas. Similarly, patterns of increased lead frequencies are present in the Antarctic, where for instance north of the coastline a band of increased lead frequencies is visible. Additionally, lead frequencies increase where islands and deep sea features in the bathymetry are present, that is, ridges and troughs. Thereby, frequencies exceed 0.4 (Arctic) and 0.2 (Antarctic) in several regions.

Based on the presented algorithm, a data set for both hemispheres was produced which includes daily fields of sea ice leads and the pixel-wise lead retrieval uncertainty. The lead data contains the classes of sea ice, leads, artefacts, cloudmask, landmask, and areas of open water.

4. Discussion

In the presented algorithm, we consider leads as pixels with a significant local temperature anomaly, which suggests that the fluxes of latent and sensible heat are enhanced at identified leads [2,3]. Leads also contribute to the formation of dense water due to the production of new ice and the associated brine rejection, which ultimately affects the ocean circulation [1,8,9,10]. The mentioned processes associated to leads imply that our results represent a data set, which can be used for for example, high-resolution modelling studies. Although the spatial resolution was increased compared to the product of References [23,27], further research needs to be done to derive leads with higher spatial resolution on a circum-polar scale, since References [6,7] show that particularly narrow leads effectively contribute to these exchange processes.

However, our presented algorithm allows the first comparable observation of sea ice leads in both hemispheres. The definition of leads is consistent in both hemispheres and allows a better inter-hemispheric comparison. To increase the quality of our results, we derive temperature-, shape- and texture-based metrics, for example, the linearity as an indicator for sea ice leads. In doing so, we include a number of independent metrics, which all are solely based on IST data and are subsequently used to separate artefacts from true leads. A major improvement—compared to the previous study by Reference [23] and other studies using fixed thresholds, for example, References [16,27]—is the use of an adaptive local thresholding technique which ensures the identification of potential sea ice leads, particularly when the local temperature contrast is weak due to warm air advection. Consequently, more potential sea ice leads are identified. However, we only make use of clear-sky situations and constrain our lead detection to the winter months to benefit from a generally high temperature contrast between open water and sea ice.

Because of the sea ice drift, leads might be relocated during the course of one day. Our procedure aims to provide data from which one can infer where a lead, that is, a significant local surface temperature anomaly, was identified during the course of one day, regardless of the drift. In the final data product, a strong drift induces an increase in uncertainty to the margins of a lead due to a decreased number of daily lead observations per pixel. Since the ice motion is in some areas on the order of approximately 10 km/d ([31,32], narrow leads in regions of strong ice drift are affected the most by this circumstance. The advantage of our approach including pixel-based uncertainties is, in this regard, that we do not have to make a decision on whether to include observations of drifting leads to the daily map or not, but rather to assign an individual uncertainty value to single lead identifications, which will in turn address the local impact of the respective lead on exchange processes.

To compensate for cloud artefacts, we apply the FCAF that was successfully used in Reference [23] and use different input data and apply specific rules for each hemisphere, respectively (Table 2) to ensure a high data quality. Since the largest source for errors is unidentified clouds, the FCAF is designed to recognize cloud artefacts. Rather than assessing the identified lead objects by a chain of several tests (Bulk lead detection in Reference [27]), we apply the FCAF to assess the derived metrics with respect to true leads and cloud artefacts simultaneously. We support our derived lead maps with pixel-wise uncertainties which can be used as a quality flag. The above mentioned sea ice drift and displacement of sea ice leads as well as large-scale warm air advection result in an increased uncertainty of a detected lead. However, the pixels in the core of a lead as well as slow moving leads receive lower uncertainties and thereby provide higher confidences. The resulting artefact class might be used as an extension for the MODIS cloud mask. With respect to the inter-hemispheric comparison of lead retrieval uncertainties, Figure 8 indicates that uncertainties for the Antarctic are generally higher than for the Arctic, which is caused by a generally higher cloud fraction (Table 1) and a smaller repetition rate of satellite overpasses due to the geographical extent. This results in less frequent clear-sky observations. However, uncertainties also drop below 10% for the highest LS classes, indicating that it is possible to detect leads with high confidence but at the cost of loosing more true leads to the artefact class.

As mentioned in, for example, Reference [16] the observed leads depend highly on the data used. For surface temperature data where the local temperature contrast between leads and the surrounding sea ice is crucial, differences to other retrieval algorithms using passive or active microwave data, for example, AMSR-E or SAR, (e.g., References [20,22]) can be expected not only because of the spatial resolution but also because of the satellite sensor specification and acquisition mode. Reference [20] rely on passive microwave data and identify leads broader than 3 km, which results in less lead observations compared to our results. Also the broadly used SIC data from passive microwave data are not capable of resolving smaller leads as it is demonstrated for the Arctic in Reference [23]. Although we use multiple overpasses by the satellite sensors to fill data gaps, some areas are persistently covered by clouds throughout a day, which means that data gaps remain in the daily lead maps. A multi-day average or merging with other data products, for example, Reference [20], might be a valuable approach to fill remaining data gaps.

Several hot spots where sea ice leads are predominantly present can be identified, for example, the Beaufort Gyre, Greenland Sea, and Barents Sea (Arctic) and the Weddell Sea and Ross Sea (Antarctic). Similar to the studies by Reference [24] for the Arctic and Reference [33] for the Antarctic, we calculated the long-term average lead frequency based on the filtered data (Figure 10), which reveals persistent lead locations in both hemispheres with respect to lead occurrences, where frequencies of 0.4 (Arctic) and 0.2 (Antarctic) are exceeded in several regions, for example, along the continental shelf break and bathymetric features in the deep sea. Compared with the long-term average of potential leads in the Antarctic as shown in Reference [33] (Figure 1), the filtered lead frequencies are lower due to the application of the FCAF, which removes artefacts from the potential lead maps. However, the overall pattern with increased frequencies along the shelf break as well as over troughs and ridges are preserved after the filtering.

The derived daily lead maps can be used for different applications. First, we consider them as a useful boundary field for regional climate and ocean modeling. Especially with the provided uncertainty, an assimilation of daily lead maps becomes feasible. Second, the lead maps can be interpreted in comparison to other lead products (e.g., References [15,26]) and third, the lead data can be used to analyze temporal and spatial patterns in lead characteristics and potential forcings in both hemispheres.

5. Conclusions and Outlook

This study presents a new and robust algorithm to produce daily maps of sea ice leads for the Arctic (November to April) and Antarctic (April – September). Based on thermal satellite imagery from MODIS, we first process all individual swaths and identify potential sea ice leads and further metrics, and second remove cloud artefacts emerging from deficits in the MODIS cloud mask with the FCAF. Finally, we conduct a manual quality control and calculate pixel-wise uncertainties and obtain daily circum-polar maps of sea ice leads. With the developed algorithm, we present an update for the Arctic and introduce a new lead data set for the Antarctic and present maps of the long-term average lead frequencies for both hemispheres.

The pixel-wise uncertainty will allow for an assimilation of the presented lead maps into boundary conditions for regional climate models and thereby support improved heat flux calculations. In the follow-up studies, we plan to study the spatial and temporal dynamics of sea ice leads for both hemispheres in detail. By doing so, we aim to reveal the long-term evolution of sea ice leads in both hemispheres with respect to atmospheric and oceanographic forcings. The comparison of our produced lead data with others is also planned and will help to improve our understanding of the small scale sea ice dynamics.