GPS/BDS-2/Galileo Precise Point Positioning Ambiguity Resolution Based on the Uncombined Model
Abstract
1. Introduction
2. Methodology
2.1. Basic Code and Carrier Phase Observation Equation
2.2. Uncombined PPP with Ambiguity Resolution
2.3. FCB Estimation
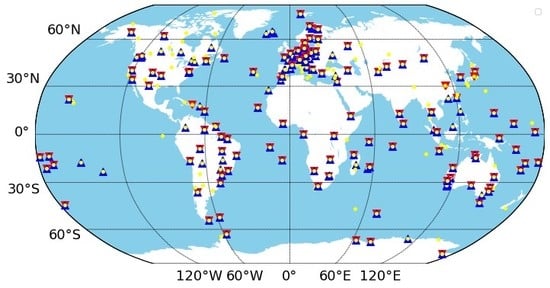
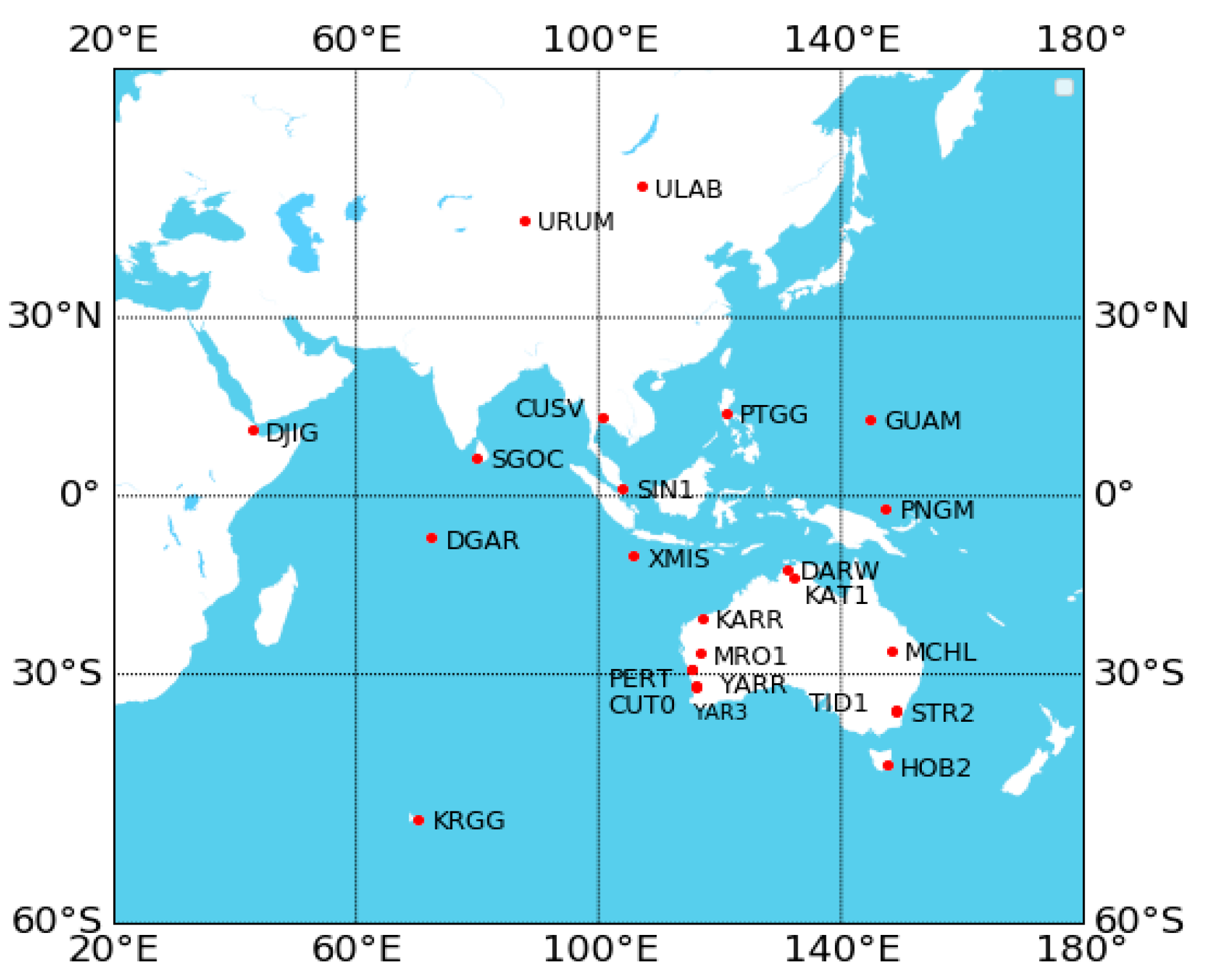
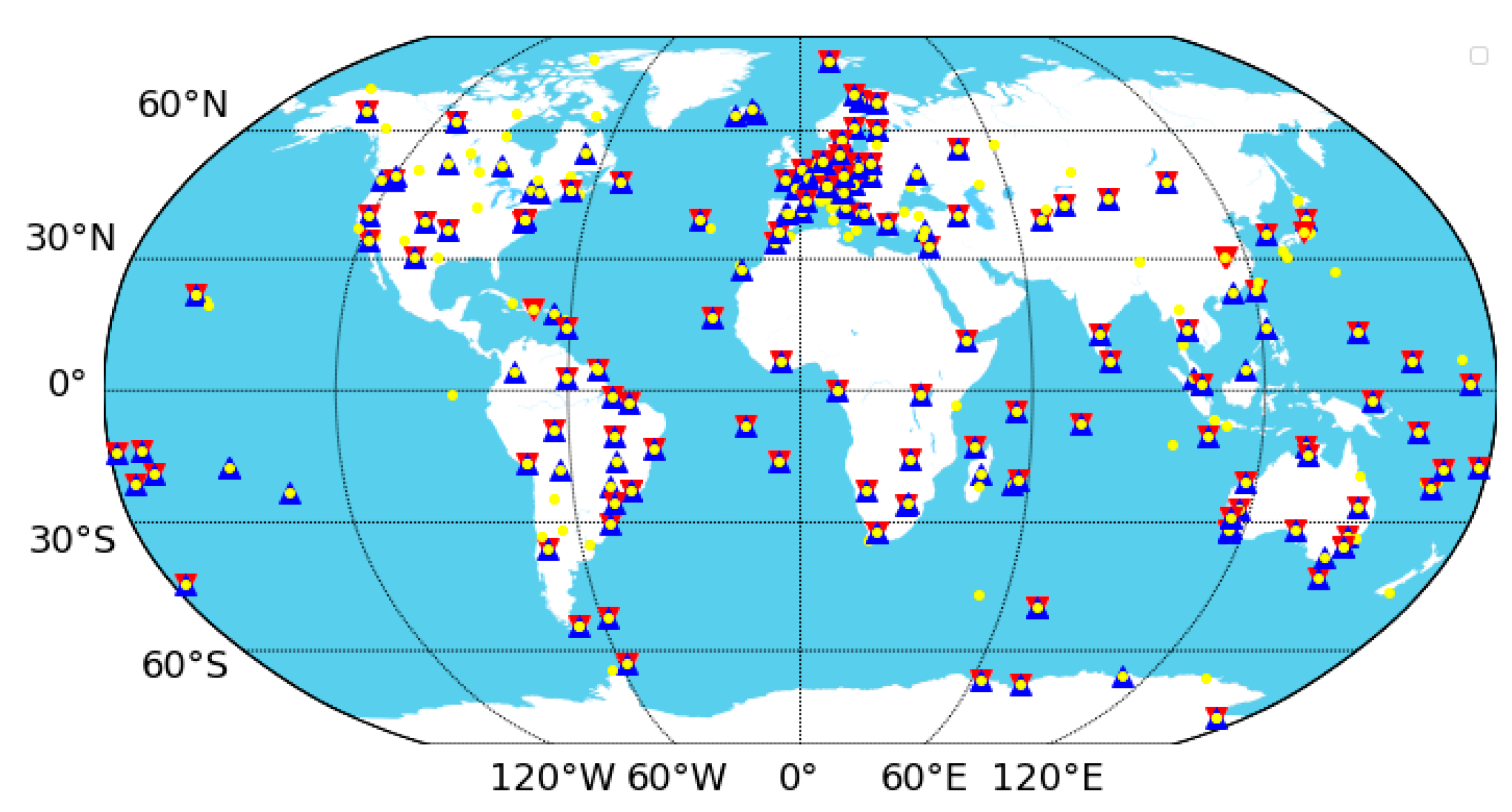
3. Data and Processing Strategy
4. Analysis Results
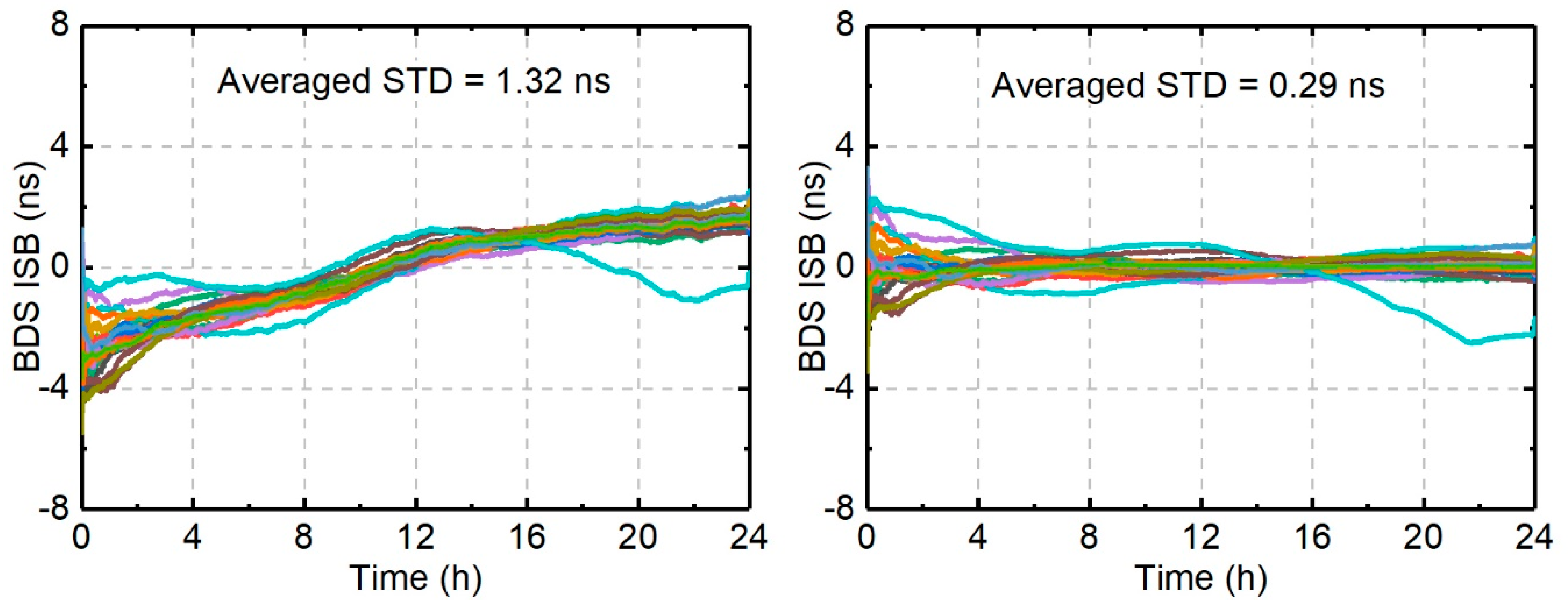
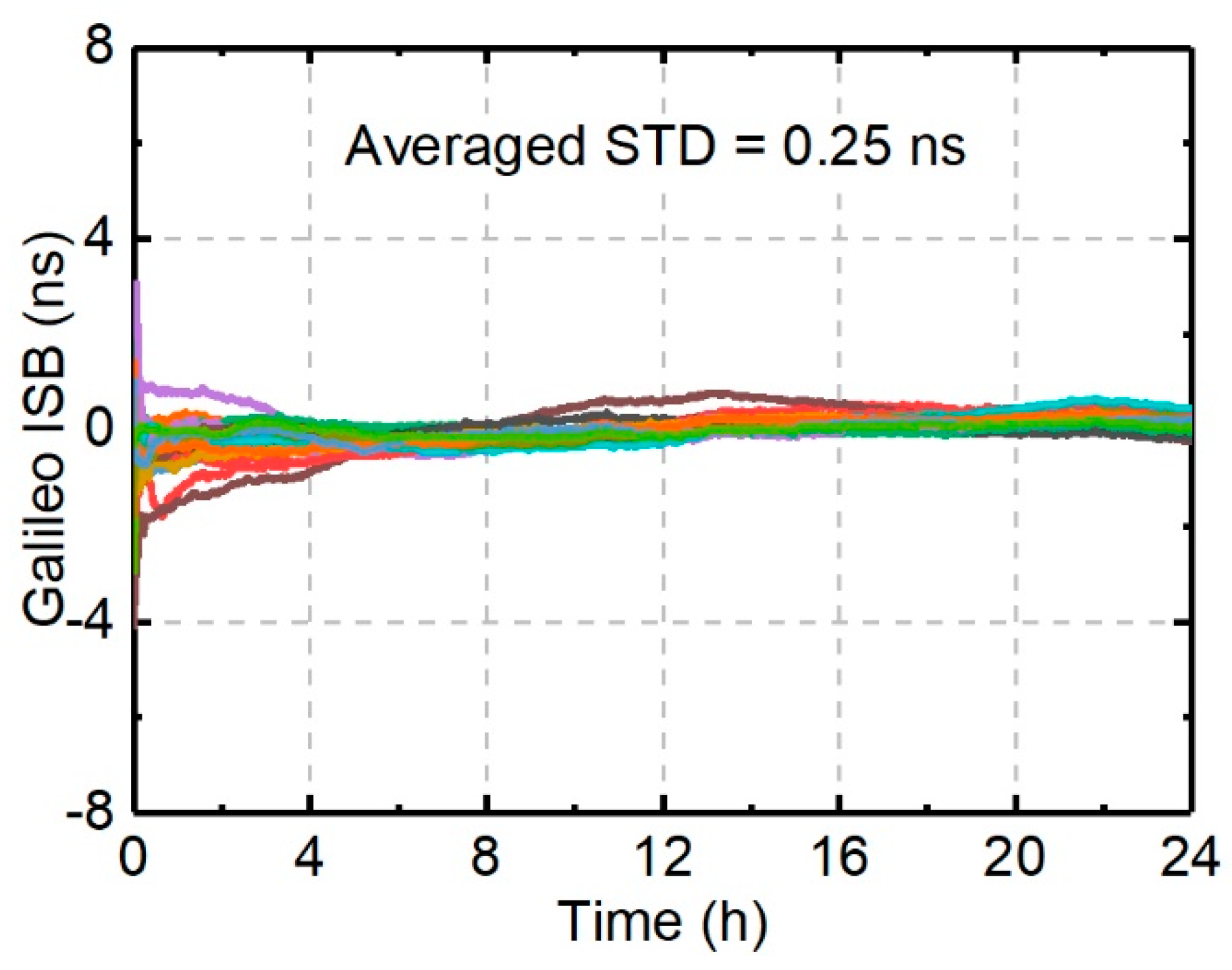
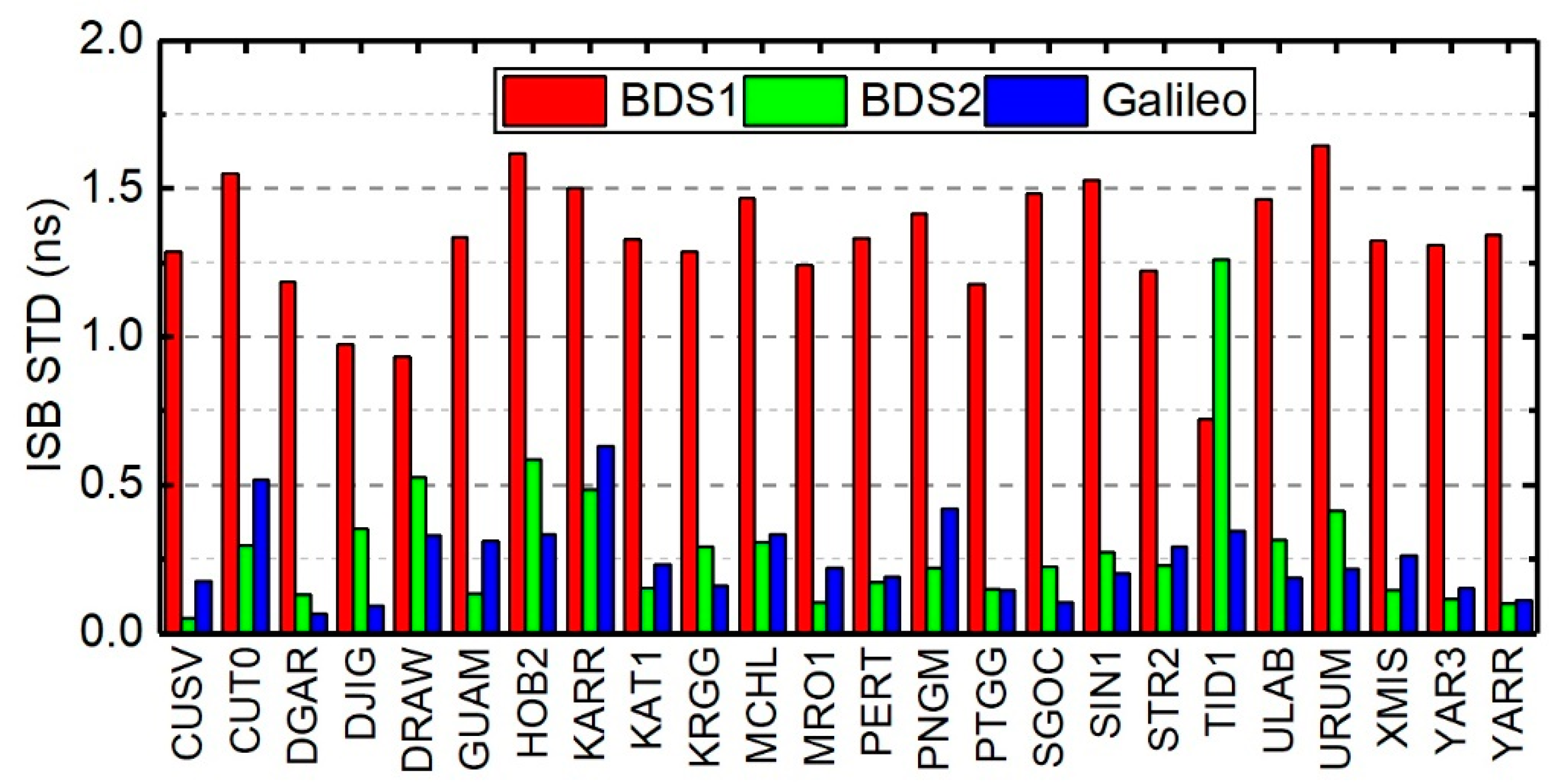
4.1. ISB Stability
4.2. FCB Results
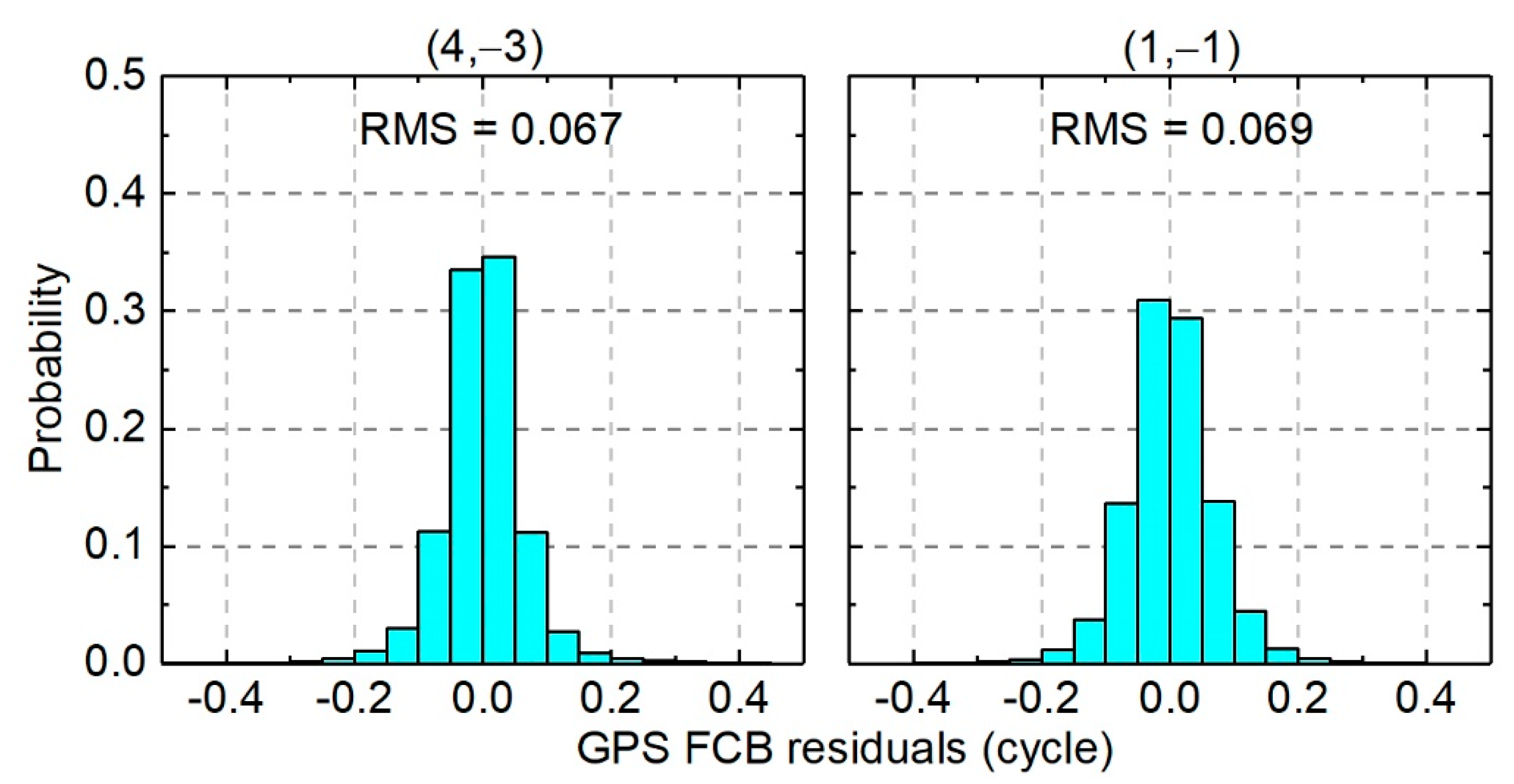
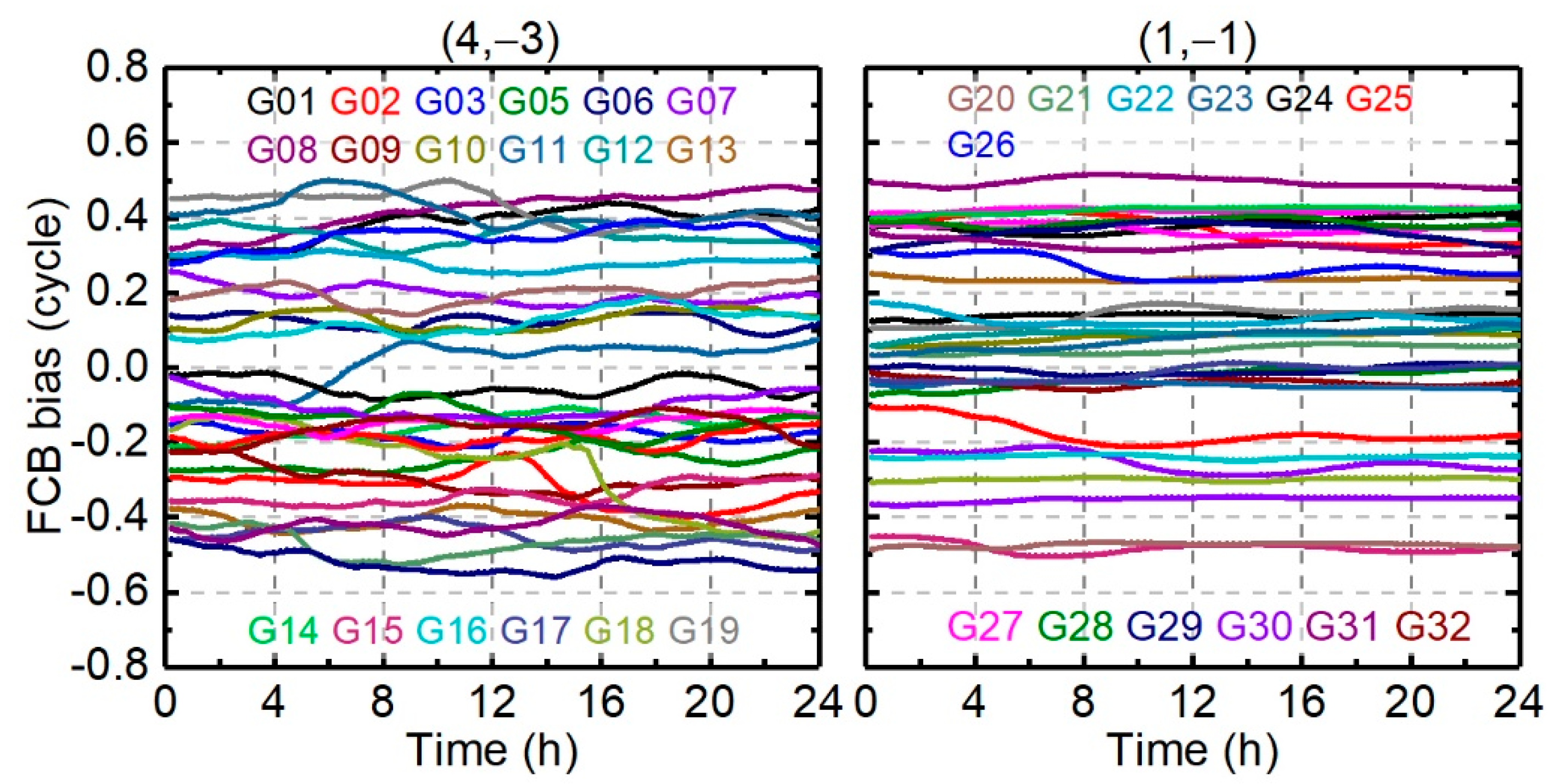
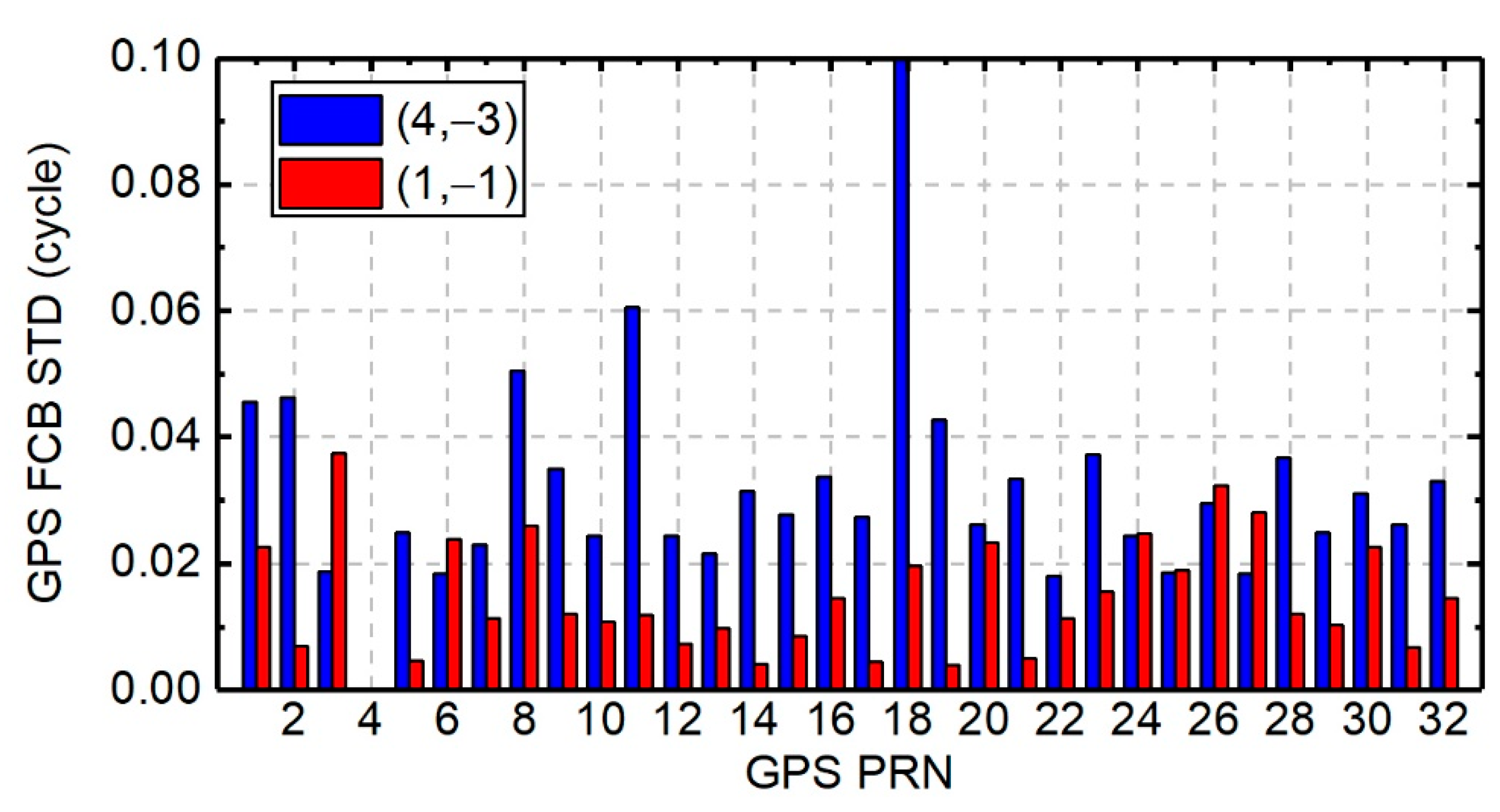
4.2.1. GPS FCB Results
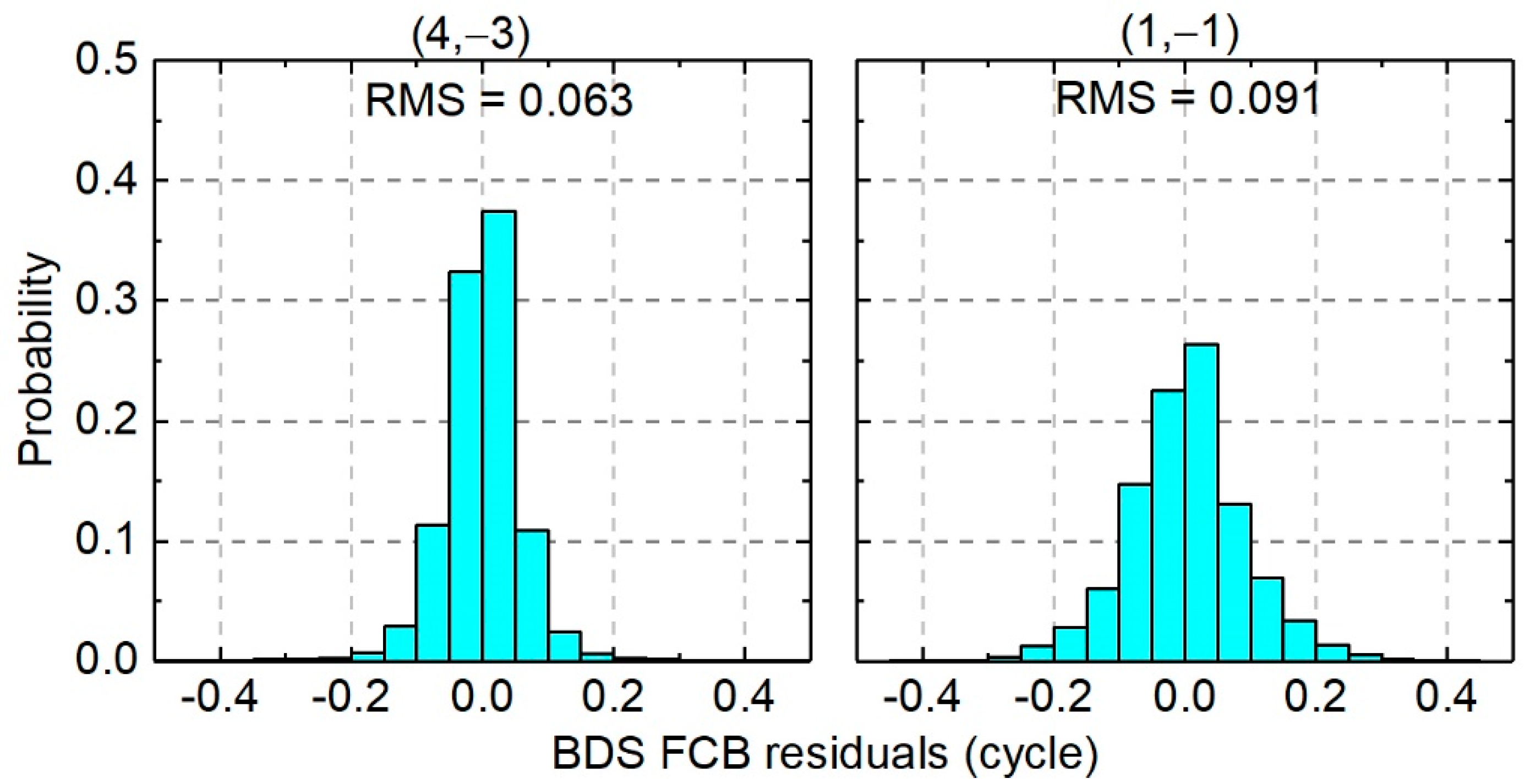
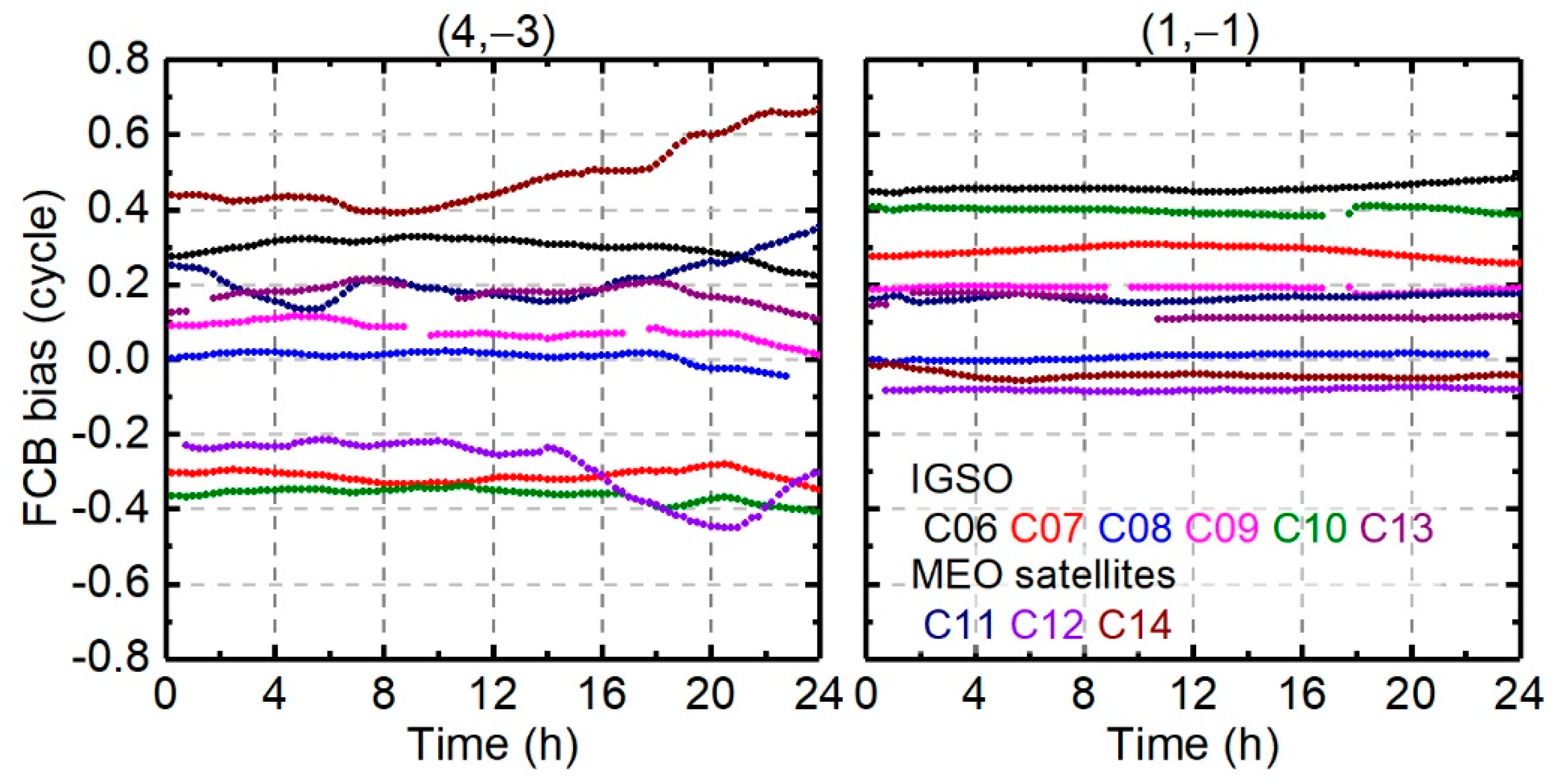
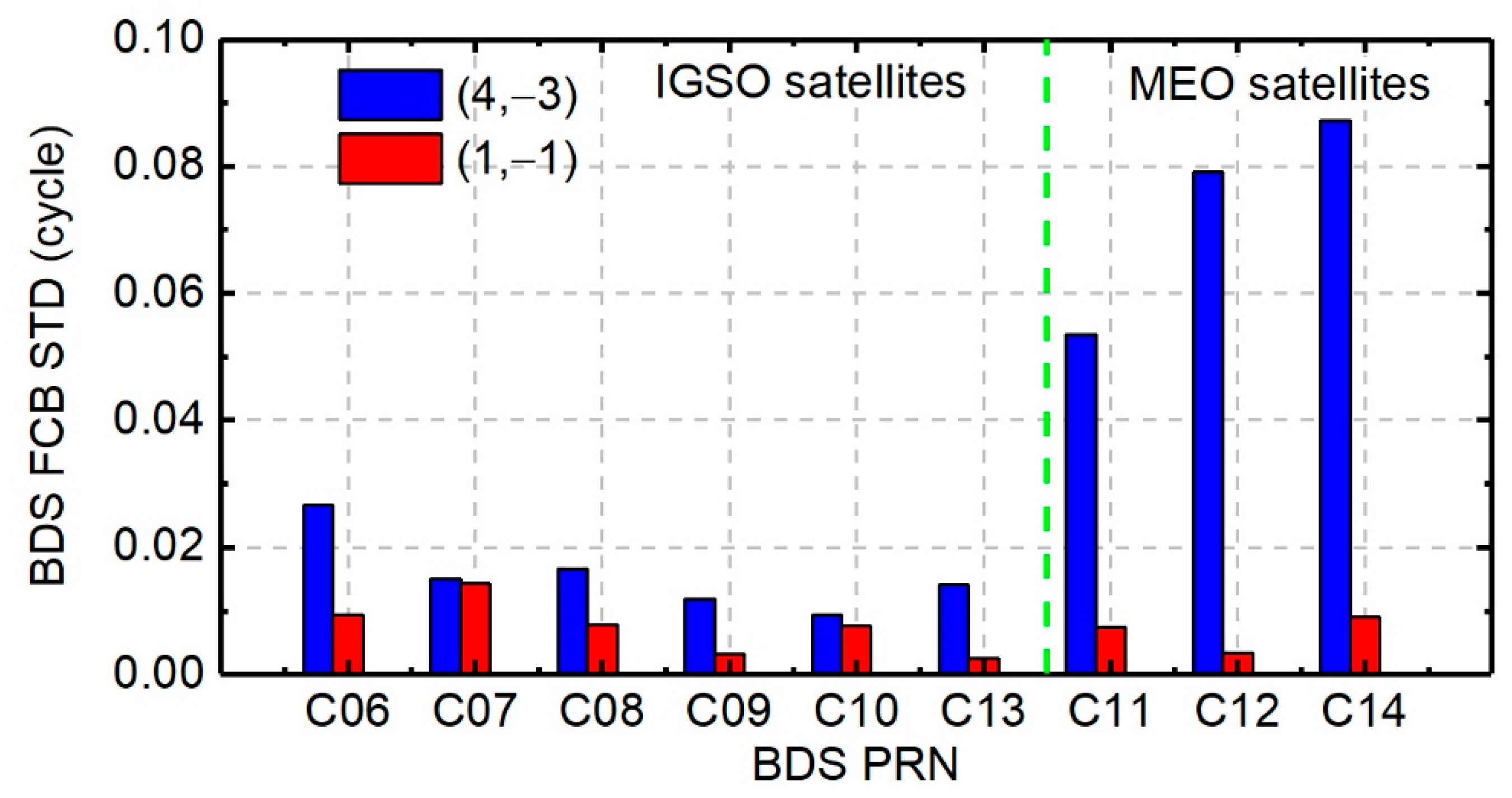
4.2.2. BDS-2 FCB Results
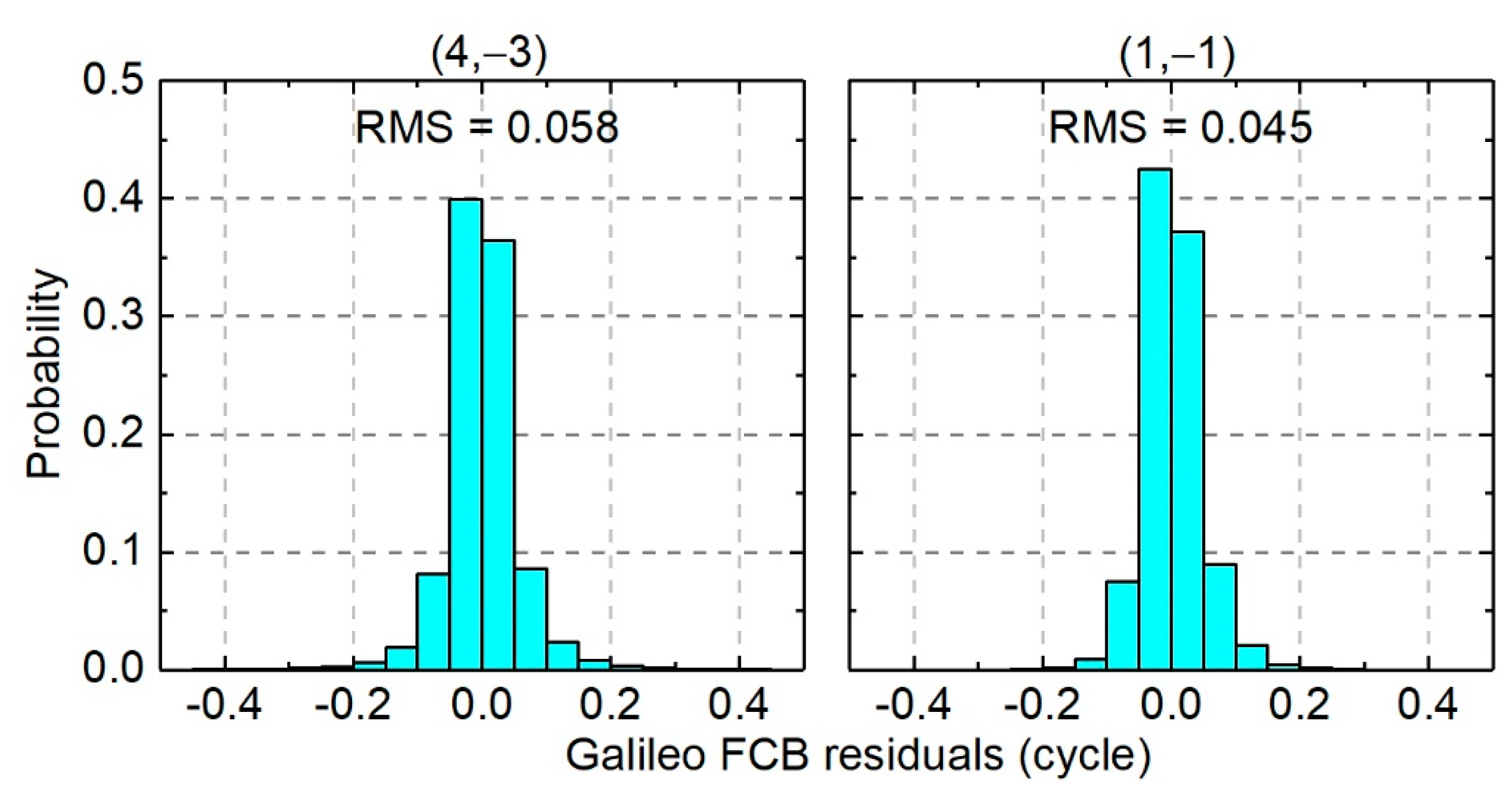
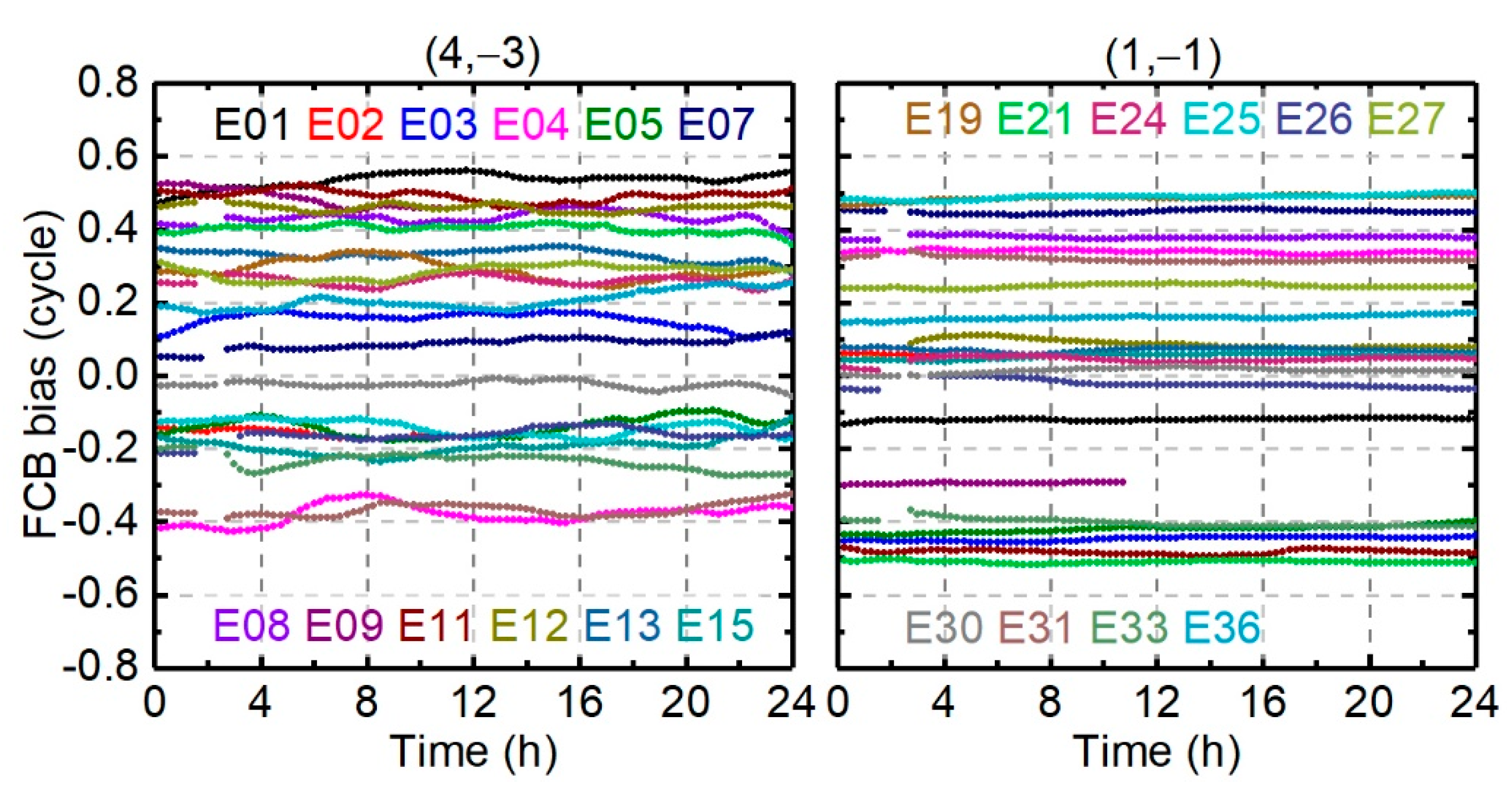
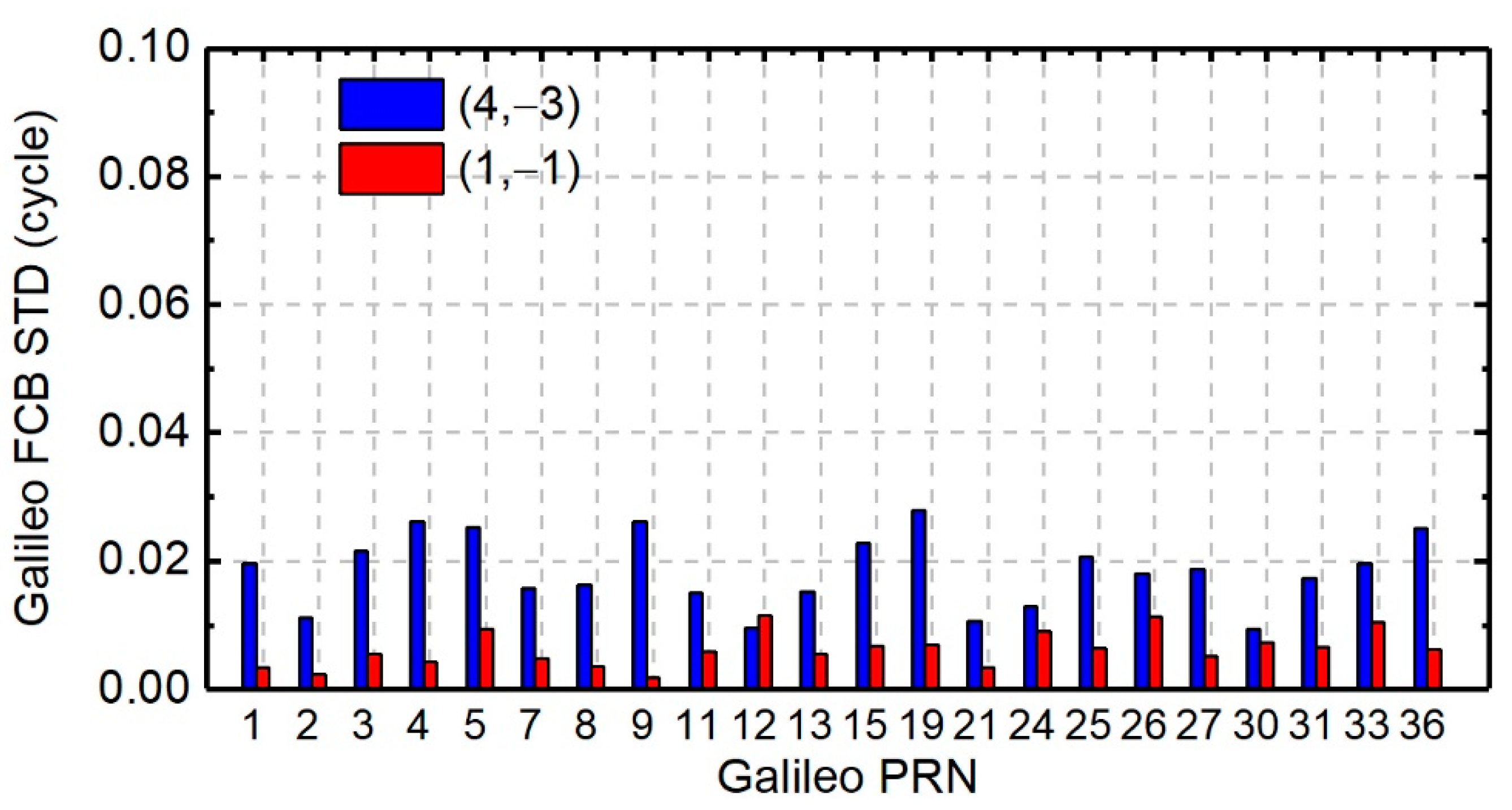
4.2.3. Galileo FCB Results
4.3. Positioning Results
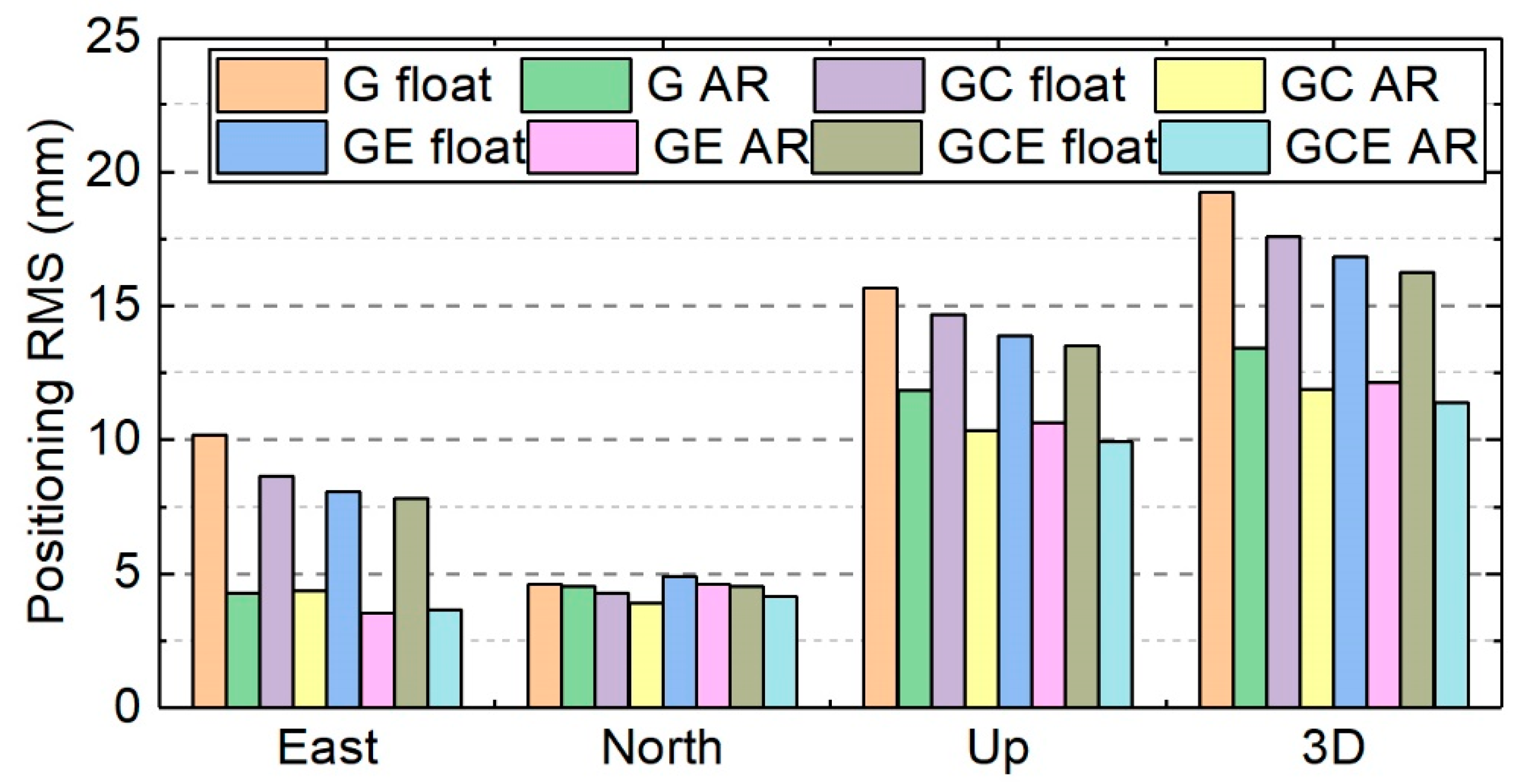
4.3.1. PPP AR Accuracy
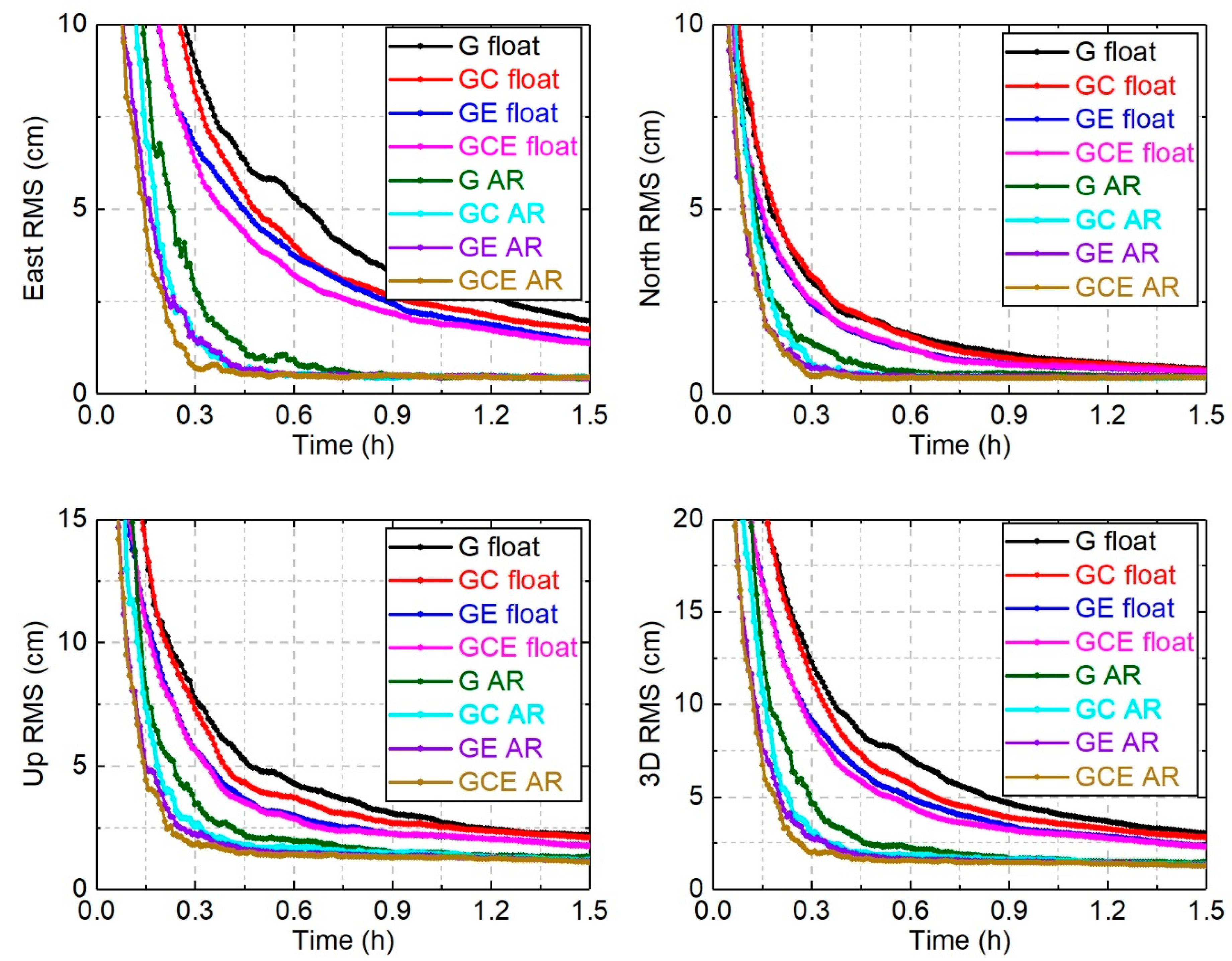
4.3.2. Convergence Time
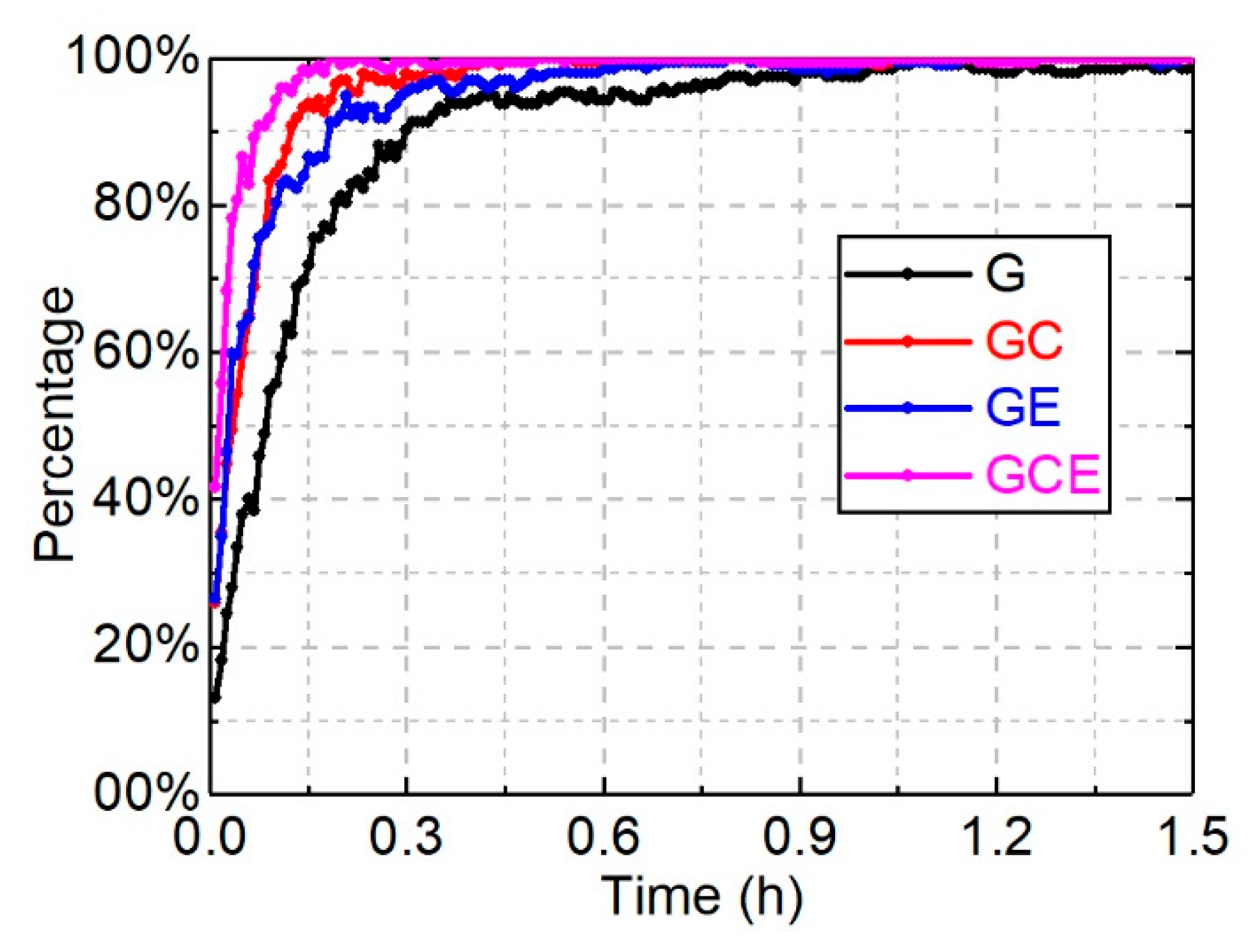
4.3.3. Ambiguity Success Fixing Rate
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kouba, J.; Héroux, P. Precise Point Positioning Using IGS Orbit and Clock Products. GPS Solut. 2001, 5, 12–28. [Google Scholar] [CrossRef]
- Bisnath, S.; Gao, Y. Current State of Precise Point Positioning and Future Prospects and Limitations. In Observing our Changing Earth; Sideris, M.G., Ed.; Springer: Berlin/Heidelberg, Germany, 2008; Volume 133, pp. 615–623. [Google Scholar]
- Guo, J.; Li, X.; Li, Z.; Hu, L.; Yang, G.; Zhao, C.; Fairbairn, D.; Watson, D.; Ge, M. Multi-GNSS precise point positioning for precision agriculture. Precis. Agric. 2018, 19, 895–911. [Google Scholar] [CrossRef]
- Su, K.; Jin, S.; Ge, Y. Rapid displacement determination with a stand-alone multi-GNSS receiver: GPS, Beidou, GLONASS, and Galileo. GPS Solut. 2019, 23, 54. [Google Scholar] [CrossRef]
- Ge, M.; Gendt, G.; Rothacher, M.; Shi, C.; Liu, J. Resolution of GPS carrier-phase ambiguities in Precise Point Positioning (PPP) with daily observations. J. Geod. 2008, 82, 389–399. [Google Scholar] [CrossRef]
- Collins, P. Precise Point Positioning with Ambiguity Resolution Using the Decoupled Clock Model. In Proceedings of the 21st international Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2008), Savannah, GA, USA, 16–19 September 2008; pp. 1315–1322. [Google Scholar]
- Laurichesse, D.; Mercier, F.; Berthias, J.-P.; Broca, P.; Cerri, L. Integer Ambiguity Resolution on Undifferenced GPS Phase Measurements and Its Application to PPP and Satellite Precise Orbit Determination. Navigation 2009, 56, 135–149. [Google Scholar] [CrossRef]
- Wang, J.; Huang, G.; Yang, Y.; Zhang, Q.; Gao, Y.; Xiao, G. FCB estimation with three different PPP models: Equivalence analysis and experiment tests. GPS Solut. 2019, 23, 93. [Google Scholar] [CrossRef]
- Cai, C.; Gao, Y. Performance Analysis of Precise Point Positioning Based on Combined GPS and GLONASS; Fort Worth Convention Center: Fort Worth, TX, USA, 2007; pp. 858–865. [Google Scholar]
- Cai, C.; Gao, Y. Modeling and assessment of combined GPS/GLONASS precise point positioning. GPS Solut. 2013, 17, 223–236. [Google Scholar] [CrossRef]
- Li, P.; Zhang, X. Integrating GPS and GLONASS to accelerate convergence and initialization times of precise point positioning. GPS Solut. 2014, 18, 461–471. [Google Scholar] [CrossRef]
- Yigit, C.O.; Gikas, V.; Alcay, S.; Ceylan, A. Performance evaluation of short to long term GPS, GLONASS and GPS/GLONASS post-processed PPP. Surv. Rev. 2014, 46, 155–166. [Google Scholar] [CrossRef]
- Ge, M.; Zhang, H.; Jia, X.; Song, S.; Wickert, J. What is Achievable with Current COMPASS Constellations? In Proceedings of the 25th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2012), Nashville, TN, USA, 17–21 September 2012; pp. 331–339. [Google Scholar]
- Li, M.; Qu, L.; Zhao, Q.; Guo, J.; Xing, S.; Li, X. Precise Point Positioning with the BeiDou Navigation Satellite System. Sensors 2014, 14, 927–943. [Google Scholar] [CrossRef]
- Xia, F.; Ye, S.; Xia, P.; Zhao, L.; Jiang, N.; Chen, D.; Hu, G. Assessing the latest performance of Galileo-only PPP and the contribution of Galileo to Multi-GNSS PPP. Adv. Space Res. 2019, 63, 2784–2795. [Google Scholar] [CrossRef]
- Cai, C.; Gao, Y.; Pan, L.; Zhu, J. Precise point positioning with quad-constellations: GPS, BeiDou, GLONASS and Galileo. Adv. Space Res. 2015, 56, 133–143. [Google Scholar] [CrossRef]
- Lou, Y.; Zheng, F.; Gu, S.; Wang, C.; Guo, H.; Feng, Y. Multi-GNSS precise point positioning with raw single-frequency and dual-frequency measurement models. GPS Solut. 2016, 20, 849–862. [Google Scholar] [CrossRef]
- Liu, T.; Yuan, Y.; Zhang, B.; Wang, N.; Tan, B.; Chen, Y. Multi-GNSS precise point positioning (MGPPP) using raw observations. J. Geod. 2017, 91, 253–268. [Google Scholar] [CrossRef]
- Cao, X.; Li, J.; Zhang, S.; Pan, L.; Kuang, K. Performance assessment of uncombined precise point positioning using Multi-GNSS real-time streams: Computational efficiency and RTS interruption. Adv. Space Res. 2018, 62, 3133–3147. [Google Scholar] [CrossRef]
- Odijk, D.; Zhang, B.; Teunissen, P.J.G. Multi-GNSS PPP and PPP-RTK: Some GPS+BDS Results in Australia. In China Satellite Navigation Conference (CSNC) 2015 Proceedings: Volume II; Sun, J., Liu, J., Fan, S., Lu, X., Eds.; Springer: Berlin/Heidelberg, Germany, 2015; Volume 341, pp. 613–623. [Google Scholar]
- Li, P.; Zhang, X.; Guo, F. Ambiguity resolved precise point positioning with GPS and BeiDou. J. Geod. 2017, 91, 25–40. [Google Scholar]
- Liu, X.; Jiang, W.; Li, Z.; Chen, H.; Zhao, W. Comparison of convergence time and positioning accuracy among BDS, GPS and BDS/GPS precise point positioning with ambiguity resolution. Adv. Space Res. 2019, 63, 3489–3504. [Google Scholar] [CrossRef]
- Wang, M.; Chai, H.; Li, Y. Performance analysis of BDS/GPS precise point positioning with undifferenced ambiguity resolution. Adv. Space Res. 2017, 60, 2581–2595. [Google Scholar] [CrossRef]
- Liu, Y.; Ye, S.; Song, W.; Lou, Y.; Gu, S. Rapid PPP ambiguity resolution using GPS+GLONASS observations. J. Geod. 2017, 91, 441–455. [Google Scholar] [CrossRef]
- Liu, Y.; Lou, Y.; Ye, S.; Zhang, R.; Song, W.; Zhang, X.; Li, Q. Assessment of PPP integer ambiguity resolution using GPS, GLONASS and BeiDou (IGSO, MEO) constellations. GPS Solut. 2017, 21, 1647–1659. [Google Scholar] [CrossRef]
- Pan, Z.; Chai, H.; Kong, Y. Integrating multi-GNSS to improve the performance of precise point positioning. Adv. Space Res. 2017, 60, 2596–2606. [Google Scholar] [CrossRef]
- Hu, J.; Zhang, X.; Li, P.; Ma, F.; Pan, L. Multi-GNSS fractional cycle bias products generation for GNSS ambiguity-fixed PPP at Wuhan University. GPS Solut. 2020, 24, 15. [Google Scholar] [CrossRef]
- Villiger, A.; Dach, R. International GNSS Service Technical Report 2018 (IGS Annual Report). IGS Central Bureau and University of Bern; Bern Open Publishing: Bern, Switzerland, 2019. [Google Scholar]
- Chen, J.; Zhang, Y.; Wang, J.; Yang, S.; Dong, D.; Wang, J.; Qu, W.; Wu, B. A simplified and unified model of multi-GNSS precise point positioning. Adv. Space Res. 2015, 55, 125–134. [Google Scholar] [CrossRef]
- Odijk, D.; Zhang, B.; Khodabandeh, A.; Odolinski, R.; Teunissen, P.J.G. On the Estimability of Parameters in Undifferenced, Uncombined GNSS Network and PPP-RTK User Models by Means of S-system Theory. J. Geod. 2016, 90, 15–44. [Google Scholar] [CrossRef]
- Wübbena, G.; Schmitz, M.; Bagge, A. PPP-RTK: Precise point positioning using state-space representation in RTK networks. In Proceedings of the ION GNSS, Long Beach, CA, USA, 13–16 September 2005; pp. 13–16. [Google Scholar]
- Li, X.; Zhang, X.; Ge, M. Regional reference network augmented precise point positioning for instantaneous ambiguity resolution. J. Geod. 2011, 85, 151–158. [Google Scholar] [CrossRef]
- Zhang, B.; Teunissen, P.J.G.; Odijk, D. A Novel Un-differenced PPP-RTK Concept. J. Navig. 2011, 64, S180–S191. [Google Scholar] [CrossRef]
- Teunissen, P.J.G.; Khodabandeh, A. Review and principles of PPP-RTK methods. J. Geod. 2015, 89, 217–240. [Google Scholar] [CrossRef]
- Nadarajah, N.; Khodabandeh, A.; Wang, K.; Choudhury, M.; Teunissen, P.J.G. Multi-GNSS PPP-RTK: From Large- to Small-Scale Networks. Sensors 2018, 18, 1078. [Google Scholar] [CrossRef]
- Laurichesse, D.; Privat, A. An Open-source PPP Client Implementation for the CNES PPP-WIZARD Demonstrator. In Proceedings of the ION GNSS 2015, Tampa, FL, USA, 14–18 September 2015; pp. 2780–2789. [Google Scholar]
- Collins, P.; Bisnath, S.; Lahaye, F.; Héroux, P. Undifferenced GPS Ambiguity Resolution Using the Decoupled Clock Model and Ambiguity Datum Fixing. Navigation 2010, 57, 123–135. [Google Scholar] [CrossRef]
- Tu, R.; Zhang, H.; Ge, M.; Huang, G. A real-time ionospheric model based on GNSS Precise Point Positioning. Adv. Space Res. 2013, 52, 1125–1134. [Google Scholar] [CrossRef]
- Wang, J.; Huang, G.; Zhou, P.; Yang, Y.; Zhang, Q.; Gao, Y. Advantages of Uncombined Precise Point Positioning with Fixed Ambiguity Resolution for Slant Total Electron Content (STEC) and Differential Code Bias (DCB) Estimation. Remote Sens. 2020, 12, 304. [Google Scholar] [CrossRef]
- Xiang, Y.; Gao, Y. Improving DCB Estimation Using Uncombined PPP. Navigation 2017, 64, 463–473. [Google Scholar] [CrossRef]
- Li, X.; Ge, M.; Zhang, H.; Wickert, J. A method for improving uncalibrated phase delay estimation and ambiguity-fixing in real-time precise point positioning. J. Geod. 2013, 87, 405–416. [Google Scholar] [CrossRef]
- Gu, S.; Lou, Y.; Shi, C.; Liu, J. BeiDou phase bias estimation and its application in precise point positioning with triple-frequency observable. J. Geod. 2015, 89, 979–992. [Google Scholar] [CrossRef]
- Li, P.; Zhang, X.; Ge, M.; Schuh, H. Three-frequency BDS precise point positioning ambiguity resolution based on raw observables. J. Geod. 2018, 92, 1357–1369. [Google Scholar] [CrossRef]
- Xiao, G.; Li, P.; Gao, Y.; Heck, B. A Unified Model for Multi-Frequency PPP Ambiguity Resolution and Test Results with Galileo and BeiDou Triple-Frequency Observations. Remote Sens. 2019, 11, 116. [Google Scholar] [CrossRef]
- Cheng, S.; Wang, J.; Peng, W. Statistical analysis and quality control for GPS fractional cycle bias and integer recovery clock estimation with raw and combined observation models. Adv. Space Res. 2017, 60, 2648–2659. [Google Scholar] [CrossRef]
- Zhou, F.; Dong, D.; Li, P.; Li, X.; Schuh, H. Influence of stochastic modeling for inter-system biases on multi-GNSS undifferenced and uncombined precise point positioning. GPS Solut. 2019, 23, 59. [Google Scholar] [CrossRef]
- Zang, N.; Li, B.; Nie, L.; Shen, Y. Inter-system and inter-frequency code biases: Simultaneous estimation, daily stability and applications in multi-GNSS single-frequency precise point positioning. GPS Solut. 2020, 24, 18. [Google Scholar] [CrossRef]
- Li, X.; Ge, M.; Dai, X.; Ren, X.; Fritsche, M.; Wickert, J.; Schuh, H. Accuracy and reliability of multi-GNSS real-time precise positioning: GPS, GLONASS, BeiDou, and Galileo. J. Geod. 2015, 89, 607–635. [Google Scholar] [CrossRef]
- Jiang, N.; Xu, T.; Xu, Y.; Xu, G.; Schuh, H. Assessment of Different Stochastic Models for Inter-System Bias between GPS and BDS. Remote Sens. 2019, 11, 989. [Google Scholar] [CrossRef]
- Zeng, A.; Yang, Y.; Ming, F.; Jing, Y. BDS–GPS inter-system bias of code observation and its preliminary analysis. GPS Solut. 2017, 21, 1573–1581. [Google Scholar] [CrossRef]
- Jiang, N.; Xu, Y.; Xu, T.; Xu, G.; Sun, Z.; Schuh, H. GPS/BDS short-term ISB modelling and prediction. GPS Solut. 2017, 21, 163–175. [Google Scholar] [CrossRef]
- Geng, J.; Meng, X.; Dodson, A.H.; Teferle, F.N. Integer ambiguity resolution in precise point positioning: Method comparison. J. Geod. 2010, 84, 569–581. [Google Scholar] [CrossRef]
- Xiao, G.; Li, P.; Sui, L.; Heck, B.; Schuh, H. Estimating and assessing Galileo satellite fractional cycle bias for PPP ambiguity resolution. GPS Solut. 2018, 23, 3. [Google Scholar] [CrossRef]
- Zhou, F.; Dong, D.; Li, W.; Jiang, X.; Wickert, J.; Schuh, H. GAMP: An open-source software of multi-GNSS precise point positioning using undifferenced and uncombined observations. GPS Solut. 2018, 22, 33. [Google Scholar] [CrossRef]
- Xiao, G.; Sui, L.; Heck, B.; Zeng, T.; Tian, Y. Estimating satellite phase fractional cycle biases based on Kalman filter. GPS Solut. 2018, 22, 82. [Google Scholar] [CrossRef]
- Dilssner, F.; Springer, T.; Schönemann, E.; Enderle, W. Estimation of Satellite Antenna Phase Center Corrections for BeiDou. In Proceedings of the IGS Workshop 2014, Pasadena, CA, USA, 23–27 June 2014. [Google Scholar]
- Wanninger, L.; Beer, S. BeiDou satellite-induced code pseudorange variations: Diagnosis and therapy. GPS Solut. 2015, 19, 639–648. [Google Scholar] [CrossRef]
- Teunissen, P.J.G. The least-squares ambiguity decorrelation adjustment: A method for fast GPS integer ambiguity estimation. J. Geod. 1995, 70, 65–82. [Google Scholar] [CrossRef]
- Katsigianni, G. Improving Galileo orbit determination using zero-difference ambiguity fixing in a Multi-GNSS processing. Adv. Space Res. 2018, 63, 2952–2963. [Google Scholar] [CrossRef]
- Yan, X.; Huang, G.; Zhang, Q.; Liu, C.; Wang, L.; Qin, Z. Early analysis of precise orbit and clock offset determination for the satellites of the global BeiDou-3 system. Adv. Space Res. 2019, 63, 1270–1279. [Google Scholar] [CrossRef]
- Zhang, X.; Wu, M.; Liu, W.; Li, X.; Yu, S.; Lu, C.; Wickert, J. Initial assessment of the COMPASS/BeiDou-3: New-generation navigation signals. J. Geod. 2017, 91, 1225–1240. [Google Scholar] [CrossRef]
- Yang, Y.; Xu, Y.; Li, J.; Yang, C. Progress and performance evaluation of BeiDou global navigation satellite system: Data analysis based on BDS-3 demonstration system. Sci. China Earth Sci. 2018, 61, 614–624. [Google Scholar] [CrossRef]
- Zhao, Q.; Wang, C.; Guo, J.; Wang, B.; Liu, J. Precise orbit and clock determination for BeiDou-3 experimental satellites with yaw attitude analysis. GPS Solut. 2018, 22, 4. [Google Scholar] [CrossRef]
- Li, Z.; Chen, W.; Ruan, R.; Liu, X. Evaluation of PPP-RTK based on BDS-3/BDS-2/GPS observations: A case study in Europe. GPS Solut. 2020, 24, 38. [Google Scholar] [CrossRef]
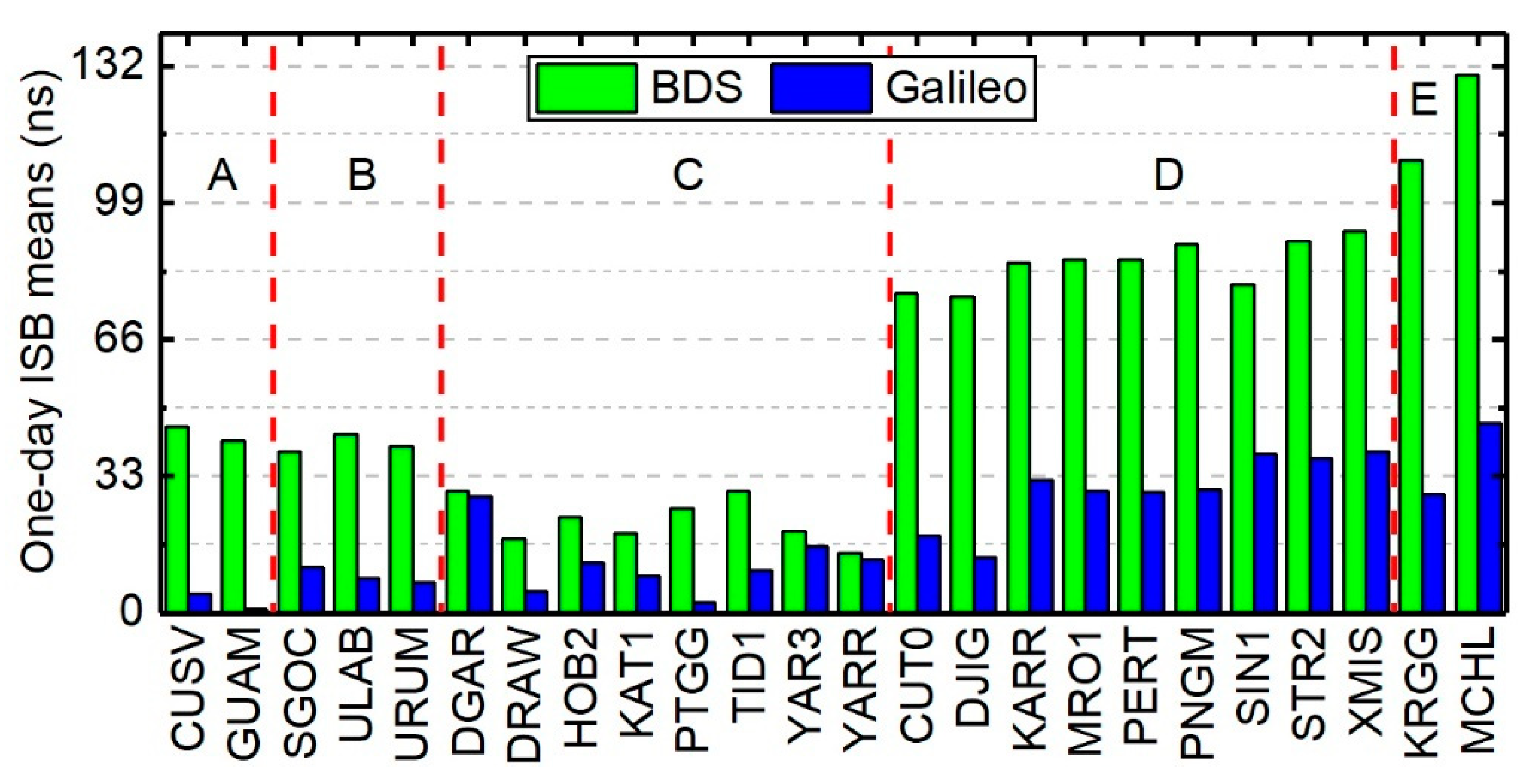
| Receiver Type | Sum of Stations | Mean (ns) | STD (ns) | ||
|---|---|---|---|---|---|
| BDS-2 | Galileo | BDS-2 | Galileo | ||
| A | 2 | 43.16 | 2.85 | 2.38 | 2.46 |
| B | 3 | 40.77 | 8.85 | 2.12 | 1.85 |
| C | 8 | 22.32 | 11.99 | 5.48 | 7.76 |
| D | 9 | 84.32 | 29.64 | 5.67 | 8.75 |
| E | 2 | 119.54 | 37.20 | 14.45 | 12.18 |
| System | 3D Positioning Accuracy (cm) at Different Processing Intervals | ||||||
|---|---|---|---|---|---|---|---|
| 10 min | 20 min | 30 min | 60 min | 120 min | 180 min | ||
| G | Float | 19.8 | 11.2 | 7.8 | 4.3 | 2.5 | 1.9 |
| AR | 10.9 | 3.9 | 2.4 | 1.7 | 1.4 | 1.3 | |
| Improvement | 45% | 65% | 69% | 61% | 43% | 30% | |
| GC | Float | 19.7 | 10.2 | 6.5 | 3.7 | 2.4 | 1.8 |
| AR | 9.0 | 2.7 | 1.8 | 1.6 | 1.4 | 1.2 | |
| Improvement | 54% | 74% | 72% | 57% | 44% | 32% | |
| GE | Float | 15.6 | 8.4 | 5.7 | 3.2 | 2.1 | 1.7 |
| AR | 6.9 | 2.6 | 1.8 | 1.5 | 1.3 | 1.2 | |
| Improvement | 55% | 69% | 69% | 53% | 38% | 28% | |
| GCE | Float | 15.4 | 7.9 | 5.2 | 3.0 | 2.0 | 1.6 |
| AR | 5.7 | 2.0 | 1.6 | 1.4 | 1.2 | 1.1 | |
| Improvement | 63% | 75% | 70% | 53% | 39% | 30% | |
| System | Float (min) | AR (min) | Improvement |
|---|---|---|---|
| G | 22 | 10.5 | 52% |
| GC | 20.5 | 9.5 | 54% |
| GE | 16.5 | 8 | 52% |
| GCE | 16 | 7.5 | 53% |
| Time (min) | Ambiguity Success Fixing Rate | |||
|---|---|---|---|---|
| G | GC | GE | GCE | |
| 10 | 75.5% | 94.3% | 86.5% | 99.0% |
| 20 | 91.1% | 99.0% | 96.4% | 99.0% |
| 30 | 93.8% | 100.0% | 97.4% | 100.0% |
| 60 | 97.9% | 99.5% | 100.0% | 99.5% |
| 120 | 99.5% | 100.0% | 99.5% | 100.0% |
| 180 | 97.9% | 99.5% | 99.5% | 100.0% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Huang, G.; Zhang, Q.; Gao, Y.; Gao, Y.; Luo, Y. GPS/BDS-2/Galileo Precise Point Positioning Ambiguity Resolution Based on the Uncombined Model. Remote Sens. 2020, 12, 1853. https://doi.org/10.3390/rs12111853
Wang J, Huang G, Zhang Q, Gao Y, Gao Y, Luo Y. GPS/BDS-2/Galileo Precise Point Positioning Ambiguity Resolution Based on the Uncombined Model. Remote Sensing. 2020; 12(11):1853. https://doi.org/10.3390/rs12111853
Chicago/Turabian StyleWang, Jin, Guanwen Huang, Qin Zhang, Yang Gao, Yuting Gao, and Yiran Luo. 2020. "GPS/BDS-2/Galileo Precise Point Positioning Ambiguity Resolution Based on the Uncombined Model" Remote Sensing 12, no. 11: 1853. https://doi.org/10.3390/rs12111853
APA StyleWang, J., Huang, G., Zhang, Q., Gao, Y., Gao, Y., & Luo, Y. (2020). GPS/BDS-2/Galileo Precise Point Positioning Ambiguity Resolution Based on the Uncombined Model. Remote Sensing, 12(11), 1853. https://doi.org/10.3390/rs12111853