Abstract
In the field of iceberg and glacier calving studies, it is important to collect comprehensive datasets of populations of icebergs. Particularly, calving of lake-terminating glaciers has been understudied. The aim of this work is to present an object-based method of iceberg detection and to create an inventory of icebergs located in a proglacial lagoon of San Quintín glacier, Northern Patagonia Icefield, Chile. This dataset is created using high-resolution WorldView-2 imagery and a derived DEM. We use it to briefly discuss the iceberg size distribution and area–volume scaling. Segmentation of the multispectral imagery produced a map of objects, which were classified with use of Random Forest supervised classification algorithm. An intermediate classification product was corrected with a ruleset exploiting contextual information and a watershed algorithm that was used to divide multiple touching icebergs into separate objects. Common theoretical heavy-tail statistical distributions were tested as descriptors of iceberg area and volume distributions. Power law models were proposed for the area–volume relationship. The proposed method performed well over the open lake detecting correctly icebergs in all size bands except 5–15 m2 where many icebergs were missed. A section of the lagoon with ice melange was not reliably mapped due to uniformity of the area in the imagery and DEM. The precision of the DEM limited the scaling effort to icebergs taller than 1.7 m and larger than 99 m2, despite the inventory containing icebergs as small as 4 m2. The work demonstrates viability of object-based analysis for lacustrine iceberg detection and shows that the statistical properties of iceberg population at San Quintín glacier match those of populations produced by tidewater glaciers.
1. Introduction
Lacustrine calving of glaciers is mechanical detachment of icebergs when a glacier terminates in fresh water [1,2]. The phenomenon of iceberg calving in lakes differs slightly from the more widely known tidewater calving. In the case of sea- and ocean-terminating glaciers, an interplay between tidal action, thermal undercutting by subglacial plumes and buoyancy forces leads to calving processes [2]. However, in the case of glaciers terminating in lakes, buoyancy forces [1] are the primary calving factor, promoting formation of tabular icebergs, as observed in proglacial lakes of, e.g., Patagonia [1] and Alaska [3]. While freshwater calving does not contribute to the global sea level rise as strongly as the tidewater calving, it influences dynamics of proglacial lakes, which have potential to store large amounts of meltwater [4] and provide water for agriculture and even hydropower downstream [5].
Nowadays, radar imagery is widely used for detection and monitoring of large icebergs in marine contexts [6,7]. Optical imagery, both satellite and aerial, is employed when detection of small icebergs is of concern [8,9]. On these datasets, both object- and pixel-based analyses are performed to arrive at iceberg positions and inventories. The major differences, relevant for remote sensing, between lacustrine and tidewater calving are the size of icebergs and color of the surrounding water. Lacustrine calving very often produces small icebergs which are hardly detectable on medium resolution satellite data. This is the case also with small tidewater glaciers. In such cases, methods which measure the calving events instead of the floating iceberg population are used to quantify ice fluxes, such as LiDAR scanning, seismic and acoustic measurements [10] or time-lapse terrestrial photography [11,12]. These in-situ techniques do not differ significantly in application near tidewater or lake-terminating glaciers. Lacustrine calving happens in freshwater ice bodies, often with high sediment load, which changes the water color. Therefore, icebergs covered with sufficient amount of debris can be mistaken for water on multispectral images. Scarcity of lacustrine iceberg and calving datasets was pointed out as a factor hindering research into the calving’s impact on lake-terminating glacier dynamics [12].
The size distribution of icebergs is a lingering topic in the glaciological literature [13,14,15]. Data on size distribution of calved ice bodies contribute to understanding of calving mechanisms [8] and iceberg decay processes [15,16], and they are used in modeling efforts to parameterize the freshwater influx from glaciers and icesheets [17]. Earlier studies prove that heavy-tailed distributions are best approximates of iceberg size frequencies [15,18]. Most of them, however, were focused on iceberg populations observed in front of calving tidewater glacier fronts [18], or coming from decay of icesheet margins [14]. Studies of size distributions of lacustrine icebergs are lacking; lacustrine calving literature focuses on detailed calving event descriptions [12] or studies of calving mechanisms [3]. The only size frequency-related work in Patagonia estimates iceberg volume from time-lapse imagery and surface wave measurements [11].
Object-Based Image Analysis (OBIA) is a paradigm of analysis of raster data (image analysis) that relies on segments identified within the image [19]. Instead of operating on properties of individual pixels, OBIA employs properties of groups of pixels to perform classifications. The advantage of OBIA compared to the pixel based object analysis is that the list of properties available to the classification algorithm is much wider. In the case of the pixel-based operations only the values of pixels in the available bands can be used, while OBIA can include geometrical features of segments, textural measures and statistical properties of pixel populations enclosed by segments. In the cryospheric research, OBIA finds uses in studies dealing with mapping features that would have been otherwise problematic to discern due to spectral overlap between surface types. Examples include mapping of debris-covered glaciers [20,21], glacier surface facies [22] or glacial lakes [23]. The advantages of OBIA can easily be exploited in iceberg detection as well. On multispectral imagery of floating icebergs, there are sharp boundaries between bright ice and dark water. The dark, debris-covered specimens, or ones with lines of sediment embedded in their faces stand out texturally against smooth water surface. OBIA has already been used successfully to study ocean-borne icebergs on radar [6] and high-resolution aerial optical [24] imagery, showing that the method is viable for iceberg research.
In this work we intend to expand the usefulness of OBIA method to the field of lacustrine iceberg detection. The objective of this paper is to present a method of mapping of icebergs with use of OBIA techniques on high-resolution optical satellite imagery. The novelty of our work is in proposition of a method to detect icebergs in the environment where the spectral contrast between ice and water is not always clearly visible. We develop an inventory of icebergs in a lagoon surrounding the San Quintín glacier and prove its usefulness by deriving size distributions and area–volume scaling laws. We test whether the sizes and relationship between cross-sectional surface area and total volume follow power law in lacustrine setting.
2. Study Area
San Quintín glacier is the largest outlet glacier of Northern Patagonia Icefield (NPI) [25], located in southern Chile (Figure 1). It has an area of 793 km2 and has an extensive tongue that forms much of the ablation area of the icefield [26].
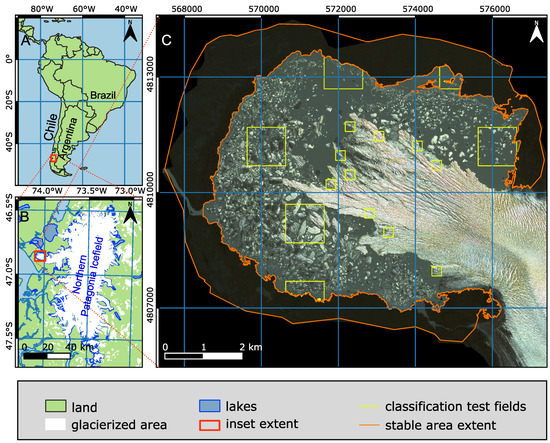
Figure 1.
Map of the study area: (A) location of the Northern Patagonia Icefield within the South America; (B) location of the San Quintín terminus and lagoon in the region; and (C) WV-2 image of the study area. Coordinates of (C) in UTM 18S coordinate system.
The glacier went through a period of oscillation in the 20th century with alternating advance and retreat episodes culminated with a very fast retreat, starting 1995 [27]. A rapid disintegration of the snout occurred between 1999 and 2013, which resulted in San Quintín’s acceleration, greater than in the case of other NPI outlets [28]. The retreat, however, paused between 2013 and 2015, with a part of the snout rapidly advancing [28]. Radar measurements of ice movements showed higher velocity in the middle of the glacier’s tongue compared to its margins and a diverse velocity field at the entrance to the lagoon [29] in line with reports of a variegated advance speed of the snout.
The surface of the lakes at the fronts of San Quintín glacier has increased from 5.42 to 42.37 km2 between 1979 and 2013 together with the glacier’s retreat of 4.5 km [30]. The lagoon into which the glacier terminates is surrounded by push moraines created during the glacier’s advance in the second half of the 20th century [27]. The lake is drained to the Pacific Ocean by a narrow, meandering stream which prevents iceberg evacuation. Consequently, icebergs calved off San Quintín’s snout have no means of escaping the lagoon and remain in the lake for their entire life cycle. Melting of sediment-laden icebergs and influx of meltwater drive large amounts of sediment to the lagoon changing the water’s color. The terminal lagoon of San Quintín increased in area between 1947 and 2011 and is the largest of the proglacial lagoons surrounding NPI [4]. In such environment, OBIA promises better classification results than a pixel-based study thanks to its ability to classify objects by analyzing features other than just spectral response in four bands. The dirty icebergs blend with the dirty water, but they differ from water with their elevation, image texture or contrast between pixels, properties which can only be analyzed within groups of pixels.
3. Data and Methods
3.1. Datasets Used and Imagery Preprocessing
We used a WorldView-2 (WV-2) satellite image composed of a four-band multispectral file and a separate file with the panchromatic band (Table 1). The product was acquired as a set of OrthoReady (OR2A level) images subject exclusively to radiometric and sensor correction [31]. In addition to the multispectral and panchromatic imagery, we included a Digital Elevation Model (DEM) in the study. Our DEM was created with the WorldView-2 stereoimage pair, of which our WV-2 scene was a part. The DEM was created in ERDAS IMAGINE photogrammetry suite with a workflow that included correlation-based matching of two stereoimages [32]. For quality assessment of the DEM, we used a freely available TanDEM-X DEM at 90 m/pixel spatial resolution [33,34].

Table 1.
List of the datasets used for iceberg inventory creation and DEM quality assessment.
For this study, we chose a less oblique photo of the pair (ID 17FEB04145515-M2AS-059470802010_01_P001). We subjected the imagery to a pre-processing routine before any analysis (Figure 2).
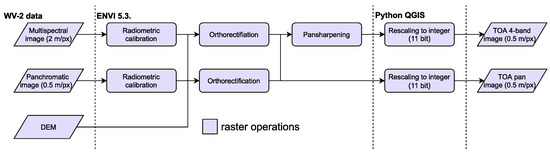
Figure 2.
Procedure of pre-processing applied to the WV-2 images.
The raw images obtained from vendor were radiometrically calibrated to the Top of Atmosphere (TOA) reflectance, orthorectified and the multispectral image was pansharpened to the resolution of the panchromatic band (0.5 m/pixel). We performed these operations in ENVI 5.3. In the orthorectification step, we used the WV-2 DEM as an elevation model. The final product was a pair of orthorectified TOA reflectance images—single-band panchromatic and four-band multispectral—in 0.5 m/pixel spatial resolution. The bitrange of the WV-2 is 11 bits [31] and it was preserved along the whole preprocessing routine. Finally, we computed Normalized Difference Snow Index (NDSI) [36] with use of green and NIR bands.
3.2. DEM Preprocessing
A drawback of all feature-matching DEM generation methods is their unreliability in smooth areas devoid of distinct features [37,38]. In our case, this resulted in a “hilly” topography in areas where flat water table would be expected. We rectified this error semi-manually (Figure 3).

Figure 3.
Procedure of determination of elevation of lagoon’s water table.
Water table elevation was measured as the mean elevation of a 10 m wide strip of pixels distanced 10 m from the coastline. This way we made sure to exclude land area from the calculations. The coastline was outlined with an NDVI mask calculated and digitized in eCogniton. All pixels falling beneath this mask were assigned a unique value of 16.85 m a.s.l. To enable calculation of overwater elevation of icebergs, we created a relative elevation () map (Digital Relative Elevation Model (DREM)). The surface of reference was the level of the water table of the lagoon. Its elevation above the sea level was subtracted from all elevations in the DEM. At the end, we produced a modified DREM. We found artifacts in the original DREM that showed negative relative elevation, probably stemming from incorrect detection of parallax by the stereoimaging algorithm or from movement of icebergs in the short time between acquisition of two stereoimages. We created a DREM0 where all values are replaced by 0.
3.3. DEM Uncertainty Assessment
To assess precision of the DREM, we used freely available TanDEM-X DEM with 90 m/pixel spatial resolution [34] as a reference model (Figure 4). We resampled the WV-2 DEM to the 90 m/pixel of the TanDEM-X DEM and isolated an area of land surrounding the lagoon. This part of the image was assumed to not undergo elevation changes between the date of WV-2 image and TanDEM-X acquisition period and is sufficiently flat to ensure good quality of the radar DEM. We created a map of differences between the two products and filtered it to 10th–90th percentile bounds.

Figure 4.
Procedure of the WV-2 DEM accuracy determination.
We assumed that elevation differences are spatially correlated over a limited distance. Such spatial correlation impacts measurement of averaged difference and its variance [39]. We used a semivariogram-based method of Rolstad et al. [39] to estimate the range of correlation and the variance of the difference between DEM and TanDEM-X DEM (Equation (2)). We computed the empirical semivariogram of the TanDEM-X-WV-2DEM difference map in SAGA, then fitted a synthetic variogram and found its properties in MATLAB. The —standard deviation of the elevation differences—and —a partially-correlated error of the mean difference—served as candidate measures of DREM precision. The method is identical to one used in [38] for assessment of TanDEM-X DEM precision over a small area.
In these equations, is the standard deviation of a spatially non-correlated DEM difference map, is the standard deviation of a partially correlated DEM difference map, is the spatial resolution of our dataset, L is the radius of a circular region whose S equals S of the averaging region and N is the number of pixels included in averaging.
3.4. Iceberg Map Creation
Our method for iceberg map creation and analysis uses several tools for different tasks (Figure 5 and Table A1 in Appendix A).
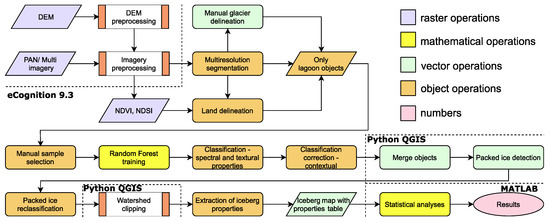
Figure 5.
Entire procedure of iceberg inventory creation. Steps enclosed in white-brown rectangular boxes are shown in detail on other figures.
We used eCognition Developer 9.3. [40] to extract iceberg contours from the imagery. In the first step, we used the Multiresolution Segmentation algorithm to divide the satellite image into a collection of objects. This algorithm works by clumping neighboring pixels according to criteria of similarity of raster values and compactness of the resulting shape [40]. All image bands and DREM were used for segmentation. The abstract parameter of the algorithm governing the size of the resulting segments was set at 100.
As we intended to detect icebergs in the lake, we excluded two land cover categories (Land and Glacier) from the classification. We discriminated land area from the lagoon using the Normalized Difference Vegetation Index (NDVI) [41]. Objects whose mean NDVI was above 0.1 were classified as “Land”, while remaining land cover types (water, glacier, iceberg and sediment-covered ice) remained unclassified. Only these unclassified objects were included in further classifications. In addition, any sections of the image located within the land area where were reclassified to “Land” to avoid contamination of the final results by water puddles or rock outcrops outside the lagoon. We manually added areas of sandy and rocky beaches to the “Land” class after classification, as they were only discovered as members of “Dirty Ice” class when classification was finished.
We outlined the extent of the San Quintín glacier snout manually. The reason for a non-automated discrimination of the glacier was the presence of dense ice melange concentrated in front of the glacier tongue. This area of the image is too chaotic to allow for reliable determination of glacier margin by automated means. We sketched a line along the margin of the glacier, creating a loop of objects enclosing the whole ice body. Thanks to the division of the image into objects, the interpreter did not have to precisely trace the margin pixel-by-pixel, but rather object-to-object, which significantly sped up the digitization effort. All objects inside the hand-drawn boundary were classified as “Glacier” and excluded from the iceberg detection procedure.
We used Random Forest (RF) algorithm implemented in eCognition to divide the set of objects into classes. Random Forest is a supervised classification method, which uses a collection of decision-tree predictors (a forest) to sort objects into classes [42,43]. The eCognition implementation is based on the OpenCV version of the algorithm [44]. We selected manually samples of classes from objects located on the lake. Table 2 shows the classes and their brief characteristics, while Table 3 lists all independent parameters used for training of the algorithm and their importance as reported by the eCognition classifier. At this stage, we performed Principal Component Analysis (PCA) to identify the object properties most important for the classification. We exported the table of properties of the classified objects and ran PCA in MATLAB on the dataset to obtain Principal Components (PC) and the loadings of particular properties on each of the PCs.

Table 2.
Description of image classes used to classify the image objects.

Table 3.
List of properties of image objects used as variables during the Random Forest classification and results of PCA analysis of their importance. “RF imp.” stands for “Random Forest Importance”, as returned by eCognition. Columns 3–6 list loadings of properties in the four Principal Components with largest explained variance in the classified objects dataset. Absolute loadings higher than 0.25 and properties carrying them are shown in bold. All minima, maxima, means and standard deviations are computed from pixels within a single object.
The setting of the San Quintín lagoon—isolated from the ocean—leads to accumulation of sediments brought into the lake with melting icebergs. As a result, the water of the lagoon is spectrally similar to surfaces covered in the local sediment—such as sky-facing surfaces of debris-covered icebergs. Moreover, the setting causes the areas of brash ice—clusters of icebergs too small to resolve on the available images—to look similarly to debris covered iceberg with a mixture of bright and dark objects producing a grainy texture. Therefore, corrections of the initial classification were needed to rectify the misclassified objects. Just as initial classification used statistical properties of the data within the polygons, the correction step looked at the contextual information available on the classified map of objects. We used properties such as neighborhood of particular classes, object shape and number of “holes” inside an object to move objects between classes. In this step, we assigned the objects classified initially as “Shadow” to one of the other classes. While discrimination of shadows cast by icebergs was necessary in the spectral classification step, the shadows themselves do not present value as a separate class of objects, being either sections of icebergs (e.g., in crevasses) or surface of water shadowed by a tall piece of ice. The section of ice melange in the vicinity of the glacier’s margin was also reclassified with use of contextual and spectral rules. The exact extent of this area was selected as a sum of all “Ice”, “Dirty Ice” and “Brash Ice” polygons which touch the glacier margin. These polygons were dissolved in QGIS 3 and used as an area-of-interest template to select objects in eCognition warranting the reclassification. A set of rules, different from the classification correction rules mentioned before, was developed to divide the ice melange area into four classes: “Large Icebergs”, “Small Icebergs”, “Water” and “Brash Ice”. It is worth noting that in this case we did not use any classification algorithm, just a set of rules dividing the population of objects into classes basing on their geometric, spectral and topographic properties.
We exported the shapefile map of the “Iceberg” class (a joint set of “Dirty Ice” and “Ice” classes). The post-processing of shapefile map of icebergs has been done within QGIS 3.8 environment. The polygons in the “Iceberg” class have been merged into a set reflecting the contours of icebergs, regardless of their color. In many cases, the icebergs were touching each another or were in other cases way too close to be correctly separated during the classification, resulting in single polygons covering several icebergs. We used the watershed algorithm to separate the icebergs in such cases. Watershed algorithm is an image analysis method for separation of parts of images which overlap or touch, first proposed by Beucher [45]. We used the OpenCV implementation of the algorithm in the Python 3 language [46].
Our workflow progressed on a “per-berg” basis to avoid memory-intensive graphic processing of the entire high-resolution image (Figure 6). Only icebergs larger than 100 m2 were cut. The division workflow starts with a conversion of the iceberg vector polygon to a binary raster image where the value of “1” corresponds to iceberg presence and “0” to iceberg absence. With morphological erosion, thin “isthmuses” between icebergs were deleted, leading to disconnection of iceberg kernels. The watershed algorithm filled the space between the kernels, leaving pixel-lines in places where contours of recreated iceberg polygons met. These lines were vectorized and used to cut the initial vector iceberg polygon, dividing a shape of connected icebergs into several smaller polygons.
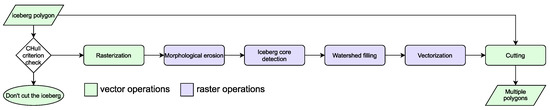
Figure 6.
Procedure of watershed cutting of a single iceberg.
Finally, we imported the divided iceberg map to eCognition and extracted statistical properties (Table 3) of pixel populations enclosed by the iceberg contours. Additionally, we computed the volume of each iceberg with use of the Equation (4):
where V (m3) is the iceberg’s entire (under- and overwater) volume, (m) is the mean elevation above the water table and S (m2)—the surface area of the waterline cross-section. We assumed ice density kg m−3 and water density kg m−3, as the lagoon is filled with fresh water. This amounts to an assumption that 90% of iceberg volume is submerged.
The mean relative elevation of an iceberg was multiplied by 9 to obtain iceberg’s total height. The lower multiplier in this case stems from an assumption of irregular shape of an iceberg. The draft of an iceberg computed by multiplying its freeboard by the ice density ratio was shown to overestimate the iceberg’s depth [47].
3.5. Iceberg Map Uncertainty Assessment
We provide two measures of uncertainty of the iceberg map created with the method described above: the error of the number of icebergs detected by the algorithm and the error of the surface area of an extracted iceberg. To obtain these values, we compared the classified iceberg map to a manually created map. Such approach has been previously used [24], albeit our procedure is not identical to it. We divided the area of the lagoon without the proximal ice melange field into a grid of squares with 500 m long sides. We randomly chose 10% of the squares as verification fields (VF, see Figure 1) and manually digitized all icebergs located within them on the map of segments produced in eCognition. A manual map of icebergs was exported as a shapefile and compared to a subset of the iceberg inventory overlapping with the VF. We calculated area error by overlying the two shapefiles and subtracting the areas of the overlapping polygons. We also counted false positives and false negatives. The former are icebergs from the automatically classified dataset which do not overlap with any icebergs from the manual dataset. The latter are those of the manually digitized polygons that do not have counterparts in the classified dataset. The same procedure was repeated on the ice melange area but with a grid of 250 m wide squares. We calculated area error by comparing areas of polygons of icebergs produced by classification () with area of manually digitized iceberg polygons (). To ensure comparability between area errors between many size scales, we computed unitless relative error of area () with Equation (5).
Histograms of frequency of area were produced, as well as 2D histograms of to present the classification quality assessment results.
3.6. Data Filtering
Before fitting area–volume scaling model, we applied filters to the obtained iceberg inventory to discard cases, which were unreliable due to the DREM imperfection:
- We used k-nearest neighbors (knn) clustering algorithm to discard outlying data points. All items which had fewer than four neighbors within radius of 0.2 in the log area–log volume space were considered outliers.
- All icebergs with were discarded. We assumed objects to be unreliable when their elevation measurements are below the precision of the DREM.
- We filtered out icebergs which were unrealistically high with respect to their width. We used a formula proposed in [48] (Equation (6)) for the critical width/height ratio at which an iceberg capsizes. We assumed that any iceberg with width/height below the critical ratio should capsize and thus the elevation measurement is not realistic.where is the critical ratio, equal to under our assumed ice and water densities.
In addition, we divided the iceberg population into sub-populations of small and large icebergs. To determine the threshold for the division, we created a volume variance signal by sorting the dataset by area and computing mean volume variance within a 100-wide running window. We found a change point (Vvar) in this signal by dividing the signal into two parts at many candidate points and choosing the one at which the sum of deviations from the mean within each section is minimal.
3.7. Area and Volume Distribution
We investigated statistical distributions of volume and area of icebergs with use of powerlaw package implemented in Python 3 programming language [49]. This suite of functions uses fitting methods described by Clauset et al. [50] to accurately fit power law, exponential and log-normal distributions to datasets. We fitted power law, exponential, log-normal and exponentially truncated power law to the vectors of surface area and volume of icebergs. Both datasets were filtered to remove icebergs smaller than 4 m2 (corresponding to 1 pixel on the 2 m/pixel DEM, smallest available size). We assessed the quality of fit of the curves with Kolmogorov–Smirnov (K-S) measure provided by the power law [49]. In addition, normal distribution curves were fitted to histograms of logarithm of area and volume of filtered dataset with the least squares method in MATLAB. Only icebergs larger than 1 m2 were used for the fitting effort.
3.8. Area–Volume Scaling
We searched for the area–volume scaling model with use of MATLAB. We fitted models to the area–volume data points in two cases: with volumes computed with DREM and DREM0. We fitted power law model to the entire unfiltered inventory, to the unfiltered sections on the two sides of the Vvar threshold and to the fully filtered dataset. In addition, a linear model was fitted to the log area–log volume filtered data. The fits were performed with non-linear least squares method in case of power law fitting and linear least squares for log-log model fitting. We used two measures to assess the quality of fitted models:
- of the fit; and
- —the product of k-fold cross-validation (CV) of a model. We divided the area–volume dataset into 10 subsets (folds) and performed the fitting with 9 subsets leaving one of them out for verification. of the volumes computed with the fitted line vs. the measured volumes was computed at each of the repetitions and the mean of these s is reported as .
4. Results
4.1. DEM Accuracy Assessment
The pixel-wise difference between WV-2 DEM and TanDEM-X 90 DEM does not follow a normal distribution (Figure 7). Thus, the typical measures of bias and precision of an elevation model, mean and standard deviation of , could not be used as DEM quality measures. The second reason against these values is the presence of spatial correlation within the elevation models. It invalidates the use of as precision measure, as this value is computed under assumption of lack of spatial correlation of individual pixels. We calculated the correlation distance to be 1381.15 m on the difference map. The parameters of semi-variograms led us to a value of the m, used as a measure of DREM precision further on.
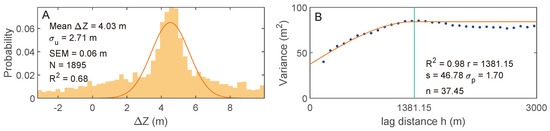
Figure 7.
Results of the accuracy assessment of the WV-2 DEM as compared to the TanDEM-X 90 m/pixel DEM: (A) histogram of the values of the WV-2 DEM-TanDEM-X DEM difference map, where the orange line represents the normal distribution fitted to the histograml and (B) empirical (blue dots) and fitted (orange line) semivariogram of the same difference map with parameters of the fitted synthetic variogram, where the green line indicates the correlation range.
4.2. Dataset and Filtering
The iceberg inventory consists of over 38,000 records (Figure 8 and Table 4) each corresponding to a single detected iceberg. the majority of icebergs are between 10 and 1000 m2 of area with just around 24% of cases outside these bounds. The largest icebergs ( m2) contribute only under 1% of the unfiltered dataset.

Figure 8.
Final result of the iceberg map creation process: (A) example of iceberg map in the lagoon area; (B) example of iceberg map in the ice melange area; and (C) the overview of the classification over the whole lagoon and its surroundings. Coordinates in UTM 18S coordinate system.

Table 4.
Statistical summary of the subsets of icebergs generated by different filtering methods.
The impact of the three filters on the dataset has been highly variable, as each filter discards a different subset of icebergs (Figure 9). The k-nearest neighbors filter eliminates only a small number of data points outlying from the clustered bulk and its impact is the lowest of the three filters. Elimination of the icebergs with mean elevation below the precision of the DREM trims the entire lower part of the cluster, corresponding to almost 70% of all data points (Figure 9).
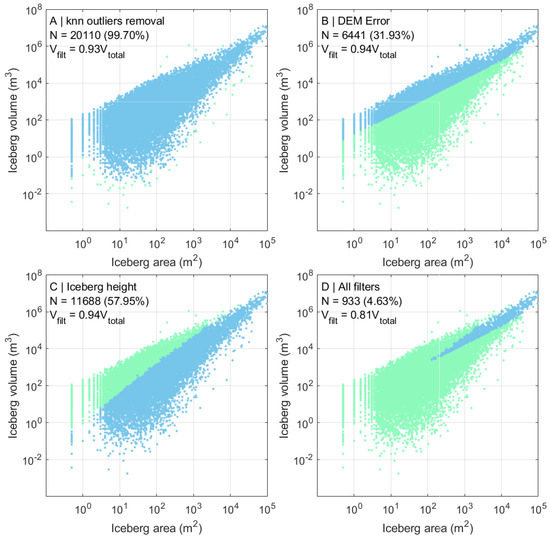
Figure 9.
Subsets of the area–volume dataset produced by applying different filters. Discarded data points shown in green: (A) outliers removal with knn clustering; (B) icebergs with m removed; (C) icebergs with width/height ratio below 0.73 removed; and (D) all filters applied together. Discarded points shown in green, and the accepted ones in blue.
Despite that, the icebergs remaining in the pool constitute 94% of the entire volume of icebergs found in the lagoon. The iceberg stability filter operates in an opposite manner to the previously described one. What remains after removal of the icebergs too high to be stable from the dataset, are the data points located in the lower part of the cluster and a subset of the largest icebergs (Figure 9). This filter is less restrictive than the DEM Error (over 57% of icebergs remaining) but the summary volume of the remaining icebergs is slightly lower (92% of the total). Application of all three filters to the dataset leaves only a small group of 933 icebergs, corresponding to 4.63% of the entire sample (Figure 9), which is, however, responsible for nearly 80% of the total volume of the lagoon’s floating ice.
4.3. Classification Accuracy Assessment
The overall number of icebergs detected by the classification in the open-lagoon verification fields is very close to the number produced by manual digitization within the open-lagoon VF (3184 vs. 3213 icebergs, Table 5). The icebergs’ frequency of occurrence for particular sizes is also similar between the manually and the automatically mapped icebergs (Figure 10). The only exception is underestimation of the number of icebergs with the sizes in the 5–15 m2 range. This is the size band in which the majority (247) of false negatives are found. A sizeable group of undetected icebergs (151) is also present among the smallest growlers (0–5 m2). These two groups account for the underestimation of iceberg count in these bands on the histogram. The remaining 96 false positives are all below 300 m2.

Table 5.
Quantities of icebergs used in classification quality assessment. Ncla stands for number of classified icebergs, Nman – number of manually digitized icebergs and VF – Verification Fields.
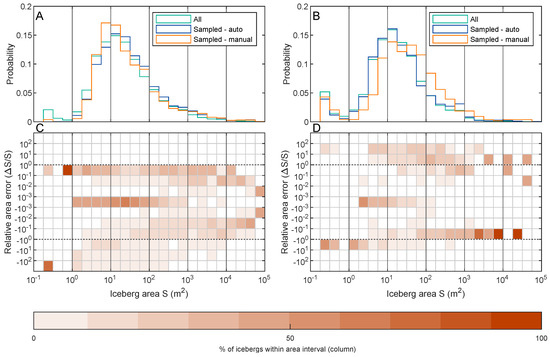
Figure 10.
Results of quality assessment of iceberg map: (A,B) histograms of frequency of iceberg areas; and (C,D) 2D histograms of unsigned relative error of manually digitized icebergs compared to automatically mapped ones. Plots (A,C) relate to the lagoon, while (B,D) to the fields of ice melange. Dashed lines show the lines of 100% relative error. Values within each column add up to 100%. Relative differences were computed as . X-axis divisions spaced by equal for histogram readability.
The area error increases gradually with the increase of area of a manual iceberg (Figure 10). A trend of positive area errors close to or at 100% of the actual area (indicating detected icebergs significantly smaller than their manual counterparts) is a trace of the false negatives. Relative area errors of icebergs in the lagoon assume diverse, mostly negative, values but are concentrated between and 1.
The classification method used in the ice melange area performed visibly worse than the RF-classification of the lagoon. It has to be noted, however, that the RF-classification on the ice melange region returned an entirely unreliable map of "icebergs" consisting only of a few very large polygons with holes filled with brash ice inside and between them. The histogram of manually picked icebergs is shifted, showing that the ruleset we used underestimates the number of large icebergs and overestimates frequency of small ones (Figure 10). Contrary to the lagoon area, in this case, the errors of area compared to manually picked bergs are less diverse in the large area bands and decidedly higher for the small icebergs than for the big ones. The largest error of this case is a large overestimation of the total number of iceberg compared to the manual set (Table 5). Many of the classified polygons overlap partially with the manual polygons. This explains low number of false positives.
In both cases, the area frequency of the whole iceberg populations are nearly identical to the frequencies of the automatically classified populations from within the verification fields showing the representativeness of the verification areas for the entire dataset. The percentage of verification icebergs relative to the entire inventory (8.21% in the lagoon and 18.35% in the ice melange region) is also satisfactory.
Four principal components explain over 97% of variability between the classified objects (Table 3). Results of PCA show that reflectances in the visual bands are the most important feature of objects for the Random Forest classifier. Minima and maxima of the red, green, blue and panchromatic bands bear highest loadings on the four PCs (Table 3). Among the other properties, only GLCM Contrast and Border Contrast on the panchromatic band are important for the PC values, although only in the final two PCs, which are together responsible for only about 3% of the overall variability.
4.4. Area and Volume Distribution
The statistical distribution which fits both the area and volume histograms best is the log-normal distribution, as evidenced by the highest K-S measures of all tested models (Figure 11 and Figure 12). In the case of area distribution, K-S = 0.03, while, for volume distribution, it is slightly higher (K-S = 0.04). In both cases, the value is lower than that of exponentially truncated power law (K-S = 0.08 in both cases). Goodness measures of power law and exponential distributions are several times higher than those of log-normal distributions. Exponential distribution shows the poorest fit to the area frequency among the four tested models (K-S = 0.54). The very poor fit of power law to volume histogram is worth noting. Its K-S (0.50) is higher even than that of the exponential model (0.46). The area distribution seems to adhere to power law on a limited section, but the model fails to recreate the tail of the dataset, corresponding to the largest icebergs (Figure 11). In the case of distribution of volume, the log-normal distribution seems imperfect at the extreme ends of the distribution, near the smallest and largest icebergs (Figure 12).
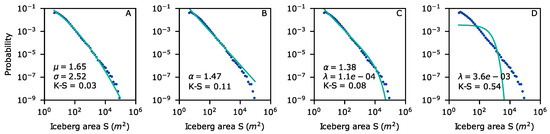
Figure 11.
Fitting of heavy-tailed distributions (green lines) to logarithmically binned area data (blue dots): (A) log-normal ; (B) power law ; (C) exponentially truncated power law ; and (D) exponential .
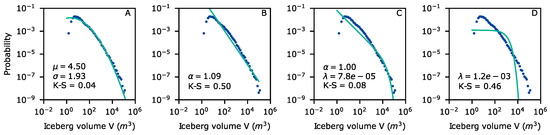
Figure 12.
Fitting of heavy-tailed distributions (green lines) to logarithmically binned volume data (blue dots): (A) log-normal ; (B) power law ; (C) exponentially truncated power law ; and (D) exponential .
The log-normality of these distributions is confirmed by fitting the normal distribution curves to the histograms of logarithms of the respective measures (Figure 13 and Figure 14). These achieve high values (over 0.9) regardless of whether a complete or filtered dataset is used. The exception to that is the filtered dataset of DREM0-based data where the of the Gaussian distribution fitted to the area and volume histogram are and .
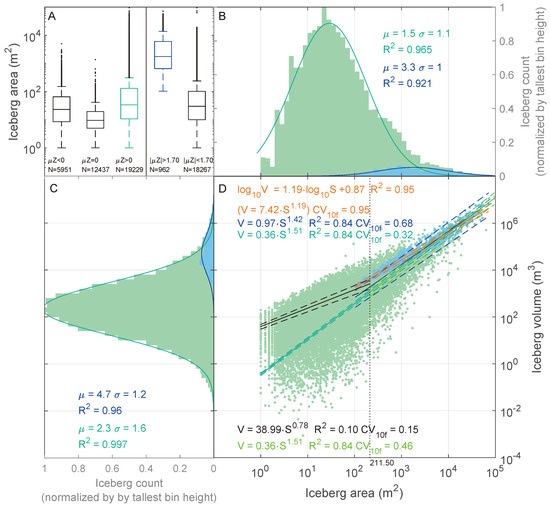
Figure 13.
Results of filtering and model fitting to the area–volume data. Unmodified DREM with negative values used: (A) area distributions of iceberg classes selected by ; (B) histograms of iceberg area; (C) histograms of iceberg volume; and (D) power law relationship fitted to the area/volume data. Green fields indicate whole dataset, blue—data filtered. Green lines are models (Gaussian distributions in (B,C), power law models in (D)) fitted to unfiltered data, blue—to the filtered data. Orange line is a linear model fitted to the log-log data. Dashed lines indicate 95% confidence intervals of fitting.
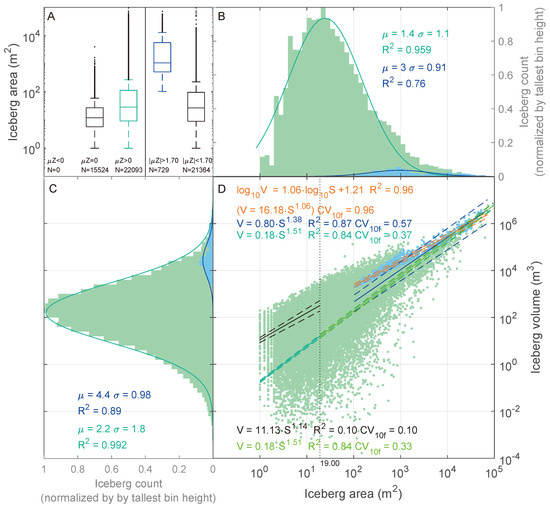
Figure 14.
Results of filtering and model fitting to the area–volume data. DREM0 with negative values replaced with 0 used: (A) area distributions of iceberg classes selected by ; (B) histograms of iceberg area; (C) histograms of iceberg volume; and (D) power law relationship fitted to the area/volume data. Green fields indicate whole dataset, blue—data filtered. Green lines are models (Gaussian distributions in (B,C), power law models in (D)) fitted to unfiltered data, blue—to the filtered data. Orange line is a linear model fitted to the log-log data. Dashed lines indicate 95% confidence intervals of fitting.
4.5. Area–Volume Scaling
Replacement of negative relative elevation () values with 0 in DREM0 distorts the log-normality of the volume distribution by introducing to the population a large number of small icebergs. This is manifested by a slightly lower of the Gaussian distribution fitted to the histogram of the modified volumes and over-representation of low-volume cases. (compare Figure 13 and Figure 14). The number of icebergs with is also higher when the modified DREM is used, showing large population of icebergs which did not contain any positive DREM values within their outlines. On the other hand, the population of icebergs (green box plots in Figure 13 and Figure 14) has also increased, hinting at presence of cases where the negative values over-weighed positives on DREM, but the positive values shifted the mean above 0 in DREM0. Apparently, certain number of such individuals is found even in the filtered dataset, among the fairly large ( m2) icebergs, as evidenced by lowering of median iceberg area in the filtered dataset used for fitting (Figure 13 and Figure 14). The imperfections introduced to the dataset and uncertain status of the negative measurements led us to assume the unmodified DREM as the basis for further analyzes.
The choice of a fitting method of the model visibly impacts the result. The linear model fitted to the logarithms of the areas and volumes () shows better than power law models fitted to the untransformed data and performs better in the K-fold cross-validation test (Figure 13). Depending on the subset of data and fitted model, the area–volume scaling model assumes different values and its quality varies. The best fit is achieved by a linear model fitted to the logarithms of areas and volumes. The log-linear model fitted to the filtered dataset achieves better fit () and performance (K-fold CV score ) than other models. This model can be transformed into a power law form of . The power law scaling laws assume different forms when fitted to the different subsets of the inventory. The power law fitted to the same filtered dataset as the log-linear model produces best quality measures (). This variant has the widest confidence intervals and visibly deviates from the point cloud below 1000 m2 of area. A model fitted to the whole dataset with the scaling formula sports similar , but much worse .
We fitted two additional scaling models using the unfiltered dataset bisected with the volume-variance threshold. These yielded two very different products. The model fitted to the subpopulation of small icebergs ( m2) performed very poorly (), its scores lowest of all fits. The model based on the large icebergs, in turn, has identical formula to the model fitted to the entirety of the dataset, albeit with wider fitting confidence intervals (). Its is also identical, while differs in favor of the more limited model.
5. Discussion
5.1. Iceberg Classification
Results of the classification present that the Random Forest classification of objects gives very good results in iceberg detection in environments where the floating icebergs can be easily discerned from the background (water). In areas where icebergs are crowded without much space between them and in the presence of small growlers lying on top of large icebergs, neither Random Forest classification nor manually tuned classification ruleset could succeed in correctly discerning individual objects. A challenge encountered in the setting of the San Quintín lagoon was the spectral similarity of the sediment-laden water to the sediment-covered icebergs. While in most cases the elevation criterion was a sufficient determinant of whether an object belongs to the “Dirty Ice” or “Water” class, the objects located in the icebergs’ marginal zones were often flat. We have tackled this problem at the post-processing stage of classification by eliminating objects which were located between “Water” and “Dirty Ice” classes and had very elongated shape (length to width ratio greater than 3). These cases represented sections of image where an intensity gradient was present between the darker iceberg and more uniform water. The segmentation algorithm separated such group of pixels as an entity separate from the wide, uniform field of water and different from the more grainy surface of the iceberg. At the same stage we eliminated from the “Ice” class objects which represented underwater ice visible as gradient of brightened water color. Due to lagoon water’s spectral similarity to the debris, these underwater portions of clear, white ice were often classified as “Dirty Ice”. We predict that our method will perform better on imagery of fjords where reflection from deep and dark water contrasts strongly to very bright ice.
The same spectral overlap hindered the multi-scale approach to object-based classification. In this method, the image is segmented and classified several times with smaller or larger objects at each level in order to detect icebergs of different size [6]. On our image, where borders between icebergs and water are sometimes fuzzy, large scale classifications, instead of separating largest icebergs from their surroundings, produced polygons which included sections of water or brash ice within the “Dirty Ice” class. Therefore, we had to classify the entire image at a low level—subdivided into a larger number of smaller objects—to detect subtle borders between debris-covered icebergs and their surroundings.
Our attempt at mapping icebergs tightly packed in the area proximal to the San Quintín glacier snout has not been fully successful. In large parts of this region ice melange resembles more a continuous field of bright ice than a collection of discrete icebergs or a grainy section of small ice pieces similar to brash ice. In others, the borders between particular icebergs, or even between the glacier and free-floating ice, were challenging to discern even by visual inspection, not to mention automated methods. The lack of clearly delimited shapes together with a spectral and textural similarity of image sections led to imperfect segmentation and erroneous classification. The properties of very tightly packed, bright ice melange are very similar to those of solid pieces of clear ice. Therefore, the classification algorithm has problems differentiating between these two surface types. Actual icebergs, and only large specimens, could be separated in the ice melange environment by following edges and shadows. A different method of detection would be needed for such cases, one that would unify OBIA with pixel-based methods such as edge detection and denoising.
Our workflow as presented in this work relies on many different software suites. Use of proprietary eCognition and MATLAB was motivated by their interactivity—it was possible for us to control quality of the outputs at each stage of the development of the method. As the method relies on generic algorithms (intensity-based segmentation, Random Forest classifier, Watershed cutting and property-based object reclassification), it could be theoretically implemented within a single environment, e.g. in Python programming language, in which all necessary algorithms are already available as existing libraries [43,46,51]. This article demonstrates the use of our proposed method on very high resolution image of lacustrine icebergs. There are however no technical reasons that would prevent upscaling the study to a different environment (tidewater calving), larger size or number of lakes and imagery with different spatial resolutions. Together with the aforementioned possibility of translating our method to a more unified software environment, we believe in very wide applicability of the proposed workflow.
Pre-eminence of reflectance as most important property during RF classification further lifts hopes for use of our method on different and larger datasets. DEMs are not always readily available, particularly in multi-temporal studies. Large loadings of maximum and minimum of reflectances in visual bands demonstrate that OBIA carries added value to the iceberg detection efforts. Division of polygons into classes can be done more effectively when statistical properties of pixels within objects can be used than just by comparison of reflectances of individual pixels. In the San Quintín lagoon where spectral differences between icebergs and water are not always unambiguous, statistical measures derived from populations of pixels provide more reliable means of differentiating between water (where difference between highest and lowest reflectances within an object is low), ice (with low reflectivity range but high minimal reflectivity) and dirty ice (where low maximum reflectivity with potentially high range of values can be expected)
5.2. Iceberg Inventory
Our iceberg inventory is a reliable source of knowledge about areas and spectral or textural properties of icebergs in the open part of the terminal lagoon of San Quintín glacier. The object-based iceberg mapping allows for collection of diverse information about icebergs that can be used for glaciological studies. The in-depth analysis of relationships between these properties is outside the scope of this work. A potential use for a high resolution iceberg inventory is as a training set for lower-resolution remote sensing exercises. A 10-30-meter-wide Sentinel or Landsat pixel can contain clear water, several very small icebergs or a part of a big one, with a possibility for clear and dirty ice in each case. Spatially detailed inventory could be used to produce datasets of iceberg density or color in grids collocated with a lower resolution image. Such basemaps could be used to improve assessment of iceberg coverage with popular medium- and low-resolution spaceborne sensors. A similar work could be conducted to create maps of surface properties relevant for radar imaging (such as volume or angularity within a pixel), if iceberg elevation data were available.
The results of the filtering show great importance of the large icebergs for the calculation of the total volume of the floating ice. This is a consequence of the heavy-tailed distribution the set adheres to. Very wide range of size scales, ranging from less than 1 m2 to several tens of thousands m2, means that a single, very large iceberg will contribute more ice to the lake than even several hundred smaller ones. The relationship is even more pronounced when ice volume is considered, a property which has higher order of magnitudes, and thus higher absolute differences between largest and smallest cases. Despite the very restrictive filtering imposed upon our iceberg inventory, resulting low fraction of reliable records accounts for nearly 80% of the ice in the lagoon. This value might, however, be inaccurate due to the uncertainty of height of the icebergs. Fitting of a power law model to the subset of small icebergs showed very little correlation between their areas and volumes. This lack of relationship is an argument for their exclusion from the scaling law determination. In the realm of small areas and low freeboards, the 1.7 m of DEM uncertainty introduces noise much stronger than the actual signal.
5.3. Volume Assessment
The quality of the DEM is a constraint on the calculation of the area–volume relationship. Filtering of icebergs lower than the 1.7 m threshold of precision effectively eliminated the majority of small icebergs. The criterion of iceberg stability also favors large icebergs, filtering out the small and tall ones. The large number of unrealistically tall icebergs testifies to overestimation of elevation by our DEM. The low precision naturally impacts small, low icebergs the most. At the critical width/height ratio of , the precision limit of m of overwater height translates to a minimum width of a stable iceberg at m m, leading to the minimal critical area of m2 of waterline cross-section area assuming perfectly cylindrical model of iceberg. Any smaller iceberg taller than the 1.7 m would be forced to capsize. Thus, 99 m2 is a theoretical lower limit of iceberg area about which meaningful elevation information can be obtained from our DREM. Despite the availability of icebergs as small as 4 m2 in our inventory, the precision of the DEM (1.7 m as compared to TanDEM-X DEM) limited our fitting effort to just the icebergs taller than the precision limit and larger than 99 m2. In the case of large icebergs, the very large number of pixels and high general elevation diminishes the impact of elevation uncertainty on the volume estimate. Moreover, large icebergs tend to have rich texture which lends more potential tie-points to the stereo correlation algorithm used to produce DEM. The elevations detected on highly crevassed or multi-colored icebergs can thus be considered more reliable than those computed from uniformly colored ones, particularly dark ones easily blending with surrounding water.
5.4. Area–Volume Scaling and Distributions
It was shown on an example of a tidewater glacier that the the distribution of iceberg size is different close to the calving terminus (iceberg source) than in sections of fjord farther away from a glacier [15]. Close to the source, the size of fresh icebergs follows power law distribution, which changes to log-normal as the distance from the calving front increases and icebergs have more time to decay. A pronounced log-normal distribution visible in our dataset (both areas and volumes) suggests that the old icebergs dominate the population. This is an expected result, as the lagoon serves as a trap in which icebergs decay in nearly unchanged conditions for their entire life cycle without removal of old bergs by other means than melting into the lake. It was shown that calving rates of lacustrine calving fronts are typically smaller than those of tidewater glaciers [52], albeit lake terminating glaciers calving more intensely than neighboring tidewater ones were also reported [53]. These factors working together mean that, compared to a typical marine-terminating glacier, we are looking at an increased number of old icebergs and decreased influx of fresh ice bodies. These trends increase proportion of old icebergs in the overall population and strengthen the log-normality of the distribution.
Kirkham’s iceberg inventory had its lower bound at around 900 m2 of waterline cross-sectional area [15], while our dataset extends the range of sizes down to 4 m2 hinting at universality of the physical processes that lead to the log-normal size distribution of older icebergs. Not only does the law hold in smaller sizes, it is also possible to find it in a lacustrine setting in temperate climate zone where conditions for iceberg decay are drastically different than in an Arctic fjord.
Better and scores of linear model fitted to log-log data than of power law model fitted to untransformed data hints that the power law might not be the optimal model to explain the relationship between waterline cross-sectional area of an iceberg and its total volume. The straight line on a log-log plot, often assumed as the prime indicator of the presence of a power law, can appear also when other models are actually involved [50], as evidenced by our investigation of the distribution of the iceberg sizes. It is often the case that a power law holds only over a section of the dataset, while the extreme ends deviate from this trend [50]. There is a possibility that power law is a sufficient model to explain area–volume scaling over only a portion of the iceberg population we used for fitting. In such case, below (or above) some size threshold a different mathematical relationship would take over.
Sulak et al. [18] performed a area–volume scaling exercise similar to ours on a population of icebergs derived from Landsat imagery and a WV-2 based DEM. The exponents obtained by these authors were spread between 1.26 and 1.33. Our values of and provide a similar, but wider range. Both the models of Sulak et al. [18] and ours were fitted to a multi-scale population of icebergs (size range between and m2) with the least squares method. This fitting technique minimizes squares of residuals between the observed and modeled values. In a multi-scale study such as iceberg size analysis, the residuals in the heavy tail of the population (where absolute values of areas and volumes are very high) are much higher than in the lower orders of magnitude. Therefore, an algorithm intended to minimize these residuals will always favor fits that perform well in the region of very big icebergs and will neglect smaller ones. This approach is not necessarily bad when one tries to model the overall volume of ice because, as briefly shown above, the largest icebergs contribute the majority of ice volume in the set. This behavior of least squares is also highlighted by identical formulas of the power law model fitted to the entire population of icebergs and just the m2 part (Figure 13). The weight of the largest icebergs is so great that the addition of a large, uncorrelated subset to the fitting did not change the course of the line. The specifics of least-squares fitting may be the reason why fitting a linear model to log-log data performed better. In this case the least squares algorithm operates on a range of values within a single order of magnitude (from to in our dataset), which does not involve the scale problems and leads to a more robust fit.
6. Conclusions
We present a method of classification of lacustrine icebergs within object-based image analysis paradigm. We propose Random Forest classification, context-based corrections and watershed cutting as a workflow to classify open-water icebergs. Our method correctly estimates the number of icebergs in the image and provides decent measurements of their cross-sectional area. The disappointing performance of ruleset-based classification of ice melange region demonstrates the need of a specialized approach to iceberg detection in cases of densely packed icebergs. An object-based inventory of icebergs can serve as a rich source of optical and geometrical information about the studied objects. High impact of reflectance information, as compared to elevation or image texture, on the result of classification gives hope that the workflow could be used with diverse datasets. Universality of the method is realized by its reliance on generic algorithms, which allows it to be implemented within various programs or programming languages.
We used our method to map icebergs floating in the lagoon surrounding the snout of San Quintín glacier, NPI. We show that log-normal distribution is the best approximation of iceberg area and volume frequencies in a population of lacustrine icebergs. This result suggests that there are mostly old icebergs in the lake and the iceberg decay may follow universal principles regardless of whether it occurs in freshwater or in a marine setting.
We found a power law relationship between iceberg area and volume in the form of . The values of the parameters are in line with an earlier publication. Nevertheless, our model comes from conversion of a linear trend fitted to the of the iceberg volumes and waterline cross-sectional areas. This, as well as a limited size range of the data valid for fitting (only icebergs larger than 99 m2), leaves open a question of whether the power law is the best model of the scaling. More work with more precise elevation models would be needed to accurately constrain the model and extend it to smaller icebergs and growlers.
Author Contributions
J.P. wrote all computer code, performed most of analyses and wrote the majority of the manuscript. M.P. conceived the idea of the work and designed the study, provided data and contributed to manuscript writing and interpretation of results. All authors have read and agreed to the published version of the manuscript.
Acknowledgments
This work was funded with ANID FONDECYT INICIACIÓN 11170937 grant and was partially financed as a part of the statutory activity from the subvention of the Ministry of Science and Higher Education in Poland. CECs is a non-profit research organization funded by the Basal Finance program of ANID, among others. JP is supported by International Environmental Doctoral School associated with the Centre for Polar Studies at the University of Silesia in Katowice. We thank Johannes Reinthaler for preparing the WV-2 DEM.
Conflicts of Interest
The authors declare no conflict of interest. The funding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript and in the decision to publish the results.
Appendix A

Table A1.
Summary of processing steps, tools used for their execution and input data at each step.
Table A1.
Summary of processing steps, tools used for their execution and input data at each step.
| Processing Step | Tool | Input Data | Flowchart |
|---|---|---|---|
| WV-2 imagery preprocessing | ENVI 5 | WV-2 raw images | Figure 2 |
| DREM creation | QGIS 3.10 | WV-2 DEM | Figure 3 |
| DREM uncertainty assessment | QGIS 3.10, SAGA, MATLAB | WV-2 DEM, TanDEM-X DEM | Figure 4 |
| Image segmentation and classification | eCognition 9.3 | WV-2 processed images, DREM | Figure 5 |
| Watershed cutting | Python 3 | Shapefile map of icebergs | Figure 6 |
| Iceberg detection quality assessment | MATLAB | Cut shapefile map of icebergs | - |
| Iceberg properties extraction | eCognition 9.3 | Cut shapefile map of icebergs | Figure 5 |
| Statistical analysis | MATLAB | Table of iceberg properties | - |
References
- Warren, C.; Benn, D.; Winchester, V.; Harrison, S. Buoyancy-driven lacustrine calving, Glaciar Nef, Chilean Patagonia. J. Glaciol. 2001, 47, 135–146. [Google Scholar] [CrossRef]
- Benn, D.I.; Warren, C.R.; Mottram, R.H. Calving processes and the dynamics of calving glaciers. Earth-Sci. Rev. 2007, 82, 143–179. [Google Scholar] [CrossRef]
- Trüssel, B.L.; Motyka, R.J.; Truffer, M.; Larsen, C.F. Rapid thinning of lake-calving Yakutat Glacier and the collapse of the Yakutat Icefield, southeast Alaska, USA. J. Glaciol. 2013, 59, 149–161. [Google Scholar] [CrossRef]
- Loriaux, T.; Casassa, G. Evolution of glacial lakes from the Northern Patagonia Icefield and terrestrial water storage in a sea-level rise context. Glob. Planet. Chang. 2013, 102, 33–40. [Google Scholar] [CrossRef]
- Schoolmeester, T. The Andean Glacier and Water Atlas: The Impact of Glacier Retreat on Water Resources; UNESCO GRID-Arenal: Paris, France; Arendal, Norway, 2018. [Google Scholar]
- Mazur, A.; Wåhlin, A.; Krężel, A. An object-based SAR image iceberg detection algorithm applied to the Amundsen Sea. Remote Sens. Environ. 2017, 189, 67–83. [Google Scholar] [CrossRef]
- Soldal, I.; Dierking, W.; Korosov, A.; Marino, A. Automatic Detection of Small Icebergs in Fast Ice Using Satellite Wide-Swath SAR Images. Remote Sens. 2019, 11, 806. [Google Scholar] [CrossRef]
- Neuhaus, S.U.; Tulaczyk, S.M.; Begeman, C.B. Spatiotemporal distributions of icebergs in a temperate fjord: Columbia Fjord, Alaska. Cryosphere 2019, 13, 1785–1799. [Google Scholar] [CrossRef]
- Scheick, J.; Enderlin, E.M.; Hamilton, G. Semi-automated open water iceberg detection from Landsat applied to Disko Bay, West Greenland. J. Glaciol. 2019, 65, 468–480. [Google Scholar] [CrossRef]
- Köhler, A.; Pętlicki, M.; Lefeuvre, P.M.; Buscaino, G.; Nuth, C.; Weidle, C. Contribution of calving to frontal ablation quantified from seismic and hydroacoustic observations calibrated with lidar volume measurements. Cryosphere 2019, 13, 3117–3137. [Google Scholar] [CrossRef]
- Minowa, M.; Podolskiy, E.A.; Sugiyama, S.; Sakakibara, D.; Skvarca, P. Glacier calving observed with time-lapse imagery and tsunami waves at Glaciar Perito Moreno, Patagonia. J. Glaciol. 2018, 64, 362–376. [Google Scholar] [CrossRef]
- Mallalieu, J.; Carrivick, J.L.; Quincey, D.J.; Smith, M.W. Calving Seasonality Associated with Melt-Undercutting and Lake Ice Cover. Geophys. Res. Lett. 2020, 47. [Google Scholar] [CrossRef]
- Dowdeswell, J.A.; Forsberg, C.F. The size and frequency of icebergs and bergy bits derived from tidewater glaciers in Kongsfjorden, northwest Spitsbergen. Polar Res. 1992, 11, 81–91. [Google Scholar] [CrossRef]
- Tournadre, J.; Bouhier, N.; Girard-Ardhuin, F.; Rémy, F. Antarctic icebergs distributions 1992–2014. J. Geophys. Res. Ocean. 2016, 121, 327–349. [Google Scholar] [CrossRef]
- Kirkham, J.D.; Rosser, N.J.; Wainwright, J.; Jones, E.C.V.; Dunning, S.A.; Lane, V.S.; Hawthorn, D.E.; Strzelecki, M.C.; Szczuciński, W. Drift-dependent changes in iceberg size-frequency distributions. Sci. Rep. 2017, 7, 1–10. [Google Scholar] [CrossRef]
- Crocker, G. Size distributions of bergy bits and growlers calved from deteriorating icebergs. Cold Reg. Sci. Technol. 1993, 22, 113–119. [Google Scholar] [CrossRef]
- Stern, A.A.; Adcroft, A.; Sergienko, O. The effects of Antarctic iceberg calving-size distribution in a global climate model. J. Geophys. Res. Ocean. 2016, 121, 5773–5788. [Google Scholar] [CrossRef]
- Sulak, D.J.; Sutherland, D.A.; Enderlin, E.M.; Stearns, L.A.; Hamilton, G.S. Iceberg properties and distributions in three Greenlandic fjords using satellite imagery. Ann. Glaciol. 2017, 58, 92–106. [Google Scholar] [CrossRef]
- Blaschke, T.; Hay, G.J.; Kelly, M.; Lang, S.; Hofmann, P.; Addink, E.; Feitosa, R.Q.; van der Meer, F.; van der Werff, H.; van Coillie, F.; et al. Geographic Object-Based Image Analysis—Towards a new paradigm. ISPRS J. Photogramm. Remote Sens. 2014, 87, 180–191. [Google Scholar] [CrossRef]
- Rastner, P.; Bolch, T.; Notarnicola, C.; Paul, F. A Comparison of Pixel- and Object-Based Glacier Classification With Optical Satellite Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 853–862. [Google Scholar] [CrossRef]
- Robson, B.A.; Nuth, C.; Dahl, S.O.; Hölbling, D.; Strozzi, T.; Nielsen, P.R. Automated classification of debris-covered glaciers combining optical, SAR and topographic data in an object-based environment. Remote Sens. Environ. 2015, 170, 372–387. [Google Scholar] [CrossRef]
- Jawak, S.D.; Wankhede, S.F.; Luis, A.J. Exploration of Glacier Surface Facies Mapping Techniques Using Very High Resolution Worldview-2 Satellite Data. Proceedings 2018, 2, 339. [Google Scholar] [CrossRef]
- Mitkari, K.V.; Arora, M.K.; Tiwari, R.K. Extraction of Glacial Lakes in Gangotri Glacier Using Object-Based Image Analysis. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 5275–5283. [Google Scholar] [CrossRef]
- McNabb, R.W.; Womble, J.N.; Prakash, A.; Gens, R.; Haselwimmer, C.E. Quantification and Analysis of Icebergs in a Tidewater Glacier Fjord Using an Object-Based Approach. PLoS ONE 2016, 11, e0164444. [Google Scholar] [CrossRef] [PubMed]
- Aniya, M.; Enomoto, H. Glacier Variations and Their Causes in the Northern Patagonia Icefield, Chile, Since 1944. Arct. Alp. Res. 1986, 18, 307. [Google Scholar] [CrossRef]
- Le Bris, R.; Paul, F.; Rastner, P.; Schaub, Y. GLIMS Glacier Database; National Snow and Ice Data Center: Boulder, CO, USA, 2018. [Google Scholar]
- Harrison, S.; Warren, C.R.; Winchester, V.; Aniya, M. Onset of rapid calving and retreat of Glaciar San Quintin, Hielo Patagónico Norte, southern Chile. Polar Geogr. 2001, 25, 54–61. [Google Scholar] [CrossRef]
- Aniya, M. Glacier variations of Hielo Patagónico Norte, Chile, over 70 years from 1945 to 2015. Bull. Glaciol. Res. 2017, 35, 19–38. [Google Scholar] [CrossRef]
- Di Tullio, M.; Nocchi, F.; Camplani, A.; Emanuelli, N.; Nascetti, A.; Crespi, M. Copernicus Big Data And Google Earth Engine For Glacier Surface Velocity Field Monitoring: Feasibility Demonstration on San Rafael and San Quintin Glaciers. ISPRS-Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, XLII-3, 289–294. [Google Scholar] [CrossRef]
- Dixon, L.; Ambinakudige, S. Remote Sensing Study of Glacial Change in the Northern Patagonian Icefield. Adv. Remote Sens. 2015, 4, 270–279. [Google Scholar] [CrossRef][Green Version]
- DigitalGlobe. Base Product Series FAQ. 2016. Available online: https://www.c-agg.org/wp-content/uploads/DigitalGlobe-Base-Product-FAQ.pdf (accessed on 9 April 2020).
- Eisank, C.; Rieg, L.; Klug, C.; Kleindienst, H.; Sailer, R. Semi-Global Matching of Pléiades Tri-Stereo Imagery to Generate Detailed Digital Topography for High-Alpine Regions. GI_Forum 2015, 1, 168–177. [Google Scholar] [CrossRef]
- Rizzoli, P.; Martone, M.; Gonzalez, C.; Wecklich, C.; Tridon, D.B.; Bräutigam, B.; Bachmann, M.; Schulze, D.; Fritz, T.; Huber, M.; et al. Generation and performance assessment of the global TanDEM-X digital elevation model. ISPRS J. Photogramm. Remote Sens. 2017, 132, 119–139. [Google Scholar] [CrossRef]
- Wessel, B.; Huber, M.; Wohlfart, C.; Marschalk, U.; Kosmann, D.; Roth, A. Accuracy assessment of the global TanDEM-X Digital Elevation Model with GPS data. ISPRS J. Photogramm. Remote Sens. 2018, 139, 171–182. [Google Scholar] [CrossRef]
- DigitalGlobe. WorldView-2 Data Sheet and Core Imagery Product Guide. 2016. Available online: https://dg-cms-uploads-production.s3.amazonaws.com/uploads/document/file/98/WorldView2-DS-WV2-rev2.pdf (accessed on 9 April 2020).
- Hall, D.K.; Riggs, G.A. Normalized-Difference Snow Index (NDSI). In Encyclopedia of Snow, Ice and Glaciers; Singh, V.P., Singh, P., Haritashya, U.K., Eds.; Springer: Amsterdam, The Netherlands, 2011; pp. 779–780. [Google Scholar]
- Haala, N.; Rothermel, M. Dense Multi-Stereo Matching for High Quality Digital Elevation Models. Photogramm. Fernerkund. Geoinf. 2012, 2012, 331–343. [Google Scholar] [CrossRef]
- Podgórski, J.; Kinnard, C.; Pętlicki, M.; Urrutia, R. Performance Assessment of TanDEM-X DEM for Mountain Glacier Elevation Change Detection. Remote Sens. 2019, 11, 187. [Google Scholar] [CrossRef]
- Rolstad, C.; Haug, T.; Denby, B. Spatially integrated geodetic glacier mass balance and its uncertainty based on geostatistical analysis: Application to the western Svartisen ice cap, Norway. J. Glaciol. 2009, 55, 666–680. [Google Scholar] [CrossRef]
- Trimble Geospatial. Trimble eCognition Suite for Windows Operating System. 2017. Available online: http://www.infoserve.co.jp/doc/Trimble/v9_3/ReleaseNotes.pdf (accessed on 29 May 2020).
- Rouse, J.W., Jr.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring vegetation systems in the Great Plains with ERTS. In Goddard Space Flight Center 3d ERTS-1 Symp. Sect. A; Freden, S.C., Mercanti, E.P., Becker, M.A., Eds.; NASA: Washington, DC, USA, 1974; Volume 1, pp. 309–317. [Google Scholar]
- Bradski, G. The OpenCV Library. Dr. Dobb’s J. Softw. Tools 2000. Available online: https://www.drdobbs.com/open-source/the-opencv-library/184404319 (accessed on 12 May 2020).
- OpenCV. OpenCV 2.4.13.7 Documentation. Random Trees. 2019. Available online: https://docs.opencv.org/2.4/modules/ml/doc/random_trees.html (accessed on 24 April 2020).
- Trimble Geospatial. In Trimble Documentation eCognition Developer 9.3 Reference Book; Trimble Germany GmbH: Munich, Germany, 2018.
- Beucher, S. Use of watersheds in contour detection. In Proceedings of the International Workshop on Image Processing (CCETT), Marne-la-Vallée, France, 26–28 March 1979. [Google Scholar]
- Mordvintsev, A.; Abid, K. Image Segmentation with Watershed Algorithm. In OpenCV 2.4.13.7 Documentation. 2013. Available online: https://opencv-python-tutroals.readthedocs.io/en/latest/py_tutorials/py_imgproc/py_watershed/py_watershed.html (accessed on 3 December 2019).
- Scheick, J.; Enderlin, E.; Miller, E.; Hamilton, G. First-Order Estimates of Coastal Bathymetry in Ilulissat and Naajarsuit Fjords, Greenland, from Remotely Sensed Iceberg Observations. Remote Sens. 2019, 11, 935. [Google Scholar] [CrossRef] [PubMed]
- Wagner, T.J.; Stern, A.A.; Dell, R.W.; Eisenman, I. On the representation of capsizing in iceberg models. Ocean Model. 2017, 117, 88–96. [Google Scholar] [CrossRef]
- Alstott, J.; Bullmore, E.; Plenz, D. powerlaw: A Python Package for Analysis of Heavy-Tailed Distributions. PLoS ONE 2014, 9, e85777. [Google Scholar] [CrossRef]
- Clauset, A.; Shalizi, C.R.; Newman, M.E.J. Power-Law Distributions in Empirical Data. SIAM Rev. 2009, 51, 661–703. [Google Scholar] [CrossRef]
- Bunting, P.; Clewley, D.; Lucas, R.M.; Gillingham, S. The Remote Sensing and GIS Software Library (RSGISLib). Comput. Geosci. 2014, 62, 216–226. [Google Scholar] [CrossRef]
- Truffer, M.; Motyka, R.J. Where glaciers meet water: Subaqueous melt and its relevance to glaciers in various settings. Rev. Geophys. 2016, 54, 220–239. [Google Scholar] [CrossRef]
- Larsen, C.F.; Motyka, R.J.; Arendt, A.A.; Echelmeyer, K.A.; Geissler, P.E. Glacier changes in southeast Alaska and northwest British Columbia and contribution to sea level rise. J. Geophys. Res. 2007, 112. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).