Land Cover Classification of Nine Perennial Crops Using Sentinel-1 and -2 Data
Abstract
1. Introduction
2. Methods
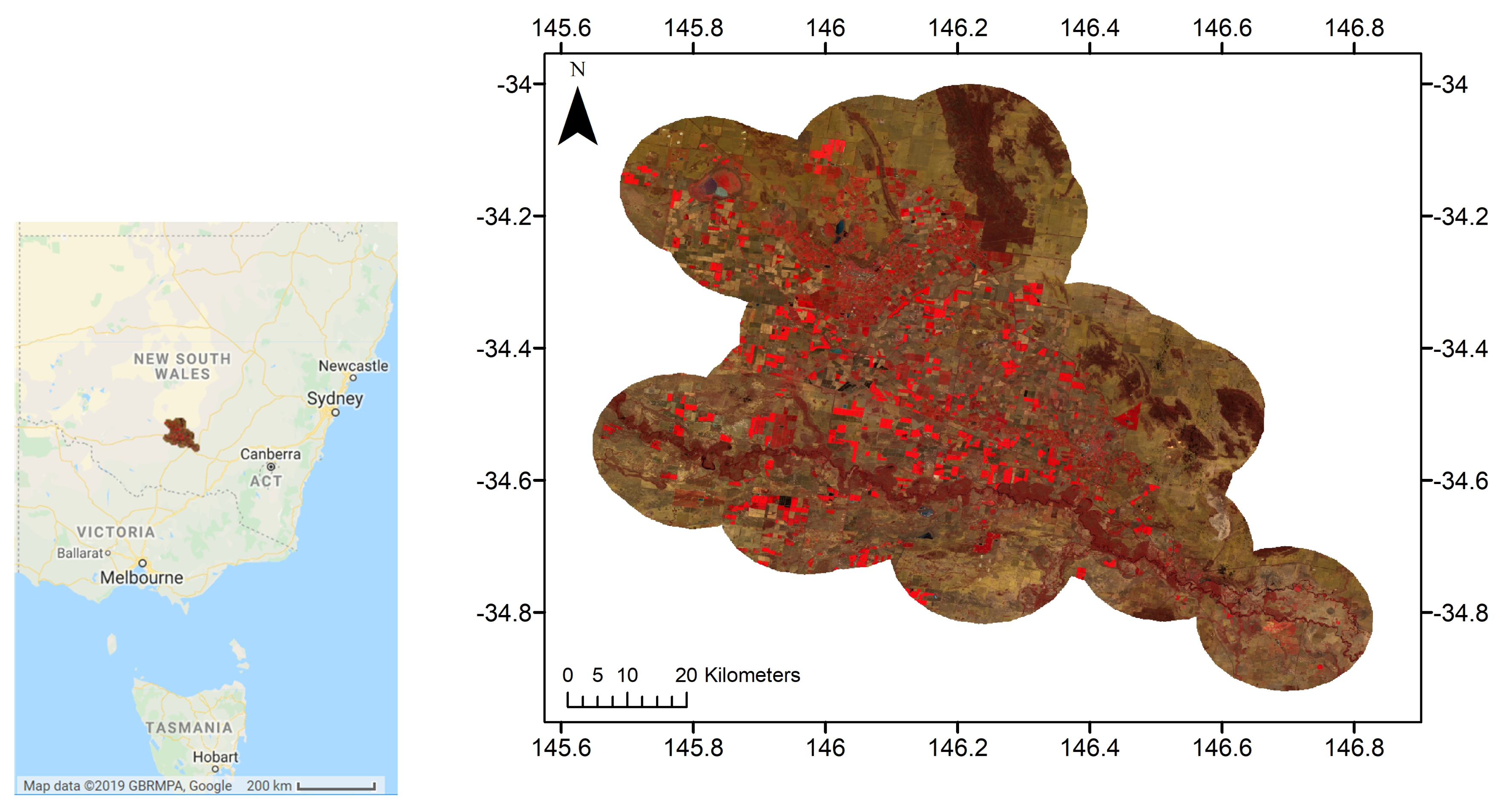
2.1. Study Area
2.2. Definitions of the Twelve Land Cover Classes
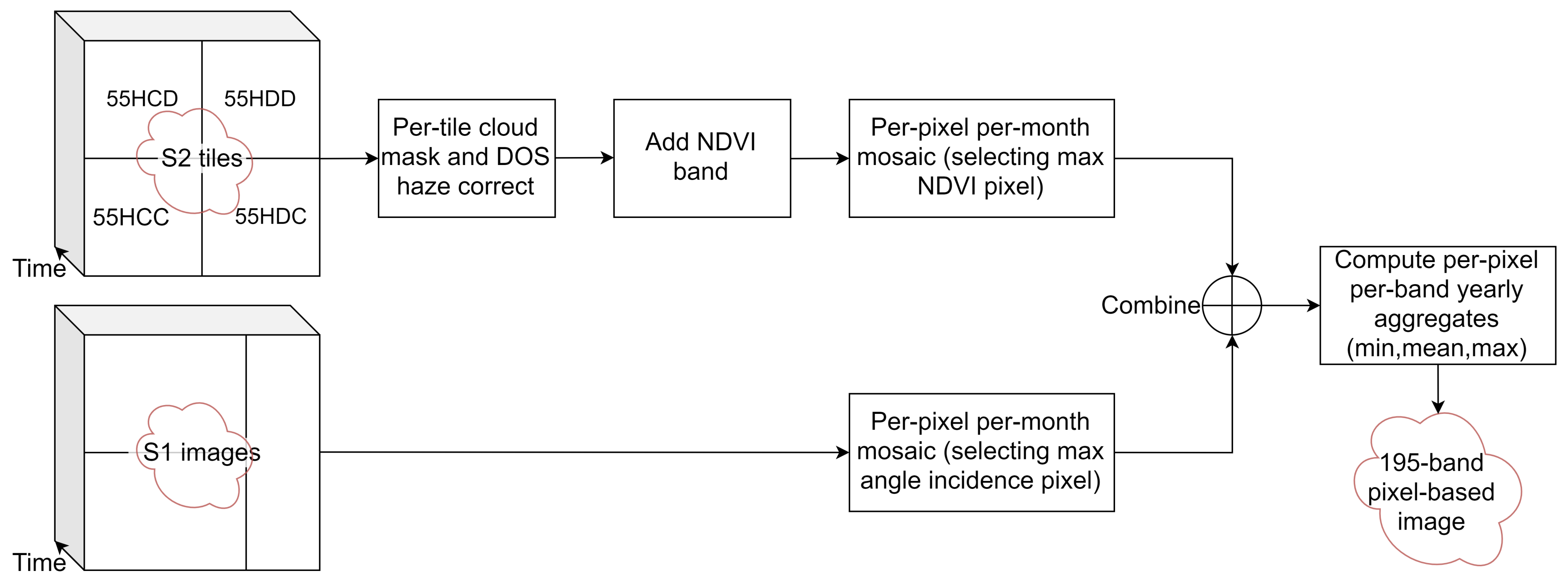
2.3. Image Sources and Pre-Processing
- The four image tiles intersecting with the area of interest (55HCD, 55HDD, 55HCC and 55HDC) from 1 May 2018 to 30 April 2019 were collected. This included 579 tiles, giving an average of 48 tiles per month, or 12 acquisition dates per month.
- Clouds in each tile were masked using the quality band metadata.
- Dark Object Subtraction (DOS) haze correction [38] was applied to each tile to obtain psuedo surface reflectance values.
- NDVI = (NIR − R)/(NIR + R) was computed.
- The four 10 m resolution bands, six 20 m resolution bands (see Table 2) and NDVI were selected, giving 11 bands per tile.
- A single mosaic was generated for each month. As multiple images are available for each month, the monthly images were generated using a quality mosaic method, selecting the image per-pixel with the highest NDVI, similar to [39]. This produces twelve images, each with eleven bands.
- The bands were renamed with the band name followed by mosaic month with the format YYMM. For example, the NIR band from May 2018 was named NIR_1805. The twelve image mosaics were flattened into a single 12 month × 11 band = 132 band image.
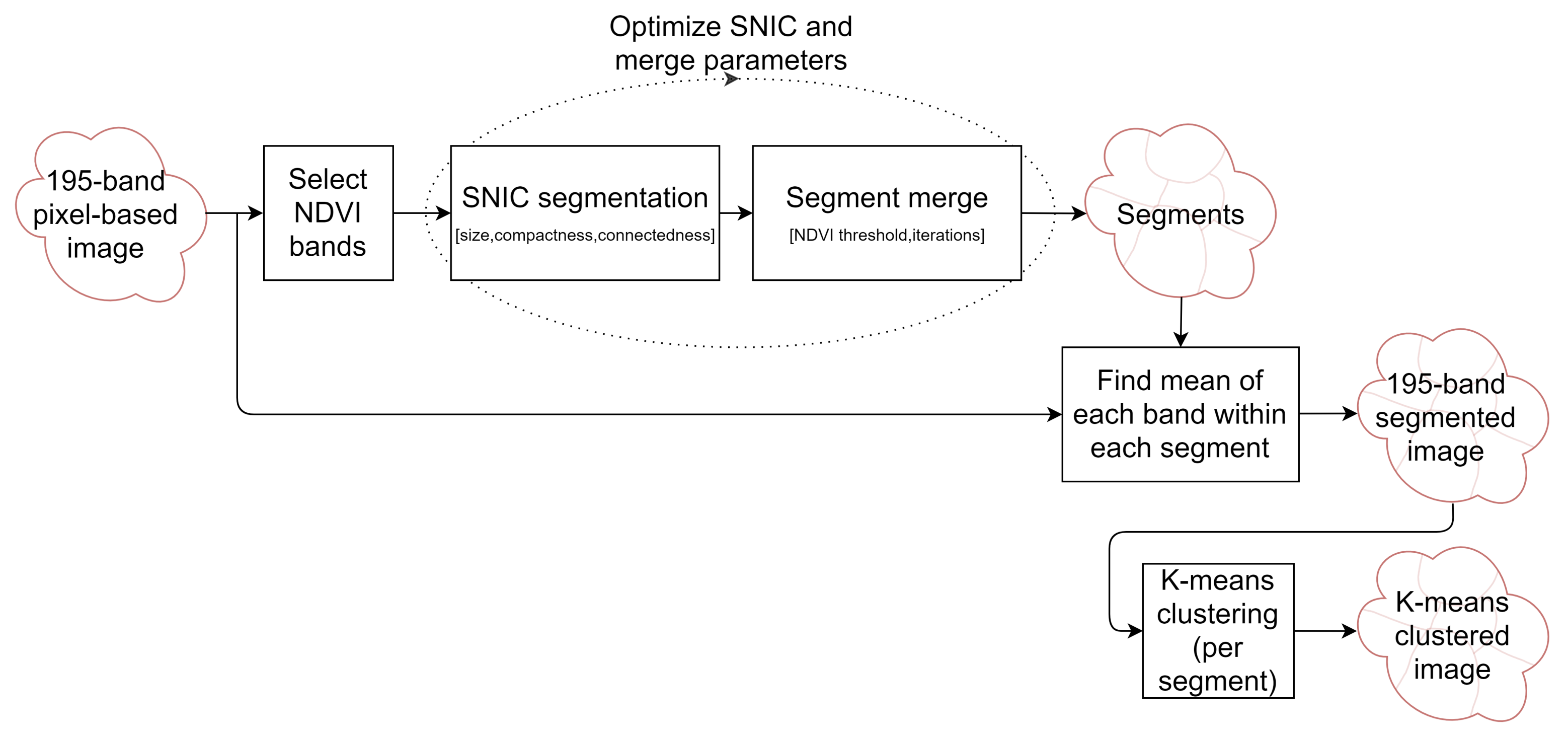
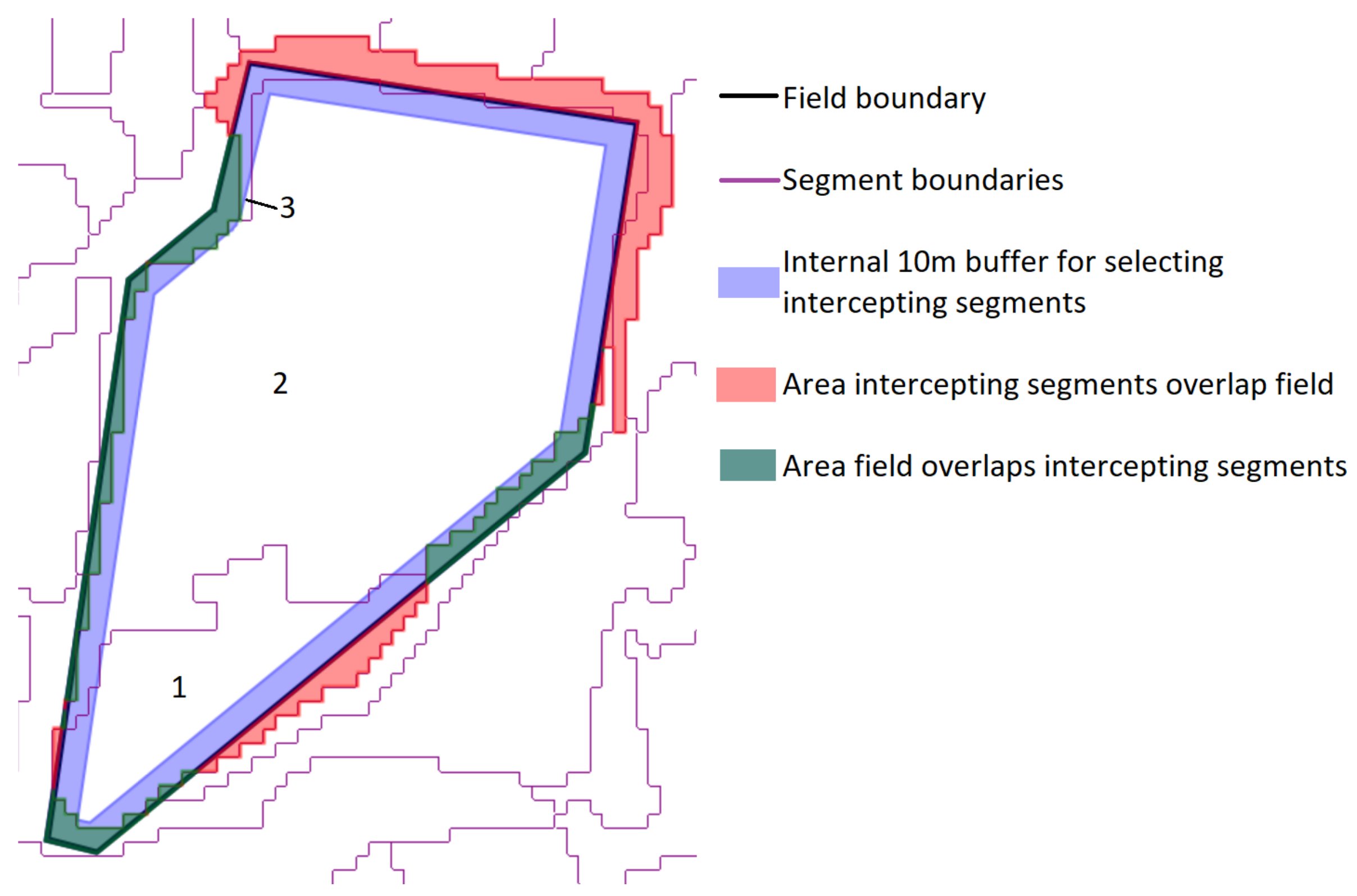
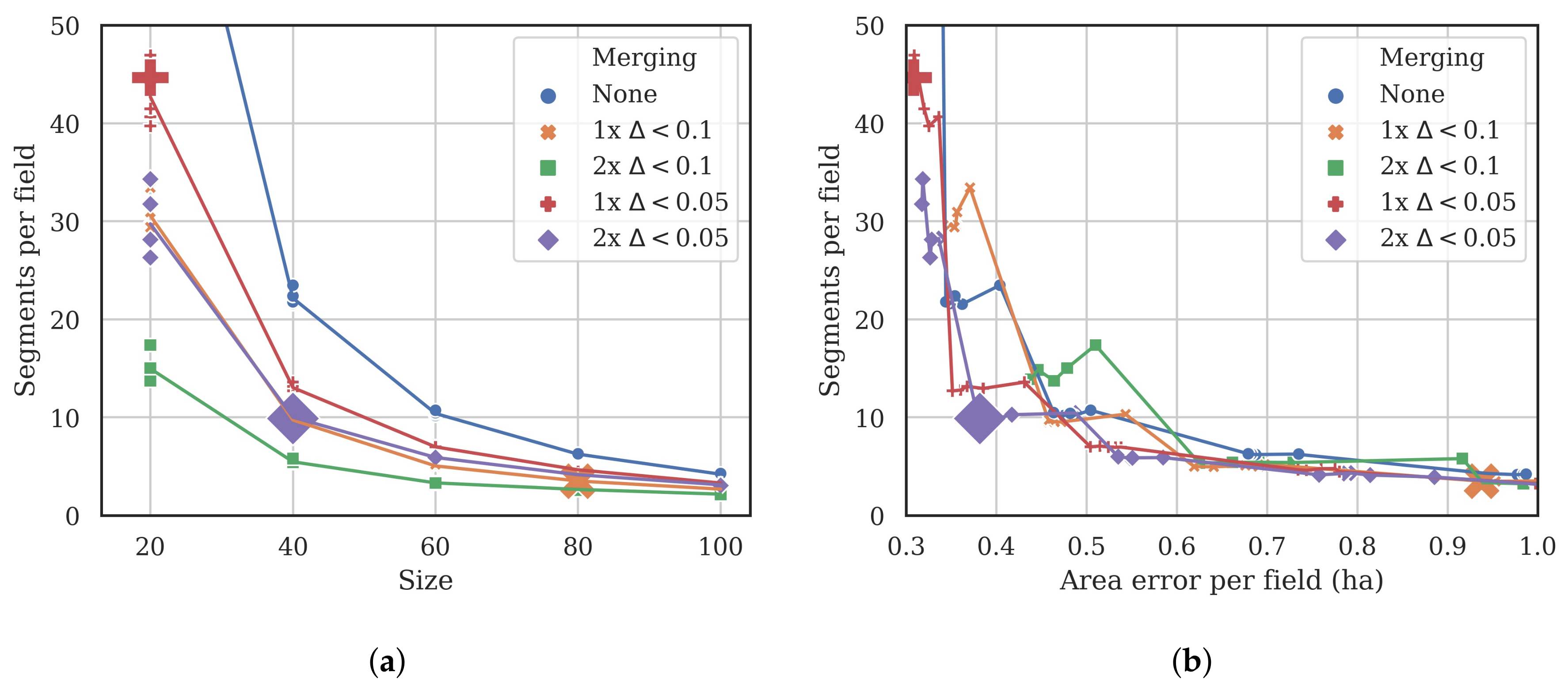
2.4. Segmentation Optimization for Object-Based Image Analysis
- The total area error, which is the sum of two components:
- Omission errors, that is the area of the test geometries that are not covered by the intercepting segments (green area in Figure 4).
- Commission errors, that is the area of the intercepting segments that overlap the test geometries (red area in the figure).
- The total number of segments intercepting the 75 test objects (3 in the example shown in Figure 4).
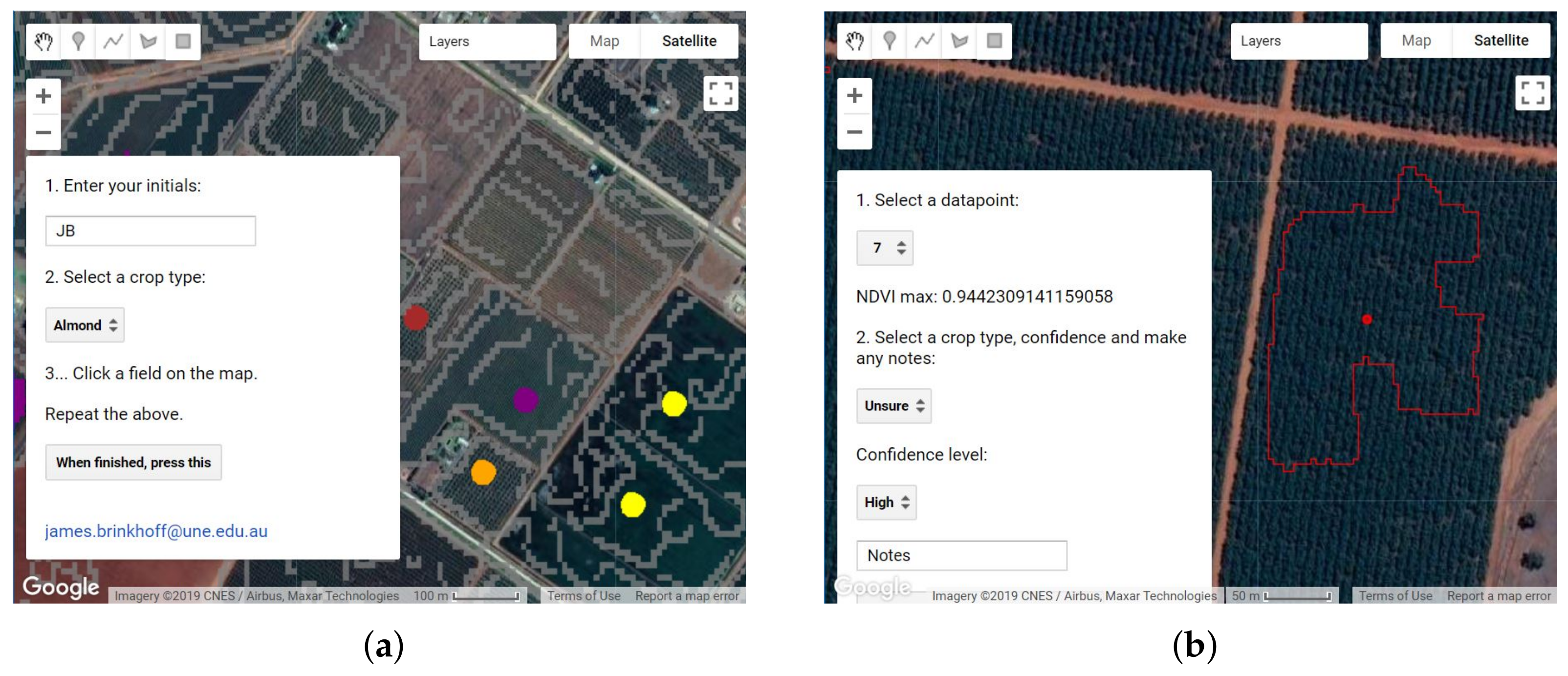
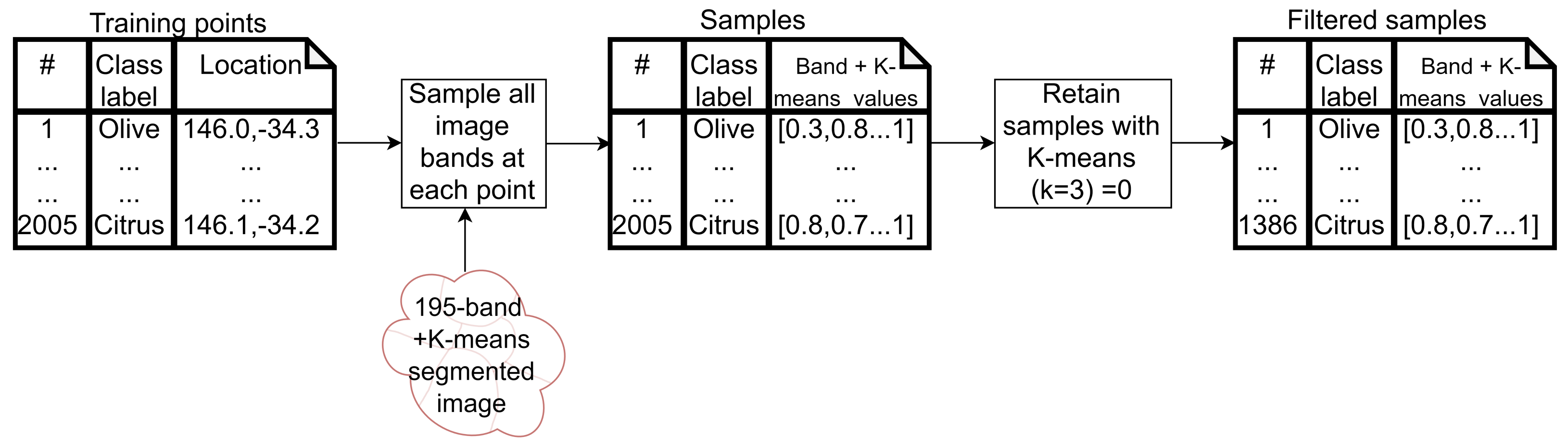
2.5. Training Data Collection and Cleaning
- Points marking new perennial plantings, where the canopy cover is small relative to the row and tree spacing. The 10 m Sentinel pixels contain more soil than canopy in these areas, and thus, are not able to classify these areas accurately.
- Points marking annual cropping areas that were fallow in the study year.
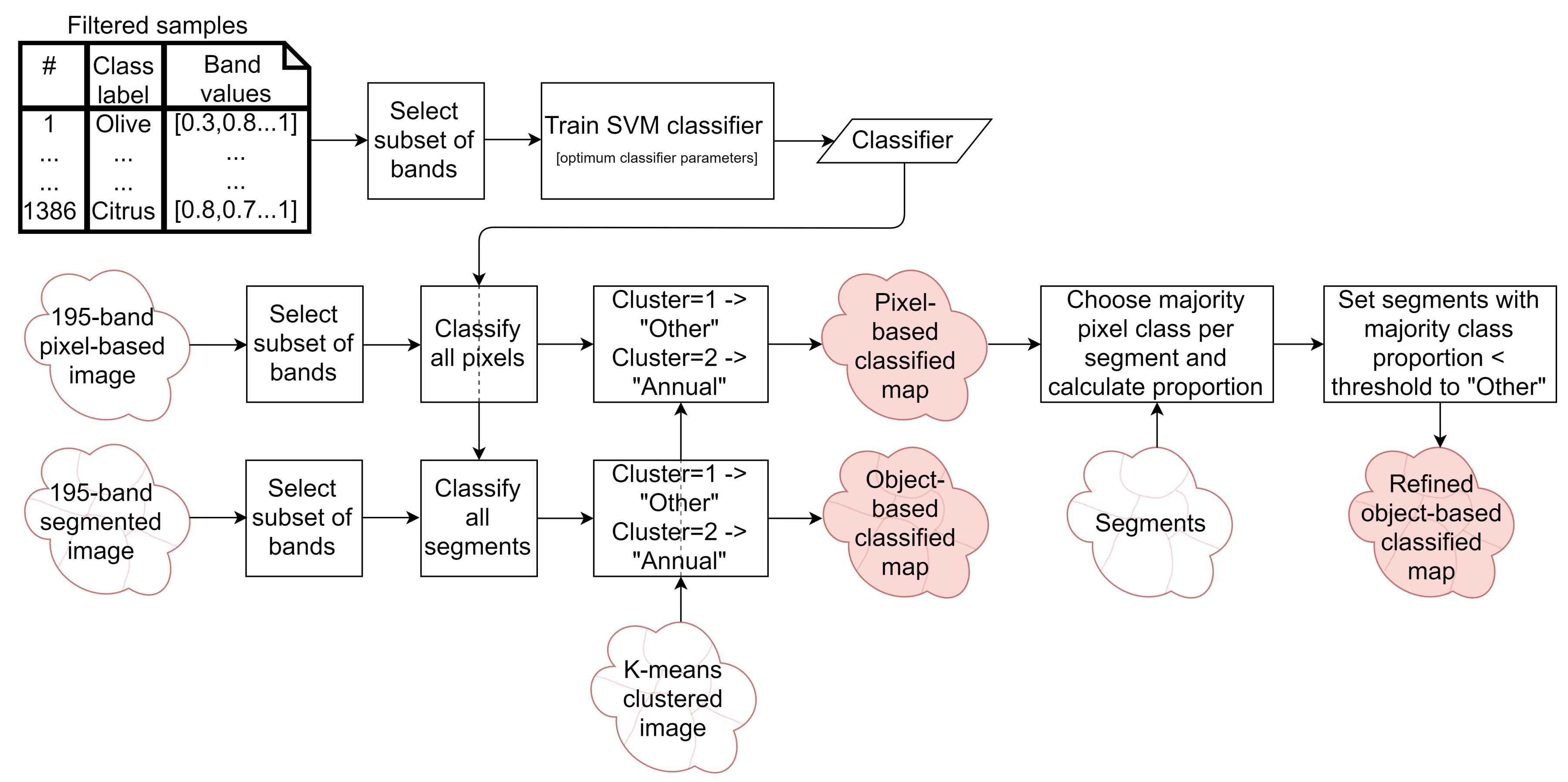
2.6. Classification
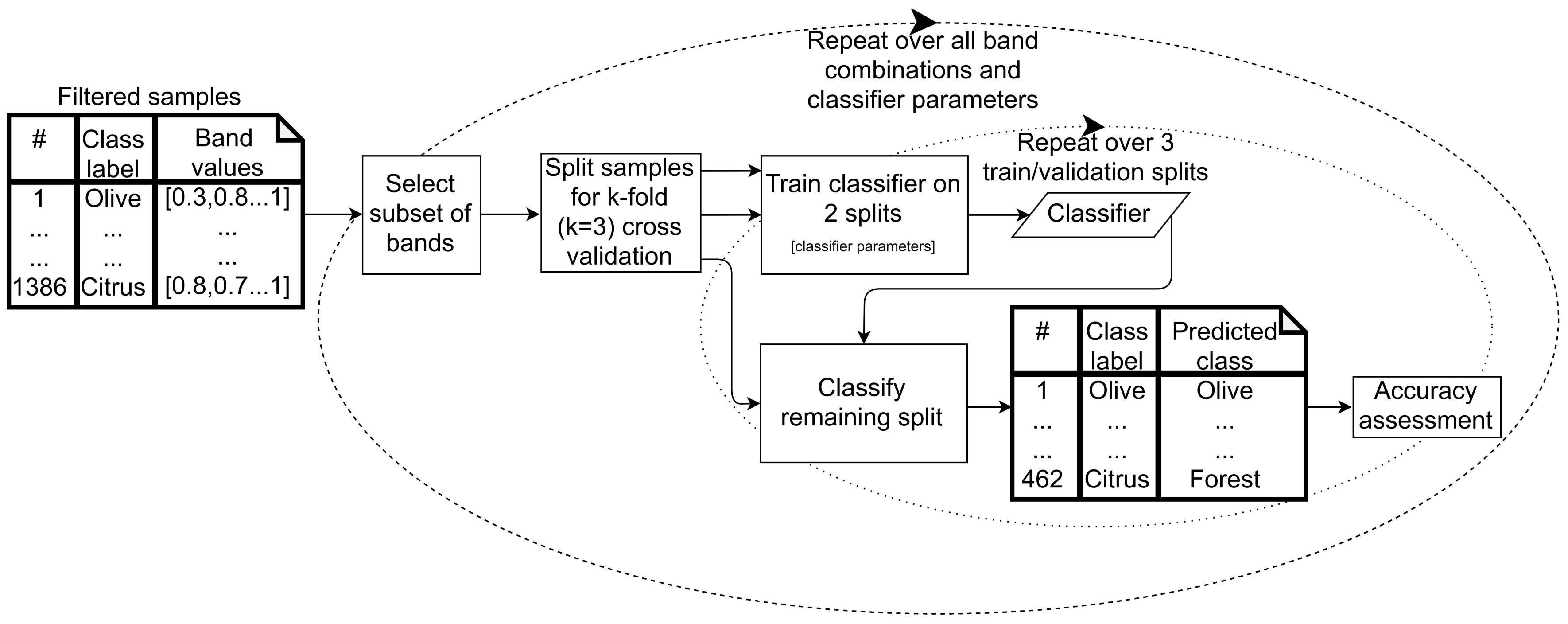
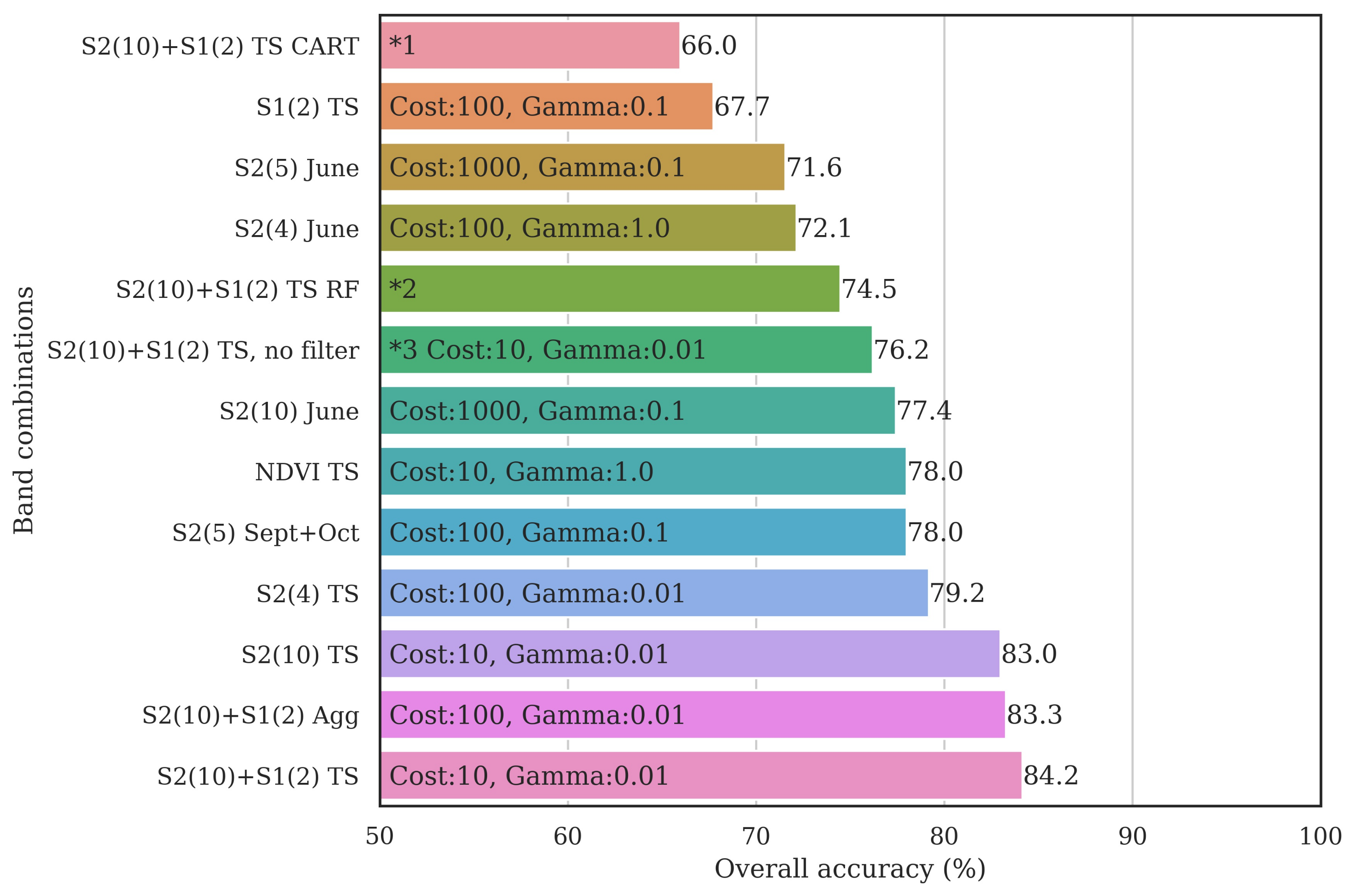
2.6.1. Supervised Classifier Optimization
- Classification and regression tree (CART), a decision tree algorithm, which classifies data points using successive decisions based on feature values.
- Random forest (RF), which uses the average of multiple decision trees, each trained on different subsets of training data and features, to arrive at a classification for each data point.
- Support vector machine (SVM), which classifies data points based on finding hyperplanes (surfaces defined by combinations of input features) that optimally separate the classes based on training data. SVM with linear and radial basis function (RBF) kernels were assessed.
2.6.2. Classified Map Generation
- The classifier was run pixel-by-pixel on the un-segmented original image, producing a pixel-based classified map.
- The classifier was run segment-by-segment on the segmented image, producing an object-based map.
- The pixel-based classified map was transformed into an object-based map by finding the majority pixel class within each segment, producing the refined object-based map.
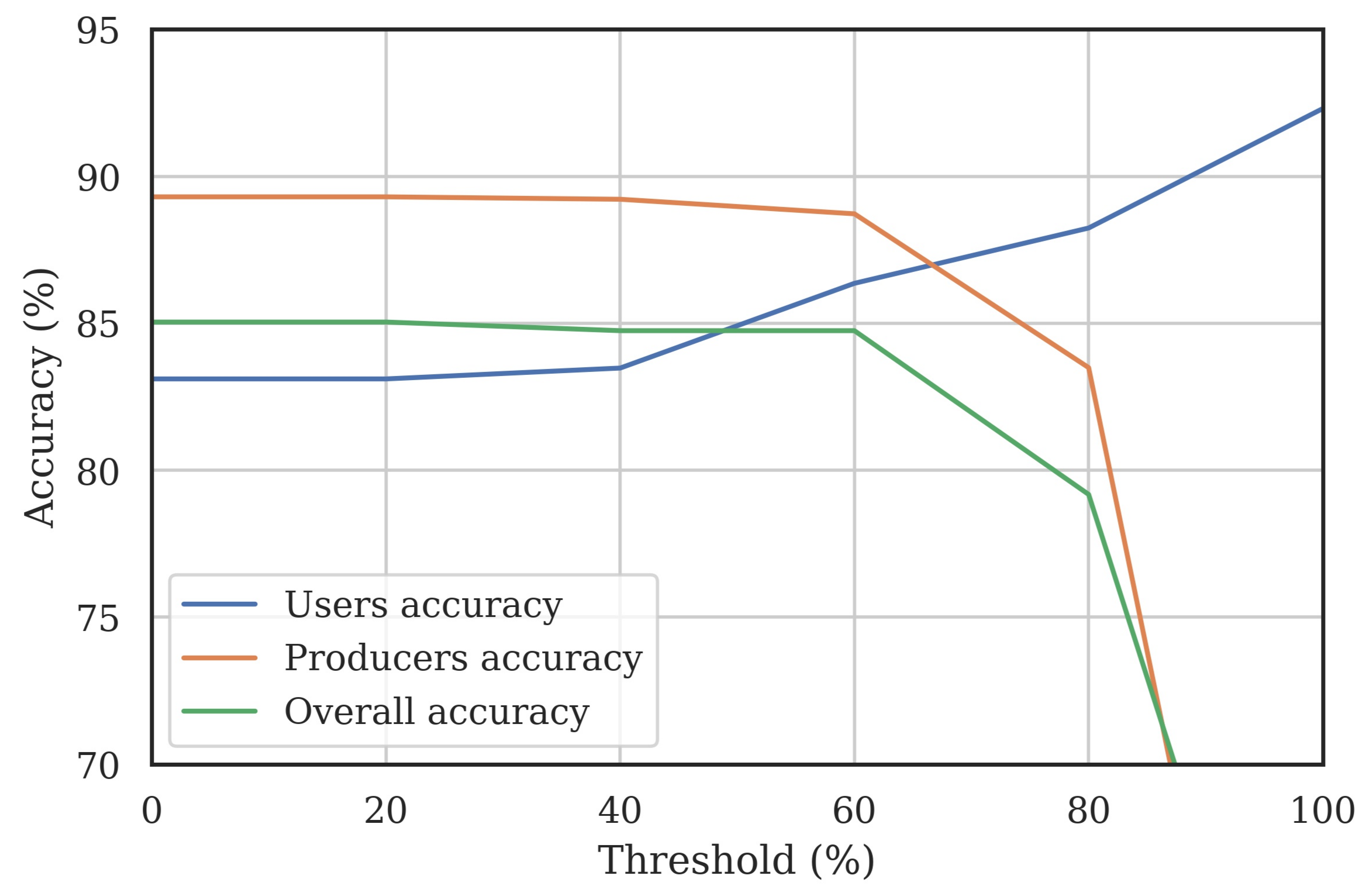
2.6.3. Classified Map Accuracy Assessment
3. Results
3.1. Segmentation Optimization
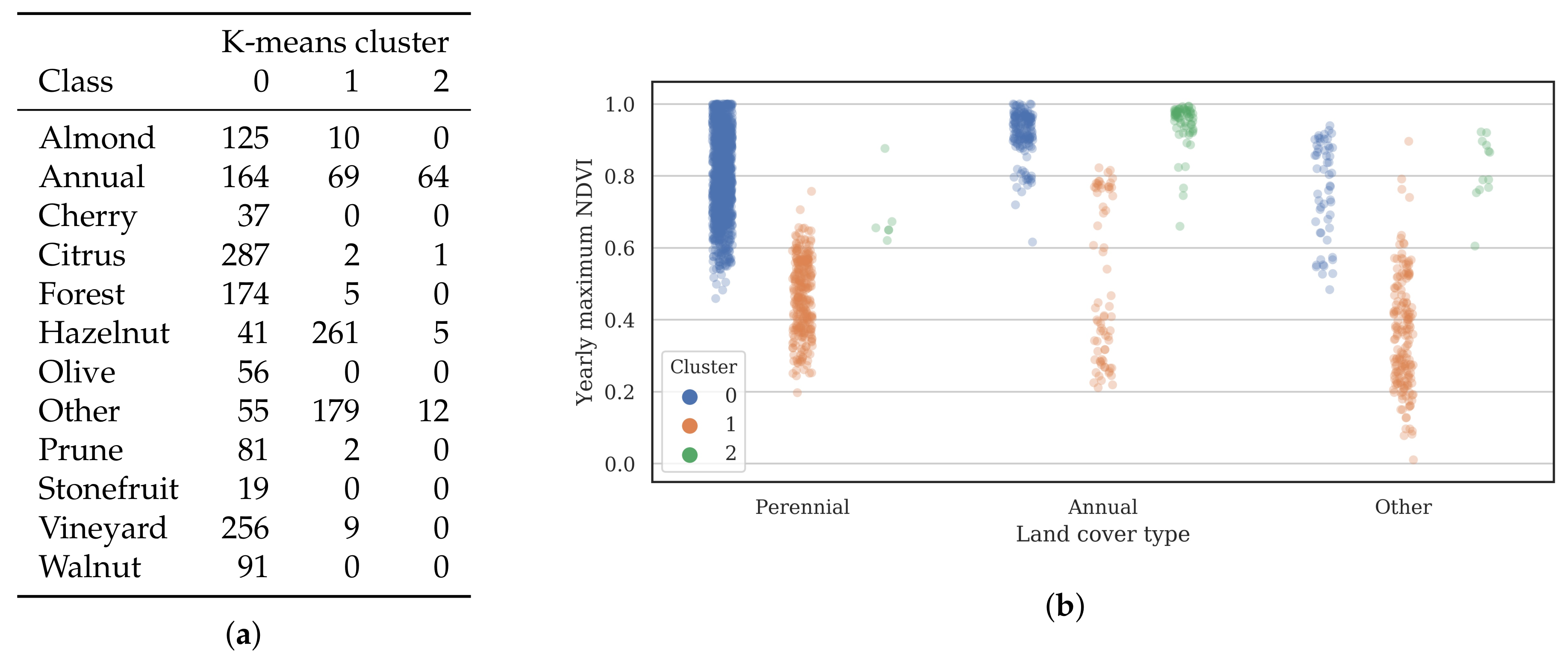
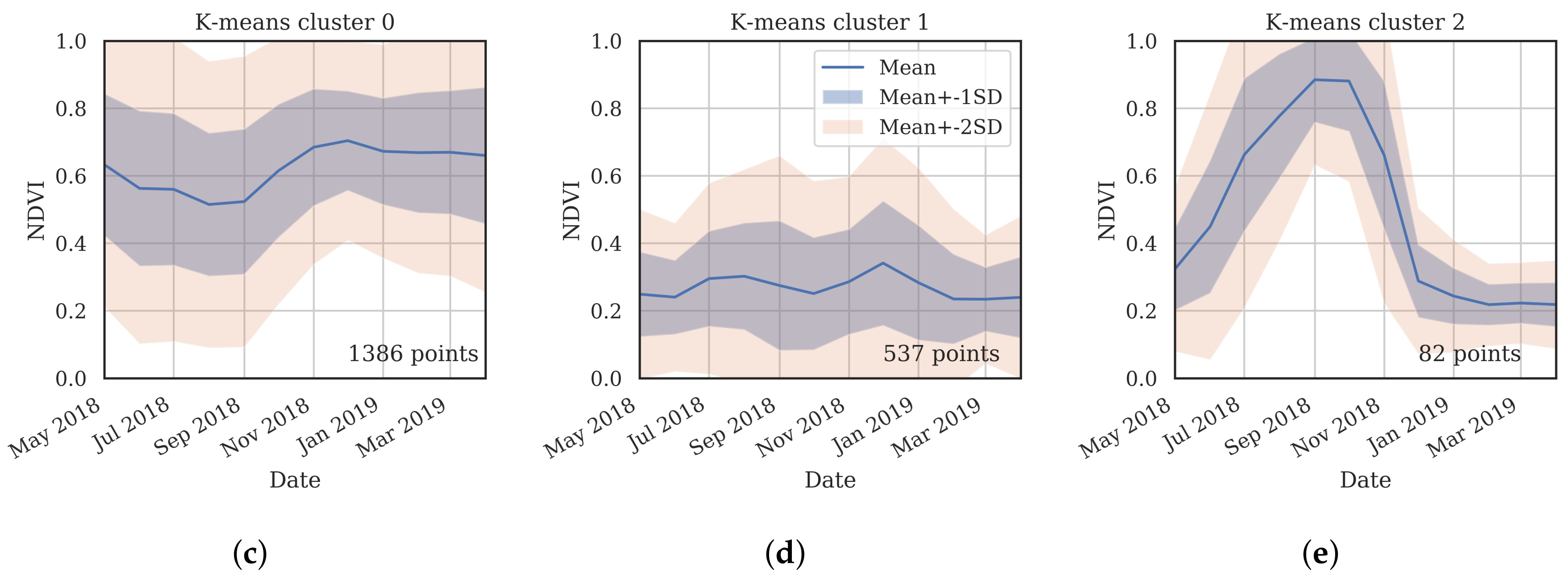
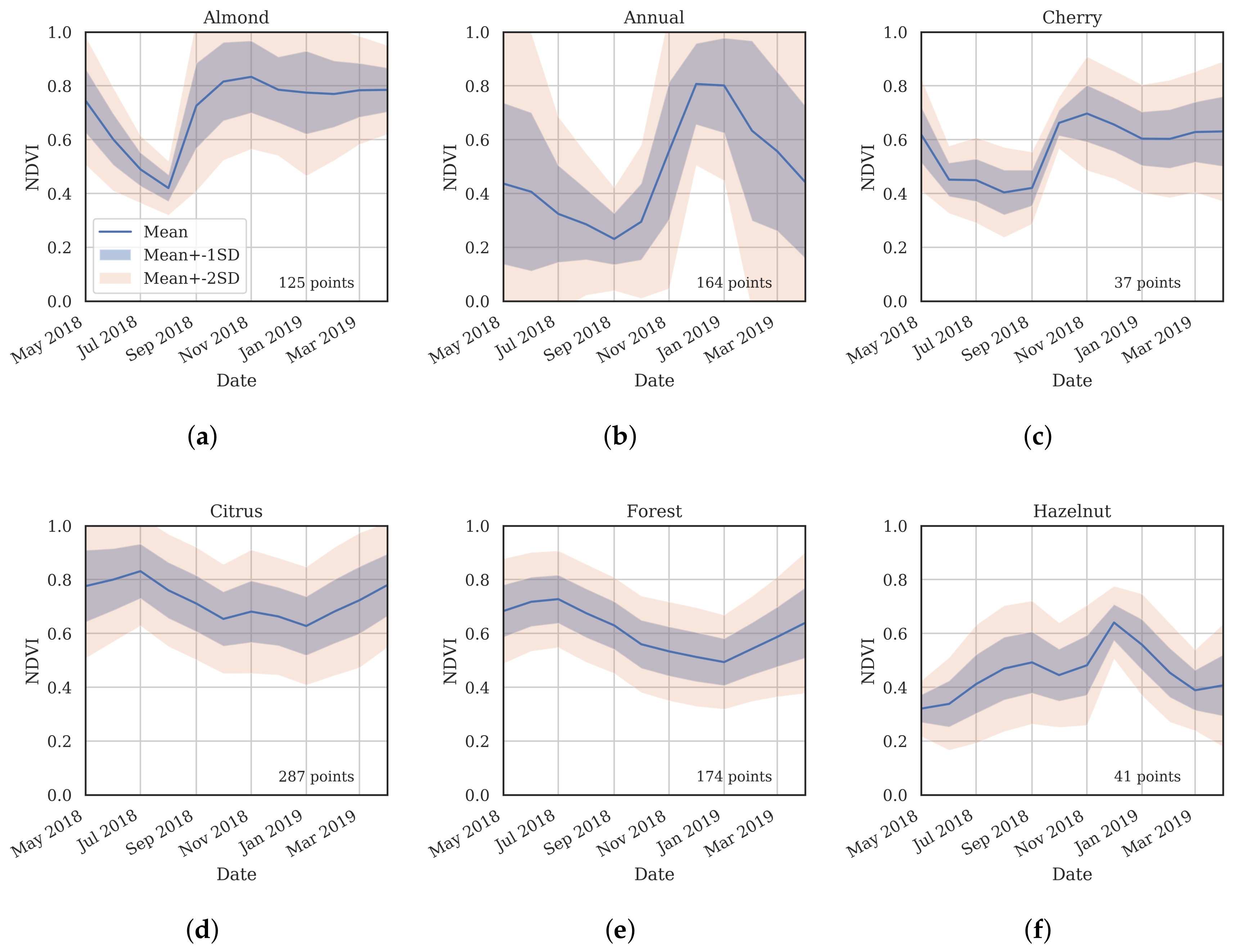
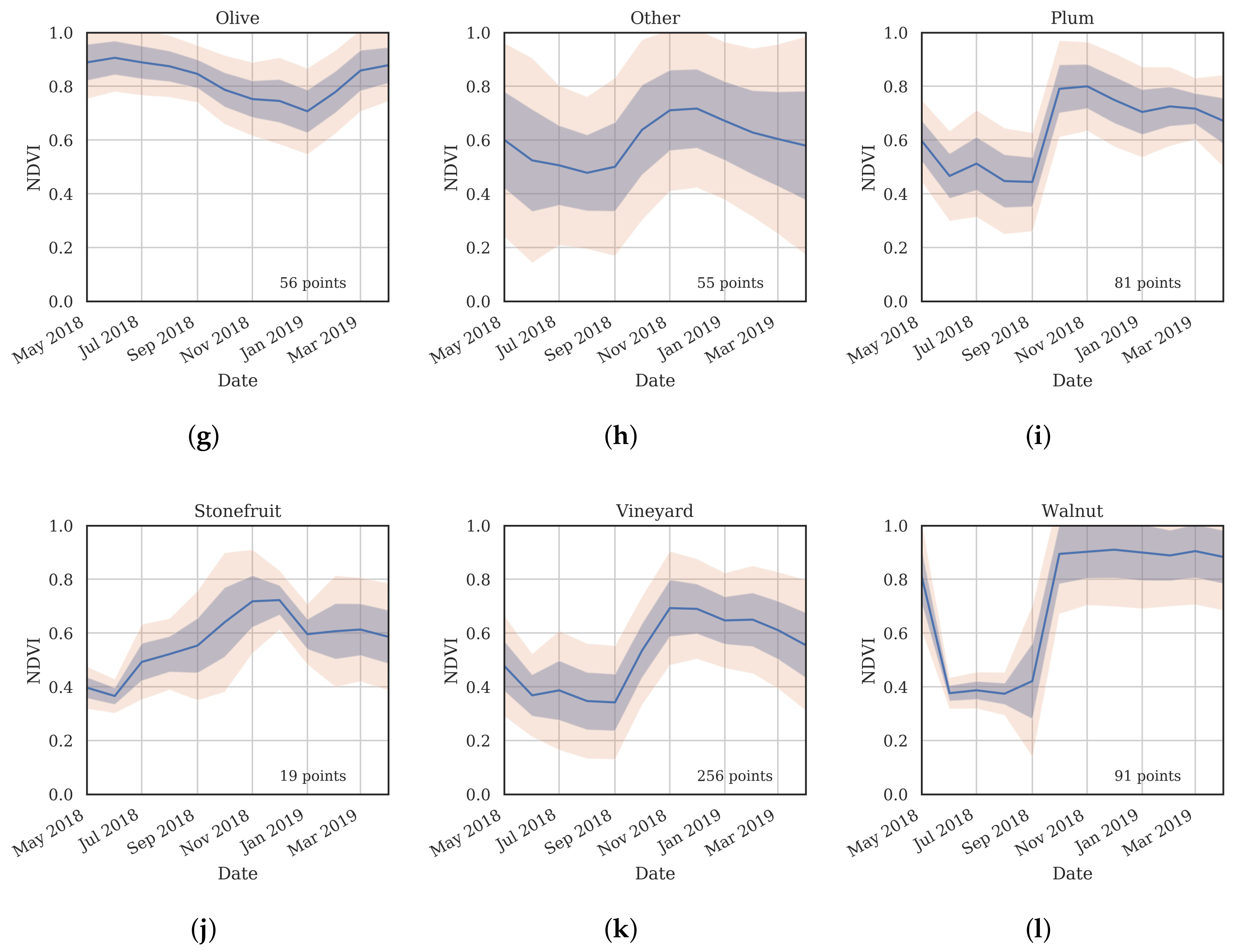
3.2. Training Data
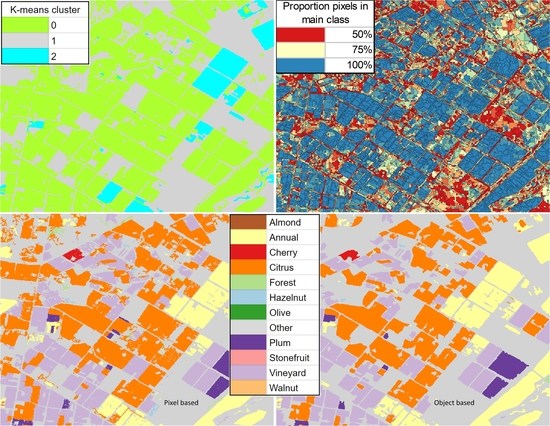
- Cluster 0 includes most of the perennial crop and Forest points, as well as the majority of the Annual points and some Other points. The NDVI time series shows that the cluster includes areas with dominant growth over the late spring to early autumn months (October to April) and areas with evergreen growth.
- Cluster 1 includes points with low NDVI, corresponding to areas with little vegetation. The Annual points in this cluster are annual cropping areas that were fallow in the study year. The perennial points in this cluster were young or very sparse plantings (which is the case in much of the Hazelnut growing area), with insufficient canopy to be detectable using the 10 m imagery. The majority of the Other points are in this cluster, corresponding to unplanted areas, built up areas and water bodies.
- Cluster 2 has high NDVI over the late winter to early spring months (July to November). This cluster is dominated by a significant number of Annual points. Therefore, this cluster identifies winter-grown annual crops.
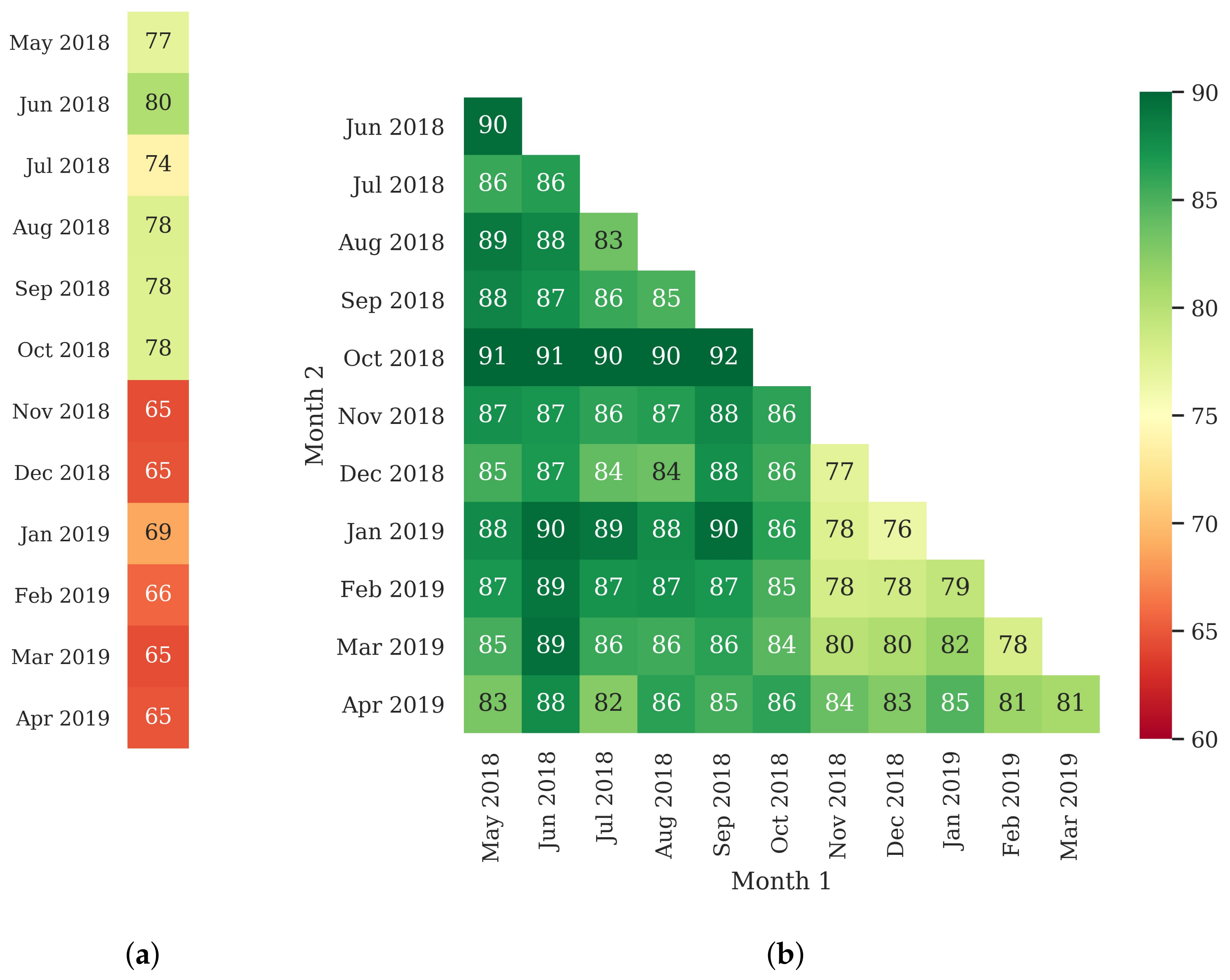
3.3. Classifier Optimization Using the Filtered Samples
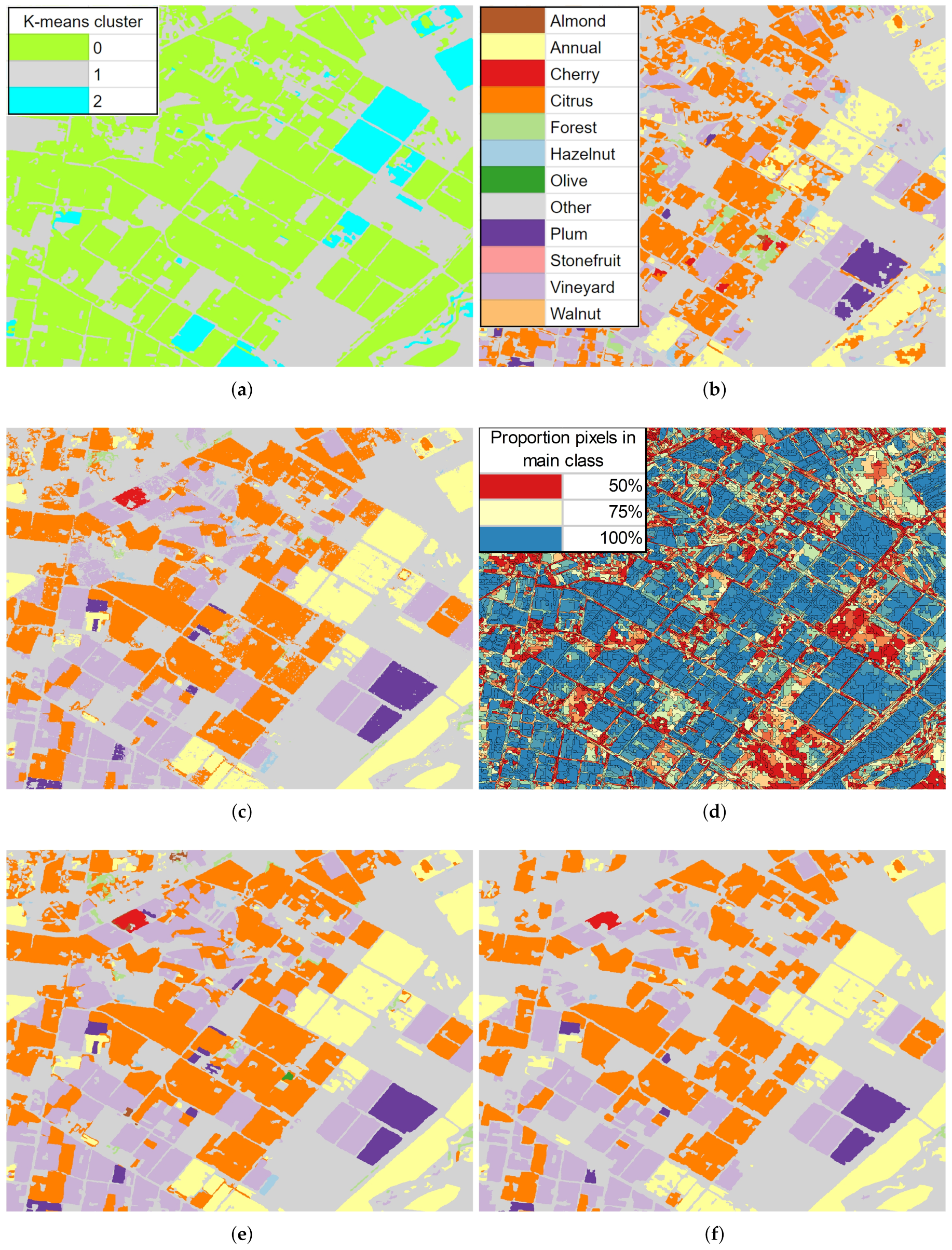
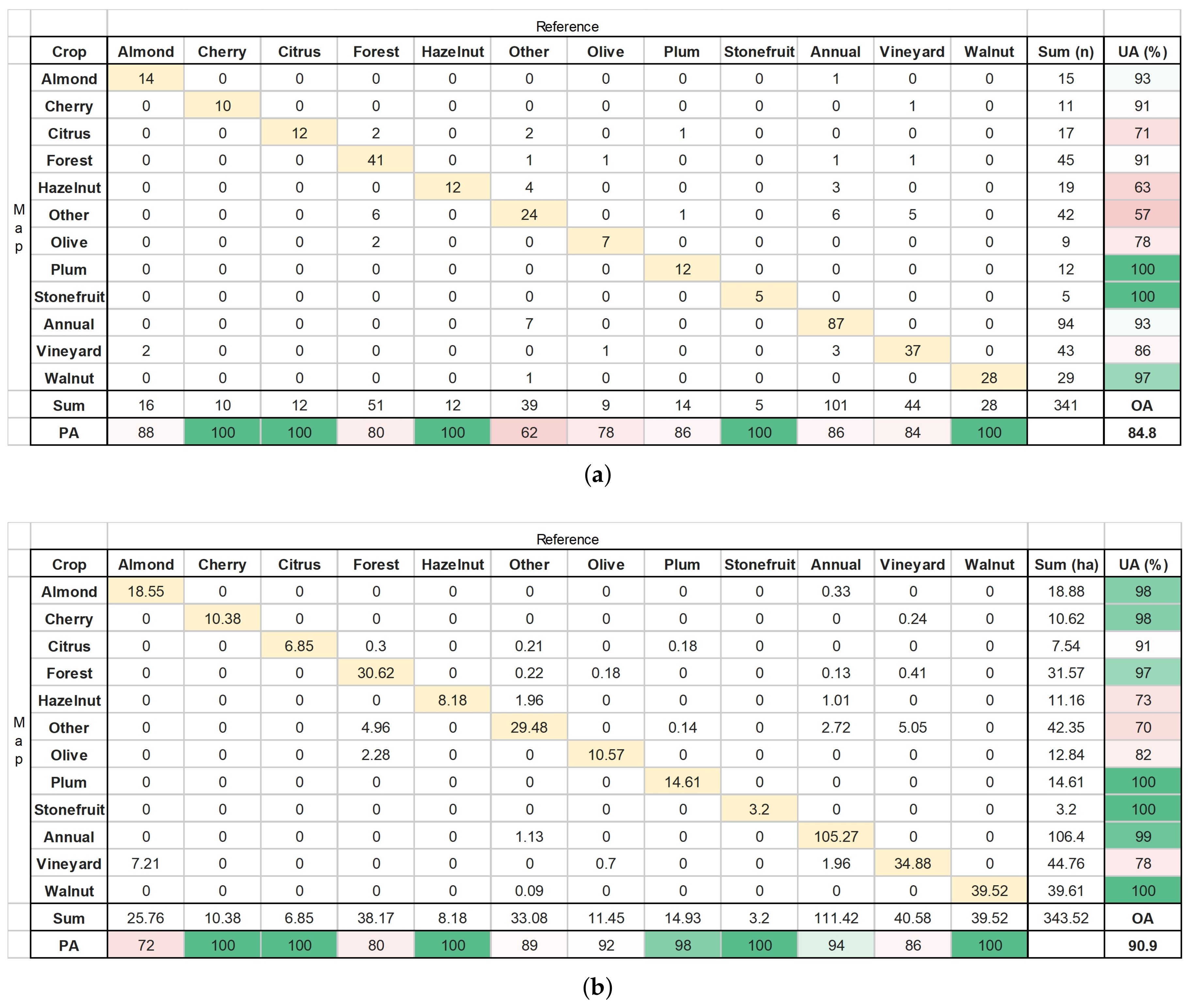
3.4. Classified Map Generation and Comparison
Final Map and Accuracy Assessment
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lesslie, R.; Barson, M.; Smith, J. Land use information for integrated natural resources management—A coordinated national mapping program for Australia. J. Land Use Sci. 2006, 1, 45–62. [Google Scholar] [CrossRef]
- Tang, Z.; Engel, B.A.; Pijanowski, B.C.; Lim, K.J. Forecasting land use change and its environmental impact at a watershed scale. J. Environ. Manag. 2005, 76, 35–45. [Google Scholar] [CrossRef] [PubMed]
- Verburg, P.H.; Schot, P.P.; Dijst, M.J.; Veldkamp, A. Land use change modelling: Current practice and research priorities. GeoJournal 2004, 61, 309–324. [Google Scholar] [CrossRef]
- Teluguntla, P.; Thenkabail, P.S.; Xiong, J.; Gumma, M.K.; Congalton, R.G.; Oliphant, A.; Poehnelt, J.; Yadav, K.; Rao, M.; Massey, R. Spectral matching techniques (SMTs) and automated cropland classification algorithms (ACCAs) for mapping croplands of Australia using MODIS 250-m time series (2000–2015) data. Int. J. Digit. Earth 2017, 10, 944–977. [Google Scholar] [CrossRef]
- Schauer, M.; Senay, G.B. Characterizing Crop Water Use Dynamics in the Central Valley of California Using Landsat-Derived Evapotranspiration. Remote Sens. 2019, 11, 1782. [Google Scholar] [CrossRef]
- Gumma, M.K.; Tsusaka, T.W.; Mohammed, I.; Chavula, G.; Ganga Rao, N.V.P.R.; Okori, P.; Ojiewo, C.O.; Varshney, R.; Siambi, M.; Whitbread, A. Monitoring Changes in the Cultivation of Pigeonpea and Groundnut in Malawi Using Time Series Satellite Imagery for Sustainable Food Systems. Remote Sens. 2019, 11, 1475. [Google Scholar] [CrossRef]
- Pfleeger, T.G.; Olszyk, D.; Burdick, C.A.; King, G.; Kern, J.; Fletcher, J. Using a Geographic Information System to identify areas with potential for off-target pesticide exposure. Environ. Toxicol. Chem. 2006, 25, 2250–2259. [Google Scholar] [CrossRef]
- Doraiswamy, P.C.; Sinclair, T.R.; Hollinger, S.; Akhmedov, B.; Stern, A.; Prueger, J. Application of MODIS derived parameters for regional crop yield assessment. Remote Sens. Environ. 2005, 97, 192–202. [Google Scholar] [CrossRef]
- Lebourgeois, V.; Dupuy, S.; Vintrou, É.; Ameline, M.; Butler, S.; Bégué, A. A Combined Random Forest and OBIA Classification Scheme for Mapping Smallholder Agriculture at Different Nomenclature Levels Using Multisource Data (Simulated Sentinel-2 Time Series, VHRS and DEM). Remote Sens. 2017, 9, 259. [Google Scholar] [CrossRef]
- Ashourloo, D.; Shahrabi, H.S.; Azadbakht, M.; Aghighi, H.; Nematollahi, H.; Alimohammadi, A.; Matkan, A.A. Automatic canola mapping using time series of sentinel 2 images. ISPRS J. Photogramm. Remote Sens. 2019, 156, 63–76. [Google Scholar] [CrossRef]
- Niel, T.G.V.; McVicar, T.R. A simple method to improve field-level rice identification: Toward operational monitoring with satellite remote sensing. Aust. J. Exp. Agric. 2003, 43, 379. [Google Scholar] [CrossRef]
- Haerani, H.; Apan, A.; Basnet, B. Mapping of peanut crops in Queensland, Australia using time series PROBA-V 100-m normalized difference vegetation index imagery. J. Appl. Remote. Sens. 2018, 12, 036005. [Google Scholar] [CrossRef]
- Sitokonstantinou, V.; Papoutsis, I.; Kontoes, C.; Lafarga Arnal, A.; Armesto Andrés, A.P.; Garraza Zurbano, J.A. Scalable Parcel-Based Crop Identification Scheme Using Sentinel-2 Data Time-Series for the Monitoring of the Common Agricultural Policy. Remote Sens. 2018, 10, 911. [Google Scholar] [CrossRef]
- Stoian, A.; Poulain, V.; Inglada, J.; Poughon, V.; Derksen, D. Land Cover Maps Production with High Resolution Satellite Image Time Series and Convolutional Neural Networks: Adaptations and Limits for Operational Systems. Remote Sens. 2019, 11, 1986. [Google Scholar] [CrossRef]
- Rozenstein, O.; Karnieli, A. Comparison of methods for land-use classification incorporating remote sensing and GIS inputs. Appl. Geogr. 2011, 31, 533–544. [Google Scholar] [CrossRef]
- Peña, M.A.; Brenning, A. Assessing fruit-tree crop classification from Landsat-8 time series for the Maipo Valley, Chile. Remote Sens. Environ. 2015, 171, 234–244. [Google Scholar] [CrossRef]
- Peña, M.A.; Liao, R.; Brenning, A. Using spectrotemporal indices to improve the fruit-tree crop classification accuracy. ISPRS J. Photogramm. Remote Sens. 2017, 128, 158–169. [Google Scholar] [CrossRef]
- Räsänen, A.; Virtanen, T. Data and resolution requirements in mapping vegetation in spatially heterogeneous landscapes. Remote Sens. Environ. 2019, 230, 111207. [Google Scholar] [CrossRef]
- Peña-Barragán, J.M.; Ngugi, M.K.; Plant, R.E.; Six, J. Object-based crop identification using multiple vegetation indices, textural features and crop phenology. Remote Sens. Environ. 2011, 115, 1301–1316. [Google Scholar] [CrossRef]
- Tian, F.; Wu, B.; Zeng, H.; Zhang, X.; Xu, J. Efficient Identification of Corn Cultivation Area with Multitemporal Synthetic Aperture Radar and Optical Images in the Google Earth Engine Cloud Platform. Remote Sens. 2019, 11, 629. [Google Scholar] [CrossRef]
- Van Tricht, K.; Gobin, A.; Gilliams, S.; Piccard, I. Synergistic Use of Radar Sentinel-1 and Optical Sentinel-2 Imagery for Crop Mapping: A Case Study for Belgium. Remote Sens. 2018, 10, 1642. [Google Scholar] [CrossRef]
- Potgieter, A.B.; Apan, A.; Dunn, P.; Hammer, G. Estimating crop area using seasonal time series of Enhanced Vegetation Index from MODIS satellite imagery. Aust. J. Agric. Res. 2007, 58, 316–325. [Google Scholar] [CrossRef]
- Stefanski, J.; Mack, B.; Waske, B. Optimization of Object-Based Image Analysis With Random Forests for Land Cover Mapping. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 2492–2504. [Google Scholar] [CrossRef]
- Crabbe, R.A.; Lamb, D.W.; Edwards, C. Discriminating between C3, C4, and Mixed C3/C4 Pasture Grasses of a Grazed Landscape Using Multi-Temporal Sentinel-1a Data. Remote Sens. 2019, 11, 253. [Google Scholar] [CrossRef]
- Zhong, L.; Hawkins, T.; Biging, G.; Gong, P. A phenology-based approach to map crop types in the San Joaquin Valley, California. Int. J. Remote Sens. 2011, 32, 7777–7804. [Google Scholar] [CrossRef]
- Immitzer, M.; Vuolo, F.; Atzberger, C. First Experience with Sentinel-2 Data for Crop and Tree Species Classifications in Central Europe. Remote Sens. 2016, 8, 166. [Google Scholar] [CrossRef]
- Delenne, C.; Durrieu, S.; Rabatel, G.; Deshayes, M.; Bailly, J.S.; Lelong, C.; Couteron, P. Textural approaches for vineyard detection and characterization using very high spatial resolution remote sensing data. Int. J. Remote Sens. 2008, 29, 1153–1167. [Google Scholar] [CrossRef]
- Maschler, J.; Atzberger, C.; Immitzer, M. Individual Tree Crown Segmentation and Classification of 13 Tree Species Using Airborne Hyperspectral Data. Remote Sens. 2018, 10, 1218. [Google Scholar] [CrossRef]
- Blaschke, T. Object based image analysis for remote sensing. ISPRS J. Photogramm. Remote Sens. 2010, 65, 2–16. [Google Scholar] [CrossRef]
- Yu, Q.; Gong, P.; Clinton, N.; Biging, G.; Kelly, M.; Schirokauer, D. Object-based Detailed Vegetation Classification with Airborne High Spatial Resolution Remote Sensing Imagery. Photogramm. Eng. Remote Sens. 2006, 72, 799–811. [Google Scholar] [CrossRef]
- Zhang, Y.J. A survey on evaluation methods for image segmentation. Pattern Recognit. 1996, 29, 1335–1346. [Google Scholar] [CrossRef]
- Ortiz, A.; Oliver, G. On the use of the overlapping area matrix for image segmentation evaluation: A survey and new performance measures. Pattern Recognit. Lett. 2006, 27, 1916–1926. [Google Scholar] [CrossRef]
- Radoux, J.; Bogaert, P. Good Practices for Object-Based Accuracy Assessment. Remote Sens. 2017, 9, 646. [Google Scholar] [CrossRef]
- Stehman, S.V.; Foody, G.M. Key issues in rigorous accuracy assessment of land cover products. Remote Sens. Environ. 2019, 231, 111199. [Google Scholar] [CrossRef]
- Miller, A.J.; Gross, B.L. From forest to field: Perennial fruit crop domestication. Am. J. Bot. 2011, 98, 1389–1414. [Google Scholar] [CrossRef]
- Aschbacher, J.; Milagro-Pérez, M.P. The European Earth monitoring (GMES) programme: Status and perspectives. Remote Sens. Environ. 2012, 120, 3–8. [Google Scholar] [CrossRef]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Chavez, P.S. An improved dark-object subtraction technique for atmospheric scattering correction of multispectral data. Remote Sens. Environ. 1988, 24, 459–479. [Google Scholar] [CrossRef]
- Jakubauskas, M.E.; Legates, D.R.; Kastens, J.H. Crop identification using harmonic analysis of time series AVHRR NDVI data. Comput. Electron. Agric. 2002, 37, 127–139. [Google Scholar] [CrossRef]
- Achanta, R.; Susstrunk, S. Superpixels and Polygons Using Simple Non-iterative Clustering. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 4895–4904. [Google Scholar] [CrossRef]
- Géron, A. Hands-On Machine Learning with Scikit-Learn and TensorFlow: Concepts, Tools, and Techniques to Build Intelligent Systems; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2017. [Google Scholar]
- Liu, S.; Qi, Z.; Li, X.; Yeh, A.G.O. Integration of Convolutional Neural Networks and Object-Based Post-Classification Refinement for Land Use and Land Cover Mapping with Optical and SAR Data. Remote Sens. 2019, 11, 690. [Google Scholar] [CrossRef]
- North, H.C.; Pairman, D.; Belliss, S.E. Boundary Delineation of Agricultural Fields in Multitemporal Satellite Imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 237–251. [Google Scholar] [CrossRef]
- Gao, Q.; Zribi, M.; Escorihuela, M.J.; Baghdadi, N.; Segui, P.Q. Irrigation Mapping Using Sentinel-1 Time Series at Field Scale. Remote Sens. 2018, 10, 1495. [Google Scholar] [CrossRef]
- Gašparović, M.; Jogun, T. The effect of fusing Sentinel-2 bands on land-cover classification. Int. J. Remote Sens. 2018, 39, 822–841. [Google Scholar] [CrossRef]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I. Textural Features for Image Classification. IEEE Trans. Syst. Man Cybern. 1973, SMC-3, 610–621. [Google Scholar] [CrossRef]
- Warner, T.A.; Steinmaus, K. Spatial Classification of Orchards and Vineyards with High Spatial Resolution Panchromatic Imagery. Photogramm. Eng. Remote Sens. 2005, 71, 179–187. [Google Scholar] [CrossRef]

| Group | Class | Notes |
|---|---|---|
| Perennial crops | Citrus | Includes common oranges (mainly the Valencia) and navel oranges Citrus sinensis. There are also some Grapefruit Citrus paradisi, Lemon Citrus limon and Mandarin Citrus reticulata orchards. |
| Almond | Prunus dulcis. | |
| Cherry | Prunus avium. | |
| Plum | Prunus domestica, which in this area are mainly used to produce dried prunes. | |
| Stonefruit | Other stonefruit, which includes small areas of Nectarines Prunus persica var. nucipersica, Peaches Prunus persica and Apricots Prunus armeniaca. | |
| Olive | Olea europaea. | |
| Hazelnut | Corylus avellana. | |
| Walnut | Juglans regia. | |
| Vineyard | Vitis vinifera, mainly used to grow grapes for wine production in this area. | |
| Other areas | Annual | Annual crops, which includes those mainly grown over the summer (such as rice, cotton and maize) and those grown over the winter (such as barley, canola and wheat) as well as melons and vegetables. |
| Forest | Trees other than those used to produce a crop, such as native forest areas, mainly consisting of evergreen Eucalyptus. | |
| Other | All other areas, including water, buildings, grass and cropping areas not planted during the study year. |
| Grouping | Band | Abbreviation | Approx. Band Center | Resolution (m) |
|---|---|---|---|---|
| S1(2) | VV | VV | 5.4 GHz | 10 |
| VH | VH | 5.4 GHz | 10 | |
| S2(4) | Blue | B | 490 nm | 10 |
| Green | G | 560 nm | 10 | |
| Red | R | 660 nm | 10 | |
| Near infrared | NIR | 830 nm | 10 | |
| S2(10) (includes S2(4)) | Red edge 1 | RE1 | 700 nm | 20 |
| Red edge 2 | RE2 | 740 nm | 20 | |
| Red edge 3 | RE3 | 780 nm | 20 | |
| Near infrared narrowband | NIRN | 860 nm | 20 | |
| Short wave infrared 1 | SWIR1 | 1610 nm | 20 | |
| Short wave infrared 2 | SWIR2 | 2200 nm | 20 |
| Designation | Bands | Months | Features |
|---|---|---|---|
| S1(2) TS | VV, VH | 1805, 1806, …, 1904 | 24 |
| S2(4) 1 month | B, G, R, NIR | 1806 | 4 |
| S2(5) 1 month | B, G, R, NIR, NDVI | 1806 | 5 |
| S2(10) 1 month | B, G, R, NIR, RE1, RE2, RE3, NIRN, SWIR1, SWIR2 | 1806 | 10 |
| S2(5) 2 month | B, G, R, NIR, NDVI | 1809, 1810 | 10 |
| NDVI TS | NDVI | 1805, 1806, …, 1904 | 12 |
| S2(4) TS | B, G, R, NIR | 1805, 1806, …, 1904 | 48 |
| S2(10) TS | B, G, R, NIR, RE1, RE2, RE3, NIRN, SWIR1, SWIR2 | 1805, 1806, …, 1904 | 120 |
| S2(10) + S1(2) Agg | B, G, R, NIR, RE1, RE2, RE3, NIRN, SWIR1, SWIR2, VV, VH | Min, Mean, Max | 36 |
| S2(10) + S1(2) TS | B, G, R, NIR, RE1, RE2, RE3, NIRN, SWIR1, SWIR2, VV, VH | 1805, 1806, …, 1904 | 144 |
| Size | Compactness | Merging | Area Error Per Field (ha) | Segments Per Field |
|---|---|---|---|---|
| 20 | 0.4 | 1 × 0.05 | 0.31 | 44.65 |
| 40 | 0.4 | 2 × 0.05 | 0.38 | 9.88 |
| 80 | 0.2 | 1 × 0.1 | 0.94 | 3.48 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brinkhoff, J.; Vardanega, J.; Robson, A.J. Land Cover Classification of Nine Perennial Crops Using Sentinel-1 and -2 Data. Remote Sens. 2020, 12, 96. https://doi.org/10.3390/rs12010096
Brinkhoff J, Vardanega J, Robson AJ. Land Cover Classification of Nine Perennial Crops Using Sentinel-1 and -2 Data. Remote Sensing. 2020; 12(1):96. https://doi.org/10.3390/rs12010096
Chicago/Turabian StyleBrinkhoff, James, Justin Vardanega, and Andrew J. Robson. 2020. "Land Cover Classification of Nine Perennial Crops Using Sentinel-1 and -2 Data" Remote Sensing 12, no. 1: 96. https://doi.org/10.3390/rs12010096
APA StyleBrinkhoff, J., Vardanega, J., & Robson, A. J. (2020). Land Cover Classification of Nine Perennial Crops Using Sentinel-1 and -2 Data. Remote Sensing, 12(1), 96. https://doi.org/10.3390/rs12010096