Assessment of Landslide Susceptibility Using Statistical- and Artificial Intelligence-Based FR–RF Integrated Model and Multiresolution DEMs
Abstract
:1. Introduction
2. Materials and Methods
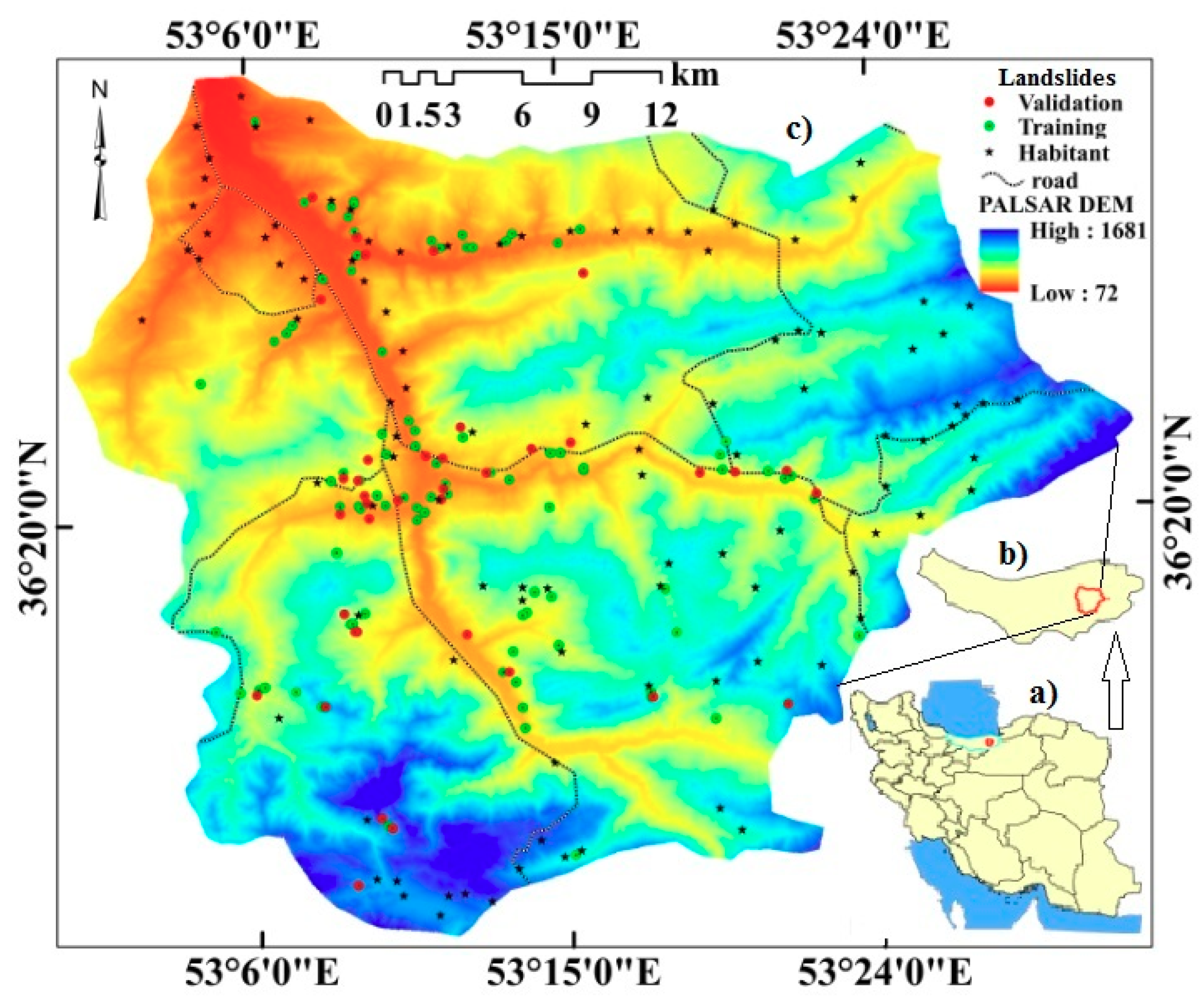
2.1. Study Area
2.2. Data Collection (Landslide Inventory Map and Landslide Conditioning Factors [LCFs])
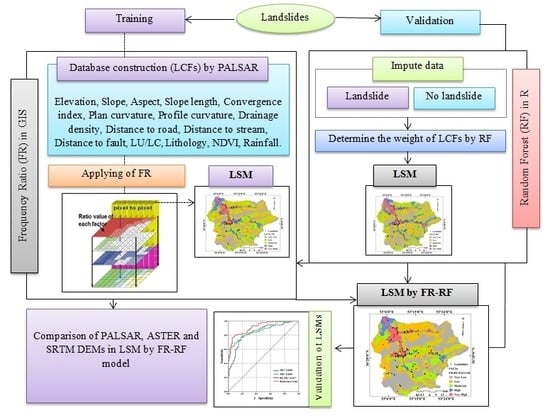
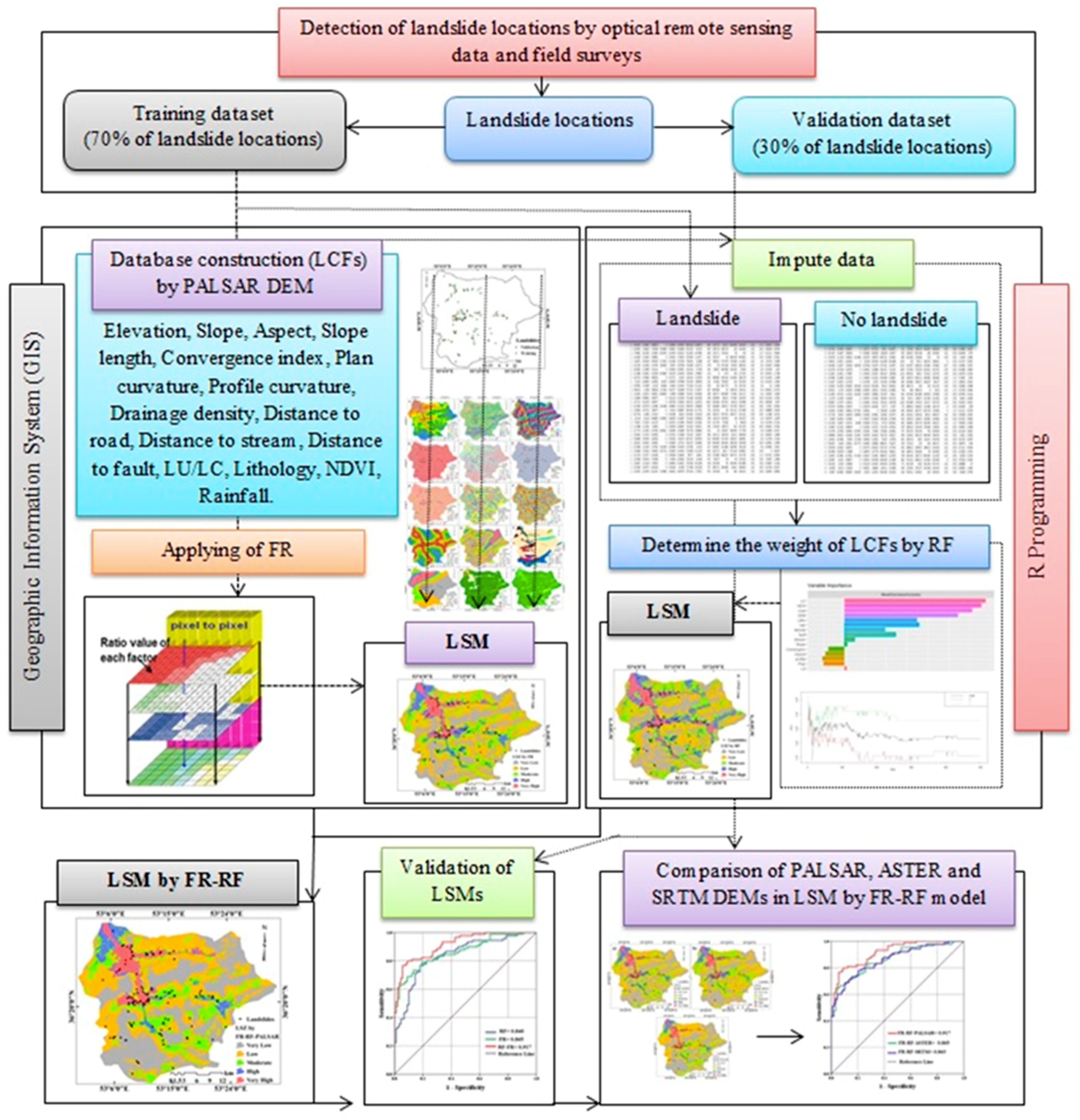
2.3. Methodology
2.4. Models
2.4.1. FR
2.4.2. RF
2.4.3. Ensemble of FR and RF (FR–RF)
2.5. Validation of models
3. Results
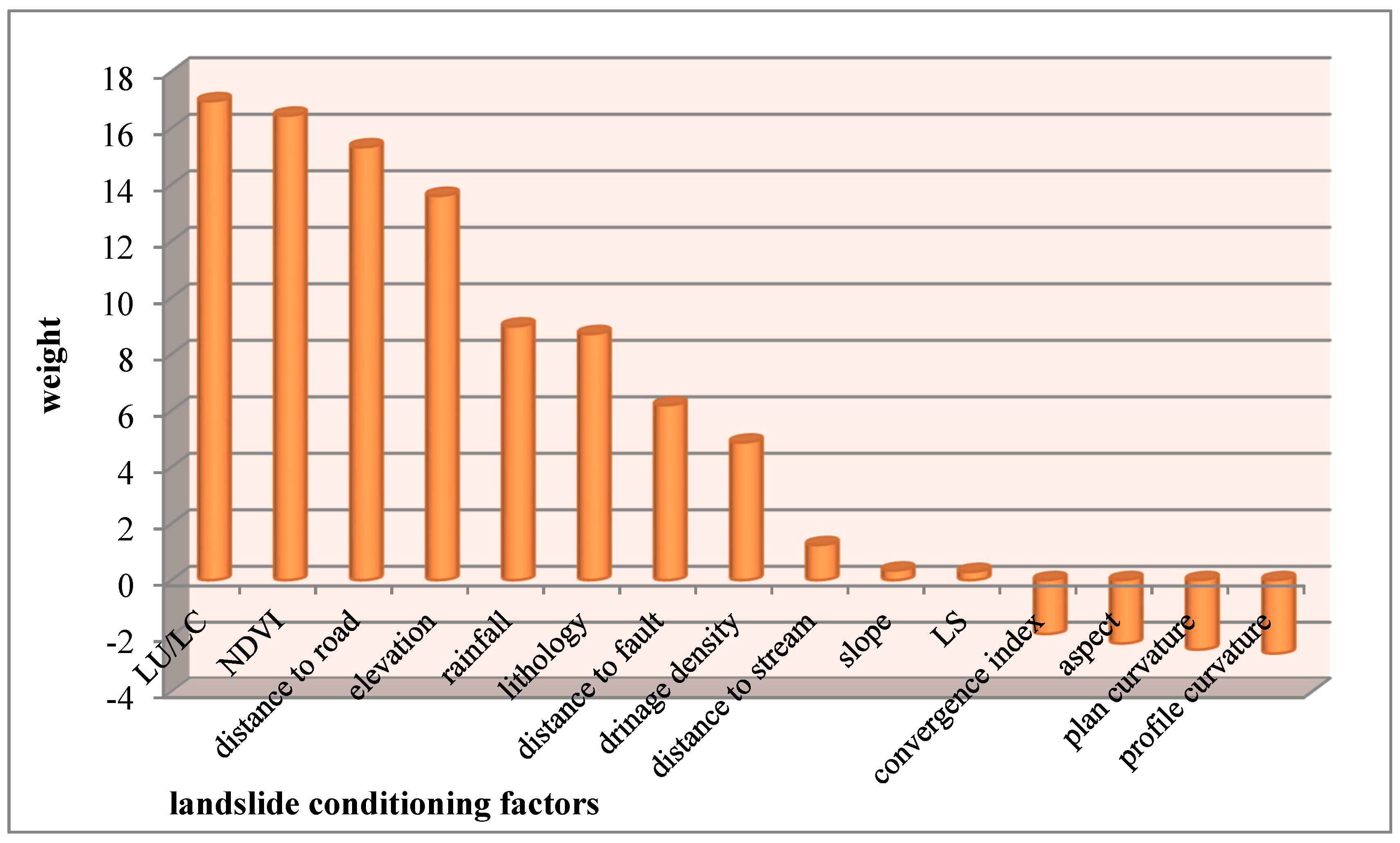
3.1. Multicollinearity Test
3.2. Application of FR Model
3.3. Application of RF Model
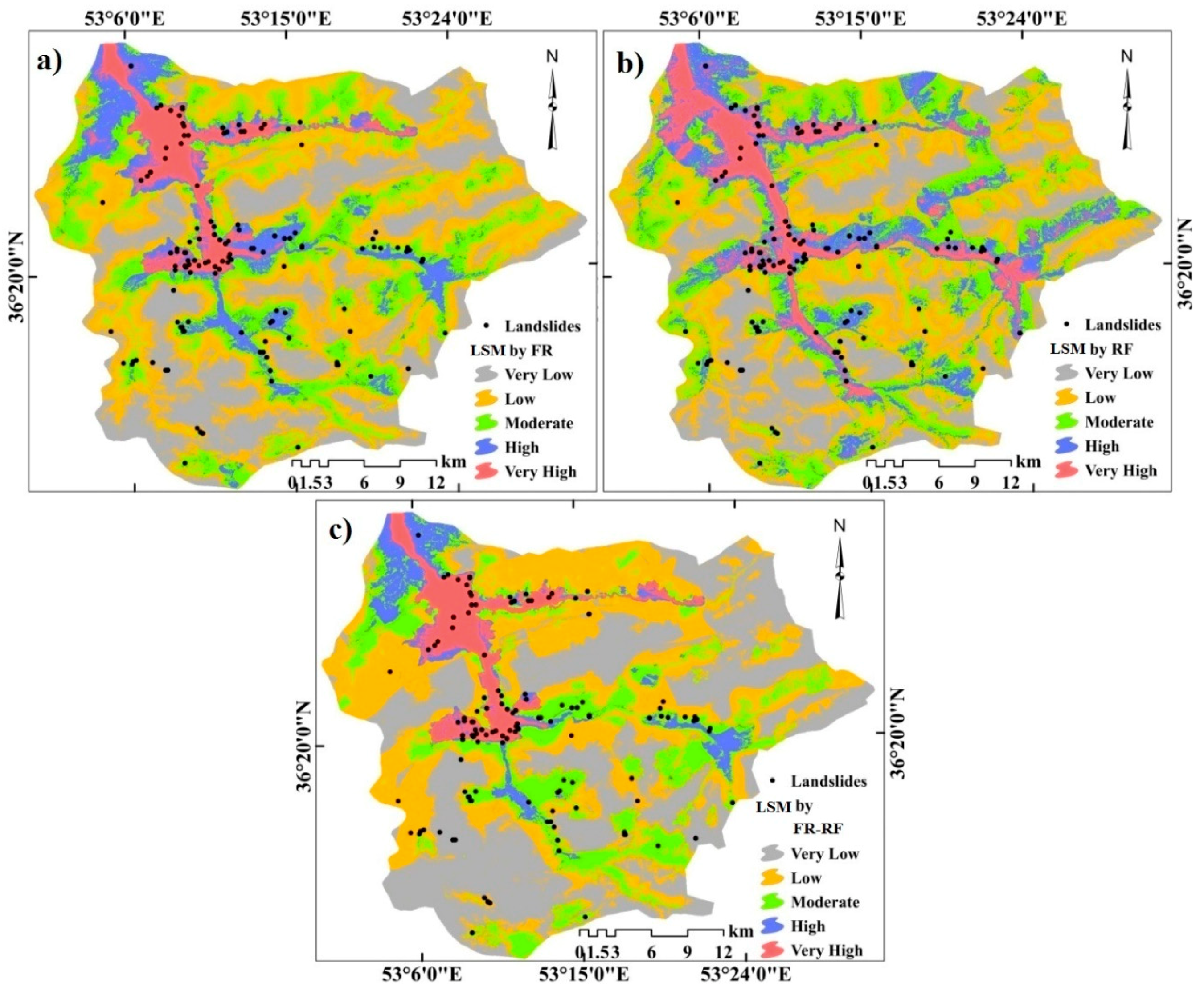
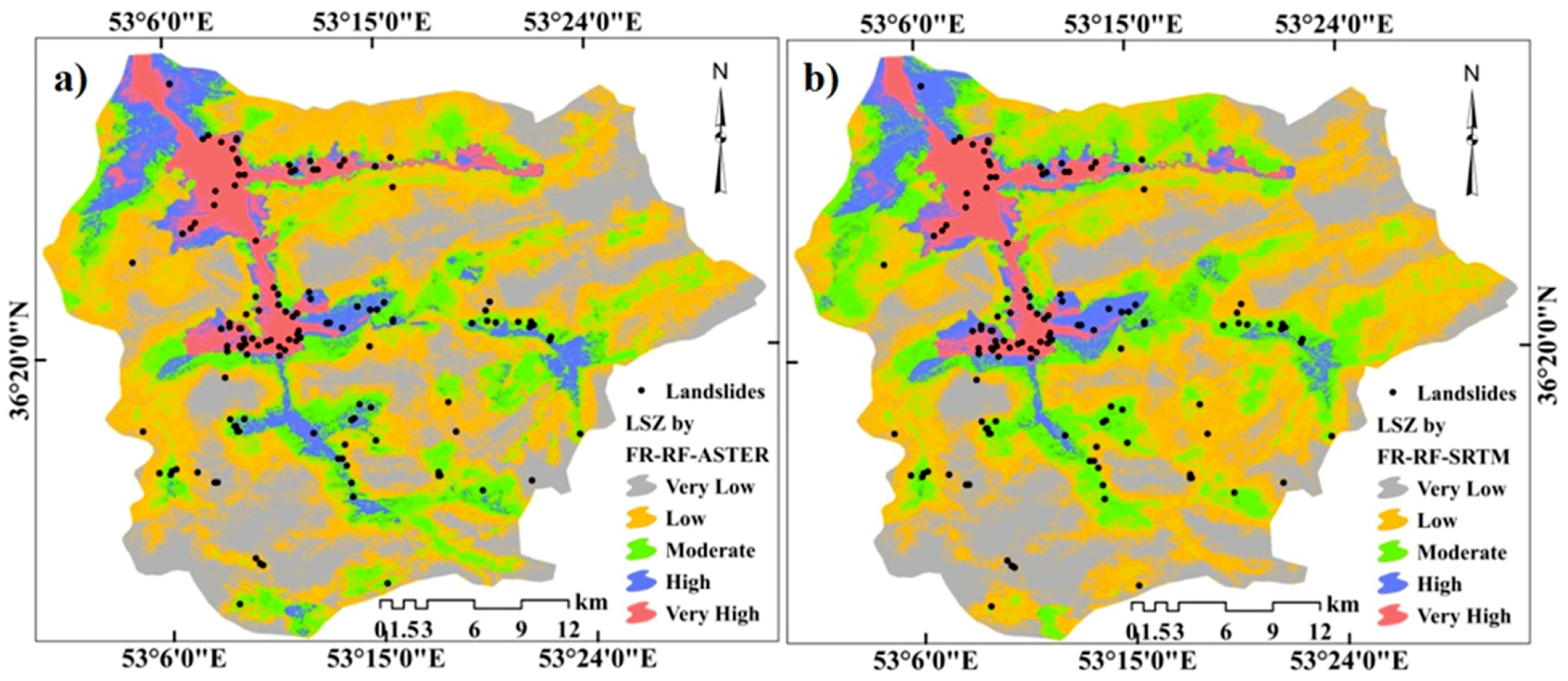
3.4. Application of FR–RF Integrated Model
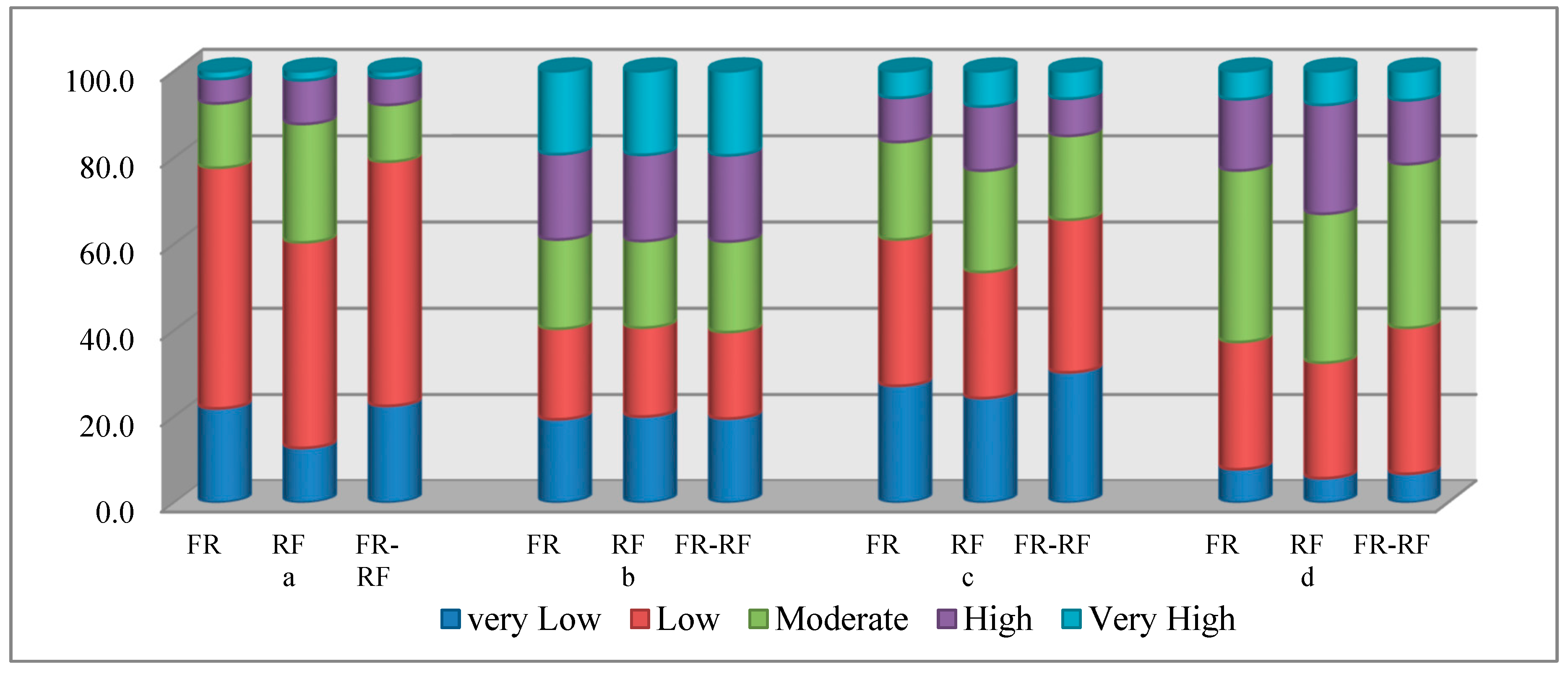
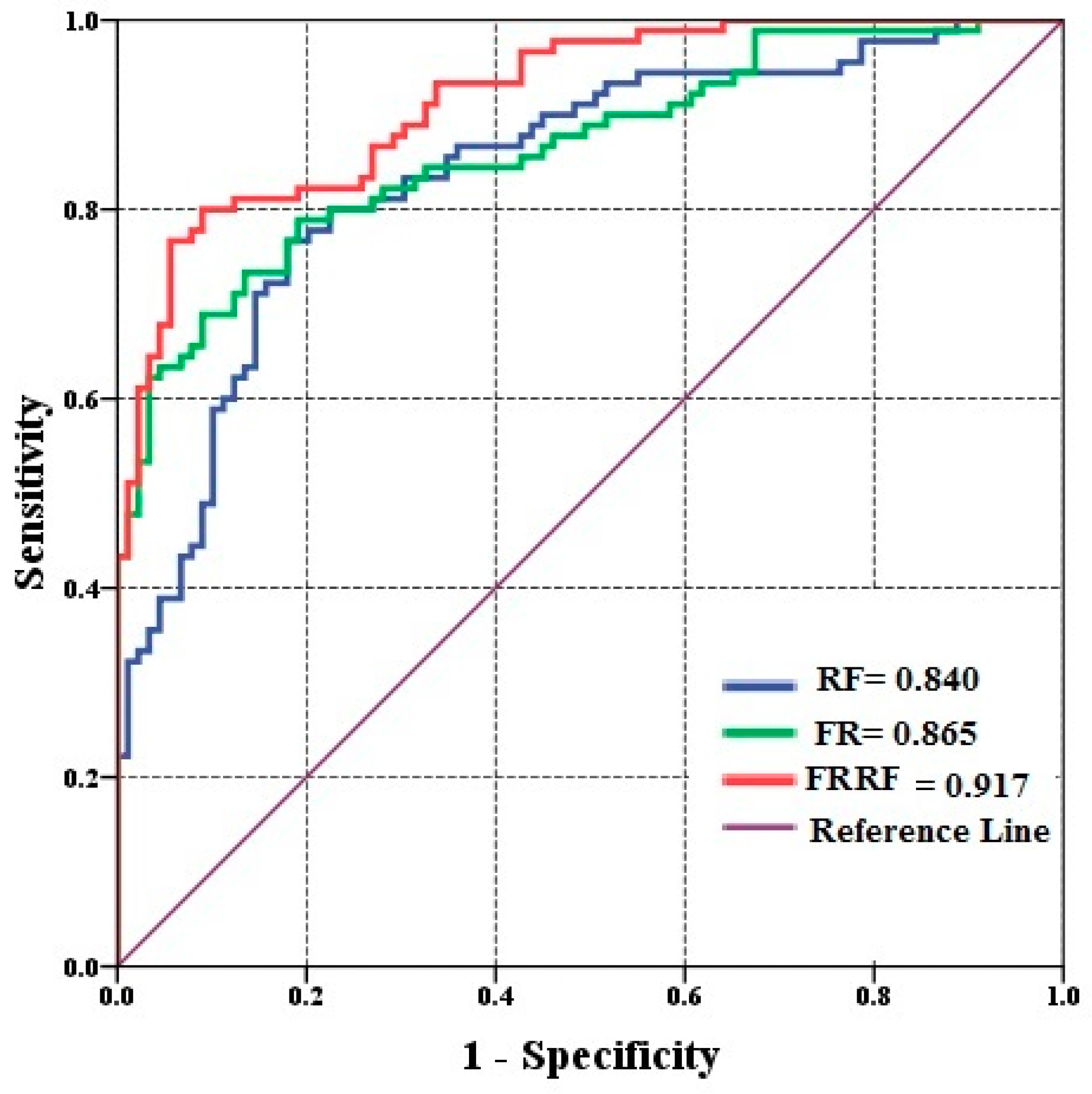
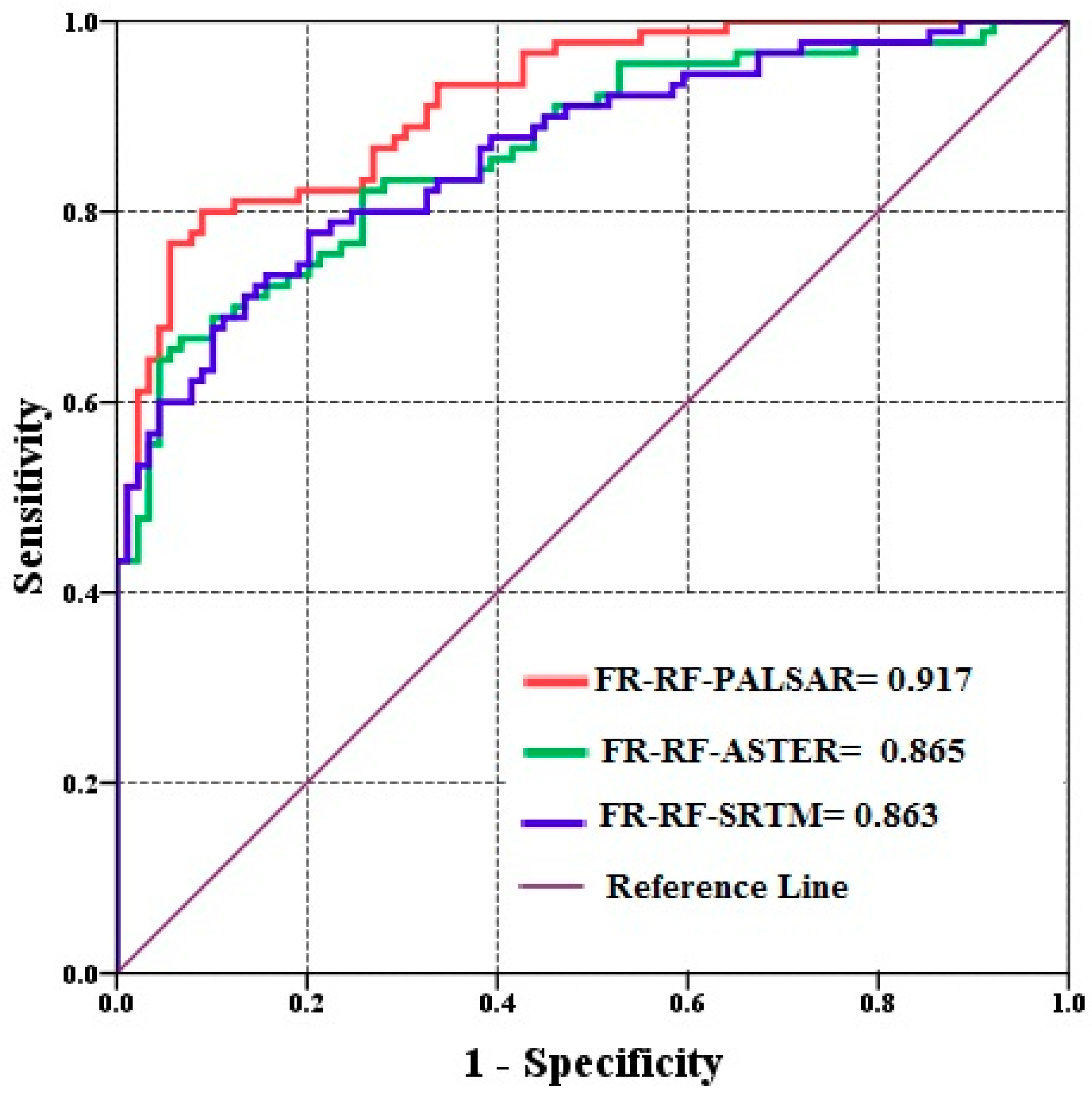
3.5. Model Validation
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chen, W.; Li, W.; Hou, E.; Bai, H.; Chai, H.; Wang, D.; Wang, Q. Application of frequency ratio, statistical index, and index of entropy models and their comparison in landslide susceptibility mapping for the Baozhong Region of Baoji, China. Arabian J. Geosci. 2015, 8, 1829–1841. [Google Scholar] [CrossRef]
- Blöchl, A.; Braun, B. Economic assessment of landslide risks in the Swabian Alb, Germany –research framework and first results of homeowners and experts surveys. Nat. Hazard. Earth Syst. Sci. 2005, 5, 389–396. [Google Scholar] [CrossRef]
- Komakpanah, A.; Hafezi Moghadas, S. Method of landslide hazard zonation. In Proceedings of the first workshop examined strategies to reduce landslide losses in the country, Tehran, Iran, 1995. [Google Scholar]
- Arabameri, A.R.; Pourghasemi, H.R.; Yamani, M. Applying different scenarios for landslide spatial modeling using computational intelligence methods. Environ. Earth Sci. 2017, 76, 832. [Google Scholar] [CrossRef]
- Cruden, D.M. A simple definition of a landslide. Bulletin Int. Assoc. Eng. Geol. 1991, 43, 27–29. [Google Scholar] [CrossRef]
- Cruden, D.M.; Varnes, D.J. Landslide types and processes. In Landslides, Investigation and Mitigation; Turner, A.K., Schuster, R.L., Eds.; Transportation Research Board: Washington, DC, USA, 1996; pp. 36–75. ISSN 0360–859X. ISBN 030906208X. [Google Scholar]
- Feizizadeh, B.; Blaschke, T. Landslide risk assessment based on GIS multi-criteria evaluation: A case study in Bostan-Abad County, Iran. J. Earth Sci. Eng. 2011, 1, 66–71. [Google Scholar]
- Akgun, A.; Kıncal, C.; Pradhan, B. Application of remote sensing data and GIS for landslide risk assessment as an environmental threat to Izmir city (west Turkey). Environ. Monit. Ass. 2012, 184, 5453–5470. [Google Scholar] [CrossRef] [PubMed]
- Pradhan, B. Landslide hazard and risk analyses at a landslide prone catchment area using statistical based geospatial model. Int. J. Remote Sens. 2011, 32, 4075–4087. [Google Scholar] [CrossRef]
- Fell, R.; Hartford, D. Landslide risk management. In Proceedings of the international workshop on landslide risk assessment, Honolulu, HI, USA, 19–21 February 1997; pp. 51–109. [Google Scholar]
- Kavzoglu, T.; Sahin, E.K.; Colkesen, I. Landslide susceptibility mapping using GIS-based multi-criteria decision analysis, support vector machines, and logistic regression. Landslides 2014, 11, 425–439. [Google Scholar] [CrossRef]
- Arabameri, A.; Pradhan, B.; Rezaei, K.; Sohrabi, M.; Kalantari, Z. GIS-based landslide susceptibility mapping using numerical risk factor bivariate model and its ensemble with linear multivariate regression and boosted regression tree algorithms. J. Mt. Sci 2019, 16, 595–618. [Google Scholar] [CrossRef]
- Brabb, E.E. Innovative approaches to landslide hazard mapping. In Proceedings of the 4th International Symposium on Landslides, Toronto, Japan, 4 October 1984; pp. 307–324. [Google Scholar]
- Guzzetti, F.; Reichenbach, P.; Ardizzone, F.; Cardinali, M.; Galli, M. Estimating the quality of landslide susceptibility models. Geomorphology 2006, 81, 166–184. [Google Scholar] [CrossRef]
- Varnes, D.J. IAEG Commission on Landslides and Other Mass-Movements Landslide Hazard Zonation: A Review of Principles and Practice; UNESCO Press: Paris, France, 1984; Available online: https://www.scirp.org/(S(i43dyn45teexjx455qlt3d2q))/reference/ReferencesPapers.aspx?ReferenceID=1768332 (accessed on 25 April 2019).
- Wang, L.j.; Kazuhide, S.; Shuji, M. Landslide susceptibility analysis with logistic regression model based On FCM sampling strategy. Comput. Geosci. 2013, 57, 81–92. [Google Scholar] [CrossRef]
- Kumar, R.; Anbalagan, R. Landslide susceptibility mapping using analytical hierarchy process (AHP) in Tehri reservoir rim region, Uttarakhand. J. Geol. Soc. India 2016, 87, 271–286. [Google Scholar] [CrossRef]
- Zhang, G.; Cai, Y.; Zheng, Z.; Zhen, J.; Liu, Y.; Huang, K. Integration of the statistical index method and the analytic hierarchy process technique for the assessment of landslide susceptibility in Huizhou, China. CATENA 2016, 142, 233–244. [Google Scholar] [CrossRef]
- Shahabi, H.; Khezri, S.; Ahmad, B.B.; Hasim, M. Landslide susceptibility mapping at central Zab basin, Iran: A comparison between analytical hierarchy process, frequency ratio and logistic regression models. CATENA 2014, 155, 55–70. [Google Scholar] [CrossRef]
- Kumar, R.; Anbalagan, R. Landslide susceptibility zonation in part of Tehri reservoir region using frequency ratio, fuzzy logic and GIS. J. Earth Syst. Sci. 2015, 124, 431–448. [Google Scholar] [CrossRef]
- Youssef, A.M.; Al-Kathery, M.; Pradhan, B. Landslide susceptibility mapping at Al-Hasher Area, Jizan (Saudi Arabia) using GIS-based frequency ratio and index of entropy models. Geosci. J. 2015, 19, 113–134. [Google Scholar] [CrossRef]
- Roșian, G.; Csaba, H.; Kinga-Olga, R.; Boțan, C.N.; Gavrilă, I.G. Assessing landslide vulnerability using statistical analysis and the frequency ratio model. Case study: Transylvanian Plain (Romania). Geomorphology 2016, 60, 359–371. [Google Scholar]
- Razavizadeh, S.; Solaimani, K.; Massironi, M.; Kavian, A. Mapping landslide susceptibility with frequency ratio, statistical index, and weights of evidence models: A case study in northern Iran. Environ. Earth Sci. 2017, 76, 499. [Google Scholar] [CrossRef]
- Nicu, L.C. Application of analytic hierarchy process, frequency ratio, and statistical index to landslide susceptibility: An approach to endangered cultural heritage. Environ. Earth Sci. 2018, 77, 79. [Google Scholar] [CrossRef]
- Chandra Pal, S.; Chowdhuri, I. GIS-based spatial prediction of landslide susceptibility using frequency ratio model of Lachung River basin, North Sikkim, India. SN Appl. Sci. 2019, 1, 416. [Google Scholar]
- Costanzo, D.; Chacón, J.; Conoscenti, C.; Irigaray, C.; Rotigliano, E. Forward logistic regression for earth-flow landslide susceptibility assessment in the Platani river basin (southern Sicily, Italy). Landslides 2014, 11, 639–653. [Google Scholar] [CrossRef]
- Zhang, T.; Han, L.; Han, J.; Li, X.; Zhang, H.; Wang, H. Assessment of Landslide Susceptibility Using Integrated Ensemble Fractal Dimension with Kernel Logistic Regression Model. Entropy 2019, 21, 218. [Google Scholar] [CrossRef]
- Tsangaratos, P.; Ilia, I. Comparison of a logistic regression and Naïve Bayes classifier in landslide susceptibility assessments: The influence of models complexity and training dataset size. Catena 2016, 145, 164–179. [Google Scholar] [CrossRef]
- Cama, M.; Conoscenti, C.; Lombardo, L.; Rotigliano, E. Exploring relationships between grid cell size and accuracy for debris-flow susceptibility models: A test in the Giampilieri catchment (Sicily, Italy). Environ. Earth Sci. 2016, 75, 238. [Google Scholar] [CrossRef]
- Tsangaratos, P.; Ilia, I.; Hong, H.; Chen, W.; Xu, C. Applying Information Theory and GIS-based quantitative methods to produce landslide susceptibility maps in Nancheng County, China. Landslides 2017, 14, 1091–1111. [Google Scholar] [CrossRef]
- Pradhan, B.; Abokharima, M.H.; Jebur, M.N.; Tehrany, M.S. Land subsidence susceptibility mapping at Kinta Valley (Malaysia) using the evidential belief function model in GIS. Nat. Hazards 2014, 73, 1019–1042. [Google Scholar] [CrossRef]
- Du, G.; Zhang, Y.; Iqbal, J. Landslide susceptibility mapping using an integrated model of information value method and logistic regression in the Bailongjiang watershed, Gansu Province, China. J. Mount. Sci. 2017, 14, 249. [Google Scholar] [CrossRef]
- Borrelli, L.; Ciurleo, M.; Gullà, G. Shallow landslide susceptibility assessment in granitic rocks using GIS-based statistical methods: The contribution of the weathering grade map. Landslides 2018, 15, 1127–1142. [Google Scholar] [CrossRef]
- Kumar, V.; Singh, K. Effectiveness of Remote Sensing and GIS-Based Landslide Susceptibility Zonation Mapping Using Information Value Method. Sustain. Eng. 2019, 17, 225–234. [Google Scholar]
- Ma, Z.; Qin, S.; Cao, C.; Lv, J.; Li, G.; Qiao, S.; Hu, X. The Influence of Different Knowledge-Driven Methods on Landslide Susceptibility Mapping: A Case Study in the Changbai Mountain Area, Northeast China. Entropy 2019, 21, 372. [Google Scholar] [CrossRef]
- Hong, H.; Chen, W.; Xu, C.; Youssef, A.M.; Pradhan, B.; Tien Bui, D. Rainfallinduced landslide susceptibility assessment at the Chongren area (China) using frequency ratio, certainty factor, and index of entropy. Geocarto. Int. 2017, 32, 139–154. [Google Scholar]
- Akgün, A.; Türk, N. Mapping erosion susceptibility by a multivariate statistical method: A case study from the Ayvalık region, NW Turkey. Comput. Geosci. 2011, 37, 1515–1524. [Google Scholar] [CrossRef]
- Conoscenti, C.; Ciaccio, M.; Caraballo-Arias, N.A.; Gómez-Gutiérrez, Á.; Rotigliano, E.; Agnesi, V. Assessment of susceptibility to earth-flow landslide using logistic regression and multivariate adaptive regression splines: A case of the Belice River basin (western Sicily, Italy). Geomorphology 2015, 242, 49–64. [Google Scholar] [CrossRef]
- Constantin, M.; Bednarik, M.; Jurchescu, M.C.; Vlaicu, M. Landslide susceptibility assessment using the bivariate statistical analysis and the index of entropy in the Sibiciu Basin (Romania). Environ. Earth Sci. 2011, 63, 397–406. [Google Scholar] [CrossRef]
- Chen, W.; Pourghasemi, H.R.; Naghibi, S.A. Prioritization of landslide conditioning factors and its spatial modeling in Shangnan County, China using GIS-based data mining algorithms. Bull. Eng. Geo. Environ. 2018, 77, 611. [Google Scholar] [CrossRef]
- Murillo-García, F.G.; Alcántara-Ayala, I. Landslide Susceptibility Analysis and Mapping Using Statistical Multivariate Techniques: Pahuatlán, Puebla, Mexico. Available online: https://link.springer.com/chapter/10.1007/978–3-319–11053–0_16 (accessed on 26 April 2019).
- Arnone, E.; Francipane, A.; Noto, L.V.; Scarbaci, A.; La Loggia, G. Strategies investigation in using artificial neural network for landslide susceptibility mapping: Application to a Sicilian catchment. J. Hydroinf. 2014, 16, 502–515. [Google Scholar] [CrossRef]
- Gelisli, K.; Kaya, T.; Babacan, A.E. Assessing the factor of safety using an artificial neural network: Case studies on landslides in Giresun, Turkey. Environ. Earth Sci. 2015, 73, 8639–8646. [Google Scholar] [CrossRef]
- Tien Bui, D.; Tuan, T.A.; Klempe, H.; Pradhan, B.; Revhaug, I. Spatial prediction models for shallow landslide hazards: A comparative assessment of the efficacy of support vector machines, artificial neural networks, kernel logistic regression, and logistic model tree. Landslides 2016, 13, 361–378. [Google Scholar] [CrossRef]
- Chen, W.; Xie, X.; Wang, J.; Pradhan, B.; Hong, H.; Tien Bui, D.; Duan, Z.; Ma, J. A comparative study of logistic model tree, random forest, and classification and regression tree models for spatial prediction of landslide susceptibility. Catena 2017, 151, 147–160. [Google Scholar] [CrossRef]
- Ren, F.; Wu, X.; Zhang, K.; Niu, R. Application of wavelet analysis and a particle swarm-optimized support vector machine to predict the displacement of the Shuping landslide in the Three Gorges, China. Environ. Earth Sci. 2015, 73, 4791–4804. [Google Scholar] [CrossRef]
- Tien Bui, D.; Pham, B.T.; Nguyen, Q.P.; Hoang, N.D. Spatial prediction of rainfall-induced shallow landslides using hybrid integration approach of least-squares support vector machines and differential evolution optimization: A case study in Central Vietnam. Int. J. Digit. Earth 2016, 9, 1077–1097. [Google Scholar] [CrossRef]
- Tien Bui, D.; Tuan, T.A.; Hoang, N.D.; Thanh, N.Q.; Nguyen, D.B.; Van Liem, N.; Pradhan, B. Spatial prediction of rainfall-induced landslides for the Lao Cai area (Vietnam) using a hybrid intelligent approach of least squares support vector machines inference model and artificial bee colony optimization. Landslides 2017, 14, 447–458. [Google Scholar] [CrossRef]
- Kumar, D.; Thakur, M.; Dubey, C.S.; Shukla, D.P. Landslide susceptibility mapping & prediction using support vector machine for Mandakini River Basin, Garhwal Himalaya, India. Geomorphology 2017, 295, 115–125. [Google Scholar]
- Kim, J.C.; Lee, S.; Jung, H.S.; Lee, S. Landslide susceptibility mapping using Random Forest and boosted tree models in Pyeong-Chang, Korea. J. Geocarto. Int. 2018, 33, 1000–1015. [Google Scholar] [CrossRef]
- Tien Bui, D.; Pradhan, B.; Lofman, O.; Revhaug, I.; Dick, O.B. Landslide susceptibility mapping at Hoa Binh province (Vietnam) using an adaptive neurofuzzy inference system and GIS. Comput. Geosci. 2012, 45, 199–211. [Google Scholar] [CrossRef]
- Dehnavi, A.; Aghdam, I.N.; Pradhan, B.; Morshed, V.M.H. A new hybrid model using step-wise weight assessment ratio analysis (SWARA) technique and adaptive neuro-fuzzy inference system (ANFIS) for regional landslide hazard assessment in Iran. Catena 2015, 135, 122–148. [Google Scholar] [CrossRef]
- Pradhan, B. A comparative study on the predictive ability of the decision tree, support vector machine and neuro-fuzzy models in landslide susceptibility mapping using GIS. Comput. Geosci. 2013, 51, 350–365. [Google Scholar] [CrossRef]
- Wang, L.J.; Guo, M.; Sawada, K.; Lin, J.; Zhang, J.A. comparative study of landslide susceptibility maps using logistic regression, frequency ratio, decision tree, weights of evidence and artificial neural network. Geosci. J. 2016, 20, 117–136. [Google Scholar] [CrossRef]
- Hong, H.; Liu, J.; Bui, D.T.; Pradhan, B.; Acharya, T.D.; Pham, B.T.; Zhu, A.X.; Chen, W.; Ahmad, B.B. Landslide susceptibility mapping using J48 Decision Tree with AdaBoost, Bagging and Rotation Forest ensembles in the Guangchang area (China). Catena 2018, 163, 399–413. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Kerle, N. Random forests and evidential belief function-based landslide susceptibility assessment in Western Mazandaran Province, Iran. Environ. Earth Sci. 2016, 75, 1–17. [Google Scholar] [CrossRef]
- Taaleb, K.; Cheng, T.; Zhang, Y. Mapping landslide susceptibility and types using Random Forest. Big Earth Data. 2018. [CrossRef]
- Jordan, M.I.; Mitchell, T.M. Machine learning: trends, perspectives, and prospects. Science 2015, 349, 255–260. [Google Scholar] [CrossRef]
- Aditian, A.; Kubota, T.; Shinohara, Y. Comparison of GIS-based landslide susceptibility models using frequency ratio, logistic regression, and artificial neural network in a tertiary region of Ambon, Indonesia. Geomorphology 2018, 318, 101–111. [Google Scholar] [CrossRef]
- Arabameri, A.; Rezaei, K.; Pourghasemi, H.R.; Lee, S.; Yamani, M. GIS-based gully erosion susceptibility mapping: A comparison among three data-driven models and AHP knowledge-based technique. Environ. Earth Sci. 2018, 77, 628. [Google Scholar] [CrossRef]
- Arabameri, A.; Rezaei, K.; Cerda, A.; Conoscenti, C.; Kalantari, Z. A comparison of statistical methods and multi-criteria decision making to map flood hazard susceptibility in Northern Iran. Sci. Total Environ. 2019, 660, 443–458. [Google Scholar] [CrossRef] [PubMed]
- Abedini, M.; Tulabi, S. Assessing LNRF, FR, and AHP models in landslide susceptibility mapping index: A comparative study of Nojian watershed in Lorestan province, Iran. Environ. Earth Sci. 2018, 77, 405. [Google Scholar] [CrossRef]
- Immitzer, M.; Atzberger, C.; Koukal, T. Tree species classification with random forest using very high spatial resolution 8-band WorldView-2 satellite data. Remote Sens. 2012, 4, 2661–2693. [Google Scholar] [CrossRef]
- Arabameri, A.; Rezaei, K.; Cerda, A.; Lombardo, L.; Rodrigo-Comino, J. GIS-based groundwater potential mapping in Shahroud plain, Iran. A comparison among statistical (bivariate and multivariate), data mining and MCDM approaches. Sci. Total Environ. 2019, 658, 160–177. [Google Scholar] [CrossRef]
- Arabameri, A.; Pradhan, B.; Rezaei, K. Gully erosion zonation mapping using integrated geographically weighted regression with certainty factor and random forest models in GIS. J. Environ. Manag. 2019, 232, 928–942. [Google Scholar] [CrossRef]
- Yu, K.; Yao, X.; Qiu, Q.; Liu, J. Landslide spatial prediction based on random forest model. J. Chem. Inf. Model. 2017, 47, 2490–2504. [Google Scholar]
- Arabameri, A.; Pradhan, B.; Pourghasemi, H.R.; Rezaei, K.; Kerle, N. Spatial Modelling of Gully Erosion Using GIS and R Programing: A Comparison among Three Data Mining Algorithms. Appl. Sci. 2018, 8, 1369. [Google Scholar] [CrossRef]
- Kornejady, A.; Pourghasemi, H.R.; Afzali, S.F. Presentation of RFFR New Ensemble Model for Landslide Susceptibility Assessment in Iran. Available online: https://link.springer.com/chapter/10.1007/978-3-319-77377-3_7 (accessed on 28 April 2019).
- I.R. of Iran Meteorological Organization (IRIMO). Available online: http://www.mazan daranmet.ir (accessed on 23 October 2018).
- Geology Survey of Iran (GSI). 1997. Available online: http://www.gsi.ir/Main/Lang_en/ index.html. (accessed on 27 October 2018).
- Guzzetti, F.; Mondini, A.C.; Cardinali, M.; Fiorucci, F.; Santangelo, M.; Chang, K.T. Landslide inventory maps: new tools for and old problem. Earth Sci. Rev. 2012, 112, 42–66. [Google Scholar] [CrossRef]
- Regmi, A.D.; Devkota, K.C.; Yoshida, K.; Pradhan, B.; Pourghasemi, H.R.; Kumamoto, T.; Akgun, A. Application of frequency ratio, statistical index, and weights-of-evidence models and their comparison in landslide susceptibility mapping in Central Nepal Himalaya. Arabian J. Geosci. 2014, 7, 725–742. [Google Scholar] [CrossRef]
- Paliaga, G.; Luino, F.; Turconi, L.; Faccini, F. Inventory of geo-hydrological phenomena in Genova municipality (NW Italy). J. Maps 2018, 15, 28–37. [Google Scholar] [CrossRef]
- Forestry, Rangeland and Watershed Organization (RWO). List of landslides in the Iran. Study Group on Landslides. Office of Engineering and Design Evaluation. 2013. Available online: http://www.frw.org.ir/02/Fa/default.aspx (accessed on 28 April 2019).
- Varnes D., J. Slope movements, type and processes. In Landslide analysis and control, Transportation Research Board; Schuster, R.L., Krizek, R.J., Eds.; Special Report 176; National Academy Sciences: Washington, DC, USA, 4 May 1978; pp. 11–33. [Google Scholar]
- Hungr, O.; Leroueil, S.; Picarelli, L. The Varnes classification of landslide types, an update. Landslides 2014, 11, 167–194. [Google Scholar] [CrossRef]
- Wang, Q.; Li, W.; Wu, Y.; Pei, Y.; Xie, P. Application of statistical index and index of entropy methods to landslide susceptibility assessment in Gongliu (Xinjiang, China). Environ. Earth Sci. 2016, 75, 599. [Google Scholar] [CrossRef]
- Wu, Y.; Li, W.; Liu, P. Application of analytic hierarchy process model for landslide susceptibility mapping in the Gangu County, Gansu Province, China. Environ. Earth Sci. 2016, 75, 422. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Moradi, H.R.; Fatemi Aghda, S.M. Landslide susceptibility mapping by binary logistic regression, analytical hierarchy process, and statistical index models and assessment of their performances. Nat. Hazards 2013, 69, 749–779. [Google Scholar] [CrossRef]
- Wang, Y.T.; Seijmonsbergen, A.C.; Bouten, W.; Chen, Q.T. Using statistical learning algorithms in regional landslide susceptibility zonation with limited landslide field data. J. Mount Sci. 2015, 12, 268–288. [Google Scholar] [CrossRef]
- Achour, Y.; Boumezbeur, R.A.; Hadji, R.; Chouabbi, A.; Cavaleiro, V.; Bendaoud, E.A. Landslide susceptibility mapping using analytic hierarchy process and information value methods along a highway road section in Constantine. Arab J. Geosci. 2017, 10, 194. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Rossi, M. Landslide susceptibility modeling in a landslide prone area in Mazandarn Province, north of Iran: A comparison between GLM, GAM, MARS, and M-AHP methods. Theor. Appl. Climat. 2016, 130, 1–25. [Google Scholar] [CrossRef]
- Tay, L.T.; Lateh, H.; Hossain, M.K.; Kamil, A.A. Landslide science for a Safer Geoenvironment. Volume 2: Methods of landslide studies Landslide hazard mapping using a poisson distribution: A case study in Penang Island, Malaysia. In Landslide Science for a Safer Geoenvironment; Springer: Cham Switzerland, 29 April 2014; pp. 521–525. [Google Scholar]
- Ozdemir, A. GIS-based groundwater spring potential mapping in the Sultan Mountains (Konya, Turkey) using frequency ratio, weights of evidence and logistic regression methods and their comparison. J. Hydr. 2011, 411, 290–308. [Google Scholar] [CrossRef]
- Lee, S.; Pradhan, B. Landslide hazard mapping at Selangor, Malaysia using frequency ratio and logistic regression models. Landslides 2007, 4, 33–41. [Google Scholar] [CrossRef]
- Chan, C.; Lewis, B. A basic primer on data mining, Information Systems Management. J. Inf. Syst. Manag. 2002, 19, 56–69. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Biau, G. Analysis of a random forests model. J. Mach. Learn. Res. 2012, 13, 1063–1095. [Google Scholar]
- Cutler, D.R.; Edwards, T.C.; Beard, K.H.; Cutler, A.; Hess, K.T. Random Forests for Classification in Ecology. Ecology 2007, 88, 2783–2792. [Google Scholar] [CrossRef] [PubMed]
- Simpson, G.L.; Birks, H.J.B. Statistical learning in palaeolimnology. In Tracking Environmental Change Using Lake Sediments; Springer: Berlin, Germany, 2012. [Google Scholar]
- Lee, S.; Kim, J.-C.; Jung, H.S.; Lee, M.J.; Lee, S. Spatial prediction of flood susceptibility using random-forest and boosted-tree models in Seoul metropolitan city, Korea. Geomat. Nat. Hazards Risk 2017, 8, 1185–1203. [Google Scholar] [CrossRef]
- Liaw, A.; Breiman, W.M. Cutler’s Random Forests for Classification and Regression. Available online: https://www.rdocumentation.org/packages/randomForest (accessed on 1 April 2018).
- Arabameri, A.; Pradhan, B.; Rezaei, K.; Yamani, M.; Pourghasemi, H.R.; Lombardo, L. Spatial modelling of gully erosion using Evidential Belief Function, Logistic Regression and a new ensemble EBF–LR algorithm. Land Degradation Develop. 2018b, 29, 4035–4049. [Google Scholar] [CrossRef]
- Arabameri, A.; Pradhan, B.; Rezaei, K.; Saro, L.; Sohrabi, M. An Ensemble Model for Landslide Susceptibility Mapping in a Forested Area. Geocarto Int. 2019. [Google Scholar] [CrossRef]
- Arabameri, A.; Pradhan, B.; Rezaei, K. Spatial prediction of gully erosion using ALOS PALSAR data and ensemble bivariate and data mining models. Geosci. J. 2019, 1–18. [Google Scholar] [CrossRef]
- Arabameri, A.; Pourghasemi, H.R. Spatial Modeling of Gully Erosion Using Linear and Quadratic Discriminant Analyses in GIS. In Spatial Modeling in GIS and R for Earth and Environmental Sciences, 1st ed.; Pourghasemi, H.R., Gokceoglu, C., Eds.; Elsevier: Berlin, Germany, 2019. [Google Scholar]
- Shirani, K.; Pasandi, M.; Arabameri, A. Landslide susceptibility assessment by Dempster–Shafer and Index of Entropy models, Sarkhoun basin, Southwestern Iran. Nat. Hazards 2018, 93, 1379–1418. [Google Scholar] [CrossRef]
- Yesilnacar, E.; Topal, T. Landslide susceptibility mapping: a comparison of logistic regression and neural networks methods in a medium scale study, Hendek region (Turkey). Eng. Geol. 2005, 79, 251–266. [Google Scholar] [CrossRef]
- Oh, H.J.; Lee, S.; Hong, M. Landslide Susceptibility Assessment Using Frequency Ratio Technique with Iterative Random Sampling. J. Sensors 2017, 2017, 1–22. [Google Scholar] [CrossRef]
- Youssef, A.M.; Pourghasemi, H.R.; Pourtaghi, Z.S.; Al-Katheeri, M.M. Landslide susceptibility mapping using random forest, boosted regression tree, classification and regression tree, and general linear models and comparison of their performance at Wadi Tayyah Basin, Asir Region, Saudi Arabia. Landslides 2016, 13, 839–856. [Google Scholar] [CrossRef]
- Chen, T.; Niu, R.; Jia, X. A comparison of information value and logistic regression models in landslide susceptibility mapping by using GIS. Environ. Earth Sci. 2016, 75, 867. [Google Scholar] [CrossRef]
- Yalcin, A. GIS-based landslide susceptibility mapping using analytical hierarchy process and bivariate statistics in Ardesen (Turkey): Comparisons of results and confirmations. Catena 2008, 72, 1–12. [Google Scholar] [CrossRef]
- Calvello, M.; Ciurleo, M. Optimal use of thematic maps for landslide susceptibility assessment by means of statistical analyses: case study of shallow landslides in fine grained soils. In Proceedings of the 12th International Symposium on Landslides, Napoli, Italy, 12–19 June 2016. [Google Scholar]
- Wechsler, S.P. Uncertainties associated with digital elevation models for hydrologic applications: A review. Hydrol. Earth Syst. Sci. 2007, 11, 1481–1500. [Google Scholar] [CrossRef]
- Garosia, Y.; Sheklabadia, M.; Pourghasemib, H.R.; Besalatpourc, A.A.; Christian Conoscentid, C.; Van Ooste, K. Comparison of differences in resolution and sources of controlling factors for gully erosion susceptibility mapping. Geoderma 2018, 330, 65–78. [Google Scholar] [CrossRef]
| Code | Description | Formation | Age |
|---|---|---|---|
| Qm | Swamp and shale | - | Quaternary |
| Plc | Polymictic conglomerate and sandstone | - | Pliocene |
| Mm, s, l | Marl, calcareous sandstone, sandy limestone and minor conglomerate | - | Miocene |
| PeEm | Marl and gypsiferous marl locally gypsiferous mudstone | - | Paleocene–Eocene |
| K2l2 | Thick-bedded to massive limestone | - | Late Cretaceous |
| K2l1 | Hyporite-bearing limestone | - | Late Cretaceous |
| DCkh | Yellowish, thin to thick-bedded, fossiliferous argillaceous limestone, dark grey limestone, greenish marl and shale, locally including gypsum | - | Devonian |
| Pel | Medium to thick-bedded limestone | - | Paleocene–Eocene |
| Jk | Conglomerate, sandstone and shale with plant remains and coal seams | Kashafrud | Middle Jurassic |
| Jl | Light grey, thin-bedded to massive limestone | Lar | Jurassic–Cretaceous |
| TRJs | Dark grey shale and sandstone | Shemshad | Triassic–Jurassic |
| Ktzl | Thick-bedded to massive, white to pinkish orbitolina bearing limestone | Tizkuh | Early Cretaceous |
| Factor | Source | Resolution | Classes | Method | Reference |
|---|---|---|---|---|---|
| Elevation | PALSAR, ASTER and SRTM DEMs | 12.5, 30 and 90 m | (1) <338 m; (2) 338–536 m; (3) 536–721 m; (4) 721–909 m; (5) 909–1136 m; (6) >1136 m | Natural break | [4] |
| Slope | PALSAR, ASTER and SRTM DEMs | 12.5, 30 and 90 m | (1) <7.1°; (2) 7.1°–13°; (3) 13°–18.8°; (4) 18.8°–25.2°; (5) 25.2°–32.6°; (6) >32.6° | Natural break | [78] |
| Aspect | PALSAR, ASTER and SRTM DEMs | 12.5, 30 and 90 m | (1) Flat (−1°); (2) North (337.5°–360°, 0°–22.5°); (3) Northeast (22.5°–67.5°); (4) East (67.5°–112.5°; (5) Southeast (112.5°–157.5°); (6) South (157.5°–202.5°); (7) Southwest (202.5°–247.5°); (8) West (247.4°–292.5°); (9) Northwest (292.5°–337.5°) | Equal interval | [12] |
| Convergence index | PALSAR, ASTER and SRTM DEMs | 12.5, 30 and 90 m | (1) <−29.41); (2) −29.41 to −9.01; (3) −9.01 to 7.45; (4) 7.45–27.84; (5) >27.84 | Natural break | [4] |
| SL | PALSAR, ASTER and SRTM DEMs | 12.5, 30 and 90 m | (1) <22.06 m; (2) 22.06–50.3 m; (3) 50.3–77.9 m; (4) 77.9–103.4 m; (5) >103.4 m | Natural break | [79] |
| Plan curvature | PALSAR, ASTER and SRTM DEMs | 12.5, 30 and 90 m | (1) Concave (<0); (2) Flat (0); (3) Convex (>0) | Natural break | [45] |
| Profile curvature | PALSAR, ASTER and SRTM DEMs | 12.5, 30 and 90 m | (1) <−1.13; (2) −1.13 to −0.35; (3) −0.35 to 0.28; (4) 0.28–1.12; (5) >1.12 | Natural break | [80] |
| Drainage density | PALSAR, ASTER and SRTM DEMs | 12.5, 30 and 90 m | (1) <0.38 km/km2; (2) 0.38–0.74 km/km2; (3) 0.74–1.12 k m/km2; (4) >1.12 km/km2 | Natural break | [60] |
| Distance to stream | PALSAR, ASTER and SRTM DEMs | 12.5, 30 and 90 m | (1) < 227 m; (2) 227–483 m; (3) 483–745 m; (4) 745–1035 m; (5) >1035 m | Natural break | [81] |
| Distance to road | Topographic map | 1:50,000 | (1) <1,204 m; (2) 1204–2564 m; (3) 2564–4041 m; (4) 4041–5712 m; (5) >5712 m | Natural break | [45] |
| Distance to fault | Geological map | 1:100,000 | (1) <649 m; (2) 649–1492 m; )3) 1492–2575 m; (4) 2575–3924 m; (5) >3924 m | Natural break | [82] |
| Lithology | Geology map | 1:100,000 | (1) DCkh; (2) Jk; (3) Jl; (4) K2l1; (5) K2l2; (6) Ktzl; (7) Mm, s, l; (8) PeEm; (9) Pel; (10) Plc; (11) Qm; (12) TRJs | Lithological units | - |
| Rainfall | Raining data | - | (1) <798.3 mm; (2) 798.3–911 mm; (3) 911–1041.3 mm; (4) 1041–1196 mm; (5) >1196 m m | Natural break | [45] |
| LU/LC | Landsat-8 image | 30 m | (1) Agriculture; (2) Dense forest; (3) Low forest; (4) Agri-orchard; (5) Agri-forest; (6); Dry farming forest; (7) Water | Supervisedclassification | - |
| NDVI | Landsat-8 image | 30 m | (1) <0.3; (2) 0.3–0.43; (3) >0.43 | Natural break | [12] |
| Model | Unstandardised Coefficients | Standardised Coefficients | t | Sig. | Collinearity Statistics | ||
|---|---|---|---|---|---|---|---|
| B | Std. Error | Beta | Tolerance (TOL) | Variance Inflation Factor (VIF) | |||
| (Constant) | 1.163 | 0.483 | 2.408 | 0.017 | |||
| Slope | −0.010 | 0.009 | −0.157 | −1.070 | 0.286 | 0.154 | 6.510 |
| Stream power index (SPI) | 0.034 | 0.057 | 0.125 | 0.590 | 0.556 | 0.074 | 13.476 |
| Topographic wetness index (TWI) | −0.059 | 0.052 | −0.262 | −1.143 | 0.255 | 0.063 | 15.948 |
| LS | 0.001 | 0.001 | 0.062 | 1.039 | 0.300 | 0.939 | 1.064 |
| NDVI | −1.063 | 0.349 | −0.220 | −3.048 | 0.003 | 0.632 | 1.582 |
| Plan | 0.057 | 0.060 | 0.082 | 0.944 | 0.346 | 0.442 | 2.264 |
| Rainfall | 0.000 | 0.000 | −0.091 | −1.001 | 0.318 | 0.401 | 2.494 |
| Convergence | −0.005 | 0.002 | −0.178 | −2.315 | 0.022 | 0.558 | 1.791 |
| Elevation | 0.000 | 0.000 | −0.185 | −1.611 | 0.109 | 0.251 | 3.980 |
| Dis. to fault | −8.000 × 10−5 | 0.000 | −0.201 | −3.201 | 0.002 | 0.836 | 1.197 |
| Dis. to road | −9.013 × 10−6 | 0.000 | −0.036 | −0.514 | 0.608 | 0.691 | 1.447 |
| Dis. to stream | 0.000 | 0.000 | 0.129 | 1.557 | 0.121 | 0.479 | 2.087 |
| Aspect | −1.151 × 10−5 | 0.000 | −0.002 | −0.040 | 0.968 | 0.955 | 1.047 |
| Lithology | 0.024 | 0.045 | 0.042 | 0.547 | 0.585 | 0.565 | 1.769 |
| LU/LC | 0.059 | 0.020 | 0.243 | 2.985 | 0.003 | 0.499 | 2.003 |
| Profile | −0.0011 | 0.051 | −0.015 | −0.215 | 0.830 | 0.689 | 1.452 |
| Drainage | 0.217 | 0.107 | 0.176 | 2.020 | 0.045 | 0.437 | 2.286 |
| Factor | Classes | Pixels in Domain | Landslides | FR | |||
|---|---|---|---|---|---|---|---|
| No. | % | No. | % | ||||
| Elevation (m) | <338 | 137,911 | 11.5753 | 33 | 37.0787 | 3.2032 | |
| 338–536 | 234,710 | 19.7000 | 22 | 24.7191 | 1.2548 | ||
| 536–721 | 259,859 | 21.8108 | 21 | 23.5955 | 1.0818 | ||
| 721–909 | 263,398 | 22.1079 | 8 | 8.9888 | 0.4066 | ||
| 909–1136 | 190,367 | 15.9781 | 4 | 4.4944 | 0.2813 | ||
| >1136 | 105,177 | 8.8279 | 1 | 1.1236 | 0.1273 | ||
| Slope (°) | <7.1 | 182,669 | 15.3320 | 13 | 14.6067 | 0.9527 | |
| 7.1–13 | 291,575 | 24.4729 | 32 | 35.9551 | 1.4692 | ||
| 13–18.8 | 278,341 | 23.3621 | 23 | 25.8427 | 1.1062 | ||
| 18.8–25.2 | 219,564 | 18.4287 | 11 | 12.3596 | 0.6707 | ||
| 25.2–32.6 | 153,604 | 12.8925 | 5 | 5.6180 | 0.4358 | ||
| >32.6 | 65,669 | 5.5118 | 5 | 5.6180 | 1.0193 | ||
| Aspect | F | 132,288 | 9.8337 | 6 | 6.1856 | 0.6290 | |
| N | 255,671 | 19.0054 | 10 | 10.3093 | 0.5424 | ||
| NE | 92,803 | 6.8986 | 8 | 8.2474 | 1.1955 | ||
| E | 103,340 | 7.6818 | 14 | 14.4330 | 1.8788 | ||
| SE | 123,821 | 9.2043 | 9 | 9.2784 | 1.0080 | ||
| SE | 125,536 | 9.3318 | 12 | 12.3711 | 1.3257 | ||
| SW | 106,245 | 7.8978 | 12 | 12.3711 | 1.5664 | ||
| W | 115,393 | 8.5778 | 10 | 10.3093 | 1.2019 | ||
| NW | 136,325 | 10.1338 | 8 | 8.2474 | 0.8139 | ||
| Convergence (100/m) | <−29.41 | 85,228 | 7.1535 | 9 | 10.1124 | 1.4136 | |
| −29.41 to −9.01 | 254,471 | 21.3586 | 14 | 15.7303 | 0.7365 | ||
| −9.01 to 7.45 | 471,169 | 39.5469 | 45 | 50.5618 | 1.2785 | ||
| 7.45–27.84 | 290,876 | 24.4142 | 18 | 20.2247 | 0.8284 | ||
| >27.84 | 89,675 | 7.5267 | 3 | 3.3708 | 0.4478 | ||
| SL (100/m) | <22.06 | 108,816 | 18.2882 | 12 | 13.4831 | 0.7373 | |
| 22.06–50.3 | 96,539 | 16.2249 | 9 | 10.1124 | 0.6233 | ||
| 50.3–77.9 | 107,115 | 18.0023 | 8 | 8.9888 | 0.4993 | ||
| 77.9–103.4 | 105,363 | 17.7079 | 44 | 49.4382 | 2.7919 | ||
| 103.4–128.2 | 106,179 | 17.8450 | 16 | 17.9775 | 1.0074 | ||
| >128.2 | 70,994 | 11.9316 | 0 | 0.0000 | 0.0000 | ||
| Plan curvature (100/m) | Concave | 564,975 | 47.4202 | 41 | 46.0674 | 0.9715 | |
| Flat | 37,478 | 3.1457 | 0 | 0.0000 | 0.0000 | ||
| Convex | 588,969 | 49.4341 | 48 | 53.9326 | 1.0910 | ||
| Profile curvature (100/m) | <−1.13 | 68,989 | 5.7905 | 7 | 7.8652 | 1.3583 | |
| −1.13 to −0.35 | 250,549 | 21.0294 | 16 | 17.9775 | 0.8549 | ||
| −0.35 to 0.28 | 502,333 | 42.1625 | 42 | 47.1910 | 1.1193 | ||
| 0.28–1.12 | 292,982 | 24.5910 | 20 | 22.4719 | 0.9138 | ||
| >1.12 | 76,569 | 6.4267 | 4 | 4.4944 | 0.6993 | ||
| Drainage density (km/km2) | <0.38 | 330,170 | 27.7123 | 5 | 5.6180 | 0.2027 | |
| 0.38–0.74 | 365,514 | 30.6788 | 18 | 20.2247 | 0.6592 | ||
| 0.74–1.12 | 320,115 | 26.8683 | 37 | 41.5730 | 1.5473 | ||
| >1.12 | 175,623 | 14.7406 | 29 | 32.5843 | 2.2105 | ||
| Distance to stream (m) | <227 | 340,196 | 28.5538 | 45 | 50.5618 | 1.7708 | |
| 227–483 | 304,400 | 25.5493 | 22 | 24.7191 | 0.9675 | ||
| 483–745 | 260,354 | 21.8524 | 15 | 16.8539 | 0.7713 | ||
| 745–1035 | 196,123 | 16.4613 | 4 | 4.4944 | 0.2730 | ||
| >1035 | 90,349 | 7.5833 | 3 | 3.3708 | 0.4445 | ||
| Distance to road (m) | <1204 | 320,797.2 | 26.9256 | 50 | 56.1798 | 2.0865 | |
| 1204–2564 | 276,105.2 | 23.1744 | 12 | 13.4831 | 0.5818 | ||
| 2564–4041 | 238,790.2 | 20.0425 | 12 | 13.4831 | 0.6727 | ||
| 4041–5712 | 199,267.2 | 16.7252 | 6 | 6.7416 | 0.4031 | ||
| >5712 | 1,564,62.2 | 13.1324 | 9 | 10.1124 | 0.7700 | ||
| Distance to fault (m) | <649 | 494,487 | 41.5039 | 34 | 38.2022 | 0.9204 | |
| 649–1492 | 329,948 | 27.6936 | 32 | 35.9551 | 1.2983 | ||
| 1492–2575 | 196,680 | 16.5080 | 19 | 21.3483 | 1.2932 | ||
| 2575–3924 | 107,320 | 9.0077 | 3 | 3.3708 | 0.3742 | ||
| >3924 | 62,987 | 5.2867 | 1 | 1.1236 | 0.2125 | ||
| Lithology | DCkh | 112 | 0.0094 | 0 | 0.0000 | 0.0000 | |
| Jk | 15,756 | 1.3225 | 1 | 1.1236 | 0.8496 | ||
| Jl | 14,742 | 1.2373 | 1 | 1.1236 | 0.9081 | ||
| K2l1 | 135,059 | 11.3359 | 3 | 3.3708 | 0.2974 | ||
| K2l2 | 45,114 | 3.7866 | 0 | 0.0000 | 0.0000 | ||
| Ktzl | 1253 | 0.1052 | 0 | 0.0000 | 0.0000 | ||
| Mm, s, l | 803,209 | 67.4160 | 61 | 68.5393 | 1.0167 | ||
| PeEm | 9010 | 0.7562 | 0 | 0.0000 | 0.0000 | ||
| Pel | 71,877 | 6.0329 | 2 | 2.2472 | 0.3725 | ||
| Plc | 56,750 | 4.7632 | 15 | 16.8539 | 3.5384 | ||
| Qm | 34,118 | 2.8636 | 6 | 6.7416 | 2.3542 | ||
| TRJs | 4422 | 0.3712 | 0 | 0.0000 | 0.0000 | ||
| Rainfall (mm) | <798.3 | 448,287 | 37.6262 | 45 | 50.5618 | 1.3438 | |
| 798.3911 | 305,254 | 25.6210 | 12 | 13.4831 | 0.5263 | ||
| 911–1041.3 | 195,091 | 16.3746 | 9 | 10.1124 | 0.6176 | ||
| 1041–1196 | 98,934 | 8.3039 | 2 | 2.2472 | 0.2706 | ||
| >1196 | 143,855 | 12.0742 | 21 | 23.5955 | 1.9542 | ||
| LU/LC | Agriculture | 976 | 0.0819 | 0 | 0.0000 | 0.0000 | |
| Dense forest | 941,148 | 78.9937 | 39 | 43.8202 | 0.5547 | ||
| Low forest | 17,995 | 1.5104 | 0 | 0.0000 | 0.0000 | ||
| Agri-orchard | 90,665 | 7.6098 | 38 | 42.6966 | 5.6107 | ||
| Agri-forest | 183 | 0.0154 | 0 | 0.0000 | 0.0000 | ||
| Dry farming forest | 136,585 | 11.4640 | 12 | 13.4831 | 1.1761 | ||
| Water | 3870 | 0.3248 | 0 | 0.0000 | 0.0000 | ||
| NDVI | <0.3 | 116,202 | 9.7532 | 26 | 29.2135 | 2.9953 | |
| 0.3–0.43 | 177,729 | 14.9174 | 29 | 32.5843 | 2.1843 | ||
| >0.43 | 897,490 | 75.3294 | 34 | 38.2022 | 0.5071 | ||
| Observed | Predicted | |
|---|---|---|
| 0 | 1 | |
| 0 | 54 | 10 |
| 1 | 17 | 44 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arabameri, A.; Pradhan, B.; Rezaei, K.; Lee, C.-W. Assessment of Landslide Susceptibility Using Statistical- and Artificial Intelligence-Based FR–RF Integrated Model and Multiresolution DEMs. Remote Sens. 2019, 11, 999. https://doi.org/10.3390/rs11090999
Arabameri A, Pradhan B, Rezaei K, Lee C-W. Assessment of Landslide Susceptibility Using Statistical- and Artificial Intelligence-Based FR–RF Integrated Model and Multiresolution DEMs. Remote Sensing. 2019; 11(9):999. https://doi.org/10.3390/rs11090999
Chicago/Turabian StyleArabameri, Alireza, Biswajeet Pradhan, Khalil Rezaei, and Chang-Wook Lee. 2019. "Assessment of Landslide Susceptibility Using Statistical- and Artificial Intelligence-Based FR–RF Integrated Model and Multiresolution DEMs" Remote Sensing 11, no. 9: 999. https://doi.org/10.3390/rs11090999
APA StyleArabameri, A., Pradhan, B., Rezaei, K., & Lee, C.-W. (2019). Assessment of Landslide Susceptibility Using Statistical- and Artificial Intelligence-Based FR–RF Integrated Model and Multiresolution DEMs. Remote Sensing, 11(9), 999. https://doi.org/10.3390/rs11090999