1. Introduction
Applications that attempt to track pedestrian motion level (walking distance) for health purposes require an accurate step detection and stride length estimation (SLE) technique [
1]. Walking distance is used to assess the physical activity level of the user, which helps provide feedback and motivate a more active lifestyle [
2,
3] Another type of application based on walking distance is navigation applications. Among various indoor localization methods, pedestrian dead reckoning (PDR) [
4] has become a mainstream and practical method, because PDR does not require any infrastructure. In addition to the general applications, involving asset and personnel tracking, health monitoring, precision advertising, and location-specific push notifications, PDR is available for emergency scenarios, such as anti-terrorism action, emergency rescue, and exploration missions. Furthermore, smartphone-based PDR mainly benefits from the extensive use of smartphones—pedestrians always carry smartphones that have integrated inertial sensors. Stride length estimation is a key component of PDR, the accuracy of which will directly affect the performance of PDR systems. Therefore, in addition to providing more accurate motion level estimation, precise stride length estimation based on built-in smartphone inertial sensors enhances positioning accuracy of PDR. Most visible light positioning [
5,
6], Wi-Fi positioning [
7,
8,
9], and magnetic positioning [
10,
11,
12] critically depend on PDR. Hence, motion level estimation based on smartphones contributes to assisting and supporting patients undergoing health rehabilitation and treatment, activity monitoring of daily living, navigation, and numerous other applications [
13].
The methods for estimating pedestrian step length are summarized as two categories: the first is direct methods, based on the integration of acceleration; the second is indirect methods that leverage a model or assumption to compute step length. The double integration of the acceleration component in the forward direction is the best method to compute the stride length of pedestrians because it does not rely on any model or assumption, and does not require training phases or individual information (leg length, height, weight) [
14]. Kourogi et al. [
15] leveraged the correlation between vertical acceleration and walking velocity to estimate walking speed, and calculated stride length by multiplying walking speed with step interval. However, the non-negligible bias and noise of the accelerometers and gyroscopes resulted in the distance error growing boundlessly and cubically in time [
14]. Moreover, it is difficult to obtain the acceleration component in the forward direction from the sensor’s measurements, as well as constantly maintaining the sensor heading parallel to the pedestrian’s walking direction [
16]. Additionally, low-cost smartphone sensors are not reliable and accurate enough to estimate the stride length of a pedestrian by double integrating the acceleration [
17]. Developing a step length estimation algorithm using MEMS (micro-electro-mechanical systems) sensors is recognized as a difficult problem.
Considerable research based on models or assumptions has been conducted to improve the accuracy of SLE, and summarized as empirical relationships [
18,
19], biomechanical models [
18,
20,
21], linear models [
22], nonlinear models [
23,
24,
25], regression-based [
22,
26], and neural networks [
27,
28,
29,
30]. One of the most renowned SLE algorithms was presented by Weinberg [
23]. To estimate the walk distance, he leveraged the range of the vertical acceleration values during each step, according to Equation (1).
where
and
denote the maximum and minimum acceleration values on the Z-axis in each stride, respectively.
k represents the calibration coefficient, which is obtained from the ratio of the actual distance and the estimated distance.
As shown in Equation (2), Kim et al. [
24] developed an empirical method, based on the average of the acceleration magnitude in each stride during walking, to calculate movement distance.
where
represents the measured acceleration value of the
sample in each step, and
N represents the number of samples corresponding to each step.
k is the calibration coefficient.
To estimate the travel distance of a pedestrian accurately, Ladetto et al. [
22] leveraged the linear relationship between step length and frequency and the local variance of acceleration to calculate the motion distance with the following equation:
where f is the step frequency, which represents the reciprocal of one stride interval, v is the acceleration variance during the interval of one step,
α and
β denote the weighting factors of step frequency and acceleration variance, respectively, and
γ represents a constant that is used to fit the relationship between the actual distance and the estimated distance.
Kang et al. [
31] simultaneously measured the inertial sensor and global positioning system (GPS) position while walking outdoors with a reliable GPS fix, and regarded the velocity from the GPS as labels to train a hybrid multiscale convolutional and recurrent neural network model. After that, Kang leveraged the prediction velocity and moving time to estimate the traveled distance. However, it is challenging to obtain accurate labels, since GPS contains a positional error. Zhu et al. [
32] measured the duration of the swing phase in each gait cycle by accelerometer and gyroscope, and then combined the acceleration information during the swing phase to obtain the step length. Xing et al. [
29] proposed a stride length estimation algorithm based on a back propagation artificial neural network, using a consumer-grade inertial measurement unit. To eliminate the effect of the accelerometer bias and the acceleration of gravity, Cho et al. [
28] utilized a neural network method for step length estimation. Martinelli et al. [
33] proposed a weighted, context-based step length estimation (WC-SLE) algorithm, in which the step lengths computed for different pedestrian contexts were weighted by the context probabilities. Diaz et al. [
34] and Diaz [
35] leveraged an inertial sensor mounted on the thigh and the variation amplitude of the leg’s pitch as a predictor to build a linear regression model. To reduce overfitting, Zihajehzadeh and Park [
36,
37] used lasso regression to fit the linear model by minimizing a penalized version of the least squares loss function. However, these methods required the user to wear a special device in a specific position on the body. In our previous work [
38], a stride length estimation method based on long short-term memory (LSTM) and denoising autoencoders (DAE), termed Tapeline, was proposed. Tapeline [
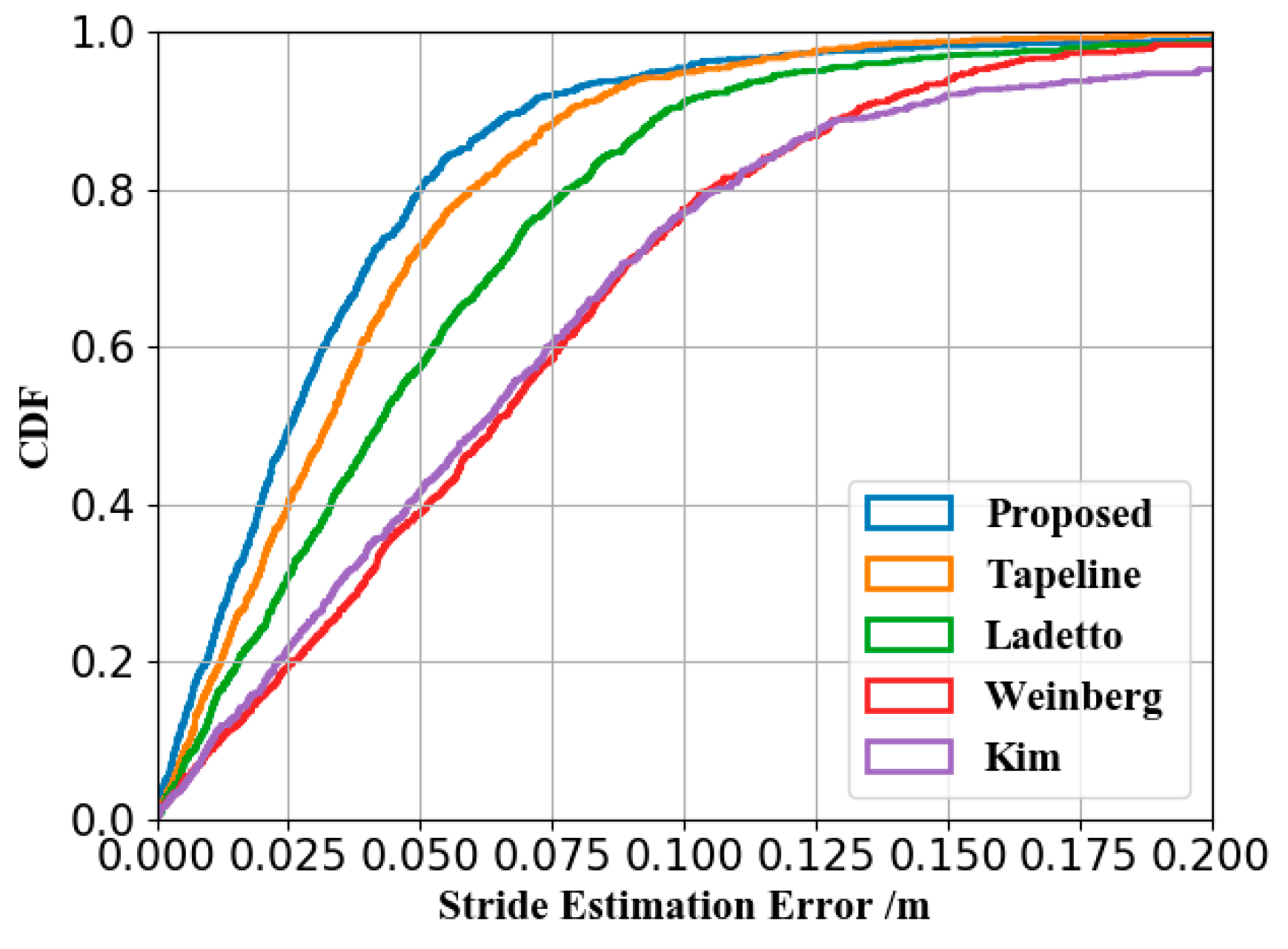
38] first leveraged a LSTM network to excavate the temporal dependencies and extract significant features vectors from noisy inertial sensor measurements. Afterwards, denoising autoencoders were adopted to sanitize the inherent noise and obtain denoised feature vectors automatically. Finally, a regression module was employed to map the denoised feature vectors to the resulting stride length. Tapeline achieved superior performance, with a stride length error rate of 4.63% and a walking distance error rate of 1.43%. However, the LSTM network and denoising processes result in a large number of computational overheads. The most significant drawback of the Tapeline was that pedestrians should hold their phone horizontally with their hand in front of their chest.
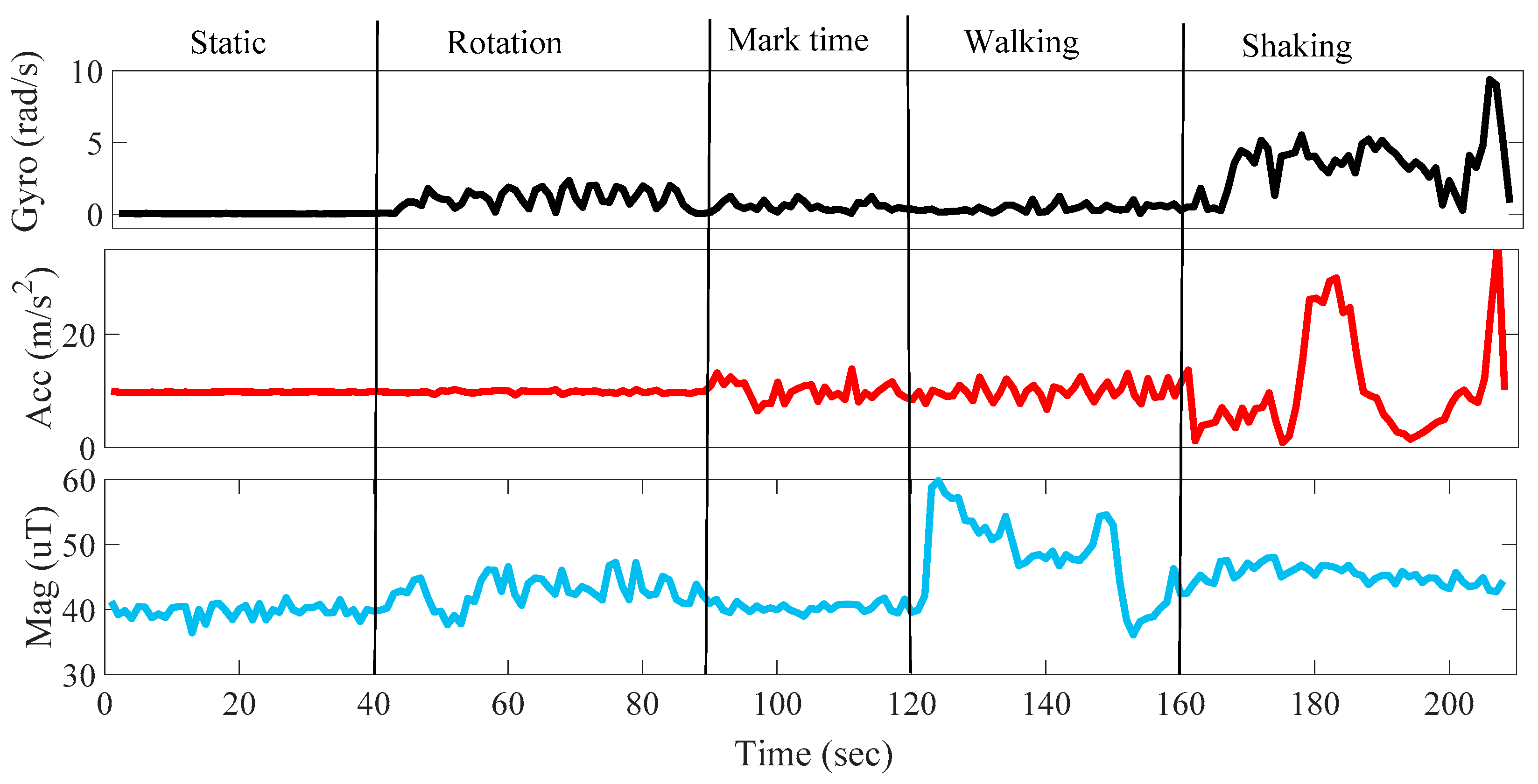
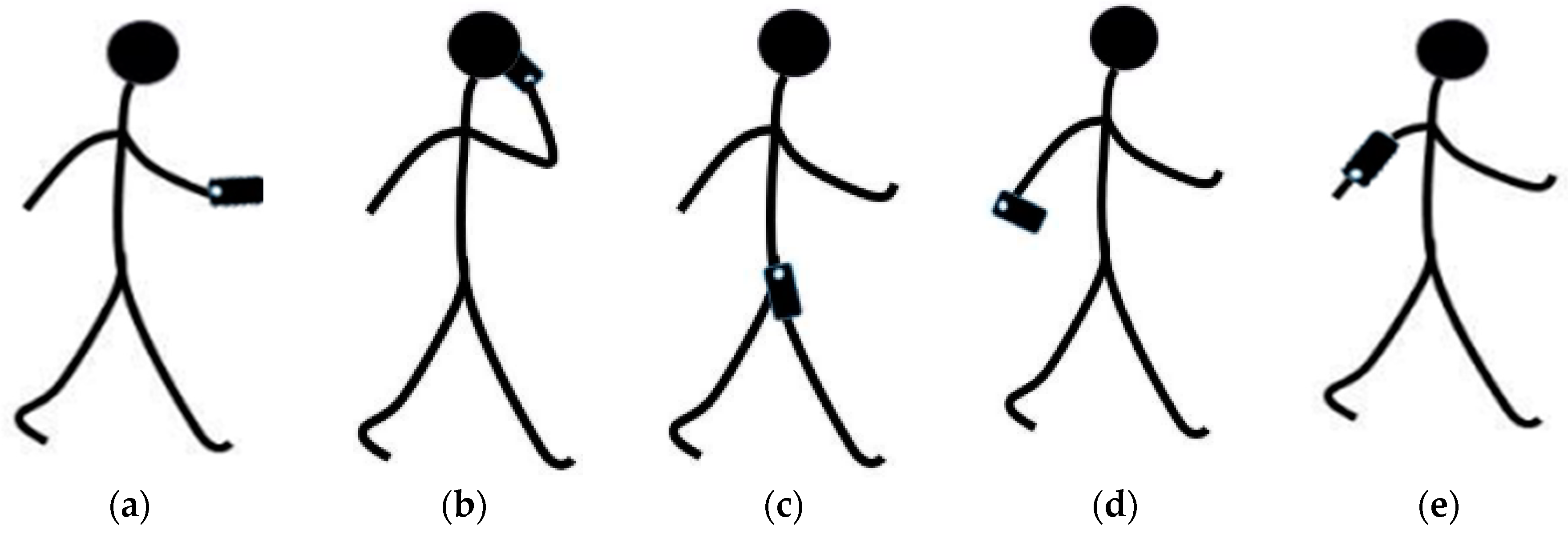
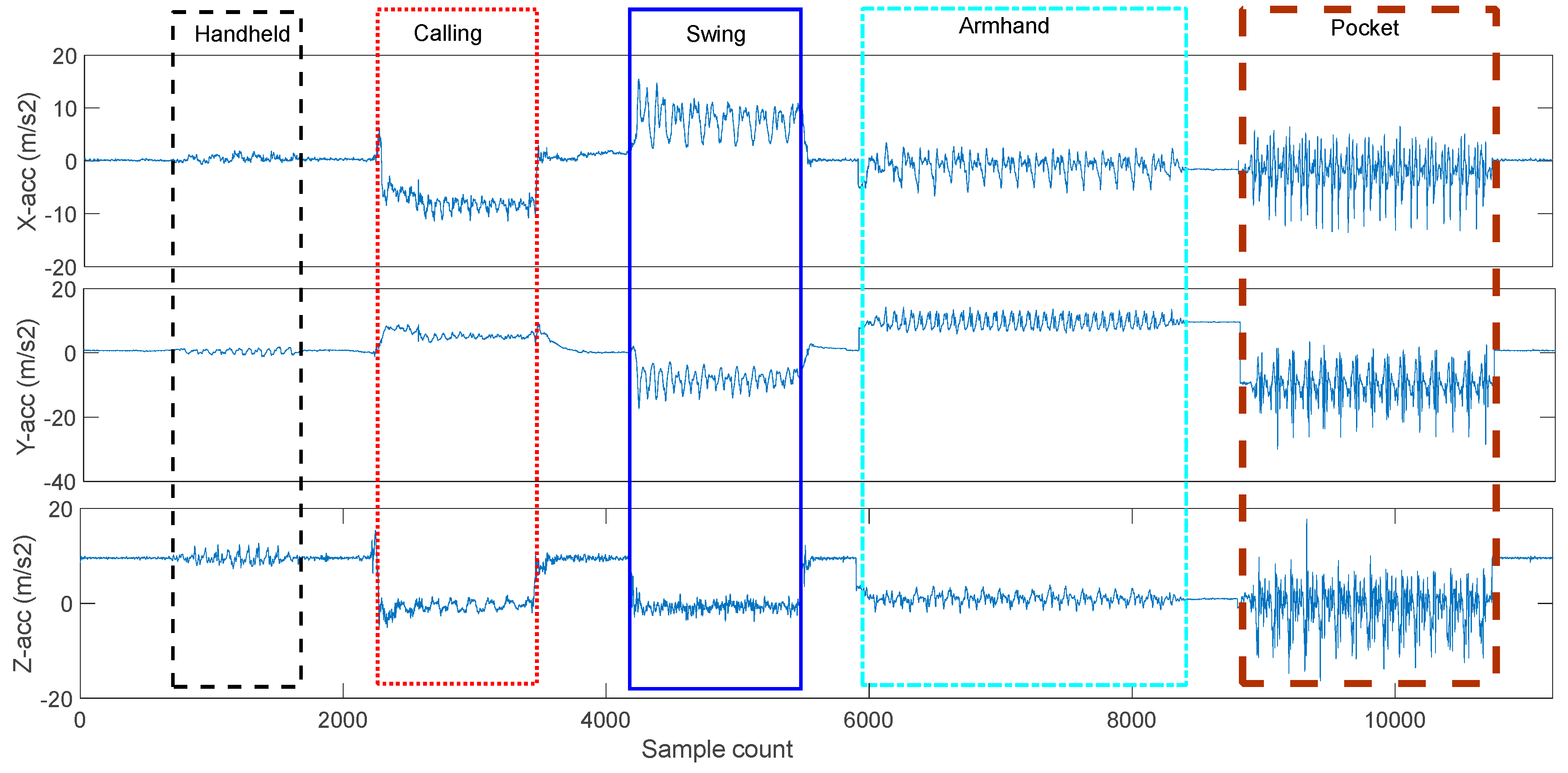
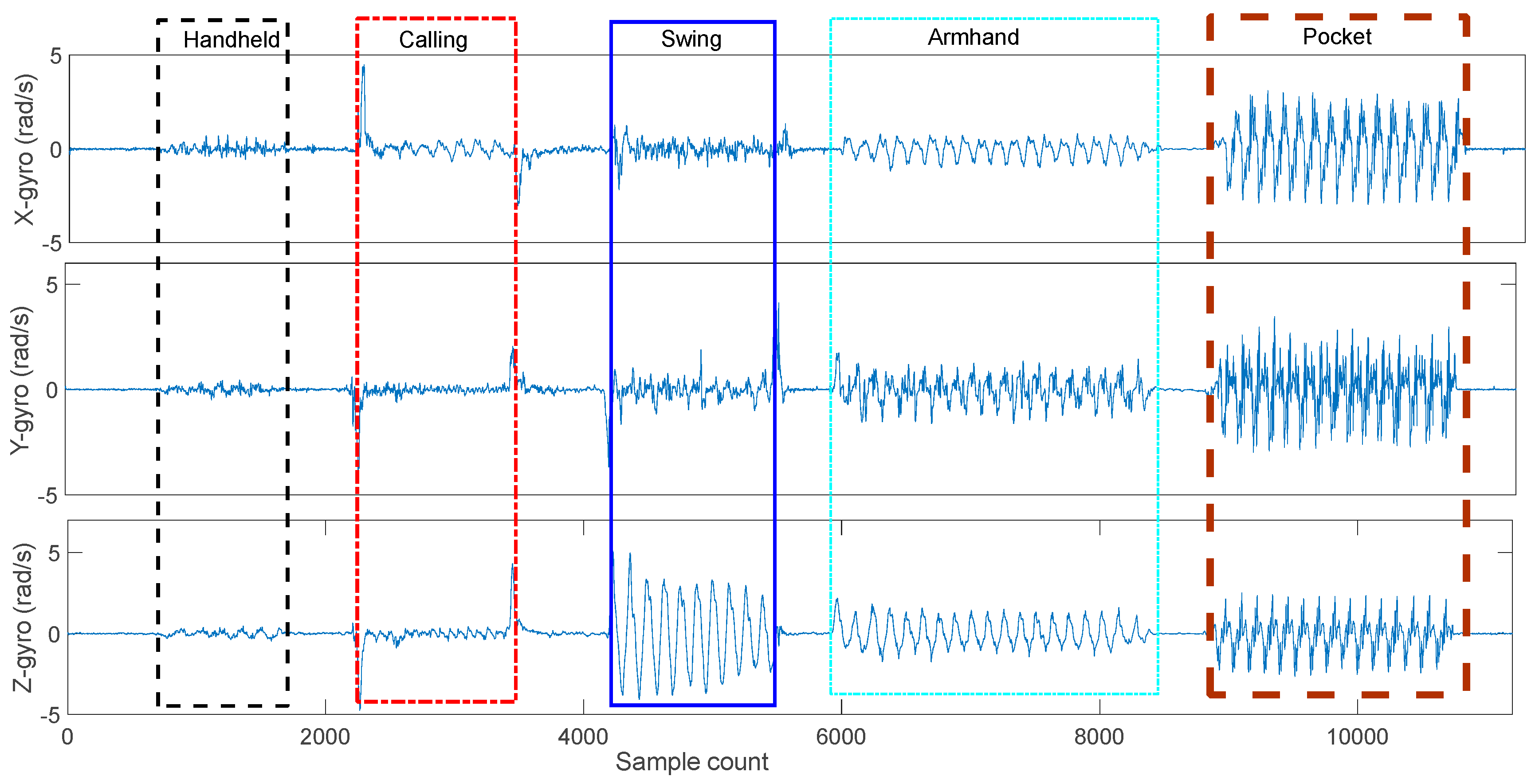
Stride length and walking distance estimation from smartphones’ inertial sensors are challenging because of the various walking patterns and smartphone carrying methods. These SLE algorithms perform well in the case of walking at normal speed under fixed mode. Unfortunately, the pedestrian may walk arbitrarily in different directions and may stop from time to time. Moreover, real paths always including turns, sidesteps, stairs, variations in speed, or various actions performed by the subject, which will result in unacceptable SLE accuracy. Eventually, these algorithms’ performances are shown to be highly sensitive to the carrying position of a smartphone (smartphone modes) on the user’s body. As shown in
Table 1, there are significant differences in the mean and standard deviation of acceleration and gyroscope collected under different carrying position.
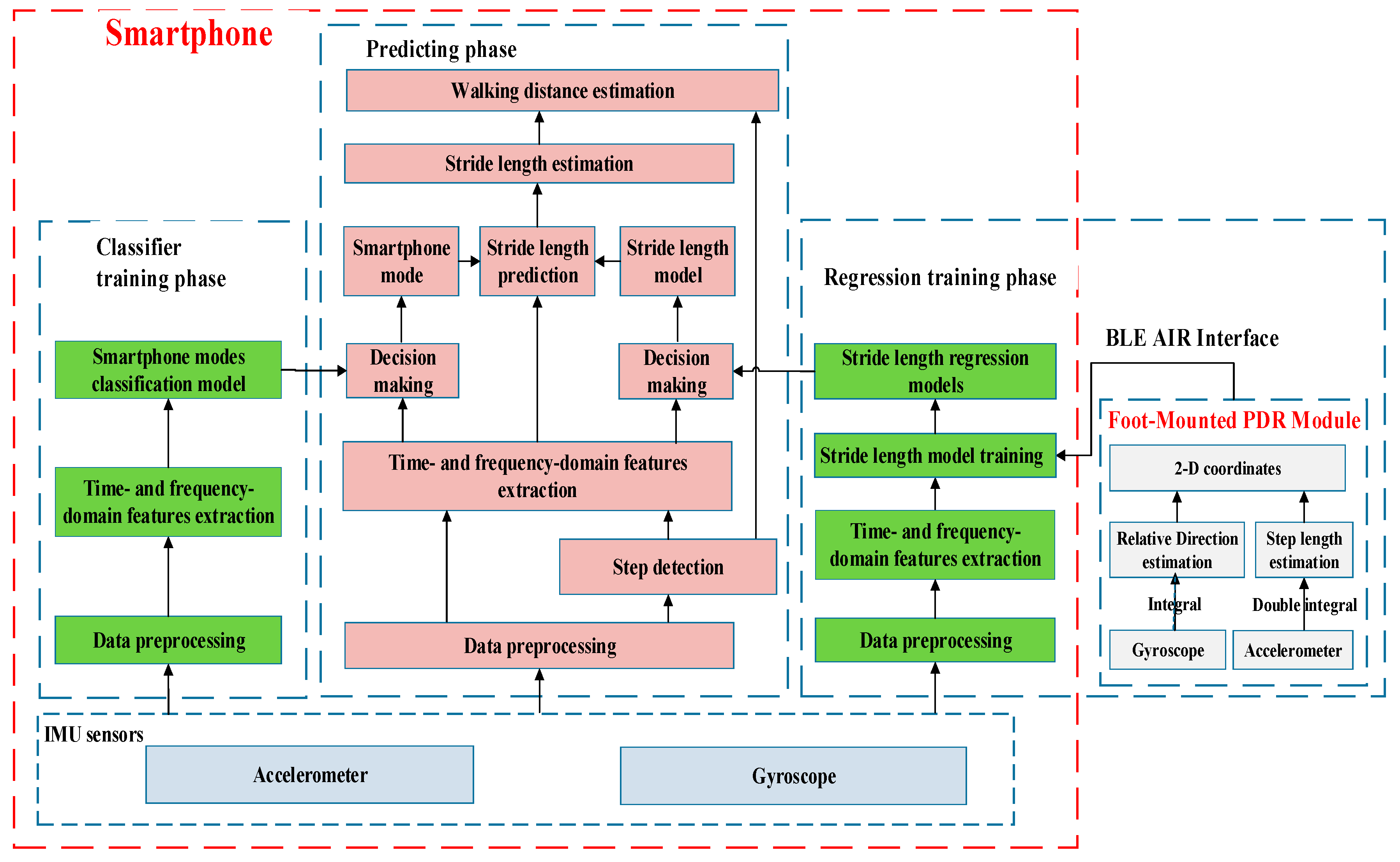
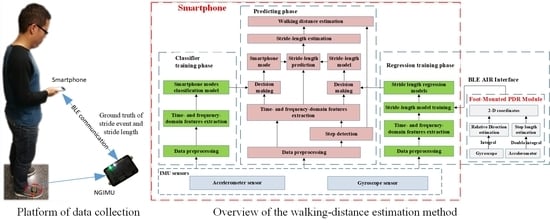
To overcome the shortcomings above of previous works, we proposed a pedestrian walking distance estimation method independent of smartphone mode. We first recognized the smartphone modes automatically by a position classifier, and then selected the most suitable stride length model for each smartphone mode. To our knowledge, we are the first to estimate the stride length and walking distance based on smartphone mode recognition, which aims to mitigate the impact of different smartphone carrying modes, thus significantly improving its stride length estimation accuracy. The key contributions of our study are as follows:
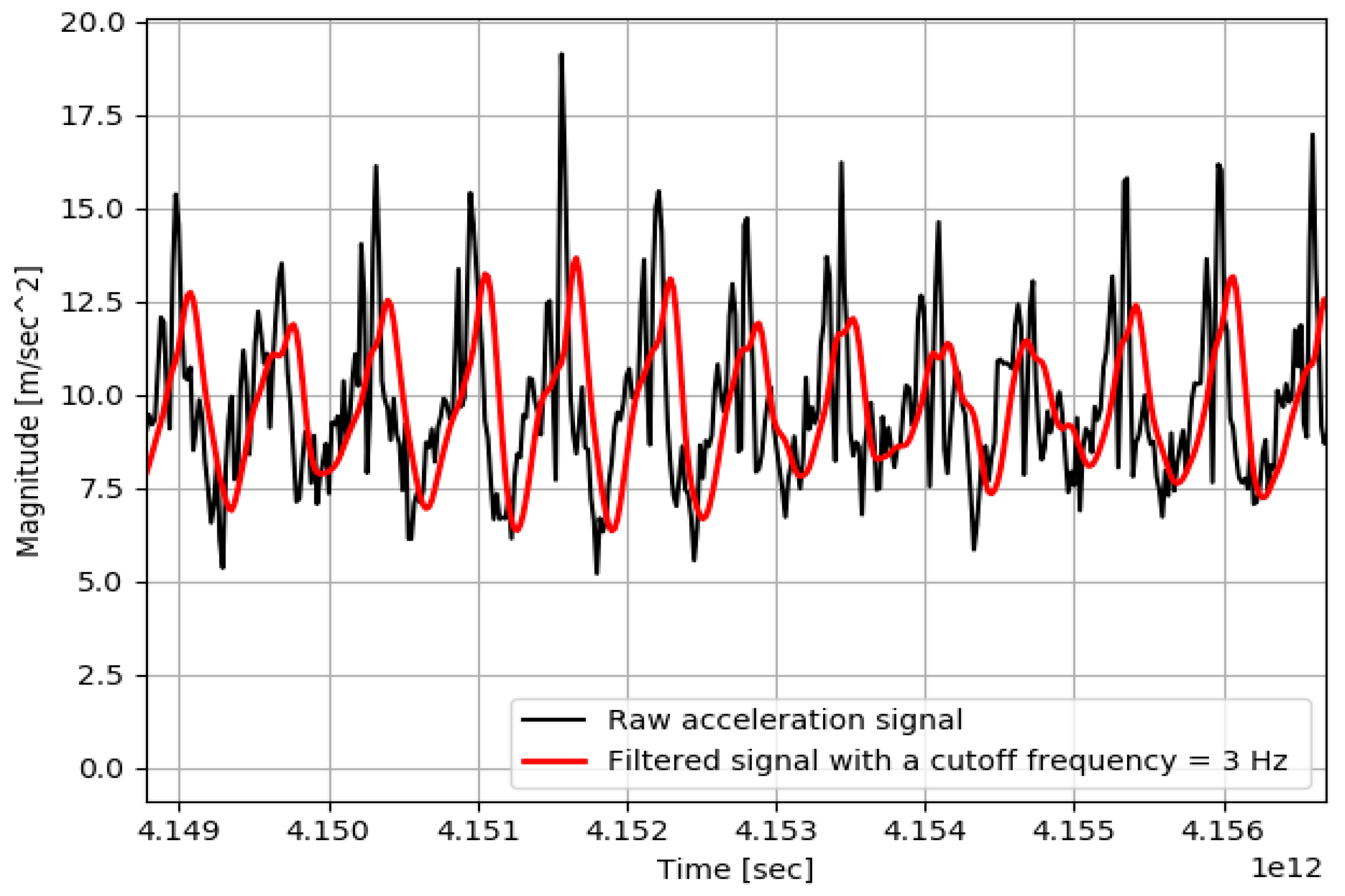
In addition to the combination of time-domain and frequency-domain features of accelerometers and gyroscopes during the stride interval, we also built higher-order features based on the acknowledged studies to model the stride length.
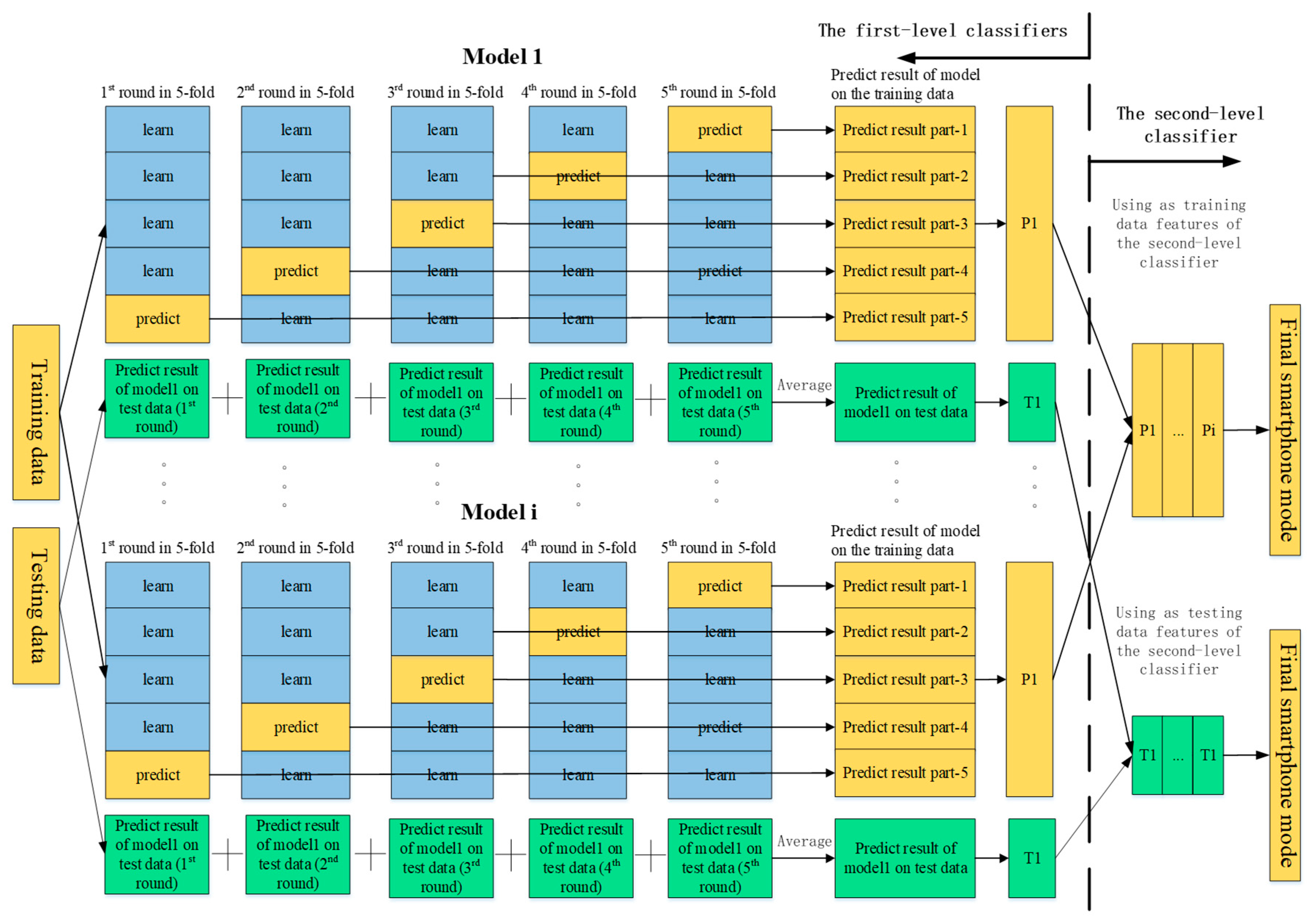
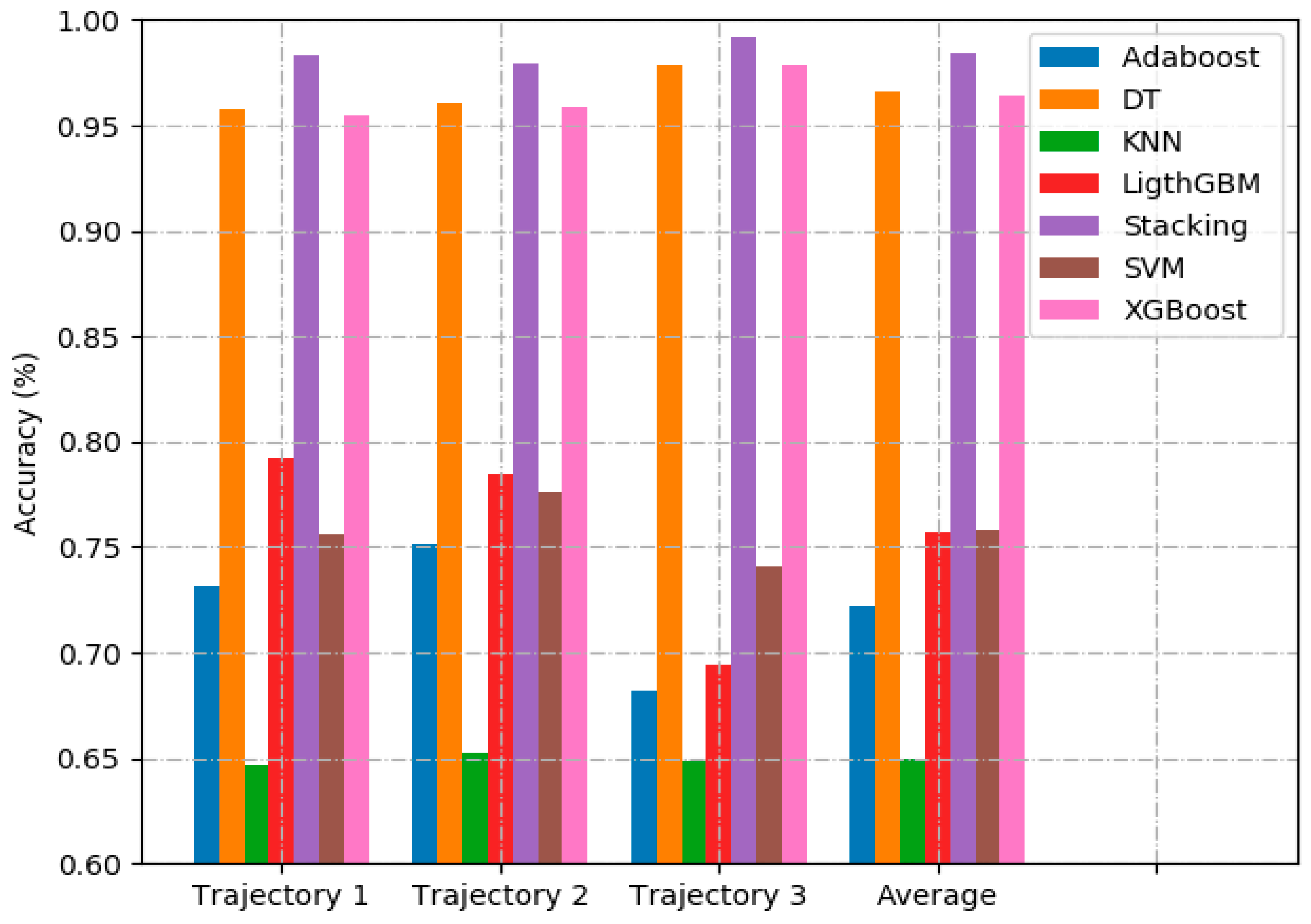
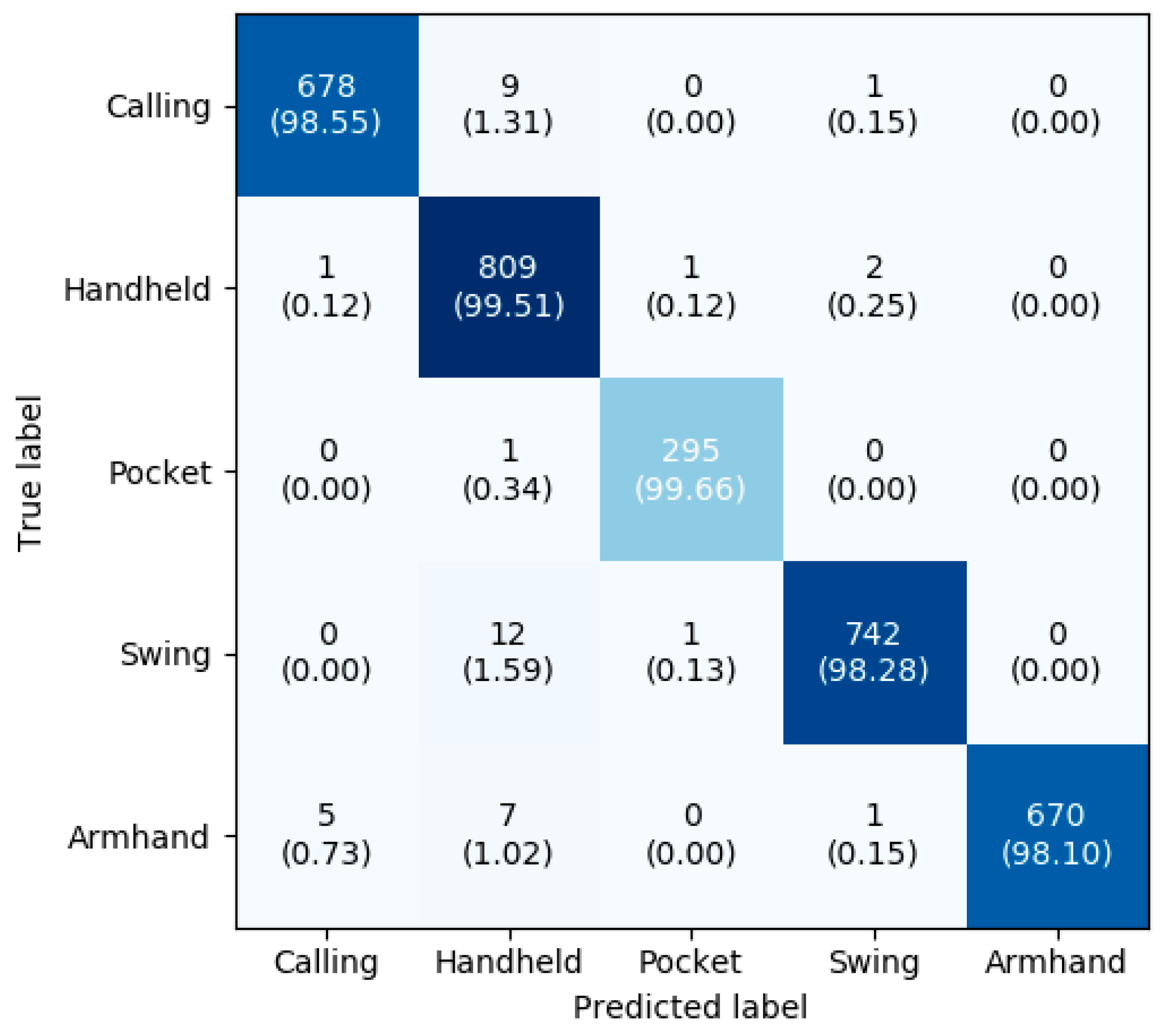
We developed a computational lightweight smartphone mode recognition method that performed accurately using inertial signals. The proposed smartphone mode recognition method achieved a recognition accuracy of 98.82% by using a two layer stacking model.
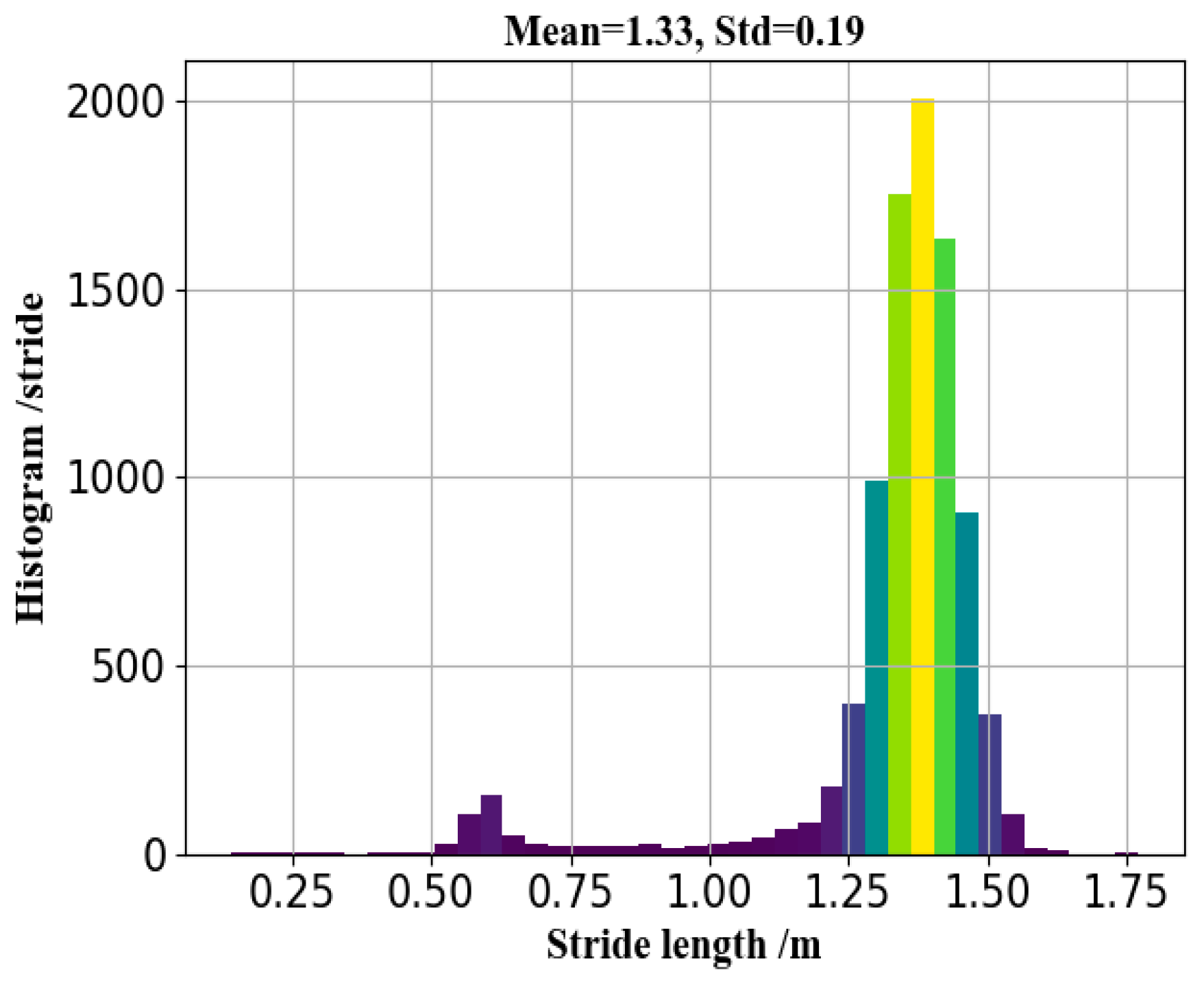
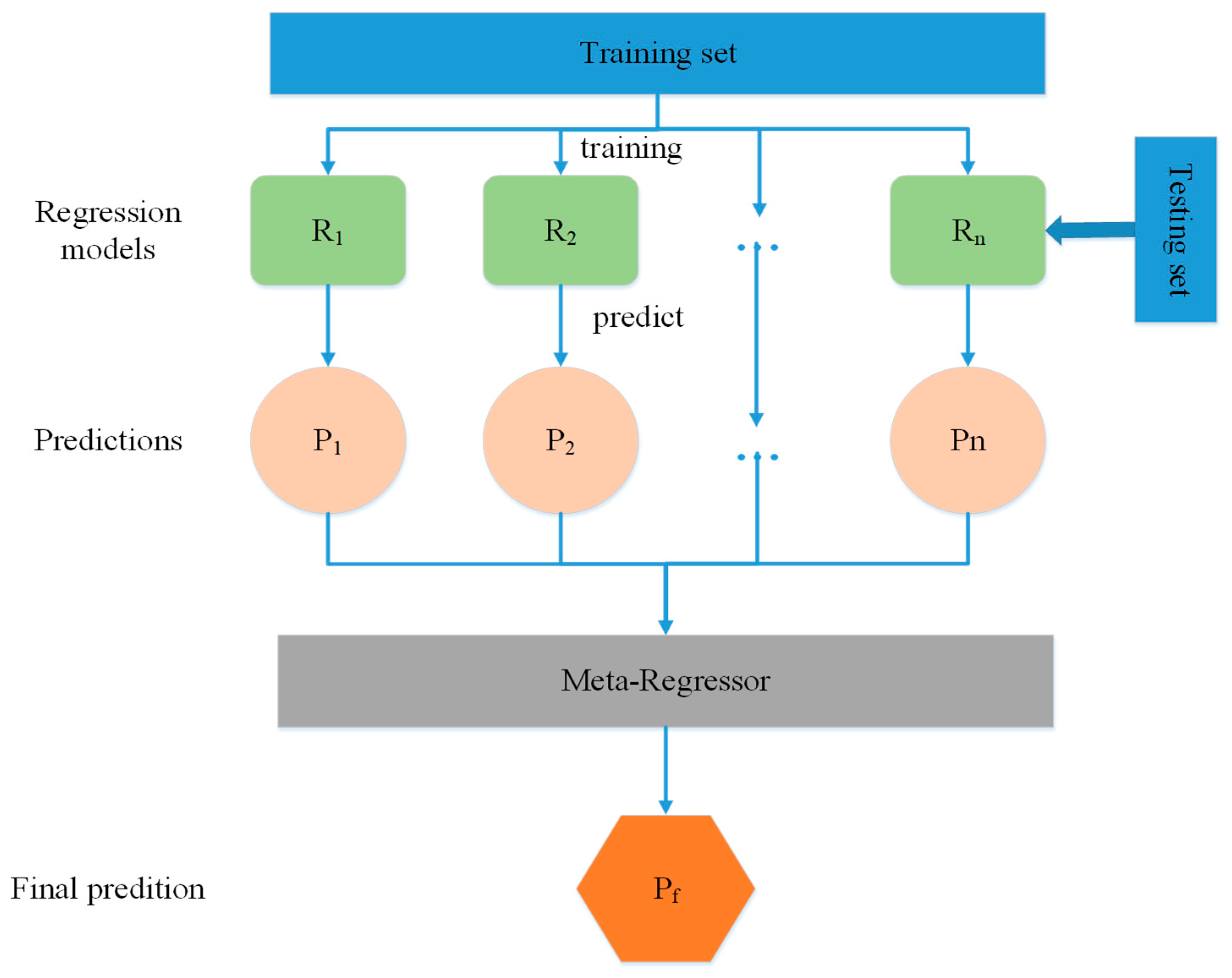
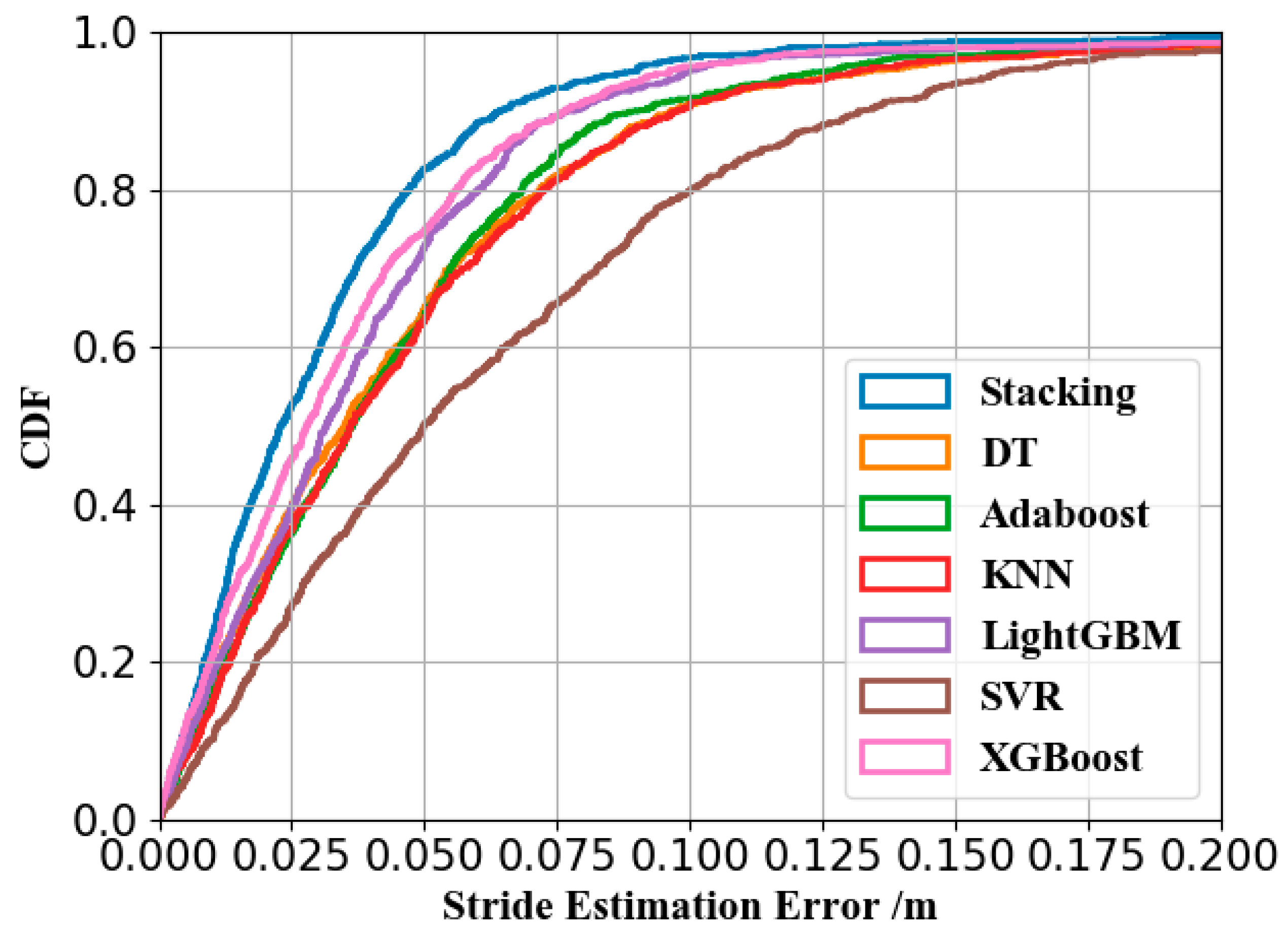
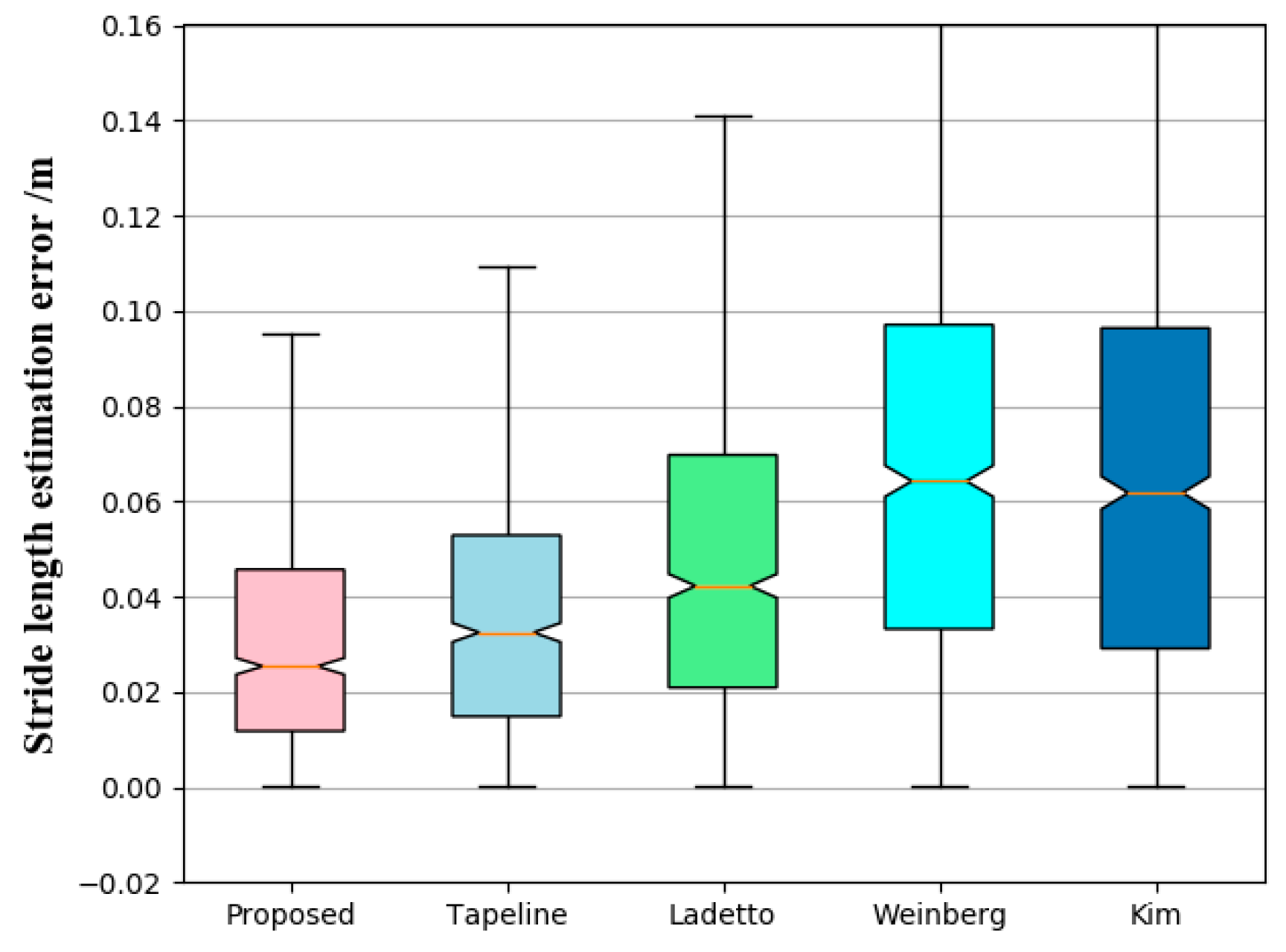
We fused multiple regression predictions from different regression models in machine learning using a stacking regression model, so that we obtained an optimal stride length estimation accuracy with an error rate of 3.30%, dependent only on the embedded smartphone inertial sensor data.
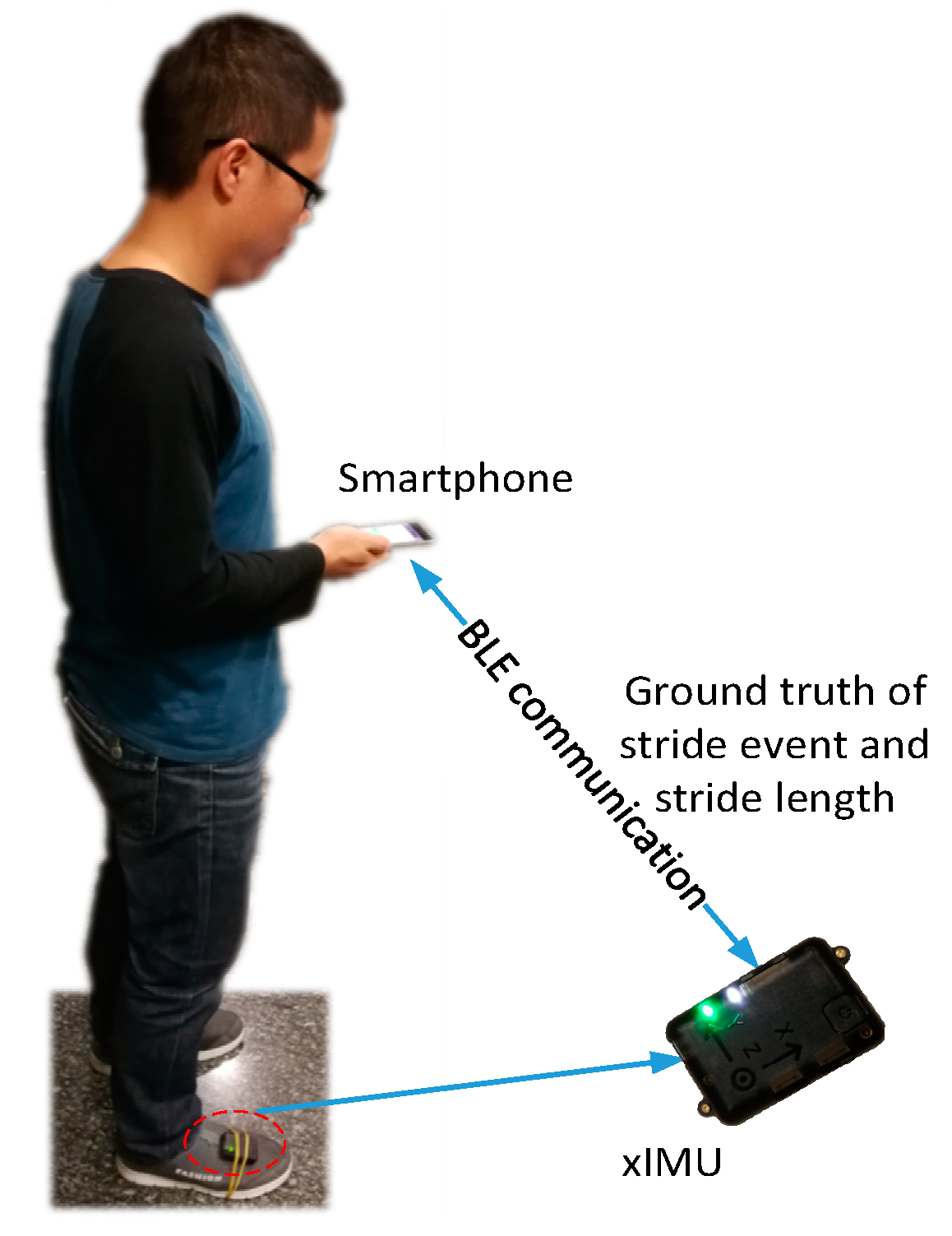
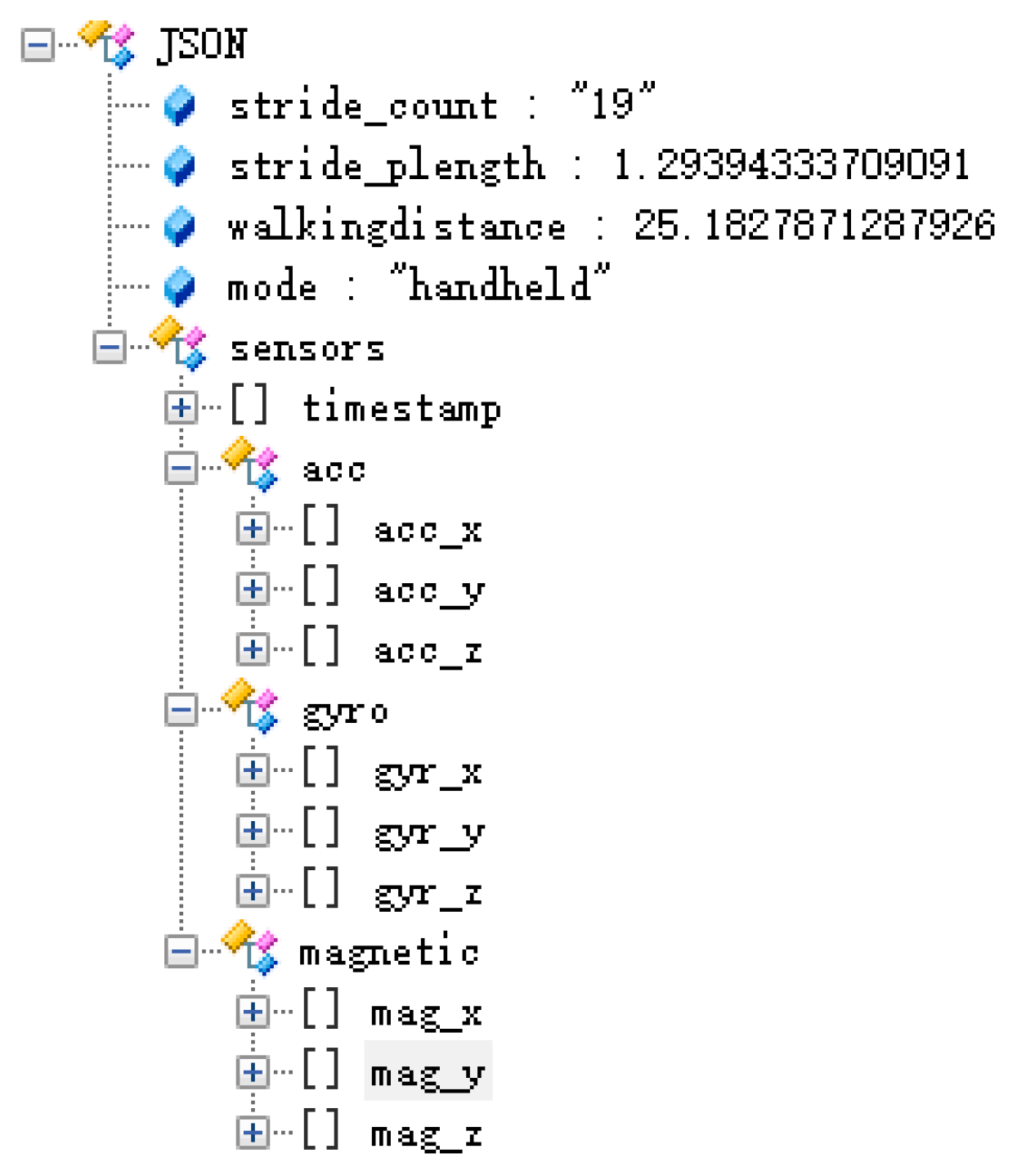
We established a benchmark dataset with ground truth from a FM-INS (foot-mounted inertial navigation system, x-IMU [
39] from x-io technologies) module for step counting, smartphone mode recognition, and stride length or walking distance estimation. We trained different stride length models for common smartphone modes and estimated the walking distance of the pedestrian by automatically recognizing the smartphone modes and selecting the most suitable stride length model. The proposed method achieved a superior performance to traditional methods, with a walking distance error rate of 2.62%.
The rest of the paper is organized as follows: In
Section 2, we describe the benchmark dataset and the feature extraction, then detail the solution of smartphone mode recognition and stride length estimation. In
Section 3, numerical results and performance comparison are presented in detail. In
Section 4, we provide a discussion and conclusion that summarizes the importance and limitations of our proposed work, and give suggestions for future research.
4. Discussion and Conclusions
Concerning the inaccuracy of the traditional nonlinear method, we presented a walking distance estimation method consists of a smartphone mode recognition and stride length estimation based on the regression model using the inertial sensors of the smartphone. We proposed a smartphone mode recognition algorithm using a stacking ensemble classifier to effectively distinguish different smartphone modes, achieving an average recognition accuracy of 98.82%. The proposed walking distance estimation method obtained a superior performance, with a single stride length error rate of 3.30% and a walking distance error rate of 2.62%. The proposed method outperformed the commonly used nonlinear step length estimation method (Kim [
24], Weinberg [
23], Ladetto [
22]) in both single stride length and walking distance estimation. In comparison to Tapeline, this method possessed the advantages of smaller computational overhead, faster training speed, and fewer training samples. In addition to improving the performance of pedestrian dead reckoning, this technique can be used to assess the physical activity level of the user, providing feedback and motivating a more active lifestyle.
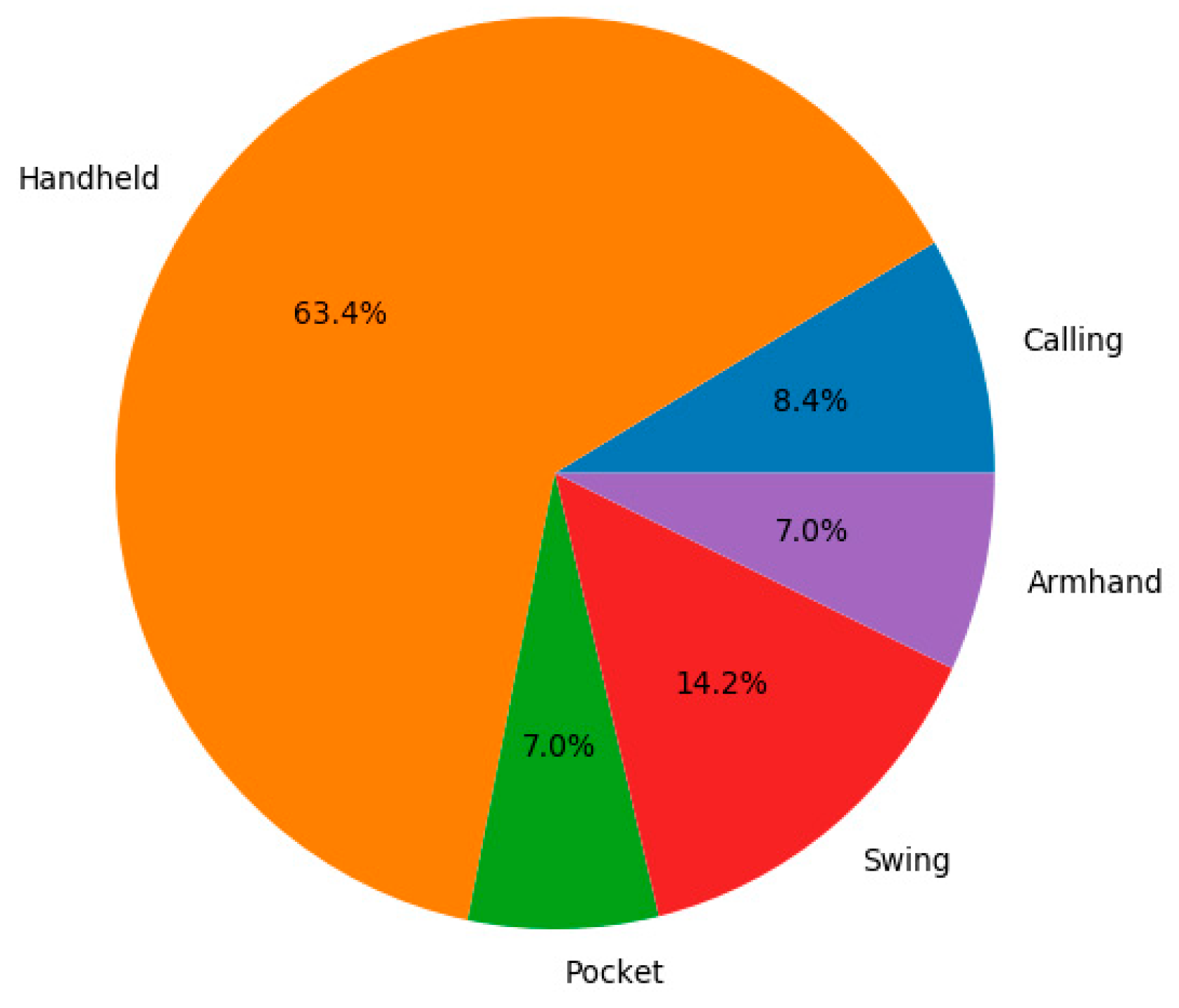
However, there are still some limitations that may be important to address in our future work. For example, only five smartphone modes (handheld, swing, pocket, arm-hand, and calling) were analyzed. More smartphone modes, such as those involving the smartphone in belts and bags, need to be further studied using similar methodologies. Additionally, we focused on the normal walk status, while other pedestrian motion states such as walking backward, lateral walking, running, and jumping will be studied in the future to construct a more viable walking distance estimation. Moreover, humans are flexible structures, it is difficult to ensure that the movement of mobile phones equals the movement of pedestrians. Extra actions (standing still, playing games, reading) result in inaccurate stride length estimation. Finally, the trained model may be not suitable for non-healthy adults (e.g., Parkinson’s patients), children, and elderly. In the future, we will investigate how to obtain training data by crowdsourcing automatically, then train a personalized SLE model in the form of online learning to mitigate user and device heterogeneity.