Gravity Recovery and Climate Experiment (GRACE) Storage Change Characteristics (2003–2016) over Major Surface Basins and Principal Aquifers in the Conterminous United States
Abstract
1. Introduction
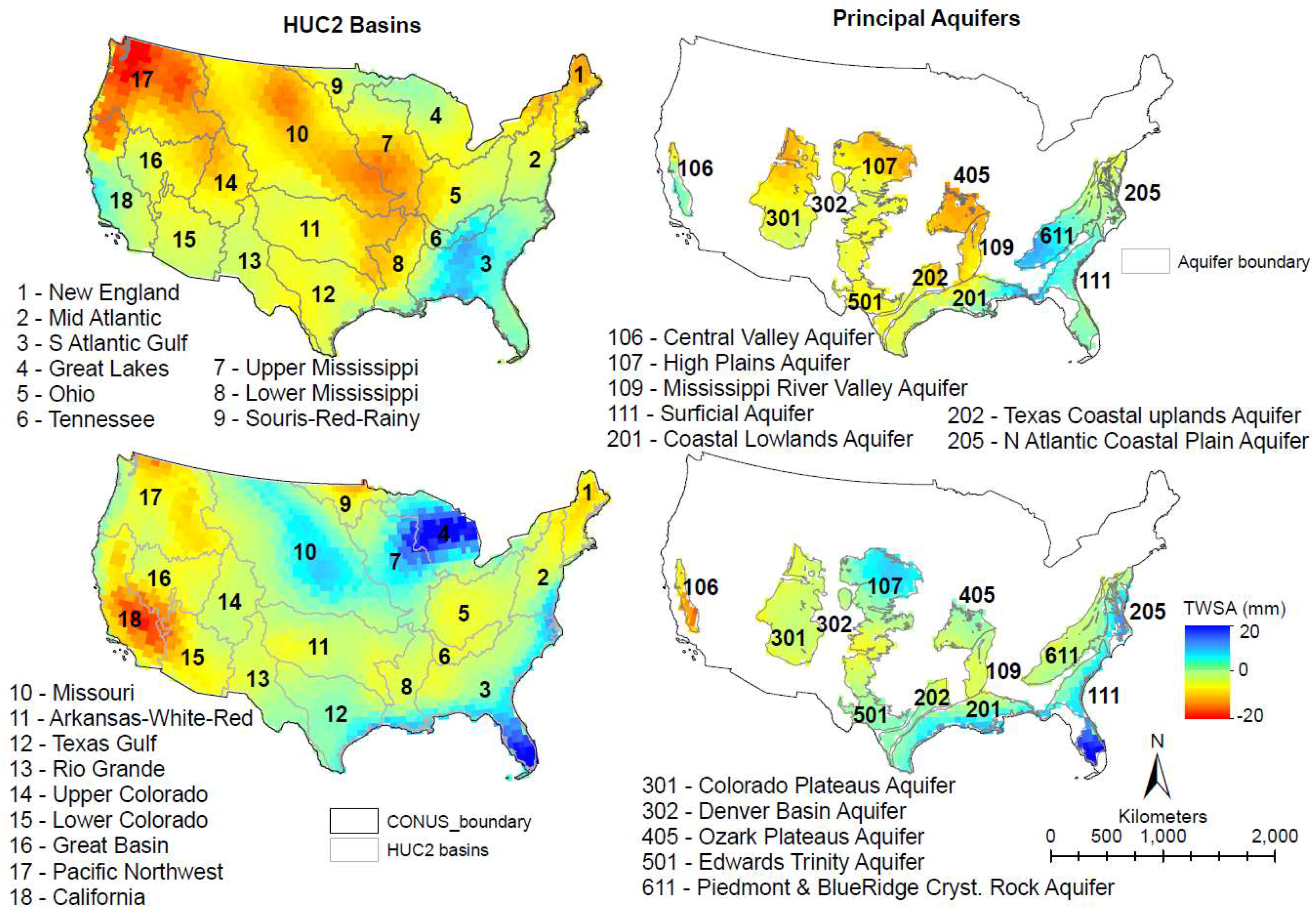
2. Materials and Methods
2.1. Data Used
2.2. Analysis of Temporal Variability and Magnitude in TWSA
2.3. Analysis of Storage Cycle and Periodicity in Storage
2.4. Analysis of Primary Explanatory Variable of Storage
2.5. Analysis of Change in Storage
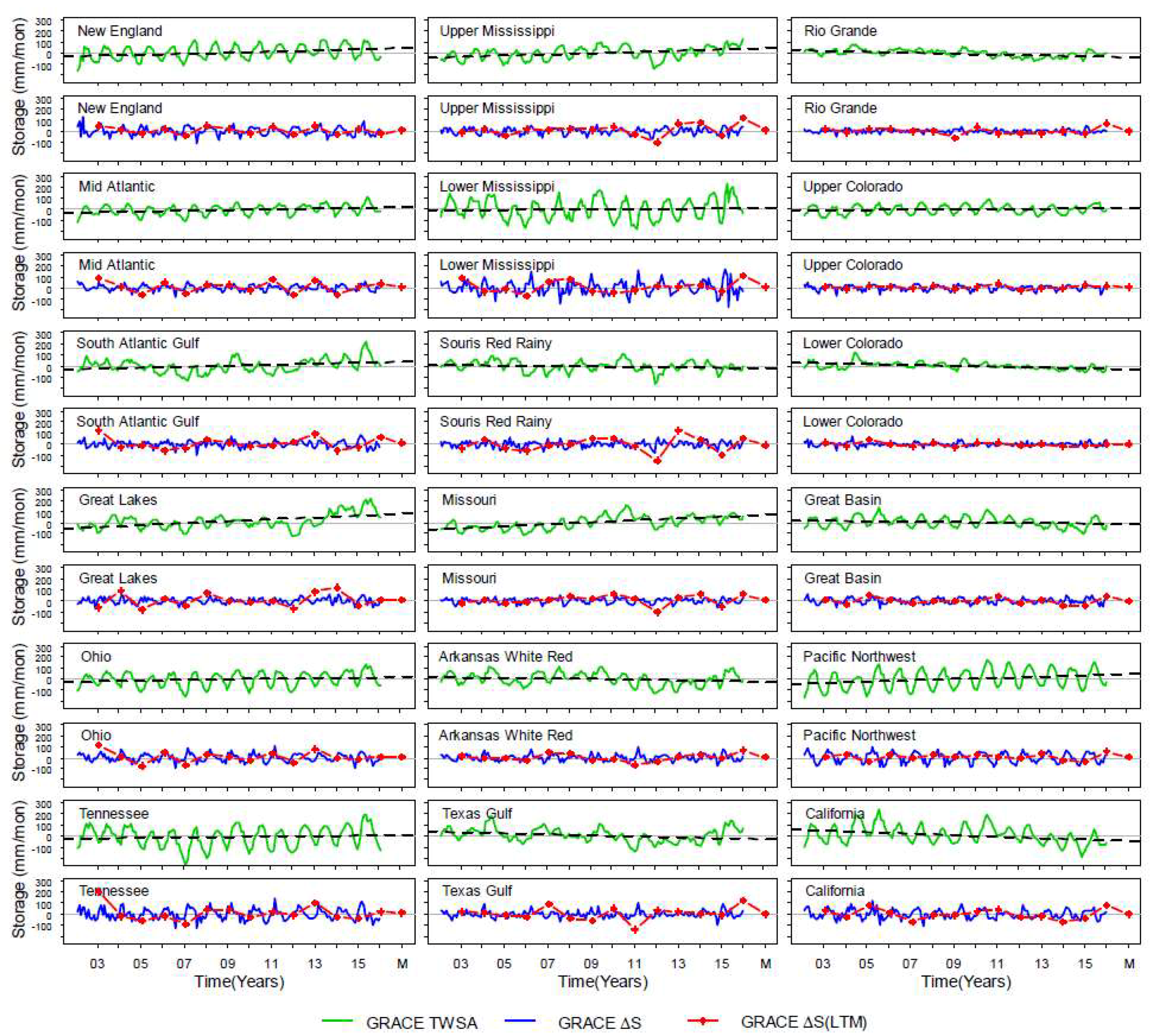
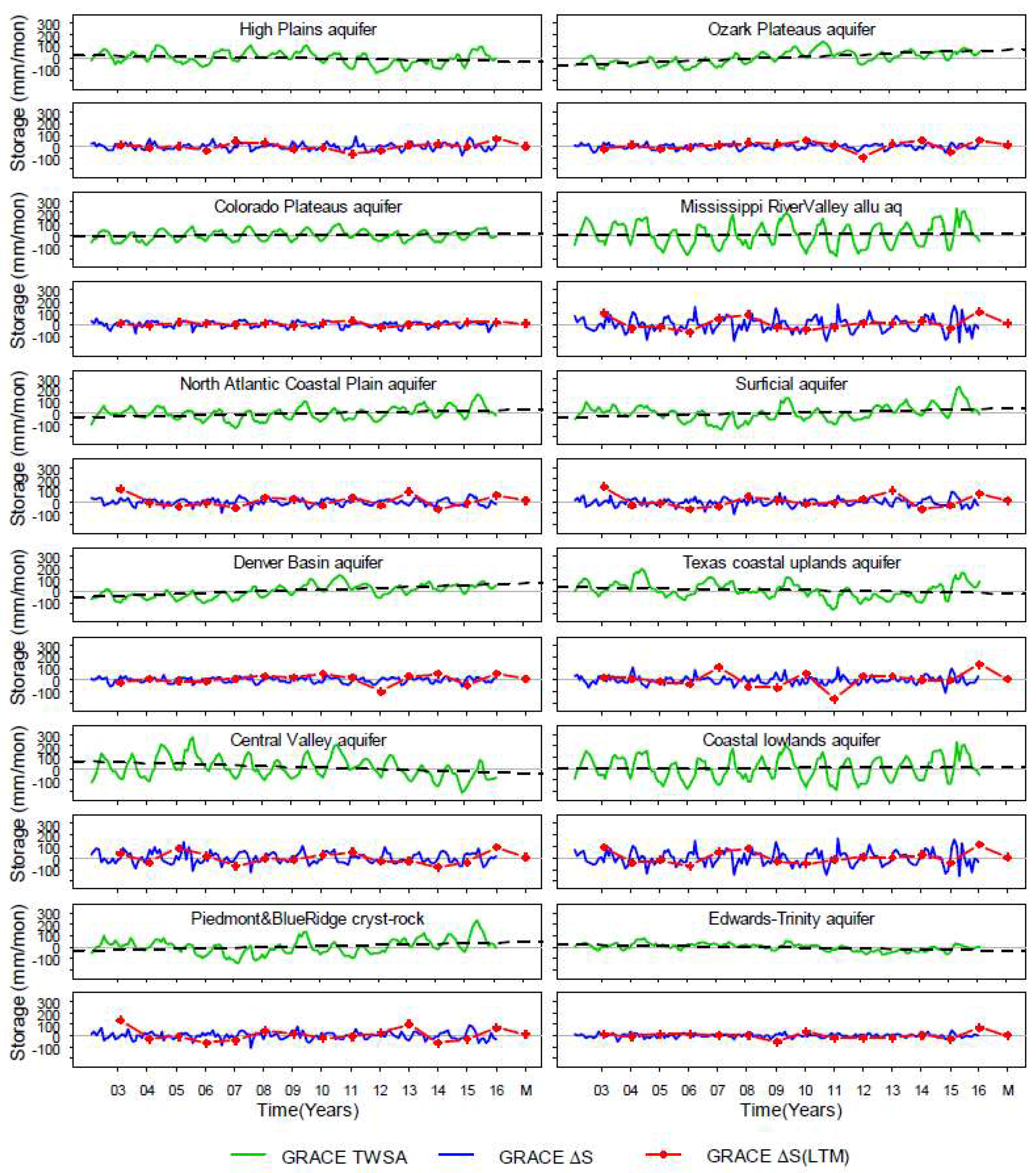
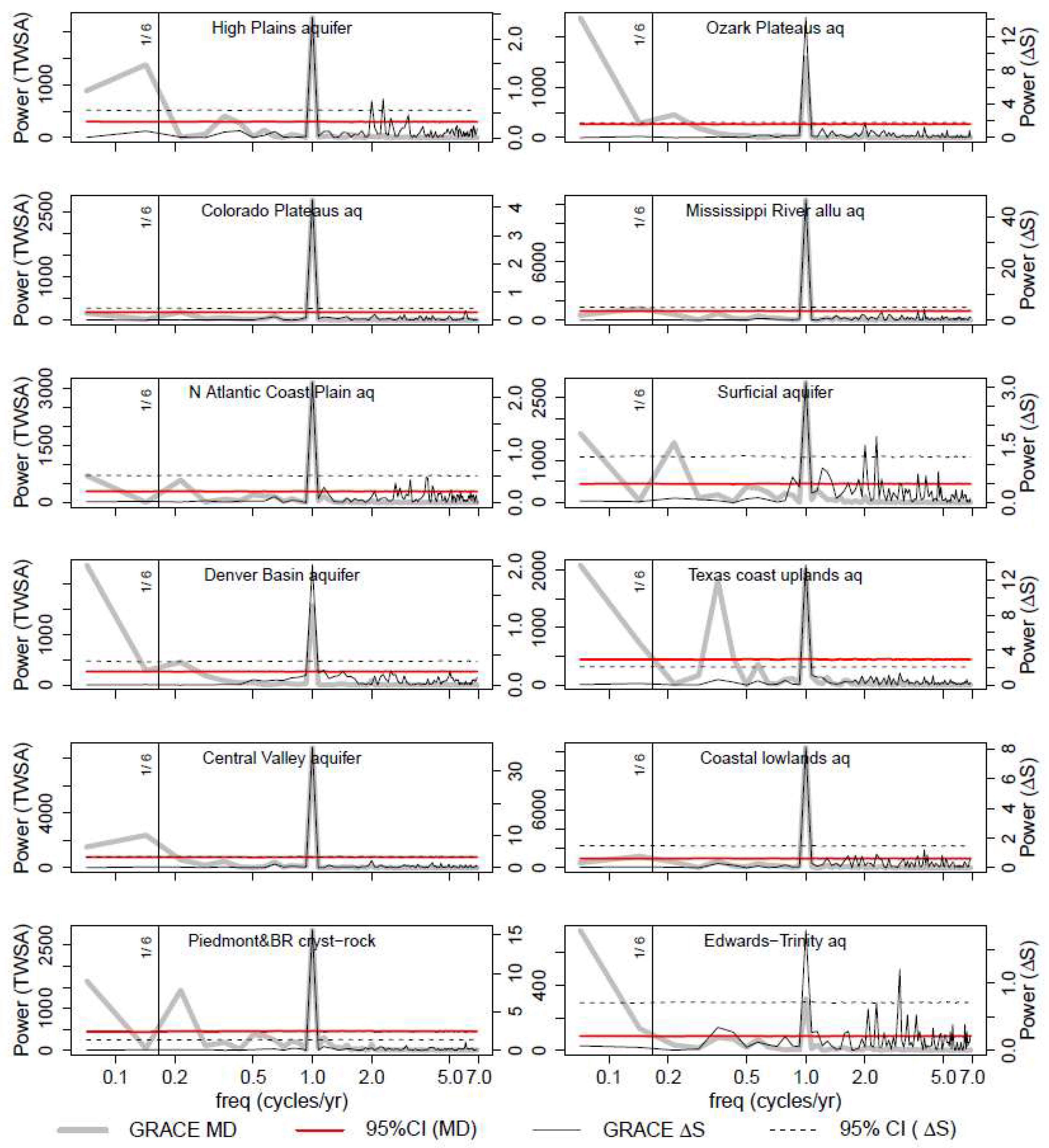
3. Results
3.1. Analysis of Temporal Variability and Magnitude in Storage (2003–2016)
3.2. Analysis of Storage Cycle and Periodicity in Storage
3.3. Analysis of Primary Explanatory Variable of Storage
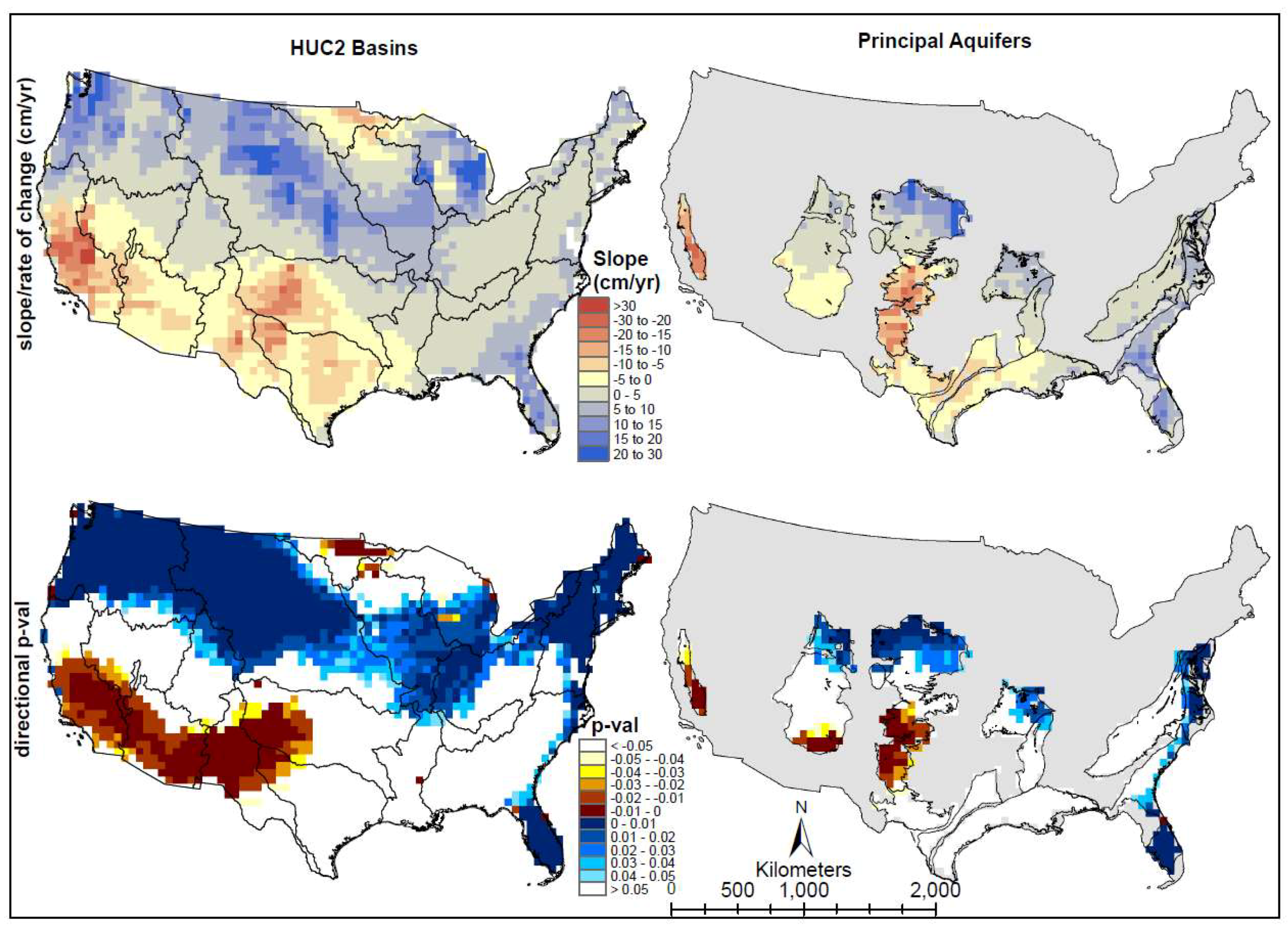
3.4. Analysis of Change in Storage
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| No | Basin Name | P-TWSA | SM-TWSA | Q-TWSA | ET-TWSA | SWE-TWSA |
|---|---|---|---|---|---|---|
| HUC2 Surface Basins | ||||||
| 1 | New England | 5 | 1 | −1 | −4 | 2 |
| 2 | Mid−Atlantic | −6 | 1 | 0 | −4 | 1 |
| 3 | South Atlantic Gulf | −5 | 1 | 0 | −4 | 2 |
| 4 | Great Lakes | 1 | 4 | 2 | −1 | 4 |
| 5 | Ohio | −2 | 1 | 0 | −4 | 1 |
| 6 | Tennessee | −1 | 2 | 3 | −3 | 4 |
| 7 | Upper Mississippi | −2 | 1 | 0 | −3 | 3 |
| 8 | Lower Mississippi | −1 | 2 | 2 | −3 | −1 |
| 9 | Souris−Red−Rainy | −3 | 0 | −1 | −4 | 1 |
| 10 | Missouri | −1 | 2 | −1 | −2 | 4 |
| 11 | Arkansas−White−Red | −2 | 2 | −1 | −3 | 4 |
| 12 | Texas−Gulf | −3 | 2 | 1 | −4 | 2 |
| 13 | Rio Grande | −4 | 2 | −2 | −4 | 2 |
| 14 | Upper Colorado | 6 | 1 | −2 | −3 | 3 |
| 15 | Lower Colorado | −5 | 1 | 1 | −4 | 2 |
| 16 | Great Basin | 4 | 2 | −1 | −3 | 3 |
| 17 | Pacific Northwest | 4 | 2 | −1 | −3 | 4 |
| 18 | California | 3 | 1 | 0 | −4 | 2 |
| Aquifers | ||||||
| 1 | High Plains | 3 | 1 | 0 | −4 | 3 |
| 2 | Colorado Plateaus | −2 | 2 | −2 | −3 | 3 |
| 3 | N Atlantic Coastal Plain | −1 | 2 | −1 | −3 | 2 |
| 4 | Denver Basin | −10 | −10 | −5 | −9 | −1 |
| 5 | Central Valley | −4 | 1 | 1 | −4 | 5 |
| 6 | Piedmont and Blue Ridge | −2 | 1 | 0 | −4 | 3 |
| 7 | Ozark Plateaus | −4 | 1 | 0 | −4 | 1 |
| 8 | Mississippi River Valley | −4 | 2 | −2 | −2 | 2 |
| 9 | Surficial | −3 | 1 | −2 | −2 | 3 |
| 10 | Texas Coastal Uplands | −1 | 1 | −1 | −3 | 2 |
| 11 | Coastal Lowlands | −2 | 2 | −2 | −3 | 2 |
| 12 | Edwards−Trinity | −4 | 1 | 0 | −4 | 1 |
References
- Reager, J.; Famiglietti, J.S. Characteristic mega-basin water storage behavior using GRACE. Water Resour. Res. 2013, 49, 3314–3329. [Google Scholar] [CrossRef] [PubMed]
- Rodell, M.; Chen, J.; Kato, H.; Famiglietti, J.S.; Nigro, J.; Wilson, C.R. Estimating groundwater storage changes in the Mississippi River basin (USA) using GRACE. Hydrogeol. J. 2007, 15, 159–166. [Google Scholar] [CrossRef]
- Rodell, M.; Famiglietti, J. Detectability of variations in continental water storage from satellite observations of the time dependent gravity field. Water Resour. Res. 1999, 35, 2705–2723. [Google Scholar] [CrossRef]
- Rodell, M.; Famiglietti, J.; Wiese, D.; Reager, J.; Beaudoing, H.; Landerer, F.; Lo, M.-H. Emerging trends in global freshwater availability. Nature 2018, 557, 651. [Google Scholar] [CrossRef] [PubMed]
- Long, D.; Pan, Y.; Zhou, J.; Chen, Y.; Hou, X.; Hong, Y.; Scanlon, B.R.; Longuevergne, L. Global analysis of spatiotemporal variability in merged total water storage changes using multiple GRACE products and global hydrological models. Remote Sens. Environ. 2017, 192, 198–216. [Google Scholar] [CrossRef]
- Rodell, M.; Famiglietti, J. An analysis of terrestrial water storage variations in Illinois with implications for the Gravity Recovery and Climate Experiment (GRACE). Water Resour. Res. 2001, 37, 1327–1339. [Google Scholar] [CrossRef]
- Seneviratne, S.I.; Viterbo, P.; Lüthi, D.; Schär, C. Inferring changes in terrestrial water storage using ERA-40 reanalysis data: The Mississippi River basin. J. Clim. 2004, 17, 2039–2057. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Zhang, Z.; Save, H.; Sun, A.Y.; Schmied, H.M.; van Beek, L.P.; Wiese, D.N.; Wada, Y.; Long, D.; Reedy, R.C. Global models underestimate large decadal declining and rising water storage trends relative to GRACE satellite data. Proc. Natl. Acad. Sci. USA 2018, 115, E1080–E1089. [Google Scholar] [CrossRef]
- Fung, F.; Lopez, A.; New, M. Water Availability in+ 2 C and+ 4 C Worlds. Available online: https://royalsocietypublishing.org/doi/full/10.1098/rsta.2010.0293 (accessed on 17 April 2019).
- Wahr, J.; Molenaar, M.; Bryan, F. Time variability of the Earth’s gravity field: Hydrological and oceanic effects and their possible detection using GRACE. J. Geophys. Res. Solid Earth 1998, 103, 30205–30229. [Google Scholar] [CrossRef]
- Save, H.; Bettadpur, S.; Tapley, B.D. High-resolution CSR GRACE RL05 mascons. J. Geophys. Res. Solid Earth 2016, 121, 7547–7569. [Google Scholar] [CrossRef]
- Famiglietti, J.S.; Rodell, M. Water in the balance. Science 2013, 340, 1300–1301. [Google Scholar] [CrossRef] [PubMed]
- Houborg, R.; Rodell, M.; Li, B.; Reichle, R.; Zaitchik, B.F. Drought indicators based on model-assimilated Gravity Recovery and Climate Experiment (GRACE) terrestrial water storage observations. Water Resour. Res. 2012, 48, 1–17. [Google Scholar] [CrossRef]
- Thomas, A.C.; Reager, J.T.; Famiglietti, J.S.; Rodell, M. A GRACE-based water storage deficit approach for hydrological drought characterization. Geophys. Res. Lett. 2014, 41, 1537–1545. [Google Scholar] [CrossRef]
- Chen, J.L.; Wilson, C.R.; Tapley, B.D. The 2009 exceptional Amazon flood and interannual terrestrial water storage change observed by GRACE. Water Resour. Res. 2010, 46, 1–12. [Google Scholar] [CrossRef]
- Reager, J.; Famiglietti, J. Global terrestrial water storage capacity and flood potential using GRACE. Geophys. Res. Lett. 2009, 36, 1–6. [Google Scholar] [CrossRef]
- Doell, P.; Mueller Schmied, H.; Schuh, C.; Portmann, F.T.; Eicker, A. Global-scale assessment of groundwater depletion and related groundwater abstractions: Combining hydrological modeling with information from well observations and GRACE satellites. Water Resour. Res. 2014, 50, 5698–5720. [Google Scholar] [CrossRef]
- Becker, M.; Meyssignac, B.; Xavier, L.; Cazenave, A.; Alkama, R.; Decharme, B. Past terrestrial water storage (1980–2008) in the Amazon Basin reconstructed from GRACE and in situ river gauging data. Hydrol. Earth Syst. Sci. 2011, 15, 533–546. [Google Scholar] [CrossRef]
- Ni, S.; Chen, J.; Wilson, C.R.; Li, J.; Hu, X.; Fu, R. Global Terrestrial Water Storage Changes and Connections to ENSO Events. Surv. Geophys. 2018, 39, 1–22. [Google Scholar] [CrossRef]
- Kusche, J.; Eicker, A.; Forootan, E.; Springer, A.; Longuevergne, L. Mapping probabilities of extreme continental water storage changes from space gravimetry. Geophys. Res. Lett. 2016, 43, 8026–8034. [Google Scholar] [CrossRef]
- Sun, A.; Scanlon, B.; AghaKouchak, A.; Zhang, Z. Using GRACE Satellite Gravimetry for Assessing Large-Scale Hydrologic Extremes. Remote Sens. 2017, 9, 1287. [Google Scholar] [CrossRef]
- Ramillien, G.; Frappart, F.; Seoane, L. Application of the regional water mass variations from GRACE Satellite Gravimetry to large-scale water management in Africa. Remote Sens. 2014, 6, 7379–7405. [Google Scholar] [CrossRef]
- Awange, J.; Forootan, E.; Kuhn, M.; Kusche, J.; Heck, B. Water storage changes and climate variability within the Nile Basin between 2002 and 2011. Adv. Water Resour. 2014, 73, 1–15. [Google Scholar] [CrossRef]
- Senay, G.B.; Velpuri, N.M.; Bohms, S.; Demissie, Y.; Gebremichael, M. Understanding the hydrologic sources and sinks in the Nile Basin using multisource climate and remote sensing data sets. Water Resour. Res. 2014, 50, 8625–8650. [Google Scholar] [CrossRef]
- Syed, T.; Famiglietti, J.; Chen, J.; Rodell, M.; Seneviratne, S.; Viterbo, P.; Wilson, C. Total basin discharge for the Amazon and Mississippi River basins from GRACE and a land-atmosphere water balance. Geophys. Res. Lett. 2005, 32, 1–5. [Google Scholar] [CrossRef]
- Yeh, P.J.F.; Swenson, S.; Famiglietti, J.; Rodell, M. Remote sensing of groundwater storage changes in Illinois using the Gravity Recovery and Climate Experiment (GRACE). Water Resour. Res. 2006, 42, 1–7. [Google Scholar] [CrossRef]
- Swenson, S.; Yeh, P.J.F.; Wahr, J.; Famiglietti, J. A comparison of terrestrial water storage variations from GRACE with in situ measurements from Illinois. Geophys. Res. Lett. 2006, 33, 1–5. [Google Scholar] [CrossRef]
- Zmijewski, K.; Becker, R. Estimating the Effects of Anthropogenic Modification on Water Balance in the Aral Sea Watershed Using GRACE: 2003–12. Earth Interact. 2014, 18, 1–16. [Google Scholar] [CrossRef]
- Daly, C.; Smith, J.W.; Smith, J.I.; McKane, R.B. High-resolution spatial modeling of daily weather elements for a catchment in the Oregon Cascade Mountains, United States. J. Appl. Meteorol. Climatol. 2007, 46, 1565–1586. [Google Scholar] [CrossRef]
- Daly, C.; Taylor, G.; Gibson, W.; Parzybok, T.; Johnson, G.; Pasteris, P. High-quality spatial climate data sets for the United States and beyond. Trans. ASAE 2000, 43, 1957–1962. [Google Scholar] [CrossRef]
- Senay, G.B.; Bohms, S.; Singh, R.K.; Gowda, P.H.; Velpuri, N.M.; Alemu, H.; Verdin, J.P. Operational evapotranspiration mapping using remote sensing and weather datasets: A new parameterization for the SSEB approach. J. Am. Water Resour. Assoc. 2013, 49, 577–591. [Google Scholar] [CrossRef]
- Tedesco, M.; Kelly, R.; Foster, J.L.; Chang, A.T.C. AMSR-E/Aqua Monthly L3 Global Snow Water Equivalent EASE-Grids. Version 2; NASA DAAC at the National Snow and Ice Data Center: Boulder, CO, USA, 2004; Available online: http://dx.doi.org/10.5067/AMSR-E/AE_MOSNO.002 (accessed on 15 April 2019).
- Xia, Y.; Mitchell, K.; Ek, M.; Sheffield, J.; Cosgrove, B.; Wood, E.; Luo, L.; Alonge, C.; Wei, H.; Meng, J. Continental-scale water and energy flux analysis and validation for the North American Land Data Assimilation System project phase 2 (NLDAS-2): 1. Intercomparison and application of model products. J. Geophys. Res. Atmos. 2012, 117, 1–27. [Google Scholar] [CrossRef]
- Seaber, P.R.; Kapinos, F.P.; Knapp, G.L. Hydrologic Unit Maps. U.S. Geological Survey Water-Supply Paper 2294. Available online: http://pubs.usgs.gov/wsp/wsp2294/index.html (accessed on 16 March 2015).
- Reager, J.; Thomas, B.; Famiglietti, J. River basin flood potential inferred using GRACE gravity observations at several months lead time. Nat. Geosci. 2014, 7, 588–592. [Google Scholar] [CrossRef]
- Montgomery, D.C.; Peck, E.A.; Vining, G.G. Introduction to Linear Regression Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Kroll, C.N.; Song, P. Impact of multicollinearity on small sample hydrologic regression models. Water Resour. Res. 2013, 49, 3756–3769. [Google Scholar] [CrossRef]
- Long, D.; Chen, X.; Scanlon, B.R.; Wada, Y.; Hong, Y.; Singh, V.P.; Chen, Y.; Wang, C.; Han, Z.; Yang, W. Have GRACE satellites overestimated groundwater depletion in the Northwest India Aquifer? Sci. Rep. 2016, 6, 24398. [Google Scholar] [CrossRef] [PubMed]
- Rodell, M.; Velicogna, I.; Famiglietti, J.S. Satellite-based estimates of groundwater depletion in India. Nature 2009, 460, 999. [Google Scholar] [CrossRef]
- Famiglietti, J.; Lo, M.; Ho, S.; Bethune, J.; Anderson, K.; Syed, T.; Swenson, S.; De Linage, C.; Rodell, M. Satellites measure recent rates of groundwater depletion in California’s Central Valley. Geophys. Res. Lett. 2011, 38, 1–4. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Faunt, C.C.; Longuevergne, L.; Reedy, R.C.; Alley, W.M.; McGuire, V.L.; McMahon, P.B. Groundwater depletion and sustainability of irrigation in the US High Plains and Central Valley. Proc. Natl. Acad. Sci. USA 2012, 109, 9320–9325. [Google Scholar] [CrossRef] [PubMed]
- Breña-Naranjo, J.A.; Kendall, A.D.; Hyndman, D.W. Improved methods for satellite-based groundwater storage estimates: A decade of monitoring the high plains aquifer from space and ground observations. Geophys. Res. Lett. 2014, 41, 6167–6173. [Google Scholar] [CrossRef]
- Hirsch, R.M.; Slack, J.R. A nonparametric trend test for seasonal data with serial dependence. Water Resour. Res. 1984, 20, 727–732. [Google Scholar] [CrossRef]
- Di Luzio, M.; Johnson, G.L.; Daly, C.; Eischeid, J.K.; Arnold, J.G. Constructing retrospective gridded daily precipitation and temperature datasets for the conterminous United States. J. Appl. Meteorol. Climatol. 2008, 47, 475–497. [Google Scholar] [CrossRef]
- Sauer, V.B.; Meyer, R. Determination of Error in Individual Discharge Measurements. U.S. Geological Survey Open-File Report 92-144; 1992. Available online: https://pubs.usgs.gov/of/1992/ofr92-144/ (accessed on 15 April 2019).
- Velpuri, N.M.; Senay, G.B.; Singh, R.K.; Bohms, S.; Verdin, J.P. A comprehensive evaluation of two MODIS evapotranspiration products over the conterminous United States: Using point and gridded FLUXNET and water balance ET. Remote Sens. Environ. 2013, 139, 35–49. [Google Scholar] [CrossRef]
- Kelly, R.E.; Chang, A.T.; Tsang, L.; Foster, J.L. A prototype AMSR-E global snow area and snow depth algorithm. IEEE Trans. Geosci. Remote Sens. 2003, 41, 230–242. [Google Scholar] [CrossRef]
- Xia, Y.; Sheffield, J.; Ek, M.B.; Dong, J.; Chaney, N.; Wei, H.; Meng, J.; Wood, E.F. Evaluation of multi-model simulated soil moisture in NLDAS-2. J. Hydrol. 2014, 512, 107–125. [Google Scholar] [CrossRef]

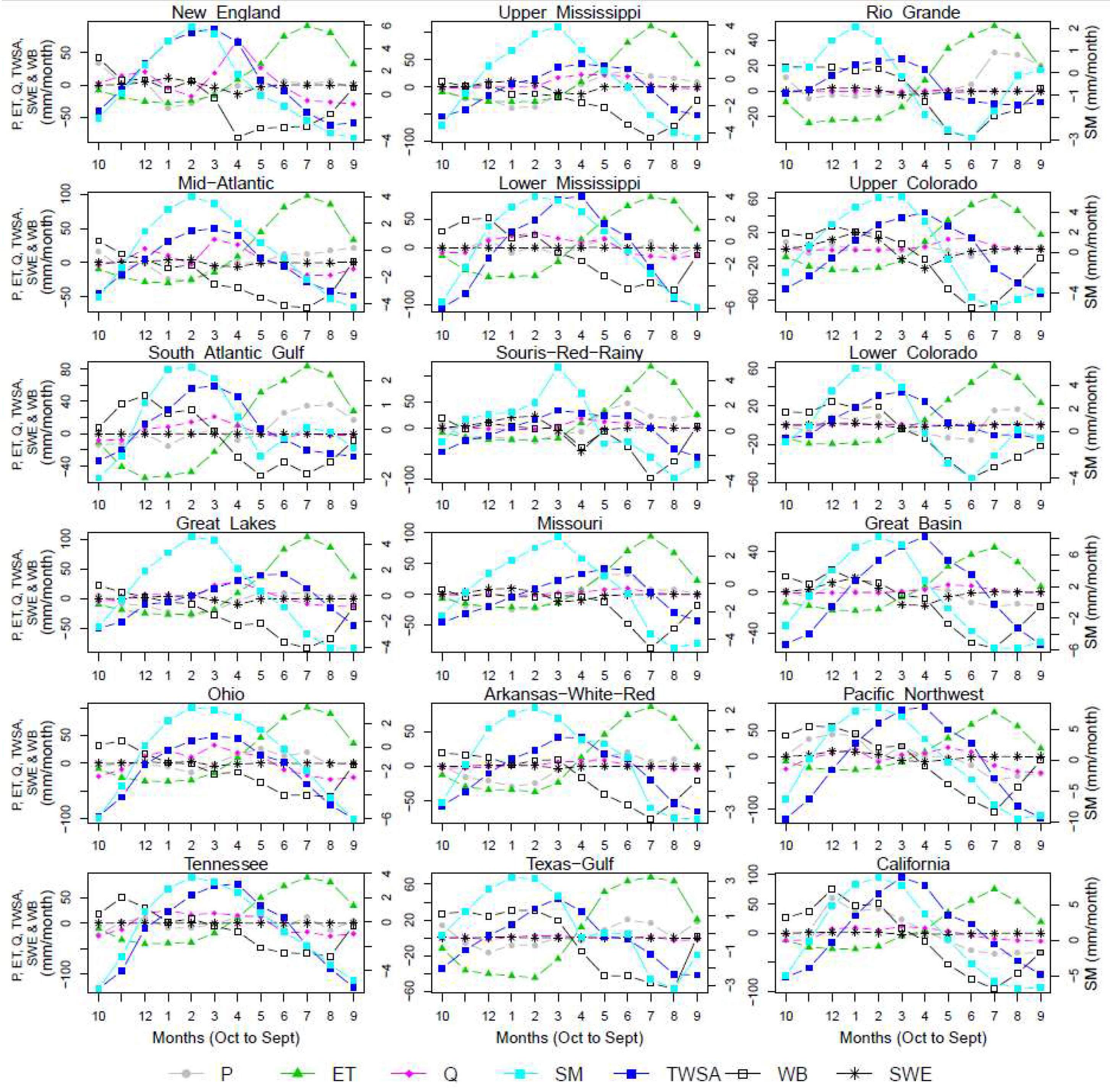
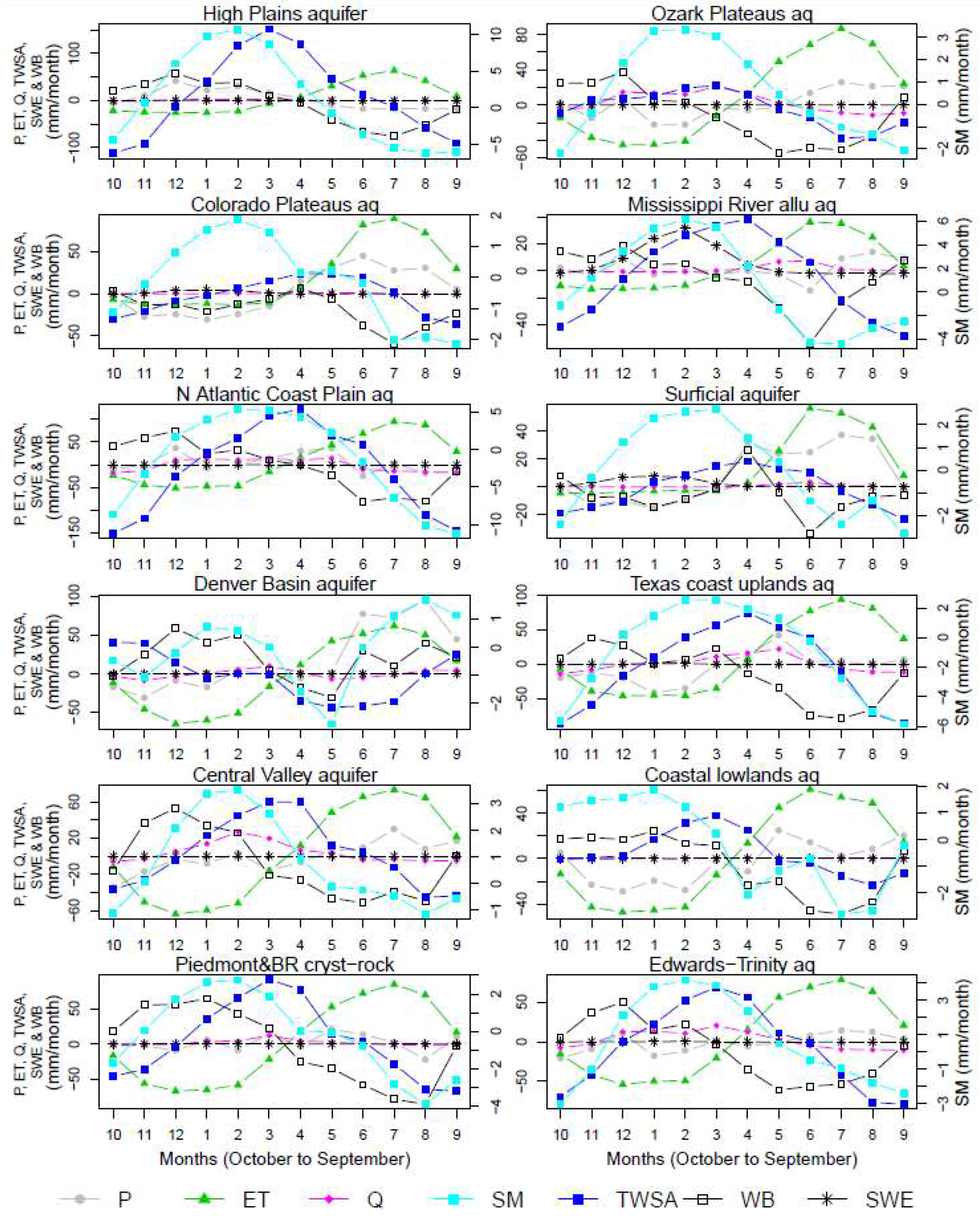
| HUC 2 Surface Basins | Annual ΔS/P (%) | Aquifer | Annual ΔS/P (%) | ||||
|---|---|---|---|---|---|---|---|
| Max | Min | DM | Max | Min | DM | ||
| New England | 0.7 | −0.7 | 0.05 | High Plains | 0.8 | −2.4 | −0.10 |
| Mid−Atlantic | 0.7 | −0.9 | −0.01 | Colorado Plateaus | 1.1 | −0.9 | 0.02 |
| South Atlantic Gulf | 0.9 | −0.9 | 0.01 | N Atlantic Coastal Plain | 0.7 | −1.0 | 0.00 |
| Great Lakes | 1.1 | −1.1 | 0.05 | Denver Basin | 0.6 | −0.6 | −0.02 |
| Ohio | 1.2 | −1.2 | 0.06 | Central Valley | 5.4 | −9.9 | −1.28 |
| Tennessee | 1.7 | −1.8 | 0.03 | Piedmont and Blue Ridge Cryst. Rock | 0.9 | −1.4 | 0.01 |
| Upper Mississippi | 1.1 | −1.7 | 0.04 | Ozark Plateaus | 1.4 | −0.8 | 0.09 |
| Lower Mississippi | 1.1 | −1.0 | 0.03 | Mississippi River Valley | 1.6 | −1.2 | 0.06 |
| Souris−Red−Rainy | 1.5 | −3.9 | −0.28 | Surficial | 0.8 | −1.0 | 0.00 |
| Missouri | 0.9 | −2.5 | 0.02 | Texas Coastal Uplands | 1.7 | −4.4 | −0.20 |
| Arkansas−White−Red | 0.7 | −1.5 | −0.06 | Coastal Lowlands | 0.7 | −1.2 | −0.01 |
| Texas Gulf | 1.3 | −5.3 | −0.32 | Edwards Trinity | 1.2 | −8.7 | −0.57 |
| Rio Grande | 0.8 | −3.7 | −0.26 | ||||
| Upper Colorado | 1.3 | −1.1 | 0.04 | ||||
| Lower Colorado | 1.2 | −1.6 | −0.20 | ||||
| Great Basin | 1.9 | −1.8 | −0.17 | ||||
| Pacific Northwest | 1.1 | −0.9 | 0.07 | ||||
| California | 2.2 | −3.2 | −0.35 | ||||
| HUC2 Surface Basins | Average STP ± SD (Months) | Aquifers | Average STP ± SD (Months) |
|---|---|---|---|
| New England | 12 ± 1 | High Plains | 10 ± 3 |
| Mid-Atlantic | 12 ± 1 | Colorado Plateaus | 12 ± 1 |
| South Atlantic Gulf | 9 ± 4 | N Atlantic Coastal Plain | 12 ± 2 |
| Great Lakes | 10 ± 3 | Denver Basin | 10 ± 3 |
| Ohio | 12 ± 1 | Central Valley | 12 ± 1 |
| Tennessee | 11 ± 2 | Peidmont and BR cryst-rock | 9 ± 4 |
| Upper Mississippi | 10 ± 3 | Ozark Plateaus | 10 ± 3 |
| Lower Mississippi | 11 ± 2 | Mississippi River Valley | 12 ± 3 |
| Souris-Red-Rainy | 10 ± 3 | Surficial aquifer | 9 ± 3 |
| Missouri | 10 ± 3 | Texas Coastal Uplands | 7 ± 4 |
| Arkansas-White-Red | 10 ± 3 | Coastal lowlands | 12 ± 3 |
| Texas Gulf | 7 ± 4 | Edwards-Trinity | 6 ± 3 |
| Rio Grande | 6 ± 3 | ||
| Upper Colorado | 12 ± 1 | ||
| Lower Colorado | 9 ± 3 | ||
| Great Basin | 12 ± 1 | ||
| Pacific Northwest | 12 ± 1 | ||
| California | 12 ± 1 |
| ID | Basin | Partial Regression Coefficients (%) for the Variables in the Best Fit Model | Model adj. R2 | PEV | Individual r (TWSA vs. PEV) | ||||
|---|---|---|---|---|---|---|---|---|---|
| P | Q | ET | SWE | SM | |||||
| HUC 2 Basins | |||||||||
| 1 | New England | 2 | 2 | NA | 2 | 93 | 0.98 * | SM | 0.96 |
| 2 | Mid-Atlantic | NA | NA | 1 | 2 | 97 | 0.97 * | SM | 0.97 |
| 3 | South Atlantic Gulf | 31 | 34 | 1 | 0.5 | 20 | 0.95 * | Q | 0.93 |
| 4 | Great Lakes | 15 | NA | 17 | NA | 68 | 0.96 * | SM | 0.42 |
| 5 | Ohio | 1 | NA | NA | NA | 99 | 0.97 * | SM | 0.98 |
| 6 | Tennessee | NA | NA | 5 | NA | 95 | 0.92 * | SM | 0.94 |
| 7 | Upper Mississippi | NA | 48 | 7 | 4 | 41 | 0.98 * | Q | 0.88 |
| 8 | Lower Mississippi | NA | NA | 12 | NA | 88 | 0.93 * | SM | 0.74 |
| 9 | Souris-Red-Rainy | NA | 30 | 12 | 21 | 37 | 0.96 * | SM | 0.63 |
| 10 | Missouri | 1 | NA | 22 | 1 | 69 | 0.96 * | SM | 0.61 |
| 11 | Arkansas-White-Red | 10 | 30 | 19 | 3 | 38 | 0.95 * | SM | 0.84 |
| 12 | Texas-Gulf | 13 | 75 | NA | 12 | NA | 0.76 * | Q | 0.73 |
| 13 | Rio Grande | 26 | NA | NA | 22 | 52 | 0.67 * | SM | 0.57 |
| 14 | Upper Colorado | NA | 6 | 19 | NA | 75 | 0.96 | SM | 0.67 |
| 15 | Lower Colorado | 12 | 88 | NA | NA | NA | 0.82 * | Q | 0.85 |
| 16 | Great Basin | NA | 5 | 16 | 4 | 75 | 0.94 * | SM | 0.64 |
| 17 | Pacific Northwest | NA | NA | 16 | 6 | 78 | 0.56 * | SM | 0.77 |
| 18 | California | NA | 89 | NA | 11 | NA | 0.87 * | Q | 0.89 |
| Principal aquifers | |||||||||
| 1 | Central Valley | NA | 82 | NA | NA | 18 | 0.84 * | Q | 0.82 |
| 2 | High Plains | NA | 88 | NA | 12 | NA | 0.77 * | Q | 0.84 |
| 3 | Missi. River Valley | NA | NA | 17 | NA | 83 | 0.88 * | SM | 0.88 |
| 4 | Surficial | NA | NA | 100 | NA | NA | 0.37 * | ET | −0.59 |
| 5 | Coastal Lowlands | NA | 92 | 8 | NA | NA | 0.66 * | Q | 0.82 |
| 6 | Texas Coastal Uplands | NA | 32 | 14 | NA | 54 | 0.88 * | SM | 0.77 |
| 7 | N Atlantic Coast. Plain | 22 | 69 | 9 | NA | NA | 0.90 * | Q | 0.9 |
| 8 | Colorado Plateaus | NA | 36 | NA | 64 | NA | 0.66 * | SWE | 0.6 |
| 9 | Denver Basin | 4 | 12 | NA | 6 | 78 | 0.88 * | SM | 0.66 |
| 10 | Ozark Plateaus | NA | NA | 6 | 2 | 92 | 0.96 * | SM | 0.93 |
| 11 | Edwards-Trinity | 60 | 40 | NA | NA | NA | 0.54 * | P | −0.53 |
| 12 | Piedmont and BR | 1 | 73 | 22 | 4 | NA | 0.90 * | Q | 0.9 |
| No | Name | GRACE TWSA | Basin/Aquifer Area (%) under | |||
|---|---|---|---|---|---|---|
| Rate of Change (cm/yr) | P value | Negative Change | Positive Change | No Change | ||
| HUC2 Surface Basins | ||||||
| 1 | New England | 4.3 | 0.0009 | 2 | 98 | 0 |
| 2 | Mid-Atlantic | 3.8 | 0.0188 | 0 | 77 | 23 |
| 3 | South Atlantic Gulf | 5.9 | 0.2232 | 0 | 25 | 75 |
| 4 | Great Lakes | 8.8 | 0.0348 | 5 | 63 | 32 |
| 5 | Ohio | 4.2 | 0.0431 | 0 | 56 | 44 |
| 6 | Tennessee | 3.1 | 0.4078 | 0 | 3 | 97 |
| 7 | Upper Mississippi | 7 | 0.0298 | 3 | 74 | 23 |
| 8 | Lower Mississippi | 1.7 | 0.6456 | 1 | 5 | 94 |
| 9 | Souris-Red-Rainy | −2.1 | 0.3875 | 31 | 6 | 63 |
| 10 | Missouri | 9.9 | 0.003 | 0 | 82 | 18 |
| 11 | Arkansas-White-Red | −4.6 | 0.2361 | 32 | 1 | 67 |
| 12 | Texas-Gulf | −6 | 0.2196 | 14 | 0 | 86 |
| 13 | Rio Grande | −5.1 | 0.0104 | 67 | 0 | 33 |
| 14 | Upper Colorado | 1.8 | 0.2267 | 3 | 31 | 66 |
| 15 | Lower Colorado | −4.9 | 0.003 | 79 | 0 | 21 |
| 16 | Great Basin | −2.8 | 0.1774 | 18 | 3 | 79 |
| 17 | Pacific Northwest | 7.9 | 0.0006 | 1 | 86 | 12 |
| 18 | California | −9.1 | 0.0279 | 60 | 7 | 33 |
| Principal Aquifers | ||||||
| 1 | High Plains | −4.1 | 0.2304 | 33 | 40 | 26 |
| 2 | Colorado Plateaus | 1.5 | 0.2475 | 20 | 19 | 61 |
| 3 | N Atlantic Coastal Plain | 3.9 | 0.1332 | 0 | 63 | 38 |
| 4 | Denver Basin | 10 | 0.0023 | 17 | 17 | 67 |
| 5 | Central Valley | −8.8 | 0.0332 | 80 | 0 | 20 |
| 6 | Piedmont and Blue Ridge crystalline-rock | 5.3 | 0.2451 | 0 | 5 | 95 |
| 7 | Ozark Plateaus | 10 | 0.0023 | 0 | 33 | 68 |
| 8 | Mississippi River Valley alluvial | 1.4 | 0.6005 | 0 | 11 | 89 |
| 9 | Surficial | 5.3 | 0.2451 | 0 | 52 | 48 |
| 10 | Texas Coastal Uplands | −5.6 | 0.2406 | 0 | 0 | 100 |
| 11 | Coastal lowlands | 1.4 | 0.6005 | 0 | 0 | 100 |
| 12 | Edwards-Trinity | −4.9 | 0.0118 | 7 | 0 | 93 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Velpuri, N.M.; Senay, G.B.; Driscoll, J.M.; Saxe, S.; Hay, L.; Farmer, W.; Kiang, J. Gravity Recovery and Climate Experiment (GRACE) Storage Change Characteristics (2003–2016) over Major Surface Basins and Principal Aquifers in the Conterminous United States. Remote Sens. 2019, 11, 936. https://doi.org/10.3390/rs11080936
Velpuri NM, Senay GB, Driscoll JM, Saxe S, Hay L, Farmer W, Kiang J. Gravity Recovery and Climate Experiment (GRACE) Storage Change Characteristics (2003–2016) over Major Surface Basins and Principal Aquifers in the Conterminous United States. Remote Sensing. 2019; 11(8):936. https://doi.org/10.3390/rs11080936
Chicago/Turabian StyleVelpuri, Naga Manohar, Gabriel B. Senay, Jessica M. Driscoll, Samuel Saxe, Lauren Hay, William Farmer, and Julie Kiang. 2019. "Gravity Recovery and Climate Experiment (GRACE) Storage Change Characteristics (2003–2016) over Major Surface Basins and Principal Aquifers in the Conterminous United States" Remote Sensing 11, no. 8: 936. https://doi.org/10.3390/rs11080936
APA StyleVelpuri, N. M., Senay, G. B., Driscoll, J. M., Saxe, S., Hay, L., Farmer, W., & Kiang, J. (2019). Gravity Recovery and Climate Experiment (GRACE) Storage Change Characteristics (2003–2016) over Major Surface Basins and Principal Aquifers in the Conterminous United States. Remote Sensing, 11(8), 936. https://doi.org/10.3390/rs11080936






